Complete determination of the crystallographic orientation of ReX2 (X = S, Se) by polarized Raman spectroscopy†
Yun
Choi
a,
Keunui
Kim
a,
Soo Yeon
Lim
a,
Jungcheol
Kim
a,
Je Myoung
Park
a,
Jung Hwa
Kim
b,
Zonghoon
Lee
bc and
Hyeonsik
Cheong
 *a
*a
aDepartment of Physics, Sogang University, Seoul 04107, Korea. E-mail: hcheong@sogang.ac.kr
bSchool of Materials Science and Engineering, Ulsan National Institute of Science and Technology, Ulsan 44919, Korea
cCenter for Multidimensional Carbon Materials, Institute for Basic Science (IBS), Ulsan 44919, Korea
First published on 23rd September 2019
Abstract
Polarized Raman spectroscopy on few-layer ReS2 and ReSe2 was carried out to determine the crystallographic orientations. Since monolayer ReX2 (X = S or Se) has a distorted trigonal structure with only an inversion center, there is in-plane anisotropy and the two faces of a monolayer crystal are not equivalent. Since many physical properties vary sensitively depending on the crystallographic orientation, it is important to develop a reliable method to determine the crystal axes of ReX2. By comparing the relative polarization dependences of some representative Raman modes measured with three different excitation laser energies with high-resolution scanning transmission electron microscopy, we established a reliable procedure to determine all three principal directions of few-layer ReX2, including a way to distinguish the two types of faces: a 2.41 eV laser for ReS2 or a 1.96 eV laser for ReSe2 should be chosen as the excitation source of polarized Raman measurements; then the relative directions of the maximum intensity polarization of the Raman modes at 151 and 212 cm−1 (124 and 161 cm−1) of ReS2 (ReSe2) can be used to determine the face types and the Re-chain direction unambiguously.
New conceptsThe crystallographic anisotropy of rhenium disulfide and diselenide (ReS2 and ReSe2) gives additional degrees of freedom in manipulating device properties. In addition to having in-plane anisotropy, the two sides of these crystals are not equivalent because of the low symmetry of Ci. Since the electrical and optical properties depend sensitively on the anisotropic orientation of the crystals, it is very important to develop a reliable method to determine the crystallographic orientation, including a method to determine the up- and down-side of the crystals. In this work, we developed the first comprehensive and unambiguous method to determine the crystallographic orientation of few-layer ReS2 and ReSe2 by combining polarized Raman spectroscopy with high-resolution electron microscopy. The results are confirmed by flipping a sample over and repeating the measurements on both sides of the same sample. To our surprise, the choice of the excitation laser turns out to be crucial, especially for ReSe2. We also found that the maximum intensity polarization direction of the Raman mode is slightly offset from the principal axis in the case of a monolayer, whereas the two directions match for thicker samples. Such detailed information is crucial in precisely determining the crystal axes for other applications. |
Introduction
The 2-dimensional (2D) layered transition metal dichalcogenides (TMDs) ReX2 (X = S, Se), are attracting much interest for application in optoelectronic devices because ReS2 has a direct bandgap for all thicknesses from monolayer (1L) to bulk unlike other TMDs such as MoX2 and WX2 (X = S, Se) which have a direct bandgap only for the monolayer case.1–4 The optical bandgap energy of ReS2 varies in the visible range, from 1.47 eV for the bulk to 1.61 eV for 1L, depending on the number of layers,5–7 making it an attractive candidate for optoelectronic devices. On the other hand, ReSe2 has an indirect (nearly direct) band gap of 1.2 eV in a monolayer and 1.3 eV in bulk.8–11 Unlike group-VI TMDs, extra electrons of ReX2 (group-VII TMDs) make Re–Re bonds resulting in Peierls distortion.5,12–14 Due to this covalent bonding of the transition metal atoms (Re–Re), ReX2 has a distorted trigonal structure (1T′) in which the principal axes are not normal to each other, i.e., the triclinic structure with the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (No. 2).8,13,15–19 Because of the 1T′ structure, ReX2 has in-plane anisotropy like black phosphorus20 or WTe2,21,22 which leads to anisotropic optical and electronic properties23–30 that can be utilized for a polarization-sensitive photodetector31,32 or orientation-dependent thin film transistors.26 Furthermore, since 1L ReX2 has only one inversion center in the primitive cell. The two faces of 1L ReX2 are not equivalent. For optoelectronic devices, determining the orientation of the ReX2 layer (up or down) is as important as identification of the in-plane crystallographic orientation. Therefore, an easy method to determine both the in-plane crystallographic orientation and the vertical orientation (up or down) of ReX2 is needed to fabricate devices with orientation-dependent properties.
(No. 2).8,13,15–19 Because of the 1T′ structure, ReX2 has in-plane anisotropy like black phosphorus20 or WTe2,21,22 which leads to anisotropic optical and electronic properties23–30 that can be utilized for a polarization-sensitive photodetector31,32 or orientation-dependent thin film transistors.26 Furthermore, since 1L ReX2 has only one inversion center in the primitive cell. The two faces of 1L ReX2 are not equivalent. For optoelectronic devices, determining the orientation of the ReX2 layer (up or down) is as important as identification of the in-plane crystallographic orientation. Therefore, an easy method to determine both the in-plane crystallographic orientation and the vertical orientation (up or down) of ReX2 is needed to fabricate devices with orientation-dependent properties.
Raman spectroscopy is widely used in 2D materials research for characterization of several basic properties including the number of layers, strain, doping, etc. Polarized Raman spectroscopy, in particular, has proven to be a powerful tool to determine the crystal structures of 1D or 2D nanomaterials such as nanowires or black phosphorus crystals.19–22,33–38 Some polarized Raman spectroscopy studies have been carried out to determine the orientation of ReX2.37,38 The in-plane crystal axes of bulk and few-layer ReX2 could be determined by comparing the polarization directions of some Raman modes with the transmission electron microscopy (TEM) measurements.19,37 However, as we shall show in this work, the choice of the excitation laser energy is crucial because the polarization directions of the Raman modes depend on the excitation laser energy sensitively. In addition, the two vertical orientations were identified in bulk crystals of ReX2, but similar work on few-layer ReX2 has not been reported. Here, we report on a comprehensive set of polarized Raman measurements on few-layer ReX2 using several excitation energies in combination with high-resolution scanning transmission electron microscopy (HR-STEM) to determine the in-plane axis and the vertical orientation simultaneously. We show that the 633 nm (1.96 eV) excitation for ReSe2 and the 514.5 nm (2.41 eV) excitation for ReS2, respectively, are most suitable for reliable determination of the crystallographic orientations.
Results and discussion
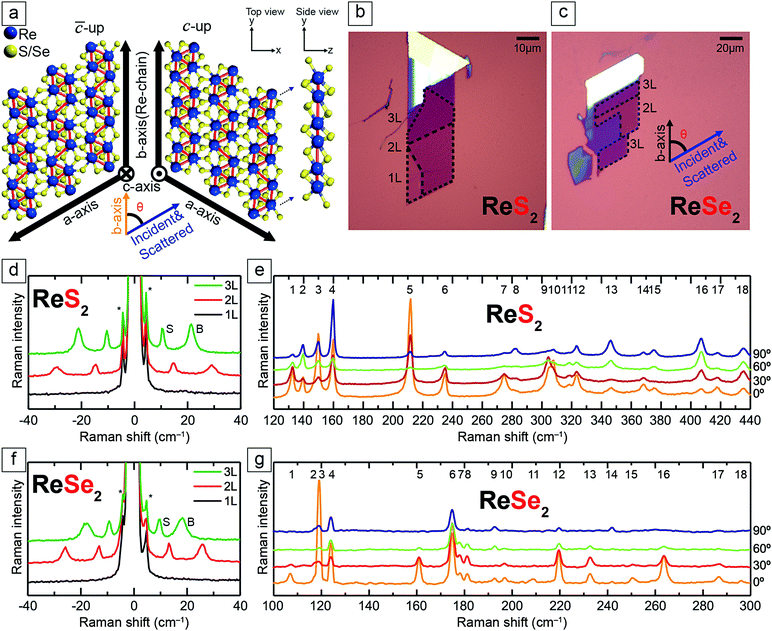
Fig. 1a shows the crystal structure of 1L ReX2, which comprises a rhenium layer sandwiched between two sulfur layers. Because 1L ReX2 belongs to the point group Ci which has inversion symmetry only, it has two types of top-view as shown in Fig. 1a.19,39 The Re chain direction is taken as the b-axis and the other in-plane principal axis is taken as the a-axis. Then the (bulk) c-axis has opposite directions in the two types. We identify the two orientations in terms of the relative direction of the c-axis of the bulk crystal. The orientation in which the bulk c-axis is coming out of the plane will be called the ‘c-up’ type and the other as the ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ type. We should note that because the c-axis is not orthogonal to the a- or b-axis due to the triclinic structure, the c-axis is slightly tilted from the face normal. Some of the cleaved edges of exfoliated ReX2 samples are found to be approximately 60° or 120° with respect to each other as shown in Fig. 1b and c, and are usually assumed to be a- or b-axis.19,38,40 However, as we will see below, assigning the crystallographic direction from the edge directions is often inaccurate.
-up’ type. We should note that because the c-axis is not orthogonal to the a- or b-axis due to the triclinic structure, the c-axis is slightly tilted from the face normal. Some of the cleaved edges of exfoliated ReX2 samples are found to be approximately 60° or 120° with respect to each other as shown in Fig. 1b and c, and are usually assumed to be a- or b-axis.19,38,40 However, as we will see below, assigning the crystallographic direction from the edge directions is often inaccurate.
The unit cell of 1L ReX2 has 12 atoms, and the irreducible representation can be written as Γ = 18(Ag + Au), among which Ag modes are Raman active.8,18,41 The 18 Raman-active Ag type modes of ReS2 are observed in the range of 130 to 440 cm−1 and those of ReSe2 in the range of 100 to 300 cm−1, as shown in Fig. 1e and g, respectively18,25,39 (see the ESI,† Fig. S1 for Raman spectra measured with different excitation energies). These modes are labelled in the order of the frequency as mode 1 through mode 18 as indicated and the peak positions are tabulated in Table S1 (ESI†). Raman spectra measured in several polarization directions are shown for comparison; the relative angle between the b-axis (Re-chain direction) and the polarization directions of the excitation and scattered photons (parallel polarization configuration) is varied. Some of the modes show prominent polarization dependences (see the ESI,† Fig. S2 for the polarization dependence of all 18 modes of 1L ReX2). In addition, the inter-layer shear and breathing modes in the ultralow-frequency range below 40 cm−1 measured in the parallel polarization configuration are observed for 2L or thicker samples as shown in Fig. 1d and f. These modes are the most reliable indicators of the number of layers.42,43 Although there have been reports in which the polarization dependences of these modes were examined for the determination of the crystal structures. However, we concentrate on the higher-frequency intralayer vibration modes that are common to all thicknesses. We also observed the Brillouin-scattering peak from the Si substrate (∼5 cm−1) which is marked by ‘*’ in Fig. 1d and f.44–46 Among the 18 first-order intra-layer Raman modes, the lower frequency modes tend to be stronger and have more straightforward polarization dependences. We focused on the 5 lowest frequency intra-layer modes for the polarization analysis (see the ESI,† Fig. S3 and S4 for the polarization dependence of 5 lowest frequency modes of few-layer ReX2). For ReS2, modes 1, 3, and 5 are relatively strong and have simple polarization dependences. Also, because these modes do not overlap with other modes, it is easier to analyze the polarization dependence from the spectra. We compared modes 3 and 5 for the analysis. For ReSe2, modes 1, 4, and 5 are spectrally isolated and have relatively simple polarization dependences. Since mode 1 is rather weak, we chose modes 4 and 5 for the analysis. Although all the modes are Ag type, the polarization dependences are dramatically different.19,42 The polarization dependence can be analysed in terms of the Raman tensors of the Ag modes of the Ci point group:37,42
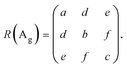 | (1) |
In anisotropic 2D materials, the polarization-dependent absorption and birefringence can be taken into account by expressing the Raman tensor elements in complex forms.20,21,42,47–53 The Raman tensors can be written as
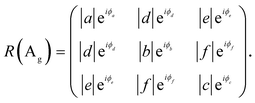 | (2) |
The Raman intensity for excitation and detection in the z-direction is,
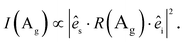 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0), and the Raman intensity is
θ, 0), and the Raman intensity is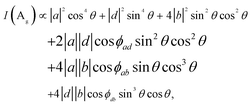 | (4) |
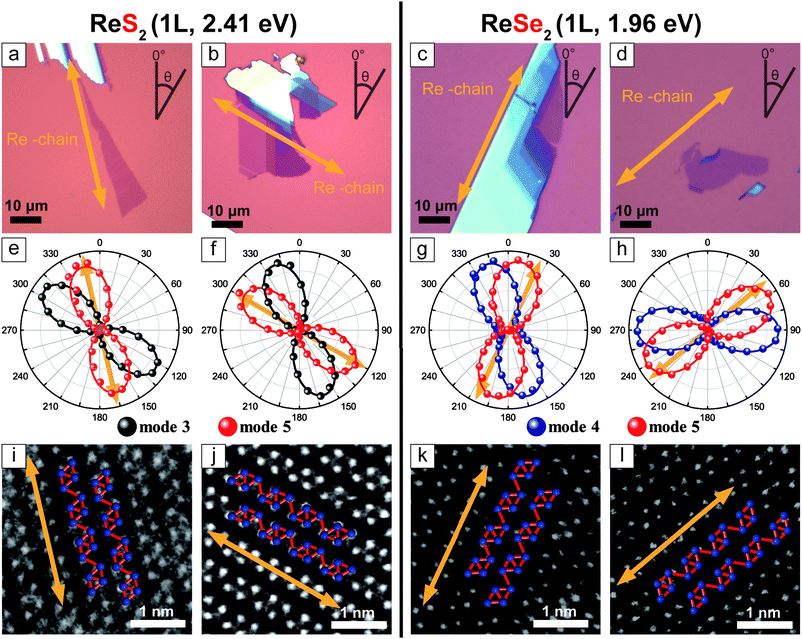
Fig. 2a–d are optical microscope images of some representative 1L ReX2 samples. The corresponding polar plots (Fig. 2e–h) show the polarization dependences of the intensities of the two chosen modes (3 and 5 for ReS2 and 4 and 5 for ReSe2) measured in the parallel polarization configuration. There are two types of the relative orientations of the two modes: in Fig. 2e (Fig. 2g), the maximum direction of mode 3 (Fig. 4) is slightly rotated in the counter-clockwise direction with respect to that of mode 5, whereas in Fig. 2f (Fig. 2h) the relative rotation is clockwise. In order to correlate these types with the crystallographic orientations, we determined the Re-chain direction (b-axis) from HR-STEM measurements shown in Fig. 2i–l. The HR-STEM images show that the two different types of the relative orientations of the two Raman modes correspond to the two different in-plane structures, i.e., vertical orientations: by comparing with the crystal structure of Fig. 1a, 2i and k corresponds to the ‘c-up’ type and Fig. 2j and l the ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ type. The Re-chain directions thus determined are also shown in the optical images and the polar plots of the Raman intensities by yellow arrows. It is obvious that the Re-chain direction does not necessarily correspond with the edge direction of a sample. We also note that the maximum intensity directions of the Raman modes do not correspond to the crystallographic orientation exactly. In order to confirm that the two-types of samples correspond to the two vertical orientations, we measured the two sides of an identical sample by placing the sample on a transparent quartz substrate.
-up’ type. The Re-chain directions thus determined are also shown in the optical images and the polar plots of the Raman intensities by yellow arrows. It is obvious that the Re-chain direction does not necessarily correspond with the edge direction of a sample. We also note that the maximum intensity directions of the Raman modes do not correspond to the crystallographic orientation exactly. In order to confirm that the two-types of samples correspond to the two vertical orientations, we measured the two sides of an identical sample by placing the sample on a transparent quartz substrate.
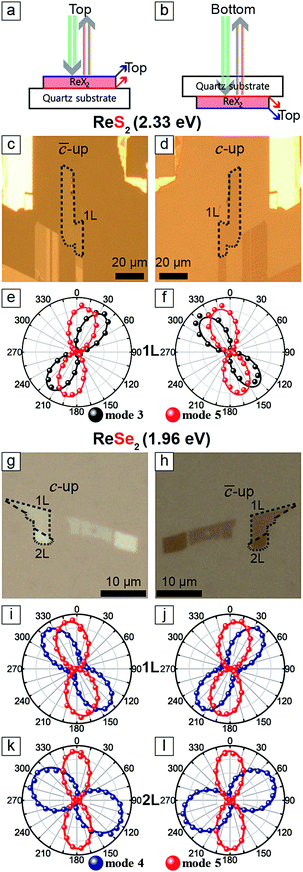
Fig. 3c and d are optical images of an 1L ReS2 sample taken by flipping the sample over as shown in Fig. 3a and b. The relative polarization dependences of modes 3 and 5, shown in Fig. 3e and f, correspond to those of the ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ and the ‘c-up’ cases in Fig. 2. Similar measurements on 1L and 2L ReSe2 also yield consistent results as shown in Fig. 3. These experiments unambiguously confirm that the relative rotation of the maximum intensity polarization directions of the two modes is a reliable indicator of the vertical orientation.
-up’ and the ‘c-up’ cases in Fig. 2. Similar measurements on 1L and 2L ReSe2 also yield consistent results as shown in Fig. 3. These experiments unambiguously confirm that the relative rotation of the maximum intensity polarization directions of the two modes is a reliable indicator of the vertical orientation.
In order to correlate the polarization dependence of Raman peaks with the in-plane crystallographic axes, we carried out polarized Raman measurements with three excitation energies each for ReS2 and ReSe2. Fig. 4a shows the polarization dependences of modes 3 and 5 of 1L to 3L ReS2 with the fitting curves to eqn (4), for three excitation energies of 1.96, 2.33, and 2.41 eV. The Re-chain direction (b-axis) determined from HR-STEM measurements is set to 0°. In order to ensure that the crystal axes in samples with different thicknesses are properly aligned, we measured a sample with all three thicknesses in a single contiguous flake. The polarization dependences for the ‘c-up’ and ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ cases are mirror images of each other with respect to the b-axis (0°). Both modes show ‘figure 8’ type polarization dependences for all excitation energies and thicknesses. The maximum intensity direction of mode 5 is approximately along the b-axis. For 1L, it is rotated with respect to the b-axis direction by 5°, −10°, and −3° for the ‘c-up’ case for excitation energies of 1.96, 2.33, and 2.41 eV, respectively. For 2L and 3L, the offset angle is zero within the experimental uncertainties. Although all three excitation energies are adequate for determination of the crystal axes, we propose that 2.41 eV is most suitable because the offset between the b-axis and the maximum intensity direction of mode 5 is smallest for the 1L case. It is much more complicated for ReSe2. Fig. 4b shows that the polarization dependences of modes 4 and 5 change dramatically with the excitation energy and thickness. The two modes maintain ‘figure 8’ polarization dependences only for the 1.96 eV excitation energy. Here, the offset between the b-axis and the maximum intensity direction of mode 5 is −10° for the ‘c-up’ type of 1L and is zero for thicker layers. Fig. 4 shows the polarization dependences of Raman modes (ReS2: 3 and 5, ReSe2: 4 and 5) tabulated with excitation source energies and thickness of ReX2. The correlation between the maximum intensity polarization directions of the modes and the crystal axes can be qualitatively understood in terms of the normal mode vibrations. For both ReS2 and ReSe2, mode 5 involves vibrations of the Re atoms along the b-axis.5,25 Therefore, it is reasonable that the maximum polarization direction (almost) matches that of the b-axis. On the other hand, mode 3 of ReS2 involves vibrations of Re and S atoms along the a-axis5 and the maximum intensity direction is approximately in that direction. Since the relative angles between the a- and b-axes are opposite for the two vertical orientations, it can be used to identify the vertical orientations. For ReSe2, mode 4 involves vibrations of Re and Se atoms in different directions, with several atoms in the unit cell vibrating in directions somewhat tilted from the a-axis,25 which we presume is why mode 4 is approximately aligned along the a-axis but the polarization dependence varies significantly with the excitation energy.
-up’ cases are mirror images of each other with respect to the b-axis (0°). Both modes show ‘figure 8’ type polarization dependences for all excitation energies and thicknesses. The maximum intensity direction of mode 5 is approximately along the b-axis. For 1L, it is rotated with respect to the b-axis direction by 5°, −10°, and −3° for the ‘c-up’ case for excitation energies of 1.96, 2.33, and 2.41 eV, respectively. For 2L and 3L, the offset angle is zero within the experimental uncertainties. Although all three excitation energies are adequate for determination of the crystal axes, we propose that 2.41 eV is most suitable because the offset between the b-axis and the maximum intensity direction of mode 5 is smallest for the 1L case. It is much more complicated for ReSe2. Fig. 4b shows that the polarization dependences of modes 4 and 5 change dramatically with the excitation energy and thickness. The two modes maintain ‘figure 8’ polarization dependences only for the 1.96 eV excitation energy. Here, the offset between the b-axis and the maximum intensity direction of mode 5 is −10° for the ‘c-up’ type of 1L and is zero for thicker layers. Fig. 4 shows the polarization dependences of Raman modes (ReS2: 3 and 5, ReSe2: 4 and 5) tabulated with excitation source energies and thickness of ReX2. The correlation between the maximum intensity polarization directions of the modes and the crystal axes can be qualitatively understood in terms of the normal mode vibrations. For both ReS2 and ReSe2, mode 5 involves vibrations of the Re atoms along the b-axis.5,25 Therefore, it is reasonable that the maximum polarization direction (almost) matches that of the b-axis. On the other hand, mode 3 of ReS2 involves vibrations of Re and S atoms along the a-axis5 and the maximum intensity direction is approximately in that direction. Since the relative angles between the a- and b-axes are opposite for the two vertical orientations, it can be used to identify the vertical orientations. For ReSe2, mode 4 involves vibrations of Re and Se atoms in different directions, with several atoms in the unit cell vibrating in directions somewhat tilted from the a-axis,25 which we presume is why mode 4 is approximately aligned along the a-axis but the polarization dependence varies significantly with the excitation energy.
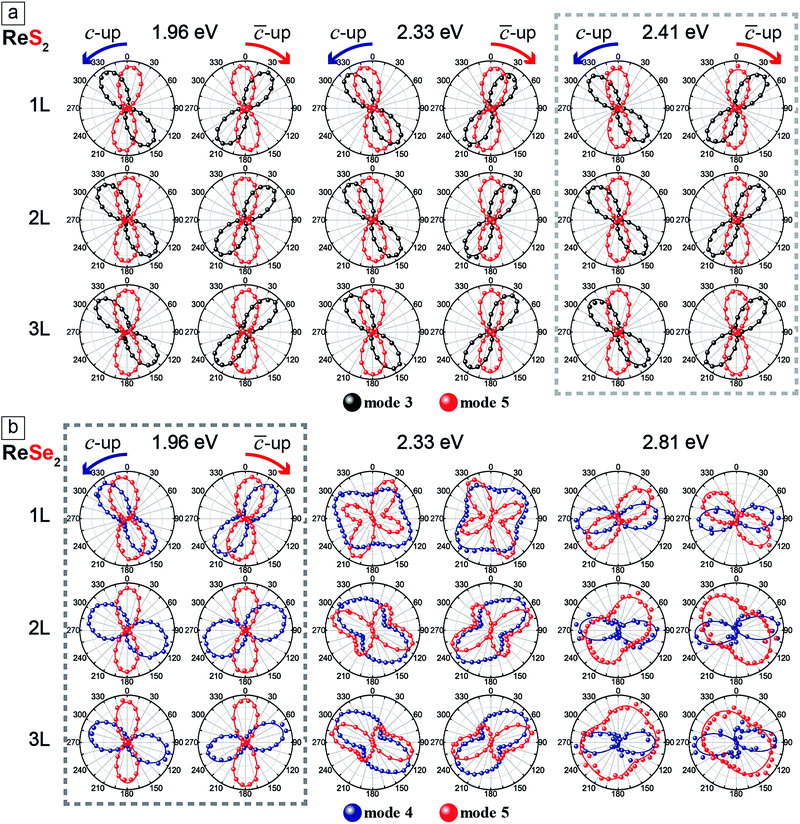 | ||
| Fig. 4 Polarization dependences of Raman modes (ReS2: 3 and 5, ReSe2: 4 and 5) tabulated with excitation source energies and thickness of ReX2. The solid curves are fits to eqn (4). | ||
The slight offset between the b-axis and the maximum intensity direction of mode 5 in the 1L samples of both ReS2 and ReSe2 is intriguing. We have measured multiple samples to confirm that this is reproducible. Some possible causes of the offset are residual strain in the sample and the influence of the SiO2/Si substrate. In order to check this possibility, we compared the polarization dependence of mode 5 of a free-standing ReS2 sample with that from a sample on a substrate and found no difference (see the ESI,† Fig. S5). We also examined the effect of a uniaxial strain by exfoliating a ReS2 sample on a flexible substrate and applying a tensile strain, but the polarization dependences of modes 3 and 5 were not affected (see the ESI,† Fig. S6). We also fabricated a ReS2 sample with contiguous 1 to 3L regions on hBN and found that the relative rotation of the mode 5 in 1L ReS2 with respect to those in 2L and 3L regions was identical to the case of the samples on SiO2/Si (see the ESI,† Fig. S7). Therefore, we conclude that the slight offset of the maximum polarization direction of mode 5 with respect to the b-axis direction in the 1L case is an intrinsic property. In the literature, there are conflicting reports on the alignment of the maximum intensity direction of mode 5 in ReX2 with the b-axis. Our results show beyond experimental uncertainty that the two are aligned in 2L and 3L but there is a clear offset in the 1L case. We suspect that the details of the band structure would be responsible for the peculiar polarization for the 1L case. For example, Gehlmann et al. examined the band structure of ReS2 and found that the top of the valence band maximum at the Γ point is very flat unlike other thicknesses.7
Experimental
Few-layer ReX2 samples were prepared by mechanical exfoliation from ReX2 flakes (HQ graphene) on Si substrates with a 280 nm SiO2 layer and on 0.5 cm quartz substrates. It has been reported that ReS2 can exist in two different polytypes: isotropic-like (IS) and anisotropic-like (AI).54 Since IS types are much more common, we selected only IS-type samples for our study. For ReSe2, we found only one type of sample judged from their Raman spectra. In the case of ReSe2, the samples were kept in a vacuum to avoid degradation because the thin ReSe2 sample seems to degrade after being measured with the 2.81 eV laser although the sample remained stable under ambient conditions without laser exposure. We identified the number of layers by comparing the optical contrast and Raman measurements.The Raman measurements were performed by using a home-built confocal micro-Raman system using the excitation sources of the 2.81 eV (441.6 nm) line of a He–Cd laser, the 2.41 eV (514.5 nm) line of an Ar ion laser, the 2.33 eV (532 nm) line of a diode-pumped-solid-state laser, and the 1.96 eV (632.8 nm) line of a He–Ne laser. ReSe2 samples were kept in an optical vacuum chamber to avoid laser-induced damage to the sample, whereas ReS2 samples were measured under ambient conditions. A 50× objective lens (0.8 NA) and a 40× objective lens (0.6 NA) were used to focus the laser beam onto the sample and to collect the scattered light (backscattering geometry). The Raman signal was dispersed with a HORIBA iHR550 spectrometer (2400 grooves per mm) and detected with a liquid-nitrogen-cooled back-illuminated charge-coupled-device (CCD) detector. The laser power was kept below 0.1 mW. Three volume holographic notch filters (OptiGrate) were used to observe the low frequency region (<100 cm−1). An achromatic half-wave plate was used to rotate the polarization of the linearly polarized laser beam to the desired direction. All measurements were conducted in the parallel-polarization configuration, where the analyzer angle was set such that photons with the polarization parallel to the incident polarization pass through. Another achromatic half-wave plate was placed in front of the spectrometer to keep the polarization direction of the signal entering the spectrometer constant with respect to the groove direction of the grating.
The TEM measurements were performed after polarized Raman measurements using an aberration-corrected FEI Titan cube G2 60-300 with a monochromator, operated at 80 kV. Scanning TEM (STEM) analysis was applied for the analysis of definitive orientation of the diamond shaped rhenium chains. For TEM measurements, exfoliated ReX2 flakes on the SiO2/Si substrate were transferred onto a TEM grid using the wet direct transfer method without poly(methyl methacrylate) (PMMA).55 The orientation of the sample was carefully aligned before and after the transfer in order to match with the orientation of the sample in the polarized Raman measurements.
Conclusions
Based on our results, we suggest the following procedure for determining the vertical orientation and the in-plane Re-chain direction of ReX2. First, a 2.41 eV laser for ReS2 or a 1.96 eV laser for ReSe2 should be chosen as the excitation source of polarized Raman measurements. In the case of ReS2, other excitation energies can be used, but then a different offset value should be used in the case of 1L ReS2. For ReSe2, other laser energies should be avoided. From the polarization dependences of modes 3 and 5 (4 and 5) of ReS2 (ReSe2), the vertical orientation can be determined: if mode 3 (mode 4) is somewhat rotated counter-clockwise with respect to mode 5, the sample corresponds to the ‘c-up’ type ReS2 (ReSe2), and the ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ type if the rotation is clockwise. Then the b-axis corresponds to the maximum intensity direction of mode 5 for 2L or thicker samples. For 1L ReS2 (ReSe2), the b-axis is offset by 3° (10°) in the clockwise direction with respect to the maximum intensity direction of mode 5 for the ‘c-up’ case, and in the opposite direction for the ‘
-up’ type if the rotation is clockwise. Then the b-axis corresponds to the maximum intensity direction of mode 5 for 2L or thicker samples. For 1L ReS2 (ReSe2), the b-axis is offset by 3° (10°) in the clockwise direction with respect to the maximum intensity direction of mode 5 for the ‘c-up’ case, and in the opposite direction for the ‘![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) -up’ case.
-up’ case.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Research Foundation (NRF) grants funded by the Korean government (MSIT) (NRF-2019R1A2C3006189, 2018R1A2A2A05019598 and 2017R1A5A1014862: SRC program (vdWMRC)), by a grant (2013M3A6A5073173) from the Center for Advanced Soft Electronics under the Global Frontier Research Program of MSIT, and by IBS-R019-D1.References
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef.
- A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS.
- Z. G. Yu, Y. Cai and Y.-W. Zhang, Sci. Rep., 2015, 5, 13783 CrossRef.
- S. Tongay, H. Sahin, C. Ko, A. Luce, W. Fan, K. Liu, J. Zhou, Y.-S. Huang, C.-H. Ho, J. Yan, D. F. Ogletree, S. Aloni, J. Ji, S. Li, J. Li, F. M. Peeters and J. Wu, Nat. Commun., 2014, 5, 3252 CrossRef.
- O. B. Aslan, D. A. Chenet, A. M. van der Zande, J. C. Hone and T. F. Heinz, ACS Photonics, 2016, 3, 96–101 CrossRef CAS.
- M. Gehlmann, I. Aguilera, G. Bihlmayer, S. Nemšák, P. Nagler, P. Gospodarič, G. Zamborlini, M. Eschbach, V. Feyer, F. Kronast, E. Młyńczak, T. Korn, L. Plucinski, C. Schüller, S. Blügel and C. M. Schneider, Nano Lett., 2017, 17, 5187–5192 CrossRef CAS.
- D. Wolverson, S. Crampin, A. S. Kazemi, A. Ilie and S. J. Bending, ACS Nano, 2014, 8, 11154–11164 CrossRef CAS.
- J. V. Marzik, R. Kershaw, K. Dwight and A. Wold, J. Solid State Chem., 1984, 51, 170–175 CrossRef CAS.
- C. H. Ho, Y. S. Huang, J. L. Chen, T. E. Dann and K. K. Tiong, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 15766–15771 CrossRef CAS.
- C. H. Ho and C. E. Huang, J. Alloys Compd., 2004, 383, 74–79 CrossRef CAS.
- S. P. Kelty, A. F. Ruppert, R. R. Chianelli, J. Ren and M.-H. Whangbo, J. Am. Chem. Soc., 1994, 116, 7857–7863 CrossRef CAS.
- B. Jariwala, D. Voiry, A. Jindal, B. A. Chalke, R. Bapat, A. Thamizhavel, M. Chhowalla, M. Deshmukh and A. Bhattacharya, Chem. Mater., 2016, 28, 3352–3359 CrossRef CAS.
- M. Rahman, K. Davey and S.-Z. Qiao, Adv. Funct. Mater., 2017, 27, 1606129 CrossRef.
- N. W. Alcock, A. Kjekshus, A. Kjekshus, S. Gronowitz, R. A. Hoffman and A. Westerdahl, Acta Chem. Scand., 1965, 19, 79–94 CrossRef CAS.
- H. H. Murray, S. P. Kelty, R. R. Chianelli and C. S. Day, Inorg. Chem., 1994, 33, 4418–4420 CrossRef CAS.
- H.-J. Lamfers, A. Meetsma, G. A. Wiegers and J. L. de Boer, J. Alloys Compd., 1996, 241, 34–39 CrossRef CAS.
- Y. Feng, W. Zhou, Y. Wang, J. Zhou, E. Liu, Y. Fu, Z. Ni, X. Wu, H. Yuan, F. Miao, B. Wang, X. Wan and D. Xing, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054110 CrossRef.
- L. Hart, S. Dale, S. Hoye, J. L. Webb and D. Wolverson, Nano Lett., 2016, 16, 1381–1386 CrossRef CAS.
- J. Kim, J.-U. Lee, J. Lee, H. J. Park, Z. Lee, C. Lee and H. Cheong, Nanoscale, 2015, 7, 18708–18715 RSC.
- M. Kim, S. Han, J. H. Kim, J.-U. Lee, Z. Lee and H. Cheong, 2D Mater., 2016, 3, 034004 CrossRef.
- Y. Cao, N. Sheremetyeva, L. Liang, H. Yuan, T. Zhong, V. Meunier and M. Pan, 2D Mater., 2017, 4, 035024 CrossRef.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS.
- Y.-C. Lin, H.-P. Komsa, C.-H. Yeh, T. Björkman, Z.-Y. Liang, C.-H. Ho, Y.-S. Huang, P.-W. Chiu, A. V. Krasheninnikov and K. Suenaga, ACS Nano, 2015, 9, 11249–11257 CrossRef CAS.
- H. Zhao, J. Wu, H. Zhong, Q. Guo, X. Wang, F. Xia, L. Yang, P. Tan and H. Wang, Nano Res., 2015, 8, 3651–3661 CrossRef CAS.
- E. Liu, Y. Fu, Y. Wang, Y. Feng, H. Liu, X. Wan, W. Zhou, B. Wang, L. Shao, C.-H. Ho, Y.-S. Huang, Z. Cao, L. Wang, A. Li, J. Zeng, F. Song, X. Wang, Y. Shi, H. Yuan, H. Y. Hwang, Y. Cui, F. Miao and D. Xing, Nat. Commun., 2015, 6, 6991 CrossRef CAS.
- M. K. Jana, A. Singh, D. J. Late, C. R. Rajamathi, K. Biswas, C. Felser, U. V. Waghmare and C. N. R. Rao, J. Phys.: Condens. Matter, 2015, 27, 285401 CrossRef PubMed.
- J. L. Webb, L. S. Hart, D. Wolverson, C. Chen, J. Avila and M. C. Asensio, Phys. Rev. B, 2017, 96, 115205 CrossRef.
- H. Jang, C. R. Ryder, J. D. Wood, M. C. Hersam and D. G. Cahill, Adv. Mater., 2017, 29, 1700650 CrossRef PubMed.
- A. Arora, J. Noky, M. Drüppel, B. Jariwala, T. Deilmann, R. Schneider, R. Schmidt, O. Del Pozo-Zamudio, T. Stiehm, A. Bhattacharya, P. Krüger, S. Michaelis de Vasconcellos, M. Rohlfing and R. Bratschitsch, Nano Lett., 2017, 17, 3202–3207 CrossRef CAS.
- F. Liu, S. Zheng, X. He, A. Chaturvedi, J. He, W. L. Chow, T. R. Mion, X. Wang, J. Zhou, Q. Fu, H. J. Fan, B. K. Tay, L. Song, R.-H. He, C. Kloc, P. M. Ajayan and Z. Liu, Adv. Funct. Mater., 2016, 26, 1169–1177 CrossRef CAS.
- E. Liu, M. Long, J. Zeng, W. Luo, Y. Wang, Y. Pan, W. Zhou, B. Wang, W. Hu, Z. Ni, Y. You, X. Zhang, S. Qin, Y. Shi, K. Watanabe, T. Taniguchi, H. Yuan, H. Y. Hwang, Y. Cui, F. Miao and D. Xing, Adv. Funct. Mater., 2016, 26, 1938–1944 CrossRef CAS.
- I. Zardo, S. Conesa-Boj, F. Peiro, J. R. Morante, J. Arbiol, E. Uccelli, G. Abstreiter and A. Fontcuberta i Morral, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245324 CrossRef.
- C. Fasolato, M. De Luca, D. Djomani, L. Vincent, C. Renard, G. Di Iorio, V. Paillard, M. Amato, R. Rurali and I. Zardo, Nano Lett., 2018, 18, 7075–7084 CrossRef CAS.
- T. M. G. Mohiuddin, A. Lombardo, R. R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. M. Basko, C. Galiotis, N. Marzari, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205433 CrossRef.
- D. Yoon, Y.-W. Son and H. Cheong, Phys. Rev. Lett., 2011, 106, 155502 CrossRef.
- D. A. Chenet, O. B. Aslan, P. Y. Huang, C. Fan, A. M. van der Zande, T. F. Heinz and J. C. Hone, Nano Lett., 2015, 15, 5667–5672 CrossRef CAS.
- S. Zhang, N. Mao, N. Zhang, J. Wu, L. Tong and J. Zhang, ACS Nano, 2017, 11, 10366–10372 CrossRef CAS.
- A. McCreary, J. R. Simpson, Y. Wang, D. Rhodes, K. Fujisawa, L. Balicas, M. Dubey, V. H. Crespi, M. Terrones and A. R. Hight Walker, Nano Lett., 2017, 17, 5897–5907 CrossRef CAS.
- H. Wang, E. Liu, Y. Wang, B. Wan, C.-H. Ho, F. Miao and X. G. Wan, Phys. Rev. B, 2017, 96, 165418 CrossRef.
- N. R. Pradhan, A. McCreary, D. Rhodes, Z. Lu, S. Feng, E. Manousakis, D. Smirnov, R. Namburu, M. Dubey, A. R. Hight Walker, H. Terrones, M. Terrones, V. Dobrosavljevic and L. Balicas, Nano Lett., 2015, 15, 8377–8384 CrossRef CAS.
- E. Lorchat, G. Froehlicher and S. Berciaud, ACS Nano, 2016, 10, 2752–2760 CrossRef CAS.
- R. He, J.-A. Yan, Z. Yin, Z. Ye, G. Ye, J. Cheng, J. Li and C. H. Lui, Nano Lett., 2016, 16, 1404–1409 CrossRef CAS.
- X. Zhang, W. P. Han, J. B. Wu, S. Milana, Y. Lu, Q. Q. Li, A. C. Ferrari and P. H. Tan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115413 CrossRef.
- J. R. Sandercock, Phys. Rev. Lett., 1972, 28, 237–240 CrossRef CAS.
- M. H. Kuok, S. C. Ng, Z. L. Rang and D. J. Lockwood, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 12902–12908 CrossRef CAS.
- T. Strach, J. Brunen, B. Lederle, J. Zegenhagen and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1292–1297 CrossRef CAS.
- H. B. Ribeiro, M. A. Pimenta, C. J. S. De Matos, R. L. Moreira, A. S. Rodin, J. D. Zapata, E. A. T. De Souza and A. H. Castro Neto, ACS Nano, 2015, 9, 4270–4276 CrossRef CAS.
- N. Mao, J. Wu, B. Han, J. Lin, L. Tong and J. Zhang, Small, 2016, 12, 2627–2633 CrossRef CAS.
- X. Ling, S. Huang, E. H. Hasdeo, L. Liang, W. M. Parkin, Y. Tatsumi, A. R. T. Nugraha, A. A. Puretzky, P. M. Das, B. G. Sumpter, D. B. Geohegan, J. Kong, R. Saito, M. Drndic, V. Meunier and M. S. Dresselhaus, Nano Lett., 2016, 16, 2260–2267 CrossRef CAS.
- C. Kranert, C. Sturm, R. Schmidt-Grund and M. Grundmann, Phys. Rev. Lett., 2016, 116, 127401 CrossRef.
- M. Li, Y. Wu, T. Li, Y. Chen, H. Ding, Y. Lin, N. Pan and X. Wang, RSC Adv., 2017, 7, 48759–48765 RSC.
- W. Zheng, J. Yan, F. Li and F. Huang, Photonics Res., 2018, 6, 709 CrossRef CAS.
- X.-F. Qiao, J.-B. Wu, L. Zhou, J. Qiao, W. Shi, T. Chen, X. Zhang, J. Zhang, W. Ji and P.-H. Tan, Nanoscale, 2016, 8, 8324–8332 RSC.
- W.-H. Lin, T.-H. Chen, J.-K. Chang, J.-I. Taur, Y.-Y. Lo, W.-L. Lee, C.-S. Chang, W.-B. Su and C.-I. Wu, ACS Nano, 2014, 8, 1784–1791 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00487d |
| This journal is © The Royal Society of Chemistry 2020 |