Beyond the paradigm of nanomechanical measurements on cells using AFM: an automated methodology to rapidly analyse thousands of cells†
S.
Proa-Coronado
 abd,
C.
Séverac
b,
A.
Martinez-Rivas‡
*ac and
E.
Dague‡
abd,
C.
Séverac
b,
A.
Martinez-Rivas‡
*ac and
E.
Dague‡
 *d
*d
aENCB-Instituto Politécnico Nacional (IPN), Av. Wilfrido Massieu, Unidad Adolfo López Mateos, 07738, Mexico City, Mexico. E-mail: nanobiomex@hotmail.com
bITAV-CNRS, Université de Toulouse, CNRS, Toulouse, France
cCIC-Instituto Politécnico Nacional (IPN), Av. Juan de Dios Bátiz S/N, Nueva Industrial Vallejo, 07738, Mexico City, Mexico
dLAAS-CNRS, Université de Toulouse, CNRS, Toulouse, France. E-mail: edague@laas.fr
First published on 15th August 2019
Abstract
Nanomechanical properties of cells could be considered as cellular biomarkers. The main method used to access the mechanical properties is based on nanoindentation measurements, performed with an operator manipulated Atomic Force Microscope (AFM) which is time-consuming and expensive. This is one of the reasons that prevent the transfer of AFM technology into clinical laboratories. In this paper we report a methodology which includes an algorithm (transferred to a script, executed on a commercial AFM) able to automatically move the tip onto a single cell and through several cells to record force curves combined with a smart strategy of cell immobilization. Cells are placed into microwells of a microstructured polydimethylsiloxane (PDMS) stamp. Inside a classical 100 × 100 μm2 AFM field, 100 cells can be immobilized. In an optimal configuration we were able to measure, within 4 h, a population of 900 Candida albicans cells both native and caspofungin treated, which represents an unprecedented performance. We discovered that the population is heterogeneous and can be divided, on the basis of nanomechanical properties, into 2 subgroups.
New conceptsThe current concept in Bio-AFM is to perform manually hundreds or thousands of force curves on a few cells. In contrast, in our work, we went beyond this concept and performed automatically nanomechanical measurements on hundreds of cells. The paper reports and demonstrates nanoindentations on organized living cells, automatically, which represents a major step forward in the field of nanotechnology. The massive nanomechanical data, acquired on 900 cells, open the door to the heterogeneity of populations, inaccessible in the framework of measuring only a few cells. We discovered in a classical C. albicans culture, 2 subpopulations of cells that can be distinguished on the basis of their nanomechanical properties. This will lead to a better understanding and use of nanomechanical data because their statistical significance power is higher than that in previously reported studies. Awakening AFM to statistics will enhance its potential use to analyze bionanomechanical properties and maybe pave the way for mechanopathology. |
Introduction
Medical doctors constantly have to face the issues of diagnosis, prognosis or evaluation of treatment efficiency. To tackle these issues there is a constant need to develop and adapt new, more accurate and sensitive biomarkers, able to help in differential diagnosis or predict as early as possible the disease evolution. In this aspect cell mechanical properties have the potential of being used as label free biomarkers for some pathologies.1 Indeed, cell mechanical properties have the potential to address the diagnosis of cancer1–4 as it has been reported that cancerous cells change their mechanical phenotype, presenting a lower Young modulus5–7 and adhesion7–9 than normal cells. Other authors have reported that cell mechanical properties are modified during proliferation,10 by comparing their elastic modulus to differentiate normal cells from cancerous cells11 or normal cells from cells treated for example with H2O2, N-ethylmaleimide and chymotrypsin.12 In the field of cardiology, it is also known that erythrocyte interactions with fibrinogen, as probed by AFM, are modified in ischemia and that the stiffness of red blood cells is altered.13 Cardiomyocytes are difficult to handle, and then works have reported the characterization of 1 to 30 cardiomyocytes14–20 in about 6–8 h, which is too small an amount of cells to provide statistically relevant information in the context of human diseases and therefore will never be reliable enough for clinicians. Mechanical properties have also helped in understanding the effects of antimicrobial molecules on bacteria or yeast cell's walls.21 Another example in the bacteria field is the work of Francius et al.22 They reported that S. aureus exposed to lysostaphin presented a decrease in elasticity and stiffness of its cell membrane. Also, Feuillie et al.23 reported in their paper that upon treating bacteria with a peptide derived from β-neurexin, it blocks the surface protein SdrC which impacts the cell adhesion. Formosa et al.24 reported the increase of the cell wall elastic modulus and an overexpression of the adhesive protein Als1p upon exposing Candida albicans to some incremental doses of caspofungin. Mechanical properties help in understanding the microorganisms’ cell wall structure, their resistance mechanisms, and adhesion processes.25,26Atomic Force Microscopy (AFM)27 is the technique of reference to acquire mechanical properties of cells.28,29 The classical procedure to obtain force curves from an AFM can be described by the following steps: first the tip is calibrated, then the sample is placed on the microscope stage, next a topographic image is acquired to determine the position of the cells, and the tip is moved to the central region of each cell. AFM indentations at different locations of the cell are performed, and force curves are obtained and recorded. Finally, when all the cells are measured, the stage is moved so that new cells are brought into the AFM field of view. This cycle is performed manually, and its throughput is low (<1 cell/10 min).30 To date this technique is neither used in the pharmaceutical industry nor in the antimicrobial drug discovery process. AFM is perceived as a research tool and indeed, the works reported so far have one common factor, which is the limited number of cells analyzed by an AFM. This limited number prevents the analysis of a cell population and therefore prohibits statistically relevant general conclusions or decisions. To be able to transfer the AFM technology to hospitals or the pharmaceutical industry a mandatory step is to achieve high throughput results in order to analyze cell populations rather than single cells.21,31
Wang et al.32 developed an automated system which uses image processing to identify Raji cell locations so that the AFM tip can move exactly above the cells and take measurements. The location and measurement of the cells are done within 3 s per cell, but their system had some requirements: the cells needed to be of round shape (which is usually the sign of dying cells), as the algorithm could only recognize round shaped cells confining the system to a specific cell geometry. Moreover, the cell substrate had to be completely flat and the agglomeration of cells was to be avoided, because the system did not withdraw the tip from the sample. Finally, the authors tested their system with 4 cells per scanning area, but they did not report the number of cells analyzed per hour. In another effort to develop AFM measurements on tissues Roy et al.33 developed a system that used image processing to align the AFM probe with a tissue of interest; they were able to obtain in an area of 80 μm × 150 μm up to 480 force curves in ∼80 min. Nevertheless, the aim of their semi-automated system consisted in analyzing changes in the tissue architecture not being adapted for single cell analysis. Another approach reported by Favre et al.34 focused on maximizing the number of cells analyzed by AFM. They developed an array of cantilevers that are controlled by one AFM acquiring images from different regions of a sample at the same time. However, to apply this technology to a cell population the cantilever arrays should be fabricated with the same dimensions as the cell arrays. Another example was the parallelism of AFM which was reported by Sadeghian et al.35 Their tool involved the miniaturization of AFMs, and they reported a maximum of 44 miniaturized AFMs in an area of 450 mm (wafer like area). Each AFM was capable of working independently from the others with different kinds of analysis. The authors tested the system by obtaining topographical images of colloidal gold nanoparticles (10 nm in diameter) deposited on mica. However, the distribution of AFM heads was very particular, and the cell array had to be adapted. Moreover, the locations of regions of interest were determined manually, meaning that human intervention was still predominant. Both parallel solutions did not consider a way to automatically bring new cells (or another cell array) inside the field of view of the AFM, consuming a vast amount of time.
Very recently Antoine Dujardin et al.36 reported a solution where an automated procedure allowed an AFM to accomplish biomechanical analysis on prokaryotes. A python script was implemented in a Dimension Fast Scan-Bio AFM (Bruker, Santa Barbara, CA, USA); however, this process takes considerable time to realign the photodetector and perform the engagement each time to finally analyze 501 areas in 8 h 35 min. They tested the system with fixed Yersinia pseudotuberculosis and living Mycobacterium bovis BCG bacteria. To identify the bioelements, a force volume image was performed in each well. This image was used to determine the bacteria positions (on the basis of their height) and the identified positions were imaged (2 × 2 μm2 area). The reported images are height and peak force-error signals discarding the option to perform a mechanical analysis on the analyzed bacteria.
In the present work an original automated methodology, previously submitted as a patent31 to measure cellular mechanical properties is reported. Our methodology combines a purposely developed copyright algorithm37 executed as a script on commercial AFMs with a smart strategy of cell immobilization (ESI,† Fig. S2). The script automatically moves the tip from cell to cell to record force curves of each cell of a cell population. Cells are immobilized at known locations into microwells of a microfabricated PDMS stamp.38 Once the tip has scanned all the cells of the scanning area, a motor stage moves automatically and brings a new cell array into the scanning area to re-initiate the methodology.
We tested this AFM based automated methodology on the eukaryote C. albicans because it is known as an opportunistic pathogenic yeast which represents one of the main causes of hospital-acquired infections. We decided to compare native C. albicans cells with caspofungin treated C. albicans cells. Caspofungin is a last change antifungal drug from the echinocandin class, known to modify the mechanical properties of the yeast cell wall.24 In our test, the automated methodology takes an average time of 12 seconds to perform 9 nanoindentations per cell and per microwell, giving a large number of force curves that is between 8000 to 9000 in 4 h, providing a method for high throughput measurements of a cell population. This automated process can be considered as the first step for a viable future diagnostic tool.31 Thanks to this development we present for the first time the mechanical properties of a cell population (800–900 cells) measured by AFM pointing out that the mechanical properties within the cell population is not homogeneous and may explain the conflicting results reported in the literature.
Results and discussion
Fig. 1 shows the execution of the program developed for this work (recommendations to initialize the algorithm: Fig. S1 and description of the algorithm in Fig. S2 and S3, ESI†); Fig. 1A and B show how the cantilever moves from one scanning area to another. The centering algorithm takes ∼40 s to be executed on each microwell. Fig. 1C shows the displacement among the microwells in one scanning area, the movement is from the center of one microwell to the center of other microwell. The program takes ∼12 s to finish the 9 indentations per microwell and ∼13 min per area, that is 64 wells per scanning area. Then Fig. 1D shows the nanoindentation on different regions inside a microwell. This result can be seen in the video in the ESI.†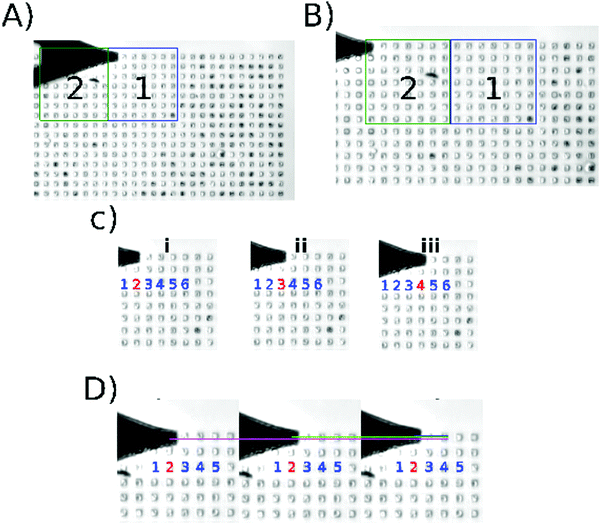 | ||
| Fig. 1 Algorithm execution. Screenshots taken from the supplementary video (ESI†). (A) Location of the center of the first microwell in the current scanning area. (B) Position of the tip after moving the motor stage; area 2 is the active scanning area at this moment. (C) shows the data acquisition through different microwells (i–iii). (D) shows the data acquisition inside one microwell; the indentation is performed in different regions of the same microwell (magenta/green/blue). | ||
The force curves were obtained from C. albicans cells immobilized inside the micro-fabricated wells. Four experiments were conducted with the objective to establish the repeatability and reliability of the results. Native and caspofungin treated cells were independently prepared as mentioned in the Methods section and immobilized the day they were used. The decision to use caspofungin is because its action on the yeast cell wall is still under debate.24,42 The script was executed and 1021 cells were analyzed for the first experiment (native cells), 957 cells for the second experiment (native cells), 1000 cells for the third (caspofungin), and 574 cells for the fourth experiment (caspofungin). For experiments 1 and 3, 16 indentations per cell were taken; meanwhile, for experiments 2 and 4, 9 nanoindentations were taken.
Experiments 1, 2, 3, and 4 are independent duplicates. The cell cultures were independent and were not performed the same day. Four experiments were performed, two of them (experiments 1 and 2) with native cells and two (experiments 3 and 4) with caspofungin treated cells. The objective of this setup was to obtain a comparable number of analyzed cells (for native and treated) and to determine the maximum number of cells analyzed in a fixed time (4 h).
Following the previous criteria Table 1 presents the number of cells analyzed, the number of force curves discarded, and the time taken to analyze each well.
| Experiment | Force curves | Wells analyzed | Cells analyzed | Time per well (s) | Discarded force curves (%) | |
|---|---|---|---|---|---|---|
| Native cells | 1 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 927 |
1021 | 1021 | 9 | 4.31 |
| 2 | 8620 | 959 | 957 | 12 | 12.87 | |
| Treated cells | 3 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
1018 | 1000 | 9 | 8.19 |
| 4 | 5180 | 579 | 574 | 12 | 20.88 |
The force curves obtained were analyzed using the JPK data processing software, and based on the work published by El-Kirat-Chatel42 we extracted the cell spring constant from all the force curves. However, the filling rate of the PDMS stamp is not 100% (actually ∼86%). In the ESI† dealing with the acquisition and analysis of force curves, the parameters used to exclude curves recorded from the cells are described (ESI,† Fig. S4). To filter the force curves the following criteria were implemented:
• The contact point is used to determine whether the force curves are from the bottom of the well, so all the curves with a contact point value below 4.15 μm are discarded.
• Curves with a negative slope are discarded.
• We assumed that the cell spring constant should be lower than that of the PDMS measured at 150 pN nm−1, hence we discarded all force curves giving a spring constant higher than 150 pN nm−1.
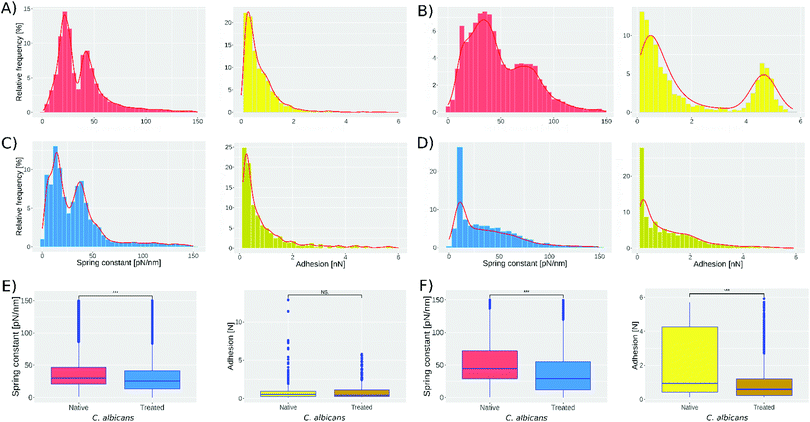
Fig. 2 presents the spring constant and adhesion histograms for C. albicans cells in native conditions (A and B) and treated with caspofungin (C and D). Fig. 2A and B, left, show the spring constant histograms, and the number of cells analyzed in the first two experiments was 1021 and 959 respectively; both are obtained by analyzing independently the cultured native cells. Analyzing the two histograms with the k-means method they can be deconvoluted into 2 populations that are slightly different in the 2 experiments. The first population has a mean spring constant of 21 ± 6 pN nm−1 (experiment 1) and 30 ± 13 pN nm−1 (experiment 2) while the second population has a spring constant of 48 ± 9 pN nm−1 (experiment 1) and 80 ± 18 pN nm−1 (experiment 2). For experiments 3 and 4 (Fig. 2C and D, left) 1018 and 579 cells were analyzed. According to the literature,42 treated cells present a softening of the cell wall because of the caspofungin treatment.
This shift can be seen in Fig. 2, comparing experiments 1 and 3. The peak present at 21 pN nm−1 (Fig. 2A-left) shifts to 13 pN nm−1 (Fig. 2C-left) and the peak at 48 pN nm−1 shifts to 42 pN nm−1. For experiments 2 and 4 (Fig. 2B and D, left, respectively) the peak present at 30 pN nm−1 shifts to 15 pN nm−1 and the peak at 80 pN nm−1 shifts to 52 pN nm−1. Fig. 2E and F show the one-way ANOVA test; Fig. 2E-left was obtained comparing spring constant data of Fig. 2A and C reducing both sets to 1018 cells; meanwhile, Fig. 2F-left was obtained by comparing spring constant data of Fig. 2B and D reducing both sets to 579. The one way test is used to compare the native cell results against those of treated cells obtaining a p < 0.001 (represented by ***).
Fig. 2A-right shows that the adhesion force between the bare tip and native cells was 0.64 ± 0.6 nN in the first experiment, while in the second experiment still on native cells, 2 subpopulations were found: the first has a mean adhesion force of 0.7 ± 1.4 nN while the second has 4.5 ± 1.5 nN. The treatment with caspofungin has no significant effect on the adhesion if experiments 1 and 3 are considered (one way ANOVA test, Fig. 2E-right shows no significant difference) but it seems that caspofungin induces a decrease in the adhesion to the tip and a reduction of the population adhesion heterogeneity.
Discussion
The protocol used to immobilize the cells was the one described by Formosa et al.;38 nevertheless, in this work a modification was made to go from ∼50% to ∼85% of microwells filled with cells (see Methods section). The number of nanoindentations were 16 for experiments 1 and 3 and 9 for experiments 2 and 4. The objective of varying the number of nanoindentations was to observe whether a significant change will be present in the histograms, and as can be seen the two subpopulations start to merge when we decrease the number of measurements; however, with nine indentations it is still possible to see the two subpopulations (Fig. 2).We extracted the spring constant from every force curve we obtained with the automated procedure. Based on the results published by El-Kirat-Chatel42 a shift in the results for the treated cells with respect to the native cells was expected; these can be confirmed by looking at Fig. 2(A and C, B and D). In contrast, the presence of the two peaks in the histograms that we observed in all four experiments was unexpected. Indeed, experiments performed on single cells24,42 only demonstrated a homogeneous distribution of the nanomechanical properties. The difference in the spring constant absolute value for the two independent experiments on native cells may come from uncontrollable differences in the cell cultures. Indeed, the maximum applied force, the tip velocity, the cantilever spring constant, the buffer, the temperature, etc., were the same. It is important to note that C. albicans is actually an extremely versatile microbe43 able to sense and adapt to its environment. As a consequence, the growth phases of C. albicans are difficult to control and an unmeasurable difference in the initial culture conditions may result through the butterfly effect to the difference that we observe between experiments 1 and 3. A further interesting experiment would be to follow a cell culture in order to monitor its evolution throughout the time. But, most importantly, we reproduced, two times, the distribution of the cells into two distinct populations. Dague E. et al.44 reported a heterogeneity of the Young modulus of Saccharomyces cerevisiae cells analyzed under the same conditions. Nevertheless, the numbers were really low (5 cells) and it was therefore impossible to draw a general conclusion at the population scale. Sub-populations in C. albicans have been described since more than ten years in the context of biofilms. They are reported to be responsible for biofilm resistance to chelating agents45 and to antifungal drugs like amphotericin B.46 In this last publication, the authors demonstrated that the sub-population was associated with ergosterol and beta 1–6 glucan pathway genes. They both are important components of the fungal cell wall and we know from previous investigations of the team47 that their expression level is correlated with the nanomechanical properties of the cells. More recently, Rosenberg et al. showed that antifungal tolerance was a sub-population effect.48 It therefore seems that sub-populations in C. albicans are common. In our work there is no particular reason for the 2 sub-populations, and we must admit that we have no clue of their origin. Globally, we can hypothesize that sub-populations in C. albicans are an adaptation mechanism probably responsible for the remarkable expansion of this microbe, usually being a commensal but also an opportunistic pathogen.
To our knowledge this work is the first that reports the use of AFM to analyze hundreds of cells which demonstrates that a microbe population is mechanically heterogeneous. Fig. S6(A and B) (ESI†) shows the presence of the two populations at all times during the experiment. This means that the sub-populations are not due to the alteration or modification of the cells during the experiments. The two populations exist from the beginning to the end of the experiments. We also wondered whether the subpopulations could be due to an artifact linked with the tip position above the cell/well. To eliminate this hypothesis, we examined the distribution of stiffness constants for each position of the tip. This analysis, presented in Fig. S6C and D (Fig. S6, ESI†), shows that the spring constants are distributed according to the same sub-population distribution for each analysis point. There is, therefore, no one position category that contributes to one sub-population and another position category that contributes to the other sub-population. These subpopulations are really linked to differences in spring constant between cells and really reflect the biological reality, complexity, variability of a Candida albicans cell population.
To be sure we also calculated the average value of each cell and represented these values on a histogram (ESI,† Fig. S5). These representations show 2 sub-populations, centered on the same values as those of the global distribution histograms.
Our strategy to achieve a few force curves (9 to 16) over a large number of cells marks a break with the traditional approach to mechanical measurements, by AFM, on living cells. Nevertheless, we compared our results with those in the literature to validate the approach. Indeed, if the measurement on hundreds of cells was theoretically to open the door to the observation of sub-population, the decrease in the number of force curves, per cell, may also have negative effects. El Kirat-Chatel et al.42 performed 256 nanoindentations on a single cell, and they found a stiffness value of 51 ± 9 pN nm−1 for cells not treated with caspofungin and 27 ± 10 pN nm−1 for cells treated with caspofungin. Our results are of the same order of magnitude (spring constant ranging from 21 ± 6 to 81 ± 19 pN nm−1 for native cells) and we observe the same tendency of decreasing the spring constant with caspofungin treatment (spring constant ranging from 13 to 52 pN nm−1, in our experiments, for caspofungin treated cells).
In another paper Formosa et al.24 showed that Candida albicans cells treated with caspofungin became harder. Their results are based on the analysis of 1024 nanoindentations performed on a cell. This inconsistency could be explained if authors selected an untreated cell from the softest subpopulation and a treated cell from the hardest subpopulation. Having no means at that time to access the sub-populations, the 2 results were accurate but incomplete. These inconsistencies are numerous in the literature and have partly motivated our work.
The results of the adhesion measurements are particularly interesting and highlight the limitations with which our method could be confronted. Indeed, it is known that Candida albicans is able to express on its surface a large number of different adhesins, in variable quantities.43,49 The conditions of expression of some of them are known but, for example, the conditions of amyloid aggregation described in ref. 41 have not been demonstrated. It seems that it could be triggered by mechanical stimulation (force induced nanodomain Alsteens PNAS ALS550) but this has not been demonstrated in Candida. Our adhesion results were different from one experiment to another, although the culture conditions were the same or at least we were under the impression that they were the same, the usual microbiological techniques being implemented. This probably means that the expression of adhesins and/or their organization on the cell surface in experiments 1 and 2 were different. Our method is not designed to analyse single cells in high detail and therefore the detection of nanodomains is impossible. It means that the traditional approach is not an antagonist of our new method and that they provide additional information. Moreover, the differences in spring constant between the nanodomains and the “normal” cell wall are not in the order of magnitude of the 2 sub-populations. Stiffer nanodomains are 13.4 ± 0.2 nN μm−1 when the rest of the cell wall is 12.4 ± 0.3 nN μm−1.41 In the present work we report a sub-population at 21 ± 6 nN μm−1 and the second at 48 ± 9 nN μm−1. This means that the differences due to the nanodomains are included in the error bar of our measurement.
Thus, our results would no longer be incomplete because they would not consider the heterogeneity of the cell population but incomplete because we would lack control over the biological sample produced. Candida albicans is known for its versatility43 and in this context is more suitable for this demonstration than any other cell model.
Conclusions
An automated methodology for AFM force curve acquisition on cell population was successfully developed and implemented on a JPK Nanowizard II. The portability of the algorithm was tested on a JPK Nanowizard III. The results demonstrate that increasing drastically the number of cells analyzed (from tens to hundreds) makes it possible to describe a cell population from the nanomechanical point of view. Moreover, we showed that the number of measurements per cell has no impact on the significance of the result.Our results, in addition to being consistent with those in the literature, show for the first time the presence of at least 2 subcellular populations. These are distinguished by differences in mechanical properties and cell wall adhesion. This discovery could have important implications for understanding the pathogenicity of Candida albicans. Indeed, the adhesion of cells to the host represents the first stage of infection and the mechanical environment of Candida is known to induce transformation from the yeast form to the invasive hypha form. Different subpopulations in terms of adhesion and mechanical properties are thus potentially responsible for one or the other of these key stages of Candida albicans infection.
Methods
Cell culture
The cell cultures were prepared as previously reported.24,41C. albicans was stored at −80 °C, and four independent cultures were prepared with the C. albicans revivified on Yeast Peptone Dextrose (YPD) agar, and each were grown in 5 ml YPD broth for 20 h at 30 °C under static conditions. In two of these four independent cultures 9.4 μl of caspofungin at 0.1 mg ml−1 (4xMIC) concentration were added and allowed to stand under static conditions for 24 h at 30 °C. Yeast cells (native and treated) were concentrated by centrifugation, washed two times in acetate buffer, and resuspended in acetate buffer just before performing AFM experiments.Sample preparation
600 μl were taken from the resuspended cell solution and centrifuged, to separate the buffer from the cells. The supernatant is deposited onto a PDMS stamp, prepared as described in ref. 38 and degassed for about 40 min. After 40 min the buffer is removed from the PDMS surface, and 200 μl of the cell solution are deposited and allowed to stand for 15 min at room temperature. The cells were then placed in the microstructures of the stamp by convective/capillary assembly as described in ref. 38.The PDMS stamp with cells was finally fixed on a Petri dish (FluoroDish FD35-100) and it was filled with 5 ml of acetate buffer solution to maintain the cells in liquid media.
AFM measurements
For all experiments, commercially available silicon nitride triangular cantilevers (Bruker MLCT) with spring constants and sensitivity ranging respectively from 0.0110 N m−1 to 0.0405 N m−1 and from 31.8 nm V−1 to 54.2 nm V−1 were used. Cantilevers were calibrated using the thermal tune method. The parameters used to engage the tip on the stamp surface were as follows: IGain = 70 Hz, PGain = 0.002, setpoint = 0.559 nN. The topographic image used to determine W1 and W2 coordinates was recorded in the force map mode (64 × 64 pixels, maximum applied force 1 nN, tip velocity 10 μm s−1). The maximum applied force used to record force curves was set to 1 nN and the piezo and motor stage speed were 10 μm s−1 and 200 μm s−1 respectively. The AFM field was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm2 (100 μm × 100 μm).
000 μm2 (100 μm × 100 μm).
The AFM automation has been implemented on a JPK Nanowizard II, with a motorized precision stage MotStage Zeiss AxioObserver (S/N SM-01-0017) on an inverted optical microscope Zeiss Axiovert 200M. The AFM control software (SPM version 4) runs under Ubuntu 10.04 LTS (Lucid Lynx); the script is executed by using the experiment planner module, included in the JPK SPM software control. Indeed, the experiment planner mode offers a Jython scripting interface to control the AFM, hence the software program for automation has been developed in Jython programming language.
Statistical analysis: k-means method
The k-means method has been used to group the subpopulations observed in the results. The method is based on the Hartigan and Wong algorithm;39 it divides M points in N dimensions into K clusters, and the cluster centers are at the mean of their Voronoi set40 (the set of data points which are nearest to the group center). The procedure is to minimize the within-cluster sum of squares, so the dimension of the clusters will be changed until the items in the same cluster are similar as possible and items in different clusters are different as possible.The k-means method was used to divide the stiffness and adhesion results into groups for analysis.
Authors contribution
E. Dague and A. Martinez-Rivas designed the research and experiments. S. Proa-Coronado and C. Séverac wrote the automation program. S. Proa-Coronado, C. Séverac, and E. Dague conducted the experiments. All the authors contributed to the writing and critical proofreading of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We want to acknowledge FONCYCYT of CONACYT (Mexico), the ministry of Foreign affairs of France and the Université Paris 13, though the financial support of the international collaborative ECOS-NORD project named Nano-palpation for diagnosis, No. 263337 (Mexico) and MI5P02 (France). AMR would like to thank the financial support of the SIP project No. 20195489, from IPN. SPC is supported by a PhD fellowship from CONACYT (No. 288029) and IPN through the cotutelle agreement to obtain double PhD certificate (IPN-UPS). ED is a researcher at Centre National de la Recherche Scientifique (CNRS).References
- E. M. Darling and D. Di Carlo, Annu. Rev. Biomed. Eng., 2015, 17, 35–62 CrossRef CAS.
- S. E. Cross, Y.-S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS PubMed.
- K. S. Kim, C. H. Cho, E. K. Park, M.-H. Jung, K.-S. Yoon and H.-K. Park, PLoS One, 2012, 7, e30066 CrossRef CAS PubMed.
- M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, R. Y. H. Lim and C.-A. Schoenenberger, Nat. Nanotechnol., 2012, 7, 757–765 CrossRef CAS.
- M. Lekka, P. Laidler, D. Gil, J. Lekki, Z. Stachura and A. Z. Hrynkiewicz, Eur. Biophys. J., 1999, 28, 312–316 CrossRef CAS.
- M. E. Grady, R. J. Composto and D. M. Eckmann, J. Mech. Behav. Biomed. Mater., 2016, 61, 197–207 CrossRef CAS.
- R. Omidvar, M. Tafazzoli-shadpour, M. A. Shokrgozar and M. Rostami, J. Biomech., 2014, 47, 3373–3379 CrossRef.
- L. Bastatas, D. Martinez-Marin, J. Matthews, J. Hashem, Y. J. Lee, S. Sennoune, S. Filleur, R. Martinez-Zaguilan and S. Park, Biochim. Biophys. Acta, Gen. Subj., 2012, 1820, 1111–1120 CrossRef CAS.
- G. Smolyakov, B. Thiebot, C. Campillo, S. Labdi, C. Severac, J. Pelta and É. Dague, ACS Appl. Mater. Interfaces, 2016, 8, 27426–27431 CrossRef CAS.
- M. G. Haugh, C. M. Murphy, R. C. McKiernan, C. Altenbuchner and F. J. O’Brien, Tissue Eng., Part A, 2010, 17, 1201–1208 CrossRef.
- A. Charlotte, G. Bruno and M. Jean-Baptiste, Biol. Cell., 2017, 109, 167–189 CrossRef.
- Y.-Q. Chen, C.-W. Chen, Y.-L. Ni, Y.-S. Huang, O. Lin, S. Chien, L. A. Sung and A. Chiou, J. Biophotonics, 2014, 7(8), 647–655 CrossRef CAS.
- A. F. Guedes, F. A. Carvalho, I. Malho, N. Lousada, L. Sargento and N. C. Santos, Nat. Nanotechnol., 2016, 11, 687–692 CrossRef CAS.
- J. Domke, W. J. Parak, M. George, H. E. Gaub and M. Radmacher, Eur. Biophys. J., 1999, 28, 179–186 CrossRef CAS.
- G. Genet, C. Guilbeau-Frugier, B. Honton, E. Dague, M. D. Schneider, C. Coatrieux, D. Calise, C. Cardin, C. Nieto, B. Payré, C. Dubroca, P. Marck, C. Heymes, A. Dubrac, D. Arvanitis, F. Despas, M.-F. Altié, M.-H. Seguelas, M.-B. Delisle, A. Davy, J.-M. Sénard, A. Pathak and C. Galés, Circ. Res., 2012, 110, 688–700 CrossRef CAS PubMed.
- Y. Liu, J. Feng, L. Shi, R. Niu, Q. Sun, H. Liu, J. Li, J. Guo, J. Zhu and D. Han, Nanoscale, 2011, 4, 99–102 RSC.
- W. S. Yoshikawa, K. Nakamura, D. Miura, J. Shimizu, K. Hashimoto, N. Kataoka, H. Toyota, H. Okuyama, T. Miyoshi, H. Morita, K. F. Kusano, T. Matsuo, M. Takaki, F. Kajiya, N. Yagi, T. Ohe and H. Ito, Circ. J., 2013, 77, 741–748 CrossRef CAS.
- J. C. Benech, N. Benech, A. I. Zambrana, I. Rauschert, V. Bervejillo, N. Oddone and J. P. Damián, Am. J. Physiol., 2014, 307, C910–C919 CrossRef CAS PubMed.
- E. Dague, G. Genet, V. Lachaize, C. Guilbeau-Frugier, J. Fauconnier, C. Mias, B. Payré, L. Chopinet, D. Alsteens, S. Kasas, C. Severac, J. Thireau, C. Heymes, B. Honton, A. Lacampagne, A. Pathak, J.-M. Sénard and C. Galés, J. Mol. Cell. Cardiol., 2014, 74, 162–172 CrossRef CAS.
- A. B. Mathur, A. M. Collinsworth, W. M. Reichert, W. E. Kraus and G. A. Truskey, J. Biomech., 2001, 34, 1545–1553 CrossRef CAS.
- C. Formosa-Dague, R. E. Duval and E. Dague, Semin. Cell Dev. Biol., 2018, 73, 165–176 CrossRef CAS.
- G. Francius, O. Domenech, M. P. Mingeot-Leclercq and Y. F. Dufrêne, J. Bacteriol., 2008, 190, 7904–7909 CrossRef CAS PubMed.
- C. Feuillie, C. Formosa-Dague, L. M. C. Hays, O. Vervaeck, S. Derclaye, M. P. Brennan, T. J. Foster, J. A. Geoghegan and Y. F. Dufrêne, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3738–3743 CrossRef CAS.
- C. Formosa, M. Schiavone, H. Martin-Yken, J. M. François, R. E. Duval and E. Dague, Antimicrob. Agents Chemother., 2013, 57, 3498–3506 CrossRef CAS.
- M. Li, N. Xi, Y. Wang and L. Liu, Nano Res., 2019, 12, 703 CrossRef CAS.
- B. Nathwani, W. M. Shih and W. P. Wong, Biophys. J., 2018, 115, 2279–2285 CrossRef CAS.
- G. Binnig, C. F. Quate and Ch. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef.
- H. Schillers, C. Rianna, J. Schäpe, T. Luque, H. Doschke, M. Wälte, J. J. Uriarte, N. Campillo, G. P. A. Michanetzis, J. Bobrowska, A. Dumitru, E. T. Herruzo, S. Bovio, P. Parot, M. Galluzzi, A. Podestà, L. Puricelli, S. Scheuring, Y. Missirlis, R. Garcia, M. Odorico, J.-M. Teulon, F. Lafont, M. Lekka, F. Rico, A. Rigato, J.-L. Pellequer, H. Oberleithner, D. Navajas and M. Radmacher, Sci. Rep., 2017, 7, 5117 CrossRef.
- I. Sokolov, M. E. Dokukin and N. V. Guz, Methods, 2013, 60, 202–213 CrossRef CAS.
- D. Di Carlo, J. Lab. Autom., 2012, 17, 32–42 CrossRef CAS.
- A. Martínez-Rivas, E. Dague, S. Proa-Coronado, C. Séverac and G. González-Quijano 2018 Patent: WO2019112414 (A1)—2019-06-13, https://patentscope.wipo.int/search/es/detail.jsf?docId=WO2019112414&tab=PCTBIBLIO&maxRec=1000.
- Z. Wang, L. Liu, Y. Wang, N. Xi, Z. Dong, M. Li and S. Yuan, J. Lab. Autom., 2012, 17, 443–448 CrossRef.
- R. Roy, W. Chen, L. Cong, L. A. Goodell, D. J. Foran and J. P. Desai, IEEE Trans. Autom. Sci. Eng., 2013, 10, 462–465 Search PubMed.
- M. Favre, J. Polesel-Maris, T. Overstolz, P. Niedermann, S. Dasen, G. Gruener, R. Ischer, P. Vettiger, M. Liley, H. Heinzelmann and A. Meister, J. Mol. Recognit., 2011, 24, 446–452 CrossRef CAS.
- H. Sadeghian, R. Herfst, B. Dekker, J. Winters, T. Bijnagte and R. Rijnbeek, Rev. Sci. Instrum., 2017, 88, 033703 CrossRef.
- A. Dujardin, P. D. Wolf, F. Lafont and V. Dupres, PLoS One, 2019, 14, e0213853 CrossRef CAS PubMed.
- D. Etienne, P. C. Sergio, S. Childerick and M. R. Adrian, AUTOMATIP: Automation of Biophysical measurements on cells by Atomic Force Microscope (AFM). Copyright: 03-2017-113012552200-01. (Instituto Politecnico Nacional, 2017).
- C. Formosa, F. Pillet, M. Schiavone, R. E. Duval, L. Ressier and E. Dague, Nat. Protoc., 2015, 10, 199–204 CrossRef.
- J. A. Hartigan and M. A. Wong, J. R. Stat. Soc. Ser. C Appl. Stat., 1979, 28, 100–108 Search PubMed.
- R Core Team, R: A Language and Enviroment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2018.
- C. Formosa, M. Schiavone, A. Boisrame, M. L. Richard, R. E. Duval and E. Dague, Nanomedicine, 2015, 11, 57–65 CrossRef CAS PubMed.
- S. El-Kirat-Chatel, A. Beaussart, D. Alsteens, D. N. Jackson, P. N. Lipke and Y. F. Dufrêne, Nanoscale, 2013, 5, 1105–1115 RSC.
- D. Poulain, Crit. Rev. Microbiol., 2015, 41, 208–217 CrossRef CAS.
- E. Dague, E. Jauvert, L. Laplatine, B. Viallet, C. Thibault and L. Ressier, Nanotechnology, 2011, 22, 395102 CrossRef CAS.
- J. J. Harrison, R. J. Turner and H. Ceri, FEMS Microbiol. Lett., 2007, 272, 172–181 CrossRef CAS.
- P. D. Khot, P. A. Suci, R. L. Miller, R. D. Nelson and B. J. Tyler, Antimicrob. Agents Chemother., 2006, 50, 3708–3716 CrossRef CAS PubMed.
- M. Schiavone, S. Déjean, N. Sieczkowski, M. Castex, E. Dague and J. M. François, Front. Microbiol., 2017, 8, 1806 CrossRef PubMed.
- A. Rosenberg, I. V. Ene, M. Bibi, S. Zakin, E. S. Segal, N. Ziv, A. M. Dahan, A. L. Colombo, R. J. Bennett and J. Berman, Nat. Commun., 2018, 9, 2470 CrossRef.
- P. W. J. de Groot, O. Bader, A. D. de Boer, M. Weig and N. Chauhan, Eukaryotic Cell, 2013, 12, 470–481 CrossRef CAS.
- D. Alsteens, M. C. Garcia, P. N. Lipke and Y. F. Dufrêne, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20744–20749 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00438f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |