Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photonic hook formation in near-infrared with MXene Ti3C2 nanoparticles†
Marat
Spector
a,
Angeleene S.
Ang
 a,
Oleg V.
Minin
a,
Oleg V.
Minin
 b,
Igor V.
Minin
b,
Igor V.
Minin
 b and
Alina
Karabchevsky
b and
Alina
Karabchevsky
 *a
*a
aSchool of Electrical and Computer Engineering, Ben-Gurion University of the Negev, Beer-Sheva 8410501, Israel. E-mail: alinak@bgu.ac.il
bNational Research Tomsk State University, Tomsk, 634050, Russia
First published on 22nd September 2020
Abstract
MXenes, a recently developed class of 2D materials, have attracted considerable attention because of their graphene-like but highly tunable properties. It appears that the metallic properties of MXene titanium carbide are pronounced in near-infrared with well-defined localised surface plasmon resonance (LSPR). Here, we report on a curved photonic nanojet, known as the photonic hook, applied on a titanium carbide nanoparticle for the particle's optomechanical manipulation. We show that the optical forces generated and applied on titanium carbide nanoparticles of various shapes are based on the LSPR excitation in near-infrared. We compare the obtained results to traditional plasmonic gold nanoparticles which exhibit LSPR in visible. Considering the diversity of the MXene family, this study is a first step towards photonic devices that utilize optomechanical manipulation in near-infrared for biomedical research, optical trapping and others.
1 Introduction
MXenes, first discovered in 2011,1 are a diverse novel family of two dimensional nanomaterials formed from transition metal carbides and carbonitrides. These materials are derived from Mn+1AXn, MAX phases, where n = 1 to 4, and M is an early transition metal produced by selectively etching the A-layers.2 The derived phase is labeled MXene to emphasize their graphene-like morphology.3 MXenes are environmentally benign, with strong hydrophilic properties due to their unique layered structure and chemical stability. These materials have demonstrated their potential as electrode materials of Li-ion batteries, supercapacitors, and sensors.4,5 One of the most widely studied and most promising members of the MXene materials is titanium carbide (Ti3C2). It can be readily fabricated by selectively etching aluminum from Ti3AlC2.6 This material is used in applications such as electrochemical capacitors,2 electromagnetic wave shielding,7 integratable photodetectors,8 transparent electrodes,9 metal ion batteries,10 supercapacitors,11 and many others.The plasmonic properties of MXenes remain largely unexplored, but limited work on the subject exists.12–20 Mauchamp et al. revealed that Ti3C2Tx (Tx denotes surface-terminated moieties such as –O or –F) is a plasmonic material;16 a comprehensive study of the surface plasmons on the material has been performed at infrared (IR) wavelengths.13 The applications of MXene nanostructures have been investigated as a broadband absorber.15 Integrating MXenes into SPR sensors has significantly improved sensitivity compared to the set-up without the 2D material.12,14
While the studies on MXenes are focused towards their use as a 2D material, they can also exist as nanoparticles,6,21 flakes,13 and nanostructured films.15 In addition, the plasmonic properties of the MXene Ti3C2 can be used to enhance light–matter interactions. Among the most popular candidates for plasmonic applications is gold, due to its bulk plasmon performance in the visible range.22 Given sufficiently small objects, one can manipulate the movement of particles using focused laser light.23 Although optical manipulation is usually applied to dielectric objects, the aforementioned strong light–matter interaction arising from plasmonic resonances has been used to trap, move, rotate, and align metallic nanoparticles.22,24–27
One of the drawbacks of using conventional laser-based optical manipulation is the diffraction-limited trapping volume.27 An alternative proposed in order to achieve sub-diffraction manipulation has been explored using a high-intensity narrow light beam generated by dielectric structures, referred to as photonic nanojets.28–32 Photonic nanojets are usually generated using symmetric structures, usually spherical, subjected to external illumination.28,33 Previous work has explored a curved photonic nanojet, called the photonic hook, and its capacity for optical manipulation under continuous plane wave illumination34 and pulsed plane waves.35 It was shown that the maximum magnitude of the optical force generated by the photonic hook is near the wavelength of plasmon resonance excitation.
It should be emphasized that the metallic properties and plasmon resonance of titanium carbide are clearly defined in the near-infrared range, whereas the plasmon resonance of gold is in the visible range. This limits the application of gold in biomedical research, since its penetration depth is short. Using near-infrared wavelengths will increase the penetration depth, making it suitable for optical manipulation beneath biological layers like tissues. Moreover, optical forces on MXene particles have never been explored.
In this paper, we report for the first time the possibility of optomechanical manipulation of Ti3C2 nanoparticles with cylindrical symmetry and movement of Ti3C2 nanospheres in a curved trajectory utilising Ti3C2 localized surface plasmon resonance (LSPR) properties in near-infrared. The studied system is shown in Fig. 1 with a plane wave illuminating the cuboid and a generated photonic hook force applied on the Ti3C2 particle. We compare our results to the magnitude trajectory of gold nanospheres moved using the photonic hook curved light force. In addition, we explore the polarizability of Ti3C2 given different particle geometries such as the nanodisk and nanorod. We will show that for the case of titanium carbide nanoparticles, the creation of the photonic hook can be successfully tuned to near-infrared.
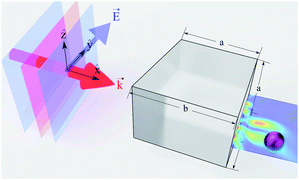 | ||
Fig. 1 Illustration of the plane wave illuminating asymmetric auxiliary structure cuboid in the direction of vector 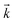 . The cuboid size parameters a = 3 and b = 4 are obtained from ref. 33. . The cuboid size parameters a = 3 and b = 4 are obtained from ref. 33. | ||
2 Ti3C2 LSPR
Here we study how to manipulate a particle in near-infrared utilizing optical forces generated on Ti3C2. This effect can occur in case the localised surface plasmon is excited. At the interface where the real part of the dielectric function changes sign, such as a metal–dielectric interface, the electron oscillations occur.36–42 Confining the surface plasmon in a nanoparticle to a size smaller than the wavelength of light used to excite the plasmon produces a localized surface plasmon.43,44 This results in the enhancement of electric fields near the particle surface, and the absorption of the particle is maximized at the plasmon resonant frequency.We compare two plasmonic materials: the commonly used gold and the novel MXene Ti3C2. The dielectric functions of gold45 and titanium carbide46 are included in the ESI file.† As opposed to gold nanoparticles, whose LSPR is located in the visible range, the location of LSPR in the case of Ti3C2 is in near-infrared.
The spectral location of the LSPR depends on the geometry of the plasmonic nanostructure and material43,47 and is directly related to the following expression
| εm(λ) + Gεd(λ) = 0; | (1) |
We investigate the excitation of LSPR under continuous wave (CW) illumination. Physically, this means that we do not take into account any heating effects which has to be taken into account for the case of a Gaussian beam. While the dependence of the dielectric function of gold on the temperature of either electrons or the lattice is very well known45,50 and was in detail discussed in our previous article,51 there is still a lack of experimental data regarding the dependence of the dielectric function of MXenes on the temperature of either electrons or the lattice. Consequently, we focus on comparison between MXenes and gold nanoparticles under CW illumination. Furthermore, we assume that the incident intensity is very low, meaning that we can neglect the dependence of the dielectric function of MXenes on temperature,52,53 which is directly related to photon absorption in near-infrared.
3 Nanosphere
Assuming that the radius of the nanosphere is much smaller than the incident wavelength, the polarizability of the nanosphere is given by54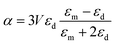 | (2) |
The normalized polarizability 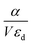 of gold and Ti3C2 nanospheres embedded in different lossless media such as air, water or silica is presented in Fig. 2. The dispersion of the dielectric function of water and silica is based on the experimental data,55,56 while the dielectric function of air is assumed to be independent of the incident wavelength of the laser beam.
of gold and Ti3C2 nanospheres embedded in different lossless media such as air, water or silica is presented in Fig. 2. The dispersion of the dielectric function of water and silica is based on the experimental data,55,56 while the dielectric function of air is assumed to be independent of the incident wavelength of the laser beam.
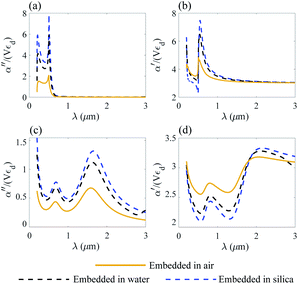 | ||
| Fig. 2 Nanosphere polarizability spectrum in air, water and silica: (a) α′′ of gold; (b) α′ of gold; (c) α′′ of Ti3C2; (d) α′ of Ti3C2. | ||
Fig. 2 shows that the location of LSPR is tuned to near-infrared for the case of Ti3C2 nanoparticles as compared to gold. Specifically, Fig. 2c and d show that the polarizability of Ti3C2 nanospheres attains its maximum (minimum) for the imaginary (real) part when the incident wavelength is λ ≈ 1.5 μm. We also note that the gold nanoparticle is a linear function of the studied media in which the nanoparticle is embedded, i.e., the real and imaginary parts of the polarizability increase as the refractive index of the surrounding medium increases. In comparison, the polarizability of Ti3C2 in this region shows a very different behavior. The imaginary part of the polarizability increases as the medium changes from air to water, while the real part decreases. Analysis shows that both the materials used as embedded media show a negligible wavelength dependence of the dielectric function. Thus, the unusual behavior of the Ti3C2 nanoparticle polarizability is strictly related to the optical properties of Ti3C2.
4 Optical force applied on a Ti3C2 nanosphere
We analyze the optical force acting on Ti3C2 and gold nanoparticles, with the photonic hook illumination system shown in Fig. 1. The optical force F and the acceleration a acting on the nanoparticle are given according to the following expressions57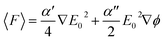 | (3a) |
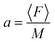 | (3b) |
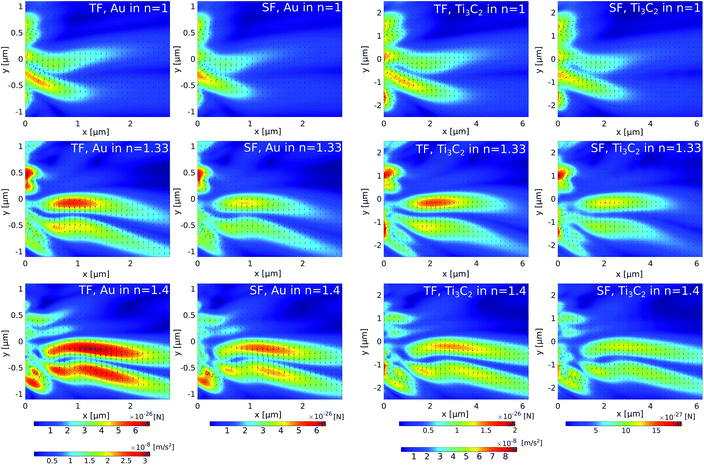
Assuming that the radius of the nanoparticle is R = 30 nm and the density ρ = 2 g cm−3 of Ti3C2,58 the optical force is presented for the case of gold and the Ti3C2 nanosphere embedded in different media in Fig. 3. The size of the nanoparticle is kept constant as changing the particle size would only change the magnitude of the optical force.
The cuboid, as illustrated in Fig. 1, is used to generate the photonic hook. It is composed of a cube with an attached wedge. The wedge provides the asymmetry required to generate the asymmetric photonic jet. For the photonic jet/hook to be generated, there needs to be a specific material contrast between the cuboid and the surrounding environment. It is known that an illuminated cuboid embedded in air34,35 creates a hook for ncuboid in air = 1.4, corresponding to fused silica. For an illuminated cuboid embedded in other media, the material needs to be adjusted in order to preserve the material contrast. Specifically, the effective refractive index of the cuboid in the medium for the cases of a cuboid embedded in water with an index of n = 1.44 is 1.862 and 2.016, respectively.
For the simulation, we built a model using commercial software Lumerical finite-difference time-domain method (FDTD). Using the scattered field formalism with an initial plane wave propagating along x and the electric field polarized along y, we obtain the photonic hook field by illuminating the cuboid. The mesh was refined along x and y to have a size of 5 nm. We define the shadow side of the cuboid at x = 0. The field data were then transferred to Matlab where a script using the central difference method was used to calculate the field derivatives needed to obtain the optical force fields.
The analysis of Fig. 3 shows that different media have a negligible effect on the maximum optical force values. Instead, it affects the shape of the optical force. Moreover, the comparison of optical forces applied on different nanoparticles shows that the magnitude of the total optical force applied on a gold nanosphere is higher than the magnitude of the total optical force applied on a Ti3C2 nanosphere. However, due to the lower density of the Ti3C2 nanoparticle, its acceleration is approximately higher by an order of magnitude. Thus, we conclude that the Ti3C2 nanosphere can be successfully used for either trapping or moving nanoparticles when the incident wavelength is in near-infrared.
However, the spherical symmetry of the nanoparticles is an idealization of the problem. In general, the particles are not spherical and different types of geometry should be considered. To highlight the differences between the gold and Ti3C2 nanoparticles, we analyse the non-spherical geometry of the nanoparticles in the following section.
5 Non-spherical particles
We assume that generating the nanojet is not related to the polarizability of the nano-particle. The outcome of the nanojet which is the optical force acting on the nanoparticle depends on the geometry of the nanoparticle and its dielectric function. Here, we consider several types of nanoparticles assuming that their polarizability which is strictly related to the optical force acting on the nanoparticle can be calculated based on Rayleigh approximation. In this section, we analyze the effect of non-spherical symmetry on the polarizability α of the studied Ti3C2 and gold nanoparticles, which in turn affects the optical force, as given by eqn (3), acting on the nanoparticle. We study the nanodisk geometry with the radius much larger compared to the height (h/r ≪ 1). Here, we calculate the nanoodisk of height 2 nm and radius of 30 nm. For the nanorod, we assume (r/h ≪ 1). Specifically, we calculate the nanorod with a radius of 2 nm and length of 30 nm.The most obvious extension of nanospheres is the ellipsoidal geometry. In this case, the polarizability depends on the direction of the electric field. The polarizability component in the direction of the i-th axis of the ellipsoid, with three orthogonal axes, is given by59
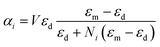 | (4) |
Assuming the semi-axes of the ellipsoid in the three orthogonal directions ax, ay and az, respectively, the depolarization factor Ni related to orthogonal directions is given by
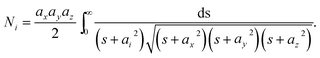 | (5) |
Due to the rotational symmetry of the sphere, spherical particles have three equal depolarization factors, i.e., 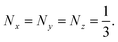
In Section 3, gold and Ti3C2 nanospheres embedded in different lossless media were analyzed. In the following section, we consider two limiting cases of ellipsoidal geometry, namely a disk, whose depolarization factors are given by (1 0 0) and a needle (0 1/2 1/2).
5.1 Nanodisk
For the case of the nanodisk, the polarizability is given by60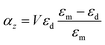 | (6a) |
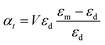 | (6b) |
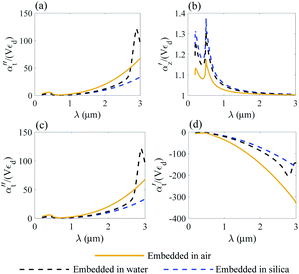 | ||
| Fig. 4 Normalized polarizability of the gold nanodisk embedded in different media. Longitudinal αz (a and b) and transverse αt (c and d) components are shown. | ||
We compare the polarizability of gold and Ti3C2 nanodisks embedded in different loss-less media. From an analysis of Fig. 4a and b, we note that for the case of gold the real and imaginary parts of αz attain their maximum values in visible. These maximum values are directly related to the interband transitions in gold. For the case of the Ti3C2 nanodisk, we note that, according to Fig. 5a and b, the maximum values of the real and imaginary parts of αz are obtained in near-infrared. Moreover, the case is much more complicated for the case of the transverse part of the nanoparticle polarizability. As can be concluded from Fig. 5c and d, it plausible to use the gold disk in near-infrared, assuming that the electric field is polarized along the transverse direction of the nanodisk.
 | ||
| Fig. 5 Normalized polarizability of the Ti3C2 nanodisk embedded in different media. Longitudinal αz (a and b) and transverse αt (c and d) components are shown. | ||
We conclude that due to the higher absolute values of the real and imaginary parts of ε of gold in near-infrared, the electric field will decay much faster from the gold nanodisk as compared to Ti3C2. Thus, the application of the Ti3C2 nanodisk is more preferable as compared to gold. Moreover, Fig. 5b shows that the real part of polarizability of the Ti3C2 nanodisk  changes its sign in a narrow spectral range. In general, the real part of polarizability is related to the gradient force which is responsible for trapping the nanoparticle. Thus, using a wideband source with a wide enough spectral range, trapping the Ti3C2 nanodisk along the z-axis can be accomplished.
changes its sign in a narrow spectral range. In general, the real part of polarizability is related to the gradient force which is responsible for trapping the nanoparticle. Thus, using a wideband source with a wide enough spectral range, trapping the Ti3C2 nanodisk along the z-axis can be accomplished.
As opposed to the nanosphere, the polarizability of either the gold or Ti3C2 nanodisk shows quite a peculiar behavior depending on the media in which these particles are embedded. Fig. 4 shows the calculated polarizability for the case of a gold nanodisk. From Fig. 4a, we note that the imaginary part of the longitudinal polarizability increases as the index of the medium increases from n = 1 (air) to n = 1.33 (water), while the real part (Fig. 4b) shows a different behavior as compared to the spherical particle. For the case of Ti3C2, both the real and the imaginary parts of the polarizability show a very different behavior when the medium changes from air to water as compared to the Ti3C2 nanosphere. This difference is associated with the geometry of the particle, while the behaviour of the spherical particle is different from that of the disk. Specifically, according to Fig. 5b, the real part of the longitudinal and transverse polarizability for the Ti3C2 nanodisk embedded in air or water is identical. This means that both air and water have the same effect on the photonic hook generation applied on titanium carbide nanoparticles.
5.2 Nanorod
For the case of a very thin nanorod, the polarizability is given as60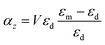 | (7a) |
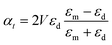 | (7b) |
We note that according to eqn (6) and (7), the longitudinal part of the dielectric polarizability of a thin nanorod is similar to the transverse part of a disk polarizability. Thus, the analysis performed in Section. 5.1 for the case of αt can be utilized in the current section.
We analyze the transverse part of dielectric polarizability αt of gold and Ti3C2 thin rods as shown in Fig. 6c, d and in Fig. 7c, d.
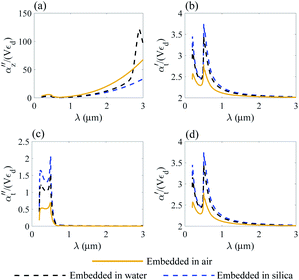 | ||
| Fig. 6 Normalized polarizability of a gold nanorod embedded in different media. Longitudinal αz (a and b) and transverse αt (c and d) components are shown. | ||
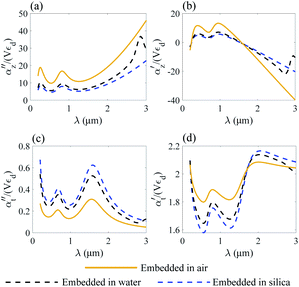 | ||
| Fig. 7 Normalized polarizability of a Ti3C2 nanorod embedded in different media. Longitudinal αz (a and b) and transverse αt (c and d) components are shown. | ||
Following the same approach as in previous section, we perform a similar analysis for the case of the transverse part of the polarizability of a thin nanorod. Thus, we conclude that the application of a Ti3C2 thin nanorod is more preferable as compared to gold. In addition, based on the results of Fig. 7d, we note that trapping of a Ti3C2 nanorod can be done using a wide enough light source.
Moreover, due to different geometry of the nanoparticle the transverse part of the Ti3C2 rod polarizability shows a different behaviour as compared to the spherical and disk geometry. Specifically, the imaginary part of the polarizability 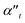 decreases as the index of the medium increases from air to water, and the real part
decreases as the index of the medium increases from air to water, and the real part 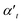 shows a more complicated behavior. Specifically, we show that at an appropriate wavelength the real part of αt is similar in all dielectric media, meaning that the media have no influence on the optical force here.
shows a more complicated behavior. Specifically, we show that at an appropriate wavelength the real part of αt is similar in all dielectric media, meaning that the media have no influence on the optical force here.
6 Summary
To summarise, we reported for the first time the effect of Photonic hook formation in near-infrared applied on MXene nanoparticles. To analyse this new effect, we explored different geometries of nanoparticles made of gold and titanium carbide for the generation of a photonic hook optical force. We showed that in comparison to plasmonic nanoparticles made of gold, experiencing LSPR in visible, the LSPR of Ti3C2 nanoparticles can be tuned to the near-infrared region. These findings are particularly important for biomedical applications for which the longer wavelengths of near-infrared radiation, as compared to visible, penetrate cells and tissues without any harmful rupture. Our findings are aimed at stimulating further research of Ti3C2 nanoparticles in the field of optomechanical manipulation in near-infrared and their applications in photonics, plasmonics, biomedical research and others.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Israel Science Foundation (2598/20). I. M. and O. M. were partially supported by the Russian Foundation for Basic Research (Grant No. 20-57-S52001) and by the Tomsk Polytechnic University Competitiveness Enhancement Program. A. K. thanks Kathleen Maleski and Yury Gogotsi for providing the dispersion data of the MXene Ti3C2.Notes and references
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS.
- J. Zhu, Y. Tang, C. Yang, F. Wang and M. Cao, J. Electrochem. Soc., 2016, 163, A785–A791 CrossRef CAS.
- J. Come, M. Naguib, P. Rozier, M. W. Barsoum, Y. Gogotsi, P.-L. Taberna, M. Morcrette and P. Simon, J. Electrochem. Soc., 2012, 159, A1368 CrossRef CAS.
- F. Wang, C. Yang, C. Duan, D. Xiao, Y. Tang and J. Zhu, J. Electrochem. Soc., 2014, 162, B16 CrossRef.
- B. Xu, M. Zhu, W. Zhang, X. Zhen, Z. Pei, Q. Xue, C. Zhi and P. Shi, Adv. Mater., 2016, 28, 3333–3339 CrossRef CAS.
- X. Yu, W. Yin, T. Wang and Y. Zhang, Langmuir, 2019, 35, 2909–2916 CrossRef CAS.
- M. Han, X. Yin, H. Wu, Z. Hou, C. Song, X. Li, L. Zhang and L. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 21011–21019 CrossRef CAS.
- K. Montazeri, M. Currie, L. Verger, P. Dianat, M. W. Barsoum and B. Nabet, Adv. Mater., 2019, 31, 1903271 CrossRef CAS.
- J. Halim, M. Lukatskaya, K. Cook, J. Lu, C. C. Smith, L.-Å. L. Näslund, S. May, L. L. Hultman, Y. Gogotsi, P. P. Eklund and M. Barsoum, Chem. Mater., 2014, 26, 2374–2381 CrossRef CAS.
- S. Kajiyama, L. Szabova, K. Sodeyama, H. Iinuma, R. Morita, K. Gotoh, Y. Tateyama, M. Okubo and A. Yamada, ACS Nano, 2016, 10, 3334–3341 CrossRef CAS.
- M. R. Lukatskaya, S. Kota, Z. Lin, M.-Q. Zhao, N. Shpigel, M. D. Levi, J. Halim, P.-L. Taberna, M. W. Barsoum, P. Simon and Y. Gogotsi, Nat. Energy, 2017, 2, 1–12 Search PubMed.
- Y. Xu, Y. S. Ang, L. Wu and L. K. Ang, Nanomaterials, 2019, 9, 165 CrossRef CAS.
- J. K. El-Demellawi, S. Lopatin, J. Yin, O. F. Mohammed and H. N. Alshareef, ACS Nano, 2018, 12, 8485–8493 CrossRef CAS.
- L. Wu, Q. You, Y. Shan, S. Gan, Y. Zhao, X. Dai and Y. Xiang, Sens. Actuators, B, 2018, 277, 210–215 CrossRef CAS.
- K. Chaudhuri, M. Alhabeb, Z. Wang, V. M. Shalaev, Y. Gogotsi and A. Boltasseva, 2017 Conference on Lasers and Electro-Optics, CLEO, 2017, p. 1 Search PubMed.
- V. Mauchamp, M. Bugnet, E. P. Bellido, G. A. Botton, P. Moreau, D. Magne, M. Naguib, T. Cabioc'h and M. W. Barsoum, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235428 CrossRef.
- Z. Jakšić, M. Obradov, O. Jakšić, D. Tanasković and D. V. Radović, 2019 IEEE 31st International Conference on Microelectronics, MIEL, 2019, pp. 91–94 Search PubMed.
- Z. Jakšić, M. Obradov, D. Tanasković, O. Jakšić and D. V. Radović, Opt. Quantum Electron., 2020, 52, 83 CrossRef.
- L. Wu, Q. You, Y. Shan, S. Gan, Y. Zhao, X. Dai and Y. Xiang, Sens. Actuators, B, 2018, 277, 210–215 CrossRef CAS.
- V. R. Sudheer, S. R. S. Kumar and S. Sankararaman, Plasmonics, 2020, 15, 457–466 CrossRef CAS.
- X. Yu, T. Wang, W. Yin and Y. Zhang, Int. J. Hydrogen Energy, 2019, 44, 2704–2710 CrossRef CAS.
- H. Yu, Y. Peng, Y. Yang and Z.-Y. Li, npj Comput. Mater., 2019, 5, 1–14 CrossRef.
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156–159 CrossRef CAS.
- J. Prikulis, F. Svedberg, M. Käll, J. Enger, K. Ramser, M. Goksör and D. Hanstorp, Nano Lett., 2004, 4, 115–118 CrossRef CAS.
- M. Righini, A. S. Zelenina, C. Girard and R. Quidant, Nat. Phys., 2007, 3, 477–480 Search PubMed.
- F. Svedberg, Z. Li, H. Xu and M. Käll, Nano Lett., 2006, 6, 2639–2641 CrossRef CAS.
- A. N. Grigorenko, N. W. Roberts, M. R. Dickinson and Y. Zhang, Nat. Photonics, 2008, 2, 365–370 CrossRef CAS.
- B. S. Luk'yanchuk, R. Paniagua-Domínguez, I. V. Minin, O. V. Minin and Z. Wang, Opt. Mater. Express, 2017, 7, 1820 CrossRef.
- A. Kovrov, A. Novitsky, A. Karabchevsky and A. S. Shalin, Ann. Phys., 2018, 530, 1800129 CrossRef.
- Y.-C. Li, H.-B. Xin, H.-X. Lei, L.-L. Liu, Y.-Z. Li, Y. Zhang and B.-J. Li, Light: Sci. Appl., 2016, 5, e16176 CrossRef CAS.
- H. Wang, X. Wu and D. Shen, Opt. Lett., 2016, 41, 1652–1655 CrossRef.
- X. Cui, D. Erni and C. Hafner, Opt. Express, 2008, 16, 13560–13568 CrossRef CAS.
- I. V. Minin and O. V. Minin, Diffractive Optics and Nanophotonics, Springer International Publishing, Cham, 2016 Search PubMed.
- A. S. Ang, A. Karabchevsky, I. V. Minin, O. V. Minin, S. V. Sukhov and A. S. Shalin, Sci. Rep., 2018, 8, 2029 CrossRef.
- M. Spector, A. Ang, O. Minin, I. Minin and A. Karabchevsky, Nanoscale Adv., 2020, 2, 2595–2601 RSC.
- A. Karabchevsky, O. Krasnykov, M. Auslender, B. Hadad, A. Goldner and I. Abdulhalim, Plasmonics, 2009, 4, 281 CrossRef CAS.
- A. Karabchevsky, O. Krasnykov, I. Abdulhalim, B. Hadad, A. Goldner, M. Auslender and S. Hava, Photonics and Nanostructures: Fundamentals and Applications, 2009, 7, 170–175 CrossRef.
- A. Karabchevsky, S. Karabchevsky and I. Abdulhalim, Sens. Actuators, B, 2011, 155, 361–365 CrossRef CAS.
- A. Karabchevsky, S. Karabchevsky and I. Abdulhalim, J. Nanophotonics, 2011, 5, 051813 CrossRef.
- A. Karabchevsky, I. Abdulhalim, C. Khare and B. Rauschenbach, J. Nanophotonics, 2012, 6, 061508 CrossRef.
- A. Karabchevsky, L. Tsapovsky, R. S. Marks and I. Abdulhalim, Biosensors, 2013, 3, 157–170 CrossRef CAS.
- A. Karabchevsky, J. S. Wilkinson and M. N. Zervas, Opt. Express, 2015, 23, 14407–14423 CrossRef CAS.
- A. Karabchevsky, A. Mosayyebi and A. V. Kavokin, Light: Sci. Appl., 2016, 5, e16164 CrossRef CAS.
- J. Pitarke, V. Silkin, E. Chulkov and P. Echenique, Rep. Prog. Phys., 2006, 70, 1 CrossRef.
- T. Stoll, P. Maioli, A. Crut, N. D. Fatti, C. Voisin and F. Vallee, Eur. Phys. J. B, 2014, 87, 260–279 CrossRef.
- K. Chaudhuri, M. Alhabeb, Z. Wang, V. M. Shalaev, Y. Gogotsi and A. Boltasseva, ACS Photonics, 2018, 5, 1115–1122 CrossRef CAS.
- D. R. Dadadzhanov, T. A. Vartanyan, P. S. Parfenov, M. A. Baranov and A. Karabchevsky, 2019, arXiv preprint arXiv:1904.06462.
- G. F. Bohren and D. Huffman, Absorption and scattering of light by small nanoparticles, Wiley, New York, 1st edn, 1983 Search PubMed.
- S. Maier, Plasmonics: Fundamentals and Applications, Springer-Science, 2nd edn, 2007 Search PubMed.
- P. Winsemius, M. Guerrisi and R. Rosei, Phys. Rev. B: Solid State, 1975, 12, 4570–4572 CrossRef CAS.
- M. Spector, A. S. Ang, O. V. Minin, I. V. Minin and A. Karabchevsky, Nanoscale Adv., 2020, 2, 2595–2601 RSC.
- Y. Ul Haq, I. Murtaza, S. Mazhar, N. Ahmad, A. A. Qarni, Z. Ul Haq, S. A. Khan and M. Iqbal, J. Appl. Polym. Sci., 2020, 137, 49197 CrossRef CAS.
- G. Baffou, F. Cichos and R. Quidant, Nat. Mater., 2020, 1–13 Search PubMed.
- B. T. Draine, Astrophys. J., 1988, 333, 848–872 CrossRef CAS.
- G. M. Hale and M. R. Querry, Appl. Opt., 1973, 12, 555–563 CrossRef CAS.
- I. Malitson, J. Opt. Soc. Am., 1965, 55, 1205–1208 CrossRef CAS.
- L. Novotny and B. Hecht, Principles of nano optics, 2006 Search PubMed.
- E. S. Muckley, M. Naguib and I. N. I. Orcid, J. Nanosci. Nanotechnol., 2018, 10, 21689–21695 CAS.
- J. D. Jackson, Classical electrodynamics, Wiley & Sons, 3rd edn, 1998 Search PubMed.
- J. Venermo and A. Sihvola, J. Electrost., 2005, 63, 101–117 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00485e |
| This journal is © The Royal Society of Chemistry 2020 |