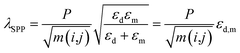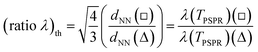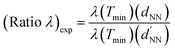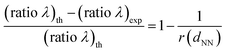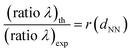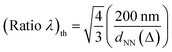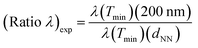Open Access Article
Open Access ArticleShort-range ordered 2D nanoholes: lattice-model and novel insight into the impact of coordination geometry and packing on their propagating-mode transmittance features
Maura
Cesaria†
 ,
Antonietta
Taurino
,
Antonietta
Taurino
 *,
Maria Grazia
Manera
*,
Maria Grazia
Manera
 and
Roberto
Rella
and
Roberto
Rella

IMM-CNR Lecce, Institute for Microelectronics and Microsystems, Campus Ecotekne, prov. le per Monteroni, 73100 Lecce, Italy. E-mail: antonietta.taurino@le.imm.cnr.it
First published on 16th July 2020
Abstract
Optically thin perforated gold films, fabricated using template colloidal masks self-assembled by following an elsewhere described simplified colloidal lithography protocol, are presented and discussed with the aim to develop a theory of short-range ordered nanoholes without straightforwardly extending concepts strictly related to periodic nanoholes. By Scanning Electron Microscopy (SEM) analysis of the evolution of nanohole short-range ordering and spatial coordination geometry under increasing interhole average spacing (dNN), unprecedented differences in the spectroscopic response are pointed out with respect to periodic systems. First, the dependence of the wavelength of a propagating plasmon mode on dNN is demonstrated to deviate from the linear relationship predicted by the grating-coupling picture developed for periodic arrays. Second, dNN cannot be straightforwardly interpreted as the counterpart of the lattice constant of periodic nanoholes, which demands to introduce a conceptually more rigorous periodicity-like length-scale. Once the impact of these findings on setting the operating parameters of a nanohole distribution is demonstrated, they are related, experimentally and by using a theoretical model developed by the authors, to the changes of the local coordination geometry (from quasi-hexagonal to quasi-square packing through mixed hexagonal–square coordination) induced by varying dNN over a wide interval. Autocorrelation analysis of SEM images is exploited to estimate a short-range periodicity-like length-scale, as a conceptual advance for laying the foundation of the concept of short-range ordered nanohole lattices and for deeper insight into the spectral response. As discussion is based on realistic, rather than simulated, evolution of colloidal arrangements, the formulated interpretative model accounts for realistic effects impacting transmission resonances.
1. Introduction
Resonantly enhanced light transmission, leading to extraordinary optical transmission (EOT) phenomena, is a fascinating property exhibited by periodic arrays of sub-wavelength holes, periodically milled in an optically thick (>100 nm) metal film.1,2 Since the seminal report on EOT,1 metal nanohole (NH) distributions have attracted worldwide interest for several applications: for instance, plasmonic solar cells and photodetectors,3 plasmonic color-filter devices,4,5 surface enhanced Raman scattering,6 surface enhanced fluorescence spectroscopy,7,8 monitoring of surface-binding events in chemical and biochemical sensing,9–11 preferably by microfluidic-chip based detection due to the benefits of a simple optical set-up, dense integration of sensors, multiplexing for parallel and selective analyte sampling in miniaturized and high throughput sensors.12,13From the fundamental standpoint, resonant transmission phenomena were first ascribed to coupling between free-space photons and Bloch-wave surface plasmon polaritons mediated by diffractive hole grating (grating-coupling model).14,15 In this picture, quasi-momentum and energy matching conditions determine the spectral position of transmission peaks depending on structural parameters (lattice geometry and periodicity), the choice of metal and dielectric environment, Bragg integer diffraction orders, the incidence angle and polarization of the excitation radiation.14,16 Further theoretical and experimental studies pointed out that the theoretical relationship predicting the spectral position of transmission resonances in the grating-coupling picture was not fulfilled in that, (i) transmission peaks are red-shifted with respect to the theoretical prediction due to hole-related scattering mechanisms,14,16–18 and (ii) transmission minima rather than maxima may be associated with propagating plasmon modes in optically thin films (<50 nm).19–21 Optically thin semi-transparent perforated metal films differ from their optically thick (>100 nm) opaque counterparts in that the propagating plasmon modes generated on both sides of the film are strongly coupled22,23 as well as transmission peaks or dips form depending on the interference between the direct reflection and transmission through the holes (incoherent path) and the radiation coupled to propagating surface plasmon polariton-modes.24,25
Interestingly, transmission peaks and dips were also found to occur in the absence of translational symmetry in quasi-periodic26,27 and short range-ordered21,28 hole arrays and to be absent in completely disordered NH distributions.29 Therefore, even if periodicity is not a crucial requirement, metal NH array distributions with positional correlation between nearest neighbors are in principle demanding to observe resonantly enhanced light transmission associated with propagating surface plasmon resonance (PSPR) modes excited along the surface of a perforated metal film and localized surface plasmon resonance (LSPR) modes with field enhancement at the edges and along the depth of the hole. In practice, nanofabrication approaches leading to short-range ordered NH arrangements are becoming an attractive low cost alternative to conventional lithography.9,30–32 Indeed, while mainly electron-beam lithography (EBL)33 and focused-ion beam (FIB) lithography34 enable manufacturing of periodic metal NH arrays with repeatability and controlled size, shape and relative positioning, they present important practical disadvantages. For instance, specialized equipment, costly procedures, and multi-step and time-consuming processing greatly limit their application for large-area (larger than a few μm2) patterning and mass production of NH lattices. Differently, short-range ordered NH distributions self-assembled by colloidal lithography are not as sensitive as periodic arrays to fabrication imperfections and can be produced massively over a large area. Also, the working principle of colloidal lithography is very simple: it relies on electrostatically driven adsorption and self-assembly of likely charged polymer colloids onto a counter-charged collector surface.35
From the fundamental standpoint, the practical convenience in fabricating short-range ordered metal NH distributions has raised questions about eventual analogies with periodic distributions in regard to spectral properties26,28,36–38 as well as the mechanisms leading to resonant transmission in the absence of long-range order.21,28,39 These studies assumed, straightforwardly and in principle, the average center-to-center distance of nearest neighbor short-range ordered NHs as the counterpart of the periodicity parameter (i.e., the lattice constant) of NH lattices.21,39 Under this assumption, since in the canonical grating-coupling picture a transmittance feature associated with a PSPR mode linearly blue-shifts for increasing lattice constant,9 the same behaviour should be expected in the case of a short-range ordered metal NH distribution versus changes of the NH-to-NH spacing. Comparative studies between ordered and short-range ordered NH systems pointed out deviations in the prediction of the resonances in the presence of short-range ordering21 and evidenced a not completely linear trend in line with the theoretical expectations of periodic NH systems.39
Recent studies on short-range ordered NH distributions40 demonstrated a general linear dependence of the spectral position of a PSPR mode on the center-to-center distance of nearest neighbour NHs, here termed dNN, varied over the 110–178 nm range. Notably, the occurrence of a slight deviation of a few data with respect to the linear trend was observed.
The aim of this paper is to extend this early study in order to clarify/unravel this point and more deeply investigate the impact of short-range ordering on the transmittance response of NH systems. Herein, short-range ordered gold NH systems, fabricated by following a simplified colloidal lithography protocol described in detail elsewhere40 and termed hereafter MNL-CL (where MNL and CL stand for monolayer and colloidal lithography, respectively), are presented. Based on these systems, the evolution of the spectral position of the transmission feature associated with a PSPR mode versus dNN ranging over a wider interval (i.e., from 110 to 203 nm) than the previously investigated one is discussed. Since transition from short-time to long-time colloid adsorption was exploited to increase the fractional coverage, the developed analysis allows a correlation between the optical response of the metal NH array and the temporal evolution of the colloid arrangement, dictated by the interplay between the active interactions, which characterizes the degree of ordering. Hence, a realistic physical insight into the mechanisms (interplay between electrostatic interparticle, colloid–collector surface interactions and capillary forces) which impact the level of positional correlated ordering during colloid self-assembly is provided.
Noteworthily, it is demonstrated that, while the spectral position of a PSPR mode doesn't vary linearly versus dNN over the entire sampled range, the linear trend is recovered over narrower contiguous ranges of dNN which correspond to distributions with different local coordination numbers of the NHs (transition of the order from locally quasi-hexagonal to locally quasi-square packing). In this respect, a conceptual interpretative model is also developed and discussed which is able to relate the observed dependence of the wavelength of a PSPR mode on dNN to the local geometry (transition from quasi-hexagonal to quasi-cubic) of NH arrangements.
The presented discussion enables to introduce the concept of a short-range ordered NH lattice, to characterize it and to rigorously assess differences with respect to periodic systems without straightforward application of the knowledge available for periodic NH arrays. For instance, we demonstrate that the interparticle distance evaluated by statistical analysis is not the counterpart of the lattice constant of periodic NH arrays.
To the best of our knowledge, results and discussion presented in this manuscript are not reported in the literature.
2. Experimental
2.1 Fabrication methods and conditions
The colloidal lithography technique was implemented for fabricating short range ordered NH distributions onto glass substrates according to the experimental procedure detailed elsewhere40 and sketched in Fig. 1. Following cleaning of microscope glass slides by ultra-sonication in acetone (Sigma Aldrich) at 60 °C for 20 minutes and isopropylic alcohol (Sigma Aldrich) at 60 °C for 20 minutes, the substrates were carefully dried by N2-blowing and their surface was made negatively charged by an oxygen-plasma treatment (100 sccm, 50 Watt, 250 mTorr, and 1 min process time). Then, a positively charged monolayer of polydiallyldimethylammonium (PDDA) (MW 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–350
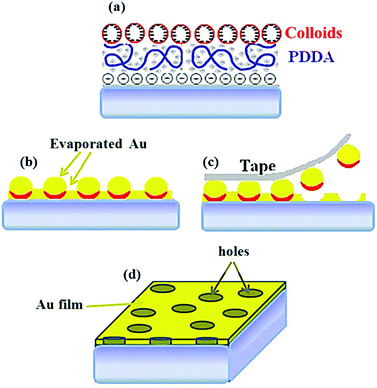
000–350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma Aldrich) polyelectrolyte was adsorbed onto the oxidized substrate from an aqueous solution (0.2 wt% in Milli-Q water) for an adsorption time ΔtPDDA ranging from 40 s to 2 min. Careful rinsing of the PDDA surface under a deionized water flow and N2 blow-drying were applied before depositing the colloidal distribution. In this respect, negatively charged commercial polystyrene nanospheres (Thermo Fisher Scientific), with diameter DPS = (80 ± 4) nm, were adsorbed onto the PDDA counter-charged layer from a salt-free aqueous solution (0.1% wt) for an adsorption time ΔtPS lasting from 25 s to 10 min. The obtained colloidal distributions were immersed for 1 minute in distilled water, previously heated up to 100 °C, and subsequently carefully N2 blow-dried.35 The colloidal distributions resulting from the above protocol (Fig. 1(a)) were covered by a thermally evaporated (20 ± 2) nm thick gold (Au) film (Fig. 1(b)). Then, the removal of the Au-capped colloids by tape stripping (Fig. 1(c)) resulted in a perforated optically thin Au film onto a glass substrate (Fig. 1(d)). Since tape stripping leaves NHs in the same positions as the polystyrene beads, the NH arrangement is dictated by the associated precursor colloidal mask. Based on several experiments devoted to exploiting the interplay between the chosen adsorption times ΔtPDDA and ΔtPS, dNN was varied from 110 to 203 nm.
000, Sigma Aldrich) polyelectrolyte was adsorbed onto the oxidized substrate from an aqueous solution (0.2 wt% in Milli-Q water) for an adsorption time ΔtPDDA ranging from 40 s to 2 min. Careful rinsing of the PDDA surface under a deionized water flow and N2 blow-drying were applied before depositing the colloidal distribution. In this respect, negatively charged commercial polystyrene nanospheres (Thermo Fisher Scientific), with diameter DPS = (80 ± 4) nm, were adsorbed onto the PDDA counter-charged layer from a salt-free aqueous solution (0.1% wt) for an adsorption time ΔtPS lasting from 25 s to 10 min. The obtained colloidal distributions were immersed for 1 minute in distilled water, previously heated up to 100 °C, and subsequently carefully N2 blow-dried.35 The colloidal distributions resulting from the above protocol (Fig. 1(a)) were covered by a thermally evaporated (20 ± 2) nm thick gold (Au) film (Fig. 1(b)). Then, the removal of the Au-capped colloids by tape stripping (Fig. 1(c)) resulted in a perforated optically thin Au film onto a glass substrate (Fig. 1(d)). Since tape stripping leaves NHs in the same positions as the polystyrene beads, the NH arrangement is dictated by the associated precursor colloidal mask. Based on several experiments devoted to exploiting the interplay between the chosen adsorption times ΔtPDDA and ΔtPS, dNN was varied from 110 to 203 nm.
2.2 Morphological and ordering characterization
Scanning electron microscopy (SEM) was applied to image and characterize the fabricated distributions of Au-capped polystyrene nanospheres, which consequently provide information about the arrangement of the associated NH distributions. A Zeiss NVISION 40 dual beam Focused Ion Beam (FIB) system, equipped with a high resolution SEM Gemini column and an Oxford 350 x-act Energy Dispersive X-ray Spectrometer (EDS), was used for acquiring SEM images that were processed by using Digital Micrograph software.41 Based on statistical analysis of the SEM images, the quantity dNN (i.e., the average center-to-center distance between nearest neighbor polystyrene nanospheres) and the corresponding fractional coverage were evaluated. The latter quantity was quoted with an uncertainty amounting to nearly 6%. Statistical histograms of the nearest neighbor distance were obtained for each nanosphere arrangement (area 5.4 μm2) under study, hence giving information about the distribution of the shortest nanosphere-to-nanosphere distance and, in particular, about the impact of capillary-induced agglomeration and nanosphere coordination on dNN. Furthermore, autocorrelation (Autocor) and Fast Fourier Transform (FFT) image processing tools were applied to analyze SEM images according to the purposes and guidelines applied by the authors for the first time to SEM images of short-range ordered colloidal distributions in a recent study.402.3 Spectral characterization analysis
The zero-order transmission spectra of the fabricated NH samples were recorded by using a Cary 500 UV-VIS-NIR Spectrometer (Varian, USA) in air at room temperature under white light incident perpendicularly on the surface of the Au NH films. All transmission spectra were acquired in the spectral range from 400 to 1000 nm with a spectral resolution Δλ = 1 nm and normalized to the transmission spectrum of a bare cleaned glass substrate.3. Results and discussion
3.1 Preliminary remarks: motivation and aim of the study
Detailed discussion about the applicability, repeatability and peculiarity of the MNL-CL protocol developed by the authors is reported elsewhere.40 To briefly summarize the main points of the experimental protocol under consideration, it is worth remarking that:(i) It uses a polyelectrolyte monolayer rather than the uppermost surface of a polyelectrolyte multi-layer, as commonly reported in the literature, to electrostatically bind colloids,
(ii) The chosen concentration of the salt-free PDDA solution guarantees flat configuration of the adsorbed chains,
(iii) dNN is varied by the interplay between the adsorption time of PDDA (ΔtPDDA), which affects the adsorption efficiency of the PDDA surface, and the adsorption time of polystyrene colloids (ΔtPS), which is tuned from short- to long-time adsorption,40
(iv) Salt-free colloidal suspensions are considered to limit detrimental effects such as clustering stemming from weakened inter-particle Coulomb repulsion and lateral capillary forces.40
Prior to presenting and discussing the results of interest for the present paper, a summary of the main conclusions concerning the spectral response of the short-range ordered NH distributions fabricated by following the MNL-CL protocol to put forward the raised fundamental questions that motivate an extended study is demanded.
(i) Unshielded rather than shielded inter-colloidal electrostatic repulsion was demonstrated to be effective to obtain short-range-ordered and well-separated NHs with controllable and tunable coverage for dNN varying from 110 to 178 nm, meaning, unlike saturated coverage commonly reported in the literature, by exploiting unsaturated adsorption conditions too.40 While resonant transmission features were observed over the whole investigated coverage range as a signature of short-range ordering, an eventual impact of correlated disorder in terms of geometry of the spatial correlation at intermediate coverage, before saturation, was not investigated and is still missing information in the literature.
(ii) Angle-resolved transmission spectra demonstrated the occurrence of a transmission peak unaffected by the incidence angle and an angle-dependent transmission dip, blue-shifting when going from normal incidence to 50°. Such a transmittance peak and dip were consequently assigned to a localized and propagating plasmon mode, respectively.40 On the basis of this assignment, the relationship between the wavelength of the propagating plasmon mode (PSPR) and dNN was discussed,40 in analogy with a periodic NH array for which a linear dependence of the PSPR wavelength on the lattice constant is theoretically predicted. In our study, a linear trend was generally confirmed, but slight deviations of a few data were observed.40
(iii) In regard to the observed deviations from a clearly linear trend of the dependence of the wavelength of the PSPR mode on dNN, agglomeration effects on the occurrence of two linear trends of unclear origin over contiguous intervals of values of dNN were hypothesized. This point would contrast with the common assumption that dNN is a universal length-scale of both periodic and short-range ordered NH systems21,39 and deserves further physical insight.
Going forward, in this paper we focus on the following main aims. First, a systematic investigation of SEM micrographs of the deposited colloidal distributions is performed to individuate any relationship between the geometry of the local coordination and ordering under changes of the fractional coverage, dictated by inter-particle interactions. While going from low to saturated coverage, the distribution of the adsorbed polystyrene nanospheres deposited by colloidal lithography is expected to change from weakly correlated arrangements of colloids, with empty spaces in between them, to electrostatically stabilized configurations with a better defined short-range geometric arrangement (e.g. triangular lattice or hexagonal coordination) and less dispersed neighboring particle distance.42
According to this picture, detailed analysis of the evolution of the colloidal arrangements under conditions of progressively increasing coverage may allow mapping their ordering formation process and individuate eventual lattice-like short-range ordered patterns. In this perspective, we studied the ordering/disordering properties of real colloidal masks rather than artificially generating disorder by random displacement of colloids. This approach allows us to realistically picture the ordering formation process depending on the active interactions and, importantly, by including the impact of lateral capillary forces on the colloidal distribution while increasing its coverage.
Second, in this study a deeper investigation of the slight deviation from the linearity of the wavelength of a PSPR mode versus dNN envisaged in a previous study is presented.40
According to the above purposes, short-range ordered NH arrangements were fabricated based on a previously experimentally validated MNL-CL protocol,40 by extending the range of values of dNN from 110–178 nm (ref. 40) to 110–203 nm. Throughout the paper the fabricated distributions of Au-capped polystyrene nanospheres will be named PS(dNN), and the associated NH sample will be straightforwardly referred to as NH(dNN).
Gold thin films are considered for two main reasons. First, deviations from the proposed theories were reported in the case of optically thin films due to not-vanishing direct transmission.24,25 Second, more localized field distribution of the bonding plasmon mode22,43 is expected to provide a spectral response less affected by loss mechanisms (absorption from the metal and scattering by the hole apertures) impacting the propagation length of propagating plasmon modes. Hence, thin films are a favourable condition to yield more general discussion of the inherent correlation between the arrangement and spectral properties of short-range ordered NH systems. From the applicative standpoint, optically thin perforated metal slabs exhibit appealing sensing behaviour of LSPR modes21 and more homogeneous and strong field enhancement inside the NH region for NH diameters around 50–70 nm.44 All of this motivated the choice of colloids with a diameter of 80 nm, leading to a smaller NH diameter of about 60 nm, due to shadow effects during Au evaporation.
3.2 Ordering and coordination analysis
Fig. 2–4 show typical SEM micrographs (left column panels) of colloidal distributions with gradually decreasing coverage, as demonstrated by the relevant values of dNN, ranging from 110 to 203 nm, derived from the statistical analyses of SEM micrographs. The distributions of the nearest inter-particle spacing are reported in the histogram of the right column panels. As overviewed in the experimental and method sections, coverage was varied by means of the interplay between the adsorption times ΔtPDDA and ΔtPS according to the principle that increasing coverage is favored by improved binding efficiency of the PDDA collector surface (i.e., ΔtPDDA > 40 s) and ΔtPS approaching the saturated adsorption.40 In practice, for a given ΔtPDDA, the simplest way to tune dNN is to interrupt the adsorption process at progressively increasing values of ΔtPS before achieving the saturation coverage.Fig. 2(a)–(c) show the arrangement of colloidal masks with dNN given as (110 ± 22) nm, (128 ± 21) nm and (141 ± 31) nm. The associated values of fractional coverage were estimated to be (26 ± 2)% for PS(110 nm), (22 ± 1)% for PS(128 nm) and (18 ± 1)% for PS(141 nm). The sparse agglomeration occurring in the case of PS(110 nm) can be ascribed to the impact of lateral capillary forces during drying favored by the high coverage of the sample under consideration. Consistently, for increasing dNN, more homogeneous arrangement with better separated units and smaller clusters was obtained.
 | ||
| Fig. 2 (a–c) SEM micrographs of the samples PS(110 nm), PS(128 nm) and PS(141 nm) and (d–f) associated histogram distributions of the nearest inter-particle spacing. | ||
The histograms in Fig. 2(d)–(f) clearly indicate the presence in this first group of colloidal distributions of agglomerated units (nearest neighbor distance < 100 nm). At the shortest dNN (i.e., PS(110 nm)), a bimodal distribution is evident, with a family of colloids, whose nearest neighbor distance varies between 50 nm (overlapped colloids) and 100 nm (nearly touching colloids), representing about 28% of the entire distribution. For increasing dNN (i.e., PS(128 nm)), the distribution proceeds through a three-modal distribution, where the family with the shortest nearest neighbor distance is emptying, whereas two families form with larger nearest neighbor distances, peaked at about 117 nm and 146 nm, respectively. Finally, in the case of PS(141 nm), a bimodal distribution is recovered, with the shortest nearest neighbor distance family representing about 20% of the entire distribution and the largest family peaked at about 153 nm.
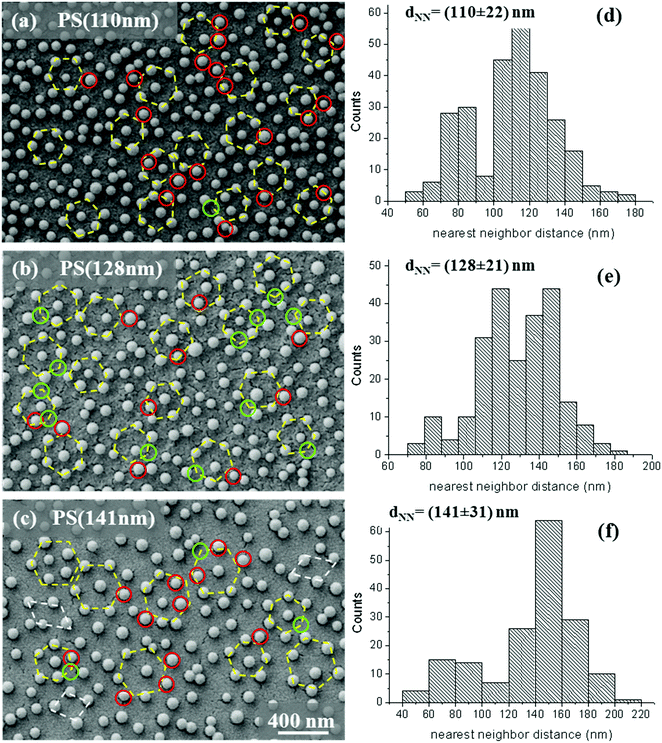
Fig. 3(a)–(c) show colloidal masks with dNN values of (156 ± 32) nm, (161 ± 32) nm, and (178 ± 30) nm. The associated values of fractional coverage were estimated to be (15.3 ± 0.9)% for PS(156 nm), (13.7 ± 0.8)% for PS(161 nm), and (10.6 ± 0.6)% for PS(178 nm). In this case, a few agglomerates are evident in the left tail of the histogram distributions (Fig. 3(d)–(f)), with overlapping phenomena disappearing for dNN larger than 161 nm.
 | ||
| Fig. 3 (a–c) SEM micrographs of the samples PS(156 nm), PS(161 nm) and PS(178 nm) and (d–f) associated histogram distributions of the nearest inter-particle spacing. | ||
Well isolated polystyrene nanospheres are observable starting from dNN ∼ 178 nm, with few units of nearly touching but not overlapping colloids.
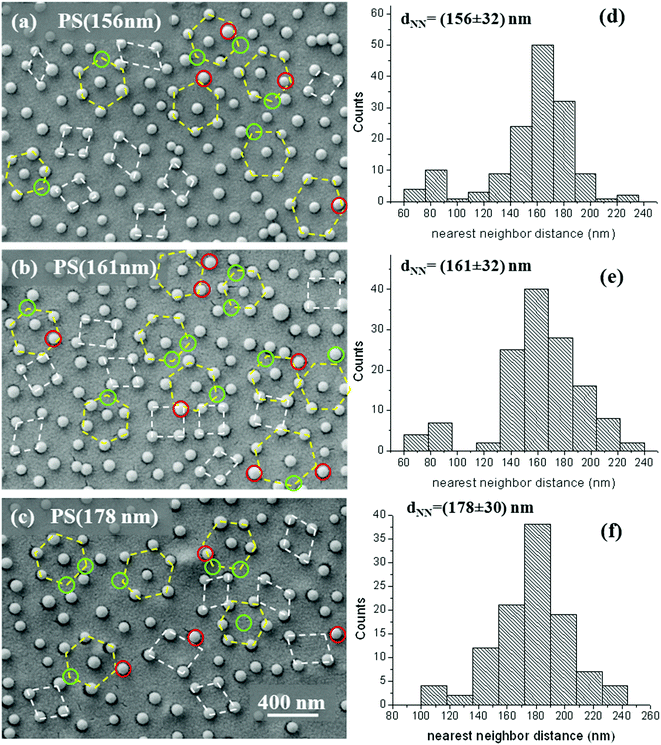
Fig. 4(a)–(d) show colloidal distributions with values of dNN given as (187 ± 31) nm, (192 ± 31) nm, (200 ± 31) nm and (203 ± 31) nm, associated with the fractional coverage values of (10.8 ± 0.6)% for PS(187 nm), (9.1 ± 0.5)% for PS(192 nm), (10.2 ± 0.6)% for PS(200 nm) and (8.2 ± 0.5)% for PS(203 nm). In these cases the distributions are monomodal (Fig. 4(e)–(h)), with a long right tail, extending up to 280–300 nm, related to the formation of voids. For increasing inter-particle spacing, the formation of void zones in between colloids is expected in not electrostatically stabilized colloidal arrangements due to short-time adsorption conditions.
 | ||
| Fig. 4 (a–d) SEM micrographs of the samples PS(187 nm). PS(192 nm), PS(200 nm) and PS(203 nm) and (e–h) associated histogram distributions of the nearest inter-particle spacing. | ||
Definitively, well-separated polystyrene nanospheres with correlated positional disorder and minimal influence of capillarity induced clustering as well as controllable and tunable coverage even at relatively closely spaced NHs (coverage up to ∼27%) have been demonstrated.
A careful analysis of SEM micrographs also allowed inspecting any change of the local-order coordination and degree of positional correlated disorder at increasing dNN. In particular, the eventual occurrence of six-nearest-neighbor coordination (triangular-like lattice) and/or four-nearest-neighbor coordination (square-like lattice) was closely inspected and it was possible to distinguish colloids organized according to a hexagonal geometry (as indicated by the dashed yellow hexagons drawn in the SEM images) and colloids which tend to be placed at the vertices of a four edge polygon (as indicated by the dashed white irregular parallelograms drawn in the SEM images). Of course, defects can be observed, such as displaced colloids (highlighted by red circles) and missing colloids (highlighted by green circles).
It is worth noticing that the samples with the shortest dNN (i.e., PS(110 nm) and PS(128 nm) in Fig. 2(a) and (b), respectively) mainly present short-range ordering with six nearest-neighbor coordination (hexagonal arrangements). In the sample PS(141 nm) (Fig. 2(c)), sparse square coordination appears, mixed with the predominant six nearest-neighbor coordination. For increasing dNN (Fig. 3(a)–(c) and 4(a)–(c)), the presence of local hexagonal arrangements progressively decreases, being replaced by local square-like coordination, which gradually becomes predominant. For the largest dNN (i.e., PS(203 nm) in Fig. 4(d)), the colloids are almost totally square-coordinated. Therefore, despite the presence of large voids and largely spaced colloids, indicative of increased disorder, the observed recurring four-nearest-neighbor coordination demonstrates local ordering even under conditions of not electrostatically stabilized arrangements.
A further remark is worth mentioning in regard to the quality of the evaporated Au film, which degrades at high coverage, exhibiting the presence of nanocracks (Fig. 2). Indeed, the high density of colloids represents a surface discontinuity in terms of topography and chemistry which affects the surface migration of the Au species during the evaporation of the Au film. With respect to using the colloidal masks as a template for the fabrication of NH arrays (Fig. 1), since the nanocracks of the Au films are much smaller than the NHs, they may have a poor scattering impact for the wavelength range sampled in the transmittance spectra of our samples (400–1000 nm). Instead, scattering effects affecting the PSPR mode may stem from NH clusters.
In order to assess more quantitatively the occurrence of short-range ordering even under the conditions of minimum coverage, Fast Fourier Transform (FFT) and autocorrelation processing of SEM images of PS(203 nm) were performed, according to the procedure established and applied for the first time by the authors to SEM images of short-range ordered colloidal distributions in a recent study.40 Notably, since the intercolloid center-to-center distance exactly corresponds to the interhole center-to-center distance (i.e., a NH distribution exactly corresponds to the arrangement of the precursor colloidal mask, according to the fabrication protocol), statistical image processing of SEM analysis may be performed on colloidal masks as well as on NH distributions without any loss of information and restrictions.
Fig. 5(a) shows the SEM micrograph of the colloidal distribution under consideration, along with the area (pointed out by a red square) considered for calculating the autocorrelation image (briefly termed “Autocor” and reported in Fig. 5(b)) and the FFT of the autocorrelation image (briefly termed “FFT(Autocor)” and reported in Fig. 5(c)).
The autocorrelation pattern presents a bright peak of correlation in the middle (corresponding to no shift of the image) and a background without evident periodicities, which suggests the absence of long range-ordering. Nevertheless, FFT(Autocor) evidences two intensity maxima, represented by two small arcs symmetrically placed around the center (highlighted by two arrows), which demonstrates short-range periodicity, associated with a spatial frequency of about (190 ± 5) nm, which is consistent with dNN = (203 ± 31) nm within the experimental uncertainty.
Definitively, the observed trend of disordering with decreasing coverage is indicative of and consistent with deviations from the electrostatically stabilized configurations. Despite the decreasing degree of short-range ordering, short-range spatial correlation was demonstrated for different coverage conditions resulting from the net interparticle interaction (including electrostatic and lateral capillary forces). Noteworthily, situations with dNN > 203 nm were not considered in experiments because the evidence that PS(200 nm) and PS(203 nm) exhibit equivalent distributions indicates that dNN > 203 nm would correspond to colloid adsorption and arrangement mainly dictated by attractive colloid–collector surface interaction rather than by interparticle repulsion. In this situation, decreasing the fractional coverage couldn't be a strategy to induce a specific coordination and/or tune the degree of ordering. Therefore, the range of values of dNN sampled in our experiments (from 110 nm to 203 nm) is the effective one to comprehensively study the impact of the correlated disorder on the spectral response of short-range ordered NH arrangements when an NH diameter is 60 nm.
3.3 Spectral characterization
On the basis of the working principle of colloidal lithography, it is known that the relative positioning of colloids evolves towards a hexagonal electrostatically stabilized coordination when going from low to high coverage.42However, in the absence of visual characterization of the colloidal distribution (allowed by SEM analysis, for instance), it is not possible to argue how the geometrical coordination evolves as a function of dNN. All of this impacts the knowledge of the relationship between the short-range ordering and spectral response of short-range ordered NH distributions.
Noteworthily, although the occurrence of locally hexagonal and locally square lattice geometry was reported while modeling the electrostatically driven formation mechanism of colloidal distributions,42 to the best of our knowledge, the impact of geometry transition and mixed-geometry on the spectral response of metal NHs has not been yet investigated. This issue is the focus of the following discussion. It is worth noting that, in comparison with the preliminary results reported in our recent publication,40 herein the spectral analyses were carried out on a wider wavelength range (going from 400 nm to 1000 nm instead of 400 nm to 800 nm) and over an extended set of dNN values, representing the comparison parameter between the spectra.
Following the SEM characterization of the fabricated colloidal masks, we turn to the discussion of the zero-order transmittance spectra of the associated gold NH samples reported in Fig. 6, which presents an extended set of data with respect to our recent publication.40 Over the acquisition wavelength range the following can be observed in all cases: (i) a transmission peak narrower and shifted with respect to the transmission maximum at 532 nm of the reference 20 nm thick continuous Au film,40 (ii) a transmission dip between 600 and 700 nm, depending on the NH sample, (iii) a further wide band transmission peak at wavelengths larger than 800 nm, and (iv) maximum transmittance intensity ranging from 45 to 65%, which is slightly lower than the 65% transmittance of the reference bare Au film because of multiple incoherent scattering from the short-range ordered NHs and metal losses.
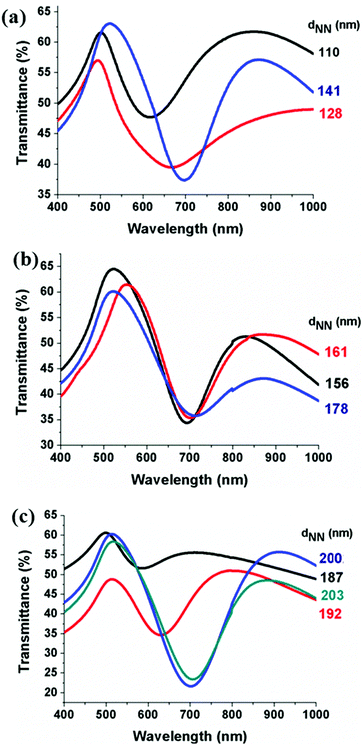 | ||
| Fig. 6 Transmittance spectra of: (a) PS(110 nm), PS(128 nm) and PS(141 nm); (b) PS(156 nm), PS(161 nm) and PS(178 nm); (c) PS(187 nm), PS(192 nm), PS(200 nm) and PS(203 nm). | ||
A less pronounced spectral dip together with a slight blue shift occurs for dNN decreasing down to 110 nm. This finding is consistent with a reduction of the contribution of the PSPR mode due to an increased density of NHs.38
Definitively, the fabricated NH samples present the transmission maxima and minima characteristics of NH arrays without any loss of spectral features over the whole sampled coverage range (from ∼8 to ∼27%), which is consistent with the presence of short-range ordering pointed out by SEM analysis.
According to previous reports on angle-dependent transmission spectra,40 the transmittance minimum between 600 and 700 nm can be associated with a PSPR wave. Based on this assignment and the general picture of free photon-hole grating coupling, we investigated how our NH samples compare with long-range ordered NH arrays.
Turning back to the possible impact of the quality of the Au film on the spectral response of our NH distributions, the rough surface and grain boundaries of the metal film45 are reported to have a negative impact on the propagation distance of PSPR modes, resulting in a reduced transmission peak and increased linewidth by light scattering and losses. In the case of short-range ordered NH distributions, the quality of the metal film is not expected to be as critical as in periodic systems because enhanced and suppressed transmission are phenomena localized to a limited number of holes rather than originating from photon-lattice coupling.28 In accordance with this discussion, Fig. 6(a) shows that the transmittance spectra of PS(110 nm), PS(128 nm) and PS(141 nm) present no particularly reduced intensity and increased linewidth compared to the other samples with a better quality of the Au film.
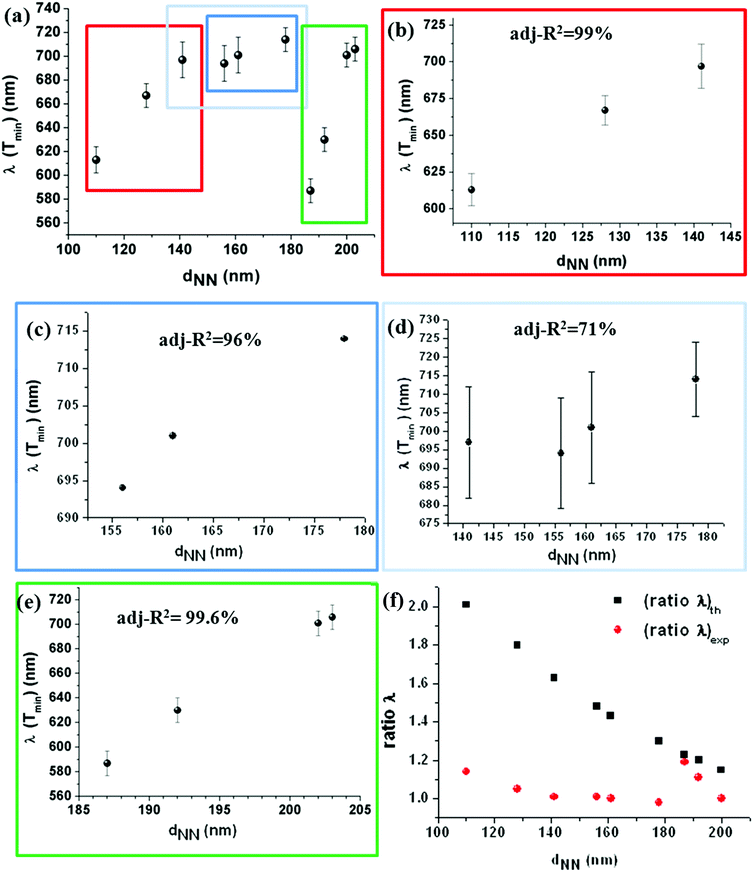
The plot showing the dependence of the wavelength of the transmittance minimum between 600 and 700 nm (referred to as λ(Tmin)) on dNN is reported in Fig. 7(a), which presents an extended set of data with respect to our recent publication.40 Interestingly, two main remarks are worth mentioning. First, λ(Tmin) varies linearly versus dNN over contiguous ranges of values of dNN without showing a general linear trend over the full dNN range from 110 to 203 nm. In contrast, it is possible to notice that there are three subsets of dNN values, highlighted by rectangles with different colors. A perfect linear dependence with adjusted-R2 = 99% for dNN in the range 110 to 141 nm (Fig. 7(b)), adjusted-R2 = 96% for dNN ranging from 156 to 178 nm (Fig. 7(c)), and adjusted-R2 = 99.6% for dNN increased from 187 to 203 nm (Fig. 7(e)) can be observed. Noteworthily, dNN ∼ 141 nm could be indicative of a transition in the distribution because the light-blue rectangle in Fig. 7(d) indicates that a linear dependence with adjusted-R2 = 71% also occurs if dNN ∼ 141 nm is added to the dNN range in Fig. 7(c). This clearly indicates that the interparticle spacing 141 nm is a border point better associated with hexagonal local coordination.
Definitively, spectral analyses indicate that the linear relationship between the spectral position of a PSPR mode and the lattice constant is not fully satisfied in the case of short-range ordering, where dNN is assumed to play the role of the periodicity length of ordered distribution. Since the spectral response of NH systems is related to geometrical arrangement and ordering properties, it is reasonable to envisage a connection between the observed unconventional (with respect to the behavior of periodic NH patterns) dependence of λ(Tmin) on dNN and the evolution of local geometric arrangements pointed out by SEM analysis of the colloidal masks presented in this study.
Notably, the above discussion points out how a lattice-like model can be developed for short-range ordered NH arrays that is not a straightforward extension of the knowledge on periodic systems. From the practical standpoint, to characterize and predict the spectral properties of short range ordered NH arrays in terms of the dependence of λ(Tmin) on dNN, the coordination geometry has to be accounted for. This point is an unprecedented result of our lattice-like analysis considering a periodicity parameter related to the occurrence of correlated disorder with degree depending on coverage and associated coordination geometry.
4. Interpretative model of the experimental results
4.1 Interpretative model: preliminary remarks and definitions
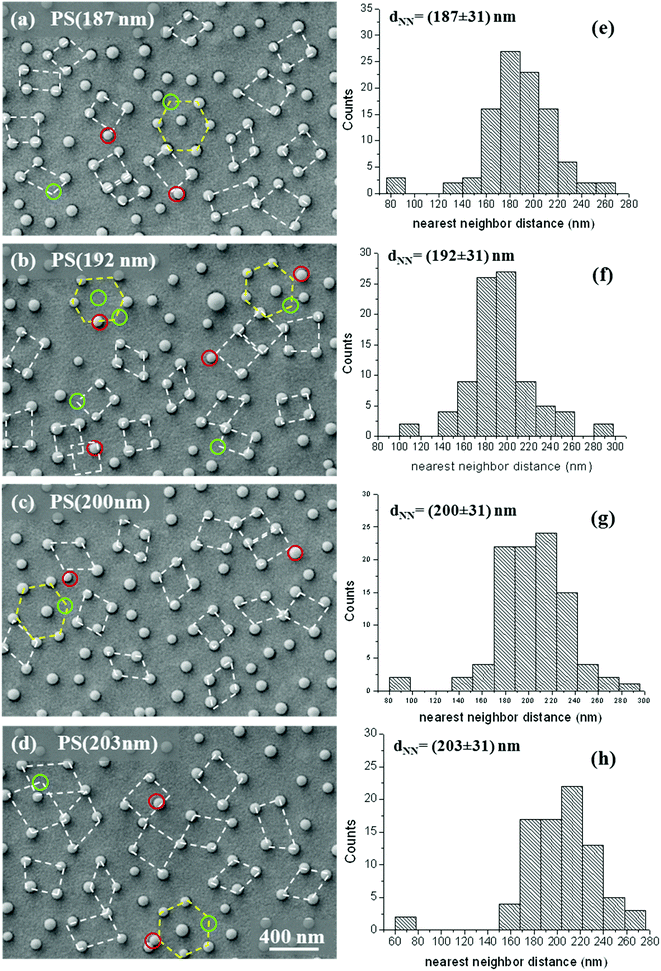
In order to gain physical insight into the nature of the observed dependence of λ(Tmin) on dNN, here we present an interpretative model relating the spectral behaviour of a PSPR mode to the geometric arrangement of NHs based on the following guidelines.A linear relationship between the transmittance resonance of a PSPR mode and the characteristic length-scale of periodically arranged NHs is expected on the basis of the momentum matching condition, that is kSPP = k∥ ± mGx ± nGy, where kSPP is the wave-vector of the surface plasmon polariton mode depending on the incident wavelength and direction, m and n are integers (Bragg integer diffraction orders), Gx and Gy are the reciprocal lattice vectors of the bidimensional hole lattice along x- and y-directions and k∥is the in-plane component of the incident photon's wave-vector (k∥ = 0 for normal incidence). As a consequence of the momentum conservation constraint, the wavelength of a PSPR mode supported by a hole lattice, under normal incidence conditions, is given by14,20
In order to gain insight into the occurrence of deviations from a general linear relationship λ(Tmin) versus dNN, we can compare the theoretical prediction of the grating-coupling model with a properly defined quantity accounting for the characteristics (short-range ordering and geometry of the local coordination) of our colloidal masks. According to this purpose, we estimate the ratio λ(□)/λ(Δ) by means of two independent procedures, as detailed here.
(i) First, we define the quantity
To implement the calculation of (ratio λ)th in the case of our experiments, we assume the statistically estimated dNN as the periodicity parameter, consistently with the general assumption adopted in the literature.21 Hence, each value of dNN is associated with a square or triangular lattice depending on the occurrence of square or hexagonal local coordination of the short-range ordered NH system.
(ii) Second, in analogy with the expression of (ratio λ)th in terms of the ratio between transmission spectral positions, we define the experimental ratio
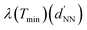 refer to the wavelength position of the transmittance minimum of our samples with average interparticle spacing dNN and
refer to the wavelength position of the transmittance minimum of our samples with average interparticle spacing dNN and 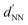 , respectively. The subscript “exp” indicates that only experimental values are considered in its evaluation. Although no geometry and/or coordination of the NH distributions were mentioned, this information is inherently accounted for (ratio λ)exp by means of the measured transmittance response. In practice, SEM analyses demonstrated that any value of dNN corresponds to a local coordination geometry (square-like or hexagonal-like or mixed).
, respectively. The subscript “exp” indicates that only experimental values are considered in its evaluation. Although no geometry and/or coordination of the NH distributions were mentioned, this information is inherently accounted for (ratio λ)exp by means of the measured transmittance response. In practice, SEM analyses demonstrated that any value of dNN corresponds to a local coordination geometry (square-like or hexagonal-like or mixed).
Additionally, in order to rationalize and gain physical insight into the difference between (ratio λ)th and (ratio λ)exp, based on simple mathematics we relate the relative variation between (ratio λ)th and (ratio λ)exp to their ratio, termed r(dNN), by means of the following formula
4.2 Interpretative model: physical insight into the role played by the geometry coordination and realistic effects
In order to implement consistently our interpretative model, while calculating (ratio λ)th and (ratio λ)exp for dNN increasing from 110 nm to 200 nm, we consider PS(200 nm) (that exhibits square-like local coordination and has the same ordering characteristics and dNN as PS(200)) as a reference square lattice. Therefore we calculateand
Since increasing dNN is associated with the changes of local coordination geometry, this procedure provides the evolution of (ratio λ)th and (ratio λ)expversus the packing geometry of the short-range ordered NH lattice.
Noteworthy, for 187 nm < dNN < 203 nm, (ratio λ)th was calculated by retaining the prefactor √4/3 rather than unity (corresponding to both square lattices) because residual random localized hexagonal coordination is still present (Fig. 4(a)–(d)). In principle, this occurrence indicates that a triangular lattice associated with large dNN is possible. As the definition of (ratio λ)th means to include inherently the presence of the two geometries observed in the real distributions, replacing the prefactor √4/3 by unit for large dNN would be, in principle and conceptually, inconsistent with the reasoning leading to the definition of (ratio λ)th that considers the wavelength positions of the same mode (i.e., (1,0,0) in our case) supported by lattices with different geometries and periodicity lengths. On the other hand, the evaluation of a prefactor weighting the contribution from simultaneously occurring different geometries is not straightforward and, in practice, is not the key point in the present discussion. In this respect, it is worth observing that the deviation between (ratio λ)th and (ratio λ)exp is more relevant over the range of values of dNN, where the prefactor √4/3 is rightly used (i.e., high and intermediate coverage regimes) than at low coverage. This observation is consistent and further supports the fact that (ratio λ)th is not able to describe realistically the distributions, including the role played by the lattice geometry. Differently, (ratio λ)exp is expected to be a more appropriate quantity that includes no a priori information about the lattice geometry and is determined by the transmittance response of the real distributions with mixed or dominant geometry.
In Fig. 7(f) the calculated (ratio λ)th and (ratio λ)exp are compared: it is possible to observe that (ratio λ)th deviates from (ratio λ)exp with a deviation that increases for decreasing dNN. The reason for such a deviation must be searched in the peculiarities of the real short-range ordered colloidal distribution and their relevant effects on (ratio λ)th and (ratio λ)exp as well as different effects accounted for (ratio λ)th and (ratio λ)exp.
As a general consideration, we can state that in the framework of short-range ordered NH arrangements, a square lattice is inherently less ordered and forms at lower coverage than an electrostatically stabilized triangular lattice.42
Hence, in principle, assuming dNN as the equivalent of the periodicity of ordered colloidal arrangements implies that it includes information about the coordination geometry through the transition of the lattice when going from low to high coverage. Since dNN decreases while adsorption drives the distribution towards the saturated configuration, unlike periodic NH arrays it is improbable that pure triangular and pure square short range lattices can occur associated with comparable dNN in the case of short-range ordered NHs.
Nevertheless, according to its meaning and statistical calculation, dNN is not always strictly representative of the geometry of the relative NH-to-NH positioning. This is the case of mixed square–hexagonal coordination where the same value of dNN represents two different types of coordination geometry; here, the assumption that dNN is the counterpart of the periodicity of ordered colloidal arrangements would be, in principle, not completely consistent.
It is therefore important to understand, on the basis of our model and by comparing (ratio λ)th and (ratio λ)exp, if and to which extent dNN can be really regarded as the periodicity length of short-range ordered colloidal systems.
From Fig. 7(f), it is evident that (ratio λ)th increases for increasing coverage. Noteworthily, different coverage is expected to affect the transmittance properties by other phenomena which are not taken into account by (ratio λ)th due to its derivation based on a hole grating-coupling model. Indeed, (ratio λ)th does not take into account any red-shift due to the finite size of NHs as well as scattering effects stemming from the correlated disorder and different degrees of ordering of square and hexagonal coordination occurring in the case of short-range ordered NH systems.42 In contrast, (ratio λ)exp exhibits a linear dependence over contiguous intervals of values of dNN consistent with the behaviour reported while studying λ(Tmin) versus dNN.
Turning to r(dNN), it was found that r(dNN) is a constant depending on the range of values of dNN, that is r(dNN) = 1.69 ± 0.08 (adjusted-R2 of 84%) for 110 nm < dNN < 141 nm, r(dNN) = 1.40 ± 0.07 (adjusted-R2 of 99.8%) for 156 nm < dNN < 178 nm and r(dNN) = 1.09 ± 0.06 (adjusted-R2 of 99.8%) for 187 nm < dNN < 203 nm.
The evidence that r(dNN) takes similar values for intervals of dNN associated with the same kind of local NH coordination (SEM analyses in Fig. 3–5) indicates that (ratio λ)exp is sensitive to the geometry of the NH arrangement. In contrast, in the case of (ratio λ)th any information about lattice geometry is assumed by dNN(□) and dNN(Δ) associated with a square and a triangular lattice, respectively.
Therefore, in regard to the relative variation between (ratio λ)th and (ratio λ)exp, two main conclusions can be remarked. First, it depends on the changes of the local coordination of our short-range ordered distributions consistently with the intervals of values of dNN individuated by SEM analysis. Second, it progressively decreases being related to the observed transition of the geometrical coordination number from hexagonal at high coverage to square at low coverage through hexagonal–square mixed coordination at intermediate coverage.
From the physical standpoint, the difference between (ratio λ)th and (ratio λ)exp that plays a role in the above discussion and conclusions is that, unlike (ratio λ)exp, (ratio λ)th doesn't account for the realistic characteristics of the NH distributions related to deviations from the periodic ordering (such as coverage-related ordering/disordering and changes of the local coordination) impacting the experimental transmission response. On this basis, the difference between (ratio λ)th and (ratio λ)exp is expected to quantitatively increase in situations where scattering effects are enhanced (such as for an increased density of NHs and capillary-induced clustering).
As a concluding remark, the developed model and the presented discussion are independent on the diameter of metal NHs. Once such a geometrical parameter if given, our conceptual model is well stated over the range of values of dNN corresponding to the evolution of the distribution from saturated adsorption to low coverage still sensitive to interparticle repulsion (i.e., dNN up to 203 nm under our experimental conditions). Indeed, under very low coverage conditions, colloid adsorption is dominated by colloid–collector attraction and interparticle repulsion poorly drives colloid self-assembly. Hence, decreasing coverage is associated with a progressively decreasing degree of correlated disorder which impacts the possibility of observing transmission resonances.
Definitively, several unprecedented results and comprehensive, both fundamental and applicative, discussion presented in this paper may lay the foundation for a fundamental description, in terms of a lattice-like model, of short-range ordered nanoholes that does not exploit straightforwardly and qualitatively concepts strictly related to periodic systems.
5. Conclusions
In this paper, the short-range order and spatial coordination geometry of NH distributions obtained by following a simplified colloidal lithography protocol in optically thin gold films have been studied based on an accurate qualitative and quantitative analysis of SEM micrographs.For each distribution, a characteristic NH-to-NH average nearest neighbor spacing dNN was derived from statistical analyses and treated, according to the common assumption, as the equivalent of the periodicity parameter of long-range ordered nanohole lattices. A transition of the order from locally quasi-hexagonal, at short dNN, to locally quasi-square, at large dNN, was observed and carefully related to the changes of the spectral response of the NH distributions as a function of fractional coverage and colloidal coordination. First, our study points out that, unlike long-range periodic distributions, the linear dependence of the wavelength of a propagating plasmon mode on the periodicity, here represented by dNN, is not demonstrated for the entire range of dNN values. An interpretative model has been developed demonstrating that, for short range ordered arrangements, dNN can be considered as the counterpart of the periodicity to a certain extent, depending on the degree of correlated disorder. Based on our model we discuss how short-range ordering, changes in the geometry of the local coordination and ordering/disordering-related scattering effects are responsible for the deviations of the spectral response of short-range ordered metal NH real distributions from ideal periodic systems.
Their effects, not accounted for in the statistical average dNN, have been found to have more impact at increasing coverage where capillary effects also impact the colloid arrangement.
To summarize the main conceptual results of our study: (i) the impact of mixed (hexagonal–square) coordination-geometry on the spectral response of short-range ordered NHs has been investigated, (ii) unlike the straightforward assumption, it has been demonstrated that dNN cannot be interpreted as the counterpart of the periodicity pitch of periodic NH arrays, and (iii) the conceptually rigorous periodicity-like length-scale has been recovered based on autocorrelation analysis of SEM images.
Therefore, unprecedented experimental results have been presented, which point out important differences between short-range and long-range ordered NHs and indicate a conceptual advance that may open the way to new directions for a deeper physical understanding of the mechanisms leading to resonant transmission features in short-range ordered metal NHs.
Noteworthily, the presented discussion points out how a lattice-like model can be developed for short-range ordered NH arrays and this model differs from the straightforwardly extended model used to describe periodic systems.
From the practical standpoint, whenever a short range ordered NH array is considered, any prediction of the trend of the dependence of λ(Tmin) on dNN has to account for the local coordination geometry as dictated by coverage.
Funding sources
This work was supported by a grant from the Ministry of Education, University and Research (MIUR) for the Scientific Program SIR2014 Scientific Independence of young Researcher (RBSI1455LK).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge Antonio Pinna for technical support during SEM experiments, Enrico Melissano (IMM-CNR, Lecce) for the thermal deposition of gold films as well as Adriana Campa (IMM-CNR, Lecce) and Maria Concetta Martucci (IMM-CNR, Lecce) for oxygen plasma treatments.References
- T. W. Ebbesen, H. J. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff, Nature, 1998, 391, 667–669 CrossRef CAS.
- C. Genet and T. W. Ebbesen, Nature, 2007, 445, 39–46 CrossRef CAS PubMed.
- H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213 CrossRef CAS PubMed.
- F. F. Mahani, A. Mokhtari and M. Mehran, Nanotechnology, 2017, 28, 385203 CrossRef PubMed.
- S. Yokogawa, S. P. Burgos and H. A. Atwater, Nano Lett., 2012, 12, 4349–4354 CrossRef CAS PubMed.
- A. G. Brolo, E. Arctander, R. Gordon, B. Leathem and K. L. Kavanagh, Nano Lett., 2004, 4, 2015–2018 CrossRef CAS.
- A. G. Brolo, S. C. Kwok, M. G. Moffitt, R. Gordon, J. Riordon and K. L. Kavanagh, J. Am. Chem. Soc., 2005, 127, 14936–14941 CrossRef CAS PubMed.
- M. Bauch, K. Toma, M. Toma, Q. Zhang and J. Dostalek, Plasmonics, 2014, 9, 781–789 CrossRef CAS PubMed.
- A. Prasad, J. Choi, Z. Jia, S. Park and M. R. Gartia, Biosens. Bioelectron., 2019, 130, 185–203 CrossRef CAS PubMed.
- A. De Leebeeck, L. K. S. Kumar, V. de Lange, D. Sinton, R. Gordon and A. G. Brolo, Anal. Chem., 2007, 79, 4094–4100 CrossRef CAS PubMed.
- M. P. Jonsson, A. B. Dahlin, L. Feuz, S. Petronis and F. Höök, Anal. Chem., 2010, 82, 2087–2094 CrossRef CAS PubMed.
- C. Escobedo, Lab Chip, 2013, 13, 2445–2463 RSC.
- A. B. Dahlin, Analyst, 2015, 140, 4748–4759 RSC.
- F. J. Garcia-Vidal, L. Martin-Moreno, T. W. Ebbesen and L. Kuipers, Rev. Mod. Phys., 2010, 82, 729–787 CrossRef.
- J. Bravo-Abad, A. Degiron, F. Przybilla, C. Genet, F. J. García-Vidal, L. Martín-Moreno and T. W. Ebbesen, Nat. Phys., 2006, 2, 120–123 Search PubMed.
- H. F. Ghaemi, T. Thio, D. E. Grupp, T. W. Ebbesen and H. J. Lezec, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6779–6782 CrossRef CAS.
- M. Sarrazin, J.-P. Vigneron and J.-M. Vigoureux, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085415 CrossRef.
- C. Genet, M. P. van Exter and J. P. Woerdman, Opt. Commun., 2003, 225, 331–336 CrossRef CAS.
- E. S. H. Kang, H. Ekinge and M. P. Jonsson, Opt. Mater. Express, 2019, 9, 1404–1415 CrossRef CAS.
- F. J. García de Abajo, Rev. Mod. Phys., 2007, 79, 1267–1290 CrossRef.
- T. Sannomiya, O. Scholder, K. Jefimovs, C. Hafner and A. B. Dahlin, Small, 2011, 7, 1653–1663 CrossRef CAS PubMed.
- J. J. Burke, G. I. Stegeman and T. Tamir, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 5186–5201 CrossRef CAS PubMed.
- F. Yang, J. R. Sambles and G. W. Bradberry, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 5855–5872 CrossRef PubMed.
- W. A. Murray, S. Astilean and W. L. Barnes, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165407 CrossRef.
- I. S. Spevak, A. Y. Nikitin, E. V. Bezuglyi, A. Levchenko and A. V. Kats, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 161406 CrossRef.
- T. Matsui, A. Agrawal, A. Nahata and Z. V. Vardeny, Nature, 2007, 446, 517 CrossRef CAS PubMed.
- F. Przybilla, C. Genet and T. W. Ebbesen, Appl. Phys. Lett., 2006, 89, 121115 CrossRef.
- D. Pacifici, H. J. Lezec, L. A. Sweatlock, R. J. Walters and H. A. Atwater, Opt. Express, 2008, 16, 9222–9238 CrossRef PubMed.
- A. Agrawal, T. Matsui, Z. V. Vardeny and A. Nahata, Opt. Express, 2008, 16, 6267–6273 CrossRef PubMed.
- C. Valsecchi, E. L. Gomez Armas and J. Weber de Menezes, Sensors, 2019, 19, 2182 CrossRef CAS PubMed.
- S.-D. Liu, P. Yue, S. Zhang, M. Wang, H. Dai, Y. Chen, Z.-Q. Nie, Y. Cui, J.-B. Han and H. Duan, Adv. Opt. Mater., 2020, 8, 1901109 CrossRef CAS.
- Q. Liu, Y. Song, P. Zeng, C. Zhang, Y. Chen, H. Wang, Y. Luo and H. Duan, Appl. Surf. Sci., 2020, 526, 146690 CrossRef CAS.
- C. Vieu, F. Carcenac, A. Pépin, Y. Chen, M. Mejias, A. Lebib, L. Manin-Ferlazzo, L. Couraud and H. Launois, Appl. Surf. Sci., 2000, 164, 111–117 CrossRef CAS.
- S. Matsui and Y. Ochiai, Nanotechnology, 1996, 7, 247–258 CrossRef CAS.
- P. Hanarp, D. S. Sutherland, J. Gold and B. Kasemo, Colloids Surf., A, 2003, 214, 23–36 CrossRef CAS.
- J. Prikulis, P. Hanarp, L. Olofsson, D. Sutherland and M. Käll, Nano Lett., 2004, 4, 1003–1007 CrossRef CAS.
- M. Q. Liu, C. Y. Zhao, B. X. Wang and X. Fang, J. Opt. Soc. Am. B, 2018, 35, 504–513 CrossRef CAS.
- F. Przybilla, C. Genet and T. W. Ebbesen, Opt. Express, 2012, 20, 4697–4709 CrossRef PubMed.
- T. H. Reilly, R. C. Tenent, T. M. Barnes, K. L. Rowlen and J. van de Lagemaat, ACS Nano, 2010, 4, 615–624 CrossRef CAS PubMed.
- M. Cesaria, A. Taurino, M. G. Manera, M. Minunni, S. Scarano and R. Rella, Nanoscale, 2019, 11, 8416–8432 RSC.
- Digital Micrograph software (DM Vers. 3.21.1374.0), https://www.myendnoteweb.com/EndNoteWeb.html?func=downloadInstallers%26cat=download%26 Search PubMed.
- S. Watanabe, M. Miyahara and K. Higashitani, J. Chem. Phys., 2005, 122, 104704 CrossRef PubMed.
- B. Brian, B. Sepúlveda, Y. Alaverdyan, L. M. Lechuga and M. Käll, Opt. Express, 2009, 17, 2015–2023 CrossRef CAS PubMed.
- K. Xiong, G. Emilsson and A. B. Dahlin, Analyst, 2016, 141, 3803–3810 RSC.
- J. Zhang, M. Irannejad, M. Yavuz and B. Cui, Nanoscale Res. Lett., 2015, 10, 238 CrossRef PubMed.
Footnote |
| † Present address: Department of Mathematics and Physics “Ennio De Giorgi”, University of Salento, prov. le Arnesano, 73100, Lecce, Italy. |
| This journal is © The Royal Society of Chemistry 2020 |