Open Access Article
Open Access ArticleFirst-principles study of Na insertion at TiO2 anatase surfaces: new hints for Na-ion battery design†
Arianna
Massaro
 a,
Ana B.
Muñoz-García
a,
Ana B.
Muñoz-García
 *b,
Pasqualino
Maddalena
b,
Federico
Bella
*b,
Pasqualino
Maddalena
b,
Federico
Bella
 c,
Giuseppina
Meligrana
c,
Claudio
Gerbaldi
c,
Giuseppina
Meligrana
c,
Claudio
Gerbaldi
 c and
Michele
Pavone
c and
Michele
Pavone
 *a
*a
aDepartment of Chemical Sciences, Università di Napoli Federico II, Comp. Univ. Monte Sant’Angelo, via Cintia 21, 80126 Naples, Italy. E-mail: michele.pavone@unina.it
bDepartment of Physics “Ettore Pancini”, Università di Napoli Federico II, Comp. Univ. Monte Sant’Angelo, via Cintia 21, 80126 Naples, Italy. E-mail: anabelen.munozgarcia@unina.it
cGAME Lab, Department of Applied Science and Technology, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129-Torino, Italy
First published on 11th June 2020
Abstract
Na-ion batteries (NIBs) are attracting widespread interest as a potentially more convenient alternative to current state-of-the-art Li-ion batteries (LIBs), chiefly for large-scale energy storage from renewables. Developing novel active materials is essential for the deployment of NIBs, especially in terms of negative electrodes that can accommodate the larger sodium ions. We focus on TiO2 anatase, which has been proposed as a promising anode material for the overall balance of performance, stability and cost. As the exposed crystal facets in different morphologies of nanostructured anatase can affect the electrochemical performances, here we report a theoretical investigation of Na+ adsorption and migration through (101), (100) and (001) surface terminations, thus explaining the different activities toward sodiation reported in the literature. Energy barriers computed by means of the CI-NEB method at the DFT+U level of theory show that the (001) surface is the most effective termination for Na+ insertion. We also provide a detailed analysis to elucidate that the energy barriers are due to structural modifications of the lattice upon sodiation. From these results we derive new design directions for the development of cheap and effective oxide-based nanostructured electrode materials for advanced NIBs.
Na-ion batteries (NIBs) are at the focus of intense research efforts both in academia and industries.1,2 The objective is replacing most dominating Li-ion based technologies, because lithium’s scarce availability and high costs have hindered their deployment in large-scale storage applications so far.3–5 On the contrary, thanks to cheap and easily available sodium raw materials, NIB-based devices are foreseen to be a key enabler for the transition to a more sustainable society: from large grid facilities, in combination with renewable energy conversion plants, to even futuristic electric transportation.6,7 Despite sharing similar operating principles, Li-ion batteries (LIBs) and NIBs sensibly differ in their constituent materials.8,9 In recent years, the energy storage community attested the resurgence toward rational optimization of various advanced electrode materials. Their thorough design in the form of nanostructures endow the electrodes with high reversible capacity, enhanced rate capability, and prolonged durability.10 However, the large Na+ radius helps in the diffusion through liquid electrolytes, but it hampers a convenient Na+ reversible storage into the structure of the electrodes.11 While this problem is less relevant for positive electrodes, including layered oxides, phosphate olivines and polyanionic compounds as those exploited in state-of-the-art LIBs,12 common negative electrodes, e.g. graphite or silicon, are not able to reversibly accommodate the larger Na+ cations.13 This has motivated the development and optimization of negative electrodes highly effective in NIBs.14
Among many proposed systems, titanium dioxide (TiO2) represents a widely investigated and convenient choice for the overall balance of performance, stability and costs. TiO2 is a versatile functional material with several applications, ranging from solar cells15 to photocatalytic water splitting16 and batteries. In Li+-based batteries, it showed comparable performances to graphitic materials, such as high reversible theoretical capacity (335 mA h g−1), low volume variation upon cycling (less than 4%) and improved safety, due to the structural robustness and high working potential, but it still suffers from poor electrical conductivity (∼1.9 10−12 S m−1) and slow ion diffusion.17 Combining TiO2 with conductive materials (e.g. graphene, mesoporous carbon, carbon nanotubes, and metal oxides) is effective for enhancing electronic conductivity,13,18 while nano-engineering is important for favourable diffusion kinetics thanks to short ion diffusion pathways and a large electrode/electrolyte contact area.19 Recent efforts have been devoted to the development and scale up of nanostructured TiO2-based materials to be applied as anode materials in lab-scale NIBs.20–25 Innovative synthetic strategies have been developed aiming at advanced functionalization of TiO2 nanoparticles (NPs) with carbon coating, thus enhancing the active material performance. Nonetheless, the amount of other components than TiO2 is rather small and plays no active role.26 Within this context, the structural features, both in terms of crystallinity and morphology, seem to be crucial in determining the activity of TiO2 NPs. For example, the work by Longoni et al.24 proves that the performances of anatase NPs as negative electrodes in NIBs depend on the exposed NP surfaces, the (100) and (001) facets being much more effective than the most stable (101) surface. From an atomistic perspective, the behavior of these different surface terminations toward Na+ uptake remains unclear and there are still open questions about the Na+ storage mechanism. Actually, to the best of our knowledge, an in-depth understanding of Na–TiO2 interactions is still missing and a conclusive theoretical interpretation of experimental evidence has not been provided yet. Longoni et al.24 suggest that different exposed surfaces in TiO2 anatase NPs can act as Na+-insertion sites. In other terms, beside the expected Na+ adsorption at NP surfaces, Na+ insertion can also occur upon cycling, as a result of the pseudocapacitive behavior detected at the electrolyte/electrode interface. Attempts to explain the anatase surface-dependent activities with just the surface adsorption fail in predicting the correct observed trend.25 In particular, adsorption can only support the experimental evidence regarding the high activity of the (100) surface, but it does not explain the high performances of the NPs exposing the (001) surface. It means that sodium coverage on the surface is not a complete nor reliable model for this electrode/electrolyte interface, where the charge and discharge also involve sodiation/desodiation processes, i.e. insertion/deinsertion through the anatase NP lattice.
In an attempt to address this knowledge gap, here we report a thorough first-principles study on Na+ adsorption and insertion at the (101), (100) and (001) TiO2 anatase surfaces. Our objective is to decouple the structural and electronic features that drive the interaction between these different anatase NP surface terminations and Na ions, thus proving the mechanism and the origin of the observed selectivity for Na+ uptake. We first built 6-layer slab models for the (101), (100) and (001) low-index surfaces of TiO2 anatase and validated our model against experimental and theoretical values from the literature (lattice parameters and surface energies are reported in Tables S1–S3†). We focus on the thermodynamically stable surfaces that have been characterized experimentally and present no significant surface reconstruction in real samples.24 To avoid fictitious numerical effects, we performed full relaxation of all the atoms in the surface slab models, thus obtaining surface energy values in agreement with the literature (Table S2 and see ref. S2†).
The slab approach is the most commonly adopted method to model NPs. On one hand, crystal surfaces are dominant over the bulk state, due to the high surface/volume ratio in NPs. On the other hand, introducing vacuum space in the extended simulation cell largely reduces the computational cost and the reliability of the model compared to the cluster approaches. The PBE+U minimum-energy structures for the surfaces under study are shown in Fig. S2.† We identified several adsorption and insertion sites as initial structures for our calculations. Insertion sites have been considered both in the subsurface layer (the first one underlying the surface layer) and in the following underlying one, along the [010] Na+ diffusion channel.23 For adsorption sites lying on top of the clean surfaces, we chose specific configurations where sodium could then be inserted into the TiO2 lattice. All the explored configurations converged to a unique structure (see the discussion below). Electronic structure analysis confirms that our model consists of a Na cation interacting with an n-type semiconductor, e.g. Na s states appear in the TiO2 conduction band (vide infra).
We calculate both Na adsorption and insertion energies for each surface as follows:
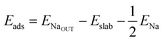 | (1) |
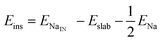 | (2) |
In order to explain the different adsorption properties for each surface, we consider that part of the energy variation in this process comes from the distortion energy, i.e. the energy required to adapt the TiO2 lattice in the pristine surface structure to the one in the Na-adsorbed state. We can define this quantity as:
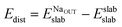 | (3) |
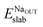 and Eslabslab are the energies of the slab at the geometry of the Na adsorbed state and in its minimum-energy structure, respectively. Table 1 lists all the energy values computed for the different surface terminations.
and Eslabslab are the energies of the slab at the geometry of the Na adsorbed state and in its minimum-energy structure, respectively. Table 1 lists all the energy values computed for the different surface terminations.
| E ads (eV) | E ins (eV) | E dist (eV) | |
|---|---|---|---|
| Bulk | 0.531 | ||
| (101) | −1.120 | 0.266 | 0.577 |
| (100) | −1.554 | 0.460 | 0.318 |
| (001) | −0.801 | 0.364 | 0.726 |
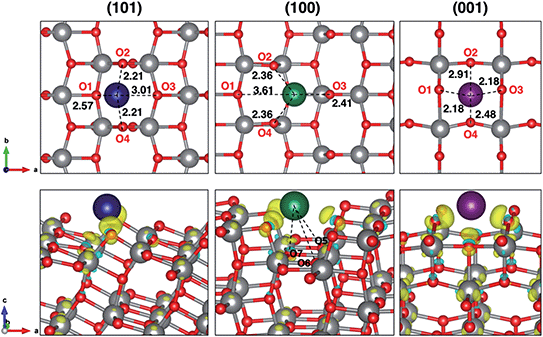
Insertion energies slightly differ for ∼0.1 eV among each other and from the bulk reference value. The distortion energies calculated for each surface are 0.577, 0.318 and 0.726 eV, for (101), (100) and (001), respectively. From our results, we can say that distortion effects clearly explain the trend in adsorption energies. The highly favourable Na adsorption on the (100) surface is also supported by three extra Na–O interactions that are peculiar on this adsorption site, as shown in Fig. 1. Further structural modifications (e.g. phase transition) are likely to be less significant when anatase is synthesized in the form of NPs.27 Indeed, the high surface/volume ratio of the NPs allows sodium to intercalate at most to the subsurface layer. Thus, the full sodiation limit is not reached. However, we addressed eventual structural effects on the subsequent insertion of another Na ion, which actually did not reveal any difference in adsorption and insertion properties.
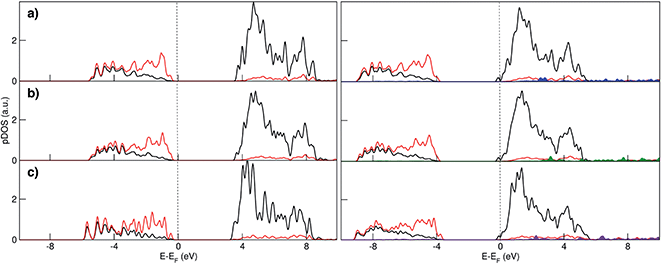
Electronic structure analysis by charge difference plots (Fig. 1, bottom panel) and PDOS (Fig. 2) show a common pattern for all the surface terminations. The adsorption of a Na atom leads to the reduction of Ti species and population of states at the edge of the TiO2 conduction band, which is consistent with the desired n-type conductivity for the NIB electrode. At the same time, there is a consistent polarization of the oxygen species that coordinate the adsorbed Na cations, determining the different relative stabilities of the resulting systems.
Besides the adsorption process, Na+ insertion at the subsurface level is very likely to occur in TiO2 anatase NPs. Thus, we considered the minimum-energy structures of Na-adsorbed (NaOUT) and Na-inserted (NaIN) systems as the initial and final equilibrium states, respectively, along the process coordinate, i.e. the migration path. We applied the climbing image-nudge elastic band (CI-NEB)28 method to compute the minimum energy path (MEP) between the two states of interest, NaOUT and NaIN, respectively. We modelled the path of Na from surface to the subsurface positions through three intermediate structures (images) that are optimized at the PBE+U level of theory according to the CI-NEB approach. Fig. 3 shows the pictorial representation of the so-obtained MEPs for each surface and their corresponding relative energies.
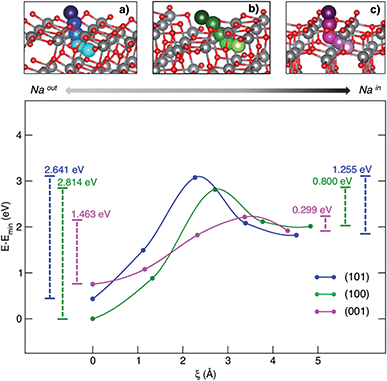 | ||
| Fig. 3 MEP (top panel) and corresponding energetics (bottom panel) for the Na-migration through the (a) (101), (b) (100) and (c) (001) surfaces. Energy barriers calculated from eqn (4) and (5) for the out/in migration are reported, respectively, at the left- and right-hand sides of the graph. | ||
The process coordinate, ξ, is defined as the Na–Na distance between two contiguous points. The computed MEPs are identical in both forward and backward processes, i.e. sodiation/desodiation.
The anatase phase shows a 3D network formed by the stacking of zigzag chains, which consist of distorted edge-sharing TiO6 octahedra. In this crystal framework, empty channels are possible interstitial sites for ion insertion and suitable-sized pathways for ion diffusion. As it can be observed in the top panel of Fig. 3, sodium moves along a given direction in the lattice, passes across the alternating Ti–O motif, that we will call the “lattice window” from this point forward, and then enters the cavity in the subsurface layer. The cavity lies on the [010] diffusion channel. The coordinates of the computed MEPs are given in the ESI.† The energy barriers associated with both sodiation and desodiation processes can be determined as:
| EOUTmigr = ENaTS − ENaOUT | (4) |
| EINmigr = ENaIN − ENaTS | (5) |
The positive values reported so far (insertion and migration energies) are consistent with the non-spontaneous sodiation of TiO2 anatase NPs. Our model is a reliable representation of an anode interface that can only be sodiated upon charge (i.e. provided an electrical potential is supplied). The inclusion in our model of other elements that in principle may lower these values, such as the presence of an electrolyte at the electrode interface and the resulting passivating layer that can be formed or an external applied potential, is beyond the aim of this work. Our purpose is to provide the simplest theoretical model that is able to explain the surface activities reported experimentally.
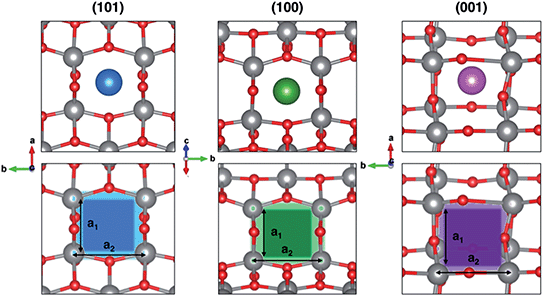
In order to rationalize such a trend, we focus on the structural features of the different surface terminations. We find that the size of the lattice window at the transition state (NaTS) provides a direct measure of the steric hindrance that the migrating sodium encounters along its path. As highlighted in Fig. 4, the lattice window is the area delimited by the Ti–O lattice and perpendicular to the path that the migrating sodium should cross in order to enter the TiO2 crystalline structure.
The total area (A) of the lattice window for each surface can be calculated straightforwardly from two Ti–Ti distances, a1 and a2. However, this descriptor does not capture the significant difference between the lowest barrier found in (001) and the two higher ones in (100) and (101), as it can be seen from Table 2. Indeed, the limiting factor in the sodium path is related to an “effective” lattice window, which is delimited by the shortest Ti–Ti distance, a1, thus defining the minimum accessible area, amin.
| A tot (Å2) | a min (Å2) | E OUTmigr (eV) | |||
|---|---|---|---|---|---|
| NaOUT | NaTS | NaOUT | NaTS | ||
| (101) | 11.4 | 12.3 | 8.7 | 9.6 | 2.641 |
| (100) | 11.4 | 12.6 | 8.7 | 9.9 | 2.814 |
| (001) | 15.2 | 14.9 | 15.1 | 14.8 | 1.463 |
The minimum accessible area (amin) indirectly correlates with the migration barrier heights calculated for the different surfaces. In fact, smaller lattice windows in (101) and (100) surfaces result in higher barriers, while the (001) surface shows the largest lattice window and, thus, the lowest barrier.
In conclusion, our results show for TiO2 anatase surfaces the most favourable adsorption of Na+ at the (100) termination, thanks to a convenient accommodation of the large cations on a surface step that maximizes the Na+–O2− interactions and does not disturb much the crystalline lattice. Moreover, we find that charge/discharge processes in TiO2 anatase NPs can effectively occur via the Na-insertion mechanism, and we prove that the (001) surface is the most active toward Na subsurface insertion thanks to its peculiar structural features: the large surface lattice window allows for an easy diffusion of the large sodium cations, thus supporting the experimental observation of high performances in NIBs with TiO2 NPs exposing the (001) surface termination. Analysis of MEPs in all the surface terminations demonstrates that the corresponding migration barrier heights depend only on structural modification of the anatase lattice upon Na+ insertion, thus unveiling the key role of surface lattice windows. The identification of this easy computable structural description can be very useful and, actually, instrumental for the rational design and development of new, high-performance materials with a potential efficient Na uptake mechanism, particularly nanostructured oxide-based materials having promising Na-host characteristics in NIBs. Our future work will pursue this direction, extending the modelling approaches that are able to correctly reproduce the capacity–voltage profiles of promising electrode materials and also focusing on the interfacial effects induced by dopants or additives, such as C-based materials and nanostructure engineering on the Na-insertion process in anatase-based anodes for NIB applications.
Methods and computational details
Spin-polarized density functional theory (DFT)29+U theory30 was employed to overcome the large self-interaction error that affects DFT when applied to mid-to-late first row transition metal oxides with tightly localized d-electrons. Our calculations were performed with projector-augmented wave (PAW) potentials and plane wave (PW) basis sets, as implemented in the Vienna ab initio simulation package (VASP) code (version 5.4.1).31 We used the Perdew–Burke–Ernzerhof (PBE)32 exchange-correlation functional with the Ueff = 3.3 eV parameter for Ti atoms33 and the standard PAW potentials. A kinetic energy of 600 eV was used to converge the PW basis set.Our surface models consist of 6-layer slabs containing 24 formula units (72 atoms). We used 2 × 2 × 1 k-point sampling based on the Monkhorst–Pack scheme. We employ the CI-NEB28 to locate minimum energy paths of Na migration from the surface to the subsurface and to compute the corresponding barrier heights. We also performed some preliminary tests on smaller cells (36 atoms, 12 f.u.) in order to model a larger sodium coverage, but no change in the observed energetics was detected (Table S6†). However, the 36 atoms-containing cells were rather too small to accommodate all the intermediate structures along Na+ migration paths, thus we needed to build up supercells in order to perform NEB calculations. Both the minimum-energy and intermediate structures have been obtained through relaxation of all layers in the slab. The projected density of states plots are computed via single-point energy calculations at the HSE06 level of theory34,35 on the PBE+U minimum-energy structures. All the results reported in the manuscript refer to perfect surfaces, although a brief discussion on adsorption and insertion energetics in reduced anatase can be found in the ESI.†
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
MP acknowledges funding from the Italian Ministry of University and Research (MIUR) under grant PRIN 2015XBZ5YA. Authors acknowledge the European Union (FSE, PON Ricerca e Innovazione 2014–2020, Azione I.1 “Dottorati Innovativi con caratterizzazione Industriale”), for funding a PhD grant to Arianna Massaro. Part of this work was carried out within the activities “Ricerca Sistema Elettrico” funded through contributions to research and development by the Italian Ministry of Economic Development. The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff;36 CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programmes. See: http://www.cresco.enea.it/english for information.References
- K. Kubota and S. Komaba, Review - Practical Issues and Future Perspective for Na-Ion Batteries, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS.
- C. Delmas, Sodium and Sodium-Ion Batteries: 50 Years of Research, Adv. Energy Mater., 2018, 8, 1703137 CrossRef.
- J. M. Tarascon, Is lithium the new gold?, Nat. Chem., 2010, 2, 510 CrossRef CAS PubMed.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, A cost and resource analysis of sodium-ion batteries, Nat. Rev. Mater., 2018, 3, 18013 CrossRef.
- A. Ponrouch and M. Rosa Palacín, Post-Li batteries: promises and challenges, Philos. Trans. R. Soc., A, 2019, 377, 20180297 CrossRef CAS PubMed.
- D. Larcher and J. M. Tarascon, Towards Greener and More Sustainable Batteries for Electrical Energy Storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- G. Yan, S. Mariyappan, G. Rousse, Q. Jacquet, M. Deschamps, R. David, B. Mirvaux, J. W. Freeland and J.-M. Tarascon, Higher energy and safer sodium ion batteries via an electrochemically made disordered Na3V2(PO4)2F3 material, Nat. Commun., 2019, 10, 585 CrossRef CAS PubMed.
- K. Chayambuka, G. Mulder, D. L. Danilov and P. H. L. Notten, Sodium-Ion Battery Materials and Electrochemical Properties Reviewed, Adv. Energy Mater., 2018, 8, 1800079 CrossRef.
- Y. Huang, Y. Zheng, X. Li, F. Adams, W. Luo, Y. Huang and L. Hu, Electrode Materials of Sodium-Ion Batteries toward Practical Application, ACS Energy Lett., 2018, 3, 1604–1612 CrossRef CAS.
- Y. Fang, X.-Y. Yu and X. W. Lou, Nanostructured Electrode Materials for Advanced Sodium-Ion Batteries, Matter, 2019, 1, 90–114 CrossRef.
- L. P. Wang, L. Yu, X. Wang, M. Srinivasan and Z. J. Xu, Recent Developments in Electrode Materials for Sodium-Ion Batteries, J. Mater. Chem. A, 2015, 3, 9353–9378 RSC.
- Z. Dai, U. Mani, H. Teng Tan and Q. Yan, Advanced Cathode Materials for Sodium-Ion Batteries: What Determines Our Choices?, Small Methods, 2017, 1, 1700098–1700124 CrossRef.
- Y. Lu, Y. Lu, Z. Niu and J. Chen, Graphene-Based Nanomaterials for Sodium-Ion Batteries, Adv. Energy Mater., 2018, 1702469 CrossRef.
- L. Li, Y. Zheng, S. Zhang, J. Yang, Z. Shao and Z. Guo, Recent progress on sodium ion batteries: Potential high-performance anodes, Energy Environ. Sci., 2018, 11, 2310–2340 RSC.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Dye-Sensitized Solar Cells, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, A Review and Recent Developments in Photocatalytic Water-Splitting Using TiO2 Or Hydrogen Production, Renewable Sustainable Energy Rev., 2007, 11, 401–425 CrossRef CAS.
- C. Jiang and J. Zhang, Nanoengineering Titania for High Rate Lithium Storage: A Review, J. Mater. Sci. Technol., 2013, 29(2), 97–122 CrossRef CAS.
- Y. C. Yang, B. Qiao, X. Yang, L. Fang, C. Pan, W. Song, H. Hou and X. Ji, Lithium Titanate Tailored by Cathodically Induced Graphene for an Ultrafast Lithium Ion Battery, Adv. Funct. Mater., 2014, 24, 4349–4356 CrossRef CAS.
- P. G. Bruce, B. Scrosati and J. M. Tarascon, Nanomaterials for Rechargeable Lithium Batteries, Angew. Chem., Int. Ed., 2008, 47, 2930–2946 CrossRef CAS PubMed.
- Y. Xu, E. M. Lotfabad, H. Wang, B. Farbod, Z. Xu, A. Kohandehghan and D. Mitlin, Nanocrystalline Anatase TiO2: A New Anode Material for Rechargeable Sodium Ion Batteries, Chem. Commun., 2013, 49, 8973–8975 RSC.
- H. Xiong, M. D. Slater, M. Balasubramanian, C. S. Johnson and T. Rajh, Amorphous TiO2 Nanotube Anode for Rechargeable Sodium Ion Batteries, J. Phys. Chem. Lett., 2011, 2, 2560–2565 CrossRef CAS.
- Y. Liu, F. Zhao, J. Li, L. Yanguang, J. A. McLeod and L. Liu, Influence of Crystal Phase on TiO2 Nanowire Anodes in Sodium Ion Batteries, J. Mater. Chem. A, 2017, 5, 20005–20013 RSC.
- F. Bella, A. B. Muñoz-Garcìa, G. Meligrana, A. Lamberti, M. Destro, M. Pavone and C. Gerbaldi, Unveiling the Controversial Mechanism of Reversible Na Storage in TiO2 Nanotube Arrays: Amorphous versus Anatase TiO2, Nano Res., 2017, 10(8), 2891–2903 CrossRef CAS.
- G. Longoni, R. L. Pena Cabrera, S. Polizzi, M. D'Arienzo, C. M. Mari, Y. Cui and R. Ruffo, Shape-Controlled TiO2 Nanocrystals for Na-ion Battery Electrodes: The Role of Different Exposed Crystal Facets on the Electrochemical Properties, Nano Lett., 2017, 17, 992–1000 CrossRef CAS PubMed.
- X. Yang, C. Wang, Y. Yang, Y. Zhang, X. Jia, J. Chen and X. Ji, Anatase TiO2 Nanocubes for Fast and Durable Sodium Ion Battery Anodes, J. Mater. Chem. A, 2015, 3, 8800–8807 RSC.
- M. N. Tahir, B. Oschmann, D. Buchholz, X. Dou, I. Lieberwirth, M. Panthöfer, W. Tremel, R. Zentel and S. Passerini, Extraordinary Performance of Carbon-Coated Anatase TiO2 as Sodium-Ion Anode, Adv. Energy Mater., 2016, 6, 1501489 CrossRef PubMed.
- W. Li, M. Fukunishi, B. J. Morgan, O. J. Borkiewicz, K. W. Chapman, V. Pralong, A. Maignan, O. I. Lebedev, J. Ma, H. Groult, S. Komaba and D. Dambournet, A Reversible Phase Transition for Sodium Insertion in Anatase TiO2, Chem. Mater., 2017, 29(4), 1836–1844 CrossRef CAS.
- G. Henkelman, B. P. Uberuagua and H. Jonsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 22, 113 Search PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864 CrossRef; W. Kohn and L. J. Sham, Self-Consistent Equation Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott Insulators: Hubbard U instead of Stoner I, Phys. Rev. B, 1991, 44, 943 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using A Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Finazzi, C. Di Valentin, G. Pacchioni and A. Selloni, Excess Electron States in Reduced Bulk Anatase TiO2: Comparison of Standard GGA, GGA+U and Hybrid DFT Calculations, J. Chem. Phys., 2008, 129, 154113 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207 ( J. Chem. Phys. , 2006 , 124 , 219906 ) CrossRef CAS.
- G. Ponti; F. Palombi; D. Abate; F. Ambrosino; G. Aprea; T. Bastianelli; F. Beone; R. Bertini; G. Bracco; M. Caporicci; B. Calosso; M. Chinnici; A. Colavincenzo; A. Cucurullo; P. Dangelo; M. D. Rosa; P. D. Michele; A. Funel; G. Furini; D. Giammattei; S. Giusepponi; R. Guadagni; G. Guarnieri; A. Italiano; S. Magagnino; A. Mariano; G. Mencuccini; C. Mercuri; S. Migliori; P. Ornelli; S. Pecoraro; A. Perozziello; S. Pierattini; S. Podda; F. Poggi; A. Quintiliani; A. Rocchi; C. Scio; F. Simoni and A. VitaThe role of medium size facilities in the HPC ecosystem: the case of the new CRESCO4 cluster integrated in the ENEAGRID infrastructure, International Conference on High Performance Computing & Simulation (HPCS), 2014, pp. 1030–1033 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: structural models, surface energies, oxygen vacancies, higher sodium coverage, CI-NEB results computed at the PBE level of theory, and atomic coordinates for all the intermediates along the Na migration path in each surface. See DOI: 10.1039/d0na00230e |
| This journal is © The Royal Society of Chemistry 2020 |