Open Access Article
Open Access ArticleBeyond linearity: bent crystalline copper nanowires in the small-to-moderate regime
Jacob
Martine
,
Robert
Lawitzki
,
Wenhao
Ma
,
Christopher
Everett
,
Guido
Schmitz
and
Gábor
Csiszár
 *
*
Chair of Materials Physics, Department of Materials Science, University of Stuttgart, Heisenbergstraße 3, 70569 Stuttgart, Germany. E-mail: Jacob.Martine@mp.imw.uni-stuttgart.de; Robert.Lawitzki@mp.imw.uni-stuttgart.de; st154509@stud.uni-stuttgart.de; Christopher.Everett@mp.imw.uni-stuttgart.de; Guido.Schmitz@mp.imw.uni-stuttgart.de; Gabor.Csiszar@mp.imw.uni-stuttgart.de
First published on 11th June 2020
Abstract
Several models can describe the nonlinear response of 1D objects to bending under a concentrated load. Successive stages consisting of geometrical and, additionally, mechanical non-linearity can be identified in moderately large extensions. We provide an explicit bending moment function with terms accounting for the linearity (Euler–Bernoulli), quasi-linearity, geometrical and finally, mechanical non-linearity as global features of a moderately large elastic deformation. We apply our method, also suitable for other metals, to the experimental data of Cu nanowires (NWs) with an aspect ratio of about 16 under different concentrated loadings. The spatial distribution of strain-hardening/softening along the wire or through the cross-section is also demonstrated. As a constitutive parameter, the strain-dependent stretch modulus represents, undoubtedly, changes in the material properties as the deformation progresses. At the highest load, the Green–Lagrange strain reaches a 12.5% extension with a corresponding ultra-high strength of about 7.45 GPa at the most strained volume still in the elastic regime. The determined stretch modulus indicates a significantly lower elastic response with an approximated Young's modulus (E ≅ 65 GPa) and a third-order elastic constant, C111 ≅ −350 GPa. Surprisingly, these constants suggest a 25–35% of that of the bulk counterparts. Ultimately, the method not only provides a quantitative description of the bent Cu NWs, but also indicates the robustness of the theory of nonlinear elasticity.
1 Introduction
One-dimensional nanowires (NWs) have gained considerable attention in the last few decades due to their outstanding optical, electrical, chemical and mechanical properties and their potential to be used as building blocks in novel nanotechnological applications such as micro/nano electromechanical systems, photocatalysis, sensing and energy conversion applications where unique functionalities are required.1–5 With use of nanowire geometry, integrated chips could utilize the vertical configuration of NWs in order to increase the device density, awakening great interest for the application of NWs in nanoscale electronic/optoelectronic devices.2,6–12 Interconnects are typical candidates for these purposes. Many kinds of one-dimensional (1D) conductive nanomaterials have been intensively investigated in order to find their long-term stability and conductivity, such as carbon nanotubes and13 metallic NWs made out of Mo,14 Ag,15–19 Au,20,21 Pt,22 TiO2 (ref. 5) and last but not least Cu.23,24 In most cases, Cu as an ideal material has been found to be the most abundant and cost-effective candidate for commercial purposes even if there are still challenges with surface oxidation or polycrystallinity.23–26 Cu NWs have great importance as the active component of nanoelectronic devices due to their high electrical and thermal conductivity. However, in operation, NWs are subjected to mechanical and electrical stresses which impact their mechanical properties.20 Generally, the fabrication of NW-based devices relies on the mechanical properties of NWs.27 Therefore, the applications of NWs inevitably require a complete understanding of their mechanical properties.From experimental perspectives, early studies investigating Sn whiskers of about 20 μm diameter showed that they exhibited an elastic strain of 2–3%, an order of magnitude higher than their bulk counterparts28 but still only 10% of the theoretical prediction.29,30 These findings encouraged the development of whisker fabrication technologies as well as theoretical studies for characterizing the mechanical properties of whiskers.31 As a result, in the last two decades the development of nano-manipulation techniques based on focus ion beam technology (FIB-SEM),32 electron microscopy (EM),33 the integration of micro-electro-mechanical systems (MEMS) into electron microscopes,34,35 and atomic force microscopy (AFM), enabled the mechanical characterization of NWs on a new level. For instance, the AFM-based three-point bending test has been used for characterizing the elastic modulus of various NWs, including Ag,36 Si,37 Ge,38 TiSi2,39 NiC,40 SiC,41 SiO2,42 ZnO,43 and CuO44 and metallic glasses.45 Alternatively, the contact resonance method in an AFM, has also become a popular non-destructive method to measure the elastic properties of NWs, such as ZnO33,46 oxidized Si47 and Si.48 As a benefit to the current experimental potentials, alternatives could reliably support the scientific achievements in this field. Furthermore, computational simulations have also provided new insights in the mechanical behavior of NWs.12,49–54 The investigated NWs have been consistently shown to exhibit unique physical properties that are significantly different to their 2D, thin film, or 3D, bulk counterparts, probably due to their extremely small physical size and high surface-to-volume ratio.55–63
From a mechanical perspective, the assumption that materials are linearly elastic is successfully used in many engineering applications. For instance, the strain ε and stress σ before yielding was derived from the load-displacement curve obtained from an AFM tip.64 In general, the stress–strain behavior was found to be more-or-less linear until apparent yielding or fracture. A previous study also showed that the modulus derived from a model allowing only bending could overestimate the strength of the NW by an order of magnitude.37 Zeng et al. investigated theoretically large deflections of nanobeams by considering only infinitesimal strains and supposed accordingly both the bulk material and the surface layer as linearly elastic.65 Yun et al. also described the bending properties of fcc metal NWs proposing a model consisting of an additional surface stress effect by utilizing only a linear material response.66 Theoretical and numerical investigation of bending properties of Cu NWs utilizing a molecular dynamics bending simulation model in a double clamped beam configuration was also conducted by employing only geometrical nonlinearity; however, a nonlinear material response may have described the deflection more realistically.67 In fact, in most cases, the elastic deformation has been characterized by using a fully linear (Euler–Bernoulli beam theory) or a partially linear approximation for the description. However, in many modern applications that involve larger strains, the deformations become inherently nonlinear (geometrically and mechanically). For example, it has been found that the mechanical strength of NWs decreases as the diameter is reduced. Short NWs are less ductile and long Cu NWs more ductile in bending tests.52 Furthermore, homogeneous isotropic non-linear elastic materials can already be found in several industrial areas such as pharmaceutical,68 aerospace,69 and food processes70 or microelectronics industry.71 Therefore, to describe the mechanical aspects of these materials, appropriate models supported by rigorous mechanical analysis are needed as they can reveal novel pathways to potential applications.72–76
The mechanical response of a homogeneous isotropic linear elastic material can fully be characterized by two physical constants. By contrast, the mechanical response of nonlinear elastic materials is described by mathematical parameters which are scalar functions of the deformation.77 There are several applied approaches to determine the appropriate parameters appearing in the mathematical models. In practice, the iterative variation of the constant coefficients in hyperelastic models has been found to be an appropriate method since the coefficients can be altered easily as they may be related directly to the linear elastic constitutive parameters.77 Therefore, we consider here a method consisting of nonlinear constitutive parameters in terms of geometrical and mechanical non-linearity for homogeneous isotropic elastic materials within the theoretical framework of finite elasticity, which in principle provides a complete description of the nonlinear elastic response of Cu NWs in bending tests as a solid, metallic, nano-crystalline material under different concentrated loadings.
The demand for a model that describes accurately the small-to-moderate range of deformation is quintessential in the application of rubber-like metallic materials. From a scientific perspective, NWs provide an ideal field for understanding the intrinsic mechanical properties of solid materials at the transition between linear and non-linear behavior. Here we report an advanced, nonlinear bending characterization method of Cu NWs synthesized via template-assisted electrodeposition from an aqueous solution. Morphological, structural and compositional investigations are also performed by using scanning electron microscopy (SEM), transmission electron microscopy (TEM) and energy-dispersive spectroscopy (STEM-EDX). Furthermore, a mesoscale technique is employed to determine the mechanical properties of NWs. With the assistance of a micromanipulator nanoprobe system installed within the SEM chamber, bending tests are conducted on individual, focused-ion-beam (FIB) fabricated NWs with a concomitant recording of the corresponding forces. Based on the deflection curve as a function of the applied forces, the nonlinear stress, nonlinear strain and, through the constant coefficients implemented in the elastic model, the incremental stretch modulus are determined numerically. This may also provide the approximated linear elastic Young's modulus.
2 Material and methods
2.1 Sample preparation
For the TEM investigation, the electrodeposition with a nominal pore size of 50 nm was conducted at a potential of E = −0.4 V for 3 minutes. After the deposition, the membrane was put into a 10 mL tube and dissolved in 0.7 mL dichloromethane (CH2Cl2) in an ultrasonic bath at a temperature of 40 °C for 3 minutes. In the following step, 0.1 mL of ethanol was added to CH2Cl2 and, without the dissolved membrane, the wires were pipetted on a nickel grid with a mesh size of 200 μm provided by Plano.
For the SEM investigation and the bending tests, the electrodeposition was conducted using a membrane with a nominal pore size of 100 nm at a potential of E = −0.4 V for 6 minutes. After the deposition, the membrane was dissolved in CH2Cl2 at a temperature of 35 °C for 30 minutes. As shown in Fig. 1, a typical SEM micrograph demonstrates the homogeneously distributed NWs in high density. The average length of the NWs grown on the sputtered gold layer amounts to 7 μm and the average diameter to 200 nm.
2.2 Characterization
3 Theory
3.1 General framework
With moderately large (<10–12%) or large deformations, the reference and deformed states can no longer be superposed. Strain and stress must be defined in both configurations leading to an Eulerian (current) and Lagrangian (reference) frame of approach. For linear elasticity theory, the difference between Lagrangian and Eulerian variables can be neglected. On the contrary, for nonlinear elasticity theory, where deformations can be large, we have to confront the difficulty that the balance of stresses is performed in the deformed state, while the constitutive relation refers to the reference configuration. For more details and fundamentals, the readers may refer to Ogden79 on non-linear elasticity theory.First, to define a nonlinear strain tensor, one can make use of the polar decomposition theorem,80 which states that: the right and left Cauchy–Green tensor (C and B, respectively) are functions of the deformation gradient tensor, F, as C = FTF and B = FFT. B and C have the same eigenvalues and therefore the principal invariants of the Cauchy–Green tensors B and C can be formulated similarly. From these basic kinematic quantities derived as functions of the principal invariants of the Cauchy–Green tensor, we can define strain tensors. Some of those routinely used tensors that combine both Lagrangian and Eulerian strain tensors are e.g. the Hencky (logarithmic or true) strain tensor,81 the Biot strain tensor,82 the Green strain tensor83 and the Almansi strain tensor.83 These strain tensors are independent of rotation, and for small elastic deformations, they are equivalent to the infinitesimal strain from the linear elastic theory.
Similar to the different nonlinear strain tensors, one can define several stress tensors e.g. the Cauchy stress tensor, or the 1st Piola–Kirchhoff or 2nd Piola–Kirchhoff stress tensor.77 It is worth noting here that one must be careful with these tensors because while e.g. the 1st Piola–Kirchhoff stress tensor, which represents the force per unit area in the reference configuration, is found suitable for describing stress, this stress tensor is not generally symmetrical in contrast to the Cauchy stress tensor, σ. On the other hand, the 2nd Piola–Kirchhoff stress tensor, due to its symmetry, is preferable in, e.g., computational approaches,84–86 but has no physical meaning. For the sake of simplicity, we restrict the discussion to the material's homogeneous isotropic hyperelastic properties that is consistent implicitly with derivatives of a strain-energy density function that depends only on the deformation gradient F and is zero at the unstressed state.77
In this study, we use the total Lagrangian formulation, where the nominal stress P (1st Piola–Kirchhoff stress) and the material stress S (2nd Piola–Kirchhoff stress) relate forces in the reference frame and the current frame to areas, dA0, in the reference configuration, defined as:
| df = P × dA0, | (1) |
| df0 = S × dA0. | (2) |
The force in the reference configuration can be deduced from the current configuration using a suitable mathematical mapping. Therefore, f0 is only a back-transformed force vector. It is worth noting here that this is only a mathematical definition. In physical reality the stress tensor can only be measured in the deformed state. The suitable mapping involves the deformation gradient tensor as follows:
| df = F × df0 | (3) |
| S = F−1 × P | (4) |
Beside the strong preferences found in computational approaches, not only can the symmetry of the 2nd Piola–Kirchhoff tensor be utilized, but it can also be shown to be an energy-conjugate to the Green–Lagrange strain tensor, E. It is therefore the standard choice for a constitutive relation.
3.2 Nonlinear elastic deformation – Green–Lagrange strain tensor
For a complete description of deformation, the chosen material stress, S, and the Green–Lagrange strain, E, with an incorporated displacement field, u = (u(x, z), v, w(x)), must be expressed for the particular sample geometry and the deformation involved in the deformation process. In this study, the concentrated load acts at the free end of the one-dimensional, cylindrical beam (NW) with a typical aspect ratio at or above 16, while the other end can be considered fixed. For the bending experiment, schematically shown in Fig. 2, the following assumptions are established: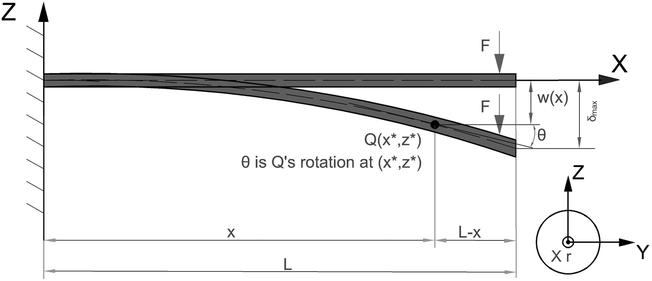 | ||
| Fig. 2 Schematic of the arrangement of the non-linearly deformed, deflected beam in terms of the reference frame. | ||
• All material points on an initial cut also align on a plane in the deformed beam. For a typical beam with an aspect ratio of about 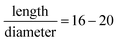 , the relative amplitude of warping is in the order of 10−3. Therefore, the warped cross-section can be neglected (εxz ≅ 0).
, the relative amplitude of warping is in the order of 10−3. Therefore, the warped cross-section can be neglected (εxz ≅ 0).
• Anticlastic deformation is negligible. Uniaxial stress gives rise to the tri-axial strain state (εyy = εzz = −ν/Eσxx). With realistic values of about ν = 1/3 and σyield/E = 10−3 − 10−2, the width or height of the beam changes up to 0.1–1%. This negligible change in the cross-sectional dimension has no effect on the deflection curve solution and the major strains/stresses (εyy = εzz ≅ 0).
• Changes of the cross-sectional shape and size of the beam are assumed to be negligible. Therefore, the displacement vector is a function of the x-coordinate (w = w(x)) only.
• Deformation develops under the assumption of planar deformation meaning that the y-component of the displacement vector vanishes (v = 0).
According to the assumptions made for the bending, the satisfying u-component (in the x-direction) of the displacement vector can be defined as a linear function of z as
| u(x, z) = uo − θ(x)z at any x, | (5) |
The deformation gradient tensor, taking into account the aforementioned assumptions, F, can now be expressed using the displacement field given in eqn (5) as
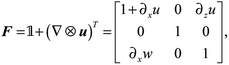 | (6) |
 | (7) |
Thus applying eqn (6), the Green–Lagrange strain tensor yields
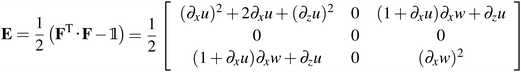 | (8) |
The most significant response derived from bending is the Exx term in E. There are several perspectives on that issue, Exz = Ezx could also be investigated, but due to the assumptions established, they play a decisive role only at extremely large bending angles. Therefore, the theoretical considerations conducted here take only the Exx tensor component into account.
To develop this point further, taking the 1st derivative of eqn (5) with respect to x, (∂xu(x, z) = ∂xuo − ∂x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(x)z) and assuming that there is no initial axial force, No (No = 0, so uo = εo = 0), Exx yields
θ(x)z) and assuming that there is no initial axial force, No (No = 0, so uo = εo = 0), Exx yields
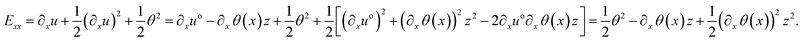 | (9) |
At moderately large/large deformations, the strain-displacement relation must be amended with higher order terms of the displacement field. For extremely large deformations (local rotation in the bending test), full non-linearity is needed. In this study, as shown in eqn (9), the quadratic approximation in u of the displacement field is applied. Consequently, as an additional feature compared to the elementary beam theory (Euler–Bernoulli), the beam axis also extends due to the rotation of the deformed cross-section as the gradient of the axial component of the displacement vector.
At a moderately large deformation, the curvature of the deflected beams must also be developed to a higher level of approximation. As illustrated in Fig. 3, it is necessary to consider the initial and deformed configuration of the beam. Contrary to the Euler–Bernoulli beam theory, which assumes ∂xw = θ, ∂xw = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is considered instead.
θ is considered instead.
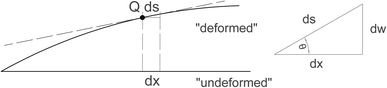 | ||
| Fig. 3 Illustration of the non-linear change of length of the deflected beam axis produced by local rotation. | ||
We also need to consider the full non-linearity of the curvature. By definition, and using the notation illustrated in Fig. 3, the curvature can be given as a function of the current length element, s, as
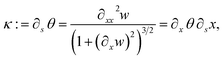 | (10) |
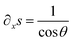 and
and 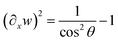 , ∂xs yields in the range of 0 < θ < 90° that
, ∂xs yields in the range of 0 < θ < 90° that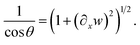 | (11) |
To conclude, eqn (9) can now be formulated as a function of the displacement vector component, w(x) and its derivatives as
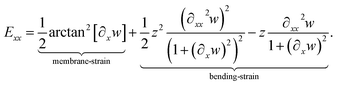 | (12) |
Eqn (12) represents the Exx – Green–Lagrange tensor component equipped by the full-nonlinearity of the curvature with a quadratic approximation in u of the displacement field (geometrical non-linearity).
3.3 The 1st Piola–Kirchhoff stress tensor
As mentioned before, the 1st Piola–Kirchhoff stress tensor, P, describes the stress in the reference configuration in a non-symmetric manner, while the symmetric, but non-physical, 2nd Piola–Kirchhoff stress tensor, S, can be shown to be the energy-conjugate to the Green–Lagrange strain tensor, E. As shown in eqn (2)–(4), the S tensor can be given by the product of the inverse deformation gradient tensor, F−1, and the 1st Piola–Kirchhoff tensor, P. Additionally, in eqn (6) and (8), the relevant components of the F−1 and E tensors are determined. Thus, the most general constitutive law| Sxx = ϕ(Exx, Exz, Ezx, Ezz) | (13) |
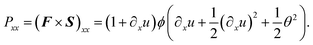 | (14) |
This equation can now be both geometrically and mechanically non-linear. To expand on this point, let 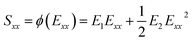 be the quadratic approximation of the relation between the 2nd Piola–Kirchhoff stress and the Green–Lagrange strain with constant coefficients of E1 and E2. It is worth noting here that this assumption for the stress–strain relation is consistent with the third-order expansion in weakly nonlinear elasticity in which the strain energy is expanded up to the third order in the power of the Green–Lagrange strain tensor. In the view of the third-order expansion, valid for every incompressible isotropic hyperelastic solid, eqn (14) turns into the following form after implementing the quadratic mechanical approximation as
be the quadratic approximation of the relation between the 2nd Piola–Kirchhoff stress and the Green–Lagrange strain with constant coefficients of E1 and E2. It is worth noting here that this assumption for the stress–strain relation is consistent with the third-order expansion in weakly nonlinear elasticity in which the strain energy is expanded up to the third order in the power of the Green–Lagrange strain tensor. In the view of the third-order expansion, valid for every incompressible isotropic hyperelastic solid, eqn (14) turns into the following form after implementing the quadratic mechanical approximation as
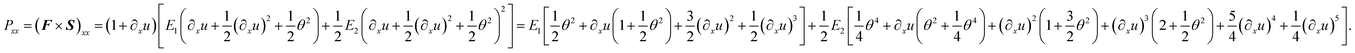 | (15) |
Since ∂xu = ε0 − ∂x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θz (see the first derivative of eqn (5) with respect to x), and keeping only the terms in ∂xu and θ to have Pxx = Pxx(∂xu, (∂xu)2, θ2, ∂xu
θz (see the first derivative of eqn (5) with respect to x), and keeping only the terms in ∂xu and θ to have Pxx = Pxx(∂xu, (∂xu)2, θ2, ∂xu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, (∂xu)2
θ2, (∂xu)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, θ4, ∂xu
θ2, θ4, ∂xu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ4) in eqn (15), the bending moment, as given by the definition of
θ4) in eqn (15), the bending moment, as given by the definition of 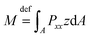 (where A is defined as the beam cross-section), can also be determined as
(where A is defined as the beam cross-section), can also be determined as
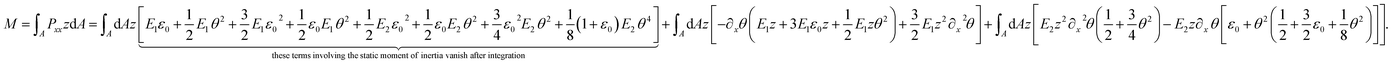 | (16) |
Incorporating the full non-linearity of the curvature defined in eqn (10), and applying −z∂x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −zκ∂xs, eqn (16) yields
θ = −zκ∂xs, eqn (16) yields
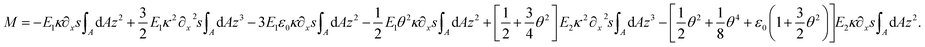 | (17) |
Since 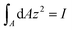 is the second moment of inertia (R4π/4 for circular cross-section),
is the second moment of inertia (R4π/4 for circular cross-section), 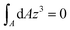 by symmetry, and by neglecting ε0, eqn (17) finally becomes
by symmetry, and by neglecting ε0, eqn (17) finally becomes
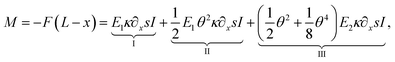 | (18) |
In eqn (18), the three distinguishable terms include different aspects with respect to elasticity. The first term (I), as a quasi-linear term, contributes to the moment similarly to E1∂2xxwI as if full linearity would be utilized (Euler–Bernoulli beam theory). In this study, on the contrary, the curvature is utilized with its full-nonlinear form (quasi-). The second term (II) contributes to M due to geometrical non-linearity (quadratic approximation in u of the displacement field). Finally, the third term (III) contributes in a mechanical sense to M. It considers the non-linear response of the material to the strain.
The eqn (18) can also be expressed in terms of the deflection function using the formula given in eqn (10). This provides an equation for the moment (eqn (18)) that consists of linear and quadratic functions of the first and second derivatives of the deflection curve with respect to x. Thus the described theoretical approach can approximate directly the constants E1 and E2 appearing in the mathematical model by employing the appropriate numerical method. In this study, through the applied numerical method, one must solve a boundary value problem by reducing it to the system of an initial value problem (shooting method).
Furthermore, the tensor component, Pxx, can also be formulated as the following,
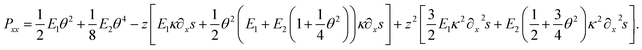 | (19) |
To expand the overall description of a strongly non-linearly deflected beam, another important quantifier similar to the Young's modulus in isotropic linear elasticity can be introduced. For this purpose, the incremental stretch modulus is introduced to study the nonlinear elastic response of an isotropic hyperelastic material under bending conditions.
The role of this elastic modulus is to reflect stiffening (or softening) in a material under strong loading. The gradient of the 1st Piola–Kirchhoff stress tensor, P, with respect to the deformation gradient, F, or equivalently, the gradient of P with respect to the displacement gradient, F − I, provides the definition of the incremental stretch modulus, Ỹincr, as
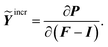 | (20) |
Applying eqn (15), the incremental stretch modulus yields its final closed form in terms of derivatives of the deflection function as
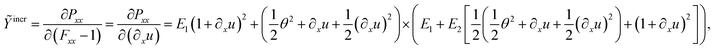 | (21) |
To bring the theoretical considerations to a conclusion, with the assistance of the determined Exx, Pxx and Ỹincr, a complete non-linear description of bending of NWs up to a quadratic order can be conducted along with experimental deflection curves.
4 Results
4.1 Mechanical bending tests
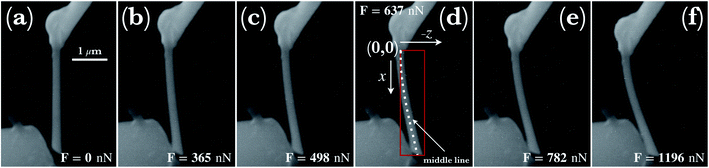
To determine the deflection curves, w(x), referring to the synthesized individual Cu NW, concentrated lateral forces are exerted by the micromanipulator at the NW's free end. While the fixed end connected to the W post was stable, the force measurement tip detected the applied lateral forces during loadings. The force measurement tip was moved in the direction perpendicular to the NW to apply gradually increasing lateral force. Furthermore, while applying the lateral force at the free end, the free end did not slip on the surface of the measurement tip away from the initial point. This means that the NW stretches during the experiment (cf.Fig. 2). Fig. 4 illustrates a series of snapshots of SEM images that display the process of bending of an individual Cu NW with a length of 3.048 ± 0.08 μm and a radius of 110 ± 12 nm. As shown in Fig. 4d, the initial point of the deflection is defined as the point where the NW is connected to the W post by Pt glue. In Fig. 4a–f, the increasing deflection indicates the gradually increased lateral force up to about a maximum force of 1196 nN, where the nanowire started to deform plastically. At higher applied forces (F > 1196 nN), residual deformation was detected. After each bending test demonstrated in Fig. 4a–f, the tip was unloaded and the deflection decreased simultaneously while the free end of the NW moved back to its initial position and restored completely its original shape without any residual plastic deformation.The investigated deflections in the load-controlled bending were conducted under the forces of 365 ± 35 nN, 498 ± 46 nN, 637 ± 52 nN, 782 ± 63 nN and 1196 ± 95 nN. The deflection paths (dots in Fig. 5) are determined by using the middle line shown schematically in Fig. 4d in a Cartesian coordinate system. As shown in Fig. 5, with increasing applied force, the maximum displacement of the wire at the free end reaches about 250 nm, 370 nm, 520 nm, 620 nm, and 840 nm, respectively, first in the elastic-, and further in the elasto-plastic/plastic region as the maximum displacement reaches 1000 nm and 1450 nm. Investigating the fitted model curves, initially, the gradient of the curvature along the wire can be approximated by a constant, however, at larger applied forces, the gradient indicates a stronger variation with respect to strain. Along the wire, towards the free end of the NW, the curvature seemingly converges to infinity. Consistently, curvature of the investigated deflections indicates that in the region closer to the fixation point, the largest bending contribution occurs and with increasing distance from the clamped end, the bending effect vanishes.
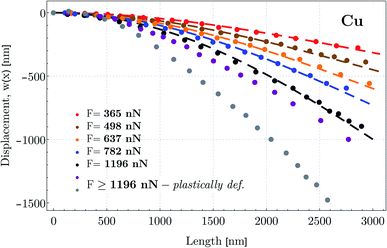 | ||
| Fig. 5 Typical deflection paths determined by displacements at points along the middle line of the NW with an average distance of about 120 nm. The first 5 deflections were conducted under lateral concentrated forces ranging from 365 nN to 1196 nN at the free end. Two additional deflections colored by violet and gray refer to those applied forces (F > 1196 nN) when the NW started to deform plastically. Additionally, deflection curves defined as the nonlinear theoretical moment functions are shown by color-coded dashed lines after solving eqn (18) numerically with the experimental data. | ||
In order to capture a fully nonlinear (higher order than quadratic approximation) effects in solids, it is now known that the fourth-order theory is the minimal model to be considered in terms of the expansion of the strain energy up to at least the fourth order of strain.83 In our model, only the third-order expansion is applied implicitly (see eqn (13)–(21); cf. Sec. 3(b), p. 8 in ref. 87). As shown in Fig. 5, the color-coded deflection curves, w(x) (dashed lines), determined by solving eqn (18), verify within 5% error in the entire range of experimental data that the third-order approximation with the determined E1 and E2 parameters is adequate in the small-to-moderate regime.
4.2 Morphology, crystalline structure and composition
The morphology of 20 nanowires has been analyzed using TEM. Their diameter was found to vary in the range of 110 ± 12 nm (cf.Fig. 6b). The surface of the cylindrical shaped wires is smooth and the diameter of a single NW varied less than ±3 nm over the total length. The SAED pattern of the region covering four nanowires represented in Fig. 6b is shown in Fig. 6a. It is obvious that the NWs are polycrystalline, which is also observed in the BF images. The grain sizes are in the range of the NWs' diameter or smaller. The observed reflections in the SAED pattern fit well to the FCC reflections expected from pure Cu, as indicated in red color, but there is a small amount of reflections that cannot be described with a FCC structure factor. In order to find their origin, the software package JEMS88 was used to simulate theoretical diffraction patterns that generate those reflections. A very good match was found with cubic copper(I)oxide (Cu2O), as indicated in blue color in Fig. 6a, which fitted all reflections that could not be indexed as FCC Cu. Since the intensity of Cu2O reflections is less, the signal probably originates from a thin shell of Cu2O.In confirmation, Fig. 6d represents a dark field (DF) image of one NW, for which a strong beam scattered in the [111] direction of Cu2O was tilted to the optical axis as indicated by the inset figure.† From the DF image it becomes clear that the Cu2O reflections originate from a thin shell with a thickness of (1.7 ± 0.4) nm around the NW. The NWs in Fig. 6b were further analyzed by EDX (cf.Fig. 6c). Besides Cu, a signal of nickel that stems from the TEM grid and a weak oxygen signal were detected by EDX. The amount of oxygen could be quantified as (1.5 ± 0.3) at% which is very close to what is expected for a thin shell of Cu2O around the NW. Theoretically, a Cu NW with a diameter of 98 nm that consists of a Cu2O shell with a thickness of 1.7 nm should contain 2.1 at% oxygen atoms considering the lattice parameters of Cu (0.3615 nm) and Cu2O (0.426 nm). The Cu2O shell could not be resolved in the EDX map, and the oxygen signal was homogeneous within the wires and thus, it can be concluded that the wires are composed of a pure copper core and a rather thin Cu2O shell.
5 Discussion
5.1 Nonlinear deflection
As shown in Fig. 7, through the bending test, the increasing applied force on NWs with an aspect ratio of about 16 resulted in specific experimental deflection paths (blue dots). From F = 365 nN to 1196 nN, the deflection does indicate a nonlinear behavior featured by a maximum displacement at the free end ranging from about 300 nm to 900 nm, respectively. For a comparison, shown in Fig. 7a–e, theoretical deflection curves were determined by applying (i) a fully linear approach (Euler–Bernoulli theory (E–B), E1∂2xxwI, the linearized first term in eqn (18); green curve), (ii) a linear appr. (E–B) with a fully nonlinear curvature consideration (E1κ∂xsI in eqn (18); brown curve), (iii) with an additional geometrical nonlinearity (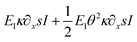 in eqn (18); red curve) and finally (iv) with a quadratic geometrical and mechanical approximation (
in eqn (18); red curve) and finally (iv) with a quadratic geometrical and mechanical approximation (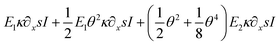 in eqn (18); black curve). In case of (i)–(iii), shown in Fig. 7, E1 and E2 are derived from the fitting result related to the case (iv). The current illustrated colored curves show that while the black curve (case (iv)) approaches accurately the experimental data in the entire region, the other model predictions match the experimental data only in the region close to the clamped end. Alternatively, other mathematical parameters were also used in the fitting procedure, however, in case of (i)–(iii) theoretical predictions failed to approach the experimental data with a discrepancy measure of about 85%. Therefore, by utilizing the least-squares method, no fitting parameters were found to be appropriate to characterize the deflection paths in the entire region except when higher order approximations in both geometry and mechanics are utilized. With respect to the shape of w(x), E1 and E2 must be positive and negative, respectively.
in eqn (18); black curve). In case of (i)–(iii), shown in Fig. 7, E1 and E2 are derived from the fitting result related to the case (iv). The current illustrated colored curves show that while the black curve (case (iv)) approaches accurately the experimental data in the entire region, the other model predictions match the experimental data only in the region close to the clamped end. Alternatively, other mathematical parameters were also used in the fitting procedure, however, in case of (i)–(iii) theoretical predictions failed to approach the experimental data with a discrepancy measure of about 85%. Therefore, by utilizing the least-squares method, no fitting parameters were found to be appropriate to characterize the deflection paths in the entire region except when higher order approximations in both geometry and mechanics are utilized. With respect to the shape of w(x), E1 and E2 must be positive and negative, respectively.
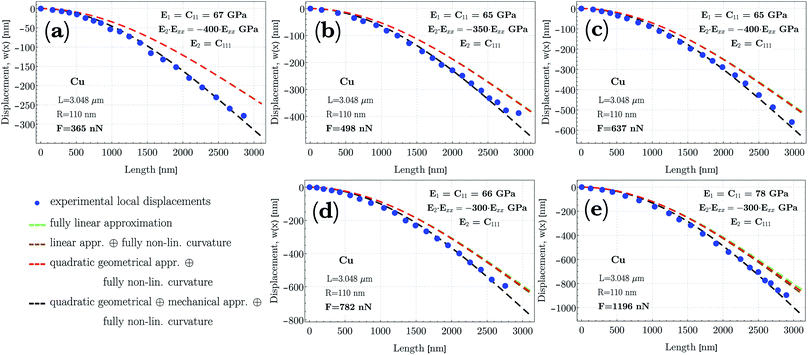 | ||
| Fig. 7 Deflection paths, w(x), as a function of position (x) along the NW determined by displacements at points (blue dots) through the middle line with an average distance of about 120 nm. The applied forces are (a) 365 nN, (b) 498 nN, (c) 637 nN, (d) 782 and (e) 1196 nN. At higher applied forces (>1196 nN), plastic deformation began to occur. Theoretical deflection curves employing eqn (18) of nonlinear deflection are also plotted for several perspectives: (i) fully linear appr. (E–B theory; green, dashed line), (ii) linear appr. with fully nonlinear curvature (brown, dashed line), (iii) quadratic geometrical appr. with fully nonlinear curvature (red, dashed line) and (iv) quadratic geometric and mechanical appr. in addition to fully nonlinear curvature (black, dashed line). Discrepancies between the shape of curves determined by either fully nonlinear or the somewhat linear-nonlinear approaches are clearly distinguishable (for more details, see text in the section ‘Discussion, Nonlinear deflection’). As mechanical properties, the approximated Young's modulus, C11, and the third-order elastic constant, C111, are also shown in the figures. | ||
In all cases attributed by some kind of linearity, the given deflection paths indicate stiffer material properties, whereas in case of a complete lack of linearity, the response of NWs indicates a relative softening. The larger the exerted force, the larger the discrepancy between the complete nonlinear and the somewhat linear descriptions of deflection. As shown in Fig. 7, the approximated linear equivalent of the Young's modulus remains constant at about E1 ≅ 65 GPa (Ebulk ≈ 110 − 128 GPa) within experimental error, suggesting that at small strains (<1%), the Cu NW exhibits massively different elastic stiffness compared to its 2D or 3D counterparts. At F = 1196 nN, the relatively higher E1 ≅ 78 GPa indicates that during deflection, close to the yield strength, the deformation became more elasto-plastic rather than being only elastic. The production and interaction of dislocations may cause the material to stiffen. As one of the major results, the magnitude of 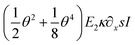 in eqn (18) considerably contributes to the calculated moment, M. In terms of consistency, we emphasize that the magnitudes of the fitting parameters of E1 and E2 may still depend on the aspect ratio on which the strength and deformation mechanism depend (cf.ref. 89).
in eqn (18) considerably contributes to the calculated moment, M. In terms of consistency, we emphasize that the magnitudes of the fitting parameters of E1 and E2 may still depend on the aspect ratio on which the strength and deformation mechanism depend (cf.ref. 89).
The impact of reduced dimensions on the mechanical properties of ultra-thin nanomaterials has also been investigated. For instance, as a core–shell structure, the crystalline cubic silicon carbide with/without a SiOx shell has shown significantly different Young's moduli in nanotensile tests.90 Moreover, a study of the core/shell structure of GaAs(core)/Al2O3(shell) has also indicated that the elastic modulus of amorphous Al2O3 increases significantly when the thickness of the layer is smaller than 5 nm.64 Hence, the Young's modulus for the composite core–shell structure changed dramatically under 5 nm. Thus, in order to attain the most appropriate fitting parameters (E1 and E2) for the relevant deflection curves, results attained from TEM and EDX analysis should also be taken into consideration. Based on findings mentioned in the section dealing with morphology, it could be confirmed that the NW is almost 100% polycrystalline Cu with a relatively negligible thin Cu2O shell formation. This shell also indicates its crystalline structure. Additionally, the bulk Young's modulus of Cu2O is in the range of E = 120 GPa, which is similar to that of the pure bulk Cu.91 Therefore, we conclude that the deflection curves with the fitting parameters can reliably be related to the Cu material.
5.2 Green–Lagrange strain, Exx
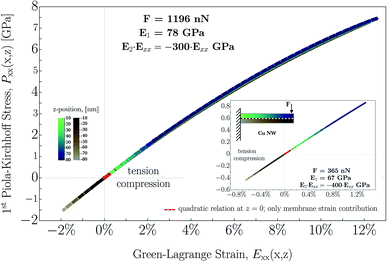
In Fig. 8a–c, the calculated Green–Lagrange strain (eqn (12)) is demonstrated in the cases with applied forces of F = 365 nN, F = 637 nN and F = 1196 nN. The middle line of NWs, shown in the schematic of Fig. 8a–c, which separates the upper (red) and bottom (blue) parts, is to help emphasize the evolving strain behavior with respect to the x and z coordinates. In Fig. 8a–c, strains referring to the upper part of NW (red) are plotted as a function of z in such a manner to be visualized at discrete values of z in the range of 10 nm to 60 nm with an increment of 10 nm. At the bottom region (blue), the plot ranges from z = −60 nm to −10 nm. At z = 0, where only the membrane strain is taken into account (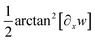 , cf.eqn (12)), the strain is illustrated by a black solid line. Strain at the highest applied force (F = 1196 nN) exhibits an enormous relative displacement of 12.5%, meaning that the elastic regime is almost an order of magnitude broader compared to that of the bulk counterpart. On the other hand, this result slightly overcomes earlier findings referring to the measurement of perfect single-crystalline Cu NWs, where the elastic limit was determined to be 7.2%.92 This difference may be due to the fact that polycrystallinity plays a crucial role in the preferred deformation mode. The seemingly large amount of strain, however, was also recorded in bent Si NWs of up to 14% total strain.20
, cf.eqn (12)), the strain is illustrated by a black solid line. Strain at the highest applied force (F = 1196 nN) exhibits an enormous relative displacement of 12.5%, meaning that the elastic regime is almost an order of magnitude broader compared to that of the bulk counterpart. On the other hand, this result slightly overcomes earlier findings referring to the measurement of perfect single-crystalline Cu NWs, where the elastic limit was determined to be 7.2%.92 This difference may be due to the fact that polycrystallinity plays a crucial role in the preferred deformation mode. The seemingly large amount of strain, however, was also recorded in bent Si NWs of up to 14% total strain.20
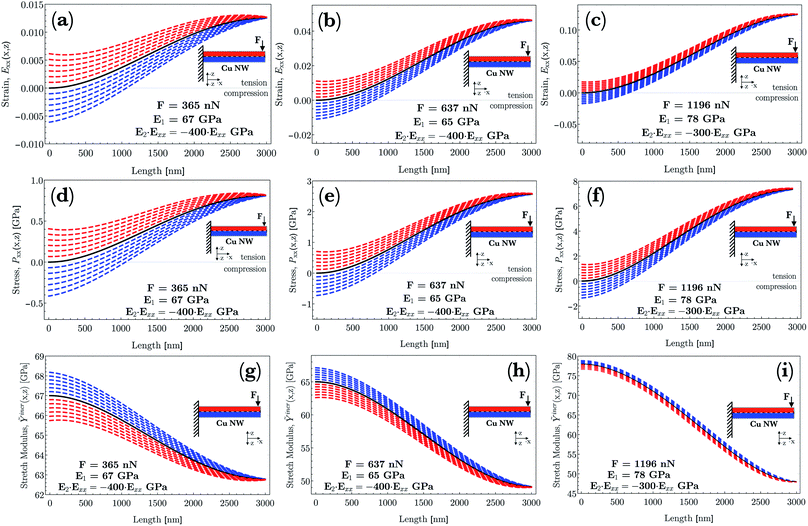 | ||
| Fig. 8 (a–c) Green–Lagrange strain, Exx, (d–f) 1st Piola–Kirchhoff stress, Pxx, and (g–i) incremental stretch modulus, Ỹincr, are plotted in a consistent way as a function of the position, x, along the NW. Derivations of strain, stress and the stretch modulus are based on the numerically determined deflection curves, w(x), shown in Fig. 7 (black dashed lines). For all demonstrated physical quantities, the recorded forces are F = 365 nN, F = 637 nN and F = 1196 nN. A schematic of the initial arrangement of NWs in the reference frame is also shown. The middle line of the NW that separates the upper (red) and bottom (blue) parts is to help emphasize the evolving (a–c) strain, (d–f) stress and (g–i) stretch modulus behavior with respect to the z coordinate. At z = 0, the corresponding physical quantities (a–i) are illustrated by black solid lines. Additionally, in (g–i), the approximated linear equivalent of the Young's modulus at each force is also illustrated concomitantly with the third-order elastic constants (E2 = C111) being almost constant at E1 ≅ 65 GPa, irrespective of the applied force. | ||
In a bending test, the bending strain and the membrane strain compete. Irrespective of the applied force, the G–L strain, Exx, at x = 0 varies only slightly asymmetrically in the range of (i) −0.0061 to +0.0063 (F = 365 nN), (ii) −0.0112 to +0.0117 (F = 637 nN) and (iii) −0.0189 to +0.0195 (F = 1196 nN) with increasing/decreasing z. This contribution is purely the bending strain, significantly large in all cases at the clamped end. To expand on this point further, the overall strain at small, increasing x values along the NWs can be characterized by a convex regime of the membrane strain added to the diminishing bending strain. After the convex regime, the strictly increasing behavior of the membrane strain becomes decreasing (concave regime) and it develops with a concomitant reduction of the prevailing bending strain. As a result, as x approaches the free end of the NWs, the membrane strain governs the overall strain. Consequently, the regions under the middle line and closer to the clamped end are still characterized by compression. However, further from this end, the overall strain becomes positive (tension) as a function of z. At larger applied forces, this phenomenon becomes even more pronounced. On the contrary, the upper region above the middle line is always characterized by tension.
5.3 First Piola–Kirchhoff stress, Pxx
As a general feature, shown in Fig. 8d–f, the stresses at x = 0 as a function of the z range only slightly asymmetrically between Pxx = −0.41 and + 0.412 GPa at a force of F = 365 nN whereas this range broadens to that of Pxx = −1.44 and +1.48 GPa at F = 1196 nN. Additionally, the determined nonlinear stress (Fig. 8f) surprisingly reaches a relatively high magnitude of Pxx ≅ + 7.45 GPa at F = 1196 nN still in the elastic regime. On the other hand, this result is slightly higher than that found in an earlier study on perfect single-crystalline Cu NWs, where the elastic limit was determined to be about 5.8 GPa.92 This result, however, is consistent with the results mentioned about the morphology where the grain size is determined to be in the range of the NWs' diameter.The different contributions of both bending and membrane strain (cf.eqn (12)) to the stress distribution along the height of the beam causes the zero stress axis to be shifted along the x axis. Thus, the zero stress point initially is inside the beam boundary, whereas it moves out of the thickness of the NW as a function of x. This implies an initial bending-, then later a tension-dominated response developed along the NW. At z = 0, illustrated by a black solid line, only the membrane stress plays a role. This feature is consistent with the result of the diminishing contribution of bending strain with a concomitant developing strain of the beam axis due to rotation (cf.Fig. 8a–c).
Another surprising phenomenon, shown in Fig. 8a & d, b & e and c & f pairwise, is that for all three given force levels, the strain vanishes at a certain position completely with a concomitant reducing stress even though the beam undergoes a moderately large deformation. As shown in eqn (19), the Pxx stress function contains additional terms, for instance 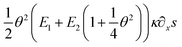 , as compared to a stress function determined by applying a linear approximation both in geometry and mechanics. Obviously, these types of terms contribute to the overall stress and additionally account for the nonlinear phenomena.
, as compared to a stress function determined by applying a linear approximation both in geometry and mechanics. Obviously, these types of terms contribute to the overall stress and additionally account for the nonlinear phenomena.
5.4 Incremental stretch modulus, Ỹincr
The incremental stretch modulus is the nonlinear counterpart of the quantifier of the isotropic linear elastic Young's modulus. In a study of the nonlinear elastic response of an isotropic hyperelastic-like material, Ỹincr plays a crucial role in reflecting stiffening (or softening) in a material as a function of a varying elastic nonlinear strain. As shown in Fig. 8g–i, the incremental stretch modulus reflects a strongly varying elastic response along the NW. As a general feature, Ỹincr decreases with increasing strain, whereas at small strains, the modulus approaches, irrespective of the applied concentrated force, to an approximated Young's modulus, E1 ≅ 65 GPa (except for F = 1196 nN). The continuous reduction in the stretch modulus is the consequence of the third-order polynomial approximation of the strain energy density function.The strain energy density, U, limiting the nonlinear features to the third order, and revisiting the aforementioned relation for Sxx, gives rise to the equation and relations as
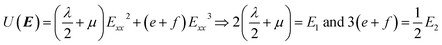 | (22) |
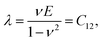 | (23) |
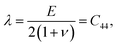 | (24) |
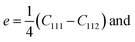 | (25) |
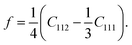 | (26) |
Since the system is isotropic, the Cauchy relation 2C44 = C11 − C12 is always fulfilled. Revisiting the assumptions regarding the negligible change of the cross-sectional dimensions, the Poisson's ratio can be assumed to be ν ≪ 1/3, and the parameters E1 and E2 finally equal E1 = C11 = E and E2 = C111. The determined coefficients of the linear and quadratic term in the stress–strain relation, E1 ≅ 65 GPa (Ebulk ≈ 110 − 128 GPa) and E2 = −400 to − 300 are found to be proportional to earlier findings,94,95 where the analyses provided similar second- and third-order elastic constants as C11 = 163.6 GPa (ref. 94) and C11 = 169 GPa,95 and C111 = −1100 GPa (ref. 94) and C111 = −1271 GPa.95 In both types of constants, the proportionality is found to be between 2.6 and 4.2.
As the strain develops along the NW with a diminishing bending and a concomitant governing membrane strain, the local strain becomes almost purely axial. As a result of E2 < 0, as the axial tensile deformation becomes larger, the stretch modulus reduces drastically. Consequently, at the highest applied load (F = 1196 nN), close to the very end of the NW, the approximated 12.5% almost pure axial strain gives rise to a reduced stretch modulus of about Ỹincr ≅ 48 GPa. Moreover, the asymmetric range of the stretch modulus as a function of z at a certain x can also be interpreted as a result of the higher-order approximation as a function of the bending- and membrane strain. Under compression, the G–L strain is slightly smaller than that in the tensile zone at the same distance (z) from the middle line (at a given x). This discrepancy through eqn (21) magnifies the asymmetry of Ỹincr in terms of the thickness of the red/blue regions. This asymmetry is clearly captured in the sequence of (g) to (i) at all x values along the NW. At z = 0, illustrated by a black solid line, the stretch modulus is based on only the membrane stress and strain.
5.5 Non-linear stress–strain relation
Finally, we focus on the relation between the arising strain and stress determined along the NW. The corresponding strain and stress values are plotted in the inset of Fig. 9 for the applied force of F = 365 nN and in Fig. 9 for F = 1196 nN. The relation between the stress and strain clearly follows a nonlinear relation as predicted by eqn (14) and (19). As given by the equations and assumptions found in the methodology, the strain is described by using a linear approximation of the displacement field (only the first-order Taylor expansion of the displacement field is applied). This may be an underestimation of the real deformation at the beam axis. On the contrary, this linear assumption causes a contribution of the overall strain to be appropriate as demonstrated by the accuracy of the shape of the generated deflection curves shown in Fig. 5 by fitting to the experimental data. However, the Green–Lagrange strain in eqn (12) could be approximated by taking higher-order terms in the Taylor expansion of the displacement field. This is, however, out of the scope of the present study. Away from the middle line, the strain is always governed by the relative ratio of the membrane- and bending strain. In general, the more membrane strain involved, the more quadratic the total strain is. Farther away from the small strain regime, a regime featured by strain larger than 2% can be identified with a quadratic feature as demonstrated in Fig. 9. To analyze the nature of stress as a function of strain, we can either concentrate on the regime demonstrated in Fig. 9 by the yellow-to-blue dashed lines or by the light-to-dark brown dashed lines. In the light-to-dark brown range, the prevailing strain gives rise to only a slightly nonlinear behavior. In the range of ε > 2%, the stress–strain relation suggests a stress–strain behavior controlled by strain-softening. This behavior is typical for e.g. biopolymer networks characterized by one of the most powerful models, the Ogden-model with 1 < α < 2.96 Surprisingly, the metallic Cu NWs do indicate similarities to hyperelastic materials.97The strong aforementioned asymmetry with respect to strain and stress is also well-visualized at the maximum applied force (F = 1196 nN). The asymmetric overall strain develops in such a manner where compression reduces the membrane strain, and tension adds an extra contribution to the membrane strain. As the concentrated load increases, the strict behavior of the increasing membrane strain is higher than the strain reduction caused by the compression under the middle line. Therefore the negative strain generated in the compression region is more intensively overcome by the membrane strain even at small distances from the clamped end. At higher applied forces, the drastically escalating membrane strain governs the corresponding stress. Thus, this asymmetry originates from the competing strain contributions, which also represents a considerable sensitivity to the signed ratios of the local membrane- and bending strains.
6 Conclusions
Successive stages consisting of geometrical and, additionally, mechanical non-linearity can be identified as a contribution in the moderately large extension of NWs. In this study, we provide an explicit bending moment function with terms accounting for the quasi-linearity, geometrical, and finally mechanical non-linearity as global features of moderately large elastic deformation. We applied the method to experimental data of Cu NWs under different concentrated loadings. Additionally, the method may also be suitable for other metals due to a lack of material specific restraints. The major findings can now be summarized as the following:(I) No fitting parameters were found to be appropriate to characterize the deflection curves in the entire region except when higher order approximations in both geometry and mechanics are utilized.
(II) The approximated Young's modulus remains constant at about E ≅ 65 GPa (Ebulk = 110 − 128 GPa) within experimental error suggesting that at small strains, the Cu NW exhibits a massively different elastic response compared to its 2D or 3D counterparts. Furthermore, the corresponding third-order elastic constant, C111 is also determined at around C111 = −300 to −400 (C111–bulk = −1271 to −1100 GPa). Both, the second- and third-order elastic constants are found to be 25–35% of that of the bulk counterparts. As one of the major results, since mechanics is introduced by a nonlinear approach, the magnitude of 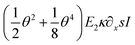 considerably contributes to the calculated moment, M.
considerably contributes to the calculated moment, M.
(III) Strain at the highest applied force (F = 1196 nN) at the free end exhibits an enormous relative displacement of 12.5% meaning that the elastic regime is almost an order of magnitude broader compared to that of the bulk counterpart.
(IV) The determined 1st Piola–Kirchhoff stress surprisingly reaches a relatively high magnitude of Pxx ≅ +7.45 GPa at F = 1196 nN while still in the elastic regime.
(V) The different contributions of both bending and membrane strain to the stress distribution along the height of the beam causes the zero stress axis to be shifted along the x axis. Thus, the zero stress point is initially inside the beam boundary and moves out of the thickness of the NW as a function of x, implying an initial bending-, and later a tension-dominated response developed along the NW.
(VI) The determined incremental stretch modulus, Ỹincr, reflects a significant softening in the material as a function of the varying elastic nonlinear strain. At the highest applied load (F = 1196 nN) close to the very end of NW, the approximated 12.5% strain gives rise to a stretch modulus of about Ỹincr ≅ 48 GPa. Otherwise, the modulus varies considerably along the NW.
(VII) The relation between the stress and strain obviously follows a nonlinear relation predicted by equations established in the theoretical considerations. Analyzing the nature of stress as a function of strain, irrespective of the applied external concentrated forces, the stress behavior in the nonlinear regime is characterized by strain-softening. This behavior is typical for e.g. biopolymer networks characterized by the Ogden-model with 1 < α < 2. Surprisingly, the metallic Cu NWs do indicate similarities in the moderate regime to hyperelastic materials.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors are thankful for the support provided by the German Research Fund (DFG) registered as (SCHM1182/14-1). The authors are grateful for Dr Orsolya Csiszár for the fruitful mathematical discussions about theoretical considerations.References
- A. Heidelberg, L. Ngo, B. Wu, M. Phillips, S. Sharma, T. Kamins, J. Sader and J. Boland, Nano Lett., 2006, 6, 1101–1106 CrossRef CAS PubMed.
- Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, H. Yan, F. Kim and H. Yan, Adv. Mater., 2003, 15, 353–389 CrossRef CAS.
- M. Chang, C. Chung, J. Deka, C. Lin and T. Chung, Nanotechnology, 2008, 19, 025710 CrossRef CAS PubMed.
- S. Lee, C. Tekmen and W. Sigmund, Mater. Sci. Eng., A, 2005, 398, 77–81 CrossRef.
- Z. Ye, H. Zhu, Y. Zheng, W. Dong and B. Chen, Mater. Sci. Eng., A, 2015, 641, 281–289 CrossRef CAS.
- D. Ferry, Science, 2008, 319, 579–580 CrossRef CAS PubMed.
- Y. Shi, H. Li, L. Chen and X. Huang, Sci. Technol. Adv. Mater., 2005, 6, 761–765 CrossRef CAS.
- S. Wang, Z. Shan and H. Huang, Adv. Sci., 2017, 4, 1600332 CrossRef PubMed.
- Y. Gao, H. Wang, J. Zhao, C. Sun and F. Wang, Comput. Mater. Sci., 2011, 50, 3032–3037 CrossRef CAS.
- G. Du and G. Van Tendeloo, Chem. Phys. Lett., 2004, 393, 64–69 CrossRef CAS.
- A. Vazinishayan, S. Yang, D. R. Lambada and Y. Wang, Results Phys., 2018, 9, 218–224 CrossRef.
- C. Peng, Y. Zhan and J. Lou, Small, 2012, 8, 1889–1894 CrossRef CAS PubMed.
- Z. Yao, C. Kane and C. Dekker, Phys. Rev. Lett., 2000, 84, 2941–2944 CrossRef CAS PubMed.
- M. Zach, K. Ng and R. Penner, Science, 2000, 290, 2120–2123 CrossRef CAS PubMed.
- Y. Sun, B. Gates, B. Mayers and Y. Xia, Nano Lett., 2002, 2, 165–168 CrossRef CAS.
- B. Wiley, Z. Wang, J. Wei, Y. Yin, D. Cobden and Y. Xia, Nano Lett., 2006, 6, 2273–2278 CrossRef CAS PubMed.
- W. Xu and S. Yu, Small, 2009, 5, 460–465 CrossRef CAS PubMed.
- L. Luo, S. Yu, H. Qian and T. Zhou, J. Am. Chem. Soc., 2005, 127, 2822–2823 CrossRef CAS PubMed.
- M. Gao, W. Xu, L. Luo, Y. Zhan and S. Yu, Adv. Mater., 2010, 22, 1977–1981 CrossRef CAS PubMed.
- L. Wang, K. Zheng, Z. Zhang and X. Han, Nano Lett., 2011, 11, 2382–2385 CrossRef CAS PubMed.
- K. Critchley, B. Khanal, M. Gorzny, L. Vigderman, S. D. Evans, E. Zubarev and N. Kotov, Adv. Mater., 2010, 22, 2338–2342 CrossRef CAS PubMed.
- G. Marzi, D. Iacopino, A. Quinn and G. Redmond, J. Appl. Phys., 2004, 96, 3458–3462 CrossRef.
- M. Mohl, P. Pusztai, A. Kukovecz, Z. Konya, J. Kukkola, K. Kordas, R. Vajtai and P. Ajayan, Langmuir, 2010, 26, 16496–16502 CrossRef CAS PubMed.
- Y. Shi, H. Li, L. Chen and X. Huang, Sci. Technol. Adv. Mater., 2005, 6, 761–765 CrossRef CAS.
- Q. Huang, C. Lilley, M. Bode and R. Divan, J. Appl. Phys., 2008, 104, 023709 CrossRef.
- A. Rathmell, M. Nguyen, M. Chi and B. Wiley, Nano Lett., 2012, 12, 3193–3199 CrossRef CAS PubMed.
- E. Gil-Santos, D. Ramos, J. Martinez, M. Fernandez-Regulez, R. Garcia, A. San Paulo, M. Calleja and J. Tamayo, Nat. Nanotechnol., 2010, 5, 641 CrossRef CAS PubMed.
- C. Herring and J. Galt, Phys. Rev., 1952, 85, 1060 CrossRef.
- L. Bragg and W. Lomer, Proc. R. Soc. London, Ser. A, 1949, 196, 171 Search PubMed.
- W. Lomer, Proc. R. Soc. London, Ser. A, 1949, 196, 182 CAS.
- A. Levitt, Whisker technology, Wiley-interscience, New York, 1970 Search PubMed.
- R. J. Young and M. V. Moore, Dual-Beam (FIB-SEM) Systems, Introduction to Focused Ion Beams: Instrumentation, Theory, Techniques and Practice, ed. L. A. Giannuzzi and F. E. Stevie, Springer, US, Boston, MA, 2005, p. 247. Search PubMed.
- G. Stan, S. Krylyuk, A. V. Davydov, I. Levin and R. Cook, Nano Lett., 2012, 12, 2599 CrossRef CAS PubMed.
- M. Haque and M. Saif, Exp. Mech., 2002, 42, 123 CrossRef CAS.
- M. Haque, H. Espinosa and H. Lee, MRS Bull., 2010, 35, 375 CrossRef.
- G. Jing, H. Duan, X. Sun, Z. Zhang, J. Xu, Y. Li, J. Wang and D. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235409 CrossRef.
- Y. Kim, K. Son, I. Choi, I. Choi, W. Park and J. Jang, Adv. Funct. Mater., 2011, 21, 279 CrossRef CAS.
- L. Ngo, D. Almécija, J. Sader, B. Daly, N. Petkov, J. Holmes, D. Erts and J. Boland, Nano Lett., 2006, 6, 2964 CrossRef CAS.
- C. Zou, G. Jing, D. Yu, Y. Xue and H. Duan, Phys. Lett. A, 2009, 373, 2065 CrossRef CAS.
- J. Du, Y. Yang, Z. Fan, Y. Xia, X. Cheng, Y. Gan, H. Hang, L. Dong, X. Li, W. Zhang and X. Tao, J. Alloys Compd., 2013, 560, 142 CrossRef CAS.
- J. Ma, Y. Liu, P. Hao, J. Wang and Y. Zhang, Sci. Rep., 2016, 6, 18994 CrossRef CAS.
- H. Ni, X. Li and H. Gao, Appl. Phys. Lett., 2006, 88, 043108 CrossRef.
- G. Jing, X. Zhang and D. Yu, Appl. Phys. A: Mater. Sci. Process., 2010, 100, 473 CrossRef CAS.
- E. Tan, Y. Zhu, T. Yu, L. Dai, C. Sow, V. Tan and C. Lim, Appl. Phys. Lett., 2007, 90, 163112 CrossRef.
- D. Magagnosc, W. Chen, G. Kumar, J. Schroers and D. Gianola, Sci. Rep., 2016, 6, 19530 CrossRef CAS PubMed.
- M. Lucas, W. Mai, R. Yang, Z. Wang and E. Riedo, Nano Lett., 2007, 7, 1314 CrossRef CAS PubMed.
- G. Stan, S. Krylyuk, A. Davydov and R. Cook, Nano Lett., 2010, 10, 2031 CrossRef CAS PubMed.
- Y.-S. Sohn, J. Park, G. Yoon, J. Song, S.-W. Jee, J.-H. Lee, S. Na, T. Kwon and K. Eom, Nanoscale Res. Lett., 2009, 5, 211 CrossRef PubMed.
- H. Zhan and Y. Gu, Comput. Mater. Sci., 2012, 55, 73–80 CrossRef CAS.
- H. Huan, B. Fu and X. Ye, Phys. Lett. A, 2017, 381, 481–488 CrossRef CAS.
- Y. Gao, F. Wang, T. Zhu and J. Zhao, Comput. Mater. Sci., 2010, 49, 826–830 CrossRef CAS.
- W.-H. Xu, L. Wang, Z. Guo, X. Chen, J. Liu and X.-J. Huang, ACS Nano, 2014, 9, 241–250 CrossRef PubMed.
- W. Liang and M. Zhou, Proc. Inst. Mech. Eng., Part C, 2004, 218, 599–606 CrossRef CAS.
- M. F. Horstemeyer and M. Baskes, J. Eng. Mater. Technol., 1999, 121, 114–119 CrossRef.
- G. Csiszár, L. Balogh, A. Misra, X. Zhang and T. Ungár, J. Appl. Phys., 2011, 110, 043502 CrossRef.
- G. Csiszár, Mater. Sci. Eng., A, 2014, 609, 185–194 CrossRef.
- Y. Chen, G. Csiszár, J. Cizek, X. Shi, C. Borchers, Y. Li, F. Liu and R. Kirchheim, Metall. Mater. Trans. A, 2016, 47, 726–738 CrossRef CAS.
- E. Huang, G. Csiszár, Y. Lo, B. Clausen, Y. Huang, W. Lee, T. Ungár and P. Liaw, Adv. Eng. Mater., 2012, 14, 902–908 CrossRef CAS.
- B. Jóni, T. Al-Samman, S. Chowdhury, G. Csiszár and T. Ungár, J. Appl. Crystallogr., 2013, 46, 55–62 CrossRef.
- M. Máthis, G. Csiszár, J. Capek, J. Gubicza, B. Clausen, P. Lukás, A. Vinogradov and S. Agnew, Int. J. Plast., 2015, 72, 127–150 CrossRef.
- M. Máthis, J. Gubicza, G. Csiszár, J. Capek, B. Clausen, V. Sima and P. Lukás, Acta Phys. Pol., A, 2015, 128, 700–703 CrossRef.
- G. Csiszár, A. Misra and T. Ungár, Mater. Sci. Eng., A, 2011, 528, 6887–6895 CrossRef.
- G. Csiszár, K. Pantleon, H. Alimadadi, G. Ribárik and T. Ungár, J. Appl. Crystallogr., 2012, 45, 61–70 CrossRef.
- C. Chen and J. Zhu, Appl. Phys. Lett., 2007, 90, 043105 CrossRef.
- D. Zeng and Q. Zheng, Acta Mech. Solida Sin., 2010, 23, 394–399 CrossRef.
- G. Yun and H. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195421 CrossRef.
- H. Zhan and Y. Gu, Comput. Mater. Sci., 2012, 55, 73–80 CrossRef CAS.
- K. I. Shingel and R. H. Marchessault, Polysaccharides for Drug Delivery and Pharmaceutical Applications, R. H. Marchessault, F. Ravenelle and X. X. Zhu, American Chemical Society, ACS Symposium Series, 2006, vol. 934, pp. 271–287. Search PubMed.
- W. Wright, Polymers in aerospace applications, Pergamon Press, 1990 Search PubMed.
- A. Akelah, Polymers in Food Processing Industries, in Functionalized Polymeric Materials in Agriculture and the Food Industry, Springer, Boston, MA, 2013 Search PubMed.
- D. Soane and Z. Martynenko, Polymers in microelectronics: fundamentals and applications, Technology & Engineering, Elsevier Science Publishers, 1989 Search PubMed.
- P. Chen, J. McKittrick and M. Meyers, Prog. Mater. Sci., 2012, 57, 1492–1704 CrossRef CAS.
- M. Destrade, M. Gilchrist and G. Saccomandi, J. Acoust. Soc. Am., 2010, 127, 2759–2763 CrossRef PubMed.
- L. Dorfmann and R. Ogden, Proc. R. Soc. A, 2017, 473, 20170311 Search PubMed.
- L. Gibson, M. Ashby and B. Harley, Cellular materials in nature and medicine, Cambridge University Press, Cambridge, UK, 2010 Search PubMed.
- R. Thurston and K. Brugger, Phys. Rev., 1964, 133, A1604–A1610 CrossRef.
- L. Mihai and A. Goriely, Proc. R. Soc. A, 2017, 473, 20170607 Search PubMed.
- M. T. Molares, J. Brötz, V. Buschmann, D. Dobrev, R. Neumann, R. Scholz, I. Schuchert, C. Trautmann and J. Vetter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 185, 192–197 CrossRef.
- R. Ogden, Non-Linear Elastic Deformation, Dover Publication, New York, 1997 Search PubMed.
- A. Goriely, The mathematics and mechanics of biological growth, Springer, New York, 2017 Search PubMed.
- H. Hencky, Z. Tech. Phys., 1928, 9, 215–220 Search PubMed.
- M. Biot, Mechanics of incremental deformations, John Wiley & Sons Inc., New York, London, Sydney, 1965 Search PubMed.
- R. Ogden, Non-Linear Elastic Deformation, Dover Publication, New York, 2nd edn, 1997 Search PubMed.
- T. Belytschko, W. Liu and B. Moran, Nonlinear finite elements for continua and structures, Wiley, New York, 2001 Search PubMed.
- P. Le Tallec, Numerical methods for three-dimensional elasticity, in Handbook of numericalanalysis, ed. P. G. Ciarlet and J. L. Lions, North-Holland, Amsterdam, The Netherlands, 1994, vol. III, pp. 465–624 Search PubMed.
- J. Oden, Finite elements of nonlinear continua, Dover Publication, New York, 2nd edn, 2006 Search PubMed.
- M. Destrade, G. Saccomandi and I. Sgura, Proc. R. Soc. A, 2017, 473, 20160811 Search PubMed.
- P. Stadelmann, Microsc. Microanal., 2003, 9, 60–61 CrossRef.
- P. Peng, H. Sun, A. Gerlich, W. Gou, Y. Zhu, L. Liu, G. Zou, C. Singh and N. Zhou, Acta Mater., 2019, 173, 163–173 CrossRef CAS.
- S. Nakata, K. Sugano, M. Negri, F. Rossi, G. Salyiati, A. Lugstein and Y. Isono, IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), 2016, pp. 543–546 Search PubMed.
- S.-R. Jian, G.-J. Chen and W.-M. Hsu, Materials, 2013, 6, 4505–4513 CrossRef PubMed.
- Y. Yue, P. Liu, Z. Zhang, X. Han and E. Ma, Nano Lett., 2011, 11, 3151–3155 CrossRef CAS PubMed.
- L. Landau and E. Lifschitz, Theory of Elasticity, Butterworth Heinemann, Oxford, 1986 Search PubMed.
- R. Lincoln, K. Kqlipfad, P. Ghate, The Phys. Rev., 2nd Series, 1967, vol. 157(3), p. 463 Search PubMed.
- V. Lubarda, J. Mech. Phys. Solids, 1997, 45, 471490 CrossRef.
- R. Ogden, Proc. R. Soc. A, 1972, 326, 565–584 CAS.
- U. Eisele, Introduction to Polymer Physics, Springer, Berlin, Heidelberg, 1990, p. 180 Search PubMed.
Footnote |
| † In order to minimize the amount of other reflections included by the objective aperture, the smallest available aperture with a diameter of 10 μm was used. |
| This journal is © The Royal Society of Chemistry 2020 |