Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational screening of transition metal-doped phthalocyanine monolayers for oxygen evolution and reduction†
Yanan
Zhou
 ab,
Guoping
Gao
b,
Wei
Chu
ab,
Guoping
Gao
b,
Wei
Chu
 *a and
Lin-Wang
Wang
*bc
*a and
Lin-Wang
Wang
*bc
aSchool of Chemical Engineering, Sichuan University, Chengdu, 610065, Sichuan, China. E-mail: chuwei1965@scu.edu.cn
bMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, 94720, California, USA. E-mail: lwwang@lbl.gov
cJoint Center for Artificial Photosynthesis, Lawrence Berkeley National Laboratory, Berkeley, 94720, California, USA
First published on 5th December 2019
Abstract
Rationally designing efficient, low-cost and stable catalysts toward the oxygen evolution reaction (OER) and the oxygen reduction reaction (ORR) is of significant importance to the development of renewable energy technologies. In this work, we have systematically investigated a series of potentially efficient and stable single late transition metal atom doped phthalocyanines (TM@Pcs, TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir and Pt) as single-atom catalysts (SACs) for applications toward the OER and ORR through a computational screening approach. Our calculations indicate that TM atoms can tightly bind with Pc monolayers with high diffusion energy barriers to prevent the isolated atoms from clustering. The interaction strength between intermediates and TM@Pc governs the catalytic activities for the OER and ORR. Among all the considered TM@Pc catalysts, Ir@Pc and Rh@Pc were found to be efficient OER electrocatalysts with overpotentials ηOER of 0.41 and 0.44 V, respectively, and for the ORR, Rh@Pc exhibits the lowest overpotential ηORR of 0.44 V followed by Ir@Pc (0.55 V), suggesting that Rh@Pc is an efficient bifunctional catalyst for both the OER and ORR. Moreover, it is worth noting that the Rh@Pc catalyst can remain stable against dissolution under the pH = 0 condition. Ab initio molecular dynamic calculations suggest that Rh@Pc could remain stable at 300 K. Our findings highlight a novel family of two-dimensional (2D) materials as efficient and stable SACs and offer a new strategy for catalyst design.
1. Introduction
Increasing energy demand and fast depletion of fossil fuels have led to search for alternative energy sources and efficient energy conversion technologies.1–3 Sustainable and renewable energy generation technologies such as water splitting cells, fuel cells, and metal–air batteries4,5 are regarded as promising approaches. These electrochemical technologies generally involve the OER and ORR, which have attracted much interest in the energy conversion research. The OER occurs on the anode side of an electrochemical water splitting cell, while as a reverse reaction of the OER, the ORR occurs on the cathode side of a fuel cell and a metal–air battery. Currently, Ru/Ir oxides4,6 and Pt oxides as well as their alloys7–9 are commonly used as the most efficient OER and ORR catalysts, respectively. However, these noble metals are rather expensive, and only a small number of surface sites can serve as catalytically active sites, which make their use rather inefficient. Therefore, the design and development of novel families of low-cost electrocatalysts whose catalytic activities are comparable or even higher than those of noble metal oxides are of significant importance.Recently, single-atom catalysts have attracted extensive attention, as metal atoms individually dispersed on supports can be promising for the maximum metal element utilization.10 However, the isolated metal atoms are easy to aggregate to form clusters or nanoparticles due to their high surface energies.11 To maintain the stability of SACs, the previous experimental and theoretical studies have demonstrated that isolated metal atoms can bind at appropriate defects or hollow sites of 2D supporting materials to avoid cluster aggregation.12,13 Moreover, due to the confinement of single atoms in the appropriate supports, the electronic properties of doped single metal atoms can be tuned with different transition metal elements which can enhance their catalytic activity.14–16 In the last few years, single metal electrocatalysts for the OER/ORR have been the subjects of extensive studies. Especially, metal and nitrogen co-doped carbon (M–Nx–C) materials have been demonstrated in many investigations to show OER/ORR performance with comparable activities to those of Ir/Pt oxides,17–21 thus suggesting a promising way to replace noble metal oxides by M–Nx–C catalysts. For example, our previous study22 found that the OER overpotential roughly decreases with the increase of the coordination number of N–TM. Wang et al.23 reported that for Co and N codoped graphene (CoNx-gra, x = 1–4), both OER and ORR overpotentials roughly decrease with the increase of the doping concentration of nitrogen. The root of the M–Nx–C materials used as electrocatalysts can be traced back to the discovery of the capability of M–N4 macrocycle complexes (e.g. porphyrin) toward the ORR.24,25
To date, a series of metal-doped phthalocyanine (MPc) monolayers, whose structure is similar to that of metal-doped porphyrins with one metal atom connecting to four nitrogen atoms, have been successfully synthesized in experiments with single metal atoms orderly and strongly anchored into the pores of the Pc.26–30 The synthesis procedure of MPc is flexible so that metal atoms can be replaced by other TM atoms.31 More importantly, due to the large surface area, unique atomic structures, and intrinsic properties of dispersed metal sites, MPc monolayers and their derivatives have been predicted to be potential candidates for spintronics,32–35 gas capture,36 and energy conversion.37–45 Using first principles calculations, Zhao et al.46 found that the 2D Cr–Pc monolayer exhibits high catalytic activity toward CO oxidation at room temperature. Wang et al.47 theoretically reported that FePc shows high activity for the ORR in an acidic solution due to the stable binding of Fe atoms with Pc monolayers and the coordinative unsaturated state of the doped active center, which has been confirmed by recent experimental work.48 All these previous studies suggest that the experimentally available TM@Pc monolayers with uniformly distributed single-atom active sites can be promising candidates for SACs.
In this work, the catalytic performance of 2D transition metal doped Pc monolayers (TM@Pc, TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, and Pt) as potential electrocatalysts toward the OER and ORR will be systematically screened with density functional theory calculations. This systematic study will be useful to help experimentalists to understand and select these transition metal elements, as these metals have exhibited OER and ORR activities in various other 2D materials.17,49,50 The advances in DFT have made it possible to accurately describe catalytic reactions,51 and the computational investigation on the OER/ORR performance of TM@Pc monolayers can shed some light on developing low-cost, effective and stable electrocatalysts, or on future improvements of the systems. Our calculations demonstrate that Rh@Pc monolayers exhibit efficient catalytic activity toward both the OER and ORR with stability both thermodynamically and kinetically.
2. Computational methods
The spin-polarized density functional theory calculations were carried out with the Vienna Ab initio Simulation Package (VASP) code.52,53 The projector augmented wave (PAW) pseudopotentials were used to describe the electron–ion interactions.54 The Perdew–Burke–Ernzerhof (PBE)55 functional of the generalized gradient approximation (GGA)56 was used to describe the electron–correction interactions. The van der Waals (vdW) interactions were described using the Grimme's DFT-D3 correction method.57 A plane-wave cutoff energy of 500 eV was adopted for all the computations to describe all atoms' valence electrons. Geometry optimizations were performed until the atomic force became less than 10−2 eV Å−1. The energy was converged to be less than 10−5 eV. A vacuum space of 20 Å was used to prevent the interaction between the periodic images. The Brillouin zone was sampled with 5 × 5 × 1 Monkhorst–Pack k-meshes.58 Bader charge analysis was performed to evaluate the charge transfer process.59 To investigate the stabilities of the screened out catalysts that possess excellent performance for the OER and ORR, the TM diffusion barriers were calculated by the climbing image nudged elastic band (CINEB) method.60,61Ab initio molecular dynamics (AIMD) calculations were also carried out to evaluate the corresponding dynamic stability. The algorithm of the Nose thermostat was used to calculate the canonical ensemble62 at 300 K for 10 ps with a time step of 2 fs. The implicit solvent model was used to simulate the solvent environment throughout the whole process using VASPsol under the water conditions.63 The details of OER and ORR calculations are provided in the ESI† as in our previous work.17 The adsorption Gibbs free energy is defined as the following eqn (1):| Gads = Gadsorbent+catalyst − Gcatalyst − Gadsorbent | (1) |
3. Results and discussion
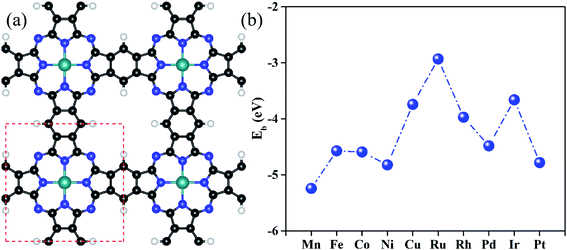
Fig. 1a shows the optimized configurations of TM@Pc monolayers in a 2 × 2 supercell, in which all the atoms are in the same plane. One unit cell of the TM@Pc monolayer contains four H atoms, twenty C atoms, eight N atoms, and one TM atom. Our calculated results for the lattice constants of TM@Pc are all about 10.7 Å, in good agreement with the experimental result of 10.8 Å and those of other theoretical studies.26,28,32,33,46 In the optimized TM@Pc monolayer structure, one TM atom binds with four inwardly projecting N atoms, forming four TM-N bonds. The binding energy (Eb) is defined as Eb = ETM@Pc − EPc − μTM, where ETM@Pc and EPc are the total energies of the TM@Pc system and the Pc substrate, respectively. μTM is the chemical potential of the TM atom calculated from its bulk crystal. Since μTM is referenced with respect to its bulk metal, negative values of Eb (Fig. 1b) indicate that the TM atoms in the Pc monolayers are stable against clustering. As shown in Fig. S1,† the strong hybridization between the 2p orbital of N and the d orbital of TM atoms demonstrates the chemical bonding of N and TM, which further explains the strong interaction between TM and Pc monolayers. The calculated bond length of TM–N, TM binding energies, and Bader charge transfer are listed in Table S1.† The Bader charge analysis results suggest that the TM centers in TM@Pc are positively charged which can serve as the active sites to bind oxygen-ended intermediate species (HO*, O* and HOO*). We then calculated the diffusion barrier of TM atoms in catalysts (using Rh@Pc and Ir@Pc as examples) from the stable si†te to further check its dynamic stability against clustering. The diffusion of Rh and Ir adatoms from their stable sites to possible neighboring metastable sites is endothermic and the calculated diffusion barrier is 3.69 and 4.36 eV, respectively (Fig. S2†). Previous studies have demonstrated that the reaction with an energy barrier below 0.70 eV can occur spontaneously at low temperature.64 Such a reaction barrier is much smaller than the TM diffusion barrier. Thus, tightly anchored Rh and Ir atoms on the Pc monolayers should be stable during the catalytic processes.The investigation of the distinct electronic properties of different types of TM atom doped Pc monolayers can help us better understand their catalytic activities. The d orbitals of the doped TM atoms on Pc monolayers were computed and are shown in Fig. S3.† In previous literature, the d band center position (εd) has been used to analyze the interaction strength between the adsorbate and the catalyst.65–69 We have thus plotted εd as the center of mass position of the d-band partial density of states (PDOS) in Fig. S3.† A shift of calculated εd to a lower energy position with respect to the Fermi level is seen as the d-electron number of the TM atom increases at least when the TMs are in the same row of the periodic table. Because the interaction between the doped TM and intermediate species occurs due to the hybridization of their electronic states, the larger d-electron number of the TM atoms and their corresponding lower energy of εd generally result in weaker interaction strength with the adsorbates.70 Thus, the expected interaction strength between TM–Pc and intermediate species should have the following trend: Mn > Fe > Co > Ni > Cu, Ru > Rh > Pd and Ir > Pt. To verify the above assumption, we plot the Gibbs free energy value of intermediates (ΔGHO*, ΔGO* and ΔGHOO*) with various d-electron numbers of the TM@Pc systems in Fig. S4.† The data can be found in Table S2.† We can conclude that with the increase of the d-electron numbers of the TM atoms in the same row of the periodic table, the adsorption Gibbs free energies of intermediates decrease. This is also consistent with the position of εd as exhibited in Fig. S3.† Thus, there is a negative correlation between εd and Gibbs free energy of intermediates, at least when the TM atoms are in the same row of the periodic table. This phenomenon was also observed in previous experimental and theoretical studies.17,18,71,72 Accordingly, the interaction strength can be modulated to an optimal value by tuning the TM doped on the Pc sheet toward OER and ORR performance.
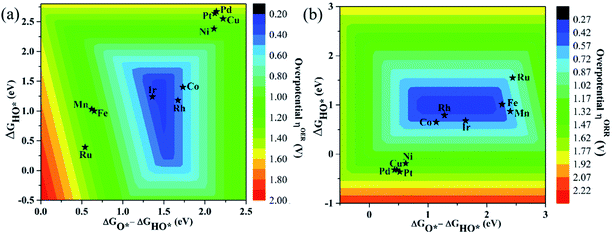
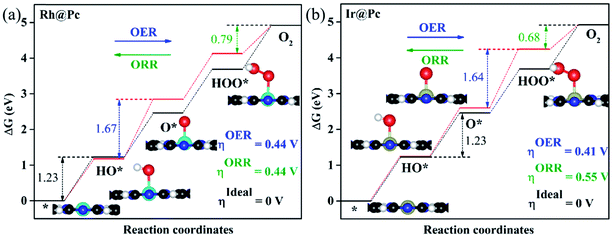
As proposed by Nørskov et al.,73 the adsorption Gibbs free energies of three intermediates (HO*, O* and HOO*) on the TM@Pc catalyst govern the intrinsic catalytic activity toward the OER and ORR. Three descriptors, Gibbs free energies of adsorbed HO*, O* and HOO*, are used to evaluate the catalytic activity of an OER/ORR electrocatalyst. According to the Sabatier principle,74 both too strong and too weak interaction strength between the intermediates and catalysts lead to adverse effects on the catalytic performance. Therefore, identifying promising electrocatalysts with moderate interaction of the reaction intermediates is one of our goals. As an ideal catalyst at the U = 0 V condition which can occur at its thermodynamic limit, it requires that the free energy barriers between two adjacent intermediate states for all the mentioned four electron transfer steps (equations from Sa to Sd in the ESI†) should be the same, that is 4.92 eV/4 = 1.23 eV. Thus, according to the equations from (S2a) to (S2e),† we can conclude that the adsorption Gibbs free energy of HO*, O* and HOO* should be 1.23, 2.46 and 3.69 eV, respectively.17,71 Thus, both the OER and ORR can occur at their thermodynamic limit and the corresponding overpotential η will be zero. In reality, the Gibbs free energy differences between two adjacent intermediate states are not equal. The overpotential of the OER (ηOER) is determined by the maximum difference between the two adjacent Gibbs free energies, while the overpotential of the ORR (ηORR) is determined by the minimum difference between the two adjacent Gibbs free energies. Obtaining the relationship among these three Gibbs free energies will simplify the analysis and the search for the optimal catalysis.75,76 Here, the scaling relationship of ΔGHO*vs. ΔGHOO* for all the considered TM@Pc catalysts is shown in Fig. 2. We found that ΔGHOO* can be expressed as a function of ΔGHO*via equation ΔGHOO* = 0.82ΔGHO* + 3.14, with a high coefficient of determination (R2 = 0.992). The slope close to unity in the correlated adsorption free energies of HO* vs. HOO* reflects the fact that both HO* and HOO* have a single bond between the O atom and TM, which is similar to the cases of metal and metal oxide surfaces.77,78 Thus, the overpotential (ηOER and ηORR) as a function of four variables (ΔGa, ΔGb, ΔGc and ΔGd) can be reduced to two independent variables (another constraint is ΔGa + ΔGb + ΔGc + ΔGd = 4.92 eV, the standard Gibbs free energy of H2O formation from O2 and 2H2).73,78 As shown in the following: ΔGa = ΔGHO*, ΔGb = ΔGO* − ΔGHO*, ΔGc = ΔGHOO* − ΔGO* = (0.82ΔGHO* + 3.14) − ΔGO* and ΔGd = 4.92 − ΔGHOO* = 4.92 − (0.82ΔGHO* + 3.14). Thus, knowing only two descriptors, ΔGHO* and ΔGO* − ΔGHO*, is sufficient for us to describe the catalytic performance of a system toward the OER and ORR. In Fig. 3a, we plot the two-dimensional volcano to exhibit the OER activity trends through ηOER as a function of two independent descriptors ΔGHO* and ΔGO* − ΔGHO*. The blue region of the plot shows the highest activity area with ηOER reaching a minimum value of 0.21 V under the optimum condition (ΔGa = ΔGb = ΔGc = 1.44 eV). Note that the minimum value of the overpotential is not zero since the relationship ΔGHOO* = 0.82ΔGHO* + 3.14 excludes the ideal case of ΔGHO* = 1.23 eV and ΔGHOO* = 3.69 eV. Different catalysts fall on different points in the volcano plot of Fig. 3. Based on this, for the OER, Ir@Pc is the best catalyst (ηOER = 0.41 V) followed by Rh@Pc (ηOER = 0.44 V). The free energy diagrams of all the intermediate states of Rh@Pc and Ir@Pc toward the OER are shown in Fig. 4a and b at U = 0 V. Notably, the calculated ηOER values of Rh@Pc and Ir@Pc are comparable or even lower than those of the current best catalysts RuO2 (ηOER = 0.42 V)78 and IrO2 (ηOER = 0.52 V).77 Co@Pc also shows good activity (ηOER = 0.50 V) for the OER with the O* formation being the rate-determining step. The ORR is the reverse reaction of the OER. In Fig. 3b the calculated η values for the ORR on various TM@Pc catalysts were compared. Under the optimal condition (−ΔGa = −ΔGd = 0.98 eV), the theoretical ηORR is found to be as low as 0.25 V. From the volcano plot in Fig. 3b, the best TM@Pc catalyst for the ORR is found to be Rh@Pc with an ηORR value of 0.44 V and the rate-determining step is the reduction of O2 to HOO* (Fig. 4b), followed by Ir@Pc (ηORR = 0.55 V). This thermodynamic limiting overpotential is even lower than that of Pt (111) (ηORR = 0.48 V).79 Fe@Pc and Co@Pc also exhibit good catalytic activities (ηORR = 0.58 and 0.58 V) for the ORR with the rate-determining steps of reduction of O* to HO* and HOO* formation, respectively. Here, it should be noted that Rh@Pc can be used as the efficient bifunctional electrocatalyst for both the OER and ORR with an ηOER value of 0.44 V and an ηORR value of 0.44 V, respectively. To evaluate the dynamic stability of this promising catalyst, we have performed AIMD simulations under 300 K condition for 10 ps (Fig. S5†) for Rh@Pc. It can be seen that the energies oscillate near the equilibrium state while the structure remains unchanged, suggesting the kinetic stability of the Rh@Pc catalyst.
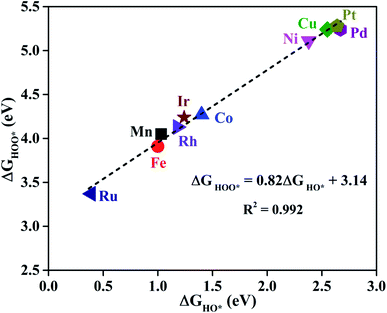 | ||
| Fig. 2 The scaling relationship between the adsorption Gibbs free energies of HO* and HOO* for all the considered TM@Pc systems. | ||
In another aspect, we have also calculated the reaction free energy (ΔGdiss) to evaluate the stability of the doped metal centers against dissolution due to the proton attack of the active region using the equation:75 TM@Pc + nH+ → nH@Pc + TMn+. Where n refers to the oxidation state for the TM atom, nH@Pc refers to the Pc monolayer with the TM vacancy adsorbed by n number of hydrogen atoms (Fig. S6†). The dissolution energy can be calculated as: ΔGdiss = G(nH@Pc) + G(TMn+) − G(TM@Pc) − nG(H+). Here, G(nH@Pc) and G(TM@Pc) can be calculated directly, and ΔG(H+) = 0.5 × G(H2) − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × kT × pH = 0.5 × [E(H2) + ZPE(H2) − TS(H2)] − ln
10 × kT × pH = 0.5 × [E(H2) + ZPE(H2) − TS(H2)] − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × kT × pH. Here, TS(H2) = 0.41 eV for the H2 gas phase at 298 K, and ZPE(H2) = 0.26 eV.17 As for G(TMn+), we take the experimental ion formation of TMn+, which is defined as: ΔG(TMn+) = G(TMn+) − G(TM,bulk). Thus: G(TMn+) = ΔG(TMn+) + G(TM,bulk), where G(TM,bulk) is calculated with DFT, and ΔG(TMn+) is obtained from the literature80 and is listed in Table. S3.† Using this approach, the dissolution energy under pH = 0 condition, ΔGdiss(0), is calculated and shown in Fig. 5. We can conclude that Rh@Pc, Pd@Pc, Ir@Pc, and Pt@Pc catalysts are stable against dissolution under the pH = 0 condition. For the other TM, their ΔGdiss(0) values are less than zero, which means they will be unstable against dissolution. However, as the pH value increases, ΔGdiss(pH) will also increase, thus, there will be a critical pH value, above which the TM@Pc catalyst will be stable. The critical value can be calculated by pHmin = −ΔGdiss(0)/(n × 0.0591) (Table S3†). Thus, when the system is sufficiently alkaline, it will always be stable against dissolution, and Rh@Pc, Pd@Pc, Ir@Pc, and Pt@Pc are stable even in a very acidic environment.
10 × kT × pH. Here, TS(H2) = 0.41 eV for the H2 gas phase at 298 K, and ZPE(H2) = 0.26 eV.17 As for G(TMn+), we take the experimental ion formation of TMn+, which is defined as: ΔG(TMn+) = G(TMn+) − G(TM,bulk). Thus: G(TMn+) = ΔG(TMn+) + G(TM,bulk), where G(TM,bulk) is calculated with DFT, and ΔG(TMn+) is obtained from the literature80 and is listed in Table. S3.† Using this approach, the dissolution energy under pH = 0 condition, ΔGdiss(0), is calculated and shown in Fig. 5. We can conclude that Rh@Pc, Pd@Pc, Ir@Pc, and Pt@Pc catalysts are stable against dissolution under the pH = 0 condition. For the other TM, their ΔGdiss(0) values are less than zero, which means they will be unstable against dissolution. However, as the pH value increases, ΔGdiss(pH) will also increase, thus, there will be a critical pH value, above which the TM@Pc catalyst will be stable. The critical value can be calculated by pHmin = −ΔGdiss(0)/(n × 0.0591) (Table S3†). Thus, when the system is sufficiently alkaline, it will always be stable against dissolution, and Rh@Pc, Pd@Pc, Ir@Pc, and Pt@Pc are stable even in a very acidic environment.
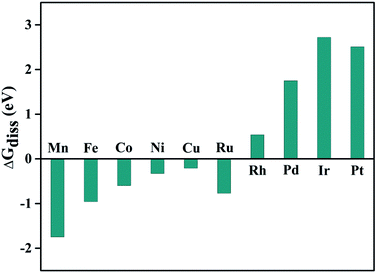 | ||
| Fig. 5 Calculated reaction free energy shows the stability of TM@Pc catalysts against doped-TM atom dissolution under the pH = 0 condition. | ||
4. Conclusion
To summarize, we have systematically screened a series of single TM atom doped Pcs as potentially efficient and stable SAC bifunctional electrocatalysts for both OER and ORR catalytic processes using a computational screening approach. Based on the computations of binding of TM atoms with Pc monolayers, we found that all the considered TM atoms exhibit a strong interaction with Pc monolayers as potentially stable SACs with high diffusion energy barriers. With the increase of the d-electron number of the doped TM atom on Pc monolayers that leads to the lower d-band center, the interaction strength between intermediates and the active doped TM atoms will decrease, which allows us to select the optimal TM@Pc catalyst toward the OER/ORR by tuning the doped TM element. According to the volcano plots of the OER and ORR, among all the studied TM@Pc catalysts, the best catalyst for the OER is Ir@Pc with an ηOER of 0.41 V followed by Rh@Pc with ηOER = 0.44 V, and for the ORR, the best catalyst is Rh@Pc with an ηORR of 0.44 V followed by Ir@Pc (ηORR = 0.55 V). It should be noted that both Rh@Pc and Ir@Pc can remain stable against dissolution under all pH conditions. This study highlights a potentially efficient new class of SACs based on the Pc monolayers toward the OER and ORR.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported through the Office of Science of the U.S. Department of Energy under award number DE-SC0004993. This theoretical work used the resources of the National Energy Research Scientific Computing Center (NERSC) that is supported by the Office of Science of the U.S. Department of Energy. We are grateful to the Chinese Scholarship Council (CSC) for providing the Ph.D. scholarship.References
- N. L. Panwar, S. C. Kaushik and S. Kothari, Renewable Sustainable Energy Rev., 2011, 15, 1513–1524 CrossRef.
- G. S. Liu, S. J. You, Y. Tan and N. Q. Ren, Environ. Sci. Technol., 2017, 51, 2339–2346 CrossRef CAS PubMed.
- M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337 CrossRef CAS PubMed.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC.
- C. G. Morales-Guio, L. A. Stern and X. L. Hu, Chem. Soc. Rev., 2014, 43, 6555–6569 RSC.
- E. A. Paoli, F. Masini, R. Frydendal, D. Deiana, C. Schlaup, M. Malizia, T. W. Hansen, S. Horch, I. E. L. Stephens and I. Chorkendorff, Chem. Sci., 2015, 6, 190–196 RSC.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- N. M. Markovic, T. J. Schmidt, V. Stamenkovic and P. N. Ross, Fuel Cells, 2001, 1, 105–116 CrossRef CAS.
- X. Q. Huang, Z. P. Zhao, L. Cao, Y. Chen, E. B. Zhu, Z. Y. Lin, M. F. Li, A. M. Yan, A. Zettl, Y. M. Wang, X. F. Duan, T. Mueller and Y. Huang, Science, 2015, 348, 1230–1234 CrossRef CAS PubMed.
- H. B. Zhang, G. G. Liu, L. Shi and J. H. Ye, Adv. Energy Mater., 2018, 8, 1701343–1701367 CrossRef.
- X. F. Yang, A. Q. Wang, B. T. Qiao, J. Li, J. Y. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed.
- J. Lin, A. Q. Wang, B. T. Qiao, X. Y. Liu, X. F. Yang, X. D. Wang, J. X. Liang, J. Li, J. Y. Liu and T. Zhang, J. Am. Chem. Soc., 2013, 135, 15314–15321 CrossRef CAS.
- G. P. Gao, Y. Jiao, E. R. Waclawik and A. J. Du, J. Am. Chem. Soc., 2016, 138, 6292–6297 CrossRef CAS PubMed.
- S. Yang, D. Y. Chung, Y. J. Tak, J. Kim, H. Han, J. S. Yu, A. Soon, Y. E. Sung and H. Lee, Appl. Catal., B, 2015, 174–175, 35–42 CrossRef CAS.
- F. Cardenas-Lizana, S. Gomez-Quero, N. Perret and M. A. Keane, Catal. Sci. Technol., 2011, 1, 652–661 RSC.
- X. P. Gao, Y. N. Zhou, Y. J. Tan, B. W. Yang, Z. W. Cheng, Z. M. Shen and J. P. Jia, Appl. Surf. Sci., 2019, 473, 770–776 CrossRef CAS.
- Y. N. Zhou, G. P. Gao, J. Kang, W. Chu and L. W. Wang, J. Mater. Chem. A, 2019, 7, 12050–12059 RSC.
- G. P. Gao, E. R. Waclawik and A. J. Du, J. Catal., 2017, 352, 579–585 CrossRef CAS.
- S. Wang, Z. Teng, C. Wang and G. Wang, ChemSusChem, 2018, 11, 2267–2295 CrossRef CAS PubMed.
- C. Zhu, Q. Shi, S. Feng, D. Du and Y. Lin, ACS Energy Lett., 2018, 3, 1713–1721 CrossRef CAS.
- Y. N. Zhou, G. P. Gao, J. Kang, W. Chu and L. W. Wang, Nanoscale, 2019, 11, 18169–18175 RSC.
- Y. N. Zhou, G. P. Gao, Y. Li, W. Chu and L. W. Wang, Phys. Chem. Chem. Phys., 2019, 21, 3024–3032 RSC.
- X. L. Zhang, Z. X. Yang, Z. S. Lu and W. C. Wang, Carbon, 2018, 130, 112–119 CrossRef CAS.
- R. Jasinski, Nature, 1964, 201, 1212–1213 CrossRef CAS.
- W. Ding, Z. D. Wei, S. G. Chen, X. Q. Qi, T. Yang, J. S. Hu, D. Wang, L. J. Wan, S. F. Alvi and L. Li, Angew. Chem., Int. Ed., 2013, 52, 11755–11759 CrossRef CAS PubMed.
- M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, J. Am. Chem. Soc., 2011, 133, 1203–1205 CrossRef CAS.
- S. Stepanow, A. L. Rizzini, C. Krull, J. Kavich, J. C. Cezar, F. Yakhou-Harris, P. M. Sheverdyaeva, P. Moras, C. Carbone, G. Ceballos, A. Mugarza and P. Gambardella, J. Am. Chem. Soc., 2014, 136, 5451–5459 CrossRef CAS.
- S. Kezilebieke, A. Amokrane, M. Abel and J. P. Bucher, J. Phys. Chem. Lett., 2014, 5, 3175–3182 CrossRef CAS.
- M. Piantek, D. Serrate, M. Moro-Lagares, P. Algarabel, J. I. Pascual and M. R. Ibarra, J. Phys. Chem. C, 2014, 118, 17895–17899 CrossRef CAS.
- S. Yang, Y. Yu, M. Dou, Z. Zhang, L. Dai and F. Wang, Angew. Chem., Int. Ed., 2019, 131, 2–9 CrossRef.
- A. Sperl, J. Kroger and R. Berndt, J. Am. Chem. Soc., 2011, 133, 11007–11009 CrossRef CAS PubMed.
- J. Zhou and Q. Sun, J. Am. Chem. Soc., 2011, 133, 15113–15119 CrossRef CAS PubMed.
- J. Zhou, Q. Wang, Q. Sun, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2012, 3, 3109–3114 CrossRef CAS PubMed.
- J. Zhou and Q. Sun, J. Chem. Phys., 2013, 138, 204706 CrossRef PubMed.
- J. Zhou and Q. Sun, Nanoscale, 2014, 6, 328–333 RSC.
- K. Lu, J. Zhou, L. Zhou, X. S. Chen, S. H. Chan and Q. Sun, J. Chem. Phys., 2012, 136, 234703 CrossRef PubMed.
- Y. H. Lu and R. G. Reddy, Electrochim. Acta, 2007, 52, 2562–2569 CrossRef CAS.
- R. R. Chen, H. X. Li, D. Chu and G. F. Wang, J. Phys. Chem. C, 2009, 113, 20689–20697 CrossRef CAS.
- J. Guo, X. M. Yan, Q. Liu, Q. Li, X. Xu, L. T. Kang, Z. M. Cao, G. L. Chai, J. Chen, Y. B. Wang and J. N. Yao, Nano Energy, 2018, 46, 347–355 CrossRef CAS.
- S. M. Zhang, H. Y. Zhang, X. Hua and S. L. Chen, J. Mater. Chem. A, 2015, 3, 10013–10019 RSC.
- W. P. Liu, Y. X. Hou, H. H. Pan, W. B. Liu, D. D. Qi, K. Wang, J. Z. Jiang and X. D. Yao, J. Mater. Chem. A, 2018, 6, 8349–8357 RSC.
- S. Mussell and P. Choudhury, J. Phys. Chem. C, 2016, 120, 5384–5391 CrossRef CAS.
- M. H. Seo, D. Higgins, G. P. Jiang, S. M. Choi, B. Han and Z. W. Chen, J. Mater. Chem. A, 2014, 2, 19707–19716 RSC.
- Z. P. Zhang, S. X. Yang, M. L. Dou, H. J. Liu, L. Gu and F. Wang, RSC Adv., 2016, 6, 67049–67056 RSC.
- Y. X. Peng, L. F. Cui, S. F. Yang, J. J. Fu, L. R. Zheng, Y. Liao, K. Li, X. Zuo and D. G. Xia, Electrochim. Acta, 2015, 154, 102–109 CrossRef CAS.
- Q. M. Deng, L. N. Zhao, X. F. Gao, M. Zhang, Y. H. Luo and Y. L. Zhao, Small, 2013, 9, 3506–3513 CrossRef CAS PubMed.
- Y. Wang, H. Yuan, Y. F. Li and Z. F. Chen, Nanoscale, 2015, 7, 11633–11641 RSC.
- X. X. Wang, B. Wang, J. Zhong, F. P. Zhao, N. Han, W. J. Huang, M. Zeng, J. Fan and Y. G. Li, Nano Res., 2016, 9, 1497–1506 CrossRef CAS.
- T. W. He, S. K. Matta, G. Will and A. J. Du, Small Methods, 2019, 3, 1800419–1800426 CrossRef.
- X. Zhang, A. Chen, Z. H. Zhang, M. G. Jiao and Z. Zhou, J. Mater. Chem. A, 2018, 6, 11446–11452 RSC.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154123 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204–084211 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106–084114 CrossRef PubMed.
- O. Lopez-Acevedo, K. A. Kacprzak, J. Akola and H. Hakkinen, Nat. Chem., 2010, 2, 329–334 CrossRef CAS PubMed.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Phys. Rev. Lett., 2004, 93, 156801 CrossRef CAS PubMed.
- V. Stamenkovic, B. S. Mun, K. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS.
- Y. Y. Liu, Y. M. Wang, B. I. Yakobson and B. C. Wood, Phys. Rev. Lett., 2014, 113, 028304–028309 CrossRef PubMed.
- F. Calle-Vallejo, A. Krabbe and J. M. Garcia-Lastra, Chem. Sci., 2017, 8, 124–130 RSC.
- M. T. de Groot and M. T. Koper, Phys. Chem. Chem. Phys., 2008, 10, 1023–1031 RSC.
- C. Y. Ling, L. Shi, Y. X. Ouyang, X. C. Zeng and J. L. Wang, Nano Lett., 2017, 17, 5133–5139 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir and L. Lindqvist, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- F. Calle-Vallejo, J. I. Martinez, J. M. García-Lastra, E. Abad and M. T. M. Koper, Surf. Sci., 2013, 607, 47–53 CrossRef CAS.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- R. L. David, CRC Handbook of Chemistry and Physics, CRC Press, New York, 1996 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00648f |
| This journal is © The Royal Society of Chemistry 2020 |