Open Access Article
Open Access ArticleHigh throughput study on magnetic ground states with Hubbard U corrections in transition metal dihalide monolayers†
Xinru
Li
 *ac,
Zeying
Zhang
bc and
Hongbin
Zhang
c
*ac,
Zeying
Zhang
bc and
Hongbin
Zhang
c
aCollege of Physics and Optoelectronic Engineering, Shenzhen University, 518060 Shenzhen, P. R. China. E-mail: xrli@szu.edu.cn
bCollege of Mathematics and Physics, Beijing University of Chemical Technology, 100029 Beijing, P. R. China
cInstitute of Materials Science, Darmstadt University of Technology, 64287 Darmstadt, Germany
First published on 4th December 2019
Abstract
We present a high throughput study of the magnetic ground states for 90 transition metal dihalide monolayers TMX2 using density functional theory based on a collection of Hubbard U values. Stable geometrical phases between 2H and 1T are first determined. Spin-polarized calculations show that 50 out of 55 magnetic TMX2 monolayers are energetically prone to the 1T phase. Further, the magnetic ground states are determined by considering four local spin models with respect to different U values. Interestingly, 23 out of 55 TMX2 monolayers exhibit robust magnetic ground orderings which will not be changed by the U values. Among them, NiCl2 with a magnetic moment of 2 μB is a ferromagnetic (FM) insulator, while the VX2, MnX2 (X = Cl, Br and I), PtCl2 and CoI2 monolayers have noncollinear antiferromagnetic (120°-AFM) ground states with a tiny in-plane magnetic anisotropic energy, indicating flexible magnetic orientation rotation. The exchange parameters for both robust FM and 120°-AFM systems are analyzed in detail with the Heisenberg model. Our high-throughput calculations give a systematic study of the electronic and magnetic properties of TMX2 monolayers, and these two-dimensional materials with versatile magnetic behavior may have great potential for spintronic applications.
I. Introduction
The demand of miniaturization and feasibility of integration of functioning devices makes two-dimensional (2D) materials remarkably promising in a wide spectrum of technological applications. Due to the breaking of translational symmetry, the 2D materials display distinct properties from the bulk systems, as supremely spotlighted by graphene.1,2 Recent highlights on 2D materials studies have moved from graphene to other layered van der Waals materials. Among them, transition metal based ultrathin materials3,4 with hexagonal structures similar to that of graphene have captured intensive attention because of their abundant electronic properties, including semiconductors with sizable band gaps, 100% spin-polarized half metals,5–7 and nontrivial topological states.8–10Such versatile electronic or magnetic properties have lead to comprehensive research in various fields like catalysis, opto-electronics, spintronics, electrodes and supercapacitors. In particular, transition metal dichalcogenide monolayers (TMDs),11 transition metal trichalcogenides MAX3,12 and 2D transition metal carbides (nitrides) as so-called MXenes13 have been systematically studied. For instance, MoS2, MoSe2, WS2 and WSe2 monolayers have sizable direct band gaps allowing applications in transistors, photodetectors, and electroluminescent devices.14,15 VS2 and VSe2 monolayers are typically metallic ferromagnets with strain-tunable magnetic ground states.5 MXenes with semiconducting band gaps around 0.25–2.0 eV yield very large Seebeck parameters around 100 K allowing high thermoelectric performance.4 van der Waals layered Cr2Ge2Te6 has been experimentally proved to be a magnetic insulator, which are regarded as a key resource for next-generation spintronic devices.16
Beyond transition metal chalcogenides, carbide and nitride transition metal halides are also found to be interesting.17 Recently, layer-dependent ferromagnetism in van der Waals CrI3 crystals has been systematically studied. It is demonstrated that the monolayer CrI3 is an Ising ferromagnet with an out-of-plane spin orientation.18 Soon after, (quasi) 2D ferromagnetic insulators have revealed many important applications in phototronics, spintronics and magnetoelectronics. For instance, Seyler et al. unveiled spontaneous circularly polarized excitation in the CrI3 monolayers.19 Jiang et al. revealed that a direct-to-indirect band gap transition can be caused by rotating the magnetic direction of CrI3 from out-of-plane to in-plane.20 Klein et al. detected the magnetic ground state and interlayer coupling in CrI3 and uncovered a field-induced metamagnetic transition.21 In addition, transition metal dihalides (TMX2) with intriguing simple lattice structures, relative large ionicity, and magnetic diversities have invigorated the enthusiasm of systematic researches. Early in 1971, layered NiCl2 and CoCl2 separated by one or two layers of graphite was proved to be a two-dimensional Heisenberg ferromagnet.22 It was shown that intercalation of graphite can weaken significantly the interaction between the TMX2 layers, so that these compounds can be regarded as 2D paramagnets. In recent years, TMX2 monolayers, especially TMX2 magnets, have attracted more attention. For instance, the ferromagnetic or antiferromagnetic properties of TMX2 (TM = 3d transition metals; X = Cl, Br, I) in both the 1T and 2H phase were investigated and the Curie temperature of magnetic transition were evaluated using Monte Carlo simulations.23 Moreover, FeX2 were proven to be half-metals24 with sufficient stability to be exfoliated from bulk layered compounds.6 Despite the achievements made on 3d transition metal dihalide monolayers, more pending questions still need to be investigated in a deeper way: (1) since fullerene-like CdCl2 closed cage structures have been successfully synthesized,25 there is a high possibility to achieve 4d or 5d TMX2 monolayers. In this case, the exotic electronic or magnetic properties of 4d or 5d TM dihalide monolayers are open to be explored. (2) Most current magnetic analyses of TMX2 monolayers are focusing on collinear magnetic ordering. However, as the TM atomic arrangements in TMX2 monolayers of both the 1T and 2H phase are triangular lattices, geometric frustration on the spin configurations is inevitable. Thus, non-collinear antiferromagnetic ordering needs to be further identified.26 (3) Previous density-functional-theory (DFT) calculations on TMX2 either neglected the local Coulomb interactions (U values) or used specific U value to estimate the electronic or magnetic properties, which may not be in accordance with future experimental results. In this regard, investigating TMX2 with a batch of U values to identify property–U relations is instructive to practical experiments.
In this work, we implement a high throughput method to identify the magnetic ground states of 90 TMX2 (TM = transition metals from Sc to Hg; X = Cl, Br, I) with four magnetic ordering configurations based on first principles calculations. 55 out of 90 TMX2 monolayers are magnetic cases and 50 magnetic TMX2 are stable in the 1T phase instead of the 2H phase. Due to the lack of experimental data when describing the correlations on d electrons of TM atoms in TMX2 monolayers, the magnetic ground states for magnetic TMX2 systems are systematically investigated with respect to Hubbard U values from 0 to 5 eV. We predict that the NiCl2 is a robust ferromagnetic insulator with magnetic moments of 2 μB and Curie temperature of 57 K. Besides, 8 TMX2 monolayers are stable in noncollinear antiferromagnetic ground states with different Hubbard U values, and the in-plane magnetic anisotropy energy is estimated to be smaller than 10 μeV indicating an easily overcome thermal fluctuation and a high-flexibility of magnetic orientation.
II. Computational method
Geometrical optimization and electronic structure calculations of the TMX2 monolayers with different magnetic orderings were carried out using the projected augmented wave method as implemented in the Vienna ab initio Simulation Package (VASP),27,28 where the exchange-correlation functional was approximated by the generalized gradient approximation (GGA)29 with Perdew–Burke–Ernzerhof (PBE)30 parametrization. The energy cutoff of 500 eV is applied to ensure convergence. The 2D Brillouin zone integration was done with a k-mesh density of 60/a, where a denotes the length of the lattice constant in the unit of Å. In order to obtain accurate magnetic anisotropic energy, a k-mesh of 120/a is applied. A vacuum slab of 25 Å was induced to prevent the image interaction from periodic supercells. A Gaussian smearing factor of 0.01 V is used. The atomic coordinates were fully optimized with a maximum residual force of 0.01 eV Å−1. Spin polarized calculations with large initial magnetic moments were carried out in order to identify magnetic and nonmagnetic systems. For the magnetic systems, four magnetic states with ferromagnetic (FM), 2 × 1 × 1 antiferromagnetic (AFM), 4 × 1 × 1 AFM and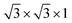 noncollinear 120° AFM orderings are generated as the prototypes, implemented in our HTP calculations. The relaxation of magnetic ground state and net magnetic moment are performed manually to avoid local minimum optimization of TMX2 systems. Regarding the effect of the correlations on the properties of the TM atoms, the Hubbard U correction from U = 1 to U = 5 was applied to account for the electronic correlation of d electrons.
noncollinear 120° AFM orderings are generated as the prototypes, implemented in our HTP calculations. The relaxation of magnetic ground state and net magnetic moment are performed manually to avoid local minimum optimization of TMX2 systems. Regarding the effect of the correlations on the properties of the TM atoms, the Hubbard U correction from U = 1 to U = 5 was applied to account for the electronic correlation of d electrons.
III. Results and discussions
A. Geometrical stability: 2H and 1T phases
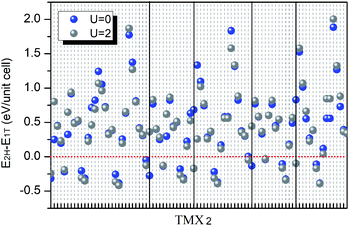
Similar to the TM dichalcogenides like MoS2,31 there are two common crystal structures for the TM dihalide monolayers, i.e., the 2H phase with trigonal prismatic D3h symmetry and the 1T phase with octahedral Oh symmetry. TMX2 with both geometries are fully optimized and the energy difference between the 2H and 1T phases with U = 0 and U = 2 are shown in Fig. 1. Obviously, most TMX2 monolayers are stable in the 1T structure, while only 21 (when U = 2) out of 90 TMX2 monolayers prefer the 2H structural phase. A stable 2H phase occurs with large possibilities in group-3 (d1) and group-4 (d2) TMX2 monolayers. For 2H systems, the energy difference between the 2H and 1T phases ranges from 10 to 139 meV per atom. Meanwhile, the energy difference between the 1T and 2H phases of MoS2 and WS2 calculated by DFT are around 283 and 300 meV per atom, respectively, which are much larger than those of TM dihalides.32 Thus, we suspect that structural phase transition can be induced in TM dihalides by plasmonic hot electron injection,33 infrared laser induction,34 and employing lithium molten salts.35 We note that the stability of the 2H and 1T structures is independent of the U value in most cases. However, as shown in Fig. 1b, in some cases such as TiBr2, TcBr2, ScI2 and TiI2, the ground structural phase can be changed by employing different U values, which are consistent with a recent theoretical study on NbSe2 which shows that DFT with the U method can tune the energy difference and improve the stability of metastable phase, explaining its detection in experiments.36On the other hand, the dynamic stability of 1T monolayers with a space group symmetry of p![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 has been studied thoroughly by previous high throughput studies. Haastrup et al. introduced the Computational 2D Materials Database (C2DB) containing 1500 2D materials distributed over 30 different crystal structures, including the 1T-CdI2 prototype. To determine the local minimum of the potential energy surface, the dynamical stabilities are analyzed by calculating the Γ-point phonons.37 It shows that 90 out of 315 1T-CdI2 prototype monolayers are of high stability. Besides, phonon dispersions without imaginary frequencies of first row 1T-TMX2 (TM = V, Mn, Fe, Co, Ni; X = Cl, Br, I) monolayers have been investigated by Kulish et al., indicating high dynamic stabilities of the 1T-TMX2 monolayers.23 Furthermore, since the most stable structure generally locates on the global free energy minimum of the potential energy surface, the corresponding potential energy surface for each TMX2 will be explored in detail in our further studies by CALYPSO software using the particle swarm optimization (PSO) algorithm.38
m1 has been studied thoroughly by previous high throughput studies. Haastrup et al. introduced the Computational 2D Materials Database (C2DB) containing 1500 2D materials distributed over 30 different crystal structures, including the 1T-CdI2 prototype. To determine the local minimum of the potential energy surface, the dynamical stabilities are analyzed by calculating the Γ-point phonons.37 It shows that 90 out of 315 1T-CdI2 prototype monolayers are of high stability. Besides, phonon dispersions without imaginary frequencies of first row 1T-TMX2 (TM = V, Mn, Fe, Co, Ni; X = Cl, Br, I) monolayers have been investigated by Kulish et al., indicating high dynamic stabilities of the 1T-TMX2 monolayers.23 Furthermore, since the most stable structure generally locates on the global free energy minimum of the potential energy surface, the corresponding potential energy surface for each TMX2 will be explored in detail in our further studies by CALYPSO software using the particle swarm optimization (PSO) algorithm.38
B. Magnetic ground states
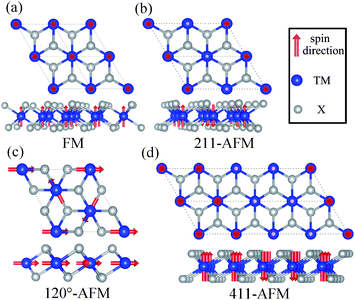
The spin structure and magnetic properties of some bulk TMX2 compounds like NiBr2 have been studied in a previous work, indicating a transition from a collinear easy-plane metamagnetic structure to an in-ab-plane spin structure.39 Since the broken translation symmetry along the z direction in a 2D magnetic monolayer can remove the magnetic ordering perpendicular to the layer plane, the magnetic properties of a 2D structure may differ from its bulk phase.17 Here, one important question is to determine the magnetic ground state of 2D TMX2 monolayers. Clearly, the TM sublattice in both the 2H and 1T phases are of the same type, i.e., a triangular lattice of TM atoms. We consider the following four possible magnetic configurations with high symmetries in 1T-TMX2 as shown in Fig. 2: (a) Ferromagnetic (FM) ordering with all initial magnetic moments pointing to the z direction perpendicular to the monolayer plane. (b) Antiferromagnetic (AFM) ordering in a 2 × 1 × 1 supercell (211-AFM). The magnetic arrangements have FM ordering within the stripes, and have AFM ordering between neighboring stripes. (c) AFM ordering in 4 × 1 × 1 (411-AFM). The magnetic arrangements have FM ordering with adjacent stripes, while they have AFM ordering between the two next neighboring stripes. (d) Due to the triangular networks of TM atoms, frustrated magnetic orderings are considered to have a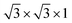 supercell with the angle of spin directions between adjacent TM atoms being 120°.
supercell with the angle of spin directions between adjacent TM atoms being 120°.
Based on the magnetic structure prototypes, DFT calculations are carried out for four such spin configurations of all 90 TMX2 monolayers. According to the total energies of different magnetic orderings obtained by the GGA+U (U = 2 eV) method, the most favorable configurations of each TMX2 in the corresponding stable geometrical phase are listed in Fig. 3. There are 55 out of 90 systems with a total magnetic moment larger than 0.2 μB in the FM configuration, which will be considered as magnetic. In accordance with Fig. 1, the stable 2H phases are mainly concentrated in the nonmagnetic (NM) TMX2 monolayers with TM atoms with d1–d2 configuration, while magnetic FeX2 (X = Cl, Br, I) and TcX2 (X = Br, I) monolayers with a stable 2H phase are exceptions to this rule. Besides, the Zn-group monolayers with a stable 1T phase are also nonmagnetic.
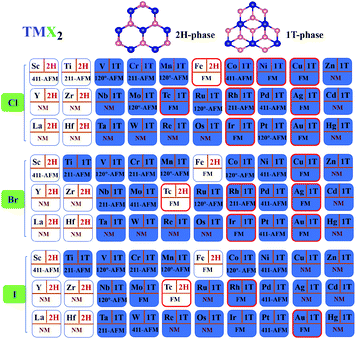 | ||
| Fig. 3 Overview of ground geometrical structure and magnetic states for all 90 transition metal dihalides with U = 2. | ||
Since the majority of magnetic TMX2 monolayers are more stable in the 1T phase, in the following discussions the magnetic and electronic structures are mainly discussed in 1T-TMX2 monolayers. As for FeX2, the energy differences between the 1T and 2H phase range from 10 to 63 meV per atom under different U, which are quite small, and 1T FeX2 monolayers have been proved to be stable in 2D materials database.6,40 Thus, our analysis of the electronic and magnetic properties of FeX2 are discussed in the 1T phases. Tc is a highly radioactive element which needs to be avoided, thus no further discussions will continue. From the magnetic point of view, it can be clearly noticed by comparing TMX2 monolayers in the sequence from 3d to 4d to 5d elements that the tendency of magnetic systems has a remarkable right-shift. It can be well explained by d band broadening which will prevent higher d transition metal based compounds from being spin polarized, i.e. magnetic. The argument is in good accordance with the magnetic behavior of d electrons in transition metal monolayers on noble metal (001) substrates in ref. 41.
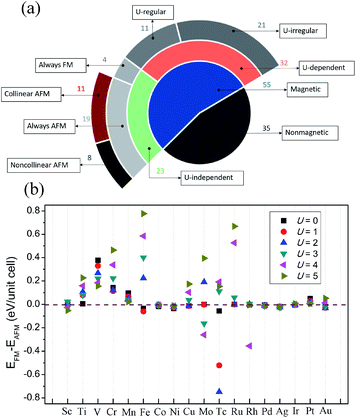
At current stage, we have obtained an overall landscape of 90 TMX2 monolayers with both geometrical and magnetic ground states clarified under the condition of U = 2. However, one threatening problem is that there is no experimental result for such 2D systems. In this case, the effect of the correlations on d electrons of TM atoms may not be described precisely without supportive experimental data. To solve these problems and to make the theoretical study more instructive, we implement HTP calculations on 55 magnetic 1T-TMX2 systems with sequential U values from 0 to 5 in a batch mode to determine the relations between U values and magnetic ground states. Magnetic ground states are evaluated by the energy difference between FM and the most stable AFM states (ΔE). The concrete classification is shown in Fig. 4a. We can clearly see from the pie-chart diagram that 55 out of 90 are magnetic systems. Taking magnetic TMCl2 monolayers for example, the energy difference as shown in Fig. 4b can intuitively reflect the changing tendency of magnetic ground state with respect to different U values from 0 to 5. Among all magnetic systems, the spin configurations are classified into two cases with respect to U values: first, 23 U-independent magnetic systems which indicate that the magnetic ground states will not be changed by different U values exhibiting robustness. The 23 TMX2 with robust magnetic ground states include TMCl2 (TM = V, Cr, Mn, Ni, Ag, and Pt), TMBr2 (TM = Ti, V, Cr, Co, Ni, Ag, and Pt), and TMI2 (TM = Sc, Ti, V, Mn, Fe, Co, Ni, Pd, and Au). Results indicate that U-independent magnetic TMX2 monolayers are mainly dominated by 3d TM dihalides, which can be explained by weaker exchange correlation potentials for lighter TM atoms. Besides, TM dihalides with IB and IIB TM atoms can also be robust magnetic systems against Hubbard U values. Second, 32 U-dependent magnetic systems which show that the magnetic properties will change among different U. Among 32 U-dependent TMX2 monolayers, there are 11 systems (U-regular cases) with magnetic ground states which can be tuned regularly by enlarging U values by the linear change of the energy difference. Meanwhile the magnetic ground states of the other 21 systems (U-irregular cases) cannot be linearly tuned by enlarging the U values.
It is worth mentioning that among the 23 magnetism-robust systems, 4 of them are robust ferromagnetic monolayers including 1 ferromagnetic insulator (NiCl2) and 3 half metals including AgCl2, AgBr2 and AuI2, while 8 out of 19 U-independent cases are noncollinear AFM monolayers. Our results for the ground states of all magnetic TMX2 monolayers are summarized in the Table in the ESI,† corresponding to the classification shown in Fig. 4a. We will make explicit analysis for these 12 1T-TMX2 monolayers with robust magnetic orderings with respect to U values in the following discussions.
Band structures with both spin-up and spin-down channels for four robust FM 1T-TMX2 monolayers with U = 2 are as shown in Fig. 5. Band curve dispersions in the whole Brillouin zone indicate similar state distributions due to the influence of the same crystalline field. The spin splitting near the Fermi level of NiCl2 is about 2.3 eV, that is, larger than the spin splittings of AgCl2, AgBr2 and AuI2, which are in the range of 0.2 to 0.5 eV. The magnetization for NiCl2, dominated by the Ni atom, is close to 2 Bohr magneton (μB) per atom indicating 8 electrons in d orbital filling with high-spin states. Meanwhile for the other Au or Ag based dihalides, the magnetization is distributed and delocalized in both Au (Ag) and halide atoms smaller than 0.5 (μB) per atom, which can also be explained from particle density of states as shown in Fig. 5. For AgCl2, AgBr2 and AuI2 monolayers, the d orbitals of Au or Ag are coupled with halide p orbitals which result in strong interaction between adjacent atoms. Besides, AgCl2, AgBr2 and AuI2 monolayers are half metals with a Fermi level only crossing one spin channel with 100% spin polarization. To ensure the reliability of the band structures of TMX2, the screened hybrid functional Heyd–Scuseria–Ernzerhof (HSE) is further implemented.42 Results indicate that both GGA+U and HSE functional do not change the energy dispersions, and orbital occupations remain similar with the two methods. An exception is represented by the band gap which in the HSE functional is larger with respect to GGA+U results. As for NiCl2, the band gap in the HSE functional is 4.48 eV. Our results are consistent with previous studies.23 However, this difference does not change other electronic and geometric properties, including exchange interactions and magnetic orderings.
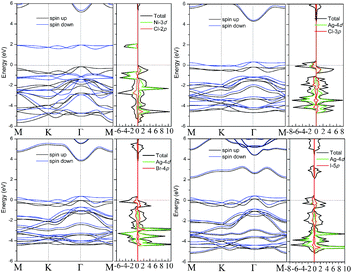 | ||
| Fig. 5 Spin polarized band structures with U = 2 for 4 U-independent FM cases: (a) NiCl2, (b) AgCl2, (c) AgBr2 and (d) AuI2, respectively. | ||
It is known that ferromagnetic insulators are in high demand in the development of next-generation quantum-spintronic devices, in particular those high symmetric systems without chemical doping or tensile strain that can only work at very low temperatures (below 16 K).43 Thus, studies of the magnetic mechanism of ferromagnetic insulator NiCl2 monolayers are further required. Since the magnetic moments are mostly located on Ni atoms, the total energies can be mapped onto a Heisenberg model:
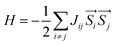 | (1) |
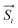 is the spin operator at site i. By considering four unequal magnetic configurations and calculating three independent total energy differences between two random configurations, we obtain the exchange parameters for the nearest neighbor J1, the second nearest neighbor exchange parameter J2 and the third nearest neighbor J3 as illustrated in Fig. 6:
is the spin operator at site i. By considering four unequal magnetic configurations and calculating three independent total energy differences between two random configurations, we obtain the exchange parameters for the nearest neighbor J1, the second nearest neighbor exchange parameter J2 and the third nearest neighbor J3 as illustrated in Fig. 6:| EFM − E211AFM = −8(J1 + J2)S2 | (2) |
| EFM − E411AFM = (−4J1 − 8J2 − 8J3)S2 | (3) |
| EFM − E120°AFM = −6(J1 + J3)S2 | (4) |
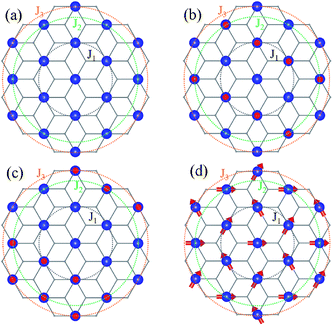 | ||
| Fig. 6 Schematic diagrams of four representative magnetic ordering arrangements corresponding to Fig. 2. Blue balls indicate TM atoms which form six trigonal lattices with nearest neighbors. The black circles identify the exchange coupling J1 between nearest neighbors (NN) of the central TM atom, the green circles identify the exchange coupling J2 between second nearest neighbors (SNN) and the orange circles identify the exchange coupling J3 between the third nearest neighbors (TNN). | ||
By combining these three equations, the three exchange parameters of ferromagnetic NiCl2 are calculated as shown in Table 1. The exchange parameters: J1 = 5.46 meV, J2 = −0.23J1, and J3 = 0.14J1 which notably indicate strong ferromagnetic ground state orderings. The Curie temperature of NiCl2 is further evaluated by mean field theory using 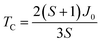 , where
, where 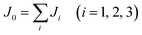 .44,45 Results show that NiCl2 is a U-independent ferromagnetic insulator with a Curie temperature of 57 K.
.44,45 Results show that NiCl2 is a U-independent ferromagnetic insulator with a Curie temperature of 57 K.
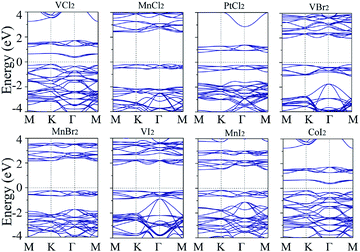
Robust AFM states with respect to U parameters in TMX2 are also worth mentioning. Previous studies have shown that antiferromagnets have typically much faster dynamics than ferromagnets, as the reorientation of antiferromagnetic moments will cost exchange energy. In particular, the insulating antiferromagnets have been proved to have significant application in optical devices. Early in 2004, Kimel et al. uncovered that the spins of the antiferromagnet TmFeO3 can be tuned on a timescale of a few picoseconds, in contrast to hundreds of picoseconds in a ferromagnet.46 Besides, Takei et al. proved theoretically that spin–superfluid transport can be realized in AFM insulator.47 In TMX2 systems, we filter 8 noncollinear AFM insulators whose magnetic ground state will not change with respect to various U, and the corresponding band structures are listed in Fig. 7. The results show that the band gaps of these noncollinear AFM insulators are in the range between 0.5 and 2.5 eV with U = 2. The NN, SNN and TNN exchange parameters listed in Table 1 are analyzed by the Heisenberg model. The positive J1 is 3.8 to 5.6 times larger than the absolute value of J2, which is consistent with the favored noncollinear AFM spin configurations. Besides, the in-plane magnetic anisotropy energy (MAE) for 8 noncollinear AFM are estimated by a rotating magnetic orientation with an interval of 10°. These results indicate that the in-plane MAE is smaller than 10 μeV per unit-cell for each noncollinear AFM TMX2, which shows that the in-plane magnetic orientation can overcome small thermal fluctuation and is of high flexibility. There is one thing worth mentioning for low-dimensional magnetic systems, especially for noncollinear cases, which is that a spin–spiral structure may exist. In previous studies, the exchange interaction parameters of the 3d transition metal chains have been evaluated by using energy dispersion relations of the spin–spiral waves. Results show that the magnetic coupling in V, Mn, Cr chains are frustrated.48 The results are in consistent with the frustrated magnetic behaviors in Mn or V based TMX2 systems. For a better understanding of the spin–spiral waves and the exchange interaction of transition metal dihalides, further studies need to be explored.
| TMX2 | J 1 | J 2 | J 3 | T C | μ B | GS |
|---|---|---|---|---|---|---|
| NiCl2 | 5.46 | −1.28 | 0.75 | 57 | 2 | FM |
| VCl2 | −28.54 | 6.26 | −3.97 | — | 3 | 120°-AFM |
| MnCl2 | −3.02 | 0.68 | −0.65 | — | 4 | 120°-AFM |
| PtCl2 | −18.06 | 4.03 | −7.63 | — | 1 | 120°-AFM |
| VBr2 | −17.07 | 3.91 | −2.32 | — | 3 | 120°-AFM |
| VI2 | −7.68 | 1.84 | −1.21 | — | 3 | 120°-AFM |
| MnI2 | −2.93 | 0.52 | −0.87 | — | 4 | 120°-AFM |
| CoI2 | −2.80 | 0.69 | −2.3 | — | 3 | 120°-AFM |
IV. Conclusions
In summary, by employing a high throughput study combined with first principles calculations, we systematically study the magnetic ground states of transition metal dihalide monolayers with respect to different Hubbard U values. The geometrical phase stability is first investigated by considering both the 2H and 1T phase in a hexagonal TMX2 lattice. The results show that 50 out of 55 magnetic TMX2 are more stable in the 1T phase except for FeX2 (X = Cl, Br and I) and TcX2 (X = Br and I), while the stable 2H phase is mainly concentrated in nonmagnetic TMX2 monolayers with a TM belonging to d1–d2 elements. The magnetic ground states for 1T-TMX2 monolayers are considered thoroughly under a batch of Hubbard U values from 0 to 5 eV by considering four typical magnetic orderings. Interestingly, we have found 23 U-independent magnetic TMX2 systems with robust magnetic ground states not changed by the U values. Among them, NiCl2 is a ferromagnetic insulator with a magnetic moment of 2 μB on Ni, and the Curie temperature estimated by Heisenberg model is 57 K. Besides, 8 TMX2 monolayers including VX2 (X = Cl, Br and I), MnX2 (X = Cl, Br and I), PtCl2 and CoI2 are proved to be noncollinear antiferromagnetic insulators. The in-plane MAE is estimated to be smaller than 10 μeV per unit-cell and such tiny MAE will not stabilize the magnetic order against thermal fluctuation, which indicates the in-plane magnetic orientation is of high flexibility. Generally, we have presented a thorough understanding of the magnetic behavior of transition metal dihalides TMX2 with respect to Hubbard U. Our studies demonstrate that TMX2 monolayers are promising for spintronic applications, and especially TMX2 monolayers with robust noncollinear antiferromagnetic orderings are possible candidates for skyrmions and quantum spin liquids.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Priority Program 1666 of the Deutsche Forschungsgemeinschaft (DFG). Xinru Li gratefully acknowledges the financial support by the Sino-German (CSC-DAAD) postdoc scholarship program and the special funds for theoretical physics of National Natural Science Foundation of China (No. 11947121). We acknowledge computing time on the Lichtenberg supercomputer at TU Darmstadt.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- Z. Liu, B. Zhou, Y. Zhang, Z. Wang, H. Weng, D. Prabhakaran, S.-K. Mo, Z. Shen, Z. Fang and X. Dai, et al. , Science, 2014, 343, 864 CrossRef CAS PubMed.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263 CrossRef PubMed.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185 CrossRef CAS.
- Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695 CrossRef CAS PubMed.
- M. Ashton, D. Gluhovic, S. B. Sinnott, J. Guo, D. A. Stewart and R. G. Hennig, Nano Lett., 2017, 17, 5251 CrossRef CAS PubMed.
- G. Gao, G. Ding, J. Li, K. Yao, M. Wu and M. Qian, Nanoscale, 2016, 8, 8986 RSC.
- S. Tang, C. Zhang, D. Wong, Z. Pedramrazi, H.-Z. Tsai, C. Jia, B. Moritz, M. Claassen, H. Ryu and S. Kahn, et al. , Nat. Phys., 2017, 13, 683 Search PubMed.
- Y.-T. Hsu, A. Vaezi, M. H. Fischer and E.-A. Kim, Nat. Commun., 2017, 8, 14985 Search PubMed.
- Y. Ma, L. Kou, X. Li, Y. Dai, S. C. Smith and T. Heine, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085427 CrossRef.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699 CrossRef CAS PubMed.
- N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425 CrossRef.
- W. Zhao, Z. Ghorannevis, L. Chu, M. Toh, C. Kloc, P.-H. Tan and G. Eda, ACS Nano, 2013, 7, 791 CrossRef CAS PubMed.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033 CrossRef CAS.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, ACS Nano, 2014, 8, 1102 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang and Y. Wang, et al. , Nature, 2017, 546, 265 CrossRef CAS PubMed.
- M. A. McGuire, Crystals, 2017, 7, 121 CrossRef.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, et al. , Nature, 2017, 546, 270 CrossRef CAS PubMed.
- K. L. Seyler, D. Zhong, D. R. Klein, S. Gao, X. Zhang, B. Huang, E. Navarro-Moratalla, L. Yang, D. H. Cobden and M. A. McGuire, et al. , Nat. Phys., 2018, 14, 277 Search PubMed.
- P. Jiang, L. Li, Z. Liao, Y. Zhao and Z. Zhong, Nano Lett., 2018, 6, 3844 CrossRef PubMed.
- D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield and J. Fernández-Rossier, et al. , Science, 2018, 360, 1218 CrossRef CAS PubMed.
- Y. S. Karimov, M. Vol’Pin and Y. N. Novikov, Journal of Experimental and Theoretical Physics Letters, 1971, 14, 142 Search PubMed.
- V. V. Kulish and W. Huang, J. Mater. Chem. C, 2017, 5, 8734 RSC.
- E. Torun, H. Sahin, S. Singh and F. Peeters, Appl. Phys. Lett., 2015, 106, 192404 CrossRef.
- R. Tenne, Chem. –Eur. J., 2002, 8, 5296 CrossRef CAS.
- A. Abdul Wasey, D. Karmakar, and G. Das, in AIP Conference Proceedings, AIP, 2013, vol. 1512, pp. 1114–1115 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Y.-C. Lin, D. O. Dumcenco, Y.-S. Huang and K. Suenaga, Nat. Nanotechnol., 2014, 9, 391 CrossRef CAS PubMed.
- K.-A. N. Duerloo, Y. Li and E. J. Reed, Nat. Commun., 2014, 5, 4214 CrossRef CAS PubMed.
- Y. Kang, S. Najmaei, Z. Liu, Y. Bao, Y. Wang, X. Zhu, N. J. Halas, P. Nordlander, P. M. Ajayan and J. Lou, et al. , Adv. Mater., 2014, 26, 6467 CrossRef CAS PubMed.
- X. Fan, P. Xu, D. Zhou, Y. Sun, Y. C. Li, M. A. T. Nguyen, M. Terrones and T. E. Mallouk, Nano Lett., 2015, 15, 5956 CrossRef CAS PubMed.
- K. Chang, X. Hai, H. Pang, H. Zhang, L. Shi, G. Liu, H. Liu, G. Zhao, M. Li and J. Ye, Adv. Mater., 2016, 28, 10033 CrossRef CAS PubMed.
- M. Calandra, Phys. Rev. Lett., 2018, 121, 026401 CrossRef CAS PubMed.
- S. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen and A. C. Riis-Jensen, et al. , 2D Materials, 2018, 5, 042002 CrossRef CAS.
- Q. Tong, J. Lv, P. Gao and Y. Wang, Chin. Phys. B, 2019, 28, 106105 CrossRef.
- P. Day and K. Ziebeck, J. Phys. C: Solid State Phys., 1980, 13, L523 CrossRef CAS.
- M. Ashton, J. Paul, S. B. Sinnott and R. G. Hennig, Phys. Rev. Lett., 2017, 118, 106101 CrossRef PubMed.
- S. Blügel, Phys. Rev. Lett., 1992, 68, 851 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- D. Meng, H. Guo, Z. Cui, C. Ma, J. Zhao, J. Lu, H. Xu, Z. Wang, X. Hu and Z. Fu, et al. , Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2873 CrossRef CAS PubMed.
- R. Rausch and W. Nolting, J. Phys.: Condens. Matter, 2009, 21, 376002 CrossRef PubMed.
- H. Walker, O. Mustonen, S. Vasala, D. Voneshen, M. Le, D. Adroja and M. Karppinen, Phys. Rev. B, 2016, 94, 064411 CrossRef.
- A. Kimel, A. Kirilyuk, A. Tsvetkov, R. Pisarev and T. Rasing, Nature, 2004, 429, 850 CrossRef CAS PubMed.
- S. Takei, B. I. Halperin, A. Yacoby and Y. Tserkovnyak, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094408 CrossRef.
- J. Tung and G. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 144403 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00588a |
| This journal is © The Royal Society of Chemistry 2020 |