Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cost-effective materials discovery: Bayesian optimization across multiple information sources†
Henry C.
Herbol
 *a,
Matthias
Poloczek‡
b and
Paulette
Clancy
*a,
Matthias
Poloczek‡
b and
Paulette
Clancy
 a
a
aDepartment of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: hherbol@jhu.edu
bUber AI, San Francisco, CA 94105, USA
First published on 8th June 2020
Abstract
Applications of Bayesian optimization to problems in the materials sciences have primarily focused on consideration of a single source of data, such as DFT, MD, or experiments. This work shows how it is possible to incorporate cost-effective sources of information with more accurate, but expensive, sources as a means to significantly accelerate materials discovery in the computational sciences. Specifically, we compare the performance of three surrogate models for multi-information source optimization (MISO) in combination with a cost-sensitive knowledge gradient approach for the acquisition function: a multivariate Gaussian process regression, a cokriging method exemplified by the intrinsic coregionalization model, and a new surrogate model we created, the Pearson-r coregionalization model. To demonstrate the effectiveness of this MISO approach to the study of commonly encountered materials science problems, we show MISO results for three test cases that outperform a standard efficient global optimization (EGO) algorithm: a challenging benchmark function (Rosenbrock), a molecular geometry optimization, and a binding energy maximization. We outline factors that affect the performance of combining different information sources, including one in which a standard EGO approach is preferable to MISO.
New conceptsBayesian optimization methods require an acquisition function (where to search next) and a surrogate model (mimicking the behavior of real systems). We create a novel algorithm that uses the only existing acquisition function capable of taking information from multiple sources (e.g., different experimental sources and/or simulation approaches) in conjunction with a new surrogate model that finds the optimal result meeting a pre-specified objective. Current surrogate models require many fitting parameters, restricting their applicability to less complex domains. Our new model minimizes the number of such hyperparameters and yet frequently performs far better than more complicated approaches. This opens the door to considering larger combinatorial problems than previously possible. We show that our new algorithm is successful at accelerating the search for optimal solutions of common materials science problems, like geometry optimization or optimal solvent choice. We identified that our multi-information source approach will work best in well-correlated systems. Noisy information sources make our approach only comparably effective to a standard EGO approach. Overall, this is an important new addition to existing Bayesian optimization tools, one that functions in decision-making more like our own brains, considering many pieces of information before deciding upon the best solution in the most effective manner. |
1 Introduction
At the forefront of materials sciences, there is a set of research topics that remain largely inaccessible, experimentally and computationally, due to their combinatorial complexity. As one topical example, the study of high entropy alloys has exploded into an almost insurmountable combinatorial problem.1 In the biological sciences, the large conformational space of protein folding has proven to be exceedingly difficult to tackle.2 In recent years, machine learning (ML) techniques have shown promise in their application to challenges in the physical and biological sciences, proving to be an effective means to tackle intractable compositional and/or high-dimensional problems. Several landmark studies are emerging, as evidenced by examples using “deep learning” approaches on protein folding such as AlphaFold,3 regression methods for transformation temperature predictions in shape change alloys,4 the use of a random forest approach to predict the thermoelectric properties of materials,5,6 the use of neural networks to predict molecular7 and atomic8 energies, and using Bayesian optimization to unravel the solution processing of the hybrid organic–inorganic perovskite (HOIP) combinatorial space.9 More nuanced applications have also arisen such as the use of deep transfer learning for materials property prediction,10 the necessity for multi-objective optimization in the case of durable antifogging superomniphobic supertransmissive nanostructured glass development,11 the use of a support vector machine (SVM) to efficiently identify potential antimicrobial peptides,12 the development of a novel molecular reaction fingerprint for the study of redox reactions,13 the use of genetic algorithms to estimate parameters in large kinetic models,14 the use of a variety of these methods to explore the organic photovoltaic (OPV) space,15,16 the use of Gaussian process regression (GPR) to model quasar emission spectra for the detection of Ly α absorbers,17 and a novel neural network design for encoding–decoding molecules to/from continuous space.18Although such studies, and many others, are demonstrating the breadth of applicability of ML to materials sciences, they invariably use a single source of data/information, which we will designate as an information source (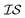 ). It is clear that improvements in speed and cost could be made by learning information from a cost-effective source and limiting predictions from other, more expensive, sources. Ultimately, using multiple information sources could lead to more robust predictions of materials' choices and/or properties, not to mention the potential for lowering the cost (in time and resources) if a cheaper information source can be used in place of a more expensive one. For materials studies, information sources could be provided by experimental data, continuum modeling predictions, molecular dynamics (MD) simulations, quantum mechanically derived density functional theory (DFT) calculations, various ML models – neural networks (NN), Gaussian processes (GPs), random forests, etc. – or even an intuitive rule of thumb. Each information source has its own inherent accuracy and cost. In this paper, we will show how to use a combination of sources of information within a Bayesian optimization framework to significantly accelerate materials discovery for common, important calculations in the computational sciences.
). It is clear that improvements in speed and cost could be made by learning information from a cost-effective source and limiting predictions from other, more expensive, sources. Ultimately, using multiple information sources could lead to more robust predictions of materials' choices and/or properties, not to mention the potential for lowering the cost (in time and resources) if a cheaper information source can be used in place of a more expensive one. For materials studies, information sources could be provided by experimental data, continuum modeling predictions, molecular dynamics (MD) simulations, quantum mechanically derived density functional theory (DFT) calculations, various ML models – neural networks (NN), Gaussian processes (GPs), random forests, etc. – or even an intuitive rule of thumb. Each information source has its own inherent accuracy and cost. In this paper, we will show how to use a combination of sources of information within a Bayesian optimization framework to significantly accelerate materials discovery for common, important calculations in the computational sciences.
Bayesian optimization, from a high-level point of view, involves the process of using Bayes rule to optimize a function. To understand why this is relevant, we must first contemplate the problem of optimizing a continuous, black-box, noisy function, g(x). If we have no way of appreciating the function, our search is blind. However, what if we can devise a function, f, that, given our observations from D = g(x), allows us to make more accurate predictions on g(x)? In essence, can we find f(x|D) ∼ g(x)? If so, we can then use f(x|D) to determine what candidate points x we should sample to maximize (or minimize) g(x). This can be accomplished using Bayes rule (eqn (1)).
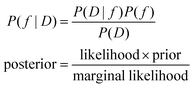 | (1) |
One approach used to consider several information sources at a time is known as cokriging.20–22 This approach uses either spatial proximity (a cross-variogram) or correlation (cross-covariance) to define a matrix, called a coregionalization matrix, to interpolate one 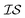 from data in another
from data in another 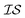 .20,23 This is illustrated in Fig. 1, in which a prediction made from a coarse
.20,23 This is illustrated in Fig. 1, in which a prediction made from a coarse 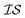 is used to glean information on a finer
is used to glean information on a finer 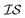 . Kriging is perhaps best known as a geostatistics term for interpolation using a GP, while cokriging is simply the extension of this interpolation to multiple, highly correlated, data sets.20 Cokriging has been used to study a wide range of geological systems, from predicting surface temperatures from elevation24 to capturing the correlation of rainfall measurements from radar to standard rain gauges.25
. Kriging is perhaps best known as a geostatistics term for interpolation using a GP, while cokriging is simply the extension of this interpolation to multiple, highly correlated, data sets.20 Cokriging has been used to study a wide range of geological systems, from predicting surface temperatures from elevation24 to capturing the correlation of rainfall measurements from radar to standard rain gauges.25
In what follows, we will use an 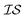 index number to denote the “accuracy” of the source (with accuracy being subjective and based on the user's viewpoint). We denote
index number to denote the “accuracy” of the source (with accuracy being subjective and based on the user's viewpoint). We denote 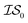 to be more accurate than
to be more accurate than 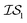 , and so on.
, and so on.
An alternative approach to handling data from several information sources was recently published as a method employing multi-information source optimization with a Knowledge Gradient (misoKG). In that work, a cost-sensitive Knowledge Gradient (csKG) acquisition function was used with a standard multivariate Gaussian process regression (MGP) surrogate model.26 These two components, an acquisition function and a surrogate model, are the building blocks of an optimization algorithm. Hence, consideration of the choices of these two components will figure prominently in the discussions below. Multi-information source optimization (MISO) works by sampling in such a way that the cost is minimized, while the accuracy of the predicted (optimal) result is maximized. The underlying csKG acquisition function allows for this by determining which point, and which source of information, to sample next. If the underlying GPR indicates no (or poor) correlation between the sources of information, then the model defaults to the well-known Knowledge Gradient (KG). At this point, we draw the reader's attention to the difference between MISO and multi-fidelity optimization: MISO can be seen as a generalization of multi-fidelity approaches from cost-effective approximations to encompass any correlated source of information.
Each approach used here builds from an underlying Gaussian process, meaning that the code will need to learn empirical fitting parameters. These parameters, called hyperparameters, can vary depending on the choice of surrogate model. With more hyperparameters, it is possible to obtain a better regression; however, this comes at a cost. To fit hyperparameters, it is common to use an approach such as the Maximum Likelihood Estimation (MLE) or Maximum A Posteriori (MAP) estimation.19 The larger the hyperparameter space, the noisier the landscape, and the more difficult it becomes to adequately learn the hyperparameters. Assuming the same model for each information source, the number of hyperparameters in MGP scales linearly with the number of information sources. Coregionalization, on the other hand, will add at most 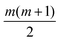 hyperparameters, being the components of a lower triangular matrix, where m is the number of information sources. This provides a strong impetus to consider coregionalization as a surrogate model.
hyperparameters, being the components of a lower triangular matrix, where m is the number of information sources. This provides a strong impetus to consider coregionalization as a surrogate model.
In this work, we present a “coregionalized csKG approach, using the csKG acquisition function with Bayesian optimization methods based on the intrinsic coregionalization model (ICM).27 Unlike the original multivariate Gaussian process regression (MGP) surrogate model, where the number of hyperparameters effectively scales with the number of information sources, we show it is possible to define the coregionalization matrix using significantly fewer hyperparameters. Further, we introduce an entirely new approach capable of generating the necessary coregionalization matrix, based on Pearson-r correlation coefficients,28 which has the considerable advantage of removing the need for additional hyperparameters altogether. We call this surrogate model the Pearson-r coregionalization model (PCM). As a “proof of concept,” we apply a unique combination of the csKG acquisition function and the new PCM surrogate model to explore complex compositional landscapes involved in the solution processing of a novel class of solar cell materials, known as hybrid organic–inorganic perovskites (HOIPs), and other common computational materials applications.
2 Nomenclature
To merge the naming conventions between the ML and DFT communities, we present two approaches to identify the models used in this paper. Within the ML community, it is common practice to identify an acquisition function/surrogate model pair by a single name. This can be seen in the case of the commonly used efficient global optimization (EGO) algorithm,29 which merges expected improvement (EI) with GPR (or, in the case of the original paper, this is referred to as “kriging”). Similarly, the misoKG algorithm uses a csKG acquisition function with an MGP surrogate model. To maintain this naming convention, we will then define “PearsonKG” to mean pairing the csKG acquisition function with the PCM surrogate model. In regards to the csKG with the ICM surrogate model, we note that a similar formulation exists with an alternative acquisition function: entropy search. This algorithm was dubbed multi-task Bayesian optimization (MTBO)30 and, as such, leads to our choice of its name as “MultiTaskKG.”This naming scheme has the benefit of recognizing an algorithm by name; however, it does not allow readers to easily parse the details of the constituent models. Within the DFT literature, the solution for naming the choices of functional and basis-set that define the overall approach is to list the two separated by a forward slash. In the spirit of the DFT naming convention, we express the specific names favored by the ML community by a combination of the underlying acquisition function and surrogate model. As a result, we identify the aforementioned combinations as follows:
• EGO = EI/GPR
• misoKG = csKG/MGP
• MultiTaskKG = csKG/ICM
• PearsonKG = csKG/PCM
Within this paper, we will refer to the algorithm name itself; however, we define the above in an effort to consolidate naming conventions within the ML and DFT literature. This extensible approach allows new researchers in the field to readily understand the taxonomy of algorithmic names in this area of machine learning.
3 Results
We benchmark three MISO surrogate models – PCM, ICM, and MGP – against a standard EGO approach using the Rosenbrock function as a first test case.31 The Rosenbrock function, with its long, narrow and very flat parabolic basin, is a difficult optimization problem that is commonly used for benchmark purposes. This test case also has probative value since it allows us to benchmark against the original misoKG paper by Poloczek et al.26 As a second test case, we study the effects of differing DFT functionals/basis sets as sources of information for the geometry optimization of carbon monoxide. Finally, we revisit the HOIP work9 and assess the benefits of using MISO approaches, in which different levels of theory within DFT are deployed as a set of information sources, as well as differing molecular systems.Running a MISO approach does not guarantee that one information source will be sampled over another. As such, given that sampling from 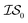 does not necessarily have the same cost as sampling from
does not necessarily have the same cost as sampling from 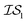 , we end up with a heterogeneous data set where cost varies between replications. This can be conceptualized by considering two experiments in which we run a MISO approach using two sources,
, we end up with a heterogeneous data set where cost varies between replications. This can be conceptualized by considering two experiments in which we run a MISO approach using two sources, 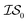 and
and 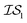 , whose costs we estimate to be 1000 and 1, respectively. If, on the first experiment, we sampled
, whose costs we estimate to be 1000 and 1, respectively. If, on the first experiment, we sampled 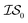 4 times and
4 times and 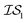 2 times, versus on the second experiment where we sampled
2 times, versus on the second experiment where we sampled 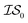 6 times, our 6th data point will be at a cumulative cost of either 4002 or 6000, depending on the experiment. As we replicate our evaluations several times for statistical significance, it is no longer possible to simply “average across all replications.” Thus, we must homogenize the sampling domain so as to average the value that first exceeds a given cost. We then plot the x associated with the maximum (or minimum, depending on the problem) posterior mean of the
6 times, our 6th data point will be at a cumulative cost of either 4002 or 6000, depending on the experiment. As we replicate our evaluations several times for statistical significance, it is no longer possible to simply “average across all replications.” Thus, we must homogenize the sampling domain so as to average the value that first exceeds a given cost. We then plot the x associated with the maximum (or minimum, depending on the problem) posterior mean of the 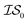 model. The “best” model is identified as the model that achieves global maximization with the least cost.
model. The “best” model is identified as the model that achieves global maximization with the least cost.
Hyperparameter optimization can be achieved in at least three different ways: (1) with data sampled across all 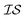 (i.e., x, if x is sampled for all
(i.e., x, if x is sampled for all 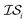 , mathematically shown as
, mathematically shown as 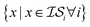 ), (2) with data sampled only within
), (2) with data sampled only within 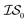 – the most expensive information source – or (3) with all sampled data. In order, we will call these
– the most expensive information source – or (3) with all sampled data. In order, we will call these  ,
, 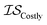 , and
, and 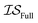 . Additional benchmarks are shown in the ESI.† In this work, we learn the hyperparameters from the data we sampled initially, and then keep them fixed for the remainder of the optimization. As such, we only concern ourselves with
. Additional benchmarks are shown in the ESI.† In this work, we learn the hyperparameters from the data we sampled initially, and then keep them fixed for the remainder of the optimization. As such, we only concern ourselves with  and
and 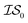 .
.
Finally, as the Bayesian optimization is performed for a combinatorial problem, we discretize the domains we wish to optimize over. The larger the discretized domain, the more complex the problem, and the harder it is to find the global extrema. This class of problem is seen as “combinatorial optimization” for “large discrete domains.” In the case of the Rosenbrock function, we illustrate below three different discretized domains as a way to illustrate the benefit of using MISO over that of using EGO, especially as the complexity of the problem increases.
3.1 The Rosenbrock function
Fig. 2 shows the results from a variety of MISO approaches in which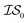 was the standard 2D Rosenbrock function (see eqn (5)), and a slightly noisier alternative was chosen as
was the standard 2D Rosenbrock function (see eqn (5)), and a slightly noisier alternative was chosen as  (in which the amplitude of the sine noise, v, was set to 0.1). To achieve better statistical significance, we ran 200 replications of each and plotted with ±2 standard error of the mean (SE). The value of a MISO approach in all panels of Fig. 2 can clearly be seen in comparison to a more standard Bayesian optimization approach like EGO, which is shown as a control. Candidate (x,y) data were sampled from [−2,2]2 in increments of 0.016, 0.008, or 0.004 (for a sampled discrete domain size of 250, 500, or 1000, respectively). This comparison of domain complexity is illustrated in Fig. 2a–c, where the superiority of MISO approaches becomes increasingly apparent. In contrast, Fig. 2d shows results from MISO approaches in which
(in which the amplitude of the sine noise, v, was set to 0.1). To achieve better statistical significance, we ran 200 replications of each and plotted with ±2 standard error of the mean (SE). The value of a MISO approach in all panels of Fig. 2 can clearly be seen in comparison to a more standard Bayesian optimization approach like EGO, which is shown as a control. Candidate (x,y) data were sampled from [−2,2]2 in increments of 0.016, 0.008, or 0.004 (for a sampled discrete domain size of 250, 500, or 1000, respectively). This comparison of domain complexity is illustrated in Fig. 2a–c, where the superiority of MISO approaches becomes increasingly apparent. In contrast, Fig. 2d shows results from MISO approaches in which  was the standard Rosenbrock function (see eqn (5)), but a significantly noisier alternative was chosen as
was the standard Rosenbrock function (see eqn (5)), but a significantly noisier alternative was chosen as  (in which the amplitude of the sine noise, v, was set to 10.0). Corresponding numerical results are shown in Table 1.
(in which the amplitude of the sine noise, v, was set to 10.0). Corresponding numerical results are shown in Table 1.
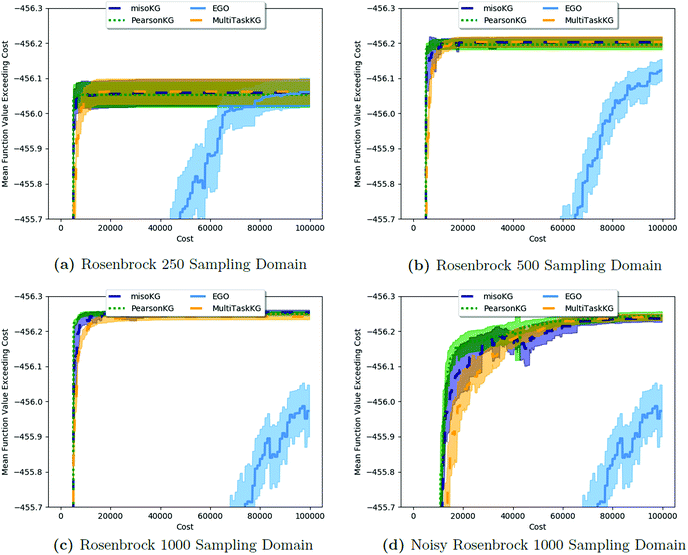 | ||
| Fig. 2 A comparison of MISO approaches to a standard EGO approach to find the minimum of the Rosenbrock function (eqn (5)). In all cases, the three MISO approaches (misoKG,26 MultiTaskKG, and PearsonKG) significantly outperform EGO (shown in blue) by converging to the global minimum of −456.3 at the least cost. This improvement is even more noticeable for the larger discretized domains of 1000 and 500 samples, which constitute a more difficult optimization problem. This figure illustrates the advantage of a MISO approach when a well-correlated alternative information source is chosen. Shaded regions indicate two standard errors of the mean obtained from up to 200 replications. | ||
![[9 with combining macron]](https://www.rsc.org/images/entities/char_0039_0304.gif) th%-tile. Values reported in this table indicate the cost taken to be below −455.3, the lowest function evaluation across all methods (with the global minimum occurring at −456.3). All values in this table have been rounded to the nearest 1000 (the cost of
th%-tile. Values reported in this table indicate the cost taken to be below −455.3, the lowest function evaluation across all methods (with the global minimum occurring at −456.3). All values in this table have been rounded to the nearest 1000 (the cost of 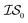 ) and then scaled by 1000 to be more easily compared
) and then scaled by 1000 to be more easily compared
| Algorithm | Acquisition function | Surrogate model | Θ training set | Mean | STD | 99.![[9 with combining macron]](https://www.rsc.org/images/entities/char_0039_0304.gif) th%-tile th%-tile |
|---|---|---|---|---|---|---|
| a Results using the same three statistical models, but for an extremely noisy Rosenbrock function. | ||||||
| EGO | EI | GPR |
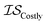
|
25 | 21 | 100 |
| misoKG | csKG | MGP |
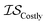
|
13 | 13 | 81 |
| MultiTaskKG | csKG | ICM |
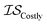
|
13 | 13 | 81 |
| PearsonKG | csKG | PCM |
|
5 | 1 | 5 |
| misoKG | csKG | MGP |

|
5 | 2 | 12 |
| MultiTaskKG | csKG | ICM |

|
5 | 1 | 7 |
| PearsonKG | csKG | PCM |

|
5 | 1 | 5 |
| misoKG | csKG | MGPa |

|
6 | 3 | 28 |
| MultiTaskKG | csKG | ICMa |

|
7 | 5 | 47 |
| PearsonKG | csKG | PCMa |

|
5 | 2 | 16 |
3.2 DFT information sources for geometry optimization in CO
We studied the ability of the same four statistical models to minimize the total energy of a carbon monoxide (CO) molecule. This effectively performs a geometry optimization, a common task using DFT, via Bayesian optimization. Information sources were taken as being either a single-point SCF calculation from a double-hybrid method, with a triple-ζ basis set (B2PLYP and Def2-TZVP),32,33 which is an accurate and expensive option, or a simple (inexpensive) Hartree–Fock approach with “three corrections”34 in which (1) a geometrical counterpoise correction to remove basis set superposition error,35–37 (2) the D3BJ dispersion correction,38 and (3) the MINIX basis set.39 Note that these information sources correlate well, with a Pearson-r correlation coefficient of 0.999. As we will show, this strong correlation is an important consideration. The results are shown in Table 2, where the ICM and PCM surrogate models perform the best (i.e., have the lowest mean cost). What is more strikingly apparent though is the improvement to the 99.9th percentile, where PearsonKG shows a 76% improvement compared to that of EGO.3.3 Physical analytics pipeLine test case for HOIP materials
A major difficulty associated with studying hybrid organic–inorganic perovskites (HOIPs) computationally lies in the fact that (1) possible candidate materials differ in composition, (2) the compositional space represents a large combinatorial problem, and (3) no MD force field exists that is suitable to use in cost-effective simulations for HOIPs candidates. As a result, computational research on HOIPs formation and growth is currently restricted largely to expensive DFT calculations.Our previous work9 showed the benefits of using Bayesian optimization to tame this complexity, and developed a probabilistic model for HOIP-solvent intermolecular binding energies. Here, we investigate the benefits of using multiple information source optimization approaches. The alternate  in this case consist of data sources in which we varied (1) the number of solvents considered to be bound to the lead salt and (2) differing DFT levels of theory (defined as differing functionals and basis sets), which can vary considerably in expense of calculation. As semi-empirical force fields for HOIPs become available in the future, these could also be used within a MISO approach.
in this case consist of data sources in which we varied (1) the number of solvents considered to be bound to the lead salt and (2) differing DFT levels of theory (defined as differing functionals and basis sets), which can vary considerably in expense of calculation. As semi-empirical force fields for HOIPs become available in the future, these could also be used within a MISO approach.
Results of these tests are shown in Fig. 3. As the MISO surrogate models require an initial sampling from all the information sources prior to running the optimizer, this produces a systematic offset on the x-axis in Fig. 3a–c (and most readily observable in Fig. 3c) indicative of this additional training cost. In contrast, EGO starts optimizing sooner since its initial training is solely against the expensive  . The largest benefits to using MISO approaches can be seen in Fig. 3a, in a test case in which the two information sources are both DFT functionals (inexpensive GGA and expensive hybrid approaches). In contrast, in Fig. 3b and c, the two different information sources concern information garnered from the number of solvent molecules bound to the lead salt (one solvent molecule vs. three solvent molecules in Fig. 3b, and three solvent molecules vs. five solvent molecules in Fig. 3c). Here, the advantage of using a MISO approach is far less apparent. The origin of this change is, we believe, a function of how noisy the energy landscape becomes as the number of solvent molecules increases which, in turn, necessitates a growing importance of adequate sampling.
. The largest benefits to using MISO approaches can be seen in Fig. 3a, in a test case in which the two information sources are both DFT functionals (inexpensive GGA and expensive hybrid approaches). In contrast, in Fig. 3b and c, the two different information sources concern information garnered from the number of solvent molecules bound to the lead salt (one solvent molecule vs. three solvent molecules in Fig. 3b, and three solvent molecules vs. five solvent molecules in Fig. 3c). Here, the advantage of using a MISO approach is far less apparent. The origin of this change is, we believe, a function of how noisy the energy landscape becomes as the number of solvent molecules increases which, in turn, necessitates a growing importance of adequate sampling.
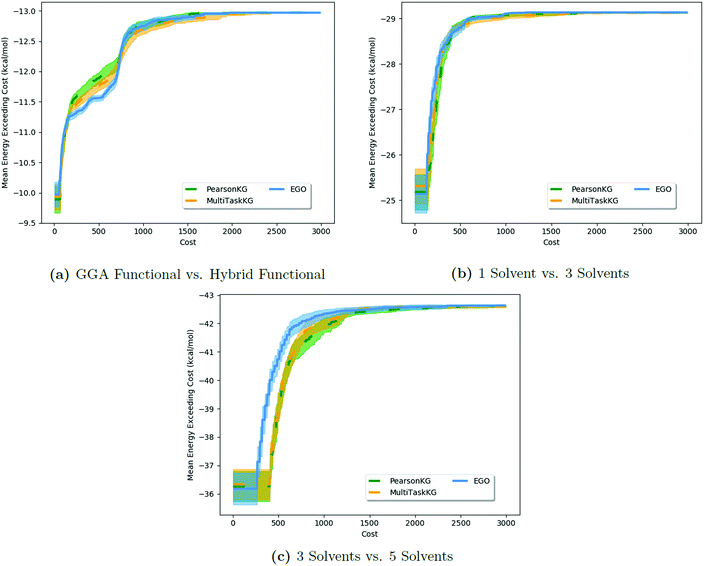 | ||
| Fig. 3 Comparison of the impact of different information sources for HOIP materials in the performance of MISO methods versus a standard EGO approach. The results show that EGO performs as well as, and at times better than, MISO methods in cases (Fig. 4b and c) where the information sources are poorly correlated. MISO methods fall back to EGO-like performance in such cases (with the exception of the x-offset due to the initial sampling). | ||
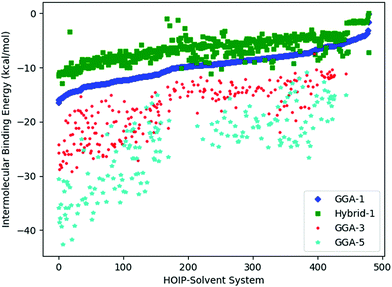
To assess the noise in the energy landscapes, we generate a cross-correlation table of possible HOIP-solvent information sources (Table 3). The various information sources are distinguished by the level of theory (GGA vs. hybrid) and the number of solvents (1, 3, or 5). The generalised gradient approximation (GGA) level of theory used was B97-D3 with a triple-ζ basis set;38,40 while the hybrid functional was PW6B95 with a triple-ζ basis set.33,41 The naming convention used was either GGA or hybrid followed by N, where N was 1, 3, or 5 (signifying the number of solvents). Results for all the information sources are plotted in Fig. 4. We find that GGA-1 correlates best with other 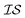 (i.e., it consistently has a correlation factor over 0.8).
(i.e., it consistently has a correlation factor over 0.8).
| Hybrid-1 | GGA-1 | GGA-3 | GGA-5 | |
|---|---|---|---|---|
| Hybrid-1 | 1.00 | 0.83 | 0.77 | 0.76 |
| GGA-1 | 0.83 | 1.00 | 0.83 | 0.83 |
| GGA-3 | 0.77 | 0.83 | 1.00 | 0.83 |
| GGA-5 | 0.76 | 0.83 | 0.83 | 1.00 |
4 Discussion
As we explore the ability of machine learning to tackle grand challenges in computational materials science, it is natural to want to take advantage of information from a variety of sources and to combine them in such a way that we can make predictions of materials properties or optimal materials discovery in the most cost-effective way possible. In this paper, we use a newly proposed acquisition function, csKG,26 in concert with several surrogate models, including a new model proposed here, that can harness multiple information sources for cost-effective predictions. This is the first application of a MISO approach to conduct common computational materials science calculations.Our first study involved using the Rosenbrock function as a test of our optimization methods, since it is a challenging non-linear, shallow-basin problem. The Rosenbrock benchmarks shown in Fig. 2 and Table 1 indicate: (1) the considerable benefits of using MISO approaches over a standard EGO approach; (2) the importance of adequate hyperparameter training in respective models; and (3) the benefits of the new PCM surrogate model, developed in this paper, over either a multivariate Gaussian process regression model (MGP) or an intrinsic coregionalization model (ICM).
For the Rosenbrock test, the improvement over EGO was 80% for each of the three MISO models we tested. In regards to hyperparameter optimization, we find that when the model includes hyperparameters that capture the interplay between information sources (as in the case of MGP and ICM), it is necessary to include data across all information sources to adequately learn these parameters. The main improvement of our new model, PCM, over that of ICM and MGP can be seen in the results for the 99.9th percentile. This improvement also comes with the considerable advantage that we no longer need additional inter-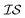 hyperparameters in this approach. As Bayesian approaches are known to be capable of optimizing noisy functions, we find that when the information sources correlate well but are inherently noisy, MISO approaches continue to outperform EGO, with the PCM surrogate model remaining the best. Finally, looking at Fig. 2, when we consider a large combinatorial space for the optimization, the MISO models perform markedly better (over EGO) than when we consider a smaller combinatorial space.
hyperparameters in this approach. As Bayesian approaches are known to be capable of optimizing noisy functions, we find that when the information sources correlate well but are inherently noisy, MISO approaches continue to outperform EGO, with the PCM surrogate model remaining the best. Finally, looking at Fig. 2, when we consider a large combinatorial space for the optimization, the MISO models perform markedly better (over EGO) than when we consider a smaller combinatorial space.
Turning towards applications of this approach to computational materials sciences, our aim is to understand the effects of including different information sources on cost-effectiveness. Performing a geometry optimization of CO using Bayesian optimization is a prime example of a common computational chemistry calculation. Here, our information sources were different DFT functionals and basis sets. This is a representative real-life issue since these sources differ greatly in cost (certainly by over an order of magnitude). Finding that we have a close-to-unity Pearson correlation coefficient between these information sources, we anticipated that the various MISO methods would perform better than EGO. And, indeed, Table 2 shows that both the MISO surrogate models (ICM and PCM) outperform a standard EGO approach by, on average, 52% in cost. Further, in the case of the 99.9th percentile, MultiTaskKG and PearsonKG outperform EGO by 71% and 76%, respectively. Commonly, local optimizers are used when performing DFT geometry optimizations; however, at times, the desire to find optimal molecular conformations/packing is desired instead. This is a global optimization problem which involves considerations of optimally packing molecules via translational and rotational changes, subsequently followed by a geometry optimization. This work shows that it is possible to use MISO methods to deploy cheap sources of information for this search space (such as Hartree–Fock) with more expensive/accurate functionals for the final calculations, greatly reducing the overall time required to find this optimal packing.
Finally, in a challenging application related to the selection of solar cell materials, hybrid organic–inorganic perovskites, we looked at the cost-effectiveness of combining different information sources within our PAL code base. For these perovskite materials, it becomes even more apparent that the reliability of the cheaper information sources, i.e., 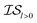 , to represent the most trusted source,
, to represent the most trusted source, 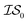 , comes under scrutiny. The results in Fig. 3a show a slight benefit in using PearsonKG, corroborated in Table 4 by the reduced mean cost to reach an optimal solution. However, this benefit is rapidly reduced as the information source changes to noisier alternatives. We find the nature of the information sources is an important factor when considering a MISO approach. This effect is clear in Fig. 4, which compares information sources that choose different ways to represent both the solvation of the lead salt and the level of DFT theory used. Choices like Hybrid-1 and GGA-1, which share a common number of solvent molecules (=1) model one another much better (i.e., are better correlated) than the alternatives (GGA-3 and GGA-5) in which the number of solvent molecules (and hence the inherent noise) varies. In the latter situation, we find no benefit to using a MISO approach (Fig. 3b and c).
, comes under scrutiny. The results in Fig. 3a show a slight benefit in using PearsonKG, corroborated in Table 4 by the reduced mean cost to reach an optimal solution. However, this benefit is rapidly reduced as the information source changes to noisier alternatives. We find the nature of the information sources is an important factor when considering a MISO approach. This effect is clear in Fig. 4, which compares information sources that choose different ways to represent both the solvation of the lead salt and the level of DFT theory used. Choices like Hybrid-1 and GGA-1, which share a common number of solvent molecules (=1) model one another much better (i.e., are better correlated) than the alternatives (GGA-3 and GGA-5) in which the number of solvent molecules (and hence the inherent noise) varies. In the latter situation, we find no benefit to using a MISO approach (Fig. 3b and c).
| Algorithm | Acquisition function | Surrogate model | Mean | STD | 99.![[9 with combining macron]](https://www.rsc.org/images/entities/char_0039_0304.gif) th%-tile th%-tile |
||
|---|---|---|---|---|---|---|---|
| EGO | EI | GPR | Hybrid-1 | — | 80 | 30 | 198 |
| MultiTaskKG | csKG | ICM | Hybrid-1 | GGA-1 | 81 | 41 | 244 |
| PearsonKG | csKG | PCM | Hybrid-1 | GGA-1 | 70 | 35 | 216 |
| EGO | EI | GPR | GGA-3 | — | 36 | 29 | 124 |
| MultiTaskKG | csKG | ICM | GGA-3 | GGA-1 | 33 | 32 | 187 |
| PearsonKG | csKG | PCM | GGA-3 | GGA-1 | 32 | 23 | 185 |
| EGO | EI | GPR | GGA-5 | — | 70 | 59 | 300 |
| MultiTaskKG | csKG | ICM | GGA-5 | GGA-3 | 87 | 62 | 300 |
| PearsonKG | csKG | PCM | GGA-5 | GGA-3 | 105 | 70 | 300 |
In summary, we have developed a new surrogate model, PCM, and shown how it performs at least as well, and often better, than ICM (where ICM can be seen as the common “go to” model when it comes to coregionalization) for several archetypal test cases in the computational materials sciences. Importantly, the new PCM model does not involve any additional hyperparameters. Further, we show how the acquisition function, csKG, can be implemented in combination with these surrogate models. This combination opens the door for computational studies to incorporate any number of data streams of varying expense in a cost-effective way. This method allows the user to exploit the availability of less accurate, lower cost, alternative sources of information. We find that the best approach to take depends heavily on the correlation between information sources and the surrogate model that defines the potential. When an information source possesses the same GPR kernel (Kx) with similar/identical hyperparameters, as in the Rosenbrock benchmark, CO geometry optimization, and the HOIP benchmark comparing Hybrid-1 versus GGA-1, using csKG with the PCM surrogate method converges significantly faster towards a global optimum. In cases where the hyperparameters differ greatly, as exemplified by GGA-5 versus GGA-3, the best course of action appears to reside in using a traditional EGO approach. Finally, we have discovered that, when it is desirable to maximize an objective with an expensive DFT functional, a MISO approach using the PCM surrogate model and a more cost-effective functional can greatly reduce the total cost.
5 Methods
5.1 The intrinsic coregionalization model
There are many methods of coregionalization, several of which are outlined in a review article by Alvarez et al.42 The intrinsic coregionalization model (ICM) approach defines a coregionalization matrix (Ks) such that K = Ks ⊗ Kx (where ⊗ is the Kronecker product and Kx is a user-defined kernel).42 The problem then arises how best to define Ks. One method involves simply allowing Ks = I, in which the hyperparameters of Kx, parameterized against all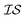 , will capture the correlation between
, will capture the correlation between 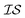 .43,44 Another method ensures a PSD matrix by having Ks = ESTSE in which E is a diagonal matrix of scalars with dimension M (the number of
.43,44 Another method ensures a PSD matrix by having Ks = ESTSE in which E is a diagonal matrix of scalars with dimension M (the number of 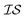 ), and S is an upper triangular matrix.45 It should be noted that there exists an equivalent expression, Ks = ELLTE, in which L is a lower triangular matrix. In general, the scalar matrix is not particularly common and, in most literature sources, we simply find that Ks is written as LLT.21
), and S is an upper triangular matrix.45 It should be noted that there exists an equivalent expression, Ks = ELLTE, in which L is a lower triangular matrix. In general, the scalar matrix is not particularly common and, in most literature sources, we simply find that Ks is written as LLT.21
5.2 The Pearson-r coregionalization model
The Pearson-r coregionalization model (PCM) was developed based on the idea that the coregionalization matrix should capture the correlation between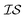 .22 From this, the coregionalization matrix was not learned, but dynamically generated from the Pearson-r correlation coefficients (ρ) of sampled data.28 Specifically, each component of the coregionalization matrix was made using eqn (2), to which eqn (3) was calculated (ρ was only calculated for data that had been sampled at all
.22 From this, the coregionalization matrix was not learned, but dynamically generated from the Pearson-r correlation coefficients (ρ) of sampled data.28 Specifically, each component of the coregionalization matrix was made using eqn (2), to which eqn (3) was calculated (ρ was only calculated for data that had been sampled at all 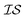 using the python package, SciPy).46 This approach eradicates the need for additional hyperparameters (ontop of those in Kx), allowing for a more scalable model.
using the python package, SciPy).46 This approach eradicates the need for additional hyperparameters (ontop of those in Kx), allowing for a more scalable model.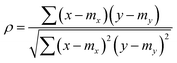 | (2) |
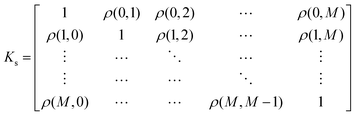 | (3) |
5.3 Analytical model
The Rosenbrock function, also known as the “banana function,” is a well known, well studied and challenging test case for global optimization.31 Further, a noisy alternate form has already been developed by Lam et al.47 As this function was used by Poloczek et al.26 to benchmark misoKG and MGP, we use it here to compare our new approach to Poloczek's misoKG. The function itself is shown in eqn (4), where a, b, c ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) .
.| fr(x) = (a − x1)2 + b(x2 − x12)2 + c | (4) |
In order to use the Rosenbrock function with MISO surrogate models, we need several  . Accordingly, we define two
. Accordingly, we define two 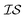 as the Rosenbrock function, plus some additional varied term. The two
as the Rosenbrock function, plus some additional varied term. The two 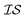 used are shown in eqn (5):
used are shown in eqn (5):
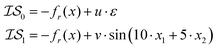 | (5) |
We can replicate the work shown in Poloczek et al.26 by setting a = 1.0, b = 100.0, c = −456.3, u = 0, v = 0.1, and a cost ratio of 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The domain for
1. The domain for  is given by
is given by 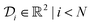 and bounded within the origin-centered-square of [−2,2]2. N, the number of discrete points of our domain
and bounded within the origin-centered-square of [−2,2]2. N, the number of discrete points of our domain 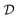 , was chosen to be either 250, 500, or 1000, in order to capture the effects of the search-space on the models. To probe the limits of our model, we expanded upon this benchmark by considering a significantly noisier secondary information source and allowing v = 10.0. Note that the global minimum of the Rosenbrock function (offset from 0) is set to c, in this case −456.3.
, was chosen to be either 250, 500, or 1000, in order to capture the effects of the search-space on the models. To probe the limits of our model, we expanded upon this benchmark by considering a significantly noisier secondary information source and allowing v = 10.0. Note that the global minimum of the Rosenbrock function (offset from 0) is set to c, in this case −456.3.
5.4 CO model
In order to model the CO molecule using multiple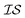 , a simple zero-mean,
, a simple zero-mean, 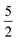 Matérn kernel was chosen.48 From this, the expensive source,
Matérn kernel was chosen.48 From this, the expensive source, 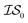 , was chosen to be a double-hybrid approach using the B2PLYP functional32 and Def2-TZVP basis set.33 The cheaper source,
, was chosen to be a double-hybrid approach using the B2PLYP functional32 and Def2-TZVP basis set.33 The cheaper source, 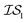 , was taken to be a corrected Hartree–Fock approach.34 All DFT calculations were performed using the Orca software.49 Since CO consists of only two atoms, x was taken as the interatomic distance (in Å), bound between [0.5, 2.0], in intervals of 0.001 Å. Five random sampled points were taken to initially train hyperparameters.
, was taken to be a corrected Hartree–Fock approach.34 All DFT calculations were performed using the Orca software.49 Since CO consists of only two atoms, x was taken as the interatomic distance (in Å), bound between [0.5, 2.0], in intervals of 0.001 Å. Five random sampled points were taken to initially train hyperparameters.
5.5 HOIP model
The probabilistic model for the HOIP system is the same as that outlined in Herbol et al.9 This is illustrated in eqn (6), with the mean given in eqn (7) and the covariance matrix in eqn (8).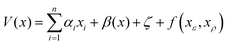 | (6) |
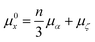 | (7) |
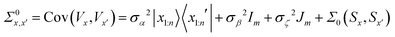 | (8) |
For Σ0(Sx,Sx′) we chose the well known 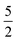 Matérn kernel, which provides the covariance between measurements made at any two points.48
Matérn kernel, which provides the covariance between measurements made at any two points.48
In the original PAL work, data points were generated to represent the intermolecular binding energy of three solvent molecules to a HOIP lead salt modeled using an ab initio GGA DFT functional. It would also be possible to generate DFT data corresponding to other situations in which a different number of solvent molecules was considered, given that a full shell surrounding the lead salt involves around 25 molecules.50 Moreover, we can use various choices of level of DFT theory which may differ significantly in accuracy and cost. Overall sampling of the solvents around the salt were performed using Packmol,51 LAMMPS,52 and the OPLS-AA force field.53 Final geometry optimizations and energy calculations were made using Orca.49
We define information sources, for example, as GGA-3, where N3 indicates the case in which three solvent molecules are considered to be bound to the lead salt, and R2 represents the level of theory indexed within the PAL codebase (the label “2” corresponding to the GGA functional B97-D3 with a triple-ζ basis set). Simply changing the number of solvents bound to the lead salt, or the level of theory used, will give rise to a different 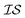 label. In that regard, we have explored the following information sources for benchmarking purposes:
label. In that regard, we have explored the following information sources for benchmarking purposes:
• GGA-5 – intermolecular binding energy of five solvent molecules to a perovskite lead salt using the GGA functional B97-D3 (179 data points).
• GGA-3 – intermolecular binding energy of three solvent molecules to a perovskite lead salt using the GGA functional B97-D3 (240 data points).
• GGA-1 – intermolecular binding energy of one solvent molecule to a perovskite lead salt using the GGA functional B97-D3 (480 data points).
• Hybrid-1 – intermolecular binding energy of one solvent molecule to a perovskite lead salt using the hybrid functional PW6B95 (480 data points).
When using multiple information sources from among these options, we chose only those that exist across all 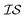 . Thus, when we used two information sources as a test case, labeling them
. Thus, when we used two information sources as a test case, labeling them 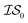 and
and 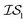 , we chose Hybrid-1 and GGA-1, for which a total of 480 data points exist. However, when
, we chose Hybrid-1 and GGA-1, for which a total of 480 data points exist. However, when 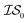 and
and 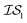 are GGA-3 and GGA-1, respectively, only the 240 intersecting points in the data sets would be used.
are GGA-3 and GGA-1, respectively, only the 240 intersecting points in the data sets would be used.
Data availability
The code for this article and the results of the benchmarks are publicly available at: https://www.github.com/clancylab/PAL, https://www.github.com/clancylab/MISO_Paper, respectively.Author contributions
H. C. H. implemented the code and benchmarks. M. P. proposed the idea of coregionalization, and H. C. H. proposed the idea of using a Pearson correlation. M. P. and P. C. advised and supervised the progress of the research. H. C. H., M. P., and P. C. wrote the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
H. C. H., P. C. and M. P. were partially supported by NSF CMMI-1536895. H. C. H. and P. C. were partially supported by funds from the Whiting School of Engineering at the Johns Hopkins University. The authors gratefully acknowledge extensive computing resources used in this work that was provided by the Maryland Advanced Research Computing Center (MARCC). MARCC was partially funded by the State of Maryland and is jointly managed by the Johns Hopkins University and the University of Maryland.References
- D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448–511 CrossRef CAS.
- P. Crescenzi, D. Goldman, C. Papadimitriou, A. Piccolboni and M. Yannakakis, J. Comput. Biol., 1998, 5, 423–465 CrossRef CAS PubMed.
- R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. F. G. Green, C. Qin, A. Zidek, A. Nelson, A. Bridgland, H. Penedones, S. Petersen, K. Simonyan, S. Crossan, D. T. Jones, D. Silver, K. Kavukcuoglu, D. Hassabis and A. W. Senior, Thirteenth Critical Assessment of Techniques for Protein Structure Prediction, 2018 Search PubMed.
- D. Xue, D. Xue, R. Yuan, Y. Zhou, P. V. Balachandran, X. Ding, J. Sun and T. Lookman, Acta Mater., 2017, 125, 532–541 CrossRef CAS.
- T. D. Sparks, M. W. Gaultois, A. Oliynyk, J. Brgoch and B. Meredig, Scr. Mater., 2016, 111, 10–15 CrossRef CAS.
- M. W. Gaultois, A. O. Oliynyk, A. Mar, T. D. Sparks, G. J. Mulholland and B. Meredig, APL Mater., 2016, 4, 053213 CrossRef.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- Y. Huang, J. Kang, W. A. Goddard and L.-W. Wang, Phys. Rev. B, 2019, 99, 064103 CrossRef.
- H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, npj Comput. Mater., 2018, 4, 51 CrossRef.
- D. Jha, K. Choudhary, F. Tavazza, W.-k. Liao, A. Choudhary, C. Campbell and A. Agrawal, Nat. Commun., 2019, 10, 5316 CrossRef PubMed.
- S. Haghanifar, M. McCourt, B. Cheng, J. Wuenschell, P. Ohodnicki and P. W. Leu, Mater. Horiz., 2019, 6, 1632–1642 RSC.
- M. W. Lee, E. Y. Lee, A. L. Ferguson and G. C. Wong, Curr. Opin. Colloid Interface Sci., 2018, 38, 204–213 CrossRef CAS PubMed.
- A. Jinich, B. Sanchez-Lengeling, H. Ren, R. Harman and A. Aspuru-Guzik, ACS Cent. Sci., 2019, 5, 1199–1210 CrossRef CAS PubMed.
- S. Katare, A. Bhan, J. M. Caruthers, W. N. Delgass and V. Venkatasubramanian, Comput. Chem. Eng., 2004, 28, 2569–2581 CrossRef CAS.
- W. Sun, Y. Zheng, K. Yang, Q. Zhang, A. A. Shah, Z. Wu, Y. Sun, L. Feng, D. Chen, Z. Xiao, S. Lu, Y. Li and K. Sun, Sci. Adv., 2019, 5(11) DOI:10.1126/sciadv.aay4275.
- W. Sun, M. Li, Y. Li, Z. Wu, Y. Sun, S. Lu, Z. Xiao, B. Zhao and K. Sun, Adv. Theory Simul., 2019, 2, 1800116 CrossRef.
- R. Garnett, S. Ho, S. Bird and J. Schneider, Mon. Not. R. Astron. Soc., 2017, 472, 1850–1865 CrossRef CAS.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules, 2017 Search PubMed.
- P. I. Frazier, A Tutorial on Bayesian Optimization, 2018 Search PubMed.
- R. Webster and M. A. Oliver, Statistics in Practice, John Wiley & Sons, Ltd, 2007, pp. 219–242 Search PubMed.
- E. V. Bonilla, K. M. Chai and C. Williams, Advances in Neural Information Processing Systems 20, Curran Associates, Inc., 2008, pp. 153–160 Search PubMed.
- M. Alvarez and N. D. Lawrence, Advances in Neural Information Processing Systems 21, Curran Associates, Inc., 2009, pp. 57–64 Search PubMed.
- M. Goulard and M. Voltz, Math. Geol., 1992, 24, 269–286 CrossRef.
- T. Ishida and S. Kawashima, Theor. Appl. Climatol., 1993, 47, 147–157 CrossRef.
- W. F. Krajewski, J. Geophys. Res.: Atmos., 1987, 92, 9571–9580 CrossRef.
- M. Poloczek, J. Wang and P. Frazier, Advances in Neural Information Processing Systems 30, NIPS, 2017, pp. 4288–4298 Search PubMed.
- P. Goovaerts, Geostatistics for Natural Resource Evaluation, Oxford University Press, 1997, ch. 4, vol. 42, pp. 75–116 Search PubMed.
- J. Benesty, J. Chen, Y. Huang and I. Cohen, Noise reduction in speech processing, Springer, 2009, pp. 1–4 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Global Optim., 1998, 13, 455–492 CrossRef.
- K. Swersky, J. Snoek and R. P. Adams, Proceedings of the 26th International Conference on Neural Information Processing Systems - Volume 2, USA, 2013, pp. 2004–2012.
- H. H. Rosenbrock, Comput. J., 1960, 3, 175–184 CrossRef.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- J. G. Brandenburg, M. Alessio, B. Civalleri, M. F. Peintinger, T. Bredow and S. Grimme, J. Phys. Chem. A, 2013, 117, 9282–9292 CrossRef CAS PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- M. A. Alvarez, L. Rosasco and N. D. Lawrence, Kernels for Vector-Valued Functions: a Review, 2011 Search PubMed.
- N. D. Lawrence and J. C. Platt, Proceedings of the Twenty-first International Conference on Machine Learning, New York, NY, USA, 2004, p. 65.
- K. Yu, V. Tresp and A. Schwaighofer, Machine Learning: Proceedings of the 22nd International Conference (ICML 2005), 2005, pp. 1012–1019.
- M. A. Osborne, S. J. Roberts, A. Rogers, S. D. Ramchurn and N. R. Jennings, 2008 International Conference on Information Processing in Sensor Networks (ipsn 2008), 2008.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. Jarrod Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. Vander Plas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- R. Lam, D. Allaire and K. Willcox, 2015.
- B. Minasny and A. B. McBratney, Geoderma, 2005, 128, 192–207 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- B. A. Sorenson, S. S. Hong, H. C. Herbol and P. Clancy, Comput. Mater. Sci., 2019, 170, 109138 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh00062k |
| ‡ This work was done while author was affiliated with the University of Arizona in Tucson, AZ, USA. |
| This journal is © The Royal Society of Chemistry 2020 |