Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Preferred orientations of organic cations at lead-halide perovskite interfaces revealed using vibrational sum-frequency spectroscopy†
Woongmo
Sung
 a,
Christian
Müller
cd,
Sebastian
Hietzschold
cd,
Robert
Lovrinčić
cd,
Nathaniel P.
Gallop
a,
Christian
Müller
cd,
Sebastian
Hietzschold
cd,
Robert
Lovrinčić
cd,
Nathaniel P.
Gallop
 e,
Artem A.
Bakulin
e,
Artem A.
Bakulin
 *e,
Satoshi
Nihonyanagi
*e,
Satoshi
Nihonyanagi
 ab and
Tahei
Tahara
ab and
Tahei
Tahara
 *ab
*ab
aMolecular Spectroscopy Laboratory, RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan. E-mail: tahei@riken.jp
bRIKEN Center for Advanced Photonics, RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan
cInnovationLab, Speyerer Str. 4, 69115 Heidelberg, Germany
dInstitute for High-Frequency Technology, TU Braunschweig, Schleinitzstrasse 22, 38106 Braunschweig, Germany
eDepartment of Chemistry, Imperial College London, Molecular Sciences Research Hub, 80 Wood Lane, London, W12 0BZ, UK. E-mail: a.bakulin@imperial.ac.uk
First published on 29th January 2020
Abstract
The structure of the interfacial layers of lead halide perovskites is expected to play a crucial role in carrier dynamics and in the performance of perovskite-based devices. However, little is known about the structure and dynamics of perovskite interfaces at the molecular level. In this study, we access molecular dynamics at perovskite interfaces by monitoring the alignment of cations in methylammonium (MA) lead bromide perovskite. For this we apply heterodyne-detected vibrational sum-frequency generation (HD-VSFG) spectroscopy with the help of DFT calculations to a range of thin-film perovskite active layers interfaced with several organic and oxide semiconducting materials. At interfaces with air, glass, TiO2 and NiO transport layers and phenyl-C61-butyric acid methyl ester (PCBM), we observed no signature of cation vibrations, indicating a randomized arrangement of cations. On the other hand, HD-VSFG spectra of 2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene (Spiro-MeOTAD)/perovskite interfaces exhibited a clear peak corresponding to the ammonium antisymmetric bending mode, indicating that the MA's ammonium moiety is preferentially oriented towards the Spiro-MeOTAD layer with a large portion of MA cations are tilted away from the surface normal. The observed interfacial anisotropy is in contrast with the general picture accepted for bulk perovskite materials. We discuss the potential consequences of the observed phenomena in the context of the local field and carrier injection at the various interfaces within the perovskite solar cells.
New conceptsOur work describes the first application of heterodyne-detected vibrational sum frequency generation spectroscopy to understand the material interfaces in hybrid perovskite solar cells by measuring the rotational behaviour of organic cations. Perovskite thin-films, integrated into multilayer structures with other optoelectronic materials, have proven themselves to be promising active elements in solution processed optoelectronics. Multiple reports have shown that the structural dynamics of these soft semiconductors, coupled with the rotational motions of organic cations, are responsible for many perovskites’ unique optoelectronic properties. However, addressing the specific structural properties of perovskite interfaces, which are extremely important for both carrier injection/extraction and internal field distribution in the device, has been challenging. Our pioneering approach reveals that, in contrast to the bulk material, cation rotation is significantly restricted close to the interface between the perovskite and certain electron/hole transporting materials. We reveal a new concept for the perovskite community, namely, that the dynamical behaviour of the perovskites’ organic sublattice, and consequently, the dynamics of the lead-halide octahedra are interface specific and should be treated differently from the bulk active layer. This has significant implications for our understanding of both local field distributions, and carrier injection properties at interfaces within perovskite solar cells. |
1. Introduction
Metal halide perovskites have generated significant interest in both academia and industry, owing to their effectiveness as absorbers in thin film photovoltaic devices and emitters in thin film light-emitting diodes.1,2 Presently, power conversion efficiencies as high as 22%3—the highest of any of the so-called 3rd generation photovoltaic technologies—have been achieved using perovskite solar cells. As well as their high power conversion efficiencies, perovskites enjoy other benefits, such as low production costs, and broad material tuneability,4 which has spurred researchers to investigate their possible use as active materials in other applications, including in solar thermoelectric materials,5 LEDs, lasers,6 and non-volatile memory.7Lead halide perovskites share an APbX3 structure, including an organic or large inorganic cation (A) and some combination of halide ions (X3). A corner sharing octahedral framework is created by the Pb and X species, with the charge-balancing A-site cation occupying the resulting central cavity. A-site cations are an essential part of the perovskite lattice, and their properties and behavior strongly influence the structure and dynamics of both the inorganic PbX3 sub-lattice and the material as a whole. It has been proposed that cation dynamics play a key role in several phenomena relevant to photovoltaic performance, including, ferroelectricity,8,9 modulation of the dielectric function,10–12 carrier transport/recombination,13–15 and ion mobility,16,17 among others. Tong et al., suggested that local field effects arising from ordered cationic domains may reduce the energy barrier for the hopping of charged defects,16 whilst an ab initio molecular dynamics simulations on perovskite observed a correlation between rotations of the methylammonium (MA) cation and migration of an iodide vacancy to an adjacent lattice site.17 In addition, a few theoretical studies have proposed that charge carrier dynamics in perovskites are strongly influenced by organic cation rotations. It has also been proposed that cation rotations are a key factor in the high dielectric constants that enable facile charge separation18 and that, in MAPbI3 dynamical reorientation of the organic sub-lattice reduces carrier scattering19 and may even work to spatially segregate electrons and holes.13,14
Because of the aforementioned phenomena, organic cation rotations have been extensively studied both theoretically and experimentally. While most studies agree that organic cations within the bulk perovskite undergo rotations at normal operating conditions for perovskite PVs, the extent of rotation may vary considerably, from total immobilization, to virtually unrestricted free rotation, depending on the pressure, temperature, chemical composition, and local environment.
Numerous experimental techniques have been used to investigate cation rotation, including: millimeter wave,10 NMR,20–22 2-dimensional IR (2D-IR),23–25 transient Optical Kerr Effect (TR-OKE),26 and quasi-elastic neutron scattering (QENS)9,27 spectroscopy. These experimental methods have been complimented by a variety of theoretical techniques, such as ab initio molecular dynamics (AIMD) and empirical force field classical molecular dynamics (CMD). Although diverse, all these modern techniques appear to identify two regimes of cation motion in MAPbI3, as well as in the less commonly utilized FAPbI3.28 These regimes are respectively: a rapid sub-ps wobbling motion around a local equilibrium aligned with the crystal axis (the so-called ‘wobbling within a cone’ or ‘frustrated librations’), and (slower) discrete ‘reorientational jumps’ of the molecular axis to an adjacent equilibrium position happening on timescales of a few-ps.23–26,28 In the case of MA and FA, cations preferentially align towards the faces of the PbI3 cage, with all faces equally favored at high temperatures, whilst certain orientational directions appear to be favored in the orthorhombic/tetragonal phases.20,29 SHG studies by Govinda et al. also appear to support a model in which the dynamics of the organic cation in the bulk do not result in either polarization or symmetry breaking.30,31
Whilst these experimental techniques have led to a relative consensus concerning the dynamics of cations in the bulk material, an understanding of cation behavior at perovskite interfaces has remained comparatively elusive. At least two recent studies have reported observations that suggest material interfaces may influence cation rotations. Zhang et al. utilized high-resolution TEM to directly observe the structure of MAPbI3, unexpectedly observing ferroelectric domains of ordered MA cations that persisted for over one second at 300 K.28,32 Such an observation is inconsistent with previously discussed findings on bulk perovskites, which predict facile cation rotation taking place on picosecond timescales. Additionally, Röhm et al. observed persistent ordered ferroelectric domains using a battery of surface sensitive techniques.33 A pioneering study by Ohmann et al. found similar evidence of orientational biasing at the surface of MAPbI3, albeit in vacuum (∼10−10 mbar), and at a temperature of 4.5 K.34 Other studies on organohalide perovskites have observed significant variation of cation rotational behavior with temperature, with cation rotation becoming significantly restricted relative to higher temperatures below 80 K.20,28 The surface sensitive nature of these techniques lies in contrast to the predominantly bulk-sensitive nature of the various spectroscopic techniques employed to date and may suggest that the dynamics of cations in metal halide perovskites vary significantly depending on their proximity to surfaces or interfaces. These differences could include a ‘freezing-out’ of cation motion close to the surface as a result of symmetry breaking.
Most perovskite optoelectronic devices are multilayer nanostructures wherein a thin slab of perovskite material is sandwiched between complementary electron and hole transporting layers, for instance organic semiconductors or metal oxides. The interfaces between the layers are essential in charge injection and extraction, as well as in energy transfer. Thus, changes in cation rotational mobility may drastically alter device performance, due to the role played by the organic cation in dictating the properties of the material. The presence of ordered cationic domains near the interface would have a significant effect on the photovoltaic performance of the perovskite, for example, by changing electrostatic barriers for charge and ion transport, or by influencing the dielectric constant close to interfaces.
Understanding of how cation reorientations vary in the bulk versus at interfaces is therefore an essential consideration in the design and development of these important materials, calling for the application of powerful surface-specific spectroscopic techniques to address the problem. Recently, Motti et al. applied homodyne VSFG spectroscopy to organic field effect transistors, and observed electric field induced orientation of the interfacial polymer moieties.35 In a similar manner to this study, Chen and coworkers investigated the interface between MAPbI3 and a polythiophene hole transport layer using homodyne VSFG, although they focused on the orientation of polymer molecules rather than MA cations in MAPbI3.36
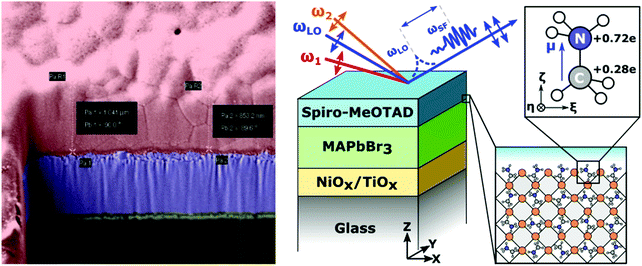
In this study, we used heterodyne-detected vibrational sum-frequency generation (HD-VSFG) spectroscopy to monitor the alignment of cations at the surface of methylammonium lead bromide perovskite thin-films and at perovskite interfaces with hole- and electron-extracting materials. HD-VSFG is a phase-resolved extension of VSFG spectroscopy and can provide both the imaginary (Im) and real (Re) parts of the second order nonlinear susceptibility (χ(2)) spectra.37,38 Im χ(2) represents the vibrational resonances and its sign provides information about the up/down orientation of the interfacial dipoles. MAPbBr3 was chosen instead of the more ubiquitous MAPbI3 as MAPbI3 is non-centrosymmetric and thus generates a background SFG signal from second-order optical process within the bulk perovskite.39 By contrast, MAPbBr3 is centrosymmetric and thus should not generate a strong bulk SFG background.40 Additionally, fluorescence from MAPbBr3 can be avoided as single photon absorption is negligible using the present ω1 wavelength and fluorescence via two-photon absorption has a much shorter wavelength (λ ∼ 500–600 nm) than the SF signal. The films were interfaced with air, glass, and several of the charge selective materials most commonly employed in perovskite devices, such as 2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene (Spiro-MeOTAD), phenyl-C61-butyric acid methyl ester (PCBM), TiO2 and NiO. At the interface of the perovskites with the air, glass, PCBM, TiO2 and NiO transport layers we observed no signature for cation vibrations, indicating a randomized, bulk-like orientation of the MA cations. Conversely, SF spectra of the Spiro-MeOTAD/perovskite interfaces exhibited a clear peak corresponding to the ammonium antisymmetric bending mode. By analyzing the Spiro-MeOTAD/MAPbBr3 SFG spectra with second-order hyper polarizabilities obtained using DFT calculations, we concluded that the ammonium moiety of the MA cation is preferentially oriented towards the Spiro-MeOTAD layer, but with most of the cations tilted away from the surface normal. Our study provides new insight into the energetic landscape of perovskite materials and devices.
2. Results and discussion
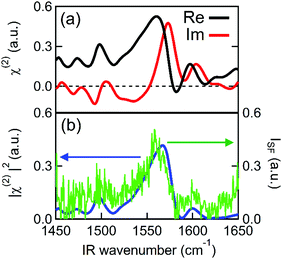
Fig. 2 shows the second order susceptibility (χ(2)) and |χ(2)|2 spectra of the Spiro-MeOTAD/MAPbBr3/TiO2 multilayer film, analogous to the active layers of perovskite solar cell devices, obtained using HD-VSFG spectroscopy. The Imχ(2) spectrum in Fig. 2(a) shows a strong clear positive peak at 1574 cm−1 and much weaker peaks at around 1490 cm−1 and 1610 cm−1. A homodyne VSFG spectrum of the same sample, which corresponds to the |χ(2)|2 spectrum, was also measured by blocking the LO pulse (Fig. 2(b), green trace). Homodyne VSFG is a more widely-utilized technique and can confidently confirm the presence of resonant peaks. Unlike HD-VSFG, however, it is unable to provide directional information. The |χ(2)|2 spectrum calculated from the complex χ(2) shown in Fig. 2(b) matches well with the homodyne spectrum, which demonstrates that the χ(2) spectra do not contain unwanted artificial signals possibly caused by heterodyning. The peak frequencies in both the |χ(2)|2 and homodyne VSFG spectra appear to be shifted from the corresponding Imχ(2) spectrum due to the mixing of the real part. Since the imaginary part is more informative, we henceforth will base our discussion and analysis on the Imχ(2) spectra.In the chosen IR frequency window, bulk MAPbBr3 has two vibrational resonances corresponding to the symmetric (δs) and antisymmetric (δas) bending modes of the ammonium moiety of the MA cation, located respectively at 1477 cm−1 and at 1585 cm−1 (Fig. S4, ESI†).41 Previously reported Raman spectra of single crystal MAPbBr3 gave similar resonance frequencies for these two bending modes (approximately 1480 cm−1 for the δs and 1590 cm−1 for the δas mode).42,43 In addition to MAPbBr3, tert-butylpyridine and the lithium triflimide salt additives used as a dopant of Spiro-MeOTAD are known to exhibit vibrational bands at ca. 1600 cm−1 and 1550 cm−1, and 1635 cm−1, respectively.44,45 However, because the concentrations of these dopants are low (approximately 30 mM and 261 mM for the lithium triflimide salt and, butylpyridine respectively), it is very unlikely that the dopant gives rise to the band observed at 1574 cm−1. In fact, the vibrational frequencies of these additives do not coincide with the band at 1574 cm−1. Therefore, the clear peak observed at 1574 cm−1 can be assigned to the δas mode of the ammonium moiety of MA cation. In contrast to the strong δas mode, we did not find a clear signature of the δs mode expected at 1477 cm−1, even though the δs mode has a larger amplitude than the δas mode in both the IR and Raman spectra. This strong mode selection, seen only in the Imχ(2) spectrum, indicates that the 1574 cm−1 band arises from the dipole contribution of oriented MA cations and that the SF signals from unoriented MA cations via electric field induced third-order process46 are negligible. Therefore, the presence of a band at 1574 cm−1, together with the absence of a band at 1477 cm−1, provides clear evidence for the preferential orientation of MA cations at the interface. Preferential orientations of the interfacial MA cations give rise to different SF signal strengths for the two ammonium bending modes. A detailed analysis of MA orientations is provided later.
To further investigate the origin of the observed SFG bands, experiments on different combinations of layers were performed. To check if our assignment for the 1574 cm−1 band to be MA cation is correct, we prepared a perovskite sample, using the same layer stacking order as the sample in Fig. 1, instead using Cs in place of the MA cation. As shown in Fig. 3(a), the Imχ(2) spectrum of the Spiro-MeOTAD/CsPbBr3/TiO2 multilayer film produces no resonance SFG signal. The disappearance of the 1574 cm−1 band upon replacing MA by Cs is consistent with our assignment of 1574 cm−1 band to be MA cation. Interestingly, however, in addition to the main feature due to MA cation, the weak bands at ∼1490 cm−1 and 1610 cm−1 seen in Fig. 2 are also absent at Spiro-MeOTAD/CsPbBr3/TiO2 multilayer. The bulk IR spectrum of MAPbBr3 does not have vibrations in these regions but Spiro-MeOTAD has a very large absorption band around 1500 cm−1 (see Fig. S3 in ESI†) as well as a small absorption at 1610 cm−1.47 Therefore, the bulk IR spectrum suggests that these bands are assignable to Spiro-MeOTAD. Nevertheless, because Spiro-MeOTAD/CsPbBr3 interface does not show the weak bands at ∼1490 cm−1 and 1610 cm−1, these bands are not attributable only to Spiro-MeOTAD but must be related with MA cations. For these reasons, we propose that these small bands at around 1490 cm−1 and 1610 cm−1 are possibly attributed to Spiro-MeOTAD directly interacting with MA cations, or vice versa, at the interface. In this case, the emergence of these bands may be indicative of a slight orientational biasing of the Spiro-MeOTAD molecules close to the interface, potentially induced by the same effects (i.e.: structural distortions and the presence of an interfacial electric field) that dictate orientational biasing of the MA cation which we discuss later. Since assignment of the bands at 1490 and 1610 cm−1 are a little ambiguous, we hereafter focus on the major band at around 1574 cm−1, which is safely assigned to the δas mode of MA cation.
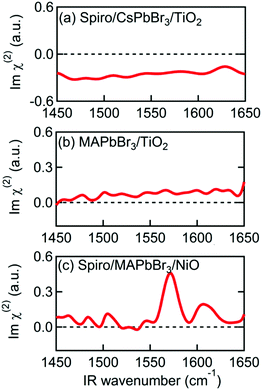 | ||
| Fig. 3 Imχ(2) spectra of various multilayer samples. (a) Spiro-MeOTAD/CsPbBr3/TiO2. (b) MAPbBr3/TiO2. (c) Spiro-MeOTAD/MAPbBr3/NiO. | ||
The MAPbBr3/TiO2 sample, without a Spiro-MeOTAD top layer, was then measured to determine which interface is responsible for alignment of the MA cation. The Imχ(2) spectrum in Fig. 3(b) shows only a small non-resonant SFG background, indicating that the MA cations at the MAPbBr3/TiO2 interface are not the main source of the resonant SFG signal within the Spiro-MeOTAD/MAPbBr3/TiO2 multilayer. Therefore, we conclude that MA cations at the Spiro-MeOTAD/MAPbBr3 interface have a net orientation.
We confirmed this by conducting experiments on samples where TiO2 was substituted by NiO. Fig. 3(c) shows the Imχ(2) spectrum of MAPbBr3 sandwiched between Spiro-MeOTAD and NiO. Excepting a small difference in the offset, the sign and the amplitude of the δas mode peak at 1574 cm−1 is almost the same as Fig. 2(a), indicating that the orientation of MA cations at the Spiro-MeOTAD/MAPbBr3 interface is hardly perturbed by the NiO bottom layer. Previously, Schulz et al. observed a ∼0.15 eV shift in the work function of MAPbBr3 due to deposition of a 5 Å thick Spiro-MeOTAD layer.48 This implies that there is a potential difference at the molecular level at the Spiro-MeOTAD/MAPbBr3 interface that exceeds the thermal energy. For our 650 nm thick MAPbBr3 film, it is expected that the distant bottom layer (TiO2 or NiO) does not alter the potential difference of the other side. Kelvin probe force microscopy (KPFM) studies on TiO2/MAPbI3/Spiro-MeOTAD devices appear to support this, finding that the region where the electric field gradient (and thus the driving force for cation reorientation) is strongest appears in a narrow region of about 50 nm on either side of the MAPbI3/Spiro interface, while the total width of nonzero electric field gradient is approximately 300 nm.49,50 It therefore appears that the depth of the layer where interfacial MA cations are oriented by this potential difference corresponds to a few unit cells of MAPbBr3. This is supported by that the 1574 cm−1 band in the Imχ(2) shown in Fig. 2(a) and 3(c) exhibit absorptive line shape as it would significantly change if the depth of oriented layer is comparable to or thicker than the length of phase mismatch (∼30 nm).46,51
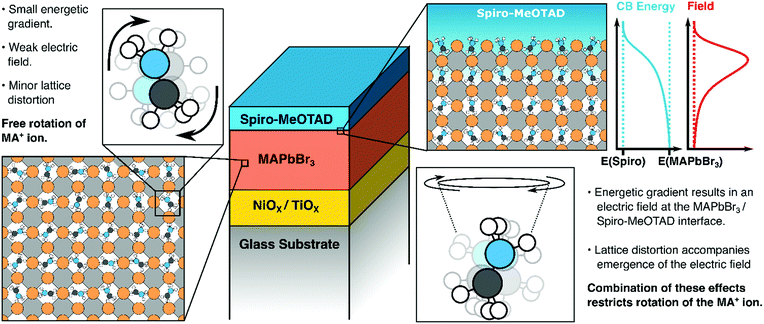
We propose that the orientational biasing of the organic cations in metal halide perovskites may be attributed to a combination of two separate effects: distortion of the inorganic PbX3 lattice52 and the aforementioned presence of an electric field close to the interface. Both effects have been discussed previously in the context of electronic and structural measurements. For example, NMR studies by Bernard et al. suggest that certain cation orientations are preferred in the tetragonal and orthorhombic phases of MAPbI3.20 The transition from the high-temperature cubic phase of MAPbI3 to the lower temperature orthorhombic/tetragonal phases is associated with a distortion of the inorganic lattice, which may explain the emergence of an orientational bias in these structures. Alternatively, a recent investigation by Birkhold et al. has also provided evidence for field induced orientational biasing of the organic cation. In their study, thermally stimulated current (TSC) peaks were observed at the orthorhombic to tetragonal phase transition, which the authors attribute to (de)polarization of the MA cations.53 Moreover, the presence of an applied electric field was found to enhance, or even reverse the polarity of the TSC peak, suggesting that applied electric fields may enhance the spontaneous polarization of the organic cation. However, the aforementioned KPFM studies performed by Jiang et al. and Guerrero et al. on TiO2/MAPbI3/Spiro-MeOTAD devices found that the MAPbI3/TiO2 interface exhibits a far greater electric field gradient compared to the MAPbI3/Spiro-MeOTAD interface, suggesting that the presence of an interfacial electric field alone is not able to induce an orientational bias.49,50 Whilst MAPbBr3 interfaces have not been profiled using KPFM, we believe it is likely that similar results would be obtained and thus we think it is apparent that the existence of an electric field gradient alone is not sufficient to explain orientational biasing in perovskites.
In addition to Spiro-MeOTAD, we also studied the possibility of MA cation preferential orientation at the interface with the PCBM electron transport layer. The LUMO level of PCBM is lower than the conduction band minimum of MAPbBr3 by 0.6 eV,54 comparable to the difference between the HOMO level of Spiro-MeOTAD and the MAPbBr3 valence band maximum (0.8 eV).48 This local field might induce orientation of MA cations at the PCBM/MAPbBr3 interface. However, Fig. 4(a) and (b), displaying the Imχ(2) spectra obtained from PCBM/MAPbBr3/TiO2 and PCBM/MAPbBr3/NiO, provide no clear evidence for ordered interfacial MA cations. From this we suggest that the strength of the interfacial local electric field at the PCBM/MAPbBr3 interface is not strong enough to orient the interfacial MA cations. This may indicate different distributions of charge at the PCBM/MAPbBr3 interface compared to Spiro-MeOTAD/MAPbBr3. This is possible as electrons are much more delocalized in fullerene aggregates then holes on the amorphous Spiro-MeOTAD molecules.55,56 Alternatively, the difference between PCBM and Spiro-MeOTAD may indicate that a combination of local lattice deformations and the electric field is responsible for the interfacial cation motions. These interface specific environments may also be the origin of the ∼10 cm−1 variation in the peak position in the Imχ(2) spectrum (1574 cm−1) compared to the IR and Raman spectra (1585–1590 cm−1). A previous modelling study by Ghosh et al. suggested that distortion of the inorganic sublattice can result in frustrated cation rotation and lead to the formation of a local electric field, further complicating the picture.52 Additional studies will be necessary to elucidate the interplay between lattice effects and the local electric field effect, and ultimately, to fully understand what effect causes the orientational biasing in perovskites.
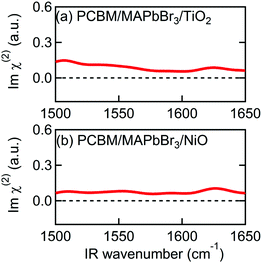 | ||
| Fig. 4 Imχ(2) spectra of multilayer samples consisting of PCBM. (a) PCBM/MAPbBr3/TiO2. (b) PCBM/MAPbBr3/NiO. | ||
From the sign of the Imχ(2) spectrum of the Spiro-MeOTAD/MAPbBr3 interface, information regarding the molecular orientation of interfacial MA cations can be inferred directly. For this purpose, several points need to be considered as follows. Firstly, the contribution of un-oriented MA cations via electric field induced χ(3) processes or quadrupole mechanisms is negligible, as mentioned previously. Secondly, the band gap energy of the MAPbBr3 perovskite at room temperature is ∼540 nm,57–59 which is far from the SF signal (∼715 nm). In this case, we can assume that the SF signal from the perovskite sample surface reflects only vibrational resonances, i.e., electronically nonresonant conditions. Finally, the Fresnel factor at the Spiro-MeOTAD/MAPbBr3 changes only moderately around 1570 cm−1 region (see Fig. S8, ESI†), hence it should not influence the Imχ(2) spectrum. These conditions ensure that the sign of the Imχ(2) spectrum is directly related to the orientational angle θ of the ammonium C–N dipole with respect to the surface normal, which is shown below.
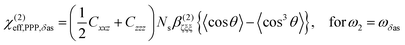 | (1) |
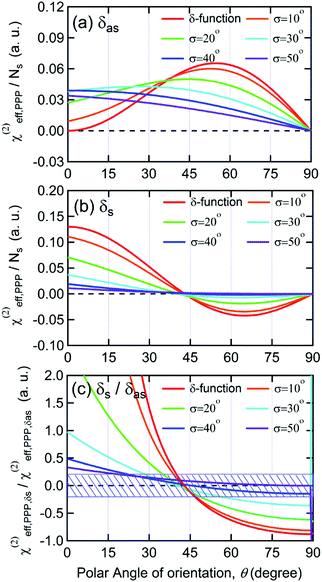
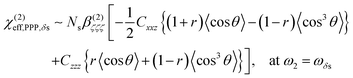 | (2) |
As shown in Fig. 5(a), the χ(2)eff,PPP of the δas mode has a maximum at a polar angle of approximately 57° when the distribution of MA polar angles with a δ-function distribution (i.e.: when all MA ions are oriented at a particular angle). The maximum angle gradually shifts to a lower angle as the distribution of MA orientation angle get broader. In the case of the δs mode, the χ(2)eff,PPP in Fig. 5(b) shows a zero crossing point at around 42° with a δ-function distribution. When the distribution width (σ) gets larger, the χ(2)eff,PPP of the δs mode is much smaller at any orientation angles compared to that of δas mode. Fig. 5(c) shows the ratio δs/δas for various distribution width, which can be directly compared to the amplitude ratio of two different vibrational bands in the observed Imχ(2) spectrum. The Imχ(2) spectrum in Fig. 2(a) does not show any clear vibrational resonance from 1450 to 1500 cm−1 (corresponding to the frequency of the δs mode). Therefore, the experimentally obtained ratio δs/δas, is less than the inverse of the signal-to-noise ratio, (i.e., 0.2, demarcated by the shaded area in Fig. 5(c)). This implies that MA cations have orientation angles in the range of 30–60° unless they have a very large angle distribution (σ ≥ 30°). At the moment, we cannot determine the orientation angle and distribution width independently, but we note that even in the case that the angle distribution is very large (σ = 40° or 50°), MA has an orientation angle larger than 20°. Consequently, it can be concluded that MA dipoles are on average pointing toward Spiro layer but a large portion of them are substantially tilted from the surface normal.
According to recent pump–probe IR experiments on MAPbX3 perovskites, MA cations in bulk MAPbBr3 exhibit a fast “wobbling in a cone” motion, with characteristic timescales of 0.3 ps, whereas secondary large angle jumping motions occur on 1.5 ps timescales.23–26,28 We conclude from the present experiments that, at the Spiro-MeOTAD/MAPbBr3 interface, the jumping motion of MA cation is unfavorable because of the large energy cost that is required to counteract the interfacial built-in electric field. Thus only the “wobbling-in a cone” motion still occurs, with its corresponding small angle displacement. This small angle displacement motion results in a finite width of the polar angle distribution, probably corresponding to the “tilted” orientation indicated by the experiment.
Although the present study was performed at room temperature, we expect that MA cations at the Spiro-MeOTAD/MAPbBr3 interface exhibit somewhat different preferential orientation at low temperature at which structure of MAPbBr3 are in tetragonal (150–230 K) or orthorhombic phase (<150 K). One MD simulation study on MAPbBr3 indicated that MA cations are aligned along the plane consisting of two smallest lattice constants below 150 K, and it was claimed that this alignment is driven by hydrogen bonding between the hydrogen atom in MA cation and the halide atom in PbX3 inorganic cage.9,60 Experimentally, a recent STM study on cleaved surface of MAPbBr3 at 4.5 K showed lateral alignment of surface MA cations with azimuthal anisotropy.34 By applying HD-VSFG spectroscopy to the Spiro-MeOTAD/MAPbBr3 interface over a wide temperature range covering the phase transition, we may be able to investigate the importance of the H⋯X hydrogen bonding with respect to the MA dipole-electric field interaction.
Our key findings are illustrated in Fig. 6. Above, we have suggested that both lattice distortions and local field effects may influence the orientational bias of the MAPbBr3 lattice close to the interface with the hole/electron transporting material. The degree to which the local electric field influences the orientation of the organic cation is unclear as no evidence of orientational bias was observed when PCBM was interfaced with the perovskite. This may be because the band offset between PCBM and the MAPbBr3 layer may be insufficiently large to result in polarization, as suggested previously. Alternatively, differences in the degree of delocalization of charge at the PCBM/perovskite interface versus the Spiro-MeOTAD interface may also affect the thickness of the space-charge layer and thus the strength of the local electric field at the interface. It may also suggest that other effects are in play. For example, an ab initio study by Torres et al. investigated the effect of methoxy group adsorption on perovskites, using anisole (Ph–O–H3) as an analogue for more complex methoxy-containing charge transfer layers (such as Spiro-MeOTAD).61 Interestingly, a significant distortion of the PbI3 lattice was observed upon absorption of the anisole molecule, which may lock the orientation of the organic cation. Thus, it may be that differences in surface interactions between the perovskite absorber and the hole transporting material (possibly due to the presence of a bulky C60 group on PCBM) may distort the lattice to different degrees and thus suppress the rotational freedom of the MA cation by different amounts. Whilst structural effects may introduce some degree of anisotropy, we would like to emphasise that the presence of an electric field is necessary to favor certain orientations of the MA cations (i.e., with the NH3 moiety facing towards or away from the organic charge transport layer). Potentially, this makes HD-VSFG spectroscopy a useful technique for probing the nature of the space-charge layer in other materials. We hope that new experiments, conducted across a range of different transport layers will provide new insights into the nature of interfaces in perovskite-based optoelectronic devices.
3. Conclusion
In summary, we have, for the first time, successfully observed oriented MA cations at the Spiro-MeOTAD/MAPbBr3 using HD-VSFG spectroscopy. The Imχ(2) spectrum shows a positive band, corresponding to the antisymmetric ammonium bending mode, whereas the symmetric bending mode signal is hardly distinguishable. From determination of the effective second-order susceptibility, supported by DFT calculations, we find that interfacial MA cations have a “dipole-up” orientation, possessing tilted polar angle, as described in Fig. 6. Since MA cations exhibit a sub-picosecond wobbling motion at room temperature, we suggest a substantial distribution of polar angles for the interfacial MA cations, but with large angle jumping motions restricted due to the built-in electric field at the interfacial region. We believe that these findings—namely that interfacial MA cations can have preferential orientations at interfaces to charge extraction layers are important for understanding interfacial structures, space-charge layers as well as carrier injection and transport in perovskite-based devices.4. Sample preparation and experimental procedure
4.1. Preparation of MAPbBr3 and CsPbBr3 perovskite thin films
HD-VSFG measurements were conducted on thin film stacks resembling full devices or their constituent sub-components (Fig. 1a and b). Use of FTO transparent electrodes was avoided, as FTO is non-centrosymmetric and thus generates a strong SFG background. Metal top electrodes were not deposited to allow the IR pulses to penetrate into the active layer.TiO2 layers were spin coated on clean glass substrates from a titanium diisopropoxide bis(acetylacetonate) solution in ethanol, with subsequent annealing at 500 °C in an oven. The perovskite films were processed under a nitrogen atmosphere. For the CsPbBr3 films, CsBr (128 mg) and PbBr2 (220 mg) were dissolved in DMSO (1.5 ml). The solution was stirred at 65 °C until all precipitates dissolved. Subsequently, the solution was spin coated through a 0.2 μm filter onto pre-heated (50 °C) substrates. The films were annealed at 65 °C for one hour. For the MAPbBr3 films, MABr (128 mg) and PbBr2 (459 mg) were dissolved in a mixture of DMSO (0.2 ml) and DMF (0.8 ml). The solution was spin-coated onto substrates pre-heated to 50 °C. The spin-coating was performed in two steps, initially at 1000 rpm (with a ramp speed of 200 rpm s−1) for 10 seconds and subsequently at 4000 rpm (with a ramp speed of 1000 rpm s−1) for 30 s. The anti-solvent, toluene, was dropped on the spinning samples about 15 s before the end of the spin-coating process. Thereafter, the films were annealed at 100 °C for 30 minutes. A solution of Spiro-MeOTAD was prepared by dissolving 50 mg Spiro-MeOTAD in 625 μl of chlorobenzene. To this solution was added 11 μl of a 1.81 M solution of lithium bis(trifluoromethylsyfonyl)imide (LiTFSI) salt in acetonitrile and 28.5 μl 4-tert-butylpyridine. The Spiro-MeOTAD films were subsequently prepared by spin-coating from the doped solution described above. PCBM films were spin-coated from chlorobenzene and annealed at 50 °C for 5 minutes. The Spiro-MeOTAD and PCBM top layers are completely transparent in the 700–800 nm window used for the HD-VSFG measurements described below. For details regarding surface characteristics, thickness determination, and IR spectra, the reader is advised to consult the ESI.† CsPbBr3 films produced using the same synthetic method were separately analysed using XRD, to establish that our as-synthesized samples are predominantly in the cubic phase. The obtained XRD pattern is provided in Fig. S8 (ESI†). Comparison with the standard patterns of the tetragonal (ICSD 109295) and cubic (ICSD 29073) phases of CsPbBr3 (Fig. S9, ESI†) suggest that the cubic phase dominates in our samples. For additional detail, the reader is advised to consult Section S5 in the ESI.†
4.2. Heterodyne-detected vibrational sum-frequency generation (HD-VSFG) spectroscopy
Detailed schemes of the HD-VSFG spectroscopy setup are described elsewhere37,38,62 In this study, we used a Ti:Sapphire regenerative amplifier system (Spectra Physics, Solstice, 3.5 W, 100 fs, 800 nm centre wavelength) as our primary light source. Mid-IR (2) probe pulses were obtained using a commercial optical parametric amplifier and difference frequency generation system (Light Conversion, TOPAS-prime). The mid-IR probe had a pulse-energy of approximately 4 μJ, a central frequency of ∼1550 cm−1, and a ∼200 cm−1 bandwidth. The beam path of ω2 was purged with dry nitrogen (RH < 4%) to prevent energy loss due to water vapor absorption. The visible probe beam (ω1), obtained by narrowing a portion of the laser output using a spatial filter with a 4F grating system, had a pulse energy of ∼5 μJ, a center wavelength of ∼795 nm (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579 cm−1), and a bandwidth of ∼1 nm (∼16 cm−1). The ω1 and ω2 beams were focused onto a gold surface, which generates a local oscillator (LO), and were subsequently refocused onto the sample stage by means of a concave mirror. The incident angles of ω1 and ω2 are ∼50° and ∼40°, respectively. The LO pulse is delayed by ∼4.8 ps with respect to the SF signal from the sample surface by passing the pulse through a 3 mm fused silica plate. The SF signal and LO were sent to a polychromator (Shamrock, SR-303i) and a CCD detector (Andor Technology, Newton-DU970P-BV) to obtain a frequency-domain interferogram. The raw interferograms were Fourier-transformed to the time-domain, and then a 2 ps width filter function was applied to extract the time-domain heterodyned SF signal appearing at −4.8 ps relative to the LO pulse. After inverse fast Fourier transformation, the filtered heterodyned SF signal of the sample in the frequency-domain was normalized by the heterodyned SF signal of an air/z-cut quartz interface. To calibrate the frequency of the ω2 axis, another SF spectrum of an air/z-cut quartz interface without dry nitrogen purging (RH ∼ 30%) was measured, and then compared to a FTIR spectrum of water vapor. The probe beams and the detected SF signal are all p-polarized (PPP polarization combination). The typical acquisition time of an HD-VSFG measurement for a perovskite sample was 15 minutes; a total of 5 spectra, each taken at different lateral positions, were averaged to remove any potential spatial inhomogeneity. The perovskite samples containing CsPbBr3 and PCBM layers were measured in another HD-VSFG setup. The FWHM bandwidth of ω1 (center wavelength ∼795 nm) in this setup was about 1.5 nm, corresponding to a spectral resolution of 24 cm−1 for the HD-VSFG spectra.
579 cm−1), and a bandwidth of ∼1 nm (∼16 cm−1). The ω1 and ω2 beams were focused onto a gold surface, which generates a local oscillator (LO), and were subsequently refocused onto the sample stage by means of a concave mirror. The incident angles of ω1 and ω2 are ∼50° and ∼40°, respectively. The LO pulse is delayed by ∼4.8 ps with respect to the SF signal from the sample surface by passing the pulse through a 3 mm fused silica plate. The SF signal and LO were sent to a polychromator (Shamrock, SR-303i) and a CCD detector (Andor Technology, Newton-DU970P-BV) to obtain a frequency-domain interferogram. The raw interferograms were Fourier-transformed to the time-domain, and then a 2 ps width filter function was applied to extract the time-domain heterodyned SF signal appearing at −4.8 ps relative to the LO pulse. After inverse fast Fourier transformation, the filtered heterodyned SF signal of the sample in the frequency-domain was normalized by the heterodyned SF signal of an air/z-cut quartz interface. To calibrate the frequency of the ω2 axis, another SF spectrum of an air/z-cut quartz interface without dry nitrogen purging (RH ∼ 30%) was measured, and then compared to a FTIR spectrum of water vapor. The probe beams and the detected SF signal are all p-polarized (PPP polarization combination). The typical acquisition time of an HD-VSFG measurement for a perovskite sample was 15 minutes; a total of 5 spectra, each taken at different lateral positions, were averaged to remove any potential spatial inhomogeneity. The perovskite samples containing CsPbBr3 and PCBM layers were measured in another HD-VSFG setup. The FWHM bandwidth of ω1 (center wavelength ∼795 nm) in this setup was about 1.5 nm, corresponding to a spectral resolution of 24 cm−1 for the HD-VSFG spectra.
Abbreviations
| MA | Methylammonium |
| HD-VSFG | Heterodyne-detected vibrational sum-frequency generation |
| Spiro-MeOTAD | 2,2′,7,7′-Tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene |
| Imχ(2) | Imaginary part of the second order susceptibility. |
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
AAB is a Royal Society University Research Fellow. AAB acknowledges JSPS Invitation Fellowships (Short-term). This work was also supported by JSPS KAKENHI Grant Number JP18H05265 to T. T. This project has also received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 639750).References
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007 CrossRef CAS.
- D. A. Egger, A. Bera, D. Cahen, G. Hodes, T. Kirchartz, L. Kronik, R. Lovrincic, A. M. Rappe, D. R. Reichman and O. Yaffe, Adv. Mater., 2018, 30, 1800691 CrossRef PubMed.
- W. S. Yang, B. W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Il Seok, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402 CrossRef CAS PubMed.
- Y. He and G. Galli, Chem. Mater., 2014, 26, 5394–5400 CrossRef CAS.
- Q. Zhang, R. Su, W. Du, X. Liu, L. Zhao, S. T. Ha and Q. Xiong, Small Methods, 2017, 1, 1700163 CrossRef.
- D. Liu, Q. Lin, Z. Zang, M. Wang, P. Wangyang, X. Tang, M. Zhou and W. Hu, ACS Appl. Mater. Interfaces, 2017, 9, 6171–6176 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kochelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O’Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- G. Grancini, A. R. Srimath Kandada, J. M. Frost, A. J. Barker, M. De Bastiani, M. Gandini, S. Marras, G. Lanzani, A. Walsh and A. Petrozza, Nat. Photonics, 2015, 9, 695–701 CrossRef CAS PubMed.
- V. D’Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Nat. Commun., 2014, 5, 3586 CrossRef PubMed.
- C. Quarti, E. Mosconi and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 9394–9409 RSC.
- J. Ma and L. W. Wang, Nano Lett., 2015, 15, 248–253 CrossRef CAS PubMed.
- J. Gong, M. Yang, X. Ma, R. D. Schaller, G. Liu, L. Kong, Y. Yang, M. C. Beard, M. Lesslie, Y. Dai, B. Huang, K. Zhu and T. Xu, J. Phys. Chem. Lett., 2016, 7, 2879–2887 CrossRef CAS PubMed.
- C. J. Tong, W. Geng, O. V. Prezhdo and L. M. Liu, ACS Energy Lett., 2017, 2, 1997–2004 CrossRef CAS.
- E. Mosconi and F. De Angelis, ACS Energy Lett., 2016, 1, 182–188 CrossRef CAS.
- Z. Yang, A. Surrente, K. Galkowski, N. Bruyant, D. K. Maude, A. A. Haghighirad, H. J. Snaith, P. Plochocka and R. J. Nicholas, J. Phys. Chem. Lett., 2017, 8, 1851–1855 CrossRef CAS PubMed.
- X. Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- G. M. Bernard, R. E. Wasylishen, C. I. Ratcliffe, V. Terskikh, Q. Wu, J. M. Buriak and T. Hauger, J. Phys. Chem. A, 2018, 122, 1560–1573 CrossRef CAS PubMed.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055–10061 CrossRef CAS PubMed.
- O. Selig, A. Sadhanala, C. Müller, R. Lovrincic, Z. Chen, Y. L. A. Rezus, J. M. Frost, T. L. C. Jansen and A. A. Bakulin, J. Am. Chem. Soc., 2017, 139, 4068–4074 CrossRef CAS PubMed.
- A. A. Bakulin, O. Selig, H. J. Bakker, Y. L. A. Rezus, C. Müller, T. Glaser, R. Lovrincic, Z. Sun, Z. Chen, A. Walsh, J. M. Frost and T. L. C. Jansen, J. Phys. Chem. Lett., 2015, 6, 3663–3669 CrossRef CAS PubMed.
- V. C. A. Taylor, D. Tiwari, M. Duchi, P. M. Donaldson, I. P. Clark, D. J. Fermin and T. A. A. Oliver, J. Phys. Chem. Lett., 2018, 9, 895–901 CrossRef CAS PubMed.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X. Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S. H. Lee, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286 RSC.
- N. P. Gallop, O. Selig, G. Giubertoni, H. J. Bakker, Y. L. A. Rezus, J. M. Frost, T. L. C. Jansen, R. Lovrincic and A. A. Bakulin, J. Phys. Chem. Lett., 2018, 9, 5987–5997 CrossRef CAS PubMed.
- J. S. Bechtel, R. Seshadri and A. Van Der Ven, J. Phys. Chem. C, 2016, 120, 12403–12410 CrossRef CAS.
- G. Sharada, P. Mahale, B. P. Kore, S. Mukherjee, M. S. Pavan, C. De, S. Ghara, A. Sundaresan, A. Pandey, T. N. Guru Row and D. D. Sarma, J. Phys. Chem. Lett., 2016, 7, 2412–2419 CrossRef PubMed.
- S. Govinda, B. P. Kore, M. Bokdam, P. Mahale, A. Kumar, S. Pal, B. Bhattacharyya, J. Lahnsteiner, G. Kresse, C. Franchini, A. Pandey and D. D. Sarma, J. Phys. Chem. Lett., 2017, 8, 4113–4121 CrossRef CAS PubMed.
- D. Zhang, Y. Zhu, L. Liu, X. Ying, C. E. Hsiung, R. Sougrat, K. Li and Y. Han, Science, 2018, 359, 675–679 CrossRef CAS PubMed.
- H. Röhm, T. Leonhard, M. J. Hoffmann and A. Colsmann, Energy Environ. Sci., 2017, 10, 950–955 RSC.
- R. Ohmann, L. K. Ono, H. S. Kim, H. Lin, M. V. Lee, Y. Li, N. G. Park and Y. Qi, J. Am. Chem. Soc., 2015, 137, 16049–16054 CrossRef CAS PubMed.
- S. G. Motti, L. S. Cardoso, D. J. C. Gomes, R. M. Faria and P. B. Miranda, J. Phys. Chem. C, 2018, 122, 10450–10458 CrossRef CAS.
- M. Xiao, S. Joglekar, X. Zhang, J. Jasensky, J. Ma, Q. Cui, L. J. Guo and Z. Chen, J. Am. Chem. Soc., 2017, 139, 3378–3386 CrossRef CAS PubMed.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Chem. Phys., 2009, 130, 204704 CrossRef PubMed.
- S. Nihonyanagi, J. A. Mondal, S. Yamaguchi and T. Tahara, Annu. Rev. Phys. Chem., 2013, 64, 579–603 CrossRef CAS PubMed.
- Y. Rakita, O. Bar-Elli, E. Meirzadeh, H. Kaslasi, Y. Peleg, G. Hodes, I. Lubomirsky, D. Oron, D. Ehre and D. Cahen, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5504–E5512 CrossRef CAS PubMed.
- Y. Rakita, E. Meirzadeh, T. Bendikov, V. Kalchenko, I. Lubomirsky, G. Hodes, D. Ehre and D. Cahen, APL Mater., 2016, 4, 051101 CrossRef.
- T. Glaser, C. Müller, M. Sendner, C. Krekeler, O. E. Semonin, T. D. Hull, O. Yaffe, J. S. Owen, W. Kowalsky, A. Pucci and R. Lovrinčić, J. Phys. Chem. Lett., 2015, 6, 2913–2918 CrossRef CAS PubMed.
- L. Q. Xie, T. Y. Zhang, L. Chen, N. Guo, Y. Wang, G. K. Liu, J. R. Wang, J. Z. Zhou, J. W. Yan, Y. X. Zhao, B. W. Mao and Z. Q. Tian, Phys. Chem. Chem. Phys., 2016, 18, 18112–18118 RSC.
- T. Yin, Y. Fang, X. Fan, B. Zhang, J.-L. Kuo, T. J. White, G. M. Chow, J. Yan and Z. X. Shen, Chem. Mater., 2017, 29, 5974–5981 CrossRef CAS.
- 4-tert-BUTYLPYRIDINE – FTIR Spectrum – SpectraBase, Compound ID = L9DGwhhSPqi, SpectraBase Spectra ID = 7AdxerwnkM7, https://spectrabase.com/spectrum/7AdxerwnkM7, (accessed 30 September 2019).
- Lithium triflimide – FTIR Spectrum – SpectraBase, Compound ID = 5Kif9YtoqEG, SpectraBase Spectra ID = 1IZXcUr8w8J, https://spectrabase.com/spectrum/1IZXcUr8w8J, (accessed 30 September 2019).
- P. E. Ohno, H. F. Wang and F. M. Geiger, Nat. Commun., 2017, 8, 1032 CrossRef PubMed.
- J. Wang, J. Li, X. Xu, Z. Bi, G. Xu and H. Shen, RSC Adv., 2016, 6, 42413–42420 RSC.
- P. Schulz, E. Edri, S. Kirmayer, G. Hodes, D. Cahen and A. Kahn, Energy and Environmental Science, Royal Society of Chemistry, 2014, vol. 7, pp. 1377–1381 Search PubMed.
- C. S. Jiang, M. Yang, Y. Zhou, B. To, S. U. Nanayakkara, J. M. Luther, W. Zhou, J. J. Berry, J. Van De Lagemaat, N. P. Padture, K. Zhu and M. M. Al-Jassim, Nat. Commun., 2015, 6, 8397 CrossRef CAS PubMed.
- A. Guerrero, E. J. Juarez-Perez, J. Bisquert, I. Mora-Sero and G. Garcia-Belmonte, Appl. Phys. Lett., 2014, 105, 133902 CrossRef.
- Y. C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- D. Ghosh, P. Walsh Atkins, M. S. Islam, A. B. Walker and C. Eames, ACS Energy Lett., 2017, 2, 2424–2429 CrossRef CAS.
- S. T. Birkhold, H. Hu, P. T. Höger, K. K. Wong, P. Rieder, A. Baumann and L. Schmidt-Mende, J. Phys. Chem. C, 2018, 122, 12140–12147 CrossRef CAS.
- M. Hu, C. Bi, Y. Yuan, Z. Xiao, Q. Dong, Y. Shao and J. Huang, Small, 2015, 11, 2164–2169 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. Van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- H. Bässler and A. Köhler, Top. Curr. Chem., 2012, 312, 1–65 Search PubMed.
- J. H. Heo and S. H. Im, Adv. Mater., 2016, 28, 5121–5125 CrossRef CAS PubMed.
- N. K. Noel, B. Wenger, S. N. Habisreutinger, J. B. Patel, T. Crothers, Z. Wang, R. J. Nicholas, M. B. Johnston, L. M. Herz and H. J. Snaith, ACS Energy Lett., 2018, 3, 1233–1240 CrossRef CAS.
- M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He, G. MacUlan, A. Goriely, T. Wu, O. F. Mohammed and O. M. Bakr, Nat. Commun., 2015, 6, 7586 CrossRef PubMed.
- A. Mattoni, A. Filippetti, M. I. Saba and P. Delugas, J. Phys. Chem. C, 2015, 119, 17421–17428 CrossRef CAS.
- A. Torres and L. G. C. Rego, J. Phys. Chem. C, 2014, 118, 26947–26954 CrossRef CAS.
- A. Kundu, S. Tanaka, T. Ishiyama, M. Ahmed, K. I. Inoue, S. Nihonyanagi, H. Sawai, S. Yamaguchi, A. Morita and T. Tahara, J. Phys. Chem. Lett., 2016, 7, 2597–2601 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Sample morphology characterization, (2) sample IR characterization, (3) calculation on Fresnel factors, and (4) DFT calculation and second-order hyperpolarizability. See DOI: 10.1039/c9mh01394f |
| This journal is © The Royal Society of Chemistry 2020 |