Role of partial charge assignment methods in high-throughput screening of MOF adsorbents and membranes for CO₂/CH₄ separation

Abstract

Metal organic frameworks (MOFs) have great potential for CO₂ separation and there is a strong need to determine the best-performing MOFs due to the rapidly increasing number of materials. High-throughput computational screening of MOFs for CO₂ separation has a tremendous value to identify the most promising MOF candidates to direct the experimental efforts to the best materials. Computational identification of promising MOF candidates using molecular simulations depends on the accurate description of electrostatic interactions between CO₂ molecules and MOFs and computing these interactions requires partial charge assignment to MOF atoms. Quantum-chemistry based charge assignment methods are highly accurate but computationally expensive when very large numbers of MOFs are considered. Approximate methods can quickly define the charges of MOFs with less computational expense. In this work, we examined the role of partial charge assignment methods in high-throughput computational screening of MOFs for CO₂/CH₄ separation. A quantum based, density-derived electrostatic and chemical charge method (DDEC) and an approximate charge equilibration method (Qeq) were used to compute the adsorption of CO₂/CH₄ mixtures in 1500 MOFs under two different operating conditions. The results of molecular simulations utilizing different charge assignment methods were used to predict the performance evaluation metrics of MOF adsorbents and membranes. The results showed that although calculated metrics quantitatively varied depending on the method, the rankings of DDEC- and Qeq-charged MOFs based on individual performance metrics were highly correlated. On the other hand, the identity of the best performing MOF candidates was found to change based on the type of charge assignment method used in simulations.

---

Design, System, Application

Metal organic frameworks (MOFs) are porous crystalline materials composed of metal complexes connected by organic linkers. MOFs have been considered as promising materials for CO₂ capture and molecular simulations have been widely used to examine CO₂/CH₄ separation potentials of MOFs. We aimed to uncover the role of partial charge assignment methods used in molecular simulations of MOFs by performing a high-throughput computational screening of 1500 structures. The CO₂/CH₄ mixture adsorption data of MOFs were computed using two different charge assignment methods, a highly accurate density functional theory-based method and an efficient approximate charge assignment method. Performance metrics such as adsorption selectivity, working capacity, adsorbent performance score, regenerability, gas permeability and membrane selectivity were calculated and compared to assess the impact of using different charge methods on the identification of the most promising MOF adsorbents and membranes. Calculated performance metrics were found to quantitatively change depending on the charge method but the rankings of MOFs based on different metrics were not significantly affected from the charge method. The results of this work will provide an assessment for the choice of charge assignment methods used in the high-throughput screening of MOF adsorbents and membranes for efficient CO₂/CH₄ separation.

1. Introduction

Discovery of new adsorbent materials for separation of CO₂ from natural gas and landfill gas is highly important as currently applied solvent-based absorption technology is energy-intensive.^1,2 Metal organic frameworks (MOFs) are porous crystalline materials composed of metal complexes connected by organic linkers and they have been considered as promising adsorbent materials for CO₂ capture.^3,4 The number of MOFs which are experimentally synthesized and deposited into the Cambridge Structural Database (CSD) has already exceeded 90 000. Due to this large material space, experimental testing of every single MOF material is impractical. Computational methods play a very important role in assessing gas storage and separation performances of a large number of MOFs.^5,6

The number of studies on high-throughput computational screening of MOFs for CO₂ capture is increasing rapidly.^7–9 These studies are based on molecular simulations of a very large number of MOFs to compute CO₂ adsorption and in some rare cases, CO₂ diffusion in the materials' pores. Due to the quadrupole moment of CO₂, electrostatic interactions between the MOF atoms and CO₂ molecules are important in determining gas adsorption and transport.¹⁰ Partial atomic charges are needed for the framework atoms to calculate these electrostatic interactions. Many different charge assignment approaches based on quantum mechanics are available in the literature such as charges from electrostatic potentials using a grid-based method (ChelpG),¹¹ the repeating electrostatic potential extracted atomic charge method (REPEAT),¹² and the density-derived electrostatic and chemical charge method (DDEC).¹³ Although density functional theory (DFT)-based approaches are highly accurate, they are very costly especially when very large numbers of MOFs are simulated in high-throughput screening studies. Alternatively, an approximate charge assignment method, named charge equilibration (Qeq),¹⁴ has been introduced. Modifications on the Qeq method to better approximate the DFT-based charges led to different versions such as periodic Qeq (PQeq),¹⁵ extended Qeq (EQeq),¹⁶ MOF-electrostatic potential optimized Qeq (MEPO-Qeq),¹⁷ formal charge Qeq (FC-Qeq) and ionizing Qeq (IQeq)¹⁸ methods, which were discussed and compared in detail in a recent review.¹⁹ Approximate charge assignment methods have been established based on a restricted set of MOFs and it is not possible to experimentally validate the partial charges of MOFs. Therefore, Qeq methods have been generally compared with DFT-based methods to understand how well they represent the CO₂ adsorption properties of MOFs.

Wilmer et al.¹⁶ compared the experimental CO₂ adsorption data of 12 MOFs with the simulated adsorption results obtained using Qeq, EQeq, ChelpG, and REPEAT charges. Simulations using ChelpG charges showed the best agreement with the experimental results whereas results obtained with EQeq-charges were comparable to them. Comparison of the CO₂ adsorption data of 14 MOFs calculated using ChelpG charges with those obtained using Qeq charges showed that both methods give the same predictions for the best and worst performing MOFs.²⁰ PQeq and DDEC charges were compared for evaluating CO₂/N₂ separation performances of 489 MOFs.¹⁵ It was shown that using PQeq charges gives sufficiently close results to the ones obtained with quantum chemistry-based charge methods for the initial screening of MOFs based on the Henry's law constants but results under real mixture conditions were found to differ significantly. Kadantsev and coworkers¹⁷ established MEPO-Qeq with a training set of 543 MOFs and applied it to 693 MOFs to predict CO₂ adsorption. Good agreements were observed for the CO₂ uptakes and heats of adsorption values of MOFs obtained using MEPO-Qeq and DFT-derived charges.

Nazarian et al.²¹ established the DDEC-charged computation ready experimental MOF (CoRE MOF) database consisting of 2932 experimentally synthesized MOFs and calculated the selectivity for tert-butyl mercaptan over CH₄ based on the Henry's law constants using DDEC and EQeq charges. Their work showed that the adsorption selectivities of MOFs can differ significantly when calculated with EQeq and DDEC charges. 1627 MOFs were screened based on the Henry's law constants for CO₂/N₂/H₂O separation using DDEC and EQeq charges and 8 out of the top 15 MOFs with the highest CO₂/H₂O selectivity were found to be common among the results obtained with either charge method.²² Collins et al.²³ used the split-charge equilibration (SQE)-MEPO method to better reproduce the quantum mechanical electrostatic potential inside the pores of 559 hypothetical MOFs and 45 hypothetical porous polymer networks. Compared to the MEPO method, the results obtained using the SQE-MEPO method showed a better agreement with those obtained using the REPEAT method for CO₂ uptakes and heat of adsorption values.

DDEC-charged CoRE MOF is currently the only database that provides computation-ready structures with partial charges for 2932 MOFs and offers great potential for high-throughput computational screening of MOFs for CO₂ adsorption. The approximate charge assignment method, Qeq, on the other hand, has been already implemented in several simulation packages and it can be used to quickly assign partial charges to very large numbers of MOFs but with less accuracy compared to the DDEC method. As we reviewed above, most of the studies comparing Qeq- and DFT-based methods either focused on the Henry's law constants of gases or single-component gas uptakes. Therefore, the impact of using different charge assignment methods on the simulated CO₂ separation performances of MOFs in high-throughput screening studies is still unknown.

In this work, we aim to uncover the role of partial charge assignment methods used in the high-throughput computational screening of MOFs by studying both adsorption-based and membrane-based CO₂/CH₄ separation. With this motivation, we used two different charge assignment methods, a DFT-based method, DDEC, and an approximate method, Qeq, and performed molecular simulations to compute the adsorption of CO₂/CH₄ mixtures in 1500 different MOF structures considering two different operating conditions and gas compositions. Results of molecular simulations were then used to calculate several adsorbent performance evaluation metrics for MOFs including adsorption selectivity, working capacity, adsorbent performance score, and regenerability, in addition to membrane performance evaluation metrics including gas permeability and membrane selectivity. These performance metrics obtained from simulations using DDEC and Qeq charges were compared in detail to explore the impact of the type of charge assignment method on the ranking and identification of the top MOF adsorbents and membranes. We also investigated the structural properties of MOFs that make the predicted performance of materials more sensitive to the choice of charge assignment method.

2. Computational details

The DDEC method utilizes the electron and spin density distributions of structures to efficiently reproduce the electrostatic potential of MOFs with chemically meaningful partial charges and therefore, it is considered as one of the most accurate partial charge assignment methods. The DDEC method was tested on 52 different periodic and non-periodic structures containing 31 different chemical elements in total.²⁴ The Qeq method utilizes the ionization potential, electron affinity and radius of atoms to efficiently and quickly approximate the electrostatic potential. It was discussed that the DDEC method assigns larger charges than the Qeq method for most of the elements except alkali metals, and the Qeq method underestimates the charges of the main attractive sites for CO₂ adsorption in MOFs compared to the DDEC method.^19,21 In agreement with these previous findings, our results also showed that for most of the MOFs, the DDEC method assigned higher charges than the Qeq method which led to higher CO₂ uptakes as we will discuss in detail below. Overall, the algorithm and the input parameters used in the charge assignment methods have an impact on the resulting charges. Although the Qeq method was shown to fail in the presence of alkali metals, it was found to be comparable in terms of accuracy with the most recent variants.¹⁹ At that point, we note that the ultimate aim of this work is to investigate the effect of using different charge assignment methods on the predicted adsorbent and membrane performances and hence ranking of MOFs but not to discuss the accuracy of these methods which already exists in the literature.¹⁹

We started with a MOF database consisting of 2932 MOFs for which DDEC charges were assigned.²¹ We computed the pore limiting diameters (PLDs), the largest cavity diameters (LCDs), and the accessible surface areas (ASAs) of MOFs using the Zeo++ software²⁵ (version 0.3). The MOF database was then constrained to only cover materials with non-zero ASAs and PLDs >3.75 Å so that both CO₂ (kinetic diameter of 3.3 Å) and CH₄ (kinetic diameter of 3.73 Å) molecules can pass through the pores for the adsorption and membrane-based CO₂/CH₄ separation. The QEq²⁰ method as implemented in the RASPA simulation package²⁶ was used to assign the partial point charges to framework atoms. MOFs for which partial charge assignment using the Qeq method could not produce reasonable results were excluded. We finally ended up with 1500 different MOF structures and performed GCMC simulations to compute the adsorption of CO₂/CH₄ mixtures in all MOFs. We note that the DDEC-charged MOFs used in this work were not geometry-optimized and therefore the only difference between DDEC-charged and Qeq-charged MOFs was the partial charges of the atoms in the frameworks.

A single-site spherical Lennard-Jones (LJ) 12–6 potential was used to model CH₄ molecules while CO₂ molecules were modeled as three-site rigid molecules with the LJ 12–6 potential and their partial point charges were positioned at the center of each site.^27,28 The united atom model for CH₄ molecules was selected based on the accurate representation of the bulk properties of CH₄ such as experimental vapor–liquid coexistence curves.²⁷ It was previously shown that the non-charged, united-atom representation of CH₄ molecules (the TraPPE model as used in this work) well represents the adsorption properties of MOFs compared to a five-site, charged CH₄ model.²⁹ This model increases the computational efficiency due to less number of interaction sites compared to the five-site model, therefore high-throughput computational screening studies including ours have generally used this model. Potential parameters and charges used for both gas molecules are given in Table S1 of the ESI.† The potential parameters of the MOF atoms were taken from the universal force field (UFF)³⁰ since it was shown to accurately reproduce the experimental CO₂ and CH₄ adsorption data of MOFs in our previous studies.^31–33 Lorentz–Berthelot mixing rules were used to calculate the interaction parameters between different atoms. Electrostatic interactions were calculated by the Ewald summation.³⁴ The cut-off distance for the truncation of intermolecular interactions was set to 13 Å. The simulation cell lengths were increased to at least 26 Å along each dimension and periodic boundary conditions were applied in all simulations. MOFs were assumed to be rigid in their reported crystallographic structures. For GCMC simulations, five different types of moves were considered including translation, rotation, reinsertion, and swap (insertion–deletion) of a molecule with equal probability. For each MOF, simulations were carried out for 10 000 initialization cycles followed by 50 000 production cycles for taking the ensemble averages. The Peng–Robinson equation of state was used to convert pressure to the corresponding fugacity. We performed GCMC simulations at room temperature under two different conditions: (i) vacuum swing adsorption (VSA) at P_ads: 1 bar and P_des: 0.1 bar and (ii) pressure swing adsorption (PSA) at P_ads: 5 bar and P_des: 1 bar. Here, P_ads and P_des represent adsorption and desorption pressures. Simulations were conducted for two different bulk mixture compositions, 10/90 CO₂/CH₄ and 50/50 CO₂/CH₄, to represent natural gas purification and landfill gas separation, respectively.

We first used the DDEC partial charges already provided for the framework atoms in the MOF database and computed the electrostatic interactions between MOF atoms and CO₂ molecules. All GCMC simulations were then repeated using Qeq-charged MOFs to compare the effect of the partial charge assignment method on the gas adsorption results. The results of GCMC simulations, CO₂ and CH₄ uptakes, were used to calculate the four different adsorbent performance evaluation metrics of MOFs, adsorption selectivity (S_ads), working capacity (ΔN), adsorbent performance score (APS), and regenerability (R%). Mathematical definitions of these metrics can be seen in Table 1.

Table 1 Adsorbent and membrane performance evaluation metrics^a

Metric	Formula
a x: adsorbed phase gas composition; y: bulk phase gas composition; NCO2: CO2 uptake (mol kg^−1); i: gas species; Pi: gas permeability (Barrer); ci: gas loadings used in MD simulation (mol kg^−1); Dself,i: self-diffusivity of gas species (cm^2 s^−1); fi: fugacity of gas species i (Pa).
Adsorption selectivity
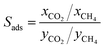
CO2 working capacity	ΔNCO2 = NCO2,ads − NCO2,des
Adsorbent performance score	APS = Sads × ΔNCO2
Percent regenerability
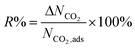
Gas permeability
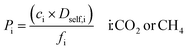
Diffusion selectivity
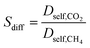
Membrane selectivity	S mem = Sads × Sdiff

---

In order to examine the effect of the charge assignment method on the gas permeability (P_i) of species i and selectivity of the selected MOF membranes (S_mem), we also performed equilibrium molecular dynamics (EMD) simulations for the 10/90 CO₂/CH₄ mixture using RASPA on selected MOFs. Gas loadings (c_i) obtained from GCMC simulations that were performed at 1 bar and 298 K for a feed mixture of 10/90 CO₂/CH₄ were used as the input of EMD simulations to compute self-diffusivities of gases (D_self,i) at their corresponding loadings. NVT ensemble was used for the EMD simulations with a time step of 1 fs. The temperature was kept constant using the Nosé–Hoover chain thermostat algorithm.³⁵ After 10 000 initialization and 10 000 equilibration cycles, 4 × 10⁶ cycles were used to obtain the mean squared displacement (MSD) data of gas molecules calculated using modified order-N algorithm at long times.²⁶ The D_self,i of gas molecules were computed from the slope of the MSD data in accordance with the Einstein relation.³⁶ These simulations were repeated three times to compute the average self-diffusivities of each gas component. Mathematical descriptions used to compute performance metrics of MOF membranes, mixture permeabilities of gas components (P_i) and mixture selectivities of membranes (S_mem), are given in Table 1.

Performance evaluation metrics computed for MOF adsorbents and membranes using two different charge assignment methods were compared. In order to explore the correlation (or the lack of correlation) between simulation results based on the atomic charge assignment method, the coefficient of determination (0 ≤ R² ≤ 1) and the Spearman's rank correlation coefficient (−1 ≤ SRCC ≤ 1) were computed. R was calculated using the formula, 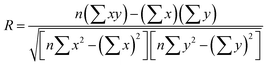, where x (y) represents the value of the metric calculated for a MOF using Qeq (DDEC) charges and n is the total number of MOFs. In order to determine the SRCC of MOFs for a given metric, we first ranked the MOFs according to the value of the metric of interest computed using either of the charge assignment method and then calculated the R value between the rankings of MOFs. Therefore, in SRCC calculation, x (y) represents the ranking of a MOF for a metric calculated using Qeq (DDEC) charges and n is the total number of MOFs. The value of the SRCC ranges from −1 to 1 where positive (negative) values represent that two rankings are highly similar (dissimilar) and SRCC becomes unity when there is a perfect correlation between the two rankings.

Before discussing the results of the adsorbent and membrane performance evaluation metrics of 1500 MOFs in detail, we compared the experimentally reported CO₂ uptakes of 10 different MOF structures taken from the literature^37–43 with our simulated CO₂ uptakes using both charge methods. Fig. S1† shows that molecular simulations using DDEC charges generally give CO₂ uptakes closer to the experimental results compared to Qeq charges. There were two MOFs (CuBTC and MIL-47) for which CO₂ uptakes obtained by the Qeq method were in a better agreement with the experiments compared to those obtained by the DDEC method. We also observed that simulated CO₂ uptakes obtained from two charge assignment methods can be similar to each other but might vary from the experimental CO₂ uptakes in some cases as shown in Fig. S1.† The comparison between experimental and simulated CO₂ adsorption isotherms computed using both charge methods is also shown for selected MOFs in Fig. S2.†

3. Results and discussion

We first examined the effect of using DDEC and Qeq charges on the adsorption of CO₂/CH₄ mixtures in 1500 MOFs. The number/type of accessible adsorption sites and van der Waals potential parameters of the framework atoms are the same regardless of the charge assignment method used in molecular simulations. Hence, the charge assignment method directly affects the electrostatic interactions between CO₂ molecules and MOF atoms. We note that partial point charges for CO₂ molecules were obtained from the TraPPE force field.²⁸ Although CH₄ was modeled as nonpolar, CH₄ uptake also changes depending on the charge assignment method due to the competition between CO₂ and CH₄ molecules in the mixture for the same adsorption sites of MOFs. The MOFs for which negligible CH₄ uptake was observed in the molecular simulations were excluded. Fig. 1 compares gas uptakes computed at 0.1, 1 and 5 bar for the 10/90 CO₂/CH₄ mixture using both charge methods. In order to facilitate the visualization of the charge effect on the simulated gas uptakes, we first identified the atom with the largest charge in a DDEC-charged MOF (q^largest_DDEC) and Qeq-charged MOF (q^largest_Qeq), and then color-coded the data points based on the difference of those charges (q^largest_DDEC − q^largest_Qeq). Fig. 1(a–c) show that the method that assigns the largest charge mostly resulted in higher simulated CO₂ uptakes compared to the other method at all pressures. However, we note that when a method assigns a larger charge to one of the atoms in the framework, this does not claim that the charges of every atom in that framework would be larger than those assigned by the other method. For most MOFs, 896 among 1500, the DDEC method assigned a higher largest charge than Qeq, while there are MOFs for which DDEC and Qeq assigned the largest charge to different atoms in the same framework.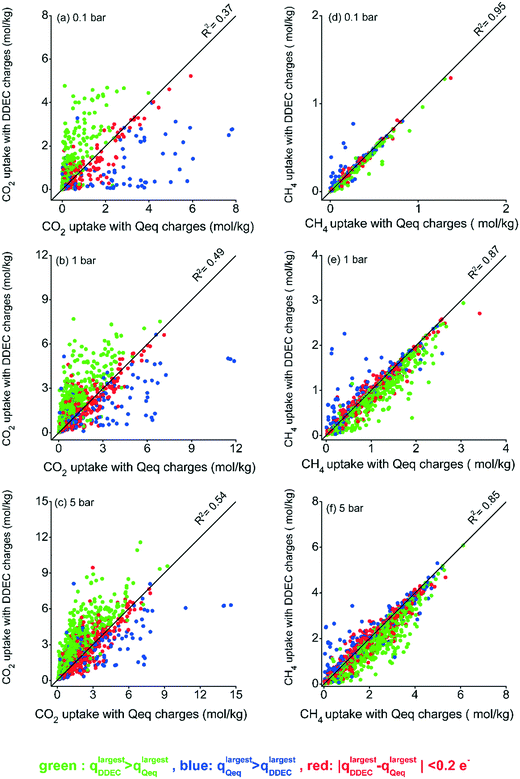

Fig. 1 CO₂ uptakes (a–c) and CH₄ uptakes (d–f) obtained from simulations using Qeq and DDEC charges at 0.1, 1, and 5 bar for the 10/90 CO₂/CH₄ mixture.

Fig. 1 shows that the discrepancy between the CO₂ uptakes obtained using DDEC- and Qeq-charged MOFs is more observable at low pressures. Gas molecules at low pressures first interact with the accessible metal centers and organic linkers of MOFs where van der Waals interaction parameters and partial charges play important roles in attracting guest molecules.⁴⁴ Due to the electrostatic interactions, atoms with the largest charges become more attractive for CO₂ molecules, and these adsorption sites are primarily saturated at low pressures. As the pressure increases and with the saturation of the most favorable adsorption sites, adsorbate–adsorbate interactions start to dominate and the effect of atomic partial charges diminishes. In order to quantify this, we computed R² values at each pressure as shown in Fig. 1. At low pressure, low R² values were observed for CO₂ uptakes obtained from simulations using two different charge assignment methods (R² of 0.37 at 0.1 bar as shown in Fig. 1(a)), showing the importance of electrostatic interactions hence the choice of charge assignment method. As the pressure increases, CO₂ uptakes obtained from different charge assignment methods become moderately similar leading to increased R² values of 0.49 and 0.54 at 1 bar and 5 bar, respectively, as shown in Fig. 1(b and c). Fig. 1(d–f) show that the type of charge assignment method had a less pronounced impact on the simulated CH₄ uptakes of MOFs compared to CO₂ uptakes. We finally note that although we used a simple representation of the effect of charges, the difference between the largest charges assigned by the two methods to an atom in a MOF (q^largest_DDEC − q^largest_Qeq), there are cases when this difference was not directly reflected on the simulated CO₂ uptakes. For example, q^largest_DDEC can be only slightly lower than q^largest_Qeq in a MOF, but the CO₂ uptake of DDEC-charged MOFs can be significantly higher than that of Qeq-charged MOFs. This occurs when the two methods assign the largest charge to different atoms which may not be equally accessible as an adsorption site for CO₂ molecules. In other words, the charges of atoms in the pore surrounding walls play an important role in describing CO₂ adsorption.

Throughout this manuscript, the results for adsorption of the 10/90 CO₂/CH₄ mixture are given while the results for adsorption of an equimolar CO₂/CH₄ mixture are provided in the ESI.† Fig. S3† shows that the effect of the charge assignment method on CO₂ uptakes is less pronounced for the 50/50 CO₂/CH₄ mixture compared to the results for the 10/90 CO₂/CH₄ mixture. Higher R² values of 0.47, 0.62, and 0.78 were observed for CO₂ uptakes at 0.1, 1, and 5 bar, respectively, for the adsorption of equimolar mixture. When the equimolar mixture was considered, there were enough CO₂ molecules in the feed to compete with CH₄ molecules and to dominate the adsorption sites at low pressures due to the electrostatic interactions with the frameworks.

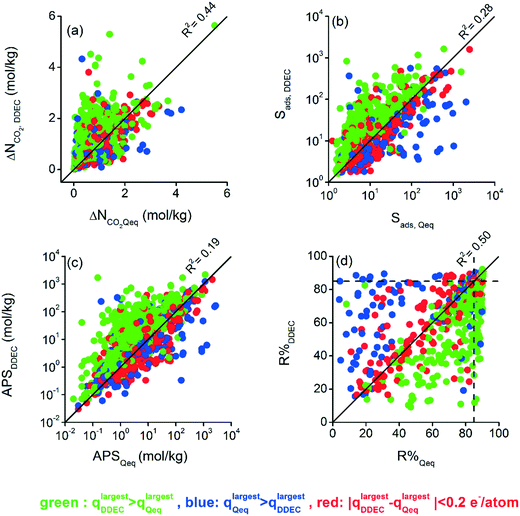
Differences between CO₂ and CH₄ uptakes of DDEC- and Qeq-charged MOFs ultimately affect the calculated adsorbent performance evaluation metrics of MOFs. We examined how these metrics change depending on the charge method used in the molecular simulations. The effect of the charge method on adsorbent metrics was more observable for the 10/90 CO₂/CH₄ mixture under VSA conditions and the results are demonstrated in Fig. 2 whereas the results for other operating conditions and mixture compositions can be found in Table S2 and Fig. S4–S6 of the ESI.†Fig. 2(a) shows that the CO₂ working capacities (ΔN_CO2) of DDEC-charged MOFs were calculated to range from 0.02 to 5.64 mol kg⁻¹ and the ΔN_CO2 values of Qeq-charged MOFs range between 0.01 and 5.51 mol kg⁻¹. Significant differences between calculated ΔN_CO2 values were observed for some MOFs based on the charge method. The calculated ΔN_CO2 values of a large number of DDEC-charged MOFs (326 MOFs) were at least double of those of Qeq-charged MOFs while the ΔN_CO2 values of many Qeq-charged MOFs (69 MOFs) were at least two times higher than those of DDEC-charged MOFs. This led to a low R² value, 0.44, for the working capacities computed by the two different methods. Similarly, we observed large differences between the adsorption selectivities (S_ads) of DDEC- and Qeq-charged MOFs as shown in Fig. 2(b). The S_ads values of DDEC-charged MOFs were calculated to range from 1.6 to 1633.8 whereas the values of Qeq-charged MOFs vary from 1.2 to 2477.7. As shown in Fig. 2(b), two orders of magnitude differences were observed in CO₂/CH₄ selectivities of some MOFs depending on the charge method, leading to a low R² of 0.28.

Fig. 2 Calculated adsorbent performance evaluation metrics using Qeq and DDEC charges under VSA conditions at 298 K, for the 10/90 CO₂/CH₄ mixture; (a) ΔN_CO2, (b) S_ads, (c) APS, and (d) R%. Dashed lines in (d) show R% = 85%.

There is generally a trade-off relationship between the selectivity and working capacity of MOFs. APS is defined as the multiplication of those two to efficiently identify the materials offering both high selectivity and high working capacity.⁴⁵Fig. 2(c) represents that the APS values of DDEC-charged MOFs vary between 0.03 and 2180 mol kg⁻¹ whereas those computed for Qeq-charged MOFs range from 0.02 to 2716 mol kg⁻¹. Since APS combined two metrics (selectivity and working capacity) computed differently by DDEC and Qeq methods, a very weak correlation, R² of 0.19, was observed. Regenerability (R%) was calculated by dividing the ΔN_CO2 of MOFs with the CO₂ uptake at the adsorption pressure. As shown in Fig. 2(d), R% values vary depending on the charge assignment method used in molecular simulations, leading to an R² of 0.50. As high R% is desired for efficient adsorption-based gas separation, we represented 85% limit with a dashed line in Fig. 2(d). 683 MOFs were found to have R% > 85% when the DDEC method was used but 36 of these MOFs were identified to have R% ≤ 85% by the Qeq method. On the other hand, there were 799 MOFs with R% > 85% when Qeq charges were used while 152 of them were computed to have R% ≤ 85% with DDEC charges. 647 common MOFs were found to have R% > 85% using either charge method.

In the high-throughput computational screening of MOFs, materials are generally ranked based on the adsorbent performance evaluation metrics to identify the most promising ones among many. We separately ranked 1500 MOFs based on their calculated S_ads, ΔN_CO2, APS, and R% metrics using the simulation results of DDEC-charged and Qeq-charged MOFs. In order to quantify how the rankings of MOFs change depending on the charge method, we computed the SRCC values and presented them in Table 2 for different compositions of the gas mixture and under different operating conditions. Although R² values were generally low for performance metrics calculated by the DDEC and Qeq methods, all the SRCC values were found to be higher than 0.7. This result indicates that although calculated performance metrics quantitatively alter depending on the charge method, the rankings of MOFs based on individual metrics are not significantly affected from the charge method used in molecular simulations. Overall, Table 2 suggests that either charge method can be used in the high-throughput screening of MOFs if the main aim of a study is to rank the materials based on one of the metrics that we considered above.

Table 2 Calculated R² and SRCC of adsorbent performance evaluation metrics between DDEC-charged and Qeq-charged MOFs under PSA and VSA conditions

	CO2/CH4: 10/90				CO2/CH4: 50/50
	R ^2		SRCC		R ^2		SRCC
	VSA	PSA	VSA	PSA	VSA	PSA	VSA	PSA
S ads	0.28	0.18	0.72	0.72	0.16	0.07	0.73	0.75
ΔNCO2	0.44	0.57	0.77	0.80	0.62	0.85	0.82	0.94
R%	0.50	0.74	0.86	0.88	0.61	0.77	0.85	0.88
APS	0.19	0.09	0.75	0.73	0.07	0.07	0.74	0.76

---

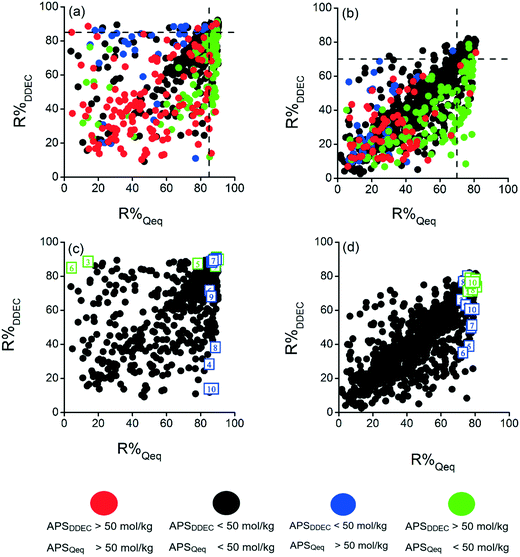
Choosing the best adsorbent material for a target gas separation process solely based on a single criterion cannot be highly accurate. For example, a MOF with a very high CO₂/CH₄ selectivity could not be suitable in practical gas separation applications if it has a low R% value. We, therefore, recently described an approach where the best material candidates having a good combination of each metric, S_ads, ΔN_CO2, and R%, were identified by solely focusing on MOFs having R% > 85% and ranking them based on their calculated APSs.^32,46 Following the same approach, we compared the R% and APS values of DDEC- and Qeq-charged MOFs as shown in Fig. 3. Due to the lower R% values obtained under PSA conditions, we set the limit to 70% under this operating condition. In Fig. 3(a) and (b), dashed lines show R% = 85 and R% = 70, respectively. We also set an arbitrary limit of APS > 50 mol kg⁻¹ as a good performance indicator considering that MOFs having ΔN_CO2 > 5 mol kg⁻¹ and S_ads > 10 would perform well for CO₂/CH₄ separation.^47,48 One important result from Fig. 3(a) is that most of the MOFs having APS > 50 mol kg⁻¹ suffer from low R% regardless of the charge assignment method. For example, majority of the Qeq-charged MOFs computed to have R% > 85% exhibited APS < 50 mol kg⁻¹ (green data points). Similarly, most of the DDEC-charged MOFs calculated to have R% > 85% were predicted to exhibit APS < 50 mol kg⁻¹ (blue data points). Fig. 3(b) shows that almost all the MOFs predicted to have APS > 50 mol kg⁻¹ by both charge methods suffered from low R% values (red data points) whereas most MOFs computed to have APS < 50 mol kg⁻¹ by both methods were found to exhibit R% ≤ 70% (black data points). In other words, either DDEC or Qeq charges can be used in high-throughput simulations to narrow down the material candidates by eliminating MOFs having low R% and low APS.

Fig. 3 Comparison of R% of DDEC and Qeq-charged MOFs under (a and c) VSA (b and d) PSA conditions for the 10/90 CO₂/CH₄ mixture. Dashed lines show R% = 85% in (a) and R% = 70% in (b). The top 10 MOFs identified by DDEC and Qeq methods are shown in green and blue, respectively.

The top 10 MOFs providing R% > 85% (70%) with the highest APSs were identified using both charge methods under VSA (PSA) conditions. We marked the top 10 MOFs identified by Qeq charges with blue and those by DDEC charges with green in Fig. 3(c and d). The main observation from Fig. 3(c) is that 5 of the top MOF adsorbents predicted from simulations using Qeq charges (blue points) suffer from very low R% when the DDEC method was used and they cannot be selected as the best candidates by the DDEC method. Similarly, 3 of the top MOFs identified using DDEC charges (green points) would be eliminated due to their low R% when the Qeq method was used. Fig. 3(d) shows that all the top 10 DDEC-charged MOFs have R% > 70 when Qeq charges were used. However, only 3 of the top 10 Qeq-charged MOFs could have R% > 70 when DDEC charges were utilized. Similar results as shown in Fig. S7† were obtained when an equimolar mixture was considered. Overall, we concluded that although the two charge methods give similar ranking of MOFs based on the individual performance metrics that we considered in this work, the identity of the top adsorbent materials was found to completely alter depending on the charge method used in simulations. Hence, if the aim of the computational screening study is to identify and name the individual best materials, selection of the charge assignment method has a critical importance.

The structural properties of MOFs are one of the intrinsic determinants that define their performances. In order to investigate the structure–performance relationship of MOFs based on the charge assignment method, we used the ratios of performance metrics calculated with DDEC charges to those calculated with QEq charges, ΔN_CO2,DDEC/ΔN_CO2,Qeq, S_ads,DDEC/S_ads,Qeq, APS_DDEC/APS_Qeq, and R%_DDEC/R%_Qeq. These ratios are shown as a function of PLDs of MOFs for the 10/90 CO₂/CH₄ mixture under VSA conditions in Fig. 4. The main message of Fig. 4 is that as the pore size increases, the effect of the charge method becomes less pronounced for all metrics (also for CO₂ uptakes as shown in Fig. S8†). The highest change in the ratio of calculated metrics was observed for APS. APS_DDEC/APS_Qeq varied between 10⁻³ and 10⁴ indicating that some of the APS values calculated with DDEC charges were orders of magnitude higher than those calculated with Qeq charges. The highest APS_DDEC/APS_Qeq values were observed for MOFs having low PLDs (<6 Å). This is due to the stronger confinement of the gas molecules in narrow pores causing a much stronger interaction with the surrounding atoms.⁴⁴ Overall, the results demonstrate that the charge assignment method does not significantly affect the predicted adsorbent performance metrics of MOFs having very large pore sizes but it has a major effect on MOFs with narrow pores.

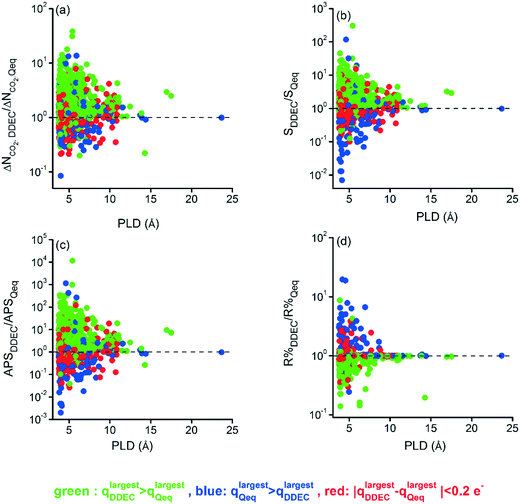Fig. 4 The ratio of (a) ΔN_CO2, (b) S_ads, (c) APS, and (d) R% computed by DDEC charges to the ones computed by Qeq charges as a function of the PLD of MOFs.

We so far examined the impact of the selected charge assignment method on the predicted performance evaluation metrics of MOF adsorbents. Combination of GCMC and EMD simulations can be used to estimate the membrane-based CO₂/CH₄ separation performances of MOFs.⁴⁹ Therefore, unlocking the effects of the charge assignment method used in both GCMC and EMD simulations on the computed gas permeabilities and selectivities of MOF membranes is also important. Performing mixture EMD simulations for a large number of MOFs is computationally challenging, therefore we specifically focused on 10 selected MOFs exhibiting a large variety of adsorption selectivities and pore sizes. Differences in the partial charges of MOF atoms led to different gas loadings and hence differences in calculated self-diffusivities and permeabilities of gases. Gas loadings obtained at the feed side of the membrane from the GCMC simulations, self-diffusivities of gases computed using EMD simulations, adsorption, diffusion and membrane selectivities of MOFs calculated using Qeq and DDEC charges are all given in Table S3.† We first compared CO₂ and CH₄ permeability obtained using different charge methods at a feed pressure of 1 bar, the permeate pressure of vacuum for the 10/90 CO₂/CH₄ mixture. The CO₂ permeability predictions of DDEC-charged MOFs, 4 × 10⁴–2 × 10⁶ Barrer, were similar to those of Qeq-charged MOFs, 3 × 10⁴–2 × 10⁶ Barrer, leading to a high R² of 0.9 as shown in Fig. 5(a). DDEC-charged MOFs were calculated to have CH₄ permeabilities of 3 × 10³–5 × 10⁵ Barrer while Qeq-charged MOFs were computed to have CH₄ permeabilities in the range of 3 × 10²–1 × 10⁶ Barrer, leading to a lower R² of 0.6. Considerably higher CH₄ permeabilities predicted by DDEC charges can be discussed with an example MOF, CAZGIT. Although the difference between the largest charges assigned by the two methods was small, the adsorbed CO₂ (CH₄) amount on Qeq-charged CAZGIT was higher (lower) than that on DDEC-charged MOF as shown in Table S3.† Due to the higher amount of total gas loading in the Qeq-charged MOF, self-diffusivities for both gases were computed to be an order of magnitude lower than those computed for the DDEC-charged MOF, resulting in gas permeabilities lower than the ones computed by using DDEC charges.

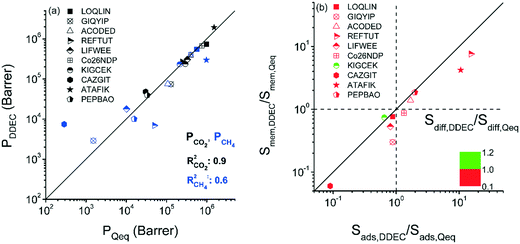Fig. 5 (a) Comparison of gas permeabilities of DDEC-charged MOFs with those of Qeq-charged MOFs. (b) Comparison of adsorption, diffusion and membrane selectivities of MOFs based on the charge method.

We finally investigated how the adsorption, diffusion and membrane selectivities of MOFs would change based on the charge method used in molecular simulations. The ratios of adsorption selectivities (S_ads,DDEC/S_ads,Qeq), diffusion selectivities (S_diff,DDEC/S_diff,Qeq), and membrane selectivities (S_mem,DDEC/S_mem,Qeq) computed with DDEC charges to the ones computed with Qeq charges are presented in Fig. 5(b). For all MOFs, S_mem,DDEC/S_mem,Qeq values depend on S_ads,DDEC/S_ads,Qeq values. For 7 MOFs, S_ads,DDEC/S_ads,Qeq values were close to 1 (0.65–1.98) and S_mem,DDEC/S_mem,Qeq values (0.30–1.86) were close to S_ads,DDEC/S_ads,Qeq values. There was a MOF, GIQYIP, for which the S_mem,DDEC/S_mem,Qeq value was calculated to be much lower than S_ads,DDEC/S_ads,Qeq. GIQYIP was computed to have higher CO₂ loading when Qeq charges were used and the diffusivity of CH₄ molecules was hindered due to its narrow pores, 3.91 Å. The difference between CH₄ diffusivities in DDEC- and Qeq-charged GIQYIP led to a very low S_diff,DDEC/S_diff,Qeq value (0.37) and eventually low S_mem,DDEC/S_mem,Qeq (0.30). LOQLIN was computed to have a similar S_ads,DDEC/S_ads,Qeq value with GIQYIP, however the membrane selectivity of the former did not notably change based on the charge method due to its large pores (13.93 Å). Gas loading and diffusivities were not significantly affected from the charge method for MOFs having large pores as previously shown in Fig. 4. For the other 3 MOFs, S_ads,DDEC/S_ads,Qeq values were significantly different than 1 which directly affected their S_mem,DDEC/S_mem,Qeq values. For example, the S_ads,DDEC/S_ads,Qeq and S_mem,DDEC/S_mem,Qeq values of REFTUT were calculated to be 15.34 and 7.60, respectively, which can be explained by the difference of the partial charges assigned by DDEC and Qeq methods to Zn atoms. Overall, it can be concluded that unless a MOF has narrow pore sizes and charges that were very differently assigned by DDEC and Qeq methods, the predicted gas permeability and membrane selectivity of that MOF using these two methods would be close to each other. We note that only 10 MOF membranes were considered in this work and studying a larger set of MOFs might provide more insights.

In this work, we aimed to understand the impact of the charge assignment method used in molecular simulations on the predicted adsorbent and membrane performance metrics of MOFs. For this aim, we used a computation-ready MOF database where crystal structures of the solvent-free MOFs mimicking the experimental activation process are directly ready to be used in molecular simulation.²¹ It is important to note that MOFs in computation ready databases might not be stable after the solvent removal and/or there might be structural problems such as missing hydrogen atoms, extra framework ions etc. as discussed in detail in our recent work.⁵⁰ We also note that the MOFs we examined in this work were limited with the ones for which DDEC charges were currently available in the literature. A final point to note is that we focused on a gas mixture where one component has a quadrupole moment, CO₂, whereas the other was nonpolar, CH₄. We believe that examining the role of charge methods used in molecular simulations for separation of a binary mixture where both components are polar, such as CO₂/H₂O, having electrostatic interactions with the MOF atoms will be interesting for future studies.

4. Conclusion

In this work, we performed a high-throughput computational screening of MOFs for CO₂/CH₄ separation using two different charge methods. The performance metrics of MOF adsorbents and membranes obtained from DDEC-charged and Qeq-charged MOFs were compared under two different operating conditions to assess the role of the charge method used in molecular simulation in predicting the CO₂ separation potential of MOFs. Results showed that the calculated CO₂ and CH₄ uptakes, CO₂ working capacities, CO₂/CH₄ selectivities, APSs, and R% of MOFs significantly alter depending on the charge method used in molecular simulations. We then ranked the MOFs based on each metric and examined the correlation between the DDEC-charged and Qeq-charged MOF rankings. Results showed that there is a high correlation between the rankings of MOFs but the best-performing MOF adsorbents identified by DDEC and Qeq methods are different. Effects of the charge method on the gas diffusivity, gas permeability and membrane selectivity of materials were also tested on a smaller set of MOF membranes and results suggested that charge methods predicted similar separation performances unless the pore size of the MOF is very narrow. Based on these results, we concluded that an approximate partial charge assignment method such as Qeq can be used to screen large numbers of MOFs in a time-efficient manner to narrow down the number of promising materials for a target application but ultimate identification of top performing materials requires using a more accurate charge assignment method like DDEC.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. K. acknowledges the ERC-2017-Starting Grant. This study has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-2017-Starting Grant, grant agreement no. 756489-COSMOS).

References

1. E. Braun, A. F. Zurhelle, W. Thijssen, S. K. Schnell, L.-C. Lin, J. Kim, J. A. Thompson and B. Smit, Mol. Syst. Des. Eng., 2016, 1, 175–188.
2. A. I. Papadopoulos, S. Badr, A. Chremos, E. Forte, T. Zarogiannis, P. Seferlis, S. Papadokonstantakis, A. Galindo, G. Jackson and C. S. Adjiman, Mol. Syst. Des. Eng., 2016, 1, 313–334.
3. D. Danaci, M. Bui, N. Mac Dowell and C. Petit, Mol. Syst. Des. Eng., 2020 10.1039/c9me00102f , Advance Article.
4. P. Müller, B. Bucior, G. Tuci, L. Luconi, J. Getzschmann, S. Kaskel, R. Q. Snurr, G. Giambastiani and A. Rossin, Mol. Syst. Des. Eng., 2019, 4, 1000–1013.
5. B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174.
6. Z. Qiao, A. K. Cheetham and J. Jiang, Mol. Syst. Des. Eng., 2019, 4, 609–615.
7. A. Sturluson, M. T. Huynh, A. R. Kaija, C. Laird, S. Yoon, F. Hou, Z. Feng, C. E. Wilmer, Y. J. Colón and Y. G. Chung, Mol. Simul., 2019, 45, 1082–1121.
8. J. Jiang, Curr. Opin. Green Sustain. Chem., 2019, 16, 57–64.
9. H. Demir, C. J. Cramer and J. I. Siepmann, Mol. Syst. Des. Eng., 2019, 4, 1125–1135.
10. I. Erucar, T. A. Manz and S. Keskin, Mol. Simul., 2014, 40, 557–570.
11. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
12. C. Campañá, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878.
13. T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468.
14. A. K. Rappe and W. A. Goddard III, J. Phys. Chem., 1991, 95, 3358–3363.
15. E. Haldoupis, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2012, 134, 4313–4323.
16. C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511.
17. E. S. Kadantsev, P. G. Boyd, T. D. Daff and T. K. Woo, J. Phys. Chem. Lett., 2013, 4, 3056–3061.
18. B. A. Wells, C. De Bruin-Dickason and A. L. Chaffee, J. Phys. Chem. C, 2015, 119, 456–466.
19. D. Ongari, P. G. Boyd, O. Kadioglu, A. K. Mace, S. Keskin and B. Smit, J. Chem. Theory Comput., 2018, 15, 382–401.
20. C. E. Wilmer and R. Q. Snurr, Chem. Eng. J., 2011, 171, 775–781.
21. D. Nazarian, J. S. Camp and D. S. Sholl, Chem. Mater., 2016, 28, 785–793.
22. W. Li, Z. Rao, Y. G. Chung and S. Li, ChemistrySelect, 2017, 2, 9458–9465.
23. S. P. Collins and T. K. Woo, J. Phys. Chem. C, 2017, 121, 903–910.
24. T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867.
25. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141.
26. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101.
27. M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577.
28. J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682.
29. M. K. Rana, H. S. Koh, H. Zuberi and D. J. Siegel, J. Phys. Chem. C, 2014, 118, 2929–2942.
30. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
31. K. B. Sezginel, A. Uzun and S. Keskin, Chem. Eng. Sci., 2015, 124, 125–134.
32. C. Altintas, G. Avci, H. Daglar, A. Nemati Vesali Azar, S. Velioglu, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 17257–17268.
33. Z. Sumer and S. Keskin, Ind. Eng. Chem. Res., 2016, 55, 10404–10419.
34. P. P. Ewald, Ann. Phys., 1921, 369, 253–287.
35. M. E. Tuckerman, J. Alejandre, R. López-Rendón, A. L. Jochim and G. J. Martyna, J. Phys. A: Math. Theor., 2006, 39, 5629–5651.
36. A. Einstein, Investigations on the Theory of the Brownian Movement, Courier Corporation, 1956.
37. B. Arstad, H. Fjellvåg, K. O. Kongshaug, O. Swang and R. Blom, Adsorption, 2008, 14, 755–762.
38. L. Du, Z. Lu, K. Zheng, J. Wang, X. Zheng, Y. Pan, X. You and J. Bai, J. Am. Chem. Soc., 2012, 135, 562–565.
39. M. Wriedt, J. P. Sculley, A. A. Yakovenko, Y. Ma, G. J. Halder, P. B. Balbuena and H. C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 9804–9808.
40. A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998–17999.
41. S. Xiang, Y. He, Z. Zhang, H. Wu, W. Zhou, R. Krishna and B. Chen, Nat. Commun., 2012, 3, 954–962.
42. P. Aprea, D. Caputo, N. Gargiulo, F. Iucolano and F. Pepe, Inorg. Chem., 2010, 55, 3655–3661.
43. A. Ö. Yazaydın, R. Q. Snurr, T.-H. Park, K. Koh, J. Liu, M. D. LeVan, A. I. Benin, P. Jakubczak, M. Lanuza and D. B. Galloway, J. Am. Chem. Soc., 2009, 131, 18198–18199.
44. C. Zheng, D. Liu, Q. Yang, C. Zhong and J. Mi, Ind. Eng. Chem. Res., 2009, 48, 10479–10484.
45. Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, Sci. Adv., 2016, 2, e1600909.
46. C. Altintas, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 3668–3679.
47. T. E. Rufford, S. Smart, G. C. Y. Watson, B. F. Graham, J. Boxall, J. C. Diniz da Costa and E. F. May, J. Pet. Sci. Eng., 2012, 94–95, 123–154.
48. M. Z. Aghaji, M. Fernandez, P. G. Boyd, T. D. Daff and T. K. Woo, Eur. J. Inorg. Chem., 2016, 2016, 4505–4511.
49. C. Altintas and S. Keskin, ACS Sustainable Chem. Eng., 2018, 7, 2739–2750.
50. C. Altintas, G. Avci, H. Daglar, A. N. V. Azar, I. Erucar, S. Velioglu and S. Keskin, J. Mater. Chem. A, 2019, 7, 9593–9608.

---

Footnote

† Electronic supplementary information (ESI) available: Potentials used for gas molecules in molecular simulations; comparison of the experimental CO₂ uptakes with the simulation results; comparison of CO₂ and CH₄ uptakes obtained from simulations using Qeq and DDEC charges for the 50/50 CO₂/CH₄ mixture; data of calculated adsorbent performance evaluation metrics computed under PSA and VSA conditions using DDEC and Qeq charges; comparison of adsorbent performance evaluation metrics using DDEC and Qeq charges; gas uptake ratios of DDEC-charged and Qeq-charged MOFs with respect to their PLD values, data for adsorption and diffusion of CO₂ and CH₄ molecules in DDEC and Qeq-charged MOFs; predicted adsorption, diffusion and membrane selectivities. See DOI: 10.1039/c9me00163h

---