Engineering porous two-dimensional lattices via self-assembly of non-convex hexagonal platelets
Nikoletta
Pakalidou
,
Junju
Mu
 ,
Andrew J.
Masters
,
Andrew J.
Masters
 and
Carlos
Avendaño
and
Carlos
Avendaño
 *
*
Department of Chemical Engineering and Analytical Science, The University of Manchester, Oxford Rd, Manchester, M13 9PL, UK. E-mail: carlos.avendano@manchester.ac.uk; Tel: +44 (0) 1613062732
First published on 5th December 2019
Abstract
In this work, a molecular-dynamics simulation study of the formation of ordered two-dimensional porous structures is presented. The structures are formed by the self-assembly of non-convex hexagonal platelets confined in a plane. By designing the interparticle interaction, a variety of structures are observed. For purely repulsive particles, the system forms a striped crystalline structure with the pmg symmetry group, which also corresponds to its close-packed structure. As the attractive interactions between the edges are turned on, the edges of close neighbours start to align (pair), but due to the non-convex shape of the platelets, only three out of six edges can be paired although there is no preference as to which particular three edges these might be. This geometric constraint promotes the formation of an unusual porous hexagonal phase with a long-range translational order but a short-range offset rotational displacement disorder in which three types of regular and irregular hexagonal pores are formed. The formation of the three hexagonal pore shapes is due to the energetic degeneracy of the three configurations. Finally, we show that when the attractive non-convex hexagonal platelets are functionalized with oligomeric chains tethered to the three main vertices of the particles, a porous hexagonal phase with the p6(632) symmetry is formed in which chiral symmetry breaking is observed despite the particles being achiral. As this functionalized platelet model does not favour one enantiomer over the other, grains with different chiral symmetries are formed, but eventually when an imbalance of the enantiomeric population takes place, a single chiral structure is formed in a similar way to that in the Viedma ripening effect.
Design, System, ApplicationThe design of two-dimensional porous ordered structures via the self-assembly of non-spherical colloidal particles is studied using molecular-dynamics simulation. The particle shape corresponds to non-convex hexagonal platelets, and the shape has been designed to promote the alignment of the particle edges with the intrinsic constraint that only three out of six edges can interact with the nearest neighbors. This geometric constraint allows the design of regular pore shapes that can be further controlled by functionalization of the surface of the particles by adding flexible functional groups. The overall effect is the design of porous and chiral structures with a long-range order using simple achiral colloidal building blocks that can be synthesized with current experimental techniques. The design of such porous materials can be used in the near future in applications such as superhydrophobic materials, antireflective coatings, and host–guest systems for macromolecules. |
1 Introduction
The design of two-dimensional (2D) ordered nanoporous networks, with pore sizes between 1 and 10 nm, has received significant attention in supramolecular chemistry due to their current and potential applications in areas such as guest molecule adsorption and immobilization of functional guest molecules in spatially ordered arrangements,1–4 enantioselective adsorption,5 fabrication of hyperthin membranes,6 sensory devices and substrate-specific tailor-made catalysts.7 These systems are typically formed at liquid/solid interfaces where the regular and open structures formed by certain molecules allow the exposure of actives sites on the substrate selectively on the nanoscale.5,8Analogous 2D ordered porous systems on the mesoscale exhibit different properties than their molecular-based counterparts as the large size of the pores and their morphologies make them ideal systems for applications such as in gas sensing,9 superhydrophobic structures,10,11 supports for the growth of organic films and semiconductors,12 antireflective coatings,13 and photonic materials.14 Fabrication of 2D mesoscopic ordered porous materials is difficult to achieve using molecular building blocks and indirect approaches are typically used for their fabrication. These experimental methods include lithography15,16 and template-assisted techniques where arrays of colloidal particles, typically of spherical shape, are inverted by backfilling in the interstitial space by a matrix followed by the removal of the original template.9 These techniques allow good control of the porous structure but they are limited with respect to the morphologies that can be designed. An alternative and more direct approach is the fabrication of mesoporous 2D systems from the self-assembly of colloidal building blocks. Colloidal particles are versatile model systems used to study phenomena such as phase transition, crystallization kinetics, collective dynamics, etc.17 due to both their large size that allows one to observe them using real-space imaging and the ability to control the interparticle interactions by controlling the properties of both the particle surface (surface charge, functional groups, tethered ligands, etc.) and the continuous media.18,19 Most cases of the self-assembly of 2D colloidal structures are those that promote the formation of close-packed structures. However, some novel techniques have been developed to target 2D porous structures including colloidal deposition mediated by electrostatic and capillary forces20 and colloidal particles with directional forces.21–26
Self-assembly of particles with non-convex shapes has also been used for the design and fabrication of highly open structures as in most cases their shapes, even at their most efficient possible packing attained, hinder the formation of closed-packed structures.27–29 For example, ring-shaped30–35 wireframe,36 and branched particles37–40 exhibit the formation of three- and quasi-two-dimensional highly open porous structures when the particle geometry is highly non-convex. Examples of non-convex particles confined in 2D have also been studied experimentally and in simulations.28,41–46
In this work, a generic coarse-grained model of non-convex hexagonal platelets is used to study the effects of both non-convexity of the particles and interparticle interactions on the phase behaviour of the structures, with particular emphasis on targeting well-defined porous ordered structures.
2 Particle model and simulation details
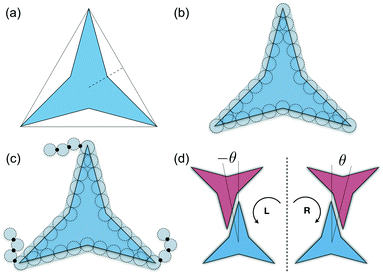
A simple coarse-grained (CG) particle model is used to represent the non-convex colloidal platelets as shown in Fig. 1. The non-convex feature of the particles is added to the system by shifting the centre of each side of an equilateral triangle towards the centre of mass by a distance equivalent to half the apothem as illustrated in Fig. 1(a). For the simulations, we use a generic model in which the particles are represented as rigid ensembles of tangent spherical beads of diameter σ as depicted in Fig. 1(b). Note that the cavity of the particles is not relevant in 2D simulations so the model represents a solid platelet. This multi-site particle model is chosen as it allows one to change efficiently the nature of the colloidal interactions by tuning the interaction parameters of each bead, instead of modelling effective interparticle interactions that depend on the distance and mutual orientations between a pair of particles which, most of the time, has to be tabulated or approximated analytically.47,48 The site–site interaction between the spherical beads is modelled using the truncated and shifted Lennard-Jones (LJ) potential given by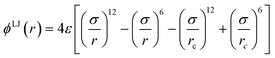 | (1) |
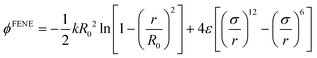 | (2) |
Molecular-dynamics (MD) simulations are used to study the phase behaviour and self-assembly of the three particle interaction models. A total of N platelets are confined in a rectangular area A of dimensions A = LxLy under periodic boundary conditions in the x and y directions. Thermodynamic properties are expressed in dimensionless units using LJ parameters where the temperature, density, packing fraction, pressure, and time are given by: T* = kBT/ε, ρ* = Nls2/A, η = NAp/A, p* = pls2/ε, and t* = t/(mσ2/ε)1/2, respectively, where T is the absolute temperature, kB is Boltzmann's constant, ls is the length of each side of the particles that in this study corresponds to ls = 5σ (see Fig. 1(b)), Ap is the area of the convex envelop of each particle that in this case is approximately Ap = 36.3σ2, p is the absolute pressure, and m is the mass of the spherical beads.
The simulations are carried out in the NVT and NPT ensembles using a time step of Δt* = 0.005. Temperature and pressure are controlled via Nosé–Hoover dynamics.51–53 The integration of the equations of motion is solved using rigid body dynamics. All simulations are performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) package.54
The formation of ordered phases is analysed using different order parameters. The l-fold symmetry of the self-assembled structures is obtained using bond-order parameter Ψl given by55–57
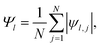 | (3) |
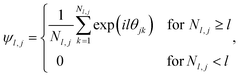 | (4) |
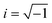 , Nl,j is the number of l nearest neighbours of particle j, and θjk is the angle made by the bond between particle j and its nearest neighbour k with respect to an arbitrary axis. The values of the bond-order parameter using Nl,j nearest neighbours rather than using all nearest neighbours calculated via Voronoi tessellation allow a better signature of the phase transition in our simulations due to the various defects observed in the crystals, the low symmetry of the particles, and the thermal fluctuations of the particles that cause deviations of their positions with respect to the perfect lattice arrangement.58,59 The nearest neighbours are determined using a cut-off distance of rc = 1.5R, where R is the radius of the circumscribed circle of the platelets. The orientation order of the system is analysed using m-fold global orientational order parameters given by
, Nl,j is the number of l nearest neighbours of particle j, and θjk is the angle made by the bond between particle j and its nearest neighbour k with respect to an arbitrary axis. The values of the bond-order parameter using Nl,j nearest neighbours rather than using all nearest neighbours calculated via Voronoi tessellation allow a better signature of the phase transition in our simulations due to the various defects observed in the crystals, the low symmetry of the particles, and the thermal fluctuations of the particles that cause deviations of their positions with respect to the perfect lattice arrangement.58,59 The nearest neighbours are determined using a cut-off distance of rc = 1.5R, where R is the radius of the circumscribed circle of the platelets. The orientation order of the system is analysed using m-fold global orientational order parameters given by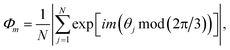 | (5) |
Chiral symmetry breaking is analysed using the following chiral order parameter Xc
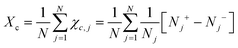 | (6) |
3 Results
3.1 Soft-repulsive non-convex hexagonal platelets
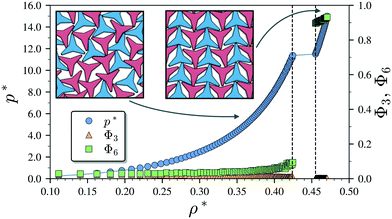
We begin by describing the results for the soft-repulsive model of non-convex triangular platelets (NCTPs), which are shown in Fig. 2. Molecular-dynamics simulation in the NPT ensemble is used to determine the equation of state (EoS) and structural behaviour of the particles. A constant temperature of T* = 1.25 is used in all simulation for this model to approximate the hard-sphere limit of the WCA potential.61,62 On sequential compression starting from a low-density state, the system exhibits a strong first-order phase transition from an isotropic state (ρ* = 0.425, η = 0.617, Φ3 = 0.009, Φ6 = 0.094) to a striped crystal structure with the pmg group symmetry63 (ρ* = 0.455, η = 0.661, Φ3 = 0.003, Φ6 = 0.897) at a pressure of P* ∼ 11.4. The crystal structure shows negligible values of the orientational order parameter Φ3 but large Φ6 values indicate that the particles can adopt either of two opposite orientations. Snapshots of representative configuration for both isotropic and crystal phases are also shown in Fig. 2. Despite the formation of a close-packed structure, the non-convex shape of these non-space filling particles prevents the tessellation of the space, that in this case is reflected on low values of the packing fraction in the order of η ∼ 2/3, which is contrary to the situation of perfect triangular platelets where particles can fill the entire space,64i.e. η ∼ 1. However, the empty space between particles, i.e. the pores, is extremely long and narrow.3.2 Attractive non-convex hexagonal platelets
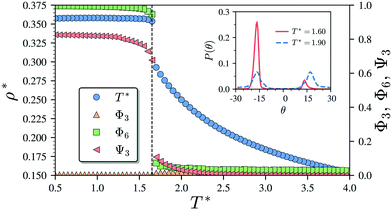
Having characterised the phase behaviour of the soft-repulsive model of NCTPs, we proceed to analyse the effect that attractive interactions have on the phase behaviour of particles. In this model, the spherical beads comprising each particle interact via the LJ potential. Since the particles tend to organise in a similar way to that in the case of the soft-repulsive model at high pressures, the phase behaviour of attractive NCTPs is therefore characterised using NPT MD simulations at a relatively low pressure, which in this case is set to P* = 1.25. As in the case of patchy particles,23 low pressures should promote the formation of open (porous) structures as the temperature is reduced due to the alignment of neighbouring particle edges. The results for attractive NCTPs are shown in Fig. 3. Sequential cooling of the system from a high temperature state results in a strong first-order phase transition from an isotropic state (ρ* = 0.293, η = 0.425, Ψ3 = 0.012, Φ3 = 0.014, and Φ6 = 0.072) to a solid state (ρ* = 0.353, η = 0.514, Ψ3 = 0.677, Φ3 = 0.004, and Φ6 = 0.947) at a temperature T* ∼ 1.675. A representative configuration of the solid structure formed by this system is shown in Fig. 4, where the very low packing fractions of the structures with values in the order of η ∼ 1/2 are evident. This structure shows remarkable differences in the crystal structure formed by the repulsive platelet model. First, the structure factor shown in the inset on the left-hand side of Fig. 4, which is calculated as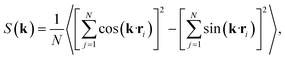 | (7) |
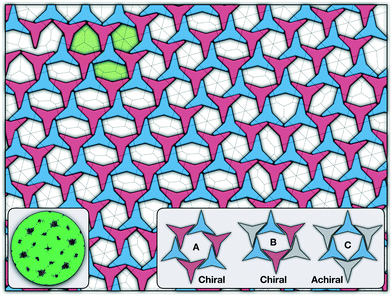
There are two additional geometrical features observed in this quasi-ordered porous structure. First, the analysis of the distribution of angular displacement, shown in the inset in Fig. 3, suggests that the majority of the particle adopt negative θ values which indicates that the pores of type A are the most recurrent in the structure. Since the structure formed in a single crystal with no grain boundaries, the small but non-negligible peak centred at θ = 15° indicates that the pores of type B are also present in the system. The second geometrical feature emerges from the chiral constraint which in a single crystal, it is not possible to observe mixed populations of the pores of type A with different chiralities, i.e. either right or left handed pores of type A are observed in a single crystal (or nucleus), and the same applies with the pores of type B. For example, in the configuration shown in Fig. 4, only the pores of types A and B shown in the inset are observed throughout the structure, but the mirror images of these pores are not present due to geometrical frustration. Since the phase transition is strongly first order, it is observed that when two nuclei of different chiralities are formed in the supercooled state, a grain boundary is formed when these two nuclei grow and meet. The lack of control of the chirality population of the pores is due to the intrinsic lack of chirality of the particles.
3.3 Attractive non-convex hexagonal platelets with tethered functional chains
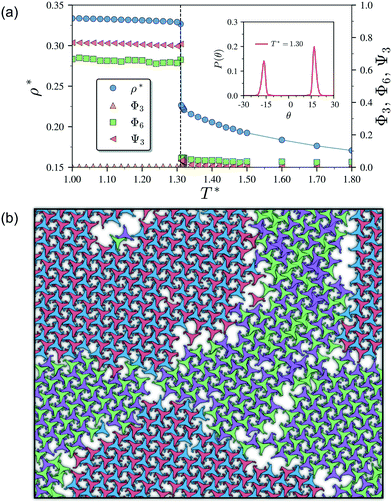
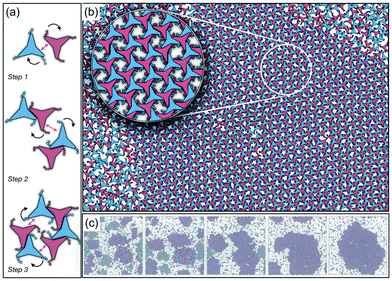
As it has already been discussed in the previous section, interacting NCTPs form crystalline structures with a short-range offset angular displacement disorder due to the degeneracy of the ground states of particle clusters forming the pores. An alternative approach to remove the degeneracy of the hexagonal pores is by introducing functional groups that ensures that once the edge of a particle aligns with another particle, then the adjacent edge is protected due to steric effects. In this way, only the pores of type A are allowed to form. For this purpose, we have explored the influence of flexible chains tethered to the three main vertices of the particles. This model is shown in Fig. 1(c). The results for the 3-membered chain system are presented in Fig. 5(a). Sequential cooling of the system from a high temperature state results in a strong first-order phase transition from an isotropic state (ρ* = 0.2227, η = 0.329, Ψ3 = 0.042, Φ3 = 0.015, and Φ6 = 0.054) to a hexagonal crystalline state with the p6(632) symmetry (ρ* = 0.327, η = 0.474, Ψ3 = 0.760, Φ3 = 0.005, and Φ6 = 0.663) at a temperature of T* ∼ 1.311. A representative configuration of the hexagonal crystal structure formed by this system is shown in Fig. 5(b). As in the case of the attractive model of NCTPs, the solid structure exhibits large values of both the bond-order parameter Ψ3 and the orientational order parameter Φ6 indicating that a hexagonal phase with particles oriented along two opposite directions is formed.A closer inspection of the structure shown in Fig. 5(b) reveals the formation of an open porous structure, as in the case of the structure formed by the attractive platelet model described previously (cf.Fig. 4), but with the main difference that the functional chains promote the formation of long-range ordered porous structures comprising only the pores of type A, i.e. regular hexagonal pores. Since the pores of type A possess the largest area among the three types of pores, the structures observed for this system have a lower packing fraction (η < 0.5) than those observed in attractive platelets without tethered chains. The formation mechanism of a unique pore type is due to a cooperative effect involving the angular displacement of the functional chains of the particles with respect to the particle symmetry axes on either the clockwise or anticlockwise direction that confer protective steric effects of the edges. In other words, for two edges to interact, the nearest chains must rotate in the opposite directions to their alignment axes to allow maximum edge alignment thus allowing the formation of chiral dimers as depicted in the first step of Fig. 6(a). Within a dimer, the chains now prevent their adjacent edges from interacting with other particle edges due to steric effects, thus imposing the conditions that only alternating edges within a particle can be paired with other particle edges, which is a necessary condition for the formation of the pores of type A. Once two dimers of the same chirality meet, a pore starts to form as shown in step 2 of Fig. 6(a). Note that two dimers of opposite chirality, which are responsible for the formation of the pores of type B in the attractive platelet model, are not allowed to interact in this functionalized model as there is no chiral compatibility due to steric effects. Finally, a third dimer can close the loop forming a pore of type A.
As in the case of the repulsive NCTPs, the phase transition is strongly first order at the transition temperature. Nuclei of opposite chirality grow independently in different parts of the system and once they reach a critical size, crystal grains grow and meet. The probability distribution of the offset angular displacement θ shown in the inset in Fig. 5(a) exhibits two peaks centred at approximately ±17° of similar intensity, which is due to the formation of an almost equal number of crystal grains of opposite chirality. These different grains are shown with different colours in Fig. 5(b).
It is indeed striking that the combined effect of particle geometry, which prevents the efficient packing of the system, and the functional chains, which prevent two adjacent edges of a particle from interacting with other particle edges, results in chiral interactions despite the particles being achiral. In other words, each new particle in solution transferred to the crystal formed detects the correct orientation which the functional chains must adopt in order to fit into the crystal structure.
In order to observe the crystallisation of a single chiral structure, the direct coexistence method has been used to ensure the formation of a liquid/solid interface in which the crystal can grow as the temperature is varied. Simulations are performed in the NVT ensemble in a system comprising N = 4096 platelets in a rectangular box at a constant density lying within the coexistence region obtained from the NPT simulation at pressure P* = 0.05 (cf.Fig. 5). The selected density is ρ* = 0.319, which is close to the density of the solid state. Due to the steepness of the fluid–solid coexistence, the selected density is within the coexistence region over a relatively wide range of temperatures. In this case, the simulations were first equilibrated at a high temperature to ensure an isotropic state followed by quenching of the system to a temperature value of T* = 1.8. The system immediately forms enantiomeric crystal grains since the particles do not have preference for one or the other enantiomer. By running the simulations long enough, typically after 107 time steps, the population of enantiomers is unbalanced, in this case towards clusters with anticlockwise angular displacements, and a single chiral crystal dominates akin to the so-called Viedma ripening effect.66 A representative configuration of the crystal structure in coexistence with its fluid phase is shown in Fig. 6(b) where it is clear that a single chiral structure anticlockwise offset angular displacement is formed, i.e. the system exhibits chiral symmetry breaking. The dominance of single chiral crystals is particularly easy to achieve at high temperatures, such as T* = 1.8, since crystal nuclei can easily reconfigure to promote the unbalance of enantiomeric species. The ripening of the enantiomeric system is illustrated in Fig. 6(c). At the beginning, it is clear that upon quenching, the systems form small grains of different chiralities, with anticlockwise enantiomers being slightly more predominant (61%), but as the simulation evolves, all clockwise nuclei melt and reconfigure to allow the formation of a single chiral crystal phase.
4 Conclusions
In this work a molecular-dynamics simulation study of the self-assembly of non-convex hexagonal platelets has been presented. As synthesis of these non-convex platelet particles can be achieved using experimental techniques such as soft lithography,60,67,68 the results reported in this work can be used for the design of experimental 2D porous structures. When the particles interact purely via repulsive interactions, the system exhibits a first-order phase transition from an isotropic state to a striped crystal phase with the pgm group symmetry, similar to those structures previously reported for curved triangular platelets.28,45 The crystal structures for this repulsive system exhibit a packing fraction in the order of η ∼ 2/3, which is considerably lower than those observed in crystals of perfect triangular platelets that can achieve packing fractions in the order of η ∼ 1. As the attractive interparticle interactions are turned on in the model, the system exhibits the formation of a highly open (porous) monolayer, with a packing fraction of approximately η ∼ 1/2, and an unusual long-range translational order, as revealed by the signature hexagonal pattern of the structure factor, and a short-range offset rotational displacement disorder, as demonstrated by the two distinct peaks in the probability distribution function P(θ), that promotes the formation of three types of regular and irregular hexagonal pores. The formation of these three pore structures is due to the energetic degeneracy of the three configurations. Moreover, it is also observed that only the pores of types A and B (see Fig. 4) with similar chirality can coexist in the same crystal, with their mirror images being forbidden to form in the structure due to geometric frustration.Finally, we have shown that the incorporation of flexible chains tethered to the three main vertices of the attractive platelet model completely disrupts the formation of the pores of types B and C thus promoting the formation of a porous hexagonal crystal with the p6(632) group symmetry that exhibits chiral symmetry breaking and packing fractions η < 1/2 due to the pores of type A having the largest area among the three types of pores. This chiral symmetry breaking phenomenon appears due to the steric effect caused by the chains in preventing two adjacent edges of a given particle to pair with neighbouring edges of the nearest neighbours. When the simulations are repeated over larger systems, the system exhibits the formation of multiple crystal nuclei with different chiralities, but upon running the simulations long enough, only one single chiral crystal is obtained in a process akin to the so-called Viedma ripening effect.
Since the self-assembled structures obtained from the attractive models have regular pore distributions, the structures can be used for applications such as separation of nanobjects,69 selective adsorption and immobilisation of macromolecules and nanoparticles,70,71 and 2D photonic materials.72 Despite the interesting phase behaviour observed in this system, there are a few aspects that are left unexplored. For example, the effect of chain length and chain interaction must be studied to study a more realistic system of tethered functional groups (such as DNA) as well as the particle geometry. Moreover, the analysis of these systems in three-dimensions also needs to be addressed to understand how interparticle interaction, particle–substrate interactions, and non-convex effects affect the self-assembly process. These aspects will be the focus of future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Aurora Cruz Cabeza and Joshua D. Elliott from the University of Manchester for fruitful discussion with respect to the crystal structures. We thank the Computational Shared Facility of the University of Manchester for computing time.References
- S. J. H. Griessl, M. Lackinger, F. Jamitzky, T. Markert, M. Hietschold and W. M. Heckl, Langmuir, 2004, 20, 9403–9407 CrossRef CAS PubMed.
- T. Kudernac, S. Lei, J. A. A. W. Elemans and S. De Feyter, Chem. Soc. Rev., 2009, 38, 402–421 RSC.
- M. Pfeffermann, R. Dong, R. Graf, W. Zajaczkowski, T. Gorelik, W. Pisula, A. Narita, K. Müllen and X. Feng, J. Am. Chem. Soc., 2015, 137, 14525–14532 CrossRef CAS PubMed.
- K. Iritani, M. Ikeda, A. Yang, K. Tahara, M. Anzai, K. Hirose, S. De Feyter, J. S. Moore and Y. Tobe, Langmuir, 2018, 34, 6036–6045 CrossRef CAS PubMed.
- J. A. A. W. Elemans, S. Lei and S. De Feyter, Angew. Chem., Int. Ed., 2009, 48, 7298–7332 CrossRef CAS PubMed.
- D. H. McCullough and S. L. Regen, Chem. Commun., 2004, 2787–2791 RSC.
- J. Zhu, C. Yang, C. Lu, F. Zhang, Z. Yuan and X. Zhuang, Acc. Chem. Res., 2018, 51, 3191–3202 CrossRef CAS.
- B. Li, K. Tahara, J. Adisoejoso, W. Vanderlinden, K. S. Mali, S. De Gendt, Y. Tobe and S. De Feyter, ACS Nano, 2013, 7, 10764–10772 CrossRef CAS.
- L. Jia and W. Cai, Adv. Funct. Mater., 2010, 20, 3765–3773 CrossRef CAS.
- Y. Li, W. Cai, B. Cao, G. Duan, F. Sun, C. Li and L. Jia, Nanotechnology, 2005, 17, 238–243 CrossRef.
- P. Roach, N. J. Shirtcliffe and M. I. Newton, Soft Matter, 2008, 4, 224–240 RSC.
- B. Kang, M. Jang, Y. Chung, H. Kim, S. K. Kwak, J. H. Oh and K. Cho, Nat. Commun., 2014, 5, 4752 CrossRef CAS PubMed.
- B. Reid, A. Taylor, Y. Chen, B. Schmidt-Hansberg and S. Guldin, ACS Appl. Mater. Interfaces, 2018, 10, 10315–10321 CrossRef CAS.
- J. E. Wijnhoven and W. L. Vos, Science, 1998, 281, 802–804 CrossRef CAS.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- L. A. Connal and G. G. Qiao, Adv. Mater., 2006, 18, 3024–3028 CrossRef CAS.
- P. J. Lu and D. A. Weitz, Annu. Rev. Condens. Matter Phys., 2013, 4, 217–233 CrossRef CAS.
- U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Science, 2001, 292, 258–262 CrossRef CAS.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS.
- J. Aizenberg, P. V. Braun and P. Wiltzius, Phys. Rev. Lett., 2000, 84, 2997–3000 CrossRef CAS PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- Q. Chen, E. Diesel, J. K. Whitmer, S. C. Bae, E. Luijten and S. Granick, J. Am. Chem. Soc., 2011, 133, 7725–7727 CrossRef CAS.
- F. Romano and F. Sciortino, Soft Matter, 2011, 7, 5799 RSC.
- G.-R. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101 CrossRef PubMed.
- J. A. Millan, D. Ortiz, G. van Anders and S. C. Glotzer, ACS Nano, 2014, 8, 2918–2928 CrossRef CAS.
- C. Karner, C. Degallo and R. Bianchi, Nano Lett., 2019, 19, 7806–7815 CrossRef CAS PubMed.
- J. de Graaf, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2011, 107, 155501 CrossRef PubMed.
- S. Atkinson, Y. Jiao and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031302 CrossRef PubMed.
- C. Avendaño and F. A. Escobedo, Curr. Opin. Colloid Interface Sci., 2017, 30, 62–69 CrossRef.
- R. Gabbrielli, Y. Jiao and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022133 CrossRef PubMed.
- C. Avendaño and E. A. Müller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061702 CrossRef PubMed.
- C. Avendaño and E. A. Müller, Soft Matter, 2011, 7, 1694–1701 RSC.
- C. Avendaño, G. Jackson, E. A. Müller and F. A. Escobedo, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9699–9703 CrossRef PubMed.
- H. H. Wensink and C. Avendaño, Phys. Rev. E, 2016, 94, 062704 CrossRef CAS PubMed.
- C. Avendaño, G. Jackson and H. H. Wensink, Mol. Phys., 2018, 116, 2901–2910 CrossRef.
- J. M. McBride and C. Avendaño, Phys. Rev. Mater., 2018, 2, 055601 CrossRef CAS.
- K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij and M. Dijkstra, et al. , Nat. Mater., 2011, 10, 872–876 CrossRef CAS.
- W. Qi, J. de Graaf, F. Qiao, S. Marras, L. Manna and M. Dijkstra, J. Chem. Phys., 2013, 138, 154504 CrossRef.
- M. P. Arciniegas, M. R. Kim, J. De Graaf, R. Brescia, S. Marras, K. Miszta, M. Dijkstra, R. van Roij and L. Manna, Nano Lett., 2014, 14, 1056–1063 CrossRef CAS.
- A. Castelli, J. de Graaf, S. Marras, R. Brescia, L. Goldoni, L. Manna and M. P. Arciniegas, Nat. Commun., 2018, 9, 1141 CrossRef.
- K. Zhao and T. G. Mason, J. Phys.: Condens. Matter, 2014, 26, 152101 CrossRef PubMed.
- C. Michał and J. Barbasz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022402 CrossRef.
- P.-Y. Wang and T. G. Mason, J. Am. Chem. Soc., 2015, 137, 15308–15314 CrossRef CAS.
- E. S. Harper, R. L. Marson, J. A. Anderson, G. van Anders and S. C. Glotzer, Soft Matter, 2015, 11, 7250–7256 RSC.
- N. Pakalidou, D. L. Cheung, A. J. Masters and C. Avendaño, Soft Matter, 2017, 13, 8618–8624 RSC.
- A. D. Griffith and R. S. Hoy, Phys. Rev. E, 2018, 98, 042910 CrossRef CAS.
- P. G. Bolhuis, A. Stroobants, D. Frenkel and H. N. W. Lekkerkerker, J. Chem. Phys., 1997, 107, 1551–1564 CrossRef CAS.
- B. Martínez-Haya, A. Cuetos, S. Lago and L. F. Rull, J. Chem. Phys., 2005, 122, 024908 CrossRef PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- S. Melchionna, G. Ciccotti and B. Lee Holian, Mol. Phys., 1993, 78, 533–544 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- D. R. Nelson, Phys. Rev. B, 1979, 19, 2457–2484 CrossRef CAS.
- T. Schilling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036138 CrossRef PubMed.
- C. Avendaño and F. A. Escobedo, Soft Matter, 2012, 8, 4675 RSC.
- W. Mickel, S. C. Kapfer, G. E. Schröder-Turk and K. Mecke, J. Chem. Phys., 2013, 138, 044501 CrossRef PubMed.
- J. A. Anderson, J. Antonaglia, J. A. Millan, M. Engel and S. C. Glotzer, Phys. Rev. X, 2017, 7, 021001 Search PubMed.
- K. Zhao, R. Bruinsma and T. G. Mason, Nat. Commun., 2012, 3, 801 CrossRef.
- J. Gao and J. H. Weiner, J. Chem. Phys., 1989, 91, 3168–3173 CrossRef CAS.
- J. Jover, A. J. Haslam, A. Galindo, G. Jackson and E. A. Müller, J. Chem. Phys., 2012, 137, 144505 CrossRef CAS PubMed.
- D. Schattschneider, Am. Math. Mon., 1978, 85, 439–450 CrossRef.
- A. P. Gantapara, W. Qi and M. Dijkstra, Soft Matter, 2015, 11, 8684–8691 RSC.
- D. Ecija, S. Vijayaraghavan, W. Auwärter, S. Joshi, K. Seufert, C. Aurisicchio, D. Bonifazi and J. V. Barth, ACS Nano, 2012, 6, 4258–4265 CrossRef CAS.
- C. Viedma, Phys. Rev. Lett., 2005, 94, 065504 CrossRef.
- C. J. Hernandez and T. G. Mason, J. Phys. Chem. C, 2007, 111, 4477–4480 CrossRef CAS.
- K. Zhao, R. Bruinsma and T. G. Mason, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2684–2687 CrossRef CAS.
- J. He, X.-M. Lin, H. Chan, L. Vuković, P. Král and H. M. Jaeger, Nano Lett., 2011, 11, 2430–2435 CrossRef CAS PubMed.
- Q.-L. Zhu and Q. Xu, Chem, 2016, 1, 220–245 CAS.
- J. Zdarta, A. Meyer, T. Jesionowski and M. Pinelo, Catalysts, 2018, 8, 92 CrossRef.
- K. R. Phillips, G. T. England, S. Sunny, E. Shirman, T. Shirman, N. Vogel and J. Aizenberg, Chem. Soc. Rev., 2016, 45, 281–322 RSC.
| This journal is © The Royal Society of Chemistry 2020 |