Open Access Article
Open Access ArticleNear-room-temperature reversible giant barocaloric effects in [(CH3)4N]Mn[N3]3 hybrid perovskite†
Jorge
Salgado-Beceiro
 a,
Ariel
Nonato
a,
Ariel
Nonato
 b,
Rosivaldo Xavier
Silva
b,
Rosivaldo Xavier
Silva
 c,
Alberto
García-Fernández
c,
Alberto
García-Fernández
 a,
Manuel
Sánchez-Andújar
a,
Manuel
Sánchez-Andújar
 a,
Socorro
Castro-García
a,
Socorro
Castro-García
 a,
Enric
Stern-Taulats
a,
Enric
Stern-Taulats
 d,
María Antonia
Señarís-Rodríguez
d,
María Antonia
Señarís-Rodríguez
 *a,
Xavier
Moya
*a,
Xavier
Moya
 *d and
Juan Manuel
Bermúdez-García
*d and
Juan Manuel
Bermúdez-García
 *ad
*ad
aUniversity of A Coruna, QuiMolMat Group, Dpt. Chemistry, Faculty of Science and Advanced Scientific Research Center (CICA), Zapateira, Coruña 15071 A, Spain. E-mail: m.senaris.rodriguez@udc.es; j.bermudez@udc.es
bCoordenação de Ciências Naturais, Universidade Federal do Maranhão, Campus do Bacabal, Bacabal, 65700-000, MA, Brazil
cCoordenação de Ciências Naturais, Universidade Federal do Maranhão, Campus VII, Codó, 65400-000, MA, Brazil
dDepartment of Materials Science, University of Cambridge, Cambridge CB3 0FS, UK. E-mail: xm212@cam.ac.uk
First published on 25th September 2020
Abstract
We report giant reversible barocaloric effects in [(CH3)4N]Mn[N3]3 hybrid organic–inorganic perovskite, near its first-order cubic-monoclinic structural phase transition at T0 ∼ 305 K. When driving the transition thermally at atmospheric pressure, the transition displays a large change in entropy of ∼80 J K−1 kg−1 and a small thermal hysteresis of ∼7 K, as well as a large change in volume of ∼1.5%. When driving the transition with pressure near room temperature, the transition displays large changes in entropy of ∼70 J K−1 kg−1, which represent a giant barocaloric response. Hybrid perovskites with similar barocaloric response and lower operating temperatures may find applications in environmentally friendly cooling.
In recent years, barocaloric materials have arisen as promising solid-state replacements to commercial refrigerant fluids, which are strong volatile greenhouse contributors that are often flammable or toxic.1–3 Similarly to refrigerant fluids, barocaloric materials display large thermal changes under application and removal of hydrostatic pressure, which are typically parameterised as pressure-driven isothermal changes in entropy ΔS, or pressure-driven adiabatic changes in temperature ΔT.1 However, due to their solid nature, barocaloric materials ultimately represent an environmentally friendly cooling solution.
With this motivation, a number of materials families have been investigated for barocaloric applications, which include magnetic alloys,4–9 polymers,10 oxyflourides,11–14 ferroelectric oxides,15,16 ferrielectric salts,17 superionic conductors,18,19 plastic crystals,20–23 and hybrid organic–inorganic perovskites.24–26 The latter have the potential to operate at hydrostatic pressures that are similar to those available in commercial compressors (≤150 bar), specifically in the case of dicyanamide hybrid perovskites.24,25 Moreover, hybrid perovskites have the advantage that they can be synthesized using fast, economic, simple and escalable methods, and their chemical composition can be easily modified by using different building-blocks, which can lead to an optimization of their barocaloric parameters depending on the application of interest.26
Dicyanamide perovskites have been shown to display giant barocaloric effects only at temperatures well above room temperature (≥330 K).24,25 Here we bring the operating temperature of hybrid perovskites closer to room temperature, by demonstrating giant barocaloric effects in a [(CH3)4N]Mn[N3]3 azide perovskite at ∼310 K and above. Near its non-isochoric cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to monoclininc (P21/m) phase transition,27,28 we find pressure-driven entropy changes |ΔS| of ∼70 J K−1 kg−1 that can be driven reversibly using changes in applied pressure p of |Δp| = |p − patm| ∼ |p| ∼ 1 kbar (patm is atmospheric pressure). Our results improve upon the performance of state-of-the-art barocaloric hybrid perovskites, by increasing twofold or more the barocaloric entropy change, and decreasing operating temperatures by ∼25 K or more, at the expense of larger driving pressures.
m) to monoclininc (P21/m) phase transition,27,28 we find pressure-driven entropy changes |ΔS| of ∼70 J K−1 kg−1 that can be driven reversibly using changes in applied pressure p of |Δp| = |p − patm| ∼ |p| ∼ 1 kbar (patm is atmospheric pressure). Our results improve upon the performance of state-of-the-art barocaloric hybrid perovskites, by increasing twofold or more the barocaloric entropy change, and decreasing operating temperatures by ∼25 K or more, at the expense of larger driving pressures.
Colourless polycrystalline powders of [(CH3)4N]Mn[N3]3 were synthesised via liquid diffusion.27,28 0.5 M of NaN3 and 0.5 M of [(CH3)4N]Cl were dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of methanol
1 mixture of methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water of volume 2.5 mL, in a glass tube. The solution was then covered by 1 ml of methanol, followed by 4 ml of 0.1 M of MnCl2·4H2O (0.1 M) in methanol, and the glass tube was sealed. Polycrystalline powders [(CH3)4N]Mn[N3]3 were obtained after leaving the sealed glass tube undisturbed for three days.
water of volume 2.5 mL, in a glass tube. The solution was then covered by 1 ml of methanol, followed by 4 ml of 0.1 M of MnCl2·4H2O (0.1 M) in methanol, and the glass tube was sealed. Polycrystalline powders [(CH3)4N]Mn[N3]3 were obtained after leaving the sealed glass tube undisturbed for three days.
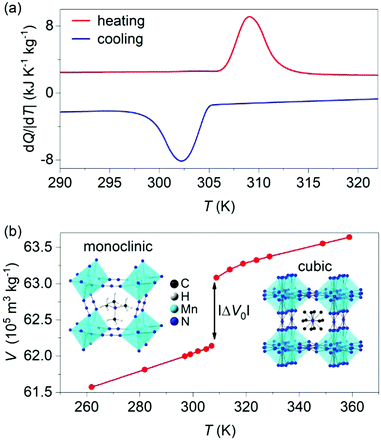
X-ray diffraction data taken on the synthesized powder at atmospheric pressure and room temperature confirmed single-phase character (Fig. S1 of ESI†). Differential scanning calorimetry at atmospheric pressure (Fig. 1a) confirmed the first-order cubic-monoclinic phase transition at Th ∼ 309 K on heating (identified using the peak in heat flow dQ/|dT|), and at Tc ∼ 302 K on cooling (identified using the peak in heat flow dQ/|dT|), with a small thermal hysteresis of ΔT = Th − Tc ∼ 7 K.
The thermally driven latent heat and entropy change for the transition (obtained via suitable integration1,2 of the peaks in heat flow dQ/|dT|) where |Q0| = 25 ± 1 kJ kg−1 and |ΔS0| = 80 ± 1 J K−1 kg−1, respectively, in good agreement with literature values.27,28
The large values of |Q0| and |ΔS0| arise primarily due to large changes in the degree of ordering27 of the nitrogen atoms within the azide ligands (N3), and of the monoclinic phase, N = exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ΔS0/R), is 12 (R is the universal gas constant). When undergoing the phase transition from the monoclinic to the cubic phase, the azide N atoms get disordered over 4 different positions and the tetramethylammonium C atoms get disorder over twelve different positions.27 This type of order–disorder phase transitions have been identified as mechanisms for potential barocaloric effects.29
(ΔS0/R), is 12 (R is the universal gas constant). When undergoing the phase transition from the monoclinic to the cubic phase, the azide N atoms get disordered over 4 different positions and the tetramethylammonium C atoms get disorder over twelve different positions.27 This type of order–disorder phase transitions have been identified as mechanisms for potential barocaloric effects.29
Variable-temperature powder X-ray diffraction data (Fig. 1b) revealed a large increase in specific volume of |ΔV0| ∼ 9.40 ± 0.03 × 10−6 m3 kg−1 on heating across the transition, which represents a relative change of ∼1.5%. The Clausius–Clapeyron equation (dT0/dp) = (ΔV0/ΔS0) returns a value of barocaloric tunability25 dT0/dp of ∼11.7 ± 0.2 K kbar−1 that is large but smaller than those obtained in dicyanamide perovskites.24,25
Variable-pressure differential scanning calorimetry (Fig. 2a) confirmed our calculated barocaloric tunability, with dTh/dp ∼ dTc/dp ∼ 12 K kbar−1 (Fig. 2b). Using these quasi-direct measurements,1 we calculated pressure-driven isothermal changes in entropy (Fig. 3) by taking the difference between thermally driven changes in entropy measured at two different pressures (Fig. S2 of ESI†). Additional changes in isothermal entropy17 that arise due to volumetric thermal expansion either side of the transition (Fig. 1a) were not considered because the coefficient of thermal expansion may decrease significantly under pressure for this compound.30 These additional changes-if taken into account-will increase the magnitude of the here presented barocaloric effect, so the values of ΔS that we present are underestimated. We found giant isothermal changes in entropy |ΔS| of ∼33 ± 1 J K−1 kg−1 that can be driven reversibly using changes in applied pressure of ∼0.7 kbar. On increasing applied pressure further, we found |ΔS| ∼ 70 ± 1 J K−1 kg−1 for |p| ∼ 1.1 kbar, which is in agreement with a previous indirect prediction.26
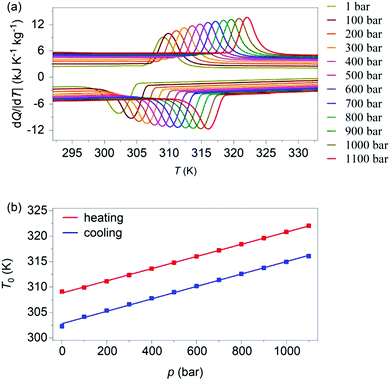 | ||
| Fig. 2 (a) Heat flow dQ/|dT| as a function of temperature, at finite applied pressures. (b) Transition temperatures versus pressure, identified using the peak in heat flow dQ/|dT|. | ||
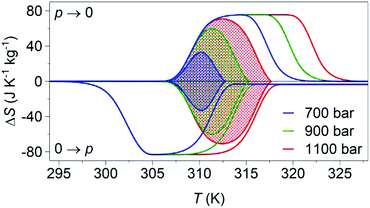 | ||
| Fig. 3 Pressure-driven isothermal changes in entropy on applying (0 → p) and removing (p → 0) selected hydrostatic pressures. Data shaded using different colours represent the reversible18 barocaloric response at different pressures. | ||
Our calculated pressure-driven changes in entropy were confirmed via direct measurements1 of barocaloric heat (Fig. 4), which are rare, as few existing calorimeters permit the application of variable pressure. At 311 K, application and removal of ∼900 bar drives reversibly our largest barocaloric entropy change of |ΔS| ∼ 70 ± 1 J K−1 kg−1 (obtained via suitable integration of the peaks in heat flow dQ/|dp|). At higher temperatures, higher pressures are required to drive the transition reversibly but |ΔS| remains nominally constant. [(CH3)4N]Mn[N3]3 improves upon the performance of [TPrA]Mn[dca]3 and [TPrA]Cd[dca]3 dicyanamide perovskites (Table 1), by increasing twofold or more the barocaloric entropy change, and decreasing operating temperatures by ∼25 K or more, at the expense of larger driving pressures.
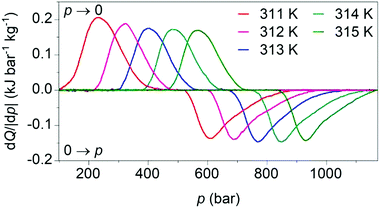 | ||
| Fig. 4 Heat flow dQ/|dp| on applying (0 → p) and removing (p → 0) hydrostatic pressure, after baseline subtraction, at different tempertures. | ||
| Barocaloric material | T 0 (K) | T h − Tc (K) | |ΔS0| (J kg−1 K−1) | |ΔV0| 10−6 m3 kg−1 | |dT0/dp| (K kbar−1) | |ΔS| (J K−1 kg−1) | Δp (bar) | Ref. | |
|---|---|---|---|---|---|---|---|---|---|
| T 0 = transition temperature averaged from the peaks maximum on heating and cooling, Th − Tc = thermal hysteresis calculated from the peaks maximum on heating and cooling, |ΔS0| = thermally driven entropy change averaged from peaks integration on heating and cooling, |ΔV0| = volume change calculated on heating, |dT0/dp| = barocaloric tunability averaged from heating and cooling, |ΔS| = reversible pressure-driven isothermal entropy change obtained by quasi-direct methods, Δp = corresponding driving pressure for |ΔS|. | |||||||||
| Hybrid | [(CH3)4N]Mn[N3]3 | 305 | 7 | 80 | 9.4 | 12 | 70 | 900 | This work |
| [TPrA]Mn[dca]3 | 330 | 0.9 | 42.5 | 10 | 23.1 | 30.5 | 70 | 24 | |
| [TPrA]Cd[dca]3 | 386 | 1.4 | 16.2 | 5.3 | 38.2 | 11.5 | 70 | 25 | |
| Organics | (CH3)2C(CH2OH)2 | 311 | 25 | 372 | 46 | 10.3 | 445 | 2500 | 20 |
| (CH3)C(CH2OH)3 | 354 | 12 | 482 | 38 | 8.7 | 490 | 2400 | 21 | |
| (CH3)3C(CH2OH) | 251 | 33 | 200.5 | 45.5 | 17 | 290 | 2600 | 21 | |
| Fullerite C60 | 257 | 3 | 26.5 | 4.6 | 17 | 42 | 4100 | 23 | |
| Inorganics | (NH4)2SO4 | 222 | 3 | 65 | 2.9 | 5.1 | 60 | 1000 | 17 |
| AgI | 420 | 24 | 64 | 7.4 | 13.4 | 60 | 2500 | 18 | |
| Fe49Rh51 | 314 | 10 | 12.5 | 1 | 5.9 | 12.5 | 2500 | 7 | |
| MnCoGeB0.03 | 290 | 18 | 47 | 5 | 10 | 30 | 1700 | 9 | |
The larger barocaloric entropy change arises due to the larger change in configurational order when driving the transition with pressure, cf. N ∼ 12 for [(CH3)4N]Mn[N3]3, whereas it is ∼8 and ∼2.6 for the Mn-dicyanamide perovskite and the Cd-dicyanamide perovskite, respectively. The lower transition temperatures may arise due to a lower Goldschmidt tolerance factor, which is close to the ideal value of 131,32 for [(CH3)4N]Mn[N3]3. The higher driving pressure is a consequence of the smaller barocaloric tunability, (dT0/dp) = (ΔV0/ΔS0), as expected for systems with similar ΔV0 but larger ΔS0. Moreover, a larger thermal hysteresis also contributes to the need of a larger driving pressure for obtaining a reversible barocaloric effect upon cycling.
On the other hand, when comparing the azide perovskite with the best barocaloric organic and/or inorganic materials up to date, this perovskite exhibits a larger reversible barocaloric effect than most of the listed materials (except polyalcohols), with the advantage of working under lower pressures (Table 1).
In the future, it will be interesting to explore multicaloric effects33 in this (and related) compounds, given that the monoclinc phase of [(CH3)4N]Mn[N3]3 is magnetic and antiferroelectric.27
Experimental methods
Caution
Azide compounds can be potentially explosive and should be handled with caution.Sample synthesis
The following chemicals were used in the synthesis, as-purchased without further purification: MnCl2·4H2O (≥98%, Aldrich), [(CH3)4N]Cl (purum ≥98%, Fluka), NaN3 (≥99%, Aldrich), and CH3OH (99.5%, Panreac).Powder X-ray diffraction
Powder X-ray diffraction at room temperature was performed using a Siemens D-5000 diffractometer, with CuKα radiation (λ = 1.5418 Å). The recorded spectra was compared with an spectra that was simulated using existing single-crystal data and Mercury 3.5.1 software.Variable-temperature powder X-ray diffraction using λ = 0.412483 Å at beamline BL04 – MSPD, Alba Synchrotron. For this experiment, ∼5 mg of [(CH3)4N][Mn(N3)3] were inserted in a borosilicate capillary of diameter ϕ = 0.5 mm, and the capillary was rotated during data collection. The recorded patterns were fitted using the Le Bail method.
Differential scanning calorimetry
Variable-pressure differential scanning calorimetry was performed using a Setaram μDSC7 EVO microcalorimeter equipped with a 260D Isco pressure pump that utilised nitrogen gas a pressure-transmitting media. Samples of ∼100 mg of [(CH3)4N][Mn(N3)3] were inserted in commercial pressure sample holders provided by Setaram and connected to the Isco pump. For quasi-direct barocaloric measurements, samples were swept in temperature at ±1.2 K min−1. For direct barocaloric measurements, the same amount of sample was swept in pressure at ±10 bar min−1.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors are grateful for financial support from Ministerio de Economía y Competitividad MINECO and EU-FEDER (MAT2017-86453-R), Xunta de Galicia (ED431G/09), FAMEPA (COOPI-07771/17), and ERC Starting Grant no. 680032. The authors acknowledge Alba Synchrotron beamline BL04 − MSPD. J. M. B. G. acknowledges Xunta de Galicia for a Postdoctoral Fellowship. X. M. and E. S. T. are grateful for support from the Royal Society.Notes and references
- X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439 CrossRef CAS.
- L. Mañosa and A. Planes, Adv. Mater., 2017, 29, 1603607 CrossRef.
- S. Crossley, N. D. Mathur and X. Moya, AIP Adv., 2015, 5, 067153 CrossRef.
- S. Yüce, M. Barrio, B. Emre, E. Stern-Taulats, A. Planes, J.-L. Tamarit, Y. Mudryk, K. A. Gschneidner Jr, V. K. Pecharsky and L. Mañosa, Appl. Phys. Lett., 2012, 101, 071906 CrossRef.
- L. Mañosa, D. González-Alonso, A. Planes, M. Barrio, J.-L. Tamarit, I. S. Titov, M. Acet, A. Bhattacharyya and S. Majumdar, Nat. Commun., 2011, 2, 595 CrossRef.
- L. Mañosa, D. González-Alonso, A. Planes, E. Bonnot, M. Barrio, J.-L. Tamarit, S. Aksoy and M. Acet, Nat. Mater., 2010, 9, 478–481 CrossRef.
- E. Stern-Taulats, A. Planes, P. Lloveras, M. Barrio, J.-L. Tamarit, S. Pramanick, S. Majumdar, C. Frontera and L. Mañosa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214105 CrossRef.
- D. Matsunami, A. Fujita, K. Takenaka and M. Kano, Nat. Mater., 2015, 14, 73–78 CrossRef CAS.
- A. Aznar, P. Lloveras, J.-Y. Kim, E. Stern-Taulats, M. Barrio, J. L. Tamarit, C. F. Sánchez-Valdés, J. L. Sánchez-Llamazares, N. D. Mathur and X. Moya, Adv. Mater., 2019, 31, 1903577 CrossRef.
- E. L. Rodriguez and F. E. Filisko, J. Appl. Phys., 1982, 53, 6536–6540 CrossRef.
- I. N. Flerov, A. V. Kartashev, M. V. Gorev, E. V. Bogdanov, S. V. Mel’nikova, M. S. Molokeev, E. I. Pogoreltsev and N. M. Laptashf, J. Fluorine Chem., 2016, 183, 1–9 CrossRef CAS.
- M. Gorev, E. Bogdanov, I. N. Flerov, A. G. Kocharova and N. M. Laptash, Phys. Solid State, 2010, 52, 167–175 CrossRef CAS.
- M. Gorev, I. N. Flerov, E. Bogdanov, V. N. Voronov and N. M. Laptash, Phys. Solid State, 2010, 52, 377–383 CrossRef CAS.
- I. N. Flerov, M. V. Gorev, A. Tressaud and N. M. Laptash, Crystallogr. Rep., 2011, 56, 9 CrossRef CAS.
- E. Stern-Taulats, P. Lloveras, M. Barrio, E. Defay, M. Egilmez, A. Planes, J.-L. Tamarit, L. Mañosa, N. D. Mathur and X. Moya, APL Mater., 2016, 4, 091102 CrossRef.
- Y. Liu, J. Wei, P.-E. Janolin, I. C. Infante, X. Lou and B. Dkhil, Appl. Phys. Lett., 2014, 104, 162904 CrossRef.
- P. Lloveras, E. Stern-Taulats, M. Barrio, J.-L. Tamarit, S. Crossley, W. Li, V. Pomjakushin, A. Planes, L. Mañosa, N. D. Mathur and X. Moya, Nat. Commun., 2015, 6, 8801 CrossRef CAS.
- A. Aznar, P. Lloveras, M. Romanini, M. Barrio, J.-L. Tamarit, C. Cazorla, D. Errandonea, N. D. Mathur, A. Planes, X. Moya and L. Mañosa, Nat. Commun., 2017, 8, 1851 CrossRef.
- J. Min, A. K. Sagotra and C. Cazorla, Phys. Rev. Mater., 2020, 4, 015403 CrossRef CAS.
- P. Lloveras, A. Aznar, M. Barrio, P. H. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko, N. D. Mathur, X. Moya and J.-L. Tamarit, Nat. Commun., 2019, 10, 1803 CrossRef CAS.
- A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. D. Mathur, X. Moya and J.-L. Tamarit, J. Mater. Chem. A, 2020, 8, 639–647 RSC.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S.-I. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS.
- J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J.-L. Tamarit and P. Lloveras, J. Mater. Chem. A, 2020 10.1039/D0TA05399F.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 15715 CrossRef.
- J. M. Bermúdez-García, S. Yáñez-Vilar, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga, M. Dilshad, X. Moya and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2018, 6, 9867 RSC.
- J. M. Bermúdez-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, J. Phys. Chem. Lett., 2017, 8, 4419 CrossRef.
- L. C. Gómez-Aguirre, B. Pato-Doldán, A. Stroppa, L. M. Yang, T. Frauenheim, J. Mira, S. Yáñez-Vilar, R. Artiaga, S. Castro-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, Chem. – Eur. J., 2016, 22, 7863–7870 CrossRef.
- F. A. Mautner, S. Hanna, R. Cortés, L. Lezama, M. G. Barandika and T. Rojo, Inorg. Chem., 2002, 38, 4647–4652 CrossRef.
- C. Cazorla, Appl. Phys. Rev., 2019, 6, 041316 Search PubMed.
- D. Walsh and P. Zoller, Standard pressure volume temperature data for polymers, CRC Press, 1995 Search PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, A. Alegría and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 11680 CrossRef.
- E. Stern-Taulats, T. Castán, L. Mañosa, A. Planes, N. D. Mathur and X. Moya, MRS Bull., 2018, 43, 295–299 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Powder X-ray diffraction spectra, isobaric entropy–temperature curves. See DOI: 10.1039/d0ma00652a |
| This journal is © The Royal Society of Chemistry 2020 |