Bioinspired self-similar all-dielectric antennas: probing the effect of secondary scattering centres by Raman spectroscopy

Abstract

All-dielectric optical antennas offer unique advantages in fabrication of highly reproducible Raman probes and light management at the meso- and nano-scale. Hot-spot engineering is a key step for enhancing the local field and promoting light channelling from far- to near-field. However, unlike the case of plasmonic antennas, hot-spot design and implementation in all-dielectric systems is still largely underdeveloped. Inspired by building-up principles that govern absorption, trapping and scattering of visible light in a variety of biological structures and guided by finite element optical simulations, here we explored the potential of self-similar dielectric optical antennas in light coupling with Mie-type modes. The systems investigated were based on the combination of primary and secondary antennas, made of micron- and nano-sized TiO₂ nanoshells. Different types of configurations, including randomly and hierarchically organized antennas were tested. Raman experiments revealed that hierarchically ordered structures offer superior SERS performances in terms of field enhancement and reproducibility in comparison to the randomly arranged counterparts, which are in turn more efficient, yet less reproducible, than simple micro-sized antennas taken as a reference. These results open the door to further investigations in view of developing next-generation platforms for SERS and photocatalysis.

---

1. Introduction

Optical antennas are intensively investigated for a wide range of applications that can take advantage of their unique capability to concentrate free-space propagating light within extremely localized spatial regions (hot-spots).¹ In particular, hot-spot engineering can remarkably enhance Raman scattering and photocatalysis in plasmonic nanostructures.^2–7

Optical antennas based on semiconductors or, in general, dielectrics, are gaining ever-increasing interest for Surface Enhanced Raman Scattering (SERS) and optical sensing, because of their multiple edges over the plasmonic counterparts in terms of low invasiveness, reproducibility and recycling.⁸ For example, SiO₂/TiO₂ core/shell (T-rex) colloids enabled plasmon-free enhanced Raman scattering, allowing chemical reactions to be monitored under real-world conditions, as well as unique multimodal detection in combination with mass spectrometry or optical sensing.^9–14 At the heart of those systems is the optical cavity obtained by alternating low-refractive index cores and high-refractive index shells, which promotes efficient light trapping and direct exploitation of morphology-dependent resonances. Our pristine study on T-rex systems demonstrated that the replacement of silica cores with air, which gives rise to TiO₂ hollow shells (T-horex), provides a systematic further enhancement of the Raman response. This effect is associated to the change of the core refractive index, which, at the wavelengths between 600 nm and 700 nm, decreases from 1.45 (SiO₂) to 1 (air), determining a consequent increase of the shell/core refractive index ratio.⁹

However, the study of non-plasmonic systems for SERS and photocatalysis is still at its infancy, making optical mode engineering very important. All the spectroscopic techniques based on microscopy (micro-Raman, micro-FTIR, micro-fluorescence…) operating through backscattering setups leverage on the efficient channelling of light from far- to near-field and vice versa. At the excitation stage, the incoming light should be collected and concentrated within subwavelength regions, maximizing its interaction with that part of substrate surface and any adsorbed molecular species (in-coupling). On the other hand, backscattering collection of the outcoming light passes through the same reverse pathway, in which the optical signal originated from near-field enhancement should be efficiently returned to the microscope objective and conveyed to the detector (out-coupling). Finding a way to optimize in-and out-coupling of light is a key step to improve the overall performance of those methods.

Biological systems offer many sources of inspiration in this regard, as most of them are organized with integrated sets of optical components that are able to collect and steer incoming and outcoming light. Animal eyes, exoskeletons and skins are only a few examples of sophisticated optical systems that have been able to solve most of the problems discussed above.^15–18 In particular, opal-made colloidal crystals and chitin spherules, which determines structural colors in many insects, offer a very simple strategy for light management that is based on the physics of photonic crystals.¹⁹ The basic units of different architectures are sub-micron spheroidal units. Playing with size, refractive index contrast, length-scale, periodicity and dimensionality, light can be selectively absorbed, emitted or reflected, giving rise to fascinating optical effects that open a variety of intriguing applications.²⁰

The combination of building blocks with identical shapes but different size results in the formation of self-similar structures, which can be either randomly or hierarchically organized.

Inspired by those biological examples, in this work we investigate the effects of combining micron- and nanosized T-horex in view of generating self-similar non-plasmonic antennas that could be applied for SERS and photocatalytic purposes.

2. Experimental

2.1. Fabrication of self-similar optical antennas

The fabrication of μm-sized TiO₂ hollow shell spheres (T-horex) utilized as primary antennas in all the experiments of this work follows the general strategy utilized to prepare SiO₂/TiO₂ core/shell T-rex and described in detail in our previous papers.⁹ Briefly, dielectric cores made of polystyrene spheres (size: 2 μm) were conformally coated with either a 100 or 120 nm thick layer of TiO₂ by Atomic Layer Deposition (ALD). Annealing at 715 °C in air for 4 h decomposes the polystyrene cores, yielding to the final hollow-shell structures. Self-similar antennas resulted from the combination of ∼2 μm-sized TiO₂ hollow shell spheres (air core size: 2 μm-sized, TiO₂ shell layer: 100 nm) with smaller (105 or 411 nm-sized) polystyrene cores spheres that were further coated with a 20 nm-thick overlayer of TiO₂. The samples were annealed at 715 °C in air for 4 h. The fabrication of randomly dispersed (M.o.S. type I and II) or hierarchically ordered (HT-horex) self-similar antennas was based on the control of concentration of small particles suspension. In particular, HT-horex were obtained by soaking T-horex in 1 wt% suspension of polystyrene spheres overnight, with subsequent deposition of TiO₂ and annealing operated as described above. 0.5 wt% suspensions of 105 or 411 nm-sized polystyrene spheres were utilized to prepare multimer-on-sphere (M.o.S.) type I and II, respectively. A more general and detailed introduction to surface relief patterns that can be achieved by the combination of binary spheres can be found in ref. 27.

2.2. SEM characterization

The scanning electron microscopy (SEM) secondary-electrons images were acquired by means of a field emission SEM LEO 1525 (ZEISS, Germany) operated at low beam voltage (3–5 kV range) without any sample preparation, in order to observe the pristine sample morphology.

2.3. Optical simulations

Optical simulations of the fields scattered by the antennas were run using finite element method implemented in the Wave Optics module of COMSOL, version 5.3a. The incident light is a plane wave propagating in the orthogonal direction with respect to the substrate normal (z-axis) and with a linearly polarized electric field. The structures are modelled exploiting their axial and rotational symmetries to reduce the computational load. T-horex and sphere-on-sphere (S.o.S.) structures are modelled using 2D simulations with axial symmetry around the z-axis. Plane wave expansion using cylindrical coordinate system is implemented to simulate plane wave incident field. Dimer-on-sphere (D.o.S.) structures are modelled using 3D simulations exploiting axial symmetries at the xz and yz planes. The discretization of the structures is performed using a tetrahedral mesh with maximum element size of one fifth of the wavelength. Smaller geometrical features are discretized reducing the element size down to one fiftieth of the wavelength. Further details are reported in Results and discussion session.

2.4. Raman experiments

Raman spectra were acquired with a LabRam HR-800 microRaman (Horiba, Jobyn-Yvon). Laser source: He–Ne (632.8 nm), microscope objective: 100× (N.A.: 0.9). The Raman spectra analysed in Fig. 4 were acquired from 10 different individual spheres per sample, selected from mono- or multilayers directly supported by the silicon substrate. The reference spectra of the TiO₂ planar films were acquired in flat regions nearby the spheres. The spectra reported in the figures are raw data. Before the analysis of the intensity ratio the spectral background was fitted and subtracted by means of the instrument software Labspec6®.

3. Results and discussion

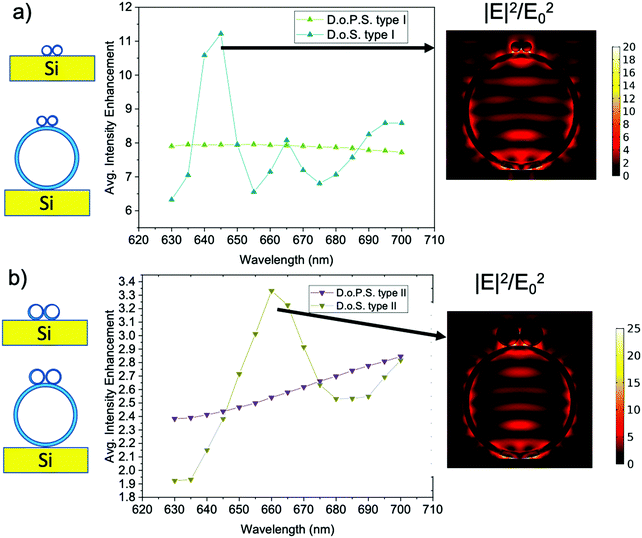
The rationale for the fabrication of self-similar dielectric antennas is given by the optical simulations shown in Fig. 1. Apart from the reference, represented by a ∼2 μm diameter TiO₂ hollow shell, all types of the antennas are formed by the combination of primary (μm-sized) and secondary (nm-sized) hollow shell antennas (T-horex). The following configurations were considered (Fig. 1):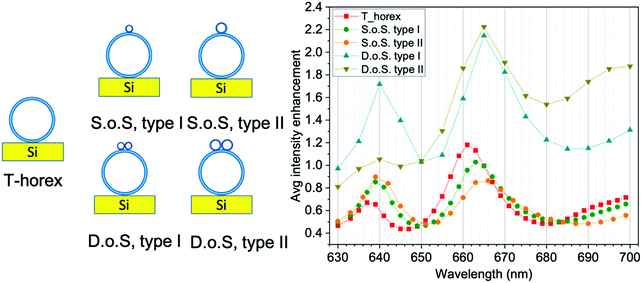

Fig. 1 Intensity enhancement of the electromagnetic field as a function of the wavelengths for different configurations.

(1) ∼2 μm-diameter TiO₂ hollow shell (T-horex). The core is a 2 μm-sized sphere of air (refractive index: 1), shell is made of 120 nm-thick layer of TiO₂ (anatase, refractive index: 2.5). This is taken as a reference for primary antennas.

(2) ∼2 μm-diameter sphere-on-sphere antenna, type I. This antenna consists of a 125 nm-sized T-horex (secondary antenna), made of an air core (diameter: 105 nm) and TiO₂ (anatase) shell layer (20 nm), which is placed on the top of a 2.1 μm-sized T-horex (primary antenna, air core: 2 μm, TiO₂ shell: 120 nm).

(3) ∼2 μm-diameter sphere-on-sphere antenna, type II. This antenna consists of a 431 nm-sized T-horex (secondary antenna), made of an air core (diameter: 411 nm) and TiO₂ (anatase) shell layer (20 nm), which is placed on the top of a 2.1 μm-sized T-horex (primary antenna, air core: 2 μm, TiO₂ shell: 120 nm).

(4) ∼2 μm-diameter dimer-on-sphere antenna, type I. This antenna consists of a dimer of 125 nm-sized T-horex (secondary antenna), which is placed on the top of a 2.1 μm-sized T-horex (primary antenna, air core: 2 μm, TiO₂ (anatase) shell: 120 nm). Each sphere of the dimer is made of an air core (diameter: 105 nm) and TiO₂ shell layer (20 nm).

(5) ∼2 μm-diameter dimer-on-sphere antenna, type II. This antenna consists of a dimer of 431 nm-sized T-horex (secondary antenna), which is placed on the top of a 2.1 μm-sized T-horex (primary antenna) air core: 2 μm, TiO₂ (anatase) shell: 120 nm. Each sphere of the dimer is made of an air core (diameter: 411 nm) and TiO₂ shell layer (20 nm).

The antennas lay on a single crystal silicon substrate (refractive index: 3.5) and surrounding medium is air. We used the finite element method implemented in COMSOL to numerically obtain the fields scattered by the antennas. Fig. 1b plots the averaged intensity enhancement of the electromagnetic field, defined as 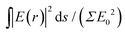where the integral 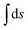is a surface integral limited to the antenna outermost surface, Σ is the antenna outermost surface area, and E₀ is the amplitude of the incident electric field of each system for wavelengths from 630 nm to 700 nm. This simulation reproduces the conditions of a microRaman experiment carried out using a He–Ne laser source (λ = 632.8 nm) focused through the objective of an optical microscope (numerical aperture, N.A.: 0.9), spanning the Raman shift range 0–1517 cm⁻¹. The intensity enhancement follows a qualitatively similar trend for all configurations, showing oscillations with local maxima around 640 and 660–665 nm. The increasing shoulder at 685 nm suggests the presence of further oscillations at λ > 700 nm. A quantitative comparison between T-horex and self-similar antennas with different configurations reveals that the use of single small spheres (sphere-on-sphere, S.o.S. type I and II) does not result in a significant enhancement of the local field (average enhancement intensity <1). On the other hand, the use of dimers (dimer-on-sphere, D.o.S. type I and II) has a pronounced effect on field enhancement, which is more than doubled at 665 nm. This result is further investigated by comparing the surface field enhancement achieved by dimers directly placed on flat silicon substrates (dimer-on-planar substrate, D.o.P.S., type I and II) with that of D.o.S. type I and II (Fig. 2). To provide a fair comparison between the two configurations, the intensity enhancement is calculated by considering only the surface Σ′ of the dimer, thus ignoring the large core–shell in dimers-on-spheres type I and II.

Fig. 2 Comparison between two dimers with the same size deposited on either planar substrates or T-horex primary antennas. (a) Dimer-on-sphere, type I; (b) dimer-on-sphere, type II. The spatial map of the electric field distribution at the enhancement maximum is shown for both the configurations. See the main text for details.

The field enhancement produced by dimers in the absence of T-horex is almost constant in the case of dimer-on-planar substrate type I and shows a monotonic increase for dimer-on-planar substrate type II. On the other hand, the optical modes of T-horex couple with those of dimers to give rise to a remarkable increase of the surface field, which is maximum for dimer-on-sphere type I (∼11.5 at 645 nm). These data confirm that T-horex is at the origin of the field oscillation and its optical coupling to dimers can be a key factor to generate local “hot-spots” on the antenna surface. The simulations of the field distribution at the resonant wavelengths of dimer-on-sphere type I and II (Fig. 2) reveal that the field is strongly concentrated at the dimer-T-horex touching points, as well as at the T-horex-silicon substrate interface. Dimer-on-sphere appears to be a more advantageous configuration to enhance the electric field intensity compared to the sphere-on-sphere. This is due to the lower intensity enhancement achieved by the single sphere compared to the dimer.

The optical simulations suggest that self-similar dimer-on-sphere antennas could offer advantages in light coupling and management from far- to near-field and back. In order to assess those predictions, different types of colloidal antennas were prepared and tested in Raman experiments.

Fig. 3 shows some representative SEM images of the antennas. In addition to the primary antennas (i.e. the ∼2 μm-sized T-horex spheres), which are the reference samples (Fig. 3a), three different types of self-similar samples were prepared. Fig. 3b shows the primary antenna decorated with secondary antennas, which have been distributed on its surface before titania coating. The secondary antennas have the same size of type I architectures (105 nm before and 125 nm after TiO₂ coating) and are assembled with a random distribution of single-, dimeric- and multimeric aggregates. These samples encompass the design of both sphere-on-sphere and dimers-on-sphere type I, providing a higher density of dielectric hot-spots on the T-horex surface. For this reason, they will be referred as multimer-on-sphere (M.o.S.) type I samples.

Fig. 3 SEM images of the four types of antennas considered in this work. (a) T-horex; (b) multimers-on-sphere type I; (c) multimers-on-sphere type II; (d) HT-horex. Scale bars: 1 μm.

Analogous considerations apply to multimer-on-sphere type II samples, obtained by coupling ∼430 nm-sized small spheres with the primary micron-sized antenna (Fig. 3c). In this case the larger size of the secondary antennas enabled a better control of their distribution on the 2 μm-sized T-horex. As a result, monomeric (S.o.S.) and dimeric (D.o.S.) secondary antennas are the prevalent types of configurations observed in these samples, and both types of antennas typically coexist in individual spheres. The combination of random self-similar scattering centres was already explored as a strategy to localize light in disordered media by Wiersma and co-workers.^21,22

Finally, a third type of architecture (Fig. 3d) was fabricated. This takes direct inspiration from the hierarchical organization of many biological structures with optical functions, like those involved in realizing structural colours. Here primary antennas are assembled to form either monolayers or three-dimensional colloidal crystals. Trimers or, in general, multimers made of ∼430 nm-sized small spheres are precisely located at the intersection between the primary antennas, giving rise to an ordered, hierarchical distribution of primary and secondary antennas in a photonic crystal. This type of structures, which will be referred as hierarchical T-horex (HT-horex), will give us the opportunity to investigate the influence of precise spatial ordering of secondary antennas, comparing the effects of hierarchical and random distributions.

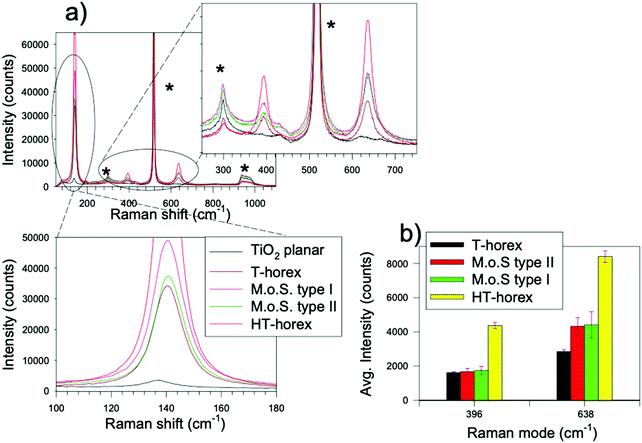
The first level of comparison was addressed to the Raman analysis of individual antennas in monolayers deposited on silicon substrates. The evaluation of the spectral intensity of the anatase modes provides a straightforward indication on the absolute efficiency of Raman scattering in these systems in the absence of any other effects (charge transfer, adsorption…) related to the presence of a given analyte. Moreover, the direct contact of the antennas with the silicon substrate allows to obtain useful information on light trapping/dissipation by inspecting the silicon Raman modes.^9,23Fig. 4 shows an example of the typical Raman spectra obtained from different samples. Ten different antennas of each sample were analysed. We note that the spatial resolution of the laser beam utilized for excitation is below 2 μm, which means that each self-similar antenna can be individually selected and analysed. All the antennas exhibit the typical TiO₂-anatase Raman modes, at about 143 cm⁻¹ (E_g(1)), 192 cm⁻¹ (E_g(2)), 396 cm⁻¹ (B_1g(1)), 518 cm⁻¹ (A_1g + B_1g(2), hidden by the overlapping main peak of Si in spectra acquired from single antennas, yet observable in spectra acquired from multilayers, vide infra) and 638 cm⁻¹ (E_g(3)).^9,24 As already reported in our previous work, the spherical antennas exhibit a systematic strong enhancement of the Raman intensity in comparison to planar thin films with the same thickness. For example, based on the analysis of the E_g(1) mode of TiO₂-anatase, the signal of T-horex exceeds that of planar titania by a factor of ∼100 (30 000/300 counts), and this factor further increases for the other antennas. In particular, hierarchically ordered antennas (HT-horex) shows a remarkable enhancement of the Raman spectra (the intensity of E_g(1) mode saturates and that of B_1(g1) and E_g(3) modes is about three times that of the corresponding modes of T-horex). These results are particularly relevant and deserve further analysis. First of all, we note that during Raman acquisition the exciting laser is focused on the region of primary antenna (T-horex). From this viewpoint, the situation is identical to that experienced by a normal T-horex. However, the presence of secondary scattering centres, represented by the small antennas hierarchically organized around the T-horex borders, contributes with a further confinement of light on the surface of the sample, which is expected to play a major role in determining the strong enhancement of the Raman signal. These results also demonstrate the importance of controlling the spatial localization of secondary antennas in self-similar aggregates, as already observed in many bioinspired optical systems.^25,26 On the other hand, the Raman response of multimer-on-sphere type I and II is more complex. In general, these types of antennas do not exhibit any relevant Raman enhancement in comparison to T-horex. On the other hand, they are significantly outperformed by the hierarchically organized systems (HT-horex). Going back to the optical simulations shown in Fig. 1, we note that the averaged enhancement of the field at 632.8 nm (the wavelength of the laser utilized as source for the Raman analysis) is not significant (∼1), which may suggest the origin of such a negligible improvement. Moreover, unlike T-horex and HT-horex, which are both characterized by a quite low relative standard deviation of the Raman intensity (∼4%, which is comparable with that reported for silica-based T-rex), multimer-on-sphere samples exhibit larger values (ranging between 12–17%). For a more general comparison, we observe that the relative standard deviation values for conventional plasmonic SERS typically exceed 20%. Such a relative decrease of reproducibility can be probably ascribed to the random distribution of the secondary antennas on the T-horex surface. In addition, the intensity ratio between E_g(3) and B_1(g1) modes, which is about 2 for both T-horex and HT-horex, is 2.5 in the case of multimer-on-sphere samples. These data suggest that multimer-on-sphere type I and II antennas boost the intensity of the E_g(3) mode. The wavelength associated to this mode is ∼660 nm, which is very near to the enhancement peak predicted by simulations shown in Fig. 1. In parallel, the B_1(g1) mode corresponds to a wavelength of 650 nm, which is a local minimum between the two maxima for both T-horex and multimer-on-sphere samples. In this regard there is a very good quantitative agreement between the experimental intensity ratios and the values extracted from numerical simulations. These observations suggest that the local enhancement of the Raman field around 660 nm could be at the origin of the anomalous intensity of the E_g(3) mode and quantitatively accounts for the E_g(3)/B_1(g1) intensity ratio.

Fig. 4 (a) Raman spectra of individual self-similar antennas and references (planar TiO₂ thin films with the same thickness and T-horex), acquired for 10 s with a 0.9 N.A. objective from individual spheres selected from a monolayer. The Raman modes of the silicon substrate are indicated by an asterisk; (b) average intensity counts for B_1(g1) (396 cm⁻¹) and E_g(3) (638 cm⁻¹) modes for the different configurations described in the text.

Finally, the intensity of the modes associated with the Si substrate measured in the case of HT-horex and T-horex is significantly lower than those observed in the case of multimer-on-sphere samples.

Interestingly, the analysis of the acoustic silicon mode at 300 cm⁻¹ clearly reveals that the intensity of silicon supporting the multimer-on-sphere samples is even higher than that observed from planar samples, which suggests that multimeric secondary antennas distributed on the T-horex surface are more effective in channelling light through the primary antenna, creating a sort of “lens”-effect.

This analysis indicates that, among the configurations taken into account, the hierarchically ordered (HT-horex) antennas is the most efficient in light harvesting on the surface of primary antennas, giving rise to superior Raman enhancement and reproducibility of the signal. In view of obtaining bioinspired colloidal platforms for SERS purposes, the case of three- dimensional (3D) colloidal crystals were also considered. In general, due to the maximization of light trapping and reduced optical losses through the substrate, 3D colloidal crystals of T-rex and T-horex spheres are characterized by superior Raman efficiency in comparison to the monolayered counterparts.^13,14 This evidence is confirmed also in the case of HT-horex antennas, which exhibit remarkable Raman signals even for a limited time of acquisition (2 s, Fig. 5). The Raman spectra of 3D HT-horex are characterized by a significant enhancement in comparison to 3D T-horex samples taken as a reference. However, more in-depth analysis reveals that the relative enhancement ratio between HT-horex and T-horex reduces from ∼3 to ∼2 by moving from the 2D to 3D case. This indicates that 3D assembly allows the Raman spectra of T-horex to reach excellent levels of efficiency and, in parallel, that the hierarchical organization of secondary and primary antennas is more efficient in enhancing the field at the surface of the colloidal crystal.

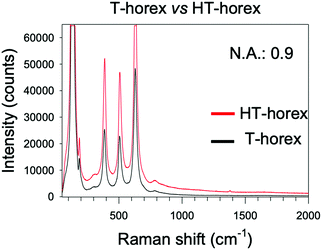Fig. 5 Raman spectra of 3D colloidal crystals made of T-horex (black) and HT-horex (red). Acquisition time: 2 s, N.A.: 0.9.

In view of possible applications of all-dielectric self-similar antennas in Raman sensors, we have compared the performances of HT-horex in detection of environmental CO₂ (ESI,† S1). These data further confirm the superior Raman enhancement that can achieved by using self-similar dielectric antennas in HT-horex configuration, which suggests many possible applications for sensing.

4. Conclusion

This study investigated the role of the distribution of secondary antennas in self-similar all-dielectric colloids that could be applied as plasmon-free SERS-active substrates or photocatalytic supports. Optical simulations indicated that multimeric secondary antennas are effective in promoting the concentration of the electromagnetic field on the surface of primary antennas. Experiments carried out on randomly and hierarchically organized self-similar antennas revealed that the Raman scattering can be significantly influenced by the presence and distribution of the secondary antennas, both in terms of overall signal intensity and efficiency of backscattering of Raman radiation originated by specific vibrational modes that are directly coupled to the local field enhancement. In particular, hierarchically ordered antennas exhibit a remarkable enhancement of Raman scattering, which is superior to that obtained by the random-distributed counterparts. These preliminary results open exciting perspectives for non-plasmonic sensing²⁸ and photocatalysis^29,30 and deserve further experimental and theoretical investigations.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This project was partially supported by the Biomass Hub Project-EU-Regione Lombardia POR FESR 2014–2020. L. C. was supported by Università degli Studi di Padova (STARS-StG-PULSAr).

References

1. L. Novotny and B. Hecht, Optical antennas. Principles of Nano-Optics, Cambridge University Press, Cambridge, 2nd edn, 2012, pp. 414–447 DOI:10.1017/CBO9780511794193.015.
2. S. Y. Ding, E. M. You, Z. Q. Tian and M. Moskovits, Electromagnetic theories of surface-enhanced Raman spectroscopy, Chem. Rev. Soc., 2017, 46, 4042–4076.
3. V. Giannini, A. I. Fernandez-Dominguez, S. C. Heck and S. A. Maier, Plasmonic Nanoantennas: Fundamentals and their use in controlling the radiative properties of Nanoemitters, Chem. Rev., 2011, 111, 3888–3912.
4. S. Linic, P. Christopher and D. B. Ingram, Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy, Nat. Mater., 2011, 10, 911.
5. M. L. Brongersma, N. J. Halas and P. Nordlander, Plasmon-induced hot carrier science and technology, Nat. Nanotechnol., 2015, 10, 25.
6. E. Cortés, Efficiency and Bond Selectivity in Plasmon-Induced Photochemistry, Adv. Opt. Mater., 2017, 5, 1700191.
7. S. Chavez, U. Aslam and S. Linic, Design Principles for Directing Energy and Energetic Charge Flow in Multicomponent Plasmonic Nanostructures, ACS Energy Lett., 2018, 3, 1590–1596.
8. I. Alessandri and J. R. Lombardi, Enhanced Raman scattering with dielectrics, Chem. Rev., 2016, 116, 14921–14981.
9. I. Alessandri, Enhancing Raman Scattering without plasmons: unprecedented sensitivity achieved by TiO₂ shell-based resonators, J. Am. Chem. Soc., 2013, 135, 5541–5544.
10. I. Alessandri, I. Vassalini, M. Bertuzzi, N. Bontempi, M. Memo and A. Gianoncelli, “RaMassays”: Synergistic Enhancement of Plasmon-Free Raman Scattering and Mass Spectrometry for Multimodal Analysis of Small Molecules, Sci. Rep., 2016, 6, 34521.
11. N. Bontempi, I. Vassalini, S. Danesi and I. Alessandri, ZORRO: zirconium oxide resonators for all-in-one Raman and whispering-gallery-mode optical sensing, Chem. Commun., 2017, 53, 10382–10385.
12. N. Bontempi, I. Vassalini and I. Alessandri, All-dielectric core/shell resonators: From plasmon-free SERS to multimodal analysis, J. Raman Spectrosc., 2018, 49, 943–953.
13. N. Bontempi, L. Carletti, C. De Angelis and I. Alessandri, Plasmon-free SERS detection of environmental CO₂ on TiO₂ surfaces, Nanoscale, 2016, 8, 3226–3231.
14. I. Alessandri and L. E. Depero, All-Oxide Raman-Active Traps for Light and Matter: Probing Redox Homeostasis Model Reactions in Aqueous Environment, Small, 2014, 10, 1294–1298.
15. B. A. Palmer, D. Gur, S. Weiner, L. Addadi and D. Oron, The Organic Crystalline Materials of Vision: Structure-function Considerations from the Nanometer to the Millimeter scale, Adv. Mater., 2018, 30, 1800006.
16. S. Vignolini, E. Moyroud, B. J. Glover and U. Steiner, Analysing photonic structures in plants, J. R. Soc., Interface, 2013, 10, 20130394.
17. M. Burresi, L. Cortese, L. Pattelli, M. Kolle, P. Vukusic, D. S. Wiersma, U. Steiner and S. Vignolini, Bright-white beetle scales optimise multiple scattering of light, Sci. Rep., 2014, 4, 6075.
18. J. Syurik, G. Jacucci, O. D. Onelli, H. Hölscher and S. Vignolini, Bio-inspired Highly Scattering Networks via Polymer Phase Separation, Adv. Funct. Mater., 2018, 28, 1706901.
19. M. Lopez-Garcia, et al., Light-induced dynamic structural color by intracellular 3D photonic crystals in brown algae, Sci. Adv., 2018, 4, 917.
20. N. Vogel, et al., Color from hierarchy: Diverse optical properties of micron-sized spherical colloidal assemblies, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10845–10850.
21. D. S. Wiersma, P. Bartolini, A. Lagendijk and R. Righini, Localization of light in a disordered medium, Nature, 1997, 390, 671–673.
22. F. Riboli, et al., Engineering of light confinement in strongly scattering disordered media, Nat. Mater., 2014, 13, 720–725.
23. I. Alessandri, N. Bontempi and L. E. Depero, Colloidal lenses as universal Raman scattering enhancers, RSC Adv., 2014, 4, 38152–38158.
24. O. Frank, M. Zukalova, B. Laskova, J. Kurti, J. Koltai and L. Kavan, Raman spectra of titanium dioxide (anatase, rutile) with identified oxygen isotopes (16, 17, 18), Phys. Chem. Chem. Phys., 2012, 14, 14567–14572.
25. S. Tadepalli, J. M. Slocik, M. K. Gupta, R. R. Naik and S. Singamaneni, Bio-Optics and Bio-Inspired Optical Materials, Chem. Rev., 2017, 117, 12705–12763.
26. H.-B. Yao, H.-Y. Fang, X.-H. Wang and S.-H. Yu, Hierarchical assembly of micro-/nano-building blocks: Bio-inspired rigid structural functional materials, Chem. Soc. Rev., 2011, 40, 3764–3785.
27. V. Kitaev and G. A. Ozin, Self-assembled surface patterns of binary colloidal crystals, Adv. Mater., 2003, 15, 75–77.
28. I. Vassalini, O. Sisman, E. Comini and I. Alessandri, The role of morphology in all-dielectric SERS: A comparison between conformal (T-rex) and non conformal TiO₂ shells, Vib. Spectrosc., 2020, 109, 103085.
29. M. Salmistraro, A. Schwartzberg, W. Bao, L. E. Depero, A. W. Bargioni, S. Cabrini and I. Alessandri, Triggering and monitoring plasmon-enhanced reactions by optical nanoantennas coupled to photocatalytic beads, Small, 2013, 9, 3301–3307.
30. I. Vassalini and I. Alessandri, Switchable stimuli-responsive heterogeneous catalysis, Catalysts, 2018, 8, 569–594.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison of T-rex and HT-horex antennas in sensing of environmental CO₂. See DOI: 10.1039/d0ma00509f

---