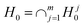Open Access Article
Open Access ArticleFormulation of mix design for 3D printing of geopolymers: a machine learning approach
Ali
Bagheri
 *a and
Christian
Cremona
b
*a and
Christian
Cremona
b
aFaculty of Science Engineering and Technology, Swinburne University of Technology, Melbourne, Australia. E-mail: a-bagheri@hotmail.com
bDirector, Technical Division, Bouygues TP, Guyancourt, France
First published on 3rd June 2020
Abstract
This work evaluates the application of machine learning in the formulation of construction materials. The aim is to introduce a feasible approach to classify geopolymer samples made via additive manufacturing technique. Using an experimentally acquired conversion factor 2.95, this study employs popular recursive-partitioning functions including rpart and ctree to build separate classification models being compared at the end. According to the findings, these functions demonstrate great ability to create classification models for 3D-printed geopolymers with up to 100% positive predictive value in ctree function and up to 81% positive predictive value in the rpart function. However, rpart function with 70% cumulative accuracy expressed slightly better performance compared to 63% for that of ctree function. Locating the content of slag and the ratio of boron ions respectively in the roots of ctree and rpart decision trees implies the significance of them in the compressive strength of samples.
1. Introduction
The history of using additive manufacturing (AM) in construction can be traced back to as far as Thomas Edison's single-pour concrete house,1 which was a well-documented failure due to the highly complex nature of the proposed novel system. Three-dimensional (3D) printing technology has been tested in some constructing projects in recent years. Khoshnevis2 from the University of Southern California (USA) developed a largescale Construction digital fabrication (CDF) system called “Contour Crafting” in 1998. In 2007, an Italian engineer Enrico Dini3 invented a substantial powder-based 3D printer so-called D-shape. Andy Rudenko4 constructed a castle shape structure using a largescale 3D printer in 2015. The structural components were printed individually using cement mortar and assembled at the building site.Nonetheless, a huge amount of ordinary Portland cement has been consumed in these projects, which results in high autogenous shrinkage, the heat of hydration, and cost. Moreover, cement manufacturing is known as a high greenhouse gas emission industry. The associated CO2 emission in addition to embodied energy consumption deteriorates sustainability performance of 3D printed concrete structures. Geopolymer has been recognised as a promising construction material for 3D printing process due to its fast-setting, cost-effective and eco-friendly nature.5,6 Apart from these, the fire resistance7 and durability8,9 of geopolymers make them superior to the conventional cement composites.
Geopolymers are normally formed by activating of aluminosilicate resources in a caustic environment.10 Silicate and hydroxide compounds of alkali metals, such as sodium silicate and sodium hydroxide, are commonly utilised to activate silicon and aluminium species.11 Studying geopolymers has been performed based on a large variety of aluminosilicate resources and alkaline solutions used for preparing geopolymer.12–18 This diversity in two main parts of geopolymers has formed one of their main interesting facets. Iron-making slag and fly ash, as the aluminosilicate resources, as well as the combination of sodium silicate and sodium hydroxide, as the activator, are the most popular constituents.
Despite the benefits of geopolymers, using silicate compounds can be disadvantageous not only because of environmental problems but also for its corrosive character. Hence, changing the composition of alkaline activator of geopolymers in order to introduce new binders has been the topic of many types of research.19–23 Many efforts have been made to substitute the silicon and aluminium atoms of the geopolymer matrix with other elements. Boron-based geopolymer is one of them that was introduced in previous studies.24
The huge volume of data produced in many engineering disciplines, especially civil and construction engineering, can be employed in order to learn patterns and classifications. As learning from data is a complex procedure, it is necessary to use computational methods. The use of machine to learn from data that is produced in materials design and its significance can be found in ref. 34–38 Supervised machine learning is a group of modern computational approaches that can be considered for data classification.25–27 The conditional inference trees (ctree) and recursive partitioning (rpart) methods are supervised machine learning functions that are frequently utilised for data mining. The aim of this study is to build a model that predicts a target variable according to certain input variables.28 Recursive-partitioning (RP) algorithm approximate a regression correlation through binary recursive partitioning in a conditional inference framework. These algorithms work in the following stages. Step (1) examining the global null hypothesis of independence between any of the input data and the targets. It stops if the hypothesis could not be rejected. Otherwise, it selects the input parameter with the highest contribution to the target variable. Their association is calculated via a p-value relating to an exam for the partial null hypothesis of a single input data and the corresponding response. Step (2) implementing a binary sub-division in the chosen input parameter. Step (3) recursively repeating previous steps. Step (4) creating a visual flowchart mapping the entire classification process.
2. Significance of the work
The compressive strength of geopolymer binders is dependent on many factors including but not limited to: the nature and characteristics of raw materials (aluminosilicate resources); the chemical composition of the aluminosilicate resources; type and formulation of the alkaline activator; the content of alkaline ions in the activator; the fraction of silicate to hydroxide compounds in the activator; the water to binder ratio; the formulation of aggregates.7,8,29 Particularly when geopolymer binder is 3D printed, the number of effective factors on the strength is expanded by the printing parameters, which include the printing method, the resolution of layers, the shape of the extrusion (circular, ovular or rectangular), linear rates of extrusion, the orientation of manufacture (vertical or horizontal) etcetera, as well as preparation and formulation of materials.Given an innumerable number of independent variables, the prediction of the compressive strength of printed geopolymer samples without the use of a machine will generate a high level of error. For instance, one can predict the strength of samples that are classified into four categories with 75% error. However, the use of machine learning would reduce this error significantly as can be seen further in this work. The most efficient way is to learn from the existing data through machine learning. One approach is to take the printing variables constant and investigate the effective factors of the mix. Another way is to take the mix constantly and change the printing parameters. The current study has focused on the former approach. Among the mentioned effective parameters, the content of the fly ash, the content of the ground granulated blast furnace slag (GGBFS), as well as the ratio of boron ions, silicon ions, and sodium ions in the alkaline solution have the most significant impact on the compressive strength.19
3. Methodology
3.1. 3D printing process
A custom-made small-scale 3D printing device (designed and manufactured in the laboratory for experiments) was used for the printing process as shown in ref. 30 The apparatus has a piston-operated extruder, where fresh geopolymer is extruded from a 45° rectangle extrusion nozzle with the dimension of 30 mm × 15 mm. An external vibration was applied to the extruder while loading the fresh mix to ensure the mix inside the extruder received adequate compaction. The specimens were printed in line with the printing direction as the extruder moves in a horizontal direction at a constant velocity. Geopolymer filaments with the dimensions of L = 250 mm × W = 30 mm × H = 15 mm are deposited in two layers for each sample. The dimension of each sample would be 250 × 30 × 30 mm. The time interval between layers, also known as the printing time interval or delay time, is 2 minutes.3.2. Data acquisition and definition
The data obtained from the compressive strength examination of boron-based geopolymer mix is evaluated and converted to that of binders when 3D printed. The preliminary examinations confirmed that the compressive strength of geopolymeric bulk specimens is within the range of 1.6–2.3 times of the compressive strength of layered samples derived from the 3D printing process. The data used in this paper was acquired from previous studies.27 Five parameters are selected as input, which include the weight percentage of the fly ash (%F), the weight percentage of the GGBFS (%S), as well as the ratio of boron ions (B/AA), the ratio of silicon ions (Si/AA) and the ratio of sodium ions (Na/AA) in the alkaline solution. The contribution of ions is representing respectively the content of borax, sodium silicate, and sodium hydroxide in the solution. The target parameter is the compressive strength of BASG samples after 7 days curing at room temperature. The sample preparation and testing procedure are similar to that of ref. 19 The content of GGBFS and fly ash is in the range of 0, 9, 30, 50, 70, 91 and 100 wt%. The concentration of sodium hydroxide solution differs in 3, 5 and 8 molar. The statistical information of the input parameters is shown in Table 1.| %F | %S | B/AA | Si/AA | Na/AA | |
|---|---|---|---|---|---|
| Minimum | 0.00 | 0.00 | 0.00 | 0 | 0.273 |
| Maximum | 100 | 100 | 0.310 | 0.500 | 1.00 |
| Mean | 66.9 | 33.1 | 0.088 | 0.224 | 0.521 |
| STD | 44.9 | 44.5 | 0.096 | 0.176 | 0.175 |
A total number of 114 targets were measured, and the average conversion factor 1.95 was applied to the dataset. Fig. 1 is the statistical presentation of dependent variable (compressive strength). It illustrates the one-dimensional data distribution graph of the target values. The box plot shown in this figure reveals the distribution of the targets into their quartiles, highlighting the mean value and the outliers. The whiskers, which are the lines extending vertically out of boxes, indicate dispersion out of the upper and lower quartiles, and any point outside the whiskers is considered an outlier.
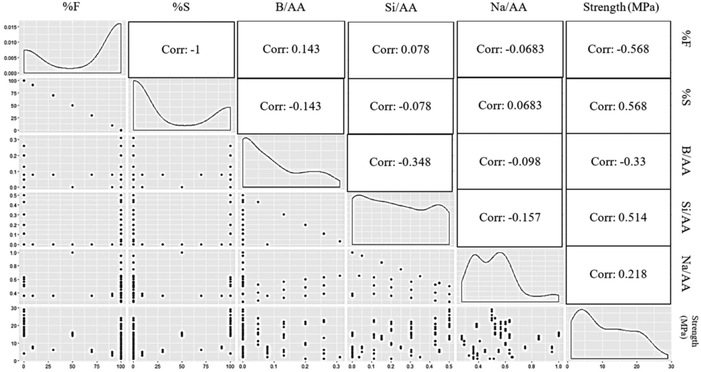
To perceive the relationship of the predictors with the response variable, an initial exploratory data visualization is performed as illustrated by the plot matrix of Fig. 2. It includes the scatter plots of individual parameter combination, in addition to their density plots and the correlations coefficient between pair of variables. The density plots visualise the distribution of response variable over a continuous interval. These charts demonstrate the variation of a histogram that utilises centre smoothing to chart values, providing smoother distribution by smoothing out the noise. Where values of the variables are concentrated over the interval are shown by the peaks of density plots.
According to Fig. 2, there has not been noticed any strong correlation between any of the variables and the response values. Lack of a reliable correlation coefficient between dependent and independent variables results in an inaccurate linear regression model. However, it would be conceivable to transform a regression problem into a classification problem. In other words, the values of the compressive strength to be predicted might be transformed into discrete brackets. The target data visualised in Fig. 1 are then classified into four classes of A, B, C and D as described in Table 2. The “cut” function, which is used to break up a continuous variable, divides the target values into four classes.
| Class | A | B | C | D |
|---|---|---|---|---|
| Compressive strength (MPa) | <5 | ≥5 & <10 | ≥10 & <15 | ≥15 |
| Number of data in each class | 34 | 24 | 22 | 34 |
3.3. Modelling details
The selected model creates conditional distribution that corelates a dependent variable (Y) to m number of independent variables with a final illustration of a tree flowchart. They include both regression and classification problems and are used for both categorical and continuous variables. The mentioned m-dimensional covariate vector is taken from a specified sample space (X = [X1, …, Xm]). Both reflex variable and the covariate vector can be taken at an arbitrary attempt. We pre-assume that a distribution D(Y|X), which is from the response Y to the covariates X, relies on a function f of the covariates as D(Y|X) = D(Y|X1, …, Xm) = D(Y|f(X1, …, Xm)). The generic algorithm for both models is a transparent two-step algorithm in which the input observations are partitioned by univariate divisions in a recursive way. Secondly, it fits a constant model in each cell of the resulting partition.33The present study relies on the R package, which is freely available through their website (r-project.org) to researchers for computer programming, to create classification tree of the compressive strength of 3D-printed boroaluminosilicate geopolymers.
4. Results and discussion
4.1. ctree function results
At the first stage of ctree function, it is necessary to decide whether any information exists about the targets covered by any of the m independent covariates. Then, in each node characterised by specific case weights (w), the global hypothesis of independence is formulated in terms of the m partial hypotheses Hj0 with global hypothesis H0.| Hj0: D(Y|Xj) = D(Y) |
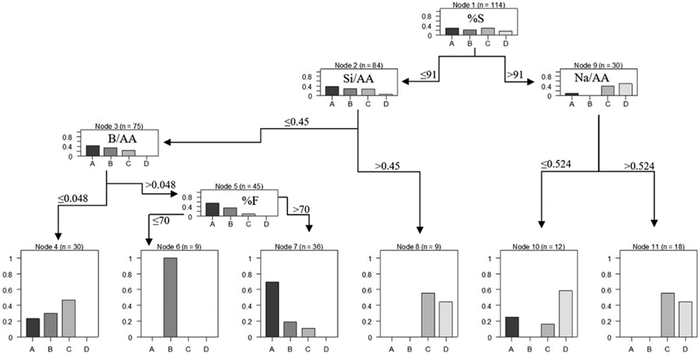
where Y is a target variable, Xj is an independent variable with m dimension, j = (1,…m) and D(Y|Xj) is the conditional distribution. When it is not possible to reject H0 at level α, the recursion stops. However, if the global hypothesis is rejected, the association between Y. and each of the independent variables Xj,j = (1, …,m) is measured by test statistics or P-values indicating the deviation from the partial hypotheses Hj0. Once an independent variable is selected in the first step of the algorithm, the split itself can be established by any split criterion, including those established by.31,32 The decision tree (DT) created by the ctree function is presented in Fig. 3. It is necessary to identify important terminologies on DT by looking at the flowchart presented in Fig. 3. Node 1 is a root node that represents the entire population of data. It further is divided into two homogeneous sets. Splitting is a process of breaking a node into two sub-nodes (nodes 2 and 9). Where a sub-node is divided into further sub-nodes, it is a decision node as Nodes 3 and 5. A node that does not split is a terminal node as Nodes 4, 6, 7, 8, 10 and 11. The sub-section of a whole tree is named as a branch. A node that is split into certain sub-nodes is a parent node of the sub-nodes while the sub-nodes are the children of the parent node.
The interpretation of the ctree DT allows prediction of optimal formulation of geopolymer with high strength. Geopolymer formulation is defined by the DT rules along with corresponding population and accuracy values. Table 3 provides this formulation based on the rules of created network.
| Strength category | Population of the bin (%) | Accuracy (%) | Rule |
|---|---|---|---|
| A [<5] MPa | 32 | 70 | %F > 70 & B/AA > 0.048 & Si/AA ≤ 0.45 |
| B [5–10] MPa | 8 | 100 | 9 < %F ≤ 70 & B/AA > 0.048 & Si/AA ≤ 0.45 & 30 < %S ≤ 0.91 |
| C [10–15] MPa | 8 | 56 | Si/AA > 0.45 & %S ≤ 0.91 |
| C [10–15] MPa | 26 | 47 | B/AA ≤ 0.048 & Si/AA ≤ 0.45 & %S ≤ 0.91 |
| C [10–15] MPa | 15 | 56 | Na/AA > 0.524 & %S > 0.91 |
| D [>15] MPa | 11 | 59 | Na/AA ≤ 0.524 & %S > 0.91 |
At the first glance, this formulation confirms the significance of the contribution of slag in the geopolymer mix design. The slag-dominated mix designs (samples with high content of slag) result in higher compressive strength. This is confirmed by the Fig. 3, where sub-node 9 with 26% of the population will end at categories of C and D. Among them, samples with higher ratios of sodium in the alkali-activator have lower compressive strength. It is observed from terminal node 10 with dominant class D to node 11 with dominant class C while the content of sodium ions increased from contents lower than 0.524 to higher than 0.524. This phenomenon has previously been observed in boron-based geopolymers if ref. 19 and 22 It is reported that the increase in the content of boron can raise the contribution of sodium ions and deteriorate the compressive strength.19 On the other hand, however, the lower the slag content, the less the compressive strength. It is observed by comparing the sub-nodes 2 and 9. Furthermore, an increase in the ratio of silicate to above 0.45 increases the compressive strength (less than 5 MPa for A to 10–15 MPa for C). The contribution of silicate in the mix design is vital for strength development as not only is silicate necessary for the initiation of polycondensation reactions but also silicate increases crosslinking phenomenon in geopolymerisation. Moreover, declining boron ions ratio in the alkaline solution from lower than 0.048 (terminal node 4) to the higher contents (terminal nodes 6 and 7) regresses the compressive strength from class C to the classes A and B.
More details about the performance of the predicted model can be obtained by looking at the confusion matrices that are demonstrated in Tables 4 and 5. The true positive rates and false negative rates of the prediction made by ctree function are stated in Table 4. According to Table 4, the maximum true positive rate of 83% belongs to samples with a compressive strength between 10 MPa and 15 MPa. It implies that a large portion of these samples, which constitute almost one-third of the population, are predicted correctly. However, the maximum false negative rate of 64% relates to the samples with a compressive strength between 5 MPa and 10 MPa that comprise one-fifth of the population. Table 5 shows the performance of the prediction in the opposite way to that of Table 4. Given the number of predictions in each category and the corresponding positive predictive values ranging from 51% to 100%, the total true prediction value of this approach is 63%.
| Actual values (%) | |||||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Predicted values (%) | A | 71 | 28 | 11 | 0 |
| B | 0 | 36 | 0 | 0 | |
| C | 20 | 36 | 83 | 63 | |
| D | 9 | 0 | 6 | 37 | |
| True positive rate (%) | 71 | 36 | 83 | 37 | |
| False negative rate (%) | 29 | 64 | 17 | 63 | |
| Actual values (%) | Positive predictive value (%) | False discovery rate (%) | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||
| Predicted values (%) | A | 70 | 19 | 11 | 0 | 70 | 30 |
| B | 0 | 100 | 0 | 0 | 100 | 0 | |
| C | 12 | 16 | 51 | 21 | 51 | 49 | |
| D | 25 | 0 | 17 | 58 | 58 | 42 | |
4.2. rpart function results
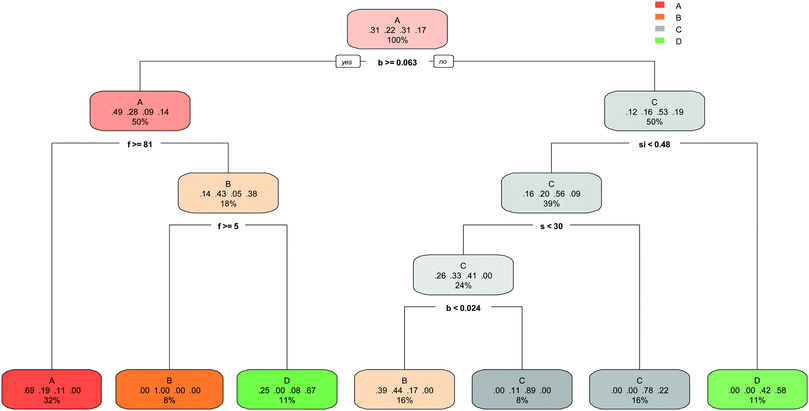
The decision tree created by the rpart function is presented in Fig. 4. Each node of the DT shown in this figure contains the predicted class (A, B, C and D), the predicted probability of each class and the percentage of observations in the node.The prediction of optimal formulation of geopolymer with high strength can be achieved by the interpretation of the rpart DT. DT rules along with corresponding population and accuracy values define geopolymer formulation. Table 6 provides this formulation based on the rules of created network by the rpart function.
| Strength category | Population of the bin (%) | Probability (%) | Rule |
|---|---|---|---|
| A [≤5] MPa | 32 | 69 | %F ≤ 81 & B/AA ≥ 0.063 |
| B [5–10] MPa | 8 | 100 | 5 < %F ≤ 81 & B/AA ≥ 0.63 |
| B [5–10] MPa | 16 | 44 | 0.024 > B/AA & %S < 30 & Si/AA < 0.48 |
| C [10–15] MPa | 8 | 89 | 0.024 < B/AA < 0.063 & %S < 30 & Si/AA < 0.48 |
| C [10–15] MPa | 16 | 78 | B/AA < 0.063 & %S < 30 & Si/AA < 0.48 |
| D [>15] MPa | 11 | 67 | 5 > %F & B/AA ≥ 0.63 |
| D [>15] MPa | 11 | 58 | Si/AA ≥ 0.48 & B/AA < 0.063 |
It is notable that unlike the ctree function, the rpart function has not used the ratio of sodium ions to create the prediction model. The root node has used the ratio of boron to split the samples into two main sets. One set is fly ash-based samples with high amount of boron, which is graded in A and B classes with compressive strength lower than 5 MPa and between 5 and 10 MPa respectively. The second set include samples with very low ratio of boron (lower than 0.024), samples with high content of slag, as well as specimens with high ratio of silicate. The efficiency of rpart model can be assessed from confusion matrices that are illustrated in Table 7 and 8. The true positive rates and false negative rates of the prediction are stated in Table 7 according which the maximum true positive rate of 79% was obtained for samples with a compressive strength greater than 15 MPa. On the other side, 37% of the 3D-printed geopolymer samples with a compressive strength between 10 MPa and 15 MPa are predicted incorrectly. Given the number of observations in each class of compressive strength and their true positive rates, 70% of the observations are predicted in the correct category of compressive strength. Table 8 reflects the positive predictive values for correct predictions and the false discovery rates for incorrect predictions. From almost one-third of the whole predictions falling within class A, 70% was correctly predicted. The highest positive predictive value of 81%, however, relates to class C with a compressive strength between 10 MPa and 15 MPa. This category composed 24% of the whole predictions. Given the number of predictions in each category and the corresponding positive predictive values ranging from 63% to 81%, the total true prediction value of this approach is 70%.
| Actual values (%) | |||||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Predicted values (%) | A | 71 | 28 | 11 | 0 |
| B | 20 | 68 | 9 | 0 | |
| C | 0 | 4 | 63 | 21 | |
| D | 9 | 0 | 17 | 79 | |
| True positive rate (%) | 71 | 68 | 63 | 79 | |
| False negative rate (%) | 29 | 32 | 37 | 21 | |
| Actual values (%) | Positive predictive value (%) | False discovery rate (%) | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||
| Predicted values (%) | A | 70 | 19 | 11 | 0 | 70 | 30 |
| B | 26 | 63 | 11 | 0 | 63 | 37 | |
| C | 0 | 4 | 81 | 15 | 81 | 19 | |
| D | 13 | 0 | 25 | 63 | 63 | 37 | |
5. Validation of results
For the validation, 20 specimens are tested, the predictor variables are set into the both algorithms, and the results are compared to the actual values of compressive strength. Table 9 compares the results of obtained from compressive strength test and from the prediction.| No. | Formulation F–S–B–Si–Naa | Compressive strength (MPa) | Predicted strength by ctree | Predicted strength by rpart |
|---|---|---|---|---|
| a F = %F; S = %S; B = B/AA; Si = Si/AA; Na = Na/AA. | ||||
| 1 | 100–0–0.21–0.313–0.428 | A (4) | A | A |
| 2 | 100–0–0.259–0.26–0.418 | A (2) | A | A |
| 3 | 100–0–0.22–0.33–0.45 | A (2) | A | A |
| 4 | 100–0–0.23–0.324–0.446 | A (3) | C | B |
| 5 | 100–0–0.11–0.34–0.55 | B (9) | C | B |
| 6 | 100–0–0.19–0.39–0.42 | B (5) | C | B |
| 7 | 100–0–0.31–0.11–0.58 | A (1) | C | B |
| 8 | 100–0–0.31–0.08–0.61 | A (1) | C | B |
| 9 | 100–0–0.235–0.237–0.528 | A (3) | C | B |
| 10 | 100–0–0.102–0.334–0.564 | B (7) | C | B |
| 11 | 100–0–0.232–0.298–0.47 | A (3) | A | A |
| 12 | 100–0–0.255–0.344–0.401 | A (4) | A | A |
| 13 | 100–0–0.219–0.306–0.475 | A (4) | A | A |
| 14 | 100–0–0.198–0.295–0.507 | A (2) | A | A |
| 15 | 100–0–0.187–0.301–0.512 | A (4) | A | A |
| 16 | 30–70–0.044–0.396–0.56 | D (23) | D | D |
| 17 | 0–100–0–0.417–0.583 | D (34) | D | D |
| 18 | 50–50–0.086–0.382–0.532 | D (19) | D | D |
| 19 | 50–50–0.098–0.318–0.584 | D (17) | D | C |
| 20 | 30–70–0.038–0.389–0.573 | D (24) | D | C |
| Total true prediction | 13 | 14 | ||
The accuracy of each prediction can be assessed by dividing the number of true predictions to the total number of examinations. Accordingly, the accuracy of ctree and rpart function are 65% and 70% respectively, which are in excellent agreement with results acquired before.
6. Conclusions
Supervised machine learning algorithms were utilised for classifying the 3D-printed boron-based geopolymer concrete. A total of 114 observations were categorised in four classes of A, B, C and D according to their compressive strength variation. Decision trees were built by ctree and rpart functions and the performance of the modelling was statistically evaluated. The predictions could be compared in two efficient ways. First, the simplicity of the model could be assessed based on the predictions rules and comprising the number of parameters. Accordingly, rpart function is far more uncomplicated with only two parameters for 50% of the predictions and three parameters for another half. Whereas, ctree function used four factors for 74% of the predictions and two factors for only 26% of the predictions. Secondly, the cumulative accuracy of each prediction function was used as a comparing criterion. The cumulative accuracy factor was obtained by multiplying the number of predictions in each category and the appropriate positive predictive value. Acquiring 70% cumulative accuracy for rpart function with respect to 63% for that of ctree function evidenced similar but slightly better performance for rpart function to predict compressive strength of 3D-printed boron-based geopolymer samples. Moreover, the importance of the percentage of slag and the ratio of boron ions can be seen in the decision trees created by ctree and rpart functions respectively.Obtaining false discovery rate is more related to the complexity of correlation between compressive strength and covariates. This study can be an excellent starting point for developing a guide/standard that maps the 3D-printed boron-based geopolymer samples into categories based on compressive strength.
Conflicts of interest
In this paper, there are no conflicts to declare.Acknowledgements
The authors acknowledge the Swinburne University of Technology, particularly Professor Jay Sanjayan and Dr Ali Nazari, for providing the opportunity to conduct this research.References
- B. Khoshnevis, et al., Contour crafting simulation plan for lunar settlement infrastructure buildup, in Earth and Space 2012: Engineering, Science, Construction, and Operations in Challenging Environments. 2012. 1458-1467.
- B. Khoshnevis and R. Dutton, Innovative rapid prototyping process makes large sized, smooth surfaced complex shapes in a wide variety of materials, Materials Technology, 1998, 13(2), 53–56 CrossRef.
- D. Enrico, Design of D-shape printers, Monolite UK Ltd, 2007 Search PubMed.
- A. Rudenko, 3D concrete house printer, Total Kustom, 2015 Search PubMed.
- B. Panda, et al., Additive manufacturing of geopolymer for sustainable built environment, J. Cleaner Prod., 2017, 167, 281–288 CrossRef CAS.
- B. Panda, et al., Current challenges and future potential of 3D concrete printing: Aktuelle Herausforderungen und Zukunftspotenziale des 3D-Druckens bei Beton, Materialwiss. Werkstofftech., 2018, 49(5), 666–673 CrossRef.
- A. Bagheri, et al., Molecular simulation of water and chloride ion diffusion in nanopores of alkali-activated aluminosilicate structures, Ceram. Int., 2018, 44(17), 20723–20731 CrossRef CAS.
- S. Moukannaa, et al., Alkaline fused phosphate mine tailings for geopolymer mortar synthesis: Thermal stability, mechanical and microstructural properties, J. Non-Cryst. Solids, 2019, 511, 76–85 CrossRef CAS.
- A. Nazari, et al., Thermal shock reactions of Ordinary Portland cement and geopolymer concrete: Microstructural and mechanical investigation, Constr. Build. Mater., 2019, 196, 492–498 CrossRef CAS.
- J. Davidovits, Geopolymer chemistry and applications, Geopolymer Institute, France, 2008 Search PubMed.
- B. Singh, et al., Effect of activator concentration on the strength, ITZ and drying shrinkage of fly ash/slag geopolymer concrete, Constr. Build. Mater., 2016, 118, 171–179 CrossRef CAS.
- A. Bagheri and A. Nazari, Compressive strength of high strength class C fly ash-based geopolymers with reactive granulated blast furnace slag aggregates designed by Taguchi method, Mater. Des., 2014, 54, 483–490 CrossRef CAS.
- A. Gharzouni, E. Joussein, B. Samet, S. Baklouti and S. Rossignol, Effect of the reactivity of alkaline solution and metakaolin on geopolymer formation, J. Non-Cryst. Solids, 2015, 410, 127–134 CrossRef CAS.
- A. Nazari, A. Bagheri and S. Riahi, Properties of geopolymer with seeded fly ash and rice husk bark ash, Mater. Sci. Eng., A, 2011, 528(24), 7395–7401 CrossRef CAS.
- A. Nazari, S. Riahi and A. Bagheri, Designing water resistant lightweight geopolymers produced from waste materials, Mater. Des., 2012, 35, 296–302 CrossRef CAS.
- S. Selmani, A. Sdiri, S. Bouaziz and S. Rossignol, Geopolymers based on calcined tunisian clays: Effects of alkaline solution on vibrational spectra and mechanical properties, Int. J. Miner. Process., 2017, 165, 50–57 CrossRef CAS.
- F. N. Okoye, J. Durgaprasad and N. B. Singh, Effect of silica fume on the mechanical properties of fly ash based-geopolymer concrete, Ceram. Int., 2016, 42(2), 3000–3006 CrossRef CAS.
- K. K. Deevasan and R. V. Ranganath, Geopolymer concrete using industrial byproducts, Proc. Inst. Civ. Eng.: Constr. Mater., 2010, 164(1), 43–50 Search PubMed.
- A. Bagheri, A. Nazari, J. G. Sanjayan and P. Rajeev, Alkali activated materials vs geopolymers: Role of boron as an eco-friendly replacement, Constr. Build. Mater., 2017, 146, 297–302 CrossRef CAS.
- J. W. Phair and J. S. J. Van Deventer, Characterization of fly-ash-based geopolymeric binders activated with sodium aluminate, Int. J. Miner. Process., 2002, 41(17), 4242–4251 CAS.
- L. Xin, X. Jin-yu, L. Weimin and B. Erlei, Effect of alkali-activator types on the dynamic compressive deformation behavior of geopolymer concrete, Mater. Lett., 2014, 124, 310–312 CrossRef CAS.
- A. Bagheri, A. Nazari, J. G. Sanjayan, P. Rajeev and W. Duan, Fly ash-based boroaluminosilicate geopolymers: Experimental and molecular simulations, Ceram. Int., 2017, 43(5), 4119–4126 CrossRef CAS.
- G. F. Huseien, J. Mirza, M. Ismail and M. W. Hussin, Influence of different curing temperatures and alkali activators on properties of GBFS geopolymer mortars containing fly ash and palm-oil fuel ash, Constr. Build. Mater., 2016, 125, 1229–1240 CrossRef CAS.
- A. Bagheri, et al., Microstructural study of environmentally friendly boroaluminosilicate geopolymers, J. Cleaner Prod., 2018, 189, 805–812 CrossRef CAS.
- S. C. Paul, B. Panda and A. Garg, A novel approach in modelling of concrete made with recycled aggregates, Measurement, 2018, 115, 64–72 CrossRef.
- A. Garg, et al., An artificial intelligence model for computing optimum fly ash content for structural-grade concrete, Adv. Civ. Eng. Mater., 2019, 8(1), 56–70 Search PubMed.
- A. Bagheri, A. Nazari and J. Sanjayan, The use of machine learning in boron-based geopolymers: Function approximation of compressive strength by ANN and GP, Measurement, 2019, 141, 241–249 CrossRef.
- L. Rokach and O. Z. Maimon, Data mining with decision trees: theory and applications, World Scientific, Singapore, 2008, vol. 69 Search PubMed.
- S. Al-Qutaifi, A. Nazari and A. Bagheri, Mechanical properties of layered geopolymer structures applicable in concrete 3D-printing, Constr. Build. Mater., 2018, 176, 690–699 CrossRef CAS.
- S. H. Bong, et al., Fresh and hardened properties of 3D printable geopolymer cured in ambient temperature, RILEM International Conference on Concrete and Digital Fabrication, Springer, Zurich, 2018 Search PubMed.
- Y.-S. Shih, A note on split selection bias in classification trees, Comput. Stat. Data Anal., 2004, 45(3), 457–466 CrossRef.
- L. Breiman, Some properties of splitting criteria, Mach. Learn., 1996, 24(1), 41–47 Search PubMed.
- A. Samimi, P. Rajeev, A. Bagheri, A. Nazari, J. Sanjayan, A. Amosoltani, M. S. Esfahani and S. Zarinabadi, Use of data mining in the corrosion classification of pipelines in Naphtha Hydro-Threating Unit (NHT), Pipeline Sci. Technol., 2019, 3(1), 14–21 CrossRef CAS.
- S. Shi, et al., Multi-scale computation methods: Their applications in lithium-ion battery research and development, Chin. Phys. B, 2015, 25(1), 018212 CrossRef.
- Y. Liu, et al., Multi-Layer Feature Selection Incorporating Weighted Score-Based Expert Knowledge toward Modeling Materials with Targeted Properties, Adv. Theory Simul., 2020, 3(2), 1900215 CrossRef CAS.
- Y. Liu, et al., Predicting the onset temperature (Tg) of GexSe1−x glass transition: a feature selection based two-stage support vector regression method, Sci. Bull., 2019, 64(16), 1195–1203 CrossRef CAS.
- Y. Liu, et al., The onset temperature (Tg) of AsxSe1−x glasses transition prediction: A comparison of topological and regression analysis methods, Comput. Mater. Sci., 2017, 140, 315–321 CrossRef CAS.
- Y. Liu, et al., Materials discovery and design using machine learning, J. Materiomics, 2017, 3(3), 159–177 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |