Evaluation of microflow configurations for scale inhibition and serial X-ray diffraction analysis of crystallization processes

Abstract

The clean and reproducible conditions provided by microfluidic devices are ideal sample environments for in situ analyses of chemical and biochemical reactions and assembly processes. However, the small size of microchannels makes investigating the crystallization of poorly soluble materials on-chip challenging due to crystal nucleation and growth that result in channel fouling and blockage. Here, we demonstrate a reusable insert-based microfluidic platform for serial X-ray diffraction analysis and examine scale formation in response to continuous and segmented flow configurations across a range of temperatures. Under continuous flow, scale formation on the reactor walls begins almost immediately on mixing of the crystallizing species, which over time results in occlusion of the channel. Depletion of ions at the start of the channel results in reduced crystallization towards the end of the channel. Conversely, segmented flow can control crystallization, so it occurs entirely within the droplet. Consequently, the spatial location within the channel represents a temporal point in the crystallization process. Whilst each method can provide useful crystallographic information, time-resolved information is lost when reactor fouling occurs and changes the solution conditions with time. The flow within a single device can be manipulated to give a broad range of information addressing surface interaction or solution crystallization.

---

Introduction

Crystallization is fundamental to many fields including environmental science,^1–3 biomineralization,^4–6 and solid-state physics.^7–9 Despite this, many questions remain about the mechanisms of crystal nucleation and growth,¹⁰ where this can be attributed to the challenges associated with characterizing the molecular-scale processes that govern these phenomena.^11–13 Further, the majority of crystallization experiments are performed in large reaction volumes (≥1 mL), which experience non-uniform mixing during the early stages of the reaction and inevitably contain impurities.^13–15 Thanks to the ever-improving accessibility of microfabrication techniques, microfluidic devices are now drawing increasing attention as a means of performing crystallization, where these offer clean and controllable reaction environments.^16–20

An additional benefit of utilizing microfluidics is the ability of lab-on-a-chip devices to be coupled to characterization techniques, such as X-ray scattering and diffraction, which can facilitate in situ analysis of crystallization and other assembly processes. Importantly, performing these types of analyses require highly controlled and low X-ray absorbing sample environments, where microfluidic devices seem like a natural choice, since their small channel size provides efficient and well-defined heat and mass transport and minimises the required beam path through a sample. Indeed, while originally used simply to grow high quality protein crystals for subsequent off-chip X-ray diffraction (XRD),²¹ microfluidic devices comprising thin, low X-ray scattering windows are now becoming increasingly utilized for on-chip X-ray analysis.²² This has enabled progress in de novo protein structure determination²³ and fixed-target serial crystallography²⁴ and also allowed researchers to investigate dynamic processes such as the shear-induced alignment of liquid crystals^25,26 and surfactants,^27,28 the arrangement/assembly of biomolecular structures,^29,30 the nucleation of nanoparticles^31,32 and the growth of crystals.³³

Previous work in developing microfluidic sample environments for in situ X-ray analysis has been focused on small-angle X-ray scattering (SAXS). Many of these devices have been proof-of-concept and limited in the observable residence time, i.e. the device window allows only a few seconds of the flow to be analysed and/or the short channel length limits on-chip reaction times. We recently introduced a new technique, droplet microfluidics-coupled X-ray diffraction (DMC-XRD), and used it to perform wide-angle X-ray scattering (WAXS) analysis of crystal nucleation and growth over long observable residence times (>2 min).³⁴ DMC-XRD is analogous to injector-based serial crystallography in that diffraction patterns at each time point are obtained by combining reflections from a series of flowing crystals rather than from a single crystallite.³⁵

Here, we further explore this technique and the accompanying insert-based microfluidic platform and weigh the merits of continuous versus segmented flow for analysing the crystallization of sparsely soluble materials. Using calcium carbonate as a model system, the inlet mixing configuration and surface wettability are shown to be crucial to minimising scale build-up that changes solution conditions over time, effecting analytical results. We additionally show that nucleating agents that promote crystallization in the “bulk” of the droplet further reduce scaling and are an excellent system for studying with DMC-XRD. The seeding of crystallising solutions with a target material is of great importance in the pharmaceutical and chemical industries,^36–39 and has recently been recognized as a way to reduce the clogging of flow crystallisers.⁴⁰ The results presented here demonstrate that foreign material which promotes heterogeneous nucleation in solution can also reduce scale build-up on reactor surfaces.

Materials and methods

Design of microfluidic platform

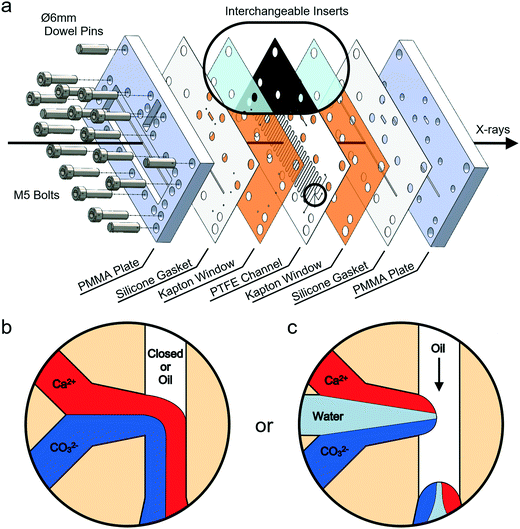
Experiments were conducted using a versatile, insert-based microfluidic platform that has been introduced previously.³⁴ Briefly, the core of the device is a polytetrafluoroethylene (PTFE) insert into which the flow channel is cut, and this is sandwiched between two laser-cut polyimide (Kapton) X-ray windows, two silicone rubber gaskets and two poly(methyl methacrylate) (PMMA) plates comprising central slits that allow the passage of X-rays (Fig. 1a and S1‡). The PTFE insert used has a serpentine flow channel with a cross section of 300 μm × 300 μm and a total length of 85 cm. This passes under the X-ray slits 36 times, enabling data collection at these positions. The PTFE insert also carries a T-junction droplet generator with two inlets for aqueous solutions and a third inlet for the introduction of the continuous oil phase (Fig. 1b). The same insert was additionally used for continuous flow experiments, where this was achieved by plugging the inlet to the third channel. Inserts with a fourth inlet situated between the two aqueous inlets were also used to provide a “buffer” flow of solvent (water) that delays mixing of counter-ions before droplet break-up and can reduce fouling at the inlet (Fig. 1c). Importantly, the insert-based design approach allows inserts made from different materials and bearing different channel layouts to be interchanged based on the requirements of the particular chemical application or analysis technique (Fig. 1a, inset). An assembled device with the current inserts and the view through the transparent X-ray window using a back-illuminated microscope are presented in Fig. 2.

Fig. 1 (a) 3D computer-aided design (CAD) of the insert-based XRD device in an exploded view displaying the laser-cut inserts and other device components. The inset demonstrates the ability to exchange window and channel inserts. (b) The 1st design of the T-junction utilised for continuous flow or segmented flow. (c) The 2nd design of the T-junction used for providing a buffer (water) flow between reagents in segmented flow experiments.

Fig. 2 (a) An assembled device with cartridge heater and thermocouple inserted. (b) View of the T-junction and positions 1 and 2 through the top PMMA slit. Distortion at the edges of the image is due to reflections coming from the side walls of the top PMMA piece.

A blind bore in one side of the bottom PMMA plate is used for the insertion of a ceramic cartridge heater (6 mm diameter) and a K-type thermocouple (Fig. 2a). Located directly beneath the solution inlets, this enables the creation of a temperature gradient along the channel. The solutions are heated immediately upon entering the chip and allowed to cool as they travel downstream. In this way, crystallization can be observed at a range of temperatures within a single experiment.

Crystallization experiments: continuous flow

We investigated the effect of different flow conditions on device scaling using the key inorganic model system,⁴¹ calcium carbonate (CaCO₃), an essential chemical additive and a common cause of scale build-up in industry.^42,43 CaCO₃ precipitation was studied in continuous flow at ambient temperatures and under heated conditions. CaCO₃ has three anhydrous crystalline polymorphs that can be found at ambient temperatures and pressures: these are calcite, aragonite and vaterite. Calcite is the most thermodynamically stable polymorph at room temperature, but other polymorphs can form depending on the reaction conditions, such as at high supersaturations or temperatures or in the presence of additives.^44,45 Each polymorph also has a characteristic habit, with calcite typically appearing as large rhombohedral single crystals, aragonite as needle-like crystals or aggregates, and vaterite as polycrystalline spherulites.⁴ CaCO₃ also has an amorphous phase, amorphous calcium carbonate (ACC), which often serves as a precursor to more stable crystalline polymorphs.^46,47

Experiments at elevated temperatures were performed by heating the reaction solutions once they entered the device using the embedded heater; the heater was allowed to equilibrate before flows were introduced. Due to the small mass flow rate (<0.2 mg s⁻¹), the solutions heat rapidly once on-chip. 8 mM equimolar solutions of CaCl₂ (Sigma Aldrich) and Na₂CO₃ (Fisher) were used for CaCO₃ precipitation (4 mM final Ca²⁺ and CO₃²⁻ concentrations). Solutions were pumped with neMESYS low-pressure syringe drivers (Cetoni), and each solution was set at a flow rate of 7 μL min⁻¹ (for a total of 14 μL min⁻¹), which corresponds to an average total velocity of 2.6 mm s⁻¹ in the main channel and a total solution residence time of 326 s (∼5.44 min).

Crystallization experiments: segmented flow

CaCO₃ precipitation was also investigated in segmented flow with a fluorinated oil (Fluorinert™ FC-40) containing 2 wt% triblock copolymer surfactant⁴⁸ serving as the continuous phase. Such non-ionic surfactants have been shown to have little effect on CaCO₃ crystallization.⁴⁹ Higher reagent concentrations than for continuous flow experiments were utilised in order to obtain crystals within the residence time of the chip, recognising crystallization in droplets is significantly slower than in bulk.⁵⁰ Two different concentrations were studied in segmented flow: 12.5 mM Ca²⁺/50 mM CO₃²⁻ and 50 mM Ca²⁺/50 mM CO₃²⁻ final concentrations. For the latter concentration, two experiments were performed: one without a nucleating agent and one in which the CaCl₂ solution was seeded with 0.01 wt% of ground 58S porous bioactive glass (Naomi's Nucleant, Molecular Dimensions; Fig. S2‡) to promote faster crystal growth.³⁴ The total flow rates utilised ranged from 16–32 μL min⁻¹ which corresponds to an average total velocity of 3.0–5.9 mm s⁻¹ in the main channel and a total residence time of 143–286 s (∼2.38–4.76 min). All solutions were filtered with a 0.22 μm Millipore syringe filter before being loaded into syringes (the CaCl₂ solution was filtered before adding the bioactive glass). The solution saturation index was calculated for each condition using Visual MINTEQ (Tables S1 and S2‡).^51,52

X-ray experiments at Diamond I11

Continuous flow data were collected at beamline I11 of the Diamond Light Source (Fig. S3‡).⁵³ Microfluidic devices were mounted on a translational stage, and analysis was performed in transmission mode using a highly collimated X-ray beam of 200 × 200 μm² spot size at 15 keV and a CCD area detector (Pixium RF4343, Thales Group). It is important to note that the X-ray beam on I11 is normally unfocussed to achieve high resolution diffraction, and it was slit down to the size required to pass through the microchannel. During device assembly, a silicon calibrant powder (NIST standard) was loaded into a secondary channel (Fig. 2a), so that the sample-to-detector distance could be calibrated for each individual device. After assembly, devices were fastened to the stage using an optical rail and rail carriage (Thorlabs), which enables devices to be quickly and reproducibly mounted and exchanged between experiments. Once calibrated using the silicon standard, the device is raised so that the primary slit is in the beam path. Using short X-ray exposures along with the computer-aided design (CAD) file of the chip, the position of the beam in relation to the device can be mapped. The known diffraction patterns of PTFE and PMMA are then used to find the centre of each analysis position (i.e. the beam is in the centre of the channel when diffraction from these materials is minimised). The characteristic background scattering profiles from the various device components are shown in Fig. S4 in the ESI.‡

Once each position is mapped, flow is then initiated (for ambient temperature reactions). Alternatively, if experiments are to be conducted at higher temperatures, the cartridge heater embedded in the bottom plate is switched on and allowed to equilibrate prior to initiating flow. Individual experiments were run for approximately 40 min, during which time XRD data were collected from individual channel positions using 60–120 s long exposures (i.e. integrating all collected photons over this time into a single image). Two-dimensional (2D) diffraction patterns collected from the area detector were viewed with Data Analysis WorkbeNch (DAWN)⁵⁴ and Matlab® (MathWorks). These 2D patterns were processed with a custom Matlab script (link available in the ESI‡) and integrated to attain the one-dimensional (1D) diffraction patterns that were analysed with Matlab.

X-ray experiments at ESRF ID13

Devices were mounted on a translational stage at beamline ID13 of the European Synchrotron Radiation Facility for segmented flow experiments (Fig. S1‡). Analysis was performed in transmission mode using a microfocused X-ray beam of 12 × 15 μm² spot size at 13 keV using a hybrid photon counting detector (EigerX 4M, Dectris). This beam size was obtained by defocusing from the regular focused beam size of 3 × 2 μm². The beamline is equipped with an optical microscope that can be lowered into the beam path when the beam shutter is closed. The focal point of this microscope is pre-aligned with the focal point of the beam, meaning that accurate positioning can be obtained by finding the desired analysis points on the device with the microscope and then saving the corresponding stage coordinates. The sample-to-detector distance was determined by placing a CeO₂ calibrant-filled capillary in the microscope focal point and collecting a diffraction pattern at the same distance used during experiments – eliminating the need to pre-load a calibrant powder into each device.

After device assembly, mounting and positioning, the flow was initiated and discrete frame-by-frame patterns were obtained consecutively at 50 Hz for 10 s to perform DMC-XRD (500 frames acquired, ∼4 μs dead time between frames). Diffraction patterns were collected from various positions along the device for 45–60 min, where individual frames from each position were processed and combined to construct a composite 2D diffraction pattern according to the method developed by Levenstein et al.³⁴ A link to the freely available code and a more detailed description of the processing routine are included in the ESI.‡ Additional beam and detector parameters at both beamlines can be found in Tables S3 and S4 in the ESI.‡

Optical and scanning electron microscopy

Time-resolved synchrotron XRD results were complemented by in situ optical microscopy and ex situ scanning electron microscopy (SEM). Continuous and segmented flow experiments were conducted as above, with the device being mounted on the stage of an M165 FC stereomicroscope (Leica). Images and videos were captured with a USB 3.0 DMC2900 colour camera with a 3.1 megapixel CMOS sensor using the Leica Application Suite (LAS) software. After flow experiments, the devices were disassembled and the bottom Kapton windows were rinsed with water and ethanol and allowed to dry at room temperature. The windows were then cut to fit on aluminium SEM stubs, coated with 4 nm of iridium (208HR sputter coater, Cressington), and imaged with a Nova NanoSEM 450 (FEI).

Results

Crystallization in continuous flow

Fluid mixing inside the device under continuous flow conditions was characterized using solutions of coloured dyes. In the T-junction, the input solutions begin to mix immediately adjacent to their interface. This interfacial region grows as the solutions travel downstream, until the solutions are fully mixed. This occurs at approximately position 1 (9.7 s) with a flow rate of 14 μL min⁻¹ (Fig. S5‡), which demonstrates that mixing is rapid as compared with the total device residence time of 5.44 min (at position 36). Mixing of 8 mM CaCl₂ and Na₂CO₃ solutions under continuous flow was also simulated using finite element modelling (COMSOL Multiphysics®) and showed good agreement with the experiments (Fig. S5‡). It is noted mixing experiments and simulations only describe the initial conditions within the flow channel, as some ions will be sequestered by crystal growth after crystals form.

CaCO₃ crystallization was initially performed under continuous flow conditions at ambient temperature (23 °C). Focusing on the T-junction, optical microscopy revealed the presence of crystals within 5 min after flow initiation, where these were located at the interface between the CaCl₂ and Na₂CO₃ flows (Fig. 3a). XRD recorded after 10 and 15 minutes corresponded to calcite, while some vaterite was also seen after 20 min (Fig. 4a). Concurrent growth of vaterite and calcite was observed at the T-junction for the remainder of the experiment. Ex situ analysis of the channel walls using SEM revealed the presence of elongated calcite crystals that were aligned with the flow, together with smaller rhombohedral calcite crystals and vaterite spherulites (Fig. 3a and S6a‡). Fewer and smaller crystals were observed at subsequent positions on the device and detected later by XRD (Fig. S7–S9‡). These experiments show CaCO₃ scale build-up on the walls of the device was greatest near the T-junction, and then decreased in quantity until dropping below our limit of detection at position 3 and beyond (Fig. 5a).

Fig. 3 Time-resolved images of the T-junction during continuous flow experiments at (a) ambient and (b) elevated temperatures and segmented flow experiments (c) without a buffer flow and (d) with a buffer flow and a nucleating agent. The last panels display SEM micrographs of the final state of the T-junction after the respective experiment. Scale bars are 200 μm in optical images and are 50 μm in SEM images.

Fig. 4 Time-resolved diffraction patterns revealing scale build-up at the T-junction during continuous flow experiments at (a) ambient and (b) elevated temperatures. Peaks are labelled with their corresponding polymorph, calcite (C) or vaterite (V). Some peaks correspond to the channel insert (PTFE).

Fig. 5 Spatially-resolved diffraction patterns from the (a) continuous flow at ambient temperature, (b) continuous flow with temperature gradient, (c) segmented flow without buffer and (d) segmented flow with buffer and nucleating agent experiments. Peaks are labelled with their corresponding polymorph, calcite (C) or vaterite (V). Some peaks correspond to the channel insert (PTFE). (d) Used with permission from Wiley-VCH Verlag GmBH & Co. KGaA.

Continuous flow with a temperature gradient

CaCO₃ precipitation was also studied under a temperature gradient created by an embedded cartridge heater, which was set at 130 °C using a thermocouple and proportional–integral–derivative (PID) controller (RS). IR thermography was used to determine the temperature inside the channel, and the temperatures at the T-junction, position 1 and position 2 were measured as 48.6 ± 1, 38.3 ± 1 and 33.3 ± 1 °C, respectively (Fig. S10‡). In common with the ambient condition experiments, few crystals were observed at subsequent positions.

Initial precipitation was observed within the T-junction (Fig. 3b), where XRD at 5 min revealed the presence of vaterite and a scattering band corresponding to amorphous calcium carbonate (ACC) (Fig. 4b and S11‡).^55,56 Longer durations resulted in a massive build-up of vaterite at the T-junction (Fig. 3b), and a reduction in ACC (Fig. 4b). This large-scale precipitation resulted in reduced crystal growth at positions 1, 2 and beyond, even compared to experiments at ambient temperature (Fig. 5b and S12‡).

Crystallization in segmented flow without a buffer flow

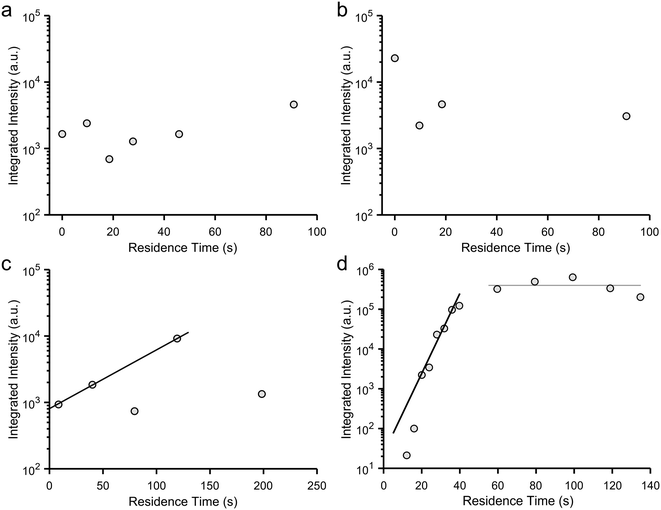
Crystallization was studied using two segmented flow configurations. In the first, CaCl₂ and Na₂CO₃ flows were combined at the T-junction with no buffer flow of water between the aqueous reagent inlets (Fig. 1b). Droplets were formed containing 12.5 mM Ca²⁺/50 mM CO₃²⁻, and at this supersaturation, precipitation occurred at the point of mixing (Fig. 3c). Precipitates would periodically detach themselves within the flow, but continued build-up of crystals eventually caused permanent occlusion of the T-junction after ca. 10 min. In spite of this, precipitate was also observed within the droplets (Movie S1 and Fig. S13‡). This was principally ACC at position 1, together with some calcite, as identified by DMC-XRD (Fig. 5c). The microfocused X-ray beam (ESRF ID13) utilised for segmented flow experiments allows a larger portion of the beam path to be occupied by the diffracting crystal (i.e. higher crystal to solvent volume ratio), and the high frame rate of the detector allowed removal of frames not displaying crystalline diffraction to be neglected.³⁴ Together, these two features provide greater contrast between background scattering and crystalline diffraction when compared to continuous flow experiments (i.e. greater signal-to-noise ratio; Fig. 5).

The area under each diffraction pattern, or integrated intensity, increased by an order of magnitude from position 1 to 15 (8.5 to 119.3 s residence time), demonstrating further crystal nucleation and growth (Fig. 5c and 6c). However, the amount of diffraction recorded at each position became less consistent after 5–10 min of flow – likely due to continued fouling of the T-junction partially blocking the channel – leading to several positions presenting lower or even zero diffraction intensity. The fouling at the T-junction also makes it unclear whether the measured diffraction is from crystals that nucleated within droplets or from material that had detached from the mixer walls. SEM examination of the Kapton window after 40 minutes of flow revealed that fouling extended from the T-junction to position 1 (Fig. 3c and S14‡).

Fig. 6 Integrated intensity of diffraction patterns as a function of residence time for the (a) continuous flow at ambient temperature, (b) continuous flow with temperature gradient, (c) segmented flow without buffer and (d) segmented flow with buffer and nucleating agent experiments. In continuous flow experiments diffraction intensity does not increase with residence time, indicating crystal growth happens in early positions. Whereas both segmented flow experiments follow a trend of intensity increasing with residence time, indicating crystals growing in flow. The black lines in (c) and (d) are first-order exponential fits of the initial increase in intensity. The horizontal grey line in (d) is a guide to the eye.

Segmented flow with buffer and hydrophobic treatment

In order to overcome the problems arising from fouling at the T-junction, a second segmented flow configuration was explored. This design introduced a buffer flow of water between the reagents to delay mixing until after droplet break-up (Fig. 1c) and made use of a commercial hydrophobic agent (Aquapel)⁵⁷ to minimise wetting of the aqueous phase on channel walls. This configuration resulted in better initial droplet production and much slower scale formation compared to the condition without a buffer flow or chemical treatment (Fig. S15a‡). Finite element simulations of the buffer configuration demonstrate its effectiveness in slowing the mixing of Ca²⁺ and CO₃²⁻ ions, where concentrations of both ions are kept to below 1.5 mM – compared to a final concentration of 50 mM – in mixed regions before droplet break-up (Fig. S16‡).

DMC-XRD patterns were recorded along the device (Fig. S15b‡), but owing to the high supersaturation and the fact that crystallization typically proceeds more slowly in droplets,⁵⁸ most precipitate was ACC. Thus, the induction time of crystal nucleation for this condition is greater than the residence time of the chip (2.38 min). Scale formation at the T-junction increased after 15 min of flow, where detached fragments from this build-up or secondary scaling are likely responsible for the isolated diffraction observed at position 30 (Fig. S15b and c‡).

Segmented flow with a nucleating agent

We also studied the influence of a calcite nucleating agent, porous bioactive glass,³⁴ on scale build-up within the device. Such additives are being explored for clogging mitigation during continuous synthesis processes⁴⁰ and can be used to nucleate target materials.^59,60 In this case, fouling was prevented for the duration of the experiment – even at the highest concentration employed (50 mM Ca²⁺/CO₃²⁻) – as confirmed by SEM (Fig. 3d). Under these conditions, precipitation was observed in droplets from position 1 (Movie S2‡), but reflections from crystalline material were not detected by DMC-XRD until position 3 (12 s, Fig. 5d and 6d). The material seen at early positions was therefore primarily ACC. Rapid growth of calcite then occurred between positions 3 and 10 (12 s to 40 s residence time), as seen by the four orders of magnitude increase in the diffraction intensities, before attaining a constant value at ≈60 s due to the depletion of ACC (Fig. 6d). The entire crystallization pathway – from initial precipitation of ACC, through crystal nucleation, crystal growth, and the termination of growth – could therefore be observed using a single device.

Finally, the suitability of this configuration for serial data collection was demonstrated by the similarity between DMC-XRD data collected from the same position at different experiment times (Fig. S17‡). XRD patterns collected approximately 15 minutes apart at position 10 contained the same major calcite peaks and were of similar intensities (total integrated intensity: 1.22 × 10⁵ a.u. versus 1.33 × 10⁵ a.u.). Further, image analysis in Matlab revealed both 2D diffraction patterns to have a similar number of discrete features, thus comprising a comparable number of individual crystalline reflections (within 96%). Considering both patterns come from only 500 frames collected from ∼20 droplets (Fig. S18‡), these measurements demonstrate high reproducibility and illustrate the consistent conditions provided by segmented flow when scaling is minimised.

Discussion

These experiments provide valuable insight into the crystallization of sparingly soluble materials within continuous and segmented flow devices and illustrate how these can be employed to study crystallization mechanisms. Continuous flow is employed industrially in the manufacturing and purification of many particulate materials including pharmaceuticals, fine chemicals and nanomaterials, where the ability to control the size, shape and structure of the end-products is critical. Fouling is also a key issue in such systems and can negatively affect the consistency of the product material. On-line analysis is therefore critical to understand the impact of different reaction conditions (e.g. flow rate, solution composition and impurities) on the product and to avoid fouling and aggregation. While many industrial processes are performed at larger length scales, our results provide broad guidance on fouling mitigation and are directly applicable to recent developments in miniaturised industrial platforms including oscillatory baffled reactors (OBRs),⁶¹ continuous stirred tank-reactors (CSTRs),⁶² and automated “plug-and-play” systems.⁶³

Our experiments demonstrate that significant precipitation occurred on the channel walls under continuous flow at both ambient and elevated temperatures (Fig. 3). The majority of crystals precipitated close to the mixing point, and remained adhered to the surface, although large aggregates could become detached under flow. Further, crystals located on the device walls grow over time, changing the supersaturation of the solution and decreasing precipitation at subsequent positions downstream (Fig. 7a). Diffraction patterns collected from the same position at different times therefore do not represent the same growth conditions and cannot be merged to create a composite dataset. We also observed that the crystals were often preferentially oriented on the channel walls which reduces the quality of the diffraction data, and in particular, its value in identifying different polymorphs. Continuous flow devices are therefore poorly suited to fundamental studies of crystallization mechanisms unless surface interaction is of specific interest, and most importantly, cannot be used for serial data collection.

Fig. 7 Examples of microfluidic X-ray analysis of crystallization in (a) continuous and (b) well-segmented flow. In (a), surface growth at early channel positions lowers the supersaturation of the solution resulting in less growth downstream, where this is apparent from decreased diffraction intensity. In (b), growth occurs in the bulk of droplets as they travel downstream, resulting in increasing diffraction intensity.

Segmented flow, in contrast, provides an excellent environment for studying crystallization mechanisms. Use of a buffer flow between the inlet flows of the reactants, chemical treatment of device walls, and adjustment of solution conditions ensured that fouling was virtually eliminated and that precipitation occurred uniquely within the droplets. All droplets passing a particular location are therefore at the same point in the crystallization pathway, and data can be combined to give a representative diffraction pattern. In contrast to continuous flow, crystals growing in droplets constantly tumble within their internal recirculating flow field,⁶⁴ such that random orientations are presented to the beam (Fig. 7b). This suggests that by analysing enough droplets, a powder XRD pattern representative of a non-oriented sample will be generated.

However, segmented flow does present some challenges. In situ X-ray characterization of segmented flow is more demanding on hardware and data analysis than continuous flow. XRD patterns from continuous flow systems can be readily collected using long (≥1 min) detector exposures, where the data is incorporated into a single frame. This approach cannot be used for segmented flow systems, as the significant scattering from the continuous oil phase masks the diffraction from the crystals (Fig. S19‡). Individual frames must therefore be collected from the droplets and oil, and this must be carried out to satisfy the Nyquist–Shannon criterion, which states that the sampling rate should be at least two times the highest frequency of the signal.⁶⁵ In the case of DMC-XRD, the ‘signal’ is the droplets/crystals, their ‘frequency’ is the speed at which they pass by the beam, and the ‘sampling rate’ is the frame rate of the X-ray detector (Fig. S20‡). The X-ray exposure time must therefore be shorter than half the interval between incoming droplets, which is challenging for many detectors, and long run times may be required to accumulate sufficient signal from droplets containing small numbers of crystals. These problems were overcome at beamline ID13 (ESRF), which provides high flux density, microfocused X-rays, and a detector with a maximum frame rate much higher than our droplet generation rates (Tables S3 and S4‡).

Conclusions

These experiments contrast the use of continuous and segmented flow microfluidic devices to study the crystallization of sparingly soluble compounds. Continuous flow devices are shown to have significant problems with scale build-up and fouling, where massive precipitation occurs close to the input channels at which the reaction solutions combine. Segmented flow systems, in turn, can offer highly reproducible reaction environments. With the use of a buffer flow between the reactant flows at the input T-junction, a routine chemical treatment to render the channel walls hydrophobic, and a nucleating agent, these devices could be operated for an hour without fouling. Segmented flow is therefore strongly preferred, where the stable chemical conditions at each position make it possible to perform injector-based serial crystallography-on-a-chip, thereby allowing a crystallization pathway to be mapped with time.

Author contributions

F. C. M. and N. K. conceived and supervised the project. M. A. L. designed and fabricated the insert-based microfluidic devices. M. A. L., Y.-Y. K., C. A.-C., C. G. N., S. J. D., S. L., W. J. M., C. C. T., M. B., F. C. M., and N. K. performed synchrotron experiments. M. A. L. and L. H. performed laboratory-based experiments. M. A. L., L. H., and P. A. L. performed scanning electron microscopy. M. A. L. developed the X-ray diffraction pattern processing routines, performed simulations, and analysed all the data. M. A. L., F. C. M., and N. K. wrote the paper with contributions from all authors.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by a UK Engineering and Physical Sciences Research Council (EPSRC) Platform Grant (EP/N002423/1) and received funding from the European Research Council (ERC) under the project DYNAMIN – DLV-788968. The authors acknowledge Diamond Light Source for time on beamline I11 under commissioning time and proposals EE10425 and EE12352 and the European Synchrotron Radiation Facility for time on beamline ID13 under proposals CH4555 and CH4928. We thank beamline scientists Britta Weinhausen, Michael Sztucki and Stephen Thompson for assistance. The authors also thank Diego Pontoni, Peter van der Linden and Pierre Lloria of the Partnership for Soft Condensed Matter (PSCM) for support during ESRF beamtimes. We additionally thank Naomi Chayen from providing the 58S bioactive glass and Graham Brown and Andrew Pickering for the device fabrication services of the EPSRC National Facility for Innovative Robotic Systems. M. A. L. acknowledges support from the US-UK Fulbright Commission and the Leeds International Research Scholarship.

References

1. R. P. Sear, Int. Mater. Rev., 2012, 57, 328–356.
2. J. D. Atkinson, B. J. Murray, M. T. Woodhouse, T. F. Whale, K. J. Baustian, K. S. Carslaw, S. Dobbie, D. O'Sullivan and T. L. Malkin, Nature, 2013, 498, 355–358.
3. J. Vergara-Temprado, A. K. Miltenberger, K. Furtado, D. P. Grosvenor, B. J. Shipway, A. A. Hill, J. M. Wilkinson, P. R. Field, B. J. Murray and K. S. Carslaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2687–2692.
4. F. C. Meldrum and H. Colfen, Chem. Rev., 2008, 108, 4332–4432.
5. T. Mass, A. J. Giuffre, C.-Y. Sun, C. A. Stifler, M. J. Frazier, M. Neder, N. Tamura, C. V. Stan, M. A. Marcus and P. U. P. A. Gilbert, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7670.
6. D. Kim, B. Lee, S. Thomopoulos and Y. S. Jun, Nat. Commun., 2018, 9, 9.
7. S. John, Nat. Mater., 2012, 11, 997–999.
8. P. B. Roder, B. E. Smith, X. Zhou, M. J. Crane and P. J. Pauzauskie, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15024–15029.
9. I. Polishchuk, N. Bianco-Stein, A. Lang, M. Kurashvili, M. Caspary Toroker, A. Katsman, J. Feldmann and B. Pokroy, Adv. Funct. Mater., 2020, 30, 1910405.
10. J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760.
11. T. Y. Gong, J. Y. Shen, Z. B. Hu, M. Marquez and Z. D. Cheng, Langmuir, 2007, 23, 2919–2923.
12. Z. Hammadi, N. Candoni, R. Grossier, M. Ildefonso, R. Morin and S. Veesler, C. R. Phys., 2013, 14, 192–198.
13. I. Lignos, S. Stavrakis, A. Kilaj and A. J. deMello, Small, 2015, 11, 4009–4017.
14. J. Leng and J. B. Salmon, Lab Chip, 2009, 9, 24–34.
15. T. W. Phillips, I. G. Lignos, R. M. Maceiczyk, A. J. deMello and J. C. deMello, Lab Chip, 2014, 14, 3172–3180.
16. M. Ildefonso, N. Candoni and S. Veesler, Cryst. Growth Des., 2011, 11, 1527–1530.
17. X. Gong, Y.-W. Wang, J. Ihli, Y.-Y. Kim, S. Li, R. Walshaw, L. Chen and F. C. Meldrum, Adv. Mater., 2015, 27, 7395–7400.
18. S. B. Li, M. L. Zeng, T. Gaule, M. J. McPherson and F. C. Meldrum, Small, 2017, 13, 10.
19. Y. Y. Kim, C. L. Freeman, X. Q. Gong, M. A. Levenstein, Y. W. Wang, A. Kulak, C. Anduix-Canto, P. A. Lee, S. B. Li, L. Chen, H. K. Christenson and F. C. Meldrum, Angew. Chem., Int. Ed., 2017, 56, 11885–11890.
20. S. Zhang, C. J. J. Gerard, A. Ikni, G. Ferry, L. M. Vuillard, J. A. Boutin, N. Ferte, R. Grossier, N. Candoni and S. Veesler, J. Cryst. Growth, 2017, 472, 18–28.
21. C. L. Hansen, E. Skordalakes, J. M. Berger and S. R. Quake, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16531–16536.
22. A. Ghazal, J. P. Lafleur, K. Mortensen, J. P. Kutter, L. Arleth and G. V. Jensen, Lab Chip, 2016, 16, 4263–4295.
23. S. L. Perry, S. Guha, A. S. Pawate, A. Bhaskarla, V. Agarwal, S. K. Nair and P. J. A. Kenis, Lab Chip, 2013, 13, 3183–3187.
24. S. Sui, Y. X. Wang, K. W. Kolewe, V. Srajer, R. Henning, J. D. Schiffman, C. Dimitrakopoulos and S. L. Perry, Lab Chip, 2016, 16, 3082–3096.
25. R. Dootz, H. Evans, S. Köster and T. Pfohl, Small, 2007, 3, 96–100.
26. A. Otten, S. Köster, B. Struth, A. Snigirev and T. Pfohl, J. Synchrotron Radiat., 2005, 12, 745–750.
27. R. Barrett, M. Faucon, J. Lopez, G. Cristobal, F. Destremaut, A. Dodge, P. Guillot, P. Laval, C. Masselon and J. B. Salmon, Lab Chip, 2006, 6, 494–499.
28. A. S. Poulos, M. Nania, P. Lapham, R. M. Miller, A. J. Smith, H. Tantawy, J. Caragay, J. Gummel, O. Ces, E. S. J. Robles and J. T. Cabral, Langmuir, 2016, 32, 5852–5861.
29. O. Saldanha, M. E. Brennich, M. Burghammer, H. Herrmann and S. Köster, Biomicrofluidics, 2016, 10, 024108.
30. O. Saldanha, R. Graceffa, C. Hemonnot, C. Ranke, G. Brehm, M. Liebi, B. Marmiroli, B. Weinhausen, M. Burghammer and S. Köster, ChemPhysChem, 2017, 18, 1220.
31. R. Stehle, G. Goerigk, D. Wallacher, M. Ballauff and S. Seiffert, Lab Chip, 2013, 13, 1529–1537.
32. K. S. Krishna, C. V. Navin, S. Biswas, V. Singh, K. Ham, G. L. Bovenkamp, C. S. Theegala, J. T. Miller, J. J. Spivey and C. Kumar, J. Am. Chem. Soc., 2013, 135, 5450–5456.
33. T. Beuvier, E. A. C. Panduro, P. Kwasniewski, S. Marre, C. Lecoutre, Y. Garrabos, C. Aymonier, B. Calvignac and A. Gibaud, Lab Chip, 2015, 15, 2002–2008.
34. M. A. Levenstein, C. Anduix-Canto, Y.-Y. Kim, M. A. Holden, C. González Niño, D. C. Green, S. E. Foster, A. N. Kulak, L. Govada, N. E. Chayen, S. J. Day, C. C. Tang, B. Weinhausen, M. Burghammer, N. Kapur and F. C. Meldrum, Adv. Funct. Mater., 2019, 29, 1808172.
35. D. A. Shapiro, H. N. Chapman, D. DePonte, R. B. Doak, P. Fromme, G. Hembree, M. Hunter, S. Marchesini, K. Schmidt, J. Spence, D. Starodub and U. Weierstall, J. Synchrotron Radiat., 2008, 15, 593–599.
36. W. Beckmann, K. Nickisch and U. Budde, Org. Process Res. Dev., 1998, 2, 298–304.
37. P. Barrett, B. Smith, J. Worlitschek, V. Bracken, B. O'Sullivan and D. O'Grady, Org. Process Res. Dev., 2005, 9, 348–355.
38. L. Durak, M. Kennedy, M. Langston, C. Mitchell, G. Morris, M. E. Perlman, K. Wendl, F. Hicks and C. D. Papageorgiou, Org. Process Res. Dev., 2018, 22, 296–305.
39. M. A. Levenstein, L. E. Wayment, C. D. Scott, R. A. Lunt, P.-B. Flandrin, S. Day, C. Tang, C. C. Wilson, F. C. Meldrum, N. Kapur and K. Robertson, Anal. Chem., 2020, 92, 7754–7761.
40. G. Giri, L. Yang, Y. Mo and K. F. Jensen, Cryst. Growth Des., 2019, 19, 98–105.
41. L. B. Gower, Chem. Rev., 2008, 108, 4551–4627.
42. O. A. Jimoh, K. S. Ariffin, H. B. Hussin and A. E. Temitope, Carbonates Evaporites, 2018, 33, 331–346.
43. M. Nergaard, R. Beck, M. Seiersten and J. P. Andreassen, Chem. Eng. Technol., 2014, 37, 1321–1328.
44. F. C. Meldrum, Int. Mater. Rev., 2003, 48, 187–224.
45. L. Dupont, F. Portemer and M. Figlarz, J. Mater. Chem., 1997, 7, 797–800.
46. Y. W. Wang, Y. Y. Kim, C. J. Stephens, F. C. Meldrum and H. K. Christenson, Cryst. Growth Des., 2012, 12, 1212–1217.
47. J. Ihli, W. C. Wong, E. H. Noel, Y. Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169.
48. C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angile, C. H. J. Schmitz, S. Köster, H. Duan, K. J. Humphry, R. A. Scanga, J. S. Johnson, D. Pisignano and D. A. Weitz, Lab Chip, 2008, 8, 1632–1639.
49. A. S. Schenk, Y.-Y. Kim, A. N. Kulak and F. C. Meldrum, Chem. Geol., 2012, 294–295, 259–262.
50. C. J. Stephens, Y. Y. Kim, S. D. Evans, F. C. Meldrum and H. K. Christenson, J. Am. Chem. Soc., 2011, 133, 5210–5213.
51. L. N. Plummer and E. Busenberg, Geochim. Cosmochim. Acta, 1982, 46, 1011–1040.
52. L. Brecevic and A. E. Nielsen, J. Cryst. Growth, 1989, 98, 504–510.
53. C. A. Murray, J. Potter, S. J. Day, A. R. Baker, S. P. Thompson, J. Kelly, C. G. Morris, S. H. Yang and C. C. Tang, J. Appl. Crystallogr., 2017, 50, 172–183.
54. M. Basham, J. Filik, M. T. Wharmby, P. C. Y. Chang, B. El Kassaby, M. Gerring, J. Aishima, K. Levik, B. C. A. Pulford, I. Sikharulidze, D. Sneddon, M. Webber, S. S. Dhesi, F. Maccherozzi, O. Svensson, S. Brockhauser, G. Naray and A. W. Ashton, J. Synchrotron Radiat., 2015, 22, 853–858.
55. M. Faatz, F. Grohn and G. Wegner, Adv. Mater., 2004, 16, 996–1000.
56. J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Mineral. Mag., 2008, 72, 283–286.
57. L. Mazutis, J. Gilbert, W. L. Ung, D. A. Weitz, A. D. Griffiths and J. A. Heyman, Nat. Protoc., 2013, 8, 870–891.
58. C. C. Tester, M. L. Whittaker and D. Joester, Chem. Commun., 2014, 50, 5619–5622.
59. Y. Diao, T. Harada, A. S. Myerson, T. A. Hatton and B. L. Trout, Nat. Mater., 2011, 10, 867–871.
60. E. Saridakis and N. E. Chayen, Trends Biotechnol., 2009, 27, 99–106.
61. T. McGlone, N. E. B. Briggs, C. A. Clark, C. J. Brown, J. Sefcik and A. J. Florence, Org. Process Res. Dev., 2015, 19, 1186–1202.
62. M. R. Chapman, M. H. T. Kwan, G. King, K. E. Jolley, M. Hussain, S. Hussain, I. E. Salama, C. González Niño, L. A. Thompson, M. E. Bayana, A. D. Clayton, B. N. Nguyen, N. J. Turner, N. Kapur and A. J. Blacker, Org. Process Res. Dev., 2017, 21, 1294–1301.
63. A.-C. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann, J. Torosian, B. Yue, K. F. Jensen and T. F. Jamison, Science, 2018, 361, 1220.
64. J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127–9133.
65. C. E. Shannon, Proc. Natl. Acad. Sci. U. S. A., 1949, 37, 10–21.

---

Footnotes

† The data associated with this paper are openly available from the University of Leeds data repository. https://doi.org/10.5518/755.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00239a

§ Present address: Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, 1206 W Green Street, Urbana, IL, 61801, USA.

¶ Present address: Alba Synchrotron Light Source, Carrer de la Llum 2-26, 08290 Cerdanyola del Vallès, Barcelona, Spain.

|| Present address: School of Optoelectronic Engineering, Chongqing University, Chongqing 400044, China.

---