Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synchrotron hard X-ray chemical imaging of trace element speciation in heterogeneous samples: development of criteria for uncertainty analysis†
Jonas
Wielinski
 *ab,
Francesco Femi
Marafatto
*ab,
Francesco Femi
Marafatto
 ac,
Alexander
Gogos
ac,
Alexander
Gogos
 ad,
Andreas
Scheidegger
ad,
Andreas
Scheidegger
 a,
Andreas
Voegelin
a,
Andreas
Voegelin
 *a,
Christoph R.
Müller
*a,
Christoph R.
Müller
 e,
Eberhard
Morgenroth
e,
Eberhard
Morgenroth
 ab and
Ralf
Kaegi
ab and
Ralf
Kaegi
 a
a
aEawag, Swiss Federal Institute of Aquatic Science and Technology, Überlandstrasse 133, 8600 Dübendorf, Switzerland. E-mail: jonas.wielinski@eawag.ch; andreas.voegelin@eawag.ch; Tel: +41 58 765 5336 Tel: +41 58 765 5470
bETH Zürich, Institute of Environmental Engineering, 8093 Zürich, Switzerland
cSwiss Light Source, Paul-Scherrer-Institute (PSI), 5232 Villigen, Switzerland
dEMPA, Swiss Federal Laboratories for Materials Science and Technology, 9014 St. Gallen, Switzerland
eETH Zürich, Institute of Energy Technology, 8092 Zürich, Switzerland
First published on 30th January 2020
Abstract
Synchrotron hard X-ray spectroscopy with focussing optics allows recording X-ray fluorescence (XRF) maps at energies around element specific X-ray absorption edges. Stacking multiple XRF maps along the energy axis yields chemical images that contain spatially resolved information on the speciation of the absorber in the sample matrix at the micrometre scale. Short dwell times needed to keep measurement time and radiation-induced sample changes within acceptable limits result in spectral noise that affects the uncertainty in data analysis. In this study, we develop a model to quantify the uncertainty associated with the processing of XRF image stacks using Bayesian inference. To demonstrate the potential of our approach, the model is applied to stacks of XRF maps collected around the copper (Cu) K-edge (pixel size: 3 × 3 μm2, map sizes: 500 × 500 μm2). The investigated samples include digested sewage sludge spiked with either CuO nanoparticles (NP) or dissolved CuSO4 and their corresponding ashes obtained through incineration. The chemical imaging data reveal differences in species distribution between sludge spiked with CuO NP or dissolved Cu. These differences disappear during the incineration process and the resulting ashes exhibit almost identical Cu species distribution. The uncertainty analysis approach developed in this study can be used for data interpretation, but can also be used for the planning of chemical imaging experiments at synchrotron beamlines.
1 Introduction
X-ray absorption spectroscopy (XAS) is widely used to investigate the speciation of major and trace elements in a wide range of sample matrices, including complex environmental samples.1–4 With XAS, the average speciation of selected elements in homogenised samples can be evaluated using wide spread X-ray beams with lateral and horizontal extensions of hundreds of micrometres to a few millimetres.4 Over the last two decades, advanced synchrotron light sources and beamlines providing higher photon fluxes and the ability to focus the beam to small sizes enabled investigations of chemical (speciation) heterogeneities at the micrometre scale.5 Based on elemental distribution maps (micro X-ray fluorescence (XRF) spectroscopy) that provide information on the elemental distributions and their correlations, points of interest (POI) can be selected to investigate the speciation of individual elements by micro-focused X-ray absorption near-edge structure (XANES) or extended X-ray absorption fine structure (EXAFS) spectroscopy, e.g.6–9 The further development of dedicated beamlines capable of focussing hard (>4.5 keV) X-rays10 and the advancement of detection systems11 meanwhile allow to perform chemical imaging analyses. In this approach, XRF maps of the same area are recorded at multiple energies around an absorption edge to obtain spatially resolved speciation information at the micrometre scale.12,13 In micro-focused X-ray experiments for chemical imaging (sometimes also called ‘Chemical-state maps’, e.g.13), a large fraction of the beam is focused onto a micrometre sized spot on the sample using slits and/or Kirkpatrick–Baez (KB) mirrors.5,10 High photon flux densities allow users to obtain chemical images of absorbers at low concentrations in complex matrices such as environmental samples within a few hours.1,4,10,12 However, the complex and heterogeneous matrices and the redox sensitivity of certain absorber atoms may lead to radiation-induced speciation changes in the sample commonly referred to as beam damage, which has previously been reported for, e.g., Cu.14,15 To limit beam-induced transformation of the sample/absorber, the exposure time to the beam can be reduced and the sample can be cooled to cryogenic temperatures. Further, the exposure of the sample to the X-ray beam can be reduced by collecting data only at selected energies of interest containing diagnostic spectral features instead of scanning over the whole absorption edge at high energy resolution. The most relevant energies of interest are commonly identified based on the XAS data of reference materials.16The new possibilities offered by the chemical imaging attracted increased attention in environmental sciences12,13,17–21 where elements of interest often occur at low concentrations (e.g., Cu in digested sewage sludge 480–700 mg kg−1) and unevenly distributed in the sample matrix.12 Because of the potential beam damage induced by high photon flux densities, only a limited number (typically ranging from 3–10)13,17 of XRF maps around an X-ray absorption edge of a specific element of interest may be recorded to derive the chemical speciation of the absorber atom at the micrometre scale.22 Nevertheless, caused by the short dwell times (few milliseconds) and low element concentrations, data acquired with even the most advanced detector systems23 contains increased amounts of noise compared to spectra recorded on bulk samples using longer dwell times (up to seconds).12 Therefore, speciation information may be limited to the oxidation state of the absorber, or to major species classes rather than individual chemical forms. XAS and chemical imaging data processing, including the determination of the appropriate number of spectral components using principle component analysis, have considerably improved over the last decades.24–26 Furthermore, strategies and guidelines to reduce uncertainty by optimizing measurement conditions are available in the literature.27,28 Studies investigating the uncertainty associated with species information extracted from hard X-ray of chemical image stacks are still lacking, however. In this study, we therefore developed a model/algorithm to quantitatively assess the impact of uncertainty on the interpretability of chemical images derived from spatially resolved XRF maps. The usefulness of the model/algorithm was demonstrated based on chemical images recorded on digested sewage sludge that had been spiked with copper oxide nanoparticles (CuO-NP) or dissolved Cu2+ (CuSO4) as well as on their corresponding ashes. These samples that have previously been examined by bulk XAS, but information on the spatial distribution of Cu and of individual Cu species in the sludge and corresponding ashes may be relevant as well for the risk and life cycle assessment of engineered nanomaterials (details in the ESI Section S1†).
2 Materials and methods
2.1 Sample preparation and characterization of experimental samples
Two digested sludge samples were spiked with either CuO-NP (SLG NP) or dissolved CuSO4 (SLG AQ) and kept under anaerobic conditions for 24 h to allow for a sulfidation of the Cu. The sludge was dewatered, dried at 105 °C and incinerated in a pilot scale bubbling bed type fluidized bed reactor resulting in the ashes ASH NP from SLG NP and ASH AQ from SLG AQ. A detailed description of the samples and their generation can be found in Wielinski et al.29 The samples SLG NP, SLG AQ, ASH NP and ASH AQ correspond to D-NP, D-AQ, D-NP-ap and D-AQ-ap, in Wielinski et al.29 The sludge and ash samples (ASH NP and ASH AQ) were dried, embedded into an epoxy resin (one part EpoFix Hardener and seven parts EpoFix Resin, both Struers) at 180 mbar (Citovac, Struers), allowed to harden for 24 h, cut into thin sections (d = 30 μm) and mounted on 1 × 1 cm2 pre-cut 250 μm-thick Si Wafers (TED PELLA, Inc.). Bulk Cu concentrations were determined using inductively coupled plasma mass spectrometry (ICP-MS, 7500cx, Agilent Technologies, Inc.) after acid digestion of 10 to 20 mg of sample (2 mL H2O2 and 9 mL aqua regia for the sludge samples or 9 mL HNO3 and 200 μL HF for the ash samples) in a microwave system (ETHOS 1, MLS GmbH) for the sludge samples and in an ultraclave (MLS GmbH) for the ash samples. The visibly clear digests were diluted to 50 mL in DI water. The limit of quantification (LOQ) in the digests was 0.02 ppb, resulting in a LOQ of 0.05 mg Cu per kg sample. Chemicals for the acid digestions (37% HCl and 40% HF, both Merck, 69% HNO3, Roth and 30% H2O2, Sigma-Aldrich) were used as received.2.2 Synchrotron experiments
Synchrotron X-ray experiments were conducted at the X05LA beamline (‘microXAS’) at the Swiss Light Source (SLS) in Villigen, Switzerland.10 A double crystal monochromator (Si(111)) was used to select the energy of the X-ray beam produced by a minigap in-vacuum undulator. KB mirrors focused the beam to a 3 × 3 μm2 spot on the sample. The flux at the beamline is around 2 × 1012 photons per s at a beam current of 400 mA. A 16-element (2048 channel) Silicon Drift detector (Ketek GmbH) was used to record the XRF signals. A total of seven Cu-Kα XRF maps recorded around the Cu K-edge were collected in ‘on-the-fly’ mode for each sample (area: 500 × 500 μm2, resolution: 3 × 3 μm2 for the samples SLG NP, SLG AQ and ASH AQ and of 350 × 350 μm2 at the same pixel resolution for ASH NP). An additional Ti-Kα XRF map was recorded from the same areas for aligning the individual XRF maps. In the on-the-fly acquisition mode, the sample stage was moved in the horizontal direction perpendicular to the beam at a constant velocity and the fluorescence detector was set to accumulate the XRF signal over a time of 100 ms. The fluorescence detector and the sample were placed at 90° and 10° with respect to the incoming beam, respectively. For the normalization of the spectra, one XRF map was collected below (8950 eV) and one above (9080 eV) the Cu K-edge (E0 = 8979 eV). The remaining five maps were collected at energies representing diagnostic features observed in XANES reference spectra (8981.0, 8986.5 8995.0, 9007.0 and 9051.5 eV) (Fig. S1†). In total, each pixel was exposed to the beam for 0.7 s.Complementary XAS measurements of small areas (3 × 3 μm2) referred to as point-XANES (pXANES) were conducted on selected points of interest (POI). POI were identified based on the Cu distribution maps. pXANES spectra were recorded from 8958 eV to 9060 eV corresponding to −21 eV pre- and 81 eV post-edge. The step size was 2 eV up to 10 eV before the edge, 0.5 eV up to 60 eV past the edge and 1.5 eV up to 81 eV above the edge. The integration time was 400 ms per energy step, leading to 88 s total exposure time per POI. Three spectra were recorded on each POI.
Reference materials (CuS (covellite), CuFeS2 (chalcopyrite), CuO (tenorite), CuSO4 (copper sulphate), CuFe2O4 (cuprospinel) and Cu2O (cuprite)) were prepared as 7 mm pellets in a cellulose matrix and measured in transmission mode using an ion chamber (I0) and a X-ray diode (It). Reference materials of Cu(+I/+II) bound to humic acid were frozen into ceramic windows (4 × 8 mm) and stored in liquid nitrogen. An aliquot of the CuO-NP that were spiked to the digested sewage sludge29 were prepared as 7 mm pellet and XAS data was acquired in transmission mode. The XANES data was identical to the tenorite XANES, which was therefore used for further evaluations.
All samples (XRF maps and pXANES) and reference materials were measured at cryogenic temperatures using a liquid nitrogen cryo jet (Oxford Instruments plc.) and setting the temperature at the nozzle to 100 K.
2.3 Data treatment
XRF peak intensities (counts within regions of interest (ROI)) and ion chamber currents were stored for each position (pixel) in a text file. All XRF maps of each sample were aligned to the same spatial grid using linear interpolation. The new grid was set very close to the old grid to preserve the shape of the data as good as possible and to keep the ROI count changes through interpolation to a minimum. This alignment was necessary due to slight variations in the acceleration and velocity of the sample stage, which were not always correctly captured by the triggering mode of the detector. Additionally, changes in the incident beam energy led to sub-pixel vertical changes in the beam position. To account for these shifts, the Ti-Kα XRF maps recorded at each energy were used to calculate the shift, which was then applied to the Cu XRF maps.30 A map typically contained around 28′000 pixels ((500 × 500 μm2)/(3 × 3 μm2 per pixel) ≈ 27′778 pixels). The spatial distribution of Cu was obtained by plotting the difference between the XRF intensity at the post- and pre-edge energy. If not stated otherwise, XRF Cu peak intensities were pixel-wise normalized by subtracting the intensity recorded before the absorption edge (8950.0 eV) and dividing by the intensity recorded at the highest energy above the edge (9080 eV). Often a first-order polynomial is used to approximate the background, which is especially relevant for measurements conducted in transmission mode. However, our measurements were conducted in fluorescence mode and we, thus, used a constant function defined by the absorption measured close to the absorption edge for the background removal. In some cases, at low absorber concentrations and consequently small edge-jumps, the pre- and post-edge background is better characterized by a second-order polynomial compared to a linear regression. To avoid evaluating and subsequently misinterpreting such cases, only pixels with associated signal intensities satisfying certain quality criteria (e.g., if the post-edge Cu-Kα XRF intensity was at least ten times the pre-edge intensity) were considered for further evaluation of the Cu speciation.The spectra of the reference materials and pXANES spectra were imported into Athena31 for merging and normalization. For linear combination fits (LCF) to XRF maps, the reference material spectra were treated as described for the XRF maps. For LCFs to the pXANES spectra data treatment was done as for bulk XANES. LCFs were performed over the entire energy range (−21 eV ≤ E0 ≤ 81 eV). If not indicated otherwise, data processing and evaluation was performed using Matlab R2017b.
2.4 Model for chemical imaging
The experimental XAS spectra can be decomposed into variable fractions of selected reference spectra using linear combination fitting (LCF), a technique well established in the analysis of XAS data.1 These linear combinations are generally expressed by:![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) sample = μreferences sample = μreferences![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) + + ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) , , | (1) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) sample contains the normalized X-ray absorption coefficients at different energies E1, …, E7:
sample contains the normalized X-ray absorption coefficients at different energies E1, …, E7:![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) sample = [μsample(E1),μsample(E2), …, μsample(E7)]T. sample = [μsample(E1),μsample(E2), …, μsample(E7)]T. | (2) |
The matrix μreferences is a 7 × 6 matrix containing the normalized X-ray absorption coefficients at different energies E1, …, E7 of the six selected reference materials (Fig. S1†). The vector ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) contains the fitting parameters (with ∀xi ≥ 0) in the experimental spectrum (
contains the fitting parameters (with ∀xi ≥ 0) in the experimental spectrum (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) sample) where
sample) where ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) = [ε1, …, ε7]T cumulates the experimental errors. The vector
= [ε1, …, ε7]T cumulates the experimental errors. The vector ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) represent the fractions of the respective spectral components (reference spectra) best reproducing the experimental spectrum. In XAS data analyses, multiple regression tools or least square methods embedded in different software packages are routinely employed to solve such mathematical problems.31–33 In a previous study, we used principle component analysis and target transform to show that our samples were best described by a linear combination of six reference spectra.29 We assumed that the error term
represent the fractions of the respective spectral components (reference spectra) best reproducing the experimental spectrum. In XAS data analyses, multiple regression tools or least square methods embedded in different software packages are routinely employed to solve such mathematical problems.31–33 In a previous study, we used principle component analysis and target transform to show that our samples were best described by a linear combination of six reference spectra.29 We assumed that the error term ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) contained all elements of
contained all elements of ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) sample that were not represented by the six references. The entries of the error term were considered as noise, although they may include contributions of additional unidentified spectral components.
sample that were not represented by the six references. The entries of the error term were considered as noise, although they may include contributions of additional unidentified spectral components.
2.5 Observation model for the uncertainty evaluation of chemical images
X-ray absorption data can be measured in transmission or fluorescence mode.4 In fluorescence mode, (energy dispersive) XRF detectors convert incoming photons into digital signals, whose integration over time (and energy) leads to a fluorescence spectrum that can be used to derive physical–chemical characteristics of the sample under investigation.27 For the development of an observation model describing the noise in the data and its discussion we only consider the fluorescence mode.Abe et al.28 recommended categorizing the noise related to beamline properties and detection systems into (i) stochastic noise, (ii) electronic noise, (iii) X-ray instability and (iv) mechanical motion of sample and optics. These recommendations were not specifically drafted for chemical imaging but X-ray absorption fine structure (XAFS) measurements in general. For further simplification of the present computations, we combined the points (i) and (ii) and points (iii) and (iv) and refer to them by the uncertainty resulting from the electronics/detection system and the sample matrix–beam-interactions, respectively. The former will be referred to by σ(d) (d: detector), the latter one by σ(m)j (m: matrix). The matrix uncertainty cumulates all uncertainties related to the sample and the sample stage, e.g., uncertainty derived from the linear interpolation assumption (Section 2.3) correcting for the imprecision of the stage setting (in micrometre) compared to the heterogeneities within the sample and the dimension of the beam (here 3 × 3 μm2). Time dependencies were neglected as all measurements were performed with constant integration times. By ‘uncertainty’ we refer to the standard deviation of a normal distribution with the mean at the determined value of the normalized X-ray absorption coefficient. This will be discussed in detail in the following paragraphs.
To derive the distribution of the uncertainty we evaluated a Cu-Kα1 and Cu-Kα2 emission spectra recorded by an energy-dispersive fluorescence detector. While the Cu-Kα1,2 emission spectrum can be described by multiple narrow Lorentzians,34 the geometry of the recorded fluorescence peak is mainly determined by the energy resolution of the detector35 (black curve, Fig. 1a, in more detail in Fig. S3†).
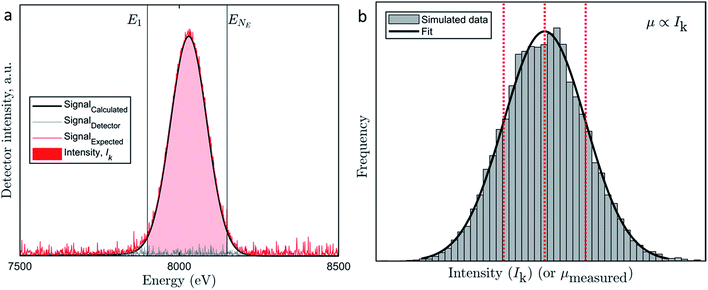 | ||
| Fig. 1 (a) Graphical representation of the observation model. The black curve represents the calculated Cu Kα fluorescence signal (Signalcalculated) reproduced from Sun et al.,35 the grey curve represents the signal related to detector noise (Signaldetector) and the red curve represents the expected signal (Signalexpected = Signalcalculated + Signaldetector). The red shaded area between the two vertical grey lines E1 and ENE represents the intensity Ik which corresponds to the integration of the expected signal (Signalexpected) over all detector channels between E1 and ENE. (b) Histogram of the frequency of occurrence of intensities Ik. Contributions to Ik were balanced between I(m)k and I(d)k, thus neither contribution dominated the other. The dotted lines indicate the mean value and ± one standard deviation. Although the computation was done for Ik, the distribution also represents the distribution of μmeasured, because, μ ∝ Ik where the mean is μmean and the standard deviation is σ(m)j + σ(d) (compare eqn (8)). | ||
The detector noise can never be smaller than zero counts and the detection system is tuned such that most likely zero counts occur during a blank measurement. Non-zero measurements are induced through, e.g., background scatter.28 Therefore, we can approximate the distribution of counts by an exponential distribution. To represent the detector induced uncertainty, a random sample drawn from an exponential distribution parameterized by λ is added at each point in Ei (or each channel of the detector, compare Fig. 1a, grey curve).
Signaldetector(Ei) ∼ λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ × y) exp(−λ × y) | (3) |
Note that we use the tilde ‘∼’ to indicate that a random sample was drawn from a distribution. The expected signal can now be described as a function of Ei (Fig. 1a, red curve):
| Signalexpected(Ei) = Signalcalculated(Ei) + Signaldetector(Ei) | (4) |
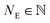 . To obtain the intensity of the measurement (Ik, the index k represents the k-th measurement on the same spot), we sum over the measured signal at the discrete energies E1,2,…,NE:
. To obtain the intensity of the measurement (Ik, the index k represents the k-th measurement on the same spot), we sum over the measured signal at the discrete energies E1,2,…,NE: | (5) |
The intensity Ik (red shaded area, Fig. 1a) can be converted to the normalized X-ray absorption coefficient for evaluation. Further, the intensity Ik can be separated into a contribution from the absorber in the matrix I(m)k and a contribution from the detection system I(d)k, where usually I(m)k ≫ I(d)k. However, I(d)k can still be relevant in very dilute samples.28
 | (6) |
According to our model, and assuming that the measurement is repeated k times at the exact same spot on the sample and neglecting beam damage, I(m)k of each repetition will have the exact same value (fluorescence is a stochastic process as well, however its variance is small compared to the processes discussed further down and not considered here). In contrast, I(d)k (contains stochastic and electronic noise) will vary slightly as this value was sampled from an exponential distribution in each detector bin. In practice, however, the monochromator is set to a specific energy and the stage is moved with a given velocity line by line. Ik is obtained by integrating the signal over a selected time period. The ‘width’ of a pixel is calculated as the product of the scan speed and the integration time (νstageΔtintegration = Wpixel). After completion of one XRF map at a certain energy, the energy is changed and an additional XRF map is recorded, etc. Ideally, the stage should be located at the exact same position at time t for every energy map. However, the locations of the stage will vary slightly, and even the smallest deviations between positions of consecutive energy maps will result in different ‘absorber environments’ of a specific location (pixel) at different energies. These differences, unfortunately, cannot be corrected entirely (Section 2.3). This situation is comparable to XAS at standard XAS beamlines at advanced synchrotron facilities with beam extensions of a few hundreds of micrometres, where the X-ray beam may slightly shift or change spatial flux density as a function of the energy and even tiny heterogeneities, diffraction artefacts or ‘pinholes’ in the sample can distort the absorption spectrum.
Furthermore, minor variations in I(m)k may arise from, e.g., resonant X-ray inelastic scattering (RIXS) at the absorber or elastic and inelastic scattering at any matrix element.28,36,37 In RIXS, the splitting of the photon emission energy at pre-edge energies of conventional XANES measurements as previously observed for CuO36 may eventually increase the uncertainty in the pre-edge region. However, the distortion introduced by the RIXS contributions is small compared to the intensity of the absorption edge and further obscured by the energy resolution of the XRF detector.35,38 The removal of spectra distorted with contributions from elastic and inelastic scattering is discussed in Section 2.7. Differently, the change in the mean X-ray penetration depth before and after the absorption edge at spots with strong absorber concretions that extend into the Z direction, e.g., over the total thin section height, might artificially enhance the contribution of the XRF intensity on the low energy side of the edge. This may be important, especially if the speciation changes in Z direction.
The resulting distribution of Ik to some extent depends on the assumption for the variation of I(m)k. However, the tendency towards a normal distribution is imposed by the variation of I(d)k. The spatial deviations of the stage position from the intended position between consecutive energy maps can be approximated by a normal distribution indicating a close to zero mean displacement (7 × 10−7 μm) and a standard deviation of 3 × 10−4 μm (Fig. S2†). Thus, for 95% of all pixels, the displacement is less than 1/2300 of the side length of a pixel. However, X-ray absorption is extremely sensitive to the absorber concentration and coordination. Therefore, larger displacements from the exact location of the pixel relative to the beam induce larger uncertainties. This consideration qualifies the selection of a normal distribution to describe the uncertainty in I(m)k. Also, a normal distribution is most suitable to capture the sum of all uncertainties of the processes that were deemed relevant previously but cannot be assessed in detail. 28 In plain language, the size of the area underneath the black curve between the grey horizontal lines is sampled from a normal distribution (Fig. 1a). The result of the listed effects can be illustrated if k = 1,2, …, 104 synthetic replicate measurements at one pixel are simulated and one arrives at another normal distribution (Fig. 1b).
By collecting sufficient repetitions of I(m)k + I(d)k, the mean of Ik and sum of two parameters σ(m)j and σ(d) can be obtained (red dotted lines, Fig. 1b). These describe the most likely and mean values of the uncertainty introduced by different elements of the beamline. The uncertainty σ(m)j will be different for each map j, but σ(d) will be the same as long as the experimental setup remains unaltered. The uncertainty in the X-ray absorption coefficient (μ) can be derived as outlined below.
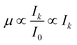 | (7) |
The value of I0 is obtained using an ion chamber and thus the uncertainty in the measurement of I0 is very small and can thus be neglected here. Due to the linear relationship between μ and Ik the uncertainty in μ can also be described by a normal distribution. Thus, any measured normalized X-ray absorption coefficient (μmeasured) can be sampled from a normal distribution (N) where the mean is the corresponding, (presumably) true normalized X-ray absorption coefficient (μmean) and the standard deviation reflects the sum of the normalized uncertainties introduced by the matrix and the detector:
| μmeasured ∼ N(μmean, [σ(m)j + σ(d)]). | (8) |
Eqn (8) indicates that the total uncertainty (σ(m)j + σ(d)) is an absolute quantity. However, in the present study, the X-ray absorption coefficients μ were normalized to values between 0 and 1, hence uncertainties obtained for different datasets are comparable.
Due to practical constraints (e.g. available beam time, beam damage), XRF maps at a given energy were only recorded once. This, however, hampers the determination of the measurement uncertainty through assessing the standard deviations. Consequently, we cannot determine the uncertainty directly related to the XRF intensities, only the uncertainty relative to a LCF result. Therefore, a proper choice of spectra from reference materials is critical for capturing the XAS signal originating from Cu species in the sample (compare Section 2.4 and eqn (1)). In this section, we argued that the uncertainty related to XRF signal production is comparable for each XRF measurement at every energy for all pixels. Thus, Bayesian inference can be used to evaluate the uncertainties according to eqn (8). We performed Markov Chain Monte Carlo (MC) Simulations using JAGS (“Just Another Gibbs Sampler”) Version 4.3.0, based on BUGS (“Bayesian inference Using Gibbs Sampling”),39 through the R library “rjags”40 in RStudio Version 1.1.456 under R Version 3.4.4 (ref. 41) to quantify σ(m)j and σ(d). Details of the computation and the computer code are available in the ESI (Section S5†). Briefly, in the MC, the standard deviations σ(m)j and σ(d) (eqn (8)) are treated as two normal distribution that are each characterized by a mean and standard deviation, which are to be determined (eqn S3 and S4†).
2.6 Synthetic data for model testing and calibration of the data interpretability
For model testing a synthetic dataset was prepared that covered a large variety of combinations of the six reference spectra. For each synthetic dataset, we created 1000 pixels (measurements or data points) where the (input) fractions were sampled from a Dirichlet distribution.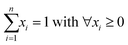 | (9) |
2.7 Quality criteria and benchmarking
Fit quality benchmarking was performed using the previously described synthetic datasets augmented with specific quantities of uncertainty (noise) (Fig. S7†). Thereafter, LCFs were performed to each pixel in each dataset, resulting in output fractions. The larger the uncertainty added to a dataset, the lager the expected discrepancy between the input and the output fractions. The generated input fractions of each data point (pixel) were sorted by their weight and compared to the computed output fractions, which were equally sorted. A score ranging from 0 to 6 was assigned to each pixel reflecting the agreement between the sorted input and the output fractions. A zero means that the first (largest) fractions is wrongly assigned, an one means that the largest fraction is correctly assigned, etc. Finally, a six means that the fractions of the reference spectra used for the LCF fits decreased in the same order for the input and for the output fractions. The scores of the total dataset were then averaged. Furthermore, the percentage of pixels was calculated, for which the reference spectra with the largest spectral component (reference material spectrum) contributing to the LCF fit was correctly identified (score ≥ 1). The scores and the percentage of pixels (Correct largest Spectral Component Identified: CSCI) as described above can be used to assess the quality of the fits at different levels of uncertainty. Arguments in the favour of the introduction of the score and CSCI are given in the ESI (Section S6†).3 Results and discussion
3.1 Validation of the uncertainty analysis technique
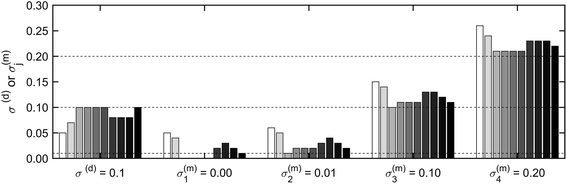
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i) were recovered with the MC approach by sampling 103 times from the model per pixel after initiating the model for 2 × 103 iterations. The long initiation phase ensured sampling under constant conditions. With this approach, the introduced uncertainties in synthetic spectra were successfully reproduced (Fig. 2), although the recovered values for the noise were slightly higher compared to the noise in the synthetic dataset (≈5%). Also, a correlation between σ(d) and σ(m)j was evident: lower values of σ(d) led to higher values of σ(m)j and vice versa (Fig. S8†). This is caused by the linear dependence of these two parameters, which add up to the same uncertainty (eq. (8)). As a consequence, all σ(m)j and σ(d) were subsequently combined to σ(d) + σ(m)j = σj. Recovering σj from four additional datasets with σj = [0, 0.01, 0.1, 0.2] during 10 repetitions yielded σj = [0.0014 ± 8 × 10−4, 0.0103 ± 10−4, 0.0988 ± 2 × 10−4, 0.2032 ± 5 × 10−4]. The standard error varied between 1.87 × 10−3 and 1.38 × 10−2. These results demonstrate that our approach recovers uncertainties in the synthetic dataset with high precision (standard error ≤ 1.4%) and accuracy (relative deviation ≤ 1.6%). The dataset σj = 0 was not included in the evaluation of the accuracy of the uncertainty as relative deviations were difficult to calculate.
i) were recovered with the MC approach by sampling 103 times from the model per pixel after initiating the model for 2 × 103 iterations. The long initiation phase ensured sampling under constant conditions. With this approach, the introduced uncertainties in synthetic spectra were successfully reproduced (Fig. 2), although the recovered values for the noise were slightly higher compared to the noise in the synthetic dataset (≈5%). Also, a correlation between σ(d) and σ(m)j was evident: lower values of σ(d) led to higher values of σ(m)j and vice versa (Fig. S8†). This is caused by the linear dependence of these two parameters, which add up to the same uncertainty (eq. (8)). As a consequence, all σ(m)j and σ(d) were subsequently combined to σ(d) + σ(m)j = σj. Recovering σj from four additional datasets with σj = [0, 0.01, 0.1, 0.2] during 10 repetitions yielded σj = [0.0014 ± 8 × 10−4, 0.0103 ± 10−4, 0.0988 ± 2 × 10−4, 0.2032 ± 5 × 10−4]. The standard error varied between 1.87 × 10−3 and 1.38 × 10−2. These results demonstrate that our approach recovers uncertainties in the synthetic dataset with high precision (standard error ≤ 1.4%) and accuracy (relative deviation ≤ 1.6%). The dataset σj = 0 was not included in the evaluation of the accuracy of the uncertainty as relative deviations were difficult to calculate.
3.2 The uncertainty in the case study datasets
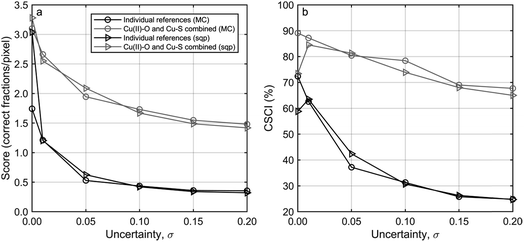
The uncertainties in four experimental datasets recorded on digested sewage sludge spiked with CuO-NP or CuSO4 and the resulting ashes were assessed using the approach described above. The levels of uncertainty were then compared to those in Section 3.1.2 and information on the quality of the extracted LCF fits were obtained. Briefly, XRF maps of the CuO spiked sludge (SLG NP), the CuSO4 spiked sludge (SLG AQ) and ash derived from SLG AQ (ASH AQ) were 500 × 500 μm2 in size with a 3 μm lateral resolution. The map of the ash derived from SLG NP (ASH NP) was 350 × 350 μm2 with the same lateral resolution.For initial and comparative analyses, all pixels with a non-normalized (NN) post edge XRF intensity of at least three times the NN pre-edge XRF intensity were included in the analysis. The correlation between σ(m)j and σ(d), previously observed in the synthetic data, was also observed in the experimental data (Fig. S9†). Therefore, we combined these uncertainties into σj(σ(d) + σ(m)j = σj) and found σj = [0.18, 0.17, 0.13, 0.33] for the experimental datasets SLG NP, SLG AQ, ASH NP and ASH AQ, respectively (Fig. S10†). Similar to the analysis of the synthetic datasets, the uncertainty was represented by a normal distribution around the values of σj. The uncertainty estimated for the two sludge samples was almost identical, likely due to the comparable sample matrix and Cu concentrations. The larger σj of ASH AQ may be explained by the granular texture of the ASH AQ sample resulting in an investigated area, dominated by an ash grain with rather low Cu concentrations.
Based on the results obtained with the synthetic dataset, uncertainties in the range of 0.13–0.18 as obtained for the experimental dataset translate into Cu(II)–O and Cu–S combined scores of around 1.5 and CSCI between 65 and 70%. An uncertainty of 0.33, leading to a score of <1.5 and a CSCI < 60% (ASH AQ), however, is too large to make reliable statements concerning the speciation of Cu in the sample (Section 3.1.2).
To obtain more reliable datasets associated with a lower uncertainty, we introduced a second criterion for the inclusion of individual pixels. In addition to the ‘relative threshold’ (NN post edge XRF intensity ≥ φ times NN pre edge XRF intensity), where φ varied between 3 and 50, an ‘absolute threshold’ (NN post-edge XRF intensity ≥ χ) was introduced and varied between 500 and 1000.
The uncertainties determined at different levels of φ or χ are reported in Fig. S11 and Table S2.† Our results suggest that it is important to quantify the uncertainty as a function of different pixel inclusion criteria when analysing different samples. In each dataset, we had to make a compromise between the number of included pixels (spectra) and the resulting uncertainty by trying to include as many pixels as possible while keeping the uncertainty as low as possible. The results of this evaluation are tabulated (Table 1) and the chemical images based on the selected inclusion criteria are visualized (Fig. 4) and discussed in the following section.
| Map | SLG NP | SLG AQ | ASH NP | ASH AQ |
| Threshold type | Relative (φ) | Relative (φ) | Absolute (χ) | Absolute (χ) |
| Level (φ or χ) | 10 | 10 | 1000 | 3000 |
| # pixels included | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 278 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
9198 | 6048 |
| Pixels included, % | 87.05 | 56.01 | 64.95 | 21.68 |
| Uncertainty | 0.18 | 0.18 | 0.09 | 0.13 |
| Score (individual references) | 0.36 | 0.36 | 0.45 | 0.39 |
| CSCI (individual references) (%) | 25.2 | 25.2 | 32.48 | 28.00 |
| Score (combined references) | 1.51 | 1.51 | 1.77 | 1.62 |
| CSCI (combined references) (%) | 68.22 | 68.22 | 78.80 | 72.76 |
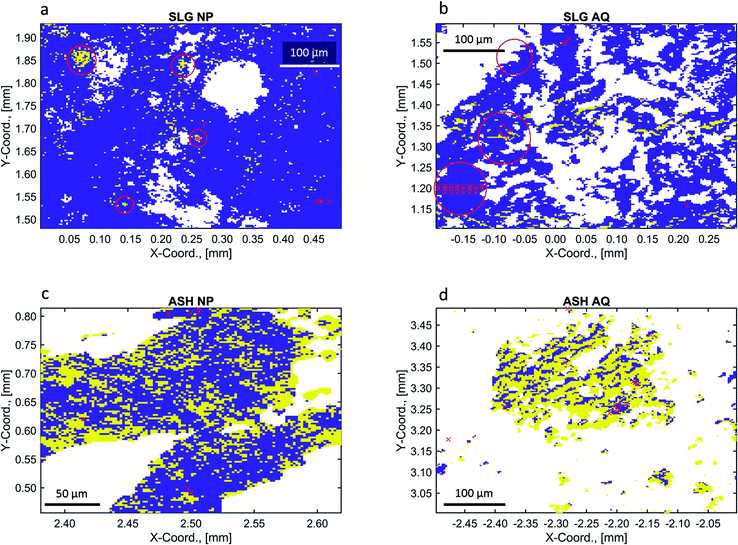 | ||
| Fig. 4 Chemical images of the experimental samples ((a): SLG NP, (b): SLG AQ, (c): ASH NP and (d): ASH AQ) using combined references (yellow: fraction (Cu(II)–O) > fraction (Cu–S), blue: fraction (Cu(II)–S) > fraction (Cu–O)) and applying the exclusion criteria listed in Table 1. White pixels reflect excluded data points. The CSCIs were 68, 68, 79 and 73% for SLG NP, SLG AQ ASH NP and ASH AQ, respectively. The coordinates (in mm) represent the coordinates relative to the beam in the centre of the sample. The red crosses and labels indicate the locations of the recorded pXANES. For their assignment to individual spectra, refer to Fig. 5. LCF was performed using a sequential quadratic programming (sqp) method.42,43 | ||
Furthermore, it can be shown using the results from SLG NP that binning multiple pixels into larger pixels reduces the uncertainty in the dataset (Table S3†). Binning of 2 × 2 = 4 pixels reduces the uncertainty drastically (Δσ = 0.04). A further increase of the binning from 2 × 2 = 4 to 4 × 4 = 16 pixels results in a linear decrease of σ (Fig. S12†). Increasing the pixel binning to 5 × 5 = 25, however, only results in a moderate decrease in uncertainty. The large initial decrease of the uncertainty observed when 2 × 2 pixels were binned may be explained by the smoothing of residual shifts from the sample stage setting and from the beam location shift that are now small relative to the (binned) pixel size. The further decrease with increasing binning of pixels results from the improved counting statistics, which however, is associated with a decrease in the lateral resolution and in agreement with the dose limited resolution criteria.46
3.3 The spatial distribution of the Cu speciation in sludge samples and corresponding ashes
Cu concentrations in the samples SLG NP, SLG AQ, ASH NP and ASH AQ were 1120 ppm, 1340 ppm, 1860 ppm and 2400 ppm, respectively. Based on the difference between the non-normalized intensities at the post- and pre-edge energy (ΔIi), the distribution patterns of Cu were obtained (Fig. 5). In the sludge samples, the Cu distribution was uneven and textural differences were observed between the SLG NP and the SLG AQ samples. The Cu concentration pattern of SLG NP appeared dotted with spot sizes between 10 and 20 μm (yellow/orange spots against the green/blue background, Fig. 5a). In contrast, the Cu distribution in the SLG AQ followed Schlieren-like structures with a few larger objects with diameters up to 70 μm (red circles, Fig. 5b). These observations are consistent with results from previous studies investigating the spatial Cu distribution in fresh biosolids, which also showed an uneven Cu distribution.12,47 The Cu distribution patterns in the sludge are in stark contrast to the Cu distribution patterns observed in both ash samples, where Cu was more evenly distributed in the ash grains (Fig. 5c and d). Therefore, the textural differences observed in the sludge samples largely disappeared during the incineration process.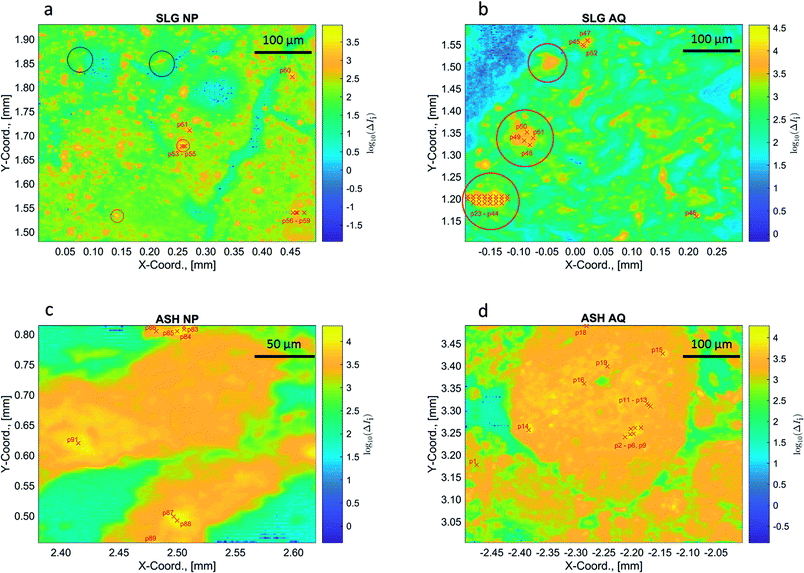 | ||
| Fig. 5 An approximation of the Cu concentrations in the samples ((a): SLG NP, (b): SLG AQ, (c): ASH NP and (d): ASH AQ) reflecting the difference between the non-normalized intensity of the post- and pre-edge energy (ΔIi). The intensities are displayed on a logarithmic scale. The coordinates (in mm) represent the coordinates relative to the beam in the centre of the sample. The red crosses and labels indicate the locations of the recorded pXANES. The pXANES, the reference material spectra and the results of a LCF analysis are given in the ESI (Fig. S14–S20†). Where multiple pXANES were recorded close to each other, the labels were combined, e.g., p2–p6, p9 in the sample ASH AQ. The location of the individual pXANES areas are given in the ESI (Section S8†). | ||
LCF to bulk-EXAFS on the same samples indicated that SLG AQ can be described by 80% CuxS (amorphous) and 20% chalcopyrite (Table 2).29 For SLG NP, identical analyses returned a similar fraction of CuxS (81%), but in addition to chalcopyrite (11%) a comparable fraction (8%) was associated with Cu(II)–O references (tenorite and copper sulphate).29 To compare the integrated LCF fractions determined from the spatially resolved XAS data with the fractions derived from bulk EXAFS LCF, the spatially resolved XAS data were weighted with the intensity difference between the pre- and post-edge (ΔIi).
| Reference material group | Individual reference material | SLG NP | SLG AQ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sum of the LCF fractions over all pixels in %. Normalized by ΔIi | Sums of previous column, % | Fractions based on pixel association in %. Normalized by ΔIi | EXAFS LCF, %a | Sums of previous column, %a | Sum of the LCF fractions over all pixels in %. Normalized by ΔIi | Sums of previous column, % | Fractions based on pixel association, % normalized by ΔIi | EXAFS LCF, %a | Sums of previous column, %a | ||
| a Fourth and fifth column: EXAFS LCF results of a previous study on the same samples given in ref. 29 (the samples SLG NP and SLG AQ, were referred to by D-NP and D-AQ, respectively). LCF was performed using a sequential quadratic programming (sqp) method.42,43 | |||||||||||
| Cu–S | CuxS | 39 | 78 | 96 | 81 | 92 | 45 | 80 | 95 | 85 | 100 |
| CuS | 28 | 0 | 25 | 0 | |||||||
| CuFeS2 | 11 | 11 | 10 | 15 | |||||||
| Cu(II)–O | CuO | 13 | 22 | 4 | 7 | 8 | 10 | 20 | 5 | 0 | 0 |
| CuSO4 | 4 | 1 | 3 | 0 | |||||||
| CuFe2O4 | 5 | 0 | 7 | 0 | |||||||
Using the selected criteria for including individual XANES spectra (Table 1), chemical images that discriminate between Cu(II)–O (yellow pixels) and Cu–S (blue pixels) were extracted from each dataset (Fig. 4) and their integrated LCF fractions were evaluated (Table 2). In general, the integrated LCF results of SLG NP and SLG AQ were comparable, with 78 and 80% of the integrated experimental spectra assigned to the Cu–S reference spectra and 22% and 20% assigned to Cu(II)–O reference spectra, respectively (Table 2). If each pixel is binary associated with either Cu–S or Cu(II)–O spectra (Fig. 4) the fractions of Cu–S were 96% (SLG NP) and 95% (SLG AQ), respectively (Table 2).
In the chemical images of both sludge samples Cu was dominantly coordinated to sulphide, represented by the blue colour (Fig. 4a and b). However, the LCF analyses of the bulk spectra, returned a higher fraction of Cu(II)–O species for the sludge samples spiked with CuO-NP and it was previously speculated that either the formation of CuxS coatings protected the CuO core from further sulfidation and/or that the agglomeration of CuO-NP substantially decreased the sulfidation kinetics.48 The resolution (3 × 3 μm2) used in the present experiments does not allow to assess whether CuO–CuxS core–shell structures formed on an individual particle level, however, agglomerates of several particles in the sludge were well within the resolution limit of the experimental setup. In SLG NP, round Cu(II)–O objects were observed within the Cu–S matrix (red circles, Fig. 4a). Two of these objects were also associated with elevated Cu concentrations relative to the background Cu (red circles, Fig. 5a). We interpret these structures as agglomerates of CuO-NP that remained untransformed during the anaerobic digestion process. The other two objects were not associated with significantly elevated Cu concentrations (black circles, Fig. 5a) and may, therefore, represent CuO-NP, where Cu remained untransformed due to locally limited/restricted availability of bisulfide or Cu bound to O functional groups from the organic matrix of the sludge. A chemical image with binned pixels (3 × 3 = 9) confirmed these observations at a lower resolution but with higher score and CSCI (Fig. S13†). The three prominent spots observed on the sample SLG AQ reflecting locally elevated Cu concentrations (red circles, Fig. 5b) did not translate into local Cu(II)–O clusters (red circles, Fig. 4b) and may thus likely reflect agglomerates of CuS particles precipitated during the CuSO4 spiking.
The locations of recorded pXANES are indicated by a series of red ‘x’ (Fig. 5 and 4). The spectra, reference material spectra, LCFs, resulting fractions and an in-depth analysis and discussion are given in the ESI (Section S8†). Briefly, the results derived from the evaluation of pXANES were consistent with the observations made on the chemical images (Fig. 4). In SLG NP, the pXANES p53–p55 showed coordination of Cu(II) to O, all other pXANES recorded on this sample revealed coordination of Cu to S. In SLG AQ, all recorded pXANES suggest Cu associated with S. In both ash samples the pXANES revealed strong local variations of the Cu oxidation state.
Transmission electron microscopy and dynamic light scattering measurements did not show agglomeration at the micrometre scale (10–20 μm) in the spiking dispersion.29 Therefore, the results of the present study support the hypothesis that the agglomeration occurred after CuO-NP were spiked to the digested sludge. Furthermore, the results showed that although the speciation of Cu in the two sludge samples was comparable, important textural differences based on the Cu concentrations (dotted versus Schlieren-type structures and large agglomerates) remained. Such differences were only observed in the sludge and were absent in the ash samples.
The Cu speciation in sludge samples spiked with either CuO-NP or CuSO4 converged with the speciation of Cu related to presence of Cu in unspiked sludge within hours.48 Nevertheless, spatial heterogeneities caused by different forms of Cu (nanoparticles vs. dissolved) added to the wastewater stream might outlive wastewater treatment including anaerobic digestion. A similar convergence of speciation has been observed for Zn during anaerobic sludge digestion.49 A recent study showed that lysimeter aged sludge obtained from a pilot wastewater treatment plant (WWTP) spiked with ZnO-NP inhibited the reproduction of earthworms to a higher degree compared to sludge produced by spiking dissolved Zn2+ to the same pilot WWTP.50 The Zn speciation as well as the total Zn concentrations were almost identical in both sludges. The authors, therefore, speculated that the morphological or spatial differences between the ZnS phases formed after spiking ZnO-NP or ZnSO4 to the pilot WWTP were responsible for the observed differences in growth inhibitions.50 However, suitable tools to investigate spatial heterogeneities at the micrometre scale were not available and the hypothesis remained speculative. As Cu and Zn both classify as chalcophile transition metals51 the results from this study on Cu may also be transferrable to Zn. Structural differences of the sludge at the micrometre scale or even below may have influenced the Zn bioavailability and, thus, also have contributed to the increased eco-toxicity of the ZnO-NP-spiked versus the dissolved Zn spiked sludge reported in the study of Lahive et al.50
4 Conclusion and outlook
We presented a model and related algorithms to quantify the uncertainty associated with hard X-ray derived chemical images. The model and algorithm were evaluated using a synthetic dataset. Two newly introduced data quality benchmarks (score and CSCI) to assess the reliability of the chemical images were evaluated using a synthetic dataset and applied to experimental data of a case study. Eventually, the model/algorithms can also be adapted to evaluate uncertainties associated with data interpretations in other settings where LCF methods are used, e.g., electron energy loss spectroscopy.52The model/algorithm also offers a suitable tool for planning and conducting chemical imaging experiments. To the end of the latter, multiple XRF maps of a small area can be recorded and the presented algorithms can be used to quantitatively evaluate the resulting uncertainties and noise levels associated with LCF data interpretations under the given end-station settings. The model output can then be used to tune the end station settings to achieve a desired level of spectra interpretability (decision tree in Fig. S25†).
Progress in the quantitative assessment of the uncertainties may further enhance the interpretability of chemical images derived from synchrotron based hard X-rays. As demonstrated in this study, the evaluation and interpretation of chemical imaging data requires a detailed understanding of the underlying uncertainties, especially at short dwell times. The present model is purely empirical and future modifications will be directed towards a more rigorous treatment of physical processes (e.g., undulator based spatial beam structure development with energy changes, beam polarisation, elastic and inelastic scattering, RIXS, self-absorption, beam damage, etc.), which will reveal future possibilities and also current limitations associated with the data interpretation of chemical images of heterogeneous samples with low absorber concentrations.
Code availability
The computer code extracting the uncertainty (σ) from (linearized) chemical images can be found in the Eawag Research Data Institutional Repository (ERIC) under: https://doi.org/10.25678/0001MF. The package includes a comprehensive README file and the data displayed in Fig. 3, 4, S12 and S13.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Paul-Scherrer-Institute (PSI) and the Swiss Light Source (SLS) for allocating beam time and Mr Dario Ferreira Sanchez (X05LA “microXAS” beamline/end station, SLS) for his support during the data acquisition. We acknowledge funding from the Swiss National Science Foundation (SNF) through grant 5221.01038 and as well as discretionary funding from Eawag and PSI. Further, we acknowledge the library of ETH Zürich for covering the APC for open access publishing.References
- M. Gräfe, E. Donner, R. N. Collins and E. Lombi, Anal. Chim. Acta, 2014, 822, 1–22 CrossRef PubMed.
- D. E. Sayers, E. A. Stern and F. W. Lytle, Phys. Rev. Lett., 1971, 27, 1204–1207 CrossRef CAS.
- E. A. Stern, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 10, 3027–3037 CrossRef CAS.
- P. Willmott, An introduction to synchrotron radiation: techniques and applications, John Wiley & Sons, 2011 Search PubMed.
- M. A. Marcus, A. A. MacDowell, R. Celestre, A. Manceau, T. Miller, H. A. Padmore and R. E. Sublett, J. Synchrotron Radiat., 2004, 11, 239–247 CrossRef CAS PubMed.
- A. Manceau, N. Tamura, M. A. Marcus, A. A. MacDowell, R. S. Celestre, R. E. Sublett, G. Sposito and H. A. Padmore, Am. Mineral., 2002, 87, 1494–1499 CrossRef CAS.
- A. Manceau, N. Tamura, R. S. Celestre, A. A. MacDowell, N. Geoffroy, G. Sposito and H. A. Padmore, Environ. Sci. Technol., 2003, 37, 75–80 CrossRef CAS PubMed.
- S. D. Kelly, D. Hesterberg and B. Ravel, Analysis of soils and minerals using X-ray absorption spectroscopy, Methods of soil analysis. Part 5, Mineralogical methods, ASA-CSSA-SSSA, 5th edn, 2008 Search PubMed.
- A. Lanzirotti, L. Lee, E. Head, S. R. Sutton, M. Newville, M. McCanta, A. H. Lerner and P. J. Wallace, Geochim. Cosmochim. Acta, 2019, 267, 164–178 CrossRef CAS.
- C. N. Borca, D. Grolimund, M. Willimann, B. Meyer, K. Jefimovs, J. Vila-Comamala and C. David, J. Phys.: Conf. Ser., 2009, 186, 012003 CrossRef.
- R. Kirkham, P. A. Dunn, A. J. Kuczewski, D. P. Siddons, R. Dodanwela, G. F. Moorhead, C. G. Ryan, G. D. Geronimo, R. Beuttenmuller, D. Pinelli, M. Pfeffer, P. Davey, M. Jensen, D. J. Paterson, M. D. d. Jonge, D. L. Howard, M. Küsel and J. McKinlay, AIP Conf. Proc., 2010, 1234, 240–243 CrossRef CAS.
- B. E. Etschmann, E. Donner, J. Brugger, D. L. Howard, M. D. de Jonge, D. Paterson, R. Naidu, K. G. Scheckel, C. G. Ryan and E. Lombi, Environ. Chem., 2014, 11, 341–350 CrossRef CAS.
- M. A. Marcus, B. M. Toner and Y. Takahashi, Mar. Chem., 2018, 202, 58–66 CrossRef CAS.
- J. G. Mesu, A. M. J. van der Eerden, F. M. F. de Groot and B. M. Weckhuysen, J. Phys. Chem. B, 2005, 109, 4042–4047 CrossRef CAS PubMed.
- J. Yang, T. Regier, J. J. Dynes, J. Wang, J. Shi, D. Peak, Y. Zhao, T. Hu, Y. Chen and J. S. Tse, Anal. Chem., 2011, 83, 7856–7862 CrossRef CAS PubMed.
- M. A. Marcus, TrAC, Trends Anal. Chem., 2010, 29, 508–517 CrossRef CAS.
- C. M. Rico, M. G. Johnson, M. A. Marcus and C. P. Andersen, Environ. Sci.: Nano, 2017, 4, 700–711 RSC.
- M. I. Heller, P. J. Lam, J. W. Moffett, C. P. Till, J.-M. Lee, B. M. Toner and M. A. Marcus, Geochim. Cosmochim. Acta, 2017, 211, 174–193 CrossRef CAS.
- P. J. Lam, D. C. Ohnemus and M. A. Marcus, Geochim. Cosmochim. Acta, 2012, 80, 108–124 CrossRef CAS.
- L. E. Mayhew, S. M. Webb and A. S. Templeton, Environ. Sci. Technol., 2011, 45, 4468–4474 CrossRef CAS PubMed.
- B. M. Toner, S. L. Nicholas and J. K. C. Wasik, Environ. Chem., 2014, 11, 4–9 CrossRef CAS.
- C. M. Rico, M. G. Johnson and M. A. Marcus, Environ. Sci.: Nano, 2018, 5, 1807–1812 RSC.
- C. G. Ryan, D. P. Siddons, R. Kirkham, P. A. Dunn, A. Kuczewski, G. Moorhead, G. D. Geronimo, D. J. Paterson, M. D. d. Jonge, R. M. Hough, M. J. Lintern, D. L. Howard, P. Kappen and J. Cleverley, AIP Conf. Proc., 2010, 1221, 9–17 CrossRef CAS.
- E. R. Malinowski, Factor analysis in chemistry, Wiley, 2002 Search PubMed.
- E. R. Malinowski, Anal. Chim. Acta, 1978, 103, 339–354 CrossRef CAS.
- A. Manceau, M. Marcus and T. Lenoir, J. Synchrotron Radiat., 2014, 21, 1140–1147 CrossRef CAS PubMed.
- S. Heald, J. Synchrotron Radiat., 2015, 22, 436–445 CrossRef CAS PubMed.
- H. Abe, G. Aquilanti, R. Boada, B. Bunker, P. Glatzel, M. Nachtegaal and S. Pascarelli, J. Synchrotron Radiat., 2018, 25, 972–980 CrossRef CAS PubMed.
- J. Wielinski, A. Gogos, A. Voegelin, C. Müller, E. Morgenroth and R. Kaegi, Environ. Sci. Technol., 2019, 53, 11704–11713 CrossRef CAS PubMed.
- M. Guizar-Sicairos, S. T. Thurman and J. R. Fienup, Opt. Lett., 2008, 33, 156–158 CrossRef PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- M. Newville, J. Phys.: Conf. Ser., 2013, 430, 012007 CrossRef.
- S. M. Webb, Phys. Scr., 2005, 2005, 1011 CrossRef.
- M. Deutsch, G. Hölzer, J. Härtwig, J. Wolf, M. Fritsch and E. Förster, Phys. Rev. A, 1995, 51, 283–296 CrossRef CAS PubMed.
- Y. Sun, S.-C. Gleber, C. Jacobsen, J. Kirz and S. Vogt, Ultramicroscopy, 2015, 152, 44–56 CrossRef CAS PubMed.
- H. Hayashi, R. Takeda, Y. Udagawa, T. Nakamura, H. Miyagawa, H. Shoji, S. Nanao and N. Kawamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045122 CrossRef.
- H. Hayashi, AIP Conf. Proc., 2007, 882, 833–837 CrossRef CAS.
- P. Glatzel, T.-C. Weng, K. Kvashnina, J. Swarbrick, M. Sikora, E. Gallo, N. Smolentsev and R. A. Mori, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 17–25 CrossRef CAS.
- D. J. Lunn, A. Thomas, N. Best and D. Spiegelhalter, Stat. Comput., 2000, 10, 325–337 CrossRef.
- M. Plummer, JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling, Proceedings of the 3rd international workshop on distributed statistical computing, Vienna, Austria, 2003, vol. 124, No. 125,10, pp. 1–10 Search PubMed.
- RCoreTeam, R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, 2017, http://https://www.R-project.org/ Search PubMed.
- M. J. Powell, in Numerical analysis, Springer, 1978, pp. 144–157 Search PubMed.
- M. J. Powell, in Nonlinear programming 3, Elsevier, 1978, pp. 27–63 Search PubMed.
- J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, SIAM J. Optim., 1998, 9, 112–147 CrossRef.
- R. A. D. Pattrick, J. F. W. Mosselmans, J. M. Charnock, K. E. R. England, G. R. Helz, C. D. Garner and D. J. Vaughan, Geochim. Cosmochim. Acta, 1997, 61, 2023–2036 CrossRef CAS.
- A. Rose, in Advances in Electronics and Electron Physics, ed. L. Marton, Academic Press, 1948, vol. 1, pp. 131–166 Search PubMed.
- E. Donner, D. L. Howard, M. D. d. Jonge, D. Paterson, M. H. Cheah, R. Naidu and E. Lombi, Environ. Sci. Technol., 2011, 45, 7249–7257 CrossRef CAS PubMed.
- A. Gogos, A. Voegelin and R. Kägi, Environ. Sci.: Nano, 2018, 5, 2560 RSC.
- E. Lombi, E. Donner, E. Tavakkoli, T. W. Turney, R. Naidu, B. W. Miller and K. G. Scheckel, Environ. Sci. Technol., 2012, 46, 9089–9096 CrossRef CAS PubMed.
- E. Lahive, M. Matzke, M. Durenkamp, A. J. Lawlor, S. A. Thacker, M. G. Pereira, D. J. Spurgeon, J. M. Unrine, C. Svendsen and S. Lofts, Environ. Sci.: Nano, 2017, 4, 78–88 RSC.
- F. Albarede, in Encyclopedia of Astrobiology, ed. M. Gargaud, R. Amils, J. C. Quintanilla, H. J. Cleaves, W. M. Irvine, D. L. Pinti and M. Viso, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 283–283, DOI:10.1007/978-3-642-11274-4_261.
- S. Yakovlev and M. Libera, Micron, 2008, 39, 734–740 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00394k |
| This journal is © The Royal Society of Chemistry 2020 |