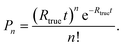Open Access Article
Open Access ArticleSingle particle inductively coupled plasma mass spectrometry: investigating nonlinear response observed in pulse counting mode and extending the linear dynamic range by compensating for dead time related count losses on a microsecond timescale†
Ingo
Strenge
 a and
Carsten
Engelhard
a and
Carsten
Engelhard
 *ab
*ab
aUniversity of Siegen, Department of Chemistry and Biology, Adolf-Reichwein-Str. 2, D-57076 Siegen, Germany. E-mail: engelhard@chemie.uni-siegen.de; Fax: +49 271 740 2041
bCenter of Micro- and Nanochemistry and Engineering, University of Siegen, Adolf-Reichwein-Str. 2, D-57076 Siegen, Germany
First published on 25th November 2019
Abstract
In single particle inductively coupled plasma mass spectrometry (spICP-MS) the detection of small nanoparticles (NP) usually requires utilization of the pulse counting signal, which entails the risk of nonlinear response for larger NP. In this work, the suitability of a traditional dead time correction (DTC) method applied to both millisecond (msTR) and microsecond (μsTR) time-resolved spICP-MS is evaluated. A custom data acquisition system was used to record the pulse counting signal at a sustained rate of 2 × 105 samples per second. Model transients from microdroplets containing different concentrations of a thallium element standard and generated via a custom droplet introduction system were studied (Part A). Findings were compared to the analysis of eleven gold NP suspensions covering a size range of 10–100 nm, introduced via regular solution nebulization (Part B). Applying DTC to μsTR spICP-MS data allowed to increase the maximum number of counts tolerated per particle or droplet four- to fifteen-fold, resulting in a linear dynamic range (LDR) of 10–60 instead of 10–40 nm AuNP, or 9–4500 instead of 9–300 μg L−1 Tl. For Part B a cross-calibration between standard and attenuated sensitivity mode could be established, further extending the LDR (10–100 nm AuNP). Findings support the theory of dead time related count losses being the main reason for nonlinear response in pulse counting spICP-MS. However, results also indicate that DTC can lead to slightly distorted particle size distributions.
Introduction
In 1993, Nomizu et al. demonstrated the first implementation of a novel detection scheme for the analysis of single particles via inductively coupled plasma mass spectrometry (ICP-MS).1 The concept evolved from a technological curiosity to a well-recognized method for the rapid determination of particle size distribution (PSD) and particle number concentration (PNC) in liquid suspensions, routinely performed on off-the-shelf instrumentation.2 Nowadays this method is referred to as single particle ICP-MS (spICP-MS) and is commonly mentioned along with other established techniques for characterization of nanoparticles (NP) based on separation or fractionation, light scattering, electron microscopy, and spectroscopy.3–5The recently published technical specification (TS) for determination of PSD and PNC via spICP-MS, ISO/TS 19590, requires “a proper validation of the response for each size range of each composition of nanoparticle”.6 Obtaining a viable linear dynamic range (LDR) for transient ICP-MS signals from single particles (“transients”), however, is known to be a challenging task.7 Apart from quantitative atomization and ionization of each particle, representative sampling and transfer, and reproducible transmission downstream the mass analyser, it is crucial to detect the corresponding ion cloud properly, and to acquire the resulting short (but potentially strong) signal adequately. Unfortunately, the latter two aspects have often been overlooked in the past.
Instrument response in spICP-MS is expected to be proportional to particle mass. Therefore, the analysis of solid spherical NP across a size range of only 1–250 nm requires more than seven orders of magnitude of LDR with respect to transient signals. Because earlier spICP-MS publications mostly cover narrow size ranges and large particles, sensitivity may not have been of highest priority and a limited LDR may have inadvertently stayed unnoticed: for instance, from 2003 to 2006 Degueldre et al. described the analysis of TiO2 and FeOOH (400 nm),8 Zr (100 nm),9 Au (80–250 nm),10 and UO2 (0.1–10 μm)11 colloids. Regarding the latter two studies, spICP-MS results were found to agree with PSD obtained by scanning electron microscopy (Au) or optical single particle counting (UO2). The quotient qm of highest and lowest Au particle mass which still show linear response, however, amounts to only (250 nm)3/(80 nm)3 = 30. In case of the UO2 colloids, analytes with low abundancy (235U, 238U16O) were selected to avoid “the shut down of the detector gate”11 due to otherwise excessive signals from larger particles.
In contrast, Nomizu et al. observed nonlinear response already in 2002 for the analysis of airborne Zn particles. They were one of the first to propose it may be caused by “limitations in the pulse-counting capability of [the corresponding] digital circuit, or […] the limited linearity of the channel electron multiplier in pulse-counting mode”.12 Later, Olesik and Gray utilized spICP-MS for the mass determination of SiO2 microparticles and found similar limitations (LDR: 400–1077 nm, qm: 20).13 They proposed several possible reasons including incomplete ionization of particles, local plasma cooling, and competing rates of particle vaporization vs. diffusion of ions. However, they also emphasized the importance of considering the “impact of detector dead time” on the count rate “near the peak of [each] transient signal”.13 At the time, droplet desolvation and particle atomization,14 local plasma cooling,15 and the diffusion of ion clouds16 from single droplets or particles were investigated by Niemax and co-workers. Fuchs et al. recently complemented these studies with experimental and simulated data addressing the impact of particle diameter on ion cloud formation for 13 AuNP suspensions (10–100 nm).17 Linear response by spICP-MS was obtained from 15 to 83 nm (qm: 170), while 100 nm AuNP were biased low. They found this to agree with the computationally modelled ionization behaviour for particles of such size and given plasma conditions. However, ion cloud duration or cloud length (which may help to understand whether the cause is related solely to ionization effects, count losses, or a combination of them) were not reported for 100 nm AuNP.
Though Liu et al. initially observed similar limitations in a case study on AuNP when operating the instrument in standard mode (LDR: 20–70 nm, qm: 40), a 40-fold attenuation of the instrument's sensitivity allowed to shift (LDR: 50–200 nm) and extend (qm: 64) the range towards much larger particles.18 Shaw and Donard instead utilized an unmodified sector-field ICP-MS instrument featuring a pulse-only detector with fast detection electronics to overcome nonlinear response.19 With a dead time of less than 6 ns (usually 30–50 ns), the relative mass range covered (qm: 500) is one of the largest and the sensitivity achieved (LDR: 5–40 nm) among the highest reported to date for the analysis of AuNP. Rush et al. recently explored an inherently different approach: “Collisional dampening via addition of a collision gas”20 allowed to prolong the average cloud duration from <2 ms to >10 ms, ultimately extending the LDR for AuNP analysed in pulse-counting (PC) mode from 20–60 nm (qm: 27) to 20–80 nm (qm: 64).
Signal suppression due to incomplete vaporization is generally known to occur for large microparticles.21,22 According to some of the findings cited above 13–17 and two further studies that simulate vaporization and diffusion rates of single particles23,24 it may need to be considered even for much smaller NP. However, the fact that linearity can be regained by attenuating the signal,18 utilizing a detector with shorter dead time,19 or extending the ion cloud duration20 (i.e., after the ions have been sampled) supports a different theory: nonlinear response of the pulse counting signal to particles within the nanometre size range is most likely attributable to count losses caused by a finite dead time of the detection electronics.
With respect to recent advances such as the transfer of this method to time-of-flight25 (ICP-ToF-MS) and sector-field26,27 (ICP-SF-MS) platforms, the use of alternative sample introduction techniques,28,29 the development of custom data acquisition systems,30–32 or simply the improved sensitivity of latest generation quadrupole instruments (ICP-Q-MS), the limited LDR will become a severe constraint with respect to the viability of spICP-MS. Therefore, “continued research on both the hardware and software aspects of ICP-MS, and specifically spICP-MS” is required to further “improve the applicability of this technique toward a wider array of research problems”.33
In this work, a home-built prototype data acquisition system (protoDAQ) is utilized to study individual transients on a microsecond time scale and to explore the feasibility for compensation of dead time related count losses in spICP-MS. A custom sample introduction system is deployed to generate a large set of uniform mass spectrometric signals in short time. Conventional dead time correction (DTC) is applied both to millisecond and microsecond time-resolved spICP-MS data, and results before and after correction are thoroughly discussed. To verify the theory of count losses being one of the main factors for nonlinear response, the idea of microsecond dead time corrected spICP-MS data is combined with the concept of a controlled signal attenuation, following the work described by Liu et al.18 Both attempts are first investigated using model transients of monodisperse microdroplets entering the ICP (Part A). They are then applied to the analysis of eight commercial AuNP suspensions and three AuNP reference materials (RM) ranging from 10 nm to 100 nm (Part B). To identify and extract transients from single AuNP in the continuous stream of data, a simple and parameterizable algorithm is presented. Cross-calibration of measurements performed with and without signal attenuation is evaluated. Ultimately, the potential impact of microsecond dead time correction on the resulting PSD is studied for two of the analysed AuNP RM.
Theory
Detection electronics used for counting of electric pulses caused by single photons or ions typically exhibit a certain time constant: after one pulse is counted, no subsequent pulse can be registered for a certain period of time τ, the so-called dead time.34 Knowledge about the necessity to correct for count losses associated with this dead time dates back to the early beginnings of photon- and ion-counting in spectrometric systems.35,36 Fundamentals on the role of dead time in counting applications, methods to determine the dead time, and concepts to correct for dead-time related count losses have been published in the past, for example by Ingle and Crouch,37 Nelms et al.,38 and Fahey.39 The following shall, therefore, only serve as a brief overview:Typically, three different types of pulse counting circuits, namely type Ia and Ib “paralyzable” and type II “nonparalyzable” circuits are differentiated in the literature. In paralyzable counting circuits each subsequent pulse that occurs during the current dead time extends the period until a new pulse can be resolved. In nonparalyzable counting circuits, by contrast, a fixed dead time exists that does not prolong, even if one or more additional pulses occur during this period. All three types are limited in their maximum pulse resolving rate, but they differ in their probability for pulse-overlap. Hence, they each require a different correction model.
For the ICP-MS instrument used in this work, both the pulse width (8–10 ns) and the minimum pulse period (45–55 ns) observed for high ion currents were found to be largely independent of the actual pulse frequency, detector voltages, and the chosen discriminator value (exemplary oscilloscope traces of the pulse-counting output during acquisition of an excessive 40Ar+ signal shown in Fig. S-1†). According to Ingle and Crouch, this behaviour indicates a type II nonparalyzable detection circuitry.37 Assuming a pulse period of ∼50 ns to be a good estimate of the instrument's actual dead time, the maximum resolvable count rate, Rmax, is limited to 2 × 107 counts per second (cps). Due to possible pulse overlap, however, even for count rates far below Rmax the experimentally observed count rate, Rexp, is lower than the actual count rate, Rtrue.
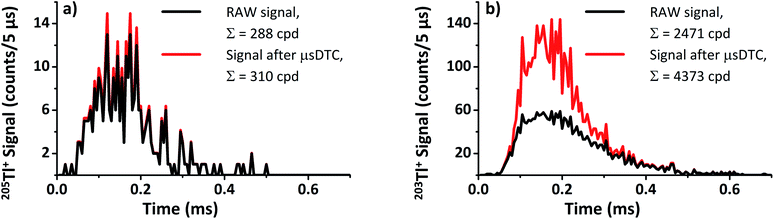
Provided Rtrue is constant during a known time interval t, the average number of lost counts can still be estimated as follows. The probability Pn of counting n randomly emitted pulses is given by Poisson's equation:
The probability for n = 0 pulses to be found during an interval of t = τ (i.e., no further pulse occurred during the dead time), therefore, is:
| P0 = e−Rtrueτ. |
With this, the average experimentally observed count rate Rexp for a given true count rate Rtrue can be calculated as:
| Rexp = P0Rtrue = e−RtrueτRtrue. |
For type II counting circuits, Rexp has been previously shown37 to be approximately equal to
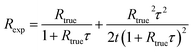 | (1) |
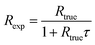 | (2) |
To calculate the estimated true count rate Rtrue from an experimentally observed count rate Rexp, eqn (2) is than rearranged as follows:
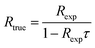 | (3) |
For Rexp ≤ 50 counts/5 μs, t ≥ 2 μs, and τ = 0.05 μs the results from eqn (1) and (2) differ by less than 1%. Therefore, in the following DTC is performed based on the simplified eqn (3).
Instrumentation
ICP-Q-MS
All work presented in the following was performed on a model iCap Qc (Thermo Fisher Scientific, Bremen, Germany) ICP-Q-MS instrument. The corresponding vendor software (Qtegra ISDS 2.4) was primarily used for instrument control and monitoring purposes, while all spICP-MS data were acquired using the protoDAQ (see below). The standard skimmer cone insert was replaced by the shorter high-sensitivity insert (type “2.8”, Glass Expansion, Melbourne, Australia). A second roughing pump (UNO 030 B, Pfeiffer Vacuum, Asslar, Germany) was added to the first vacuum stage to improve the overall instrument sensitivity and to maintain sufficient interface vacuum even during operation under argon (Ar)/helium (He) mixed-gas conditions. The standard quartz torch injector with an inner diameter (ID) of 2.5 mm was replaced by either a 1.5 mm (Part A) or a 1.0 mm (Part B) ID injector (both Thermo Fisher Scientific). A model DSO-X 2024 digital storage oscilloscope (Agilent Technologies, Santa Clara, CA, USA) was used for validation of the different data acquisition schemes, fine-tuning of the pre-acquisition delay (see below), and for experimental determination of the aforementioned pulse width and minimum pulse period.spICP-MS operating conditions
To achieve conditions suitable for spICP-MS, measurements of only one isotope (197Au+, 203Tl+, or 205Tl+, resolution “normal”, no interference correction) were performed with the dwell time set to 10 ms (vendor software, monitoring) and 5 μs (protoDAQ, acquisition). The “Counting Threshold”, a parameter responsible for (de)activation of the detector's pulse counting section, was increased from 20 to 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in order to force the detection electronics to stay in pulse counting mode. To minimize any possible “blind time” even in the unlikely case that a very strong signal still exceeds this threshold, the “Counting Threshold Timeout” (i.e., the minimum time the pulse counting section of the detector stays deactivated once the Counting Threshold is triggered) was set to the lowest valid value of 20 μs.
000 in order to force the detection electronics to stay in pulse counting mode. To minimize any possible “blind time” even in the unlikely case that a very strong signal still exceeds this threshold, the “Counting Threshold Timeout” (i.e., the minimum time the pulse counting section of the detector stays deactivated once the Counting Threshold is triggered) was set to the lowest valid value of 20 μs.
Signal attenuation
For the “Attenuated Sensitivity” mode, the CCT Focus Lens voltage was decreased by 30 V after successful optimization of operating conditions, whereas all other parameters were left unchanged. After investigation of different possibilities to attenuate the ICP-MS signal in a fast and reproducible manner, a moderate manipulation of the CCT Focus Lens voltage was found to provide sufficient attenuation (see below for further explanation) with no pronounced analyte-dependency for the monitored isotopes.Data acquisition
A home-built prototype data acquisition system, specifically tailored to the needs of spICP-MS, was used for acquisition of all data shown in the following. An earlier version of this protoDAQ was mentioned first by the authors in 2016,30 but was constantly improved and adapted to different use cases since then,40 and a more advanced version was utilized recently in two studies performed by Mozhayeva et al.41,42 In its current version, the protoDAQ allows to acquire and transfer data to a host computer for virtually any measurement time at a sustained data rate of up to 2 × 105 samples per second (i.e., with a highest time resolution of 5 μs) and with a duty cycle of 100% (no reset time between two subsequent data points). In this study, it captured the pulse counting signal directly behind the preamplifier/discriminator stage of the instrument's detection electronics, providing an uninterrupted stream of data that represents the number of pulses observed in each dwell (“RAW data”). An input sampling rate of 250 MHz (i.e., 4 ns−1) ensures that every pulse generated by the detection electronics is registered properly. Furthermore, the protoDAQ can be operated either in “continuous, free-running” or in “triggered, segmented” mode:The “free-running” mode simply yields the count rate as a function of time in a continuous fashion, acquired at the chosen dwell time and for the desired measurement duration. In spICP-MS, this mode proves useful any time the frequency of transient events varies or is unknown (e.g., the analysis of suspensions through conventional nebulization, as performed in Part B). It also depicts the preferable mode during tuning and optimization. However, for transients that recur strongly periodically (e.g., the on-demand introduction of monodisperse droplets into the ICP, as performed in Part A) the “segmented” acquisition mode can greatly simplify the process of data handling and processing: each time a trigger signal is registered, only a short segment of the pulse counting signal is acquired as described above. Segment length, trigger condition, and pre-acquisition delay (an optional idle time between detection of the trigger signal and start of the acquisition) can be configured according to requirements. Because acquisition takes place only while transient signals are expected to occur, the overall amount of data is reduced significantly. Depending on the remaining droplet jitter (the difference between observed and expected time of occurrence for the periodically generated droplets, which also limits the minimum useful segment length) and the resulting signal-to-noise ratio (transient signal vs. average signal that is not part of the transient), this mode may even render subsequent data extraction and processing steps redundant.
Part A: analysis of Tl+ in microdroplets
In the first part of this work, a custom microdroplet sample introduction interface (MDI) was used to study transient signals and to explore the feasibility for compensation of dead-time related count losses in spICP-MS. The interface allows on-demand generation and transfer of single droplets into the ICP. If adjusted carefully, droplets emerging from the droplet generator show a uniform size distribution and follow a stable droplet trajectory through the MDI. Desolvation along this flight path transforms the droplets into small airborne particles, enabling the transport of any non-volatile compound contained in the former droplet further downstream in a spatially and temporally confined manner. Ultimately, a transient mass spectrometric signal comparable to the signal from a single NP can be detected for each airborne particle that reaches the ICP.Experimental
Transfer of the droplets into the ICP was achieved by means of a custom-machined MDI. It represents the successor of a design presented in an earlier study,29 which in turn was inspired by other interfaces such as the one described by Gschwind et al.28 The MDI consists of a dispenser head mounting which is sealed towards a glass transfer tube, two independent gas inlets (henceforth referred to as “carrier” and “make-up” gas), an LED strobe light, as well as camera and lens mountings incorporated into a detachable aluminium body (Fig. S-2†). The camera is positioned right below the nozzle of the dispenser head, with the strobe light facing the camera from behind.
For optimum desolvation and transport of the microdroplets, He was passed both through the dispenser head (sheath gas) and the first gas inlet position (carrier gas), as it has been reported in the past to effectively dry droplets in short time even at room temperature.28,43 Ar was passed through the T-junction of the MDI near the end of the vertical transfer tube (make-up gas) for final transfer of the droplets towards the horizontal torch injector.
Four aqueous sample solutions were prepared by diluting a standard stock solution of 1000 mg L−1 Tl (Inorganic Ventures) with double-distilled water to final concentrations of 29, 44, 444, and 6600 μg L−1 Tl in 0.5% HNO3 (CertiPUR). Thallium shows a natural isotopic abundance of 70.48% 205Tl and 29.52% 203Tl. However, the isotopic ratio is not accessible during analysis, because typically only a single isotope is monitored in spICP-MS at a given time. Therefore, the four sample solutions were treated as eight monoisotopic samples containing either 9, 13, 131, and 1949 μg L−1 of 203Tl, or 20, 31, 313, and 4651 μg L−1 of 205Tl. This approach required only three changes of the sample solution to obtain in total eight data points for determination of the dynamic range, ultimately reducing the risk of a potential change in the droplet volume between different samples to a minimum.
Data acquisition and processing
Acquisition of each data segment was triggered by the “Ready” signal of the MDS (output of a short 5 V pulse with generation of each droplet). The droplet frequency was kept at 20 Hz, and every measurement was carried out for 180 s (i.e., 3600 individual droplets per sample, isotope, and sensitivity mode) using a dwell time of 5 μs. The protoDAQ's pre-acquisition delay was adjusted for each of the four sample solutions utilizing the DSO, because interruptions of the droplet generation process led to small variations in the average droplet transit time through the MDI.
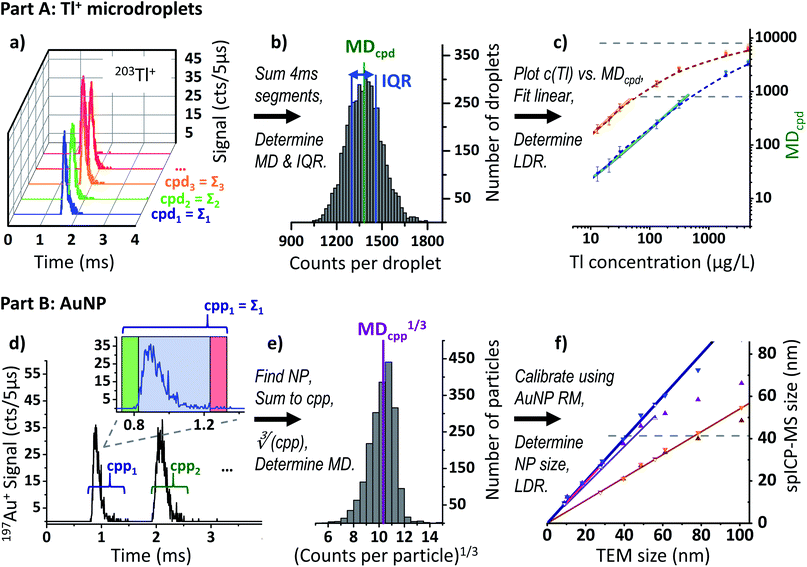 | ||
| Fig. 2 Data acquisition and processing scheme. (a) Transients of five subsequent droplets (131 μg L−1 203Tl), protoDAQ operated in segmented acquisition mode. (b) Histogram after frequency analysis of obtained cpd values including median (MDcpd) and IQR. (c) Log–log plot of Tl concentration vs. MDcpd, see also Fig. 3. (d) Time-resolved 197Au+ signal for 50 nm AuNP, protoDAQ operated in continuous acquisition mode. Zoom-in detail: algorithm for identification of NP events applied to first transient (green: scurr ≥ thstart, red: scurr ≤ thend). (e) Histogram after frequency analysis of obtained cpp1/3 values including median (MDcpp1/3). (f) TEM size vs. spICP-MS size plot after calibration using RM AuNP, see also Fig. 6. | ||
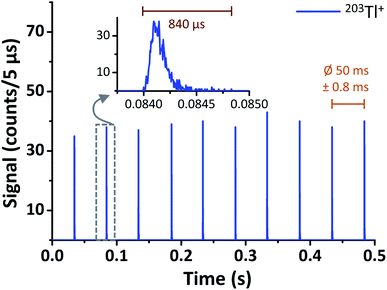
To obtain the typical number of counts per droplet (cpd) for a given dataset, first the cpd value for each of the contained segments was calculated. For this, the 800 consecutive RAW data points found in each row were simply summed up, row by row. Subsequently, the median cpd (MDcpd) and the corresponding interquartile range (IQR, as a measure of the spread of the population and to allow for a weighted linear regression) across the 3600 resulting sums were calculated for each dataset (Fig. 2b). With this, a robust estimate of the typical cpd is derived, even in case a dataset contains a moderate number of outliers. Because the approach is solely based on the sum of counts in each 4 ms segment and does not make use of the protoDAQ's improved time resolution, it is referred to as “millisecond time-resolved (msTR)” data in the following. It should be noted, however, that by virtue of the triggered acquisition these datasets do not exhibit artefacts from so-called “split-particle events” (cases where the signal of a single transient is split up between two subsequent dwells) otherwise known to occur in msTR spICP-MS.
Results and discussion
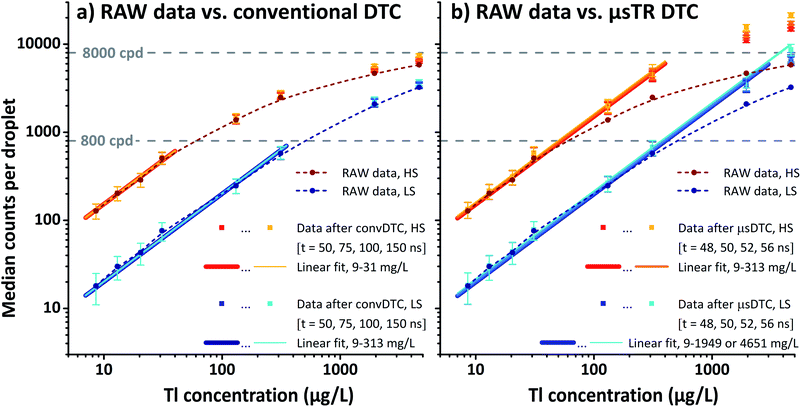 | ||
| Fig. 3 Instrument response obtained for Tl-containing microdroplets in high (red) and low sensitivity (blue) mode. Data points show MDcpd (dots and squares, n = 3600) and IQR (error bars) as a function of the analyte concentration (mass of either 203Tl or 205Tl per volume). Both plots contain RAW data (dark red/blue dots) and data after either (a) convDTC or (b) μsDTC (squares in brighter shades of red/blue). Data after convDTC (a) using a dead time of 50, 75, 100, or 150 ns is virtually indistinguishable and mostly obscured by RAW data. In contrast, data after μsDTC (b) using a dead time of 48, 50, 52, or 56 ns shows significant differences to the RAW data. Solid lines of different width (after DTC) represent the corresponding fit functions from linear regression, while dashed lines (RAW data) are added to guide the eye. For individual plots, see also Fig. S-3a–c.† | ||
Instrument response ranges from approximately 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cpd in HS mode, and 15 to 4000 cpd in LS mode. The LDR observed for these short transients, however, is small – regardless whether data before or after convDTC are taken into account and independent of the actual dead time applied. Not even for exceptionally high values of τ (100 ns, 150 ns) a noticeable impact on the data can be provoked. Both in HS and LS mode the response is only linear up to a few hundred cpd, and in all cases deviation from the expected linear relation is observed with the first data point above 1000 cpd (Fig. 3a, aid line at 800 cpd). In HS mode, this range covers only the first four data points, or up to 500 cpd (linear regression: 9 μg L−1 203Tl to 31 μg L−1 205Tl; R2 = 0.995). In LS mode, a linear response is obtained for at least the first six data points, or up to 600 cpd (9 μg L−1 203Tl to 313 μg L−1 205Tl; R2 = 0.988 to 0.989 depending on τ). It should be noted, however, that attenuation of the instrument's sensitivity by a factor of approximately 6.8 results in only 18 ± 7 cpd (MD ± IQR) for the lowest Tl concentration analysed. At this point, the relative dynamic concentration range and the bottom end of the absolute signal scale converge. Consequently, it is safe to assume that the Tl concentration range utilized, and the attenuation factor chosen, cover the entire LDR available with respect to short transient signals.
000 cpd in HS mode, and 15 to 4000 cpd in LS mode. The LDR observed for these short transients, however, is small – regardless whether data before or after convDTC are taken into account and independent of the actual dead time applied. Not even for exceptionally high values of τ (100 ns, 150 ns) a noticeable impact on the data can be provoked. Both in HS and LS mode the response is only linear up to a few hundred cpd, and in all cases deviation from the expected linear relation is observed with the first data point above 1000 cpd (Fig. 3a, aid line at 800 cpd). In HS mode, this range covers only the first four data points, or up to 500 cpd (linear regression: 9 μg L−1 203Tl to 31 μg L−1 205Tl; R2 = 0.995). In LS mode, a linear response is obtained for at least the first six data points, or up to 600 cpd (9 μg L−1 203Tl to 313 μg L−1 205Tl; R2 = 0.988 to 0.989 depending on τ). It should be noted, however, that attenuation of the instrument's sensitivity by a factor of approximately 6.8 results in only 18 ± 7 cpd (MD ± IQR) for the lowest Tl concentration analysed. At this point, the relative dynamic concentration range and the bottom end of the absolute signal scale converge. Consequently, it is safe to assume that the Tl concentration range utilized, and the attenuation factor chosen, cover the entire LDR available with respect to short transient signals.
Usually, a reduction of the instrument's sensitivity is accompanied by a deteriorated limit of detection. In conventional ICP-MS the operation in LS mode would, thus, only be seen as a shift and not as an extension of the applicable concentration range. When analysing particulate matter by spICP-MS, however, it is not possible to reduce the amount of analyte from a single particle that reaches the ICP at a given time in the classical sense (e.g., higher dilution of the suspension, lower sample uptake rate, or decreased transport efficiency). In this case, adjustments to the instrument's sensitivity or multiple analyses of the same sample using two or more sensitivity regimes can be considered genuine strategies to extend the LDR. Because convDTC has been found to be unable to provide a significant improvement over the uncorrected data for transients in the sub-ms regime, an appropriate attenuation factor may currently even depict the only way to handle strong transient signals in msTR spICP-MS.
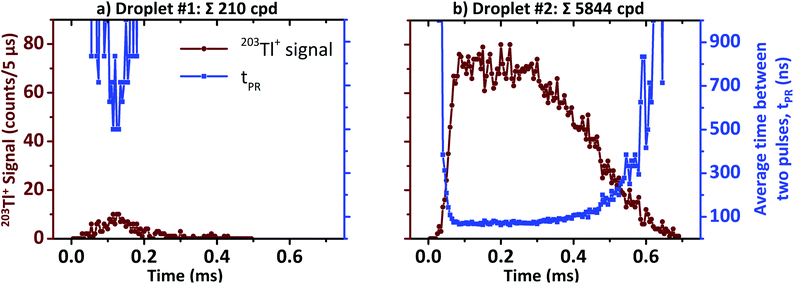
In case of μsTR spICP-MS, providing an 800× higher time resolution compared to msTR spICP-MS, the prerequisite of a constant pulse frequency over at least one dwell can be considered fulfilled again. Fig. 5 shows two exemplarily chosen transients before and after μsDTC has been performed on every 5 μs dwell. The total number of counts per droplet are either 288 and 2471 cpd (black, before μsDTC), or 310 and 4373 cpd (red, after μsDTC with τ = 50 ns). As can be seen, only a marginal correction for count losses occurs for count rates <15 counts/5 μs (i.e., <3 × 106 cps – the typical upper limit for pulse counting signals in ICP-Q-MS). Similarly, the probability for pulse overlap at these frequencies is still rather low. Dwells showing 20–40 counts/5 μs experience a moderate correction for count losses, resulting in count rates that are 20% (24 instead of 20 counts/5 μs) to 70% (68 instead of 40 counts/5 μs) higher than the corresponding uncorrected data. Accurate correction for count losses by means of a statistical model, however, is limited to a certain scale and reliable results may not be expected in case of severe pulse overlap. As soon as the cumulative duration of the observed pulses occupies a considerable fraction of the integration time, even minor differences in the actual count rate or in the dead time used for correction have a significant effect on the resulting number of pulses after correction: as can be seen in Fig. 5, application of μsDTC to dwells with count rates >50 counts/5 μs results in 100–150% higher values (τ = 50 ns). Moreover, variation of the observed count rate by only ±1 count, or variation of τ by only ±2 ns, affects the resulting count rate after μsDTC by more than ±4 counts. A case-specific evaluation of the maximum pulse frequency suitable for application of μsDTC and an accurate determination of τ are, therefore, highly recommended to avoid additional artefacts arising from the correction itself.
Considering both HS and LS data, the best combination of LDR covered and coefficient of determination obtained is achieved using τ = 52 ns. Likewise, the minimum pulse repetition time observed with a DSO has been determined to be approximately 48 ns (Fig. S-1,† measured utilizing the strong ion current ever-present for 40Ar+). Taking the DSO's limited bandwidth of only 200 MHz (which equals an effective time resolution of 5 ns) into account, these two independent approaches to estimate the instrument's dead time are considered to be in good agreement.
Summary
Overall, application of μsDTC results in up to a fifteen-fold increase of the upper end of the LDR compared to convDTC or uncorrected data with respect to transient signals from single droplets or airborne particles, if data is acquired in pulse counting mode. Because the expected signal of a single transient cannot be altered in the classical sense to meet the optimum intensity range when using spICP-MS, combining μsDTC with a controlled attenuation approach allows to further increase the LDR. Determination of a maximum count rate that can be tolerated in spICP-MS and used for μsDTC is difficult: among others, it depends on the average duration of the transient signals, the steepness of signals' rising and falling edges, and the instrument's dead time. Based on the data evaluated above, and with reference to the instrument and conditions used in this study, an upper count rate limit of 50 counts/5 μs (+100% compensation for τ = 50 ns), not to be exceeded for an extended period of time throughout a transient, is proposed.Part B: analysis of gold nanoparticles
Up to this point, the benefits of μsDTC have been demonstrated only for the analysis of monodisperse droplets in combination with a custom MDI. However, due to transport characteristics inherent to this particular sample introduction technique the corresponding transients are often more uniform compared to transients from single NP analysed using a standard sample introduction system (Fig. S-4 and S-5†). The presented findings may, therefore, not be considered representative with respect to conventional spICP-MS. Hence, in the second part of this work the same μsDTC approach is applied to data obtained from a more common spICP-MS experiment: the analysis of monodisperse AuNP suspensions in the size range from 10 to 100 nm by means of pneumatic solution nebulization, performed both in HS and LS mode.Experimental
Monodisperse, solid, spherical AuNP with tannic acid surface functionalization (“NanoXact Tannic”) and sizes (TEM diameter ± first standard deviation as reported in the corresponding certificate of analysis, COA) of 10 (10.4 ± 0.7), 20 (18.2 ± 1.9), 30 (28.6 ± 3.2), 40 (39.5 ± 3.8), 50 (48.6 ± 6.4), 60 (61.2 ± 6.0), 80 (78.3 ± 6.0), and 100 (100.9 ± 12.1) nm were purchased from NanoComposix (San Diego, CA, USA). Citrate-stabilized AuNP reference materials RM 8011, RM 8012, and RM 8013 with sizes of 10 (8.9 ± 0.1), 30 (27.6 ± 2.1), and 60 (56.0 ± 0.5) nm (TEM mean diameter ± expanded uncertainty as stated in the corresponding report of investigation, ROI)45–47 were purchased from NIST (Gaithersburg, MD, USA). All samples were stored in darkness at approximately 2 °C prior to analysis. Suspensions were shaken for 30 s before being diluted to a final particle number concentration of 2 × 105 NP mL−1 with double-distilled water. Sample analysis was performed immediately after dilution.
Data acquisition and processing
Similar to the data processing approach described in Part A, the resulting files for each material and sensitivity mode were directly imported into separate OriginPro 2015 (OriginLab) worksheets. The number of counts per particle (cpp) were obtained by simply summing up the counts observed for each row or NP event. Subsequently, the median cpp (MDcpp) was determined for each of the datasets. In addition, the cubic root of each cpp value, cpp1/3, as well as the respective median, MDcpp1/3, were computed (see Fig. 2e and section “Size calibration” below).
It should be noted that particle sizes obtained by TEM and spICP-MS are not expected to show perfect agreement. In fact, both techniques represent independent physical measures, each one biased by its own characteristic distortions. For TEM, information on the size of a particle is directly accessible from its corresponding surface projection, while in spICP-MS it is derived from a signal proportional to particle mass. In case of the commercial AuNP suspensions, TEM characterization is typically carried out only on a rather small number of particles (N < 300), which may induce an additional bias. Ultimately, mean and median are different central tendency estimates and deviations are to be expected anytime size distributions differ from a normal distribution.
Results and discussion
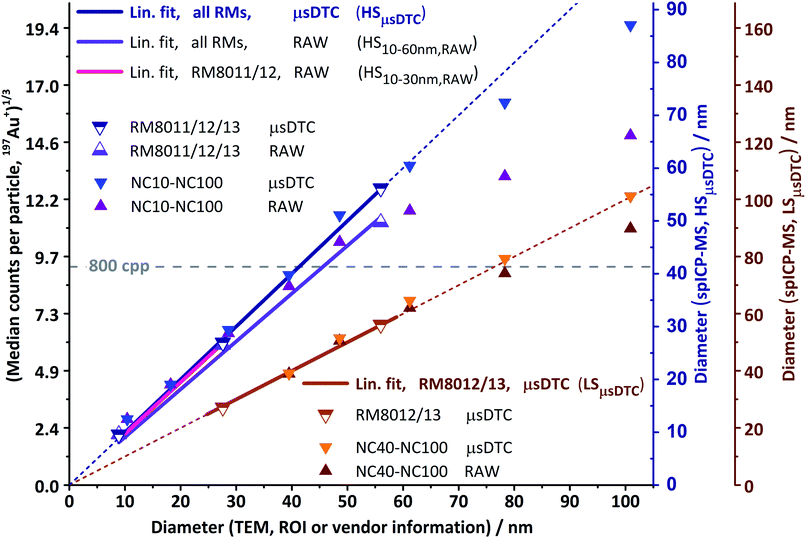
In Fig. 6, the size-proportional MDcpp1/3 values obtained from the subsequent analysis of eight monodisperse AuNP suspensions (“NC10–NC100”, solid triangles) and three RM (“RM8011/12/13”, semi-open triangles) are plotted against the corresponding TEM diameter. The figure includes data acquired both in HS (blue/purple) and LS mode (orange/brown), as well as before and after μsDTC (triangles pointing up and down, respectively). Also shown are four different linear fit functions (bold lines), with the best fit for each of the two sensitivity modes extended to full axis range (thin lines) and chosen as the size scale for the corresponding y-axis. Depending on sensitivity and linear range obtained for a particular dataset, either the smaller two, the larger two, or all three AuNP RM have been considered for absolute size calibration.Application of μsDTC to the HS dataset (blue triangles pointing down) extends the linear range towards RM8013 and leads to virtually identical slopes, regardless whether only the smaller two or all three RM are used (“HSμsDTC”, blue, mC = 0.22464 cpp1/3 nm−1, R2 = 0.9999). Sizing using the HSμsDTC calibration also enables reproduction of the reported TEM diameter for NC60 (MDcpp = 1588 cpp before and 2505 cpp after μsDTC). However, as mentioned before the ability to compensate for dead-time related count losses is fundamentally limited by the instrument's dead time, the dwell time used for acquisition, and the rate at which a transient's pulse frequency changes. For signals from single AuNP the instrument response in HS mode has been found to tail off just beyond 60 nm, resulting in a slightly underestimated size for NC80 (MDcpp = 2264/4309 cpp). The signal for NC100 (MDcpp = 3287/7488 cpp), although raised by more than 220% due to μsDTC, still suffers from count losses that cannot be fully corrected for: with >3000 detected pulses in 0.5 ms (each pulse provoking a dead time of 50 ns) the detection circuitry is blocked and unable to count any further pulses for more than 30% of the transient's total duration.
Attenuation of the instrument's sensitivity by a factor of approximately 6.3 (LS mode, brown triangles pointing up) resulted in linear response of the uncorrected data for the calibrants RM8012 and RM8013, as well as for NC40, NC60, and NC80 (MDcpp = 729 cpp). However, RM8011, NC10, and NC20 now fell beyond the lower limit of detection (expected signal, based on the response for RM8012: 1.3, 2.0, and 10.8 cpp, respectively). Therefore, calibration could only be performed using RM8012/13. The resulting linear fit functions before and after μsDTC are virtually identical (“LSμsDTC”, brown, mD = 0.12145 cpp1/3 nm−1, R2 = 0.999), and even without any dead time correction spICP-MS size and reported TEM diameter are in good agreement up to NC80. Despite the attenuated sensitivity, MDcpp for NC100 still exceeds 800 cpp and, therefore, its spICP-MS size before μsDTC appears slightly underestimated.
Application of μsDTC to the LS dataset (orange triangles pointing down) predominantly changed the MDcpp values for NC100 and (to a much lesser extent) NC80, while leaving the data for all smaller NP virtually unchanged. Eventually, linear response now ranges from 30 to 100 nm and covers all AuNP detectable in LS mode. Furthermore, when using the LSμsDTC calibration for sizing the discrepancy between derived median spICP-MS size and reported mean TEM size is less than ±1 nm for both the smallest (RM8012) and largest (NC100) AuNP suspension analysed.
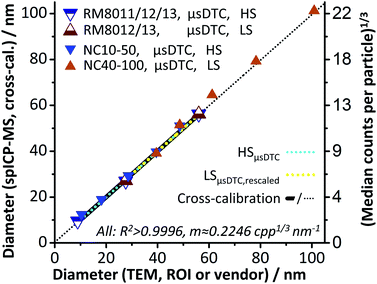
Ultimately, and within limits of accuracy for the reported mean TEM sizes, a linear relation between AuNP size and spICP-MS response over the entire size range of 8.9 to 100.9 nm is achieved by combining the concepts of μsDTC and a controlled signal attenuation. Furthermore, the findings indicate that moderate manipulation of the CCT Focus Lens voltage maintains the instrument's underlying response function for the given experimental setup and may be used to further attenuate the signal, if necessary.
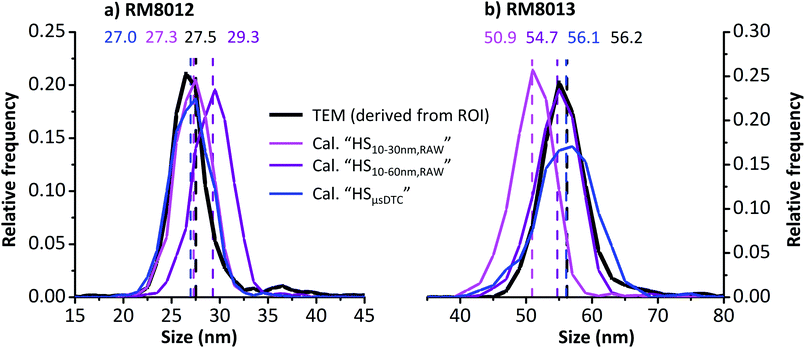
To identify possible distortions arising from μsDTC, size distributions of RM8012 and RM8013 as obtained by spICP-MS in HS mode are compared to TEM distributions published in the corresponding ROI. The spICP-MS distributions shown in Fig. 8 are based either on data before (HS10–30 nm,RAW, pink and HS10–60 nm,RAW, purple) or after μsDTC (HSμsDTC, blue), while the TEM distributions (black) have been derived from the respective histograms46,47 through manual image processing. Dashed vertical lines and labels of matching colour indicate the corresponding mean sizes (minimal deviations between the reported and the derived TEM mean size are likely due to inevitable rounding errors from histogram transformation). A rather coarse bin width of 2 nm has been chosen to minimize any bias due to histogram quantization effects and to allow for best comparability.
The RM8012 size distributions as reported by TEM (Fig. 8a, black) and obtained for spICP-MS after μsDTC and using all three AuNP RM (Fig. 8a, blue) show a close match. For data before μsDTC, a similar agreement is only achieved when considering the smaller HS10–30 nm,RAW calibration range (Fig. 8a, pink). Resulting mean sizes of 27.3 and 27.0 nm represent deviations of less than −1.9% from the TEM mean size of 27.5 nm. The RM8012 size distribution obtained for spICP-MS before μsDTC but using the larger HS10–60 nm,RAW calibration range (Fig. 8a, purple), however, is shifted to the right and shows an overestimation of the mean size by more than 2 nm (+6.5%). On the contrary, a first visual assessment of the RM8013 size distribution using the very same calibration approach indicates a good match between spICP-MS and TEM (Fig. 8b, purple). Closer examination, however, reveals a noticeable overrepresentation of NP < 53 nm at the expense of NP > 60 nm, ultimately resulting in a slightly smaller mean size of 54.7 nm compared to 56.2 nm by TEM (−2.7%). The size distribution obtained using the narrow HS10–30 nm,RAW calibration range (Fig. 8b, pink) is strongly shifted to the left, though, and results in an underestimation of the mean size by more than 5 nm (−9.4%). Again, only spICP-MS after μsDTC (Fig. 8b, blue) is able to reproduce the TEM mean size with less than −0.2% deviation and independent of the calibration range.
Notably, the size distribution for RM8013 obtained after μsDTC (Fig. 8b, blue) is slightly broader than the corresponding TEM distribution. So far it is assumed that μsDTC is able to compensate for dead-time related count losses known to occur in spICP-MS, eventually diminishing the systematic underestimation of stronger transients and providing the correct mean size of monodisperse NP suspensions within an extended size range. At the same time, however, the approach may still not be accurate enough to yield a correct result on a per-particle basis, resulting in an artificial broadening of the size distribution. In the end, and depending on individual requirements, accuracy of the central tendency estimate for NP size may need to be traded off against precision of the obtained size distribution by considering either μsDTC data (in combination with a more universal calibration) or uncorrected RAW data (calibrated only across a narrow size window).
Summary
Similar to the findings in Part A, results show that μsDTC allows for a significant improvement of the LDR over uncorrected spICP-MS data. Application of μsDTC to the HS dataset leads to a four-fold increase of qm and enables the use of all three RM for calibration (LDR: 8.9–61.2 nm, qm: 325). Application of μsDTC to the LS dataset only changes the MDcpp values for the largest AuNP suspensions, eventually resulting in a linear response for AuNP ranging from 30 to 100 nm (qm: 50). Cross calibration between HS and LS mode after μsDTC results in virtually identical calibration parameters but is now based on five instead of only two or three data points. By combining the concepts of μsDTC and a controlled signal attenuation, a linear relation between AuNP size and spICP-MS response over the entire size range analysed (LDR: 8.9–100.9 nm, qm: 1460) is achieved. Furthermore, the RM8012 size distributions as reported by TEM and obtained for spICP-MS after μsDTC are in good agreement. For RM8013, a slight broadening of the distribution can be observed that is not apparent in the uncorrected dataset. Therefore, pros and cons of μsDTC may need to be balanced regarding the LDR required, and the accuracy of the size distribution aimed at within this range.Conclusions
A sustained, artefact-free sampling of the pulse counting signal from hundreds of thousands of droplets and NP using a home-built prototype data acquisition system and a time resolution of 5 μs allowed for an extensive investigation and better understanding of the challenges associated with the analysis of short transients in spICP-MS. Oversampling of each transient enabled a functional compensation for dead-time related count losses, ultimately improving the LDR by approximately one order of magnitude towards higher count rates. However, it also revealed the fundamental limitations of this approach with respect to the detection electronics found in today's ICP-Q-MS instruments.Measurements performed after signal attenuation through a provoked reduction of the ion transmission (i.e., after sampling of the ions) revealed that the relative response between different analyte concentrations, as well as different NP sizes, stayed essentially unchanged. Therefore, a cross-calibration between two sensitivity regimes could be established, improving the LDR by approximately another order of magnitude towards higher particle masses. Furthermore, findings support the proposed theory of dead-time related count losses being one of the main reasons for nonlinear response in pulse counting spICP-MS.
Due to the low number of atoms (and, in consequence, ions) present when analysing nanomaterials of small size or low density, of more complex chemical compositions, or from elements with low isotopic abundancy, the extremely sensitive (high-gain, but limited linearity) pulse counting mode is likely to stay indispensable in the future. But while it has been shown in this work that compensation for count losses is possible with manifold oversampling of the transient signals, and despite the fact that counting electronics with ultra-low dead times could further improve the LDR, other ways must be explored to extend the top end of the tolerated particle mass range and, thereby, the methods' applicability and usability.
Future work is expected to expand the concept of acquiring and processing microsecond time-resolved data towards (low-gain, but higher linearity) analogue mode spICP-MS, combining previous improvements such as the elimination of particle coincidence and split-events with a detection scheme that is unaffected by dead time effects as a matter of principle.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support by the glassblower and the machine shop services at the Institute for Inorganic and Analytical Chemistry, University of Muenster, and the Department of Chemistry and Biology, University of Siegen, are gratefully acknowledged.References
- T. Nomizu, S. Kaneco, T. Tanaka, T. Yamamoto and H. Kawaguchi, Determination of Femto-gram Amounts of Zinc and Lead in Individual Airborne Particles by Inductively Coupled Plasma Mass Spectrometry with Direct Air-Sample Introduction, Anal. Sci., 1993, 9, 843–846 CrossRef CAS.
- F. Laborda, E. Bolea and J. Jiménez-Lamana, Single particle inductively coupled plasma mass spectrometry: a powerful tool for nanoanalysis, Anal. Chem., 2014, 86, 2270–2278 CrossRef CAS.
- K. Leopold, A. Philippe, K. Worle and G. E. Schaumann, Analytical strategies to the determination of metal-containing nanoparticles in environmental waters, TrAC, Trends Anal. Chem., 2016, 84, 107–120 CrossRef CAS.
- F. Laborda, E. Bolea, G. Cepria, M. T. Gomez, M. S. Jimenez, J. Perez-Arantegui and J. R. Castillo, Detection, characterization and quantification of inorganic engineered nanomaterials: a review of techniques and methodological approaches for the analysis of complex samples, Anal. Chim. Acta, 2016, 904, 10–32 CrossRef CAS.
- O. A. Sadik, N. Du, V. Kariuki, V. Okello and V. Bushlyar, Current and Emerging Technologies for the Characterization of Nanomaterials, ACS Sustainable Chem. Eng., 2014, 2, 1707–1716 CrossRef CAS.
- ISO/TS 19590:2017, Nanotechnologies – Size distribution and concentration of inorganic nanoparticles in aqueous media via single particle inductively coupled plasma mass spectrometry.
- M. Tanner and D. Günther, Short transient signals, a challenge for inductively coupled plasma mass spectrometry, a review, Anal. Chim. Acta, 2009, 633, 19–28 CrossRef CAS.
- C. Degueldre and P. Y. Favarger, Colloid analysis by single particle inductively coupled plasma-mass spectroscopy: a feasibility study, Colloids Surf., A, 2003, 217, 137–142 CrossRef CAS.
- C. Degueldre, P. Y. Favarger and C. Bitea, Zirconia colloid analysis by single particle inductively coupled plasma-mass spectrometry, Anal. Chim. Acta, 2004, 518, 137–142 CrossRef CAS.
- C. Degueldre, P. Y. Favarger and S. Wold, Gold colloid analysis by inductively coupled plasma-mass spectrometry in a single particle mode, Anal. Chim. Acta, 2006, 555, 263–268 CrossRef CAS.
- C. Degueldre, P. Y. Favarger, R. Rosse and S. Wold, Uranium colloid analysis by single particle inductively coupled plasma-mass spectrometry, Talanta, 2006, 68, 623–628 CrossRef CAS.
- T. Nomizu, H. Hayashi, N. Hoshino, T. Tanaka, K. Kitagawa and S. Kaneco, Determination of zinc in individual airborne particles by inductively coupled plasma mass spectrometry with digital signal processing, J. Anal. At. Spectrom., 2002, 17, 592–595 RSC.
- J. W. Olesik and P. J. Gray, Considerations for measurement of individual nanoparticles or microparticles by ICP-MS: determination of the number of particles and the analyte mass in each particle, J. Anal. At. Spectrom., 2012, 27, 1143–1155 RSC.
- C. C. Garcia, A. Murtazin, S. Groh, V. Horvatic and K. Niemax, Characterization of single Au and SiO2 nano- and microparticles by ICP-OES using monodisperse droplets of standard solutions for calibration, J. Anal. At. Spectrom., 2010, 25, 645–653 RSC.
- S. Groh, C. C. Garcia, A. Murtazin, V. Horvatic and K. Niemax, Local effects of atomizing analyte droplets on the plasma parameters of the inductively coupled plasma, Spectrochim. Acta, Part B, 2009, 64, 247–254 CrossRef.
- K. Niemax, Considerations about the detection efficiency in inductively coupled plasma mass spectrometry, Spectrochim. Acta, Part B, 2012, 76, 65–69 CrossRef CAS.
- J. Fuchs, M. Aghaei, T. D. Schachel, M. Sperling, A. Bogaerts and U. Karst, Impact of the Particle Diameter on Ion Cloud Formation from Gold Nanoparticles in ICPMS, Anal. Chem., 2018, 90, 10271–10278 CrossRef CAS.
- J. Liu, K. E. Murphy, R. I. Maccuspie and M. R. Winchester, Capabilities of Single Particle Inductively Coupled Plasma Mass Spectrometry for the Size Measurement of Nanoparticles: A Case Study on Gold Nanoparticles, Anal. Chem., 2014, 86, 3405–3414 CrossRef CAS.
- P. Shaw and A. Donard, Nano-particle analysis using dwell times between 10 μs and 70 μs with an upper counting limit of greater than 3 × 107 cps and a gold nanoparticle detection limit of less than 10 nm diameter, J. Anal. At. Spectrom., 2016, 31, 1234–1242 RSC.
- L. A. Rush, M. C. Endres, M. Liezers, J. D. Ward, G. C. Eiden and A. M. Duffin, Collisional dampening for improved quantification in single particle inductively coupled plasma mass spectrometry, Talanta, 2018, 189, 268–273 CrossRef CAS.
- P. Goodall, M. E. Foulkes and L. Ebdon, Slurry Nebulization Inductively-Coupled Plasma Spectrometry – the Fundamental Parameters Discussed, Spectrochim. Acta, Part B, 1993, 48, 1563–1577 CrossRef.
- G. Xiang, B. Hu, Z. Jiang and C. Gong, A comparison of slurry sampling electrothermal vaporization and slurry nebulization inductively coupled plasma mass spectrometry for the direct determination of trace impurities in titanium dioxide powder, J. Mass Spectrom., 2006, 41, 1378–1385 CrossRef CAS.
- K. S. Ho, K. O. Lui, K. H. Lee and W. T. Chan, Considerations of particle vaporization and analyte diffusion in single-particle inductively coupled plasma-mass spectrometry, Spectrochim. Acta, Part B, 2013, 89, 30–39 CrossRef CAS.
- W. W. Lee and W. T. Chan, Calibration of single-particle inductively coupled plasma-mass spectrometry (SP-ICP-MS), J. Anal. At. Spectrom., 2015, 30, 1245–1254 RSC.
- O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, A prototype of a new inductively coupled plasma time-of-flight mass spectrometer providing temporally resolved, multi-element detection of short signals generated by single particles and droplets, J. Anal. At. Spectrom., 2013, 28, 226–233 RSC.
- J. Tuoriniemi, G. Cornelis and M. Hassellov, Size discrimination and detection capabilities of single-particle ICPMS for environmental analysis of silver nanoparticles, Anal. Chem., 2012, 84, 3965–3972 CrossRef CAS.
- K. Shigeta, H. Traub, U. Panne, A. Okino, L. Rottmann and N. Jakubowski, Application of a micro-droplet generator for an ICP-sector field mass spectrometer – optimization and analytical characterization, J. Anal. At. Spectrom., 2013, 28, 646–656 RSC.
- S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Günther, Capabilities of inductively coupled plasma mass spectrometry for the detection of nanoparticles carried by monodisperse microdroplets, J. Anal. At. Spectrom., 2011, 26, 1166–1174 RSC.
- B. Franze, I. Strenge and C. Engelhard, Single particle inductively coupled plasma mass spectrometry: evaluation of three different pneumatic and piezo-based sample introduction systems for the characterization of silver nanoparticles, J. Anal. At. Spectrom., 2012, 27, 1074–1083 RSC.
- I. Strenge and C. Engelhard, Capabilities of fast data acquisition with microsecond time resolution in inductively coupled plasma mass spectrometry and identification of signal artifacts from millisecond dwell times during detection of single gold nanoparticles, J. Anal. At. Spectrom., 2016, 31, 135–144 RSC.
- A. J. Managh, D. N. Douglas, K. M. Cowen, H. J. Reid and B. L. Sharp, Acquisition of Fast Transient Signals in ICP-MS with Enhanced Time Resolution, J. Anal. At. Spectrom., 2016, 31, 1688–1692 RSC.
- S. I. Miyashita, A. S. Groombridge, S. I. Fujii, A. Minoda, A. Takatsu, A. Hioki, K. Chiba and K. Inagaki, Highly efficient single-cell analysis of microbial cells by time-resolved inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2014, 29, 1598–1606 RSC.
- M. D. Montano, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Single Particle ICP-MS: advances toward routine analysis of nanomaterials, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef CAS.
- R. D. Evans, in The Atomic Nucleus, McGraw Hill, New York, NY, 1955, ch. 28 Search PubMed.
- M. L. Franklin, G. Horlick and H. V. Malmstadt, Basic and practical considerations in utilizing photon counting for quantitative spectrochemical methods, Anal. Chem., 1969, 41, 2–10 CrossRef CAS.
- F. T. Arecchi, E. Gatti and A. Sona, Measurement of Low Light Intensities by Synchronous Single Photon Counting, Rev. Sci. Instrum., 1966, 37, 942–948 CrossRef.
- J. D. Ingle and S. R. Crouch, Pulse overlap effects on linearity and signal-to-noise ratio in photon counting systems, Anal. Chem., 1972, 44, 777–784 CrossRef CAS.
- S. M. Nelms, C. R. Quetel, T. Prohaska, J. Vogl and P. D. P. Taylor, Evaluation of detector dead time calculation models for ICP-MS, J. Anal. At. Spectrom., 2001, 16, 333–338 RSC.
- A. J. Fahey, Measurements of dead time and characterization of ion counting systems for mass spectrometry, Rev. Sci. Instrum., 1998, 69, 1282–1288 CrossRef CAS.
- B. Franze, I. Strenge and C. Engelhard, Separation and detection of gold nanoparticles with capillary electrophoresis and ICP-MS in single particle mode (CE-SP-ICP-MS), J. Anal. At. Spectrom., 2017, 32, 1481–1489 RSC.
- D. Mozhayeva and C. Engelhard, Separation of Silver Nanoparticles with Different Coatings by Capillary Electrophoresis Coupled to ICP-MS in Single Particle Mode, Anal. Chem., 2017, 89, 9767–9774 CrossRef CAS.
- D. Mozhayeva, I. Strenge and C. Engelhard, Implementation of Online Preconcentration and Microsecond Time Resolution to Capillary Electrophoresis Single Particle Inductively Coupled Plasma Mass Spectrometry (CE-SP-ICP-MS) and Its Application in Silver Nanoparticle Analysis, Anal. Chem., 2017, 89, 7152–7159 CrossRef CAS PubMed.
- J. Koch, L. Flamigni, S. Gschwind, S. Allner, H. Longerich and D. Günther, Accelerated evaporation of microdroplets at ambient conditions for the on-line analysis of nanoparticles by inductively-coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2013, 28, 1707–1717 RSC.
- DIN 38402-51:2017-05, German standard methods for the examination of water, waste water and sludge: calibration of analytical methods – Linear Calibration.
- J. A. Small and R. L. Watters, RM 8011 Report of Investigation, National Institute of Standards and Technology, Gaithersburg, MD, USA, 2015 Search PubMed.
- J. A. Small and R. L. Watters, RM 8012 Report of Investigation, National Institute of Standards and Technology, Gaithersburg, MD, USA, 2015 Search PubMed.
- J. A. Small and R. L. Watters, RM 8013 Report of Investigation, National Institute of Standards and Technology, Gaithersburg, MD, USA, 2015 Search PubMed.
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, Critical considerations for the determination of nanoparticle number concentrations, size and number size distributions by single particle ICP-MS, J. Anal. At. Spectrom., 2013, 28, 1220 RSC.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Determining transport efficiency for the purpose of counting and sizing nanoparticles via single particle inductively coupled plasma mass spectrometry, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00327d |
| This journal is © The Royal Society of Chemistry 2020 |