Efficient separation and high-precision analyses of tin and cadmium isotopes in geological materials

Abstract

This paper presents a new method for the separation of Sn and Cd from geological matrices followed by high-precision isotope analyses that include low abundance isotopes (<1.25%). The new technique is of specific interest for the detection of small mass-independent nucleosynthetic or cosmogenic isotope variations in meteorites and other planetary materials. We also report a new precise estimate for Sn isotope abundances. The method employs a combination of ion exchange and extraction chromatography together with multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS). Tin is separated from the sample matrix using an anion-exchange resin, followed by removal of remaining matrix elements and organics using the TRU and Pre-filter resins, respectively. The matrix fraction from the TRU resin step is further purified to isolate Cd using a two-stage anion exchange procedure. Analyses of Sn and Cd standard solutions doped with interfering elements were employed to define thresholds for tolerable amounts of interference producing elements. Our data demonstrate that our new procedure produces purified Sn and Cd solutions with sufficiently low levels of contaminants for high precision Sn and Cd isotope analyses. Removal of U is important for Sn isotope data because of doubly charged U ions. The internally normalised Sn isotope data of the two standard solution (NIST SRM 3161a and SPEX CLSN2-2Y) are in excellent agreement with previous data. Based on repeated analysis of independently processed lake sediment aliquots, an external reproducibility (intermediate precision) (2SD) is achieved of ±110 ppm for ¹¹²Sn/¹²⁰Sn, ±170 ppm for ¹¹⁴Sn/¹²⁰Sn, ±160 ppm for ¹¹⁵Sn/¹²⁰Sn, ±21 ppm for ¹¹⁷Sn/¹²⁰Sn, ±13 ppm for ¹¹⁸Sn/¹²⁰Sn, ±20 ppm for ¹¹⁹Sn/¹²⁰Sn, ±22 ppm for ¹²²Sn/¹²⁰Sn and ±24 ppm for ¹²⁴Sn/¹²⁰Sn. Replicate Sn analyses of the carbonaceous chondrite Allende are in excellent agreement with those of the lake sediments. For Cd isotope analyses, the lake sediment yields an external reproducibility (2SD) of ±170 ppm for ¹⁰⁶Cd/¹¹¹Cd, ±200 ppm for ¹⁰⁸Cd/¹¹¹Cd, ±34 ppm for ¹¹⁰Cd/¹¹¹Cd, ±18 ppm for ¹¹²Cd/¹¹¹Cd, ±24 ppm for ¹¹³Cd/¹¹¹Cd and ±15 ppm for ¹¹⁴Cd/¹¹¹Cd.

---

1. Introduction

The Sn isotope composition has been studied in detail since the mid 1960s. Most work was carried out by thermal ionisation mass spectrometry (TIMS) and focused on improving the analytical techniques to precisely determine the Sn isotope abundances and atomic weights.^1–4 Another goal was the search for isotopic anomalies in meteorites.^5,6 With the introduction of MC-ICP-MS and its capability for measuring elements with high ionisation potentials at high precision (e.g.ref. 7), research shifted to the investigation of mass-dependent Sn isotope fractionation associated with the formation of cassiterite for provenance analysis.^8–14 Other studies used Sn to identify mass-independent nuclear field shift effects during chemical exchange reaction using crown ether¹⁵ and during methylation and demethylation.¹⁶ Most recent research focused on mass-dependent Sn isotope fractionation during igneous differentiation and on the Sn isotope composition of the bulk silicate Earth (BSE) using a double-spike approach.^17,18

Tin isotopes are of special interest for geochemical and cosmochemical studies due to various reasons. With a 50% condensation temperature of 704 K for a gas of solar composition at a total pressure of 10⁻⁴ bar, Sn is cosmochemically classified as a moderately volatile element.^19,20 Moreover, the primitive mantle of the Earth is depleted in Sn by a factor of 33 ± 3 relative to the CI chondrites.²¹ Therefore, mass-dependent Sn isotope fractionation is a promising tool to better constrain the mechanism of volatile depletion in the solar system. Geochemically, Sn is moderately siderophile to chalcophile, and incompatible during silicate differentiation.²¹ The behaviour of Sn during differentiation depends on its oxidation state, coordination in the crystal lattice and melt composition.^22,23 Based on this, Sn isotope fractionation likely occurs during igneous processes and published Sn isotope data support this conclusion.^17,18

Similarly, Cd is another moderately volatile element with a 50% condensation temperature of 652 K ²⁰ that has been studied for its mass-dependent isotope composition to address the origin of volatile depletion in rocky planets (e.g.ref. 24–27). More recently, it has also been shown that Cd isotopes not only fractionate due to volatility related processes e.g. in chondrites,²⁶ but also during magmatic differentiation, with the crust displaying a slightly heavier Cd isotope composition.²⁸

In recent years, nucleosynthetic isotope variations have become a powerful tool in cosmochemistry. These are mass-independent isotope variations identified in meteorites and terrestrial planets. They are caused by the heterogeneous distribution of presolar dust that survived the formation of the solar system and kept the extreme isotopic compositions of their stellar sources (e.g. AGB-star or supernovae).²⁹ The distinct nucleosynthetic compositions of planetary materials can be used to investigate important processes in the early solar system, such as mixing or the physical conditions (e.g. temperatures) that prevailed in the protoplanetary disk, and influenced the composition of solar system material (e.g.ref. 30 and 31). Tin is the element with the highest number of stable isotopes with ten stable isotopes, formed by the p-process (¹¹²Sn and ¹¹⁴Sn), s-process (¹¹⁶Sn), the r-process (¹²⁴Sn), or mixtures thereof (¹¹⁵Sn, ¹¹⁷Sn, ¹¹⁸Sn, ¹¹⁹Sn, ¹²⁰Sn and ¹²²Sn), and therefore an ideal candidate to study nucleosynthetic isotope variations in the solar system. Cadmium provides an excellent companion with its eight stable isotopes also produced by a variety of nucleosynthetic processes: ¹⁰⁶Cd and ¹⁰⁸Cd by the p-process, ¹¹⁰Cd by the s-process, and ¹¹¹Cd to ¹¹⁶Cd by a combination of the s- and the r-process in different proportions.^32,33 Cadmium has a mainly chalcophile affinity as opposed to the more siderophile nature of Sn, indicating that Cd and Sn may reside in different carrier phases within meteorites. Therefore, the combined study of Sn and Cd may provide a powerful tool to assess the origin of the current lack of resolvable nucleosynthetic isotope variations of moderately volatile elements at the bulk meteorite scale. However, since these mass-independent nucleosynthetic variations are generally small, mostly less than 0.1 per mil (e.g. for Zr,³⁰ Mo³⁴ and Ru³⁵), an improved analytical procedure for mass-independent Sn and Cd isotope analyses is required.

In addition to nucleosynthetic variations, meteorites and lunar samples can experience mass-independent modification of their isotopes through exposure to galactic cosmic rays in space. Such modifications are, for example, reported for Cd isotopes in lunar samples.^26,36 This is important to note, because the investigation of the mass-dependent Sn and Cd isotope compositions in meteorites and lunar samples using the double-spike method also depends on their mass-independent isotope composition. This is because the double spike method assumes a constant natural isotope composition that is only altered by mass-dependent isotope fractionation. In order to obtain precise and accurate data using the double-spike approach, one must identify whether the Sn or Cd isotope composition was subject to mass-independent processes, i.e. has a different mass-independent composition and if so, the double spike calculation needs adaption (e.g.ref. 37).

Available analytical methods for Sn or Cd isotope analyses (e.g.ref. 14 and 27) were not designed to obtain such mass-independent isotope data at sufficiently high precision to address these issues. Therefore, we developed a new analytical procedure to obtain high precision Sn and Cd isotope data from the same sample aliquot. The method includes a three-stage chromatographic procedure to efficiently separate Sn from complex rock matrices, followed by anion-exchange chromatography to purify Cd. The resulting Sn and Cd sample solutions are analysed on a Nu Plasma II MC-ICP-MS, thereby determining all Sn and Cd isotopes at high precision. Spectral interferences and matrix effects from traces of elements remaining after sample purification can hamper data quality during MC-ICP-MS analyses. This is in particular an issue when improving the analytical precision, because effects, which were unproblematic at lower precision, can be resolved at high precision. For this reason, we performed extensive test with Cd and Sn standard solutions doped with critical elements. The accuracy and precision of the new procedure was also verified using two geological samples processed through the chromatographic procedure: a lake sediment and the carbonaceous chondrite Allende. The new technique is powerful because it can be applied for the search of nucleosynthetic or cosmogenic Sn and Cd isotope variations in extraterrestrial materials. Since extraterrestrial materials are in general rare and therefore analyses are sample limited, the combined Sn and Cd isotope analyses on the same sample aliquot constitute a significant advantage. Here, the method is also used for a new accurate estimate of Sn isotope abundances.

2. Samples and analytical procedures

2.1 Samples and standard materials

Two Sn standard solutions were employed: the NIST SRM 3161a (Lot 070330) bought in 5% HNO₃–1% HF and the SPEX CLSN2-2Y (Lot CL6-83SNY) in 1% HNO₃–1% HF. These standards were chosen because no certified Sn isotope reference standard currently exists, and they were already used in previous studies.^13,14,18 For Cd, an Alfa Aesar Cd standard in 5% HNO₃ was employed and on two measurement days the NIST SRM 3108 Cd standard (Lot 060531) was analysed for comparison. A sample of a sediment core from Lake Zürich (ZH 09-05 23.3) referred to here as Lake Zürich I, as well as, the basaltic USGS standard rock (BHVO-2) and the CV3 chondrite Allende were used to test the developed separation procedure.

2.2 Materials and reagents

Mineral acids of reagent grade were purified once (HF, 1TD) or twice (HCl, HNO₃, 2TD) by sub-boiling distillation in Savillex™ Teflon stills. Millipore Super-Q (SQ) water with a resistivity of 18 MΩ was used for mixing reagents.

2.3 Sample digestion

Powdered aliquots of Lake Zürich I and BHVO-2 in sizes of 0.1 to 1 g were digested on a hotplate using 60 ml Savillex beaker made from perfluoroalkoxy alkanes (PFA). First, the samples were digested in 1.5 ml concentrated HNO₃ and 12 ml concentrated HF at 140 °C for one day. After dry down, the samples were re-dissolved in 30 ml 7 M HNO₃ at 110 °C overnight and taken to dryness again. Samples with high organic contents (lake sediments) were additionally treated with 7.5 ml 10 M HCl and 2.5 ml 14 M HNO₃ for 3 days at 80 °C and taken to dryness. In the final digestion step, each sample was re-dissolved in 20 ml 6 M HCl and evaporated at low temperatures (80–90 °C) to prevent the Sn loss in the form of SnCl₄,^14,38 which becomes volatile at 114 °C.³⁹ An aliquot (0.1 g) of Lake Zürich I (referred to as Lake Zürich I bomb) and two 1 g powder aliquots of the CV3 carbonaceous chondrite Allende (split each over 5 vials) were digested in precleaned PFA vials in a Parr© bomb using for each vial 0.7 ml concentrated HNO₃ and 3 ml concentrated HF for 4.5 days at 170 °C, followed by dry-down and dissolution with 5 ml 6 M HCl at 90–100 °C.

2.4 Tin separation procedure

Tin was purified from the sample matrix using a three-stage separation procedure (Table 1). The first stage uses a modified method of Fehr et al.⁴⁰ to separate Sn, Cd, and Zn from the matrix elements. For each separation, a fresh resin bed of 2 ml anion-exchange resin (AG 1-X8, 200–400 mesh) was prepared in BioRad PolyPrep® chromatography columns. Up to 0.5 g of sample was loaded on one individual column, while larger sample sizes were split over several columns. The digested sample was dissolved in 3.37 ml 3 M HCl prior to ion exchange chemistry and refluxed overnight on a hotplate. Before centrifuging, 6.73 ml SQ water was added to achieve a final concentration of 1 M HCl and the sample was refluxed for another hour. After centrifuging, precipitates, if present, were washed twice with 1 ml 1 M HCl for 30 min. This procedure was repeated twice. Small aliquots (0.1 ml) were taken before loading the solution onto the column to determine the yields of the separation procedure. After cleaning and conditioning the resin with 10 ml 1 M HNO₃ and 10 ml 1 M HCl, the sample was loaded in 10 ml 1 M HCl. Following the loading, the column was rinsed with 20 ml 1 M HCl and more matrix elements (e.g. Ag) were eluted using 10 ml 6 M HCl and 2 ml 1 M HNO₃. Tin was then recovered from the resin with 5 ml 1 M HNO₃. To prevent Sn precipitation, 0.17 ml 4 M HF per ml solution was added to the beaker prior to the Sn collection.⁴¹ The second stage of the chromatographic procedure (Table 1) uses a modified separation method based on Eichrom TRU resin^11,14,41 in conjunction with an Eichrom Pre-filter resin to remove organics eluting from the resin. Eichrom Pre-filter resin (40 μl) was filled in Teflon columns, followed by 120 μl Eichrom TRU resin. After cleaning and conditioning of the resin with 5 ml 1 M HNO₃, 5 ml 0.1 M HCl–0.3 M HF (U removal from the resin) and 5 ml 1 M HCl, samples were loaded in 1 ml 1 M HCl. The resin was rinsed with 5 ml 1 M HCl to separate Sn from Cd and the remaining matrix (Zn) before eluting Sn in 3.5 ml 1 M HNO₃ into PFA beakers containing 10 μl ml⁻¹ solution 1 M HF. The matrix fraction of this separation was further cleaned for Cd isotope analysis (see Section 2.5).

Table 1 Tin separation procedure

Eluent	Volume (ml)	Step
(1) Column: 2 ml BioRad AG1-X8 anion-exchange resin (200–400 mesh)
1 M HNO3	10	Resin cleaning
1 M HCl	10	Resin conditioning
1 M HCl	10	Sample loading
1 M HCl	20	Matrix elution
6 M HCl	10	Matrix elution
1 M HNO3	2	Matrix elution
1 M HNO3	5	Sn, Cd, Zn
(2) Column: 40 μl Eichrom Pre-filter resin (100–150 μm) + 120 μl Eichrom TRU resin (100–150 μm)
1 M HNO3	5	Resin cleaning
0.1 M HCl–0.3 M HF	5	Resin cleaning (U)
1 M HCl	5	Resin conditioning
1 M HCl	1	Sample loading
1 M HCl	5	Cd, Zn
1 M HNO3	3.5	Sn
(3) Column: 160 μl Eichrom Pre-filter resin (100–150 μm) – organics removal
1 M HCl	5	Resin cleaning
0.1 M HCl–0.3 M HF	5	Resin cleaning (U)
1 M HNO3	5	Resin conditioning
1 M HNO3–0.01 M HF (sample solution)	3.5	Sn
1 M HNO3	1	Sn

---

The Eichrom Pre-filter resin (40 μl) used in the second stage was not sufficient to remove all organic compounds (octyl(phenyl)-N,N-diisobutylcarbamoylmethylphosphine oxide (CMPO) and tributyl phosphate (TBP)) of the TRU resin. For further organic removal, an additional column using solely Pre-filter resin was introduced (Table 1). The eluted Sn fraction of the second column was directly loaded on a Teflon column with Eichrom Pre-filter (160 μl). The resin was pre-cleaned and conditioned with 5 ml 1 M HCl, 5 ml 0.1 M HCl–0.3 M HF and 5 ml 1 M HNO₃. Tin was directly collected upon loading and in an additional 1 ml 1 M HNO₃.

2.5 Cadmium separation procedure

The Cd–Zn fraction from the second separation step for Sn (Table 1) was purified for Cd using a two-stage anion exchange procedure (Table 2), which is based on the method of Wombacher et al.²⁷ It employs 2 ml anion-exchange resin (AG 1-X8, 100–200 mesh) prepared in quartz glass columns. The Cd–Zn fraction from the Sn separation was dried down and redissolved in 5 ml 6 M HCl for 30–40 minutes at 120 °C. The sample solution was diluted to 3 M HCl by adding 5 ml MQ water and further refluxed for 10–15 minutes before cooling and loading onto the cleaned and preconditioned resin. Remaining matrix elements were removed using 0.5 M HCl, 1 M HCl and 2 M HCl. The procedure of ref. 27 includes an additional elution step using 8 M HCl to specifically remove Ag from the sample. However, Ag is already separated in the first Sn ion exchange column and therefore this step was omitted here. To efficiently elute Zn from the resin, a total of 21 ml 0.5 M HNO₃–0.1 M HBr mixture was used. This solution was always prepared fresh each day because HNO₃ and HBr slowly react with each other over time (e.g.ref. 27). Afterwards, 2.5 ml 2 M HNO₃ was added, followed by the collection of Cd in 4 ml 2 M HNO₃. Another 4 ml 2 M HNO₃ was used to elute the last fraction (Cd post fraction; Table 2), that was checked for its Cd content. On average, this cut contained <5% of the total eluted Cd and was therefore discarded.

Table 2 Cadmium ion exchange procedure

Eluent	Volume (ml)	Step
a The Cd-containing fraction of the (2) column from the Sn separation procedure (Table 1) was dried down and dissolved in 3 M HCl as sample load.
2 ml BioRad AG 1-X8 anion-exchange resin (100–200 mesh)
2 M HNO3	10	Resin cleaning
H2O	1	Rinse
0.5 M HCl	1	Conditioning (conversion to Cl^− form)
6 M HCl	20	Conditioning
0.5 M HCl	11	Conditioning
3 M HCl	10	Sample loading^a
3 M HCl	1	Matrix elution
0.5 M HCl	30	Matrix elution
1 M HCl	10	Matrix elution
2 M HCl	10	Matrix elution
0.5 M HNO3–0.1 M HBr	1	Elute remaining HCl
0.5 M HNO3–0.1 M HBr	20	Zn
2 M HNO3	2.5	Matrix elution
2 M HNO3	4	Cd
2 M HNO3	4	Cd (post fraction)
160 μl BioRad AG 1-X8 anion-exchange resin (100–200 mesh)
2 M HNO3	2	Resin cleaning
H2O	0.1	Rinse
0.5 M HCl	1	Conditioning (conversion to Cl^− form)
3 M HCl	1	Sample loading
0.5 M HCl	0.2	Matrix elution
0.5 M HNO3–0.1 M HBr	0.1	Elute remaining HCl
0.5 M HNO3–0.1 M HBr	1.6	Zn
2 M HNO3	0.25	Matrix elution
2 M HNO3	0.4	Cd
2 M HNO3	0.4	Cd (post fraction)

---

The second separation step is a downscaled version of the first (by a factor of ∼10) using ∼160 μl anion-exchange resin (AG 1-X8, 100–200 mesh) prepared in Teflon columns (Table 2). It was specifically designed to remove remaining Zn required for samples with a ⁶⁶Zn/¹¹¹Cd ratio above ∼0.01. This ratio was calculated based on mass-scans performed on the Nu Plasma II MC-ICP-MS that was used for Cd isotope analysis. This ratio is the threshold determined for obtaining accurate ¹⁰⁶Cd and ¹⁰⁸Cd isotope data (see below) onto which Zn argides can interfere. The sample was prepared prior to loading as before, but with 0.5 ml 6 M HCl and 0.5 ml MQ water. The Cd fraction was collected in 0.4 ml 2 M HNO₃. The post-Cd elution contained on average <5% of the total eluted Cd. However, on one occasion, a column processed standard contained ∼7% of the total Cd in this post-cut and was thus recombined with the main Cd fraction.

3. Mass spectrometry

3.1 Instrumentation

The samples were analysed on a Nu Plasma II MC-ICP-MS (Nu Instruments) at ETH Zürich using a DSN 100 desolvator as a sample introduction system (Table S1†). Measurements were performed in low-resolution. For Sn analyses, a wet-plasma sampler cone and a dry-plasma skimmer cone were used. For Cd, another set of dry-plasma sampler and skimmer cones were used. The nebuliser uptake rate was about 50–60 μl min⁻¹ and prior to each analysis a peak centre routine was performed.

3.2 Tin data collection and reduction

In order to analyse all ten Sn isotopes and to monitor all isobaric interferences, the measurements were performed in dynamic mode (Table 3). In the first measurement line, all Sn isotopes and ¹¹¹Cd were analysed, while the second line was mainly used for correction of isobaric interferences (¹²⁵Te, ¹²⁶Te, ¹²⁹Xe) (Table 3). One analysis consisted of 20 cycles with 10 s integration time for the first measurement line and 5 s in the second, and 3 s of magnet settle time after the magnet jumped. At the beginning of each analysis an electronic baseline was measured via electrostatic analyser deflection lasting 30 s. A 0.5 M HNO₃–0.005 M HF solution was used to rinse the nebuliser for 240 s after each analysis. Interspersed between the samples, a second 0.5 M HNO₃–0.005 M HF solution was analysed with the same measurement routine as the samples as background monitor. The recorded signals were used for the background correction and in particular to account for the Ar₃ interference on mass 120 (Table 3). The sample measurements were bracketed to a NIST 3161a SRM Sn standard solution at concentrations within ±20% of the sample. A single measurement took about 10 minutes and used around 100–120 ng Sn. The total ion beam sensitivity ranged from 2.7 × 10⁻¹² to 4.8 × 10⁻¹² A ppb⁻¹ using 10¹¹ Ω resistors. Before analysis, each sample was checked for potential remaining impurities of Cd, Mo, Pd, Ru, Rh, Te, U and Zr by scanning through their mass range and comparing to a multi-element standard. All collected data were first corrected for the electronic baseline, followed by the subtraction of background measurement. The data were internally normalised to a ¹¹⁶Sn/¹²⁰Sn ratio of 0.4460 (ref. 2) using the exponential law to correct for instrumental mass bias (in addition data was also tested for normalisations to ¹²²Sn/¹¹⁸Sn = 0.19125 and ¹¹⁸Sn/¹²⁰Sn = 0.742935 calculated based on the ¹¹⁶Sn/¹²⁰Sn ratio of 0.4460 (ref. 2)). The normalisation ratio of ¹¹⁶Sn/¹²⁰Sn was chosen to ease the comparison to earlier studies, which already used it. Moreover, this ratio offers a wide range of advantages such as the relatively large spread of isotope masses, the minor effects of interfering isotopes from neighbouring elements, the relatively small uncertainties of the data compared to when other ratios are employed and the use of even isotope masses only. The latter ascertains that the normalisation ratio is not affected by non-mass-dependent effects such as nuclear field shift or magnetic isotope effects.

Table 3 Cup configuration for Sn isotope analysis and interference elements

	^111Cd	^112Sn	^113Cd	^114Sn	^115Sn	^116Sn	^117Sn	^118Sn	^119Sn	^120Sn	^122Sn	^124Sn	^125Te	^126Te	^129Xe
Collector configuration
Line 1	L3	L2	L1	Ax	H1	H2	H3	H4	H5	H6	H7	H8
Line 2							L4	L3	L2	L1	H1	H3	H4	H5	H7
Isotope abundances of Sn and isobaric interferences
Cd	12.8	24.1	12.2	28.7		7.5
Sn		0.97		0.66	0.34	14.5	7.7	24.2	8.6	32.6	4.6	5.8
In			4.3		95.7
Te										0.10	2.6	4.8	7.1	19.0
Xe												0.09		0.09	26.4
Major molecular interferences
M^1H	^110Pd (11.7)
	^110Cd (12.5)	^111Cd (12.8)	^112Cd (24.1)	^113Cd (12.2)	^114Cd (28.7)
						^115In (95.7)
											^121Sb (57.2)	^123Sb (42.8)
													^124Sn (5.8)
															^128Te (31.7)
M^14N	^97Mo (9.5)	^98Mo (24.1)		^100Mo (9.6)
			^99Ru (12.7)	^100Ru (12.6)	^101Ru (17.0)	^102Ru (31.5)		^104Ru (18.6)
							^103Rh (100)
								^104Pd (11.1)	^105Pd (22.3)	^106Pd (27.3)	^108Pd (26.4)	^110Pd (11.7)
												^110Cd (12.5)	^111Cd (12.8)	^112Cd (24.0)
															^115In (95.7)
M^16O	^95Mo (15.9)	^96Mo (16.6)	^97Mo (9.5)	^98Mo (24.1)		^100Mo (9.6)
					^99Ru (12.7)	^100Ru (12.6)	^101Ru (17.0)	^102Ru (31.5)		^104Ru (18.6)
									^103Rh (100)
										^104Pd (11.1)	^106Pd (27.3)	^108Pd (26.4)		^110Pd (11.7)
														^110Cd (12.5)	^113Cd (12.2)
													^109Ag (48.1)
M^40Ar	^71Ga (39.7)
		^72Ge (27.6)	^73Ge (7.7)	^74Ge (35.8)
						^76Se (9.3)	^77Se (7.6)	^78Se (23.7)		^80Se (49.4)	^82Se (8.7)
					^75As (100)
									^79Br (50.5)
										^40Ar–^40Ar–^40Ar (99.6)
											^82Kr (11.5)	^84Kr (56.8)		^86Kr (17.2)
													^85Rb (71.9)
														^86Sr (9.8)
															^89Y (100)
M^++						^232Th (100)			^238U (99.3)

---

Isobaric interferences (Table 3) were corrected using ¹¹¹Cd, ¹²⁵Te and ¹²⁹Xe signals as monitors as follows. First a Cd correction was performed on ¹¹⁶Sn by subtracting ¹¹⁶Cd (using ¹¹⁶Cd/¹¹¹Cd = 0.563754 (ref. 6)) without mass bias correction. For the mass bias correction, the corrected ¹¹⁶Sn signal was then used to determine the fractionation factor (β) of the exponential law:

R_true = R_meas × (m₁/m₂)^β (1.1)

where R_true is the ^xSn/^ySn (x = 116, 118, 122; y = 118 or 120, ratio identical to that used for internal normalisation of the Sn isotope data) corrected for mass bias, R_meas the measured ^xSn/^ySn ratio, m₁ and m₂ refer to the masses of nominator and denominator isotopes ^xSn and ^ySn, respectively. Afterwards β was iteratively refined until convergence using the newly determined β for interference correction of Cd on ¹¹⁶Sn in the subsequent loop. For Te/Sn ratios >3 × 10⁻³ an additional Te correction on ¹²⁰Sn is necessary to correctly determine β. Here, a ¹¹⁷Sn/¹¹⁹Sn ratio of 0.893266 (based on ¹¹⁷Sn/¹²⁰Sn = 0.235313 and ¹¹⁹Sn/¹²⁰Sn = 0.26343 (ref. 7)) was used to determine the mass bias before performing the Cd and Te correction on ¹¹⁶Sn and ¹²⁰Sn. Again, the final fractionation factor β was obtained by iteratively solving for it. This final fractionation factor was then used for mass-bias correction and interference correction on all ratios. The results are reported in epsilon notation relative to ¹²⁰Sn:

ε^xSn = ((^xSn/¹²⁰Sn_sample/^xSn/¹²⁰Sn_{NIST 3161a}) − 1) × 10 000 (1.2)

where ^xSn/¹²⁰Sn_sample is the isotopic ratio of the sample measured relative to the isotopic ratio ^xSn/¹²⁰Sn_{NIST 3161a} of the Sn standard solution NIST 3161a. Reported uncertainties are 2 standard deviation (SD) of repeat analyses, whereas for single analyses, the 2SD of the daily bracketing standard is displayed.

Solutions for yield and blank determination were analysed on an Element XR. The blanks from digestion and those from the chemical separation procedure were dried down and taken up in 0.5 M HNO₃–0.005 M HF for analysis. To estimate the yields of the separation procedure, small aliquots (5% of sample material) of the Sn fraction collected in the first and third stage were compared to a small aliquot (1% of sample material) taken before the chromatographic procedure. These aliquots were also analysed in a 0.5 M HNO₃–0.005 M HF media.

3.3 Cadmium data collection and reduction

Similar to Sn, Cd isotope analyses were performed in dynamic mode to allow measurements of all Cd isotopes and Pd, In and Sn isotopes for direct isobaric interference corrections. In the first line, all Cd isotopes, ¹¹⁵In and ¹¹⁸Sn were measured. In the second, ¹⁰⁵Pd, ¹⁰⁸Cd and ¹¹¹Cd were collected. Each analysis comprised of 30 dynamic isotope measurements, using 10 s (first line) and 5 s (second line) integrations, and a 2 s magnet delay time. Before each measurement, an electronic baseline was measured for 30 s. After each analysis, the nebuliser was rinsed with 0.5 M HNO₃ for 150 s. On-peak backgrounds were measured in 0.5 M HNO₃ before and after three standard and/or sample analyses. Background corrections were applied to sample and standard measurements using the average of background analyses before and after these measurement blocks. Samples were bracketed to an Alfa Aesar Cd standard with a matching concentration to within ±20% on average. Each measurement lasted ∼12 minutes consuming between ∼120–150 ng Cd. The total ion beam intensity ranged from 1.5 × 10⁻¹² to 3.3 × 10⁻¹² A ppb⁻¹ using 10¹¹ Ω resistors. The column processed samples were checked for purity using 2–5% aliquots on the Nu Plasma II by scanning them for potentially interfering elements including Zn, Zr, Mo, Ge, Ru, Ga, Pd, In and Sn. These aliquots were also scanned for their Cd content, which was used to calculate the final yields following the full separation procedure by comparison with the 1% aliquot taken prior to the first Sn column chemistry (Section 2.4).

After baseline and background correction, the Cd isotope data were internally normalised to a ¹¹⁶Cd/¹¹¹Cd ratio of 0.578505 ⁴² with the exponential law. This ratio was chosen to ascertain a large spread, which improves precision, but also to minimize the effects of interferences from neighbouring elements (i.e. Pd) and to avoid isotopes affected by neutron capture (¹¹³Cd, ¹¹⁴Cd) during galactic cosmic ray irradiation in space.⁴³

Interferences from Pd, In and Sn were corrected for using a similar iterative approach as described for the Sn data reduction (see Section 3.2). Results are reported in the epsilon notation relative to ¹¹¹Cd:

ε^xCd = ((^xCd/¹¹¹Cd_sample/^xCd/¹¹¹Cd_{Alfa Aesar}) − 1) × 10 000 (1.3)

where x denotes the mass of the isotope of interest, with ^xCd/¹¹¹Cd_sample giving the isotopic ratio of the sample relative to the ratio of the Cd Alfa Aesar standard.

4. Results and discussion

4.1 Yields and blanks

The Sn yields of the first and the combined yields of the second and third column are around 90–100% and 80–100%, respectively. The yield of the total Sn separation procedure was generally >80%. The total yield for the separation of Cd was on average >70%.

The total Sn procedural blank ranged typically between 1.4 and 2.2 ng for samples of 0.5–1 g. The Sn blanks of the reagents differed, concentrated HCl (twice Teflon distilled) contained 16–30 pg ml⁻¹, while concentrated HNO₃ (twice Teflon distilled) and SQ water contained less than 2 pg ml⁻¹ Sn. The total procedural blank was therefore strongly dependent on the digestion procedure. While the complete separation procedure usually yielded a blank of 0.4 ng Sn, the digestion of the sample alone resulted in blank values from 0.27 ng per beaker in a Parr bomb digestion, up to 2 ng blank for the digestion of 0.5–1 g sample material in 60 ml vials on the hotplate. Generally, the Sn content of the analysed lake sediment and basalt aliquots was above 500 ng resulting in a blank contribution of <1%, which is therefore negligible.

The Cd blanks after the Sn column chemistry in the Cd–Zn cut were ≤14 pg, and including the subsequent Cd ion exchange chemistry ≤87 pg, on average. The sample digestion and the complete separation procedure together yielded blanks of <90 pg Cd. Considering that the Cd contents of all lake sediments and column processed standards were ∼150 ng or higher, this results in a negligible blank contribution of <0.1%.

4.2 Eluted organics from TRU resin

It has been shown that organics eluted from the TRU resin during extraction chromatography can affect the instrumental mass bias of Cd (ref. 44 and 45) and therefore compromise the quality of isotopic analysis. Several other studies also reported that these organic compounds elute from the TRU resin into sample fractions.^14,46 High contents of organics, furthermore, influence the nebuliser uptake rate and the sensitivity of the instrument, and may affect the dissolution of the sample after dry-down. The Sn fractions after the second separation stage, consisting of TRU Spec resin and Pre-filter resin, contained up to 250 μg P, most likely bound to the organic extractants (CMPO and TBP) of the TRU resin, because both compounds are phosphor bound organic species. After the additional clean-up column (third stage) containing the Pre-filter resin, the phosphorous content of the Sn fractions was reduced to <20 ng. Phosphorus is efficiently separated from Cd by the employed Cd anion-exchange chemistry (Table 2). The final purified Cd solutions contained on average <12 ng P.

4.3 Interferences

Isobaric interferences. The Sn NIST SRM 3161a standard solution (100–200 ppb Sn) was doped with various amounts of Cd (0.005–0.075 ppb), In (0.005 ppb), Te (0.05–4 ppb) and U (0.005–0.015 ppb) to evaluate the robustness of the interference correction. Ratios for Cd/Sn of up to 2 × 10⁻⁴ can be adequately corrected to yield accurate Sn isotope data (Fig. 1a and b). After column chemistry, the Sn fractions had generally Cd/Sn ratios below these limits (<1 × 10⁻⁴). The isotope ¹¹⁵Sn is very sensitive to small In contaminations due to the large difference in abundances of ¹¹⁵In (95.7%) and ¹¹⁵Sn (0.34%). Without In interference correction, In/Sn of 5 × 10⁻⁶ already resulted in an offset of ε¹¹⁵Sn = +17.7. Moreover, ¹¹³In, the monitor isotope for In correction, is also the low abundance isotope (4.29%) of In and subject to Cd interferences. Taken together this leads to large uncertainties on ε¹¹⁵Sn due to error magnification (In correction results in an uncertainty on ε¹¹⁵Sn of ±40 (2SD). The uncertainty on ε¹¹⁵Sn without In correction is only ±1.6 (2SD), see ESI Fig. S1†). Although most analysed aliquots of Lake Zürich I, BHVO-2 and Allende tend to lower (negative) ε¹¹⁵Sn values compared to the NIST 3161a Sn standard, their ε¹¹⁵Sn values are indistinguishable from each other considering their analytical uncertainty (Table 4). The ε¹¹⁵Sn data for the column processed Sn standard solutions (NIST 3161a, SPEX CLSN2-2Y) show similar negative offsets. First and most importantly, this shows that samples processed through the new analytical procedure yield accurate data relative to each other. Therefore, no In interference correction was applied to our data. Second, these observations also indicate that the consistent negative offsets are caused by small In impurities in the NIST SRM 3161a standard solution, while In is virtually quantitatively removed during our chromatographic separation procedure. This leads to an artificially induced higher ε¹¹⁵Sn value for the NIST SRM 3161a standard analyses, while the sample data is not affected by this problem. Ideally, the NIST SRM 3161a standard should also be further purified for In.

Fig. 1 Tin isotope ratios for a 100 and 200 ppb NIST SRM 3161a standard solution doped with Cd, U and Te. Data points show the average of individual analyses and the dotted line marks the tolerance level for each element. Closed symbols indicate interference corrected data, open symbols data without interference correction. Uncertainties are 2SD of repeat analyses. For three standards (Cd/Sn = 0.5 × 10⁻⁴ and 3.5 × 10⁻⁴, U/Sn = 1.5 × 10⁻⁴) only one measurement was performed and the uncertainty is the 2SD of the daily bracketing standard. The grey band represents the reproducibility (2SD) of NIST SRM 3161a at 200 ppb. (d–f) No Te correction on ¹²⁰Sn. (g–i) Te correction on ¹²⁰Sn.

Table 4 Sn isotope ratios of column processed samples

Sample	Sn (ppb)^f	Cd/Sn	Te/Sn		N	ε ^112Sn	ε ^114Sn	ε ^115Sn	ε ^117Sn	ε ^118Sn	ε ^119Sn	ε ^122Sn	ε ^124Sn
a Indicates the number of analysed standards within one analytical session, instead of the number (N) of analytical sessions for standard solutions or individual measurements for the other samples. b Denotes ε^115Sn measured relative to SPEX CLSN2-2Y and corrected for difference between SPEX CLSN2-2Y and NIST SRM 3161a. c Measured with Aridus II on a Nu Plasma II. d Uncertainty refers to 95% confidence interval t0.95,n−1 × SD/√n). e For the lake sediment, two aliquots were digested. “bomb” refers to the Parr bomb digestion, the second aliquot was digested on the hotplate. NIST: NIST SRM 3161a; SPEX: SPEX CLSN2-2Y; Lake Zürich Ix: x refers to separate column chemistry. f Sn (ppb) concentration refers to measurement solution.
Sn standard solutions
NIST SRM 3161a	200	1.4 × 10^−5	3.6 × 10^−5	20		0.0 ± 0.9	0.0 ± 1.3	0.0 ± 1.2	0.00 ± 0.16	0.00 ± 0.11	0.00 ± 0.17	0.00 ± 0.21	0.00 ± 0.31
	100			11		0.0 ± 1.4	0.0 ± 2.3	0.0 ± 2.0	0.00 ± 0.22	0.00 ± 0.13	0.00 ± 0.21	0.00 ± 0.25	0.00 ± 0.39
	40			29^a		0.0 ± 2.6	0.2 ± 4.9	0.1 ± 5.4	0.00 ± 0.20	0.00 ± 0.21	0.01 ± 0.39	0.00 ± 0.35	0.01 ± 0.40
	25			25^a		0.0 ± 5.0	0 ± 11	0.1 ± 6.7	0.01 ± 0.50	0.01 ± 0.26	0.02 ± 0.71	0.00 ± 0.91	0.00 ± 0.75
	9			19^a		−1 ± 11	0 ± 23	1 ± 21	−0.1 ± 1.4	0.04 ± 0.61	0.1 ± 1.9	0.1 ± 1.9	0.2 ± 1.7
	5.5			21^a		0 ± 28	1 ± 49	0 ± 42	0.0 ± 1.6	−0.02 ± 0.91	0.0 ± 1.6	0.0 ± 2.6	0.0 ± 2.5
SPEX CLSN2-2Y	100	2.4 × 10^−5	6.2 × 10^−5	20^a		0.0 ± 1.2	0.1 ± 1.8	7.3 ± 2.2	−0.05 ± 0.18	0.01 ± 0.11	−0.03 ± 0.19	−0.05 ± 0.27	−0.13 ± 0.44
Column processed Sn standard solutions
NIST + Cd	200	1.6 × 10^−5	3.3 × 10^−5		1	−0.4 ± 1.0	−0.3 ± 1.7	−0.6 ± 1.1	0.18 ± 0.18	0.01 ± 0.13	0.11 ± 0.18	−0.14 ± 0.16	−0.16 ± 0.27
NIST + Cd	100	2.8 × 10^−5	2.6 × 10^−5		1	0.6 ± 1.7	1.3 ± 2.3	0.1^b ± 1.7	0.02 ± 0.23	0.10 ± 0.20	0.04 ± 0.15	−0.03 ± 0.14	−0.17 ± 0.27
SPEX	100	8.6 × 10^−6	2.8 × 10^−5		1	−0.6 ± 1.6	−1.6 ± 2.1	−1.1^b ± 1.5	−0.09 ± 0.25	−0.04 ± 0.10	−0.15 ± 0.10	−0.18 ± 0.27	−0.48 ± 0.36
SPEX Ag1x8	100	7.3 × 10^−6	1.8 × 10^−5		1	−0.1 ± 1.6	−0.1 ± 2.1	−0.5^b ± 1.5	0.05 ± 0.25	0.08 ± 0.10	0.18 ± 0.10	0.00 ± 0.27	0.15 ± 0.36
SPEX TRU	100	1.3 × 10^−5	1.2 × 10^−4		1	−1.2 ± 1.6	−1.0 ± 2.1	−1.0^b ± 1.5	0.08 ± 0.25	−0.03 ± 0.10	0.10 ± 0.10	−0.06 ± 0.27	−0.09 ± 0.36
Allende (CV3)
Allende bomb 1a	200	4.3 × 10^−5	3.6 × 10^−5		1	0.4 ± 1.0	1.9 ± 1.7	−2.8 ± 1.1	0.05 ± 0.18	0.04 ± 0.13	0.10 ± 0.18	−0.07 ± 0.16	−0.13 ± 0.27
Allende bomb 1a	200	4.4 × 10^−5	6.8 × 10^−5		1	0.27 ± 0.83	0.9 ± 1.1	−2.6 ± 1.1	0.16 ± 0.23	0.10 ± 0.12	0.04 ± 0.21	0.02 ± 0.24	−0.06 ± 0.41
Allende bomb 1b	200	1.2 × 10^−4	3.3 × 10^−5		1	−0.11 ± 0.92	1.9 ± 1.4	−0.09 ± 0.94	0.08 ± 0.22	0.02 ± 0.11	0.09 ± 0.14	0.17 ± 0.24	0.03 ± 0.24
Allende bomb 1b	200	2.3 × 10^−5	5.1 × 10^−5		1	0.33 ± 0.57	−0.13 ± 0.82	−2.38 ± 0.81	0.20 ± 0.12	−0.03 ± 0.10	0.00 ± 0.15	−0.23 ± 0.19	−0.21 ± 0.23
With additional Pre-filter clean up
Allende bomb 2a	200	5.8 × 10^−5	4.0 × 10^−5		1	−0.17 ± 0.84	0.90 ± 1.15	−2.5 ± 1.4	0.07 ± 0.16	0.10 ± 0.12	0.12 ± 0.16	−0.02 ± 0.20	0.00 ± 0.38
Allende bomb 2b	200	4.5 × 10^−5	4.5 × 10^−5		1	−0.26 ± 0.84	0.64 ± 0.93	−2.20 ± 0.92	0.21 ± 0.12	0.10 ± 0.08	0.17 ± 0.23	0.09 ± 0.12	−0.14 ± 0.25
Allende bomb 2a + 2b^c	200	4.9 × 10^−5	3.0 × 10^−5		1	−0.9 ± 1.1	−0.22 ± 1.62	−0.3^b ± 1.7	0.26 ± 0.18	0.03 ± 0.10	0.07 ± 0.21	−0.04 ± 0.25	−0.16 ± 0.37
Allende bomb 1 mean	200				4	0.23 ± 0.46	1.1 ± 2.0	−2.0 ± 2.5	0.12 ± 0.14	0.03 ± 0.11	0.06 ± 0.09	−0.03 ± 0.34	−0.09 ± 0.21
					4^d	0.23 ± 0.36	1.1 ± 1.6	−2.0 ± 2.0	0.12 ± 0.11	0.03 ± 0.09	0.06 ± 0.08	−0.03 ± 0.27	−0.09 ± 0.16
Allende bomb 2 mean	200				3	−0.44 ± 0.85	0.4 ± 1.3	−1.7 ± 2.4	0.18 ± 0.19	0.07 ± 0.11	0.12 ± 0.17	0.01 ± 0.21	−0.10 ± 0.31
Basalts
BHVO-2 1a	100	1.2 × 10^−5	3.0 × 10^−5		1	−1.1 ± 1.7	−2.4 ± 2.3	0.3^b ± 1.7	−0.08 ± 0.23	−0.17 ± 0.20	0.13 ± 0.15	0.20 ± 0.14	0.06 ± 0.27
BHVO-2 1b	100	2.3 × 10^−5	2.7 × 10^−5		1	0.4 ± 1.7	1.9 ± 2.3	−0.2^b ± 1.7	0.08 ± 0.23	−0.03 ± 0.20	−0.01 ± 0.15	0.10 ± 0.14	0.08 ± 0.27
BHVO-2 2	100	1.4 × 10^−5	3.2 × 10^−5		1	−0.3 ± 1.7	−1.0 ± 2.3	0.3^b ± 1.7	−0.06 ± 0.23	−0.14 ± 0.20	0.03 ± 0.15	0.07 ± 0.14	0.16 ± 0.27
Lake sediment
Lake Zürich Ia	200	3.5 × 10^−5	3.6 × 10^−5		1	1.1 ± 1.0	1.3 ± 1.7	−1.5 ± 1.1	0.13 ± 0.18	0.03 ± 0.13	−0.04 ± 0.18	−0.16 ± 0.16	−0.17 ± 0.27
Lake Zürich Ia	200	3.3 × 10^−5	2.8 × 10^−5		1	−0.45 ± 0.92	0.6 ± 1.4	−1.86 ± 0.94	−0.10 ± 0.22	−0.09 ± 0.11	0.20 ± 0.14	0.24 ± 0.24	−0.07 ± 0.24
Lake Zürich Ib	200	1.5 × 10^−5	3.2 × 10^−5		1	0.1 ± 1.0	0.0 ± 1.7	−1.7 ± 1.1	0.09 ± 0.18	0.04 ± 0.13	0.02 ± 0.18	0.00 ± 0.16	−0.05 ± 0.27
Lake Zürich Ib	200	1.3 × 10^−5	3.0 × 10^−5		1	−0.31 ± 0.92	−1.1 ± 1.4	−1.96 ± 0.94	−0.10 ± 0.22	−0.08 ± 0.11	0.06 ± 0.14	−0.06 ± 0.24	0.05 ± 0.24
Lake Zürich Ib	200	1.5 × 10^−5	4.0 × 10^−5		1	0.0 ± 1.2	0.4 ± 2.0	−2.0 ± 1.4	0.13 ± 0.19	0.08 ± 0.12	−0.16 ± 0.11	−0.08 ± 0.21	−0.14 ± 0.29
Lake Zürich Ic	200	1.8 × 10^−5	2.8 × 10^−5		1	0.09 ± 0.92	0.8 ± 1.4	−1.64 ± 0.94	0.05 ± 0.22	0.15 ± 0.11	0.01 ± 0.14	−0.16 ± 0.24	−0.33 ± 0.24
Lake Zürich Ic	200	2.2 × 10^−5	2.8 × 10^−5		1	−0.68 ± 0.92	−0.5 ± 1.4	−1.86 ± 0.94	−0.18 ± 0.22	−0.02 ± 0.11	0.01 ± 0.14	−0.17 ± 0.24	−0.21 ± 0.24
Lake Zürich Ic	200	8.8 × 10^−6	4.0 × 10^−5		1	0.3 ± 1.2	−0.7 ± 2.0	−2.7 ± 1.4	0.04 ± 0.19	0.03 ± 0.12	−0.06 ± 0.11	−0.02 ± 0.21	−0.10 ± 0.29
With additional Pre-filter clean up
Lake Zürich Id	200	8.0 × 10^−5	3.4 × 10^−5		1	−0.25 ± 0.94	−0.5 ± 1.4	−0.9 ± 1.1	−0.10 ± 0.12	0.03 ± 0.11	−0.11 ± 0.17	−0.07 ± 0.22	−0.16 ± 0.38
Lake Zürich Ie	200	5.1 × 10^−5	3.3 × 10^−5		1	−0.8 ± 1.1	−0.3 ± 1.6	0.0 ± 1.7	−0.10 ± 0.18	0.02 ± 0.10	−0.10 ± 0.21	−0.03 ± 0.25	−0.10 ± 0.37
Lake Zürich I bomb a	200	1.1 × 10^−4	3.7 × 10^−5		1	0.14 ± 0.84	1.4 ± 1.2	−0.5 ± 1.4	−0.13 ± 0.16	−0.01 ± 0.12	−0.03 ± 0.16	−0.01 ± 0.20	−0.03 ± 0.38
Lake Zürich I bomb b	200	2.9 × 10^−5	3.3 × 10^−5		1	0.24 ± 0.94	0.2 ± 1.4	−0.6 ± 1.1	0.00 ± 0.12	0.11 ± 0.11	−0.21 ± 0.17	−0.14 ± 0.22	−0.19 ± 0.38
Lake Zürich I bomb b	200	2.4 × 10^−5	2.8 × 10^−5		1	−0.6 ± 1.1	0.5 ± 1.6	−0.9 ± 1.7	−0.12 ± 0.18	−0.01 ± 0.10	0.03 ± 0.21	0.06 ± 0.25	0.10 ± 0.37
Lake Zürich I bomb c	200	8.1 × 10^−5	3.7 × 10^−5		1	0.38 ± 0.78	1.20 ± 0.97	−0.6 ± 1.0	−0.08 ± 0.14	−0.04 ± 0.10	−0.18 ± 0.16	−0.13 ± 0.18	−0.20 ± 0.21
Lake Zürich I bomb c	200	8.1 × 10^−5	2.2 × 10^−5		1	−0.59 ± 0.73	−0.56 ± 0.97	−0.3 ± 1.2	−0.01 ± 0.12	−0.07 ± 0.11	−0.02 ± 0.14	0.11 ± 0.20	0.03 ± 0.27
Lake Zürich I bomb c	200	8.5 × 10^−5	1.5 × 10^−5		1	−0.80 ± 0.91	−0.8 ± 1.3	−0.4 ± 1.4	0.06 ± 0.18	−0.04 ± 0.13	−0.22 ± 0.16	−0.22 ± 0.22	−0.33 ± 0.35
Lake Zürich I bomb c	200	8.4 × 10^−5	1.5 × 10^−5		1	0.38 ± 0.91	1.1 ± 1.3	0.1 ± 1.4	0.07 ± 0.18	0.07 ± 0.13	−0.10 ± 0.16	0.01 ± 0.22	−0.12 ± 0.35
Lake Zürich I bomb c^c	200	8.4 × 10^−5	2.7 × 10^−5		1	−1.2 ± 1.1	0.4 ± 1.6	−1.9^b ± 1.7	−0.19 ± 0.18	−0.04 ± 0.10	−0.07 ± 0.21	−0.07 ± 0.25	0.00 ± 0.37
Lake Zürich I bomb c	200	9.4 × 10^−5	2.7 × 10^−5		1	0.29 ± 0.91	1.5 ± 1.3	−0.7 ± 1.4	−0.16 ± 0.18	−0.01 ± 0.13	0.00 ± 0.16	0.09 ± 0.22	−0.04 ± 0.35
Lake Zürich I bomb c	200	8.1 × 10^−5	2.7 × 10^−5		1	0.2 ± 1.1	1.5 ± 1.2	−0.9 ± 1.0	−0.07 ± 0.12	−0.07 ± 0.07	−0.09 ± 0.11	−0.05 ± 0.19	0.06 ± 0.25
Measured with Aridus II on NU3
Lake Zürich Ib	100	2.8 × 10^−5	3.9 × 10^−5		1	0.1 ± 1.3	0.7 ± 2.7	−1.0 ± 2.0	−0.13 ± 0.14	0.04 ± 0.16	−0.05 ± 0.21	−0.15 ± 0.22	−0.31 ± 0.33
Lake Zürich Id	100	2.3 × 10^−5	2.3 × 10^−5		1	0.0 ± 1.2	0.3 ± 2.9	−2.1 ± 1.7	−0.07 ± 0.13	−0.07 ± 0.09	−0.18 ± 0.22	−0.01 ± 0.25	0.07 ± 0.53
Lake Zürich Ie	100	6.5 × 10^−5	2.2 × 10^−5		1	−0.2 ± 1.2	0.4 ± 2.3	0.3 ± 2.7	0.01 ± 0.27	0.00 ± 0.18	−0.14 ± 0.27	0.09 ± 0.31	−0.18 ± 0.57
Lake Zürich I bomb b	100	3.2 × 10^−5	1.8 × 10^−5		1	0.0 ± 1.2	0.4 ± 2.9	−0.8 ± 1.7	−0.02 ± 0.13	−0.06 ± 0.09	−0.33 ± 0.22	0.15 ± 0.25	0.00 ± 0.53
Lake Zürich I bomb c	40	8.0 × 10^−5	1.3 × 10^−5		1	−3.3 ± 2.6	−3.9 ± 4.9	3.2 ± 5.4	−0.13 ± 0.20	0.12 ± 0.21	−0.17 ± 0.39	0.15 ± 0.34	−0.14 ± 0.40
Lake Zürich I bomb c	9	1.0 × 10^−4	−5.7 × 10^−5		1	−1 ± 11	−10 ± 23	−7 ± 21	0.8 ± 1.4	0.16 ± 0.61	−0.8 ± 1.9	−1.1 ± 1.9	−0.3 ± 1.7
Lake Zürich I bomb c	5.5	−3.8 × 10^−5	1.9 × 10^−4		1	0 ± 28	25 ± 49	3 ± 42	−0.4 ± 1.6	0.13 ± 0.91	−0.5 ± 1.6	−0.7 ± 2.6	−1.4 ± 2.5
Lake Zürich I mean	200				20	−0.1 ± 1.1	0.3 ± 1.7	−1.1 ± 1.6	−0.04 ± 0.21	0.00 ± 0.13	−0.05 ± 0.20	−0.04 ± 0.22	−0.10 ± 0.24
	100				4	0.0 ± 0.2	0.4 ± 0.3	−0.9 ± 2.0	−0.05 ± 0.12	−0.02 ± 0.10	−0.18 ± 0.23	0.02 ± 0.27	−0.11 ± 0.35
	40				1	−3.3 ± 2.6	−3.9 ± 4.9	3.2 ± 5.4	−0.13 ± 0.20	0.12 ± 0.21	−0.17 ± 0.39	0.15 ± 0.34	−0.14 ± 0.40
	9				1	−1 ± 11	−10 ± 23	−7 ± 21	0.8 ± 1.4	0.16 ± 0.61	−0.8 ± 1.9	−1.1 ± 1.9	−0.3 ± 1.7
	5.5				1	0 ± 28	25 ± 49	3 ± 42	−0.4 ± 1.6	0.13 ± 0.91	−0.5 ± 1.6	−0.7 ± 2.6	−1.4 ± 2.5

---

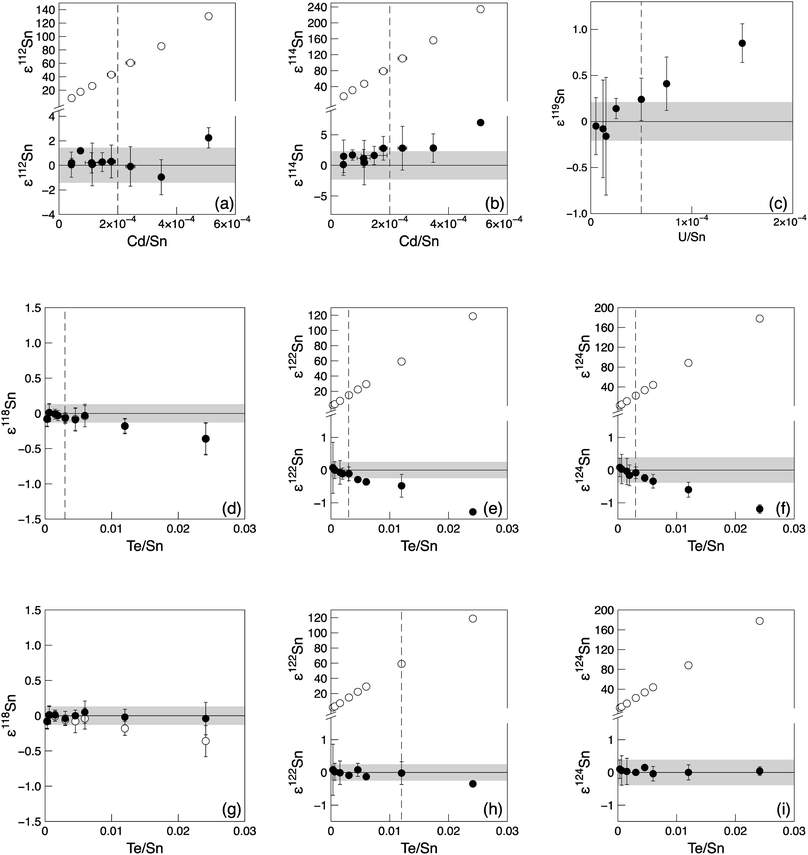
Because of the high abundances of ¹²⁰Sn, ¹²²Sn and ¹²⁴Sn, the Te interference correction can tolerate larger amounts of Te compared to Cd or In. Without Te correction on the denominator isotope ¹²⁰Sn, Te/Sn ratios of up to 3 × 10⁻³ can be tolerated (Fig. 1d–f). If an additional Te interference correction on ¹²⁰Sn is applied, a Te/Sn ratio of up to 1.2 × 10⁻² still yields accurate Sn isotope results (Fig. 1g–i). The Te/Sn ratios of the analysed samples after the chemical separation procedure were generally below 8.0 × 10⁻⁵. The Te interferences were monitored using ¹²⁵Te and ¹²⁶Te and the results after interference correction with each isotope were compared. Our data show that interference correction using ¹²⁵Te results in a slightly better reproducibility, because ¹²⁶Te needs an additional correction for ¹²⁶Xe and this increases the uncertainty of the correction (Table S2†). A proportionally higher background was observed for ¹²⁵Te compared to ¹²⁶Te, and this elevated ¹²⁵Te background correlated with the signal intensity of Sn. This increased background signal was likely caused by ¹²⁴Sn-hydrides. Therefore, the correction with ¹²⁵Te results in slightly lower ¹²²Sn/¹²⁰Sn and ¹²⁴Sn/¹²⁰Sn ratios when compared to the ¹²⁶Te corrected data (Table S2†). However, this difference is smaller than the uncertainties of the analyses.

Uranium (²³⁸U) can interfere on ¹¹⁹Sn as double-charged ions. Tests show that the production rate of U⁺⁺ is ca. 4% and that U/Sn ratios of up to 5 × 10⁻⁵ leave the results unaffected (Fig. 1c). This demonstrates that relatively small blank amounts of U can already affect the data and thus U requires a clean separation from the Sn fraction. The U content of samples after our chemical separation procedure were generally below this threshold.

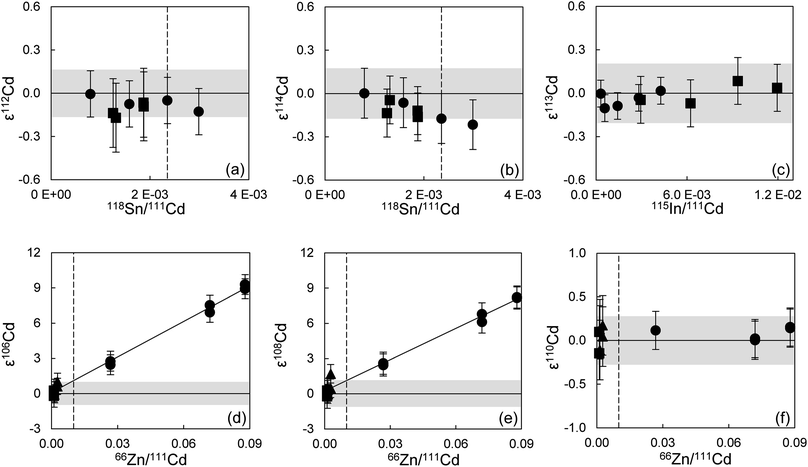
The limits for adequate and reliable isobaric interference corrections for Cd isotope analyses were also assessed. To this end, the 200 ppb Alfa Aesar Cd standard solution was doped with different amounts of Sn (0.050–0.200 ppb), In (0.005–0.200 ppb) and Pd (0.005–0.075 ppb) (Fig. 2 and ESI Fig. S2†). The tolerance levels were defined as the relative signal ratios of the isotopes used for interference correction (¹¹⁸Sn, ¹¹⁵In and ¹⁰⁵Pd) against ¹¹¹Cd. This allows a direct comparison with samples scanned for purity before analysis. Standards with a ¹⁰⁵Pd/¹¹¹Cd ratio of up to ∼5.5 × 10⁻⁴ (0.075 ppb Pd, Pd/Cd = 3.8 × 10⁻⁴) and a ¹¹⁵In/¹¹¹Cd ratio of up to ∼1.2 × 10⁻² (0.200 ppb In, In/Cd = 1.0 × 10⁻³) can still be accurately corrected for (Fig. S2a–c† and 2c). For Sn, the tolerance threshold was determined at ¹¹⁸Sn/¹¹¹Cd of ∼2.4 × 10⁻³ (0.150 ppb Sn, Sn/Cd = 7.5 × 10⁻⁴) (Fig. 2a and b). Column processed standards and samples in general yielded ratios below these limits (Table S3†).

Fig. 2 Cadmium isotope ratios measured for a 200 ppb Alfa Aesar Cd standard solution doped with Sn (a, b), In (c) and Zn (d–f) after interference correction. Symbols represent different measurement sessions, with each data point showing the result of one analysis and the dotted vertical lines the derived tolerance thresholds. The grey bands show the average daily reproducibility of the 200 ppb Alfa Aesar Cd standard solution (2SD). The individual error bars denote the reproducibility (2SD) of the bracketing standard on the day of measurement. The ¹¹⁸Sn/¹¹¹Cd and the ¹¹⁵In/¹¹¹Cd values were determined from the measured signal intensities of these isotopes during analysis. The ⁶⁶Zn/¹¹¹Cd ratios were obtained from mass-scans performed prior to analysis.

Molecular interferences. After the chromatographic separation procedure, Sn and Cd sample solutions were analysed for remaining elements that form molecular interferences. The influence of elements (Mo, Rh, Zr), generating molecular interferences on Sn isotopes were tested with doped standards up to the level identified in the sample solutions or above. For the following elemental ratios, no effect on the ε^xSn values of the affected isotope were observed: Mo/Sn = 1 × 10⁻², Pd/Sn = 1.25 × 10⁻³, Ru/Sn = 1.5 × 10⁻³, Rh/Sn = 7.5 × 10⁻⁴, Zr/Sn = 5 × 10⁻⁴, Ca/Sn = 1.5 × 10⁻¹, Cr/Sn = 3.3 × 10⁻¹.

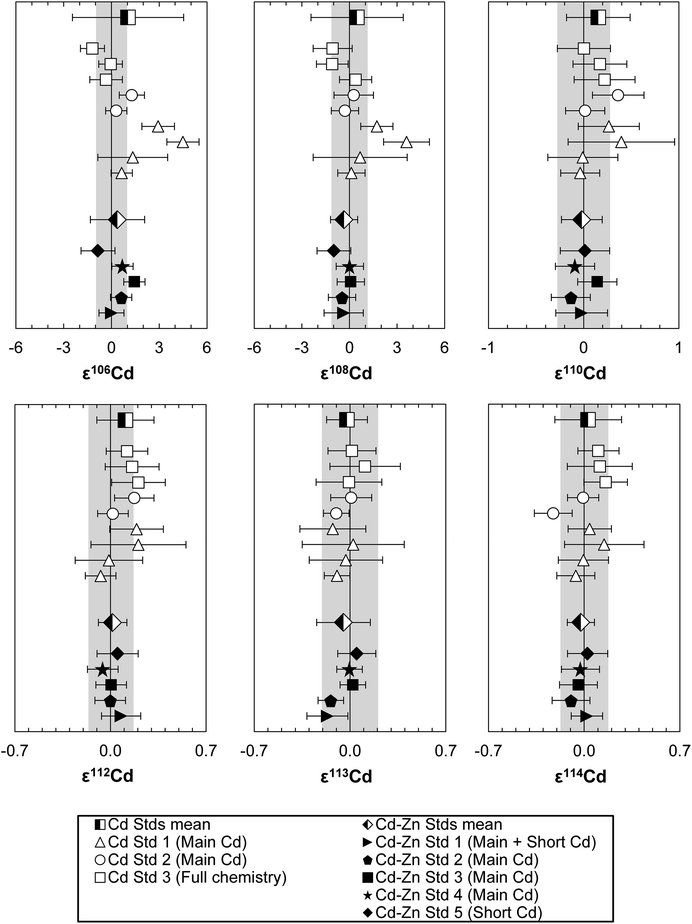
For Cd analyses, major molecular interferences originate from Zn, Zr and Mo, that in particular influence the two least abundant Cd isotopes, ¹⁰⁶Cd and ¹⁰⁸Cd.²⁷ Standard solutions doped with up to 0.400 ppb Mo (Mo/Cd = 2 × 10⁻³, ⁹⁵Mo/¹¹¹Cd ∼ 1.3 × 10⁻³ from mass-scans) and 0.030 ppb Zr (Zr/Cd = 1.5 × 10⁻⁴, ⁹⁰Zr/¹¹¹Cd ∼ 3.0 × 10⁻⁴) yield accurate Cd isotope data and thus these levels can be tolerated in the final sample solutions (ESI Fig. S2d–f†). For Zn, a tolerance threshold on ⁶⁶Zn/¹¹¹Cd of ∼1 × 10⁻² was estimated (∼1 ppb Zn, Zn/Cd ∼ 5 × 10⁻³) (Fig. 2d–f). These limits were in general achieved for Cd–Zn standards and samples passed through both Cd ion exchange columns (Table S3†). However, the Zn blank of sample solutions often increased following dry-down and redissolution to levels above this tolerance threshold, as can be observed for samples where repeat analyses were possible (Cd Std 1 and Lake Zürich If, Table S3†). This issue was noted early during establishing our method and was combatted by adopting a more thorough cleaning regime of the pipette tips and vials used, and by working with PE gloves instead of vinyl. This ensured that Zn levels remained low. This is reflected by the last two measurements of Cd Std 1 that already show a much more constant Zn/Cd ratio than before, and also from the low Zn/Cd ratio of later processed standards and samples.

4.4 Precision and accuracy of the solution standards and the determination of Sn isotope abundances

Tin. The long-term average for a 200 ppb NIST SRM 3161a Sn solution over 15 months and 17 analytical sessions is ¹¹²Sn/¹²⁰Sn = 0.029823 ± 4, ¹¹⁴Sn/¹²⁰Sn = 0.020190 ± 4, ¹¹⁵Sn/¹²⁰Sn = 0.010361 ± 2, ¹¹⁷Sn/¹²⁰Sn = 0.235320 ± 28, ¹¹⁸Sn/¹²⁰Sn = 0.742945 ± 29, ¹¹⁹Sn/¹²⁰Sn = 0.263479 ± 32, ¹²²Sn/¹²⁰Sn = 0.142095 ± 11, ¹²⁴Sn/¹²⁰Sn = 0.177583 ± 35. Table 5 shows the comparison of the long-term average of NIST SRM 3161a and SPEX CLSN2-2Y against previously determined ratios (ref. 2 (using double spike),^7,47 normalising to a ¹¹⁶Sn/¹²⁰Sn ratio of 0.4460). Our results are in good agreement with previous work. The NIST SRM 3161a and SPEX CLSN2-2Y standards show a small difference on ¹¹⁵Sn/¹²⁰Sn of 7.3ε (Table 5). The difference between SPEX CLSN2-2Y and NIST SRM 3161a disappears, when these Sn standard solutions are treated through our chemical separation procedure (Table 4) and is therefore likely related to a higher In content of SPEX CLSN2-2Y (+7.76 per mil In is indicated by elevated ε¹¹⁵Sn value of the SPEX CLSN2-2Y solution). This In interference cannot be adequately corrected without introducing large uncertainties on this ratio (In correction results in a ¹¹⁵Sn/¹²⁰Sn ratio of 0.010297 ± 42).

Table 5 Comparison of Sn isotope ratios of NIST SRM 3161a and SPEX CLSN-2Y with previously published data

Ratio	ETH^a (200 ppb)			ETH^a (100 ppb)			Lee and Halliday (1995)			Rosman et al. (1984)			Devillers et al. (1983)^c
	NIST 3161a			SPEX1			Johnson Matthey AAS standard solution			Johnson Matthey Sn oxide and metal^b			VENTRON metallic wire, Alfa Products
	Mean	2SD	2SD (ppm)	Mean	2SD	2SD (ppm)	Mean	2SD	2SD (ppm)	Mean	2SD	2SD (ppm)	Mean	2SD	2SD (ppm)
a External reproducibility (n sessions). b “Specpure” tin oxide (JMC 530 laboratory S8346) and tin metal (JM 540 laboratory S2807). c Absolute ratios determined using a ^116Sn–^122Sn double spike.
^112Sn/^120Sn	0.029823	0.000004	149	0.029826	0.000008	266	0.029812	0.000004	134	0.029860	0.000050	1674	0.029840	0.000100	3351
^114Sn/^120Sn	0.020190	0.000004	206	0.020194	0.000007	346	0.020195	0.000014	693	0.020220	0.000050	2473	0.020000	0.000100	5000
^115Sn/^120Sn	0.010361	0.000002	193	0.010369	0.000002	228	0.010366	0.000007	675	0.010390	0.000040	3850	0.011000	0.000100	9091
^116Sn/^120Sn	0.446000			0.446000			0.446000			0.446000			0.446000	0.001100	2466
^117Sn/^120Sn	0.235320	0.000028	119	0.235302	0.000023	100	0.235313	0.000048	204	0.235380	0.000080	340	0.235500	0.000700	2972
^118Sn/^120Sn	0.742945	0.000029	39	0.742929	0.000024	32	0.742935	0.000076	102	0.742950	0.000200	269	0.743200	0.001100	1480
^119Sn/^120Sn	0.263479	0.000032	121	0.263447	0.000027	103	0.263430	0.000046	175	0.263450	0.000130	493	0.263400	0.000400	1519
^122Sn/^120Sn	0.142095	0.000011	80	0.142081	0.000007	48	0.142086	0.000013	91	0.142110	0.000070	493	0.142010	0.000280	1972
^124Sn/^120Sn	0.177583	0.000035	197	0.177549	0.000027	152	0.177588	0.000052	293	0.177530	0.000100	563	0.177600	0.000550	3097
n	17			7

---

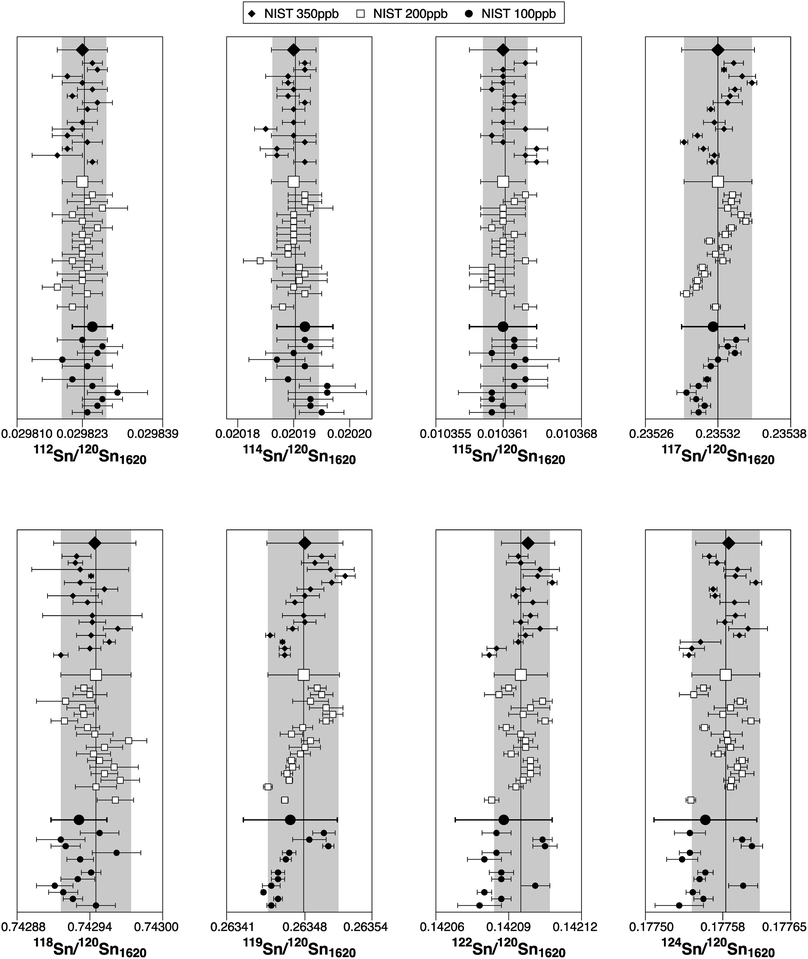
The associated uncertainties on the ratios are generally more precise than in previous studies. Nevertheless, the ratios ¹¹⁷Sn/¹²⁰Sn, ¹¹⁸Sn/¹²⁰Sn and ¹¹⁹Sn/¹²⁰Sn are affected by drifting (long-term and during a session) (Fig. 3). Therefore, for sample analyses, the measurements were bracketed with NIST SRM 3161a to correct for these drifts. The reason for the long-term drifts is unclear. It could indicate that the Faraday cups do not behave completely linear due to differences in cup efficiencies, however, the relatively prominent drifts on the odd/even isotope ratios ¹¹⁷Sn/¹²⁰Sn and ¹¹⁹Sn/¹²⁰Sn may also suggest nuclear field shift effect⁴⁸ or the magnetic isotope effect⁴⁹ as a potential source (Fig. 3). The typical reproducibility (2SD) of the NIST SRM 3161 200 ppb solution (drift corrected) within a single session was 0.9 for ε¹¹²Sn, 1.3 for ε¹¹⁴Sn, 1.2 for ε¹¹⁵Sn, 0.16 for ε¹¹⁷Sn, 0.11 for ε¹¹⁸Sn, 0.17 for ε¹¹⁹Sn, 0.21 for ε¹²²Sn and 0.31 for ε¹²⁴Sn.

Fig. 3 Tin isotope ratios of NIST SRM 3161a at concentrations of 100 ppb, 200 ppb and 350 ppb over a period of 15 months. Each data point and associated 2SD represents the average of an individual analytical session, while the grey band indicates the typical reproducibility (2SD) of NIST SRM 3161a at 200 ppb within a single session. Subscript 1620 refers to the ¹¹⁶Sn/¹²⁰Sn ratio that was employed for instrumental mass bias corrections.

Based on the long-term average for a 200 ppb NIST SRM 3161a Sn solution (Table 5), new Sn isotope abundances were calculated. The new Sn isotope abundances are more precise and in good agreement with the previous recommendation of IUPAC 2001 (ref. 50) (Table 6).

Table 6 Sn isotope abundances in mole fraction^a

	ETH^b	2SD	Böhlke (2005)^c
a The 2SD uncertainties in parenthesis refer to last digits. b Abundances and associated uncertainties were calculated based on data for NIST SRM 3161a 200 ppb (Table 5). c Representative Sn isotope composition from Böhlke.^50
112	0.0097220	(15)	0.0097(1)
114	0.0065822	(14)	0.0066(1)
115	0.0033775	(7)	0.0034(1)
116	0.1453838	(45)	0.1454(9)
117	0.0767065	(94)	0.0768(7)
118	0.242175	(12)	0.2422(9)
119	0.085883	(11)	0.0859(4)
120	0.325973	(23)	0.3258(9)
122	0.0463168	(40)	0.0463(3)
124	0.057880	(12)	0.0579(5)

---

Cadmium. The long-term average for a 200 ppb Alfa Aesar Cd standard solution measured over 17 months (corresponding to 40 measurement days) is ¹⁰⁶Cd/¹¹¹Cd = 0.098544 ± 24, ¹⁰⁸Cd/¹¹¹Cd = 0.069914 ± 12, ¹¹⁰Cd/¹¹¹Cd = 0.977034 ± 69, ¹¹²Cd/¹¹¹Cd = 1.878560 ± 60, ¹¹³Cd/¹¹¹Cd = 0.950066 ± 72 and ¹¹⁴Cd/¹¹¹Cd = 2.227640 ± 107. For comparison with literature,^42,51,52 our data was internally normalised to ¹¹⁰Cd/¹¹⁴Cd = 0.438564 after Rosman et al.⁵² (Table S4†). The ratios obtained in this study show a good agreement with previously published results. Small variations are present between the newly obtained Cd isotope data and literature for the most and least abundant isotopes and may stem from interferences or mass bias that was not fully corrected for. Importantly, the Cd isotope data obtained in this study for the Alfa Aesar Cd standard represents a long-term average of a total of 1061 individual analyses, whereas previous studies reported significantly fewer measurements (Table S4†). The average daily reproducibility (2SD) achieved over this period was 1.2 for ε¹⁰⁶Cd, 1.1 for ε¹⁰⁸Cd, 0.30 for ε¹¹⁰Cd, 0.19 for ε¹¹²Cd, 0.26 for ε¹¹³Cd and 0.27 for ε¹¹⁴Cd. Some of the Cd ratios, in particular ¹¹⁰Cd/¹¹¹Cd and ¹¹³Cd/¹¹¹Cd, also showed drifts during and between measurement sessions. When using ¹¹⁰Cd/¹¹⁴Cd for internal normalisation, the ratios involving the odd isotopes of Cd (¹¹³Cd/¹¹⁴Cd and the ¹¹¹Cd/¹¹⁴Cd) showed the most pronounced drifts between measurement sessions. Within a measurement session, however, the ¹¹⁶Cd/¹¹⁴Cd ratio showed the most drift. The reason for such drifts is unclear, but may be related to the same effects as described for Sn (differences in Faraday cup efficiencies and/or nuclear field shifts). Overall, this highlights the importance to bracket the sample measurements to the Alfa Aesar Cd standard, as done in this study. By applying a drift correction to the standard data, a slightly improved average daily reproducibility of 1.0 for ε¹⁰⁶Cd, 1.1 for ε¹⁰⁸Cd, 0.28 for ε¹¹⁰Cd, 0.16 for ε¹¹²Cd, 0.20 for ε¹¹³Cd and 0.17 for ε¹¹⁴Cd was achieved.

4.5 Precision and accuracy of the sample measurements

Tin. The lake sediment (Lake Zürich I) with a high Sn concentration (67 ppm) and the CV3 meteorite Allende (0.63 ppm) were used to determine the reproducibility (termed intermediate precision by ISO) and accuracy of the method. Eight aliquots of two individual digestions of Lake Zürich I were processed independently through the newly established procedure. The reproducibility (2SD, n = 20) obtained for Lake Zürich I is slightly larger than the reproducibility of the NIST SRM 3161a Sn standard: −0.1 ± 1.1 for ε¹¹²Sn, 0.3 ± 1.7 for ε¹¹⁴Sn, −1.1 ± 1.6 for ε¹¹⁵Sn, −0.04 ± 0.21 for ε¹¹⁷Sn, 0.00 ± 0.13 for ε¹¹⁸Sn, −0.05 ± 0.20 for ε¹¹⁹Sn, −0.04 ± 0.22 for ε¹²²Sn and −0.10 ± 0.24 for ε¹²⁴Sn (Table 4, Fig. 4). Most Sn data of the analysed lake sediments overlap with the composition of the 200 ppb NIST SRM 3161a Sn standard solution within uncertainties. Similarly, the analysed aliquots of Allende overlap in their Sn isotope composition with the NIST SRM 3161a Sn standard and Lake Zürich I considering the analytical uncertainty (Table 4 and Fig. 5). Exceptions are observed for ε¹¹⁵Sn. The different aliquots of Lake Zürich I and Allende consistently tend to negative ε¹¹⁵Sn values, which implies the presence of small In impurities in the NIST SRM 3161a Sn standard as previously discussed (Table 4).

Fig. 4 The Sn isotope composition for repeated analyses of eight independently processed aliquots of a lake sediment (Lake Zürich I). The shaded area represents the typical reproducibility (2SD) of NIST SRM 3161a 200 ppb within a single session, while the individual error bars represent the analytical precision of the NIST bracketing standard during the measurement session. Black symbols – no additional Pre-filter stage, open symbols – additional Pre-filter stage. Half-filled symbol – average of all the single analysis, uncertainty – 2SD.

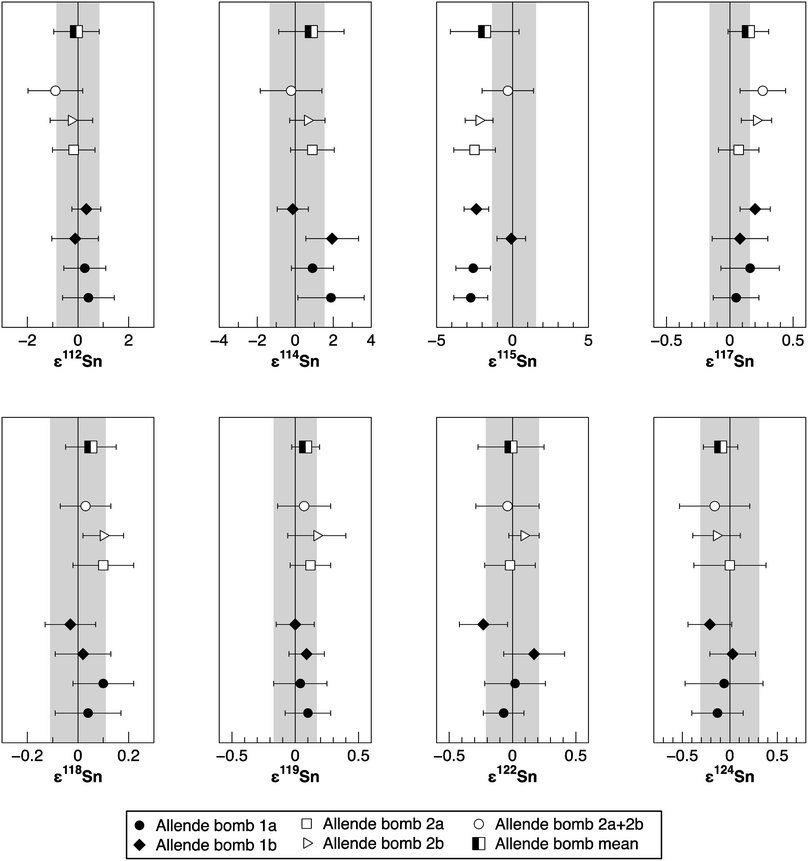Fig. 5 The Sn isotope composition for repeated analyses of two independently digested aliquots of Allende. Symbols and uncertainties are the same as in Fig. 4.

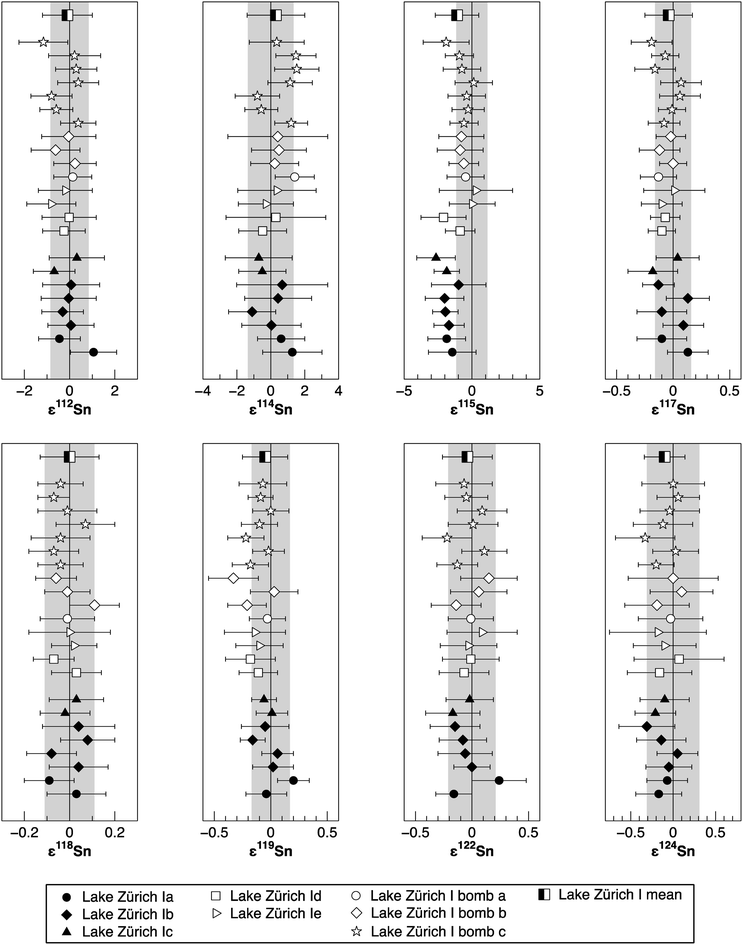
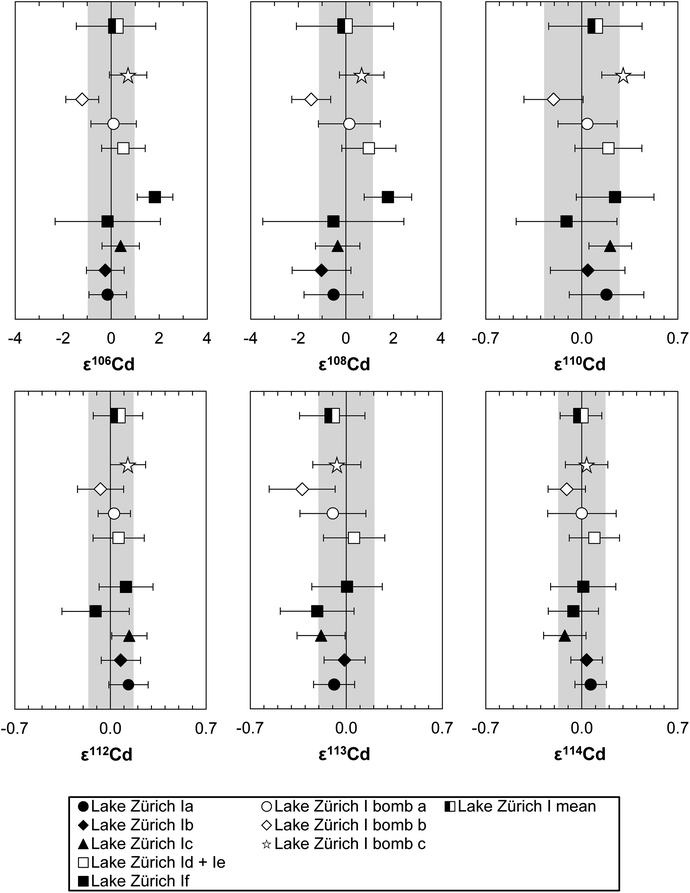
To verify the method and to check for analytical artifacts associated with organics released by the TRU Spec resin, aliquots of lake sediments were analysed using different introduction systems (Aridus II versus DSN). The isotopic composition of the lake sediment Lake Zürich I measured with two different desolvating systems, DSN 100 and Aridus II, are in good agreement (Table 4). In addition, aliquots of samples prepared by using the two-stage chromatographic separation procedure only were measured and compared to samples with the additional Pre-filter stage. Similar results are obtained when comparing samples before and after additional treating with Pre-filter resin (Table 4 and Fig. 4). The exception are the lake sediments with additional Pre-filter treatment, which show a tendency to higher ε¹¹⁵Sn values and therefore are closer to the values obtained for the NIST SRM 3161a Sn standard solution. The reason behind this is unclear, but may indicate that these samples pick up a small additional In blank during Pre-filter treatment. Alternatively, organics may be partly responsible for the observed negative shift in ε¹¹⁵Sn. However, considering the analytical uncertainty, all isotopic ratios measured with or without the third stage column (Pre-filter resin) are identical.

Cadmium. The same lake sediment (Lake Zürich I) with a Cd concentration of ∼14 ppm, as well as column processed aliquots of the Alfa Aesar Cd standard with (Cd–Zn Std 1 to 4: 200 ng Cd + 80 000 ng Zn, Cd–Zn Std 5: 200 ng Cd + 20 ng Zn) and without additions of Zn (500 ng Cd each), were used to calibrate and test the accuracy and reproducibility of our separation procedure for Cd isotope analyses. The standard aliquots were passed through various stages of the column chemistry (Table S3†), and display on average the same Cd isotope composition as the unprocessed Alfa Aesar standard once Zn has been efficiently removed (Fig. 6). The Cd isotope data of Lake Zürich I display a similar to slightly larger reproducibility (2SD, n = 9), compared to the Alfa Aesar Cd standard, of 0.2 ± 1.7 for ε¹⁰⁶Cd, 0.0 ± 2.0 for ε¹⁰⁸Cd, 0.10 ± 0.34 for ε¹¹⁰Cd, 0.06 ± 0.18 for ε¹¹²Cd, −0.10 ± 0.24 for ε¹¹³Cd and −0.01 ± 0.15 for ε¹¹⁴Cd (Table S3,†Fig. 7). In general, the Cd isotope data of the lake sediment overlap with the composition of the Alfa Aesar Cd standard, apart from the second measurement of Lake Zürich If with an elevated ε¹⁰⁶Cd and ε¹⁰⁸Cd data, which is likely due to Zn contamination.

Fig. 6 The Cd isotope composition of column processed Alfa Aesar Cd aliquots with (Cd–Zn Std 1 to 4: 200 ng Cd + 80 000 ng Zn, Cd–Zn Std 5: 200 ng Cd + 20 ng Zn) and without additions of Zn (500 ng Cd each). Open symbols represent pure Cd standard aliquots, closed symbols Cd–Zn standards and half-filled symbols the averages. The ion exchange procedure which each standard was subjected to is indicated in brackets: “Main Cd” – first Cd column chemistry, “Short Cd” – last down-scaled Cd column chemistry, “Full chemistry” – entire separation procedure performed using all four column chemistries. Error bars show the reproducibility (2SD) of the 200 ppb Alfa Aesar Cd standard measured in the same session, except for the averages where the 2SD of the repeat measurements are given. The grey bands indicate the average daily reproducibility (2SD) of the 200 ppb Alfa Aesar Cd standard.

Fig. 7 The Cd isotope composition of the measured lake sediment (Lake Zürich I) aliquots. Symbols are the same as in Fig. 4. Uncertainties are the same as in Fig. 6.

Summary. The consistency of the high precision Sn and Cd isotope data obtained for geological samples (Table 4 and S3†) show that our new analytical procedure for the separation of Sn and Cd from the same sample aliquot successfully produces high-purity Sn and Cd sample fractions. These fractions can be analysed by MC-ICPMS and produce accurate and precise data thereby demonstrating the validity of the method.

5. Conclusion

We developed and validated a new analytical method to separate Sn and Cd from geological samples for isotope analysis by MC-ICPMS at high precision. The new separation technique yields purified Sn fractions with minimal amounts of Cd, Te and other interfering elements and high Sn recoveries (>80%). Interference tests with doped Sn solutions show that besides Cd, In and Te, in particular the removal of U is critical because of the relatively high U⁺⁺ production rates that can reach 4% depending on instrument conditions. Solutions require U/Sn ratios of less than 5 × 10⁻⁵ for accurate data. Tellurium interference correction on Sn isotopes yields better precision when using ¹²⁵Te (instead of ¹²⁶Te) for correction. Moreover, our data indicate that both the NIST SRM 3161a and SPEX CLSN-2Y Sn standard solution contain small traces of In that affect the ¹¹⁵Sn data. The differences in ε¹¹⁵Sn between the two standards suggests that the SPEX solution contains 0.76 per mil more In than NIST SRM 3161a.

For Cd isotope analyses, the purified Cd fractions contain Pd, Sn and In below their determined tolerance limits and Zn is efficiently separated to enable accurate ¹⁰⁶Cd and ¹⁰⁸Cd isotope data. Inference tests demonstrate that notably high Zn levels (⁶⁶Zn/¹¹¹Cd > 1 × 10⁻²) yield inaccurate ¹⁰⁶Cd and ¹⁰⁸Cd data due to interfering Zn-argides formed in the plasma. Such levels can be easily generated as blank contribution during the analytical procedure and therefore need careful monitoring, if the low abundance Cd isotopes are targeted.

Our new analytical procedure allows for the simultaneous detection of all ten Sn isotopes and the correction of direct isobaric interferences. Similarly, it also includes the simultaneous measurement of all eight Cd isotopes including Pd, In and Sn isotopes for isobaric interference correction. The new data obtained for the NIST SRM 3161a Sn standard is in excellent agreement with those previously determined.^2,7,47 Based on our data, more precise absolute abundances of natural Sn were determined. The precisions for Sn and Cd isotope data achieved using our new procedure are sufficient to identify potential small nucleosynthetic or cosmogenic effects in meteorites. Our findings also illustrate the challenges related to extending an analytical method to low abundance isotopes or improving the measurement precision through increased counting statistics and improved instrumentation available. It requires careful attention to potential interferences. Molecular interferences (e.g., argides or oxides) as well as double charged ions formed in the plasma, or contamination of single standard solutions, previously unproblematic, can hamper the data quality when moving to higher precision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Adrian Gilli for the provision of the sample from Lake Zurich. The research leading to these results has received funding from the Swiss National Science Foundation (Project 200021_149282). Parts of this work have been carried out within the framework of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation. We would also like to thank Tim Conway and Matthias Sieber for their helpful input regarding the early Zn blank issue and Maria Kirchenbaur, Morten Andersen and Tim Elliot for helpful discussion.

References

1. J. R. De Laeter and P. M. Jeffery, J. Geophys. Res., 1965, 70, 2895–2903.
2. C. Devillers, T. Lecomte and R. Hagemann, Int. J. Mass Spectrom. Ion Phys., 1983, 50, 205–217.
3. N. J. McNaughton and K. J. R. Rosman, Geochim. Cosmochim. Acta, 1991, 55, 499–504.
4. K. J. R. Rosman and N. J. McNaughton, Int. J. Mass Spectrom. Ion Processes, 1987, 75, 91–98.
5. J. R. De Laeter and P. M. Jeffery, Geochim. Cosmochim. Acta, 1967, 31, 969–985.
6. R. D. Loss, K. J. R. Rosman and J. R. de Laeter, Geochim. Cosmochim. Acta, 1990, 54, 3525–3536.
7. D.-C. Lee and A. N. Halliday, Int. J. Mass Spectrom. Ion Processes, 1995, 146–147, 35–46.
8. D. Berger, E. Figueiredo, G. Brügmann and E. Pernicka, J. Archaeol. Sci., 2018, 92, 73–86.
9. G. Brügmann, D. Berger and E. Pernicka, Geostand. Geoanal. Res., 2017, 41, 437–448.
10. R. Clayton, P. Andersson, N. H. Gale, C. Gillis and M. J. Whitehouse, J. Anal. At. Spectrom., 2002, 17, 1248–1256.
11. M. Haustein, C. Gillis and E. Pernicka, Archaeometry, 2010, 52, 816–832.
12. A. H. Mason, W. G. Powell, H. A. Bankoff, R. Mathur, A. Bulatović, V. Filipović and J. Ruiz, J. Archaeol. Sci., 2016, 69, 110–117.
13. E. Yamazaki, S. Nakai, Y. Sahoo, T. Yokoyama, H. Mifune, T. Saito, J. Chen, N. Takagi, N. Hokanishi and A. Yasuda, J. Archaeol. Sci., 2014, 52, 458–467.
14. E. Yamazaki, S. i. Nakai, T. Yokoyama, S. Ishihara and H. Tang, Geochem. J., 2013, 47, 21–35.
15. F. Moynier, T. Fujii and P. Telouk, Anal. Chim. Acta, 2009, 632, 234–239.
16. D. Malinovskiy, L. Moens and F. Vanhaecke, Environ. Sci. Technol., 2009, 43, 4399–4404.
17. N. Badullovich, F. Moynier, J. Creech, F. Z. Teng and P. A. Sossi, Geochem. Perspect. Lett., 2017, 24–28,  DOI:10.7185/geochemlet.1741.
18. X. Wang, Q. Amet, C. Fitoussi and B. Bourdon, Geochim. Cosmochim. Acta, 2018, 228, 320–335.
19. A. M. Davis, in Meteorites and the Early Solar System II, ed. D. S. Lauretta and H. Y. McSween, University of Arizona Press, 2006, vol. 1, pp. 295–307.
20. K. Lodders, Astrophys. J., 2003, 591, 1220.
21. K. P. Jochum, A. W. Hofmann and H. M. Seufert, Geochim. Cosmochim. Acta, 1993, 57, 3585–3595.
22. F. Farges, R. L. Linnen and G. E. Brown, Can. Mineral., 2006, 44, 795–810.
23. R. L. Linnen, M. Pichavant, F. Holtz and S. Burgess, Geochim. Cosmochim. Acta, 1995, 59, 1579–1588.
24. K. J. R. Rosman and J. R. De Laeter, Geochim. Cosmochim. Acta, 1974, 38, 1665–1677.
25. K. J. R. Rosman and J. R. De Laeter, Earth Planet. Sci. Lett., 1988, 89, 163–169.
26. F. Wombacher, M. Rehkämper, K. Mezger, A. Bischoff and C. Münker, Geochim. Cosmochim. Acta, 2008, 72, 646–667.
27. F. Wombacher, M. Rehkämper, K. Mezger and C. Münker, Geochim. Cosmochim. Acta, 2003, 67, 4639–4654.
28. C. S. Palk, M. Schönbächler, M. Rehkämper and B. J. Wood, Lunar Planet. Sci., 2015, 46, 2822.
29. E. Zinner, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Elsevier, Oxford, 2nd edn, 2014, pp. 181–213.
30. W. Akram, M. Schönbächler, S. Bisterzo and R. Gallino, Geochim. Cosmochim. Acta, 2015, 165, 484–500.
31. A. Trinquier, J.-L. Birck and C. J. Allègre, Astrophys. J., 2007, 655, 1179–1185.
32. C. Arlandini, F. Käppeler, K. Wisshak, R. Gallino, M. Lugaro, M. Busso and O. Straniero, Astrophys. J., 1999, 525, 886–900.
33. S. Bisterzo, R. Gallino, O. Straniero, S. Cristallo and F. Käppeler, Mon. Not. R. Astron. Soc., 2011, 418, 284–319.
34. C. Burkhardt, T. Kleine, F. Oberli, A. Pack, B. Bourdon and R. Wieler, Earth Planet. Sci. Lett., 2011, 312, 390–400.
35. M. Fischer-Gödde and T. Kleine, Nature, 2017, 541, 525–527.
36. D. G. Sands, J. R. De Laeter and K. J. R. Rosman, Earth Planet. Sci. Lett., 2001, 186, 335–346.
37. J. Y. Hu and N. Dauphas, J. Anal. At. Spectrom., 2017, 32, 2024–2033.
38. M. Kirchenbaur, A. Heuser, A. Bragagni and F. Wombacher, Geostand. Geoanal. Res., 2018, 42, 361–377.
39. A. F. Holleman, E. Wiberg and N. Wiberg, Lehrbuch der Anorganischen Chemie, Walter de Gruyter, 2007.
40. M. A. Fehr, M. Rehkämper and A. N. Halliday, Int. J. Mass Spectrom., 2004, 232, 83–94.
41. W. Yi, A. N. Halliday, D.-C. Lee and J. N. Christensen, Geochim. Cosmochim. Acta, 1995, 59, 5081–5090.
42. F. Wombacher, M. Rehkämper and K. Mezger, Geochim. Cosmochim. Acta, 2004, 68, 2349–2357.
43. E. R. Toth, M. Schönbächler, M. Friebel and M. A. Fehr, Meteorit. Planet. Sci., 2017, 52, A353.
44. M. Gault-Ringold and C. H. Stirling, J. Anal. At. Spectrom., 2012, 27, 449.
45. K. Murphy, M. Rehkämper, K. Kreissig, B. Coles and T. van de Flierdt, J. Anal. At. Spectrom., 2016, 31, 319–327.
46. C. Pin and J. Rodriguez, in Treatise on Geochemistry, ed. K. K. Turekian, Elsevier, Oxford, 2nd edn, 2014, pp. 147–170.
47. K. J. R. Rosman, R. D. Loss and J. R. De Laeter, Int. J. Mass Spectrom. Ion Processes, 1984, 56, 281–291.
48. J. Bigeleisen, J. Am. Chem. Soc., 1996, 118, 3676–3680.
49. A. L. Buchachenko, J. Phys. Chem. B, 2013, 117, 2231–2238.
50. J. K. Böhlke, J. Phys. Chem. Ref. Data, 2005, 34, 57.
51. S. Ripperger and M. Rehkämper, Geochim. Cosmochim. Acta, 2007, 71, 631–642.
52. K. J. R. Rosman, I. L. Barnes, L. J. Moore and J. W. Gramlich, Geochem. J., 1980, 14, 269–277.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00289h

---