Open Access Article
Open Access ArticleEffect of particle size distribution on rheological properties of chocolate†
Annika
Feichtinger
 ,
Elke
Scholten
and
Guido
Sala
*
,
Elke
Scholten
and
Guido
Sala
*
Physics and Physical Chemistry of Foods, Wageningen University & Research, P.O. Box 17, 6700 AA Wageningen, The Netherlands. E-mail: guido.sala@wur.nl
First published on 27th October 2020
Abstract
This study focused on the influence of the particle size distribution (PSD) of ingredients used for chocolate preparation (cocoa powder and sugar) on viscosity of model chocolates with different fat contents. Model chocolates with varying PSDs and two particle size ratios (cocoa particles![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sugar of 1
sugar of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) were prepared by mixing highly defatted cocoa powder as a fine fraction and sugar as coarse fraction in several proportions. Samples containing spherical quartz beads were included as a reference to gain insight into the role of particle properties. Comparing chocolate samples with the same composition, but different particle size ratio, the largest difference in viscosity was found at a proportion of coarse fraction of 0.6. This shows that at this proportion of coarse particles, the highest maximum packing fraction was reached, which is in accordance with theoretical predictions. However, for the investigated chocolate samples, the lowest viscosity values were obtained at a proportion of the coarse fraction of 0.8 or 1. This could be attributed to parameters other than PSD, such as a decrease in surface area with an increasing amount of coarse particles. Also the morphology and surface properties were shown to influence viscosity. Compared to cocoa and sugar particles, spherical and smooth quartz beads led to an improved particle packing, and therefore a lower viscosity. The addition of lecithin led to a decrease in viscosity due to a decrease in particle–particle interactions, particularly for hydrophilic sugar particles. The knowledge obtained in this study provides possible approaches on how to reduce fat content of chocolates.
6) were prepared by mixing highly defatted cocoa powder as a fine fraction and sugar as coarse fraction in several proportions. Samples containing spherical quartz beads were included as a reference to gain insight into the role of particle properties. Comparing chocolate samples with the same composition, but different particle size ratio, the largest difference in viscosity was found at a proportion of coarse fraction of 0.6. This shows that at this proportion of coarse particles, the highest maximum packing fraction was reached, which is in accordance with theoretical predictions. However, for the investigated chocolate samples, the lowest viscosity values were obtained at a proportion of the coarse fraction of 0.8 or 1. This could be attributed to parameters other than PSD, such as a decrease in surface area with an increasing amount of coarse particles. Also the morphology and surface properties were shown to influence viscosity. Compared to cocoa and sugar particles, spherical and smooth quartz beads led to an improved particle packing, and therefore a lower viscosity. The addition of lecithin led to a decrease in viscosity due to a decrease in particle–particle interactions, particularly for hydrophilic sugar particles. The knowledge obtained in this study provides possible approaches on how to reduce fat content of chocolates.
1. Introduction
Chocolate is an appreciated food product and, especially in Europe, is consumed in considerable amounts. In 2017, 8.8 kg of chocolate was consumed per capita in Switzerland, and 5.1 kg in the Netherlands.1 Around 30 wt% of chocolate consists of fat,2 the macronutrient with the highest caloric density.3 Therefore, chocolate is among the food products richest in calories, and can contribute to overweight. Depending on the type of chocolate, the caloric content varies between 510 and 530 kcal per 100 g. Fat reduced chocolate would provide an attractive alternative for consumers, but as fat is the main constituent and continuous phase of chocolate, it is difficult to achieve fat reductions whilst keeping desirable flow properties.2From a colloidal point of view, chocolate can be defined as a dense dispersion of solid particles (sugar, cocoa powder and milk solids) in a continuous phase of fat.4,5 A minimum fat content is required to include all the present solid particles in the system and to provide a pleasant mouthfeel when melted in the mouth. The dispersed particles, which constitute 65–70 wt% of chocolate, determine the rheological behaviour of molten chocolate to a great extent, as during deformation each particle interacts with many other neighbouring particles. Decreasing the fat content in chocolate is accompanied with an increase in the dispersed phase. This results in more contact between the dispersed solid particles, which gives rise to more friction and leads to an increase in viscosity.6 The viscosity of chocolate is an important parameter concerning sensorial attributes. An increased viscosity has been shown to lead to an unpleasant, pasty mouthfeel.7 Besides affecting mouthfeel, the fat content also has an effect on the technological properties of the product. Viscosity is important for the handling of the product during production, for example during pumping and mixing, and determines its suitability for the final product application, like enrobing or dipping.4 The volumetric proportion of particles is one of the most important factors influencing the viscosity of a dispersion; a higher proportion of particles limits chocolate flowability.2 The Krieger–Dougherty equation relating the volume fraction of dispersed particles, φ, to viscosity is valid for concentrated dispersions8 and is therefore appropriate for chocolate with high volume fractions of dispersed particles. According to the Krieger–Dougherty equation, the viscosity, η, depends on the volume fraction of dispersed particles as
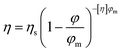 | (1) |
The viscosity of chocolate can thus be decreased by increasing φm of the dispersed sugar and cocoa particles. Such an increase of φm can be achieved by broadening of the particle size distribution (PSD), i.e. by increasing the polydispersity of the particles. If fine particles are added to coarser ones, the fine ones will fill the voids between the coarser ones, thereby increasing the maximum packing fraction. As was shown experimentally, this effect on φm is especially pronounced for a size ratio higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, i.e. with coarse particles with a size at least sevenfold the size of fine particles.11,12 Small particles may even lubricate the coarser particles just like the continuous phase, leading to a higher flowability and subsequent viscosity reduction.5 Such an effect of a change of the PSD is considerable for more concentrated suspensions, as in these systems local dilatations become necessary to enable layers of particles to slide past each other. On the contrary, for suspensions with φ ≤ 0.2, small variations of the PSD, i.e. the value of φm, do not show an effect on viscosity.11 In the case of multiple particle sizes, the viscosity will be affected by the specific ratio of fine, medium and coarse fractions. Table 1 shows the optimal composition of non-interacting fine and coarse particles to reach a maximal φm at a specific volume fraction of 0.64 of dispersed particles, based on theoretical calculations. For volume fractions of dispersed particles larger than 0.64, the optimal composition to reach a minimum viscosity shifts to larger proportions of coarse fraction, whereas for volume fractions of dispersed particles lower than 0.64, smaller proportions of coarse fraction are optimal.13 The work of Metzner11 shows that for viscosity reduction, the additional benefit of a trimodal distribution compared to a bimodal one is relatively small.
7, i.e. with coarse particles with a size at least sevenfold the size of fine particles.11,12 Small particles may even lubricate the coarser particles just like the continuous phase, leading to a higher flowability and subsequent viscosity reduction.5 Such an effect of a change of the PSD is considerable for more concentrated suspensions, as in these systems local dilatations become necessary to enable layers of particles to slide past each other. On the contrary, for suspensions with φ ≤ 0.2, small variations of the PSD, i.e. the value of φm, do not show an effect on viscosity.11 In the case of multiple particle sizes, the viscosity will be affected by the specific ratio of fine, medium and coarse fractions. Table 1 shows the optimal composition of non-interacting fine and coarse particles to reach a maximal φm at a specific volume fraction of 0.64 of dispersed particles, based on theoretical calculations. For volume fractions of dispersed particles larger than 0.64, the optimal composition to reach a minimum viscosity shifts to larger proportions of coarse fraction, whereas for volume fractions of dispersed particles lower than 0.64, smaller proportions of coarse fraction are optimal.13 The work of Metzner11 shows that for viscosity reduction, the additional benefit of a trimodal distribution compared to a bimodal one is relatively small.
| Mode | Bimodal | Trimodal | Tetramodal |
|---|---|---|---|
| Very fine | — | — | 16.5% |
| Fine | 37% | 22.5% | 21.5% |
| Medium | — | 32% | 27% |
| Coarse | 63% | 45.5% | 35% |
It should be noted that besides the volume fraction, also the particle size and shape often affect viscosity, although this is not taken into account in the Krieger–Dougherty equation. In food products, dispersed particles are often non-spherical, and next to the particle shape also surface roughness and particle density vary. These parameters need to be taken into account, as they affect the maximum packing fraction and interactions between particles. In the case of non-spherical particles, a lower maximum packing fraction can be expected.5,11 An understanding about how these parameters influence the rheological properties can help in designing chocolate.
In previous research, it was attempted to prepare chocolate with a bimodal PSD of the dispersed particles with different methods: (i) by adding a coarse sugar fraction to cocoa and milk powder milled to a smaller particle size, (ii) by milling of two fractions containing all ingredients to two different size classes,14 and (iii) by addition of two different sized sugar fractions to the remaining pre-grinded ingredients.15 Due to the technical difficulty of preparing chocolate with a distinct fine and coarse particle fraction, i.e. a bimodal PSD, in the mentioned studies only multimodal or broad, almost unimodal PSDs were obtained. Therefore, these studies did not lead to concrete conclusions on the role of PSD on chocolate viscosity. Do et al.16 were able to obtain a more defined particle distribution. They studied the effect of PSD on the rheology of sugar model systems consisting of sugar, cocoa butter and lecithin only, i.e., no cocoa particles. Varying PSDs were obtained by mixing a fine and a coarse sugar fraction in different ratios. Compared to the studies performed on chocolate, the differences in PSDs between samples with varying proportions of fine and coarse sugar fraction were more pronounced and PSDs were partly bimodal, but also here the coarse sugar fraction on its own already showed a relatively broad PSD with a noticeable shoulder. Considering these different approaches and results of studies performed so far, it becomes clear that a more systematic approach needs to be used to obtain conclusions in systems with a composition resembling that of chocolate. Samples need to contain both sugar and cocoa particles, and the PSD should be varied systematically, i.e. including samples with a monomodal PSD for both the finer and coarser particles, as well as mixtures thereof in different mixing proportions. In addition, the effect of a comparably large size ratio of fine and coarse particles should be studied. The inclusion of two size ratios of fractions also provides a simple approach to draw conclusions on the mixing ratio of fine and coarse particles to achieve the maximum packing fraction. The maximum packing fraction is obtained for the mixing ratio at which the largest difference in viscosity is seen for an increased particle size ratio.11,17 Accordingly, in this study we combined the aspect of working with a model system having a composition typical of dark chocolates with a systematic variation of the PSD at several particle volume fractions. Contrary to previous researches, our starting point was a fine cocoa powder and a coarse sugar fraction, which both had a relatively narrow PSD and no shoulder peaks. Such a narrow size distribution was obtained by sieving. The PSDs of our samples included, next to a monomodal PSD for the fine particle fraction and a monomodal PSD for coarser particle size fractions, clear bimodal PSDs obtained for different mixing ratios of the fine and coarse fraction. Samples varied not only in the mixing proportion of fine and coarse particles, but were also prepared at two size ratios of the dispersed particles; besides a particle size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, we also included a larger particle size ratio of 1
4, we also included a larger particle size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, which was closer to the expected optimal ratio to achieve a pronounced effect on the maximum packing.
6, which was closer to the expected optimal ratio to achieve a pronounced effect on the maximum packing.
2. Materials and methods
2.1 Materials
To first evaluate the stability of cocoa particles during sample preparation, three different sources of cocoa were used. Cocoa press cake was supplied by Royal Duyvis Wiener B.V. (Koog aan de Zaan, The Netherlands). Krüger cocoa powder (Krüger GmbH & Co. KG, Bergisch Gladbach, Germany), Raw Organic Food Cacao Nibs (De Smaakspecialist, Ulvenhout, The Netherlands) and Reddy sunflower oil (Vandemoortele Nederland BV, Zeewolde, The Netherlands) were purchased at local supermarkets. For fat extraction, laboratory-grade n-hexane (Sigma-Aldrich, St Louis, U.S.) was used.For the preparation of model chocolates, icing sugar was obtained from Silver Spoon (Peterborough, UK). The icing sugar contained small amounts of tricalcium phosphate as anti-caking agent. As tricalcium phosphate is not surface-active and was present in very small amounts, this component was assumed to have no influence on the rheological properties of samples. Soy lecithin LECIPRIME™ 1400 IPM for the particular use in chocolate was provided by Cargill (Minneapolis, Minnesota, USA), and Bensdorp Red D-light cocoa powder (Barry Callebaut Cocoa AG, Zürich, Switzerland) and cocoa butter (Barry Callebaut Belgium N.V., Lebbeke-Wieze, Belgium) by Barry Callebaut. Quartz beads with a median of 20 μm were obtained from Tatsumori Ltd (Koriyama-city Fukushima, Japan).
2.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) were created by mixing cocoa powder as fine fraction (Bensdorp Red D-light, d4,3 of 9.6 μm) with either a medium (d4,3 of 40.6 μm) or a coarse (d4,3 of 52.4 μm) icing sugar fraction in five different mixing ratios (proportion coarse by volume 0, 0.3, 0.6, 0.8 and 1). These volumetric proportions of powder fractions were determined based on their density and mass. Additionally, sugar model systems were prepared by mixing a fine (d4,3 of 10.9 μm) and a medium (d4,3 of 40.6 μm) sugar fraction, resulting in a particle size ratio of 1
6) were created by mixing cocoa powder as fine fraction (Bensdorp Red D-light, d4,3 of 9.6 μm) with either a medium (d4,3 of 40.6 μm) or a coarse (d4,3 of 52.4 μm) icing sugar fraction in five different mixing ratios (proportion coarse by volume 0, 0.3, 0.6, 0.8 and 1). These volumetric proportions of powder fractions were determined based on their density and mass. Additionally, sugar model systems were prepared by mixing a fine (d4,3 of 10.9 μm) and a medium (d4,3 of 40.6 μm) sugar fraction, resulting in a particle size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. Quartz beads model systems with a particle size ratio of 1
4. Quartz beads model systems with a particle size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 were prepared by mixing a fine (d4,3 of 11 μm) and coarse (d4,3 of 55.2 μm) quartz beads fraction. These sugar and quartz beads model systems with a fat content of 28% had PSDs comparable to the respective chocolate samples. For all fat contents, the same model chocolate, sugar and quartz beads systems were also prepared with additional lecithin to evaluate the effect of particle interactions. A summary of the different sample series is provided in Table 2.
5 were prepared by mixing a fine (d4,3 of 11 μm) and coarse (d4,3 of 55.2 μm) quartz beads fraction. These sugar and quartz beads model systems with a fat content of 28% had PSDs comparable to the respective chocolate samples. For all fat contents, the same model chocolate, sugar and quartz beads systems were also prepared with additional lecithin to evaluate the effect of particle interactions. A summary of the different sample series is provided in Table 2.
| Sample type | Size ratio | Fat content (%) | Lecithin addition |
|---|---|---|---|
Model chocolate samples (fine fraction:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cocoa powder coarse fraction: cocoa powder coarse fraction:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sugar) sugar) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
28 | Yes |
| No | |||
| 30 | Yes | ||
| No | |||
| 36 | Yes | ||
| No | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
28 | Yes | |
| No | |||
| 30 | Yes | ||
| No | |||
| 36 | Yes | ||
| No | |||
| Sugar model systems (fine and coarse fraction sugar) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
28 | Yes |
| No | |||
| Quartz beads model systems (fine and coarse fraction quartz beads) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
28 | Yes |
| No |
Table 3 gives an overview of how samples were composed. Attention was paid to keep volume fractions constant, by taking the different densities of the different dry ingredients (cocoa powder, sugar, quartz beads) into account. Densities used for calculations were 1.535 g cm−3 for cocoa powder as determined by pycnometry, 1.587 g cm−3 for sugar20 and 2.5 g cm−3 for quartz beads, according to the product data sheet of the manufacturer. The method for the preparation of model chocolate samples and model systems was based on the method of Zhao et al.21 with some adjustments. In short, the required amount of cocoa butter was melted in a beaker glass on a heating plate until it was liquefied. Subsequently, the cocoa butter was stirred with a 2-bladed propeller stirrer fitted to an IKA RW20 digital overhead stirrer (IKA®-Werke GmbH & Co. KG, Staufen, Germany) until a temperature of approximately 60 °C was reached. Then the pre-mixed dry ingredients, i.e. sugar and cocoa powder, were slowly added to the cocoa butter during a period of 5 min at a stirring speed of 350 rpm. For samples containing lecithin, the lecithin was subsequently added to the mixture of cocoa butter and dry ingredients within these first 5 min. Stirring was continued for another 25 min at 1200 rpm at 60 ± 3 °C to achieve homogeneous systems and a good coating of the particles with fat and lecithin.
| Lecithin | Proportion coarse fraction | Cocoa butter | Lecithin | Fine particles (cm3) | Coarse particles (cm3) | |||
|---|---|---|---|---|---|---|---|---|
| (g) | (wt%) | (g) | (wt%) | |||||
Model chocolate samples, 28% fat (size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1 4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) 6) |
No | 0.0 | 3.92 | 28.00 | — | 6.57 | 0.00 | |
| 0.3 | 3.92 | 27.80 | — | 4.60 | 1.97 | |||
| 0.6 | 3.92 | 27.60 | — | 2.63 | 3.94 | |||
| 0.8 | 3.92 | 27.47 | — | 1.31 | 5.25 | |||
| 1.0 | 3.92 | 27.34 | — | 0.00 | 6.57 | |||
| Yes | 0.0 | 3.82 | 27.28 | 0.10 | 0.72 | 6.57 | 0.00 | |
| 1.0 | 3.82 | 27.28 | 0.10 | 0.72 | 0.00 | 6.57 | ||
Sugar model systems, 28% fat (size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) 4) |
No | 0.6 | 3.92 | 27.34 | — | 2.63 | 3.94 | |
| Yes | 0.6 | 3.82 | 26.64 | 0.10 | 0.70 | 2.63 | 3.94 | |
Quartz beads model systems, 28% fat (size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) 5) |
No | 0.6 | 3.92 | 19.28 | — | 2.63 | 3.94 | |
| Yes | 0.6 | 3.82 | 18.78 | 0.10 | 0.50 | 2.63 | 3.94 | |
An overview of characteristic parameters, i.e. d4,3, span and SSA, of all powder mixtures used for sample preparation is provided in Table 4. The values of d4,3, span and SSA of the mixtures were calculated as average values from the values measured for the single powder fractions, i.e. fine cocoa particles and coarse sugar particles, taking into account the different proportions. Fig. 1 provides light microscopy images of the different powder fractions. The cocoa powder particles (Fig. 1a) were irregularly shaped, with a rough surface. Also the sugar particles of different size fractions (Fig. 1b–d) had an irregular shape, with a smoother surface, but sharp edges. The quartz beads had a smooth surface and a particle shape close to perfect spheres (Fig. 1e and f). Fig. 2 provides the PSDs of the model chocolate samples. The single powder fractions showed a relatively narrow PSD without shoulders. The cocoa powder was mixed as fine fraction with either a medium or coarse sugar fraction to obtain a different size ratio of cocoa and sugar particles of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, respectively. They were mixed in different weight ratios to obtain different volumetric proportions; a proportion of 0 refers to only cocoa, i.e. only a fine fraction, and a proportion of 1 refers to only sugar, i.e. only a coarse fraction. The mixing resulted in three samples with bimodal PSDs with a proportion of 0.3, 0.6 and 0.8. In Fig. 2, bimodality is clearly seen especially for the PSDs of samples with a size ratio of 1
6, respectively. They were mixed in different weight ratios to obtain different volumetric proportions; a proportion of 0 refers to only cocoa, i.e. only a fine fraction, and a proportion of 1 refers to only sugar, i.e. only a coarse fraction. The mixing resulted in three samples with bimodal PSDs with a proportion of 0.3, 0.6 and 0.8. In Fig. 2, bimodality is clearly seen especially for the PSDs of samples with a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, as here the single fractions differed more in size and therefore showed less overlap of the separate peaks representing the separate particle fractions. As can be seen from Table 4, the samples containing a mixture of two differently sized fractions showed a higher span value, which in theory would lead to a higher value of φm.
6, as here the single fractions differed more in size and therefore showed less overlap of the separate peaks representing the separate particle fractions. As can be seen from Table 4, the samples containing a mixture of two differently sized fractions showed a higher span value, which in theory would lead to a higher value of φm.
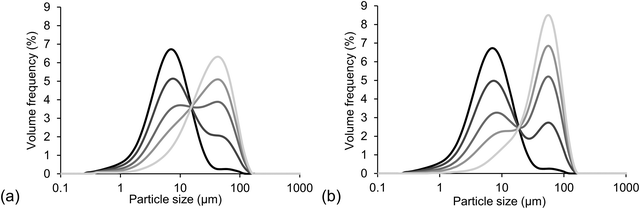 | ||
Fig. 2 PSDs of model chocolate samples with a particle size ratio of (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and (b) 1 4 and (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and a proportion of coarse fraction of 0, 0.3, 0.6, 0.8 and 1 (black to light grey). 6 and a proportion of coarse fraction of 0, 0.3, 0.6, 0.8 and 1 (black to light grey). | ||
| Proportion coarse fraction | d 4,3 (μm) | Span | SSA (m2 g−1) | |
|---|---|---|---|---|
Model chocolate samples, size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
0.0 | 9.6 | 2.22 | 1.333 |
| 0.3 | 18.9 | 5.07 | 1.034 | |
| 0.6 | 28.2 | 3.90 | 0.741 | |
| 0.8 | 34.4 | 2.68 | 0.549 | |
| 1.0 | 40.6 | 2.14 | 0.359 | |
Model chocolate samples, size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
0.0 | 9.6 | 2.22 | 1.333 |
| 0.3 | 22.4 | 6.20 | 0.991 | |
| 0.6 | 35.3 | 3.18 | 0.656 | |
| 0.8 | 43.8 | 2.10 | 0.436 | |
| 1.0 | 52.4 | 1.66 | 0.219 | |
| Sugar model systems | 0.0 | 10.9 | 1.81 | 1.161 |
| 0.3 | 19.8 | 3.68 | 0.915 | |
| 0.6 | 28.7 | 3.37 | 0.673 | |
| 0.8 | 34.7 | 2.69 | 0.515 | |
| 1.0 | 40.6 | 2.14 | 0.359 | |
| Quartz beads model systems | 0.0 | 11.0 | 1.43 | 1.070 |
| 0.3 | 24.3 | 4.71 | 0.834 | |
| 0.6 | 37.5 | 1.93 | 0.608 | |
| 0.8 | 46.4 | 1.48 | 0.460 | |
| 1.0 | 55.2 | 1.18 | 0.314 |
2.2.6.1 Viscosity and yield value. Rheological measurements were performed in a shear-controlled Physica MCR 301 rheometer with a concentric cylinder system. The bob model CC17/Ti with a diameter of 16.66 mm was used together with the cup model C-CC17/T200/Ti with a diameter of 18.1 mm (Anton Paar GmbH, Graz, Austria). This measurement geometry was chosen because of the higher reproducibility of the results compared to plate–plate or plate–cone geometries.22 Before measurements, samples were liquefied under stirring on a heating plate and kept at 50 ± 3 °C for an additional 25 min to ensure that no fat crystals remained in the sample. Around 4 mL of sample was placed in the bob. The measurement protocol was set up according to the official ICA (International Confectionary Association)-method (ICA analytical method 46), with an additional waiting time of 600 s before the actual measurement started, to ensure temperature equilibration. Temperature was set to 40 °C. The shear stress was recorded while the shear rate was increased from 2 to 50 s−1 within 180 s, held at 50 s−1 for 60 s, and again decreased to 2 s−1 within 180 s. Measurements were performed in duplicate. To characterize the flow properties of samples, two values were extracted from the flow curves following the ICA-method: apparent viscosity was taken at a shear rate of 40 s−1, and, in addition, the shear stress at a shear rate of 5 s−1 was determined as the yield stress, both on the decreasing shear rate ramp. As shown by Servais et al.,23 this method provides better reproducible and repeatable results than the more commonly used Casson model. By determining the shear stress at low shear rate, the yield value is reflected more accurately, as errors resulting from data extrapolation are avoided.23
2.2.6.2 Thixotropy. Another parameter that was used to describe the rheological properties of the samples is thixotropy. We chose to determine thixotropy based on the hysteresis loop resulting from increase and subsequent decrease in shear rate, which is a commonly used method to characterise thixotropy in chocolate research.16,24–26 Thixotropy values were obtained by subtracting the value of apparent viscosity at 40 s−1 determined at decreasing shear rate from the apparent viscosity obtained at 40 s−1 upon increasing shear rate, as described by Servais et al.23 This value was multiplied by 402 (s−2), resulting in a value for thixotropy in Pa. This method was shown to result in similar values as the determination of the loop area, but to have a better repeatability.23
3. Results and discussion
3.1 Influence of PSD on viscosity
The apparent viscosity values (η40) of model chocolate samples, sugar and quartz beads model systems obtained for varying proportions of coarse fraction are shown in Table 5. For some of the model chocolate samples viscosity values were too high to be measured. This was for example the case for the model chocolate samples containing a large amount of fine fraction (proportion of coarse fraction of 0 or 0.3) at a fat content of 28% and 30%. For the quartz bead systems, all viscosities were low enough to be measured. This difference between model chocolate samples and quartz beads systems can be explained by the differences in particle shape. The maximum packing fraction of irregularly shaped particles like sugar and cocoa particles was lower, which contributes to generally higher viscosity values of model chocolates compared to quartz beads systems.11,27 Also, the irregular shape and less smooth surface of sugar and cocoa particles compared to quartz beads was not taken into account in the calculation of the specific surface area (SSA). Therefore, even though the obtained values of the SSA were similar for quartz beads systems and model chocolate samples (Table 4), the SSA of sugar and cocoa particles was in reality larger. This explains why for chocolate samples more fat was needed to coat the particle surfaces to lower the viscosity.6| Sample type/fat content | Size ratio of fractions | Lecithin | Proportion coarse fraction | Apparent viscosity (Pa s) | σ 5 (Pa) | Thixotropy (Pa) |
|---|---|---|---|---|---|---|
*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) No duplicate measurement could be done. No duplicate measurement could be done. |
||||||
| Model chocolate samples/36% | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
Yes | 0.3 | 13.29 ± 0.15 | 108.2 ± 1.9 | 1240 ± 170 |
| 0.6 | 3.18 ± 0.03 | 23.6 ± 0.1 | 390 ± 60a,b | |||
| 0.8 | 1.58 ± 0.04 | 10.2 ± 0.5a | 100 ± 1a,c | |||
| 1.0 | 1.17 ± 0.02 | 6.7 ± 0.1 a | 220 ± 10 b,c | |||
| No | 0.3 | 12.68 ± 0.05 | 97.8 ± 0.0 | 1500 ± 110 | ||
| 0.6 | 3.42 ± 0.01 | 23.8 ± 0.3 | 390 ± 80a,b | |||
| 0.8 | 1.83* | 12* |
270*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,c a,c |
|||
| 1.0 | 1.55 ± 0.06 | 8.0 ± 0.3 | 440 ± 20b,c | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
Yes | 0.3 | 10.84 ± 0.59 | 91.1 ± 1.3 | 1000 ± 100 | |
| 0.6 | 2.42 ± 0.05a,b | 18.2 ± 0.2 | 290 ± 110 a | |||
| 0.8 | 1.40 ± 0.04 a,c | 8.4 ± 0.1a | 320 ± 40a | |||
| 1.0 | 1.52 ± 0.01b,c | 7.9 ± 0.2 a | 720 ± 30 | |||
| No | 0.3 | 10.74 ± 0.20 | 83.8 ± 3.5 | 770 ± 50 | ||
| 0.6 | 2.54 ± 0.03a | 18.2 ± 0.5a | 490 ± 10 | |||
| 0.8 | 1.53 ± 0.01 | 9.0 ± 0.2 b | 420 ± 40 | |||
| 1.0 | 2.82 ± 0.26a | 15.2 ± 1.3a,b | 1370 ± 520 | |||
| Model chocolate samples/30% | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
Yes | 0.3 | Not measurable | ||
| 0.6 | 10.90 ± 0.09 | 90.1 ± 0.8 | 1600 ± 350 | |||
| 0.8 | 4.32 ± 0.19 | 29.7 ± 1.0 | 730 ± 230 | |||
| 1.0 | 3.07 ± 0.14 | 17.6 ± 0.7 | 830 ± 100 | |||
| No | 0.3 | Not measurable | ||||
| 0.6 | 11.17 ± 0.19 | 82.0 ± 2.0 | 1580 ± 120 | |||
| 0.8 | 4.76 ± 0.02 a | 31.0 ± 0.0 a | 740 ± 50 | |||
| 1.0 | 6.50 ± 0.70a | 36.2 ± 4.5a | 490 ± 610 | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
Yes | 0.3 | Not measurable | |||
| 0.6 | 7.70 ± 0.24 | 59.5 ± 2.7 | 760 ± 240 | |||
| 0.8 | 4.09 ± 0.12 | 26.6 ± 0.4 | 1370 ± 80 | |||
| 1.0 | Not measurable | |||||
| No | 0.3 | Not measurable | ||||
| 0.6 | 7.84 ± 0.07 | 59.6 ± 1.0 | 590 ± 120 | |||
| 0.8 | 4.76 ± 0.08 | 30.7 ± 1.0 | 1890 ± 130 | |||
| 1.0 | Not measurable | |||||
| Model chocolate samples/28% | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
Yes | 0.3 | Not measurable | ||
| 0.6 | 16.68 ± 2.16 | 126.7 ± 15.4 | 4810 ± 980 | |||
| 0.8 | 6.68 ± 0.14a | 49.5 ± 0.7a | 740 ± 160 a | |||
| 1.0 | 4.83 ± 0.13 a | 27.8 ± 0.9 a | 2050 ± 200a | |||
| No | 0.3 | Not measurable | ||||
| 0.6 | 15.74 ± 2.62 | 95.0 ± 17.4 | 5910 ± 2900 | |||
| 0.8 | 7.29 ± 0.31 | 50.3 ± 2.9 | 960 ± 8 | |||
| 1.0 | Not measurable | |||||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
Yes | 0.3 | Not measurable | |||
| 0.6 | 12.21 ± 0.50 | 98.3 ± 1.1 | 2520 ± 300 | |||
| 0.8 | 6.09 ± 1.08 | 41.8 ± 1.1 | 2950 ± 80 | |||
| 1.0 | Not measurable | |||||
| No | 0.3 | Not measurable | ||||
| 0.6 | 12.66 ± 0.70 | 93.0 ± 2.7 | 2320 ± 150 | |||
| 0.8 | 7.30 ± 0.50 | 51.0 ± 5.0 | 1900 ± 500 | |||
| 1.0 | Not measurable | |||||
| Sugar model systems/28% | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
Yes | 0.3 | — | ||
| 0.6 | 4.00 ± 0.03a | 32.4 ± 0.6 | 220 ± 40 a | |||
| 0.8 | 3.80 ± 0.02 a | 26.8 ± 0.6 a | 650 ± 30a | |||
| 1.0 | 4.83 ± 0.13 | 27.8 ± 0.9a | 2050 ± 200 | |||
| No | 0.3 | — | ||||
| 0.6 | 12.20 ± 0.70 | 65.8 ± 2.5 | 1500 ± 530 | |||
| 0.8 | 7.59 ± 0.11 | 42.3 ± 2.6 | 1360 ± 420 | |||
| 1.0 | Not measurable | |||||
| Quartz beads model systems/28% | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
Yes | 0.3 | 6.83 ± 0.04 | 131.2 ± 2.4 | 70 ± 8a |
| 0.6 | 5.00 ± 0.10 | 108.5 ± 3.2 | −90 ± 30 | |||
| 0.8 | 4.26 ± 0.02 | 92.3 ± 0.14 | 10 ± 20a | |||
| 1.0 | 5.79 ± 0.04 | 76.4 ± 0.6 | 740 ± 40 | |||
| No | 0.3 | 9.69 ± 0.28 | 167.9 ± 0.7 | 90 ± 70a | ||
| 0.6 | 6.44 ± 0.21 a | 107.7 ± 1.1a | −300 ± 80 b | |||
| 0.8 | 6.72 ± 0.02a | 114.4 ± 3.5a | −50 ± 120a,b | |||
| 1.0 | 8.14 ± 0.06 | 96.2 ± 1.5 | 670 ± 50 | |||
Regarding the proportion of coarse fraction for which the lowest viscosity was obtained for the different sample types, we will first consider the samples without added lecithin. For the quartz beads systems with a particle shape close to perfect spheres and a fat content of 28%, viscosity was lowest at a proportion of coarse fraction of 0.6. For a larger proportion of fine or coarse quartz beads, the viscosity was higher, even though it should be noted that the difference in viscosity values was statistically not significant for the values obtained for a proportion of coarse fraction of 0.6 and 0.8. A minimum viscosity at a proportion of coarse fraction of 0.6 matches the predictions from theoretical calculations: for a bimodal mixture of spheres with a particle volume fraction of 0.64, the proportion of coarse fraction that leads to the highest value of φm, thus lowest viscosity, is 0.63 (see Table 1). This indicates that the quartz beads model systems prepared in this study behave close to an ideal suspension of spherical particles, for which viscosity is only affected by the value of φm.5
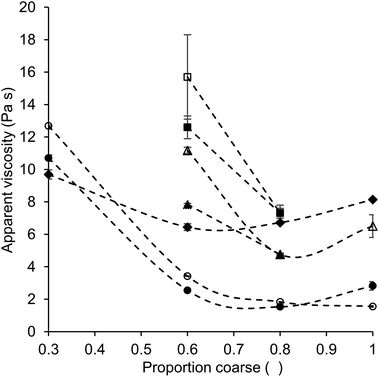
For the model chocolate samples (without lecithin), the influence of a variation of the proportion of coarse fraction on viscosity was generally similar to that observed for quartz beads systems. Also here, based on theory, the lowest viscosity would be expected for a proportion of coarse fraction of around 0.6 for samples with a fat content of 28%, and at even lower proportions of coarse fraction for samples with a higher fat content.13Fig. 3 shows the apparent viscosity versus the proportion of coarse particles for some of the different systems. It can be seen that also for model chocolate samples, the minimum viscosity is indeed mostly observed for a bimodal distribution of particles, following the from the Krieger–Dougherty equation (eqn (1)) expected effect of PSD on viscosity. However, in the model chocolate samples (without lecithin), the minimum viscosity was found at a proportion of coarse fraction of 0.8 instead of 0.6 for all sample sets, except for the samples with 36% fat and a particle size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. For these samples, the viscosity was lowest at a proportion of coarse fraction of 1. These results show that for suspensions of non-spherical particles like chocolate, also other factors, next to φm, had a noticeable effect on viscosity. One of these factors is the specific surface area (SSA), which influences the interactions between particles and therefore leads to deviations from the theoretical predictions based on particle packing and the Krieger–Dougherty equation. The influence of the SSA was visible in the different viscosity values for model chocolates containing either only a fine (cocoa) or only a coarse (sugar) fraction. In both cases, as only one fraction of a certain monomodal particle size was present, the PSD was narrow, which resulted in a comparably high value of φm. Therefore, according to the Krieger–Dougherty equation, in a system where viscosity is only determined by the value of φm, a comparably high viscosity would be expected for the samples, independently of the particle size. However, due to the influence of the SSA next to that of particle packing (φm), less particle–particle interactions and a lower viscosity were found for samples with only a coarse (monomodal) fraction, which had a lower SSA compared to samples with only a fine fraction (Table 4). This influence of the SSA on viscosity also explains the lowest viscosity values for a proportion of coarse particles of 1 for the model chocolate samples with a fat content of 36%. Especially at a high fat content, when the volume fraction of dispersed particles φ was not close to φm yet, the ability of the particles to pack well due to a more effective distribution of particle sizes, i.e. the value of φm, had a minor impact. Instead, viscosity was more determined by particle size. With an increasing particle size, i.e. an increasing proportion of coarse fraction, the SSA decreases, and less particle–particle interactions are present, leading to a viscosity reduction. Thus, the influence of SSA explains that the lowest viscosity values for chocolate samples were reached at a larger proportion of coarse particles as expected from theory on particle packing. However, the influence of the SSA is mainly important at high fat content and low particle size ratio, which is shown by the fact that for the samples with a fat content of 36% and a size ratio of 1
4. For these samples, the viscosity was lowest at a proportion of coarse fraction of 1. These results show that for suspensions of non-spherical particles like chocolate, also other factors, next to φm, had a noticeable effect on viscosity. One of these factors is the specific surface area (SSA), which influences the interactions between particles and therefore leads to deviations from the theoretical predictions based on particle packing and the Krieger–Dougherty equation. The influence of the SSA was visible in the different viscosity values for model chocolates containing either only a fine (cocoa) or only a coarse (sugar) fraction. In both cases, as only one fraction of a certain monomodal particle size was present, the PSD was narrow, which resulted in a comparably high value of φm. Therefore, according to the Krieger–Dougherty equation, in a system where viscosity is only determined by the value of φm, a comparably high viscosity would be expected for the samples, independently of the particle size. However, due to the influence of the SSA next to that of particle packing (φm), less particle–particle interactions and a lower viscosity were found for samples with only a coarse (monomodal) fraction, which had a lower SSA compared to samples with only a fine fraction (Table 4). This influence of the SSA on viscosity also explains the lowest viscosity values for a proportion of coarse particles of 1 for the model chocolate samples with a fat content of 36%. Especially at a high fat content, when the volume fraction of dispersed particles φ was not close to φm yet, the ability of the particles to pack well due to a more effective distribution of particle sizes, i.e. the value of φm, had a minor impact. Instead, viscosity was more determined by particle size. With an increasing particle size, i.e. an increasing proportion of coarse fraction, the SSA decreases, and less particle–particle interactions are present, leading to a viscosity reduction. Thus, the influence of SSA explains that the lowest viscosity values for chocolate samples were reached at a larger proportion of coarse particles as expected from theory on particle packing. However, the influence of the SSA is mainly important at high fat content and low particle size ratio, which is shown by the fact that for the samples with a fat content of 36% and a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, the minimum viscosity was found for a proportion of coarse fraction of 0.8 instead of 1. Mixing two differently sized fractions leads to a more pronounced increase of φm at a larger particle size ratio, as a large size difference between the two fractions facilitates the particle packing.11,17 Therefore, the proportion of coarse fraction has a larger effect on the viscosity at a larger particle size ratio, whereas the effect of SSA is less dominant.
6, the minimum viscosity was found for a proportion of coarse fraction of 0.8 instead of 1. Mixing two differently sized fractions leads to a more pronounced increase of φm at a larger particle size ratio, as a large size difference between the two fractions facilitates the particle packing.11,17 Therefore, the proportion of coarse fraction has a larger effect on the viscosity at a larger particle size ratio, whereas the effect of SSA is less dominant.
Next, we will consider the results obtained for model chocolates containing lecithin. Also here, the minimum viscosity was obtained for a proportion of coarse fraction of 0.8 or 1, and not the expected 0.6 based on theoretical predictions. For model chocolate samples with 36% fat, i.e. a relatively low volume fraction of dispersed particles, lecithin addition did not have a large influence on the viscosity, nor on the effect of the proportion of fine and coarse particles. However, in the case of model chocolate sample sets with 30 and 28% fat, i.e. a higher particle volume fraction, addition of lecithin showed a larger effect on viscosity and the optimum proportion of coarse particles. At a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
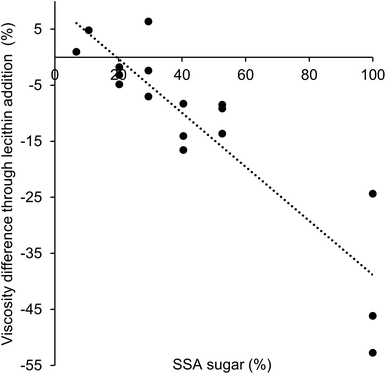
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, when no lecithin was present, the lowest viscosity was observed at a proportion of coarse fraction of 0.8. Instead, when lecithin was added, the lowest apparent viscosity was found for a proportion of coarse fraction of 1 (Table 5). This result is explained by differences in the effect of lecithin on viscosity depending on the particle type. As different particle types were used as fine and coarse fraction, i.e. cocoa and sugar, the interactions between the different particles will depend on the specific proportion. The sugar particles are more hydrophilic than the cocoa particles, and will therefore show higher particle–particle interactions in a hydrophobic environment. The amphiphilic lecithin will coat the particles, thereby decreasing the particle–particle interactions, and the largest decrease in viscosity is then expected for hydrophilic particles.2 Therefore, it is expected that the viscosity-decreasing effect of lecithin will be larger for samples with a larger proportion of sugar particles and a smaller proportion of cocoa particles. The extent of the viscosity reduction is thus mostly affected by sugar particle interactions, which depends on the sugar SSA. Fig. 4 shows the difference in viscosity as a function of the sugar SSA. A linear relation can be found between the difference in viscosity and the amount of sugar SSA in samples, and the highest viscosity reduction was indeed found for a larger proportion of sugar (high sugar SSA). This confirmed that lecithin had a more pronounced viscosity-decreasing effect for the sugar particles used as coarse fraction than for the cocoa particles providing the fine fraction. This effect of lecithin dominated the resulting viscosity of lecithin-containing model chocolates samples (with 30 and 28% fat and a size ratio of 1
4, when no lecithin was present, the lowest viscosity was observed at a proportion of coarse fraction of 0.8. Instead, when lecithin was added, the lowest apparent viscosity was found for a proportion of coarse fraction of 1 (Table 5). This result is explained by differences in the effect of lecithin on viscosity depending on the particle type. As different particle types were used as fine and coarse fraction, i.e. cocoa and sugar, the interactions between the different particles will depend on the specific proportion. The sugar particles are more hydrophilic than the cocoa particles, and will therefore show higher particle–particle interactions in a hydrophobic environment. The amphiphilic lecithin will coat the particles, thereby decreasing the particle–particle interactions, and the largest decrease in viscosity is then expected for hydrophilic particles.2 Therefore, it is expected that the viscosity-decreasing effect of lecithin will be larger for samples with a larger proportion of sugar particles and a smaller proportion of cocoa particles. The extent of the viscosity reduction is thus mostly affected by sugar particle interactions, which depends on the sugar SSA. Fig. 4 shows the difference in viscosity as a function of the sugar SSA. A linear relation can be found between the difference in viscosity and the amount of sugar SSA in samples, and the highest viscosity reduction was indeed found for a larger proportion of sugar (high sugar SSA). This confirmed that lecithin had a more pronounced viscosity-decreasing effect for the sugar particles used as coarse fraction than for the cocoa particles providing the fine fraction. This effect of lecithin dominated the resulting viscosity of lecithin-containing model chocolates samples (with 30 and 28% fat and a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4), whereas the effect of PSD was less important. Nevertheless, for samples with a size ratio of 1
4), whereas the effect of PSD was less important. Nevertheless, for samples with a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, a minimum viscosity was observed for a proportion of coarse fraction of 0.8, independently of the presence of lecithin. This again shows that the PSD has a more dominant effect on the viscosity at a larger size ratio (1
6, a minimum viscosity was observed for a proportion of coarse fraction of 0.8, independently of the presence of lecithin. This again shows that the PSD has a more dominant effect on the viscosity at a larger size ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 instead of 1
6 instead of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4), whereas additional effects next to the PSD, such as SSA and lecithin, are then less important in determining viscosity.
4), whereas additional effects next to the PSD, such as SSA and lecithin, are then less important in determining viscosity.
Also for the sugar model systems (size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 28% fat), i.e. samples containing only sugar particles in two different sizes, the minimum viscosity was found for a proportion of coarse fraction of 0.8, independently of the presence of lecithin (Table 5). In these samples the particle type did not change and therefore the effect of lecithin was not dependent on the proportion.
4, 28% fat), i.e. samples containing only sugar particles in two different sizes, the minimum viscosity was found for a proportion of coarse fraction of 0.8, independently of the presence of lecithin (Table 5). In these samples the particle type did not change and therefore the effect of lecithin was not dependent on the proportion.
Next to considering the optimal proportion of coarse and fine fraction to obtain a low viscosity, also conclusions regarding the impact of PSD variation on viscosity as a function of fat content can be drawn. In the case of a lower fat content, a variation of the proportion of coarse fraction had a more pronounced effect on viscosity, which is clear when comparing the slopes obtained for model chocolate samples with a proportion of coarse fraction of 0.6 and 0.8 (Fig. 3). For samples with a lower fat content (high particle volume fraction), the volume fraction of dispersed particles (φ) was closer to φm than in systems with a higher fat content (low particle volume fraction). Therefore, for a high particle volume fraction, PSD variations, i.e. variations of φm, had a stronger impact on viscosity (eqn (1)).
In conclusion, a variation of the PSD and the resulting changes in φm had a large effect on viscosity, as expected from the Krieger–Dougherty equation. However, for most model chocolate and sugar systems, the minimum viscosity was observed at a proportion of coarse fraction of 0.8, which deviated from theoretical predictions. This indicates that next to the PSD, also other parameters played a role in determining viscosity. These other parameters were linked to particle–particle interactions, since factors as the surface area (SSA) and lecithin addition influenced the viscosity of samples. For samples with low fat content or high particle size ratio (i.e. large difference between particle sizes), the PSD was the main important factor, whereas additional parameters next to the PSD were mainly important at high fat contents and a low particle size ratio (i.e. small difference between particle sizes).
3.2 Influence of particle size ratio on viscosity
For model chocolates, samples were obtained with two particle size ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6). Fig. 5 shows the change of apparent viscosity of model chocolate samples when the particle size ratio was increased from 1
6). Fig. 5 shows the change of apparent viscosity of model chocolate samples when the particle size ratio was increased from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to 1
4 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
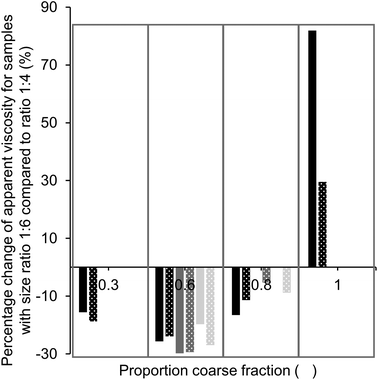
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, i.e., a more pronounced bimodal particle size distribution. For samples without as well as with lecithin, only values for samples with 36% fat (black bars) are given at a proportion of coarse particles of 0.3 and 1, as the viscosity could not be measured for samples with a lower fat content. In both cases, the largest viscosity decrease achieved by increasing the particle size ratio was found for a proportion of coarse fraction of 0.6, with viscosity reductions between 20 and 30%. Viscosity reductions can be explained by a higher value of φm due to the larger particle size ratio. At a proportion of coarse particles of 1, we see that the viscosity increased when the size ratio was increased. Theoretically, we expected that the value of φm and therefore also the viscosity would be the same for samples of both size ratios (d4,3 of medium and coarse sugar fraction 40.6 and 52.4 μm).11,17 This discrepancy may be explained by the difference in the PSD of the two sugar fractions; the coarse sugar fraction had a narrower PSD than the medium sugar fraction (Table 4). Such a narrow PSD would lead to a lower value of φm,11 and therefore a higher viscosity (eqn (1)).
6, i.e., a more pronounced bimodal particle size distribution. For samples without as well as with lecithin, only values for samples with 36% fat (black bars) are given at a proportion of coarse particles of 0.3 and 1, as the viscosity could not be measured for samples with a lower fat content. In both cases, the largest viscosity decrease achieved by increasing the particle size ratio was found for a proportion of coarse fraction of 0.6, with viscosity reductions between 20 and 30%. Viscosity reductions can be explained by a higher value of φm due to the larger particle size ratio. At a proportion of coarse particles of 1, we see that the viscosity increased when the size ratio was increased. Theoretically, we expected that the value of φm and therefore also the viscosity would be the same for samples of both size ratios (d4,3 of medium and coarse sugar fraction 40.6 and 52.4 μm).11,17 This discrepancy may be explained by the difference in the PSD of the two sugar fractions; the coarse sugar fraction had a narrower PSD than the medium sugar fraction (Table 4). Such a narrow PSD would lead to a lower value of φm,11 and therefore a higher viscosity (eqn (1)).
Based on theoretical predictions, we expected the viscosity reduction to be the highest for the sample with the highest value of φm,11,17i.e. at a proportion of coarse fraction of 0.6 (Table 1). Even though the viscosity was not the lowest at this proportion, the effect of an increased particle size ratio (from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to 1
4 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) was the largest at this proportion (Fig. 5), independent of the presence of lecithin. This indicates that samples with a proportion of coarse fraction of 0.6, with and without lecithin, have indeed the highest φm, which is in accordance with mathematical predictions for mixtures of spheres (Table 1). The discrepancy with the optimal proportion of coarse fraction for the lowest viscosity shows the importance of other factors that influence viscosity. These are, for example, the decreasing surface area (SSA) with an increasing amount of coarse particles and changing compositions regarding the particle type, which was, as discussed previously, especially relevant for the samples containing lecithin. To draw conclusions on the proportion of coarse fraction for which the highest value of φm is achieved, a comparison of the viscosity values of sample sets with different size ratios as shown in Fig. 5 is therefore more reliable than the determination of the minimum viscosity of samples with a changing proportion of coarse fraction.
6) was the largest at this proportion (Fig. 5), independent of the presence of lecithin. This indicates that samples with a proportion of coarse fraction of 0.6, with and without lecithin, have indeed the highest φm, which is in accordance with mathematical predictions for mixtures of spheres (Table 1). The discrepancy with the optimal proportion of coarse fraction for the lowest viscosity shows the importance of other factors that influence viscosity. These are, for example, the decreasing surface area (SSA) with an increasing amount of coarse particles and changing compositions regarding the particle type, which was, as discussed previously, especially relevant for the samples containing lecithin. To draw conclusions on the proportion of coarse fraction for which the highest value of φm is achieved, a comparison of the viscosity values of sample sets with different size ratios as shown in Fig. 5 is therefore more reliable than the determination of the minimum viscosity of samples with a changing proportion of coarse fraction.
3.3 Influence of particle properties on viscosity
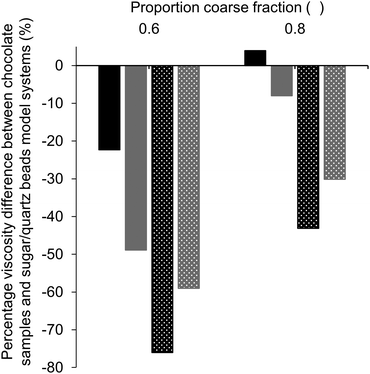
To investigate the influence of different particle properties, i.e. particle shape, surface roughness and hydrophilicity, viscosity values of model chocolate samples with 28% fat were compared to those of the model systems with sugar and quartz beads with the same fat content and comparable PSDs. For these samples, the d4,3 values varied by no more than 6.3%, and were therefore considered as similar enough to draw valid conclusions from comparisons (Table 4). Quartz beads model systems represented suspensions of spherical particles with a smooth surface, whereas chocolate samples and sugar model systems were suspensions of more randomly shaped particles. Fig. 6 shows the difference in percentage of apparent viscosity comparing the sugar model systems and quartz beads model systems with the respective model chocolate samples.We will first consider the comparisons of samples without lecithin (solid bars). The sugar model systems had a lower viscosity at a proportion of coarse fraction of 0.6 compared to the corresponding model chocolate samples. At a proportion of coarse fraction of 0.8, the sugar model systems had a slightly higher viscosity than the model chocolate systems. However, this difference was statistically not significant. Therefore, if no lecithin is present, sugar is assumed to have two counteracting effects: on the one hand, sugar particles have a lower SSA compared to cocoa particles due to a smoother surface, which leads to lower viscosity values due to less particle–particle interactions; on the other hand, compared to cocoa particles, sugar particles are more hydrophilic, which means that particles show a higher tendency to network formation, and therefore also have a viscosity-increasing effect, especially when present in larger amounts. Apparently, for a proportion of sugar particles of 0.6, the effect of a lower SSA is more relevant, whereas at a higher proportion of 0.8 increased particle interactions seem to become more important. The lower SSA could be explained with a smoother or more spherical surface of the particles. Considering the results obtained for the optimum proportion of coarse fraction for model chocolates, which was larger as expected from theory, it becomes apparent that the overall SSA determined viscosity more than the effect of an enhanced particle aggregation due to the hydrophilic nature of sugar. If the effect of aggregation of sugar particles would be dominant, viscosity would increase instead of decrease at larger proportions of coarse sugar fraction, and the optimum proportion of coarse fraction would be found at lower values as expected from theory. Quartz beads systems had the lowest viscosity of the three model systems, as quartz beads had a lower SSA (more spherical, smoother) in comparison to sugar and cocoa particles. Particles with a more spherical shape also lead to a higher value of φm and, therefore, a lower viscosity.11,27
When looking at samples with lecithin (patterned bars), the considerably lower viscosity of sugar model systems compared to that of model chocolate samples underlines the effect of lecithin on particle–particle interactions. For suspensions containing sugar particles, the viscosity-decreasing effect of lecithin was much larger than for suspensions containing cocoa particles. This was most likely due to the high hydrophilicity of sugar compared to the more hydrophobic nature of cocoa powder.2 Upon addition of lecithin, the strong sugar particle interactions were reduced due to the coating of the particles by lecithin. At a proportion of coarse particles of 0.8, the differences in composition of the compared model chocolate sample and sugar model system were generally smaller, as the chocolate sample contained less cocoa particles and more sugar particles than for a proportion of coarse fraction of 0.6. Therefore, also the differences in viscosity were smaller.
Comparing the sugar and quartz beads systems, the sugar systems had a lower viscosity than quartz beads systems when lecithin was present, whereas the quartz beads systems had a lower viscosity than the sugar systems when no lecithin was present. The larger effect of lecithin addition on sugar particles than on quartz beads could be due to several reasons: (i) interactions between sugar particles may be stronger due to their higher hydrophilicity, (ii) sugar model systems may have an overall larger SSA due to their irregular shape and less smooth surface, (iii) higher affinity of lecithin for the sugar particles than for quartz beads.
3.4 Influence of PSD on yield stress
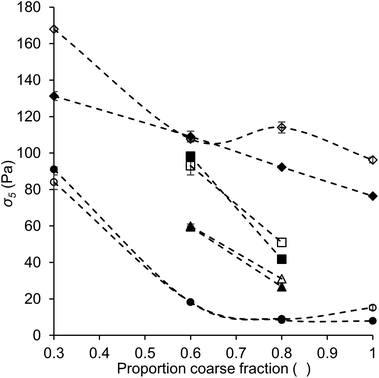
The yield stress plays an important role in several chocolate functionalities, for instance pattern holding, formation of feet and tails, and the incorporation of air bubbles.28 In this research, instead of determining the actual yield stress at zero shear rate, we used the value of the shear stress at a shear rate of 5 s−1 (σ5) as an alternative measure. The value of σ5 has proven to be more reproducible than the Casson yield value, which is often used for chocolate, due to the avoidance of data regression,22,23 and has been discussed to be a good representative for the yield stress.16,23,29 All values obtained are shown in Table 5.Fig. 7 shows the values of σ5 as a function of the proportion of coarse fraction for some samples. For the quartz beads model systems (diamonds), a clear relation between σ5 and an increasing proportion of coarse fraction was found. The yield stress, or in this case the stress at low shear rate, is known to depend on the number of contact points between particles and therefore is expected to correlate with the SSA, and therefore also with the proportion of coarse fraction.15 Such a relation between σ5 and the proportion of coarse fraction or SSA can indeed be seen for the quartz beads model systems. On the contrary, for sugar model systems (data not shown) and chocolate model samples (squares, triangles and circles), no clear relation between σ5 and the proportion of coarse fraction was observed. Instead, for these samples the dependence of σ5 on the proportion of coarse fraction followed the same trend as found for the dependence of the viscosity values on the proportion of coarse fraction.
These results indicate that for the quartz beads systems, the behaviour at low shear rate was dominated by the SSA, and therefore the degree of contact between the particles. In the case of the model chocolate samples, the SSA was not the dominating factor. Instead, the PSD and particle interaction (the effect of lecithin) played a more important role. The differences in the most dominating factor for quartz beads and chocolate samples is most likely related to the differences in morphology of the particles of the two systems: particles were close to perfect spheres in quartz beads model systems, and irregularly shaped in model chocolates (Fig. 1). For the quartz beads, therefore a clear correlation between particle size and surface area (i.e. contact points) exists. In the case of the cocoa particles, the determination of the exact SSA is more difficult. SSA is calculated assuming that the particles are spherical. In reality, the cocoa and sugar particles are irregularly shaped, and therefore the real SSA may not depend proportionally on the particle size. This may partially explain why no clear relationship is seen. Furthermore, for irregularly shaped particles the resulting contact area is not directly linked to the SSA or the size of the particles, but is also determined by various arrangements and spatial distribution. As the total surface area becomes less relevant, the impact of the PSD on σ5 for model chocolate samples at low shear becomes more important. These results show that for chocolate, the PSD is not only a relevant parameter to control viscosity, but also plays an important role in determining the shear stress at low shear rate. Considering the absolute values obtained for σ5, the values for quartz beads systems were mostly higher than those obtained for sugar and model chocolate samples with the same fat content, indicating more extensive particle aggregation. These results suggest that even though SSA and hydrophilicity of quartz beads were lower than those of sugar particles, particle interactions were stronger among quartz beads than among sugar particles. A possible explanation for the higher interactions between quartz beads is a difference in surface morphology. In the case of smoother surfaces, the probability for direct surface–surface contact is larger and adhesion forces therefore may be more pronounced.30–32 These results also indicate that a high yield stress does not necessarily lead to a high viscosity, as quartz beads systems give lower viscosity values than the other systems, as discussed in the previous section. Viscosity is not only determined by the interactions between the particles, but more by particle packing effects.
3.5 Influence of PSD on thixotropy
The thixotropy value is another parameter to characterize the properties of viscous materials. Thixotropy describes the time-dependent behaviour during shearing and provides information on the extent of structural breakdown in the sample. Table 5 shows the outcome for the determined thixotropy values, based on a comparison between the viscosity determined at increasing and decreasing shear rate. The values of thixotropy of quartz beads model systems were generally very low compared to model chocolate samples. This indicates that interactions between particles were stronger in quartz beads systems than in chocolate model samples, and therefore only little structure breakdown was observed. This is in accordance with the results obtained for the yield value; the yield value was generally higher for quartz beads than for model chocolate samples and sugar model systems. A possible reason for the stronger interactions in quartz beads systems is their smoother surface, which facilitates contact between particles, and also results in stronger adhesion forces.30–32 For some of the quartz beads systems, even negative values were obtained. This indicates a more effective network formation between the dispersed particles over time, which leads to an increase in the viscosity. A possible explanation is the formation of shear-induced aggregates due to the increased occurrence of particle collisions during shearing.33Even though for a considerable number of model chocolate samples the differences between thixotropy values within a sample set were statistically not significant, the results showed that fat content and PSD had an influence on thixotropy (Table 5). Lower thixotropy values were observed for samples with a higher fat content as well as for samples containing a mixture of two differently sized fractions, i.e. for samples with a higher value of φm. Low values indicate that the structure does not undergo a lot of structural changes or rearrangements. In this case, the lower thixotropy can be explained by a lower degree of network formation. When there is initially less structure, less structural breakdown is then observed during a measurement. For the chocolate samples, both a higher fat content and a higher value of φm lead to a lower extent of structure formation, as more of the continuous fat phase was available to ensure that particles were dispersed well. The obtained results show that a variation of the PSD and fat content has an influence on thixotropy values, yield values and viscosity, and that the interactions between particles and packing efficiency play a large role in determining different rheological parameters.
4. Conclusions
In this study, the influence of a bimodal particle size distribution (PSD) and particle size ratio on rheological properties of model chocolate samples was investigated. A bimodal PSD was obtained using cocoa powder as fine fraction and sugar as coarse fraction in different ratios. From the decreased viscosity values obtained for samples containing two fractions with particles of different size, we concluded that a bimodal PSD leads to a higher maximum packing fraction, and thus less contact between the particles. The largest effect was seen for a larger size difference between small and large particles, i.e. a more pronounced bimodal distribution, and thus an improved particle packing. This particle packing was mainly relevant for samples with a high particle volume fraction, i.e. a low fat content, and subsequent high viscosity. At lower particle volume fraction, the particle surface becomes more relevant: for a size ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, an increasing proportion of coarse sugar particles and subsequent decrease in particle surface area led to a decrease in viscosity. For such hydrophilic particles, addition of lecithin had a large effect on viscosity, as this decreased the interactions among the particles. These additional factors had an effect on the optimum proportion of coarse fraction, which was 0.8 in most model chocolate samples. This value increased further when the particle volume fraction was low and particles were of more similar size, as then the effects of surface area or lecithin addition were more important than the effect of particle packing. For spherical quartz beads, the optimum proportion of coarse particles was closer to 0.6, as predicted by theory. This shows that especially for suspensions of non-spherical particles like chocolate, next to the PSD, other factors such as particle shape, particle size ratio, surface roughness and hydrophilicity all contribute to changes in viscosity and other rheological parameters, such as yield stress and thixotropy. The obtained knowledge on how chocolate rheology can be changed by altering PSD, fat content and lecithin addition can be used to optimize the composition of chocolate samples with respect to the rheological properties and nutritional value.
4, an increasing proportion of coarse sugar particles and subsequent decrease in particle surface area led to a decrease in viscosity. For such hydrophilic particles, addition of lecithin had a large effect on viscosity, as this decreased the interactions among the particles. These additional factors had an effect on the optimum proportion of coarse fraction, which was 0.8 in most model chocolate samples. This value increased further when the particle volume fraction was low and particles were of more similar size, as then the effects of surface area or lecithin addition were more important than the effect of particle packing. For spherical quartz beads, the optimum proportion of coarse particles was closer to 0.6, as predicted by theory. This shows that especially for suspensions of non-spherical particles like chocolate, next to the PSD, other factors such as particle shape, particle size ratio, surface roughness and hydrophilicity all contribute to changes in viscosity and other rheological parameters, such as yield stress and thixotropy. The obtained knowledge on how chocolate rheology can be changed by altering PSD, fat content and lecithin addition can be used to optimize the composition of chocolate samples with respect to the rheological properties and nutritional value.
Conflicts of interest
There are no conflicts of interests to declare.References
- Statista, https://www.statista.com/statistics/819288/worldwide-chocolate-consumption-by-country/, (accessed October 2018).
- S. T. Beckett, Industrial chocolate manufacture and use, John Wiley & Sons, 2011 Search PubMed.
- S. F. Schakel, B. Jasthi, N. Van Heel and L. Harnack, Adjusting a nutrient database to improve calculation of percent calories from macronutrients, J. Food Compos. Anal., 2009, 22, S32–S36 CrossRef CAS.
- S. T. Beckett, The science of chocolate, Royal Society of Chemistry, 2018 Search PubMed.
- C. Servais, R. Jones and I. Roberts, The influence of particle size distribution on the processing of food, J. Food Eng., 2002, 51, 201–208 CrossRef.
- R. W. Hartel, H. Joachim and R. Hofberger, Confectionery science and technology, Springer, 2018 Search PubMed.
- E. V. Gonçalves and S. C. d. S. Lannes, Chocolate rheology, Food Sci. Technol., 2010, 30, 845–851 CrossRef.
- P. Walstra, Physical chemistry of foods, CRC Press, 2002 Search PubMed.
- J. G. Berryman, Random close packing of hard spheres and disks, Phys. Rev. A, 1983, 27, 1053 CrossRef CAS.
- K. W. Desmond and E. R. Weeks, Random close packing of disks and spheres in confined geometries, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051305 CrossRef.
- A. B. Metzner, Rheology of suspensions in polymeric liquids, J. Rheol., 1985, 29, 739–775 CrossRef CAS.
- R. K. McGeary, Mechanical packing of spherical particles, J. Am. Ceram. Soc., 1961, 44, 513–522 CrossRef CAS.
- R. J. Farris, Prediction of the viscosity of multimodal suspensions from unimodal viscosity data, Trans. Soc. Rheol., 1968, 12, 281–301 Search PubMed.
- S. Bolenz, M. Holm and C. Langkrär, Improving particle size distribution and flow properties of milk chocolate produced by ball mill and blending, Eur. Food Res. Technol., 2014, 238, 139–147 CrossRef CAS.
- G. Mongia and G. R. Ziegler, The role of particle size distribution of suspended solids in defining the flow properties of milk chocolate, Int. J. Food Prop., 2000, 3, 137–147 CrossRef CAS.
- T. A. Do, J. M. Hargreaves, B. Wolf, J. Hort and J. R. Mitchell, Impact of particle size distribution on rheological and textural properties of chocolate models with reduced fat content, J. Food Sci., 2007, 72, E541–E552 CrossRef CAS.
- J. Zheng, W. B. Carlson and J. S. Reed, The packing density of binary powder mixtures, J. Eur. Ceram. Soc., 1995, 15, 479–483 CrossRef CAS.
- Malvern Instruments., Ltd, Mastersizer, 3000 user manual, no. 2.1, 2013 Search PubMed.
- T. A. Do, J. Vieira, J. M. Hargreaves, J. R. Mitchell and B. Wolf, Structural characteristics of cocoa particles and their effect on the viscosity of reduced fat chocolate, LWT–Food Sci. Technol., 2011, 44, 1207–1211 CrossRef CAS.
- F. Cardarelli, Materials handbook: a concise desktop reference, Springer Science & Business Media, 2008 Search PubMed.
- H. Zhao, B. Li and B. J. James, Structure-fracture relationships in chocolate systems, LWT–Food Sci. Technol., 2018, 96, 281–287 CrossRef CAS.
- J. M. Aeschlimann and S. T. Beckett, International inter-laboratory trials to determine the factors affecting the measurement of chocolate viscosity, J. Texture Stud., 2000, 31, 541–576 CrossRef.
- C. Servais, H. Ranc and I. D. Roberts, Determination of chocolate viscosity, J. Texture Stud., 2003, 34, 467–497 CrossRef.
- E. O. Afoakwa, A. Paterson and M. Fowler, Effects of particle size distribution and composition on rheological properties of dark chocolate, Eur. Food Res. Technol., 2008, 226, 1259–1268 CrossRef CAS.
- M. Hinneh, D. Van de Walle, J. Haeck, E. E. Abotsi, A. De Winne, A. D. Saputro, K. Messens, J. Van Durme, E. O. Afoakwa and L. De Cooman, Applicability of the melanger for chocolate refining and Stephan mixer for conching as small-scale alternative chocolate production techniques, J. Food Eng., 2019, 253, 59–71 CrossRef CAS.
- V. Glicerina, F. Balestra, M. Dalla Rosa and S. Romani, Microstructural and rheological properties of white chocolate during processing, Food Bioprocess Technol., 2015, 8, 770–776 CrossRef CAS.
- S. Mueller, E. Llewellin and H. Mader, The effect of particle shape on suspension viscosity and implications for magmatic flows, Geophys. Res. Lett., 2011, 38, L13316 Search PubMed.
- E. S. Seguine, Casson plastic viscosity and yield value: What they are and what they mean to the confectioner, Manuf. Confect., 1988, 11, 57–63 Search PubMed.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Comparison of rheological models for determining dark chocolate viscosity, Int. J. Food Sci. Technol., 2009, 44, 162–167 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2011 Search PubMed.
- A. S. Moussa, M. Lattuada, B. N. O. Conchúir, A. Zaccone, M. Morbidelli and M. Soos, Flow-induced aggregation and breakup of particle clusters controlled by surface nanoroughness, Langmuir, 2013, 29, 14386–14395 CrossRef CAS.
- K. Kendall, Molecular adhesion and its applications: the sticky universe, Springer Science & Business Media, 2007 Search PubMed.
- J. Mewis and N. J. Wagner, Thixotropy, Adv. Colloid Interface Sci., 2009, 147, 214–227 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0fo01655a |
| This journal is © The Royal Society of Chemistry 2020 |