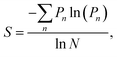Open Access Article
Open Access ArticleOptical costs and benefits of disorder in biological photonic crystals†
Sébastien R.
Mouchet
 ab,
Stephen
Luke
a,
Luke T.
McDonald‡
ab,
Stephen
Luke
a,
Luke T.
McDonald‡
 a and
Pete
Vukusic
*a
a and
Pete
Vukusic
*a
aSchool of Physics, University of Exeter, Physics Building, Stocker Road, Exeter EX4 4QL, UK. E-mail: P.Vukusic@exeter.ac.uk
bDepartment of Physics, Namur Institute of Structured Matter (NISM), University of Namur, Rue de Bruxelles 61, 5000 Namur, Belgium
First published on 9th September 2020
Abstract
Photonic structures in ordered, quasi-ordered or disordered forms have evolved across many different animal and plant systems. They can produce complex and often functional optical responses through coherent and incoherent scattering processes, often too, in combination with broadband or narrowband absorbing pigmentation. Interestingly, these systems appear highly tolerant of faults in their photonic structures, with imperfections in their structural order appearing not to impact, discernibly, the systems’ optical signatures. The extent to which any such biological system deviates from presenting perfect structural order can dictate the optical properties of that system and, thereby, the optical properties that system delivers. However, the nature and extent of the optical costs and benefits of imperfect order in biological systems demands further elucidation. Here, we identify the extent to which biological photonic systems are tolerant of defects and imperfections. Certainly, it is clear that often significant inherent variations in the photonic structures of these systems, for instance a relatively broad distribution of lattice constants, can consistently produce what appear to be effective visual appearances and optical performances. In this article, we review previously investigated biological photonic systems that present ordered, quasi-ordered or disordered structures. We discuss the form and nature of the optical behaviour of these structures, focusing particularly on the associated optical costs and benefits surrounding the extent to which their structures deviate from what might be considered ideal systems. Then, through detailed analyses of some well-known 1D and 2D structurally coloured systems, we analyse one of the common manifestations of imperfect order, namely, the extent and nature of positional disorder in the systems’ spatial distribution of layers and scattering centres. We use these findings to inform optical modelling that presents a quantitative and qualitative description of the optical costs and benefits of such positional disorder among ordered and quasi-ordered 1D and 2D photonic systems. As deviation from perfectly ordered structures invariably limits the performance of technology-oriented synthetic photonic processes, we suggest that the use of bio-inspired fault tolerance principles would add value to applied photonic technologies.
Introduction
Animal and plant colour appearances most often result from spectrally selective pigments or from what are commonly known as structural colour mechanisms or from a combination of these. Specifically, structural colours arise from the interaction of incident light with physical structures embedded in or on the system in question.1–4 They are invariably responsible for the brightest and most conspicuous colour appearances and can give rise to other interesting optical phenomena such as iridescence and polarisation-dependent reflectance. Such physical structures comprise elements possessing alternating higher and lower refractive indices on a scale commensurate with visible wavelengths (i.e., a few hundred nanometres). In some biological systems, these structures appear highly periodic, sometimes three-dimensionally, and in such cases, are referred to, or modelled as, photonic crystals. However, most frequently encountered in biological systems are thin films, multilayers, diffraction gratings, and quasi-ordered and disordered structures. Photonic structures have been identified as a common feature in diverse structurally coloured biological systems, some dating to more than 500 million years,2,4 for instance: in molluscs,5,6 in fish,7,8 in amphibians,9 in reptiles,10,11 in mammals,12 in birds,13–19 in arachnids,20–22 in insects,1,23–29 in bacterial colonies,30–34 and in plants.35–38Perfectly periodic photonic crystals are idealised structures. From a theoretical perspective, they should be periodic along either one, two or three dimensions and have an infinite size. In biological systems, photonic structures are neither perfectly ordered nor spatially very large. Many photonic structures appear highly periodic on first inspection, exhibiting what appear to be only small variations from a perfect lattice due to their physical morphology; such variations manifest via positional disorder, size disorder or shape disorder of the scattering elements, irregular interfaces or defects in the refractive index of the materials. Such imperfections have been ascribed to cellular noise during morphogenesis.39,40 For example, the long-studied butterflies from the Morpho genus, one of the archetypes for research related to structurally coloured insects,24,26,41,42 are known for their striking blue iridescent colours. These are produced by their wings, in which longitudinal ridges run parallel to the main axis of the upper lamina. The ridges comprise several lamellae, spaced such that they form effective multilayer reflectors that confer distinct periodic profiles to the (Christmas tree-like) cross-sections. Despite the appearance of strong periodic order in these structures, demonstrable structural irregularity and elements of disorder persist in variables associated with the ridge alignment, ridge heights and the lamellar period.43–48 The consequences of these relatively low measures of structural irregularity, or disorder, in Morpho typically translate to lower peak reflectance, broader spectral reflectance, a wider solid-angle in which light scattering takes place (namely, more diffuse reflectance) and a weakening of iridescence, the former two resulting visually in a less saturated colour appearance. Studies confirm that various degrees of disorder prevail, sometimes concurrently, among a range of biological systems.45,49–52
Unexpectedly, disordered structures can also enhance reflectance.53,54 One example is the silvery appearance of the skins of certain fishes, which is due to guanine platelets in the cytoplasm of cells called iridophores.53,55 These structures form multiple localised multilayer reflectors. In the case of two species in the family Trichiuridae, the thickness of each layer was described as random over a given interval, resulting in a so-called “chaotic” reflector displaying high reflectance in the visible spectrum.53 Another example lies in the epicuticular wax structures occurring on Tradescantia pallida “purpurea” leaves. They were shown to reflect incident light strongly at yellow wavelengths, thus producing a golden shine.56 Conversely, biological systems that actively enhance transparency have also been described. For instance, Greta spp. butterflies are known for their highly transparent non-scale-bearing wings.57,58 Surface structures described as close-packed thin pillars with cone-shaped pedestals cover the wing membranes. These cones are positioned in a quasi-ordered arrangement. Owing to an impedance matching mechanism between the wing material and the surrounding air, they suppress light reflection from the wings, acting as antireflectors. In the case of the G. oto butterfly, it was demonstrated that the random height distribution of these pillars helped to increase wing transparency irrespective of the observation angle.58
For the purposes of this work, we propose classifying biological structurally coloured systems, including those with black or white appearances, into three different regimes: (1) highly ordered photonic systems, (2) quasi-ordered photonic systems and (3) disordered photonic systems.
Strong coherent scattering by highly periodic photonic crystals gives rise to photonic bandgaps, i.e., wavelength ranges within which light cannot propagate through the system and is therefore strongly reflected.59–61 The extent to which light propagation is supported or inhibited is a function of several variables, such as the incident wavelength, the angles of incidence and observation, the number of periods and the refractive index contrast. In the absence of light absorption by the system, photonic crystals that have a sufficiently large number of periods and refractive index contrast can achieve 100% reflectance for wavelengths corresponding to the system bandgap.
Compared to perfectly ordered photonic structures, quasi-order is characterised by the partial absence of organisation in a system’s physical morphology. Examples in biological photonic systems include scattering elements or layers that are unimodal in size and interscatterer distance but exhibit a general lack of spatial organisation, as defined in Prum and co-workers’ seminal papers,13,14,62,63 but we also include among quasi-ordered systems those exhibiting spatial organisation with scattering elements that are not unimodal in size or whose nearest neighbour distances have a distribution of values rather than a single value. Optical coherent scattering from quasi-ordered structures can produce vivid colours if there is sufficient order; however, quasi-ordered structurally coloured systems tend to exhibit reduced or no discernible iridescence.13,14,62,63
On the other hand, the interaction of incident light with disordered structures gives rise to incoherent scattering. Systems comprising groups of scattering centres, for instance, particles with sizes comparable to visible incident wavelengths, scatter light indiscriminately, with the result that any colours produced are non-iridescent. In this size regime, Mie scattering theory predicts the response of spherical scatterers.64–66 Two well-known classical examples of Mie scattering are the white colours of clouds and snow. For non-spherical particles, no exact solutions can be calculated analytically using the T-matrix method.67 Scattering by particles smaller than the wavelength is predicted by Rayleigh scattering theory.68–70 Rayleigh scattering is recognised as the underlying mechanism explaining celestial colours, that is blue during the day, red-shifting at sunset or sunrise and the “green flash”.71 Recently, UV reflectance peaks from poultry eggshells were attributed to Mie backscattering caused by spherical pores.72
In addition, biological photonic systems are known to exhibit structural disorder at longer length scales, such as on the micrometric scale. This creates multilength-scale optical effects, such as additive colour mixing and the minimisation of iridescence. For instance, many arthropods, including butterflies and beetles, conventionally display structural colours that originate from intra-wing-scale structures that can exhibit various photonic structures at different length scales.1–4,29 Where they occur, elements associated with micrometric disorder often manifest as misalignment or disorientation within the arrays of juxtaposed scales,45,50,73 or as the close juxtaposition of differently oriented photonic crystal domains, lattice parameters or morphologies.36,50,74,75
Many aspects of disorder can be characterised using a statistical approach relying on measurements of physical features, for example: the distances between scattering centres, their sizes and shapes (e.g., number of sides or ellipticity), or their orientations, radial distribution functions or structure factors.32,52–54,76–78 In this paper, we suggest that the distributions of these measured quantities represent a useful measure of the extent of a system’s disorder. For some systems, a measure of structural entropy has been defined.51,79 For instance, in the cases of the Chrysina gloriosa79 and Eupholus magnificus51 beetles, optical and electron micrographs were used to characterise the extent of polygonal order. To this end, the number of nearest neighbours of each lattice point was analysed using a method suited to structural pattern analysis, namely, Voronoi diagrams.80,81 This approach divides the micrographs into polygons, called “cells”. Thus, the structural entropy S was defined as
Given the myriad factors involved in, and variables associated with, the formation and growth of biological material, imperfect structural order in systems adapted for optical purposes is understandable if not inevitable. However, it may be more than a by-product of morphogenetic processes. There is strong evidence to suggest that specific forms of quasi-order may have evolved through natural selection to perform distinct functional roles, such as in inter- or intra-specific visual communication. For example, Prum et al. have described non-iridescent structurally coloured caruncles, comprising quasi-ordered photonic structures, in phylogenetically distinct bird species, indicating multiple instances of independent evolution.63 Moreover, Moyroud et al. posited that the extent of disorder in the optical structures among the petals of angiosperms demonstrates convergent evolution.77 They reported structures comprising parallel striations in the cuticle on the epidermis of the petal, which diffract light and lead to directional scattering in the UV and blue wavelength regions. In this case, the quasi-order is associated with the size and the spacing of the striations within single organs, and was shown to contribute significantly to the diffraction effect, thereby enhancing pollinator signalling.
Despite significant progress over three decades in the understanding and fabrication of synthetic photonic crystals,83–86 imperfections and defects still remain critical limiting factors for many technological applications in photonics. In manufactured photonic structures, imperfections and variations in the size or shape of scattering centres, or in their positional order, arising from limitations of the fabrication processes, are unwanted occurrences as defect-induced optical scattering often reduces the performance efficiency of photonic devices.
We propose that naturally evolved photonic systems can provide valuable insights into the optical costs and benefits of deviating from perfectly periodic photonic structures. Crucially, one specific and particularly interesting feature associated with biological photonic structures is their tolerance to morphological imperfections and unintended imperfect order, as evidenced by their functional optical adaptations. This ascribed tolerance lends increased resilience to their related functional optical effects which, arguably, are thereby cheaper to deliver. Invariably, despite systems’ major photonic defects and deviation away from perfect periodicity, the visual appearances of structurally coloured biological systems and their related adapted functions are reproduced effectively by all but the most outlying specimens of a given species. This tolerance to faults or imperfect structural periodicity is, we suggest, particularly valuable from the perspective of applied bioinspired technologies. Therefore, biological photonic structures have the potential to form a basis for enhancing the resilience of manufacturability of future applications and devices. An example of this relates to optical anti-counterfeiting devices.87
This article reviews some key examples of natural photonic structures that exhibit various extents of quasi-order and disorder. Furthermore, we use analyses of 1D and 2D photonic crystal structures to inform optical modelling with the intention of providing a platform to evaluate the optical costs and benefits of positional disorder among ordered and quasi-ordered structures.
Ordered gyroids in butterfly scale bodies
Butterfly species including Callophrys rubi,88–93Parides sesostris,90,94–96Teinopalpus imperialis,90,96,97Cyanophrys remus,74,76,90Callophrys gryneus (formerly known as Mitoura gryneus),90,95,96Callophrys dumetorum,90,95,96Cyanophrys herodotus96 and Thecla opisena98 exhibit complex 3D photonic crystal structures incorporated within the lumens of scales covering regions of their wings (Fig. 1). These structures have been modelled as single gyroid structures with different filling fractions and lattice parameters.90,96 Gyroids are intricate structures divided into two regions that are complexly interlaced and separated by a bicontinuous triply periodic minimal surface. Mathematically, the surface defining a gyroid can be described by the function:F(X, Y, Z) = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y + sin Y + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z + cos Z + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z = t, Z = t, |
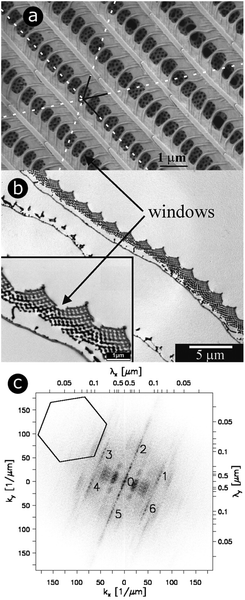 | ||
| Fig. 1 For scales covering the dorsal wings of Cyanophrys remus, scale lumens comprise gyroid photonic structures that give rise to regular patterns in 2D-FFT analysis. Both SEM (a) and TEM (b) observations (of the top view and a cross-section, respectively) reveal the presence of ridges separated by cross-ribs in the upper lamina of the scale. Visible through the windows, formed by the ridges and cross-ribs, are highly ordered photonic structures (seen here as a hexagonal lattice of small holes) that were demonstrated to be gyroid structures. Different periodic patterns can be observed: (1) parallel ridges; (2) parallel rows of windows and (3) hollow pattern in the gyroid structure. The dotted white lines correspond to the axes of the hexagonal lattice of small holes. A 2D-FFT of the SEM image of the top view exhibits a regular pattern (c). White relates to null intensity and black to maximal intensity. A line of peaks forming a 23° angle with the vertical direction passes through (0 μm−1, 0 μm−1). These peaks are separated by a distance Δk = 3.64 μm−1 and correspond to the parallel ridges (interspacing of 1726 nm angled at 23° with respect to the horizontal direction). 11.01 μm−1 from these aligned peaks (to the left and the right), two strong blurred parallel lines of peaks are observed. These correspond to the windows (interspacing of 566 nm). The blurring is due to the lack of uniformity in the size of these windows. Two more blurred lines of second-harmonic peaks are also observed. The numbers 0 to 6 highlight the peaks of a hexagonal lattice of small holes observed from the gyroid structure. The pattern is symmetrical. The 35.9 μm−1 distance between 1–6 and 0 corresponds to the 175 nm spacing of adjacent holes. The central line 0 is repeated 6 times along the hexagonal lattice with no apparent additional blurring. This means the hexagonal lattice has long-range order and is coherent. Reproduced from ref. 74, with permission from the American Physical Society (APS). | ||
Order and quasi-order in beetle scale bodies
The bodies and elytra of many weevils and longhorn beetles are adorned with scales, showcasing a multifarious colour palette adapted for diverse environmental pressures. Numerous weevils, including Pachyrrhynchus congestus pavonius,99,100Lamprocyphus augustus,101,102Entimus imperialis,75,103–107Eupholus cuvieri,108Eupholus magnificus51 and Phyllobius/Polydrusus sp.,109 exhibit ordered photonic crystal structures (Fig. 2). As with the gyroid morphology discussed in the previous section, these structures have also been described as two interlaced regions divided by a bicontinuous triply periodic minimal surface. However, this surface has been characterised as a diamond structure,90,104,105 the mathematical representation of which isF(X, Y, Z) = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(X + Y) + sin sin(X + Y) + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(X − Y) = t. cos(X − Y) = t. |
 | ||
| Fig. 2 The matt green non-iridescent colour in the elytral pits of the E. imperialis weevil (a) is due to scales displaying brilliant colours ranging from blue to orange (b and c). Complex triply periodic bicontinuous networks exhibiting diamond symmetry are found within these scales (d). The juxtaposition of several domains with different crystallographic orientations contributes to additive colour mixing by a multilength-scale effect. Reproduced from ref. 75. | ||
Typically, such biological photonic structures exhibit high periodicity and regularity (Fig. 2d, 3a and b), which is confirmed by 2D-FFTs of their electron micrographs, as shown here for the yellow-green scales of E. magnificus (Fig. 3c). The spatial distribution of the intensity spots in the 2D-FFT image (Fig. 3c) can be associated with an element of positional disorder. Furthermore, similar to the gyroid structures identified in several of the aforementioned butterflies (e.g., P. sesostris, C. rubi or C. remus), many weevils have intra-scale juxtaposed domains with different crystallographic orientations that lead to additive colour mixing (Fig. 2).75,105,106 This effect is particularly striking for E. imperialis, whose crystal domains are large enough to be resolved (just) by the naked eye. Consequently, the elytral pits in which the weevil’s vividly coloured scales are concentrated display a distinctive pointillistic appearance. The non-iridescent matt green colour of this weevil arises from the additive, and thereby averaging, effect of combining many brilliantly coloured photonic domains, ranging from blue to orange, with typical lengths of 30 μm and intra-domain periodicities of approximately 200 nm.
 | ||
| Fig. 3 E. magnificus weevils exhibit bands of yellow-green (a and b) and blue (d and e) scales on their elytra. In the yellow-green scales, a highly ordered 3D photonic structure is observed in each domain (a and b). This structure is modelled by a triply periodic bicontinuous network with a diamond symmetry. The 2D-FFT of an SEM image from a single domain (c) yields a pattern with a hexagonal symmetry. Black relates to null intensity and white to maximal intensity. By contrast, the blue scales contain a quasi-ordered structure (d and e). For these scales, the 2D-FFT of an SEM image generates a complex pattern (f). Two main components are observed: (1) a diffuse disk, which is a sign of long-range disorder due to several length-scale spatial frequencies, and (2) 12 intense peaks positioned at the edge of the disk, corresponding to a shorter range spatial frequency. The annulus formed by these peaks indicates spatial isotropy and is a signature of quasi-order. Scale bars represent 10 μm (a and d) and 2 μm (b and e). Reproduced from ref. 51, with permission from the Optical Society of America (OSA). | ||
Interestingly, in addition to lateral bands of yellow-green scales, E. magnificus also displays lateral bands of blue scales spanning its elytra. In direct contrast to the highly ordered photonic structures in the scales from the yellow-green regions, the colour of the blue scales is produced by quasi-ordered structures (Fig. 3d and e). A 2D-FFT of an electron micrograph of these structures produces an intensity pattern (Fig. 3f) that reveals their quasi-order.
Other structures in beetle scales have also been identified, including gyroids, close-packed spheres, perforated multilayers and inverse columns.28,52,110–115 These structures also exhibit various ranges of disorder. For instance, Bermúdez-Ureña et al. highlighted the presence of various extents of disorder in structurally coloured scales of the Sulawesiella rafaelae longhorn beetle.52 This beetle displays green, orange and turquoise hues due to perforated multilayer structures (Fig. 4A–C). Differing distributions in the layer orientations give rise to variable iridescence and scattering properties (Fig. 4D–F). The authors also calculated 2D-FFTs of scanning electron microscopy (SEM) images of scale cross-sections (insets in Fig. 4D–F). The green scales, with the narrowest layer orientation distribution, correspond to a 2D-FFT of a highly ordered system, with small spots of high intensity that are symmetrically distributed. The most disordered structure, namely the one occurring in the turquoise scales, gives rise to a distinct annulus in the 2D-FFT image, which is the signature of quasi-order. The quasi-order in these scales results in diminished iridescence.52
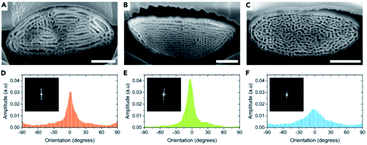 | ||
| Fig. 4 The Sulawesiella rafaelae longhorn beetle displays orange (A and D), green (B and E) and turquoise (C and F) coloured areas due to perforated multilayer structures embedded in the scales covering the beetle elytra. Based on SEM images of the scale cross-sections (A–C), variable distributions in the layer orientations (D–F) were measured and 2D-FFT analyses were performed (insets in D–F). The different extents of disorder in these scales give rise to various iridescence and scattering properties. Scale bars: 2 μm (A–C). Reproduced from ref. 52, License CC-BY-NC-ND. | ||
Local variations in structurally ordered scales
Male Argyrophorus argenteus butterflies display broadband silver-coloured wings (Fig. 5a). This colour arises from scales, the upper lamina of which exhibits a symmetric sawtooth profile whereas the basal lamina is approximately flat116 (Fig. 5b and c). This morphology gives rise to elongated air gaps, akin to corridors, under the ridges. Because of continual thickness variations in the gap and upper lamina thickness, the scales appear brilliantly multi-coloured when viewed under an optical microscopy. Macroscopically, from a distance, these closely juxtaposed multi-coloured bands combine additively to form a silver appearance that, owing to the extensive localised structural variations, is remarkably diffuse. Arguably, the structural colour principles underpinning this broadband colour reflection effect might loosely be considered to include aspects of disorder. Conversely, the system could equally be described as being based on the organised incorporation of a range of periodicities.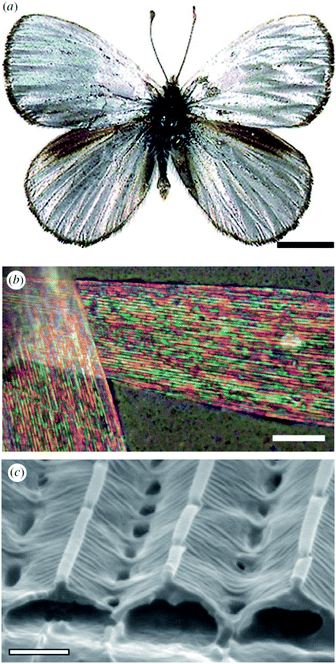 | ||
| Fig. 5 The silver colouration of the wings of male A. argenteus butterflies (a) is due to an additive colour mixing process arising from multiply coloured bands (b). Variations in the lamina thickness of the air gaps (c) are responsible for this range of microscopic colours. Scale bars: 0.5 cm (a), 15 μm (b) and 0.8 μm (c). Reproduced from ref. 116. | ||
In other systems, localised curvatures of the scattering structures may also be a source of disorder. For instance, the blue colour of Maratus nigromaculatus peacock spiders73 arises from ultra-dense diffraction gratings covering the scales. In addition to disorder in the arrangement of scales, local microscopic disorder was observed in the grating period due to the scale curvature.
Quasi-ordered photonic structures in damselflies
In the late 1990s and early 2000s, structural colours produced by coherent scattering were attributed to the quasi-ordered structures of many natural organisms, including bird caruncles,62,63 bird feathers,13,14,117–125 mammalian derma,12 dragonflies and damselflies.126,127 These structures have diverse morphologies that include twisted channels and amorphous packing arrangements of spheres or fibres. In the case of bird feathers, they are believed to form by self-assembly, through phase separation of β-keratin from cytoplasm in medullary cells.119Prior to these studies, Tyndall and Rayleigh scattering, which are incoherent scattering processes, were believed to be the underlying cause behind the colours of these integumentary structures. For instance, in the case of the blue-coloured familiar bluet damselfly, Enallagma civile, spherical nanostructures are embedded within living epidermal cells lying below the cuticle (Fig. 6a).126 These spheres are closely packed in the endoplasmic reticulum of these cells. 2D-FFT analysis of transmission electron microscopy (TEM) images of these spheres gives rise to annuli at intermediate spatial frequencies (Fig. 6b). This 2D-FFT pattern implies that the spherical scattering elements are not spatially disordered but quasi-ordered, with unimodal and isotropic distributions of sphere size and spacing. Any scattering occurring within these integuments must therefore be coherent. However, as the system is quasi-ordered rather than ordered, the associated structural colour of the damselfly is not iridescent.
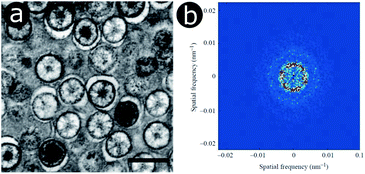 | ||
| Fig. 6 Within the epidermal cells lying below the cuticle of the Enallagma civile damselfly, light scattering spheres are found in the endoplasmic reticulum, as observed here by TEM (a). The 2D-FFT of a TEM image exhibits ring-shaped patterns of the Fourier power (b) corresponding to a dominant periodicity at intermediate spatial frequencies along all directions. Scale bar: 500 nm (a). Reproduced from ref. 126, with permission from The Company of Biologists. | ||
Whereas examples of natural angle-independent blue and green colours due to such quasi-ordered structures are common, their red counterparts are conspicuously rare. This can be explained by the tendency of these close-packed particles to backscatter light more strongly in the blue wavelength range.128 Using Ewald sphere construction, Maiwald et al. demonstrated that natural quasi-ordered photonic structures are particularly well suited for light scattering at shorter blue and green wavelengths but much less so for longer red wavelengths.82 Using FDTD simulations, it was later suggested that high red colour purity and saturation cannot be produced by such quasi-ordered structures.129
Biological quasi-ordered structures have inspired the development of fabricated systems that hope to replicate the non-iridescent structural colours of their biological counterparts. In general, these bioinspired structures are synthesised through the self-assembly of colloidal spheres.130–132
White colours due to highly disordered structures in insect wings
Highly disordered photonic structures occur in the integumentary ultrastructures of several insects, including the scales of certain butterflies,133–136 longhorn137 and scarab beetles,138–140 as well as the wings of some damselflies.141 In terms of appearance, disordered structures are typically manifested as matt white colours. Examples include the scales of Pontia protodice, Pieris rapae and Delias nigrina butterflies, where ovoid-shaped pterin beads are located between the longitudinal parallel ridges and the cross-ribs that interconnect these ridges (Fig. 7).133–136 These pterin bead scattering centres appear randomly distributed and have sizes of the order of a few hundred nanometres. They scatter incident white light diffusely, resulting in a bright white colour appearance. The reflectance intensity is determined by the density of scattering centres.133,135,136 Additional pigments can be incorporated alongside these ovoid pterin beads. This is the case for male P. rapae, the scales of which also comprise xanthopterin and leucopterin.142 | ||
| Fig. 7 Randomly disordered granules acting as scatterers in the scales of male Pontia protodice dorsal wings. Scale bar: 1 μm. Reproduced from ref. 135. | ||
In contrast, the diffuse white colours of the longhorn beetle Calothyrza margaritifera137 and the scarab beetles Cyphochilus sp. and Lepidiota stigma138,139 originate purely from incoherent light scattering by highly disordered networks of chitin beads or fibrils (Fig. 8), respectively. The structural anisotropy in the optical systems of Cyphochilus sp. and L. stigma enhances the brightness through increased out-of-plane scattering.138–140,143 Moreover, this evolutionarily optimised scattering has drawn interest for paper coating technologies through a bioinspiration approach.144 Other longhorn beetles, such as Celosterna pollinosa sulfurea, Phosphorus virescens and Trictenotoma childreni, also combine disordered structures with yellow and fluorescent pigments in order to produce a range of yellow hues.145,146
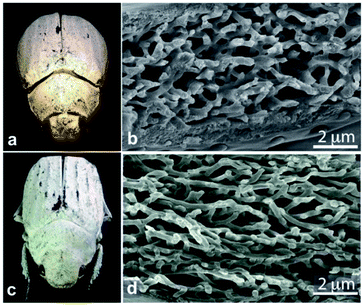 | ||
| Fig. 8 Chitin fibrils in the scales of Cyphochilus sp. and Lepidiota stigma scarab beetles (a and c) result in white colour appearances. SEM observations of scale cross-sections enable observation of the structural anisotropy exhibited by the fibrils (b and d). This anisotropy was shown to enhance scale brightness. Reproduced from ref. 139, License CC-BY. | ||
Positional disorder in periodic multilayer structures
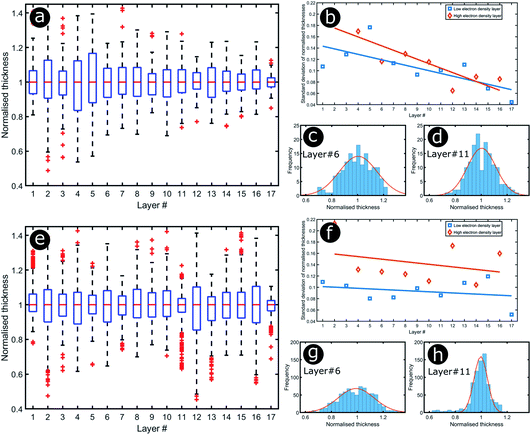
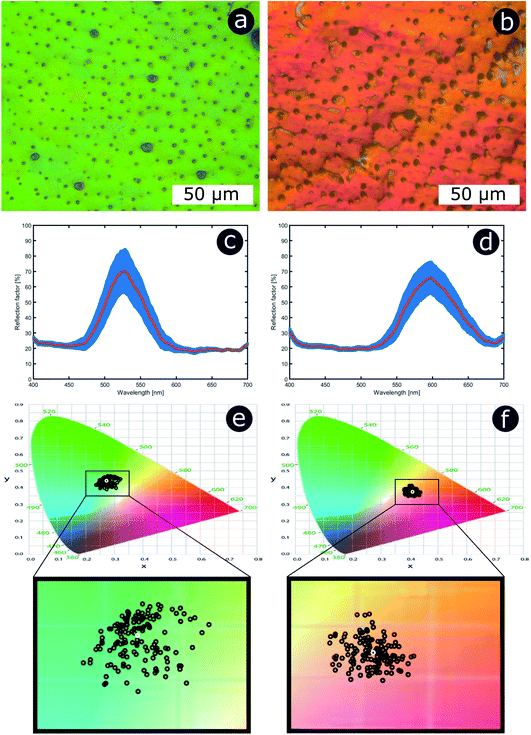
Significant interest lies in understanding the prevalence and extent of structural disorder in highly adapted biological systems whose functions include the generation of colour appearances and the general control of colour and light flow. To this end, we undertook an analysis of such disorder, its effects and the optical costs and benefits with which it is associated.Structural colour effects in beetles belonging to the genus Chrysochroa, for example, C. rajah,147,148C. fulgidissima,149–153C. vittata154–156 and C. fulminans,148 have been studied extensively and are well established. As with many buprestid beetles, the species of the Chrysochroa genus typically have a shiny iridescent metallic-coloured carapace, which is predominantly green but is often augmented by stripes that range from violet to red. All relevant studies showed that the colours are the result of periodic multilayers embedded within the topmost few micrometres of the exocuticles.147–156 In the case of C. rajah, each elytron is highly iridescent green with a single orange or red stripe147 (Fig. 9). The variation in the thickness of each layer comprising the elytral colour-generating multilayer structures, as observed by TEM, was analysed statistically (see Materials and methods section). This variation may be described as one type of positional disorder. In TEM images, these multilayers appear as repetitions of electron-dense and electron-lucent layers (Fig. 9c and d). As reported in previous publications, multilayers comprising up to a total of twenty layers are typical; Noyes et al. reported nine electron-lucent layers and eight electron-dense layers for both the green and orange areas in C. rajah (Fig. 9 and 10). Greyscale contrast in TEM images is a proxy for contrast in electron density across the TEM section and results from the differential uptake of heavy metal staining in the preparation process. It has been closely associated with the presence of melanin-rich regions in structurally coloured biological samples.157 Hence, TEM greyscale contrast is a proxy for the refractive index contrast that underpins a system’s optical properties. For the purposes of this narrative, we describe the positional disorder in C. rajah’s layers as that corresponding to the variation in layer thickness (Fig. 9c and d) across each single layer within the TEM image width. For this analysis, the thicknesses of the 17 layers in our sample were measured from TEM images of the multilayer cross-sections. In total, we obtained N = 152 sample profiles from the C. rajah green region and N = 771 sample profiles from the C. rajah orange region. Each profile comprised adjacent positions over widths of approximately 300 nm and 1000 nm, respectively. For this positional disorder analysis, each measured layer thickness was normalised with respect to the median value of each layer, which is common practice where it is useful to compare similar distributions.158 The extent of variation, or disorder, in the thickness of each individual layer was assessed via the distribution of these normalised layer thicknesses (Fig. 10, S1 and S2, ESI†) using conventional box and whisker plots of the normalised thickness distributions (Fig. 10a and e). The layer-by-layer thickness distribution comparison (Fig. 10) provides a visual measure of disorder for systems generally described as archetypal well-ordered multilayers. The two colour regions of C. rajah appear to comprise multilayers that exhibit similar variations in thickness, i.e., the thicknesses of each of their layers are similarly disordered. In general, this disorder decreases with depth below the surface, especially in the case of the green elytral region (Fig. 10b and f). The elytral lamellar structure of the beetle cuticle develops from the epithelium during morphogenesis, starting with the outermost layers.159–161 During the overlaying process, it is possible that disorder decreases as a result of the metabolic formation of the epithelium and mechanical constraints arising from the previously developed layers. Fig. 10 also shows that the extent of disorder tends to be larger for the electron-dense layers (Fig. 10b and f), especially for the orange coloured elytral region. We suggest that the variations in layer thicknesses, exemplified by the positional disorder illustrated in Fig. 10, underpin the variations in the colour appearance observed in both the green and orange regions of the elytra of C. rajah (Fig. 11). In optical micrographs featuring areas typically several hundred microns wide, such as those in Fig. 11a and b, a range of hues are observed (greens and yellows in Fig. 11a; reds, oranges, yellows and greens in Fig. 11b). Macroscopically, these juxtaposed colours combine additively for a homogeneous mono-coloured, albeit iridescent, appearance.106,157,162 Reflected light from both surface regions was quantified by microspectrophotometry (Fig. 11c–f). Normal incidence reflectance spectra, measured as intensity normalised with respect to a white reflectance standard, were collected from a large number of different spots (N = 150 per region) with a size of approximately 0.3 mm2, and from elytral positions separated by at least 0.7 mm. These spectra, and their variation, were compared (Fig. 11c–f). Specifically, at the two reflectance maxima, located at 527 nm and 597 nm for the green and orange regions, respectively, the standard deviations describing the variation in normalised intensity between the sampled spots were 15% (for the elytral green region; N = 150) and 11% (for the orange elytral region; N = 150) (Fig. 11c and d). Each of these 300 experimental spectra are represented by black coloured data points on the CIE diagrams (Fig. 11e and f); the white circles represent the mean of each series of spectra. Unsurprisingly, the experimentally measured CIE coordinates of the reflected colours from the beetle elytra are well distributed around the mean colour coordinates for both the green and the orange regions. Although the width of the detection spots from which the optical measurements were collected was larger than the widths of the TEM images from which the disorder in layer thicknesses was analysed (Fig. 9), we suggest that positional disorder in the layer thicknesses contributes directly to the variation of colours observed by optical microscopy and microspectrophotometry.
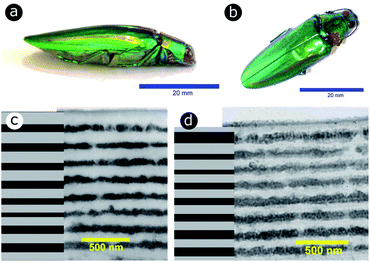 | ||
| Fig. 9 The elytra of C. rajah are iridescent green with orange stripes (a and b).147 These colours are produced by multilayer structures embedded within the exocuticle of the beetle. The multilayer structure was investigated using TEM for both the orange (c) and green (d) regions of the elytra. Reproduced from ref. 147, with permission from the Optical Society of America (OSA). | ||
In order to model the theoretical variation in the optical response that arises from positional disorder in multilayer systems like these, the reflectance, transmittance and absorption spectra were calculated (Fig. 12a–d) at normal incidence for a system based on the structure of C. rajah (using the formulation of Noyes et al.147). To incorporate layer-thickness disorder into these models and investigate the associated optical effects, the layer thicknesses were generated as follows. The refractive indices of both electron-dense and electron-lucent layers were set using values reported in the literature for Chrysochroa spp. multilayer systems, namely n = 1.68 + 0.03i for electron-dense layers and n = 1.55 + 0.14i for electron-lucent layers.147 Positional disorder was introduced into the model by increasing or decreasing individual layer thicknesses in the system from their starting values of 92 nm and 60 nm for the high and low refractive index layers, respectively.147 The thickness of each layer in each computed model was increased or decreased by an arbitrary value, the random choice of which was dictated by the full width at half maximum (FWHM) of an associated normal distribution of layer thicknesses for the model Chrysochroa spp. system. Thus, the extent of disorder applied to each modelled system was controlled by the variable representing the FWHM, with FWHM = 0 nm corresponding to a perfectly ordered multilayer, with alternating layer thicknesses of 92 nm and 60 nm. For each chosen FWHM value (representing systems with lower or higher thickness disorder) 100 structure models were generated. The spectra for all 100 simulations for each chosen FWHM value were analysed by calculating their mean spectral intensities and their associated standard deviations. This data is shown in Fig. 12. Perhaps surprisingly, Fig. 12 demonstrates that as the FWHM increases (i.e., the disorder in the layer thicknesses increases), the peak reflectance intensity and wavelength position, as well as the signal-to-background intensity ratio, do not change significantly for FWHM values below ca. 15 nm. This is interesting from the perspective of the system’s optical tolerance to the applied disorder in layer thickness. Above this FWHM-based disorder threshold, the peak intensity of the mean reflectance decreases and the standard deviation of the intensity variation increases, especially at the foot of the mean reflectance peak. These features, arguably indicators of ‘poor’ optical performance, are the direct result of more significant variation in the peak reflectance wavelength position among each set of 100 simulated spectra. This arises from increased disorder in the layer thicknesses. In the CIE diagrams (Fig. S3, ESI†), the predicted colours become more widely distributed with increased values of FWHM. For FWHM values exceeding ca. 25 nm, the colour desaturation of the mean reflectance spectra is particularly evident. These results indicate the extent to which simple multilayers are resistant to, or tolerant of, layer thickness disorder. In the case of C. rajah’s multilayers, the layers exhibited standard deviations of the normalised thickness distribution ranging from 4% to 22% of their median values (Fig. 10). For the C. rajah structure model (Fig. 12), a normalised standard deviation of 4% corresponds to a FWHM of ca. 5 nm, whereas a normalised standard deviation of 22% corresponds to FWHM of ca. 20 nm and ca. 30 nm for the low and high refractive index layers, respectively. Hence we infer that the multilayers in C. rajah combine highly ordered and relatively disordered layers. However, most layer thicknesses in the C. rajah exocuticle have a standard deviation of about 12%, which corresponds to a FWHM of ca. 10 nm and ca. 15 nm for the low and high refractive index layers, respectively. In sum, the layers in C. rajah appear to be sufficiently ordered so that the resulting peak reflectance intensity and the signal-to-background intensity ratio are not affected significantly by the structural imperfections in the system.
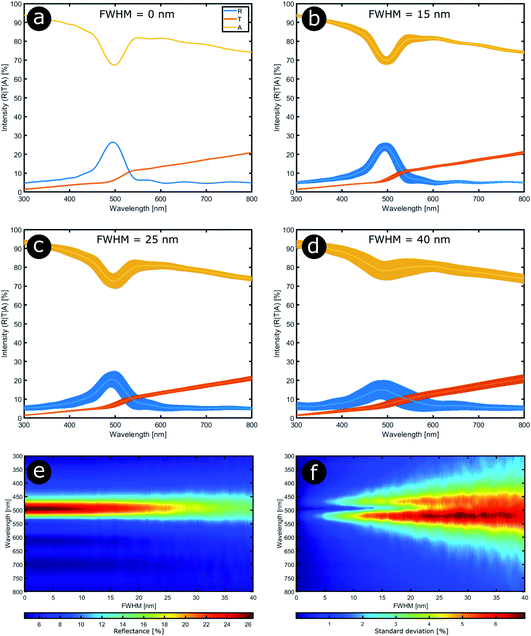 | ||
| Fig. 12 Stability in the optical response of natural photonic structures arises from their high resilience to positional defects. Reflectance (R), transmittance (T) and absorption (A) spectra calculated at normal incidence from a typical multilayer model in which positional disorder is added progressively (a–d). The multilayer model comprises 9 bilayers,147 and the high (n = 1.68 + 0.03i) and low (n = 1.55 + 0.14i) refractive index layers have randomly selected thicknesses following normal distributions with mean parameters equal to 92 nm and 60 nm, respectively. The FWHM of these normal distributions were varied from 0 nm to 40 nm in 0.2 nm steps (e and f). (a–d) correspond to FWHM = 0 nm, 15 nm, 25 nm and 40 nm, respectively. | ||
Positional disorder in 2D photonic structures
In the case of photonic structures exhibiting 2D order or quasi-order, positional disorder is distinct from size disorder, with these disorder parameters represented by represented by, for example, the scattering centre nearest neighbour distance distribution and the scattering centre size distribution, respectively. In addition to spectral effects, an increase in 2D disorder is expected to lead to an increase in the scattering solid angle. This section focuses on the former, with reference to several biological 2D structurally coloured systems.Prum and co-workers performed extensive investigations of structural colours generated by 2D structures in dermal collagen for a range of bird species (Fig. 13).62,63,163,164 The birds investigated in these works exhibited non-iridescent structural colours ranging from yellow to blue, with a number of species also demonstrating scattering at UV wavelengths. Prum and co-workers showed that the structurally coloured caruncles of these birds often contain quasi-ordered dermal arrays of parallel collagen fibres that collectively give rise to coherent scattering. These 20–100 μm-long fibres exhibit circular cross-sections and are surrounded by mucopolysaccharide. They run approximately parallel to the skin surface. Each TEM observation shows similar fibre diameters (varying from 5 μm to 20 μm depending on the species) and interfibre distances. In most cases, the fibres do not present a perfect geometrically symmetric organisation. 2D-FFT analyses of the TEM images revealed the familiar patterns of approximately concentric rings over a range of spatial frequencies corresponding to the refractive index variations that account for the observed colours. These studies postulated that this colour production mechanism had evolved convergently in several tens of bird species. By contrast, in a few species, such as the blue and green of Philepitta castanea, these fibres were found to be organised in regular hexagonal arrays,163,164 the 2D-FFTs of which revealed regular hexagonal patterns. Despite this structural order, iridescence is suppressed by long-range disorder, via variations in the orientation of the collagen fibre bundles. The bird caruncles investigated by Prum and co-workers included examples of scattering at longer wavelengths, such as the orange facial and lappet skin of the pheasant Tragopan caboti (Fig. 13F) and the yellow facial skin of Ramphastos toco (Fig. 13H). These colours were found to arise from the interplay between photonic structures and pigments such as carotenoids.63 In the case of Gymnopithys leucapsis (Fig. 13J), nanostructures were identified that may also give rise to UV scattering.164
 | ||
| Fig. 13 TEM images of cross-sections of dermal collagen arrays for a selection of birds, in which parallel collagen fibres are embedded in a mucopolysaccharide matrix. Through coherent scattering, these arrays give rise to non-iridescent colours ranging from orange to blue (A–I, K and L), as well as possible UV scattering (J).63 Pictures of the related birds are inserted, with an arrow pointing to a specific zone added when required. The orange visual appearance (F) arises from the interplay between the collagen array and pigments (presumably carotenoids).62 (A) Oxyura jamaicensis, light blue; (B) Numida meleagris, dark blue; (C) Tragopan satyra, dark blue; (D) Tragopan caboti, dark blue; (E) Tragopan caboti, light blue; (F) Tragopan caboti, orange; (G) Syrigma sibilatrix, blue; (H) Ramphastos toco, dark blue; (I) Philepitta castanea, light blue; (J) Gymnopithys leucapsis, light blue; (K) Procnias nudicollis, green and (L) Terpsiphone mutata, dark blue. All scale bars represent 200 nm. This figure was reproduced from ref. 63, with permission from The Company of Biologists. Insets were reproduced from John Mosesso Jr, https://commons.wikimedia.org/wiki/File:Oxyura_jamaicensis_NBII2.jpg, public domain (A); Diego Delso, delso.photo, License CC-BY-SA-4.0 (B); Kuribo, https://commons.wikimedia.org/wiki/File:Satyr_Tragopan_Osaka.jpg, License CC-BY-SA-3.0 (C); A. Ocram, https://commons.wikimedia.org/wiki/File:Sekret%C3%A4r_Vogel.JPG, public domain (D–F); Jimmy Baikovicius, https://commons.wikimedia.org/wiki/File:Syrigma_sibilatrix_-Punta_del_Este,_Uruguay-8.jpg, License CC-BY-SA-2.0 (G); Bernard Gagnon, https://commons.wikimedia.org/wiki/File:Toco_toucan_in_Igua%C3%A7u_National_Park.jpg, License CC-BY-SA-4.0,3.0,2.5,2.0,1.0 (H); Frank Vassen, https://commons.wikimedia.org/wiki/File:Velvet_asity_(Philepitta_castanea),_Ranomafana_National_Park,_Madagascar.jpg, License CC-BY-2.0 (I); Dick Daniels, https://commons.wikimedia.org/wiki/File:Bicolored_Antbird_RWD7.jpg, License CC-BY-SA-3.0 (J); Ben Tavener, https://commons.wikimedia.org/wiki/File:Procnias_nudicollis.jpg, License CC-BY-2.0 (K) and Kris Norvig, https://commons.wikimedia.org/wiki/File:Terpsiphone_mutata_001.jpg, License CC-BY-SA-3.0 (L). | ||
We consider three other documented cases of 2D biological systems here: the setae of the polychaete worm Pherusa sp. (Fig. 14a), self-organised bacterial colonies of Cellulophaga lytica (Fig. 14b), and the blue feathers of the male peacock Pavo cristatus (Fig. 14c). The structure within the setae of Pherusa sp. comprises water-filled chitin cylinders arranged in close-packed domains of hexagonal order (Fig. 14a).165 These hollow cylindrical channels are packed into monocrystalline domains of different orientations that create a polycrystalline effect overall. The water-filled cylinders have a diameter that is linearly dependent on the seta diameter and typically measures from 120 nm to 170 nm.165
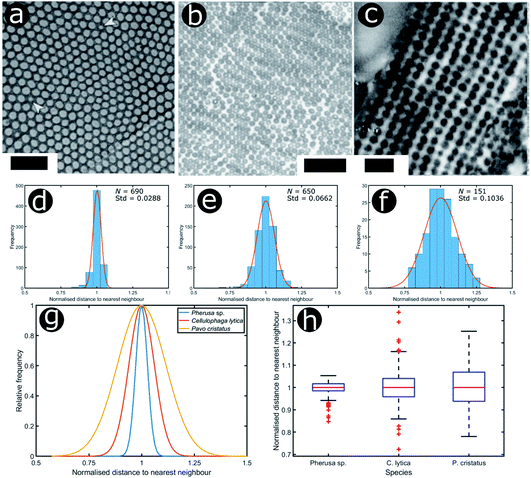 | ||
| Fig. 14 Structural colours can be generated by 2D morphologies with various extents of positional disorder. TEM images showing the cross-sections of 2D photonic crystal structures present in the sea mouse Pherus sp. (a), the colony structure of the marine bacterium C. lytica (b) and the blue feather barbules of the peacock P. cristatus (c). The statistical analysis (histograms and Gaussian fits) of the distributions of normalised nearest neighbour distances facilitates assessment of the extent of disorder in the photonic systems related to Pherus sp. (d), C. lytica (e) and P. cristatus (f) (N = 690, N = 650 and N = 151, respectively). Comparing the Gaussian fits of the statistical distributions (g) and the related box and whisker plots (h) allows the extent of disorder in these photonic structures to be evaluated. Scale bars: 1 μm (a), 2 μm (b) and 400 nm (c). (a) was reproduced from ref. 165 with permission from the American Physical Society (APS). (b) was reproduced from ref. 32, License CC-BY-4.0. (c) was reproduced from ref. 16, with permission from the authors. | ||
Similarly, several rod-shaped bacteria (phylum Bacteroidetes), specifically from the orders Flavobacteriales and Cytophagales, were found to produce structural colours when forming colonies, with large domains of close-packed structures displaying hexagonal quasi-order.31–34 The refractive index contrast between the bacteria (n = 1.38 (ref. 32 and 166–168)) and their host medium (typically agar with a refractive index of n = 1.34 (ref. 32 and 169) in the laboratory) underpins striking photonic colours, such as in the case of the bacterium C. lytica, which is found on the surface of sea anemones and exhibits a predominantly iridescent green appearance, although a diverse colour palette (including red, orange, yellow, green, cyan, blue and magenta) was observed for various angles of incidence and observation, most notably at the edges of the colonies.30–32
The blue feathers of the male peacock Pavo cristatus represent another 2D photonic structure that has received considerable attention from researchers. Here, melanin rodlets (called melanosomes), arranged in a square array, sit in a keratin matrix (interlaced with air gaps).16,17,170–172 The colours of all blue, green, yellow and orange neck and breast feathers are caused by identical optical effects in the observed 2D photonic crystals. The difference in reflected hue simply arises from different periodicities, typically 150 nm for blue feathers and closer to 190 nm for the yellow and green feathers.16,17,170 More recently, it was shown that simple effective-medium multilayer modelling is suited to modelling these feather colour appearances.171,172
To analyse the extent of order or disorder in these systems, a Delaunay triangulation algorithm173 was applied to TEM images of the cross-sections of these structures and the avian dermal structures studied by Prum et al. (Fig. 13 and 14), using the method described in ref. 31 and 165. This approach allows direct measurement of the distribution of the distance from each scattering centre (collagen fibre, chitin channel, melanin rodlet or bacterium) to its nearest neighbour (e.g., Fig. 14d–f). The distribution widths of these distances, normalised to their median values, represent the deviation from a perfectly ordered structure. All distributions were relatively narrow and, accordingly, their associated standard deviations were small. This is illustrated by the range of box and whisker plots shown in Fig. 15. The standard deviations of the distributions of the nearest neighbour distances in each system range from 2.9% of the median value for the sea worm Pherusa sp., to 15.3% of the median value for the green skin of the bare-throated bellbird Procnias nudicollis. The most ordered arrangements in avian dermal structures were observed for the cases of the light blue and green regions of the velvet asity P. castanea (standard deviations equal to 3.7% and 5.7% of the median value, respectively, Fig. S4, ESI†). In fact, they correspond to the same probability distribution (using a two-sample Kolmogorov–Smirnov test, p-value = 0.1946, significance level α = 0.001); this implies that the extent of positional disorder is the same in the tissues of both the light blue and the green regions of the wattle of P. castanea. In other words, two different colours arise from analogous structures, but with different size collagen fibres, and both have the same level of positional disorder regarding their scattering elements. One interesting case to consider lies in the caruncular colours of the bird T. caboti. The dark and light blue regions both exhibit a relatively low extent of positional disorder, with the normalised nearest neighbour distance distributions in each system having standard deviations of 6.4% and 6.8%, respectively, with respect to their median values (Fig. 15 and S4, ESI†). However, this is in direct contrast to the distribution of nearest neighbour distances in the array of collagen fibres found in the orange-coloured dermal region, the standard deviation of which is 11.4% of its median value and which, alongside the dermis of P. nudicollis, is among the most disordered systems displaying functional structural colours documented to date (Fig. 15 and S4, ESI†). The disorder in the dark and light blue integuments of this specimen was found to be identical (two-sample Kolmogorov–Smirnov test, p-value = 0.3371, α = 0.001). However, a comparison of the distributions of normalised nearest neighbour distances identified differences between the dark blue and orange areas (two-sample Kolmogorov–Smirnov test, p-value = 4.8462 × 10−6, α = 0.001) as well as in the light blue and orange areas (two-sample Kolmogorov–Smirnov test, p-value = 7.9124 × 10−5, α = 0.001). It is possible that the extent of positional disorder in the structurally coloured caruncles of T. caboti evolved to deliver specific visual signals (such as scattering angle) in certain regions of tissue but not in others. We performed a similar analysis using TEM images of the green dermis of P. nudicollis (Fig. 16) from two different studies.62,63 This showed that these two measured distributions correspond to the same probability distribution (based on a two-sample Kolmogorov–Smirnov test, p-value = 0.0740, α = 0.001).
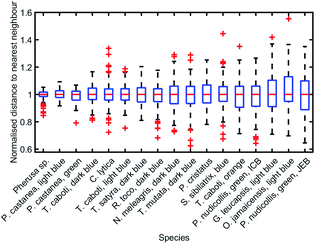 | ||
| Fig. 15 Positional disorder occurs frequently in 2D biological photonic structures. The box and whisker plots of the distributions of normalised nearest neighbour distances show that structural colours can be produced by structures with various extents of disorder. The results from the analysis of TEM images from: ref. 165 for Pherusa sp.; ref. 63 for the light blue area of P. castanea, the dark blue area of T. caboti, the light blue area of T. caboti, the dark blue area of T. satyra, the dark blue area of R. toco, the dark blue area of N. meleagris, the dark blue area of T. mutata, the blue area of S. sibilatrix, the orange area of T. caboti, the light blue area of G. leucapsis, the light blue area of O. jamaicensis and the green area of P. nudicollis; ref. 62 for the blue area of P. castanea and the green area of P. nudicollis; ref. 31 for C. lytica; and ref. 16 for the blue feathers of P. cristatus. The labels “ICB” and “JEB” associated with the green area of P. nudicollis correspond to ref. 62 and 63, respectively. | ||
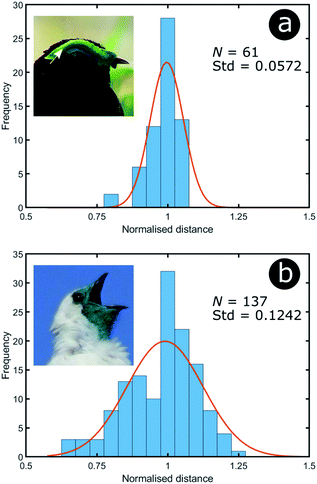 | ||
| Fig. 16 Green colour can arise from relatively different levels of disorder: the green area of P. castanea exhibits a low level of disorder in its collagen fibres whereas the structure within the dermis of P. nudicollis corresponds to a higher extent of disorder. The data results from the analysis of TEM images from ref. 62. Insets were reproduced from Frank Vassen, https://commons.wikimedia.org/wiki/File:Velvet_asity_(Philepitta_castanea),_Ranomafana_National_Park,_Madagascar.jpg, License CC-BY-2.0 (a) and Ben Tavener, https://commons.wikimedia.org/wiki/File:Procnias_nudicollis.jpg, License CC-BY-2.0 (b). | ||
Moreover, TEM images of cross-sections of the setae of the polychaete worm Pherusa sp. (Fig. 14a), the self-organised bacteria C. lytica in colony biofilms (Fig. 14b) and the blue feathers of the male peacock P. cristatus (Fig. 14c) were also analysed using this approach. These systems exhibit differing extents of disorder, as observed from the box and whisker plots of their normalised nearest neighbour distance distributions (Fig. 14h). In the case of Pherusa sp., the structures are highly ordered, with a standard deviation of the normalised distance distribution equal to 2.9% of the median value (Fig. 14d and g). Conversely, the analysis showed that C. lytica colonies are quasi-ordered systems, with a standard deviation of the normalised distance distribution equal to 6.6% of the median value (Fig. 14e and g). Both structures exhibit hexagonal packing. A two-sample Kolmogorov–Smirnov test confirmed that these structures correspond to two different probability distributions (p-value = 1.3623 × 10−15, α = 0.001). The barbule ultrastructure in the blue feathers of P. cristatus resembles a quasi-ordered square arranged lattice (Fig. 14f and g), with a standard deviation of the normalised distance distribution equal to 10.4% of the median value.
Finite element method (FEM) modelling, using Comsol Multiphysics® (http://www.uk.comsol.com), was used to determine how the distribution of periodicities within the three structures affects their optical response. Positional disorder was introduced into the 2D photonic structures such that the nearest neighbour distributions of the models were analogous to the 2D biological systems observed via electron microscopy (Fig. 14). This involved displacing the scattering centres (i.e., chitin channels, bacteria or melanin rodlets) from their positions in an initially ordered lattice. Our TEM image structural analysis also informed on the scattering centre sizes and the distribution of periodicities. Periodic boundary conditions for the model were used to minimise diffraction effects associated with finite cell size, with the models represented by a large computational supercell (typically 15 μm wide). This ensured that the models comprised a large number of cylindrical elements (N > 1000) and that the dominant optical effects were those associated with the scattering centres. These simulations showed that infusing a perfectly ordered system with disorder modifies its total reflectance spectrum (Fig. 17). The primary components of the change in reflectance, once a certain disorder threshold are reached, are a lower peak reflectance intensity and a higher background intensity. As the width of the reflectance peak does not seem to change significantly, its reduced intensity is likely the principal factor underlying any positional disorder-induced changes to the perceived saturation or brightness. The disorder-induced increase in background reflectance is indicative of an increase in diffuse scattering, which corresponds to scattering of the reflected light at a wider solid angle.
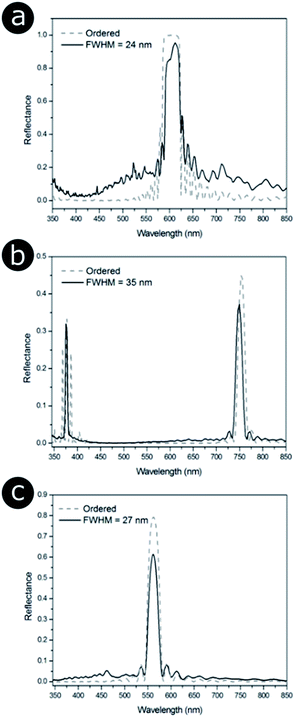 | ||
| Fig. 17 Positional disorder affects the optical response from 2D photonic structures. Modelled total reflectance spectra for 2D photonic structures identified in three natural samples (Fig. 14), namely (a) the setae of the polychaete worm Pherusa sp., (b) the colonies of the marine bacterium C. lytica and (c) the feather barbules of the male peacock P. cristatus. (a) and (b) correspond to a hexagonal lattice, whereas (c) is related to a square array. The solid lines represent the total reflectance spectra for structure models in which disorder was introduced so that it matched the distribution of nearest neighbour distances observed experimentally (Fig. 14). Different FWHM were chosen for the distributions of nearest neighbour distances. P. cristatus barbules were described as the most disordered structure in terms of the distribution of normalised nearest neighbour distances; however, the median distance is shorter (122 nm) than that for both the Pherusa sp. setae (135 nm) or the C. lytica colonies (258 nm). This demonstrates that a larger FWHM does not necessarily translate to greater disorder when comparing different lattice geometries. The dashed lines correspond to the predicted total reflectance spectra associated with perfectly ordered structure models. | ||
As described earlier in relation to the 1D multilayers of C. rajah, there are parameters other than positional disorder to consider in such optical systems. For 2D systems, this includes refractive index contrast, particle shape, size distribution and lattice geometry. It is clear from a simple comparison of Fig. 17a and b, for example, that while these systems exhibit relatively low values for the standard deviations of their respective normalised nearest neighbour distance distributions (2.9% and 6.6%, respectively, Fig. 14g and h), there are marked differences in their reflectance spectra. For all three cases modelled in Fig. 17, a similar number of periods were considered, which, for the perfectly ordered Pherusa sp. model (Fig. 17a), was sufficient to create a band with 100% reflectance. However, for the perfectly ordered P. cristatus model, a similar number of periods results in a reflectance peak with an intensity of approximately 80% (Fig. 17c). The key difference between these structures, other than the positional disorder and the lattice arrangement, is their associated inherent refractive index contrast. For the channels in Pherusa sp., the refractive index contrast of the materials (namely, chitin and water with refractive indices equal to 1.56 (ref. 24, 152, 174 and 175) and 1.33,176 respectively) is relatively higher than for P. cristatus barbules in which melanin rodlets (refractive index assumed to be equal to 1.67 (ref. 177 and 178)) are surrounded by keratin (refractive index assumed to be equal to 1.56).175 Unsurprisingly, the contrast between the refractive indices of the scattering centres and the matrix medium plays a key role. Furthermore, and as mentioned in the specific case of the P. castanea dermis, other factors, such as additional length-scale disorder and polycrystallinity, affect the optical response of a photonic structure.106,157,162
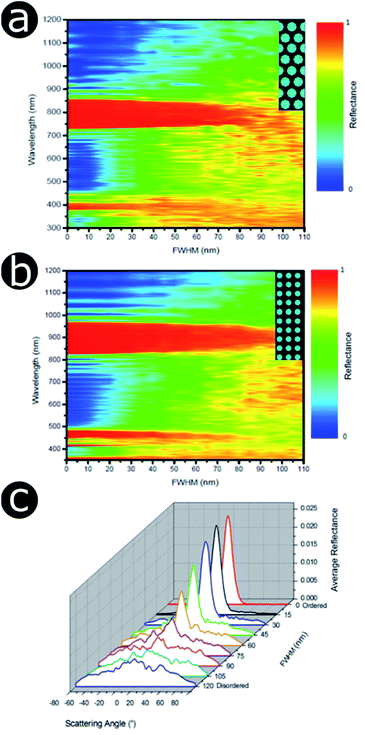
As with the 1D examples described earlier, the multi-variable nature of these systems makes the disorder-focused modelling of the full parameter space extremely complex. Therefore, more manageable models with reduced parametric variability were generated. To this end, two 2D photonic structure models with cylindrical scattering elements were chosen, representing the hexagonal and square lattice geometries, respectively (Fig. 18a and b). The mean periodicity and the scattering particle radii were fixed at 400 nm and 100 nm, respectively, whilst the cylindrical elements and the surrounding medium were assigned refractive indices of 1.50 and 1.00, respectively. Positional disorder was implemented by displacing the individual cylindrical elements of the model from their lattice positions. As described in our earlier analyses, disorder was introduced to the model via nearest neighbour distance distributions. For each particle, positional disorder was generated randomly following a normal distribution of the nearest neighbour distances with FWHM ranging, in a controlled manner, from 0 nm to 110 nm. Thus, the extent of disorder was controlled by the active selection of the FWHM value, with FWHM = 0 nm corresponding to a model with a perfectly ordered structure. Each model comprised a large unit cell featuring at least 1000 individual elements. Incidence was normal to the upper boundary of the cell. For low FWHM values, the simulated total reflectance spectra (Fig. 18) display very intense and well-defined reflectance peaks due to coherent backscattering. The reflectance peaks are centred at wavelengths of ca. 800 nm and ca. 900 nm for the hexagonal and square arrays, respectively. This is an artefact of the primary scattering planes within the hexagonal model being closer together than those in the square model for equivalent periodicity; therefore, the principal reflectance peaks associated with scattering from these planes occur at shorter wavelengths in the hexagonal lattice model than for the corresponding square lattice model.
From these spectra (Fig. 18a and b), it is evident that the principal reflectance peaks are remarkably resilient to the application of positional disorder with respect to the scattering centre distribution. This is particularly true for the square structure model, for which the main reflectance peak is relatively intact even for high FWHM values of the nearest neighbour distance distribution (ca. 80–90 nm). Nevertheless, whilst the reflectance peak remains relatively unchanged, the background reflectance levels increase with increasing disorder. Furthermore, as the intensity of the background reflectance increases, it spreads over a wider solid angle (Fig. 18c). This is expected. For a perfectly ordered model (FWHM = 0 nm), the backscattered power is concentrated entirely in the specular direction (although its finite width arises from the angular width of the incident beam, approximately 10°, used in the modelling). As the positional disorder in the model increases (accompanied by an increase in the FWHM value), an increase in the background scattering manifested as a broad-angled reflectance distribution is predicted. Notably, however, the central specular maximum is maintained in a similar fashion to the reflectance peak position in the total reflectance spectrum (Fig. 18a). As the positional disorder within the model structures increases, the angular distribution flattens to an approximately Lambertian scattering profile, as expected for a random arrangement of scattering elements.
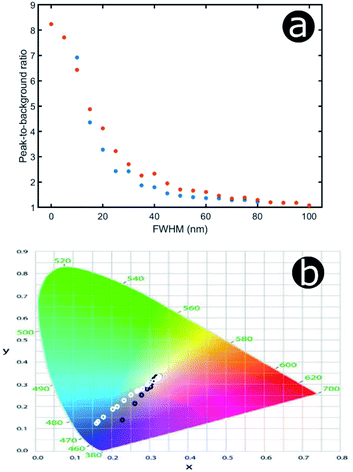
An increase in background reflectance leads to reduced saturation of the reflected colour because a high-intensity narrowband reflection is normally required to achieve bright saturated hues. One of the primary factors representing this is the ratio of the reflectance peak to the background reflectance level (Fig. 19a). For both the hexagonal and the square geometry, the ratio of peak-to-background reflectance is attenuated rapidly with increasing positional disorder. A strong negative correlation is observed, with the steepest gradient associated with the initial increase in background reflectance. This is to be expected; for zero and very low extents of positional disorder, diffuse scattering is minimal and therefore background levels are low. As positional disorder is introduced, the diffuse scattering intensity rises, as observed in the reflectance colour maps (Fig. 18a and b): the greatest change in background intensity occurs between FWHM values of 0 nm and 30–40 nm. This rapid initial rise in background scattering explains the shape of the peak-to-background ratio (Fig. 19a); however, the peak reflectance is not impacted appreciably until mid-to-high FWHM values are implemented (Fig. 18a and b). The main factor responsible for changing the peak-to-background ratio appears to be the increase in background reflectance, which occurs for relatively low extents of positional disorder.
Unsurprisingly, the models confirm that highly saturated reflected colours correspond to structural order (Fig. 19b), owing to strong narrowband reflectance in parallel with low off-peak levels of scattering. Neither model reflects fully saturated colour, principally owing to the choice of structural parameters (i.e., the geometries and refractive indices). These parameters produced reflectance peaks on the fringes of the visible wavelength range, namely 380–700 nm. The primary reflectance peaks for both modelled structures fall just outside of this range, whereas the short-wavelength peak is located at blue wavelengths for the square model and at the UV-visible boundary for the hexagonal model. For both lattice arrangements, as positional disorder increases, the reflected colours desaturate and converge to the neutral point (0.33, 0.33) of the 1931 CIE chromaticity diagram (Fig. 19b). This corroborates the transition from narrowband to broadband reflectance as the structures are infused with increasing levels of positional disorder. Interestingly, this trend is not homogeneous for the two geometries under consideration. For the hexagonal model, the reflectance desaturates in an approximately exponential manner, in line with the trend observed for the peak-to-background ratio (Fig. 19a). The square model, on the other hand, demonstrates less dramatic desaturation, following a more linear trend.
Materials and methods
Electron microscopy and statistical analyses of positional disorder
TEM observations of cross-sections of C. rajah elytra from both green and orange areas were performed using a JEOL 100S TEM instrument. Prior to analysis, the samples were fixed in 3% glutaraldehyde at 21 °C for 2 hours followed by rinsing in sodium cacodylate buffer and fixing in 1% osmic acid in buffer for 1 hour. This step was followed by block staining in 2% aqueous uranyl acetate for 1 hour, dehydration through an acetone series (ending in 100% acetone) and embedding in Spurr resin.179 After microtoming, sample cross-sections were stained with lead citrate. All other TEM images were taken from the literature.16,32,62,63,165 We assumed all TEM sections to be have been taken perpendicular to the long axes of the scattering structures, namely, the collagen fibres of the bird caruncles, the chitin cylinders within the setae of Pherusa sp., the colony of the marine bacterium C. lytica and the melanin rodlets of P. cristatus barbules.Detailed investigation of C. rajah cross-sections was performed by statistical analysis of the thicknesses of the layers embedded within the elytral exocuticle. The thicknesses of these layers were measured from the TEM images along N = 152 sample profiles from the green region and N = 771 sample profiles for the orange region. The profiles comprised adjacent positions on the exocuticle surface over widths of 298 nm and 962 nm, respectively. Thus, N = 152 and N = 771 greyscale profiles were obtained. In order to calculate the layer thicknesses, we defined the layer interfaces as the mean grey scale values between two consecutive extrema within a single profile. To highlight positional disorder, we normalised the measured layer thicknesses to the median values for each layer. Unlike the mean value, the median value is known for being less skewed by small numbers of extremely large or small values.158 In addition, this normalisation allowed appropriate consideration of existing systematic errors. The extent of positional disorder was measured by the distribution of these normalised thicknesses.
Statistical analyses of the 2D scattering structures observed by TEM were performed after preliminary image processing steps, including the removal of the background and the binarisation of the TEM images. The resulting binary images allowed discrimination of the scattering particles from the background material. For each particle, the centroid coordinates were computed. Using Delaunay triangulation,173 the nearest neighbour distances were computed. As described earlier, the nearest neighbour distance distributions were normalised to their median values. Therefore, the extent of positional disorder was measured by the distribution of these normalised nearest neighbour distances. To test whether two different measured distributions corresponded to the same probability distribution, we used the two-sample Kolmogorov–Smirnov test with significance level α = 0.001.180,181
Optical microscopy and microspectrophotometry
Optical microscopy observations of the green and orange regions of C. rajah elytra were performed using a Zeiss Axioskop 2 MAT MOT microscope, a Zeiss AxioCam MRc 5 camera, a Zeiss HAL 100 light source and a Zeiss LD Epiplan 50×/0.50 HD DIC objective. The elytra of the investigated specimens were detached from the bodies and placed on microscope slides. Images were captured from elytral regions exhibiting the least surface curvature; however, owing to the curvature of the elytral surface, an extended depth of focus function was used to generate in-focus microscopic images.The reflection factor spectra R = (I − B)/(W − B) were defined as the ratios between the intensity I reflected by the sample and the intensity W reflected by a Labsphere white reflectance standard, with noise corrections B. They were measured with an Ocean Optics USB2000 fibre spectrophotometer connected to the optical microscope described herein, the Zeiss HAL 100 light source and a Zeiss LD Epiplan 100×/0.75 HD objective. The analysed area spanned approximately 0.3 mm2. Several sets of N = 150 spectra were measured. The distance between two measurement spots was at least 0.7 mm. The integration time of the spectrophotometer was chosen to be 300 ms and each spectrum was averaged over 15 measurements. Because of the microscope configuration, all incidence and detection directions were normal to the sample surface. From the measured spectra, the related colours were represented by chromaticity diagrams as defined by the Commission Internationale de l’Éclairage (CIE) in 1931, assuming the D65 standard illuminant also defined by the CIE in 1931.182,183
Optical simulations
Reflectance spectra of the typical multilayer models were calculated using a thin-film modelling computer code based on 1D scattering matrix formalism184 to rigorously solve Maxwell’s equations in the case of planar layered photonic structures. Simulations were performed for unpolarised light at normal incidence. The generated models were based on the TEM analysis of C. rajah’s multilayers in terms of dimensions and the extent of positional disorder. They were composed of 9 bilayers. The high (n = 1.68 + 0.03i) and low (n = 1.55 + 0.14i) refractive index layers147 had thicknesses that were generated randomly with probabilities weighted by envelopes shaped by normal distributions that had mean parameters equal to 92 nm and 60 nm, respectively, for each layer type following ref. 147. The FWHM of these normal distributions were varied from 0 nm to 40 nm in 0.2 nm steps. This FWHM parameter was used to control the extent of disorder in each multilayer model. The refractive indices of the incident and emergent media were equal to 1.00 and 1.68 + 0.03i, respectively.Finite element method (FEM) modelling, using Comsol Multiphysics® (http://www.uk.comsol.com), was used to determine the way in which the distribution of periodicities within the three 2D photonic structures, namely the extent of disorder applied, affects their optical response. Two different 2D FEM models were created, one with hexagonal geometry and one with square geometry, each comprising cylindrical scattering centres. Positional disorder of the scattering centres was incorporated such that the nearest neighbour distributions of the models matched the experimental observations (Fig. 14). The mean periodicity and the scattering particle radius were chosen to be 400 nm and 100 nm, respectively. The cylindrical elements and the surrounding medium were assumed to have refractive indices equal to 1.50 and 1.00, respectively. Positional disorder was introduced by displacing the cylindrical elements from their original perfectly ordered geometric positions. The positions of the cylindrical elements in each model iteration were generated randomly so that the ranges of nearest neighbour distances followed a normal distribution, with FWHM ranging from 0 nm to 110 nm. The extent of applied positional disorder was controlled by the selection of the chosen distribution associated with a given FWHM. Periodic boundary conditions were used for each model. To minimise any optical effects introduced by this periodicity, a large FWHM supercell was generated (typically 15 μm wide). This ensured that the models comprised a large number of cylindrical elements (N > 1000) and that the dominant optical effects were those associated with the positional disorder of the scattering elements, rather than those associated with the discrete size of the periodic FEM cell. The total reflectance spectra were simulated for normal incidence.
Conclusions
Coherent scattering from ordered and quasi-ordered photonic structures, a common phenomenon in many animals and plants, gives rise to a range of structurally coloured appearances. Highly scattering diffuse broadband appearances or highly absorbing appearances result from disordered structures in systems presenting white or grey appearances, respectively. The inherent extent of order, quasi-order or disorder in such systems contributes to their optical signatures through, for example, reflected colour saturation or enhancement of the specular or diffuse nature of the reflection. In this work, we have reviewed a range of examples of natural photonic systems that exhibit differing extents of order, quasi-order and disorder. We have explored and discussed the optical costs and benefits associated with systems that diverge from perfectly periodic photonic structures to generate their appearances. We discussed what appears to be a valuable feature of biological photonic systems, namely their tolerance to natural variations, defects, faults or ranges of imperfections in their photonic structures. Despite this phenotypic diversity, or what might be described as biological noise, these systems nevertheless produce visual appearances throughout the animal and plant kingdoms, with distinct optical signatures that are effective and highly functional and are reproduced by the vast majority of specimens of a single animal or plant species. In comparison, optical scattering associated with the presence of imperfectly ordered structures in synthetic technology-based systems usually reduces their efficiency and effective performance. Exploiting the tolerance of biological photonic systems to faults and imperfections would be valuable for bioinspired technological applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. R. M. was partly supported by the Belgian National Fund for Scientific Research (FRS-FNRS) as a Postdoctoral Researcher (91400/1.B.309.18F).Notes and references
- S. Berthier, Iridescences, les couleurs physiques des insectes, Springer, 2003 Search PubMed.
- P. Vukusic and J. R. Sambles, Nature, 2003, 424, 852–855 CrossRef CAS.
- P. Vukusic, Structural colour effects in Lepidoptera, in Structural Colors in Biological Systems: Principles and Applications, ed. S. Kinoshita and S. Yoshioka, Osaka University Press, 2005 Search PubMed.
- S. Kinoshita, Structural Colors in the Realm of Nature, 2008 Search PubMed.
- T. L. Tan, D. Wong and P. Lee, Opt. Express, 2004, 12, 4847–4854 CrossRef CAS.
- A. L. Holt, S. Vahidinia, Y. L. Gagnon, D. E. Morse and A. M. Sweeney, J. R. Soc., Interface, 2014, 11, 20140678 CrossRef.
- E. Denton, Sci. Am., 1971, 224, 64–72 CrossRef.
- L. M. Mäthger, M. F. Land, U. E. Siebeck and N. J. Marshall, J. Exp. Biol., 2003, 206, 3607–3613 CrossRef.
- A. V. Zabuga, M. I. Arrigo, J. Teyssier, S. R. Mouchet, K. Nishikawa, M. Matsui, M. Vences and M. C. Milinkovitch, Soft Matter, 2020, 16, 1714–1721 RSC.
- S. V. Saenko, J. Teyssier, D. Van Der Marel and M. C. Milinkovitch, BMC Biol., 2013, 11, 105 CrossRef.
- J. Teyssier, S. V. Saenko, D. Van Der Marel and M. C. Milinkovitch, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- R. O. Prum and R. H. Torres, J. Exp. Biol., 2004, 207, 2157–2172 CrossRef.
- R. O. Prum, R. H. Torres, S. Williamson and J. Dyck, Nature, 1998, 396, 28–29 CrossRef CAS.
- R. O. Prum, R. H. Torres, S. Williamson and J. Dyck, Proc. R. Soc. London, Ser. B, 1999, 266, 13–22 CAS.
- J. Zi, X. Yu, Y. Li, X. Hu, C. Xu, X. Wang, X. Liu and R. Fu, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12576–12578 CrossRef CAS.
- S. Yoshioka and S. Kinoshita, Forma, 2002, 17, 169–181 Search PubMed.
- Y. Li, Z. Lu, H. Yin, X. Yu, X. Liu and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 010902 CrossRef.
- J.-P. Vigneron, J.-F. Colomer, M. Rassart, A. I. Ingram and V. Lousse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021914 CrossRef.
- H. Yin, L. Shi, J. Sha, Y. Li, Y. Qin, B. Dong, S. Meyer, X. Liu, L. Zhao and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051916 CrossRef.
- G. S. Oxford and R. G. Gillespie, Annu. Rev. Entomol., 1998, 43, 619–643 CrossRef CAS.
- A. L. Ingram, A. D. Ball, A. R. Parker, O. Deparis, J. Boulenguez and S. Berthier, J. Arachnol., 2009, 37, 68–71 CrossRef.
- A. L. Ingram, O. Deparis, J. Boulenguez, G. Kennaway, S. Berthier and A. R. Parker, Arthropod Struct. Dev., 2011, 40, 21–25 CrossRef CAS.
- P. Vukusic, J. R. Sambles and H. Ghiradella, Photonics Sci. News, 2000, 6, 61–66 Search PubMed.
- P. Vukusic, J. R. Sambles, C. R. Lawrence and R. J. Wootton, Proc. R. Soc. London, Ser. B, 1999, 266, 1403–1411 Search PubMed.
- A. E. Seago, P. Brady, J.-P. Vigneron and T. D. Schultz, J. R. Soc., Interface, 2009, 6, S165–S184 CrossRef.
- S. Berthier, Photonique des Morphos, Springer, 2010 Search PubMed.
- L. P. Biró and J.-P. Vigneron, Laser Photonics Rev., 2011, 5, 27–51 CrossRef.
- V. Saranathan, A. E. Seago, A. Sandy, S. Narayanan, S. G. J. Mochrie, E. R. Dufresne, H. Cao, C. O. Osuji and R. O. Prum, Nano Lett., 2015, 15, 3735–3742 CrossRef CAS.
- S. R. Mouchet and P. Vukusic, Adv. Insect Physiol., 2018, 54, 1–53 Search PubMed.
- B. Kientz, A. Ducret, S. Luke, P. Vukusic, T. Mignot and E. Rosenfeld, PLoS One, 2012, 7, e52900 CrossRef CAS.
- B. Kientz, P. Vukusic, S. Luke and E. Rosenfeld, Appl. Environ. Microbiol., 2012, 78, 2092–2099 CrossRef CAS.
- B. Kientz, S. Luke, P. Vukusic, R. Péteri, C. Beaudry, T. Renault, D. Simon, T. Mignot and E. Rosenfeld, Sci. Rep., 2016, 6, 19906 CrossRef CAS.
- V. E. Johansen, L. Catón, R. Hamidjaja, E. Oosterink, B. D. Wilts, T. S. Rasmussen, M. M. Sherlock, C. J. Ingham and S. Vignolini, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2652–2657 CrossRef CAS.
- L. Schertel, G. T. van de Kerkhof, G. Jacucci, L. Catón, Y. Ogawa, B. D. Wilts, C. J. Ingham, S. Vignolini and V. E. Johansen, J. R. Soc., Interface, 2020, 17, 20200196 CrossRef.
- D. W. Lee and J. B. Lowry, Nature, 1975, 254, 50–51 CrossRef.
- S. Vignolini, P. J. Rudall, A. V. Rowland, A. Reed, E. Moyroud, R. B. Faden, J. J. Baumberg, B. J. Glover and U. Steiner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15712–15715 CrossRef CAS.
- S. Vignolini, B. J. Glover and U. Steiner, Photonic Structures in Plants, in Biomimetics in Photonics, ed. O. Karthaus, CRC Press, 2012 Search PubMed.
- S. Vignolini, E. Moyroud, B. J. Glover and U. Steiner, J. R. Soc., Interface, 2013, 10, 20130394 CrossRef.
- I. G. Johnston, B. Gaal, R. Pires das Neves, T. Enver, F. J. Iborra and N. S. Jones, PLoS Comput. Biol., 2012, 8, e1002416 CrossRef CAS.
- L. S. Tsimring, Rep. Prog. Phys., 2014, 77, 026601 CrossRef.
- S. Yoshioka and S. Kinoshita, Proc. R. Soc. London, Ser. B, 2004, 271, 581–587 Search PubMed.
- S. Berthier, E. Charron and J. Boulenguez, Insect Sci., 2006, 13, 145–157 CrossRef.
- S. Kinoshita, S. Yoshioka, Y. Fujii and N. Okamoto, Forma, 2002, 17, 103–121 Search PubMed.
- S. Kinoshita, S. Yoshioka and K. Kawagoe, Proc. R. Soc. London, Ser. B, 2002, 269, 1417–1421 Search PubMed.
- J. Boulenguez, S. Berthier and F. Leroy, Appl. Phys. A, 2012, 106, 1005–1011 CrossRef CAS.
- V. E. Johansen, Appl. Opt., 2014, 53, 2405–2415 CrossRef.
- K. Yamashita, M. Fukihara, Y. Hirai, Y. Kuwahara and A. Saito, Jpn. J. Appl. Phys., 2020, 59, 052009 CrossRef CAS.
- K. Yamashita, Y. Kuwahara and A. Saito, Proc. SPIE, 2020, 11374, 1137406 Search PubMed.
- S. Kinoshita and S. Yoshioka, ChemPhysChem, 2005, 6, 1442–1459 CrossRef CAS.
- J.-P. Vigneron, V. Lousse, V. L. P. Biró, Z. Vértesy and Z. Bálint, Proc. SPIE, 2005, 5733, 308–315 CrossRef.
- C. Pouya, D. G. Stavenga and P. Vukusic, Opt. Express, 2011, 19, 11355–11364 CrossRef CAS.
- E. Bermúdez-Ureña, C. Kilchoer, N. P. Lord, U. Steiner and B. D. Wilts, iScience, 2020, 23, 101339 CrossRef.
- D. R. McKenzie, Y. Yin and W. D. McFall, Proc. R. Soc. London, Ser. A, 1995, 451, 579–584 CrossRef.
- T. M. Jordan, J. C. Partridge and N. W. Roberts, J. R. Soc., Interface, 2014, 11, 20140948 CrossRef CAS.
- E. Denton, Sci. Am., 1971, 224, 64–72 CrossRef.
- G. T. van de Kerkhof, L. Schertel, R. Poon, G. Jacucci, B. J. Glover and S. Vignolini, Faraday Discuss., 2020 10.1039/D0FD00024H.
- D. G. Stavenga, Mater. Today: Proc., 2014, 1S, 109–121 Search PubMed.
- R. H. Siddique, G. Gomard and H. Hölscher, Nat. Commun., 2015, 6, 6909 CrossRef CAS.
- S. John, Phys. Rev. Lett., 1987, 58, 2486–2489 CrossRef CAS.
- E. Yablonovitch, Phys. Rev. Lett., 1987, 58, 2059–2062 CrossRef CAS.
- J. D. Joannopoulos, S. G. Johnson, J. N. Winn and R. D. Meade, Photonic Crystals: Molding the Flow of Light, Princeton University Press, 2008 Search PubMed.
- R. O. Prum and R. H. Torres, Integr. Comp. Biol., 2003, 43, 591–602 CrossRef.
- R. O. Prum and R. H. Torres, J. Exp. Biol., 2003, 206, 2409–2429 CrossRef.
- G. Mie, Ann. Phys., 1908, 330, 377–445 CrossRef.
- M. Born and E. Wolf, Principles of Optics, Pergamon Press, 1975 Search PubMed.
- E. Hecht, Optics, Addison Wesley Longman, 1998 Search PubMed.
- M. I. Mishchenko, L. D. Travis and D. W. Mackowski, J. Quant. Spectrosc. Radiat. Transfer, 1996, 55, 535–575 CrossRef CAS.
- J. W. Strutt, London, Edinburgh Dublin Philos. Mag. J. Sci., 1871, 41, 447–454 CrossRef.
- L. Rayleigh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1881, 12, 81–101 CrossRef.
- A. T. Young, Appl. Opt., 1981, 20, 533–535 CrossRef CAS.
- M. Maunder, Lights in the Sky: Identifying and Understanding Astronomical and Meteorological Phenomena, Springer, 2007 Search PubMed.
- M. Ladouce, T. Barakat, B.-L. Su, O. Deparis and S. R. Mouchet, Faraday Discuss., 2020 10.1039/D0FD00034E.
- B. D. Wilts, J. Otto and D. G. Stavenga, Nanoscale Adv., 2020, 2, 1122–1127 RSC.
- K. Kertész, Z. Bálint, Z. Vértesy, G. I. Márk, V. Lousse, J.-P. Vigneron, M. Rassart and L. P. Biró, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021922 CrossRef.
- S. R. Mouchet, J.-P. Vigneron, J.-F. Colomer, C. Vandenbem and O. Deparis, Proc. SPIE, 2012, 8480, 848003 CrossRef.
- G. I. Márk, Z. Vértesy, K. Kertész, Z. Bálint and L. P. Biró, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051903 CrossRef.
- E. Moyroud, T. Wenzel, R. Middleton, P. J. Rudall, H. Banks, A. Reed, G. Mellers, P. Killoran, M. M. Westwood, U. Steiner, S. Vignolini and B. J. Glover, Nature, 2017, 550, 469–474 CrossRef CAS.
- V. E. Johansen, O. D. Onelli, L. M. Steiner and S. Vignolini, Photonics in Nature: From Order to Disorder, in Functional Surfaces in Biology III, ed. S. N. Gorb and E. V. Gorb, Springer Nature, 2017 Search PubMed.
- V. Sharma, M. Crne, J. O. Park and M. Srinivasarao, Science, 2009, 325, 449–451 CrossRef CAS.
- F. Aurenhammer, ACM Comput. Surv., 1991, 23, 345–405 CrossRef.
- A. Okabe, B. Boots, K. Sugihara and S. N. Chiu, Spatial Tessellations – Concepts and Applications of Voronoi Diagrams, John Wiley and Sons, 2000 Search PubMed.
- L. Maiwald, S. Lang, D. Jalas, H. Renner, A. Y. Petrov and M. Eich, Opt. Express, 2018, 26, 11352–11365 CrossRef CAS.
- E. Yablonovitch, T. J. Gmitter and K. M. Leung, Phys. Rev. Lett., 1991, 67, 2295–2298 CrossRef CAS.
- T. F. Krauss, R. M. De La Rue and S. Brand, Nature, 1996, 383, 699–702 CrossRef CAS.
- J. S. Foresi, P. R. Villeneuve, J. Ferrera, E. R. Thoen, G. Steinmeyer, S. Fan, J. Joannopoulos, L. C. Kimerling, H. I. Smith and E. P. Ippen, Nature, 1997, 390, 143–145 CrossRef CAS.
- A. A. Erchak, D. J. Ripin, S. Fan, P. Rakich, J. D. Joannopoulos, E. P. Ippen, G. S. Petrich and L. A. Kolodziejski, Appl. Phys. Lett., 2001, 78, 563–565 CrossRef CAS.
- D. Pavlović, M. D. Rabasović, A. J. Krmpot, V. Lazovic, S. Čurcic, D. V. Stojanovic, B. Jelenkovic, W. g. Zhang, D. Zhang, N. Vukmirovic, D. Stepanenko, B. Kolaric and D. V. Pantelic, J. Biophotonics, 2019, 12, e201900218 CrossRef.
- R. B. Morris, J. Entomol., Ser. A: Gen. Entomol., 1975, 49, 149–154 Search PubMed.
- A. C. Allyn and J. C. Downey, Bull. Allyn Mus., 1976, 40, 1–6 Search PubMed.
- K. Michielsen and D. G. Stavenga, J. R. Soc., Interface, 2008, 5, 85–94 CrossRef CAS.
- K. Michielsen, H. De Raedt and D. G. Stavenga, J. R. Soc., Interface, 2010, 7, 765–771 CrossRef CAS.
- G. E. Schröder-Turk, S. Wickham, H. Averdunk, F. Brink, J. D. Fitz Gerald, L. Poladian, M. C. J. Large and S. T. Hyde, J. Struct. Biol., 2011, 174, 290–295 CrossRef.
- B. Wintera, B. Butza, C. Diekera, G. E. Schröder-Turkb, K. Meckec and E. Spieckera, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12911–12916 CrossRef.
- P. Vukusic and J. R. Sambles, Proc. SPIE, 2001, 4438, 85–95 CrossRef.
- R. O. Prum, T. Quinn and R. H. Torres, J. Exp. Biol., 2006, 209, 748–765 CrossRef.
- V. Saranathan, C. O. Osuji, S. G. J. Mochrie, H. Noh, S. Narayanan, A. Sandy, E. R. Dufresne and R. O. Prum, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11676–11681 CrossRef CAS.
- A. Argyros, S. Manos, M. C. J. Large, D. R. McKenzie, G. C. Cox and D. M. Dwate, Micron, 2002, 33, 483–487 CrossRef CAS.
- B. D. Wilts, B. Apeleo Zubiri, M. A. Klatt, B. Butz, M. G. Fischer, S. T. Kelly, E. Spiecker, U. Steiner and G. E. Schröder-Turk, Sci. Adv., 2017, 3, e1603119 CrossRef.
- V. L. Welch, V. Lousse, O. Deparis, A. R. Parker and J.-P. Vigneron, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041919 CrossRef.
- B. D. Wilts and V. Saranathan, Small, 2018, 14, 1802328 CrossRef.
- J. W. Galusha, L. R. Richey, J. S. Gardner, J. N. Cha and M. H. Bartl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 050904 CrossRef.
- R. Ebihara, H. Hashimoto, J. Kano, T. Fujii and S. Yoshioka, J. R. Soc., Interface, 2018, 15, 20180360 CrossRef.
- O. Deparis and J.-P. Vigneron, Mater. Sci. Eng., B, 2010, 169, 12–15 CrossRef CAS.
- B. D. Wilts, K. Michielsen, H. De Raedt and D. G. Stavenga, J. R. Soc., Interface, 2012, 9, 1609–1614 CrossRef.
- B. D. Wilts, K. Michielsen, J. Kuipers, H. De Raedt and D. G. Stavenga, Proc. R. Soc. London, Ser. B, 2012, 279, 2524–2530 Search PubMed.
- S. R. Mouchet, J.-F. Colomer, C. Vandenbem, O. Deparis and J.-P. Vigneron, Opt. Express, 2013, 21, 13228–13240 CrossRef.
- X. Wu, A. Erbe, D. Raabe and H.-O. Fabritius, Adv. Funct. Mater., 2013, 23, 3615–3620 CrossRef CAS.
- B. D. Wilts, N. IJbema, K. Michielsen, H. De Raedt and D. G. Stavenga, Mater. Res. Soc. Symp. Proc., 2013, 1504, mrsf12-1504-v08-03 CrossRef.
- L. T. McDonald, S. Narayanan, A. Sandy, V. Saranathan and M. E. McNamara, Biol. Lett., 2020, 16, 20200063 CrossRef.
- J.-P. Vigneron, J.-F. Colomer, N. Vigneron and V. Lousse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061904 CrossRef.
- F. Liu, B. Q. Dong, X. H. Liu, Y. M. Zheng and J. Zi, Opt. Express, 2009, 17, 16183–16191 CrossRef CAS.
- B. Q. Dong, X. H. Liu, T. R. Zhan, L. P. Jiang, H. W. Yin, F. Liu and J. Zi, Opt. Express, 2010, 18, 14430–14438 CrossRef CAS.
- B. Q. Dong, T. R. Zhan, X. H. Liu, L. P. Jiang, F. Liu, X. H. Hu and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011915 CrossRef CAS.
- J.-F. Colomer, P. Simonis, A. Bay, P. Cloetens, H. Suhonen, M. Rassart, C. Vandenbem and J.-P. Vigneron, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 011907 CrossRef.
- S. R. Mouchet, M. Lobet, B. Kolaric, A. M. Kaczmarek, R. Van Deun, P. Vukusic, O. Deparis and E. Van Hooijdonk, Mater. Today: Proc., 2017, 4, 4979–4986 Search PubMed.
- P. Vukusic, R. Kelly and I. Hooper, J. R. Soc., Interface, 2009, 6, S193–S201 Search PubMed.
- J. Veron, A. O’Farrell and B. Dixon, Tissue Cell, 1974, 6, 613–626 CrossRef CAS.
- M. D. Shawkey and G. E. Hill, J. Exp. Biol., 2006, 209, 1245–1250 CrossRef CAS.
- E. R. Dufresne, H. Noh, V. Saranathan, S. G. J. Mochrie, H. Cao and R. O. Prum, Soft Matter, 2009, 5, 1792–1795 RSC.
- H. Noh, S. F. Liew, V. Saranathan, S. G. J. Mochrie, R. O. Prum, E. R. Dufresne and H. Cao, Adv. Mater., 2010, 22, 2871–2880 CrossRef CAS.
- V. Saranathan, J. D. Forster, H. Noh, S.-F. Liew, S. G. J. Mochrie, H. Cao, E. R. Dufresne and R. O. Prum, J. R. Soc., Interface, 2012, 9, 2563–2580 CrossRef.
- H. Yin, B. Dong, X. Liu, T. Zhan, L. Shi, J. Zi and E. Yablonovitch, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10798–10801 CrossRef CAS.
- J. Tinbergen, B. D. Wilts and D. G. Stavenga, J. Exp. Biol., 2013, 216, 4358–4364 CrossRef.
- T. Ueta, G. Fujii, G. Morimoto, K. Miyamoto, A. Kosaku, T. Kuriyama and T. Hariyama, Europhys. Lett., 2014, 107, 34004 CrossRef.
- C. D’Ambrosio, D. C. Skigin, M. E. Inchaussandague, A. Barreira and P. Tubaro, Phys. Rev. E, 2018, 98, 032403 CrossRef.
- R. O. Prum, J. A. Cole and R. H. Torres, J. Exp. Biol., 2004, 207, 3999–4009 CrossRef.
- M. J. Henze, O. Lind, B. D. Wilts and A. Kelber, J. R. Soc., Interface, 2019, 16, 20180785 CrossRef CAS.
- S. Magkiriadou, J.-G. Park, Y.-S. Kim and V. N. Manoharan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062302 CrossRef.
- G. Jacucci, S. Vignolini and L. Schertel, 2020, arXiv:2006.05230v1, 1–6.
- J. D. Forster, H. Noh, S. F. Liew, V. Saranathan, C. F. Schreck, L. Yang, J.-G. Park, R. O. Prum, S. G. Mochrie, C. S. O’Hern, H. Cao and E. R. Dufresne, Adv. Mater., 2010, 22, 2939–2944 CrossRef CAS.
- A. Kawamura, M. Kohri, G. Morimoto, Y. Nannichi, T. Taniguchi and K. Kishikawa, Sci. Rep., 2016, 6, 33984 CrossRef CAS.
- M. Iwata, M. Teshima, T. Seki, S. Yoshioka and Y. Takeoka, Adv. Mater., 2017, 29, 1605050 CrossRef.
- D. G. Stavenga, S. Stowe, K. Siebke, J. Zeil and K. Arikawa, Proc. R. Soc. London, Ser. B, 2004, 271, 1577–1584 CAS.
- D. G. Stavenga, M. A. Giraldo and B. J. Hoenders, Opt. Express, 2006, 14, 4880–4890 CrossRef CAS.
- N. I. Morehouse, P. Vukusic and R. Rutowski, Proc. R. Soc. London, Ser. B, 2007, 274, 359–366 CrossRef CAS.
- S. M. Luke, P. Vukusic and B. Hallam, Opt. Express, 2009, 17, 14729–14743 CrossRef CAS.
- J. Lafait, C. Andraud, S. Berthier, J. Boulenguez, P. Callet, S. Dumazet, M. Rassart and J.-P. Vigneron, Mater. Sci. Eng., B, 2010, 169, 16–22 CrossRef CAS.
- P. Vukusic, B. Hallam and J. Noyes, Science, 2007, 315, 348 CrossRef CAS.
- M. Burresi, L. Cortese, L. Pattelli, M. Kolle, P. Vukusic, D. S. Wiersma, U. Steiner and S. Vignolini, Sci. Rep., 2014, 4, 6075 CrossRef CAS.
- L. Cortese, L. Pattelli, F. Utel, S. Vignolini, M. Burresi and D. S. Wiersma, Adv. Opt. Mater., 2015, 3, 1337–1341 CrossRef CAS.
- M. R. Nixon, A. G. Orr and P. Vukusic, J. R. Soc., Interface, 2017, 14, 20170036 CrossRef.
- K. Makino, K. Satoh, M. Koiki and N. Ueno, Annot. Zool. Jpn., 1952, 27, 113–114 Search PubMed.
- G. Jacucci, J. Bertolotti and S. Vignolini, Adv. Opt. Mater., 2019, 1900980, 1–6 Search PubMed.
- B. T. Hallam, A. G. Hiorns and P. Vukusic, Appl. Opt., 2009, 48, 3243–3249 CrossRef CAS.
- E. Van Hooijdonk, C. Barthou, J.-P. Vigneron and S. Berthier, J. Lumin., 2013, 136, 313–321 CrossRef CAS.
- S. R. Mouchet, C. Verstraete, A. M. Kaczmarek, D. Mara, S. van Cleuvenbergen, R. Van Deun, T. Verbiest, B. Maes, P. Vukusic and B. Kolaric, J. Biophotonics, 2019, 12, e201800470 CrossRef.
- J. A. Noyes, P. Vukusic and I. R. Hooper, Opt. Express, 2007, 15, 4351–4358 CrossRef CAS.
- S. Yoshioka, Structural Color in Nature: Basic Observations and Analysis, in Pattern Formations and Oscillatory Phenomena, ed. S. Kinoshita, Elsevier, 2013 Search PubMed.
- E. Adachi, J. Morphol., 2007, 268, 826–829 CrossRef.
- F. Schenk, B. D. Wilts and D. G. Stavenga, Bioinspiration Biomimetics, 2013, 8, 045002 CrossRef.
- D. G. Stavenga, B. D. Wilts, H. L. Leertouwer and T. Hariyama, Philos. Trans. R. Soc., B, 2011, 366, 709–723 CrossRef.
- S. Yoshioka and S. Kinoshita, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 051917 CrossRef.
- S. Yoshioka, S. Kinoshita, H. Iida and T. Hariyama, J. Phys. Soc. Jpn., 2012, 81, 054801 CrossRef.
- O. Deparis, C. Vandenbem, M. Rassart, V. L. Welch and J.-P. Vigneron, Opt. Express, 2006, 14, 3547–3555 CrossRef CAS.
- J.-P. Vigneron, M. Rassart, C. Vandenbem, V. Lousse, O. Deparis, L. P. Biró, D. l Dedouaire, A. Cornet and P. Defrance, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041905 CrossRef.
- O. Deparis, M. Rassart, C. Vandenbem, V. L. Welch, J.-P. Vigneron and S. Lucas, New J. Phys., 2008, 10, 013032 CrossRef.
- P. Vukusic, J. R. Sambles, C. Lawrence and G. Wakely, Appl. Opt., 2001, 40, 1116–1125 CrossRef CAS.
- J. Medhi, Statistical Methods: An Introductory Text, New Age International, 1992 Search PubMed.
- L. E. R. Picken, The Organization of cells and other organisms, Clarendon Press, Oxford, 1962 Search PubMed.
- J. M. Pasteels, O. Deparis, S. R. Mouchet, D. M. Windsor and J. Billen, Arthropod Struct. Dev., 2016, 45, 509–518 CrossRef.
- O. D. Onelli, T. van de Kamp, J. N. Skepper, J. Powell, T. Dos Santos Rolo, T. Baumbach and S. Vignolini, Sci. Rep., 2017, 7, 1373 CrossRef.
- J.-P. Vigneron, M. Ouedraogo, J.-F. Colomer and M. Rassart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021907 CrossRef.
- R. O. Prum, R. L. Morrison and G. R. Ten Eyck, J. Morphol., 1994, 222, 61–72 CrossRef.
- R. O. Prum, R. Torres, C. Kovach, S. Williamson and S. M. Goodman, J. Exp. Biol., 1999, 202, 3507–3522 Search PubMed.
- T. Trzeciak and P. Vukusic, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061908 CrossRef.
- K. F. A. Ross and E. Billing, J. Gen. Microbiol., 1957, 16, 418–425 CrossRef CAS.
- J. A. Valkenburg and C. L. Woldringh, J. Bacteriol., 1984, 160, 1151–1157 CrossRef CAS.
- A. P. Leis, S. Schlicher, H. Franke and M. Strathmann, Appl. Environ. Microbiol., 2005, 71, 4801–4808 CrossRef CAS.
- T.-M. Lee, F. J.-J. Toublan, A. Oldenburg, S. Sitafalwalla, W. Luo, D. L. Marks, K. S. Suslick and S. A. Boppart, Proc. SPIE, 2003, 4967, 129–134 CrossRef.
- Y. Jiang, R. Wang, L. Feng and D. Zhang, Opt. Mater., 2018, 75, 74–78 CrossRef CAS.
- P. Freyer, B. D. Wilts and D. G. Stavenga, Interface Focus, 2019, 9, 20180043 CrossRef.
- P. Freyer and D. G. Stavenga, Faraday Discuss., 2020 10.1039/D0FD00033G.
- B. Delaunay, Bull. Acad. Sci. URSS, Cl. Sci. Math. Nat., 1934, 6, 793–800 Search PubMed.
- I. B. J. Sollas, Proc. R. Soc. London, Ser. B, 1907, 79, 474–481 Search PubMed.
- H. L. Leertouwer, B. D. Wilts and D. G. Stavenga, Opt. Express, 2011, 19, 24061–24066 CrossRef CAS.
- G. M. Hale and M. R. Querry, Appl. Opt., 1973, 12, 555–563 CrossRef CAS.
- D. G. Stavenga, H. L. Leertouwer, D. C. Osorio and B. D. Wilts, Light: Sci. Appl., 2015, 4, e243 CrossRef.
- W. Song, L. Zhang, S. Ness and J. Yi, Biomed. Opt. Express, 2017, 8, 3966–3980 CrossRef CAS.
- A. R. Spurr, J. Ultrastruct. Res., 1969, 26, 31–43 CrossRef CAS.
- N. Smirnov, Ann. Math. Stat., 1948, 19, 279–281 CrossRef.
- K. L. Elmore, Weather Forecast., 2005, 20, 789–795 CrossRef.
- D. B. Judd and G. Wyszecki, Color in Business, Science and Industry, John Wiley & Sons, 1975 Search PubMed.
- G. J. Chamberlin and D. G. Chamberlin, Colour: Its Measurement, Computation and Application, Heyden International Topics in Science, 1980 Search PubMed.
- P. Yeh, Optical Waves in Layered Media, Wiley-Interscience, 2005 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0fd00101e |
| ‡ Current address: School of Biological, Earth and Environmental Sciences, University College Cork, Distillery Fields, North Mall, Cork T23 TK30, Ireland. |
| This journal is © The Royal Society of Chemistry 2020 |