Open Access Article
Open Access ArticleBiophotonics of diversely coloured peacock tail feathers
Pascal
Freyer
 and
Doekele G.
Stavenga
and
Doekele G.
Stavenga

Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747AG Groningen, The Netherlands. E-mail: p.freyer@rug.nl; d.g.stavenga@rug.nl
First published on 12th May 2020
Abstract
Peacock feathers feature a rich gamut of colours, created by a most sophisticated structural colouration mechanism. The feather barbules contain biophotonic structures consisting of two-dimensionally-ordered lattices of cylindrical melanosomes and air channels embedded in keratin. Here, we study the reflectance characteristics of the various peacock tail feather colours by applying bifurcated-probe- and micro-spectrophotometry and imaging scatterometry. We compare the experimental results with published anatomical SEM and TEM data, using a transfer-matrix based effective-medium multilayer model that includes the number and diameter of the melanosome rodlets and air channels, the lattice spacing and the keratin cortex thickness, together with the recently determined wavelength-dependence of the refractive indices of keratin and melanin. Slight variations in the parameter values cause substantial changes in the spectral position and shape of the reflectance bands. We find that the number of layers crucially determines the number of peaks in the reflectance spectra. For a small number of melanosome layers, the reflectance band shape is particularly sensitive to the properties of the uppermost layer, which provides a simple mechanism for tuning the feather colours.
Introduction
Peacocks are famous for their colourful plumage. The striking blue breast feathers, as well as the richly patterned tail feathers, are structurally coloured by arguably one of the most sophisticated photonic crystal structures found in birds.1–3 The diverse colours are created by two-dimensionally-ordered rectangular lattices in the barbules that consist of melanin rodlets (melanosomes) interlaced by air channels that are embedded in keratin.4,5In bird feathers, structural colouration is widespread,1 but the underlying optical mechanisms are diverse.2 For instance, pigeon neck feathers are coloured by keratin thin films.6–9 The barbs of many bird species, e.g. parrots, kingfishers, and rollers, contain nano-sized, spongy-structured cells that selectively reflect short-wavelength light by constructive interference.2,3,10–13 The barbules of bird-of-paradise feathers and the common bronzewing contain stacks of planar arranged melanin rodlets in keratin, which act as multilayer reflectors.14–17 Layers of hollow cylindrical melanosomes colour the feather barbules of starlings, magpies, and turkeys.18–21 The extreme iridescence of hummingbird feathers is created by stacks of air-filled melanosome platelets in the barbules.1,22–25
Peacock feather barbules contain a rectangular lattice of solid melanosomes and air channels, which is a unique arrangement compared to other iridescent birds. The anatomy of peacock feathers has been studied in extensive detail by Durrer.1,4,5 To understand the various feather colours, he treated the different photonic lattices of peacock barbules as a periodic multilayer. Applying Bragg’s law, he calculated reflectance peak wavelengths that generally corresponded to the observed colours.1,4 Subsequent spectrophotometry on peacock tail, neck and shoulder feathers yielded a variety of single- and double-peaked reflectance spectra, which were interpreted by various optical methods.26–30
We recently studied the blue feathers of the peacock’s neck and breast, applying spectrophotometry and imaging scatterometry. The measured spectra could be well explained with an effective-medium multilayer model.31 Extending this approach, here we present a detailed set of reflectance spectra of the tail feathers with a comprehensive analysis of the feathers’ rich colouration pattern, using recently determined refractive index values of bird keratin and melanin.16,32 We include all six colour regions that were characterized by Durrer1,4,5 and highlight the key optical parameters that determine the reflectance band shape. The latter crucially depends on the number of layers and furthermore is very sensitive to the uppermost layers of the photonic structure, particularly the keratin cortex, which has effects that have so far been insufficiently addressed.
Materials and methods
Peacock feathers and photography
Tail feathers of the peacock, Pavo cristatus, were collected at a children’s farm in Groningen (The Netherlands) and at a private peacock holding in the Western Cape (South Africa). Photomacrographs of the feathers were made with a Canon EOS 30D camera. Micrographs were made with an Olympus SZX16 stereomicroscope (Olympus, Tokyo, Japan) equipped with an Olympus SC30 camera and a Zeiss Universal microscope (Zeiss AG, Oberkochen, Germany) fitted with a ScopeTek DCM510 camera.Imaging scatterometry
To investigate the spatial reflection characteristics of the barbules, we performed imaging scatterometry.33–36 An isolated barbule was attached to a glass micropipette and then positioned at the first focal point of the ellipsoidal mirror of the scatterometer. Narrow-aperture scatterograms were obtained by focusing a white light beam with aperture <5° on a small circular area (diameter 13 μm) of a single barbule cell and then monitoring the spatial distribution of the far-field scattered light. The exposure times of the scatterograms were appropriately adjusted to obtain a clear image without overexposure.Spectrophotometry
Reflectance spectra of the different areas of the tail feathers were measured with a bifurcated fiber probe (Avantes FCR-7UV200), connected to a CCD detector array spectrometer (Avantes AvaSpec-2048, Apeldoorn, The Netherlands). The light source was a deuterium–halogen lamp (Avantes AvaLight-D(H)-S), and the reference was a white diffusely scattering reflection tile (Avantes WS-2). Reflectance spectra of small barbule areas were measured with a microspectrophotometer (MSP). The MSP was a Leitz OrthoLux microscope (Leitz, Wetzlar, Germany) with a LUCPlanFL N 20×/0.45 objective (Olympus, Tokyo, Japan) and a xenon arc lamp light source. The area measured with the MSP was a square (edge length 5–10 μm), determined by a diaphragm in the microscope’s image plane, which was in turn imaged at the entrance of an optical fiber connected to the detector array spectrometer. Due to the glass optics in the microscope, the MSP spectra were limited to wavelengths >360 nm. However, this limitation appeared to be unimportant, because the bifurcated probe measurements showed that the reflectance in the UV was minimal for all feather areas. The probe and MSP collect light from a limited aperture and therefore the measured reflectance depends on the spatial reflection properties of the object. Scatterometry demonstrated that the barbules are specular-reflecting. We estimated that, with a diffuse reflector as a reference, the measured probe reflectance is too large by a factor of ∼4. We therefore present the probe reflectance divided by 4. The MSP peak reflectances were scaled to the respective probe spectra and modelled spectra. In order to obtain representative spectra for the varying barbule cell colours of the different regions, we compared the modelling results with the mean of the MSP spectra that were measured from a large set of cells of a single barbule in regions 1–5. As the main aim of our study was to gain understanding of the colouration mechanism of the peacock’s tail feathers, we specifically focused on the shape of the spectrum in our analysis.Anatomy
We combined the anatomical data of peacock tail barbules from the extensive transmission electron microscopy (TEM) studies performed by Durrer and Villiger4,5,37 with the scanning electron microscopy (SEM) study by Jiang et al.38 (see Table 1). These sources did not specify the cortex thickness of the feather barbules of the peacock. We therefore started our modelling with the mean anatomical parameters of Durrer and Jiang et al.4,5,38 and then adjusted them together with the cortex thickness to obtain an optimal fit to the measured spectra.| a (nm) | b (nm) | c (nm) | D m (nm) | D a (nm) | N m | |
|---|---|---|---|---|---|---|
| a The six feather regions are given as R1 to R6; a: longitudinal period; b: lateral period; c: cortex thickness; Dm: melanosome diameter; Da: air channel diameter; Nm: number of melanosome layers. The asterisk indicates that the first air channel layer was omitted in the modelling. The values of parameter a in brackets indicate values taken for only the first melanosome period (see main text). | ||||||
| R1 black–violet | ||||||
| Durrer4,5,37 | 150–170 | 140–165 | 70–130 | 100–110 | 33 | 9–11 |
| Zi27 | 140 | 140 | — | 112 | 70 | 9–12 |
| Jiang38 | 128–151 | 116–134 | — | 113–126 | 30–40 | 9–11 |
| Model | 140 | 150 | 100 | 100 | 33 | 10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| R2 blue–green | ||||||
| Durrer4,5 | 157–175 | 150–190 | — | 100–120 | — | 9–10 |
| Yoshioka26 | 150 | 150 | — | 130 | — | 8–12 |
| Zi27 | 150 | 150 | — | 120 | 75 | 9–12 |
| Jiang38 | 153–178 | 112–131 | — | 106–119 | 52–63 | 5–8 |
| Model | 160 | 170 | 100 | 110 | 33 | 9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| R3 brown | ||||||
| Durrer4,5 | 198–223 | 135–172 | — | 100–120 | — | 5–7 |
| Zi27 | 185 | 150 | — | 120 | 75 | 6* |
| Li28 | 185 (235) | 150 | — | 120 | 75 | 6* |
| Medina29 | 198 (231) | 187 | — | — | — | 4–5 |
| Model | 190 | 150 | 70 | 110 | 50 | 5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| R4 green–yellow | ||||||
| Durrer4,5,37 | 190–220 | 115–190 | 100–160 | 100–130 | 55 | 4–6 |
| Yoshioka26 | 190 | 190 | — | 140 | — | 3–6 |
| Zi27 | 165 | 165 | — | 132 | 83 | 4 |
| Model | 195 | 150 | 130 | 120 | 55 | 5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| R5 purple | ||||||
| Durrer4,5 | 180–228 | 160–250 | — | 110–130 | — | 4–7 |
| Model | 185 (240) | 190 | 140 | 100 | 70 | 3* |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| R6 brass–green | ||||||
| Durrer4,5 | 180–240 | 140–180 | — | 110–135 | — | 3–6 |
| Model 1 | 185 | 160 | 130 | 120 | 70 | 4* |
| Model 2 | 185 (240) | 160 | 150 | 100 | 70 | 3* |
Effective-medium multilayer modelling
We interpreted the measured reflectance spectra with an effective-medium multilayer model using a transfer matrix program based on classical optical multilayer theory.39,40 Taking the previously published anatomical data,4,38 we sliced the melanosome and air channel stack into 1 nm thin layers and for each layer calculated the volume fractions of the component media, keratin, fk, melanin, fm, and air, fa, with fk + fm + fa = 1. The effective refractive index of each 1 nm layer was then calculated with these volume fractions and the refractive indices of the component media; for keratin, nk = Ak + Bkλ−2, with Ak = 1.532 and Bk = 5890 nm2; for melanin, ñm = nm − ikm, with nm = Am + Bmλ−2 and km = am![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ/bm), where Am = 1.648, Bm = 23
exp(−λ/bm), where Am = 1.648, Bm = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 nm2, am = 0.56, and bm = 270 nm;16,32 for air, na = 1. The complex effective refractive index of each 1 nm layer was then obtained:
700 nm2, am = 0.56, and bm = 270 nm;16,32 for air, na = 1. The complex effective refractive index of each 1 nm layer was then obtained:| ñeff = (fknkw + fmñmw + fanaw)1/w, | (1) |
Results
The appearance of the colour regions
Peacock tail feathers have a brightly coloured eye-like pattern at their distal end. The pattern can be categorised into six differently coloured regions with a macroscopic appearance of: (1) violet–black; (2) blue–green; (3) brown; (4) green–yellow; (5) purple; and (6) brass–green (Fig. 1a; see also ref. 4 and 5). The colours originate from the barbules, the branches of the feather barbs (Fig. 1b–d; see also ref. 5).The individual barbules consist of rows of cells with size, shape and colour depending on their location (Fig. 1e–j). Notably, the cells in the central and distal parts of the barbules display a large coloured surface. This is especially the case in feather region 2, where the barbules are very densely packed, and together create a brightly coloured area (Fig. 1d). In contrast, the barbules in region 1 show only a subdued violet in the distal part of the barbule (Fig. 1e). Here, the barbules are strongly tilted, thus creating the dark velvety-black appearance of the central feather area with a slight violet tinge (Fig. 1a; arrow head I in Fig. 1d). The proximal cells of the barbules in region 1 are less tilted and have only a brown pigmentary colour (arrow head II in Fig. 1d; anatomy shown in ref. 4).
Imaging scatterometry of the feather barbule cells
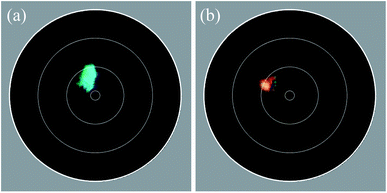
To investigate the spatial reflection characteristics of the barbules of the peacock tail feathers, we performed imaging scatterometry on single barbule cells from blue–green region 2 and brown region 3. A narrow aperture light beam, focused on a small area of a single barbule cell, yielded nearly specular reflections (Fig. 2a and b). Illumination of larger barbule cell areas yielded scattering patterns with a wider spatial distribution (not shown) due to the curved surface of the barbules (Fig. 1f and g; Fig. 3a). | ||
| Fig. 3 Anatomy of the peacock tail feather barbules (reproduced from ref. 5). (a) TEM image of the cross-section of a barbule from region 3. (b–g) TEM cross-sections of the photonic structures in the six colour regions, 1–6 (Fig. 1). The black dots represent melanin rodlets, the light grey areas are the air channels, and the darker grey is due to keratin. As in Fig. 1e–j, the number in the lower left-hand corner and the colour bar indicate the feather region. Scale bars: (a) 5 μm, (b–g) 0.5 μm. | ||
Anatomy and photonic structure of the six colour regions
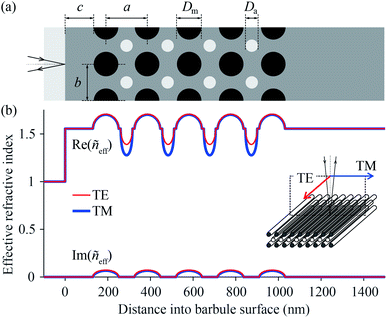
The scatterometry results can be directly understood from the barbule anatomy, as revealed by transmission electron microscopy (Fig. 3), where the cross-section of a barbule cell shows its curvature (Fig. 3a). The dark outer rim of the barbule cell indicates high melanin pigmentation (Fig. 3a). The melanin is contained in solid rodlets (melanosomes), which are arranged in a two-dimensional rectangular lattice embedded in a keratin matrix (Fig. 3b–g). The layers of melanosomes are interspersed with layers of air channels, which have a less uniform shape compared to the melanosomes.4,5 Durrer demonstrated that the arrangement and dimensions of the melanosome layers are characteristic of the colours of the different regions.4,5 The different photonic structures vary in the number of layers and the size, periodicity and ordering of the melanosomes and air channels (Fig. 3b–g); but how do these structures cause different colours?To answer this question, we derived the parameter values of the component media from the reported anatomical data (Table 1), and using eqn (1) we calculated the refractive index profiles of the various barbules as a function of wavelength and depth into the barbule surface. As an example, Fig. 4a shows a stack of 5 melanosome layers and 4 air channel layers, similar to the structure of region 4. Fig. 4b presents the corresponding effective refractive index profiles for TE- and TM-polarised light with a wavelength of 500 nm. Implementing the refractive index profiles of the different barbules in a transfer matrix program allowed the calculation of the reflectance spectra, which we compared with the measurements. In the reflectance modelling we only considered the melanosome–air channel stack on the upper side of the barbule and neglected the stack on the bottom surface. Previous modelling demonstrated that the lower melanosome–air channel stack and the randomly occurring melanosomes in the barbule interior contribute at most a very small fraction to the total reflection. Modelling of only the upper stack is therefore adequate.20,31,44
Spectrophotometry
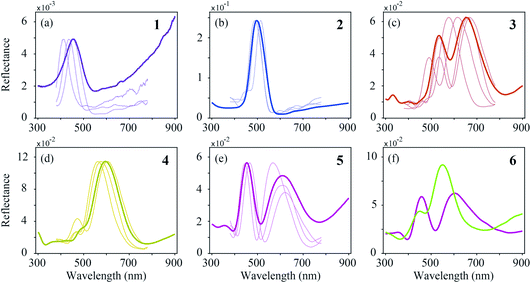
In order to reach a quantitative understanding of the colours of the different feather regions, we performed spectrophotometry using a bifurcated reflection probe (Fig. 5, bold curves). The reflectance spectrum of violet–black region 1 features a single band peaking at ∼450 nm (Fig. 5a). Its amplitude is very low, corresponding to the black appearance of region 1. The reflectance spectra of blue–green region 2 and green–yellow region 4 (Fig. 5b and d) also have single bands, peaking at ∼500 nm and ∼600 nm, respectively, but with a much larger amplitude. Quite differently, the reflectance spectra of the brown- and purple-coloured regions 3 and 5 (Fig. 5c and e) are double-peaked, with peak wavelengths at ∼530 nm and ∼660 nm (region 3) and ∼450 nm and ∼620 nm (region 5). The band structure of the reflectance spectra of brass–green region 6 strongly varies, depending on the measurement location (Fig. 5f).In the bifurcated probe measurements, the illumination area is rather large (diameter ∼1 mm), and therefore the probe spectra contain the averaged reflectance of many barbule cells. To investigate the local variation of the spectra we measured the reflectance spectra of single barbule cells with a microspectrophotometer (MSP; Fig. 5, thin curves). Although the MSP spectra measured in the various colour regions varied in peak shape and position, they were on average very similar to the local probe spectra.
Effective-medium multilayer modelling
We compared the measured reflectance spectra with modelled spectra, calculated as described in the Materials and methods section. The average of the locally measured MSP spectra (Fig. 6, solid curves) was compared with the modelled spectra (Fig. 6, dashed curves) that were computed using the parameter sets derived from the literature (Table 1). We started the modelling using these parameter values initially with a guessed cortex thickness. Subsequently, we optimized the lattice to reach an optimal fit to the experimentally measured spectra while obeying the range of variation of the literature parameters.4,5,26–28,37,38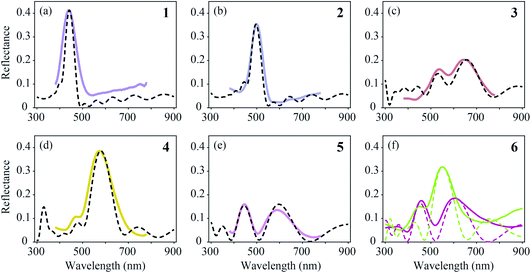 | ||
| Fig. 6 Averages of MSP spectra (solid curves) and spectra calculated by effective-medium multilayer modelling (dashed curves). (a–e) MSP and modelled spectra for regions 1–5. (f) Two probe spectra of region 6 (Fig. 5f) compared with modelled spectra. | ||
The feather regions 1, 2 and 4 have single-peaked reflectance spectra. Modelling of the spectra required only slight adjustments of the cortex thickness and the lattice period. A satisfactory correlation between the measured and modelled spectra was readily obtained for the three regions by taking the lattice periods a = 140, 160, and 195 nm, melanosome diameters Dm = 100, 110, and 120 nm, and number of melanosome layers Nm = 10, 9, and 5, respectively. For the air channel diameter we used the parameter values obtained by Durrer and Villiger:37Da = 33, 33, and 55 nm, respectively (other anatomical studies reported a large variation in the air channel diameter; see Table 1 and Fig. 3b–g). Modelling showed that varying the air channel diameter mainly affected the peak amplitude and the bandwidth of the reflectance spectra, but hardly affected the peak wavelength.
During the fitting procedure, an essential parameter governing the peak shape appeared to be the keratin cortex thickness. Since no anatomical data exists for the cortex thickness in the Pavo genus, we estimated its value for the three regions via the closest fit to the experimentally measured spectra. A value of c = 100 nm followed for regions 1 and 2, whereas for region 4 appropriate fits were obtained for c = 130 nm. These values agree well with the cortex thickness range of the violet–black and blue–green tail feather barbules of the Congo peacock, Afropavo congensis: 70–130 nm and 100–160 nm, respectively.37
The brown (region 3, Fig. 5c and 6c) and purple (region 5, Fig. 5e and 6e) feathers yielded double-peaked reflectance spectra, which could also be modelled well. For region 3 we derived a large period value, a = 190 nm, together with a small cortex thickness, c = 70 nm. In order to obtain a modelled spectrum with the same spectral shape as the measured spectra for region 5, we concluded a general lattice period of a = 185 nm, but with a first lattice period of about a = 240 nm, together with a cortex thickness of c = 140 nm.
In region 6, both single- and double-peaked reflectance spectra were measured (Fig. 6f), which resembled the spectra of regions 4 and 5, respectively (Fig. 6d and e). Modelling of the single- and double-peaked spectra of region 6 (Fig. 6f, short- and long-dashed curves) revealed that the final parameter values were similar to those of regions 4 and 5, respectively (see Table 1: R4 vs. Model 1, and R5 vs. Model 2). The single- and double-peaked spectra of region 6 could both be modelled well by changing mainly the first lattice period (a = 185 nm vs. a = 240 nm), with a slightly adjusted cortex thickness (c = 130 nm vs. c = 150 nm), melanosome diameter (Dm = 120 nm vs. Dm = 100 nm), and layer number, while keeping the remaining lattice spacing and air channel diameter constant (see Table 1: Model 1 vs. Model 2). Apparently, the single- and double-peaked reflectance spectra coexist in a single colour region by slightly varying the structure, especially that of the uppermost layers.
Discussion
Peacock tail feathers display a rich colour palette due to barbules containing basically the same photonic components but with large variation in the different feather regions, as demonstrated by the detailed anatomical studies by Durrer.1,4,5 The barbules in region 1 are closely packed and oriented nearly perpendicular to the feather plane (Fig. 1e). Normally incident light is thus scattered sideways and also inwards, resulting in a very low reflectance, similar to the case of the “super black” feathers of birds of paradise.45 Very differently, in regions 2–6 the cells in the middle and distal area of the barbules are about parallel to the feather plane (Fig. 1f–j), clearly to maximize the reflectance (Fig. 5b–f). Consequently, lowly reflecting region 1 and highly reflecting regions 2–6 together create an extreme colour contrast in the centre of the eye-like pattern of the peacock tail feathers.Yoshioka and Kinoshita measured the reflectance spectra of the blue neck feathers as well as the yellow tail covert feathers and modelled the angle dependence of the spectra with a scalar field approximation.26 Furthermore, Zi et al. studied various coloured barbules in the eye pattern of the tail feathers of a male green peafowl (Pavo muticus).27 Using a plane wave expansion method, they calculated the photonic band structure of a 2D photonic crystal and also applied a transfer matrix method to compute reflectance spectra. Here we extended the previous studies by applying effective-medium multilayer modelling, which allowed the calculation of the feathers’ reflectance spectra for various coloured regions of the tail feathers by choosing appropriate parameter values and also adding the so far neglected cortex.
The amplitude of the feather reflectance of course crucially depends on the packing density of the barbules. Notably, the feather barbules are rather loosely packed in regions 3–6. Furthermore, the barbule is curved and the barbule cells are saddle-shaped and thus reflect incident light with a large spatial angle, which makes quantitative modelling of the reflectance cumbersome. We have therefore focused on interpreting the spectral positions and shapes of the measured reflectance spectra. Using parameter values predominantly from the literature4,5,37 (Table 1), the single-peaked spectra were readily modelled, with only minor adjustments to the layer periodicity in order to match the peak wavelengths, λmax. For the modelling of double-peaked spectra that fitted well with the experimentally measured spectra, the adjustment of several parameter values was necessary.
In the classical case, where the melanosome–air-layer stack is treated as an ideal multilayer reflector, the reflectance spectrum features a single, main band. The lattice period determines its peak wavelength, and the bandwidth decreases with an increase in the number of periods (see Land,46 for instance). However, when the melanosome–air-layer stack consists of only a few periods (as in regions 3–6), minor changes in the spacing of the first layers can cause distinct modulations in the reflectance spectra.28,29 We found that the keratin cortex and the melanosome diameter in the first lattice periods play a prominent role in adjusting the peak shape. Interestingly, the effect of these peak shape modulating parameters decreases when the number of melanosome layers increases. With a large number of layers the reflectance spectrum is always single-peaked, as occurs in regions 1 and 2.
The MSP spectra measured from various areas in the same barbule vary only slightly (Fig. 5), which indicates that the dimensions of the underlying structures are similar. Subtle deviations from the anatomical parameters as stated in the literature were necessary to achieve satisfactory modelling results. This is not surprising, as the anatomical data obtained by electron microscopy inevitably represent data from a very restricted set of barbule cells. The parameter values deduced from the anatomical data can furthermore suffer from preparation artefacts, for instance the uncertainty of whether the section is perpendicular to the barbule surface.
The modelling of a specific spectrum allowed a small range of freedom, especially since the effects of each structure parameter depend on the choice of the other parameters. For instance, the number of melanosome and air channel layers, together with the air channel diameter, mainly affect the peak reflectance and bandwidth, while the cortex thickness, the melanosome diameter and the lattice-spacing prominently affect the peak wavelength and whether the spectrum is single- or double-peaked. Nonetheless, the parameter space for modelling the position and shape of the spectrum while at the same time adhering to the anatomical values appears to be restricted. The air channel diameter is strongly variable, as already noted by Durrer, who speculated that the channel size is not controlled by an active cellular process as in the case of the melanosome diameter.4,5
The distinct, single-peaked reflectance spectra obviously create a strong visual signal, and it is hence interesting to compare the spectral properties of the various colour regions with the spectral sensitivities of the peacock’s photoreceptors. Vision in the peafowl is tetrachromatic, based on VS, SWS, MWS and LWS photoreceptors with peak spectral sensitivities at 432, 477, 537 and 605 nm, respectively.47 The weakly reflecting region 1 has a reflectance peak wavelength at λmax = 450 nm, in the sensitivity range of the VS and SWS receptors, but the low reflectance is unlikely to cause any excitation, rather an area that highly contrasts with its surroundings. The brightly reflecting region 2, with λmax = 500 nm, will activate the SWS and MWS receptors; the two reflectance bands of region 3, with λmax = 530 and 660 nm, correspond to the MWS and LWS spectra. Region 4, with λmax = 600 nm, matches LWS; and the two reflectance bands of region 5, with λmax = 450 and 620 nm, are well tuned to VS and LWS. In other words, the males’ tail feather patterns, when displayed, will be properly discriminated by the visual system of the choosy females (see also Kane et al.48). The relative contribution of the various areas of the multi-coloured eyespots to the male’s mating success has been investigated by Dakin and Montgomerie.49 They concluded that the blue–green eyespot overwhelmingly influences the mating success, while the influence of the other colours is minimal, raising questions about their function. Here we show that the brown region 3 presents quite a uniform optical signal that is spatially well defined, while regions 4, 5 and 6 are more intermixed, particularly in the lower part of the eye pattern (Fig. 1a). It is therefore not surprising to see a close anatomical relationship for the spectra measured in the outer regions, specifically for the coexisting spectra of the outer brass–green region 6 (see Fig. 6c and Table 1). Besides serving as a background surface when the peacock’s feather train is raised, region 6 hence provides an excellent coat of camouflage when the train is lowered, by blending in with the surrounding greens and browns of foliage.
Our comprehensive investigation of the different colour regions of peacock tail feathers demonstrated that small geometrical changes in the barbule’s components, especially those in the uppermost surface layers, can cause large variations in the spectral reflection properties of the peacock’s feathers. The many tail feathers of a peacock nevertheless all display approximately the same colour pattern, which suggests that developmental genetic programs are adequate in controlling the arrangement of the local photonic structures, e.g. the number of melanosome layers, the melanosome diameter and the lattice spacing, to serve the creation of beautiful and even exciting optical signals for the onlooker.
Funding
This study was financially supported by the PhD scholarship programme of the University of Groningen and the Advanced Materials research program of the Zernike National Research Centre under the Bonus Incentive Scheme of the Dutch Ministry for Education, Culture and Science (to P. F.), and the Air Force Office of Scientific Research/European Office of Aerospace Research and Development AFOSR/EOARD (grant FA9550-15-1-0068, to D. G. S.).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank H. L. Leertouwer for providing excellent technical support, A. H. van Zessen for excellent MATLAB programming support and Dr B. D. Wilts for valuable comments on the manuscript.References
- H. Durrer, Denkschr. Schweiz. Naturforsch. Ges., 1977, 91, 1–126 Search PubMed.
- R. O. Prum, in Bird Colouration, Vol. 1, Function and Evolution, ed. G. E. Hill and K. J. McGraw, Harvard University Press, Cambridge, 2006, pp. 295–353 Search PubMed.
- S. Kinoshita, Structural Colors in the Realm of Nature, World Scientific, Singapore, 2008 Search PubMed.
- H. Durrer, Verh. Naturforsch. Ges. Basel, 1962, 73, 204–224 Search PubMed.
- H. Durrer, Rev. Suisse Zool., 1965, 72, 263–412 CrossRef.
- K. J. McGraw, Naturwissenschaften, 2004, 91, 125–129 CrossRef CAS PubMed.
- H. Yin, L. Shi, J. Sha, Y. Li, Y. Qin, B. Dong, S. Meyer, X. Liu, L. Zhao and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051916 CrossRef PubMed.
- S. Yoshioka, E. Nakamura and S. Kinoshita, J. Phys. Soc. Jpn., 2007, 76, 013801 CrossRef.
- E. Nakamura, S. Yoshioka and S. Kinoshita, J. Phys. Soc. Jpn., 2008, 77, 124801 CrossRef.
- M. D. Shawkey, A. M. Estes, L. M. Siefferman and G. E. Hill, Proc. R. Soc. London, Ser. B, 2003, 270, 1455–1460 Search PubMed.
- S. Kinoshita, S. Yoshioka and J. Miyazaki, Rep. Prog. Phys., 2008, 71, 076401 CrossRef.
- D. G. Stavenga, J. Tinbergen, H. L. Leertouwer and B. D. Wilts, J. Exp. Biol., 2011, 214, 3960–3967 CrossRef PubMed.
- L. D’Alba, L. Kieffer and M. D. Shawkey, J. Exp. Biol., 2012, 215, 1272–1277 CrossRef PubMed.
- D. G. Stavenga, H. L. Leertouwer, N. J. Marshall and D. Osorio, Proc. R. Soc. London, Ser. B, 2011, 278, 2098–2104 Search PubMed.
- B. D. Wilts, K. Michielsen, H. De Raedt and D. G. Stavenga, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4363–4368 CrossRef CAS PubMed.
- D. G. Stavenga, H. L. Leertouwer, D. C. Osorio and B. D. Wilts, Light: Sci. Appl., 2015, 4, 1–6 Search PubMed.
- M. Xiao, A. Dhinojwala and M. Shawkey, Opt. Express, 2014, 22, 14625 CrossRef PubMed.
- H. Durrer and W. Villiger, J. Ornithol., 1970, 111, 133–153 CrossRef.
- R. Maia, D. R. Rubenstein and M. D. Shawkey, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10687–10692 CrossRef CAS PubMed.
- D. G. Stavenga, H. L. Leertouwer and B. D. Wilts, J. Exp. Biol., 2018, 221, 174656 CrossRef PubMed.
- C. M. Eliason, P. P. Bitton and M. D. Shawkey, Proc. R. Soc. London, Ser. B, 2013, 280, 20131505 Search PubMed.
- C. H. Greenewalt, W. Brandt and D. D. Friel, J. Opt. Soc. Am., 1960, 50, 1005–1013 CrossRef.
- M. A. Giraldo, J. L. Parra and D. G. Stavenga, J. Comp. Physiol., A, 2018, 204, 965–975 CrossRef CAS PubMed.
- J. Sosa, J. L. Parra, D. G. Stavenga and M. A. Giraldo, J. Ornithol., 2020, 161, 289–296 CrossRef.
- C. M. Eliason, R. Maia, J. L. Parra and M. D. Shawkey, Evolution, 2020, 74, 447–458 CrossRef PubMed.
- S. Yoshioka and S. Kinoshita, Forma, 2002, 17, 169–181 Search PubMed.
- J. Zi, X. Yu, Y. Li, X. Hu, C. Xu, X. Wang, X. Liu and R. Fu, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12576–12578 CrossRef CAS PubMed.
- Y. Li, Z. Lu, H. Yin, X. Yu, X. Liu and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 010902 CrossRef PubMed.
- J. M. Medina, J. A. Díaz and P. Vukusic, Opt. Express, 2015, 23, 10198–10211 CrossRef CAS PubMed.
- T. Okazaki, Zool. Sci., 2018, 35, 86–91 CrossRef PubMed.
- P. Freyer, B. D. Wilts and D. G. Stavenga, J. R. Soc., Interface, 2019, 9, 20180043 Search PubMed.
- H. L. Leertouwer, B. D. Wilts and D. G. Stavenga, Opt. Express, 2011, 19, 24061–24066 CrossRef CAS PubMed.
- D. G. Stavenga, H. L. Leertouwer, P. Pirih and M. F. Wehling, Opt. Express, 2009, 17, 193–202 CrossRef CAS PubMed.
- B. D. Wilts, H. L. Leertouwer and D. G. Stavenga, J. R. Soc., Interface, 2009, 6, 185–192 CrossRef PubMed.
- P. Vukusic and D. G. Stavenga, J. R. Soc., Interface, 2009, 6, 133–148 Search PubMed.
- D. G. Stavenga, B. D. Wilts, H. L. Leertouwer and T. Hariyama, Philos. Trans. R. Soc., B, 2011, 366, 709–723 CrossRef PubMed.
- H. Durrer and W. Villiger, J. Ornithol., 1975, 116, 94–102 CrossRef.
- Y. Jiang, R. Wang, L. Feng and D. Zhang, Opt. Mater., 2018, 75, 74–78 CrossRef CAS.
- P. Yeh, Optical Waves in Layered Media, Wiley, Hoboken, NJ, 2005 Search PubMed.
- D. G. Stavenga, Mater. Today: Proc., 2014, 1, 109–121 Search PubMed.
- R. Bräuer and O. Bryngdahl, Appl. Opt., 1994, 33, 7875–7882 CrossRef PubMed.
- V. Lucarini, J. J. Saarinen, K.-E. Peiponen and E. M. Vartiainen, Kramers-Kronig Relations in Optical Materials Research, Springer, Berlin, 2005, pp. 19–26 Search PubMed.
- R. Halir, P. J. Bock, P. Cheben, A. Ortega-Moñux, C. Alonso-Ramos, J. H. Schmid, J. Lapointe, D. X. Xu, J. G. Wangüemert-Pérez, Í. Molina-Fernández and S. Janz, Laser Photonics Rev., 2015, 9, 25–49 CrossRef CAS.
- D. G. Stavenga, C. J. Van Der Kooi and B. D. Wilts, J. R. Soc., Interface, 2017, 14, 20170407 CrossRef PubMed.
- D. E. McCoy, T. Feo, T. A. Harvey and R. O. Prum, Nat. Commun., 2018, 9, 1–8 CrossRef CAS PubMed.
- M. F. Land, Prog. Biophys. Mol. Biol., 1972, 24, 75–106 CrossRef CAS PubMed.
- N. S. Hart, J. Exp. Biol., 2002, 205, 3925–3935 Search PubMed.
- S. A. Kane, Y. Wang, R. Fang, Y. Lu and R. Dakin, PLoS One, 2019, 14, 0210924 CrossRef PubMed.
- R. Dakin and R. Montgomerie, Behav. Chem. Ecol., 2013, 24, 1048–1057 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |