Open Access Article
Open Access ArticleElectrochemical exfoliation of graphite in H2SO4, Li2SO4 and NaClO4 solutions monitored in situ by Raman microscopy and spectroscopy†
Zhenyuan
Xia
 *ab,
Vittorio
Bellani
*ab,
Vittorio
Bellani
 c,
Jinhua
Sun
a and
Vincenzo
Palermo
ab
c,
Jinhua
Sun
a and
Vincenzo
Palermo
ab
aIndustrial and Materials Science, Chalmers University of Technology, Hörsalsvägen 7B, 41258 Göteborg, Sweden
bIstituto per la Sintesi Organica e la Fotoreattività, CNR, via Gobetti 101, 40129 Bologna, Italy
cDipartimento di Fisica and INFN, Università degli Studi di Pavia, via Bassi 6, 27100 Pavia, Italy
First published on 6th January 2020
Abstract
The electrochemical exfoliation of graphite is one of the cheapest and most tunable industrial techniques to produce graphene nanosheets with a tunable degree of oxidation and solubility. Anodic oxidation allows high-yield production of electrochemically exfoliated graphene oxide (EGO) in either acid or salt solutions, with the key role played by ions electrochemically driven in between the graphene sheets. This chemical intercalation is followed by a mesoscale mechanical exfoliation process, which is key for the high yield of the process, but which is still poorly understood. In this work, we use Raman spectroscopy to simultaneously monitor the intercalation and oxidation processes taking place on the surface of highly ordered pyrolytic graphite (HOPG) during electrochemical exfoliation. The mechanism of EGO formation in either acidic (0.5 M H2SO4) or neutral (0.5 M Li2SO4) electrolytes through blistering and cracking steps is discussed and described. This process is also compared to the non-destructive intercalation of graphite in an organic electrolyte (1 M NaClO4 in acetonitrile). The results obtained show how high exfoliation yield and low defectivity can be achieved by the combination of efficient, non-destructive intercalation followed by chemical decomposition of the intercalants and gas production.
Introduction
The electrochemical exfoliation of graphite is one of the cheapest and most versatile ways to produce 2-dimensional soluble nanosheets. The exfoliation can be easily tuned by varying the applied potential and electrolyte to obtain a wide range of 2D materials, from pristine graphene to highly processable graphene oxide. The electrochemical process is well-known and used industrially for the synthesis of graphite intercalated compounds (GICs) with reversible intercalation/deintercalation properties.1 One of the most relevant applications of GICs is as lithium (Li) anodes for rechargeable Li-ion batteries.2,3 Since the discovery of graphene, the electrochemical exfoliation process has also been extensively studied for the production of graphene sheets.4,5 Typically, the electrochemical exfoliation can be seen as an ‘over-oxidation’ process of the GICs, which involves the formation of GICs with unstable electrolytes in a high electric field, and the subsequent destructive delamination of GIC layers.6 The use of electrochemistry allows a step-controllable oxidation process of graphite by varying the polarity of bias applied,7,8 the use of aqueous or non-aqueous solutions,9,10 or the concentration of the active electrolytes.11,12 The tunability of electrochemistry permits better control of the oxidative damage of the sheets, an eco-friendly process with less consumption of harsh acid, and a faster production rate as compared to the traditional chemical exfoliation approach (e.g. Hummer’s method).13 The high tunability, environmental sustainability and low cost of this technique are already used for large-scale production of graphene-based materials.14Anodic exfoliation allows the high-yield production of electrochemically exfoliated graphene oxide (EGO) sheets with different degrees of oxidation. The most widely used electrochemical production technique is the anodic exfoliation of graphite in either dilute mineral acid or salt electrolytes. For example, Su et al. developed electrochemical exfoliation of EGO in 0.5 M H2SO4 using a high bias of +10 V.15 Parvez et al. reported anodic exfoliation of graphite with 0.1 M (NH4)2SO4 aqueous electrolyte to obtain low defect EGO flakes with a high yield (>80%) of one- to three-layer graphene flakes, high C/O ratio (12.3) and low sheet resistance (4.8 kΩ sq−1 for a single EG sheet).16 We previously reported EGO production with >50% mono and bilayers, C/O ratio of 12.7 and >1 μm flake size, which could be processed in electrodes with 20 Ω sq−1 sheet resistance.17
We also described a two-step exfoliation approach based on the intercalation of uncharged acetonitrile molecules with charged perchlorate, followed by decomposition due to microwave irradiation.17 More recently, Pei et al. and Cao et al. independently reported a two-step approach to achieve full exfoliation of EGO with high oxygen content, where H2SO4-GICs were formed by electrochemical intercalation and then exfoliated in dilute H2SO4 or (NH4)2SO4 electrolyte.18,19
Despite significant efforts to improve EGO production and study its chemistry, the mechanism of its formation on bulk graphite during the anodic process has rarely been reported. It is not clear which electrolyte, solvent and experimental conditions have the best potential to achieve high yield and good quality. A few studies have performed systematic comparisons, mainly based on structural analysis of the morphology of the exfoliated surface acquired by SEM or AFM.13,20 In the present work, we improve this approach by combining optical microscopy and Raman spectroscopy to map, in real time, the chemical disruption of the graphite surface during electrochemical exfoliation in different conditions.
Raman spectroscopy is a powerful non-destructive method for quantitative analysis of carbon-based materials.21 In particular, in situ Raman mapping of bulk graphite flakes allows us to directly identify the intercalation efficiency, defect concentration, and lattice disruption of graphite during the anodic oxidation process.22 We acquired Raman data with high spatial (∼3 μm) and spectral resolution (0.8 cm−1) during the exfoliation of graphite in two types of aqueous electrolytes (0.5 M H2SO4, 0.5 M Li2SO4). This revealed the intermediate reaction products during the ‘over-oxidation’ and surface deformation process. The Raman data allowed a comparison of the EGO formation mechanisms in acid and neutral sulfate ion-based aqueous solutions. The observed chemical changes were also compared with a similar anodic process under a non-aqueous electrolyte (1 M NaClO4 in acetonitrile), which instead features a non-oxidative intercalation reaction.
Experimental
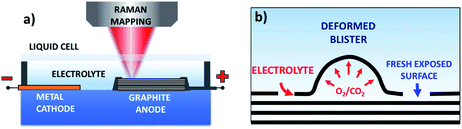
HOPG (12 mm × 12 mm × 2 mm, Grade ZYH) was purchased from GE Advanced Ceramics and exfoliated into thin pieces of size 12 mm × 12 mm × 0.05 mm using Scotch tape. Sulfuric acid (Sigma-Aldrich, 95–97%) and lithium sulfate (Sigma-Aldrich, 99%) were used as the electrolytes for the electrochemical oxidation of the HOPG surface in aqueous solution. Sodium perchlorate (Sigma-Aldrich, 98%) was used as the electrolyte for anodic intercalation of HOPG in acetonitrile solution (Sigma-Aldrich, anhydrous, 99.8%).The electrochemical exfoliation cell included a piece of HOPG, used as the working electrode, and copper foil, used as the counter electrode. Fig. 1 shows the setup of our electrochemical platform. The HOPG electrode (1.2 × 1.2 cm) was obtained by Scotch tape exfoliation and had an average thickness of around 0.05 mm, and was attached to the Cu foil through silver glue. The side faces of the working electrode were sealed with epoxy glue to prevent exposure of the HOPG edges to the electrolyte. Both the working and counter electrodes were fixed by double sided Scotch tape on a glass substrate. The electrolyte solution was added on the graphite and Cu foil surface and covered with a glass slide.
The electrolytes used in this work were 0.5 M H2SO4 (pH ≈ 0.3) or 0.5 M Li2SO4 (pH ≈ 7) in water and 1 M NaClO4 in acetonitrile. The anodic exfoliation of graphite was carried out under a potential of +3 V in acidic and mineral salt electrolytes and +5 V in organic electrolyte at room temperature. In all cases, we used a two-electrode system, and the setup value (+3 V or +5 V) was the total voltage. Raman scattering measurements were carried out with a micro-Raman spectrometer (Model: LabRAM from Horiba Jobin-Yvon), using a 50× objective (laser spot diameter ≈2 μm), laser excitation wavelength of 632.8 nm and laser power <1 mW to avoid heating of the sample. The Raman mapping mode was used over a scan area of around 63 × 63 μm. For each oxidation time step we collected ca. 800 spectra to study in particular the two band regions at 1070–1970 cm−1 (G band) and 2330 cm−1 to 3050 cm−1 (2D band).
Results and discussion
Fig. 2a and S1a–c† show the optical images of the HOPG surface (image size ≈63 × 63 μm) immersed in 0.5 M H2SO4 solution after applying a bias of +3 V for 5 s, 60 s, 300 s, and 600 s. Blistering was observed after just 5 seconds, which is consistent with previous studies on electrochemical graphite exfoliation.13,20 These blisters originated from the intercalation and oxidation of solvated anions and the subsequent evolution of gas (e.g. O2 from water electrolysis, and CO2 from carbon oxidation, see also scheme in Fig. 1b). The process is so fast and visible on the mesoscopic scale because the applied potential is much higher than the thermodynamic potential for carbon and water oxidation (Ecarbon = +0.95 V and EO2/H2O = +1.23 V). Further oxidation led to the accumulation and migration of gases in the uppermost graphite layers. Trapped gases could build up a high pressure (several thousand bar)13 inside the blisters, elastically deform the graphene multilayers, and finally erupt from the inner graphite layers with the formation of cellular structure cracks around the giant blisters, as shown in Fig. 1b, 2a and S1b.† The periodic cracking of the uppermost graphene layers and the infiltration of electrolytes through these cracks to the layers underneath results in continuous oxidation and blister evolution, and the final delamination of EGO multilayers from the surface, with a corresponding roughening visible by optical microscopy (Fig. S1c†). The scale of blistering and mechanical fragmentation caused by gas expansion limits the size of EGO sheets within a scale of tens of micrometers during the electrochemical oxidation process, in contrast to chemical methods which can yield GO sheets with sizes >100 μm.23 | ||
| Fig. 2 (a) Optical image of HOPG surface and (b) the corresponding ID/IG Raman mapping image after 60 seconds’ electrochemical oxidation in 0.5 M H2SO4 electrolyte. | ||
It is worth noting that some reports attribute the blistering and fragmentation to SO2 gas formed during the anodic exfoliation of graphite in dilute H2SO4 solution.24 However, the reduction of dilute H2SO4 is thermodynamically very difficult, while the anodic conversion of SO2 to H2SO4 is a spontaneous exothermic process.6,25 The release of SO2 only happens under extreme conditions such as “thermal shock” treatment of H2SO4-GIC composites, in which graphite is fully intercalated with concentrated H2SO4.26 In the case of acid solutions, the main gas sources are CO2 produced by corrosion of the carbon anode and oxygen produced by water electrolysis.13
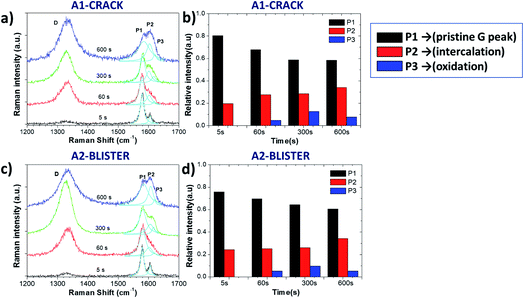
We used Raman spectroscopy to monitor the graphite surface during the anodic process, to explore the structural and chemical changes due to the intercalation and oxidation processes. A total of 3200 spectra were acquired for each sample to monitor the G and 2D bands. The G peak at ∼1580 cm−1 in the Raman spectra is the typical signature of an sp2 hybridized carbon structure; the D peak at ∼1330 cm−1 is due to inter-valley resonant Raman scattering, indicative of lattice defects, for example as caused by oxidation. The ratio of the intensity of the D peak and G peak (ID/IG) allowed us to estimate the average defect density on the graphite surface. Fig. 2b and S1d–f show the ID/IG maps acquired simultaneously with the optical images in Fig. 2a and S1a–c for the same areas of the sample. During the first 5 s of oxidation, an average ID/IG value of 0.14 ± 0.13 was observed, mainly due to small blisters and step edge sites. Further anodic oxidation (Fig. 2b and S1b†) led to a dramatic increase of the ID/IG ratio, due to SO42− intercalation and the subsequent oxidation of graphite corresponding to grain boundaries or step edges. ID/IG increased to 1.06 ± 0.16 after 60 s and 1.89 ± 0.21 after 300 s. Interestingly, the “valley” areas near giant blisters showed ID/IG values lower than the average (deep blue on the color scale in Fig. 2b and S1d–f, with red arrows indicating the “valley” regions). For example, the average ID/IG in the “valley” areas was 0.81 ± 0.12 after 60 s and 1.55 ± 0.13 after 300 s, indicating that the cracks due to blistering exposed fresh, less defective layers of the underlying bulk graphite (as exemplified in the scheme in Fig. 1b). For longer oxidation times (600 s), the ID/IG map became more uniform, with an average ID/IG value of 1.51 ± 0.08, similar for the cracks and blisters, indicating a steady state due to the continuous delamination of the uppermost EGO layers and the continuous oxidation of the inner layers.
Fig. 3 and Table 1 show more detailed Raman spectra taken from two representative areas, A1 and A2, localized on a “valley” area corresponding to a surface crack and on a blister, respectively. In both areas the increase of the D peak is similar to what we already observed for the ID/IG ratio mapping images. There was a broadening trend of the D and G peaks for both selected areas, indicating crystalline damage and amorphization of graphite layers due to oxidation (see Table 1). For example, the full width at half maximum (FWHM) value of the D peak (named ΓD) increased from 46 ± 6 cm−1 (5 s) to 64 ± 6 cm−1 (600 s), and the FWHM value of the G peak (named ΓG) increased from 14 ± 2 cm−1 (5 s) to 47 ± 6 cm−1 (600 s) in the A1 and A2 areas. During oxidation from 60 s to 300 s, the D peak increased more on the giant blister area A2 (ID/IG = 2.01) compared to the valley area A1 (ID/IG = 1.46).
| Time (s) | ω D (cm−1) | Γ D (cm−1) | ω G (cm−1) | Γ G (cm−1) | I D/IG | L a (nm) | n |
|---|---|---|---|---|---|---|---|
| A1 (0.5 M H2SO4) | |||||||
| 5 s | 1327 | 46.1 | 1579 | 13.8 | 0.24 | 186.9 | 10.1 |
| 60 s | 1330 | 50.2 | 1578 | 19.4 | 1.02 | 37.3 | 6.9 |
| 300 s | 1326 | 52.0 | 1580 | 20.0 | 1.46 | 25.9 | 6.1 |
| 600 s | 1333 | 64.3 | 1585 | 46.8 | 1.45 | 26.1 | 5.4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| A2 (0.5 M H2SO4) | |||||||
| 5 s | 1329 | 41.0 | 1579 | 12.4 | 0.09 | 425.4 | 8.2 |
| 60 s | 1333 | 52.9 | 1583 | 27.6 | 1.20 | 31.6 | 7.5 |
| 300 s | 1325 | 52.6 | 1582 | 31.9 | 2.01 | 18.9 | 7.0 |
| 600 s | 1334 | 68.0 | 1584 | 41.1 | 1.51 | 25.1 | 5.6 |
The G band also changed significantly after the 5 s oxidation process, becoming a convolution of three different peaks named P1, P2 and P3 (ref. 13) for clarity, according to their position from low to high wavenumbers:
- P1 = 1577 cm−1 corresponds to the standard G peak due to the E22g(i) mode stretching of the carbon atoms, and indicates the presence of bulk graphite.
- P2 = 1605 cm−1 is the E22g(b) mode of carbon atoms adjacent to the intercalants, and indicates the presence of intercalated graphite.
- P3 = 1617 cm−1 (also termed the D′ band) appears upon further oxidation due to large scale damage and deformation, indicative of surface oxidation.
Fig. 3b and d show the evolution of P1, P2 and P3 on the selected A1 and A2 areas. Both areas show a similar trend in the increase of the P2 peak, indicating a continuous intercalation of HSO4− into the graphite basal plane with the formation of C+HSO4−-GIC composite. The P3 peak increased initially, but decreased upon long exfoliation times. The reduction in defectivity can be explained only by the continuous mechanical removal of the upper, highly oxidised layers, exposing the pristine surface underneath.
The intensity ratio of the P1 and P2 peaks is related to the intercalation stage index n by
| P1/P2 = σi/σb × (n − 2)/2 | (1) |
We also used the ID/IG ratio to evaluate the changes in the graphite crystalline structure using the formula:29,30
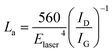 | (2) |
Besides the D and G bands, we also monitored the 2D band (Fig. S2†) on the A1 and A2 areas. The 2D band (often named G′) originates from two-phonon resonance Raman processes, and it is the second prominent band on graphite in addition to the G band. We could observe a sharp 2D peak at ∼2685 cm−1 after 5 s oxidation, similar to the pristine graphite 2D peak. The 2D peak became broader and its relative intensity was lower with longer oxidation time. The 2D band is usually used to determine graphene layer numbers; however, electrochemical oxidation broke the stacking order of adjacent graphene layers and introduced amorphization of carbon atoms. Therefore, the 2D peak was too weak to estimate the layer number information of delaminated EGO sheets.
Meanwhile, new peaks with low intensity appeared at 2880–2950 cm−1 in both the A1 and A2 areas due to the D + D′ bands, indicative of high defect density.
Besides graphite exfoliation in mild acid, we also studied exfoliation in neutral salts. Fig. 4a–d show optical images of the graphite surface upon exfoliation at +3 V in 0.5 M Li2SO4 solution, recorded at 5 s, 60 s, 300 s, and 600 s. Blistering was observed, even if less rapid than was observed in acids at similar oxidation times. The process was slower, and we could also see the migration of giant blisters and fragmentation of the superficial EGO layers with size dimensions around 30–60 μm. Meanwhile, in situ Raman mapping was performed on the graphite basal surface as well (Fig. 4e–h). The ID/IG showed much smaller increases during the oxidation going, from 0.62 ± 0.19 at 5 s to 0.66 ± 0.20 after 60 s, to 0.90 ± 0.24 after 300 s. However, we observed a clear distribution of the oxidation related defects near the step edge and blister areas, see Fig. 4e–g. After 600 s oxidation (Fig. 4h) the average ID/IG reached 1.48 ± 0.07, with the distribution of lower defective areas (ID/IG value ∼1.2) along the crack region of the graphite basal plane.
 | ||
| Fig. 4 (a–d) Optical images of the HOPG surface during electrochemical oxidation in 0.5 M Li2SO4 electrolyte and (e–h) the corresponding ID/IG Raman mapping images. | ||
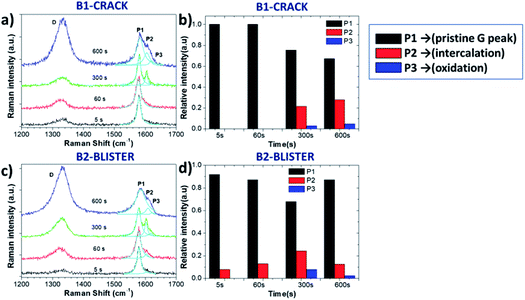
In order to perform a detailed analysis of the Raman spectra variation, in this case we also compared two representative areas, B1 and B2, on the crack and blister sites of the graphite surface, respectively (Fig. 5a and c). The D peak increased during oxidation; however, we observed no clear D peak broadening in the B1 and B2 regions (see in Table 2), only a broadening of the G peak. The ΓG value increases from 14 (5 s) to 29 (600 s) on the B1 area and from 15 (5 s) to 38 (600 s) on the B2 area. The ID/IG value on the B2 blister area increased to 0.98 after a 300 s oxidation period, significantly higher than was observed on the B1 crack area (ID/IG = 0.71). This is consistent with what was observed in acid, with a more destructive intercalation/oxidation process below the blister regions, as compared to the “valley” areas before cracking. After 600 s, the ID/IG ratio reached a value on the B2 and B1 areas of 1.68 and 1.59, respectively, indicating the full oxidation of the uppermost layers and continual intercalation/oxidation of the innermost layers.
| Time (s) | ω D (cm−1) | Γ D (cm−1) | ω G (cm−1) | Γ G (cm−1) | I D/IG | L a (nm) | n |
|---|---|---|---|---|---|---|---|
| B1 (0.5 M Li2SO4) | |||||||
| 5 s | 1331 | 46.7 | 1580 | 14.0 | 0.61 | 61.6 | — |
| 60 s | 1325 | 46.9 | 1578 | 19.4 | 0.67 | 56.4 | — |
| 300 s | 1328 | 53.2 | 1580 | 13.7 | 0.71 | 53.2 | 9.0 |
| 600 s | 1332 | 51.0 | 1584 | 29.2 | 1.59 | 23.9 | 6.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| B2 (0.5 M Li2SO4) | |||||||
| 5 s | 1329 | 48.9 | 1579 | 14.8 | 0.59 | 64.3 | 24.9 |
| 60 s | 1322 | 55.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
1578![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
19.7 | 0.68 | 56.1 | 15.6 |
| 300 s | 1327 | 50.6 | 1578 | 16.3 | 0.97 | 38.6 | 7.6 |
| 600 s | 1331 | 53.5 | 1585 | 37.8 | 1.68 | 22.6 | 17.1 |
While the evolution of the D peak was qualitatively similar to what was observed in acid, the evolution of the P1, P2 and P3 peaks was significantly different. Unlike the rapid intercalation process in acid electrolytes, sulfate anion intercalation in neutral salt solutions is a much slower process. Our observation is consistent with the report of Alsmeyer et al. for mild acid conditions, since weaker acid strength leads to a higher intercalation potential for the formation of GICs.31 The P1 peak on the crack did not vary much during the first 60 s, indicating the presence of pristine graphite. On the B2 blister, a low intensity P2 peak from G band was observed (Fig. 5a and c), attributed to the intercalation of SO42− on step edges and defect regions of graphite. For longer times (t > 300 s), the presence of the P2 and P3 peaks was instead observed in all areas, similar to the exfoliation in acid (Fig. 5b and d).
The intercalation stage index n decreased from n ≈ 25 to n ≈ 8 on the B2 area and n ≈ 7 (600 s) on the B1 area, indicating the successful intercalation of SO42− ions on graphite layers.
However, n on the B2 blister area increased again, reaching n ≈ 17 after 600 s oxidation. This cannot be explained by chemical deintercalation of sulfate ions, but was instead attributed to the delamination and removal of the uppermost EGO layers, exposing partially fresh graphite underneath.
As observed for the exfoliation in acid, here the average graphite crystalline size La also decreased, going from around a hundred nm to ∼23 nm, and the 2D band broadened (Fig. S3†).
We should underline that, in our setup, Raman spectra were acquired on the microscopic scale with high spatial resolution, in contrast to typical Raman spectra, which just report an average signal from a macroscopic area of the sample. The 3200 Raman spectra we acquired on different samples at different exfoliation stages allowed us to perform a statistical analysis of the data, correlating the different ongoing processes in each point of the sample.
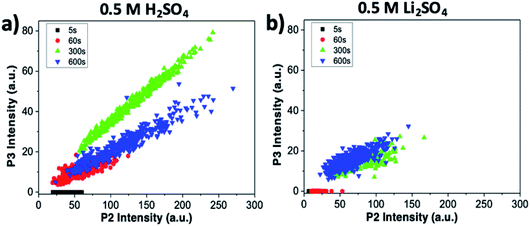
The intensity of the P2 peak (indicative of ion intercalation) and P3 peak (indicative of sample oxidation) for the sample treated in sulfuric acid are correlated in Fig. 6a. The correlation is poor at the initial stages (t = 5 and 60 s). For later stages, a clear linear correlation is observed, indicating that graphene oxidation is more intense in areas where intercalation is strong. The highest correlation is observed for t = 300 s; then, in agreement with what was observed at specific points in the sections above, the average value of P3 decreases, but the correlation between the two processes is still evident.
The same analysis for samples treated in lithium sulfate is performed in Fig. 6b. The P3 intensity is zero at t = 0 s and 60 s. Oxidation becomes significant only in later stages, but even then no clear correlation is observed, indicating that the oxidation in neutral media is much lower than in acid, and is not directly correlated to intercalation.
The combined use of P1, P2 and P3 data allowed us to obtain even more refined insight, as shown in Fig. 7. Here, the intercalation stage calculated using formula (1) is correlated with the graphene oxidation for each point of all the samples. We observe that strongly oxidized areas (on the right side of the graph) show on average lower intercalation numbers than poorly oxidized areas, again confirming that the oxidation process is directly correlated to ion intercalation. It is noteworthy that the value of n seems to reach an asymptotic value at a given treatment time and is not directly correlated to the oxidation values. Also in this case, the oxidation values decrease from t = 300 s to t = 600 s, as the first areas to be removed from the sample are the most oxidized. The average intercalation stage, however, decreases slightly, indicating that while oxidized areas exfoliated by the blisters are removed, high intercalation continues in the uncovered areas of the samples. Conversely, samples treated in lithium sulfate showed no P3 peak for t < 60 s, and only random correlation for t > 60 s (not shown).
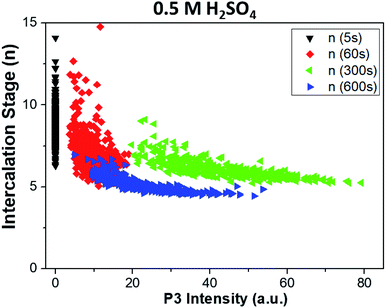 | ||
| Fig. 7 Correlation between the intercalation stage of ions in graphite (P1/P2 calculated with formula (1) in the main text) and oxidation of the sample (P3), obtained from Raman maps at different times. Graphs refer to treatment in sulfuric acid. Samples treated in lithium sulfate showed no P3 peak for t < 60 s, and only uncorrelated data for t > 60 s. | ||
The systematic optical and Raman comparison of the anodic process in acid or neutral salt solution indicates the most plausible model of EGO formation: first, solvated sulfate ions (HSO4−/SO42− in acidic media and SO42− in neutral media) intercalate into the graphite grains or step edges under a critical potential > 1.8 V (vs. RHE) with the formation of GICs.13,31 Intercalation proceeds until an intercalation stage n ≥ 5 is reached.
Second, electrolysis of the co-intercalated water molecules releases a large amount of O2 gas. Water induced hydrolysis of the GIC complex leads to oxidative cleavage of carbon atoms from the edges or defects of the graphite accompanied by CO2 gas due to the decomposition of GICs. Third, the almost simultaneous gas evolution and oxidation process driven by chemical and physical forces results in rapid blister growth. The deformed blisters crack the upper graphene layers, uncovering pristine graphite areas in the cracks between the blisters (Fig. 1b). The collapse of the giant blisters mechanically peels off the uppermost EGO flakes, and the cycle can start again. The penetration of solvated anions on the crack edges brings repeated intercalation, gas formation and graphite oxidation processes to the inner layers.
We should underline that our in situ monitoring process only focused on the basal face of graphite, in order to give a clear visualization of the surface morphology changes. However, in practical exfoliation, the side faces will also be included during the whole intercalation, oxidation and expansion steps, giving an even faster exfoliation process.
It is known that water plays an important role in EGO production. A water molecule is not only the source of oxygen gas from water electrolysis, but also the attacking nucleophile during oxidative hydrolysis of the GIC complex.
In a previous work, we estimated the average thickness of the produced EGO nanosheets using atomic force microscopy (AFM) statistical analysis. The nanosheets feature a “sandwich” structure with multilayer configurations instead of a single layer.28 The present work provides a mechanistic understanding of this limit, revealing that the intercalating anions reach an intercalation stage of at best n ≥ 5 in dilute acidic or neutral media. Furthermore, the blister–crack formation–collapse mechanism of the uppermost graphene layers limits the lateral dimension of the exfoliated EGO sheets to tens of micrometers (around 30–60 μm in our experiment).
Although EGO exfoliation in salts looks qualitatively similar to exfoliation in acids, there are still some differences between the two media. (1) Energetically favorable intercalation of sulfate anions in acidic media is evidenced from the faster growth of the P2 peak during the initial stages of oxidation (t < 60 s), indicating a more efficient intercalation process and possibly a more thermodynamically stable GIC complex in acid instead of in neutral solution:13
| Cp + HSO4− + γH2O ↔ Cp+·HSO4−·γH2O + e− | (3) |
(2) Meanwhile, the carbon corrosion potential in neutral conditions is lower than in acid conditions, corresponding to the irreversible oxidative reaction:13,32
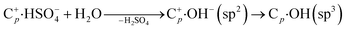 | (4) |
| Cp·OH + H2O → Cp-1 + CO2 + 3H+ + 3e− | (5) |
| 2H2O → O2 + 4H+ + 4e− | (6) |
Thus, while in acid graphite intercalation and exfoliation are directly correlated to graphite oxidative damage, in salt the two processes are not well correlated, as clearly shown by the statistical analysis in Fig. 6 and 7.
Although less blistering was observed initially in Li2SO4 compared to H2SO4 due to the lower intercalation efficiency, the fast gas evolution from neutral media resulted in a rougher morphology after a long oxidation time.
However, it should be noted that the action of water will improve the production efficiency of the gas source, which might avoid serious damage of the EGO sheets during the mechanical expansion step, but the rapid exfoliation process also leads to incomplete intercalation of graphite and the formation of more EGO multilayers. Thus, electrochemical exfoliation in neutral salts (in this case, Li2SO4) could give a higher yield but thicker graphene than exfoliation performed in dilute sulfuric acid (H2SO4).
(3) The whole process mechanically removes EGO nanosheets with a thickness of a few layers and a lateral size of tens of μm, continuously uncovering fresh areas of graphite to be exfoliated. This gives an experimental explanation for the high production speed attained with electrochemical exfoliation at an industrial level.
Finally, to further study the role of water in the electrochemical process, we used our setup to monitor the anodic graphite intercalation with a non-aqueous electrolyte. Fig. S4a–d† show the optical images of a graphite surface in 1 M NaClO4 in acetonitrile (CH3CN). To achieve a visible effect, a bias of +5 V instead of +3 V was applied for t = 0 s, 60 s, 300 s, and 600 s.
After 60 s oxidation, a few blisters formed on the graphite surface, but there was no major change in the surface morphology under prolonged treatment. Raman measurements showed the characteristic G and 2D peaks of graphite (Fig. 8a and S5†). In the G band region, two peaks of acetonitrile at 1370 cm−1 and 1449 cm−1 were observed due to the CH3 deformation vibration. Other peaks at 2248 cm−1 and 2942 cm−1 were due to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching and C–H stretching vibration modes of acetonitrile, respectively (Fig. S5†).34
N stretching and C–H stretching vibration modes of acetonitrile, respectively (Fig. S5†).34
We could not observe any D peak formation at ∼1330 cm−1 during the anodic process, even for t = 600 s. We only observed a shape change of the peak at 1370 cm−1, possibly due to the oxidative electrochemical decomposition of the CH3CN solvent.
On the other hand, the growth of a significant P2 peak (Fig. 8b) demonstrated a significant intercalation of solvated ClO4− anions, with no increase in defects (which would yield a P3 peak) and no mechanical exfoliation observed on the micron scale. The intercalation stage index n (estimated from eqn (1)) reached n ≈ 3 (600 s), showing a much more efficient intercalation as compared to sulfate ions in water (see in Table 3). Obviously, water-free electrolytes could achieve efficient intercalation of organic molecules and inorganic anions without damage to the graphite lattice, even under an anodic process. The efficient intercalation is not sufficient per se to achieve significant exfoliation but should be followed by chemical decomposition of the intercalants, with gas production. The ideal process would thus combine first the efficient intercalation of suitable ions (e.g. ClO4− in acetonitrile), followed by the successive decomposition of such ions. We have already experimentally tested this procedure in a previous work,17 in which graphite was intercalated by perchlorate ions and acetonitrile molecules under a +5 V potential for 30 minutes, and further expanded under microwave irradiation due to the degradation of the co-intercalated organic molecules. The in situ measurements performed here thus give experimental support to our empirical procedure, and demonstrate the better potential of a two-stage exfoliation procedure to achieve high yield and low defectivity at the same time.
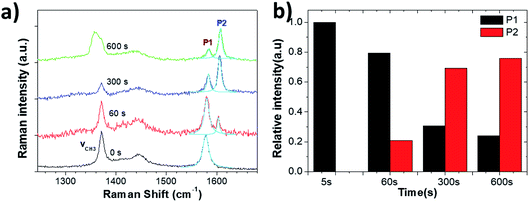 | ||
| Fig. 8 (a) Raman spectra acquired from the HOPG surface during electrochemical oxidation in 1 M NaClO4/CH3CN electrolyte. (b) Evolution with increasing time of Raman P1 and P2 peaks. | ||
| Time (s) | ω CH3 (cm−1) | Γ CH3 (cm−1) | ω G (cm−1) | Γ G (cm−1) | n |
|---|---|---|---|---|---|
| 1 M NaClO4/CH3CN | |||||
| 0 s | 1372 | 11.8 | 1578 | 14.2 | — |
| 60 s | 1371 | 9.7 | 1580 | 11.6 | 9.6 |
| 300 s | 1371 | 10.0 | 1583 | 10.4 | 2.9 |
| 600 s | 1369 | 20.6 | 1584 | 12.6 | 2.6 |
Conclusion
In summary, we compared the anodic graphite exfoliation process in dilute acid (0.5 M H2SO4) and neutral salt (0.5 M Li2SO4) electrolytes by in situ optical and Raman spectroscopy analysis. In either acidic or neutral aqueous media, blistering and cracking was observed on the uppermost graphite layers. The relative anion intercalation, graphite oxidation and mechanical expansion steps were correlated to Raman ID/IG ratio and G band splitting variations. Our observations enable a deep understanding of the mechanism of EGO formation in aqueous electrolytes. We also demonstrated the use of nonaqueous electrolyte (1 M NaClO4/CH3CN) as an alternative for efficient graphite intercalation without oxidation. The combination of efficient, non-destructive intercalation followed by chemical decomposition of the intercalants and gas production thus seems to be the best way to exfoliate graphite by an anodic intercalation process.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The research leading to these results has received funding from the European Union’s Horizon 2020 research and innovation programme under GrapheneCore2 785219 – Graphene Flagship and from the Swedish Research Council under project Janus 2017-04456.References
- M. S. Dresselhaus and G. Dresselhaus, Adv. Phys., 1981, 30, 139–326 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- C. Sole, N. E. Drewett and L. J. Hardwick, Faraday Discuss., 2014, 172, 223–237 RSC.
- A. Ambrosi and M. Pumera, Chem.–Eur. J., 2013, 19, 4748–4753 CrossRef CAS.
- S. Yang, M. R. Lohe, K. Mullen and X. L. Feng, Adv. Mater., 2016, 28, 6213–6221 CrossRef CAS.
- F. Beck, J. Jiang and H. Krohn, J. Electroanal. Chem., 1995, 389, 161–165 CrossRef.
- J. Z. Wang, K. K. Manga, Q. L. Bao and K. P. Loh, J. Am. Chem. Soc., 2011, 133, 8888–8891 CrossRef CAS.
- A. Ejigu, I. A. Kinloch and R. A. W. Dryfe, ACS Appl. Mater. Interfaces, 2017, 9, 710–721 CrossRef CAS.
- A. J. Cooper, N. R. Wilson, I. A. Kinloch and R. A. W. Dryfe, Carbon, 2014, 66, 340–350 CrossRef CAS.
- H. P. Lei, J. G. Tu, Z. J. Yu and S. Q. Jiao, ACS Appl. Mater. Interfaces, 2017, 9, 36702–36707 CrossRef CAS.
- P. Yu, Z. M. Tian, S. E. Lowe, J. C. Song, Z. R. Ma, X. Wang, Z. J. Han, Q. L. Bao, G. P. Simon, D. Li and Y. L. Zhong, Chem. Mater., 2016, 28, 8429–8438 CrossRef CAS.
- Z. Y. Xia, D. Wei, E. Anitowska, V. Bellani, L. Ortolani, V. Morandi, M. Gazzano, A. Zanelli, S. Borini and V. Palermo, Carbon, 2015, 84, 254–262 CrossRef CAS.
- Z. Y. Xia, S. Pezzini, E. Treossi, G. Giambastiani, F. Corticelli, V. Morandi, A. Zanelli, V. Bellani and V. Palermo, Adv. Funct. Mater., 2013, 23, 4684–4693 CrossRef CAS.
- M. Thompson, http://www.talgaresources.com/IRM/PDF/1742/TalgaReducesGraphiteProcessingStepsForLiionBatteries, 2016.
- C. Y. Su, A. Y. Lu, Y. P. Xu, F. R. Chen, A. N. Khlobystov and L. J. Li, ACS Nano, 2011, 5, 2332–2339 CrossRef CAS.
- K. Parvez, R. J. Li, S. R. Puniredd, Y. Hernandez, F. Hinkel, S. H. Wang, X. L. Feng and K. Mullen, ACS Nano, 2013, 7, 3598–3606 CrossRef CAS.
- Z. Y. Xia, G. Giambastiani, C. Christodoulou, M. V. Nardi, N. Koch, E. Treossi, V. Bellani, S. Pezzini, F. Corticelli, V. Morandi, A. Zanelli and V. Palermo, ChemPlusChem, 2014, 79, 439–446 CrossRef CAS.
- S. Pei, Q. Wei, K. Huang, H. M. Cheng and W. Ren, Nat. Commun., 2018, 9, 145 CrossRef.
- J. Y. Cao, P. He, M. A. Mohammed, X. Zhao, R. J. Young, B. Derby, I. A. Kinloch and R. A. W. Dryfe, J. Am. Chem. Soc., 2017, 139, 17446–17456 CrossRef CAS.
- G. Bussetti, R. Yivlialin, D. Alliata, A. L. Bassi, C. Castiglioni, M. Tommasini, C. S. Casari, M. Passoni, P. Biagioni, F. Ciccacci and L. Duo, J. Phys. Chem. C, 2016, 120, 6088–6093 CrossRef CAS.
- C. Casiraghi, S. Pisana, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Appl. Phys. Lett., 2007, 91, 233108 CrossRef.
- J. B. Wu, M. L. Lin, X. Cong, H. N. Liu and P. H. Tan, Chem. Soc. Rev., 2018, 47, 1822–1873 RSC.
- E. Treossi, M. Melucci, A. Liscio, M. Gazzano, P. Samori and V. Palermo, J. Am. Chem. Soc., 2009, 131, 15576–15577 CrossRef CAS.
- A. A. Muhsan and K. Lafdi, SN Appl. Sci., 2019, 1, 276 CrossRef CAS.
- K. Wiesener, Electrochim. Acta, 1973, 18, 185–189 CrossRef CAS.
- G. Carotenuto, A. Longo, L. Nicolais, S. De Nicola, E. Pugliese, M. Ciofini, M. Locatelli, A. Lapucci and R. Meucci, J. Phys. Chem. C, 2015, 119, 15942–15947 CrossRef CAS.
- S. Solin and H. Zabel, Graphite Intercalation Compounds, Springer-Verlag, Berlin, 1990 Search PubMed.
- G. Maccaferri, C. Zanardi, Z. Y. Xia, A. Kovtun, A. Liscio, F. Terzi, V. Palermo and R. Seeber, Carbon, 2017, 120, 165–175 CrossRef CAS.
- L. G. Cancado, K. Takai, T. Enoki, M. Endo, Y. A. Kim, H. Mizusaki, A. Jorio, L. N. Coelho, R. Magalhaes-Paniago and M. A. Pimenta, Appl. Phys. Lett., 2006, 88, 163106 CrossRef.
- M. S. Dresselhaus, A. Jorio, A. G. Souza and R. Saito, Philos. Trans. R. Soc., A, 2010, 368, 5355–5377 CrossRef CAS.
- D. C. Alsmeyer and R. L. McCreery, Anal. Chem., 1992, 64, 1528–1533 CrossRef CAS.
- A. Pandy, Z. W. Yang, M. Gummalla, V. V. Atrazhev, N. Y. Kuzminyh, V. I. Sultanov and S. Burlatsky, J. Electrochem. Soc., 2013, 160, F972–F979 CrossRef CAS.
- R. M. Tamgadge and A. Shukla, Electrochim. Acta, 2019, 325, 134933 CrossRef CAS.
- B. G. Oliver and G. J. Janz, J. Phys. Chem., 1970, 74, 3819–3822 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9fd00123a |
| This journal is © The Royal Society of Chemistry 2021 |