Open Access Article
Open Access ArticleSorption of surfactants onto sediment at environmentally relevant concentrations: independent-mode as unifying concept†
Hildo
Krop
 *a,
Pim
de Voogt
*a,
Pim
de Voogt
 *bc,
Christian
Eschauzier
d and
Steven
Droge
*bc,
Christian
Eschauzier
d and
Steven
Droge
 b
b
aKrop-Consult, Conradstraat 7, 1505KA Zaandam, The Netherlands. E-mail: h.b.krop@uva.nl; Tel: +31 614988669
bUniversity of Amsterdam (UvA), Institute for Biodiversity and Ecosystem Dynamics (IBED), Science Park 904, 1098 XH Amsterdam, The Netherlands
cKWR Water Research Institute, Groningenhaven 7, 3433 PE Nieuwegein, The Netherlands
dEschauzier Water Management, Trouringhstraat 18-1, 1055HB Amsterdam, The Netherlands
First published on 24th March 2020
Abstract
At low surfactant concentrations often non-linear sorption processes are observed when natural adsorbents like sediment or soil are involved. This sorption process is often explained by a Dual-Model (DM) model, which assumes sorption to an adsorbent to be based on a combined ionic-polar and non-polar sorption interaction term. An Independent-Mode (IM) model, however, could treat surfactant sorption as two independent sorption processes to which the non-polar and ionic-polar features of the surfactant molecule contribute differently. For both models the overall exact partition coefficient, Ktotalp, and its corresponding total standard free enthalpy of adsorption, ΔsG0total, are derived. We tested the outcome of both models against multiple published experimental sorption data sets by, (i) varying the organic carbon fraction, (ii) constructing sorption and partition isotherms over different concentration ranges, (iii) removing the organic carbon fraction, (iv) applying different types of mixtures of surfactants, and (v) explaining sorption hysteresis in desorption studies based on either continuous and successive washing steps. It turned out that only the IM model was able to explain the reported sorption phenomena. We also show that when one interaction is dominating, e.g. non-polar over ionic-polar, the ΔsG0total of the IM model can be approximated by the sum of the different ΔsG0 values, the ΔsG0total of the DM model. The exact partition coefficient, Kp(Cw) (L kg−1) = dCs (mmol kg−1)/dCw (mmol L−1), is turning each sorption isotherm into a partition isotherm that provides the Kp values required in environmental risk assessment models.
Environmental significanceThis paper addresses ad- and desorption processes of surfactants at environmentally low concentrations onto sediments. Reported models show that both the head and tail of the same surfactant molecule is involved in a single sorption process (Dual-Mode). This paper shows that all experimentally observed sorption phenomena can be explained by sorption of the tail of one surfactant molecule to one location while the head of another surfactant molecule will be adsorbed to another sorption location (Independent-Mode). The study emphasizes that only complete Langmuir isotherms are able to explain adequately many observed sorption phenomena. In applying the Independent-Mode model we define an exact Kp function. In sorption experiments of surfactants on complex adsorbents one requires to define the relevant adsorbents and apply for each fraction simple Langmuir isotherms. In ERA models one needs to estimate two sorption parameters for each relevant adsorbent. |
1. Introduction
The sorption behaviour of chemicals in the environment is characterized by the ratio of the concentration of the substance associated with water, Cw (mg L−1 or mmol L−1), and the amount of substance associated with a volume of a sorbent such as sediment, Cs (mg kg−1 or mmol kg−1). At equilibrium, this ratio is equivalent to the sediment–water partition coefficient, Kp (L kg−1), eqn (1):| Kp = Cs/Cw | (1) |
The Kp plays an important role in environmental fate models and in environmental risk assessment (ERA). For example it is required to estimate the bioavailable fraction of the sorbate in different environmental compartments. In ERA models sorption of organic substances is currently addressed only via a hydrophobic or non-polar interaction mechanism. In these models sorption is incorporated as a linear process. It is also generally found that the hydrophobic or non-polar sorption increases proportionally with increasing organic carbon fraction (foc) of the sorbent, making it logical to normalise the sediment–water partition constant, Kp, to the organic carbon fraction, Koc. These Koc values are used as dependent descriptor for structure–activity relationships (SARs) e.g. with the octanol–water partition coefficient, Kow, as independent descriptor.
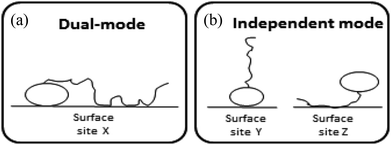
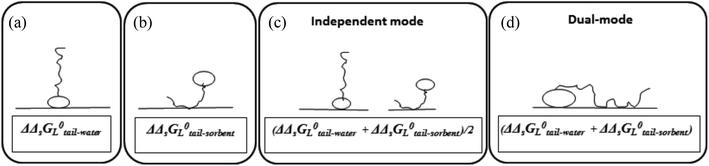
Surface-active agents (surfactants) are molecules consisting of an ionic, polar, or otherwise hydrophilic head and a hydrophobic (lipophilic) tail. Because of their amphiphilic character their sorption behaviour is different from purely hydrophobic compounds and may also include an electrostatic or ionic-polar sorption process. These sorption processes are described clearly in colloid chemistry. On pure surfaces like silica, kaolinite, or montmorillonite over a large concentration range the sorption process of many surfactants is characterised by a distinct four steps adsorption pattern.1–3 At low concentrations sorption is linear and the sorption process is only restricted to an exchange process between isolated molecules and the surface referred to as the Henry's law region. At higher concentrations surfactant molecules start to form micellar-like structures on the surface commonly denoted as admicelles and hemicelles followed by the formation and sorption of micelles. Unless waste waters enter aquatic systems without any treatment, surfactant concentrations encountered in the environment are in general so low, i.e. in the order of μg L−1 or lower, that micellar-like structures are not expected.4,5 However, even if an ionic-polar sorption process is expected to occur at a sorbent within the Henry's law region it is observed that the sediment–water partition coefficient increases with increasing carbon chain length of analogue surfactants (i.e. increasing number of CH2 or CF2-units).6–9 In environmental and colloid chemistry this is generally interpreted as an additional or non-polar sorption interaction of the tail with the sorbate.10,11 In these models both the head and the tail of the surfactant molecule are involved simultaneously in an adsorption process. In the present work this is called the Dual-Mode (DM) adsorption process because only one type of adsorbent is involved, as depicted in Fig. 1a. The DM models lead to a picture that the surfactant molecules should be (partially) absorbed into the matrix, requiring the introduction in the model of parameters that are related to the structure of the matrix.
To our best knowledge, it has not been described well in the scientific sorption literature what sorption isotherm would be obtained if sorption of surfactants to adsorbents is described by an Independent-Mode (IM) adsorption process, as an alternative to the DM model. In the IM model one surfactant molecule (or one part of the total adsorbed mass of the surfactant) is adsorbed by a non-polar mechanism to an organic-carbon like sediment component, and another surfactant molecule (or, the other part of the total adsorbed mass) is adsorbed (only) by an ionic-polar mechanism to another sediment component (e.g. clay mineral surface), as depicted in Fig. 1b.
Although Fig. 1 is overly simplistic, intuitively it makes sense that the description of these two models could lead to different conclusions on how surfactant sorption can be best described. A correct interpretation of observed sorption phenomena for surfactants is of importance for risk assessment modelling of potential contamination with such chemicals. Regulators may have to extrapolate results from the experimental boundaries to specific case studies with different features, sorbent properties, and concentration ranges. As outlined below in more detail the goal of this study was two-fold. In the theoretical considerations we derive the relevant thermodynamic equations for the standard free enthalpy change, ΔsG0total, of the sorption process for both the DM and IM model. For both models, the overall adsorption isotherm (Ktotalp) which combines both types of interactions between surfactant and the sorbent surface (non-polar and polar-ionic) is then derived. These mathematical descriptions should elucidate how the relevant partition coefficients can be derived to support environmental risk assessment for surfactants. In the model application section we evaluated outcomes of both models against multiple published experimental sorption data sets involving various sorption phenomena. By simulating the variations of several sorption parameters differences between IM and DM sorption isotherms are interpreted and compared with observed isotherms. We will show that interpretation of these differences shows full support for the IM model. The DM model is used in the development of sorption models based on thermodynamics but we will show that the same results are found using the IM model when one of the two interaction modes dominates.
2. Theoretical considerations
2.1 Introduction
In this paper it is assumed that in the environment sediment–water and/or soil/water adsorption processes are dominant particularly for the fate of surfactants. Therefore soil/air adsorption processes are excluded in the present study. In environmental chemistry one refers often to hydrophobic vs. electrostatic adsorption processes when dealing with especially ionic surfactants. This excludes the possibility for an electrostatic attraction of the non-ionic but highly polar head, like e.g., for non-ionic surfactants such as alcohol ethoxylates (AE) to sediment or soil. To include the possibility of different types of electrostatic interactions for various surfactants, we refer in the text to an ionic-polar adsorption process when the head of any surfactant is involved in the adsorption process, but in the relevant mathematical formulas we keep on using the abbreviation ‘elec’. Similarly, the hydrophobic adsorption processes of the tail of a surfactant is described in the text as a non-polar adsorption process, but we keep the abbreviation ‘hydr’ in the mathematical formulas. These abbreviations align with the mathematics of sorption models applied elsewhere.Absorption into some sorbents may also occur for surfactants, but these processes are also not within the subject of the present study on sorption to soil or sediment. It has been reported that ionic surfactants fully intercalate within phospholipid membranes.12,13 Also the solid-phase microextraction process for non-ionic surfactants such as AE with polyacrylate coated glass fibers appears to be based on absorption of the entire surfactant molecules into the rubbery polymer matrix.14,15
By far most sorption experiments of surfactants performed in the laboratory apply a short time span where aging phenomena are neglected. When applying aging processes fast and slow (into micropores of sediment or soil) ad- or desorption fractions may be observed16,17 but in this paper it will be shown that the IM model can explain such phenomena for surfactants without invoking additional adsorption into micropores (for a more fundamental discussion on the different ranges of validity of especially the kinetic Langmuir sorption–diffusion model see for example the work of Douven et al.18). All applied literature references to test our developed model are performed in a relatively short time span (hours to days).
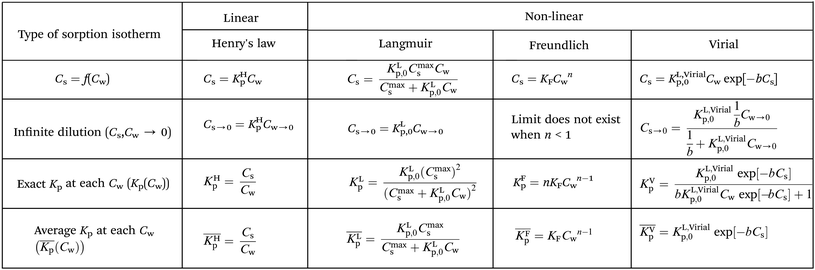
At low concentrations (usually, but not specifically, at the μg L−1 level) both non-linear and linear sorption of surfactants to pure and complex adsorbents are observed.19 The observed non-linear sorption processes are often described by a Langmuir, Freundlich, or Virial isotherm. Also more complex models like combinations of a linear and one or more Langmuir, Temkin, Toth isotherms or the non-ideal competitive adsorption (NICA)-Donnan model have been proposed.20–24 The models establish a relationship between a number of data points of measured concentrations Cs in soil or sediment and concentrations Cw in water, at equilibrium. In the present work we refer to the ratios of such measured data, obtained from the applied experimental system, as partition coefficients, Kp (L kg−1). The partition coefficients thus derived need to be linked to the molecular adsorption system to develop sorption models and/or SARs. Parameters related to molecular adsorption processes are called sorption constants, K (unit e.g. L mmol−1). In thermodynamical terms we have to distinguish two different systems here. In order to relate Kp to K, a change in (thermodynamic) system is therefore involved; from the experimental one to the molecular one. In the experimental system certain parameters, e.g., temperature or pH, are often modified to establish the variation of the partition coefficient. We show that one needs to be careful to interpret measured variation in Kp as a result of e.g., varying pH values into variations in (molecular) sorption constants, K.
From the different non-linear models the most simple one to interpret is the Langmuir model. In this case the non-linearity is caused by the limited number of sorption sites in the applied experimental system. At low concentrations where no micellization occurs it is therefore assumed that the observed non-linearity is a consequence of the availability of a limited number of sorption sites in the applied experimental system. Before any molecular adsorption process can be studied this non-linear adsorption strength in the applied experimental system must be accounted for. This is done by studying the sorption behaviour at infinite dilution. This behaviour is not only important to establish molecular sorption models but environmentally very relevant since it coincides with a dilution process. Kp values corrected for their non-linear behaviour at infinite dilution are indicated as Kp,0. Only Kp,0-values lead therefore to relevant information on the molecular sorption process(es).
The relevant sorption parameters for the IM and DM models will be derived in a stepwise approach. The first step describes the behaviour of the most common isotherms at infinite dilution to account for the limited number of sorption sites in the applied experimental system.
Non-linear sorption isotherms imply that the corresponding Kp depends on the dissolved concentration of the compound (Cw), Kp(Cw). In the second step it will be shown how the Kp(Cw) can be derived from any (non-linear) isotherm by defining an ‘exact’ partition coefficient, Kp. It will be shown that the partition coefficient from eqn (1) is an ‘average’ Kp, 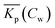 .
.
In the third step the relevant thermodynamic equations will be derived for the standard free enthalpy change, ΔsG0total, of the sorption process and for the overall partition coefficient, Ktotalp, which encompasses both the non-polar and ionic-polar interactions for both the IM and DM model. Finally the step from the experimentally derived parameter, Kp,0, to the molecular sorption constants will be discussed. In this part also attention will be given to observed rate phenomena of any adsorption or desorption process for surfactants.
2.2 Behaviour of commonly used sorption isotherms at infinite solution (Cs,Cw → 0)
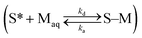 are related to each other by the Langmuir case I sorption constant, KL (L mg−1 or mmol−1) and is also equal to the ratio of the adsorption and desorption rate constants, ka/kd. The fraction of surface sites occupied, S–M/(S* + S–M), Cs/Cmaxs, can be written in the operational way cf.eqn (2):
are related to each other by the Langmuir case I sorption constant, KL (L mg−1 or mmol−1) and is also equal to the ratio of the adsorption and desorption rate constants, ka/kd. The fraction of surface sites occupied, S–M/(S* + S–M), Cs/Cmaxs, can be written in the operational way cf.eqn (2):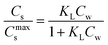 | (2) |
In dilute solutions (more accurate when KLCw ≪ 1) eqn (2) can be rewritten as eqn (3) where a Langmuir sediment–partition coefficient, KLp, can be derived that is not influenced anymore by the number of unoccupied sites, KLp,0 (L kg−1),26,27 (eqn (3a) and (3b)):
| Cs→0 = KLCmaxsCw→0 | (3a) |
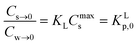 | (3b) |
Using eqn (3b), eqn (2) can then be rewritten into the (thermodynamic) expression of KLp,0 as follows, eqn (4), used throughout in this study.
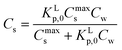 | (4) |
Reported Cs and Cw values and isotherms are usually normalised to 1 kg of sediment and 1 L of water respectively. In Annex I it is shown that eqn (4) arises from a general Langmuir sorption process, which includes the sediment concentration while neglecting the sediment volume.
It is important to realize that eqn (4) can become linear both at infinite dilution, as described above, and when Cmaxs ≫ KLp,0Cw (that is for low fraction of surfactant adsorbed in relation to a high number of sorption sites). Therefore it is assumed in this study that whenever a linear isotherm at low surfactants concentrations is observed this is not only a consequence of the Langmuir isotherm at infinite dilution but it is also equivalent to the Henry's law isotherm observed at low surfactant concentrations on pure adsorbents. The IM model therefore supposes that an observed linearity in sorption at low concentrations is a general consequence of a Langmuir isotherm where the number of occupied sorption sites in the applied experimental system is still low compared to the total number of sorption sites.
On the other hand, any observed non-linear behaviour of the Langmuir case I isotherm at higher surfactant concentrations is a consequence of a preference of one of two different processes: either Cmaxs is approached and the curvature will decrease until a plateau, Cmaxs, is reached or the curvature will increase before Cmaxs is approached which is related to the formation of admicelles, hemicelles or possible multiple layers28 on the adsorbent (neglecting for example additional chemical processes like an exchange of ligands form the adsorbent). Since at environmental concentrations micelle structures are not expected only decreasing curvature is expected for single Langmuir isotherms. In the discussion attention will be given when to be aware of possible micellization at higher surfactant concentrations.
| Kocfoc = KH,hydrp = KL,hydrp,0 = KhydrLCmaxs,hydr | (5a) |
Eqn (5a) shows that Koc is linearly related to KhydrL and foc to Cmaxs,hydr. Similarly a linear isotherm of any ionic-polar interaction derived from its corresponding Langmuir isotherm at low concentrations can be related to a still unknown sediment parameter, fsed and a normalised ionic-polar sorption parameter, eqn (5b):
| KelecLCmaxs,elec = KL,elecp,0 = KH,elecp = Knormelecfsed | (5b) |
Eqn (5a) and (5b) gives the possibility to compare Langmuir sorption constants, KL, from different types of sorption processes. Possible sediment parameters, fsed, that might be related to Cmaxs,elec will be discussed later.
Cs = KVpCw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−bCs] exp[−bCs] | (6) |
In this model the parameter b is related to the capacitance of the ionic-polar model. At infinite solution (Cs,Cw → 0) eqn (6) can be rewritten as eqn (7):
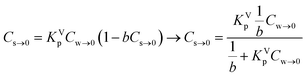 | (7) |
Eqn (7) shows that in a dilute system eqn (6) becomes equivalent to the Langmuir isotherm, eqn (4), and thus that KVp is equivalent to KL,Virialp,0 and 1/b = Cmaxs,Virial. There are two disadvantages in using the Virial over the Langmuir isotherm. Firstly it is difficult to linearize the Virial isotherm and to derive the Virial sorption parameters KVp and b. Secondly it will be described below that the way the correction factor for the non-polar interaction is introduced, corresponds only to the DM model.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Csvs. log
Csvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cw is found to be linear a Freundlich isotherm is observed. The Freundlich equation is then given by Cs = KFCwn. The Freundlich isotherm is an empirical relationship between the Cw and the Cs, the mechanism underlying the sorption process is not explained. Reported Freundlich isotherms (with surfactants) at environmentally relevant concentrations indicate in nearly all cases a value of n < 1.29 When n < 1 and Cw → 0 (physically equivalent to infinite dilution) Cs does not exist. Therefore when n < 1 one cannot derive the Freundlich sediment–water partition coefficient at infinite dilution, KFp,0 required in developing sorption models. It also remains unclear how the reported Freundlich sorption constants, KF, and n, can be transformed into the Freundlich sediment–water partition coefficient, KFp, required in the ERA model.
Cw is found to be linear a Freundlich isotherm is observed. The Freundlich equation is then given by Cs = KFCwn. The Freundlich isotherm is an empirical relationship between the Cw and the Cs, the mechanism underlying the sorption process is not explained. Reported Freundlich isotherms (with surfactants) at environmentally relevant concentrations indicate in nearly all cases a value of n < 1.29 When n < 1 and Cw → 0 (physically equivalent to infinite dilution) Cs does not exist. Therefore when n < 1 one cannot derive the Freundlich sediment–water partition coefficient at infinite dilution, KFp,0 required in developing sorption models. It also remains unclear how the reported Freundlich sorption constants, KF, and n, can be transformed into the Freundlich sediment–water partition coefficient, KFp, required in the ERA model.
2.3 Defining an average and exact partition coefficient Kp
In a sorption experiment a number of data points of the ratio of measured concentration Cs and Cw, Cs/Cw, at equilibrium are established (eqn (1)). However mathematically one determines the Kp value for each data point as the ratio of the difference in Cs and Cw between two data points being the measured value and the origin, Kp = ΔCs/ΔCw. In case Kp is determined by establishing a ratio between the measured value and the origin or between two distinct sorption data, we refer in this article to an average Kp:![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) p.
p.
When a mathematical equation is established between the measured data points it is possible to obtain both the Cs and Kp at each Cw, Cs(Cw) and Kp(Cw). Establishing the mathematical relationship between the measured data points is mathematically equivalent to taking the limiting value of ΔCw to zero, ΔCw → 0. In this case the Kp(Cw) can be established by taking the differential of Cs(Cw), dCs/dCw. In this study we speak then of an exact Kp. Although such an approach has been reported once for surfactants in the scientific literature5 it has not been elaborated further upon. In the literature invariably average Kp values (![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) p) (e.g.ref. 30 and 31) are being reported, but it is the exact Kp that needs to be used in the development of sorption models and in ERA models. An exact Kp(Cw) at each Cw is therefore obtained by differentiating Cs to Cw, dCs/dCw, while the average Kp
p) (e.g.ref. 30 and 31) are being reported, but it is the exact Kp that needs to be used in the development of sorption models and in ERA models. An exact Kp(Cw) at each Cw is therefore obtained by differentiating Cs to Cw, dCs/dCw, while the average Kp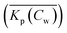 at each Cw is obtained by dividing Cs over Cw, Cs(Cw)/Cw. Exact and average partition coefficients of the most commonly used sorption isotherms are shown in Table 1. From here on Kp refers to an exact partition coefficient unless specifically indicated otherwise.
at each Cw is obtained by dividing Cs over Cw, Cs(Cw)/Cw. Exact and average partition coefficients of the most commonly used sorption isotherms are shown in Table 1. From here on Kp refers to an exact partition coefficient unless specifically indicated otherwise.
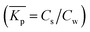 sediment–water partition constants
sediment–water partition constants
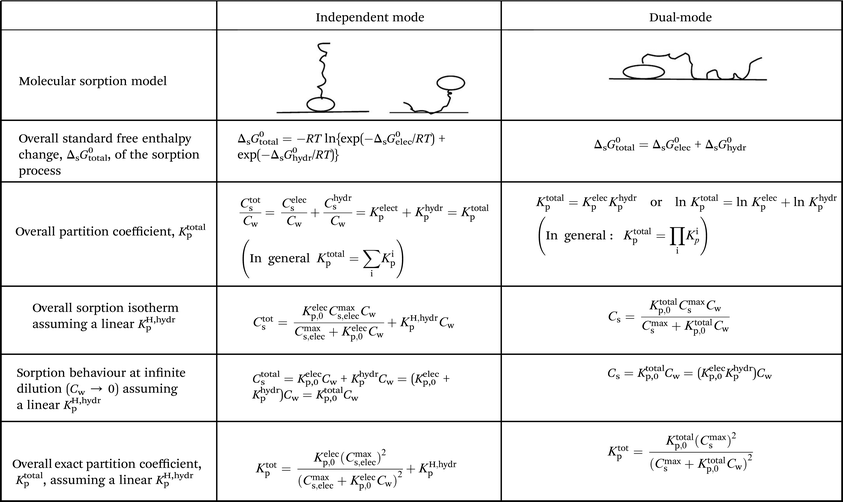
2.4 ΔsG0total and Ktotalp of the IM and DM model
The two interaction modes, depicted in Fig. 1, allow to establish the overall standard free enthalpy of the sorption process and the corresponding partition coefficients, the overall sorption isotherms and their behaviour at infinite dilution to derive the different partition coefficients, Kelecp, and Khydrp with the adsorbent (see Table 2).The equations in Table 2 are the final equations used in this study to construct and explain observed differences in the adsorption and desorption behaviour of surfactants with sediments at low concentrations. For the overall isotherm in the IM model a Langmuir isotherm for the ionic-polar interaction and a Henry's law isotherm for the non-polar interaction have been selected instead of two Langmuir isotherms. In Section 4.1 it will be justified when such an approach is feasible. However the procedure is equivalent if the non-polar interaction is given by a non-polar Langmuir isotherm. The IM model describes the sorption process in the experimental system by two completely different types of sorption sites on the same sediment or two different types of sediment, each with a specific Kp,0 and Cmaxs. In contrast, the DM model describes the experimental system by one adsorbent (e.g. organic matter) and one type of sorption location with one specific Kp,0 and Cmaxs where both type of interactions take place simultaneously. Because these experimental systems are different, the thermodynamic overall equations and the overall equations of the partition coefficients of each system are different. Table 2 shows that ΔsG0total for the DM model is a simple addition of the non-polar and ionic-polar process while this is not the case for the IM model. Otherwise stated, the total sorption coefficient Ktotalp is the sum of the non-polar and ionic-polar partition coefficient for the IM model, while it is the product of the non-polar and ionic-polar partition coefficient for the DM model.
2.5 From experimental system parameter, Kp,0, to its molecular sorption parameter(s), K
If the Kp,0-value must be related to its corresponding molecular sorption constant the value must also be corrected for its system parameter(s) because a change of thermodynamic system is considered. Therefore the KL in the Langmuir equation (cf.eqn (3)) is equivalent to the molecular sorption constant and these equilibrium values must be used as input for molecular sorption models and SARs. This procedure is equivalent to what is a common procedure in environmental chemistry: to normalise measured partition coefficients directly on the (dissolved) organic carbon (cf.eqn (5a)). However such a procedure of normalisation on organic carbon is allowed if it is assured that a non-polar interaction takes place. It seems that this procedure is not always applied correctly in sorption studies with surfactants where ionic-polar interactions are also expected.22,32–34 Incorrect conclusions on molecular sorption strength will also be drawn if variations in Kp,0-values are not corrected for the system parameter Cmaxs when different adsorbents are used.35,36The standard free enthalpy of the molecular sorption processes, ΔsG0L, can be calculated from the corresponding KL-value, ΔsG0L = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KL. This standard free enthalpy can only be calculated correctly if KL is dimensionless. Usually KL-values are reported in L mol−1. However, there is no general method to modify to a unit-less value. It is then difficult to compare similar ΔsG0L-values from different references 37 and erroneous conclusions may be drawn on the nature of the sorption process. There has been consensus on the direct use of the unit L mol−1 for non-ionic and dilute ionic solutions because the activity coefficient does not vary too much.38 In colloid chemistry KL-values are often transformed into a “dimensionless” value of mol mol−1 by transforming the liter-unit of water into mol-unit (1 L water = 55.5 mol water if the experiment was conducted in an aqueous solution). However Azizian recently challenged this transformation because a mol of an adsorbate is not equivalent to a mol of water.39 In his kinetic derivation of the Langmuir-equation he proposed to introduce a relative Cr(t) instead of a Cw(t) based on the maximum solubility of the solute in water, Csataq, Cr(t) = Cw(t)/Csataq. The modified (thermodynamic) Langmuir isotherm with a real dimensionless Langmuir constant, KML, will appear then as (eqn (8)):
KL. This standard free enthalpy can only be calculated correctly if KL is dimensionless. Usually KL-values are reported in L mol−1. However, there is no general method to modify to a unit-less value. It is then difficult to compare similar ΔsG0L-values from different references 37 and erroneous conclusions may be drawn on the nature of the sorption process. There has been consensus on the direct use of the unit L mol−1 for non-ionic and dilute ionic solutions because the activity coefficient does not vary too much.38 In colloid chemistry KL-values are often transformed into a “dimensionless” value of mol mol−1 by transforming the liter-unit of water into mol-unit (1 L water = 55.5 mol water if the experiment was conducted in an aqueous solution). However Azizian recently challenged this transformation because a mol of an adsorbate is not equivalent to a mol of water.39 In his kinetic derivation of the Langmuir-equation he proposed to introduce a relative Cr(t) instead of a Cw(t) based on the maximum solubility of the solute in water, Csataq, Cr(t) = Cw(t)/Csataq. The modified (thermodynamic) Langmuir isotherm with a real dimensionless Langmuir constant, KML, will appear then as (eqn (8)):
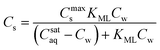 | (8) |
Although appealing, it is not clear how the term Csataq must be interpreted in the case of possible micellization.
The influence of a non-polar and ionic-polar interaction on ΔsG0 when the number of CF2 or CH2 units in the tail of the surfactant is varied, can be described as follows. If Kp,0-values of only an ionic-polar interaction of the surfactant with the adsorbent, Kelecp,0, are established then the standard free enthalpy variation of e.g. an addition of CF2-unit (NCF2) in the tail, 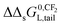 , is given by a contribution of the head which is adsorbed to the sorbent and the tail in the water cf.eqn (9a)
, is given by a contribution of the head which is adsorbed to the sorbent and the tail in the water cf.eqn (9a)
ΔsG0p,elec(NCF2) = ΔsG0L,head-sorbent + ΔΔsG0L,head-sorbentNCF2 − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cmaxs,elec Cmaxs,elec | (9a) |
ΔsG0p,hydr(NCF2) = ΔsG0L,tail-sorbent + ΔΔsG0L,tail-sorbentNCF2 − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cmaxs,hydr Cmaxs,hydr | (9b) |
In case of KL-values, the term −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cmaxs would not appear in eqn (9a) and (9b). When in the applied experimental system both interactions occur at the same time, the observed value of
Cmaxs would not appear in eqn (9a) and (9b). When in the applied experimental system both interactions occur at the same time, the observed value of 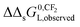 for the IM model will differ from the DM model.
for the IM model will differ from the DM model.
The fact that in a sorption experiment two thermodynamic systems must be considered has also a profound influence on its adsorption or desorption rate processes. In any rate measurement it is the experimental system which relaxes to equilibrium. In the study of Azizian40 where the Langmuir rates of adsorption (ka) and desorption (kd) are directly linked to Cs(t), it can be shown that when Cw(0) ≫ Cs(0) i.e., when the initial concentration of the solute in the water phase is very high compared to the adsorbed one, the experimentally observed rate constant is of pseudo-first order and is a combination of the adsorption and desorption Langmuir rate constants. Both Langmuir rate constants can be obtained by plotting the observed rate constant vs. the initial concentration of the solute, Cw(t = 0), which should lead to a straight line with ka as slope and kd as intercept and therefore establish the Langmuir sorption constant, KL, in another way. Owing to the existence of different kinetic regimes it is not necessary that the kinetically derived KL and the thermodynamically derived KL lead to similar values. In the same ref. 40 it is also shown that when Cw(0) ≳ Cs(0) or when the initial concentration of the solute is not too high a pseudo-second-order model is observed which leads to the Langmuir adsorption isotherm expression at equilibrium. The observed second-order rate constant is a more complex function of the initial concentration of the solute than in the case of the first-order rate constant. There are several ways to show that the Langmuir adsorption and desorption rate process are of a second order nature. In this study the derivation is given in Annex II.
3. Model application to several sorption phenomena
3.1 Overview
As stated before, well-defined substance and/or sediment parameters can be derived from the Langmuir, Henry's law and Virial isotherms at infinite dilution. Therefore only sorption data derived from these three isotherms are relevant in the model development. In addition, sorption isotherms should be established at low, and preferably at environmentally relevant, surfactant concentrations. In order to avoid experimental artefacts, direct analysis of both the sediment and water phase should have been applied. The resulting data set is small despite the large number of references dealing with sorption of surfactants to sediment (cf. Table S1, ESI†). In Table S1† the Ktotalp,0 of Matthijs et al.41 are calculated from their reported KL and Cmaxs values for the anionic surfactant C12-LAS (cf.eqn (3b)).– Section 3.2 describes then how the sorption of surfactants is influenced by various organic carbon fractions according to the IM and DM model, using the anionic surfactant C12-LAS as an example. Reported sorption values for LAS from the literature at very low and very high contents of organic carbon26,41–43 will be used to derive their model-specific partition coefficients, Khydrp, Kelec-IMp,0 and Kelec-DMp,0. After deriving the model partition coefficients, the IM and DM isotherms will be constructed again according to Table 2 by varying the organic carbon fraction (1%, 10%, 20%). The curvature at infinite dilution and the overall isotherms over the full concentration range will then be compared to experimentally observed isotherms.
– In Section 3.3, the influence of surfactants head groups and/or tail length is discussed. In Section 3.3.1 the overall sorption isotherms according to the IM and DM model of a mixture of nonylphenol ethoxylates (NPEOx) as an example where only the head varies will be constructed and compared to similar reported isotherms. In Section 3.3.2 sorption data of a mixture of LAS as an example of varying tail lengths will be compared to the individual components of the mixture.
– In Section 3.4, the incremental standard free enthalpy values 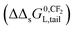 reported on varying the number of CF2-groups of perfluorinated carboxylated acids (PFCAs), will be compared to experimentally observed values when both interactions are present.
reported on varying the number of CF2-groups of perfluorinated carboxylated acids (PFCAs), will be compared to experimentally observed values when both interactions are present.
- In Section 3.5, the influence of different adsorbents on the experimentally observed adsorption isotherm will be given, and particularly will discuss how different sorption processes influence the desorption rate isotherms.
– In Section 3.6, a few published examples will be discussed where both a non-polar and ionic-polar Langmuir isotherm were observed.
3.2 Applying the IM and DM model to variable OC contents
| Case | f oc | K hydrp (L kg−1) | K elec-IMp,0 (L kg−1) | K elec-DMp,0 (L kg−1) | K totalp,0 (L kg−1) | Remark |
|---|---|---|---|---|---|---|
| 0 | 1% | 211 | From cited values (Matthijs41) | |||
| 1 | 1% | 15 | 14 | 211 | K hydrp see text. Kelecp based on DM-model | |
| 2 | 1% | 15 | 196 | 211 | K hydrp see text. Kelecp based on IM-model | |
| 3 | 10% | 150 | 196 | 346 | K elec-IMp constant and using IM model to estimate Ktotalp | |
| 4 | 20% | 300 | 196 | 496 | K elec-IMp constant and using IM model to estimate Ktotalp | |
| 5 | 10% | 150 | 14 | 2100 | K elec-DMp constant and using DM model to estimate Ktotalp | |
| 6 | 20% | 300 | 14 | 4200 | K elec-DMp constant and using DM model to estimate Ktotalp |
 | ||
| Fig. 2 C12-LAS overall sorption isotherms on varying the organic carbon fraction (1% for case 0–2; 10% for case 3 and 5; 20% for case 4 and 6) in the IM model (a) or DM model (b) in the range from 0–15 mg L−1. Case 0 is based on the sediment partition coefficient values observed in Matthijs41 with Ktotalp,0 = 211 L kg−1 and foc = 1%, from which the Kelecp,0 are derived for both the IM and DM model. Case 1 and 2 represent the two model sorption isotherms with 1% organic carbon as used in that study, whereas new sediment compositions with 10 and 20% are simulated based on these obtained Kelecp,0 values for both models. The Khydrp values increase proportional to foc and are equal for the IM and DM model, Kelecp,0 values are constantly 196 L kg−1 for IM, and constantly 14 L kg−1 for DM (details given in Table 3). | ||
Fig. 2b shows that upon increasing the organic carbon fraction the DM model remains a Langmuir isotherm albeit the isotherms become steeper at the origin. Therefore the curvature of the DM isotherms at low concentrations increases on increasing the organic carbon fraction. This is in contradiction to the isotherms constructed by the IM model (Fig. 2a). This one indicates that the isotherms become more linear near the origin on increasing foc. Such a difference in isotherm behaviour can also be extended to the Freundlich isotherm. If the DM model is valid an increase in organic carbon would lead to a change in n further from 1 but if the IM model is valid, n would become closer to 1 and the isotherm becomes more linear. This increase in linearity and n to values closer to 1 on increasing the oc-fraction is observed clearly e.g. for C12-LAS5 and for the perfluorinated sulphonates45 but much less for A13EO6.46 The IM model explains the observed sorption behaviour as a function of the organic carbon fraction when both types of interaction are present, while the DM model does not.
When deriving the IM and DM partition coefficients for foc of 0.01 from the experimental data of Matthijs (1985),41 the observed overall isotherm according to the DM model with Ktotalp,0 = 211 L kg−1 and Cmaxs,elec of 1923 mg kg−1, is nearly equivalent to the IM model isotherm (from eqn (4)) with Kelec-DMp,0 = 196 L kg−1 and Cmaxs,elec of 1923 mg kg−1, including a linear part with Khydrp = 15 L kg−1. The IM model leads to a difference between the experimental Cs and the calculated one of around 14% only at the highest applied concentration (15 mg L−1). Both isotherms are shown in Fig. 2a (case 0 and 2 respectively). It can be concluded here that the difference in Cs calculated by the IM or the DM model applied to these experimental data will become only pronounced at higher oc-fractions.
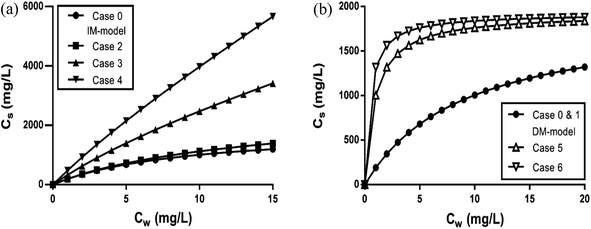
 | ||
| Fig. 3 (a–c) Sorption isotherms of LAS according to the IM and DM model with foc = 1% and foc = 20% respectively. (a and b) For the IM model, Kelecp,0 = 196 L kg−1, Cmaxs = 1923 mg kg−1, Koc = 1500 with foc = 1% (a) and foc = 20% (b). (a) and (b) include the separated adsorption isotherms of the electrostatic and hydrophobic interaction and the overall sorption isotherm. (c) shows the sorption isotherms for the DM model with foc = 1% and foc = 20%. The applied experimental concentration range by Matthijs41 for foc = 1% and for foc = 20% by Marchesi44 are indicated by the grey area. (d–f) Partition isotherms of LAS according to the IM and DM model with foc = 1% to foc = 20% respectively. (d and e) For the IM model, Kelecp,0 = 196 L kg−1, Cmaxs = 1923 mg kg−1, Koc = 1500 with foc = 1% (d) and foc = 20% (e). (d) and (e) include the separated partition isotherms of the electrostatic and linear hydrophobic interaction and the overall sorption isotherm. (f) shows the partition isotherms for the DM model with foc = 1% and foc = 20% respectively. The applied experimental concentration range by Matthijs41 for foc = 1% and for foc = 20% by Marchesi44 are indicated by the grey area. | ||
Fig. 3 shows that on using the IM model and depending on the applied concentration range and the characteristics of the sediment, the sorption process can be dominated by the ionic-polar or the non-polar interaction. For example, in Fig. 3a and d it is shown that in the experimental concentration range applied by Matthijs et al. (1985)41 (1–15 mg L−1) the total adsorbed LAS fraction and the overall partition coefficient are dominated by the ionic-polar contribution, whereas at much higher surfactant concentrations (>500 mg L−1) the total adsorbed fraction and the overall partition coefficient is dominated by the non-polar contribution. If the authors would have considered a much larger concentration range (their experimental data would allow such a consideration) then the typical characteristic S-curvature for the overall sorption isotherm would have been obtained that was observed by other authors e.g.ref. 46. At much higher oc-fractions, as in the experiments conducted by e.g. Marchesi,44 in the IM-model the total adsorbed LAS fraction and the overall partition coefficient is entirely determined by the non-polar interactions over the full concentration range, even at a very low concentration (see Fig. 3b and e). The contribution of the ionic-polar interaction does not play any significant role. This is in contradiction to the DM isotherms constructed from the same data. In both cases (foc = 1% and 20%) the sorption and the partition isotherms remain a Langmuir curve over the full concentration range (see Fig. 3c and f).
We conclude here that the IM model can explain several features in observed sorption isotherms of surfactants at different applied concentration ranges.
3.3 Applying the IM and DM model to variable surfactant structures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koc and the number of EO units, NEO, (see Fig. S1†). In bold and in italics the recalculated IM partition coefficients are indicated in Table 4. Table 5 shows the ionic-polar and non-polar partition coefficients when the DM model is used.
Koc and the number of EO units, NEO, (see Fig. S1†). In bold and in italics the recalculated IM partition coefficients are indicated in Table 4. Table 5 shows the ionic-polar and non-polar partition coefficients when the DM model is used.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kocvs. NEO correlation from Fig. S1a. The calculated KH,hydrp,0 values from the reported data for NPEO10–12 are unrealistic because the error in the reported data is in the same range as the expected KH,hydrp,0. Using the improved KH,hydrp,0-values for NPEO10–12 lead to a set of improved data. Data taken from John47
Kocvs. NEO correlation from Fig. S1a. The calculated KH,hydrp,0 values from the reported data for NPEO10–12 are unrealistic because the error in the reported data is in the same range as the expected KH,hydrp,0. Using the improved KH,hydrp,0-values for NPEO10–12 lead to a set of improved data. Data taken from John47
| NPEOx | Reported data (+SE) | K H,hydrp,0 (L kg−1) | K H,hydrp,0 (L kg−1) | Improved data | K oc | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koc Koc |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH,elecp,0 KH,elecp,0 |
||
|---|---|---|---|---|---|---|---|---|---|
| K H,elecp,0 (L kg−1) | K totalp,0 (IM) (L kg−1) | K totalp,0 (IM) | K H,hydrp,0 (L kg−1) | ||||||
a From NPEO10–12 from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kocvs. NEO QSAR (see ESI Fig. S1). ? = doubtful values because the actual value is within the SE limits. Kocvs. NEO QSAR (see ESI Fig. S1). ? = doubtful values because the actual value is within the SE limits.
|
|||||||||
| 3 | 230 + 20 | 1460 + 140 | 1230 | 1460 | 1230 | 6150 | 3.79 | 2.36 | |
| 4 | 270 + 20 | 930 + 60 | 660 | 930 | 660 | 3300 | 3.52 | 2.43 | |
| 5 | 320 + 30 | 750 + 110 | 430 | 750 | 430 | 2150 | 3.33 | 2.51 | |
| 6 | 360 + 40 | 700 + 70 | 340 | 700 | 340 | 1700 | 3.23 | 2.56 | |
| 7 | 330 + 60 | 590 + 60 | 260 | 590 | 260 | 1300 | 3.11 | 2.52 | |
| 8 | 400 + 60 | 550 + 60 | 150 | 550 | 150 | 750 | 2.88 | 2.60 | |
| 9 | 460 + 60 | 540 + 60 | 80 | 540 | 105 | 526 | 2.72 | 2.66 | |
| 10 | 480 + 60 | 450 + 80 | −30? | 71 | 551 | 71 | 357 | 2.55 | 2.68 |
| 11 | 530 + 90 | 550 + 110 | 20? | 49 | 579 | 49 | 243 | 2.38 | 2.72 |
| 12 | 590 + 120 | 750 + 180 | 160? | 33 | 623 | 33 | 165 | 2.22 | 2.77 |
| NPEOx | Reported data (+SE) | K H,hydrp,0 (L kg−1) | K oc | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koc Koc |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH,elecp,0 KH,elecp,0 |
|
|---|---|---|---|---|---|---|
| K H,elecp,0 (L kg−1) | K totalp,0 (DM) | |||||
| 3 | 230 + 20 | 1460 + 140 | 6.35 | 31.74 | 1.50 | 2.36 |
| 4 | 270 + 20 | 930 + 60 | 3.44 | 17.22 | 1.24 | 2.43 |
| 5 | 320 + 30 | 750 + 110 | 2.34 | 11.72 | 1.07 | 2.51 |
| 6 | 360 + 40 | 700 + 70 | 1.94 | 9.72 | 0.99 | 2.56 |
| 7 | 330 + 60 | 590 + 60 | 1.79 | 8.94 | 0.95 | 2.52 |
| 8 | 400 + 60 | 550 + 60 | 1.38 | 6.88 | 0.84 | 2.60 |
| 9 | 460 + 60 | 540 + 60 | 0.98 | 4.89 | 0.69 | 2.66 |
| 10 | 480 + 60 | 450 + 80 | 1.15 | 5.73 | 0.76 | 2.68 |
| 11 | 530 + 90 | 550 + 110 | 1.42 | 7.08 | 0.85 | 2.72 |
| 12 | 590 + 120 | 750 + 180 | 1.08 | 5.42 | 0.73 | 2.77 |
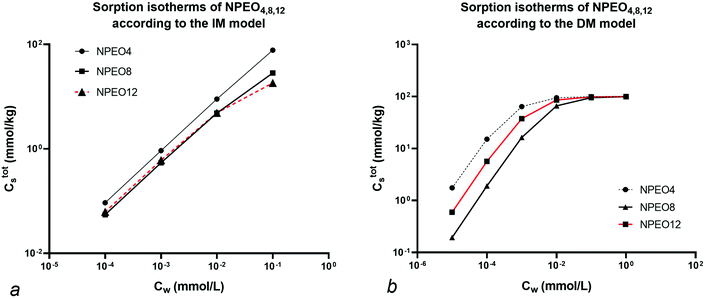
Since no value for Cmaxs,elec is cited in the specific reference an arbitrary value of 100 mmol kg−1 is chosen to show the different isotherm behaviour at low and high concentration. The resulting Ctotals isotherms for each NPEOx according to the IM and DM model for a foc = 0.20 are shown in Fig. 4.
Fig. 4 shows that at high Cw (>0.01 mmol L−1) the sequence in the IM model is NPEO4 > NPEO8 > NPEO12. In the IM model at high concentration the non-polar interaction is dominant because the ionic-polar sorption process does not contribute anymore to Cs and NPEO4 shows the largest value of Koc. This is not the case in the DM model where the sequence is NPEO4 > NPEO12 > NPEO8 which is also equivalent at low concentrations in the IM model. This is expected as in both models the sequence of the Ktotalp,0 values corresponds to NPEO4 > NPEO12 > NPEO8. Therefore it can be shown that in the IM model a reversal of the isotherm of NPEO8 and NPEO12 or on similar grounds for any similar surfactant with the same tail and a varying head can be expected when the full isotherm is established or when the concentration range is high enough that one of the two isotherms (non-polar or ionic-polar) is saturated. Such a reversal phenomenon has indeed been observed for experimental sorption of C12EO1,3,5 (ref. 48) and an increasing influence of the organic carbon fraction compared to the clay fraction at higher Cw.49 In case both the heads and tails vary as in alkylethoxylates (AEO) the chemical variation in AEO at different Cw is much more difficult to model. The IM model can explain reversals of the sequence of isotherms of a mixture of surfactants with different heads and similar tails.
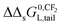 on pure and complex adsorbents have been reported.8,51,52 On a pure ionic-polar adsorbent e.g. kaolinite or a weak anion exchanger (WAX) it is assumed that the value of
on pure and complex adsorbents have been reported.8,51,52 On a pure ionic-polar adsorbent e.g. kaolinite or a weak anion exchanger (WAX) it is assumed that the value of 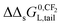 can be found by the slope on applying eqn (9a). On a pure non-polar adsorbent e.g. HLB or C18 it is assumed the slope can be found by applying eqn (9b). If both types of interactions take place at the same time then according to the IM model the adsorption processes are independent and the overall incremental value is the average value of both values (Fig. 5c). In case the DM model is considered then both interactions are simultaneously taking place and the overall incremental value is an addition of both values (Fig. 5d).
can be found by the slope on applying eqn (9a). On a pure non-polar adsorbent e.g. HLB or C18 it is assumed the slope can be found by applying eqn (9b). If both types of interactions take place at the same time then according to the IM model the adsorption processes are independent and the overall incremental value is the average value of both values (Fig. 5c). In case the DM model is considered then both interactions are simultaneously taking place and the overall incremental value is an addition of both values (Fig. 5d).
Table 6 shows reported values of slopes of PFCAs sorption processes on both pure and mixed adsorbents.
| Only non-polar assumed | Only ionic-polar assumed | Predicted ΔsΔG0L(CF2) according to the different models | Observed ΔsΔG0L(CF2) | ||
|---|---|---|---|---|---|
| ΔsΔG0L(CF2)tail-adsorbent | ΔsΔG0L(CF2)head-adsorbent | Dual-mode | Independent mode | ||
| a C. Eschauzier.51 b F. Xiao.8 c C. P. Higgins.11 d P. de Voogt.52 | |||||
| 4.70 ± 0.34 (C18)a | 2.6 ± 0.24 (WAX)a | 3.3 (org. matter)c | |||
| 4.00 ± 0.40 (HLB)a | 2.5 ± 0.23 (MAX)a | 3.4 (sediment)b | |||
| 4.7 (octanol)a | 2.6 (kaolinite)b | ||||
| 4.3 (C18)d | |||||
| Average | 4.5 | 2.6 | 7.1 | 3.5 | 3.4 |
Table 6 shows that when both interactions take place the slope follows the IM model and not the DM one.
Established KelecL or ΔsG0L values of cationic or anionic surfactants vary with the ionic strength of the solution. However this does not count for the slope of a sequence of such type of surfactants 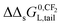 .8
.8
3.4 Applying the IM and DM model to describe desorption processes
As described before in kinetic sorption experiments two thermodynamic systems are present, the experimental one and the molecular one leading to complex molecular rate functions. In this case adsorption and desorption results between the IM and DM model can be quite different because in the IM model two different adsorbents are present each having their independent sorption isotherm.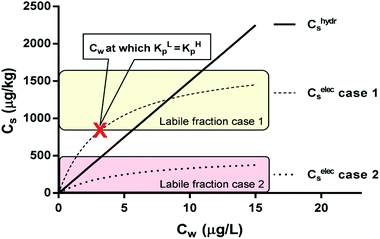 | ||
| Fig. 6 Two sorption cases of a surfactant according to the IM model. Case 1 is a combination of a linear (non-polar) and Langmuir (ionic-polar) sorption process where the Langmuir isotherm is at least partially above the linear isotherm (KL,elecp,0 > KH,hydrp) with KH,hydrp = 150 L kg−1, KL,elecp,0 = 500 L kg−1 and Cmaxs,elec = 1800 μg kg−1. Case 2 where the entire Langmuir (ionic-polar) isotherm is below the linear (non-polar) one (KL,elecp,0 < KH,hydrp) with KH,hydrp = 150 L kg−1, KL,elecp,0 = 100 L kg−1 and Cmaxs,elec = 500 μg kg−1. With these data the Cw for which KL,elecp = KH,hydrp in case 1 is equal to ∼3.0 μg L−1 according to eqn (10) and divides the adsorbed ionic-polar fraction into a labile and non-labile one. The labile (ionic-polar) fractions that will be desorbed first because they are weaker bound than the non-polar fraction are indicated by the colored sections. | ||
The value of Cw for which both the Langmuir ionic-polar and the Henry's law non-polar isotherm have the same partition coefficient, KL,elecp = KH,hydrp, can be found by equating in this case the exact Kp for the different isotherm (Table 2) leading to eqn (10)
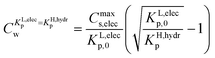 | (10) |
For the data applied in Fig. 6 this is at a Cw of ∼3 μg L−1. This equation is only valid for KL,elecp,0 > KH,elecp corresponding to case 1. The Cw where KL,elecp = KH,hydrp divides the non-linear (Langmuir) sorbed fraction in the IM model into two parts, a labile or fast one where 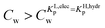 and a non-labile or slow one where
and a non-labile or slow one where 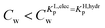 . In any desorption experiment above
. In any desorption experiment above 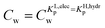 the first fraction that is removed is the labile ionic-polar adsorbed fraction followed by desorption of the non-polar adsorbed one. However below
the first fraction that is removed is the labile ionic-polar adsorbed fraction followed by desorption of the non-polar adsorbed one. However below 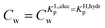 the first fraction that is removed is the non-polar adsorbed fraction followed by the stronger bound ionic-polar adsorbed one.
the first fraction that is removed is the non-polar adsorbed fraction followed by the stronger bound ionic-polar adsorbed one.
To visualize the different sorption processes Table 7 is derived from Fig. 6 indicating the mass adsorbed by the linear (non-polar) fraction and the labile and non-labile fraction from the non-linear ionic-polar isotherm.
| C w (μg L−1) | C totals (μg kg−1) | C hydrs (μg kg−1) | C elecs (non-labile) (μg kg−1) | C elecs (labile) (μg kg−1) |
|---|---|---|---|---|
| Case 1 | ||||
| 12 | 2900 | 1700 | 600 | 600 |
| 6* | 1800 | 1200 | 600 | 0 |
| 6 | 1800 | 800 | 600 | 400 |
| 1 | 600 | 200 | 400 | 0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Case 2 | ||||
| 1 | 300 | 200 | 0 | 100 |
| 6 | 1100 | 800 | 0 | 300 |
| 12 | 2100 | 1700 | 0 | 400 |
In the following, two desorption processes are distinguished, in Section 3.4.2 a continuous one and in Section 3.4.3 a successive washing one from a complex adsorbent (e.g. an adsorbent where either two or more types of sorption processes may occur or that exists out of two or more different types of pure sorbent materials).
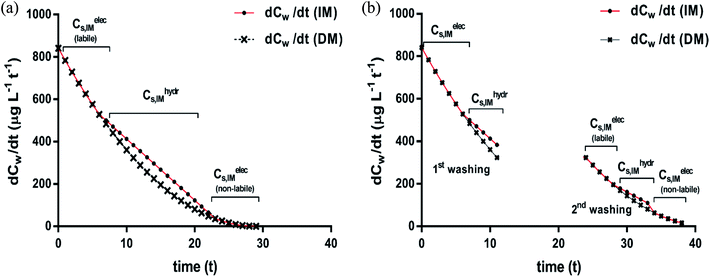 | ||
| Fig. 7 Desorption rates after a single continuous washing (a) and two successive washings (b); desorption rate curves according to the DM (×) and IM (●) model applied to case 1 in Fig. 6. The subsequent desorption fractions from the two sorption isotherms (non-polar and ionic-polar) according to the IM model are indicated. Note the different slope ranges that coincide with changes of desorption processes for the IM model and note that the adsorbed ionic-polar fraction is divided into a labile and non-labile one. The Cw where this change occurs is the Cw where KL,elecp = KH,hydrp. | ||
On similar grounds the fraction that is removed in case of case 2 is 980 μg of which 373 μg is from the complete labile bound ionic-polar fraction and an additional 637 μg from non-polar fraction. If the time between the washing process is sufficient to re-establish equilibrium a small surfactant flux of 273 μg adsorbed by a non-polar interaction will desorb and flow to the labile ionic-polar adsorbent.
We conclude here that only the IM model can lead to mixed rate desorption isotherms of first and second order processes when different sediment fractions are involved in the sorption process of the adsorbate while for the DM model only second order processes should be observed. After a washing process the IM model predicts also a mass flow of the surfactant to other adsorbents without invoking any additional physical and/or chemical process of the adsorbate or adsorbent itself.
3.5 Both non-polar and ionic-polar Langmuir isotherms: Koc and focvs. KhydrL and Cmaxs,hydr
Experiments where the non-polar interaction has been described by a Langmuir isotherm do exist but most authors do not relate the different sorption parameters Koc and foc to KhydrL and Cmaxs,hydr. One example is the sorption experiment of the cationic surfactant dodecylpyridinium (DP) onto sediment “EPA12”59 where a multisite competitive Langmuir model was developed to explain the sorption behaviour. In this model each site was characterized by a constant KLp and a specific value of Cmaxs. However by invoking a varying KLp (KLp(Cw)) and a unique value of Cmaxs for both defined interactions (ionic-polar and non-polar), this multisite competitive model changes into a much simpler model of two Langmuir isotherms according to the IM model. In this case, Cmaxs,hydr, for the non-polar interaction of DP with the sediment “EPA12” was found to be ∼75 mmol (∼25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg) dodecylpyridinium per kg sediment. This corresponds to a maximum sediment sorption capacity of around 2.5% (m/m) for DP, which is coincidentally similar to the organic carbon fraction of this sediment (2.1–2.3%).
000 mg) dodecylpyridinium per kg sediment. This corresponds to a maximum sediment sorption capacity of around 2.5% (m/m) for DP, which is coincidentally similar to the organic carbon fraction of this sediment (2.1–2.3%).
Sorption experiments of phenanthrene to marine sediment60 were described by several isotherms including Langmuir. Using the reported Langmuir data and assuming that only non-polar sorption occurs the data shows the expected linear correlation between Cmaxs,hydr (mmol kg−1) and foc (%), leading to Cmaxs,hydr = 0.68foc + 0.10 (N = 5, R2 = 0.88) and an average KhydrL = 316 L mmol−1 or Koc = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 L kg−1 (see Table S2†). Using the linear correlation a value of Cmaxs,hydr (mmol kg−1) of 1.7 mmol kg−1 sediment for ∼2.2% oc is found. Whether this difference in Cmaxs,hydr between phenanthrene (1.7 mmol kg−1 sediment) and DP (75 mmol kg−1 sediment) for the same fraction of oc of 2.2% is caused by a different type of organic carbon or by a difference in size of the molecules or both remains to be investigated. We conclude here that relating Koc values to KhydrL ones is only possible if the ratio of foc to Cmaxs,hydr is known. This can only be obtained if complete non-polar Langmuir adsorption isotherms are established until the saturating plateau. It is as yet unknown if this ratio depends on the type of organic carbon or is a purely constant one. However in the case of non-polar sorption only it has been reported that the ratio seems to be constant but that the intercept varies which was attributed to different adsorption processes to two types of organic carbon.61
400 L kg−1 (see Table S2†). Using the linear correlation a value of Cmaxs,hydr (mmol kg−1) of 1.7 mmol kg−1 sediment for ∼2.2% oc is found. Whether this difference in Cmaxs,hydr between phenanthrene (1.7 mmol kg−1 sediment) and DP (75 mmol kg−1 sediment) for the same fraction of oc of 2.2% is caused by a different type of organic carbon or by a difference in size of the molecules or both remains to be investigated. We conclude here that relating Koc values to KhydrL ones is only possible if the ratio of foc to Cmaxs,hydr is known. This can only be obtained if complete non-polar Langmuir adsorption isotherms are established until the saturating plateau. It is as yet unknown if this ratio depends on the type of organic carbon or is a purely constant one. However in the case of non-polar sorption only it has been reported that the ratio seems to be constant but that the intercept varies which was attributed to different adsorption processes to two types of organic carbon.61
4. Validation and implications
4.1 Independent-mode or dual-mode
Although the DM model is attractive due to its simple overall standard free enthalpy equation (see Table 2), we have shown that many sorption experiments of surfactants at environmentally relevant concentrations can be interpreted correctly by the IM model only. The Virial applied to LAS5 and the NICA-Donnan model applied to PFCA11 were developed to interpret an additional non-polar sorption process (Virial) or ionic-polar sorption process (NICA-Donnan). These models include the additional sorption process by an addition of the different standard free enthalpies, indicating a direct influence of the sorption strength of the head by the tail or vice versa. Table 2 shows that this corresponds to the DM model.Evaluation reveals that these two models are used in cases where a specific sorption process dominates. However if the perturbation (δ) remains small compared to the main sorption process, e.g. ΔsG0hydr ≫ ΔsG0elec, then it can be easily derived that ΔsG0total(IM) (Table 2) will lead to an equivalent expression of ΔsG0total(DM) since ln(1 + δ) ≈ δ. In that case ΔsG0total(IM) = (ΔsG0main + δΔsGper) will become equal to ΔsG0total(IM) = ΔsG0hydr + δΔsG0elec which is exactly the standard free enthalpy expression for the DM model applied in the NICA-Donnan model. A similar expression can be developed when the main adsorption process is ionic-polar in character, the basis of the Virial model and was also shown before in Fig. 2a for case 0 and 1. Consequently the defined Virial K is equal to Ktotalp,0 in the DM model (Table 2). Although mathematically ΔsG0total(IM) will become equivalent to ΔsG0total(DM) when accounting for a small perturbation of the main sorption process, the physical picture of individual molecules of surfactants adsorbed only to different sediment fractions has not changed. The Virial and NICA-Donnan models fail to describe the sorption isotherm correctly when the other process becomes more dominant, e.g. by increasing the organic carbon fraction in case of the Virial. It implies that when conducting sorption experiments at low surfactant concentrations with complex adsorbents (like sediment, soil, or even clay), one needs to consider which specific adsorbents are involved in the adsorption processes, and describe each adsorption process independently by a Langmuir isotherm. The experimentally applied system boundaries determine if the specific Langmuir isotherm will appear as a linear one or as a Langmuir one (see Section 2.2.1). In river sediments and soils the non-polar adsorbent fraction is most likely much larger than the ionic-polar one, while in sea sediments this might be the opposite. Under these conditions (one fraction much larger than the other) the overall adsorption process can often best be described by a linear term and a Langmuir one, and the desorption rate processes will show a mixed character of linear and non-linear rate constants. We note here that the same characteristics are also observed with the polar substance estrone62 and non-polar substances in general adsorbed to Sediment Organic Matter (SOM). Our sorption expressions return in the Dual-Mode (DM-SOM),29 the Distributed Reactivity Model (DRM)63 and the OM-clay model applied for non-ionic surfactants sorbing to marine sediment.48 However the interpretation of the observed values in the DM-SOM and DRM model differs with the IM model. In the IM model the linear and non-linear contributions are described by simple Langmuir adsorption isotherms related to different adsorbents, respectively. In the DM-SOM model a so-called dissolution domain, leading to a linear term is distinguished from hole-filling domains contributing to the non-linear terms. In the DRM model for natural systems, composite isotherm behaviour is considered as the resultant of a series of near-linear absorption reactions and nonlinear adsorption reactions. The IM model supports the statement that usually one linear term and one or two Langmuir terms are required to obtain “best-fit” models64,65 that describe the sorption to SOM. Finally one should realize that better statistics of one model compared to the other do not necessarily imply that the former should be selected, because the error in the measurements themselves are often not taken into consideration.
4.2 The cause of the increase of KL for ionic-polar or non-polar adsorption when varying the surfactant tail length
The observation that the KL increases and therefore its corresponding ΔsG0 decreases with a constant value when the tail-length of the surfactant increases with one CX2-unit is an important aspect in sorption models and SARs. The constant decrease of the free enthalpy of adsorption of surfactants to gaseous films has been known as Traube's rule. According to Aranow,66 the constant contribution in the free enthalpy of adsorption (ΔΔsG0L) was attributed to an increase of an entropy (ΔΔsSL0) rather than a decrease in enthalpy (ΔΔsH0L). Aranow attributed this increase of the entropy to an increase of energy levels caused by an increase of torsional oscillators of the additional CH2-group in air.Modern views on the entropy contribution are related to the decrease of the rotational and/or translational movements of the water molecules in the shell around the non-polar tail of the surfactant molecule. Two models attempt to explain this source of entropy loss, the clathrate cage model and the scaled particle cavity model.67,68 The loss of entropy is released when the surfactant is adsorbed to the sorbent. Compared to the complete release of the surfactant molecule from the bulk water phase, the entropy increase is expected to be less when an ionic-polar adsorption process prevails, because the tail still remains (partially) in the water–sorbent interface. In the case of a non-polar adsorption process the tail is adsorbed to the adsorbent out of the water interface leading to a higher free enthalpy release (ΔsG0L,hydr > ΔsG0L,elec) and a higher value of the slope (ΔΔsG0L,hydr > ΔΔsG0L,elec) is expected. In other words the main contribution factor to a decrease of the standard free enthalpy of adsorption (ΔΔsG0L < 0) when the tail length of e.g. a PFCA increases, is a relatively large increase in entropy release of the molecular system 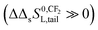 . This causes an increase in the Langmuir sorption constant KL, and not an extra enthalpy term
. This causes an increase in the Langmuir sorption constant KL, and not an extra enthalpy term 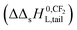 like an additional interaction of the tail with the sorbent. However, the difference in increment is different for each type of interaction (ionic-polar and non-polar).
like an additional interaction of the tail with the sorbent. However, the difference in increment is different for each type of interaction (ionic-polar and non-polar).
4.3 Sorption processes in environmental risk assessment models
The IM model can also describe observed sorption phenomena for surfactants adequately in any ERA model. Basically both types of interaction, non-polar and ionic-polar, are described by a Langmuir isotherm of the specific sediment fraction. However in an ERA model the systems considered (catchment, country) are usually quite large and thus the linear approach (cf.eqn (3a) and (3b)) is valid. When estimating the partition coefficient for an unknown surfactant one faces the problem that two parameters must be estimated for each adsorbent: KL and Cmaxs. The value of KL can be estimated from SARs. However the problem to estimate Cmaxs remains, reason why simple sediment parameters are looked for. This concept has only been applied extensively to the non-polar interactions and many SARs have been developed to estimate the Koc of a specific chemical69 based on the organic carbon fraction of the sediment, foc, as a substitute of Cmaxs,hydr.For the development of estimation methods for the ionic-polar interaction of the surfactant their corresponding KelecL and Cmaxs or their related Kelecnorm and fsed must be established. These estimation methods are hardly known due to several reasons. Firstly, several types of ionic-polar interactions are known e.g. cationic, anionic, non-ionic and zwitter-ionic. For each of these types it may be required to set up a separate Kelecnorm estimation system. Secondly, before any estimation model can be developed a set of proper Kelecnorm data must be established. These steps are lacking in the development of a sorption SAR for anionic surfactants.35 In this case the infinite dilution sorption values, correctly obtained as a first step, were not separated into their corresponding sorption processes as they should have been (see Table 2) and any possible salt effect and therefore Kp could not be corrected for the system parameter, Cmaxs, for the separate sorption processes. Consequently in the established SAR the use of foc or CEC (Cation Exchange Capacity) descriptors as independent parameters (eqn (8) and (9) in ref. 35) reflects only the variation in Cmaxscf.eqn (3), and the use of the CMC descriptor only considers a non-polar interaction parameter for the specific sorption process of the selected anionic surfactants, even though it is expected that also ionic-polar adsorption will occur.
Simple sediment parameters that estimate Cmaxs for the different types of surfactants have not been established well. Depending of the type of interaction three types of sediment parameters are found in the literature that are related to Cmaxs; (a) parameters directly related to Cmaxs (e.g. the CEC for cationic surfactants)30,59,70,71 or the Anionic Exchange Capacity (AEC) for anionic surfactants e.g. the difference in sorption capacity of PFCAs on the anionic exchangers WAX and MAX,51 (b) the specific surface area (SSA) of the sediment sorption system48,72 for non-ionic surfactants or (c) specific sediment parameters e.g. oc content or Fe/Al, Si/Al or Fe + Al/Si ratio49,50,73–76 for anionic surfactants. Currently the CEC seems to be the only sediment parameter that gives a reasonable direct correlation with Cmaxs,cat. The SSA can only be used when a single sorbent is present. In that case it can relate the adsorbed mass to the surface coverage, very useful in understanding the molecular sorption process. However if different sorbents are present that are both interacting in the sorption process each with a different Cmaxs, the SSA is only an overall sediment parameter that cannot be related to one or both of the required Cmaxs. Structural sediment parameters like foc of Fe/Al ratio have the disadvantage that their exact relationship to Cmaxs is unknown but are very useful to develop estimation methods for normalised sorption coefficients.
4.4 Possible formation of micellar structures
Sorption of some surfactants at higher concentrations may result into the formation of micellar structures at the surface of the adsorbent (hemi-micelles and/or admicelles) as is well known on pure surfaces (e.g. LAS).1,3 It is generally assumed that the surface is then fully covered by one layer of surfactant leading to an additional non-polar adsorption process by the tail until twice the Cmaxs values. However when sediment is used as adsorbent this is not observed each time, see e.g. Section 3.3.2. From a thermodynamic point of view these micellar structures will not be formed when the sorption isotherm can be represented by eqn (4) (Vsyst ≈ VL) and at Cw(aq) = CMC the value of Cmaxs/CMC (L kg−1) is (much) smaller than the minimum aggregation number required to form a micelle at the CMC. For Cmaxs of ∼8600 mg L−1, as observed in the experiments of Istok et al.,26 the ratio of Cmaxs/CMC for LAS10 (1989/500) and LAS12 (2770/125) is ∼4 and ∼22, respectively, which falls still far from the minimum aggregation number at the CMC for these two LAS-compounds, 56 and 68 respectively.77 Consequently no micellar structures at the surface of the adsorbent are observed even at these high surfactant concentrations. If the experiment would have been repeated with pure LAS-C10 and LAS-C12, the ratios would have been ∼8600/500 = ∼17 and ∼8600/125 = ∼70 respectively. A micellization process of LAS12 could have been expected at the surface of the adsorbent at these high surfactant concentrations.5. Experimental modifications and final remarks
In this study it has been shown that for sorption to complex adsorbents, such as sediment or soil, at environmentally relevant concentrations the full sorption isotherm of surfactants can be described well by the IM model. When performing such sorption experiments the most relevant adsorbents in the system must be established first. In river sediment and in soils one starts usually with the organic carbon fraction but adsorbents relevant for the possible ionic-polar interaction are often not well characterized. Once these adsorbents are characterised, the pertaining sorption process at low concentrations can be described by simple Langmuir isotherms. The experimentally applied system boundaries (the volume of the water and the fractions of adsorbents) determine how the Langmuir isotherms will appear at low concentrations. In ERA models it is assumed that these boundaries are so large that every contribution to the overall sorption process can be described by linear contributions. The main issue here is how to establish the sorption constant of the ionic-polar or non-polar adsorption process and the corresponding Cmaxs of each adsorbent so that eqn (3a) can be applied. In lab experiments with much smaller system dimensions the Cmaxs of one adsorbent may be larger than the one of another sorbent, rendering support to describe the sorption process by a combination of one Langmuir isotherm and a linear contribution or only Langmuir ones. We would like to emphasise here that such a procedure is also applicable to air/soil adsorption processes, adsorption on different types of organic carbon, inorganic sorbents, etc. Current ERA models for surfactants underestimate the adsorbed fraction in those cases where the ionic-polar interaction is substantially present, for example in sea sediments or clay-rich sediments or soils.One needs also to be careful to interpret differences in Kp,0 when varying a system parameter like pH or ionic strength of the water. According to eqn (3) the Kp,0 is a product of KL and Cmaxs. Consequently the influence of the variation on both parameters must be established. For example an increase in the Virial partition coefficient upon addition of calcium ions has been observed.5 If [Ca2+] (or any other experimental parameter, e.g. pH) is varied, the complete isotherm must be established again to derive the relevant parameters, KL,Virialp,0 or KL and b or Cmaxs. If the full Virial isotherm had been established in this case then the increase of KL,Virialp,0 could have been related either to an increase in KL (and the increase in the partition coefficient KL,Virialp,0 is caused by an increase in the sorption strength of the surfactant molecules onto the sediment), or to an increase in Cmaxs (cf.eqn (3)) (and the increase in the partition coefficient KL,Virialp,0 is caused by an increase in the number of sorption locations). In case the increase in the partition coefficient KL,Virialp,0 is caused by an increase in Cmaxs, an equivalent increase in the capacitance ‘b’ at low concentrations (eqn (6)) would also have been measured. Even this incorrect sorption model can result in a correct interpretation because, as explained in Section 4.1, such types of sorption isotherms can be observed if the non-polar adsorption constant is much smaller than of the ionic-polar one.
For modelling purposes and SAR development a variation of the tail length of the surfactant is an important molecular property.52 It is well known that the molecular sorption constant always increases for both an ionic-polar and non-polar sorption process of a surfactant when increasing the tail length. This incremental value is different for the two different adsorption processes. The most likely cause of these observations is an entropy effect rather than an enthalpy effect caused by the water molecules surrounding the tail of the surfactant.
When interpreting a variation in Kp at a specific Cw due to varying a system parameter (e.g. the fraction of sediment) the resulting exact Kp values must be compared to each other instead of using the average one. In case of a non-linear isotherm the average Kp leads to a different Kp,0 at each Cw. This would imply that the (molecular) sorption coefficient, e.g. KL in case of a Langmuir isotherm, differs at each Cw which is obviously incorrect in this case. However the exact Kp at a specific Cw can only be determined if a fitted sorption isotherm has been established through the measured data points. By calculating the exact Kp value at a specific Cw one may observe whether the exact Kp increases or decreases when varying the sediment fraction (see also Annex I). The IM model can also well explain a number of different desorption phenomena in sediment or soil. IM can define labile and non-labile desorption fractions from the same Langmuir isotherm. IM also shows that in successive washings, material flows from one adsorbent to other ones will occur because the system is forced out of equilibrium. We also showed that if one applies a Langmuir isotherm and a linear one for the different adsorbents, second order and first order desorption rates can be observed. While this has been observed for non-polar substances already, in the literature we could not find such phenomena for surfactants.
The IM model is most likely the best model to describe sorption on sediment and soil for surfactants at low concentrations. Applying the Freundlich isotherm in environmental chemistry, as is often done, needs to be avoided since the Freundlich model fails for example to derive Kp,0 relevant for the development of sorption models, nor can it properly describe the environmentally important dilution process. The Freundlich model also does not add to the understanding of the adsorption mechanism of the surfactant or any other substance on the relevant adsorbent.
Annex I
Sorption including sediment fraction as variable parameter
In a typical sorption experiment an amount of sediment, ms (kg) is added to a specific volume of water, VL (L) containing an amount of sorbate. The total volume of the experimental system, Vsyst, is then given by VL + ρms where ρ is the specific volume (L kg−1) of the sediment and ms the mass of the sediment. After the experiment an amount of substance, mx (mg), is adsorbed to the sediment while an amount, maq (mg), remains dissolved. The thermodynamic particulate matter concentration, Ctherms, is given by mx (mg substance)/ms (kg sediment) and the dissolved concentration in the experimental system, Csystw, by maq/VLVL/Vsyst,78 where maq/VL is the thermodynamic dissolved concentration, Cthermw. The experimental Langmuir case I sorption isotherm is then given by (A1)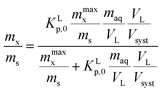 | (A1) |
 | (A2) |
(1) In case ρfsMs ≪ VL (Vsyst ≈ VL) or ρ[S]aq ≪ 1 and sorption is normalised to 1 kg of sediment (fs = 1 kg kg−1, Ms = 1 kg), eqn (A2) is approximated by eqn (A3), the thermodynamic Langmuir sorption isotherm necessary to derive the proper sorption constant KLp,0
 | (A3) |
Eqn (A3) is normally used in a typical sorption experiment where a small amount of sediment is mixed with a relatively large and constant amount of water with varying mass of surfactant and the data are normalised to 1 kg of sediment and 1 L of water.
(2) In case Ms and VL are normalised to 1 kg of sediment and 1 L respectively and in addition Cthermw = constant, then eqn (A2) turns into eqn (A4),
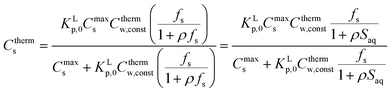 | (A4) |
Eqn (A4) shows the variation of the Ctherms with varying fractions of sediment, fs (kg kg−1), or sediment concentrations, Saq (kg L−1), present in the system keeping Cthermw = constant. Experimentally this condition is very difficult to achieve. However by establishing a series of full adsorption isotherms, each with the same total mass of the sorbate but a varying sediment fraction,5,79 one can compare the exact Kp's at a specific Cthermw.
(3) Eqn (A4) leads also to Cs → KLp,0Cthermw,const(fs/(1 + ρfs)) or Cs → KLp,0Cthermw,const(fs/(1 + ρSaq)) in the limiting condition when Cmaxs ⋙ KLp,0Cthermw,const(fs/(1 + ρfs)) or Cmaxs ⋙ KLp,0Cthermw,const(fs/(1 + ρSaq)) indicating an increasing fraction of sediment present in the experimental system. This is equivalent to the Langmuir sorption equation for infinite dilution (eqn (3b) in this paper) but corrected for the difference in system. Since under the experimental conditions ρfs is often ≪1 or ρ[S]aq ≪ 1, Cs → KLp,0Cthermw,constfs showing that sorption depends of the sediment fraction while keeping Cw constant. In case Cmaxs is very small compared to KLp,0Cthermw,const(fs/(1 + ρfs)), eqn (A4) leads to Cs → Cmaxs, which is the maximum amount of substance that can be sorbed to the sediment.
(4) The observed increase in sorption strength when the sediment fraction increases is different from the variation in sorption strength of strongly non-polar substances caused by the presence of a third phase in the water sometimes indicated as the classical solid effect. In this case it is observed that the sorption strength decreases on increasing sediment fraction, fs.
Annex II
Rate equation for Langmuir sorption process
The experimental measured adsorption–desorption rate eqn (A5) is the starting point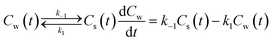 | (A5) |
The equilibrium constant KLp is related to both rate constants, KLp = k1/k−1, eqn (A6). However these system rate constants are not equivalent to the molecular adsorption–desorption rate constants since this is a different thermodynamic system. In a non-linear sorption process KLp is also a function of Cw(t) including in the infinite limit.
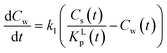 | (A6) |
Eqn (A6) is equivalent on assuming that local molecular sorption process(es) is(are) at equilibrium at each moment (KL = cst) but the overall system sorption process leading to KLp is not. Such type of processes are well known and described in non-equilibrium statistical thermodynamics.80
Table 2 gives an expression for the exact KLp and for Cs at each Cw for the Langmuir molecular sorption process which is turned into an equivalent but time dependent system one, eqn (A7).
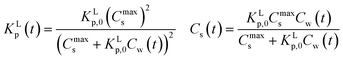 | (A7) |
Using eqn (A7) into (A6) and rearranging leads to the following rate expression for the simple case that molecular sorption process, KL, is in equilibrium at each moment but the overall system sorption process is not and when the initial concentration is not too high (Cw(0) ≳ Cs(0))
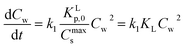 | (A8) |
Thus sorption rate processes following a Langmuir isotherm are of a simple second order nature in Cw as is overwhelmingly observed, e.g.ref. 81 and 82, while it is a more complex one for the Virial isotherm. The Freundlich isotherms fails because the infinite limit value is not defined. It is clear that when Cs(t) does not play a role in eqn (A5) (Henry's law regime), a first order rate process is observed.
List of parameters
| Parameter | Unit | Description |
|---|---|---|
| ΔsG0elec | J mol−1 | Standard free enthalpy of an electrostatic (ionic-polar) adsorption process |
| ΔsG0hydr | J mol−1 | Standard free enthalpy of a hydrophobic (non-polar) adsorption process |
| ΔsG0total | J mol−1 | Total standard free enthalpy of adsorption |
| AEC | mg or mmol anionic ions per kg sediment | Anion exchange capacity |
| CEC | mg or mmol cationic ions per kg sediment | Cation exchange capacity |
| CMC | mmol L−1 | Critical micelle concentration |
| C s | mg or mmol substance per kg sediment | Adsorbed mass fraction |
| C maxs,elec | mg or mmol substance per kg sediment | Maximum sorption capacity for an electrostatic or ionic-polar interaction |
| C maxs,hydr | mg or mmol substance per kg sediment | Maximum sorption capacity for a hydrophobic or non-polar interaction |
| C maxs,Virial | mg or mmol substance per kg sediment | Virial maximum sorption capacity |
| C maxs | mg or mmol substance per kg sediment | Maximum sorption capacity |
| C w | mg L−1 or mmol L−1 | Dissolved concentration |
| f oc | kg oc per kg sediment | Fraction organic carbon in sediment |
| f sed | kg parameter per kg sediment | Fraction of a specific parameter in sediment |
| IEC | mg or mmol ions per kg sediment | Ionic exchange concentration |
| K Hp,0 = KHp | L kg−1 | Henry's law sediment–water partition coefficient (at any Cw) |
| K F | Ln kg−1 mg−(n−1) | Freundlich sorption constant |
| K L | L mg−1 or L mmol−1 | Langmuir sorption constant |
| K L,elecp,0 | L kg−1 | Langmuir sediment–water partition coefficient at infinite dilution for an electrostatic or ionic-polar interaction |
| K L,hydrp,0 | L kg−1 | Langmuir sediment–water partition coefficient at infinite dilution for a hydrophobic or non-polar interaction |
| K elecL | L mg−1 or L mmol−1 | Electrostatic or ionic-polar Langmuir sorption constant |
| K hydrL | L mg−1 or L mmol−1 | Hydrophobic or non-polar Langmuir sorption constant |
| K Lp | L kg−1 | Langmuir sediment–water partition coefficient |
| K Lp,0 | L kg−1 | Langmuir sediment–water partition coefficient at infinite dilution |
| K elecnorm | L kg−1 parameter | Sediment normalised electrostatic or ionic-polar sediment–water partition coefficient |
| K oc | L kg−1 oc | Organic carbon normalised hydrophobic or non-polar sediment–water partition coefficient |
| K ow | Loctanol Lwater−1 | Octanol–water partition coefficient |
| K p | L kg−1 | Sediment–water partition coefficient |
| K elec-DMp,0 | L kg−1 | Electrostatic or ionic-polar sediment–water partition coefficient at infinite dilution according to the Dual-Mode model |
| K elec-IMp,0 | L kg−1 | Electrostatic or ionic-polar sediment–water partition coefficient at infinite dilution according to the Independent-Mode model |
| K L,Virialp,0 | L kg−1 | Langmuir Virial sediment–water partition coefficient at infinite dilution |
| K totalp,0 | L kg−1 | Total sediment–water partition coefficient at infinite dilution |
| K elecp | L kg−1 | Electrostatic or ionic-polar sediment–water partition coefficient |
| K Fp | L kg−1 | Freundlich sediment–water partition coefficient |
| K H,elecp | L kg−1 | Henry's law sediment–water partition coefficient for an electrostatic or ionic-polar interaction |
| K H,hydrp | L kg−1 | Henry's law sediment–water partition coefficient for a hydrophobic or non-polar interaction |
| K hydrp | L kg−1 | Hydrophobic or non-polar sediment–water partition coefficient |
| K Vp | L kg−1 | Virial sediment–water partition coefficient |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors would like to thank the valuable input from all four anonymous reviewers in improving the structuring of the manuscript and providing critical suggestions to clarify the terminology.References
- J. Scamehorn, R. Schechter and W. Wade, J. Colloid Interface Sci., 1982, 85, 463–478 CrossRef CAS.
- A. Fan, P. Somasundaran and N. J. Turro, Langmuir, 1997, 13, 506–510 CrossRef CAS.
- R. Atkin, V. S. Craig, E. J. Wanless and S. Biggs, Adv. Colloid Interface Sci., 2003, 103, 219–304 CrossRef CAS PubMed.
- P. Chandar, P. Somasundaran and N. J. Turro, J. Colloid Interface Sci., 1987, 117, 31–46 CrossRef CAS.
- J. C. Westall, H. Chen, W. Zhang and B. J. Brownawell, Environ. Sci. Technol., 1999, 33, 3110–3118 CrossRef CAS.
- P. Somasundaran, R. Middleton and K. Viswanathan, Relationship between surfactant structure and adsorption, in Anonymous, ACS Publications, 1984 Search PubMed.
- Y. Ihara, J. Appl. Polym. Sci., 1992, 44, 1837–1840 CrossRef CAS.
- F. Xiao, X. Zhang, L. Penn, J. S. Gulliver and M. F. Simcik, Environ. Sci. Technol., 2011, 45, 10028–10035 CrossRef CAS PubMed.
- S. T. Droge and K. Goss, Environ. Sci. Technol., 2013, 47, 14233–14241 CrossRef CAS PubMed.
- R. Zhang and P. Somasundaran, Adv. Colloid Interface Sci., 2006, 123, 213–229 CrossRef PubMed.
- C. P. Higgins and R. G. Luthy, Environ. Sci. Technol., 2007, 41, 3254–3261 CrossRef CAS PubMed.
- S. Droge, Environ. Sci. Technol., 2018, 53, 760–770 CrossRef PubMed.
- N. Timmer and S. Droge, Environ. Sci. Technol., 2017, 51, 2890–2898 CrossRef CAS PubMed.
- S. T. Droge, T. L. Sinnige and J. L. Hermens, Anal. Chem., 2007, 79, 2885–2891 CrossRef CAS PubMed.
- J. J. Haftka, P. Scherpenisse, G. Oetter, G. Hodges, C. V. Eadsforth, M. Kotthoff and J. L. Hermens, Environ. Toxicol. Chem., 2016, 35, 2173–2181 CrossRef CAS PubMed.
- W. J. Weber and W. Huang, Environ. Sci. Technol., 1996, 30, 881–888 CrossRef CAS.
- B. Xing and J. J. Pignatello, Environ. Toxicol. Chem., 1996, 15, 1282–1288 CrossRef CAS.
- S. Douven, C. A. Paez and C. J. Gommes, J. Colloid Interface Sci., 2015, 448, 437–450 CrossRef CAS PubMed.
- P. M. Gschwend, Environmental organic chemistry, John Wiley & Sons, 2016 Search PubMed.
- M. Ishiguro and L. K. Koopal, Adv. Colloid Interface Sci., 2016, 231, 59–102 CrossRef CAS PubMed.
- Z. Xu, J. Cai and B. Pan, J. Zhejiang Univ., Sci., A, 2013, 14, 155–176 CrossRef CAS.
- Y. Chen, J. L. Hermens and S. T. Droge, Environ. Pollut., 2013, 179, 153–159 CrossRef CAS PubMed.
- G. Limousin, J. Gaudet, L. Charlet, S. Szenknect, V. Barthes and M. Krimissa, Appl. Geochem., 2007, 22, 249–275 CrossRef CAS.
- E. M. Webster, Environ. Rev., 2014, 22, 430–444 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- J. Istok, J. Field, M. Schroth, T. Sawyer and M. Humphrey, Groundwater, 1999, 37, 589–598 CrossRef CAS.
- P. S. Bäuerlein, T. L. Ter Laak, R. C. Hofman-Caris, P. de Voogt and S. T. Droge, Water Res., 2012, 46, 5009–5018 CrossRef PubMed.
- N. Narkis and B. Ben-David, Water Res., 1985, 19, 815–824 CrossRef CAS.
- B. Xing and J. J. Pignatello, Environ. Sci. Technol., 1997, 31, 792–799 CrossRef CAS.
- R. T. Podoll, K. C. Irwin and S. Brendlinger, Environ. Sci. Technol., 1987, 21, 562–568 CrossRef CAS PubMed.
- M. L. Cano and P. B. Dorn, Environ. Toxicol. Chem., 1996, 15, 684–690 CrossRef CAS.
- S. J. Traina, D. C. McAvoy and D. J. Versteeg, Environ. Sci. Technol., 1996, 30, 1300–1309 CrossRef CAS.
- G. Pan, C. Jia, D. Zhao, C. You, H. Chen and G. Jiang, Environ. Pollut., 2009, 157, 325–330 CrossRef CAS PubMed.
- S. Droge and K. Goss, Environ. Sci. Technol., 2012, 46, 5894–5901 CrossRef CAS PubMed.
- D. M. Di Toro, L. J. Dodge and V. C. Hand, Environ. Sci. Technol., 1990, 24, 1013–1020 CrossRef CAS.
- R. Chen, Y. Zhang, F. Darabi Sahneh, C. M. Scoglio, W. Wohlleben, A. Haase, N. A. Monteiro-Riviere and J. E. Riviere, ACS Nano, 2014, 8, 9446–9456 CrossRef CAS PubMed.
- X. Zhou and X. Zhou, Chem. Eng. Commun., 2014, 201, 1459–1467 CrossRef CAS.
- P. S. Ghosal and A. K. Gupta, J. Mol. Liq., 2017, 225, 137–146 CrossRef CAS.
- S. Azizian, S. Eris and L. D. Wilson, Chem. Phys., 2018, 513, 99–104 CrossRef CAS.
- S. Azizian, J. Colloid Interface Sci., 2004, 276, 47–52 CrossRef CAS PubMed.
- E. Matthijs and H. De Henau, Tenside Deterg., 1985, 22, 299–304 CAS.
- J. Rubio, E. González-Mazo and A. Gómez-Parra, Mar. Chem., 1996, 54, 171–177 CrossRef CAS.
- M. Garcia, E. Campos, J. Sanchez-Leal and F. Comelles, Tenside, Surfactants, Deterg., 2004, 41, 235–239 CrossRef CAS.
- J. Marchesi, W. House, G. White, N. Russell and I. Farr, Colloids Surf., 1991, 53, 63–78 CrossRef CAS.
- C. P. Higgins and R. G. Luthy, Environ. Sci. Technol., 2006, 40, 7251–7256 CrossRef CAS PubMed.
- S. T. Droge and J. L. Hermens, Environ. Sci. Technol., 2007, 41, 3192–3198 CrossRef CAS PubMed.
- W. W. John, G. Bao, W. P. Johnson and T. B. Stauffer, Environ. Sci. Technol., 2000, 34, 672–679 CrossRef CAS.
- S. T. Droge, L. Yarza-Irusta and J. L. Hermens, Environ. Sci. Technol., 2009, 43, 5712–5718 CrossRef CAS PubMed.
- A. Rico-Rico, A. Temara, T. Behrends and J. L. Hermens, Environ. Pollut., 2009, 157, 377–383 CrossRef CAS PubMed.
- Y. Shen and M. Yen, Environ. Technol., 1999, 20, 425–430 CrossRef CAS.
- C. Eschauzier, Perfluoroalkyl acids in drinking water: Sources, fate and removal, Ph.D. thesis, Universiteit van Amsterdam, 2013 Search PubMed.
- P. de Voogt, L. Zurano, P. Serné and J. J. Haftka, Environ. Chem., 2012, 9, 564–570 CrossRef CAS.
- G. Cornelissen, P. C. van Noort and H. A. J. Govers, Environ. Toxicol. Chem., 1997, 16, 1351–1357 CrossRef CAS.
- M. D. Johnson, T. M. Keinath and W. J. Weber, Environ. Sci. Technol., 2001, 35, 1688–1695 CrossRef CAS PubMed.
- W. Huang, H. Yu and W. J. Weber Jr, J. Contam. Hydrol., 1998, 31, 129–148 CrossRef CAS.
- W. J. Weber Jr, W. Huang and H. Yu, J. Contam. Hydrol., 1998, 31, 149–165 CrossRef.
- E. J. LeBoeuf and W. J. Weber, Environ. Sci. Technol., 2000, 34, 3632–3640 CrossRef CAS.
- A. T. Kan, G. Fu and M. B. Tomson, Environ. Sci. Technol., 1994, 28, 859–867 CrossRef CAS PubMed.
- B. J. Brownawell, H. Chen, J. M. Collier and J. C. Westall, Environ. Sci. Technol., 1990, 24, 1234–1241 CrossRef CAS.
- G. Yang and X. Zheng, Environ. Toxicol. Chem., 2010, 29, 2169–2176 CrossRef CAS PubMed.
- P. C. Van Noort, M. T. Jonker and A. A. Koelmans, Environ. Sci. Technol., 2004, 38, 3305–3309 CrossRef CAS PubMed.
- J. Zhang, G. Yang, Q. Li, X. Cao and G. Liu, Mar. Pollut. Bull., 2013, 76, 220–226 CrossRef CAS PubMed.
- W. J. Weber Jr, P. M. McGinley and L. E. Katz, Environ. Sci. Technol., 1992, 26, 1955–1962 CrossRef.
- W. Huang, T. M. Young, M. A. Schlautman, H. Yu and W. J. Weber, Environ. Sci. Technol., 1997, 31, 1703–1710 CrossRef CAS.
- G. Xia and W. P. Ball, Environ. Sci. Technol., 1999, 33, 262–269 CrossRef CAS.
- R. H. Aranow and L. Witten, J. Chem. Phys., 1958, 28, 405–409 CrossRef CAS.
- T. P. Silverstein, J. Chem. Educ., 1998, 75, 116 CrossRef CAS.
- D. Chandler, Nature, 2005, 437, 640 CrossRef CAS PubMed.
- D. Mackay and R. Boethling, Handbook of property estimation methods for chemicals: environmental health sciences, CRC Press, 2000 Search PubMed.
- S. Xu and S. A. Boyd, Environ. Sci. Technol., 1995, 29, 312–320 CrossRef CAS PubMed.
- M. J. Brown and D. R. Burris, Groundwater, 1996, 34, 734–744 CrossRef CAS.
- B. Wang, W. Chen, H. Fu, X. Qu, S. Zheng, Z. Xu and D. Zhu, Carbon, 2014, 79, 203–212 CrossRef CAS.
- K. Inoue, K. Kaneko and M. Yoshida, Soil Sci. Plant Nutr., 1978, 24, 91–102 CrossRef CAS.
- Z. Ou, A. Yediler, Y. He, L. Jia, A. Kettrup and T. Sun, Chemosphere, 1996, 32, 827–839 CrossRef CAS.
- Y. Shen, Chemosphere, 2000, 41, 711–716 CrossRef CAS PubMed.
- S. Kang and H. Y. Jeong, J. Hazard. Mater., 2015, 284, 143–150 CrossRef CAS PubMed.
- Z. Li, Q. Gong, L. Luo, L. Zhang, S. Zhao and J. Yu, J. Dispersion Sci. Technol., 2011, 32, 167–173 CrossRef CAS.
- J. F. Pankow and S. W. Mckenzie, Environ. Sci. Technol., 1991, 25, 2046–2053 CrossRef CAS.
- B. J. Brownawell, H. Chen, W. Zhang and J. C. Westall, Environ. Sci. Technol., 1997, 31, 1735–1741 CrossRef CAS.
- D. Zubarev, V. Morozov and G. Ropke, Statistical Mechanics of Nonequilibrium Processes, Volume 1 (See 3527400834): Basic Concepts, Kinetic Theory, Wiley-VCH, 1996 Search PubMed.
- C. K. Yeh and L. C. Lin, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2003, 38, 1145–1157 CrossRef PubMed.
- Z. Du, S. Deng, Y. Bei, Q. Huang, B. Wang, J. Huang and G. Yu, J. Hazard. Mater., 2014, 274, 443–454 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9em00580c |
| This journal is © The Royal Society of Chemistry 2020 |