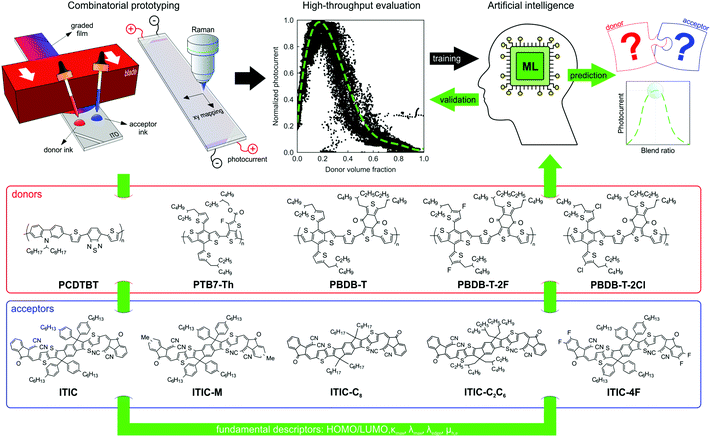
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting the photocurrent–composition dependence in organic solar cells†
Xabier
Rodríguez-Martínez
 a,
Enrique
Pascual-San-José
a,
Zhuping
Fei
a,
Enrique
Pascual-San-José
a,
Zhuping
Fei
 b,
Martin
Heeney
b,
Martin
Heeney
 b,
Roger
Guimerà
b,
Roger
Guimerà
 cd and
Mariano
Campoy-Quiles
cd and
Mariano
Campoy-Quiles
 *a
*a
aInstitut de Ciència de Materials de Barcelona, ICMAB-CSIC, Campus UAB, 08193, Bellaterra, Spain. E-mail: m.campoy@csic.es
bDepartment of Chemistry and Centre for Plastic Electronics, White City Campus, Imperial College London, London W12 0BZ, UK
cInstitució Catalana de Recerca i Estudis Avançats, ICREA, Passeig de Lluís Companys 23, 08010, Barcelona, Spain
dDepartment of Chemical Engineering, Universitat Rovira i Virgili, 43007, Tarragona, Spain
First published on 7th January 2021
Abstract
The continuous development of improved non-fullerene acceptors and deeper knowledge of the fundamental mechanisms governing performance underpin the vertiginous increase in efficiency witnessed by organic photovoltaics. While the influence of parameters like film thickness and morphology are generally understood, what determines the strong dependence of the photocurrent on the donor and acceptor fractions remains elusive. Here we approach this problem by training artificial intelligence algorithms with self-consistent datasets consisting of thousands of data points obtained by high-throughput evaluation methods. Two ensemble learning methods are implemented, namely a Bayesian machine scientist and a random decision forest. While the former demonstrates large descriptive power to complement the experimental high-throughput screening, the latter is found to predict with excellent accuracy the photocurrent–composition phase space for material systems outside the training set. Interestingly, we identify highly predictive models that only employ the materials band gaps, thus largely simplifying the rationale of the photocurrent–composition space.
Broader contextMulticomponent systems underline the significant performance improvements recently witnessed in many energy fields, from electrodes in batteries, to multication perovskites for photovoltaics and to high-ZT thermoelectric composites. Predicting the specific composition that would result in optimum performance is, however, one of the greatest unresolved problems in materials science. This is, in part, due to the fact that performance maximization is a complex multiparametric problem. Here we show that combining high-throughput experimental data with artificial intelligence (AI) algorithms enables unprecedented predicting capability. Specifically, we applied our methodology to the case of organic photovoltaics (OPV), since active layer composition is the parameter that affects more strongly OPV efficiency (e.g. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 or 0 0 or 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compositions result in zero efficiency for a blend whose optimum gives 18%). We generate thousands of data points in the performance–composition phase space for 15 different donor:acceptor blends and use the generated datasets to feed AI algorithms. Our work results in the identification of highly accurate and predictive models for the photocurrent–composition dependence unravelling the key material descriptors governing such behaviour (i.e. band gaps and charge mobility imbalance). This study paves the way for the use of AI and high-throughput experimentation to predict optimum composition in energy materials. 1 compositions result in zero efficiency for a blend whose optimum gives 18%). We generate thousands of data points in the performance–composition phase space for 15 different donor:acceptor blends and use the generated datasets to feed AI algorithms. Our work results in the identification of highly accurate and predictive models for the photocurrent–composition dependence unravelling the key material descriptors governing such behaviour (i.e. band gaps and charge mobility imbalance). This study paves the way for the use of AI and high-throughput experimentation to predict optimum composition in energy materials.
|
Introduction
The synthesis of novel conjugated semiconductors underpins the striking performance upswing that the field of organic photovoltaics (OPV) is currently experiencing.1 Photoactive blends of non-fullerene acceptors2–4 (NFAs) and low band gap donor co-polymers5,6 have demonstrated power conversion efficiencies (PCEs) over 18% in single-junction binary devices.7 Such figures result from an improved understanding of the donor:acceptor (D:A) material requirements in terms of extended light absorption, frontier energy level alignment and film morphology,8,9 as well as from enhanced charge transport properties.10 Indeed, the advanced understanding of many of the fundamental working principles in OPV combined with the inherent synthetic flexibility of conjugated materials is prompting the large-scale screening of potentially high-performing OPV material candidates. Yet, for a given material system, what could we say a priori about its OPV potential?At the molecular level, computational algorithms such as those developed in the on-going Harvard Clean Energy Project (CEP)11 serve to rapidly pre-screen millions of molecular motifs and classify them according to their theoretical OPV outcome, thus motivating their ulterior synthesis. Beyond purely in silico screening, the development of data-driven models in the OPV field has so far been mostly restricted to data mining and training of artificial intelligence (AI) algorithms using intrinsic material descriptors.12 This approach has been applied to make predictions in terms of novel materials13,14 and their corresponding expected PCE,15 as well as to guide researchers in the design of potentially top-performing materials.16 While promising, these calculations have had modest success thus far. This is due, in part, to the lack of sufficiently reproducible data in the literature; also to the difficulty to predict solid-state properties of the blend such as microstructure or gas-to-solid shifts in the optical properties and molecular energy levels; and finally, due to the fact that relevant device information is not considered in the calculations.17
At the device level, one aspect that has been modelled very successfully is the dependence of the performance on the active layer thickness. Device modelling based on transfer matrices has been demonstrated to reproduce accurately the mild oscillations of the photocurrent found experimentally.18,19 Further refinements based on advanced charge transport descriptions and unintentional doping effects have precisely described the thickness-dependent photocurrent.20
Despite acutely affecting the OPV performance,21–25 predicting the optimum D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio has been much more challenging due to the complexity of charge photogeneration and transport through the blend towards the electrodes. For semicrystalline polymers blended with fullerenes, optimum D
A ratio has been much more challenging due to the complexity of charge photogeneration and transport through the blend towards the electrodes. For semicrystalline polymers blended with fullerenes, optimum D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratios have been rationalized by the binary phase diagram.21 In particular, slightly hypoeutectic concentrations with respect to the polymer loading were found to lead to a good compromise between charge generation and appropriate percolating pathways for charges to reach the electrodes. Also the balance of charge carrier mobilities between electrons and holes has often been considered a key feature determining the shape of the photocurrent–composition curve26 (hereafter referred to as Jsc–vol%). The current OPV paradigm led by NFAs as excellent light harvesters adds another ingredient to the Jsc–vol% dependence compared to fullerene-based devices since photocurrent generation is now fully distributed between both materials. Given the intricate optoelectronic trade-off that sets the location of the optimum D
A ratios have been rationalized by the binary phase diagram.21 In particular, slightly hypoeutectic concentrations with respect to the polymer loading were found to lead to a good compromise between charge generation and appropriate percolating pathways for charges to reach the electrodes. Also the balance of charge carrier mobilities between electrons and holes has often been considered a key feature determining the shape of the photocurrent–composition curve26 (hereafter referred to as Jsc–vol%). The current OPV paradigm led by NFAs as excellent light harvesters adds another ingredient to the Jsc–vol% dependence compared to fullerene-based devices since photocurrent generation is now fully distributed between both materials. Given the intricate optoelectronic trade-off that sets the location of the optimum D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio, novel experimental approaches and data-driven predictive models are required to enhance the current understanding of the Jsc–vol% dependence in binary OPV blends.
A ratio, novel experimental approaches and data-driven predictive models are required to enhance the current understanding of the Jsc–vol% dependence in binary OPV blends.
In this work, we adopt a synergic combination of experimental high-throughput screening and AI to study the relationship between the photocurrent generation and the active layer parameters (i.e. thickness and D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio) in binary OPV devices. The experimental exploration is performed by processing orthogonal parametric gradients or libraries, which in combination with local probing techniques (namely Raman spectroscopy and photocurrent imaging) serve to assess the corresponding photocurrent phase space diagrams with minimal effort.27–32 The exploration results in a plethora of possible Jsc–vol% dependences: from strongly skewed bell shapes to bimodal distributions. Then, in an attempt to rationalize these complex relationships, we implement two different AI algorithms that take as input a series of intrinsic optoelectronic material descriptors. The first algorithm is a Bayesian machine scientist,33 which is found to complement the high-throughput experimental screening due to its large descriptive power while providing an analytical equation to describe the intricate Jsc–vol% phase spaces. Second, we use a random forest (RF) algorithm as a predictive model for the normalized Jsc–vol% dependences retrieving a mean absolute error (MAE) below 0.20 in untrained OPV binaries. In the RF models, we find that descriptors related with the alignment of the frontier energy levels and the mobility difference are statistically relevant in shaping the Jsc–vol% space. Finally, feature selection procedures reveal highly predictive models when only the donor and acceptor electronic (or optical) band gaps are employed in the training step. The RF models found herein define the Jsc–vol% curves in both NFA and fullerene-based binary blends with excellent accuracy.
A ratio) in binary OPV devices. The experimental exploration is performed by processing orthogonal parametric gradients or libraries, which in combination with local probing techniques (namely Raman spectroscopy and photocurrent imaging) serve to assess the corresponding photocurrent phase space diagrams with minimal effort.27–32 The exploration results in a plethora of possible Jsc–vol% dependences: from strongly skewed bell shapes to bimodal distributions. Then, in an attempt to rationalize these complex relationships, we implement two different AI algorithms that take as input a series of intrinsic optoelectronic material descriptors. The first algorithm is a Bayesian machine scientist,33 which is found to complement the high-throughput experimental screening due to its large descriptive power while providing an analytical equation to describe the intricate Jsc–vol% phase spaces. Second, we use a random forest (RF) algorithm as a predictive model for the normalized Jsc–vol% dependences retrieving a mean absolute error (MAE) below 0.20 in untrained OPV binaries. In the RF models, we find that descriptors related with the alignment of the frontier energy levels and the mobility difference are statistically relevant in shaping the Jsc–vol% space. Finally, feature selection procedures reveal highly predictive models when only the donor and acceptor electronic (or optical) band gaps are employed in the training step. The RF models found herein define the Jsc–vol% curves in both NFA and fullerene-based binary blends with excellent accuracy.
Results
General workflow
Fig. 1 illustrates the high-throughput evaluation, training, and prediction workflow used throughout the article. The processing of compositional libraries was accomplished by blade coating via the coalescence of pristine donor and acceptor ink drops at the blade reservoir. The blade movement induced their mixing during the coating to generate a compositional gradient perpendicularly to the displacement direction.29 In parallel, ink depletion at the front reservoir generates a thickness gradient along the blade movement direction. The dissimilar ink rheology also created film thickness fluctuations in conjunction with the D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio library (see Section I in the ESI†). Following electrode deposition, a simultaneous characterization based on Raman spectroscopy and light-beam induced-current (LBIC) mapping was used to image the heterogeneous film features including thickness and composition,34 and to correlate them to the corresponding photocurrent images. This approach allowed the efficient exploration of the photocurrent phase diagram of binary OPV blends in a combinatorial manner: the time and semiconductor material cost requirements can be as low as 90 seconds and 50 ng per data point, respectively (see Section II in the ESI†).
A ratio library (see Section I in the ESI†). Following electrode deposition, a simultaneous characterization based on Raman spectroscopy and light-beam induced-current (LBIC) mapping was used to image the heterogeneous film features including thickness and composition,34 and to correlate them to the corresponding photocurrent images. This approach allowed the efficient exploration of the photocurrent phase diagram of binary OPV blends in a combinatorial manner: the time and semiconductor material cost requirements can be as low as 90 seconds and 50 ng per data point, respectively (see Section II in the ESI†).
The highly efficient screening process generated large amounts of thickness–composition parametric combinations per D:A pair in the corresponding Jsc space (ca. 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points). This was then employed in the training and validation of AI algorithms together with fundamental optoelectronic material descriptors such as highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels, absorption coefficients (see Section III in the ESI†) and charge carrier mobilities. As detailed in Section IV in the ESI,† the descriptors extracted from literature can be selected following distinct criteria. With these data, we first validated the ability of the AI models to reconstruct the complete Jsc–vol% diagram and then predict the corresponding dependence for material combinations out of the original training set. This approach is exploited to determine the optimum active layer thickness and composition in terms of photocurrent for any D:A pair (with known input descriptors).
000 data points). This was then employed in the training and validation of AI algorithms together with fundamental optoelectronic material descriptors such as highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels, absorption coefficients (see Section III in the ESI†) and charge carrier mobilities. As detailed in Section IV in the ESI,† the descriptors extracted from literature can be selected following distinct criteria. With these data, we first validated the ability of the AI models to reconstruct the complete Jsc–vol% diagram and then predict the corresponding dependence for material combinations out of the original training set. This approach is exploited to determine the optimum active layer thickness and composition in terms of photocurrent for any D:A pair (with known input descriptors).
High-throughput experimental screening
Herein, the high-throughput experimentation strategy based on lateral parametric libraries substitutes the traditional sample-by-sample methodologies (aka Edisonian experimentation) in the screening of the Jsc–vol% space. Hence, we first verify that both approaches converge to the same figures in the normalized Jsc–vol% diagram. Fig. 2 compares the Jsc dispersion obtained following the traditional fabrication-intensive protocol (Fig. 2a and b) and the measuring-intensive strategy proposed here (Fig. 2c and d). We study two high-performing OPV binary systems, namely the workhorse PTB7-Th:ITIC blend35 as well as a novel, unreported binary formed by PBDB-T:ITIC-C2C6. The preparation of premixed inks from pristine D and A aliquots (as required in traditional experimentation procedures) enables us to estimate the corresponding D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A density ratios, ξ (see Section VII in the ESI†). In Fig. 2 we accordingly transform vol% to the more familiar D
A density ratios, ξ (see Section VII in the ESI†). In Fig. 2 we accordingly transform vol% to the more familiar D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A weight ratio typically followed in OPV sample preparation. However, the transformation from vol% to wt% does not generally lead to an acute displacement of the scattered data distributions since ξ is found to be close to unity in the here explored cases. This indicates that Jsc–vol% phase diagrams (as raw-extracted from optical probes such as Raman or ellipsometry) will generally resemble quite closely Jsc–wt% distributions. On the other hand, the observed photocurrent dispersion along the y-axis in Fig. 2a and b is mainly related to the screening of the active layer thickness as we varied the thickness at each composition in the pursuit of the optimum thickness at each blending ratio (see Section I in the ESI†). Importantly, the two systems exhibit very different Jsc–wt% curves, one being a single peak centered at ca. 40 wt% of donor, while the other appears bimodal (vide infra).
A weight ratio typically followed in OPV sample preparation. However, the transformation from vol% to wt% does not generally lead to an acute displacement of the scattered data distributions since ξ is found to be close to unity in the here explored cases. This indicates that Jsc–vol% phase diagrams (as raw-extracted from optical probes such as Raman or ellipsometry) will generally resemble quite closely Jsc–wt% distributions. On the other hand, the observed photocurrent dispersion along the y-axis in Fig. 2a and b is mainly related to the screening of the active layer thickness as we varied the thickness at each composition in the pursuit of the optimum thickness at each blending ratio (see Section I in the ESI†). Importantly, the two systems exhibit very different Jsc–wt% curves, one being a single peak centered at ca. 40 wt% of donor, while the other appears bimodal (vide infra).
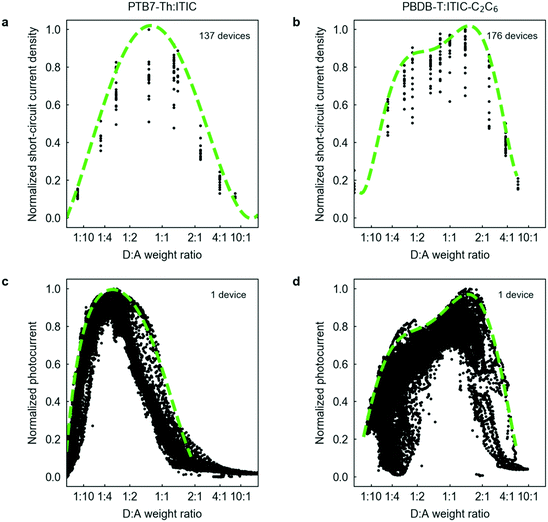 | ||
Fig. 2 (a and b) Normalized distribution of the short-circuit current density obtained in discrete devices as a function of the D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A weight ratio in PTB7-Th:ITIC and PBDB-T:ITIC-C2C6 blends. (c and d) Normalized photocurrent dispersion obtained following the high-throughput optimization approach for the same blends. Green dashed lines are polynomial fits of the high-performing envelope of photocurrent values. In each case we indicate the number of devices needed to generate these plots. The reader is referred to Section I in the ESI† for further details on device manufacture. A weight ratio in PTB7-Th:ITIC and PBDB-T:ITIC-C2C6 blends. (c and d) Normalized photocurrent dispersion obtained following the high-throughput optimization approach for the same blends. Green dashed lines are polynomial fits of the high-performing envelope of photocurrent values. In each case we indicate the number of devices needed to generate these plots. The reader is referred to Section I in the ESI† for further details on device manufacture. | ||
Notably, the high-throughput methodology reproduces the unimodal and bimodal photocurrent dispersions observed as a function of the donor loading in both binaries (Fig. 2c and d). Importantly, it does so with very large statistics, strongly reducing the uncertainty with respect to the actual shape of the curve. In this approach, the vertical Jsc dispersion originates from both active layer thickness and morphology variations, the latter being a consequence of the in situ mixing of the pristine inks in the blade reservoir. By quantifying the Raman blue-shifting of the corresponding D and A vibrational fingerprints, we have verified that devices containing compositional gradients can reproduce the degree of mixing attained when casting fully premixed solutions. Moreover, they embrace a richer catalogue of film morphologies than conventional methodologies expanding the available data to correlate microstructure and device performance (see Section II in the ESI†). Note that the high-throughput screening requires a significantly reduced amount of experimental time and resources: hundreds of discrete devices (here 137 and 176 devices in PTB7-Th:ITIC and PBDB-T:ITIC-C2C6, respectively) versus a single combinatorial device per binary.
The high-throughput methodology has, however, the caveat of measuring Jsc only rather than the full set of solar cell parameters (open-circuit voltage (Voc), fill factor (FF) and PCE). Nevertheless, since Voc remains fairly constant, the PCE correlates well with Jsc for the range of compositions of interest despite the variations observed in FF (see Section II in the ESI†), which is in excellent agreement with the overall trends depicted from data-mining studies (i.e. Jsc is the best proxy for PCE).17 Interestingly, we have determined that parameters related with morphology such as Raman (blue-)shifting and photoluminescence (PL) quenching and shifting are closely related with microstructure and FF, thus opening up the possibility to take into account their effect in the high-throughput determination of the D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio that maximizes the overall PCE (see Section II in the ESI†). On the other hand, the use of non-standardized white light for the acquisition of the Jsc data (see Section I in the ESI†) and the intrinsic uncertainty of the Raman-based determination of composition34 can explain the small differences observed in the photocurrent distributions when comparing both optimization protocols; more specifically, the ca. 15 wt% offset in the donor content that maximizes the photocurrent in PTB7-Th:ITIC devices. Nonetheless, these drawbacks are significantly outweighed by the rapid attainment of large experimental datasets, which serve as ideal seeds for training AI algorithms. Furthermore, the experimental approach demonstrates high reproducibility from batch-to-batch (see Section II in the ESI†).
A ratio that maximizes the overall PCE (see Section II in the ESI†). On the other hand, the use of non-standardized white light for the acquisition of the Jsc data (see Section I in the ESI†) and the intrinsic uncertainty of the Raman-based determination of composition34 can explain the small differences observed in the photocurrent distributions when comparing both optimization protocols; more specifically, the ca. 15 wt% offset in the donor content that maximizes the photocurrent in PTB7-Th:ITIC devices. Nonetheless, these drawbacks are significantly outweighed by the rapid attainment of large experimental datasets, which serve as ideal seeds for training AI algorithms. Furthermore, the experimental approach demonstrates high reproducibility from batch-to-batch (see Section II in the ESI†).
Implementation of artificial intelligence algorithms
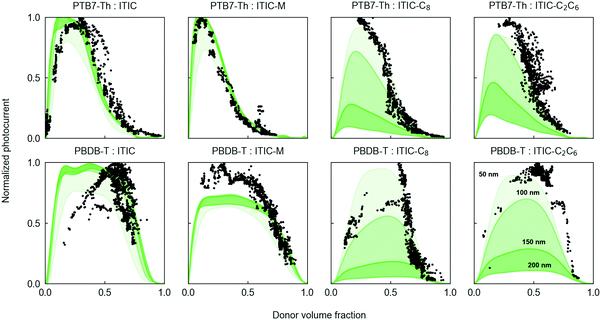
We next examine the upper crust of the scattered photocurrent distribution observed in the combinatorial samples (dashed green lines in Fig. 2c and d). These provide a large overview of the photocurrent phase space in a very efficient manner. After determining the optical properties of the D:A blends (see Section III in the ESI†) and indexing their electronic properties from the literature (see attached spreadsheet in the ESI†), we start feeding AI algorithms to elucidate the origin of the observed trends. Our tentative list of relevant descriptors contains 23 elements per D:A pair, including eight dimensionless parameters (see Section IV in the ESI†). At this stage, we did not include descriptors based on properties of the blends, such as their phase diagrams.Our first implementation of AI is a Bayesian machine scientist,33 which includes the dimensionless descriptors as inputs to develop analytical models that explore the Jsc–vol% dependence (see Section V in the ESI†). For any given set of scattered data, the Bayesian machine scientist identifies the plausible and simplest mathematical models that describe the observed trends. We applied this methodology to two families of OPV binaries (Fig. 3) with PTB7-Th and PBDB-T as donors, individually blended with four ITIC-based acceptors showing either distinct end groups (ITIC-M) or side-chains (ITIC-C8 and ITIC-C2C6). We note that, experimentally, small but non-zero photocurrent has been measured for some pristine NFAs. A full study of this goes beyond the scope of this manuscript, but it is worth noting it, even when the corresponding solar cells have comparatively low overall efficiencies.
According to the solid curves in Fig. 3, which delimit the Jsc–vol% space encountered at different active layer thickness values, the Bayesian machine scientist reproduces well the highest-performing experimental trends. The actual model equation is provided in Section V in the ESI.† While we would not rationalize any physical meaning, we use it to evaluate the parameter space. Importantly, regarding the photocurrent phase space, the modeling indicates that (i) PTB7-Th binaries are characterized by sharp and unbalanced compositional optimum peaks; (ii) PBDB-T blends are more tolerant to compositional fluctuations and their maxima are more balanced in D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A ratio; (iii) binaries containing ITIC and ITIC-M show limited thickness dependence; (iv) ITIC-C8 and ITIC-C2C6 blends are very sensitive to active layer thickness variations; and (v) the bimodal distribution is more or less pronounced depending on the actual thickness range. Despite the great descriptive power of the machine scientist in completing the exploration of the complex photocurrent phase space, it has some limitations arising from its computational complexity and the size of the training dataset, including: (i) month-scale times needed for training; (ii) poor predictive capability out of the training materials dataset due to the unfeasibility of sampling models for long enough time; and (iii) an uninformative utilization of the features, which makes it impossible to determine which of them are really important.
A ratio; (iii) binaries containing ITIC and ITIC-M show limited thickness dependence; (iv) ITIC-C8 and ITIC-C2C6 blends are very sensitive to active layer thickness variations; and (v) the bimodal distribution is more or less pronounced depending on the actual thickness range. Despite the great descriptive power of the machine scientist in completing the exploration of the complex photocurrent phase space, it has some limitations arising from its computational complexity and the size of the training dataset, including: (i) month-scale times needed for training; (ii) poor predictive capability out of the training materials dataset due to the unfeasibility of sampling models for long enough time; and (iii) an uninformative utilization of the features, which makes it impossible to determine which of them are really important.
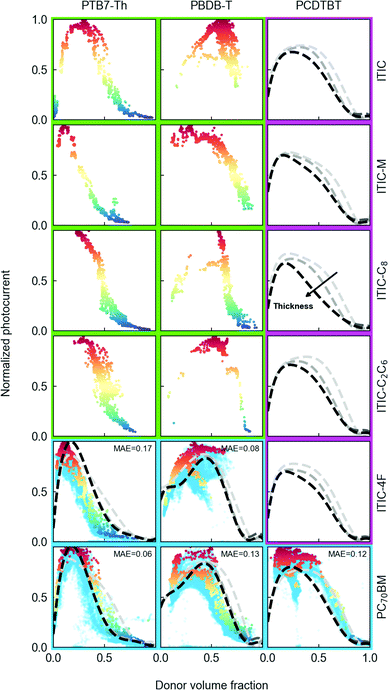
Therefore, we tested alternative ML approaches such as the random forest (RF) algorithm to improve the predictive capability of the AI models. The RF ensemble is initially trained using the same OPV binaries previously explored by the Bayesian machine scientist, which are highlighted with green frames in Fig. 4. The validation (testing) datasets are highlighted in blue while the purely predictive scenarios are framed in magenta color. Thus, Fig. 4 accordingly depicts a combinatorial matrix of the scattered Jsc–vol% dependences obtained in distinct D:A pairs following the high-throughput experimentation approach, as well as the RF model predictions (dashed lines) at different active layer thickness values (colored from grey to black). Therein, we include organic semiconductors out of the pristine training material set such as PCDTBT as donor polymer and two additional acceptors, namely a fluorinated ITIC derivative (ITIC-4F) and the workhorse fullerene, PC70BM.
As part of the RF model validation process, we first perform a leave-one-out cross-validation (LOO-cv) of the RF ensemble including the 8 training datasets (green frames in Fig. 4), as detailed in Section VI in the ESI.† Based on the extrapolation reliability found (ca. 65% of success rate), we further validated the RF model by comparing the predicted trends with the experimental results obtained in D:A pairs out of the training set selection, i.e. binaries for which either one or the two materials have not been used within the training step (blue frames in Fig. 4). This trait is precisely the main feature desired for highly predictive models.
Our results indicate that the RF model extrapolates very well (MAE < 0.20) in all validation binaries explored, both the position of the Jsc maximum and its modulation in the composition (and thickness) diagram. The results obtained are equally consistent when validating a larger combinatorial matrix including data for high performing donor polymers such as PBDB-T-2Cl (PM7) and PBDB-T-2F (PM6), see Fig. S23 in the ESI.† It is worth highlighting that regardless of the molecular nature of the materials blended, the only model inputs for the extrapolation are the corresponding optoelectronic descriptors used in the training of the RF algorithm. In this particular case, we hand-picked the HOMO/LUMO energy levels reported from cyclic voltammetry (CV) measurements only as well as the corresponding mobilities from the same references (whenever possible), as detailed in Section IV in the ESI.†
Discussion
Undoubtedly, the predictive power of the RF model is remarkable given its simplicity. From a chemical and fundamental point of view, the dissimilarities between the materials employed in the training and both PCDTBT and PC70BM (as the most distinct validation species in Fig. 4) are important. The type of moieties in the backbone and grafted side chains (for the donor polymers), as well as the chemical structure and topology (for the acceptors) are significantly different. Despite these acute differences, the RF model draws well the Jsc–vol% dependence experimentally found in the validation datasets. On the other hand, the predictive capability of the RF model (magenta panels in Fig. 4) is extremely powerful to evaluate a priori the Jsc–vol% diagram of any OPV binary, including their tolerance against blending ratio fluctuations. This latter fact has important consequences in the upscaling of any novel D:A pair and is largely acknowledged in the OPV industry. Indeed, our results are very promising considering the limited number (8) of D:A material combinations employed in our first tentative model training. Further enhancements in the predictive power can be expected when the training set is extended or additional material-specific descriptors are included, such as the molecular structures.AI models, such as the RF ensemble, also provide the so-called feature importance (FI), a magnitude that serves to identify and rank quantitatively those characteristics that mostly govern the experimental observables, i.e. the Jsc–vol% dependence. Accordingly, we first perform subsequent FI analysis using three distinct selections of optoelectronic descriptors. These differ on how the actual values are picked from the literature database (>80 references accessed): either randomly, by a consistent manual selection or calculated from the statistical medians of the scattered data. This analysis is performed to evaluate the sensitivity of the model against the consistency of the input descriptors. The accumulated analysis of the FI in each model (Fig. 5) indicates that parameters related to the HOMO/LUMO energy level alignment, such as CTe, CTh or Egap,d–a, as well as those related to the mobility of the blended species (Δμ and μimb) are, statistically, the most important descriptors in defining the Jsc–vol% dependence. These findings are in good agreement with the current understanding of the performance–composition space in OPV, as the existence of unbalanced charge carrier mobility has been considered one of the key features that influences the Jsc–vol% diagram in binary blends.26 Nevertheless, we observe that the actual selection of values for the descriptors has a large effect on the FI distribution, thus highlighting the requirement for great consistency among the experimental data selected or measured. In this regard, feature selection approaches might help in identifying those combinations of descriptors that return more robust models against experimental noise.
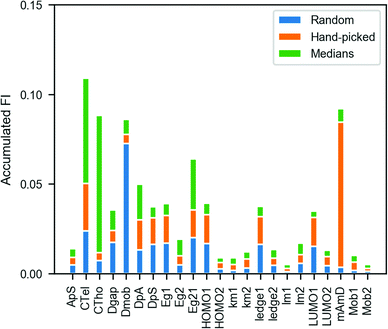 | ||
| Fig. 5 Accumulated feature importance (FI) depending on the choice of descriptor values. Since the HOMO and LUMO energy levels as well as the charge carrier mobilities are taken from the literature, we explore the effect that the actual value of the descriptors has on the FI drawn by the RF ensemble. We generally observe that descriptors related with energy level alignment (CTe, CTh, Egap,d–a) as well as those related with the mobility imbalance (Δμ = |μd − μa|, μimb = μa/μd) show the highest accumulated FI. The reader is referred to Section IV in the ESI,† for a detailed mathematical definition of the descriptors employed. | ||
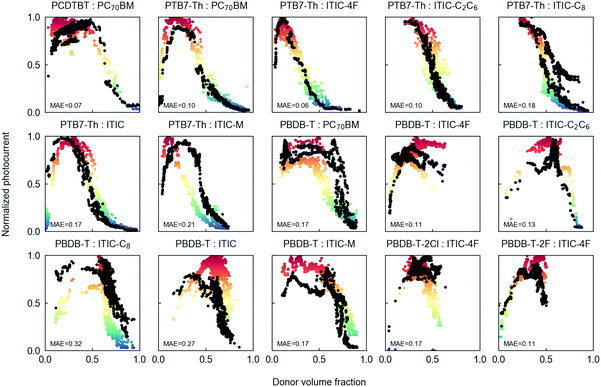
In particular, by performing a greedy MAE feature selection procedure we identify several two-parameter combinations that yield highly accurate RF models, even showing in some cases lower MAE than those models trained with a larger list of descriptors (see Section VI in the ESI†). Among them, we would like to highlight the pair formed by Egap,d and Egap,a, whose LOO-cv in 15 distinct D:A binaries is depicted in Fig. 6. This model, based on Egaps, is remarkably robust against experimental fluctuations and it extrapolates moderately well in some unseen blends, including all-polymer binaries (see Section VI in the ESI†). Moreover, successful model equations are drawn by the Bayesian machine scientist when employing these two descriptors only (see Section V in the ESI†). Finally, we observe that model training using the consistently extracted solid-state optical band gaps from Tauc plots results as well in successfully validated RF models (see Section VI in the ESI†). Hence, Egap,d and Egap,a (either electronic or optical) unify the main learning characteristics previously found by the 23-parameter model yet in a more physically intuitive approach and providing comparable predictive accuracy. Nevertheless, model predictions in workhorse D:A pairs such as P3HT:PC60BM are not successful, which we believe is a consequence of the limited extension of the training datasets employed and the absence of highly semi-crystalline donor polymers in our training dataset.
In spite of such limitations, we believe that the simplicity and accuracy of this two-parameter model are powerful for several reasons: (i) for theoretical material screening, as Egap is a byproduct of density functional theory (DFT) calculations; (ii) for combinatorial material synthesis, as organic semiconductors are usually subjected to CV to quantify the HOMO–LUMO energy levels as part of a routine set of electrochemical characterizations; and (iii) because Egap is a magnitude sufficiently unrelated to processing. We further note that similar predictive accuracy can be obtained by using easily measured solid-state optical band gaps in the model training.
These features are especially advantageous when dealing with small batches of novel materials. In this case, RF models may help researchers to tailor more effectively the optimal device features (i.e. active layer thickness and composition) and explore de facto the full photovoltaic potential of the new molecular species. The here employed training dataset initially formed by 15 D:A binaries is in constant growth; therefore, the conclusions extracted by the RF model will be progressively refined blend after blend. For this reason, we make accessible our combinatorial screening database in a public CSIC repository (http://hdl.handle.net/10261/223231), which is open to contributions from any researchers as part of a joint OPV materials screening project.
Conclusions
In this work, we have shown the synergic use of high-throughput experimentation and AI algorithms for the prediction of the Jsc–vol% space in binary bulk heterojunction organic solar cells. The generation of combinatorial libraries via blade coating and their subsequent imaging by Raman spectroscopy and LBIC mapping enables the efficient exploration of the complex performance landscape in such devices. The subsequent training of a Bayesian machine scientist is demonstrated to be useful in filling the corresponding parameter space, which serves to evaluate the sensitivity of the selected binary upon variations of composition, active layer thickness and other intrinsic optoelectronic descriptors. We finally validate RF models that are able to predict the Jsc–vol% dependence with excellent accuracy in unseen binary blends (i.e. blends that are not in the training materials set). We identify descriptors related with the HOMO/LUMO energy level alignment of the donor and acceptor materials, as well as their mobility imbalance among the most important features in shaping the Jsc–vol% predictions. Interestingly, simple intuitive models of only two features, namely the electronic (or solid-state optical) band gaps of the blended species, reproduce with large accuracy the Jsc–vol% dependence.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the Spanish Ministerio de Ciencia e Innovación under Grants PGC2018-095411-B-I00, FIS2016-78904-C3-1-P, and SEV-2015-0496 in the framework of the Spanish Severo Ochoa Centre of Excellence. We acknowledge financial support from the European Research Council through project ERC CoG 648901 and the H2020 Marie Curie actions through the SEPOMO project (grant number 722651). X. R.-M., E. P.-S.-J. and M. C.-Q. thank Dr Bernhard Dörling for designing the doctor blade controller and Mr Martí Gibert-Roca for designing the multiplexer/switcher. X. R.-M. acknowledges the departments of Physics, Chemistry and Geology of the Autonomous University of Barcelona (UAB) as coordinators of the PhD program in Materials Science. M. H. acknowledges the Royal Society and the Wolfson Foundation. The authors thank Dr Mathieu Linares and Dr Jasper Michels for inspiring discussions at the early stages of this work. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).References
- O. Inganäs, Adv. Mater., 2018, 30, 1800388 CrossRef.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 18003 CrossRef CAS.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS.
- G. Li, W.-H. Chang and Y. Yang, Nat. Rev. Mater., 2017, 2, 17043 CrossRef CAS.
- C. Liu, K. Wang, X. Gong and A. J. Heeger, Chem. Soc. Rev., 2016, 45, 4825–4846 RSC.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Nat. Mater., 2009, 8, 904–909 CrossRef CAS.
- V. D. Mihailetchi, H. X. Xie, B. de Boer, L. J. A. Koster and P. W. M. Blom, Adv. Funct. Mater., 2006, 16, 699–708 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- H. Sahu, F. Yang, X. Ye, J. Ma, W. Fang and H. Ma, J. Mater. Chem. A, 2019, 7, 17480–17488 RSC.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- W. Sun, Y. Zheng, K. Yang, Q. Zhang, A. A. Shah, Z. Wu, Y. Sun, L. Feng, D. Chen, Z. Xiao, S. Lu, Y. Li and K. Sun, Sci. Adv., 2019, 5, eaay4275 CrossRef CAS.
- H. Sahu and H. Ma, J. Phys. Chem. Lett., 2019, 10, 7277–7284 CrossRef CAS.
- S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS.
- L. A. A. Pettersson, L. S. Roman and O. Inganäs, J. Appl. Phys., 1999, 86, 487 CrossRef CAS.
- D. W. Sievers, V. Shrotriya and Y. Yang, J. Appl. Phys., 2006, 100, 114509 CrossRef.
- F. Deledalle, T. Kirchartz, M. S. Vezie, M. Campoy-Quiles, P. Shakya Tuladhar, J. Nelson and J. R. Durrant, Phys. Rev. X, 2015, 5, 011032 Search PubMed.
- C. Müller, T. A. M. Ferenczi, M. Campoy-Quiles, J. M. Frost, D. D. C. Bradley, P. Smith, N. Stingelin-Stutzmann and J. Nelson, Adv. Mater., 2008, 20, 3510–3515 CrossRef.
- P. Wolfer, P. E. Schwenn, A. K. Pandey, Y. Fang, N. Stingelin, P. L. Burn and P. Meredith, J. Mater. Chem. A, 2013, 1, 5989 RSC.
- Y. Zhang, Y. Xu, M. J. Ford, F. Li, J. Sun, X. Ling, Y. Wang, J. Gu, J. Yuan and W. Ma, Adv. Energy Mater., 2018, 8, 1800029 CrossRef.
- Z. Wen, X. Ma, X. Yang, P. Bi, M. Niu, K. Zhang, L. Feng and X. Hao, Chin. Chem. Lett., 2019, 30, 995–999 CrossRef CAS.
- S. S. van Bavel, M. Bärenklau, G. de With, H. Hoppe and J. Loos, Adv. Funct. Mater., 2010, 20, 1458–1463 CrossRef CAS.
- Y. Firdaus, V. M. Le Corre, J. I. Khan, Z. Kan, F. Laquai, P. M. Beaujuge and T. D. Anthopoulos, Adv. Sci., 2019, 6, 1802028 CrossRef.
- M. Kiy, R. Kern, T. A. Beierlein and C. J. Winnewisser, Organic Light Emitting Materials and Devices X, 2006, vol. 6333, p. 633307 Search PubMed.
- S. Langner, F. Häse, J. D. Perea, T. Stubhan, J. Hauch, L. M. Roch, T. Heumueller, A. Aspuru-Guzik and C. J. Brabec, Adv. Mater., 2020, 32, 1907801 CrossRef CAS.
- A. Sánchez-Díaz, X. Rodríguez-Martínez, L. Córcoles-Guija, G. Mora-Martín and M. Campoy-Quiles, Adv. Electron. Mater., 2018, 4, 1700477 CrossRef.
- A. Harillo-Baños, X. Rodríguez-Martínez and M. Campoy-Quiles, Adv. Energy Mater., 2020, 10, 1902417 CrossRef.
- K. Glaser, P. Beu, D. Bahro, C. Sprau, A. Pütz and A. Colsmann, J. Mater. Chem. A, 2018, 6, 9257–9263 RSC.
- E. Pascual-San-José, X. Rodríguez-Martínez, R. Adel-Abdelaleim, M. Stella, E. Martínez-Ferrero and M. Campoy-Quiles, J. Mater. Chem. A, 2019, 7, 20369–20382 RSC.
- R. Guimerà, I. Reichardt, A. Aguilar-Mogas, F. A. Massucci, M. Miranda, J. Pallarès and M. Sales-Pardo, Sci. Adv., 2020, 6, eaav6971 CrossRef.
- X. Rodríguez-Martínez, M. S. Vezie, X. Shi, I. McCulloch, J. Nelson, A. R. Goñi and M. Campoy-Quiles, J. Mater. Chem. C, 2017, 5, 7270–7282 RSC.
- Y. Lin, J. Wang, Z.-G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee02958k |
| This journal is © The Royal Society of Chemistry 2021 |