The role of bulk and interfacial morphology in charge generation, recombination, and extraction in non-fullerene acceptor organic solar cells†
Akchheta
Karki
 a,
Joachim
Vollbrecht
a,
Joachim
Vollbrecht
 a,
Alexander J.
Gillett
a,
Alexander J.
Gillett
 b,
Steven Shuyong
Xiao
c,
Yali
Yang
c,
Zhengxing
Peng
d,
Nora
Schopp
a,
Alana L.
Dixon
a,
Sangcheol
Yoon
a,
Max
Schrock
a,
Harald
Ade
d,
G. N. Manjunatha
Reddy
b,
Steven Shuyong
Xiao
c,
Yali
Yang
c,
Zhengxing
Peng
d,
Nora
Schopp
a,
Alana L.
Dixon
a,
Sangcheol
Yoon
a,
Max
Schrock
a,
Harald
Ade
d,
G. N. Manjunatha
Reddy
 *e,
Richard H.
Friend
*b and
Thuc-Quyen
Nguyen
*e,
Richard H.
Friend
*b and
Thuc-Quyen
Nguyen
 *a
*a
aCenter for Polymers and Organic Solids, University of California Santa Barbara (UCSB), Santa Barbara, California 93106, USA. E-mail: quyen@chem.ucsb.edu
bOptoelectronics Group Cavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK. E-mail: rhf10@cam.ac.uk
c1-Material Inc., 2290 Chemin St-François, Dorval, Quebec H9P 1K2, Canada
dDepartment of Physics and Organic and Carbon Electronics Laboratories (ORaCEL), North Carolina State University, Raleigh, North Carolina 27695, USA
eDepartment of Chemistry, University of Lille, CNRS, Centrale Lille Institut, Univ. Artois, UMR 8181-UCCS-Unité de Catalyse et Chimie du Solide, F-59000, Lille, France. E-mail: gnm.reddy@univ-lille.fr
First published on 4th September 2020
Abstract
Some fundamental questions in the organic solar cell (OSC) community are related to the role of bulk and interfacial morphology on key processes such as charge generation, recombination, and extraction that dictate power conversion efficiencies (PCEs). The challenges with answering these questions arise due to the difficulty in accurately controlling, as well as comprehensively characterizing the morphology in bulk-heterojunction (BHJ) OSC blends. In this work, large variations in the interfacial and bulk morphologies of different low molecular weight fraction (LMWF) PM6:Y6 blends were detected despite the blends being fabricated from ostensibly the same building blocks. A drop in PCE from ∼15% to ∼5% was observed when the concentration of LMWFs of the PM6 polymer was increased from 1% to 52%. The drop in PCEs is found to be due to the lowering of the short-circuit current density (JSC) and fill-factor (FF) values as a result of compromised charge generation efficiencies, increased bulk trap densities, reduced charge transport, and inefficient charge extraction. The origin of the high device performance in the 1% LMWF blend is rationalized by the favorable bulk and interfacial morphological features, resolved from four techniques at sub-nanometer to sub-micrometer length scales. First, the closer donor:acceptor (D:A) interactions, smaller D and A domains, and increased D:A interfacial area facilitate ultrafast electron and hole transfer at the D:A interface. Second, the better long-range ordering and optimal phase separation of the D:A regions lead to superior charge transport and extraction.
Broader contextPolymer:non-fullerene acceptor (NFA) bulk-heterojunction (BHJ) organic solar cells (OSCs) have reached unprecedented power conversion efficiencies (PCEs) of over 18%. However, there are some important fundamental questions regarding the role of morphology in the major processes dictating device performance that remain unanswered. One of the key challenges in addressing these questions is accurately characterizing the bulk and interfacial morphology in these blends. Moreover, precisely distinguishing the donor:acceptor (D:A) interactions at the BHJ interface in high performing polymer:NFA blends is challenging due to the structural similarities between the donor and acceptor molecules that lead to complex compositions, which are difficult to deconvolute. Here, we use the molecular weight fractions of the donor polymer as a tool to exert fine control over the interfacial and bulk morphology. Subsequently, from powerful 1D and 2D solid state NMR (ssNMR) spectroscopy techniques, valuable information on the nature of the D:A inter- and intra-molecular interactions could be obtained. The results from ssNMR spectroscopy are corroborated by three additional techniques at different length scales (sub-nanometer to sub-micrometer) used to attain a comprehensive understanding of the bulk and interfacial morphology in these blend systems. Ultimately, the results from this work provide recommendations on the significant bulk and interfacial morphological features that are critical for optimizing charge generation, recombination, and extraction processes to give high performing OSCs, expediting the pathway to its commercialization in the near future. |
1. Introduction
With polymer:non-fullerene acceptor (NFA) bulk-heterojunction (BHJ) organic solar cells (OSCs) reaching unprecedented power conversion efficiencies (PCEs) of over 18%,1 it has become essential to obtain an in-depth understanding of the role of bulk and interfacial morphology in the key processes determining their PCEs. However, precisely controlling and characterizing the bulk and interfacial morphology remains challenging. In this work, we investigate PM6:Y6 systems with different percentages of a low molecular weight (Mw) fraction (LMWF) in the batch of the PM6 polymer. When varying the LMWF of PM6 from 1% to 52%, large variations in the interfacial and bulk morphologies of the different LMWF blends were detected, despite being fabricated from ostensibly the same basic building-blocks. Consequently, divergent OSC performance between the different LMWF PM6:Y6 blends was obtained, highlighting the importance of carefully controlling the polymer Mw to ensure optimal device performance. Furthermore, although a few studies have previously shown that the Mw of polymers can significantly impact device performance in NFA-based OSCs,2–4 its effect on interfacial and bulk morphologies, and subsequently, the key photophysical processes from charge generation to extraction remain largely unexplored. Therefore, varying the LMWF in the PM6 polymer enables us to cleanly probe the impact of bulk and interfacial morphology on all processes of OSC operation, free of any differences in the innate chemical structures of the blend components.5In this work, we extensively characterize the 1% and 52% LMWF PM6:Y6 blends with one- (1D) and two-dimensional (2D) solid-state NMR (ssNMR) spectroscopy, allowing us to identify and accurately characterize donor:acceptor (D:A) inter- and intra-molecular interactions. Furthermore, ssNMR results are supplemented by morphological characterization using grazing incidence wide angle scattering (GIWAXS), photo-conductive AFM (pc-AFM), and resonant soft X-ray scattering (RSoXS) techniques. The use of multiple techniques to characterize the morphology at different length scales (from sub-nanometer to sub-micrometer) enables us to develop a comprehensive understanding of the bulk and interfacial morphology in the different LMWF PM6:Y6 blends. Subsequently, the role of such morphological differences on the processes dictating OSC device performance can be established; from this, we are able to provide important recommendations on the key interfacial and bulk morphological features that enable efficient NFA OSC device operation. Thus, this study provides an understanding of two fundamental and complex questions that are highly relevant to the OSC community: (i) the role of the nature of the D:A BHJ interface on charge generation and recombination processes, and (ii) the morphological factors affecting charge extraction and transport in BHJ OSCs.
2. Results and discussions
2.1. Chemical structures, energy levels, and device configuration
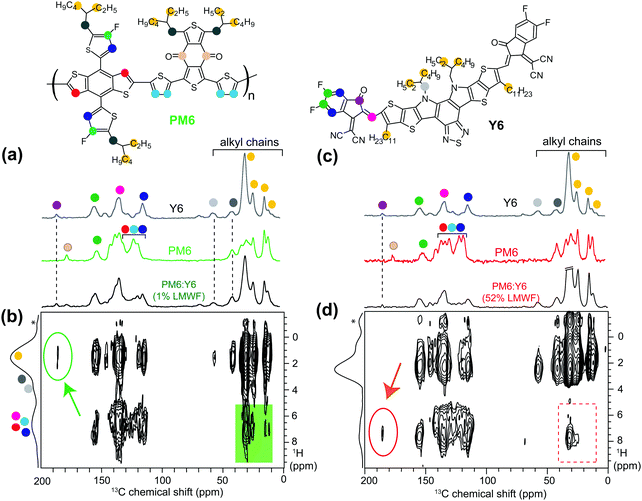
Fig. 1 shows the energy levels, device configuration, and chemical structures of the materials used in this study, as well as schematic representations of four different PM6 polymer batches that were tested with the Y6 NFA. The PM6 donor polymer batches comprised of high and low number average molecular weight (Mn) fractions, as depicted in the green and red schematics in Fig. 1c. The schematic pathway to the synthesis of the PM6 donor polymers and the extraction procedures for obtaining the different batches of polymers are described in the ESI† (Fig. S1–S3). From gel permeation chromatography (GPC) (Table S1, ESI†), it was found that the different PM6 batches contain high and low Mw fractions of Mn = 40 kDa and Mn = 2.5 kDa, respectively. It should be noted that the polymers in the LMWFs with a Mn = 2.5 kDa consists of about 4 PM6 monomers, whereas the high molecular weight fraction (HMWFs) with a Mn = 40 kDa consist of polymers with about 64 PM6 monomers. The batches vary in the ratio of low and high molecular weight fractions present, and are referred to as 1%, 7%, 9%, and 52% LMWF PM6 donor polymers as shown in Fig. 1c. To the best of our knowledge, completely removing the LMWF is not possible; there will always be a small amount (≤1%) of the LMWF PM6 fraction present in the polymer batches. Generally, GPC analyses of this low quantity of LMWF PM6 are not conducted in most studies reported in the literature.5–122.2. Solar cell characteristics
We begin this study by testing the four different batches of PM6 donor polymers containing 1%, 7%, 9%, and 52% LMWFs with the Y6 NFA. To ensure a systematic comparison between the four batches, the device configuration, D:A blend ratios, processing solvents, and annealing conditions for the devices across the different PM6 batches were kept the same. As depicted in the box plots in Fig. 2a, the PCE decreases with increasing LMWFs (1%, 7%, 9%, and 52%) of the PM6 polymer in the blends from about 15% to 5% (Table 1). To further investigate why the PCE drops with increasing LMWFs, we examine the J–V curves of the different LMWF blends in further detail. Fig. 2b shows the J–V curves at 1 sun illumination (100 mW cm−2 AM 1.5) of the four different blend systems. Since the 7% and 9% LMWF blends do not show significant differences in the PCEs, an in-depth study was conducted to understand the reasons behind the PCE differences in the 1% and 52% LMWF blend systems.| PM6:Y6 blend | V OC (V) | J SC (mA cm−2) | FF | Average PCE (max) [%] |
|---|---|---|---|---|
| 1% LMWF | 0.83 ± 0.003 | 25.5 ± 0.7 | 0.712 ± 0.02 | 15.0 ± 0.4 (15.35) |
| 7% LMWF | 0.846 ± 0.003 | 20.6 ± 1.2 | 0.681 ± 0.02 | 11.8 ± 0.6 (12.9) |
| 9% LMWF | 0.843 ± 0.005 | 20.4 ± 1 | 0.646 ± 0.02 | 11.1 ± 0.5 (12.3) |
| 52% LWMF | 0.85 ± 0.006 | 12.0 ± 0.7 | 0.51 ± 0.02 | 5.2 ± 0.5 (5.7) |
The large drop in PCEs from 15% to 5% in the 1% and 52% LMWF blends was found to be dictated by a reduction in the FF and JSC values, where the FF dropped from an average value of 0.71 to 0.51 and the JSC dropped from 25.5 to 12 mA cm−2 (Table 1). The small differences in the VOC values (0.83 V vs. 0.85 V) can be explained by the higher charge transfer voltage losses (S1-CT offset) in the 1% LMWF blend compared to the 52% LMWF blend (Fig. S4 and S5, ESI†). Fig. 2c shows the external quantum efficiency (EQE) spectra of the 1% and 52% LMWF blends which drops from an average EQE of ∼80% to ∼40% in the wavelengths of 500–800 nm. Furthermore, the integrated JSC values were found to be within 4% of the average JSC values measured via the J–V characteristics. A combined simulation and experimental approach13 was used to obtain the internal quantum efficiencies (IQEs) for the 1% and 52% LMWF blend systems. The difference in IQEs from ∼90% to ∼70% in going from the 1% LMWF to the 52% LMWF blend systems confirms the decreased charge generation and extraction efficiencies.
2.3. Morphological characterization
Next, we establish the interfacial and bulk morphological differences in the 1% and 52% LMWF PM6:Y6 blend systems. An OSC device performance is largely affected by the BHJ morphology.1,14–19 Therefore, by characterizing the bulk and interfacial morphology in the two blend systems, we can identify the effects of these differences on the processes ranging from charge generation to extraction that dictate device performance.16,18–23 To obtain a comprehensive picture of the BHJ morphology in the two PM6:Y6 blends from sub-nanometer to sub-micrometer length scales, four techniques were used.First, AFM and photo-conductive atomic force microscopy (pc-AFM) techniques were used to visualize the domain sizes and the hole- and electron-rich domains on the BHJ blend film surfaces of the 1% and 52% LMWF PM6:Y6 devices at sub-micrometer length scales. In a pc-AFM measurement, an electrically conductive platinum–chromium coated tip is used to scan the surface of the photoactive layers of the devices under white light illumination and 0 V bias such that features of high and low photocurrents in the two blend films corresponding to hole- and electron-rich regions can be spatially mapped. Fig. 3a and b shows the topography images of the 1% and 52% LMWF blends. Fig. 3c and d shows the corresponding pc-AFM images that are simultaneously scanned with the topography images. The corresponding high resolution 500 × 500 nm sized images of each blend shows identifiable differences in the domains of the two blend films. The 1% LMWF blend exhibits smaller and more defined, grain-like, and swirling patterns which can also be visualized in the photocurrent images. The corresponding photocurrent image of the 1% LMWF device reveals small phase separated domain sizes of hole- (PM6; lighter color on the photocurrent scale) and electron- (Y6; darker color on the photocurrent scale) rich regions on the film surface. Overall, the fact that there is a continuous interpenetrating network of electron and hole rich domains that can be visualized by pc-AFM suggests that there are finely phase-separated donor and acceptor networks throughout the 1% LMWF PM6:Y6 blend film surface, which can be correlated to the finely phase separated surface morphology. The higher viscosity and thickness of the 1% LMWF blend film amounts to root-mean-square (RMS) roughness values of ∼1.9 nm. Contrastingly, the 52% LMWF blend displays larger domain sizes and less defined features. The corresponding photocurrent image of the 52% LMWF blend shows that domains of hole-(PM6; lighter color on the photocurrent scale) and electron- (Y6; darker color on the photocurrent scale) rich regions are not finely and continuously separated as in the 1% LMWF case, which is consistent with the larger domain sizes seen in the height images. The lower viscosity and thickness of the 52% LMWF blend amounts to RMS roughness values of ∼1.7 nm. Overall, comparison of the pc-AFM images under white light illumination elucidate two advantages in the nanoscale morphology of the 1% LMWF blend films: an increase in the nanoscale photocurrent scale; consistent with the higher JSC values of the tested devices (Fig. 3e and f), and a continuous interpenetrating network of electron and hole rich domains suggesting finely phase-separated D and A networks throughout the film surface.
Second, grazing incidence wide-angle X-ray scattering (GIWAXS) was used to probe differences in the meso-scale structural order of the two blends (ca. tens of nanometers). Fig. S6 (ESI†) shows the GIWAXS patterns of the 1% and 52% LMWF PM6:Y6 blend films, which reveal that both blends have a primarily face-on orientation. The GIWAXS 1D line cuts corresponding to the in-plane (qxy) and out-of-plane (qz) scattering intensities are also shown in Fig. S6 (ESI†). The corresponding d-spacing, π–π and lamellae stacking distances are listed in Table S2 (ESI†). It was found that while the π–π stacking peaks corresponding to both PM6 and Y6 could be resolved in the 1% LMWF blend, at 1.75 qz (d: 0.36 nm, Lc: 2.31 nm) and 1.81 qz (d: 0.35 nm, Lc: 3.89 nm) respectively, the scattering peaks in the 52% LMWF blend corresponding to Y6 could not be resolved. The only π–π stacking peaks that could be resolved in the 52% LMWF blend was the peak corresponding to PM6 at 1.76 qz (d: 0.36 nm, Lc: 2.32 nm). In addition, it was found that the 1% LMWF blend contained additional lamellar scattering peaks from Y6 at 0.22 qxy (d: 2.85 nm, Lc: 26.30 nm) and 0.43 qxy (d: 1.46 nm, Lc: 5.91 nm), which was absent in the 52% LMWF blend. Furthermore, the 1% LMWF blend was generally found to have larger coherence lengths (Lc) for the lamellar stacking peaks. Therefore, from a qualitative inspection, we can conclude that the 1% LMWF blend exhibits a superior molecular ordering compared to the 52% LMWF blend.
Third, resonant soft X-ray scattering (RSoXS) was used to obtain information on the domain purity and the domain spacing distribution.24,25Fig. 3g and h show the Lorentz corrected and circularly averaged RSoXS profiles of the blend films. The fitting parameters are provided in Table S3 (ESI†). Long periods of ∼126 nm for the 52% LMWF blend and ∼56 nm for the 1% LMWF blend were extracted from the RSoXS profiles, which were consistent with the differences in domain sizes obtained from the pc-AFM measurements. Variations in the long period between the two LMWF blends can be explained by considering the impact of the polymer viscosity on the film formation. Previous studies have shown that blends containing more low Mw PM6 chains are less viscous and as a result have more time to undergo liquid–liquid transition, which delays the liquid–solid transitions to form larger domains.4,26–31 The root-mean-square (RMS) composition variation (which is monotonically related to the domain purity) of the 1% and 52% LMWF blends were determined by obtaining the integrated scattering intensities. A higher value for the RMS composition variation indicates larger average purity of domains in the blends. In comparison to the 1% LMWF blend, it was found that the RMS composition variation was higher for the 52% LMWF blend, indicating higher average purity. A high average purity has been shown to be related to a reduced number of molecular D:A interfacial area due to the reduced distribution of acceptor molecules in the polymer-rich phase.4,20,24,32 Therefore, the RSoXS data suggests that the 1% LMWF blend has an increased molecular D:A interfacial area in addition to the increased domain interfacial area due to the smaller average domain sizes of the polymer-rich and acceptor-rich domains. This observation is consistent with the nanoscale phase separation visualized from pc-AFM where more continuously phase separated D:A interfaces can be observed in the 1% LMWF blend.
The morphological techniques discussed so far reveal differences in the macroscopic characteristics of the 1% and 52% LMWF PM6:Y6 blends. Several theoretical and experimental studies have suggested that the nature of the molecular-level D:A interactions can affect the rates of charge transfer and recombination,33–35 electronic coupling,19,36 charge generation,19,35 and charge delocalization.37 To this end, insights into short-range structures and molecular D:A interactions of the 1% LMWF and 52% LMWF PM6:Y6 blends were obtained by employing multi-nuclear 1D and 2D solid-state NMR spectroscopy techniques.
Solid-state NMR (ssNMR) spectroscopy is a short-range technique that allows local structures and interactions in heterogeneous polymers and blends to be measured and distinguished at a sub-nanometer to nanometer resolution.16,38–44 The 1H, 13C, and 19F chemical shifts and line-shapes are sensitive to local bonding environments, non-covalent interactions, and molecular conformations in π-conjugated materials.16,38–41,45–47 In such materials, information on molecularly proximate and dipole–dipole coupled 1H–1H and 1H–X pairs (X = 13C, 15N and 19F) at sub-nanometer to nanometer distances can be obtained by the analyses of powerful 2D correlation NMR spectra. In addition, in situ and ex situ NMR techniques have been employed to understand the phases transitions, crystallization, melting and solid-to-solution transformations or vice versa.48–51 Furthermore, combined X-ray scattering, ssNMR spectroscopy, and computational modeling approaches have shown enormous potential to elucidate the structures of π-conjugated systems43,45 and packing interactions in polymer:fullerene BHJ blends.40 Such multi-technique approaches are seldom applied to study BHJ blends with non-fullerene acceptors due to the presence of structurally identical donor and acceptor moieties that lead to intrinsically complex compositions which are difficult to deconvolute. However, in this case, analyzing and comparing the structural information gained from powerful 1D and 2D NMR spectroscopy techniques, valuable insight into the nature of the D:A inter- and intra-molecular interactions in the 1% and 52% LMWF blends could be obtained.
In this study, we examined different 1H, 13C, and 19F sites in the 1% and 52% LMWF PM6 donor polymers and Y6 acceptor molecules and their respective blends. Although 1H ssNMR spectra benefit from intrinsically high sensitivity, the severely overlapped spectra of PM6:Y6 blends hinder the identification of signals corresponding to distinct aliphatic and aromatic 1H sites (Fig. S7, ESI†). 1D and 2D 19F ssNMR techniques have been employed to characterize the local 19F sites in PM6 donor and Y6 acceptors moieties (Fig. S8, ESI†). Detailed insights into through-space proximities between 1H and 13C nuclei at sub-nanometer to nanometer distances can be obtained by analyzing and comparing the 1D 13C{1H} CP-MAS and 2D 13C–1H heteronuclear correlation (HETCOR) NMR spectra of neat molecules and BHJ blends (Fig. 4 and Fig. S9–S11, ESI†). In particular, 2D 1H–13C HETCOR NMR experiments facilitate spectral simplification by distributing the 1H and 13C signals into two frequency dimensions, which allow distinct 2D 13C–1H correlation intensities to be resolved. The homonuclear decoupling was applied during the acquisition of vertical indirect 1H dimension using a DUBMO pulse sequence.52,53 The analyses of 2D 13C–1H correlation intensities of the 1% and 52% BHJ blends can be compared to the analogous signals in the 2D 13C–1H correlation spectra of neat PM6 and Y6 materials to obtain valuable information on the D:A inter- and intra-molecular interactions, as discussed below.
Fig. 4 shows the 2D 13C–1H HETCOR NMR spectra of the 1% and 52% LMWF PM6:Y6 blends together with the 1D 13C{1H} CP-MAS spectra of neat Y6, PM6, and the PM6:Y6 blends presented on the top horizontal axes (Fig. 4). Aliphatic and aromatic 1H and 13C signals associated with PM6 and Y6 molecules are shown in colored dots, as depicted in their schematic structures. Analogous 2D 13C–1H HETCOR NMR spectra of neat Y6 material and different batches of PM6 polymers were analyzed and compared (Fig. S10 and S11, ESI†). In the 2D 13C–1H spectra of the 1% LMWF (high performing) PM6:Y6 blend shown in Fig. 4b, correlation signals between 13C (13, 15 ppm) and 1H (1.5 ppm) and between 13C (25–35 ppm) and 1H (1.7–2.5) originate from –CH3 and –CH2 groups of alkyl side chains, respectively. Of particular interest is the 2D correlation signal between 13C (13 and 15 ppm) and aromatic 1H signals (6–7.5 ppm) depicted in the green color box, which indicates the close intermolecular proximity between the PM6 sidechains and Y6 aromatic groups, and/or the PM6 backbones and Y6 sidechains. By comparison, in both PM6 and Y6 molecules, the C–H moieties in the aromatic core are relatively far from the terminal methyl groups in aliphatic chains and the intramolecular C–H dipolar interactions are less likely to contribute to such 2D correlation peaks. These results are corroborated by the analysis of 2D HETCOR NMR spectra of neat Y6 and PM6 compounds shown in Fig. S10 and S11 (ESI†), which exhibited no such correlation peaks between aliphatic and aromatic C–H moieties within PM6 molecules and minimal correlation peaks within the Y6 molecules. Hence, most of the 2D correlation signals between aromatic 13C (120–150 ppm) and aliphatic 1H (1–2.5 ppm) in Fig. 4b are expected to originate from both inter- and intra-molecular through space proximities between PM6 and Y6 molecules in BHJ blends. However, these signals are partially overlapped and convoluted to be accurately distinguished and identified, which hinders the ability to extract detailed information about the intermolecular interactions between PM6 and Y6 molecules. Nevertheless, well-resolved 2D correlation intensity between the carbonyl groups of Y6 (13C, 186 ppm, purple dot) and aliphatic 1H signals of PM6 (1.2–1.5 ppm) depicted in the green oval (Fig. 4b) further validates the close spatial proximity between the Y6 aromatic groups and PM6 sidechains. In contrast, no such 2D correlations between 1H (1.2–1.5 ppm) and 13C signals (186 ppm – purple dot in Y6, and 178 ppm – ivory dot in PM6) were detected in the 2D HETCOR NMR spectra of the neat Y6 and PM6 compounds (Fig. S10 and S11, ESI†). These results indicate the close (<1 nm) intermolecular proximity between PM6 and Y6 molecules in the 1% LMWF PM6:Y6 blend.
To probe the D:A interactions in the 52% LMWF (low performing) PM6:Y6 blend, we analyzed and compared the 1D 13C{1H} CP-MAS and 2D 13C–1H HETCOR spectra of neat compounds and the BHJ blend (Fig. 4c and d). Although the 2D correlation signals between 13C (24–35 ppm) and 1H (∼1.5–2.0 ppm) and between 13C (24–35 ppm) and 1H (2.2–2.5 ppm) sites originating from –CH3 and –CH2 groups of alkyl side chains are observed, no such 2D correlation intensities associated with the intermolecular interactions between PM6 and Y6 molecules are detected in the low performing blend (red dashed rectangle). The 2D correlation intensity present in the HETCOR spectrum of the 52% LMWF blend (present within the red dashed rectangle) originates from the through-space interactions between aliphatic and aromatic sites of Y6 molecules themselves, which is also present in the 2D HETCOR spectrum of neat Y6 material (Fig. S11b, ESI†). Additionally, unlike in the 1% LMWF blend, the 2D correlation intensity associated with carbonyl groups of Y6 (13C, 186 ppm) and aliphatic 1H signals (1.2–1.5 ppm) of PM6 shown in the green oval (Fig. 4b) was not detected in the 2D 13C–1H correlation spectrum of the 52% LMWF blend (Fig. 4d). Instead, a correlation intensity between 13C signals of carbonyl groups and aromatic 1H signals (∼7 ppm) of Y6 aromatic groups (depicted within the red oval) was observed, which is expected to arise from the intramolecular 13C–1H proximity within Y6 molecules as shown in the 2D 13C–1H correlation spectrum of neat Y6 (Fig. S11b, ESI†). The absence of 2D 13C–1H correlation peaks corresponding to the D:A intermolecular interactions in the 52% LMWF blend confirms the lack of close D:A interactions, unlike those found in the 1% LMWF blend.
To summarize the morphological findings, systematic analyses using the four characterization techniques (from sub-nanometer to sub-micrometer length scales) revealed bulk and interfacial morphological differences in the 1% and 52% LMWF PM6:Y6 blends. Notably, analyses of 2D 13C–1H HETCOR spectra revealed intermolecular 13C–1H proximities between PM6 and Y6 molecules in the 1% LMWF blend, which were absent in the 52% LMWF blend. While these results imply different intermolecular packing arrangements in PM6:Y6 blends with different LMWFs of the PM6 donor polymers, we note that the development of complete three-dimensional structural models of such intrinsically complex blends using ssNMR results alone is less straightforward and is beyond the scope of this work.54 Nevertheless, ssNMR results were found to successfully resolve crucial differences in the D:A interactions between the two blends. Additionally, from a combination of the four morphological techniques, we established that the high-performing (1% LMWF) BHJ blend has better long-range ordering, a more continuous and optimal D:A phase separation, larger D:A interfacial area, and closer D:A interactions. Next, we investigate the impact of these bulk and interfacial morphological differences on the charge transfer dynamics at the D:A interface, as well as the non-geminate recombination and extraction dynamics of the 1% and 52% LMWF PM6:Y6 blends.
2.4. Charge generation dynamics
The use of transient absorption (TA) spectroscopy allows us to fully-characterize the charge generation processes in the 1% and 52% LMWF PM6:Y6 blends. Thus, a detailed understanding of the effect of BHJ morphology on the charge generation dynamics can be obtained. For the simplest picture, we begin by selectively exciting Y6 in the blends with an 800 nm pump pulse to induce hole transfer to PM6. Importantly, care was taken to ensure that identical excitation densities were used across all TA measurements for both blends (n0 ∼1 × 1017 cm−3; highly comparable to the carrier densities of devices under operating conditions discussed in the following section, Fig. S26a, ESI†), allowing for a direct comparison of the resulting photophysics. A fluence series was also conducted for these systems, where there was a clear increase in the rate of excited state decay at higher fluences, as would be expected from the extra bimolecular recombination induced by the increased excitation densities. The TA spectra for each sample at different pump fluences are included in the ESI† (Fig. S12–S15). However, we choose to focus on the lowest fluence measurements here, as they will have the smallest amount of excess bimolecular recombination and are therefore the most relevant to discuss when trying to understand the charge generation dynamics of the blends.The TA spectra and kinetics of the 1% LMWF blend after excitation with a low fluence of 0.45 μJ cm−2 are shown in Fig. 5a and b. At 0.2 ps, we observe the presence of a positive feature between 700–900 nm and a narrow photo-induced absorption (PIA) at 920 nm. By referencing the TA of a polystyrene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y6 1
Y6 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 film (Fig. S16, ESI†), we attribute the positive feature to the ground state bleach (GSB) of Y6 and the PIA to the Y6 singlet exciton (S1). Additionally, the PM6 GSB is also visible between 530–650 nm (Fig. S17, ESI†). The steady-state absorption spectra of the neat materials are shown in Fig. S18 (ESI†) to provide definitive proof that the positive signals belong to the GSB of PM6 and Y6. The presence of the polymer GSB, despite selective excitation of Y6 below the band gap of PM6, suggests that some hole transfer from Y6 occurs on ultrafast (<0.2 ps) timescales. As time progresses, the PM6 GSB continues to rise and peaks after ∼100 ps, confirming hole transfer is completed by this time. Additionally, new negative bands form between 700–800 nm and at the edge of the probe range around 950 nm. Through comparison to a reference PM6:PC60BM film (Fig. S19, ESI†), we confirm that the 950 nm band is due to the absorption of holes on PM6. Interestingly, we can associate the band between 700–800 nm to an electro-absorption (EA) feature of PM6 (Fig. S19, ESI†): the EA represents the Stark-shift of the PM6 absorption spectrum by the electric field of the separating charges.55–58 Thus, the presence of a strong EA signal is consistent with the efficient free charge generation in the 1% LMWF blend.
1.2 film (Fig. S16, ESI†), we attribute the positive feature to the ground state bleach (GSB) of Y6 and the PIA to the Y6 singlet exciton (S1). Additionally, the PM6 GSB is also visible between 530–650 nm (Fig. S17, ESI†). The steady-state absorption spectra of the neat materials are shown in Fig. S18 (ESI†) to provide definitive proof that the positive signals belong to the GSB of PM6 and Y6. The presence of the polymer GSB, despite selective excitation of Y6 below the band gap of PM6, suggests that some hole transfer from Y6 occurs on ultrafast (<0.2 ps) timescales. As time progresses, the PM6 GSB continues to rise and peaks after ∼100 ps, confirming hole transfer is completed by this time. Additionally, new negative bands form between 700–800 nm and at the edge of the probe range around 950 nm. Through comparison to a reference PM6:PC60BM film (Fig. S19, ESI†), we confirm that the 950 nm band is due to the absorption of holes on PM6. Interestingly, we can associate the band between 700–800 nm to an electro-absorption (EA) feature of PM6 (Fig. S19, ESI†): the EA represents the Stark-shift of the PM6 absorption spectrum by the electric field of the separating charges.55–58 Thus, the presence of a strong EA signal is consistent with the efficient free charge generation in the 1% LMWF blend.
For comparison, we have also excited the 52% LMWF blend at 800 nm with a low fluence of 0.50 μJ cm−2, with the resulting TA spectra and kinetics displayed in Fig. 5c and d. At 0.2 ps, we again observe the Y6 GSB. However, in clear contrast to the 1% LMWF blend, the PM6 GSB is not visible at this time. In fact, the PM6 GSB does not noticeably form until 10 ps (Fig. S20, ESI†): thereafter a particularly muted growth ensues. The peak PM6 GSB intensity occurs at 200 ps, confirming hole transfer is complete, after which time it begins to rapidly decay again. Additionally, the Y6 GSB, which remains at a relatively constant intensity in the 1% LMWF blend, also significantly decreases over the time of the experiment. Given the slow hole transfer process in this blend, it is likely that the fall in Y6 GSB intensity is due to the decay of un-dissociated Y6 S1 back to the ground state. By 2 ns, the low intensity of the remaining spectral features, including the PM6 EA and hole PIA, in the 52% LMWF blend confirms that fewer of the initially-generated excitons are successfully converted to free charges (Fig. S21, ESI†); this is fully consistent with the lower JSC and reduced performance observed in this blend.
Next, we preferentially excite PM6 at 580 nm to track the electron transfer process from PM6 to Y6. However, as there is still some absorption by Y6 at 580 nm, a small fraction of the NFA will also unavoidably be excited. Beginning with the 1% LMWF blend (Fig. S22a and b, ESI†), pumped with a low fluence of 0.67 μJ cm−2, the PM6 and Y6 GSB are both present at 0.2 ps. After this time, the spectral evolution closely resembles that of the blend after selective excitation of Y6 at 800 nm, when only hole transfer can take place. The lack of early-time spectral evolution implies that the electron transfer process is completed on ultrafast timescales. To confirm this, we have also performed TA on the near-infrared (NIR) region from 1250–1600 nm, where the S1 PIAs of PM6 and Y6 reside (Fig. S22c, ESI†). Here, we observe rapid quenching of the PM6 S1 PIA at 1250 nm within 1 ps. Thus, the electron transfer process from PM6 to Y6 also appears to be extremely efficient, in-line with the excellent performance obtained in the 1% LMWF device. In the 52% LMWF blend, excited at 580 nm with a fluence of 0.95 μJ cm−2, the resulting behavior is markedly different (Fig. S23a and b, ESI†). After peaking immediately after excitation at 0.2 ps, the PM6 GSB actually decreases in intensity over the first 10 ps. Taking a kinetic trace between 675–725 nm, which corresponds to the vibronic shoulder of the Y6 GSB, we notice this region also increases in intensity over the same timescales. Further, in the NIR region, there is an increase in the intensity of the Y6 S1 PIA as the PM6 S1 PIA is quenched (Fig. S23c, ESI†). Taken together, it is clear that a significant proportion of the PM6 S1 states undergo Förster resonance energy transfer (FRET) from PM6 to Y6 in the 52% LMWF blend; we estimate this to be 30% from the decrease in the PM6 GSB from its initial magnitude by 10 ps (Fig. S23b, ESI†). We note that FRET is not detectable in the 1% LMWF blend, where the rapid charge transfer out-competes any FRET processes. Following FRET in the 52% LMWF blend, the PM6 GSB regains intensity from 10 ps onwards and peaks at 200 ps, whilst the PM6 EA feature begins to form; this is consistent with the timescales and dynamics of the hole transfer process from Y6 to PM6.
Having now characterized the contrasting charge transfer dynamics of the two blends, we are well-positioned to rationalize the experimental behavior against the known morphological features. The key observation is that both electron and hole transfer processes are faster and more efficient in the 1% LMWF blend, which contributes to the improved JSC value. Beginning with the electron transfer process, the fact that FRET can out-compete electron transfer in the 52% LMWF blend suggests that the charge transfer process is compromised. As the 52% LMWF blend has larger D and A domains, with purer D domains, as well as a smaller D:A interfacial area, this means PM6 excitons are likely to be generated further from the D:A interface or the nearest A molecule inside the D-rich domains. Whilst charge transfer is a short range process, typically taking place between adjacent D and A molecules,59 FRET can occur over comparatively long-ranges (∼5 nm).60 Thus, FRET can compete with charge transfer if it becomes significantly diffusion-limited. In a blend where hole transfer from A to D is equally as efficient as electron transfer, FRET is unlikely to significantly harm the charge generation efficiency, though it may be considered a marker for a non-ideal morphology. However, when the hole transfer process becomes inefficient, FRET channels excitons onto the component with a lower charge transfer efficiency. This then compounds the problem of an inefficient hole transfer process, as it now becomes responsible for dissociating an even larger fraction of the excitons. We note the development of such a bottleneck in the 52% LMWF blend. This finding is reinforced by a recent report from Zhong et al. where that also discusses FRET from D to A was also observed to compete with electron transfer in the case of D excitons generated further from the D:A interface.61
Particularly interesting is the effect of morphology on the hole transfer process in the blends. Whilst there is also likely an aspect of diffusion limitation on the hole transfer rates, as discussed previously, the situation is somewhat more complex. The critical observation is the presence of some ultrafast (<0.2 ps) hole transfer taking place in the 1% LMWF blend, with this component entirely absent in the 52% LMWF blend. If diffusion was the sole factor limiting the hole transfer rate, we would expect to see a smaller, but finite, amount of ultrafast hole transfer. This is because a proportion of Y6 excitons would still be generated in close proximity to the D:A interface, regardless of the BHJ morphology. To rationalize this, we consider more deeply the nature of D:A interactions at the interface. As we have demonstrated from ssNMR, the 1% LMWF fraction blend exhibits closer D:A interactions. According to Marcus theory, the rate of charge transfer process depends on, amongst other factors, the square of the D:A electronic coupling (HDA).36 As HDA is approximately proportional to the overlap of the HOMO of D and the LUMO of A,36 the nature of the D:A interface plays a critical role in determining the charge transfer rate. It is then reasonable to assume that closer D:A interactions result in greater HOMO–LUMO overlap, increasing HDA and therefore the charge transfer rate in the 1% LMWF blend.61 As hole transfer is typically takes place over tens of ps in low offset NFA systems,61–64 it is in fine-balance with the rate of NFA exciton decay (Fig. S11, ESI†). Therefore, any unnecessary decrease in the hole transfer rate can have severe consequences for the charge transfer efficiency. The slower charge transfer is also compounded with the increasing exciton diffusion limitations in the 52% LMWF blend, resulting in the lower hole transfer efficiencies observed. Thus, we consider that close D:A interactions and moderate domain sizes, on the order of ∼56 nm, are key to maximizing the efficiency of charge photogeneration in PM6:Y6 blends.
2.5. Non-geminate recombination and charge extraction dynamics
We next measured the non-geminate recombination and charge extraction dynamics to gain further insights into the timescales of the loss processes of the 1% and 52% LMWF PM6:Y6 blends. Naturally, the goal is to minimize the charge extraction time, while maximizing the charge carrier lifetime, as this leads to a reduction of the losses caused by non-geminate recombination.16,65,66 The first step of this analysis will be the calculation of the photocurrent density Jph:| Jph = Jlight − Jdark, | (1) |
| Vcor = Vapp − J·Rseries, | (2) |
 | (3) |
 | ||
| Fig. 6 (a) Photocurrent Jph and (b) collection probability PC of the 1% and 52% LMWF PM6:Y6 batches. (c) Average extraction time τex and charge carrier lifetime τrec of the two batches. | ||
Additionally, J–V-curves at varying light intensities were measured to qualitatively inspect the non-geminate recombination mechanisms (Fig. S24, ESI†). Specifically which type of non-geminate recombination mechanism dominates can be determined by the relationship between the VOC and the light intensity I:68
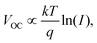 | (4) |
Nevertheless, a quantitative confirmation of the dominant loss processes requires a more advanced recombination analysis.72 Hence, a quantitative analysis based on capacitance spectroscopy was employed.65,72–74 This measurement technique yields the capacitance of the BHJ, which can be used to calculate important parameters such as the charge carrier density (n) and the effective mobility (μeff) of the studied solar cells under operating conditions (Fig. S25, ESI†).75,76 A detailed description of the procedures to determine the charge carrier densities and effective mobilities under operating conditions are described in the ESI† (Sections S7.2 and S7.3). The measured charge carrier densities for the two different batches are in a range of n = 1014–1017 cm−3, with the high performing devices (LMWF = 1%) exhibiting the highest variation (n = 9.0 × 1014 to 8.5 × 1016 cm−3) compared to the low performing devices (LMWF = 52%; n = 3.5 × 1016 to 1.7 × 1017 cm−3), which show comparatively high charge carrier densities at reverse bias (Fig. S26a, ESI†). This observation is interpreted as a sign of inefficient charge extraction, since there should be ideally a significant reduction in the carrier density at reverse biases.66 This is also consistent with the low values for the PC that have been determined for the low performing devices (LMWF = 52%). Furthermore, a clear trend can be seen for the effective mobilities, where the high performing devices exhibit mobilities more than one order of magnitude higher than their low performing counterparts (LMWF = 1%: μeff = [4.4–34.0] × 10−5 cm2 V−1 s−1; LMWF = 52%: μeff = [3.9–6.0] × 10−6 cm2 V−1 s−1; Fig. S26b, ESI†).
To obtain a quantitative understanding of the non-geminate recombination mechanisms, it is assumed that the overall measured recombination current density (Jrec = Jph,sat − Jph) is a superposition of the three aforementioned recombination mechanisms that contribute a certain part to the total recombination current density Jrec:
 | (5) |
Finally, the extraction of charge carriers has to be quantified as well to obtain a comprehensive understanding of the non-geminate recombination dynamics in the studied devices. To this end, the effective extraction time (τex) was calculated, utilizing a previously-employed approach.16 It is assumed that a charge carrier needs to traverse, on average, half of the active layer thickness, until it reaches one of the electrodes and that the active layer can be treated as an effective medium. The following relationship can be derived based on these assumptions:
 | (6) |
Overall, the results obtained for the extraction and non-geminate recombination dynamics are consistent. The low performing devices (LMWF = 52%) exhibit significantly more trap-assisted recombination in the bulk, reduced effective mobilities, and compromised charge extraction leading to the reduction in the JSC from 25.5 to 12 mA cm−2 and FF values from 0.71 to 0.51. The occurrence of trap-assisted recombination in the 52% LMWF blend can be understood by the presence of the LMWFs of PM6, which consist of small packets of polymers containing only 4 monomers. As reported in previous literature,26,78–82 low molecular weight polymers can act as trap states for charge carriers which result in reduced mobilities in the blends (Fig. S26b and S28, ESI†). Additionally, it has been shown that low molecular weight polymer chains can lead to disconnected ordered regions in films that can hinder charge transport pathways.78 Therefore, the presence of LMWFs in addition to the compromised long-range ordering and suboptimal phase-separated D:A regions in the 52% LMWF blend is the reason for its inferior charge transport and extraction.16 In summary, better long-range ordering, reduction in the LMWFs, and optimally phase-separated D:A regions are crucial for efficient charge transport and extraction in NFA OSC blends.
3. Conclusions
In summary, different amounts (1% and 52%) of LMWFs of the PM6 polymer were used as a tool to exert control over the interfacial and bulk morphology in the two PM6:Y6 blends. The use of four morphological characterization techniques from sub-nanometer to sub-micrometer length scales enabled a full characterization of the bulk and interfacial morphology in these two blend systems. The drop in PCEs from over 15% to 5% with the increased LMWFs was due to a drop in the JSC and FF values caused by compromised charge generation efficiencies, increased bulk trap densities, lower competition factors, and reduced charge transport. The origins of the high device performance in the 1% LMWF blend could be rationalized by the favorable bulk and interfacial morphological features, summarized by two main points. First, the closer D:A interactions, smaller D and A domains, and increased interfacial area facilitated ultrafast electron and hole transfer at the D:A interface. Second, the better long-range ordering and optimally phase separated D:A regions led to its superior charge transport and extraction. Therefore, this study provides insight into the detailed bulk and interfacial morphological features that are critical in achieving high PCEs of over 15% in polymer:NFA OSCs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. K., J. V., and A. J. G. contributed equally. This work is supported by the U.S. Office of Naval Research, under Award No. N000141410580. A. K. acknowledges funding by the Schlumberger foundation. J. V. acknowledges funding by the Alexander-von-Humboldt Stiftung. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. R. H. F. and A. J. G. acknowledge support from the Simons Foundation (grant no. 601946). Z. P. and H. A. are supported by the U.S. Office of Naval Research (ONR), under Award No. N000141712204. G. N. M. R. gratefully acknowledge the financial support from the IR-RMN-THC FR-3050 CNRS France for conducting some of the solid-state NMR measurements. The authors would like to thank Dr Alexander A. Mikhailovsky, Dr Viktor Brus, Alexander T. Lill, and Suraj Upadhyay for helpful discussions.References
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275 CrossRef.
- A. Wadsworth, Z. Hamid, M. Bidwell, R. S. Ashraf, J. I. Khan, D. H. Anjum, C. Cendra, J. Yan, E. Rezasoltani, A. A. Y. Guilbert, M. Azzouzi, N. Gasparini, J. H. Bannock, D. Baran, H. Wu, J. C. de Mello, C. J. Brabec, A. Salleo, J. Nelson, F. Laquai and I. McCulloch, Adv. Energy Mater., 2018, 8, 1801001 CrossRef.
- S. F. Hoefler, T. Rath, N. Pastukhova, E. Pavlica, D. Scheunemann, S. Wilken, B. Kunert, R. Resel, M. Hobisch, S. Xiao, G. Bratina and G. Trimmel, J. Mater. Chem. A, 2018, 6, 9506–9516 RSC.
- L. Ye, S. Li, X. Liu, S. Zhang, M. Ghasemi, Y. Xiong, J. Hou and H. Ade, Joule, 2019, 3, 443–458 CrossRef.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- M. Zhang, X. Guo, W. Ma, H. Ade and J. Hou, Adv. Mater., 2015, 27, 4655–4660 CrossRef CAS.
- Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515 CrossRef.
- S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, Nat. Photonics, 2020, 14, 300–305 CrossRef.
- Z. Zhou, W. Liu, G. Zhou, M. Zhang, D. Qian, J. Zhang, S. Chen, S. Xu, C. Yang, F. Gao, H. Zhu, F. Liu and X. Zhu, Adv. Mater., 2020, 32, 1906324 CrossRef.
- L. Hong, H. Yao, Z. Wu, Y. Cui, T. Zhang, Y. Xu, R. Yu, Q. Liao, B. Gao, K. Xian, H. Y. Woo, Z. Ge and J. Hou, Adv. Mater., 2019, 31, 1903441 CrossRef.
- Y. Cui, H. Yao, L. Hong, T. Zhang, Y. Tang, B. Lin, K. Xian, B. Gao, C. An, P. Bi, W. Ma and J. Hou, Natl. Sci. Rev., 2020, 7, 1239–1246 CrossRef.
- K. Jiang, Q. Wei, J. Y. L. Lai, Z. Peng, H. K. Kim, J. Yuan, L. Ye, H. Ade, Y. Zou and H. Yan, Joule, 2019, 3, 3020–3033 CrossRef CAS.
- G. F. Burkhard, E. T. Hoke and M. D. McGehee, Adv. Mater., 2010, 22, 3293–3297 CrossRef CAS.
- S. Li, C.-Z. Li, M. Shi and H. Chen, ACS Energy Lett., 2020, 1554–1567 CrossRef CAS.
- L. Zhu, M. Zhang, G. Zhou, T. Hao, J. Xu, J. Wang, C. Qiu, N. Prine, J. Ali, W. Feng, X. Gu, Z. Ma, Z. Tang, H. Zhu, L. Ying, Y. Zhang and F. Liu, Adv. Energy Mater., 2020, 1904234 CrossRef CAS.
- A. Karki, J. Vollbrecht, A. L. Dixon, N. Schopp, M. Schrock, G. N. M. Reddy and T.-Q. Nguyen, Adv. Mater., 2019, 31, 1903868 CrossRef CAS.
- A. Karki, G.-J. A. H. Wetzelaer, G. N. M. Reddy, V. Nádaždy, M. Seifrid, F. Schauer, G. C. Bazan, B. F. Chmelka, P. W. M. Blom and T.-Q. Nguyen, Adv. Funct. Mater., 2019, 29, 1901109 CrossRef.
- J. A. Love, C. M. Proctor, J. Liu, C. J. Takacs, A. Sharenko, T. S. van der Poll, A. J. Heeger, G. C. Bazan and T.-Q. Nguyen, Adv. Funct. Mater., 2013, 23, 5019–5026 CrossRef CAS.
- N. A. Ran, S. Roland, J. A. Love, V. Savikhin, C. J. Takacs, Y.-T. Fu, H. Li, V. Coropceanu, X. Liu, J.-L. Brédas, G. C. Bazan, M. F. Toney, D. Neher and T.-Q. Nguyen, Nat. Commun., 2017, 8, 79 CrossRef.
- N. A. Ran, J. A. Love, M. C. Heiber, X. Jiao, M. P. Hughes, A. Karki, M. Wang, V. V. Brus, H. Wang, D. Neher, H. Ade, G. C. Bazan and T.-Q. Nguyen, Adv. Energy Mater., 2018, 8, 1701073 CrossRef.
- S. D. Collins, N. A. Ran, M. C. Heiber and T.-Q. Nguyen, Adv. Energy Mater., 2017, 7, 1602242 CrossRef.
- P. Zalar, M. Kuik, N. A. Ran, J. A. Love and T.-Q. Nguyen, Adv. Energy Mater., 2014, 4, 1400438 CrossRef.
- J. A. Love, I. Nagao, Y. Huang, M. Kuik, V. Gupta, C. J. Takacs, J. E. Coughlin, L. Qi, T. S. van der Poll, E. J. Kramer, A. J. Heeger, T.-Q. Nguyen and G. C. Bazan, J. Am. Chem. Soc., 2014, 136, 3597–3606 CrossRef CAS.
- B. A. Collins, Z. Li, J. R. Tumbleston, E. Gann, C. R. McNeill and H. Ade, Adv. Energy Mater., 2013, 3, 65–74 CrossRef CAS.
- E. Gann, A. T. Young, B. A. Collins, H. Yan, J. Nasiatka, H. A. Padmore, H. Ade, A. Hexemer and C. Wang, Rev. Sci. Instrum., 2012, 83, 045110 CrossRef CAS.
- W. Li, L. Yang, J. R. Tumbleston, L. Yan, H. Ade and W. You, Adv. Mater., 2014, 26, 4456–4462 CrossRef CAS.
- F. P. V. Koch, J. Rivnay, S. Foster, C. Müller, J. M. Downing, E. Buchaca-Domingo, P. Westacott, L. Yu, M. Yuan, M. Baklar, Z. Fei, C. Luscombe, M. A. McLachlan, M. Heeney, G. Rumbles, C. Silva, A. Salleo, J. Nelson, P. Smith and N. Stingelin, Prog. Polym. Sci., 2013, 38, 1978–1989 CrossRef CAS.
- M. J. Banach, R. H. Friend and H. Sirringhaus, Macromolecules, 2003, 36, 2838–2844 CrossRef CAS.
- C. Müller, E. Wang, L. M. Andersson, K. Tvingstedt, Y. Zhou, M. R. Andersson and O. Inganäs, Adv. Funct. Mater., 2010, 20, 2124–2131 CrossRef.
- T. Yasuda, H. Meguro, S. Okamoto and L. Han, Polym. J., 2013, 45, 129–132 CrossRef CAS.
- J. Subbiah, B. Purushothaman, M. Chen, T. Qin, M. Gao, D. Vak, F. H. Scholes, X. Chen, S. E. Watkins, G. J. Wilson, A. B. Holmes, W. W. H. Wong and D. J. Jones, Adv. Mater., 2015, 27, 702–705 CrossRef CAS.
- K. D. Rosenthal, M. P. Hughes, B. R. Luginbuhl, N. A. Ran, A. Karki, S.-J. Ko, H. Hu, M. Wang, H. Ade and T.-Q. Nguyen, Adv. Energy Mater., 2019, 9, 1901077 CrossRef.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2009, 131, 15777–15783 CrossRef CAS.
- X.-K. Chen, M. K. Ravva, H. Li, S. M. Ryno and J.-L. Brédas, Adv. Energy Mater., 2016, 6, 1601325 CrossRef.
- B. P. Rand, D. Cheyns, K. Vasseur, N. C. Giebink, S. Mothy, Y. Yi, V. Coropceanu, D. Beljonne, J. Cornil, J.-L. Brédas and J. Genoe, Adv. Funct. Mater., 2012, 22, 2987–2995 CrossRef CAS.
- H. Oberhofer and J. Blumberger, J. Chem. Phys., 2010, 133, 244105 CrossRef.
- B. Yang, Y. Yi, C.-R. Zhang, S. G. Aziz, V. Coropceanu and J.-L. Brédas, J. Phys. Chem. C, 2014, 118, 27648–27656 CrossRef CAS.
- M. R. Hansen, R. Graf and H. W. Spiess, Chem. Rev., 2016, 116, 1272–1308 CrossRef CAS.
- H. N. Tsao, D. M. Cho, I. Park, M. R. Hansen, A. Mavrinskiy, D. Y. Yoon, R. Graf, W. Pisula, H. W. Spiess and K. Müllen, J. Am. Chem. Soc., 2011, 133, 2605–2612 CrossRef CAS.
- N. C. Miller, E. Cho, M. J. N. Junk, R. Gysel, C. Risko, D. Kim, S. Sweetnam, C. E. Miller, L. J. Richter, R. J. Kline, M. Heeney, I. McCulloch, A. Amassian, D. Acevedo-Feliz, C. Knox, M. R. Hansen, D. Dudenko, B. F. Chmelka, M. F. Toney, J.-L. Brédas and M. D. McGehee, Adv. Mater., 2012, 24, 6071–6079 CrossRef CAS.
- K. R. Graham, C. Cabanetos, J. P. Jahnke, M. N. Idso, A. El Labban, G. O. Ngongang Ndjawa, T. Heumueller, K. Vandewal, A. Salleo, B. F. Chmelka, A. Amassian, P. M. Beaujuge and M. D. McGehee, J. Am. Chem. Soc., 2014, 136, 9608–9618 CrossRef CAS.
- C. K. Lo, B. R. Gautam, P. Selter, Z. Zheng, S. D. Oosterhout, I. Constantinou, R. Knitsch, R. M. W. Wolfe, X. Yi, J.-L. Brédas, F. So, M. F. Toney, V. Coropceanu, M. R. Hansen, K. Gundogdu and J. R. Reynolds, Chem. Mater., 2018, 30, 2995–3009 CrossRef CAS.
- S. R. Chaudhari, J. M. Griffin, K. Broch, A. Lesage, V. Lemaur, D. Dudenko, Y. Olivier, H. Sirringhaus, L. Emsley and C. P. Grey, Chem. Sci., 2017, 8, 3126–3136 RSC.
- B. Yurash, D. Leifert, G. N. M. Reddy, D. X. Cao, S. Biberger, V. V. Brus, M. Seifrid, P. J. Santiago, A. Köhler, B. F. Chmelka, G. C. Bazan and T.-Q. Nguyen, Chem. Mater., 2019, 31, 6715–6725 CrossRef CAS.
- D. Dudenko, A. Kiersnowski, J. Shu, W. Pisula, D. Sebastiani, H. W. Spiess and M. R. Hansen, Angew. Chem., Int. Ed., 2012, 51, 11068–11072 CrossRef CAS.
- A. Melnyk, M. J. N. Junk, M. D. McGehee, B. F. Chmelka, M. R. Hansen and D. Andrienko, J. Phys. Chem. Lett., 2017, 8, 4155–4160 CrossRef CAS.
- G. N. M. Reddy, A. Marsh, J. T. Davis, S. Masiero and S. P. Brown, Cryst. Growth Des., 2015, 15, 5945–5954 CrossRef CAS.
- M. T. Seifrid, G. N. M. Reddy, C. Zhou, B. F. Chmelka and G. C. Bazan, J. Am. Chem. Soc., 2019, 141, 5078–5082 CrossRef CAS.
- A. Luzio, F. Nübling, J. Martin, D. Fazzi, P. Selter, E. Gann, C. R. McNeill, M. Brinkmann, M. R. Hansen, N. Stingelin, M. Sommer and M. Caironi, Nat. Commun., 2019, 10, 1–13 CrossRef CAS.
- G. N. M. Reddy, A. Huqi, D. Iuga, S. Sakurai, A. Marsh, J. T. Davis, S. Masiero and S. P. Brown, Angew. Chem. Weinheim Bergstr. Ger., 2017, 23, 2315–2322 CAS.
- G. N. M. Reddy, R. Ballesteros-Garrido, J. Lacour and S. Caldarelli, Angew. Chem., Int. Ed., 2013, 52, 3255–3258 CrossRef.
- B. Elena, G. de Paëpe and L. Emsley, Chem. Phys. Lett., 2004, 398, 532–538 CrossRef CAS.
- D. Sakellariou, A. Lesage, P. Hodgkinson and L. Emsley, Chem. Phys. Lett., 2000, 319, 253–260 CrossRef CAS.
- M. Seifrid, G. N. M. Reddy, B. F. Chmelka and G. C. Bazan, Nat. Rev. Mater. DOI:10.1038/s41578-020-00232-5.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef.
- A. C. Jakowetz, M. L. Böhm, A. Sadhanala, S. Huettner, A. Rao and R. H. Friend, Nat. Mater., 2017, 16, 551–557 CrossRef CAS.
- M. Scarongella, J. De Jonghe-Risse, E. Buchaca-Domingo, M. Causa’, Z. Fei, M. Heeney, J.-E. Moser, N. Stingelin and N. Banerji, J. Am. Chem. Soc., 2015, 137, 2908–2918 CrossRef CAS.
- S. M. Menke, A. Cheminal, P. Conaghan, N. A. Ran, N. C. Greehnam, G. C. Bazan, T.-Q. Nguyen, A. Rao and R. H. Friend, Nat. Commun., 2018, 9, 277 CrossRef.
- D. Wróbel and A. Graja, Coord. Chem. Rev., 2011, 255, 2555–2577 CrossRef.
- S. R. Scully, P. B. Armstrong, C. Edder, J. M. J. Fréchet and M. D. McGehee, Adv. Mater., 2007, 19, 2961–2966 CrossRef CAS.
- Y. Zhong, M. Causa’, G. J. Moore, P. Krauspe, B. Xiao, F. Günther, J. Kublitski, R. Shivhare, J. Benduhn, E. BarOr, S. Mukherjee, K. M. Yallum, J. Réhault, S. C. B. Mannsfeld, D. Neher, L. J. Richter, D. M. DeLongchamp, F. Ortmann, K. Vandewal, E. Zhou and N. Banerji, Nat. Commun., 2020, 11, 833 CrossRef CAS.
- C. Sun, S. Qin, R. Wang, S. Chen, F. Pan, B. Qiu, Z. Shang, L. Meng, C. Zhang, M. Xiao, C. Yang and Y. Li, J. Am. Chem. Soc., 2020, 142, 1465–1474 CrossRef CAS.
- L. Xue, Y. Yang, J. Xu, C. Zhang, H. Bin, Z.-G. Zhang, B. Qiu, X. Li, C. Sun, L. Gao, J. Yao, X. Chen, Y. Yang, M. Xiao and Y. Li, Adv. Mater., 2017, 29, 1703344 CrossRef.
- Y. Liu, L. Zuo, X. Shi, A. K.-Y. Jen and D. S. Ginger, ACS Energy Lett., 2018, 3, 2396–2403 CrossRef CAS.
- J. Vollbrecht, V. V. Brus, S.-J. Ko, J. Lee, A. Karki, D. X. Cao, K. Cho, G. C. Bazan and T.-Q. Nguyen, Adv. Energy Mater., 2019, 9, 1901438 CrossRef.
- A. Karki, J. Vollbrecht, A. J. Gillett, P. Selter, J. Lee, Z. Peng, N. Schopp, A. L. Dixon, M. Schrock, V. Nadáždy, F. Schauer, H. Ade, B. F. Chmelka, G. C. Bazan, R. H. Friend and T.-Q. Nguyen, Adv. Energy Mater., 2020, 10, 2001203 CrossRef CAS.
- J. Vollbrecht, C. Wiebeler, H. Bock, S. Schumacher and H.-S. Kitzerow, J. Phys. Chem. C, 2019, 123, 4483–4492 CrossRef CAS.
- C. M. Proctor, M. Kuik and T.-Q. Nguyen, Prog. Polym. Sci., 2013, 38, 1941–1960 CrossRef CAS.
- L. J. A. Koster, V. D. Mihailetchi, R. Ramaker and P. W. M. Blom, Appl. Phys. Lett., 2005, 86, 123509 CrossRef.
- M. M. Mandoc, F. B. Kooistra, J. C. Hummelen, B. de Boer and P. W. M. Blom, Appl. Phys. Lett., 2007, 91, 263505 CrossRef.
- V. V. Brus, Org. Electron., 2016, 29, 1–6 CrossRef CAS.
- V. V. Brus, C. M. Proctor, N. A. Ran and T.-Q. Nguyen, Adv. Energy Mater., 2016, 6, 1502250 CrossRef.
- I. Zonno, H. Zayani, M. Grzeslo, B. Krogmeier and T. Kirchartz, Phys. Rev. Appl., 2019, 11, 054024 CrossRef CAS.
- C. M. Proctor, C. Kim, D. Neher and T.-Q. Nguyen, Adv. Funct. Mater., 2013, 23, 3584–3594 CrossRef CAS.
- M. C. Heiber, T. Okubo, S.-J. Ko, B. R. Luginbuhl, N. A. Ran, M. Wang, H. Wang, M. A. Uddin, H. Y. Woo, G. C. Bazan and T.-Q. Nguyen, Energy Environ. Sci., 2018, 11, 3019–3032 RSC.
- S. Albrecht, J. R. Tumbleston, S. Janietz, I. Dumsch, S. Allard, U. Scherf, H. Ade and D. Neher, J. Phys. Chem. Lett., 2014, 5, 1131–1138 CrossRef CAS.
- D. Bartesaghi, I. del, C. Pérez, J. Kniepert, S. Roland, M. Turbiez, D. Neher and L. J. A. Koster, Nat. Commun., 2015, 6, 7083 CrossRef CAS.
- R. J. Kline, M. D. McGehee, E. N. Kadnikova, J. Liu and J. M. J. Fréchet, Adv. Mater., 2003, 15, 1519–1522 CrossRef CAS.
- R. J. Kline, M. D. McGehee, E. N. Kadnikova, J. Liu, J. M. J. Fréchet and M. F. Toney, Macromolecules, 2005, 38, 3312–3319 CrossRef CAS.
- D. Spoltore, W. D. Oosterbaan, S. Khelifi, J. N. Clifford, A. Viterisi, E. Palomares, M. Burgelman, L. Lutsen, D. Vanderzande and J. Manca, Adv. Energy Mater., 2013, 3, 466–471 CrossRef CAS.
- A. Zen, J. Pflaum, S. Hirschmann, W. Zhuang, F. Jaiser, U. Asawapirom, J. P. Rabe, U. Scherf and D. Neher, Adv. Funct. Mater., 2004, 14, 757–764 CrossRef CAS.
- S. A. Mollinger, A. Salleo and A. J. Spakowitz, ACS Cent. Sci., 2016, 2, 910–915 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee01896a |
| This journal is © The Royal Society of Chemistry 2020 |