Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatial dynamics of lithiation and lithium plating during high-rate operation of graphite electrodes†
Donal P.
Finegan
 *a,
Alexander
Quinn
*a,
Alexander
Quinn
 a,
David S.
Wragg
a,
David S.
Wragg
 b,
Andrew M.
Colclasure
b,
Andrew M.
Colclasure
 a,
Xuekun
Lu
cd,
Chun
Tan
a,
Xuekun
Lu
cd,
Chun
Tan
 cd,
Thomas M. M.
Heenan
cd,
Thomas M. M.
Heenan
 cd,
Rhodri
Jervis
cd,
Rhodri
Jervis
 cd,
Dan J. L.
Brett
cd,
Dan J. L.
Brett
 cd,
Supratim
Das
cd,
Supratim
Das
 e,
Tao
Gao
e,
Daniel A.
Cogswell
e,
Tao
Gao
e,
Daniel A.
Cogswell
 e,
Martin Z.
Bazant
e,
Martin Z.
Bazant
 e,
Marco
Di Michiel
e,
Marco
Di Michiel
 f,
Stefano
Checchia
g,
Paul R.
Shearing
f,
Stefano
Checchia
g,
Paul R.
Shearing
 cd and
Kandler
Smith
cd and
Kandler
Smith
 a
a
aNational Renewable Energy Laboratory, 15013 Denver W Parkway, Golden, CO 80401, USA. E-mail: donal.finegan@nrel.gov
bCentre for Materials and Nanotechnology, University of Oslo, 0315 Oslo, Norway
cElectrochemical Innovation Laboratory, Department of Chemical Engineering, University College London, London, WC1E 7JE, UK
dThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot, OX11 0RA, UK
eDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
fESRF-The European Synchrotron, 71 Avenue des Martyrs, 38000 Grenoble, France
gMAX IV Laboratory, University of Lund, Lund, Sweden
First published on 8th July 2020
Abstract
The principal inhibitor of fast charging lithium ion cells is the graphite negative electrode, where favorable conditions for lithium plating occur at high charge rates, causing accelerated degradation and safety concerns. The local response of graphite, both at the electrode and particle level, when exposed to fast charging conditions of around 6C is not well understood. Consequently, the conditions that lead to the onset of lithium plating, as well as the local dynamics of lithium plating and stripping, have also remained elusive. Here, we use high-speed (100 Hz) pencil-beam X-ray diffraction to repeatedly raster along the depth of a 101 μm thick graphite electrode in 3 μm steps during fast (up to 6C) charge and discharge conditions. Consecutive depth profiles from separator to current collector were each captured in 0.5 seconds, giving an unprecedented spatial and temporal description of the state of the electrode and graphite's staging dynamics during high rate conditions. The electrode is preferentially activated near the separator, and the non-uniformity increases with rate and is influenced by free-energy barriers between graphite's lithiation stages. The onset of lithium plating and stripping was quantified, occurring only within the first 15 μm from the separator. The presence of lithium plating changed the behavior of the underlying graphite, such as causing co-existence of LiC6 and graphite in the fully discharged state. Finally, the staging behavior of graphite at different rates was quantified, revealing a high dependency on rate and drastic hysteresis between lithiation and delithiation.
Broader contextFast charging of electric vehicles (EVs) to achieve full charge within 15 minutes is recognized as a critical capability for their widespread uptake. Yet, fast charging the high energy density lithium ion batteries used in EVs leads to accelerated degradation and increased risk of failure. These undesirable outcomes are primarily due to lithium plating on the graphite negative electrode during fast charging, which is the foremost limitation that is preventing EVs from charging at a rate that is competitive with refueling a combustion engine vehicle. This work focuses on understanding the conditions that lead to lithium plating on graphite. Using high speed synchrotron X-ray diffraction, real-time depth profiles of the graphite's lithiation stages are quantified during 6C charge (full charge in 10 minutes) at ambient temperature. The onset of lithium plating on the graphite is followed and can be linked to the state of the underlying graphite, facilitating a direct link between local operating conditions and the propensity of certain regions to undergo lithium plating. This clarifies the challenges faced by current high energy density electrodes and provides real-time data for guiding and validating electrochemical and multi-physics models for predicting lithium plating. |
Introduction
High energy density lithium (Li)-ion cells with high-rate capability are recognized as a necessity for widespread uptake of electric vehicles.1 The ability to charge an electric vehicle quickly, to 80% state of charge (SOC) in 10 minutes, is commonly cited as an important milestone to achieve before their widespread uptake,2,3 along with energy densities of >250 W h kg−1 and discharge power densities of >400 W kg−1 at the cell level. One promising approach to increase the energy density of Li-ion cells while using conventional cost-effective electrode materials, such as graphite and transition metal oxides, is to increase the ratio of active to inactive materials within the cell, hence manufacturing thicker electrodes relative to inactive components such as the current collector and separator. However, thick electrodes are counterproductive to improving rate capability as they impose transport limitations that deplete Li ions in the electrolyte nearer the current collector, requiring increased potential to charge the cell, especially at higher C-rates.4–6When concentration gradients in the electrolyte become increasingly severe during fast charging, particles near the separator experience higher local current densities than those near the current collector.5–8 This can lead to solid-state transport limitations within the graphite near the separator, particularly during the charging step (i.e. graphite lithiation). However, it is stressed that insufficient ionic conductivity of the electrolyte is what can cause such unfavorably high localized current densities, and tackling this challenge may be key to facilitating fast charging of thick electrodes. With regard to solid-state transport, Li+ moves mostly along the planar graphene layers within graphite, with minimal transport in the through-plane direction.9 As Li inserts into graphite, a staging sequence takes place, where the Li fills layers between graphene planes, giving rise to the naming convention of stages that describes the average number of graphene layers between each Li layer; for example, Stage I corresponds to the fully lithiated LiC6 with one plane of graphene between each Li plane, and Stage II corresponds to LiC12 with two graphene planes between each Li plane. There is still some uncertainty about the structures that occur between LiC12 and graphite; for example, Senychyn et al.10 characterized 4 phases during lithiation and 7 phases during delithiation, indicating hysteresis between charge and discharge.11,12 The stages of graphite are free energy minima, causing phase-separation within the graphite as it is lithiated and delithiated.
Each state of graphite has a unique color13 which has facilitated optical experiments that confirm co-existence of stages within and between distinct graphite particles, even after long periods of open-circuit.13–15 Classical intercalation models requiring application of diffusion coefficients16,17 do not capture equilibrium between phases, but phase-field models do, and have recently been experimentally validated at low current densities.13,14,18,19 During fast charging, where solid-state transport limitations can become significant, intercalation reaction kinetics and local transport are strongly influenced by the concentration of Li within the host graphite.13 These effects further complicate the modelling of high-rate conditions.
High rate lithiation of graphite is also conducive to Li plating where a lithium ion is reduced on the surface of the graphite rather than intercalated, which can lead to rapid degradation through side reactions with the electrolyte,20 the products of which can further inhibit transport.21 Unlike during delithiation where there are favorable conditions enabling the application of high overpotentials to drive high currents,22 during lithiation the applied overpotential is limited to going below the Li/Li+ potential, beyond which Li is likely to plate rather than intercalate.22,23 During high C-rates, polarization from Ohmic and transport limitations can become severe, leading to the surface potential falling well below the equilibrium potential of 0 V vs. Li/Li+, resulting in a large overpotential for the plating reaction.5,6,20 The rate and location of Li plating in graphite electrodes is not well understood, and the behavior of plated Li remains uncertain. This uncertainty stems from the challenging nature of capturing and quantifying the spatial dynamics of Li plating. Dismantling the cell to measure plated Li can lead to erroneous interpretations of Li plating because the system continues to be electrochemically, as well as chemically, active after operation is stopped and during the disassembly process.24 Hence, a non-destructive operando approach to quantifying Li is needed.
Li plating has previously been detected in situ and operando using a range of techniques including visual observations,14,15,24 neutron diffraction,5,25–27 nuclear magnetic resonance (NMR),21 and electron paramagnetic resonance (EPR).28 Electrochemical techniques such as monitoring voltage relaxation25 and voltage plateaus29 are also used, but are not yet quantitative nor fully reliable due to challenges in decoupling reversible and irreversible Li plating, as well as heating effects on the cells electrochemistry at high rates.30,31 Most operando studies to date have been carried out at low temperature (around 0 °C) where kinetics are slow and operando techniques that take tens of seconds to minutes, can be used to record the dynamic SOC and plating or stripping of Li.26 To date, no operando method has quantified the spatial dynamics of heterogenous lithiation and Li plating under fast charge conditions and temperatures between 20 °C and 50 °C.32 A deep understanding of the behavior of graphite when exposed to high current densities is yet to be achieved, and a detailed description of SOC heterogeneities, conditions necessary for the onset of Li plating, the spatial dynamics of Li plating, and the impact of Li plating on the performance of the cell is needed to help guide the design of electrode materials, electrolytes, and architectures to facilitate extreme fast charging conditions.
Here, high-speed depth-profiling synchrotron X-ray diffraction (XRD) is used to spatially describe lithiation and Li plating dynamics as a function of depth and time under extreme fast charge and discharge conditions of up to 6C (full charge in 10 min) in a thick (101 μm) graphite electrode. The high-energy X-ray source of the ESRF – The European Synchrotron – facilitated carrying out this experiment while the cell was housed in a standard coin-cell format, thus avoiding common concerns of bespoke operando-cell designs negatively affecting the cell's behavior, such as poor or uneven compression and high contact and ionic resistances.33 With a depth resolution of 3 μm and time resolution of 0.5 s per whole electrode scan, the state of lithiation, concurrent fractions of graphite's lithiation stages, and Li plating and stripping, are quantified. This provides the first spatial and temporal description of depth-heterogeneities of Li plating, current densities, and SOC during fast charge and discharge conditions at both 6C and 2C. In addition to quantifying the physical state of the system with time, we also describe the rate of change of the system with respect to the rates of change of the distinct lithiation stages of graphite, establishing a direct link between Li plating and local physical and dynamic state of the graphite. This work provides insight into the limitations of commercial electrode designs for fast charging and highlights graphite behavior that is currently not captured in most multi-physics modelling approaches. It is expected that the results presented here will help guide the design of high-energy density and high-rate electrodes, as well as the development of computational modelling methods that accurately simulate fast charge behavior.
Results and discussion
The impact of electrode thickness and rate
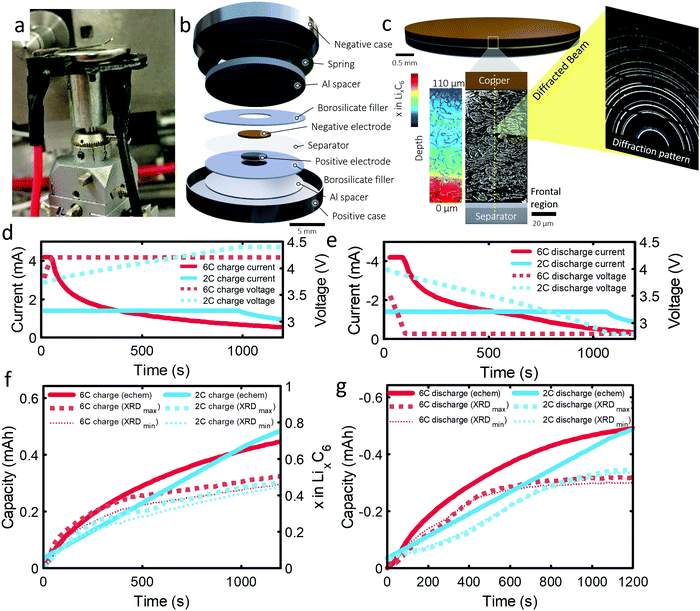
The 101 μm negative electrode was tested in a CR2032 coin-cell (Section S6, ESI†). Capacity analyses and post-mortem photographs in ESI† showed that for increasing rate and thickness of electrode, increasingly severe capacity fade and Li plating occurred. It is suspected that increasingly severe lithiation gradients and heterogeneous exchange current densities for higher rates and thicker electrodes lead to Li plating and capacity fade. The following experiment was designed to confirm this hypothesis and quantify lithium concentration gradients and Li plating/stripping during operation. As the 101 μm electrode displayed the greatest degradation and is the most desired electrode to function effectively under fast charge conditions, due to its high energy density, this work was focused entirely on it. An illustration of the cell design and XRD depth profiling overview is shown in Fig. 1(a–c). The cell was cycled several times, as discussed in the methods section. The first 6C cycle and final 2C cycle will be discussed and compared in this work, for which the current and capacity profiles are provided in Fig. 1(d–g). Electrochemical data on the other cycles are provided in Section S1 (ESI†). The constant current portion of the 6C charge and discharge lasted for about 40 s and for about 1000 s at 2C. We highlight that the cut-off voltage for the 6C step was 4.2 V and for 2C step was increased to 4.4 V. This was to increase the likelihood of Li plating as well as to prolong the constant current step for model validation.As graphite lithiates, distinct Bragg peaks appear in the diffraction pattern. A video showing the shift of peaks in q (scattering vector length) as a function of depth and time is provided as Movie S1 (ESI†). 2-Dimensional XRD data were azimuthally integrated and the stages of graphite lithiation were quantified. At room temperature and in an equilibrated state, Stage III corresponds to a composition of around ca. LiC30,34 stage II and IIL correspond to ca. LiC12 and LiC18,35 and Stage I to LiC6. Multiple phase compositions have been recorded between Stage II and graphite, including Stage III, but are challenging to characterize due to the weak splitting of Bragg peaks.10 For this work, everything between Stage II and graphite was considered to be Stage III, but as a best estimate of its exact composition the lithium contribution from Stage III was set to be linear with the d-spacing, where the limits were such that a c-axis spacing of 6.5 Å corresponded to LiC30 and a c-axis spacing of 7.05 Å corresponded to LiC12; further detail is provided in the Experimental section and ESI.† The estimation of LixC6 in Fig. 1f, and in the rest of this manuscript, was determined by summing the Li content from the measured stages of lithiation. Decoupling Stages II and IIL was not possible due to characteristic diffraction intensity peaks being obscured by peaks from the steel casing and, since we could not distinguish Stage II from IIL, the exact composition of this stage may lie between LiC12 and LiC18. A sensitivity analysis was performed in Fig. 1f and g, where we assumed Stage II/IIL consisted of either entirely LiC12 (large dotted lines labelled XRDmax) or entirely LiC18 (small dotted lines labelled XRDmin), where it was found that LixC6 was sensitive to the composition of Stage II/IIL at the beginning of the charge step, but not very sensitive to the value overall. For the remainder of the manuscript Stage II/IIL was assigned a composition of LiC12. Furthermore, using the graphite lithiation data the current was estimated and correlated reasonably well with the potentiostat current (see Section S5, ESI†) but showed a consistently lower value which indicates that some unfavorable phenomena may have been occurring during operation, such as parasitic side reactions, capacitive effects,36 undetected Li-plating, or Li-dendrites in the separator. There was a notable divergence from the potentiostat data at the beginning of the 6C discharge, which is discussed further later in the manuscript.
State of charge and phase heterogeneities
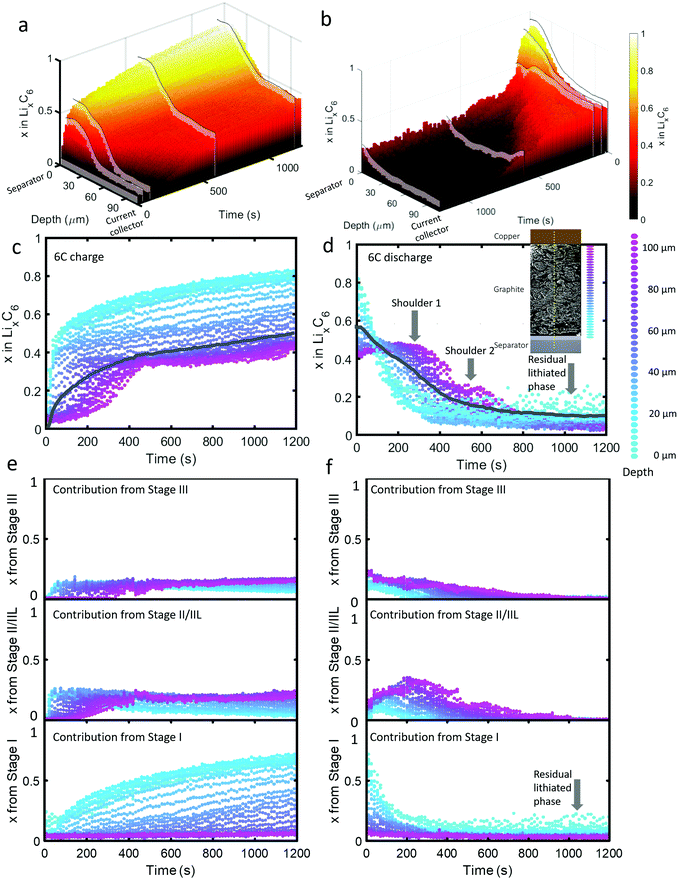 | ||
| Fig. 2 (a) 3D plot of LixC6 as a function of time and depth during 6C charge and (b) 6C discharge. Constant current operation lasted for about 40 s during charge and about 100 s during discharge, and was followed by constant voltage. Videos S2 and S3 (ESI†) show the time-resolved phase fractions as a function of depth for (a) and (b). (c and d) Scatter plots of XRD point measurements, color-coded by depth, showing LixC6 for 6C charge and discharge, and (e and f) the contributions from the individual lithiation stages to the overall value of LixC6. Inset of (d): Illustration showing the depths to which colors correspond. The grey lines in (c) and (d) represent the average x in LixC6 across all depths. The graphite electrode area was 0.12 cm2 and its capacity was ca. 0.68 mA h. | ||
As seen in Fig. 2(c), during the first 50 s of the 6C charge step, most of the intercalation occurred near the separator. The lithiation state near the frontal region reached x ≈ 0.6 before regions beyond 60 μm deep showed any change, indicating a rapid onset of severe polarization. In Fig. 2(e), the contribution to LixC6 from the individual stages is presented, i.e. the sum of x from Stage I, x from Stage II/IIL, and x from Stage III is equal to x from LixC6. Initially (<10 s), Stage I quickly formed near the separator without a major contribution from Stage II/IIL and Stage III. With small quantities of Stage I established near the separator, further local lithiation diminished and shifted closer to the current collector forming Stage II/IIL/III. After about 100 s, the region closest to the current collector began to transition from graphite into Stage II/IIL and Stage III, and lithiated until about 500 s before reaching a plateau. Beyond 500 s, only the region closest to the separator underwent any significant change, all of which included transitioning from Stage II/IIL to Stage I, while the material near the current collector became inactive.
For the 6C discharge step the concentration profile in Fig. 2(d) showed two unexpected features: first, two delithiation shoulders appeared for depths greater than about 60 μm (labelled “Shoulder 1” and “Shoulder 2”), and second, the region between 0 μm and 20 μm did not fully delithiate (labelled as “Residual lithiated phase”). Investigating the cause of Shoulder 1 by exploring the contribution to LixC6 from the distinct stages in Fig. 2(f) shows that at depths >60 μm, the quantity of Stage II/IIL increased while Stage III decreased for the first 300 s, and is then followed by a decrease of both. The opposite but equal moles of Li changes in Stage II/IIL and Stage III lead to an overall plateau in layer average x at those depths. As for why Stage II/IIL increased, this will be explored in more detail in the section on ‘Local rates of change and estimating current densities’.
Fig. 2(f) can provide further insight into the residual Li feature observed for the first 15 μm from the separator upon discharge. All of the Li that was contributing to a non-zero layer-average value of x at the end of discharge in Fig. 2(d) took the form of the fully lithiated Stage I. This indicates that for the first 15 μm, solely Stage I and graphite existed at the end of the delithiation step. Because the XRD measurements included signal from many particles along the line of sight, we cannot definitively know whether the two phases existed within particles (phase co-existence) or between particles. As seen in a later section on Li plating quantification, Li plating occurred at exactly the depths where this behavior happened, hence the two phenomena are likely to be linked. It is difficult to understand why Stage I graphite always exists in the frontal region in contact with the plated lithium, even at the end of the discharge step. We can speculate that thick SEI growth on the plated lithium prevented complete dissolution during the delithiation step, as under delithiation the SEI becomes a very poor conductor of ions and electrons.37 It might also be possible that residual lithium may have directly lithiated the grains of graphite in contact with the lithium interface.
Due to the potential difference that existed between LiC6 and graphite, it's unlikely that the two phases existed solely between well-connected particles, i.e. 100% of one particle was LiC6 and 100% of a neighboring particle was graphite. The most likely explanation is that the Li plating on particles lithiated the frontal region of the graphite while the core of the particles consisted of delithiated graphite. Phase co-existence within a single crystal of graphite has been observed previously13,14 but only phase co-existence of LiC12 with graphite, or LiC12 with LiC6, has been detected. However, phase co-existence within Li plated particles or phase co-existence during extreme fast charging conditions has not been extensively explored. The consequences of co-existence of Stage I with graphite on the kinetics of subsequent charge/discharge steps are expected to be significant because the lithiation kinetics vary greatly with the Li occupancy of graphite at and near the edge plane; for example, some occupancy of sites improves lithiation kinetics by helping separate the layers for transference of Li.
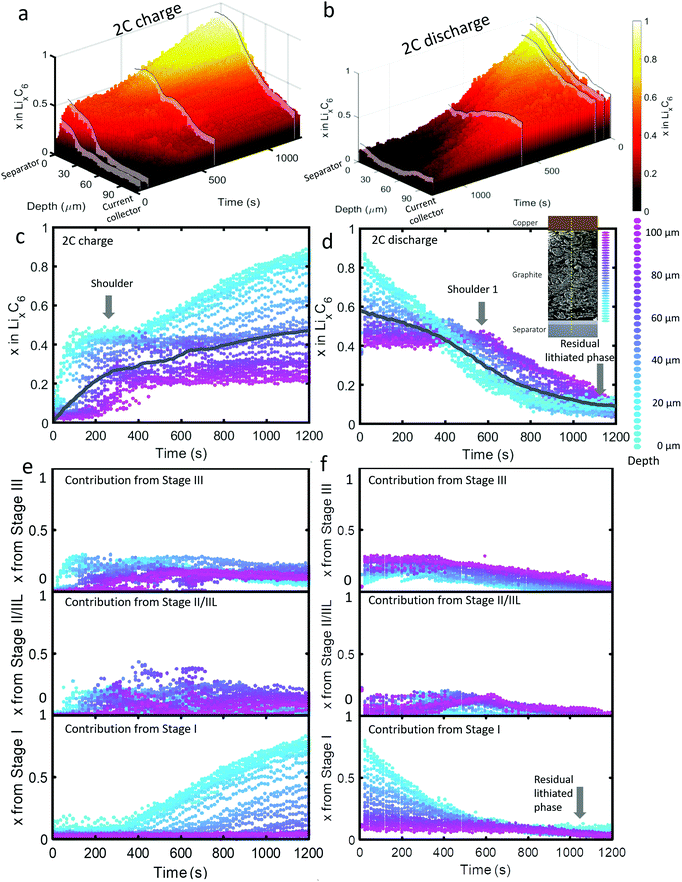 | ||
| Fig. 3 (a) 3D plot showing LixC6 value as a function of time and depth during 2C charge and (b) 2C discharge. Constant current operation lasted for about 1000 s during charge, and 1100 s during discharge, which was followed by constant voltage. Videos S4 and S5 (ESI†) show the time-resolved phase fractions as a function of depth for (a) and (b). (c and d) Scatter plots of XRD point measurements, color-coded by depth, showing LixC6 and (e and f) the contributions from the individual lithiation stages to the overall value of LixC6. Inset of (d): Illustration showing the depths to which colors correspond. The grey lines in (c) and (d) represent the average x in LixC6 across all depths. | ||
The dynamics of phase transitions greatly differed between 2C and 6C as seen in Fig. 3(c–f). During 2C charge, a shoulder in the x in LixC6 plot in Fig. 3(c) occurred, where the lithiation of the 50 μm closest to the separator reached a plateau at x ≈ 0.5. The composition at this plateau mostly consisted of Stage II/IIL and Stage III, as shown in Fig. 3(e). Upon reaching these phases, the lithiation appeared to have stopped near the frontal region, and proceeded to deeper regions for about 200 s, thereafter returning to the frontal region to complete the lithiation from Stage II/IIL to Stage I, as seen from the Stage I plot in Fig. 3(e).
This switch in depth of lithiation, from lithiating the frontal region to a deeper region, and then back to the frontal region, was related to a free energy barrier associated with the transition from Stage II to Stage I where the overpotential necessary to overcome this barrier was not achieved temporarily at the frontal region.18 Instead, deeper regions were lithiated, and when the applied overpotential further increased and the deeper regions became more lithiated, the frontal region became thermodynamically favorable for lithiation to Stage I. This did not occur for the case of 6C operation, which may be due to the applied potential being higher and sufficient to overcome the free energy barrier required for the transition from Stage II to Stage I to occur at the frontal region. This phenomenon highlights the importance of including Gibbs free energy paths necessary to reach certain lithiation stages in models, paths that are mostly non-linear and can involve overcoming barriers necessary to transition from one phase to another. As an example of how standard Newman models do not capture some of the features observed in the XRD data, a direct comparison between a Newman model prediction and the XRD data is provided in Section S8 (ESI†).
Upon discharge, a rapid delithiation of the region close to the separator occurred which mostly consisted of the transition from Stage I to Stage II/IIL and Stage III, as observed in Fig. 3(f). The deeper regions near the current collector were inactive for the first 400 s as the delithiation front progressed from the separator deeper into the electrode. It was only after about 500 s that significant change in the concentration of the electrode close to the current collector occurred, a phenomenon observed even at 2C discharge. Similar to the 6C discharge, but to a lesser extent, some residual lithium was present at the region close to the separator at the end of 2C discharge which consisted of Stage I, as seen in Fig. 3(f). In addition, a slight increase in the amount of Stage II/IIL near the current collector was observed at 400–600 s.
Time-resolved spatial quantification of Li-plating
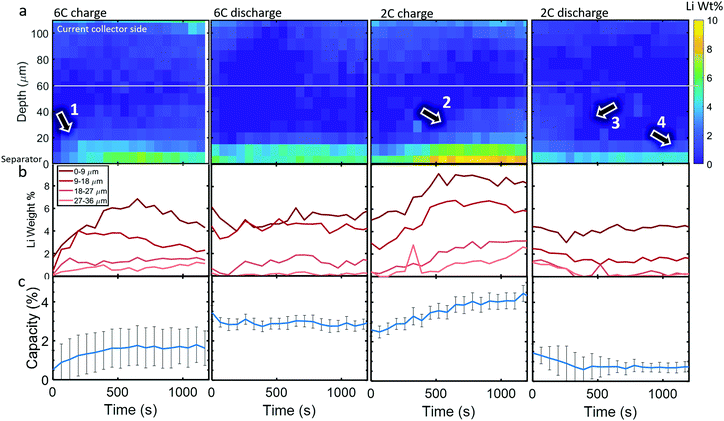
Li metal was detected (as the diffraction pattern of metallic Li) within the cell upon the first 6C charge step. The diffraction signal was weak so, to reduce the impact of noise, the data was binned for 3 depth and 5 time points, hence a spatial resolution of 9 μm and a temporal resolution of 65 s (for the whole electrode due to there being 13 s between each line-scan), to improve the signal for quantitative measurements. In Fig. 4a, colormaps of Li weight percent (wt%) are presented, for which the corresponding error maps are provided in Section S7 (ESI†) and show that the error was around 1 wt% for all points. The XRD signal became increasingly noisy at regions approaching the current collector, where peak fitting was not reliable. Hence, for quantifying the total Li mass and its corresponding capacity, only the regions below the white line in Fig. 4a were considered.During the 6C charge step, up to about 7 wt% of Li was quantified at the frontal region which increased (plated) for the first 700 s as indicated by arrow 1, and then decreased (stripped) to about 4 wt% from 700 s to 1200 s as seen in Fig. 4b. As expected, Li plating occurred mostly near the separator due to the reaction gradients previously observed, where particles near the separator were exposed to much higher current densities and overpotentials than those near the current collector. Significant Li plating was only observed within the first 20 μm from the separator, the sum of which amounted to around 1–2% of the total capacity of the graphite electrode (Fig. 4c). The increase and decrease of Li at the frontal region for 6C charge in Fig. 4b indicates that even though the graphite electrode was still being lithiated, the rate of stripping eventually exceeded the rate of plating during the lower currents of the constant voltage step. Li plating and stripping have been observed before26,28 and it has been predicted that as Li plates it concurrently strips from both the outer (electrolyte side) and inner (graphite side) interfaces;39 inner stripping further lithiates its host graphite, and outer stripping lithiates other particles via the electrolyte.26 This demonstrates that, even with in situ techniques, quantifying Li plating immediately after operation, i.e. during the relaxation period,25,39 may not capture the full picture of plating, since both plating and stripping were likely to have occurred during the charging process itself. Since current was still being applied, we could not decouple graphite lithiation that stemmed from Li stripping and lithiation that stemmed from normal operation, i.e. from the positive electrode. However, as seen previously, after 400 s most lithiation occurred at depths <40 μm with increased intercalation closest to the separator. This would be consistent with the regions of influence of Li plating where the plated regions (<20 μm) would lithiate fastest due to inner stripping, and neighboring regions (20–40 μm) would lithiate from outer stripping via the electrolyte, or via Li in the electrolyte sourced from the positive electrode.
A full cycle occurred between the 6C charge and discharge step shown in Fig. 4, hence the discontinuity between the quantities of Li plating. However, during 6C discharge, little change in the Li plating occurred, perhaps indicating that the reversible portion of Li plating had stripped before the discharge step initiated, where the residual Li plating was inactive and thus it's quantity not changing.40 During the 2C charge, plating became increasingly severe, reaching about 4% of the electrode's capacity and as the charge step continued to 500 s the Li plating reached deeper into the electrode, as indicated by arrow 2, while the frontal regions plateaued. During the 2C discharge step, the Li plating at regions >20 μm decreased (arrow 3 in Fig. 4a), while the frontal regions remained almost constant (arrow 4), further indicating that there may have been irreversible Li plating near the separator.
Local rates of change and estimating current densities
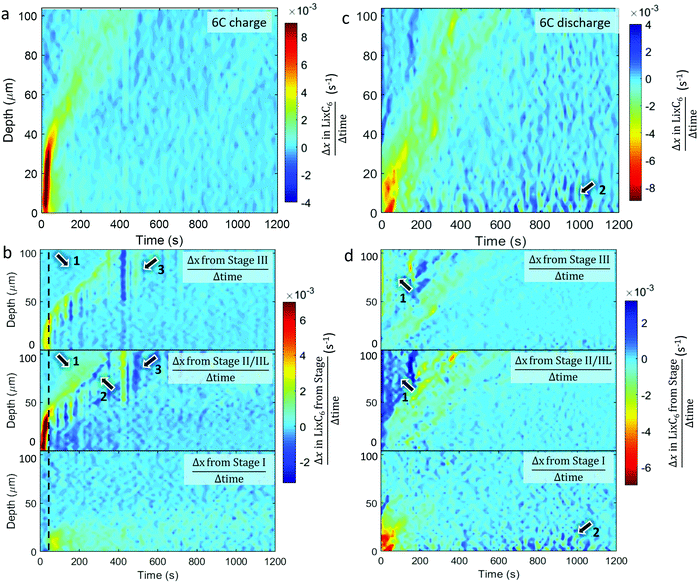
The spatial dynamics of composition and phase transitions during 6C and 2C rates were quantified by measuring the overall rate of lithiation (Δx in LixC6 divided by Δtime) as shown in Fig. 5 and 6. The respective rates of change of the distinct stages were also quantified and are presented in the form of Δx in LixC6 from the change in the quantity of a particular stage; that is to say, the sum of Δx from Stage I, Δx from Stage II/IIL, and the Δx from Stage III, equals the overall Δx in LixC6. The color bars in Fig. 5 and 6 were set such that any change opposite in direction to the overall change (e.g. negative Δx during lithiation and positive Δx during delithiation) appears dark blue.Comparing the plots for 6C and 2C shows that the spatial dynamics of lithiation and delithiation were very different. During 6C charge, a higher rate of change occurred compared to the discharge (Fig. 5a and c). Exploring the phases involved in this high rate of change in Fig. 5b shows that all of that change consisted of forming Stages II/IIL and III, without any observed change in Stage I. It was only when the rate of formation of Stage II/IIL began to decline, did the change of Stage I increase, as seen around the dashed black line in Fig. 5b. This was likely related to the physical phenomena that caused the shoulder in Fig. 3(c) where the potential difference needed to overcome the free energy barrier necessary to transition from Stage II to Stage I wasn’t achieved until well into the 2C charge step. For the 6C charge step, activation of the transition to Stage I was much sooner due to the necessary overpotential being reached much sooner, and the delayed transition from Stage II to Stage I was not observable by simply looking at the values of LixC6 in its counterpart 6C plot in Fig. 2(c).
During the 6C charge, there were also unexpected exchanges between Stages II/IIL and III at depths >40 μm, as pointed out in Fig. 5b. Close inspection of the Stage II/IIL and Stage III plots in Fig. 5b shows that a significant increase of Stage II/IIL occurred before Stage III as pointed out by arrows 1, despite Stage III being the logical first step upon lithiation. It's possible that Stage III did not exist due to the system being in a non-equilibrium state, or perhaps its fleeting presence was missed due to an insufficient temporal resolution of measurement. At 6C there was a high Li injection flux, and although the transport of Li in graphite and Stage III is expected to be fast,13 it may not have been fast enough to evenly distribute the Li. A front consisting of a phase boundary of Stage II/IIL and graphite may have formed, bypassing Stage III. This front eventually homogenized, causing a decrease in diffraction signal from Stage II/IIL and an increase in signal from Stage III, as observed and indicated by arrow 2 in Fig. 5b where a negative change (dark blue) of Stage II/IIL is seen with concurrent positive change of Stage III. The relaxation from Stage II/IIL to Stage III within a bulk electrode has previously been seen with neutron imaging27 and is thermodynamically favored. At depths from 50 μm to 100 μm at around 400 s in Fig. 5b, there was also a sudden transition from Stage III to Stage II/IIL followed by a relatively slight reversal as indicated by arrow 3. It is unclear whether this feature is related to the normal operation of a cell, but rather it might have been caused by an anomalous occurrence such as a gas pocket shifting and exposing more surface area of graphite for lithiation.
During the 6C discharge, the peak rate of local change of LixC6 was significantly lower than during charge, as seen in Fig. 5c. It is also notable that during 6C discharge the total current calculated from the graphite lithiation states was significantly lower than the potentiostat data for the first 200 s (see Section S5, ESI†). A large overpotential was applied during the first 200 s to draw the high current, and due to high-transport resistance caused by the relatively low diffusion coefficient of graphite in its LiC6 stage,41 it may have been more favorable to draw electrons from corrosion or other side reactions within the cell during this time rather than from the graphite. In general, for each depth, there was also a longer window of time in which the system was changing, indicating hysteresis. At depths of <50 μm over the first 100 s, most delithiation was associated with a decreasing presence of Stage I, as seen in Fig. 5d. A corresponding increase in lower lithiation states, as Stage I gives to II/IIL and III, was not strongly observed and is perhaps indicative of a rapid transition from Stage I to graphite of the frontal regions during the 6C constant current discharge. Within the first 200 s at depths >50 μm, an increase in Stage II/IIL and corresponding decrease in Stage III occurred as pointed out by arrows 1. This was unexpected because the material at those depths appeared to be lithiating rather than delithiating. A possible explanation for this is that the electrode was increasing in temperature due to ohmic heating from concurrent flow of electrons from delithiation of material near the separator. Extensive heating is a well-known occurrence during high rate operation with internal temperatures of commercial cells sometimes exceeding 50 °C.30,42 At elevated temperatures, it is more thermodynamically favored for concentrations close to LiC12 to take on a crystal structure akin to Stage II,18,23 hence with increasing temperature Stage III regions might have transitioned to the Stage II structure without any change in Li concentration. Furthermore, such heating may have improved transport in both the solid and liquid phases, accelerated equilibration of phases throughout the electrode,27 and helped reduce the extent of Li plating through enhanced kinetics.43 After about 600 s of discharge, some activity occurred near the region close to the separator that consisted of periods of lithiating and delithiating as seen at arrows 2 in Fig. 5(c), and upon inspection of respective phase behaviors in Fig. 5d it was seen that the activity consisted solely of Stage I. This is likely related to the residual Stage I observed at the end of the discharge and perhaps to the presence of Li plating. One hypothesis is that, at lower currents during the constant voltage step, the graphite grains that were in immediate contact with the Li plating lithiated, which were then periodically delithiated and relithiated while suppling the low currents.
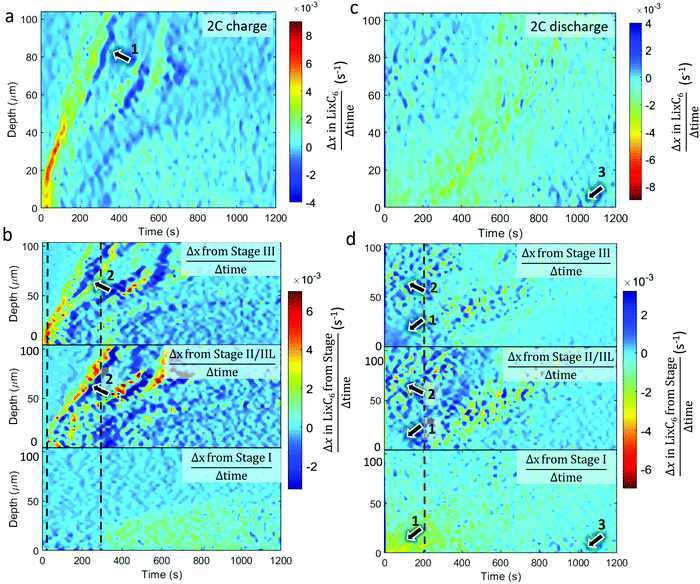
The equivalent quantitative dynamics for the 2C charge and discharge are presented in Fig. 6. During the 2C charge, a similar lithiation front moved from the separator to current collector over time, albeit with less magnitude of change. Periods of local delithiation (shown as dark blue) were observed during the charge step in Fig. 6a, which followed from periods of local lithiation as indicated by arrow 1. As the summed LixC6 was observed to continuously increase, the local periods of delithiation may have occurred due to charge balancing, which is seen in the repeated trading between Stage II/IIL and Stage III, as indicated by arrows 2 in Fig. 6b. Unlike for the 6C charge, where Stage II/IIL appeared before Stage III during lithiation, for the 2C charge Stage III occurred well-before Stage II/IIL, indicating that the solid phase sub-particle polarization was not as severe. The dotted grey lines show where Stage II/IIL and Stage I start to form. During 2C discharge in Fig. 6c, the length of time during which most delithiation occurred within the first 20 μm from the frontal region almost tripled compared to the 6C case, from about 200 s to almost 600 s. Exploring the activity of the distinct stages in Fig. 6d, it also appears that most of the Stage I material within the first 30 μm transitioned directly to Stage III or graphite, as pointed out by arrows 1. Similar to 6C discharge, activity occurred between Stages II/IIL and III at regions >50 μm over the first 200 s as indicated by arrows 2. However, rather than an absolute increase in Stage II/IIL and decrease in Stage III, as observed in Fig. 5d, in the case of 2C in Fig. 6d, the presence of Stage II/IIL and III seemingly fluctuate in accordance with each other. This may have been due to less heat being generated at 2C, reducing the extent of equilibration resulting in a moderate redistribution of lithium in a stochastic manner. As the delithiation front traveled deeper into the electrode in Fig. 6c, local delithiation for any particular depth was substantially longer than its 6C counterpart. Fluctuations between Stages II/IIL and III were also characteristic of this delithiation front, as seen in Fig. 6d. Finally, similar to the 6C case, some lithiation was observed at the graphite near the separator, as highlighted by arrows 3, which was likely connected to local Li plating.
The above quantifications of lithiation change were used to estimate the current density experienced by the graphite particles; that is, the current per unit surface area of the graphite. This is not to be confused with the current per unit area of the electrode sheet, as is often used.44 An estimate of the current density on the surface of the graphite was made by using the specific area of the graphite that was provided by the manufacturers (0.89 m2 g−1) for the volume of graphite within each of the 3 μm steps of the beam. The current density estimates for the 6C and 2C charge and discharge steps are provided in Fig. 7, and should be considered with some caveats; for example, it is assumed that current is homogeneous across the surface of the particles, that the specific area of the graphite is true for all depths into the electrode, that all surfaces of the graphite are accessible to Li-ions from the electrolyte, and that all particles are equally used for a particular depth i.e. homogenous electrical and ionic resistances.
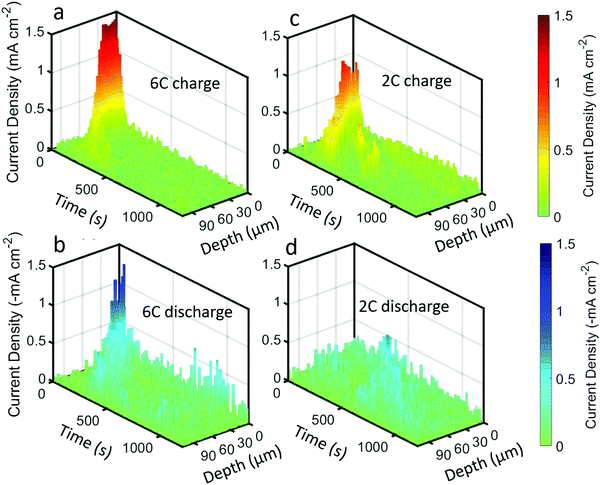 | ||
| Fig. 7 Current density plots, i.e. current per unit surface area of graphite, as a function of time and depth for (a) 6C charge, (b) 6C discharge, (c) 2C charge, and (d) 2C discharge. | ||
The highest estimate for current density during the charge step in Fig. 7a and c was ca. 1.5 mA cm−2 during 6C and ca. 1 mA cm−2 for 2C. The local current density did not scale linearly with the C-rate, indicating that the rate of transport of Li into the particles was not constant, where it is likely that at 6C the electrolyte and solid phase was transport limited. Such a transport limited system, along with a likely negative overpotential vs. Li, would have created favorable conditions for Li plating. Upon discharge in Fig. 7b and d, the maximum current densities were lower, about −1.3 mA cm−2 and −0.5 mA cm−2 for 6C and 2C respectively.
A discussion on future applications of depth-profiling XRD for analyzing fast charging phenomena
Having demonstrated high-energy XRD with 100 Hz measurements and a resolution of 3 μm, a plethora of new opportunities for understanding the limitations associated with, and effective solutions to, Li plating and transport limitations arise. For the same electrode, there remains other operating conditions that could present new insights into its function, such as operation at low rates (e.g. 0.1C) to explore whether any transport limitations occur during overnight charging conditions, as well as examining the efficacy of strategic charging methods such as pulse charging or step charging in mitigating lithiation gradients and Li plating, and separately for exploring how lithiation gradients and Li plating change upon switching to open circuit. There are also opportunities to explore the efficacy of preventative measures for mitigating Li plating, like charging at elevated temperatures which is known to help enhance kinetics, improve transport of lithium in both solid and liquid phases, and help prevent Li plating.45 There is much to be explored on lithiation kinetics at various temperatures, including at sub-zero temperatures, to simulate charging during winter conditions in high-latitude regions. Finally, electrode architectures can be designed to reduce lithiation gradients and Li plating by reducing the tortuosity and distance travelled by ions to reach the graphite host through various means. There may also be opportunity for optimizing electrode compositions (e.g. conductive carbon and binder) or the morphology and crystal architecture of particles. Having undergone a recent upgrade, The European Synchrotron is expected to soon facilitate faster imaging and higher resolution than demonstrated here, thus creating ample opportunity for applying similar experimental conditions to compare the response of next generation fast charging electrodes and cells to their conventional counterparts.Conclusions
High-speed XRD depth profiling was carried out on a 101 μm thick graphite electrode to quantify the spatial and temporal state of the electrode and concurrent Li plating during high rate (up to 6C) conditions. Extreme lithium concentration gradients were observed through the depth of the electrode during both 6C and 2C charge and discharge conditions. Local extents of lithiation were also divided into the fractional presence of lithiation stages, including Stage III, Stage II/IIL and Stage I. During charging at both 6C and 2C rates, only the half of the electrode depth that was closest to the separator reached Stage I. Periods where both full lithiation near the separator (Stage I) and no lithiation (graphite) near the current collector concurrently occurred shortly after 6C and 2C charge steps were initiated, demonstrating severe polarization caused by transport limitations through the liquid electrolyte.The evolution of the distinct lithiation stages was quantified at each depth, providing insight into the lithiation state distribution. The high free-energy barrier for Stage II to transition to Stage I was observed to have influenced the lithiation behavior of the electrode during both 6C and 2C charging. For example, when the electrode near the separator reached Stage II/IIL, further local lithiation slowed, and the lithiation front progressed to deeper regions, bringing those regions to a similar lithiation state, and then lithiation of the frontal regions resumed with the transition from Stage II/IIL to Stage I. Furthermore, there was extensive evidence of phase co-existence observed within single depths and phase co-existence of Stage I and graphite was observed after the electrode was fully delithiated at regions where Li plating was present. The Stage I and graphite continued to co-exist for at least 800 s, where solid-solution models would predict that the phases relax to some intermediate concentration. Li plating was shown to affect the equilibrium state of particles, which has raised questions for how the performance of graphite particles will be influenced by Li plating; for example, whether the plating hinders or improves further (de)lithiation, and how the transport properties of graphite are affected by the presence of plating and co-existence of LiC6 with graphite.
Asymmetric behavior was observed within graphite between charge and discharge with higher local current densities being observed during charge. At the beginning of discharge, regions close to the current collector appeared to take on a stage associated higher lithiation, which is thought to have been caused by Ohmic heating increasing the temperature and widening the stability window of the Stage II structure to include other concentrations close to LiC12 without any overall change in local lithiation. Fluctuations between Stage II/IIL and Stage III were observed at distinct depths as the delithiation process continued and at 2C, regions that were initially occupied with Stage I transitioned directly to Stage III, by-passing Stage II/IIL. Phase-field modelling methods have predicted asymmetry, and it is expected that this dataset will provide opportunity to validate such models.
In summary, we have provided a detailed experimental description of the response of a graphite electrode to fast charging and discharging conditions as well as a description of the onset of Li plating and stripping. The data presented in this work are expected to guide and validate modelling efforts for predicting fast charge and discharge behaviors. Finally, having demonstrated this technique and an easily built functioning operando cell design, this presents opportunities to investigate the efficacy of other electrode chemistries such as positive electrodes, and electrode designs with innovative architectures, in sustaining high rates. Furthermore, using different operating conditions, the non-equilibrium behavior of electrodes could be monitored in real time to validate phase and kinetic behavior within intercalation materials.
Methods
Electrode properties
A full cell with commercially relevant electrodes was used for this work to accurately capture conditions that may exist in actual field applications, such as during fast charging of electric vehicles. High-energy density electrodes were selected for this investigation. The positive electrode consisted of 90 wt% ECOPRO LiNi0.6Mn0.2Co0.2O2 (NMC622) with 5 wt% Timcal C45 and 5 wt% Solvay 5130 PVDF. In its dry state, the coating thickness was 112 μm on a 20 μm thick aluminum foil. The coating loading was 30.24 mg cm−2 with a density of 2.70 g cm−3 and a porosity of 34%. The areal capacity of the electrode was 4.60 mA h cm−2. The diameters for particle size distribution were D10 = 8.4 μm, D50 = 11.0 μm, and D90 = 14.4 μm. The negative electrode consisted of 91.83 wt% Superior graphite SLC1520P with 2 wt% Timcal C45, 6 wt% Kureha 9300 PVDF Binder, and 0.17 wt% oxalic acid. SLC1520P is a long-life graphite blend used for energy applications such as in electric vehicles, and is also a blend that is being explored within United States Department of Energy (DOE) research programs. In its dry state, the coating thickness was 101 μm on a 15 μm thick copper foil. The coating loading was 13.97 mg cm−2 with a density of 1.38 g cm−3 and porosity of 36.2%. The diameters for particle size distribution were D10 = 11.03 μm, D50 = 16.94 μm, and D90 = 26.76 μm.Operando cell design and operating conditions
The objective of this experiment was to capture phase heterogeneities, such as lithiation states and Li plating, as a function of depth and time during fast charging. This work was carried out at ESRF – The European Synchrotron – at Beamline ID15A which specializes in fast high-energy XRD with small (<1 μm) beam sizes. Depth profiling with XRD necessitated a cell with a small diameter to avoid broad diffraction peaks and ensure high accuracy of phase identification. An operando-cell was constructed to facilitate 6C charge and discharge conditions in a relevant operating environment for high-spatial resolution XRD (Fig. 1(a and b)). The cell was based on a standard CR2032 coin cell, but the typical stainless steel spacers were replaced with aluminum ones for increased X-ray transmission, and borosilicate paper was used to center a negative electrode of 3.97 mm diameter (ca. 0.68 mA h capacity) and a positive electrode of 4.76 mm diameter (ca. 0.81 mA h capacity) inside the casing, as shown in Fig. 1b. Some Li+ may have alloyed with the Al but is likely to be minimal due to the relatively long distance an ion would have had to travel to circumnavigate the electrodes. A Celgard 2320 polymer separator was used, and the entire cell was soaked in electrolyte consisting of 1.2 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (3
EMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7). Before exposure to the beam, the cell underwent two formation cycles at a constant current of C/10 between 2.8 V and 4.2 V. Several cycles were carried out with constant current followed by about 20 minutes of constant voltage: 2 cycles of 6C charge and 6C discharge cycles between 2.8 V and 4.2 V, 1 cycle of 3C charge and 3C discharge cycle (not discussed here) between 2.8 V and 4.2 V. Finally, a 2C cycle was applied which consisted of 2C constant current to 4.4 V followed by constant voltage at 4.4 V for 60 minutes. The voltage was increased to 4.4 V for the final 2C cycle to prolong the constant current step which we considered to be important for future modelling efforts and to create more favorable conditions for lithium to plate. Furthermore, this helped overcome the high ohmic resistance of the cell for a more complete lithiation of the electrode. The discharge step consisted of 2C constant current to 2.8 V followed by constant voltage at 2.8 V for 60 minutes. The 6C and 2C cycles are discussed in this work. All cycle data is provided in Section S1 (ESI†).
7). Before exposure to the beam, the cell underwent two formation cycles at a constant current of C/10 between 2.8 V and 4.2 V. Several cycles were carried out with constant current followed by about 20 minutes of constant voltage: 2 cycles of 6C charge and 6C discharge cycles between 2.8 V and 4.2 V, 1 cycle of 3C charge and 3C discharge cycle (not discussed here) between 2.8 V and 4.2 V. Finally, a 2C cycle was applied which consisted of 2C constant current to 4.4 V followed by constant voltage at 4.4 V for 60 minutes. The voltage was increased to 4.4 V for the final 2C cycle to prolong the constant current step which we considered to be important for future modelling efforts and to create more favorable conditions for lithium to plate. Furthermore, this helped overcome the high ohmic resistance of the cell for a more complete lithiation of the electrode. The discharge step consisted of 2C constant current to 2.8 V followed by constant voltage at 2.8 V for 60 minutes. The 6C and 2C cycles are discussed in this work. All cycle data is provided in Section S1 (ESI†).
XRD and data processing
X-ray diffraction was carried out at beamline ID15A at ESRF – The European Synchrotron.46 Prior to XRD measurements, the cell was aligned using X-ray radiography to position the electrode surface parallel to the X-ray beam. This was ensured by measuring the apparent thickness of the electrode in radiography – any thickness larger than 101 μm indicating that the electrode (or cell) was not aligned perfectly parallel to the beam path. Depth profiling measurements consisted of 35 point-scans 3 μm apart starting just adjacent to the Cu negative current collector and ending adjacent to the separator, thus ensuring that each line-scan encompassed the entirety of the electrode (Fig. 1c). The window of measurement was thus 105 μm along the thickness; for the 101 μm thick electrode, the final two measurements at 102 μm and 105 μm may have been capturing a dynamic front due to the swell and contraction associated with lithiation and delithiation. However, as Qi et al.47 highlight, lithiation-induced swelling may not translate proportionally into an increase in coating thickness due to some expansion narrowing the pores and instead decreasing porosity. Therefore, since the electrode only reached around 50% state of charge, it is not expected that the active material moved outside the 105 μm window, albeit there may be some measurement error associated with a travelling electrode front within and between the final 2 XRD measurements (at 102 μm ad 105 μm). The individual points were taken at 100 Hz, where each depth scan took ca. 0.5 s. A pause of 12 s was included between each depth-scan to reduce the quantity of data gathered. An exposure time of 0.005 s and a monochromatic 72.1 keV beam, with beam size of 2.5 μm × 8 μm (V × H), were used with a Dectris Pilatus3 X CdTe 2M (Dectris, Baden, Switzerland) high-energy photon-counting detector. Rietveld refinement was carried on the integrated diffraction patterns using LiC30, LiC12, LiC6, graphite, and Li phases to quantify their mass fractions, for which all wt% measurements had an error of around 1 wt%, i.e. low error. Details on Rietveld refinement are provided in ESI.† The output mass fractions were used to calculate all quantities provided in this manuscript, the steps of which are provided in ESI.† Images and videos were made using MATLAB.Author contributions
D. P. F. conceived of and conducted the experiments. M. D. M. and S. C. prepared the beamline for the experiment and guided data preparations. D. W. carried out the Rietveld refinement of the data. D. P. F., A. Q., and D. W. processed the data. A. D. C., X. L., C. T., T. M. M. H., R. J. and S. C assisted during the beamtime experiments. X. L., A. C., D. J. L. B., S. D. T. G., D. C., M. B., P. S. and K. S. assisted with guiding the experimental design and interpreting the results.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was authored by Alliance for Sustainable Energy, LLC, the manager and operator of the National Renewable Energy Laboratory for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by the U.S. Department of Energy Vehicle Technology Office. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes. These experiments were performed at beamline ID15A at the ESRF (Grenoble, France). We are grateful to the ESRF for allowing us to use their facilities. PRS acknowledges funding from the Royal Academy of Engineering (CiET1718\59). The authors acknowledge the support of The Faraday Institution under ISCF Faraday Challenge Fast Start projects on “Degradation of Battery Materials” and “Multi-scale Modelling” made available through grant EP/S003053/1 (FIRG001 and FIRG003, respectively). The authors would also like to thank Bryant Polzin and Andrew Jansen at Cell Analysis, Modeling and Prototyping (CAMP) facility at Argonne National Laboratory for manufacturing the electrodes, and Steve Harris from Lawrence Berkeley National Labs for productive discussions on interpreting the results in this manuscript.References
- D. Andre, S.-J. Kim, P. Lamp, S. F. Lux, F. Maglia, O. Paschos and B. Stiaszny, J. Mater. Chem. A, 2015, 3, 6709–6732 RSC.
- D. Howell, S. Boyd, B. Cunningham, S. Gillard and L. Slezak, Enabling Fast Charging: A Technology Gap Assessment, US Department of Energy (DOE), 2017 Search PubMed.
- Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550 CrossRef.
- Z. X. Shu, R. S. McMillan and J. J. Murray, J. Electrochem. Soc., 1993, 140, 922–927 CrossRef CAS.
- A. M. Colclasure, T. R. Tanim, A. N. Jansen, S. E. Trask, A. R. Dunlop, B. J. Polzin, I. Bloom, D. Robertson, L. Flores, M. Evans, E. J. Dufek and K. Smith, Electrochim. Acta, 2020, 337, 135854 CrossRef CAS.
- A. M. Colclasure, A. R. Dunlop, S. E. Trask, B. J. Polzin, A. N. Jansen and K. Smith, J. Electrochem. Soc., 2019, 166, A1412–A1424 CrossRef CAS.
- K. P. C. Yao, J. S. Okasinski, K. Kalaga, I. A. Shkrob and D. P. Abraham, Energy Environ. Sci., 2019, 12, 656–665 RSC.
- X. Lu, A. Bertei, D. P. Finegan, C. Tan, S. R. Daemi, J. S. Weaving, K. B. O’Regan, T. M. M. Heenan, G. Hinds, E. Kendrick, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2020, 11, 2079 CrossRef CAS PubMed.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- A. Senyshyn, O. Dolotko, M. J. Mühlbauer, K. Nikolowski, H. Fuess and H. Ehrenberg, J. Electrochem. Soc., 2013, 160, A3198–A3205 CrossRef CAS.
- D. Allart, M. Montaru and H. Gualous, J. Electrochem. Soc., 2018, 165, A380–A387 CrossRef CAS.
- X.-L. Wang, K. An, L. Cai, Z. Feng, S. E. Nagler, C. Daniel, K. J. Rhodes, A. D. Stoica, H. D. Skorpenske, C. Liang, W. Zhang, J. Kim, Y. Qi and S. J. Harris, Sci. Rep., 2012, 2, 747 CrossRef PubMed.
- Y. Guo, R. B. Smith, Z. Yu, D. K. Efetov, J. Wang, P. Kim, M. Z. Bazant and L. E. Brus, J. Phys. Chem. Lett., 2016, 7, 2151–2156 CrossRef CAS PubMed.
- K. E. Thomas-Alyea, C. Jung, R. B. Smith and M. Z. Bazant, J. Electrochem. Soc., 2017, 164, E3063–E3072 CrossRef CAS.
- S. J. Harris, A. Timmons, D. R. Baker and C. Monroe, Chem. Phys. Lett., 2010, 485, 265–274 CrossRef CAS.
- M. D. Levi and D. Aurbach, J. Phys. Chem. B, 1997, 101, 4641–4647 CrossRef CAS.
- H.-j. Guo, X.-h. Li, X.-m. Zhang, H.-q. Wang, Z.-x. Wang and W.-j. Peng, New Carbon Mater., 2007, 22, 7–10 CrossRef CAS.
- R. B. Smith, E. Khoo and M. Z. Bazant, J. Phys. Chem. C, 2017, 121, 12505–12523 CrossRef CAS.
- M. Chandesris, D. Caliste, D. Jamet and P. Pochet, J. Phys. Chem. C, 2019, 123, 23711–23720 CrossRef CAS.
- T. Waldmann, B.-I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124 CrossRef CAS.
- B. P. Matadi, S. Geniès, A. Delaille, C. Chabrol, E. de Vito, M. Bardet, J.-F. Martin, L. Daniel and Y. Bultel, J. Electrochem. Soc., 2017, 164, A2374–A2389 CrossRef CAS.
- K. Dokko, N. Nakata, Y. Suzuki and K. Kanamura, J. Phys. Chem. C, 2010, 114, 8646–8650 CrossRef CAS.
- J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170–9177 CrossRef CAS PubMed.
- C. Uhlmann, J. Illig, M. Ender, R. Schuster and E. Ivers-Tiffée, J. Power Sources, 2015, 279, 428–438 CrossRef CAS.
- C. von Lüders, V. Zinth, S. V. Erhard, P. J. Osswald, M. Hofmann, R. Gilles and A. Jossen, J. Power Sources, 2017, 342, 17–23 CrossRef.
- V. Zinth, C. von Lüders, M. Hofmann, J. Hattendorff, I. Buchberger, S. Erhard, J. Rebelo-Kornmeier, A. Jossen and R. Gilles, J. Power Sources, 2014, 271, 152–159 CrossRef CAS.
- J. Wilhelm, S. Seidlmayer, S. Erhard, M. Hofmann, R. Gilles and A. Jossen, J. Electrochem. Soc., 2018, 165, A1846–A1856 CrossRef CAS.
- J. Wandt, P. Jakes, J. Granwehr, R.-A. Eichel and H. A. Gasteiger, Mater. Today, 2018, 21, 231–240 CrossRef CAS.
- I. D. Campbell, M. Marzook, M. Marinescu and G. J. Offer, J. Electrochem. Soc., 2019, 166, A725–A739 CrossRef.
- X. Yu, Z. Feng, Y. Ren, D. Henn, Z. Wu, K. An, B. Wu, C. Fau, C. Li and S. J. Harris, J. Electrochem. Soc., 2018, 165, A1578–A1585 CrossRef CAS.
- C.-K. Lin, Y. Ren, K. Amine, Y. Qin and Z. Chen, J. Power Sources, 2013, 230, 32–37 CrossRef CAS.
- X.-G. Yang, T. Liu, Y. Gao, S. Ge, Y. Leng, D. Wang and C.-Y. Wang, Joule, 2019, 3, 3002–3019 CrossRef CAS.
- O. J. Borkiewicz, K. M. Wiaderek, P. J. Chupas and K. W. Chapman, J. Phys. Chem. Lett., 2015, 6, 2081–2085 CrossRef CAS PubMed.
- D. Billaud and F. X. Henry, Solid State Commun., 2002, 124, 299–304 CrossRef CAS.
- D. Billaud, F. X. Henry, M. Lelaurain and P. Willmann, J. Phys. Chem. Solids, 1996, 57, 775–781 CrossRef CAS.
- I. J. Ong, J. Electrochem. Soc., 1999, 146, 4360 CrossRef CAS.
- S. Das, P. M. Attia, W. C. Chueh and M. Z. Bazant, J. Electrochem. Soc., 2019, 166, E107–E118 CrossRef CAS.
- C. Mao, R. E. Ruther, J. Li, Z. Du and I. Belharouak, Electrochem. Commun., 2018, 97, 37–41 CrossRef CAS.
- S. Hein and A. Latz, Electrochim. Acta, 2016, 201, 354–365 CrossRef CAS.
- E. J. McShane, A. M. Colclasure, D. E. Brown, Z. M. Konz, K. Smith and B. D. McCloskey, ACS Energy Lett., 2020, 5, 2045–2051 CrossRef CAS.
- I. Umegaki, S. Kawauchi, H. Sawada, H. Nozaki, Y. Higuchi, K. Miwa, Y. Kondo, M. Månsson, M. Telling, F. C. Coomer, S. P. Cottrell, T. Sasaki, T. Kobayashi and J. Sugiyama, Phys. Chem. Chem. Phys., 2017, 19, 19058–19066 RSC.
- C. Forgez, D. Vinh Do, G. Friedrich, M. Morcrette and C. Delacourt, J. Power Sources, 2010, 195, 2961–2968 CrossRef CAS.
- X.-G. Yang and C.-Y. Wang, J. Power Sources, 2018, 402, 489–498 CrossRef CAS.
- K. G. Gallagher, S. E. Trask, C. Bauer, T. Woehrle, S. F. Lux, M. Tschech, P. Lamp, B. J. Polzin, S. Ha, B. Long, Q. Wu, W. Lu, D. W. Dees and A. N. Jansen, J. Electrochem. Soc., 2016, 163, A138–A149 CrossRef CAS.
- X.-G. Yang, G. Zhang, S. Ge and C.-Y. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7266–7271 CrossRef CAS PubMed.
- G. B. M. Vaughan, R. Baker, R. Barret, J. Bonnefoy, T. Buslaps, S. Checchia, D. Duran, F. Fihman, P. Got, J. Kieffer, S. A. J. Kimber, K. Martel, C. Morawe, D. Mottin, E. Papillon, S. Petitdemange, A. Vamvakeros, J.-P. Vieux and M. Di Michiel, J. Synchrotron Radiat., 2020, 27, 515–528 CrossRef CAS PubMed.
- Y. Qi and S. J. Harris, J. Electrochem. Soc., 2010, 157, A741–A747 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee01191f |
| This journal is © The Royal Society of Chemistry 2020 |