Structure and magnetism of the Rh⁴⁺-containing perovskite oxides La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

Abstract

Synchrotron X-ray powder diffraction data indicate that La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ adopt distorted perovskite structures (space group Pnma) with A-site and B-site cation disorder. A combination of XPS and ⁵⁷Fe Mössbauer data indicate the transition metal cations in the two phases adopt Mn³⁺/Rh⁴⁺ and Fe³⁺/Rh⁴⁺ oxidation state combinations respectively. Transport data indicate both phases are insulating, with ρ vs. T dependences consistent with 3D variable-range hopping. Magnetisation data reveal that La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ adopts a ferromagnetic state below T_c ∼ 60 K, which is rationalized on the basis of coupling via a dynamic Jahn–Teller distortion mechanism. In contrast, magnetic data reveal La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ undergoes a transition to a spin-glass state at T ∼ 45 K, attributed to frustration between nearest-neighbour Fe–Rh and next-nearest-neighbour Fe–Fe couplings.

---

Introduction

Transition-metal oxides which adopt the ABO₃ perovskite structure exhibit a wide variety of complex physical properties, including superconductivity, colossal magnetoresistance, ferroelectricity and a wide variety of other coupled electronic and magnetic behaviours.¹ The rich diversity of electronic and magnetic phenomena displayed by perovskite oxides can be attributed to the strong coupling between the local electronic states of the octahedrally coordinated transition-metal cations, which is facilitated by strong covalency in the B–O–B links which connect the BO₆ units.²

Recently there has been much interest in perovskite oxide compounds which combine 3d and 4d or 3d and 5d transition-metal cations, because the contrasting features of the 3d (narrow metal d-bands, large on-site electron–electron repulsion) and 4d/5d (broad d-bands, low on-site repulsion, strong spin–orbit coupling for 5d) cations can result in novel behaviour when they are combined.^3,4 For example, Sr₂FeMoO₆ exhibits half-metallic ferromagnetic behaviour attributed to the interaction between the localized 3d⁵ electronic configuration of Fe³⁺ and the delocalized 4d¹ electrons of Mo⁵⁺,⁵ with similar behaviour observed in other 3d/4d and 3d/5d systems.^6,7

In a broader context the inter-cation magnetic couplings in mixed 3d/4d and 3d/5d perovskite oxides do not generally appear to follow the Goodenough Kanamouri rules⁸ which dominate 3d systems.^9–11 However, to date only a subset of the 3d/4d and 3d/5d perovskite oxide phases which could be envisioned have been reported,¹² so it is hard to formulate broad magnetic coupling rules for this class of compound. To help address this situation, we have been studying mixed perovskite phases containing rhodium.

A range of Rh-containing perovskite oxides of the form LaM_0.5Rh_0.5O₃ have been reported (M = Cr, Mn, Fe, Co, Ni and Cu) with M/Rh cation disordered structures.^13–16 The unit cell volumes of these LaM_0.5Rh_0.5O₃ compounds are broadly consistent with an M³⁺/Rh³⁺ oxidation state combination, with the exception of LaCu_0.5Rh_0.5O₃ which appears to adopt a configuration close to a Cu²⁺/Rh⁴⁺ combination.^13,15 However, Curie constants obtained by fitting the Curie–Weiss law to temperature-dependent magnetization data deviate from values expected for combinations of M³⁺ and low-spin, S = 0 Rh³⁺, casting some doubt on this oxidation state assignment.¹³ In the case of LaCo_0.5Rh_0.5O₃ the deviations are large and temperature dependent and have been attributed to both a change in the spin-state of Co³⁺ and the presence of Co²⁺/Rh⁴⁺ oxidation state combinations.^17–19

Here we report two further cation-disordered rhodium-containing perovskite oxides, La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃. Using a combination of XPS and ⁵⁷Fe Mössbauer spectroscopy we demonstrate that, even though these compounds were prepared at ambient pressure, the rhodium cations adopt an Rh⁴⁺ oxidation state, resulting in ferromagnetic behaviour for La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and spin-glass behaviour for La_0.5Sr_0.5Fe_0.5Rh_0.5O₃.

Experimental

Synthesis

Samples of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ were prepared via a high-temperature ceramic route. Suitable quantities of La₂O₃ (99.999%, dried at 900 °C) SrCO₃ (99.994%), Rh₂O₃ (99.99%, dried at 800 °C) and either MnO₂ (99.997%) or Fe₂O₃ (99.997%) were ground together in an agate pestle and mortar and then heated in air to 1000 °C in an alumina crucible. The resulting powders were then reground and pressed into pellets. Samples of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ were then heated in air at 1300 °C for 4 periods of 48 h. Samples of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ were heated under flowing oxygen at 1300 °C for 3 periods of 48 h. All samples were reground and pressed into pellets between heating periods.

Characterization

X-ray powder diffraction data were collected using a PANalytical X′pert diffractometer incorporating an X'celerator position-sensitive detector (monochromatic Cu Kα₁ radiation). High-resolution synchrotron X-ray powder diffraction data (SXRD) were collected using the I11 instrument at the Diamond Light Source Ltd. Diffraction patterns were collected using Si-calibrated X-rays with an approximate wavelength of 0.825 Å from samples sealed in 0.3 mm diameter borosilicate glass capillaries. Rietveld refinements were performed using the GSAS suite of programs.²⁰ Magnetization data were collected using a Quantum Design MPMS SQUID magnetometer. Four-probe resistivity measurements were performed using a home-made apparatus on bars cut from sintered pellets. ⁵⁷Fe Mössbauer spectroscopy measurements utilized acrylic absorber discs with a sample area of 1.767 cm² which were loaded to present 2.16 × 10⁻³ g cm⁻² of Fe, and achieve a Mössbauer thickness of 1. Samples were homogeneously mixed with graphite to achieve this level of loading. The 14.4 keV γ-rays were supplied by the cascade decay of 25 mCi ⁵⁷Co in a Rh matrix source, oscillated at constant acceleration by a SeeCo W304 drive unit, and detected using a SeeCo 45431 Kr proportional counter operating with 1.745 kV bias voltage applied to the cathode. All measurements were calibrated relative to α-Fe foil. Spectral data were fitted using the Recoil software package,²¹ using Lorentzian line shapes.

X-ray photoelectron spectroscopy (XPS) analysis was performed using a Kratos Axis SUPRA XPS fitted with a monochromated Al K_α X-ray source (1486.7 eV), a spherical sector analyser and 3 multichannel resistive plate, 128 channel delay line detectors. All data was recorded at 150 W and a spot size of 700 × 300 μm. Survey scans were recorded at a pass energy of 160 eV, and high-resolution scans recorded at a pass energy of 20 eV. Electronic charge neutralization was achieved using a magnetic immersion lens. Filament current = 0.27 A, charge balance = 3.3 V, filament bias = 3.8 V. All sample data was recorded at a pressure below 10⁻⁸ Torr and a room temperature of 294 K. Data was analysed using CasaXPS v2.3.18PR1.0. C 1s sp³ peaks were calibrated to 284.8 eV.

Results

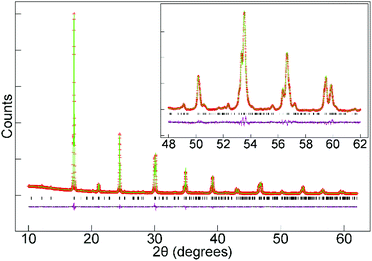
Structural characterisation of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃

SXRD data collected from La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ at room temperature could be readily indexed using an orthorhombic unit cell (a = 5.483 Å, b = 7.776 Å, 5.536 Å) with extinction conditions consistent with the Pnma (# 62) space group. A structural model was constructed based on the reported structure of LaMn_0.5Rh_0.5O₃,¹⁵ but with the La³⁺ replaced by a 1 : 1 ratio of La³⁺ : Sr²⁺. This model was refined against the SXRD data to achieve a good fit as shown in Fig. 1 and detailed in Table 1, with selected bond lengths listed in Table 2. SXRD data provide no evidence for Mn/Rh cation-order, with a model based on the reported cation-ordered structure of LaSrNiRuO₆ (space group P2₁/n)¹¹ reverting to a disordered structure when the Mn and Rh occupancies were refined.

Fig. 1 Observed, calculated and difference plots from the structural refinement of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ against SXRD data collected at room temperature. Inset shows quality of fit at large values of 2θ.

Table 1 Parameters from the structural refinement of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ against synchrotron X-ray powder diffraction data

Atom	x	y	z	Occupancy	U iso (Å^2)
La0.5Sr0.5Mn0.5Rh0.5O3 space group Pnma (#62). a = 5.4830(1) Å, b = 7.7769(1) Å, 5.5364(1) Å, volume = 236.08(1). Formula mass: 240.18 g mol^−1, Z = 4. Radiation source: Synchrotron X-ray, λ = 0.82622 Å. χ^2 = 19.75; wRp = 2.92%; Rp = 1.88%.
La/Sr	0.5181(1)	¼	0.0023(1)	0.5/0.5	0.009(1)
Mn/Rh	0	0	0	0.5/0.5	0.004(1)
O(1)	0.0000(6)	¼	0.9434(6)	1	0.009(1)
O(2)	0.2701(8)	0.0305(4)	0.2189(6)	1	0.020(1)

---

Table 2 Selected bond lengths from the structure of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃

Cation	Anion	Bond length (Å)
Mn/Rh	O(1) × 2	1.969(1)
	O(2) × 2	1.928(4)
	O(2) × 2	2.017(4)
La/Sr	O(1)	2.470(3)
	O(1)	2.662(3)
	O(1)	2.859(3)
	O(1)	3.070(3)
	O(2) × 2	2.490(4)
	O(2) × 2	2.684(4)
	O(2) × 2	2.758(3)
	O(2) × 2	3.117(4)

---

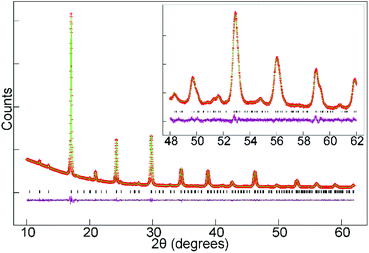
Structural and chemical characterisation of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

SXRD data collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ at room temperature could be readily indexed using an orthorhombic unit cell (a = 5.525 Å, b = 7.860 Å, 5.563 Å,) with extinction conditions consistent with the Pnma (# 62) space group. A structural model was constructed, based that used for La_0.5Sr_0.5Mn_0.5Rh_0.5O₃, and refined against the SXRD data to achieve a good fit as shown in Fig. 2 and detailed in Table 3, with selected bond lengths listed in Table 4. SXRD data provide no evidence for Fe/Rh cation-order, with a model based on the reported cation-ordered structure of LaSrNiRuO₆ (space group P2₁/n)¹¹ reverting to a disordered structure when the Fe and Rh occupancies were refined.

Fig. 2 Observed, calculated and difference plots from the structural refinement of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ against SXRD data collected at room temperature. Inset shows quality of fit at large values of 2θ.

Table 3 Parameters from the structural refinement of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ against synchrotron X-ray powder diffraction data

Atom	x	y	z	Occupancy	U iso (Å^2)
La0.5Sr0.5Fe0.5Rh0.5O3 space group Pnma (#62). a = 5.5254(3) Å, b = 7.8602(5) Å, 5.5635(4) Å, volume = 241.63(3). Formula mass: 240.63 g mol^−1, Z = 4. Radiation source: Synchrotron X-ray, λ = 0.8259 Å. χ^2 = 15.85; wRp = 2.41%; Rp = 1.54%.
La/Sr	0.5138(3)	¼	0.0012(6)	0.5/0.5	0.007(1)
Fe/Rh	0	0	0	0.5/0.5	0.003(1)
O(1)	0.9982(5)	¼	0.0369(4)	1	0.009(1)
O(2)	0.2294(3)	0.9594(1)	0.2800(2)	1	0.016(1)

---

Table 4 Selected bond lengths from the structure of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

Cation	Anion	Bond (Å)
Fe/Rh	O(1) × 2	1.976(1)
	O(2) × 2	1.958(1)
	O(2) × 2	2.033(1)
La/Sr	O(1)	2.571(4)
	O(1)	2.684(3)
	O(1)	2.856(3)
	O(1)	2.995(4)
	O(2) × 2	2.456(2)
	O(2) × 2	2.678(2)
	O(2) × 2	2.849(2)
	O(2) × 2	3.176(2)

---

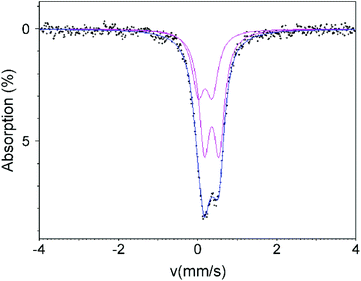
⁵⁷Fe Mössbauer analysis of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

A ⁵⁷Fe Mössbauer spectrum collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ at room temperature can be satisfactorily fitted by two doublets as shown in Fig. 3 and detailed in Table 5.

Fig. 3 ⁵⁷Fe Mössbauer spectrum collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ at room temperature.

Table 5 Parameters extracted from fit to ⁵⁷Fe Mössbauer spectrum collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ (χ² = 0.650)

Doublet	C S (mm s^−1)	Δ (mm s^−1)	HWHM (mm s^−1)	Site population (%)
1	0.361(18)	0.371(6)	0.166(16)	63(19)
2	0.195(42)	0.355(14)	0.184(24)	37(19)

---

We attribute the need to use two doublets to obtain a satisfactory fit to the Fe/Rh cation-disordered structure of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃. Each octahedral transition-metal coordination site in the perovskite framework is surrounded by 6 others. In a disordered Fe/Rh array the majority of the iron cations with have 3 iron neighbours and 3 rhodium neighbours. However there will be a significant number which have Fe₂Rh₄ or Fe₄Rh₂ surrounding them and a smaller number with Fe₁Rh₅ or Fe₅Rh₁. When we also consider that the Fe₃Rh₃ environments can be arranged as either fac or mer, and the Fe₂Rh₄ and Fe₄Rh₂ as cis or trans, it can be seen that there are a large number of local environments for the iron cations within the disordered Rh/Fe array, each with a different Mössbauer chemical shift and doublet splitting. It is not possible to resolve this large number of components from the data in a meaningful way, so we have utilized a 2-doublet fit to extract the range of C_s and Δ values spanned by the different Fe local coordination environments. Comparison with literature standards indicates these signals correspond to octahedrally coordinated Fe³⁺.^22,23

To investigate the possibility that some Fe⁴⁺ cations are present in La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ we have performed a further fit in which one doublet was fixed at C_S = 0, corresponding to Fe⁴⁺. This approach also gives a reasonable fit to the data and indicates a maximum concentration of 12(2)% Fe⁴⁺ as described in detail in the ESI.†

XPS analysis of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

A Rh 3d spectrum collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ is shown in Fig. 4a and exhibits a well resolved Rh 3d_5/2 component centred at BE = 308.9 eV (FWHM = 1.86 eV) and a Rh 3d_3/2 component centred at BE = 313.7 eV (FWHM = 2.63 eV). When combined with an O 1s–Rh 3d_5/2 separation of 219.6 eV, as shown in Fig. 4a, these values indicate an oxidation state of Rh⁴⁺.^24,25 Fe 2p spectra (Fig. S2, ESI†) exhibit a well resolved Fe 2p_3/2 component centred at BE = 710.1 eV (FWHM = 3.44 eV) and a Fe 2p_1/2 component centred at BE = 723.3 eV (FWHM = 4.65 eV), consistent with Fe³⁺.^26,27 These data, in combination with the ⁵⁷Fe Mössbauer data indicate an Fe³⁺/Rh⁴⁺ oxidation state combination for La_0.5Sr_0.5Fe_0.5Rh_0.5O₃.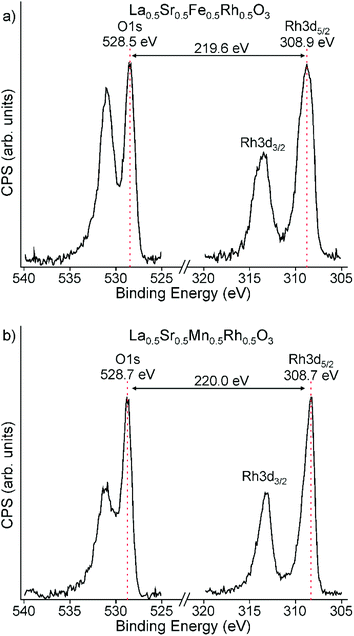

Fig. 4 Binding energy separation between O 1s and Rh 3d peaks of (a) LaSrFe_0.5Rh_0.5O₃ and (b) LaSrFe_0.5Rh_0.5O₃ which is consistent with the presence of Rh⁴⁺ in both cases.

Similarly, a Rh 3d spectrum collected from La_0.5Sr_0.5Mn_0.5Rh_0.5O₃, shown in Fig. 4b, exhibits a well resolved Rh 3d_5/2 component centred at BE = 308.7 eV (FWHM = 1.45 eV), a Rh 3d_3/2 component centred at BE = 313.4 eV (FWHM = 2.16 eV) and a O 1s–Rh 3d_5/2 separation of 220.0 eV which also indicate an oxidation state of Rh⁴⁺.^24,25 Mn 2p spectra (Fig. S3, ESI†) exhibit a well resolved Mn 2p_3/2 component centred at BE = 641.6 eV (FWHM = 3.79 eV) and a Mn 2p_1/2 component centred at BE = 652.9 eV (FWHM = 4.35 eV), consistent with Mn³⁺.^26,28 These data indicate an Mn³⁺/Rh⁴⁺ oxidation state combination for La_0.5Sr_0.5Mn_0.5Rh_0.5O₃.

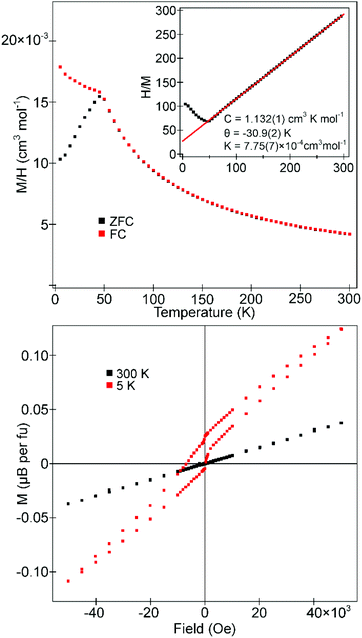
Magnetic characterisation of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃

Zero-field cooled (ZFC) and field cooled (FC) magnetization data collected from La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ in an applied field of 100 Oe (Fig. 5) diverge weekly below 100 K, before diverging more strongly below 60 K, consistent with the onset of magnetic order. Data in the range 100 < T/K < 300 do not obey the Curie–Weiss law. Magnetization-field data collected at 5 K are consistent with ferromagnetic behaviour with a coercive field of 190 Oe (as shown more clearly in Fig. S3 in the ESI†) and a saturated moment of 1.43μ_B per formula unit (2.86μ_B per Mn).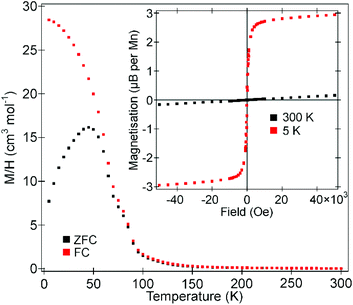

Fig. 5 ZFC and FC magnetisation data collected from La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ in an applied field of 100 Oe. Inset shows magnetisation-field isotherms collected at 300 K and 5 K.

Temperature-dependent 4-probe transport measurements indicate that La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ is highly resistive, with a semiconducting/insulating temperature dependence (δρ/δT < 0) as shown in Fig. 6. A plot of ln ρ against T^−1/4 is linear in the range 90 < T/K < 300 consistent with 3D variable range hopping.

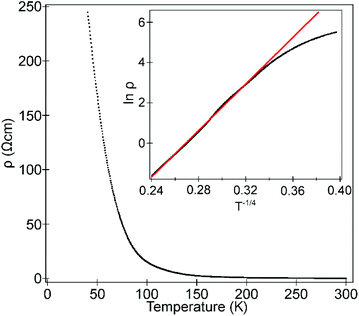Fig. 6 Temperature-dependent resistivity of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃. Inset shows fit to 3D variable-range hopping model.

Magnetic characterisation of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃

ZFC and FC data collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ (Fig. 7) can be fit by the Curie–Weiss law (χ = C/(T − θ) + K) in the temperature range 60 < T/K < 300 to yield value of C = 1.132(1) cm³ K mol⁻¹, θ = −30.9 K, K = 7.75(7) × 10⁻⁴ cm³ mol⁻¹, as shown in Fig. 6. For T < 45 K the ZFC and FC data diverge, indicative of a magnetic phase transition. Magnetization data collected at 300 K exhibit a linear field dependence. In contrast, magnetization data collected at 5 K after cooling from 300 K in an applied field of 50 000 Oe exhibit hysteresis and are displaced from the origin, indicative of spin-glass behaviour.

Fig. 7 (Top) ZFC and FC magnetisation data collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ in an applied field of 100 Oe. Inset shows Curie–Weiss law fit to the ZFC data. (Bottom) Magnetisation-field isotherms collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ at 300 K and at 5 K after field cooling from 300 K in an applied filed of 50 000 Oe.

Temperature-dependent 4-probe transport measurements indicate that La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ is highly resistive, with a semiconducting/insulating temperature dependence (δρ/δT < 0) as shown in Fig. 8. A plot of ln ρ against T^−1/4 is linear in the range 50 < T/K < 300 consistent with 3D variable range hopping.

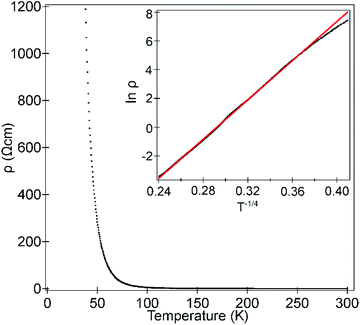Fig. 8 Temperature-dependent resistivity of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃. Inset shows fit to 3D variable-range hopping model.

Discussion

SXRD data indicate that in common with other reported La_1−xSr_xMn_0.5Rh_0.5O₃ phases,^15,29 La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ adopts a cation-disordered, a⁻a⁻c⁺ distorted, GdFeO₃-type perovskite structure. Comparison with the reported structures of LaMn_0.5Rh_0.5O₃ and La_0.75Sr_0.25Mn_0.5Rh_0.5O₃ reveals that both the unit cell volumes (V = 243.92 ų, 240.01 ų and 236.08 ų for x = 0, 0.25 and 0.5 respectively) and average (Mn/Rh)–O bond lengths ((Mn/Rh)–O = 2.019 Å, 1.995 Å and 1.971 Å for x = 0, 0.25 and 0.5 respectively) decrease on substitution of La³⁺ by Sr²⁺, consistent with oxidation of the transition metal cations. In addition it should be noted that there is no evidence of an ordered Jahn–Teller distortion (long-range orbital order) of the (Mn/Rh)O₆ octahedra in La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ (Table 2) or any other La_1−xSr_xMn_0.5Rh_0.5O₃ phases (despite the unambiguous presence of Mn³⁺ in LaMn_0.5Rh_0.5O₃)¹⁵ which is attributed to suppression by the disordered arrangement of the Mn and Rh cations.

La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ also adopts a cation-disordered, a⁻a⁻c⁺ distorted, GdFeO₃-type perovskite structure. Comparison with the reported structure of LaFe_0.5Rh_0.5O₃ ¹³ again reveals that substitution of La³⁺ with Sr²⁺ leads to a contraction in unit cell volume, consistent with oxidation of the transition metals.

XPS and ⁵⁷Fe Mössbauer data indicate the predominant oxidation state combinations of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ are Mn³⁺/Rh⁴⁺ and Fe³⁺/Rh⁴⁺ respectively. This is unexpected considering the oxide chemistry of these transition metals. For example, Mn³⁺ is not particularly stable in perovskite oxides, as illustrated by the observation that LaMnO₃ must be prepared under low oxygen partial pressures to avoid the formation of mixed-valent Mn^3+/4+ ‘LaMnO_3+δ’ phases.³⁰ In contrast the preparation of Mn⁴⁺ containing perovskite oxides, such as SrMnO₃, can be readily achieved by heating in air.³¹ Rhodium shows the opposite trend with Rh³⁺ perovskites such as LaRhO₃ being readily prepared in air,³² while Rh⁴⁺ perovskite oxides such as SrRhO₃ require high-pressure synthesis conditions.³³ It is therefore surprising that combining the two ‘more stable’ perovskite phases LaRhO₃ and SrMnO₃ to form La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ leads to a change in oxidation states from a Mn⁴⁺/Rh³⁺ combination in the ternary phases to a Mn³⁺/Rh⁴⁺ in the quaternary product. Rh⁴⁺ has been observed in perovskite oxides prepared at ambient pressure when it is combined with either electronegative elements such as Cu (LaCu_0.5²⁺Rh_0.5⁴⁺O₃)¹⁵ or elements which only exhibit a single divalent cation oxidation state (LaZn_0.5²⁺Rh_0.5⁴⁺O₃, LaMg_0.5²⁺Rh_0.5⁴⁺O₃).³⁴ However, the observation of Rh⁴⁺ in the presence of cations such as Fe³⁺ and Mn³⁺ which can be oxidized relatively easily is unexpected and suggests the 3d and 4d levels of Mn/Fe and Rh respectively are of similar energy.

Magnetic behaviour

Transport and magnetization data indicate that La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ is an electrical insulator which undergoes a transition to a ferromagnetic state at T_c ∼ 60 K. This behaviour is very similar to that reported for other perovskite oxides containing disordered arrays of Mn³⁺ cations such as LaMn_0.5Rh_0.5O₃ (T_c = 65 K)^15,16 and LaMn_0.5Ga_0.5O₃ (T_c = 70 K), with the observed saturated ferromagnetic moment of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ (2.86μ_B per Mn) also being similar to that observed for LaMn_0.5Ga_0.5O₃.^35,36

The ferromagnetic behaviour of LaMn_0.5Ga_0.5O₃ has been rationalized by observing that partial substitution of the Mn³⁺ cations in LaMnO₃ by a non-Jahn–Teller ion (e.g. Ga³⁺) suppresses the static Jahn–Teller distortion (orbital ordering) of the Mn^IIIO₆ units present in the unsubstituted phase.^35,37 In the absence of a static Jahn–Teller distortion (long-range orbital order), local dynamic Jahn–Teller distortions predominate which make all the Mn–O–Mn exchange couplings ferromagnetic, thus explaining the ferromagnetic order observed for LaMn_1−xGa_xO₃ phases with x > 0.5.^35,37 This mechanism can also be invoked to explain the ferromagnetic behaviour of LaMn_0.5Rh_0.5O₃ as it is observed that the substitution of diamagnetic, low-spin d⁶, Rh³⁺ into LaMnO₃ suppresses the static Jahn–Teller distortion of the Mn^IIIO₆ units in a manner directly analogous to Ga³⁺ substitution.^15,38

We propose that this dynamic Jahn–Teller mechanism is also the origin of the ferromagnetic behaviour of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃, as the substitution of Rh⁴⁺ for Mn³⁺ suppresses the static Jahn–Teller distortion of the manganese centres, leading to ferromagnetic couplings between Mn³⁺ cations in this cation-disordered material. It may be expected that the presence of paramagnetic Rh⁴⁺ centres would perturb the ferromagnetic Mn–O–Mn couplings, however the observation that the Curie temperature of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ (T_c ∼ 60 K) is very similar to those of LaMn_0.5Rh_0.5O₃ (T_c = 65 K)^15,16 and LaMn_0.5Ga_0.5O₃ (T_c = 70 K)^35,36 indicates any Mn–O–Rh couplings present are weak. It is not clear if the Rh spins contribute to the magnetically ordered state of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃.

Magnetization data collected from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ in the temperature range 60 < T/K < 300 exhibit the temperature-dependence of the Curie–Weiss Law (Fig. 6). However, the Curie constant extracted from these data (C = 1.132(1) cm³ K mol⁻¹) is much smaller than expected for simple paramagnetic behaviour for either an Fe³⁺/Rh⁴⁺ (C_expected = 2.375 cm³ K mol⁻¹) or an Fe⁴⁺/Rh³⁺ (C_expected = 1.50 cm³ K mol⁻¹) oxidation state combination. This indicates that strong spin–spin interactions are present in this temperature range, which is consistent with the large temperature-independent susceptibility observed (K = 7.75(7) × 10⁻⁴ cm³ mol⁻¹) which contributes ∼20% to the total susceptibility at 300 K.

On cooling below T = 45 K, La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ undergoes a transition to a spin-glass state. In order to adopt a spin-glass state a system must be crystallographically disordered, and subject to magnetic frustration. If we consider the nearest-neighbour super exchange couplings in La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ we observe Fe^III–O–Fe^III should be strongly antiferromagnetic, Rh^IV–O–Rh^IV should also be antiferromagnetic, but only weakly, and Fe^III–O–Rh^IV should be ferromagnetic.⁸ If these are the only significant magnetic couplings, a disordered Fe/Rh array would not be subject to magnetic frustration, making the observed spin-glass behaviour of La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ a little puzzling.

Battle et al. considered the spin-glass states of SrFe_0.5Ru_0.5O₃ and Sr₂Fe_0.5Ru_0.5O₄ which arise from disordered arrays of Fe³⁺ and Ru⁵⁺.^39,40 The nearest-neighbour super exchange couplings in SrFe_0.5Ru_0.5O₃ and Sr₂Fe_0.5Ru_0.5O₄ are directly analogous to those in La_0.5Sr_0.5Fe_0.5Rh_0.5O₃: Fe^III–O–Fe^III is antiferromagnetic, Ru^V–O–Ru^V is antiferromagnetic and Fe^III–O–Ru^V is ferromagnetic.

Battle et al. concluded that the order of coupling strengths is Fe^III–O–Fe^III > Ru^V–O–Ru^V ∼ Fe^III–O–Ru^V ∼ Fe^III–O–O–Fe^III where this last term is the next-nearest-neighbour Fe–Fe coupling. In this situation, frustration arises because the ferromagnetic Fe^III–O–Ru^V couplings align next-nearest neighbour Fe spins ferromagnetically, but the Fe^III–O–O–Fe^III super–super exchange coupling is antiferromagnetic and the two couplings have about the same strength. We propose that a similar frustration between nearest-neighbour Fe^III–O–Rh^IV and next-nearest-neighbour Fe^III–O–O–Fe^III couplings is responsible for the spin-glass behaviour in La_0.5Sr_0.5Fe_0.5Rh_0.5O₃.

It is interesting to note that the contrasting magnetic behaviour of La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ can be understood on the basis of the relative strengths of the different transition-metal couplings in the two systems – the dominance of 3d–3d couplings in La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ leading to ferromagnetism; the comparable strengths of 3d–3d, 3d–4d couplings in La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ resulting in spin-glass behaviour.

Conclusions

Hole doping of the perovskite phases LaMn_0.5Rh_0.5O₃ and LaFe_0.5Rh_0.5O₃ leads to the oxidation of Rh³⁺ to Rh⁴⁺ in the resulting La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ compounds. The stabilization of Rh⁴⁺ in the presence of the readily oxidizable Mn³⁺ and Fe³⁺ cations suggests that the 3d Mn/Fe states and 4d Rh states are of similar energy, so that if the electronic bandwidth of the phases could be increased, by decreasing the magnitude of the octahedral tilting distortion for example, or the 3d and 4d cations could be ordered, correlated electronic behaviour is likely, in line with computational predictions for high-valent rhodium oxides.⁴¹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Experiments at the Diamond Light Source were performed as part of the Block Allocation Group award “Oxford Solid State Chemistry BAG to probe composition–structure–property relationships in solids” (EE13284). NH acknowledges funding from the “State Programme on Education of Azerbaijani Youth Abroad in 2007–2015” by the Ministry of Education of Azerbaijan. The XPS data collection was performed at the EPSRC National Facility for XPS (“HarwellXPS”), operated by Cardiff University and UCL, under Contract No. PR16195.

Notes and references

1. R. J. D. Tilley, Perovskites: Structure-Property Relationships, John Wiley and Sons, Chichester, 2016.
2. J. B. Goodenough and J.-S. Zhou, Chem. Mater., 1998, 10, 2980–2993.
3. T. Saha-Dasgupta, Mater. Res. Express, 2020, 7, 014003.
4. A. Halder, P. Sanyal and T. Saha-Dasgupta, Phys. Rev. B, 2019, 99, 020402(R).
5. K. L. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680.
6. K. I. Kobayashi, T. Kimura, Y. Tomioka, H. Sawada, K. Terakura and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 11159–11162.
7. H. Kato, T. Okuda, Y. Okimoto, Y. Tomioka, Y. Takenoya, A. Ohkubo, M. Kawasaki and Y. Tokura, Appl. Phys. Lett., 2002, 81, 328–330.
8. J. B. Goodenough, Magnetism and the chemical bond, Wiley, New York, 1963.
9. S. Kanungo, B. H. Yan, M. Jansen and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214414.
10. X. D. Ou, Z. W. Li, F. R. Fan, H. B. Wang and H. Wu, Sci. Rep., 2014, 4(7542), 7541–7544.
11. R. Morrow, M. A. McGuire, J. Q. Yan and P. M. Woodward, Inorg. Chem., 2018, 57, 2989–3001.
12. S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1–36.
13. A. E. Smith, A. W. Sleight and M. A. Subramanian, Mater. Res. Bull., 2010, 45, 460–463.
14. P. D. Battle and J. F. Vente, J. Solid State Chem., 1999, 146, 163–167.
15. J. Ting, B. J. Kennedy, Z. Zhang, M. Avdeev, B. Johannessen and L. Y. Jang, Chem. Mater., 2010, 22, 1640–1646.
16. C. Schinzer, J. Phys. Chem. Solids, 2000, 61, 1543–1551.
17. K. Knizek, J. Hejtmanek, M. Marysko, Z. Jirak and J. Bursik, Phys. Rev. B, 2012, 85, 134401.
18. J. Li, A. E. Smith, K. S. Kwong, C. Powell, A. W. Sleight and M. A. Subramanian, J. Solid State Chem., 2010, 183, 1388–1393.
19. S. V. Streltsov, V. V. Gapontsev and D. I. Khomskii, J. Phys.: Condens. Matter, 2016, 28, 086005.
20. A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report LAUR 86-748, 2000.
21. K. Lagarec and D. G. Rancourt, Recoil: Mössbauer spectral analysis software for windows, 1998.
22. J. P. Hodges, S. Short, J. D. Jorgensen, X. Xiong, B. Dabrowski, S. M. Mini and C. W. Kimball, J. Solid State Chem., 2000, 151, 190–209.
23. Y. Takeda, K. Kanno, T. Takada, O. Yamamoto, M. Takano, N. Nakayama and Y. Bando, J. Solid State Chem., 1986, 63, 237–249.
24. E. N. K. Glover, S. G. Ellington, G. Sankar and R. G. Palgrave, J. Mater. Chem. A, 2016, 4, 6946–6954.
25. T. K. Le, D. Flahaut, H. Martinez, N. Andreu, D. Gonbeau, E. Pachoud, D. Pelloquin and A. Maignan, J. Solid State Chem., 2011, 184, 2387–2392.
26. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
27. T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441–2449.
28. E. S. Ilton, J. E. Post, P. J. Heaney, F. T. Ling and S. N. Kerisit, Appl. Surf. Sci., 2016, 366, 475–485.
29. B. Bakowski, P. D. Battle, E. J. Cussen, L. D. Noailles, M. J. Rosseinsky, A. I. Coldea and J. Singleton, Chem. Commun., 1999, 2209–2210.
30. N. Kamegashira, Y. Miyazaki and H. Yamamoto, Mater. Chem. Phys., 1984, 11, 187–194.
31. K. Kuroda, K. Shinozaki, K. Uematsu, N. Mizutani and M. Kato, J. Am. Ceram. Soc., 1980, 63, 109–110.
32. H. J. Gysling, J. R. Monnier and G. Apai, J. Catal., 1987, 103, 407–418.
33. K. Yamaura and E. Takayama-Muromachi, Phys. Rev. B, 2001, 64, 224424.
34. C. Schinzer and G. Demazeau, J. Mater. Sci., 1999, 34, 251–256.
35. J. Blasco, J. Garcia, J. Campo, M. C. Sanchez and G. Subias, Phys. Rev. B, 2002, 66, 174431.
36. E. J. Cussen, M. J. Rosseinsky, P. D. Battle, J. C. Burley, L. E. Spring, J. F. Vente, S. J. Blundell, A. I. Coldea and J. Singleton, J. Am. Chem. Soc., 2001, 123, 1111–1122.
37. J. Goodenough, R. J. Arnott, N. Menyuk and A. Wold, Phys. Rev., 1961, 124, 373–384.
38. M. T. Haque, H. Satoh and N. Kamegashira, J. Alloys Compd, 2005, 390, 115–121.
39. P. D. Battle, T. C. Gibb, C. W. Jones and F. Studer, J. Solid State Chem., 1989, 78, 281–293.
40. P. D. Battle, S. K. Bollen and A. V. Powell, J. Solid State Chem., 1992, 99, 267–275.
41. A. Halder, D. Nafday, P. Sanyal and T. Saha-Dasgupta, npj Quantum Mater., 2018, 3, 17.

---

Footnote

† Electronic supplementary information (ESI) available: Mn 2P and Fe 2P XPS from La_0.5Sr_0.5Mn_0.5Rh_0.5O₃ and La_0.5Sr_0.5Fe_0.5Rh_0.5O₃ respectively; additional fits to ⁵⁷Fe Mössbauer data from La_0.5Sr_0.5Fe_0.5Rh_0.5O₃. See DOI: 10.1039/d0dt02466j

---