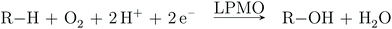Is density functional theory accurate for lytic polysaccharide monooxygenase enzymes?

Abstract

The lytic polysaccharide monooxygenase (LPMO) enzymes boost polysaccharide depolymerization through oxidative chemistry, which has fueled the hope for more energy-efficient production of biofuel. We have recently proposed a mechanism for the oxidation of the polysaccharide substrate (E. D. Hedegård and U. Ryde, Chem. Sci., 2018, 9, 3866–3880). In this mechanism, intermediates with superoxide, oxyl, as well as hydroxyl (i.e. [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺) cores were involved. These complexes can have both singlet and triplet spin states, and both spin-states may be important for how LPMOs function during catalytic turnover. Previous calculations on LPMOs have exclusively been based on density functional theory (DFT). However, different DFT functionals are known to display large differences for spin-state splittings in transition-metal complexes, and this has also been an issue for LPMOs. In this paper, we study the accuracy of DFT for spin-state splittings in superoxide, oxyl, and hydroxyl intermediates involved in LPMO turnover. As reference we employ multiconfigurational perturbation theory (CASPT2).

---

Introduction

Atmospheric oxygen is believed to have been introduced in our atmosphere 2.0–2.5 billion years ago.¹ Nature has since devised numerous ways to exploit O₂ to perform biochemical transformations, often by the use of transition metals. Copper is one of the metals employed for O₂ activation by many enzyme families.² A relatively new member of the O₂-activating enzymes is lytic polysaccharide monooxygenase (LPMO). The LPMOs were discovered in 2010^3,4 and were shown to boost polysaccharide depolymerization through oxidative chemistry. This was a paradigm shift in our understanding of how highly stable polysaccharides, such as cellulose, are decomposed, which previously was believed to be solely hydrolytic. The discovery of LPMOs have fueled the hope for production of biofuels from cellulosic biomass,^5–9 which could reduce the cost of biofuel production, because cellulose is cheap and estimated to be the most abundant polysaccharide on Earth.¹⁰

The overall oxidation reaction of the LPMOs involves O₂ and two reduction steps (cf.Scheme 1).

Scheme 1 Reaction catalyzed by LPMO, where R–H denotes a polysaccharide.

However, it should be noted that this reaction may evolve through initial generation of peroxide as it was recently shown that both O₂ and H₂O₂ can be employed as co-substrate.^11,12 Further, the substrate-free LPMO can activate O₂ and produce H₂O₂.^13–15 The active site responsible for this chemistry is shown in Fig. 1 in a form where O₂ is bound to Cu together with a part of the substrate. The figure also shows the two substrate carbon positions (C1 and C4) oxidised by LPMOs; the positions are at the glycoside link between the sugar units. The active site itself is comprised of the copper ion, coordinated by two histidine residues, one of which coordinates with both the imidazole sidechain and the (terminal) amino group. This active site is conserved among all known LPMOs, which otherwise show a rather large sequence variation.^16,17 This variation is evident even close to the active site. In the AA9 family of the LPMOs (which is the focus of the current article), there is a nearby tyrosine residue that can act as Cu ligand (depending on the copper oxidation state), whereas some other LPMO families lack this residue.

Fig. 1 General structure of AA9 LPMO Ls(AA9)A, in complex with a substrate (taken from the 5ACF structure³⁰), as well as the structure of the active site, from the QM/MM optimized structure of the [CuO₂]⁺ intermediate,³² illustrating the employed QM system.

Regardless of whether O₂ or H₂O₂ is used as co-substrate, the mechanism employed is still unknown: most structural information is obtained for the LPMO resting state without substrate or co-substrates bound.^18–27 A few crystal structures of O₂-bound LPMOs^28,29 or LPMOs complexed with substrates^30,31 have been reported. However, no structural data have been obtained for oxygen-bound intermediates complexed with substrates. Thus, the intermediate shown in Fig. 1 was obtained from a combined quantum mechanics and molecular mechanics (QM/MM) optimization.³² These calculations further showed that the species in Fig. 1 is best described as superoxide ion (O₂˙⁻) bound to a Cu(II) ion.

A key part of the LPMO mechanism is believed to be the abstraction of a hydrogen atom from the C–H bond in the C1 or C4 positions of the polysaccharide substrate. Despite efforts from both theory and experiments, the active species that abstracts the hydrogen from the polysaccharide substrate has been the matter of controversy.

Some suggestions for the mechanism employs a superoxide for the C–H abstraction,^6,19,20,33 but other suggestions have involved hydrogen abstraction from an oxyl (O˙⁻) species.^6,8,34,35 Studies on model systems have also suggested hydroxy^8,36 and hydroperoxy complexes³⁷ as the reactive species.

Rather few studies have addressed the mechanism of LPMOs with quantum mechanical (QM) methods.^{14,32,34,38–41} We and a few other groups have recently initiated investigations of the LPMO mechanism employing both QM-cluster and QM/MM calculations.^32,40,41 From these calculations we could show that hydrogen abstraction by complexes involving an intact O–O is not energetically feasible,⁴¹ whereas both oxyl^32,34,41 or hydroxy complexes^32,41 are more reactive.

While important mechanistic insight thus have been obtained from computational studies, all investigations so far have relied exclusively on density functional theory (DFT). Yet, we have for some intermediates shown how the reaction as well as spin-state energetics depend quite strongly on the choice of the DFT functional.³² Moreover, in metalloproteins whose active sites resemble LPMOs^42–45 both Cu–superoxide and Cu–oxyl species are known to involve electronic structures where DFT occasionally fails to predict the correct ground state.⁴⁶

In this study, we address the performance of DFT for the spin-state splittings in several LPMO intermediates that have been shown to be important in various parts of the LPMO mechanism, employing QM/MM optimised structures³² from our previous studies. The target intermediates are the superoxide, oxyl and hydroxyl complexes, i.e., intermediates with [CuO₂]⁺, [CuO]⁺, and [CuOH]²⁺ cores, respectively. The first intermediate is included although it is probably not relevent for C–H abstraction. However, it is still the only structurally characterized intermediate^28,29 after introduction of O₂, and its inclusion more firmly connects our study with experimentally observed intermediates. All three intermediates have singlet and triplet spin states close in energy according to DFT predictions³² and thus both spin states may be involved in the mechanism. While we are not aware of any experimental studies directly probing the spin-state splitting of the investigated species, we have for the [CuO₂]⁺ intermediate previously confirmed that a superoxide provides the best fit to the experimental structure¹⁵ and this interpretation complies with close lying triplet and singlet spin states.

The performance of DFT will here be estimated using a reference method and for this purpose we employ multiconfigurational perturbation theory to the second order, based on a complete active-space wavefunction (CASPT2),^47,48 which we compare to the results of several popular DFT functionals.

Computational details

We study three different intermediates. All structures were taken from our previous QM/MM calculations³² in which they were optimized in triplet and singlet spin-states, respectively. All were optimized with the same size of QM region; an example is provided in Fig. 1 for the intermediate with O₂ bound to copper. We will here use the short-hand notation [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺, for these three intermediates. The QM/MM calculations and their setup were described in more detail in ref. 32. Here we only note that the setup is based on the crystal structure from Frandsen et al.³⁰ (PDB: 5ACF) and the QM system included the imidazole ring of His78 and the phenol ring of Tyr164, both capped with a hydrogen atom replacing C^α. The entire His1 residue, which coordinates to Cu through both the terminal amino group and the imidazole sidechain, was also included and the neighboring Thr2 residue was included up to the C^α atom, which was replaced by a hydrogen atom. The fifth ligand (trans to the terminal NH₂ group) was either superoxide, oxyl or hydroxide, giving rise to [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺ species, respectively. In addition, the QM system also contained two glucose rings (from the substrate) and a second-sphere histidine residue (His147, protonated on the N^ε2 atom).

The three intermediates have electronic structures that can attain both singlet and triplet spin states. When necessary, we designate the spin state of the intermediate by giving the spin multiplicity (2S + 1) in superscript, e.g., ³[CuO₂]⁺ and ¹[CuO₂]⁺ in case of the superoxide species. The singlet states ¹[CuO₂]⁺ and ¹[CuO]⁺ were of open-shell nature and were optimized as unrestricted open-shell (broken-symmetry) singlets. The open-shell nature was confirmed by analyzing the spin-densities (cf.Table 2). The comparison between triplet and open-shell singlet were done directly from the obtained energies and no correction schemes were employed. For ¹[CuOH]²⁺, attempts to optimize the open-shell singlet yielded essentially the closed-shell state (the resulting spin densities were small; the Cu and O atoms in the ¹[CuOH]²⁺ moiety carried spin densities of 0.09 and 0.07 respectively). Energies of the closed- and open-shell states were within 1 kJ mol⁻¹ and the structures were identical. Therefore, we used the structure and energies of the closed-shell singlet state.

Table 1 Bond distances (in Å) and angles (in °) for the considered complexes

Complex	Cu–O1	Cu–N1	Cu–N2	Cu–N3	Cu–OTyr	O1–O2/H	Cu–O1–O2/H
^3[CuO2]^+	2.08	1.96	1.98	2.11	2.29	1.28	116
^1[CuO2]^+	2.05	1.96	1.98	2.10	2.29	1.29	117
^3[CuO]^+	1.89	1.95	1.99	2.12	2.40	—	—
^1[CuO]^+	1.85	1.95	1.95	2.11	2.40	—	—
^3[CuOH]^2+	1.93	1.96	2.00	2.13	2.32	0.99	123
^1[CuOH]^2+	1.85	1.90	1.95	2.05	2.35	0.99	117

---

Table 2 The combined weight of copper 3d and oxygen ligand (from superoxide, oxyl or hydroxyl) in orbitals with occupation numbers significantly different from 2 or 0 in Fig. 3, 4 and 5. The results are obtained with ANO basis sets

Intermediate	Occ.	3d	2p
^3[CuO2]^+	1.000	0.00	1.30
^3[CuO2]^+	0.999	0.92	0.05
^1[CuO2]^+	1.241	0.46	0.60
^1[CuO2]^+	0.757	0.44	0.72
^3[CuO]^+	1.001	0.00	0.99
^3[CuO]^+	1.009	0.90	0.13
^1[CuO]^+	1.323	0.49	0.50
^1[CuO]^+	0.677	0.45	0.55
^3[CuOH]^2+	1.003	0.01	0.96
^3[CuOH]^2+	1.005	0.95	0.05
^1[CuOH]^2+	1.688	0.43	0.44
^1[CuOH]^2+	0.310	0.53	0.46

---

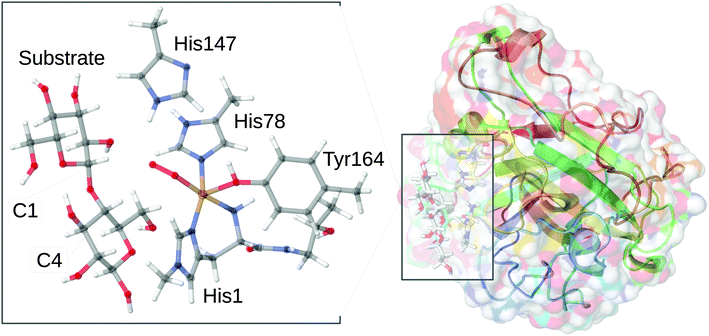
Owing to the large computational cost, the CASPT2 calculations were performed on truncated systems (called model 1), compared to the QM system used in our QM/MM calculations³² (which are called model 2). The truncated model 1 for all three studied states are shown in Fig. 2 and selected bond lengths are given in Table 1. As can be inferred from Fig. 1 and 2, the truncation in model 1 includes removal of the second-sphere histidine and the substrate, while methyl groups were replaced by hydrogen atoms. For the bidentate histidine ligand, the carbonyl C was replaced by a hydrogen atom (i.e. excluding all parts of Thr2). The structures were obtained by adding H atoms at a C–H distance of 1.10 Å along the C–C bond (in the case of the one N–C bond where C was replaced on His1, the N–H distance is 1.01 Å). No re-optimizations of the structures were performed in order to keep the structures as close to the protein structures as possible.

Fig. 2 Structures of the ³[CuO₂]⁺, ³[CuO]⁺ and ³[CuOH]²⁺ complexes used in the CASPT2 calculations. Only structures in triplet spin states are shown. The structural differences between singlet and triplet are small: up to 0.04 Å in the first coordination sphere for [CuO₂]⁺ and [CuO]⁺ and up to 0.08 Å for [CuOH]²⁺ (cf.Table 1).

The CASSCF/CASPT2⁴⁸ calculations were performed with MOLCAS 8.2.⁴⁹ The selected active space included 12 electrons in 12 orbitals, denoted CAS(12,12), for [CuO₂]⁺. We employed CAS(14,16) for [CuO]⁺ and [CuOH]²⁺. The selection of orbitals for the active space for the various species is described in more detail in the Results section. We used two different basis sets in the CASSCF/CASPT2 calculations. The first involved ANO-RCC-VQZP ([7s6p4d3f2g1h]) for Cu⁵⁰ and ANO-RCC-VTZP for the C, N and O ([4s3p2d1f]) for all and [3s1p] for H.⁵¹ The second was a Dunning correlation-consistent (cc) basis set with cc-pwCVQZ-DK for Cu,⁵² cc-pVTZ-DK for C, N and O, and cc-pVDZ-DK for H.⁵³ Scalar relativistic effects were included with the Douglas–Kroll–Hess (DKH) approach to the second order.^54–56 For the CASPT2 calculations, all valence electrons and 3s3p semi-core electrons of copper were correlated. The evaluation of two-electron integrals in MOLCAS were approximated with Cholesky decomposition and using an on-the-fly generated auxiliary basis set.⁵⁷ All PT2 calculations were performed with the standard ionisation potential–electron affinity (IPEA) Hamiltonian shift of 0.25 a.u.⁵⁸

The DFT calculations were done with the def2-TZVPP basis set on all atoms.⁵⁹ We employed four different functionals, namely TPSS,⁶⁰ TPSSh,⁶¹ B3LYP^62–64 and M06L.⁶⁵ These functionals were chosen because they represent four commonly employed functionals employing different design strategies: the TPSS and M06L functionals are both meta-GGA but while the former was constructed to satisfy exact physical constraints without empirical parameters, the latter is heavily parameterized (and includes transition metal compounds in its parameterization). The TPSSh functional is a hybrid formulation of TPSS, adding 10% exact Hartree–Fock exchange, while the B3LYP functional is an empirical hybrid functional that has been a standard method in quantum chemistry since its development in the early 90's. For non-hybrid functionals the DFT calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set (the resolution-of-identity approximation),^66,67 employing standard def2-TZVPP auxiliary basis sets. The empirical D3 dispersion corrections were included with the Becke–Johnson damping.⁶⁸ All DFT calculations were performed with the Turbomole 7.1 software.⁶⁹

We additionally carried out a series of coupled-cluster (CC) calculations employing CC with singles, doubles and perturbative triples, CCSD(T) as implemented in Turbomole 7.1. The calculations employed the cc-pVTZ basis set⁵² for Cu and def2-SV(P)⁷⁰ for the other atoms. All the CCSD(T) calculations were spin restricted. However, the D1 amplitudes for the singlet states turned out to be rather large and in all cases over the threshold D1 > 0.15,⁷¹ suggesting multiconfigurational character (0.24 for [CuO₂]⁺, 0.19 for [CuO]⁺ and 0.27 for [CuOH]²⁺). As discussed below, the CASPT2 calculations also indicated that the singlet states are multiconfigurational and hence we will not discuss the CCSD(T) results in detail.

We finally note that on several occasions only values for one representative basis set or functional are reported. Thus, all shown orbitals are obtained with ANO type basis set. The Dunning-type basis set gave rise to identical orbitals. Similarly, the reported Mulliken spin densities were for all CASPT2 calculations obtained with ANO-type basis set and also here the Dunning basis set led to very similar results. With DFT, the reported Mulliken spin densities are obtained with the TPSS functional (and def2-TZVPP basis set) and also here the same conclusions are obtained with other functionals.

Results and discussion

In this study, we compare energy splittings between the singlet and triplet spin states (ΔE_ts = E_triplet − E_singlet) obtained with either DFT or CASPT2. We consider three LPMO intermediates, [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺ and the results are discussed in separate sections.

The superoxide state

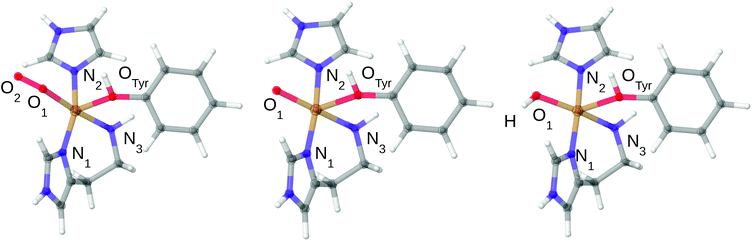
Earlier studies on LPMO^{14,32,34,38–41} and other copper enzymes^2,46 have shown that [CuO₂]⁺ is often best interpreted as a doublet superoxide radical (O₂⁻) bound to a doublet Cu(II) ion. In DFT, this can give rise to either a triplet state or an open-shell (broken-symmetry) singlet state, depending on the alignment of the two unpaired spins. To describe the [CuO₂]⁺ moiety, we employed a CAS(12,12) active space for both the singlet and triplet spin states. The chosen active-space orbitals are shown in Fig. 3 in combination with natural occupation numbers (shown below the orbitals).

Fig. 3 Active orbitals and their occupation numbers from the CAS(12,12) calculation with ANO-RCC type basis sets for the [CuO₂]⁺ species.

The active space includes one bonding ligand orbital that is located between Cu, the three nitrogen atoms of the two histidine ligands, and O₂⁻. This orbital has an occupation number close to two (1.997) for both states. It could be interpreted as O₂-antibonding orbital, albeit with large amplitude on histidine. We decided to include this orbital due to its large amplitude on O₂⁻ in both singlet and triplet species. The active space is further comprised of the five 3d orbitals, of which four are doubly occupied with occupation numbers between 1.988 and 1.989 in both the singlet and triplet states. The fifth Cu 3d_z² orbital interacts with the oxygen π* orbitals and they show a pair of partly occupied orbitals: in the triplet state, they both have occupation numbers around 1.0 and are of rather pure 3d and oxygen π* character, respectively (see Table 2 where the combined weight of the constituting atomic orbitals are given). With four of the five 3d orbitals doubly occupied, and the last 3d orbital singly occupied, an Cu(II) interpretation seems reasonable. In the singlet state, the singly occupied orbitals have occupation numbers of 1.241 and 0.757, respectively, and are more mixed between Cu 3d and O 2p character (see Table 2). The remaining five orbitals have low occupation numbers (0.005–0.012) in both triplet and singlet spin states. They are included as a second shell of d orbitals, which has previously shown to be important to obtain accurate CASPT2 energies.⁷² Overall, the orbitals for the singlet and triplet states are similar, which is desired for ensuring accurate spin-state splittings. We also note that a similar active space was employed in the study of a protein with an active site resembling the one studies here.⁴⁶

For the singlet state, a closer investigation of the underlying CASSCF wavefunction reveals that two configurations have large weights, 0.61 and 0.37, respectively. The four 3d orbitals and the O₂⁻ orbital (with occupation number 1.997) are doubly occupied in both configurations, and they differ instead in the occupation of the two orbitals with occupation numbers 1.241 and 0.757. In the first configuration, the former is doubly occupied and the latter unoccupied, whereas the opposite is true for the second configuration; in combination with the fact that the two partially occupied orbitals are a mixture of copper 3d orbitals and oxygen 2p orbitals (cf.Table 2), we assign the oxidation state as Cu(II). Thus, both spin states represent primarily a Cu(II)–superoxide state, but with different spin couplings.

The spin-state splittings from the CAS(12,12)PT2 calculations as well as the four investigated DFT functionals are shown in Table 3. The singlet–triplet splitting energies are quite small for all methods. The DFT methods predict the triplet state to be most stable, by 16–19 kJ mol⁻¹ for TPSS, TPSSh and B3LYP and by 31 kJ mol⁻¹ for M06-L. Interestingly, CASPT2 predicts that the singlet is 2 kJ mol⁻¹ more stable than triplet state, meaning that the two states are essentially degenerate.

Table 3 Singlet–triplet splitting energies ΔE_ts = E_t − E_s (kJ mol⁻¹) obtained with different methods using model 1. The CASPT2 results are with ANO basis sets (results with Dunning-type basis sets shown in parentheses). All DFT results are obtained with def2-TZVPP basis set

ΔEts (kJ mol^−1)
Intermediate	CASPT2	TPSS	TPSSh	B3LYP	M06-L
[CuO2]^+	2.4 (2.1)	−16.0	−15.5	−19.0	−30.9
[CuO]^+	−20.7 (−21.2)	7.4	5.5	4.4	−1.3
[CuOH]^2+	93.2 (92.2)	62.0	40.0	30.7	49.3

---

The results in Table 3 were obtained with model 1. For the B3LYP and TPSS functionals, we also estimated ΔE_ts with the larger model 2. The results from this investigation are shown in Table 4, showing that the larger model decreases the stability of the triplet state by 3–6 kJ mol⁻¹.

Table 4 Singlet–triplet splitting energies ΔE_ts = E_t − E_s (kJ mol⁻¹) obtained with different functionals and def2-TZVPP basis sets with model 2

ΔEts (kJ mol^−1)
Intermediate	TPSS		B3LYP
	QM^a	QM/MM^b	QM^a	QM/MM^b
a Energy obtained in vacuum for the QM/MM optimised structures with model 2. b The corresponding QM/MM energies (from ref. 32).
[CuO2]^+	−12.8	−12.3	−13.4	−15.3
[CuO]^+	−5.9	−6.9	−3.7	−3.5
[CuOH]^2+	36.1	45.1	21.0	33.8

---

Thus, our results show that care must be exercised when assessing relative spin-states with DFT for LPMO intermediates and that for the TPSS, TPSSh and B3LYP functionals, spin-states separated by 20 kJ mol⁻¹ or less can essentially not be distinguished based on DFT. The M06-L functional is further off (by 30 kJ), although this functional was parameterized employing transition-metal systems.⁶⁵ Interestingly, a previous theoretical study of a [CuO₂]⁺ moiety with several different ligands⁴⁶ showed that CAS(12,12)PT2 predicts the triplet to be most stable for most ligands, but in one case, the singlet was found to be more stable. The energy differences varied between 13 kJ mol⁻¹ and −25 kJ mol⁻¹, showing that the ligands can have large influence on the singlet–triplet splitting. Moreover, DFT does not always predict this effect correct: in particular, the M06-L functional gave qualitatively wrong spin-state splittings on several occasions.⁴⁶

The oxyl state

We next turn to the [CuO]⁺ species, which is among the states that we and others previously have suggested to be active in the C–H abstraction.^32,34,41 The [CuO]⁺ intermediate has in previous studies (see e.g.ref. 32) been interpreted as a doublet O⁻ radical bound to doublet Cu(II), giving either a triplet or an open-shell singlet state.

The CASSCF active-space orbitals and the corresponding occupation numbers are shown in Fig. 4. Our selected active spaces include the three oxygen 2p orbitals, the five Cu 3d orbitals and the five Cu 4d (double-shell) orbitals. In addition, we included the three O 3p orbitals, leading to the shown CAS(14,16) active space. This active space is slightly larger than the active space employed in ref. 46, due to the addition of the oxygen 3p orbitals. As for the [CuO₂]⁺ intermediate, the triplet state has two orbitals with occupation numbers close to 1. In [CuO]⁺, these orbitals are of Cu 3d_z² and O 2p character, showing that triplet [CuO]⁺ can be interpreted as oxyl, i.e., with one unpaired electron on Cu(II) and another on O⁻. The situation in the singlet is a bit less clear. It is again the orbitals of Cu 3d_z² and O 2p character that have occupation numbers that deviate significantly from 0 or 2: the corresponding occupation numbers are 1.323 and 0.677, respectively (cf.Fig. 4). Compared to the triplet, these two orbitals are a mix of oxygen 2p and 3d orbitals, as seen for the [CuO₂]⁺ intermediate (cf.Table 2). Investigation of the underlying CASSCF wavefunction again shows some degree of multiconfigurational nature with two configurations having significant contributions to the total wavefunction with weights 0.62 and 0.32, respectively. Similar to the [CuO₂]⁺ intermediate both configurations have four doubly occupied Cu 3d orbitals as well as two doubly occupied ligand orbitals, in this case the oxyl 2p orbitals with occupation numbers 1.973 and 1.976. In addition, the configuration with the largest weight has the orbital with occupation number 1.323 occupied, whereas the orbital with occupation number 0.677 is empty. The opposite is true for the second-largest configuration. With a similar argument as for [CuO₂]⁺, the large mixing of copper 3d orbital and ligand (oxygen) 2p orbitals for these two orbitals leads to an interpretation where Cu(II) and a O⁻ radical are spin-coupled to a singlet.

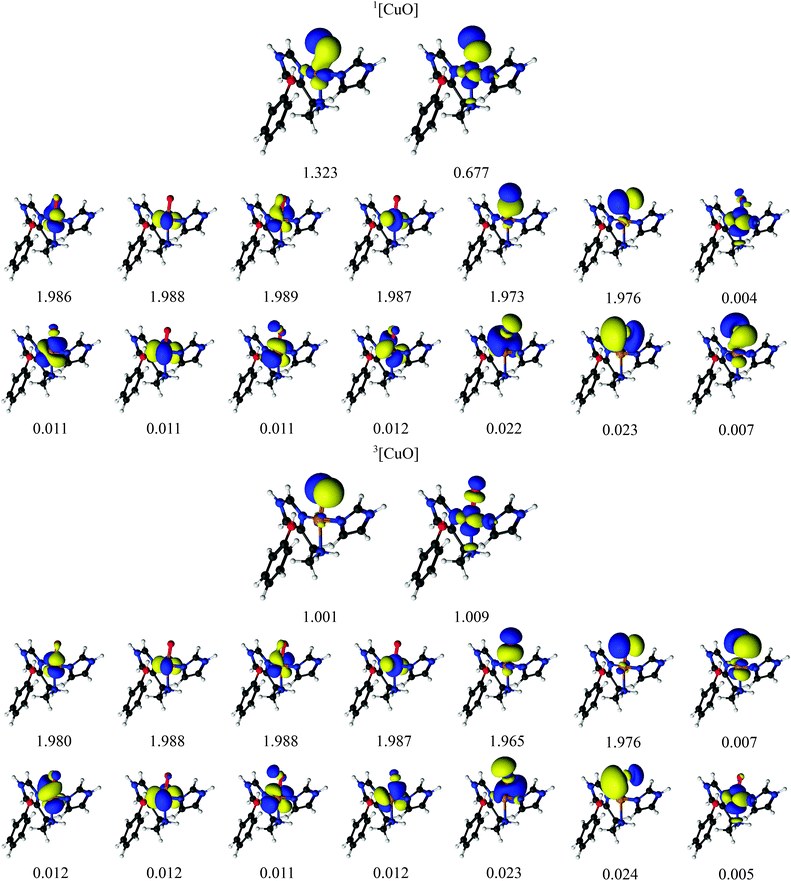Fig. 4 Active natural orbitals and their occupation numbers from a CAS(14,16) calculation with ANO-RCC type basis sets for the [CuO]⁺ species.

The singlet–triplet splittings from DFT and CASPT2 are shown in Table 3. The triplet is found to be 21 kJ mol⁻¹ more stable than the singlet state with CAS(14,16)PT2, independent of the basis set. On the other hand, the DFT calculations predict that the singlet and triplet are essentially degenerate: TPSS, TPSSh and B3LYP predict the singlet to be 4–7 kJ mol⁻¹ more stable than the triplet, whereas M06-L predicts the triplet to be 1 kJ mol⁻¹ more stable than the triplet. We note that the splitting was also predicted to be quite small with the larger model 2 and enlarging the model stabilizes the triplet by 8–14 kJ mol⁻¹, making the triplet slightly more stable in all cases (cf.Table 4). Hence, we can expect −21 kJ mol⁻¹ to be an lower limit for the singlet–triplet splitting, which is likely to increase for a larger model, assuming CASPT2 behaves similar to DFT in this regard. Since the splitting is already low, both singlet and triplet states may participate in the mechanism. We can conclude that the singlet–triplet is indeed small as predicted by DFT, and the DFT methods are in this regard in reasonable agreement with CASPT2 for the oxyl species.

The hydroxyl state

Finally, we investigated also the [CuOH]²⁺ hydroxy species. As described in ref. 32, the [CuOH]²⁺ species is readily formed by protonation of [CuO]⁺ and may also participate in the C–H abstraction in LPMOs. The [CuOH]²⁺ moiety might consist of OH⁻ bound to Cu(III). Alternatively, it could be described as a hydroxyl OH radical bound to doublet Cu(II), giving either a triplet or an open-shell singlet. Finally, the species may also be formulated as a singlet OH⁺ bound to Cu(I). With DFT, we obtained both the triplet and the singlet, the latter in both closed- and open-shell form. However, both the structure and the energy of the open-shell singlet turned out to be almost identical to those of the closed-shell singlet and the spin densities were small, and we therefore discuss only the closed-shell singlet for the DFT calculations.

In the CASPT2 calculations, we employed a CAS(14,16) active-space with orbitals and corresponding natural occupation numbers shown in Fig. 5. We use the same active space as for the [CuO]⁺ species, including five Cu 3d orbitals, five correlating Cu 4d orbitals, a pair of bonding and anti-bonding orbitals on the OH ligand as well as two lone-pair orbitals with two correlating O 3p orbitals. The two O 2p orbitals and four of the Cu 3d orbitals were found to be doubly occupied with occupation numbers close to two for both the singlet and the triplet. The fifth Cu 3d orbital (3d_z²) and one O 2p orbital were singly occupied in the triplet state with occupation numbers of 1.00, indicating a OH radical bound to a Cu(II) coupled to a total triplet state. The singlet state is again somewhat more complicated: the two orbitals having occupation numbers with significant deviation from 2.0 indicates that the singlet is not closed-shell. The two partially occupied orbitals (with occupation numbers 1.688 and 0.310, respectively) have large character of both 3d- and 2p atomic orbitals, although to varying degree (see Table 2). Investigating the underlying wave function shows (as expected) that more than one configuration contribute to the ground-state wavefunction: two configurations have large weights of 0.80 and 0.14, respectively. In the configuration with the largest weight, the four 3d orbitals as well as the three OH-based orbitals with occupation numbers 1.975, 1.980 and 1.688 are double occupied. For the configuration with smaller weight (0.14), the electrons in the orbital with occupation number 1.688 are now interchanged with the orbital with occupation number 0.310, which then becomes doubly occupied. Since the two orbitals with occupation numbers 1.688 and 0.310 are shared between Cu 3d and OH orbitals, we again suggest that the singlet state has one electron on the Cu center, which is bound to a OH radical, spin-coupled to a singlet i.e. Cu(II) and OH.

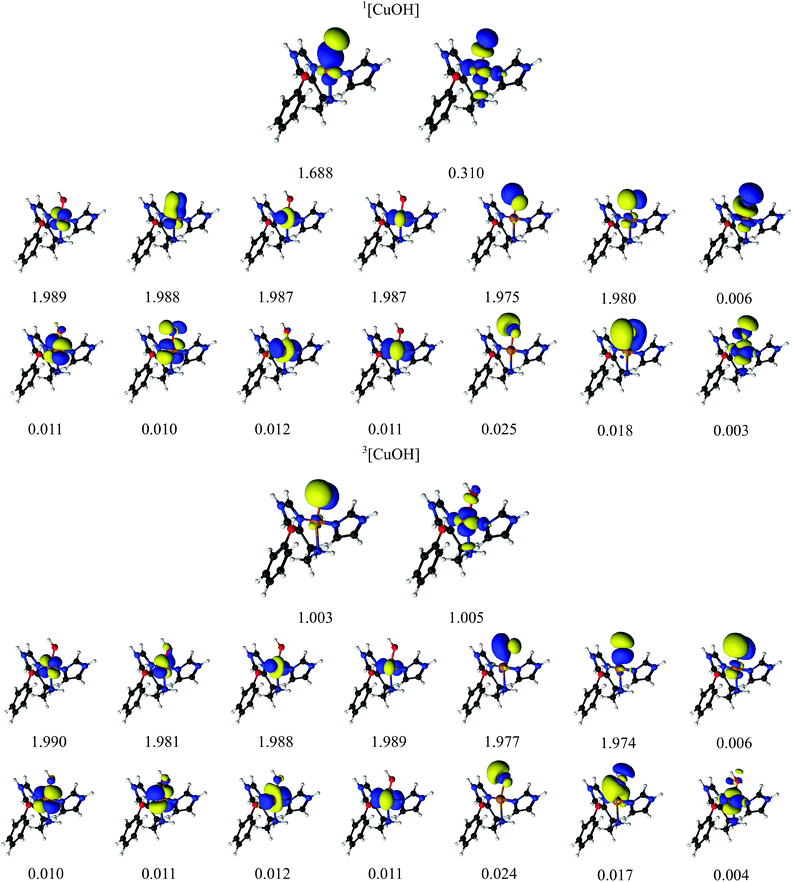Fig. 5 Active orbitals and their occupation numbers from a CAS(14,16) calculation with ANO-RCC type basis sets for the [CuOH]²⁺ species.

The calculated singlet–triplet splittings are given in Table 3 and it can be seen that CASPT2 predicts the singlet to be the more stable state by 92–93 kJ mol⁻¹. All DFT methods agree with this conclusion, but they overestimate the stability of the triplet significantly. The results depend quite strongly on the DFT functional, but the results shows differences of 31–62 kJ mol⁻¹ from CASPT2 and are thus significantly off. The TPSS functional gives results closest to CASPT2 (with a difference of 31 kJ mol⁻¹), whereas B3LYP gives the largest difference (62 kJ mol⁻¹).

The effect of enlarging the model system was again investigated by DFT and the results are compiled in Table 4. The larger model gives between 26 kJ mol⁻¹ (TPSS) and 10 kJ mol⁻¹ (B3LYP) lower singlet–triplet splitting energies, i.e. always favoring the triplet state. However, even by assuming the largest of these truncation errors (i.e. the one obtained with the TPSS functional), the singlet is still expected to be significantly more stable than the triplet.

In our previous study,³² the reaction in which [CuOH]²⁺ abstracts C–H from the substrate was found to involve both the singlet and triplet potential-energy surfaces and the reaction energy showed a rather strong dependence on employed the exchange–correlation functional.³² The present results suggest that part of the reason for this dependency is that the employed DFT functionals struggle to describe the electronic structure of the [CuOH]²⁺ singlet correctly.

Discussion

In this section, we compare the three intermediates in terms of calculated spin-densities and relate these findings to the findings from the previous section. We also comment on the expected accuracy for CASPT2 for spin-state splittings of transition metals.

Analyses of the most important configurations, as well as the active space orbitals for both triplet and singlet spin-states in the [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺ intermediates, in all cases suggested a Cu(II) oxidation state. This fits well with the Mulliken spin-densities (shown in Table 5), showing a large spin population on the copper atom for the triplet states (∼0.9 for CAS wave functions and around 0.4–0.6 for DFT). The spin-density obtained from CAS is quite similar for the three intermediates in their triplet spin states (the singlet gives per definition all zero). In addition, Table 5 includes the total Mulliken 3d occupations from the copper atom, which for all intermediates and spin-states are around 9, also in good correspondence with a Cu(II) ion.

Table 5 Mulliken spin-densities employing either a CAS wavefunction (with ANO basis set) or DFT (with def2-TZVPP basis set). For Cu, the total d-occupations are given in parentheses. The atom labels are shown in Fig. 2

Method	CASSCF			DFT (TPSS)
State	Cu	O1	O2	Cu	O1	O2
^3[CuO2]^+	0.86 (9.05)	0.25	0.80	0.35 (9.67)	0.71	0.77
^1[CuO2]^+	0.00 (9.05)	0.00	0.00	−0.33 (9.66)	0.13	0.35
^3[CuO]^+	0.84 (9.02)	1.10	—	0.54 (9.57)	1.23	—
^1[CuO]^+	0.00 (9.06)	0.00	—	−0.33 (9.56)	0.46	—
^3[CuOH]^2+	0.92 (8.95)	1.02	—	0.58 (9.53)	0.54	—
^1[CuOH]^2+	0.00 (8.99)	0.00	—	0.00 (9.44)	0.00	—

---

Similar to the spin-densities obtained from CASSCF wavefunctions, the DFT calculations show large spin-density on both copper and the oxygen ligands. Together with the total d-occupations around 9 to 9.5, this is in accordance with a Cu(II) interpretation. However, the variation among the three intermediates is larger for DFT than for CASSCF. We note that the open-shell singlet spin-states (¹[CuO₂]⁺ and ¹[CuO]⁺) calculated with DFT broken-symmetry calculations – contrary to a CAS wave function – give rise to a (non-physical) spin-density. While this is a known artifact from the broken-symmetry approach, the resulting spin densities are nevertheless reported in Table 5 to confirm that we obtained a broken-symmetry state.

The TPSS, TPSSh and B3LYP methods show the expected trend of increasing stability of the triplet state with the increasing amount of Hartree–Fock exchange in the methods (0, 10 and 20%) for all three complexes, but the heavily parametrized M06-L method (also 0%) does not follow this trend. On average, TPSS gives the most accurate results, with an mean absolute error of 26 kJ mol⁻¹, but the other methods are not much worse (32–36 kJ mol⁻¹). TPSS also has the smallest maximum error (31 kJ mol⁻¹), whereas B3LYP gives the largest error (63 kJ mol⁻¹).

Although CASPT2 is known to be a highly accurate quantum chemical model, several studies have shown that it occasionally overestimates the stability of high-spin states.^73–75 This was recently ascribed to the fact that CASPT2 can be less accurate for the correlation originating from the metal 3s3p orbitals.⁷⁶ This would imply that for [CuO₂]⁺ and [CuOH]²⁺ (for which the singlet was most stable with CASPT2), the singlet may be even lower than obtained here, while the splitting for [CuO]⁺ (where the triplet was most stable) could be smaller than calculated here. The effect was estimated to 8–12 kJ mol⁻¹ in the benchmark study by Pierloot et al.,⁷⁶ but it should be noted that the employed benchmarks set did not include any LPMO active-site model (or any other copper system). It should further be noted that a Dunning type basis set was recommended in ref. 76, prompting us to apply both ANO and Dunning-type basis sets. However, the obtained differences between the two types of basis sets were very small for our LPMOs models (less than 1 kJ mol⁻¹).

A remedy for inaccuracies in the 3s3p correlation with CASPT2 was recently suggested in which the 3s3p correlation was obtained employing a coupled cluster wavefunction.⁷⁷ Yet, due to the multiconfigurational nature of the complexes in this paper, we have refrained from this procedure.

Conclusion

In this work, we have investigated three intermediates of the LPMO enzyme with CASPT2, namely [CuO₂]⁺, [CuO]⁺ and [CuOH]²⁺ with structures taken from previous QM/MM optimizations.³² The first species is expected to be a precursor for generation of the two later intermediates, which probably are involved in the abstraction of a hydrogen atom from the polysaccharide substrate.

To obtain a first indication of the accuracy of DFT, we have calculated spin-state energy splittings of the three species, which can attain both singlet and triplet spin states; both spin states are suspected to be involved in the catalytic turnover.

Comparing the obtained energies (cf.Table 3), we see that for both [CuO₂]⁺ and [CuO]⁺, TPSS, TPSSh and B3LYP functionals give rise to some errors, although they can still be considered reasonable (errors of 18–33 kJ mol⁻¹). An analysis of the underlying CASSCF wavefunctions shows that the systems are multiconfigurational. The M06-L functional overestimates the stability of the triplet state of [CuO₂]⁺ by 33 kJ mol⁻¹, but is more accurate for [CuO]⁺ (19 kJ mol⁻¹ error). In the case of [CuOH]²⁺, DFT significantly underestimates the singlet–triplet splitting (by 31–61 kJ mol⁻¹), and this intermediate is also found to be multiconfigurational.

Thus we can conclude that the DFT methods for LPMO intermediates can give significant errors (the range found here is 18–62 kJ mol⁻¹), reflecting the multiconfigurational nature of the studied intermediates. Perhaps an even worse finding is that DFT sometimes overestimates the stability of the singlet state, while in other cases it is the stability of the triplet state that is overestimated: for instance, all DFT methods overestimate the stability of the triplet state for [CuO₂]⁺, but overestimate the stability of the singlet state for [CuO]⁺. Further, all DFT methods significantly underestimate the singlet–triplet splitting for [CuOH]²⁺ and produce a qualitatively wrong (closed-shell) description of the singlet state.

These results show that care must be taken when employing DFT for LPMOs. In future studies, we aim at employing more accurate methods also for reactions involving [CuOH]²⁺ in abstraction of hydrogen from the polysaccharide substrate.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge grants from the Swedish Research Council (project 2018-05003), The Carlsberg Foundation (CF15-0208 and CF16-0482), the European Commission (MetEmbed project 745967), the Royal Physiographic Society in Lund, the China Scholarship Council, and COST through Action CM1305 (ECOSTBio). The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University, NSC at Linköping University, and HPC2N at Umeå University.

References

1. L. R. Kump, Nature, 2008, 451, 277–278.
2. E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853.
3. P. V. Harris, D. Welner, K. C. McFarland, E. Re, J.-C. N. Poulsen, K. Brown, R. Salbo, E. Ding, H. Vlasenko, S. Merino, F. Xu, J. Cherry, S. Larsen and L. L. Leggio, Biochemistry, 2010, 49, 3305–3316.
4. G. Vaaje-Kolstad, B. Westereng, S. J. Horn, Z. Liu, M. Zhai, H. Sørlie and V. G. H. Eijsink, Science, 2010, 330, 219–222.
5. G. R. Hemsworth, G. J. Davies and P. H. Walton, Curr. Opin. Struct. Biol., 2013, 23, 660–668.
6. W. T. Beeson, V. V. Vu, E. A. Span, C. M. Phillips and M. A. Marletta, Annu. Rev. Biochem., 2015, 84, 923–946.
7. E. A. Span and M. A. Marletta, Curr. Opin. Struct. Biol., 2015, 35, 93–99.
8. P. H. Walton and G. J. Davies, Curr. Opin. Chem. Biol., 2016, 31, 195–207.
9. K. K. Meier, S. M. Jones, T. Kaper, H. Hansson, M. J. Koetsier, S. Karkehabadi, E. I. Solomon, M. Sandgren and B. Kelemen, Chem. Rev., 2018, 118, 2593–2635.
10. D. Klemm, B. Heublein, H.-P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393.
11. B. Bissaro, A. K. Røhr, G. Muller, P. Chylenski, M. Skaugen, Z. Forsberg, S. J. Horn, G. Vaaje-Kolstad and V. G. H. Eijsink, Nat. Chem. Biol., 2017, 13, 1123–1128.
12. J. A. Hangasky, A. T. Iavarone and M. A. Marletta, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4915–4920.
13. R. Kittl, D. Kracher, D. Burgstaller, D. Haltrich and R. Ludwig, Biotechnol. Biofuels, 2012, 5, 1–14.
14. C. H. Kjaergaard, M. F. Qayyum, S. D. Wong, F. Xu, G. R. Hemsworth, D. J. Walton and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8797–8802.
15. O. Caldararu, E. Oksanen, U. Ryde and E. D. Hedegård, Chem. Sci., 2019, 10, 576–586.
16. C. Tian, W. T. Beeson, A. T. Iavarone, J. Sun, M. A. Marletta, J. H. D. Cate and N. L. Glass, Proc. Natl. Acad. Sci. U. S. A., 2011, 106, 22157–22162.
17. R. M. Berka, et al. , Nat. Biotechnol., 2011, 29, 922–927.
18. R. J. Quinlan, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15079–15084.
19. C. M. Phillips, W. T. Beeson, J. H. Cate and M. A. Marletta, ACS Chem. Biol., 2011, 6, 1399–1406.
20. W. T. Beeson, C. M. Phillips, J. H. D. Cate and M. A. Marletta, J. Am. Chem. Soc., 2012, 134, 890–892.
21. S. J. Horn, G. Vaaje-Kolstad, B. Westereng and V. G. H. Eijsink, Biotechnol. Biofuels, 2012, 5, 45–56.
22. Z. Forsberg, G. Vaaje-Kolstad, B. Westereng, A. C. Bunæs, Y. Stenstrøm, A. MacKenzie, M. Sørlie, S. J. Horn and V. G. H. Eijsink, Protein Sci., 2011, 20, 1479–1483.
23. G. R. Hemsworth, E. J. Taylor, R. Q. Kim, R. C. Gregory, J. P. Lewis, S. J. Turkenburg, A. Parkin, G. J. Davies and P. H. Walton, J. Am. Chem. Soc., 2013, 135, 6069–6077.
24. G. Vaaje-Kolstad, L. A. Bøhle, S. Gåseidnes, B. Dalhus, M. Bjørås, G. Mathiesen and V. G. H. Eijsink, J. Mol. Biol., 2012, 416, 239–254.
25. F. L. Aachmann, M. Sørlie, G. Skjåk-Bræk, V. G. H. Eijsink and G. Vaaje-Kolstad, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18779–18784.
26. G. Vaaje-Kolstad, S. J. Horn, M. Sørlie and V. G. H. Eijsink, FEBS J., 2013, 280, 3028–3049.
27. G. Vaaje-Kolstad, Z. Forsberg, J. S. M. Loose, B. Bissaro and V. G. H. Eijsink, Curr. Opin. Struct. Biol., 2017, 44, 67–76.
28. W. B. O'Dell, P. K. Agarwal and F. Meilleur, Angew. Chem., Int. Ed., 2017, 56, 767–770.
29. J.-P. Bacik, S. Mekasha, Z. Forsberg, A. Y. Kovalevsky, G. Vaaje-Kolstad, V. G. H. Eijsink, J. C. Nix, L. Coates, M. J. Cuneo, C. J. Unkefer and J. C.-H. Chen, Biochemistry, 2017, 56, 2529–2532.
30. K. E. H. Frandsen, et al. , Nat. Chem. Biol., 2016, 12, 298–305.
31. T. Simmons, K. Frandsen, L. Ciano, T. Tryfona, N. Lenfant, J. Poulsen, L. Wilson, T. Tandrup, M. Tovborg, K. Schnorr, K. S. Johansen, B. Henrissat, P. H. Walton, L. L. Leggio and P. Dupree, Nature, 2017, 8, 1064.
32. E. D. Hedegård and U. Ryde, Chem. Sci., 2018, 9, 3866–3880.
33. X. Li, W. T. Beeson IV, C. M. Phillips, M. A. Marletta and J. H. D. Cate, Structure, 2012, 20, 1051–1061.
34. S. Kim, J. Ståhlberg, M. Sandgren, R. S. Patond and G. T. Beckham, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 149–154.
35. J. Y. Lee and K. D. Karlin, Curr. Opin. Chem. Biol., 2015, 25, 184–193.
36. D. Dhar and W. B. Tolman, J. Am. Chem. Soc., 2015, 137, 1322–1329.
37. B. D. Neisen, N. L. Gagnon, D. Dhar, A. D. Spaeth and W. B. Tolman, J. Am. Chem. Soc., 2017, 139, 10220–10223.
38. L. Bertini, M. Lambrughi, P. Fantucci, L. De Gioia, M. Borsari, M. Sola, C. A. Bortolotti and M. Bruschi, Inorg. Chem., 2017, 57, 86–97.
39. B. Wang, E. M. Johnston, P. Li, S. Shaik, G. J. Davies, P. H. Walton and C. Rovira, ACS Catal., 2018, 8, 1346–1351.
40. E. D. Hedegård and U. Ryde, ACS Omega, 2017, 2, 536–545.
41. E. D. Hedegård and U. Ryde, J. Biol. Inorg. Chem., 2017, 22, 1029–1037.
42. M. Conchí, F. Silvia, J. Řezáč, P. Olivier, R. Olivia, V. Moliner and A. de la Lande, Chem. – Eur. J., 2013, 19, 17328–17337.
43. E. Abad, J. B. Rommel and J. Kästner, J. Biol. Chem., 2014, 289, 13726–13738.
44. P. Chen and E. I. Solomon, J. Am. Chem. Soc., 2004, 126, 4991–5000.
45. A. Crespo, M. A. Mart, A. E. Roitberg, L. M. Amzel and D. A. Estrin, J. Am. Chem. Soc., 2006, 128, 12817–12828.
46. S. M. Huber, A. R. M. Shahi, F. Aquilante, C. J. Cramer and L. Gagliardi, J. Chem. Theory Comput., 2009, 5, 2967–2976.
47. K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
48. K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
49. F. Aquilante, et al. , J. Comput. Chem., 2016, 37, 506–541.
50. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579.
51. P.-O. Widmark, P.-Å. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306.
52. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
53. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
54. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
55. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037–2047.
56. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956.
57. T. B. Pedersen, F. Aquilante and R. Lindh, Theor. Chem. Acc., 2009, 124, 1–10.
58. G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
59. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
60. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
61. N. V. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
62. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
63. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
64. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
65. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
66. K. Eichkorn, T. Oliver, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
67. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
68. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 1456–1465.
69. TURBOMOLE V7.1 2016, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com .
70. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
71. W. Jiang, N. J. Deyonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460.
72. V. Veryazov, P.-Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338.
73. K. Pierloot, Mol. Phys., 2003, 101, 2083–2094.
74. S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582.
75. M. L. L. Daku, F. Aquilante, T. W. Robinson and A. Hauser, J. Chem. Theory Comput., 2012, 8, 4216–4231.
76. K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553.
77. Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 3961–3977.

---

Footnote

† Electronic supplementary information (ESI) available: Mulliken charges as well as XYZ-files for model 1 of the three investigated intermediates. See DOI: 10.1039/C9DT04486H

---