How to use X-ray diffraction to elucidate 2D polymerization propagation in single crystals

Abstract

Covalent long-range ordered (crystalline) sheets called 2D polymers have recently been synthesized by irradiating single crystals of suitably packed monomers. To have such an action proceed successfully, billions of bond formation processes have to be mastered exclusively in two dimensions within 3D crystals. This raises questions as to how to elucidate the mechanism of these unusual polymerizations as well as their entire strain management. The article will show that single crystal X-ray diffraction based on both Bragg and diffuse scattering are powerful techniques to achieve such goal. The very heart of both techniques will be explained and it will be shown what can be safely concluded with their help and what not. Consequently, the reader will understand why some crystals break during polymerization, while others stay intact. This understanding will then be molded into a few guidelines that should help pave the way for future developments of 2D polymers by those interested in joining the effort with this fascinating and emerging class of 2D materials.

---

A. Dieter Schlüter

A. Dieter Schlüter is currently Professor Emeritus for polymer chemistry at the Materials Department of the ETH Zürich. He studied chemistry and geophysics at the University of Munich (LMU) and worked at UC Berkeley, USA, University of Durham, UK (short term), MPI for Polymer Research, Mainz, Germany, Karlsruhe Institute of Technology, Karlsruhe, Germany, Free University of Berlin, Berlin, Germany and ETH Zürich, Switzerland. His research interests are in the area of synthetic polymer chemistry. Schlüter believes that organic chemistry is the fundament of polymer synthesis.

Thomas Weber

Thomas Weber studied mineralogy with focus on crystallography at the University of Munich (LMU), where he also received his PhD in 1998. After a three-year post-doctoral stay at the University of Berne, he moved to ETH Zurich in 2001, where he first worked as a senior scientist at the Laboratory for Crystallography. Since 2016 he has been head of the X-ray platform at the Materials Department of ETH Zurich. His research interest is the determination of real structures using diffuse X-ray scattering.

Gregor Hofer

Gregor Hofer is currently employed as a post-doc at the Materials Department of ETH Zürich. He studied earth sciences at the University of Vienna during which he specialised in crystalline phase-transitions under high pressures. He came to ETH Zurich for his PhD where he investigated the growth mechanisms of 2D polymers using a wide range of X-ray diffraction methods. His current research interests include structural changes in materials subjected to an external stimulus, which he pursues using experimental and computational methods.

---

Key learning points

(1) To understand the structural insights and limitations which the analytical tool X-ray diffraction (XRD) offers

(2) To realize that Bragg XRD analysis provides information about the average structure of a single crystal, while the analysis of the diffuse scattering of the same crystal provides information about the local structure(s). Local structural information is particularly important when monitoring the course of a chemical reaction within single crystals with XRD

(3) To learn that powder XRD, transmission electron microscopy (TEM) and electron diffraction are alternative methods to single crystal XRD for structural elucidation but that each of these methods has specific strengths and weaknesses which renders them comprehensive to one another rather than exchangeable.

(4) To understand that the mechanism of a 2D polymerization in a single crystal is in fact a complex 3D process that involves all components the crystal is composed of: monomers, templates, and solvents. Comprehensive understanding thus requires knowing the time evolution of all components from monomer to product crystal

(5) To learn that strain management is mandatory for bringing about 2D polymerization and that detailed mechanistic understanding can provide valuable hints concerning polymerization strategy and monomer design.

For small-molecule synthetic chemistry single crystal X-ray diffraction (SCXRD) is an important analytical tool, for example, to confirm a particular atom–atom connection, determine bond lengths and angles or differentiate one stereoisomer from another.¹ As long as the diffractogram displays sufficiently sharp and assignable Bragg reflections, the quality of the crystals used for the analysis is of secondary importance. The desired information is accessible despite crystal defects and crystal disorder. This situation changes when reactions within single crystals are performed and SCXRD is used to analyse and monitor the process.

When synthesizing 2D polymers in single crystals, an external stimulus (most often light) converts a layered monomer crystal into a crystal composed of stacks of regularly covalently connected layers.^2,3Fig. 1 shows a prototype example all the way from the macroscopic single crystal to the molecular structure of the product obtained.⁴ Subsequent exfoliation of these layers then provides access to thin sheet stacks and individual sheet-like macromolecules. The latter are called 2D polymers because of their molecular structure being tile-covered by topologically planar repeat units (RU),^5–7 very much in analogy to linear polymers the molecular structure of which is composed of a sequence of topologically linear RUs.⁸ 2D polymers with sizes of say a few tens of μm² require formation of millions of covalent bonds in this process, which all have to take place within each of the monomer layers. While linear polymerization in single crystals has been investigated in detail by SCXRD,^9,10 mastering and analysing the complexity of a two-dimensional growth process involving such a huge number of individual reaction events by SCXRD was unheard of until recently.¹¹

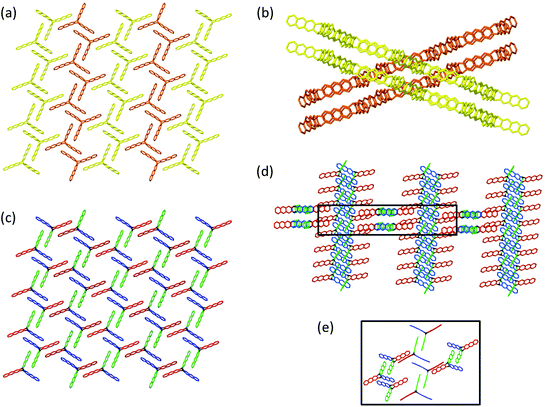
Fig. 1 Synthesizing 2D polymers in a single-crystal-to-single-crystal transformation. (a) Optical micrographs of monomer (left) and 2D polymer single crystals (right). Polymerization is triggered by light irradiation and depolymerisation by thermal treatment. (b) Sketch of the layered structure of both rhombohedral crystals. (c) Sections of a layer in the monomer crystal with three-armed molecular structure of the monomer and of the corresponding 2D polymer after the opposing olefins of neighbouring monomers have reacted with one another according to a [2+2]-cycloaddition reaction. Parts of this panel reproduced and modified with permission by the publisher (ref. 4).

There are two main prerequisites to achieve such a goal. First, the starting crystals should be as perfect as possible. Ideally, polymerization should proceed from one crystal face to the opposite face to produce the largest possible 2D polymers and must be strictly confined to the respective monomer layers. Furthermore, microstructural features such as grain boundaries resulting from mosaicity,¹² point defects, and screw dislocations are to be avoided because they can cause limited sheet size, holes in the 2D polymer sheets, and undesired connections between adjacent sheets, respectively. Second, the growth process must proceed in a way that the crystals can accommodate the strain unavoidably occurring through the structural changes associated with polymerization. Cohen and Schmidt have formulated this in the famous ‘Topochemical Postulate’ requiring a minimum of molecular movement.¹³ Elsewise single-crystal-to-single-crystal (SCSC) transformations will not be possible because cracks will form or the crystals may even shatter.

Thus, polymerizations in layered monomer crystals appear in a rather different, more challenging light and it is important to the synthetic chemist to know how SCXRD can be used to identify and to quantify them. Furthermore, 2D polymerization is a complex, concerted process and seemingly unimportant ‘spectators’ such as solvent or template molecules may have a vital function in enabling or hindering it. Consequently, the full methodological power of SCXRD needs to be applied and refinements need to involve all crystal constituents.

XRD on single crystals concerns not only the frequently used Bragg analysis but also the less commonly applied analysis of the diffuse scattering.¹⁴ While Bragg analysis provides the structure in a crystal, averaged over all unit cells, diffuse scattering provides information about the local deviations from the average structure. When monitoring polymerization in a single crystal, the analysis of diffuse scattering at different states of reaction conversion allows one to learn about the intermediates of the process. This is somewhat related to the thinking of chemists in terms of oligomers as intermediates of polymerization and bears the potential of gaining insight into events happening during this complex process. Concretely, applying SCXRD offers a number of intriguing possibilities, which include selecting the most suited starting crystals, i.e. those with the least defects, exploring fine structural features of intermediate crystals on the way to the through-polymerized final product crystals, and thus developing an understanding for how the polymerization propagates mechanistically. This last aspect shows the potential of this powerful tool for structural elucidation but also as a method supporting polymer synthesis by providing insights useful for the optimization of polymerization strategy and monomer design.

In materials chemistry, XRD also plays an indispensable role. Famous examples concern the family of metal–organic frameworks (MOF), which often are obtained and analysed in single crystalline form.^15,16 The covalent organic frameworks (COF), first reported by the Yaghi group, are another example.^17–21 However, except for two cases where single crystals were reported,^22,23 these materials are obtained as microcrystalline powders. Powders cannot be analysed by SCXRD because the small crystallites are more or less randomly oriented in space. Fortunately, correlating powder diffractograms (PXRD) with structural models provides then insights into structural properties of the specimen.

This Tutorial Review addresses students and scientists interested in chemical reactions within single crystals and wish to learn what SCXRD has to offer concerning elucidation of the processes that these reactions involve. Despite the available plethora of topochemical reactions in the literature,^24–26 the article focusses on the synthesis of 2D polymers for two reasons. First, making covalent sheets is the currently most complex chemical reaction known to take place in single crystals and therefore promises a maximum of information. Second, very recently a comprehensive study of a particular 2D polymer was completed,¹¹ which thus provides an excellent basis for the article.

This Tutorial starts out with Sections 1 and 2, which provide a more chemistry-related and a more methodical basis for the topic, respectively. Both subsections have a factual style; interpretations and the description of possible consequences are kept for later. The chemistry-related Section 1 provides the state-of-the-art in the synthesis of 2D polymers in single crystals comprising not only all known SCSC-type approaches but also related cases. In those, product crystals either shatter and could not be analysed by scattering anymore or suffer partial destruction, which prevented the use of SCXRD but still allowed other scattering techniques, for example, electron diffraction (ED) to be applied. It also contains a few other relevant cases. Thereafter the methodically oriented Section 2 explains the very nature of XRD to provide sufficient understanding for what and what not to expect from this analytical tool when applied to problems such as 2D polymerization. Additionally, the reader will understand the respective advantages and disadvantages of SCXRD and PXRD. Based on this groundwork, Section 3 will then guide the reader through the above-mentioned case in which a topochemical polymerization was studied by both Bragg and diffuse scattering resulting in rather comprehensive insights into all structural changes associated with making this 2D polymer in a single crystal. The insights gained from this section are then combined in Section 4 with the findings and facts of Sections 1 and 2 to carefully draw conclusions as to how to perform such chemistry, how to design monomers, and which polymerization strategy to follow. Section 4 will also capitalize on this understanding and try to explain why problems occurred in some of the cases presented in the chemistry-related Section 1.

1. Examples for the synthesis of 2D polymers starting from monomer single crystals

We start out with monomer 1,²⁷ carrying two groups, the anthracenes and the acetylenes, which are potentially reactive in photochemically triggered dimerization reactions. Because of the monomer's threefold symmetry, lateral growth should be possible, supposed the monomers assume an appropriate layered packing (Section 4) in which the reactive sites of neighbouring monomers are in close enough distance to allow each monomer molecule to form bonds with its three neighbours. Given high reaction conversion, this would provide access to stacks of long range ordered covalent networks, which are nothing else but 2D polymers. In fact, when crystallized from various organic solvents, rhombohedral single crystals were obtained. SCXRD proved the crystals to be layered with the layers parallel to the hexagonal face. Each layer comprises a hexagonal lattice (Fig. 2a) with the cup-shaped monomers 1 densely packed and alternatingly oriented upside down. An acetylene from one monomer overlaps with the anthracene of a neighbouring monomer right at this moiety's photochemically active 9,10-positions. The authors anticipated (and hoped) that this tight rigid arrangement would force the monomers to react irrespective of whether or not the rules of orbital symmetry apply²⁸ and putting studies on the role of defects in particular on the dimerization of anthracenes in single crystals aside for a moment.^29,30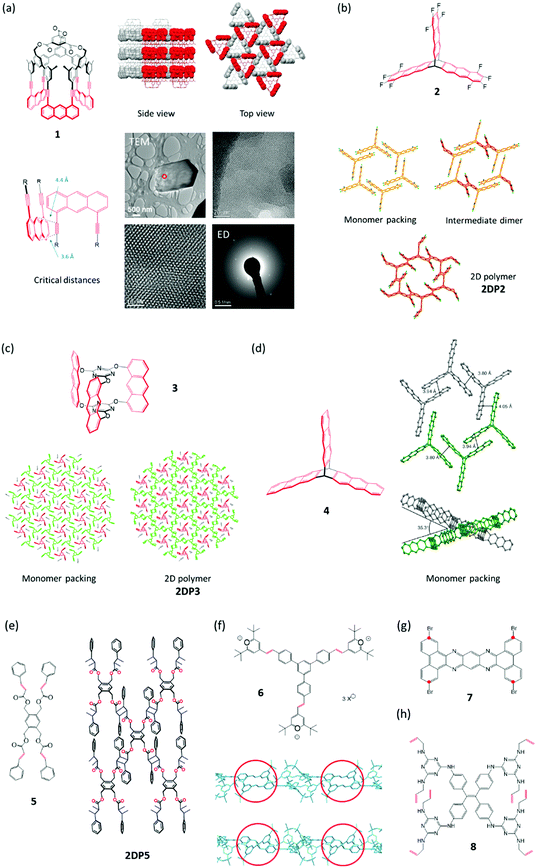

Fig. 2 Monomers investigated for 2D polymerization starting from single crystals. Potentially reactive sites are in red. (a) Cup-shaped monomer 1 with side and top views of its packing in the single crystal. The reactive parts in a space-filling representation are alternatingly oriented up (red) and down (grey). TEM micrograph of partially exfoliated irradiated crystals with two expansions processed using a Wiener filter to reduce the noise. Cryogenic electron diffractogram confirming a structure very similar to the monomer crystal. Parts of this panel reproduced with permission by the publisher (ref. 27). (b) Structure of monomer 2 and structures in the single crystal of this monomer, the dimeric intermediate, and the corresponding 2D polymer 2DP2. (c) Structure of monomer 3, its packing in a single crystal, and the structure of the corresponding 2D polymer 2DP3 in the single crystal. (d) Structure of monomer 4 and views of its packing in the single crystal. Note that not all anthracenes lie in the same plane. Parts of this panel reproduced with permission by the publisher (ref. 31). (e) Structure of tetrafunctional monomer 5 and sketch of the 2D polymer 2DP5 obtained from it. (f) Structure of monomer 6, the polymerization of which is shown in Fig. 1. Side view sections of a monomer layer and the corresponding layer of 2DP6 with red circles indicating two (of the three) reactive olefin pairs before (top) and after dimerization (bottom). Bond formation proceeds largely perpendicular to the monomer plane. (g) Structure of tetrabromide 7, the polymerization of which under dehalogenation was attempted at 500 °C. The positions supposed to react with one another are marked with red dots. (h) Structure of octafunctional monomer 8.

As with all reactions in a single crystal, the next step in which the actual bond formation takes place, is critical. The key question is whether the necessary changes in bond angles and atom/atom distances associated with the proposed bond formation would allow the crystal to remain largely intact.¹³ Section 3 will show how complex a matter this is and at this point in the Tutorial we just leave the reader with the information that photoirradiation of the crystals with light of λ = 470 nm in fact achieved virtually complete polymerization. Because the crystals could not accommodate the changes completely, however, cracks formed to a degree that rendered SCXRD not applicable anymore. Such scenario is ideally suited either for PXRD or for the complementary techniques transmission electron microscopy (TEM) imaging and ED to fill the gap. Fig. 2a displays the key results, which proved both crystallinity and the expected molecular structure of the 2D polymer 2DP1 (see Section 4). Throughout this article we will use this numbering system in which 2DP stands for two-dimensional polymer and the number (here 1) for the monomer from which the 2DP was created.

Never before had a regular covalent network been created under ambient conditions. There was only one report on the 2D polymer poly-C₆₀, which was obtained at approximately 700 K and a pressure of several GPa,³² conditions one finds in the inner of the earth. While this thus was a reason to celebrate, it was nevertheless urgent to achieve at least two more goals. The first concerned monomer accessibility and the second the desired applicability of SCXRD for not only the monomer but also the product crystals. Monomer 1 required a 25-step synthesis, which is a challenge to everyone going through such process. In addition, only a few tens of milligrams were obtained; certainly not enough to solve all the questions that 2D polymers were expected to raise. To have also the product in single crystalline form was important as XRD provides structures representative for large volume elements, while ED is restricted to small volumes and provides information that bears the risk not being representative for the whole material (see comment in Section 4).

The groups of King and one of the authors (ADS) set out in a constructive competition to address these issues. The results were monomers 2³³ and 3,³⁴ which could be obtained in much less steps and much larger quantity (Fig. 2b and c). Meanwhile, for monomer 3 even a synthesis under technical conditions is available.³⁵ Both monomers were crystallized into single crystals, which contained stacks of layered ‘reactive packings’, with neighbouring monomers forming pairs of only slightly off-set anthracenes, potentially suitable for topochemical reaction. Honestly speaking, at this point, it was more an intuition than a rational understanding that such arrangement may be suited for the crystals to ‘survive’ polymerization. However, sometimes one needs luck. Upon irradiation, both monomer crystals stayed intact and gave the corresponding stacks of polymers 2DP2 and 2DP3 (Fig. 2b and c). As evidenced by a slightly increased width at half height of the Bragg reflections, the quality of the crystals decreased somewhat, yet wet-chemical exfoliation afforded huge amounts of very thin sheet stacks and even occasionally single sheets of the corresponding 2DPs. This finding had major consequences. First, the claim of having achieved a 2D polymer was much more widely believed to be correct, now that SCXRD analyses existed for both 2DP2 and 2DP3. Resistance against the feasibility of covalently bonded, long range ordered networks faded. This showed the power XRD can develop even outside the realm of the actual structural solution. The other consequence was a first mechanistic type information which was obtained for 2DP2. Here the polymerization went through a distinct intermediate, the single crystal of dimerized monomers (Fig. 2b). Only if that state was further irradiated, 2DP2 formed. In the thinking of polymer chemistry, this suggested that the growth process was closer to what is called step-growth rather than chain growth. Section 3 will delineate which consequences in terms of feasibility this finding has, supposed it more or less applies to all 2D polymerizations. The synthesis of 2DP3 did not pass through such a distinct intermediate state, which is part of the reason why exactly this system was chosen for an in-depth XRD-monitoring (Section 3). Both polymerizations proceed quantitatively and are thermally reversible, an aspect this Tutorial will not cover.

Only a year later, the polymerization of monomer 4 was reported.³¹ In terms of all the things that can happen in a single crystal, this is a particularly interesting case, which will be discussed in detail in Section 4. Already the tilt angle of approximately 35° between anthracene units that should in principle react with one another indicates complexity (Fig. 2d). The variability of chemical reactions suitable for synthesized 2D polymers in single crystals was expanded in 2015 by Chu et al.,³⁶ who showed that monomer 5 crystallizes from ethyl acetate in layers with the four olefins of each monomer properly aligned with the olefins of its four neighbours. Exposure to sun light brings about lateral polymerization. Prior to this irradiation the authors grinded up the monomer single crystals to a fine powder. This appears somewhat unfortunate in terms of not only achieving laterally as extended 2D polymers as possible, but also concerning the aspect whether this polymerization has the potential to proceed in SCSC-fashion.

Monomer 6⁴ like monomer 5 formally uses [2+2]-cycloaddition between olefins of neighbouring monomers for the polymerization. The distance between these olefins is 3.93 Å, whereas the distance between olefins of neighbouring monomer layers is at least 7.67 Å. This explains the observed perfect in-plane reactivity. Despite the sensitivity of the monomer single crystal towards loss of solvent (methanol/acetonitrile mixture), the photoreaction could be performed in SCSC-fashion. The dimerization reactions proceed largely vertical to the main plane of the monomer layers, an important feature discussed in Section 4.

Another compound, the tetrabromide 7, was studied for its potential to give 2D polymers.³⁷ In principle, one can imagine a sequence of dehalogenation and (radical) combination to furnish a hetaromatic 2D polymer, somewhat reminiscent of graphene. In an interesting first report, the authors could obtain sheets after heating the monomer single crystals up to approximately 500 °C. While conventional AFM imaging revealed the sheets to be largely homogeneous, the exact structural features based on e.g. HR-AFM or STM imaging still wait to be reported. An aspect this chemistry has to master is the shrinkage caused by the severe mass loss associated with the necessary removal of four heavy bromine atoms. Furthermore, the movement of the molecular fragments formed after debromination needs to be steered such that the positions marked with red dots (Fig. 2g) can actually establish the desired connectivity. A thrilling next step would be to analyse the molecular structure of the sheets obtained and to use this information to back-conclude what might have happened during the thermal treatment. Given the fact that there are quite a few brominated aromatics known, such effort is certainly worthwhile.

This brings us now to the last monomer to be discussed, compound 8, which carries four urea moieties to direct the monomers into a layered packing in single crystal and eight laterally positioned allylamine groups.³⁸ The Ke group uses these moieties to connect the monomers with one another by propanedithiol, which was allowed to diffuse into the monomer crystals. In an amazingly selective, light triggered ene-thiol addition process, this connection results in a layered single crystal composed of 2D polymer sheets. This addition cannot be driven yet to 100% conversion, which is not astounding given the eight allylic groups per monomer that ideally need to be connected. The whole approach is nevertheless refreshingly novel and complements conceptually the above described strategies by introducing flexible linkers between monomers endowing the 2D polymer with considerable responsiveness. Thus, these five-atom linkers allow the polymer crystals to expand reversibly through guest up-take. This responsiveness should not only be observable for the crystals but also for individual sheets once the currently ongoing exfoliation studies have afforded them. Apart from this more application-oriented aspect, the introduction of flexible linkers also has some bearing on an aspect that Section 4 will deal with quite extensively, namely how to compensate the strain commonly associated with chemical reactions in a single crystal.

2. What we can learn about 2DPs from diffraction and what not

Single crystal X-ray structure analysis is an over 100 years old success story. Thanks to the availability of highly optimized instruments and software, more than one million crystal structures have so far been solved and stored in databases. It is therefore not a surprise that SCXRD is also the tool for studying structural properties of monomer and 2D polymer single crystals and, maybe of even greater interest, the transition from one to the other. In this section, we will discuss what lessons can be learned from routine XRD, what information is lost in the course of data treatment and how this information can be recovered with complementary methods.

Conventional XRD follows a largely standardised procedure. A crystal is selected under the microscope that appears suitable for single crystal structure analysis, i.e. its size is in the order of a few 100 μm in each direction, it shows well-developed faces and no inclusions, cracks or other inhomogeneities. In most cases, data collection and processing are automated. After raw data processing, the crystal structure is solved and refined with user-friendly software. This procedure rarely fails to deliver results that are suitable for publication, including automatic quality assessment, ready-for-submission graphical material and tables and to some extent even automatically generated text to be included in the publication. In the absence of severe disorder or twinning, the typical time span between selecting a good crystal for the experiment and the availability of material for submission to a crystal structure database is less than a day.

However, it is of importance to note that the result obtained is not the crystal structure of a material, but an incomplete and simplified representation of it. To be able to apply fully the powerful tool of crystallographic symmetry, the results of a structure analysis have to be confined to a model in which all of the nodes of an infinite perfect mathematical lattice are occupied by identical unit cells. The diffraction pattern of such an ideal crystal would consist of point-like Bragg reflections located on the nodes of the reciprocal lattice and the space between the Bragg peaks would be empty. However, real diffraction intensities deviate from this picture, on the one hand because of unavoidable experimental factors, e.g. the point spread function of the instrument or background scattering, on the other hand because real structures cannot be as ideal as theory demands: real crystals are not infinite and have defects and disorder. Even if error-free instruments were available, real diffraction experiments will always show broadened Bragg peaks and diffuse scattering located between the Bragg positions. Therefore, standard crystallographic tools cannot be applied to the as-measured experimental data, because the reality of the experimental information contradicts the theoretical requirements. There are two ways to escape this dilemma. One is chosen in PXRD, where peak broadening effects are modelled to fit to the experimental data. For single crystal experiments, such approaches have not yet been tried, mostly because the diffraction geometry of a SCXRD experiment and the amount of data to be processed are by far more demanding as compared to powder experiments. In single-crystal evaluations, an opposite approach is therefore chosen. Instead of fitting the model to the data, the data are adapted to the requirements of theory (!): Bragg peaks are integrated across their profiles and the intensities are assigned to integer reciprocal lattice nodes. Information about Bragg peak profiles and about any diffraction intensities between the Bragg reflections is lost on this path.

Before we explain which information is suppressed by such data treatment and how it can be recovered, we want to first discuss the properties of the so-called average structure, that can be extracted from the integral Bragg peak intensities. This is nothing else than the average of the content of all individual unit cells in the crystal, i.e. the information of about 10¹⁵ unit cells in a single crystal is represented by a single average cell. This drastic reduction of complexity may be accompanied by significant loss of information, but it is also the reason why X-ray crystallography has become so successful.

In the case of an ideal, perfectly long-range ordered infinite crystal, the average structure would indeed be identical to the real structure. However, in the presence of disorder, averaging results in non-physical properties. Let us illustrate this with an example and assume that we are dealing with a partially polymerized single-crystal structure in which the distribution of reacted and unbound reactive groups is not perfectly ordered. The average structure would represent the crystal such that both, the monomer and the 2D polymer substructures would fill the complete crystal at the same time, i.e. they would interpenetrate each other, what is obviously not possible in reality. The degree of conversion would be represented by the relative scattering power assigned to the two substructures. Any information about the spatial distribution of the unbound active and reacted groups and thus about the growth mechanism is lost. We will discuss this later in more detail.

At this point, we can conclude that the average crystal structure as deposited in databases does not allow direct access to local structural information. Nevertheless, careful analysis of a series of intermediate structures during the evolution of a 2D polymer combined with plausibility arguments can help to draw some conclusions about the local structure, as we will show with an example in Section 3. However, it should be kept in mind that local structural information extracted from integrated Bragg peaks must be necessarily incomplete, because experimental information has been supressed in the course of data processing, and the results are biased by assumptions. Direct experimental evidence for the conclusions drawn about the local structure is missing. Since chemistry takes place over short distances, comprehensive and accurate knowledge about local structure properties in a crystal is certainly at least as important as the knowledge of the average structure, in particular in the presence of severe disorder. The diffuse scattering between the Bragg peaks is the key to this information.

The investigation of the local structures by means of diffuse scattering is considerably more challenging than it is the case for average structures. The amount of data to be examined frequently exceeds the limits of available computer resources and compromises have to be made. In addition, since diffuse scattering represents local order, most of the methods used for average structure analysis cannot be applied owing to the lack of strict long-range order. One approach that has proven useful in clarifying the real structure of disordered crystals is the three-dimensional difference pair distribution function (3D-ΔPDF).³⁹ It is obtained by extracting and Fourier transforming the diffuse scattering from the total single crystal diffraction pattern. A 3D-ΔPDF map shows us how the local order behaves in relation to the maximum degree of disorder that would be compatible with the known average structure.

This is again best illustrated on an example. Once more, we consider the above-mentioned partially polymerized 2D polymer. In addition, we assume that the degree of conversion is 50%. In the following we will call an established bond between reactive groups B and U otherwise. In the case of a maximum degree of disorder, i.e. a random distribution of U and B, we find that the probability that a B (or a U) is neighboured by another B or U would be the same and the 3D-ΔPDF map densities would be zero for any interatomic vectors with length larger zero. In the case of an island-like growth, i.e. fully polymerized domains are enclosed by a ‘sea’ of monomers, the probabilities of finding B–B or U–U, i.e. equal pairs at short distances is much higher than in the completely random case, while U–B pairs are rare and only found close to the ‘shores’ of the islands. Such positive correlations are seen as positive signals in a 3D-ΔPDF map. In contrast, if the formation of a bond between two monomers reduces the probability of establishing another bond in the immediate vicinity, U–B pairs are dominant at short distances (= negative correlation) and the 3D-ΔPDF signals representing such short interatomic vectors will also be negative. Since 3D-ΔPDF signals are proportional to the correlations probabilities they can be quantified by least squares fitting. Similar rules as for the substitutional disorder described above can be formulated for correlated displacements (e.g. preferences for in-phase or anti-phase vibration modes) and for displacements induced by a change of the local chemistry, e.g. by the formation of a bond. In this tutorial, we will not go further into the details about the properties of the 3D-ΔPDF. For a more comprehensive discussion, the interested reader is referred to the literature.³⁹

In many cases, the qualitative interpretation of the 3D-ΔPDF maps is intuitive and straightforward.⁴⁰ However, in the case of 2DP3, which will be discussed in detail in Section 3, the overlaps of signals are high and the local structure could only be solved by trial-and-error. Results were confirmed and quantified by a least-squares refinement (Fig. 3). The accuracy of local structure investigations falls behind what is the standard for average structures. In the latter case, statistical and systematic errors are typically in the order of a very few percent (e.g. defect concentration, degree of conversion) or even better (e.g. lattice constants, atomic coordinates). The relative uncertainties of refined local structure correlations are around 10%.⁴⁰

Fig. 3 Sections from the three-dimensional reciprocal (left; hk10.2 section; degree of conversion = 22%) and 3D-ΔPDF space (right; uv0.37 section) of 2DP3. The right-hand graphics was chosen for didactic reasons although it refers to a case with 0% conversion. In both cases the experimental data, the results from the 3D-ΔPDF refinements and the difference between observed and calculated data are shown. Black and red colours indicate positive values while the negative values are shown in blue.

In the following we want to discuss which information is lost by integrating over the Bragg peak profiles. It is essentially microstructural information, i.e. mosaicity, the sizes of the mosaic blocks and microstrain and, thus, exactly the kind of information the synthetic chemist would like to have.

According to the definition of the International Union of Crystallography a mosaic crystal is a “[…] conglomerate of minute crystalline blocks, tilted to each other by fractions of a minute of arc. Each block is separated from the surrounding blocks by faults and cracks”‡.⁴¹ In principle grain boundaries may move or even disappear. However, it can be considered a reasonable assumption that such defects and cracks, if already present in a monomer single crystal, may hinder or even disable the propagation of 2D polymerization across mosaic blocks. The larger the tilt angle between mosaic blocks is the higher is the expected barrier.

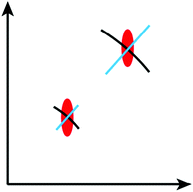
The term mosaicity refers to the orientation distribution of the mosaic blocks. Mosaicity can be measured with so-called rocking curves. The crystal is first oriented such that the Bragg condition is fulfilled. It is then rotated around this position (‘rocked’) and the change of the integral intensity of the Bragg reflection is recorded as a function of the rocking angle. The resulting curves can be understood as angular histograms of the orientation distribution of the mosaic blocks around the axis of rotation. Alternatively, one may analyse the Bragg peak profiles when recorded with area detectors. The angular distribution of the mosaic blocks is seen as arc-like broadening that follows the traces of a circle around the origin of reciprocal space (black arcs in Fig. 4).

Fig. 4 Impact on the Bragg peak profiles from mosaicity (black arcs), mosaic block sizes (red ellipsoids) and isotropic microstrain (blue lines). The axes indicate the reciprocal space coordinate system. In this example the mosaic blocks are larger along the horizontal direction (narrow peak width) than along the vertical direction (broad peak width). Note that the contributions due to limited sizes are constant in reciprocal space, while the widths of mosaicity and microstrain effects scale proportional to the distance from the origin of reciprocal space. For clarity, the effects are heavily exaggerated.

Mosaicity only quantifies the orientation distribution of the mosaic blocks, but does not allow a direct conclusion about the block size distribution. However, this information is of particular interest for synthetic chemists, since the lateral extent of a mosaic block in the final 2D polymer is the upper threshold to the size of the polymer sheets. The sizes of mosaic blocks also affect the Bragg peak profiles, but the representation in reciprocal space differs from the arcs induced by mosaicity. In contrast to mosaicity Bragg peak broadening due to limited block sizes may be along any direction in reciprocal space (red ellipsoid in Fig. 4).

Finally, also microstrain effects can be measured from the Bragg peak profiles. In intermediate 2D polymer structures the reason for microstrain may be an inhomogeneous distribution of the conversion leading to a distribution of slightly different lattice constants within the various mosaic blocks. If microstrain is isotropic it leads to a broadening of Bragg peaks along radial reciprocal space directions (blue lines in Fig. 4).

We have now seen that microstructure properties of monomers, 2D polymers and their intermediate structures may in principle be extracted from the Bragg profiles, but how easily is this done in practice? A general answer is difficult, because it heavily depends on the strength of the effect and on the experimental resolution function of the instrument used. For high-quality crystals mosaicity may be significantly less than a tenth of a degree, the sizes of mosaic blocks may extend up to a few micrometers and microstrain may be even absent. In comparison, the beam divergence of typical in-house single crystal diffractometers is in the order of a few tenths of a degree, which defines the lower detection limit of mosaicity. The coherence length of the beam is about a few tens of nanometers, i.e. any mosaic blocks or domain sizes exceeding this limit cannot be distinguished from infinite large blocks. The coherence length of the beam is also the limiting factor for the detection of microstrain. It can be experimentally observed if the root-mean-square lattice constant deviations from the average lattice constant is about 0.5% or more, i.e. if it is very strong. Looking at these figures it is clear that the microstructural effects must be very pronounced in order to be detectable with standard in-house single crystal diffractometers, which are normally optimized for intensity and not for reciprocal space resolution.

With synchrotron radiation or specially designed in-house diffractometers the detection limits may be shifted by several orders of magnitude. The resolution that can be achieved depends very much on the specific experimental setup. A detailed discussion is far beyond the scope of this tutorial. To measure the achievable experimental resolution, it is recommended to perform experiments with well-defined reference crystals of very high quality (e.g. silicon or ruby single crystals) and the same experimental setup.

In summary, measurement of microstructural properties in single crystals is a challenging task. In contrast to PXRD, where well-developed theory and powerful software for such investigations is available, such standard tools are not yet at hand for single crystal experiments. Why then are single crystal investigations carried out at all and not merely PXRD, in particular since powder samples are much easier to prepare?

The powder-intrinsic angular projection of the three-dimensional reciprocal space to one dimension leads to a considerable loss of information. Already in cases of moderately sized lattice constants or low-symmetric lattices, Bragg peaks overlap severely and the natural profiles of peaks are only accessible up to very small diffraction angles. However, accurate determination of microstructural properties would require knowledge of the evolution of peak profiles over a large range of diffraction angles. Furthermore, structure determination of unknown crystal structures is extremely time consuming and frequently fails even in cases of medium complexity. With a start model at hand that is already very close to the reality, structure refinements may be feasible, but details as they can be extracted from single crystal measurements, are still hardly accessible.

For accessing the local structure properties of disordered polycrystalline materials, the powder-based pair distribution function (PDF) method is available.⁴² The concept is very similar to the 3D-ΔPDF, however, it is the full diffraction pattern and not only the isolated diffuse scattering that is Fourier transformed when using powder data. The result is essentially a histogram of distances of atoms in the real structure, i.e. any information about the direction of interatomic vectors is lost. The powder PDF has proven to be extremely powerful to elucidate the local structure of materials with high symmetry and small lattice constants.⁴³ In cases of more complex structure, however, the applicability of this method is clearly limited and makes it challenging to extract local structure information beyond the molecular level.

PXRD may be considered to assess the quality of a 2D polymer in the cases that the scsc transformation has failed and polymerisation has been destructive for the single crystal. The observation of diffraction peaks might be considered an indication that the transformation resulted in a crystalline 2D polymer and a similarity between the peak positions and intensities of the monomer and the powdered reaction product may be considered a strong hint that the 2D polymer is similar to the monomer structure. We issue a warning here. It is true that such observations do not contradict the assumptions made, but the experimental evidence is by far too weak to allow definite conclusions. A powder peak half-width of 2° means the crystallite size is only about 5 nm what is rather considered an oligomer. Furthermore, correct indexing of peaks in a complex powder diffraction pattern is not unique, even if the position of a large number of reflections has been accurately measured. Thus, the match of only a few peak positions is all but a proof for the correctness of the presumptions. Furthermore, in molecular crystals the envelope of the diffraction intensities is mostly dictated by the atomic structure of the molecule and not by the crystal structure. If strong Bragg peaks are found at similar locations in the monomer and the reaction product it cannot necessarily be concluded that the molecular arrangements are similar. It has even been demonstrated that the same powder diffraction pattern can be well fitted with two very different structures of the same molecule.⁴⁴

Finally, a special warning about possible experimental artefacts that may cause one to overlook the existence of large 2D polymers in a powder. If a diffraction experiment is done in reflection mode, e.g. in the popular Bragg–Brentano geometry, particles with flat morphology are usually oriented with their broad faces parallel to the surface of the sample holder. For 2D polymers this is of relevance if the monomers already crystallize as platelets or if they are at least in parts exfoliated. In a standard experiment reciprocal space is probed along directions perpendicular to the sample holder surface, i.e. perpendicular to the 2D polymer layer, if preferred orientation as described is present. In such cases scans do not provide any information about the in-layer properties of the 2D polymer, only about the perpendicular direction. For example, in the case of exfoliated 2D polymer sheets one would not observe any Bragg reflections, just because there is no long-range order perpendicular to the layers! It is therefore very important to check the existence of preferred orientations and/or to use diffraction geometries that are less sensitive to such artefacts, e.g. setups with samples in capillaries.

3. Structural changes during polymerization of monomer 3 and depolymerisation of 2DP3 in the single crystal

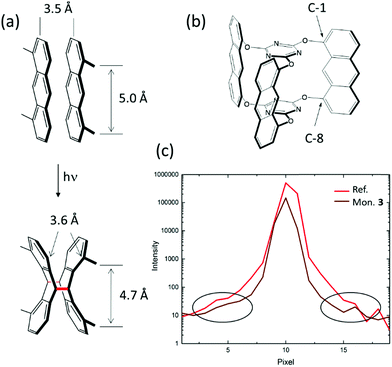
The initial considerations of why to investigate compound 3 as a potential monomer for 2D polymerization were more intuitive than fact-based. Our first intuition was that we should be able to induce the right packing of the monomers, in particular by choosing the right solvent for crystallization. Motivated by the finding that monomer 1 formed a reactive packing involving anthracenes and acetylenes more or less at the first attempt, we were optimistic not to have to test too many solvents before finding the desired packing with all monomers nicely ftf-stacked within layers (Fig. 2c). While this expectation was correct for some monomers, including 3, this is no guarantee.⁴⁵ The second intuitive consideration concerned commensurability of monomer and 2D polymer packing within each layer. An ideally perfect match between these two lattices we believed to be an effective way to avoid detrimental strain in crystals locally building up during polymerization.

When anthracene units react with one another, the distance between them shrinks from about 3.5 Å that they have in van der Waals pairs to the length of a CC-bond, which in dimers is order of 1.6 Å (Fig. 5a). This is so at least at the sites of dimerization, which are the C-9 and C-10 carbon atoms. This factor of more than two is substantial. In conventional linear polymerization, contraction is well-known and the main reason why monomer batches shrink in volume during polymer growth. In 2D polymerization, however, such shrinkage cannot be tolerated. Monomer design has to compensate for it, if polymerization should not come to a halt after a few dimerization steps because of gap formation and if the crystals should not mechanically disintegrate. This is why in monomer 3 the anthracene units were incorporated into the monomer skeleton via their C-1 and C-8 positions (Fig. 5b). Upon dimerization, the former anthracene units kink, which leaves the distance between these positions virtually identical (3.6 Å) to the distance they assume in the van der Waals pair. This simple geometric consideration combined with the hope for a ftf-packing made us synthesizing monomer 3 eventually and investigating its polymerization behaviour in the single crystal. The present section shows that these two considerations were correct, but that the reality is more complex. Additional factors have a vital role showing that our intuition was too naïve. In hindsight, giving birth to 2DP3 was thus a matter of considerable luck.

Fig. 5 (a) Distance changes by dimerization: distance in an anthracene van der Waals pair (3.5 Å) and positions C-1 and C-8 (5.0 Å) (top) as well as between the C-1 and C-8 positions across the dimer (3.6 Å) and within one of its side (4.7 Å). Newly formed CC bonds between the previous C-9 and C-10 positions in red. (b) Positions C-1 and C-8 through which the anthracene growth units of monomer 3 connect to the two central triazine units. (c) Intensity versus pixel plot of Bragg peaks of monomer 3 after repeated recrystallization from 2-cyanopyridine (brown) and of Ruby reference crystals (red). Intensity in logarithmic scale. Both reflections are virtually superimposable, suggesting that a Bragg peak in the single crystal diffractogram of monomer 3 is at the resolution limit. Image recorded at a synchrotron source. Black ellipsoids show the presence of diffuse scattering on both sides of the reflections’ onset.

The findings presented here rely on both conventional Bragg analysis and an analysis of the diffuse scattering. They involve a complete XRD-monitoring of the photochemically triggered polymerization and the thermally triggered depolymerisation steps based on more than 40 different X-ray structures recorded using both synchrotron X-ray beams and in-house X-ray equipment. To eliminate a possible impact from a too narrow sample collection, we scrutinized several different crystals of different sizes (between 100 μm and 900 μm). After repeated recrystallization from 2-cyanopyridine (cpy), the monomer single crystals had a quality illustrated by the Bragg reflection shown in Fig. 5c. This reflection has the same extraordinarily low width at half height as the ruby crystal used as reference standard in crystallography, indicating that the experiments were conducted at the resolution limit of a synchrotron experiment. Because of the high sample quality, already the Bragg analysis afforded insights beyond the common. Diffuse scattering confirmed these findings and provided additional insights based on the 3D-ΔPDF.^40,46

The following discussion is structured into the important features of the monomer packing and the local changes that take place upon bond formation during polymerization and bond breaking during depolymerization, before coming to the mechanism of polymerization in a spatial sense. As will be discussed in Section 4, for crystal integrity it is preferred to have the growth reactions evenly distributed over the crystal volume to keep the total strain, unavoidably associated with the chemical reaction, to the absolute minimum. Once we have established the mechanism and confirmed it from the diffuse scattering, we will move on to describing what else can be concluded from the pair correlation functions obtained. The full Bragg analysis is available.¹¹ A manuscript concerning the already completed analysis of the diffuse scattering is about to be submitted.

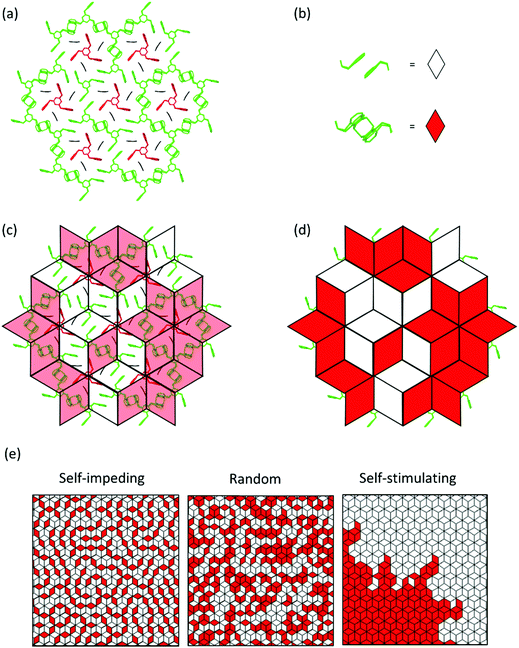
Now let us first have a look into how monomer 3 packs in the single crystal. For this, we not only consider an individual monomer layer (top view; Fig. 6a) but also the ABC-stacked columns in which the monomers are arranged vertical to the layers, thus in c-direction (side view; Fig. 6c). Within each layer, the monomer molecules are parallel to the ab plane and occupy three symmetry independent locations indicated by green, blue, and red colours. Only 2/3 of these molecules, the green and the blue ones, form a reactive packing by allowing their anthracene blades to form ftf-stacked pairs. This geometry is supported by the remaining 1/3 of the molecules, the red template. This template, while in principle the exact same monomer molecule as the green and the blue, assumes a different function. It does not act as monomer but rather fills the holes the reactive packing generates. It is thus an enabler and a spectator. The templates are turned upside down in respect to the green and blue monomers which is noticeable by the different screw sense. To complete the filling, three partially disordered cpy solvent molecules are contained in vertical direction next to the template in each hole.

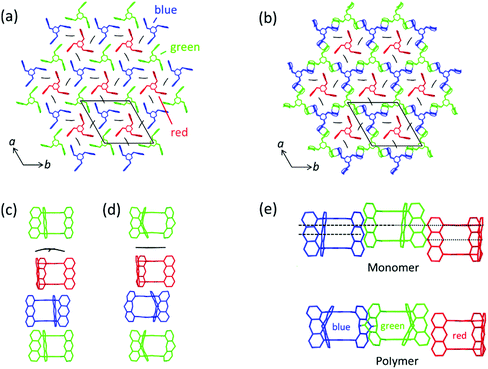Fig. 6 Aspects of the packing of compound 3 and of polymer 2DP3 in the crystal. (a) Reactive packing within a layer. The colour code indicates the different neighbourhoods and functions compound 3 assumes (green, blue, red). Green and blue molecules together form the reactive packing. (b) Structure of polymer 2DP3; green and blue moieties refer now to RUs. The red templates together with the three solvent molecules now fill the pores of 2DP3. (c and d) Columnar sequences in the side views of the layered monomer crystal and the stack of 2DP3 sheets in the polymer crystal, respectively. Note that both sequences contain one disordered solvent molecule every three layers sandwiched between the red template and the green monomer molecule. (e) Change of the average intermolecular center-to-center distances between neighbouring monomer molecules (top) and RUs (bottom), respectively, within the same layer with increasing polymerisation conversion. Parts of this panel reproduced and modified with permission by the publisher (ref. 11).

In a column, ABC sequences of three symmetry-independent molecules green, blue and red are separated by one disordered cpy molecule sandwiched in between a green monomer and a red template (Fig. 6c). All monomer molecules and the templates of each column lie on the same three-fold symmetry axis. They are not laterally offset relative to one another, as the graphical representation might suggest. Fig. 6b and d depict the same two perspectives, (top view and side view) for polymer 2DP3. Except for the red template molecule, the colour code now of course refers to repeat units (RU) created by the reaction between monomers. The bonds connecting these RUs to the polymer product 2DP3 are not shown. They are at positions C-9 and C-10 (see Fig. 5b).

When comparing monomer and polymer structures in Fig. 6a and b, there does not seem to have happened much besides the desired bond formation and perhaps some small change of lattice constant a. This impression changes when looking into how the average center-to-center distances between monomer molecules and the corresponding RUs change with polymerization. Fig. 6c and d provides this comparison for neighbouring molecules and RUs in the same column, thus across neighbouring layers, while Fig. 6e provides the same for neighbouring molecules and RUs within the same layer. Between neighbouring layers, there are noteworthy changes. First, two distances within the column decrease (green-template: by ∼0.5 Å and template-blue: by ∼0.5 Å) and one distance increases (blue-green: ∼1 Å). Second, the solvent molecules, which assume tilted orientations in the monomer crystal relative to the sandwiching monomer planes, are squeezed in between green RUs and red templates in the polymer. Consequently, their orientations are now parallel to the sandwiching polymer planes. Without going into a discussion of these changes at this point (see Section 4), it appears that the two-dimensional polymerization, which takes place predominantly within each layer of the layered monomer crystals, has components reaching out into the third dimension. This becomes even stronger by the changes within a layer (Fig. 6e). There, the out-of-plane distance between adjacent green and blue monomers vanishes almost completely during polymerization. This requires both monomers to move in opposite directions by ∼0.75 Å each. The position of the template however remains more or less unchanged despite this considerable ‘traffic’ in its direct vicinity.

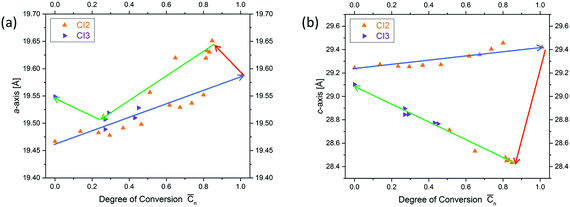
Next, we will have a look into the conversion dependent changes of lattice constants a (the one within a layer and identical to lattice constant b in a trigonal structure) and c (the one vertical to the layers). We will do this in both ways the chemical reaction can possibly proceed, which are polymerization and depolymerization. The first observation is that both lattice constants during polymerization increase with conversion (a by approx. 0.1 Å and c by approx. 0.25 Å). This is a surprising finding, because, as mentioned above, in linear polymerization volume contraction is the common scenario. The second observation concerns the changes caused by heating fully polymerized single crystals to about 60 °C. This temperature is much lower than that needed to bring about depolymerization (∼150 °C). Both lattice constants react abruptly to this procedure but in opposite direction (Fig. 7). While the in-plane constant a further expands, the out of plane constant c rather contracts. If then heating is continued at ∼150 °C such that depolymerisation slowly sets in, a expands by maximally ∼0.1 Å and c contracts by maximally ∼1.1 Å. This is clear indication for strain built up during polymerization both within the 2D polymer sheets and between them. In other words, photochemical polymerization at about 0–20 °C does allow the produced polymer sheets neither to expand nor to move closer to each other as they would like to. This is a typical signature of a kinetically trapped state and already (very) mild heating provides the energy to the system needed to relax towards a more equilibrated state. Soon after the initial major changes are implemented by the crystals, the lattice constants gradually move back to almost their initial values. Consequently, polymerization and depolymerization follow different paths. The consequences this kinetically frozen state has on 2D polymerization will be discussed in Section 4.

Fig. 7 Changes of lattice constants a (a) and c with reaction conversion (b) for two crystals (CI2 and CI3). Polymerization, annealing and depolymerization are indicated by blue, red and brown lines respectively. The reason for why both curves do not exactly return back to the initial state requires further research.

Now that we have learned about packing changes associated with polymerization of monomer 3, we move on to how polymerization (and depolymerisation) locally propagates in the entire crystal volume such that all the dimerization events required to convert a layer consisting of an almost infinite number of monomer molecules ideally into only one polymer molecule, namely 2DP3. A more physics-oriented way to phrase the same question is how a monomer phase transforms into the corresponding polymer phase. This problem was approached in three different ways. First, we measured the reaction conversion with irradiation time based on the Bragg structures of a large number of intermediate states. The obtained curve was then analysed with the help of the Avrami equation⁴⁷ which correlates the transformation propagation with transformation time via the Avrami exponent n. This exponent is an indicator for the relative amount of growth sites and the dimensionality of growth propagation at each of these growth sites. It is small when there are few growth sites which propagate linearly and large when there are multiple growth sites which propagate spherically. A detailed example for its usage in the context of 2D polymers is given in ref. 11. Second, the average distance between unreacted anthracene pairs was determined as function of polymerization conversion. While the result of such measurement alone does not prove a mechanism, it was important to see whether it was in line with the predictions based on the Avrami exponent. Finally, we analysed the diffuse scattering of various intermediate states and quantified the local spatial correlations of chemical bonds near a site where dimerization and thus bond formation had taken place. This promised to provide experimental evidence for whether or not a given dimerization influences the occurrences in its direct vicinity. If it does influence, this analysis allows concluding whether further dimerization is self-impeded or self-stimulated. If it does not, one can conclude that dimerization occurs fully random. However, the quantification of local spatial correlations promised even more than that. In contrast to the Avrami formalism, which reduces a complex problem to a single number by making many assumptions, diffuse scattering allows to directly ‘see’ all bond correlations. For 2D polymerizations it is important to note that what diffuse scattering sees is not restricted to within the monomer layer but goes well beyond in all directions and is thus a tool to decipher eventual 3D contributions to 2D polymerization. Diffuse scattering is therefore the method of choice for adequate and quantitative mechanistic descriptions of phase transformations. As will be seen, all three methods point in the same direction.

Fig. 8 provides a graphical representation of the three different main mechanistic scenarios. Fig. 8a shows a concrete intermediate situation of a reactive packing of monomer 3 (all monomers and RUs in green) with some dimers having formed and others not. Fig. 8b describes the colour code [white (unreacted), red (reacted)] which is applied to the rhombohedral lattice models in Fig. 8c and d. Fig. 8c and d show overlays of the chemical structure in (a) and colour-coded rhombille tiling in a transparent and a non-transparent fashion. Now prepared, Fig. 8e presents the three scenarios from ‘self-impeding’ via ‘random’ to ‘self-accelerating’ (from left to right). Translated into the geometry of anthracene dimers, self-impeding means that the distance or the lateral offset of not yet reacted dimers in the direct vicinity of a given dimer is increased as compared to the average monomer structure. This slows the mutual reactivity down. In the extreme case, all pairs first transform into dimers before they then start to grow further. If the opposite is true, growth is self-accelerating causing growth islands to form around an initially created dimer. These islands then continue growing through the layers and the crystal establishing ever-growing polymerization fronts, separating monomer phase from polymer phase.

Fig. 8 Simplification of partially polymerized structures and three main growth mechanisms for monomer 3. (a) depicts an arbitrarily chosen intermediate state where (b) chemical units are visually replaced by red and white rhombs. The resulting replacement is shown in (c) overlayed on top of the structure and in (d) solid colours. This visual simplification is used to describe the self-impeding, random, and self-stimulating mechanisms depicted in (e). Note that they all have the same conversion ratio.

Fig. 9a shows a typical experimental curve for the average degree of conversion C versus the irradiation time. This data gave the Avrami exponent n = 0.66 (Fig. 9b), which is an average over all polymerization data collected. Because values of n < 1 are uncommon, Monto Carlo simulations were used to predict the Avrami exponent for the phase transformation of layered monomer 3 into 2DP3. Interestingly, this simulation afforded the expected Avrami exponents of n = 1 and n = 2 for the random and self-accelerated reactivity models (Fig. 8e), respectively, but for the self-inhibited reactivity model the exponent n = 0.55 was obtained, which is in good agreement with the experimentally observed. Thus, the Avrami formalism points towards a self-impeding mechanism.

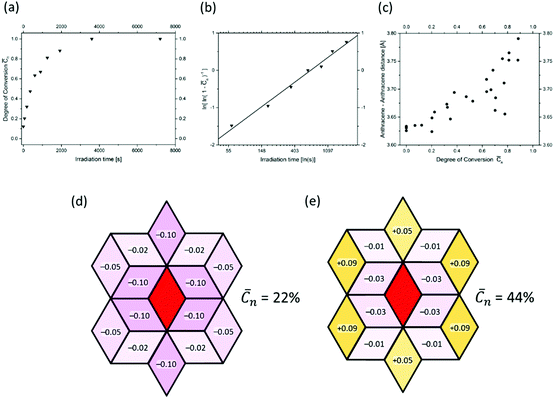Fig. 9 Evidence for the self-inhibiting mechanism of the two-dimensional polymerization mechanism of monomer 3. Details are given in the text.

Next we turned our attention to the evolution of the distance in unreacted anthracene pairs with increasing polymerization conversion. Fig. 9c shows the corresponding plot which collects data from several different experiments. Despite the scatter this causes, there is a clear trend visible. The distance increases! As it is reasonable to assume that distance changes occur in close proximity to where dimerizations have taken place, this distance increase in turn supports the self-inhibiting scenario.

After this encouraging finding, the mechanism was finally determined by analysing the diffuse scattering data. The results are shown in Fig. 9d and e again using rhombille tiles. The red tile in the center refers to a dimerized anthracene pair and the numbers in the surrounding tiles are the correlation coefficients. Coefficients range between −1 and +1, whereby −1 means that once a bond has formed (in the center) the probability of another dimerization is nil. +1 means that the bond in the center is always accompanied by another bond in the particular tile. Finally, the coefficient 0 reflects a random process. When now looking at the coefficients for two different polymerization conversions (22% and 44%) the first observation is that all values are relatively small. Thus, we are not dealing with strong effects. For the low conversion, there is a clear bias towards self-impeding, while for the high conversion, the self-impeding effect decreases and at longer distances from the central dimer can turn into a weak positive correlation. Statistical considerations might explain this.

4. The current understanding of 2D polymerization in the single crystal and what it means for the future

Now that the methodical and structural stages are set, this section addresses the understanding of many of the occurrences that can have influence on 2D polymerizations in single crystals and how this understanding can be used to improve and broaden synthesis of 2D polymers in the future. We believe that all occurrences aim at an optimum strain management, very much in line with the initial ‘Topochemical Postulate’ by Cohen and Schmidt.¹³ For convenience, we divide them in strain prevention, strain compensation, and strain distribution, although there will always be an overlap. The resulting subdivisions concern measures that allow a monomer molecule to not have to move by neither translation nor rotation, that buffer motions locally so that they are absorbed rather than passed on further, and to evenly distribute local strains over the crystal volume, respectively. The first two subdivisions refer to local phenomena, while the third subdivision concerns the global situation. Occasionally, local strain can also increase during polymerization as long as the entire strain balance is in order. As monomer 3 is arguably the best-understood case currently, we will start the discussion with this compound before expanding it mainly to monomers 4, 6 and 8. Whenever appropriate we will point to possibly more generally valid, yet still tentative conclusions and will provide recommendations.

We had stressed that the anthracene units of monomer 3 kink upon dimerization (Fig. 5) and that this is the ‘trick’ to keep the C-1 and C-8 atoms in both the unreacted pair and the dimer at more or less constant distance. While this design element is clearly important for local strain prevention, it is not the only factor enabling smooth polymerization. To understand two of the other factors we consider the columns of monomers, templates and RUs shown in Fig. 6. There are two things to note. First, during polymerization the blue and the green neighbouring monomers move towards each other out-of-plane by 0.75 Å each. This traffic totals to 14 000 km within 1 mm³ large crystals and one may ask, why this enormous movement happens, although it is seemingly against the ‘Topochemical Postulate’. Second, the space available to the solvent molecules squeezed in between the green monomer and the red template decreases upon polymerization. What are possible explanations? We believe the traffic to be necessary because it brings the reactive sites of the monomers (the C-9 and C-10 positions) closer to one another preventing the strain the product polymer would contain otherwise in form of unnaturally long C–C-bonds. This out-of-plane movement thus serves in-layer strain prevention. On the other hand, the squeezing of the solvent molecules can be interpreted in terms of buffering the vertical motion of the green monomer during polymerization. By sacrificing much of their space, the solvent molecules serve to prevent this motion from reaching and possibly detrimentally affecting the adjacent layer.

While these two factors are a wonderful symbiosis of strain prevention and strain compensation (buffering), this is not all. Surprisingly, there are two more occurrences, which we have identified so far. First, the polymer sheets formed contain some compressive strain as the increase in a upon mild thermal treatment proves (Fig. 8). Second, the sheets are kept at an artificially large distance, as the contraction in c amounting to 1.1 Å or 3.5% during annealing shows. The compressive strain may be due to the two independent effects of kinking and out-of-plane movement resulting in an accidental slight overcompensation of shrinkage, while the tensile strain may be due to facilitated translocations of the solvent molecules between the sheets during polymerization. This is suggested by their smeared-out electron density. Both these factors appear counterintuitive, as one may expect strain to be disadvantageous in all respects. What in the end however appears to truly matter is the proper strain management of the crystal supported by monomer design and monomer packing that enables the crystal to stay intact. We note that the compression may actually be beneficial in that it prevents the forming sheet from disruptions and the tensile strain may be advantageous when it comes to exfoliation, supposed this is performed prior to equilibration.

The compressive and tensile strains observed for the polymerization of monomer 3 raises an important question. Would premature annealing interrupt further growth? While there is no definite answer yet, together with the above observations, we consider the insights gained by this careful XRD analysis a warning to synthetic chemistry. This makes us formulate the first take home message:

The process of a 2D polymerization within what later will be the sheet plane is in fact an almost unpredictably complex three-dimensional process and a monomer design based on such a process therefore appears risky.

In retrospect, our own reasoning why monomer 3 could be suitable was excessively naïve. While this is not to say that monomers similar to 1–4 should not be tried but that monomers that connect perpendicular to the growing sheet may have a greater chance of success (see below).

Now that we have addressed strain prevention and strain compensation for the polymerization of monomer 3, we will deal with the third factor concerning strain distribution in a global sense. As the Bragg analysis suggested (Fig. 8) and the diffuse scattering finally proved, polymerization of monomer 3 when irradiating into the tail of the absorption curve⁴⁸ follows a self-impeding mechanism (Fig. 9). Thus, there is no polymerization front and there is no build-up of local strain just because of how the polymerization propagates spatially. This leads us to a second message:

Irrespective of what happens on the local scale, effective global strain distribution by self-impeding (or random) propagation mechanisms is ideal for 2D polymerization to happen smoothly.

Crystals are less likely to shatter and if there are a few cracks as observed for 2DP3, they will likely occur between sheets rather than vertical to them. When attempting 2D polymerization one should always have in mind, therefore, how to ensure the monomer to propagate self-impedingly.

The following example concerning monomer 4 will be rather telling in this very respect because its peculiar packing likely renders polymerization propagation to be self-accelerated. To make this point understandable, we have to describe the packing in some detail. Please note that the propagation mechanism has not been studied as for monomer 3 and that the following considerations are based on a deep look into the packing combined with the fact, that 2DP4 actually forms. Fig. 10a and b show top and side view of the packing, respectively. It is composed of two sets of symmetry-equivalent strands (brown and yellow) of monomers. These strands are tilted relative to one another by 35°, requiring polymerization to involve considerable concerted action. Although Fig. 10a mediates the impression that a desired reactive packing already exists, Fig. 10b shows that this is just an effect of projection. We draw the readers’ attention to the crossing points of the two sets of strands, because critical action will be exactly there.

Fig. 10 Structural features of monomer 4 in the single crystal. (a and b) Top and side view. (c) Top view with colour code reflecting the distance in anthracene pairs and, thus, their reactivity. (d) Crossing-points (black box) between the tilted strands in an overview (d) and in magnification (e). The projection in (e) shows the central monomers from top to better visualize the angle in the red pairs.

Fig. 10c is the same view as in Fig. 10a, however, this time using a colour code reflecting increasing monomer distance and thus decreasing reactivity towards dimerization: blue 3.7 Å, green 3.9 Å, and red 4.0 and 5.6 Å. The two distances for the red pair are a consequence of the anthracenes to be tilted caused by the tilt between the strands and thus by nearly 35°. While upon irradiation the blue and the green pairs are expected to react fastest, this cannot be the only action. Otherwise, the brown and yellow strands would form linear polymers interlocked in the crystal with no chance to align to furnish stacks of 2D polymers. Fig. 10d provides the missing ingredient using the same colour code as in Fig. 10c. It shows the two sets of strands of monomers that can polymerize. Even though in this projection it appears as if they were orthogonal to one another, the actual angle between the strands is in fact 35°. Because we know that 2D polymer 2DP4 actually forms, we propose that, possibly initiated by the dimerization action surrounding the crossing point, a first red anthracene pairs coplanarizes and subsequently connects the two forming adjacent polymer strands (Fig. 10d and e). This one motion then not only triggers neighbouring red pairs to do the same, actually in both strands of monomers, but also the other pairs to change their distance and become more reactive. By this action, the strands start to give up their topological identity and convert into sheet elements. To achieve 2D polymerization, these tiny sheet elements are required to now grow also laterally and to do so faster than new seeds of growth are formed somewhere in the crystal. Otherwise, sheet stacks titled by 35° grow towards each other and upon collision could not connect. This results in the ‘funny’ situation that on the one hand one would like to have as many seeds as possible for prevention of polymerization fronts, on the other hand one cannot accept a situation where many seeds tilted against each other dominate the action. Given the ambiguity of this aspect it may be interesting to learn that the crystals crack during irradiation to a degree that prevents SCXRD and that the flakes obtained after exfoliation are small. This might indicate that a limited number of seeds grow until they reach the size of the sheets obtained, when they then collide.

Unfortunately, the current state of research does not allow predicting which packing will result in which kind of propagation mechanism. The only recommendation one can therefore provide is:

Try to obtain monomer single crystals in different polymorphs and choose that polymorph for 2D polymerization where propagation is either self-inhibiting or random.

A first indication is whether the crystals survive polymerization. The effort involved in bringing monomer 4 into another reactive packing, for example, the one found for 2 and 3 may appear larger than it is because often already the unit cell dimensions are sufficient to conclude whether a new packing has been achieved.⁴⁹ They are obtained within a matter of minutes. The other lesson to be learned from monomer 4 is to never surrender in a seemingly hopeless situation, but rather to try irradiation in any case. There is a variety of reactions in crystals with rather unexpected outcome the most famous of which concerns 9-cyanoanthracene which forms anti-oriented reactive pairs but furnishes the syn-dimer after irradiation.⁵⁰

Next, we will come back to the issue whether the direction of bond formation should be within the plane of what will later be the polymer sheet or rather perpendicular to it. Monomer 6 provides invaluable insights here, although as for monomer 4 propagation has not yet been studied. As discussed, for monomers 1–3, all bond formations take place in the direction of the a,b-plane. Thus, the strain associated with the chemical action and the degree to which it can be compensated has a direct impact on how large the sheets will be eventually. For monomer 6 (and 5), however, this is different. Here the direction is more or less perpendicular to the plane (Fig. 2f, bottom). Importantly, this shifts a fraction of the developing strain to in between adjacent layers. As there should not be any bond formed between layers anyway, this is good news for synthesis. For monomer 6 the in-layer direction actually slightly shrinks, which is obviously being well taken care of by the propagation mechanism as judged by the sizes of the sheets and sheet stacks obtained from exfoliation.

Despite the fact that there are currently more in-plane (1–3, possibly also 4) than perpendicular-to-the-plane monomers (5, 6) and that the total number of cases is still manageable, successful mastering of the strain issue in our eyes is more promising for the latter monomers as part of the complexity is shifted to in between the growing planes. This reduces the risk of failure and we formulate the fourth take home message:

Monomers that allow for a ‘perpendicular-to-the-plane’ growth are more likely to be successful than those for ‘in-plane’ plane growth.

As with all monomers for topochemical reactions, however, molecular design and mode of polymerization alone is not all. Although this Tutorial does not touch on crystal engineering,⁵¹ we had already mentioned that achieving the right packing is an independent and important step. According to our experience, reactive packings can often be achieved by solvent screening, although there is a case, where even 70 solvates did not include the crystal desired for 2D polymerization.⁴⁵

Monomer 8 adds yet another useful facet (Fig. 11). It concerns the mechanism of strain compensation. In contrast to all other cases discussed here, neighbouring monomers are not connected photochemically. Rather, a cross-linker is diffused into the monomer crystals to connect the terminal olefin groups with one another such that the covalent sheets 2DP8 are obtained. The unit cell volume change associated with the reaction amounts to few percent, which clearly requires strain compensation. However, 2DP8 contains the flexible cross-linkers as integral structural parts and slight conformational changes of these parts can therefore easily serve to compensate strains on both a local and a global level. It is important to realize that polymers such as 2DP1–2DP4 and also 2DP5 and 2DP6 are quite rigid and do not have this option. Thus, the polymerization of 8 is a brand-new concept both in terms of the kind of cross-linking used and the way in which strain annihilation is achieved. Given the enormous degree of selectivity required for the reaction between cross-linker and monomer to bring about a 2D polymer (rather than an irregular cross-linked 2D or 3D network), however, it is expected that the cross-linker and its relative orientation in the crystal dictates a cross-linking topology. From the three dithiols tested (with two, three, and four methylene groups) only 1,3-propanedithiol gave 2DP8. As this paragraph touched upon new chemistry, we would like to mention on passing that the group of Sureshan has developed interesting topochemical reactions, which may well be suited for 2D polymerizations as well.⁵²

Fig. 11 Top and side view (a and b) of the polymer 2DP8 in the single crystal. Not all dithiolpropane bridges are resolved. These sites are marked with red spheres between which electron density is found. Possible reasons include completely missing links and links that are bonded to one olefin only. Additionally, there may be regiochemical and stereochemical isomers associated with the thiol–ene-addition reaction, which all can contribute to a smeared electron distribution.

The polymerization of monomer 8 generates another tempting thought. Would it be possible to synthesize monomers similar to 2, 3 or 4 that have built-in strain-compensation units? Would a somewhat reduced structural rigidity help not only to achieve the desired packing but also to render polymerization smoother by an internal strain buffering? The fact that monomer 3 polymerizes so smoothly makes us wonder whether this might have anything to do the presence of ether bridges which are known to be conformationally quite flexible. Thinking in this direction has great potential and therefore the fifth take home message is:

New concepts of strain management could include monomers with a somewhat increased conformational flexibility.

Ideally, such thinking goes in concert with theoretical modelling.

Finally, a few words concerning monomer 1 whose single crystals shatter upon irradiation. If there is no other way to avoid that, we have learned that PXRD and TEM/ED are tools optional to SCXRD. TEM and ED were actually applied to the product of 1 and gave the beautifully resolved images and informative diffraction patterns (Fig. 2a), which, together with other evidence, established the structure of 2DP1. Inasmuch can these beautiful images now be compared with the SCXRD patterns, which were at the core of the present Tutorial? Here it is important to note that PXRD and SCXRD are averaging techniques and therefore provide representative information for a large volume (typically an entire crystal or a heap of microcrystalline powder). In contrast, TEM and ED are local techniques providing information in small and selected volume elements of the analysed matter (see scale bars in Fig. 2a). Thus, the structural features so nicely seen in Fig. 2a may not be representative for the entire material obtained, which is a caveat. However, there are more differences between these methods. For example, while SCXRD provides bond lengths and angles with unmatched precision, TEM has the unique capability to unravel local microstructural information on e.g. cracks, grain boundaries, and defects. Such information is of clear interest to synthetic chemistry and leads to the sixth take home message:

None of the methods PXRD, TEM/ED, and SCXRD can replace either of the remaining ones; they are in the best sense complementary.

The discussion of monomer 1 will be concluded with a thought of potential general applicability. In cases where crystals brake, it may be advisable not to polymerize through to have then to apply PXRD or TEM/ED but rather to stop polymerization at a conversion low enough to still be able to apply SCXRD. Detailed structural analysis at this stage by Bragg and possibly diffuse scattering may provide invaluable information concerning the responsible factors for destruction, and by this point towards possible solutions.

So far, we have concentrated on the various facets of strain management and structural analytics. There are however also more technical and resolution issues. Obviously, the monomer crystals should have an optimal quality as already mentioned in Section 2. Recrystallization and annealing of the monomer crystal prior to polymerization can reduce mosaicity and lead to crystals with more long-ranging order. The choice of wavelength also deserves consideration. If it is chosen at or near the maximum optical absorption, the probability of the incident beam to cause dimerization is highest near the crystal surface.⁴⁸ This works against an even distribution of local strain and rather supports phase separation between monomer and polymer phases with polymerization fronts in between. The seventh take home message thus is:

Choose the wavelength such that the reactions it causes are distributed over the entire crystal volume. Otherwise, any measures taken to favour a self-impeding propagation mechanism might be counteracted.

Despite the power of SCXRD, it has limitations the synthetic chemist should know about. For example, even when performed at a synchrotron, SCXRD does not allow determining lattice site occupancy to an accuracy better than a few percent (Section 2). Thus, claiming a 2D polymer solely based on this method is insufficient. This very polymer may in fact be missing 1–2% of its RUs, an issue of obvious importance when such material shall be used e.g. as filtration membrane. In addition, SCXRD does not allow estimating the size of 2D polymer sheets in the single crystal. At best, it provides a lower threshold value, which for common diffractometer set-ups is order of a few hundred nm. Such an issue has to be addressed by imaging methods including TEM or atomic force microscopy. Finally, a comment concerning PXRD. Here, we stress again that occasionally more than one model fits a given diffractogram.⁴⁴ This turns structural assignment the more questionable the less crystalline a material is as well as the larger the materials lattice constant and the lower its symmetry are. We recommend not to apply baseline corrections although this makes diffractograms appear more beautiful, because the background can always contain critical information (degree of amorphicity and diffuse scattering).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are thankful to all our coworkers that have contributed to the field of 2D polymers for their invaluable and creative input. Their names can be found in the references. We also thank Chenfeng Ke, Dartmouth College, for helpful discussions. We are further grateful for helpful discussions enabled by the Harris German/Dartmouth Distinguished Visiting Professorship program. The Swiss National Science Foundation supported this work (grant 157157).

References

1. P. Müller, Crystallogr. Rev., 2009, 15, 57–83.
2. J. Sakamoto, J. Van Heijst, O. Lukin and A. D. Schlüter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069.
3. J. W. Colson and W. R. Dichtel, Nat. Chem., 2013, 5, 453–465.
4. R. Z. Lange, G. Hofer, T. Weber and A. D. Schlüter, J. Am. Chem. Soc., 2017, 139, 2053–2059.
5. P. Payamyar, B. T. King, H. C. Öttinger and A. D. Schlüter, Chem. Commun., 2016, 52, 18–34.
6. M. Servalli, H. C. Öttinger and A. D. Schlüter, Phys. Today, 2018, 71, 40–47.
7. W. Wang and A. D. Schlüter, Macromol. Rapid Commun., 2018, 1800719.
8. H. Staudinger, Ber. Dtsch. Chem. Ges. A/B, 1920, 53, 1073–1085.
9. G. Wegner, Makromol. Chem., 1972, 154, 35–48.
10. M. Hasegawa, Chem. Rev., 1983, 83, 507–518.
11. G. Hofer, F. Grieder, M. Kröger, A. D. Schlüter and T. Weber, J. Appl. Crystallogr., 2018, 51, 481–497.
12. C. Giacovazzo, H. L. Monaco, D. Viterbo, F. Scordari, G. Gilli, G. Zanotti and M. Catti, Fundamentals of Crystallography, Oxford Univ. Press, Oxford, 1992.
13. M. D. Cohen and G. M. J. Schmidt, J. Chem. Soc., 1964, 1996–2000.
14. T. R. Welberry and T. Weber, Crystallogr. Rev., 2016, 22, 2–78.
15. S. L. James, Chem. Soc. Rev., 2003, 32, 276–288.
16. H.-C. Zhou and S. Kitagawa, Chem. Soc. Rev., 2014, 43, 5415–5418.
17. X. Feng, X. Ding and D. Jiang, Chem. Soc. Rev., 2012, 41, 6010–6022.
18. S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568.
19. P. J. Waller, F. Gándara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053.
20. C. S. Diercks and O. M. Yaghi, Science, 2017, 355, 923.
21. S. Kandambeth, K. Dey and R. Banerjee, J. Am. Chem. Soc., 2019, 141, 1807–1822.
22. T. Ma, E. A. Kapustin, S. X. Yin, L. Liang, Z. Zhou, J. Niu, L.-H. Li, Y. Wang, J. Su, J. Li, X. Wang, W. D. Wang, W. Wang, J. Sun and O. M. Yaghi, Science, 2018, 361, 48–52.
23. A. M. Evans, L. R. Parent, N. C. Flanders, R. P. Bisbey, E. Vitakul, M. S. Kirschner, R. D. Schaller, L. X. Chen, N. C. Gianneschi and W. R. Dichtel, Science, 2018, 361, 52–57.
24. L. Addadi and M. Lahav, J. Am. Chem. Soc., 1979, 101, 2152–2156.
25. G. S. Murthy, P. Arjunan, K. Venkatesan and V. Ramamurthy, Tetrahedron, 1987, 43, 1225–1240.
26. J. W. Lauher, F. W. Fowler and N. S. Goroff, Acc. Chem. Res., 2008, 41, 1215–1229.
27. P. Kissel, R. Erni, W. B. Schweizer, M. D. Rossell, B. T. King, T. Bauer, A. D. Schlüter and J. Sakamoto, Nat. Chem., 2012, 4, 287–291.
28. R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781–853.
29. J. M. Thomas, Philos. Trans. R. Soc. London, 1974, 277, 251–286.
30. M. D. Cohen, Tetrahedron, 1987, 43, 1211–1224.
31. D. J. Murray, D. D. Patterson, P. Payamyar, R. Bhola, W. Song, M. Lackinger, A. D. Schlüter and B. T. King, J. Am. Chem. Soc., 2015, 135, 3450–3453.
32. X. Chen, S. Yamanaka, K. Sato, Y. Inoue and M. Yasukawa, Chem. Phys. Lett., 2002, 356, 291–297.
33. P. Kissel, D. J. Murray, W. J. Wulftange, V. J. Catalano and B. T. King, Nat. Chem., 2014, 6, 774–778.
34. M. Kory, M. Wörle, T. Weber, P. Payamyar, S. Van de Poll, J. Dshemuchadse, N. Trapp and A. D. Schlüter, Nat. Chem., 2014, 6, 779–784.
35. P. Tanner, G. Maier and A. D. Schlüter, Helv. Chim. Acta, 2018, 101, e1800128.
36. Z. Wang, K. Randazzo, X. Hou, J. Simpson, J. Struppe, A. Ugrinov, B. Kastern, E. Wysocki and Q. R. Chu, Macromolecules, 2015, 48, 2894–2900.
37. W. Liu, X. Luo, Y. Bao, Y. P. Liu, G.-H. Ning, I. Abdelwahab, L. Li, C. T. Nai, Z. G. Hu, D. Zhao, B. Liu, S. Y. Quek and K. P. Loh, Nat. Chem., 2017, 9, 563–570.
38. X. Jiang, X. Cui, A. J. E. Duncan, L. Li, R. P. Hughes, R. J. Staples, E. V. Alexandrov, D. M. Proserpio, Y. Wu and C. Ke, J. Am. Chem. Soc., 2019, 141, 10915–10923.
39. T. Weber and A. Simonov, Z. Kristallogr., 2012, 227, 238–247.
40. A. Simonov, T. Weber and W. Steurer, J. Appl. Crystallogr., 2014, 47, 2011–2018.
41. https://dictionary.iucr.org/Mosaic_crystal .
42. S. Billinge, Philos. Trans. R. Soc., A, 2019, 377, 20180413.
43. T. Proffen, S. Billinge, T. Egami and D. Louca, Z. Kristallogr., 2009, 218, 132–143.
44. C. Buchsbaum and M. U. Schmidt, Acta Crystallogr., 2007, 63, 926–932.
45. M. Servalli, N. Trapp, M. Solar and A. D. Schlüter, Cryst. Growth Des., 2017, 17, 3419–3432.
46. G. Hofer, PhD thesis, 2019, https://doi.org/10.3929/ethz-b-000371011.
47. M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112.
48. V. Enkelmann, G. Wegner, K. Novak and K. B. Wagener, J. Am. Chem. Soc., 1993, 115, 10390–10391.
49. M. Servalli, N. Trapp, M. Wörle and F.-G. Klärner, J. Org. Chem., 2016, 81, 2572–2580.
50. V. Ramamurthy and K. Venkatesan, Chem. Rev., 1987, 87, 433–481.
51. G. R. Desiraju, Crystal Engineering: The design of Organic Solids, Elsevier, Amsterdam, 1989.
52. B. P. Krishnan, R. Rai, A. Asokan and K. M. Sureshan, J. Am. Chem. Soc., 2016, 115, 14824–14827.

---

Footnotes

† Dedicated to Gerhard Wegner on the occasion of his 80th birthday.

‡ This definition refers only to very small tilts (‘… fractions of a minute of arc …’). In literature the term mosaicity is normally also accepted if the mosaic spread is in the order of 1°, what is observed for many organic or protein crystals. Please note that the term block has a different meaning in the context of mosaicity than for polymers.

---