Open Access Article
Open Access ArticleTowards understanding the catalytic properties of lead-based ballistic modifiers in double base propellants†
Lisette R.
Warren
,
Colin R.
Pulham
 and
Carole A.
Morrison
and
Carole A.
Morrison
 *
*
EaSTCHEM School of Chemistry, University of Edinburgh, The King's Buildings, David Brewster Road, Edinburgh, EH9 3FJ, UK. E-mail: C.Morrison@ed.ac.uk
First published on 29th October 2020
Abstract
Lead-based ballistic modifiers are additives in double base propellants (DBPs) which render the burn rate insensitive to changes in pressure within a defined pressure range, thus imparting greater control of combustion conditions. In-coming European legislation will soon ban the use of lead in propellant formulations, however, and few suitable candidate replacement materials are currently available. In an effort to understand better the unique properties offered by lead-based modifiers, we present a first-principles computational study on Pb, PbO, PbO2, SnO2 and Bi2O3, all of which have been investigated experimentally as ballistic modifier materials. Our study demonstrates that various quantifiable properties exist for the lead-based materials. Overall, they have narrower electronic band gaps, lower surface energies and lower surface work functions than the lead-free systems, indicating a greater propensity to form stable chemical surfaces with higher catalytic activity. We also show that of the set, only Pb and α-PbO can support the formation of a weakly bound layer of amorphous carbon, a key experimental observable in the burning of DBPs.
Introduction
Double base propellants (DBPs) are a form of solid rocket propellant consisting of the nitrate esters nitrocellulose (40–70%), and nitroglycerin (15–41%, see Fig. 1), which bind together to form a polymeric gel. This mixture acts as a combined fuel and oxidiser, and finds application in missile and rocket propulsion due to the rapid release and expansion of smokeless gaseous combustion products.1,2 | ||
| Fig. 1 Structures of nitroglycerin [left] and fully-nitrated nitrocellulose, 14.4% N by weight [right]. | ||
The burning rate r for DBPs is represented by Vieille's law, according to:
| r = apn | (1) |
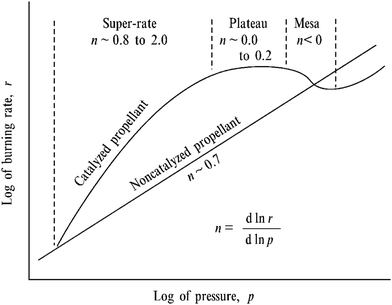 | ||
| Fig. 2 Burning rate-pressure relation for non-catalysed and catalysed DBP.8 Copyright (1974) AIAA. | ||
The first ballistic modifiers were identified during World War Two, when researchers serendipitously discovered that the use of lead-containing lubricants in the propellant manufacturing process lead to a greatly increased pressure exponent in the ambient pressure region.3 Lead-based ballistic modifiers are commonly used in the form of lead salts of organic acids such as lead acetate, lead salicylate and lead β-resorcylate, or as the oxides PbO, Pb3O4 and PbO2.8–12 To date, only these lead-based compounds support all three burn-rate effects, while the inclusion of other additives, such as copper-based products and carbon black, have been found to further increase the catalytic effect of the lead salts.2,12–14
The on-going dependence on lead is problematic as this highly toxic element presents hazards in its use and disposal, and impending European Union regulations (Reach – Registration, evaluation, authorisation and restriction of chemicals)15 will ban their use. Hewkin et al. tested a wide range of alternative modifiers including CuO, Fe2O3, ZnO, Co2O3 and SnO2 which, while increasing the combustion rate, could not support plateau burning.11 In particular, CuO and SnO2 have been found to produce extensive super-rate burning at low pressures, but fail to plateau off the burn rate as the pressure increases. A recent review on current ballistic modifiers, which documents the trends towards nano-scale particles of ballistic modifiers, maintains the dependence on lead to generate plateau burning.16 Nano-Bi2WO6 was recently reported as a promising lead-free alternative capable of achieving plateau burning, however this was observed at a considerably higher pressure range than for the lead-based modifiers which may limit its application, and no mesa effect was observed.17
In order to understand how ballistic modifiers alter the burn-rate of DBPs, the decomposition mechanism should be considered. Much of the experimental work and theory development was documented in the 1950s–1990s, and has recently been summarised in a review article.18 It is known that combustion of DBPs occurs in a succession of distinct zones, as depicted in Fig. 3.3,11 Initially the temperature rises in the conductive heat zone until thermal degradation of the DBP is significant, wherein the nitrate esters decompose (reversibly) to RO˙ and NO2 just below the burning surface. A series of simultaneous secondary reactions then occur to deliver primarily aldehyde and NO2 fragments to the burning surface. Burning surface temperatures are typically on the order of 300 °C, and do not exceed 500 °C.7 Highly exothermic gaseous oxidation and reduction reactions then occur in the fizz zone, and the temperature rapidly increases. A variety of products are produced, primarily NO, CO, CO2 and H2O.19 Temperatures at the end of the fizz zone are typically 800–1000 °C. Redox reactions of these products in the next zone (the dark zone) takes place slowly unless the pressure is particularly high. This is then followed by the flame zone, where the final combustion products of N2, CO2, CO and H2O are formed, and a luminous flame is produced.
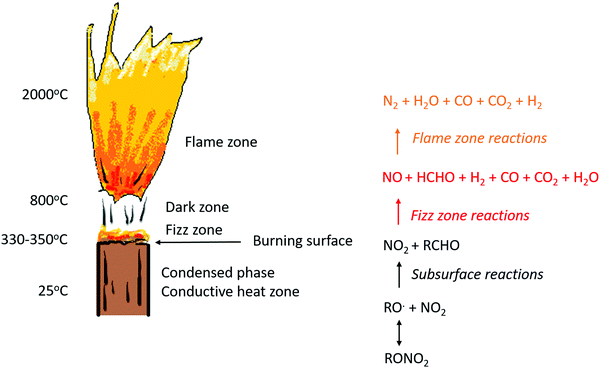 | ||
| Fig. 3 Schematic diagram of the flame regions in the DBP combustion zone. Reproduced from ref. 18 with permission from Wiley. | ||
From the perspective of DBP decomposition in the presence of ballistic modifiers, there is consensus in the literature that catalysis takes place in the fizz zone, and therefore involves reactions to produce NO2 and aldehyde fragments, and to support potential reduction/oxidation reactions, in these respective parts of the flame.5,6,9,20,21 A thermochemical study in 1984 showed that a large variety of lead salts all decompose within the temperature range of 300–500 °C, which is consistent with temperatures just below the burning surface.10 It is therefore likely that the catalytically active form of the ballistic modifier will be a decomposition product of the lead salts. Furthermore PbO and PbO2 have been directly proven to be capable of produce plateau burning,11,12,22 whilst mass spectrometry studies have identified that Pb, PbO, PbO2, H3PbO4 and elemental carbon are all formed in the decomposition of lead ballistic modifiers within the combustion process.9 Of the different lead oxide species, PbO is widely regarded as the most stable form,23 and so it is likely that other forms of lead oxide will convert to this in the combustion flame.
Notable to the catalytic decomposition of DBPs is the observation that the addition of carbon black alongside lead salts significantly improves the initial super-rate burning and plateau burning rates. Furthermore, the existence of a carbon matrix at the burning surface in the presence of lead salts has been identified in many experiments.5,7,9,11,24–26 A compelling catalytic theory for the decomposition of DBPs with ballistic modifiers is that the initial formation of this carbon soot layer is responsible for modifying the burning surface and aiding super-rate burning; the subsequent loss of the carbon matrix with increasing pressure has then been proposed for inducing the plateau-burning effect.11,18,27
As the available experimental evidence points towards the ballistic modifier decomposing to catalytically active clusters interacting at a solid/gas interface, a computational modelling investigation into the surface properties of various metal and metal oxides surfaces can offer fundamental insight into the nature of these catalytic processes. To this end, herein we simulate the electronic properties of the bulk crystalline materials of Pb, PbO and PbO2, which have demonstrated success as burn-rate modifiers when added to DBP formulations, and compare against Bi2O3 and SnO2 which, while capable of accelerating reactions at low gas pressures, have failed to support plateau or mesa burning effects.11,12 This study seeks to identify the likely surfaces that will form in the condensed phase and to compute various chemical reactivity markers, namely electronic band gaps, surface energies and surface work functions, which may help explain the differences in chemical reactivity. A layer of amorphous carbon has been deposited onto each model to investigate its propensity to support a carbon layer. In this way we identify some unique properties of the lead-based systems, in the hope that these metrics will accelerate the search for non-toxic ballistic modifier replacements.
Results and discussion
Structure and electronic properties of bulk models
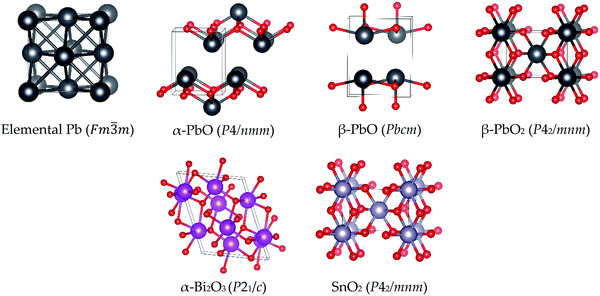
In order to investigate the catalytic properties of lead-based ballistic modifiers, condensed phase models of Pb, PbO and PbO2 have been investigated. SnO2 and Bi2O3 have also been studied to provide a comparison with lead-free alternatives, which while known to support super-rate burning, fail to achieve the plateau and mesa rate effects.As the temperature of the burning surface in DBPs does not exceed 500 °C,7 the phase of the bulk model to be considered should be stable under these conditions. For PbO there are two known stable phases: litharge α-PbO (space group P4/nmm) is the ambient temperature structure, which transitions to massicot β-PbO (space group Pbcm) at temperatures above 500 °C.28–30 As this is within the limit of the burning surface temperature, both phases of PbO have been included in this study. Both are characterised by layers orthogonal to either the c- (α-PbO) or a-axis (β-PbO), wherein all oxygen atoms are sandwiched between two Pb sub-layers (see Fig. 4). For both systems inter-layer spaces are occupied by the lone pairs on Pb(II). For PbO2, α-PbO2 is known to transform into β-PbO2 at room temperature and under ambient humidity conditions,29 whereas the reverse transition appears to only occur at high pressure.29 Thus, only the β-form (space group P42/mnm) is considered in this study. The most stable phase for SnO2 (stable up to 800 °C and high pressures)31 is isostructural with β-PbO2.32 Unlike in PbO, the Pb/Sn(IV) metal atoms are fully coordinated to oxygen atoms, resulting in an absence of metal-based lone pairs in these structures. Bismuth oxide has four known crystal phases (α-, β-, γ- and δ-); this study focuses on the monoclinic α-form (space group P21/c),33 which is the most stable phase up to 1000 K.34 To complete the study, we also include metallic lead, which has a face-centered cubic lattice (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), consisting of four atoms in the unit cell. Images of the bulk crystalline structures studied in this work are presented in Fig. 4.
m), consisting of four atoms in the unit cell. Images of the bulk crystalline structures studied in this work are presented in Fig. 4.
Input structures were taken from the ICSD, with calculations performed as described in the Computational Methods section. In order to interpret the electronic behaviour of the bulk models, the electronic band structure and projected density of states (PDOS) onto atomic orbitals were calculated (Fig. 5 and 6). A variety of functionals were tested; the hybrid HSE06 functional performed very well for semiconducting systems, and the GGA PBE functional performed best for metallic Pb. Full details of the optimised structures are recorded in the ESI;† for all models reported in the main text the optimised unit cell volumes deviated from the experimental values by no more than 2.5%. Due to the layered nature of the PbO models, lattice parameters have not been optimised for these models, as attempts to account for dispersion interactions via the Grimme D3 dispersion correction scheme did not result in a satisfactory unit cell optimisation (see ESI†). Similarly, for α-Bi2O3, the correction scheme resulted in severe over-binding of the b-axis, and so unit cell optimisation without dispersion was pursued for this model.
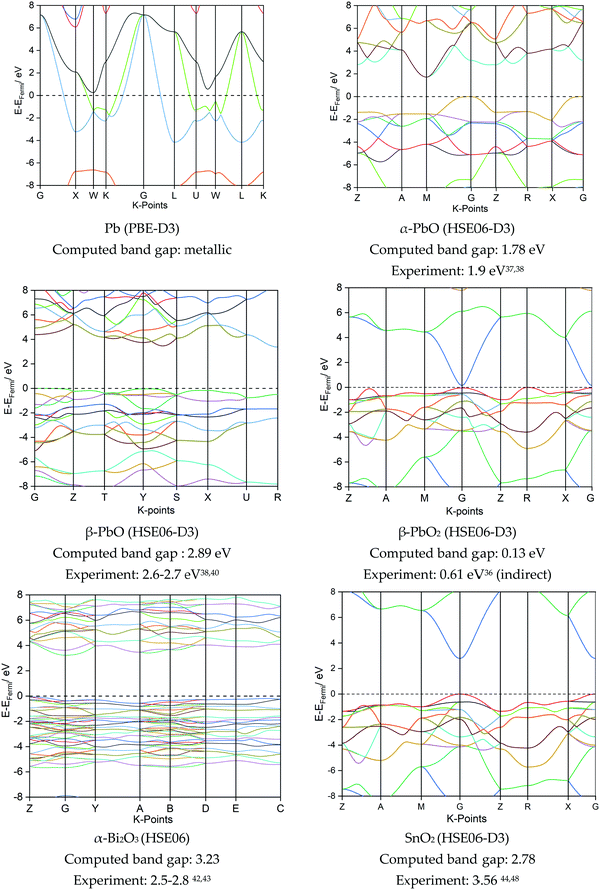 | ||
| Fig. 5 Computed band structures and band gaps for the best fitting functional for each of the lead-based and non-lead systems. Experimental band gaps also given. | ||
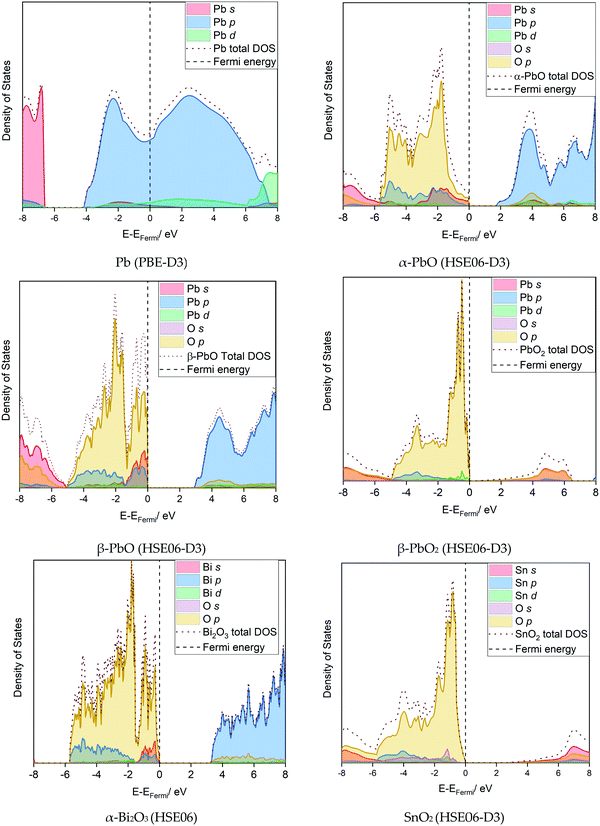 | ||
| Fig. 6 Computed density of states for the best fitting functional for the lead-based and non-lead systems. | ||
It is evident from Fig. 5 that the electronic band gaps of the lead-based materials are generally smaller than for the non-lead oxides. Pb is, as expected, metallic, whilst β-PbO2 is a semi-metal with a small band gap, in agreement with both experimental reports35,36 and other DFT calculations.35 Both α- and β-PbO are semiconductors, with the α-form presenting a smaller indirect band gap of 1.78 eV, in direct agreement with both experiment37,38 and computation.39 The β-form of PbO presents a computed band gap of 2.89 eV with the HSE06 functional, compared to an empirical value of 2.6–2.7 eV.38,40 The electronic structure for α-Bi2O3 (band gap 3.23 eV) is close to previous calculations reported for the PBE functional (2.8 eV)41 and is similar to experimental values (2.5–2.8 eV).42,43 Finally, SnO2 is found to be a direct band gap insulator; experimental data reports a direct transition of 3.56 eV,44 and our simulation matches a previous report using the same functional (2.8 eV).45 Thus, even though PbO2 and SnO2 are isostructural and present very similar electronic structures, the band gap for PbO2 is significantly shorter compared to SnO2. This can be attributed to relativistic effects: while in both cases the metal s-states form the lower conduction band, the Pb 6s states reside much lower in energy than the 5s Sn states, thereby narrowing the band gap.46
Further detail into the electronic nature of the valence band maximum (VBM) and conduction band minimum (CBM) can be gathered from the projected densities of states in Fig. 6. Comparing the lead-based systems first, the 6p states dominate the VBM near the Fermi level for Pb, where (6p)2 forms the outermost valence electrons. Both α- and β-PbO present very similar density contributions around the Fermi level; their electronic nature differs only in the magnitude of the band gap. Compared to Pb, in PbO the unoccupied Pb p-states now shift to the CBM. The valence bands are constructed from hybridised O p-states and Pb s- and p-states; the nature of this interaction has been discussed in detail by Walsh et al.,47 and is used to account for the formation of the asymmetric lone pair on Pb(II) in litharge α-PbO. Further oxidation to β-PbO2 now results in the unoccupied metal 6s state forming the major contribution to the CBM. Oxygen p-states now dominate the valence band edge, with a very minor contribution from the metal d-states. Thus, each of the lead-based systems (Pb, PbO and PbO2) present different orbital contributions around the Fermi surface, and can be considered to be chemically distinct, while overall presenting relatively small electronic band gaps.
For the lead-free materials, Bi is found in oxidation state(III) in α-Bi2O3, and therefore presents the same valence electron count as Pb(II) in α-PbO. Thus, very similar electronic contributions are observed around the Fermi surface, where interaction between the Bi 6s-states, O 2p-states, and unoccupied Bi 6p-states have also been identified to be responsible for the presence of an asymmetric lone pair.46 SnO2 is isostructural to PbO2, such that electronic contributions to the VBM and CBM are very similar for the two systems (see Fig. 6).
From these simulations, a trend emerges that the electronic band gap, which is a metric of chemical reactivity, is smaller for the Pb-based systems than for the lead-free systems. For all metal oxide models, the O 2p states dominate the valence band maximum, with contributions from metals varying depending on their oxidation state.
Properties of bare surfaces
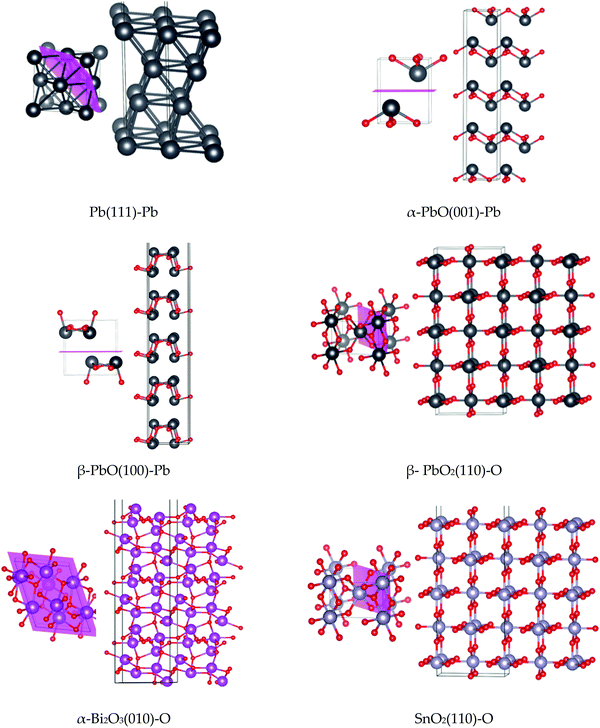
2D periodic slabs were generated to study the surface properties of the lead-based and lead-free models (see Computational methods). Atomic relaxations only were considered, and features such as surface reconstructions and defect formation effects were not included. While this may lack authenticity with the experimental observation of e.g. flow of powders (where high surface energies may be indicative of materials that clump), it can provide valuable insights into their stabilities at point of formation in a hot gas stream. Surface energies are used to understand the chemical stability of the surfaces, as well as the structural nature of each surface, while surface work functions indicate the energy required to oxidise the material, and therefore provide another metric for chemical reactivity. Structures for the other (less stable) studied surfaces with relaxed surface energies are reported in the ESI.†Ball-and-stick models of the most stable surface for each system are shown in Fig. 7. Computed surface energies and work functions are presented for both the hybrid HSE06 functional and GGA PBE functional in Table 1. We note that surface energies computed by the HSE06 hybrid method are generally greater than those obtained for the GGA PBE method. For all systems, the computed band gap of the surface is smaller than that of the bulk system (see Table 1 and Fig. 5). As with the bulk systems, a similar trend is observed where the Pb-based systems portray smaller band gaps than the Pb-free modifiers, which again suggests a more chemically reactive state. The nature of the VBM and CBM is the same as observed for the bulk models. For all surfaces, the electron density around the band gap is located largely on the exposed surface states due to the increasing chemical activity of the unsaturated valency sites (see ESI†).
| System | Band gap (eV) | γ (J m−2) HSE/PBE | Other works γ (J m−2) | φ (eV) HSE/PBE | Other works φ (eV) | Expt φ (eV) |
|---|---|---|---|---|---|---|
| Functionals:a PBE functional.b PBEsol functional.c D3 dispersion correction applied. | ||||||
| Pb(111) | Metallic | 0.33/0.32 | 0.28a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 48 |
3.8/3.8 | 3.78a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48, 3.83a 48, 3.83a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
4.2550 |
| α-PbO(001) | 1.72c | 0.34c/0.20c | 0.08b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
4.5c/3.6c | 3.60b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
4.4652 |
| β-PbO(100) | 2.89c | 0.33c/0.24c | 0.13a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 53 |
5.3c/4.6c | — | — |
| β-PbO2(110) | Metallic | 0.77/0.55 | — | 7.5/6.9 | — | — |
| α-Bi2O3(010) | 3.18 | 0.37/0.37 | 0.26a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34, 0.38b 34, 0.38b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
5.5/4.9 | 4.1b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
4.8252 |
| SnO2(110) | 2.18 | 1.26/1.04 | 1.04a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54, 1.31b 54, 1.31b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
7.5/6.6 | 7.48b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
4.55,52 4.4–5.755 |
From the perspective of forming clusters in the condensed phase of DBPs, low values for the surface energy indicate chemical stability of the surface and ease of formation, while higher values indicate an energetic barrier to formation and a higher propensity to form larger clusters. From this study, it is notable that the Pb-based surfaces all present relatively low surface energies for formation, which in turn suggests a comparative ease for these compounds to form small clusters with stable faces. The (111) surface of Pb was deduced to be the most stable, as expected for a fcc metal.56 For α-PbO and β-PbO the (001) and (100) surfaces, respectively, which arise due to the breaking of weak van der Waals interactions between the layers, were found to be the most stable, in agreement with previous reports (on isostructural SnO)57 and β-PbO.53 For β-PbO2 and SnO2, the (110) surface was deduced to be the most stable, in agreement with other DFT calculations reported for isostructural rutile TiO2,58–60 which has also been verified experimentally.61 Due to breaking of Pb–O bonds, β-PbO2(110) has a noticeably higher surface energy for formation compared to the other lead systems. Isostructural SnO2, in turn, presents a much higher surface energy value, attributed to the severance of stronger Sn–O bonds compared to Pb–O.62 Thus, SnO2 presents the highest surface energies for formation in the test set, and therefore a greater propensity to form particles of larger diameter to minimise the surface/volume ratio. This particle agglomeration effect has been observed for SnO2 in a DBP.12 Finally, in agreement with the computational study by Lei and Chen,34 the (010) surface with terminating oxygen atoms was determined to be the most stable cleaved model for α-Bi2O3.
The work function is a measure of the ease of electron removal from the valence band of the material to the vacuum. Our HSE06 computed values (see Table 1) for Pb and α-PbO match experimental values well, and the PBE computed work function matches another report using the PBEsol functional.51 For α-Bi2O3(010), both computed values are higher than previously reported,51 but match better with experiment. PbO2 and SnO2(110) predict much higher work functions than experimentally observed, but match previous theoretical works for SnO2(110).51 The reason for this disparity is likely due to the experimental ease of formation of oxygen vacancies on these surfaces, which has been found to raise the Fermi level closer to the conduction band, resulting in lower work functions.63 Despite this, the trends between experiment and theory remain consistent, and high values for the surface work functions of PbO2 and SnO2(110) remain.
With respect to chemical reactivity, the very low work function value obtained for Pb(111) indicates that the surface is easily oxidised, in accordance with the metallic nature of this material. All other surfaces are harder to oxidise. While the inclusion of O p-states to the Fermi surface will increase the work function compared to Pb (see Fig. 6 for bulk model density of states, ESI† for the surface model equivalents), all oxide surfaces retain a significant metal contribution bar β-PbO2 and SnO2 which are almost entirely composed of O p-states, and thus return the largest surface work functions of the set. We observe that the work function for α-PbO(001) is lower than that for α-Bi2O3(010), suggesting the former is more readily oxidised than the latter. β-PbO(100) is also narrowly smaller than α-Bi2O3(010). Overall, the lower work functions observed for Pb and the PbO polymorphs suggest these surfaces can be more readily oxidised than the other systems in the text set, which in turn may account for why Pb-based compounds aide the reduction of aldehyde fragments to form carbonaceous material at the burning surface in DBPs.
Thus a clear picture emerges from the computational modelling work performed on the bulk models and bare surfaces. Pb and PbO present lower (more stable) surface energies, lower surface work functions and smaller electronic band gaps, indicating these materials possess a greater chemical reactivity compared to the less stable PbO2 and the Pb-free ballistic modifiers included in the test group.
Carbon binding study to surface models
An important feature of the catalytic activity of ballistic modifiers in DBPs is their propensity to support a large amount of amorphous carbon at the burning surface. In particular, a compelling theory is that the formation of this carbon soot layer, and its subsequent loss with increasing pressure, is responsible for the super-rate and plateau/mesa burning mechanisms in DBPs.18,27 To test this hypothesis, layers of amorphous carbon have been deposited onto each of the most stable surface models identified in the previous section. The aim is to investigate the interaction between a carbon layer and the surface; if the bare surface remains intact then it becomes possible to define an adsorption energy (see ESI†). Owing to the complex nature of the amorphous layer it is not expected that the true energy minima will be obtained, but any variation in interaction across the model surfaces should yield further critical insight into the enhanced catalytic behaviour observed for the Pb-containing modifiers.Initial adsorption models, constructed in order to adsorb equivalent amounts of carbon to each surface (ca. 1 carbon atom per 1.4 Å2 of surface area) are presented in the ESI.† The output structures obtained and binding energies obtained where possible are shown in Fig. 8; optimised properties are also displayed in the ESI.†
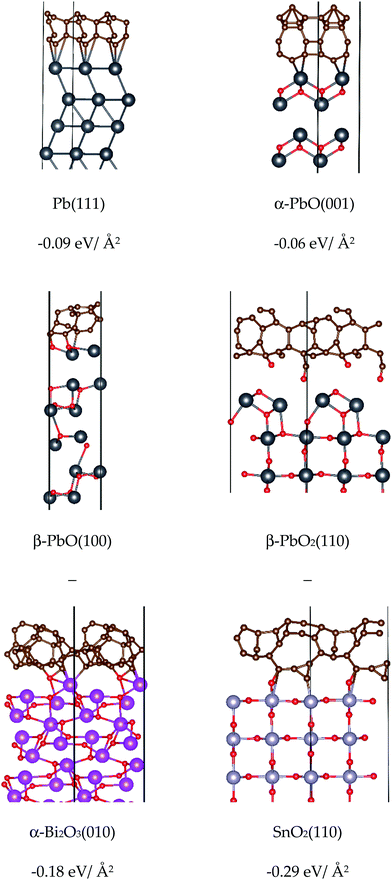 | ||
| Fig. 8 Optimised adsorption models and energies for binding amorphous carbon to bare metal and metal oxide surfaces. | ||
As observed from the negative binding energies in Fig. 8, binding of a carbon layer to all surfaces results in favourable adsorption interactions. For α-PbO(001) and Pb(111), the absence of any oxygen atoms at the binding surface means that only relatively weak Pb–C bonds can form, and it is likely that the carbon layer would be easily detached. These models therefore appear to support the build-up and reduction of an amorphous carbon layer, as postulated in the carbon soot theory to account for all three DBP burn rate effects summarised in Fig. 1.18 The β-PbO and β-PbO2 surfaces have more accessible oxygen sites that take part in binding to carbon, and structural distortion effects are observed in both which render the calculation of carbon binding energies unreliable. For the latter model the oxygen atoms are ripped out of the surface to form part of the carbon matrix. While the removal of oxygen atoms will introduce defects and likely increase the reactivity of Pb sites, it seems unlikely that this model could support stable attachment of a carbon layer. Interestingly, while SnO2(110) and PbO2(110) are structurally very similar, the SnO2 surface model remains intact upon carbon binding, again demonstrating the significantly stronger Sn–O bonds compared to Pb–O.62 Similarly, carbon binding to α-Bi2O3(010) appears to leave the surface largely intact, and strong C–O interactions results in a relatively strong surface attachment. With respect to their experimental action as ballistic modifiers, this likely explains why SnO2 is observed to build up large layers of carbon matter, sustaining super-rate burning but failing to achieve plateau/mesa-rate burning through the loss of this layer.12 In the case of α-Bi2O3 (and it's respective acidic salts), addition to double-base propellants results in accelerated burning at low pressures, but fails to achieve plateau burning at the low pressures of lead salts.64–66
Conclusions
There is a pressing need to find non-toxic replacements for lead-based ballistic modifiers in double-base propellant rocket systems. Consensus in the literature points towards decomposition of the ballistic modifier to form metal-containing clusters at the burning surface in the propellant combustion zone; these clusters act as catalytic sites to seed decomposition of the nitrate ester fuel. As no suitable lead-free alternatives exist, this study reports on a first principles simulation study to identify key metrics found for lead-based compounds.In summary, bulk electronic band structures, surface electronic properties, surface energies and surface work functions have been investigated to gain an understanding into the electronic properties of the systems studied. A carbon-binding study has also been performed to investigate the interaction between a carbon layer and the bare surface. For the bulk materials, the lead-based systems (Pb, α-PbO, and β-PbO2) present smaller electronic band gaps, suggesting a greater chemical reactivity, than the lead-free alternatives. The surface energies obtained for each model, which are indicative of the relative ease for each material to form clusters with stable faces at a gas/solid reactive interface, indicate that the presence of lead renders the bulk models more energetically favourable to cleave. Calculated surface work functions suggest that the lead-containing models are easier to oxidise than the lead-free models. Intriguingly, literature reports on Bi2WO6, introduced at the start of this paper as the first lead-free material capable of supporting plateau rate burning (at higher gas pressures than for the Pb-based salts), suggest low surface energies, a band gap smaller than that reported herein for Bi2O3, and a surface work function in the upper range of materials reported here.67 Finally, the carbon-binding study has revealed weak binding to the Pb and α-PbO surfaces, destruction of the β-PbO and β-PbO2 surface, and stronger binding to the α-Bi2O3 and SnO2 systems. This suggests that the first two systems alone are capable of supporting the growth and destruction of the amorphous carbon layer postulated to account for the modified burn-rate properties inferred by the lead-based additives. Taken together, this first principles study has highlighted important metrics that may cast light on the enhanced ballistic modifier properties offered by the current materials used, which we hope provides guidance in the on-going search to find lead-free alternatives.
Computational methods
Bulk models and surfaces: CRYSTAL17
In order to make use of hybrid DFT for accurate electronic band structures, localised basis set calculations have been performed using the ab initio periodic CRYSTAL17 code. Pseudopotentials or all-electron atom-centered Gaussian-type functions are used for basis sets through the standard LCAO method.68 An all-electron basis set was used for O (8-411d1 in the notation used by CRYSTAL),69,70 and for Pb, Bi and Sn the scalar-relativistic small-core pseudopotential developed by Metz, Stoll and Dolg71 was employed along with 22 (Pb, Sn), and 23 (Bi) valence electrons treated explicitly. For Bi2O3, PbO2 and SnO2 the valence electrons were described using Bi-4411-411-411d,72 Sn-411-51d and Pb-6111-51d notations respectively.73 For Pb and PbO, a cc-pVDZ (double zeta quality) basis set was required to describe the valence electrons due to the metal/layered nature of the structures.74For the bulk systems full optimisation of the atomic positions and lattice parameters was performed (only atomic positions were optimised for layered PbO). Tested functionals were the pure GGA PBE,75 and the B3LYP,76,77 PBE0,78 B3PW77,79 and HSE0680 hybrid functionals. The Grimme D3 dispersion correction scheme (DFT-D3)81 has been tested for all calculations, but was found to overbind the monoclinic α-Bi2O3b-axis, so was not applied to its surface and bulk models. Convergence of the k-point grid was considered for energy differences of 10−6 a.u., resulting in a Monkhorst–Pack shrinking factor82 of 14 for PbO2, SnO2 and PbO, 8 for Bi2O3, and 16 for Pb. To describe the metallic nature of Pb, the Gilat net83 was doubled to 32, and a Fermi smearing temperature of 0.01 a.u. was applied. Other computation conditions include the evaluation of the bielectronic Coulomb and exchange contributions to the Fock matrix are controlled by five overlap criteria, set in this study to 10−7, 10−7, 10−7, 10−7, and 10−14 in atomic units.83,84 Convergence criteria was determined from the root-mean-square and absolute value of both the gradients and estimated displacements.83 In addition, the energy threshold criteria between two successive optimisation steps is set to 10−7 a.u.
All conditions defined above for the bulk systems were maintained for optimising surfaces in CRYSTAL. 2D periodic boundary conditions were imposed, such that periodicity is interrupted in the z-direction.68 The only surfaces considered were Tasker-type surfaces, where the bulk lattice is cut to expose non-polar symmetric top and bottom surfaces that maintain the stoichiometry of the host crystal.85 For the surfaces, atomic positions only were optimised. The surface energies were computed in the standard way, and surface work functions were computed following the methodology of Doll (see ESI†).86
Carbon binding model: CASTEP19
These simulations were performed using the plane-wave DFT code CASTEP, version 19.1.1.87 The GGA PBE functional75 was used for all systems, with an energy cutoff of 800 eV for all metal oxides, and 350 eV for Pb, so that convergence was achieved to within 2 meV per atom. Ultrasoft pseudopotentials88 were generated “on the fly.” For the bulk systems, a Monkhorst–Pack scheme was set such that k-point spacings were less than 0.05 Å−1. The optimisation convergence tolerances for force, stress, ionic displacement, and energy were 0.01 eV Å−1, 0.02 GPa, 0.005 Å, and 5 × 10−6 eV per atom, respectively, with SCF convergence between two cycles of 1 × 10−8 eV. For PbO2 and Pb systems a temperature smearing of 0.1 eV was applied. Atomic positions only were optimised. Monkhorst–Pack k-point spacings for surfaces were 6 × 3 × 1 for β-PbO2 and SnO2(110), 5 × 5 × 1 for α-PbO(001), 4 × 4 × 1 for β-PbO(100), 14 × 14 × 1 for Pb(111), and 4 × 5 × 1 for α-Bi2O3(010). The non-periodic z-direction for the surfaces was modelled with a vacuum of 20 Å for all surfaces to fit in the carbon layer. The quantity of carbon added to each surface was calculated to maintain a consistent ca. 1 carbon atom per 1.4 Å2 of surface area across all models. All systems were tested with the Tkatchenko–Scheffler dispersion correction,89 which was applied to the layered PbO system to optimise the atomic positions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All authors kindly acknowledge Gregory W. Drake (U.S. Army Futures Command CCDC-AvMC, Redstone Arsenal, USA) for helpful discussions. Research was sponsored by the Army Research Office and was accomplished under Cooperative Agreement Number W911NF-19-2-0288. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. This work has made use of the resources provided by EaSTCHEM Research Computing Facility and the Edinburgh Compute and Data Facility (ECDF) (http://www.ecdf.ed.ac.uk/). We also gratefully acknowledge the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1).References
- H. Shekhar, Cent. Eur. J. Energ. Mater., 2012, 9, 353–364 CAS.
- H. Austruy, in Solid Rocket Propulsion Technology, ed. A. Davenas, Elsevier Ltd, 1993, pp. 369–413 Search PubMed.
- N. Kubota, Propellants and Explosives: Thermochemical Aspects of Combustion, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015 Search PubMed.
- D. R. Greatrix, Powered Flight: The Engineering of Aerospace Propulsion, Springer, London, London, 2012, pp. 323–379 Search PubMed.
- N. Kubota, T. J. Ohlemiller, L. H. Caveny and M. Summerfield, Symp. Combust., 1975, 15, 529–537 CrossRef CAS.
- N. Kubota, Symp. Combust., 1979, 17, 1435–1441 CrossRef.
- G. Lengellé, J. Brulard and H. Moutet, Symp. Combust., 1977, 16, 1257–1269 CrossRef.
- N. Kubota, T. J. Ohlemiller, L. H. Caveny, J. And and M. Summerfield, AIAA J., 1974, 12, 1709 CrossRef CAS.
- M. Farber and R. D. Srivastava, Combust. Flame, 1978, 31, 309–323 CrossRef CAS.
- H. Singh and R. K. Rao, Proc. Indiana Acad. Sci., 1984, 93, 93–97 CAS.
- D. J. Hewkin, J. A. Hicks, J. Powling and H. Watts, Combust. Sci. Technol., 1971, 2, 307–327 CrossRef CAS.
- A. P. Denisyuk and L. A. Demidova, Combust., Explos. Shock Waves, 2004, 40, 311–318 CrossRef.
- Y. Wang, Q.-L. Yan, T. An, B. Chen, Y.-P. Ji, W. Wang and F. Zhao, J. Energ. Mater., 2018, 15, 376–390 CAS.
- T. An, F.-Q. Zhao, Q.-L. Yan, Y.-J. Yang, Y.-J. Luo, J.-H. Yi and W.-L. Hong, Propellants, Explos., Pyrotech., 2018, 43, 1087–1095 CrossRef CAS.
- Lead REACH Consortium, https://ila-reach.org/.
- Q. L. Yan, F. Q. Zhao, K. K. Kuo, X. H. Zhang, S. Zeman and L. T. DeLuca, Prog. Energy Combust. Sci., 2016, 57, 75–136 CrossRef.
- T. Wei, Y. Zhang, K. Xu, Z. Ren, H. Gao and F. Zhao, RSC Adv., 2015, 5, 70323 RSC.
- L. R. Warren, Z. Wang, C. R. Pulham and C. A. Morrison, Propellants, Explos., Pyrotech., 2020, 45 DOI:10.1002/prep.202000167.
- G. Lengelle, A. Bizot, J. Duterque and J. F. Trubert, Fundamentals of Solid-Propellant Combustion, AIAA, 1984, vol. 90, pp. 361–407 Search PubMed.
- B. B. de Schor and J. E. Toni, Thermochim. Acta, 1978, 27, 347–356 CrossRef.
- N. P. Suh, G. F. Adams and C. Lenchitz, Combust. Flame, 1974, 22, 289–293 CrossRef CAS.
- A. P. Denisyuk, T. M. Kozyreva and V. G. Khubaev, Combust., Explos. Shock Waves, 1975, 11, 271–273 CrossRef.
- K. Gavrichev, A. Bolshakov, D. Kondakov, A. Khoroshilov and S. Denisov, J. Therm. Anal. Calorim., 2008, 92, 857–863 CrossRef CAS.
- H. Singh and K. R. K. Rao, Combust. Flame, 1988, 71, 205–213 CrossRef CAS.
- L. Shufen, Combust. Sci. Technol., 1998, 133, 395–401 CrossRef CAS.
- J. Sharma, G. B. Wilmot, A. A. Campolattaro and F. Santiago, Combust. Flame, 1991, 85, 416–426 CrossRef CAS.
- C. Youfang, Propellants, Explos., Pyrotech., 1987, 12, 209–214 CrossRef CAS.
- R. J. Hill, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 1281–1284 CrossRef.
- W. B. White, F. Dachille and R. Roy, J. Am. Ceram. Soc., 1961, 44, 170–174 CrossRef CAS.
- J. Moreau, J. M. Kiat, P. Gamier and G. Calvarin, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 296–299 CrossRef.
- J. Haines and J. M. Lé, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11144–11154 CrossRef CAS.
- J. Haines, J. M. Léger and O. Schulte, J. Phys.: Condens. Matter, 1996, 8, 1631–1646 CrossRef CAS.
- G. Malmros, Acta Chem. Scand., 1970, 24, 384–396 CrossRef CAS.
- Y. H. Lei and Z. X. Chen, J. Chem. Phys., 2013, 138, 054703 CrossRef.
- D. J. Payne, R. G. Egdell, W. Hao, J. S. Foord, A. Walsh and G. W. Watson, Chem. Phys. Lett., 2005, 411, 181–185 CrossRef CAS.
- D. J. Payne, G. Paolicelli, F. Offi, G. Panaccione, P. Lacovig, G. Beamson, A. Fondacaro, G. Monaco, G. Vanko and R. G. Egdell, J. Electron Spectrosc. Relat. Phenom., 2009, 169, 26–34 CrossRef CAS.
- B. Thangaraju and P. Kaliannan, Semicond. Sci. Technol., 2000, 15, 542–545 CrossRef CAS.
- R. C. Keezer, D. L. Bowman and J. H. Becker, J. Appl. Phys., 1968, 39, 2062–2066 CrossRef CAS.
- D. J. Payne, R. G. Egdell, D. S. L. Law, P. A. Glans, T. Learmonth, K. E. Smith, J. Guo, A. Walsh and G. W. Watson, J. Mater. Chem., 2007, 17, 267–277 RSC.
- J. C. Schottmiller, J. Appl. Phys., 1966, 37, 3505–3510 CrossRef CAS.
- J. Deng and Z. Y. Zhao, Comput. Mater. Sci., 2018, 142, 312–319 CrossRef CAS.
- T. P. Debies and J. W. Rabalais, Chem. Phys., 1977, 20, 277–283 CrossRef CAS.
- H. Cheng, B. Huang, J. Lu, Z. Wang, B. Xu, X. Qin, X. Zhang and Y. Dai, Phys. Chem. Chem. Phys., 2010, 12, 15468–15475 RSC.
- D. Fröhlich, R. Kenklies and R. Helbig, Phys. Rev. Lett., 1978, 41, 1750–1751 CrossRef.
- F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, S. Sanvito and A. Du, ACS Appl. Mater. Interfaces, 2016, 8, 25667–25673 CrossRef CAS.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428 CrossRef CAS.
- D. Yu and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–8 Search PubMed.
- B. Sun, P. Zhang, Z. Wang, S. Duan, X.-G. Zhao, X. Ma and Q.-K. Xue, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035421 CrossRef.
- H. B. Michaelson, J. Appl. Phys., 1977, 48, 4729 CrossRef CAS.
- Y. Hinuma, T. Toyao, T. Kamachi, Z. Maeno, S. Takakusagi, S. Furukawa, I. Takigawa and K.-I. Shimizu, J. Phys. Chem. C, 2018, 122, 29435–29444 CrossRef CAS.
- Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CrossRef CAS.
- J. Fang Lv, C. Lin Fan, X. Tong, Y. Xing Zheng and X. Li, Appl. Surf. Sci., 2019, 470, 135–142 CrossRef.
- J. Oviedo and M. J. Gillan, Surf. Sci., 2000, 463, 93–101 CrossRef CAS.
- A. Klein, C. Körber, A. Wachau, F. Säuberlich, Y. Gassenbauer, R. Schafranek, S. P. Harvey and T. O. Mason, Thin Solid Films, 2009, 518, 1197–1203 CrossRef CAS.
- J. Wang and S. Q. Wang, Surf. Sci., 2014, 630, 216–224 CrossRef CAS.
- Y. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–22 Search PubMed.
- F. Labat, P. Baranek and C. Adamo, J. Chem. Theory Comput., 2008, 4, 341–352 CrossRef CAS.
- M. Ramamoorthy, D. Vanderbilt and R. D. King-Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16721–16727 CrossRef CAS.
- R. A. Evarestov and Y. F. Zhukovskii, Surf. Sci., 2013, 608, 226–240 CrossRef CAS.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
- T. L. Cottrell, The Strengths of Chemical Bonds, Butterworths, London, 2nd edn, 1958 Search PubMed.
- K. T. Butler, J. Buckeridge, C. Richard, A. Catlow and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115320 CrossRef.
- R. M. Jorge and A. A. M. F. Filho, J. Aerosp. Technol. Manage., 2019, 11, 15–18 CAS.
- S. B. Thompson, J. L. Goodwin and A. T. Camp, US Pat., US005652409A, 1997 Search PubMed.
- J. Neidert and R. E. Askins, US Pat., US5372070A, 1994 Search PubMed.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, Appl. Surf. Sci., 2018, 427, 487–498 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–36 CAS.
- T. Bredow, K. Jug and R. A. Evarestov, Phys. Status Solidi B, 2006, 243, 10–12 CrossRef.
- M. D. Towler, N. L. Allan, N. M. Harrison, V. R. Saunders, W. C. Mackrodt and E. Apra, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5041–5054 CrossRef CAS.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS.
- E. Heifets, E. A. Kotomin, A. A. Bagaturyants and J. Maier, J. Phys. Chem. Lett., 2015, 6, 2847–2851 CrossRef CAS.
- G. Sophia, P. Baranek, C. Sarrazin, M. Rérat and R. Dovesi, Phase Transitions, 2013, 86, 1069–1084 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunel, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, 2017 Search PubMed.
- C. Pisani, R. Dovesi and C. Roetti, Hartree-Fock Ab Initio Treatment of Crystalline Systems, Springer-Verlag, 1988 Search PubMed.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- K. Doll, Surf. Sci., 2006, 600, L321–L325 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard Ii, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Krist., 2005, 220, 567–570 CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05172a |
| This journal is © the Owner Societies 2020 |