Strain effects in core–shell PtCo nanoparticles: a comparison of experimental observations and computational modelling

Abstract

Strain in Pt nanoalloys induced by the secondary metal has long been suggested as a major contributor to the modification of catalytic properties. Here, we investigate strain in PtCo nanoparticles using a combination of computational modelling and microscopy experiments. We have used a combination of molecular dynamics (MD) and large-scale density functional theory (DFT) for our models, alongside experimental work using annular dark field scanning transmission electron microscopy (ADF-STEM). We have performed extensive validation of the interatomic potential against DFT using a Pt₅₆₈Co₁₈ nanoparticle. Modelling gives access to 3 dimensional structures that can be compared to the 2D ADF-STEM images, which we use to build an understanding of nanoparticle structure and composition. Strain has been measured for PtCo and pure Pt nanoparticles, with MD annealed models compared to ADF-STEM images. Our analysis was performed on a layer by layer basis, where distinct trends between the Pt and PtCo alloy nanoparticles are observed. To our knowledge, we show for the first time a way in which detailed atomistic simulations can be used to augment and help interpret the results of ADF-STEM strain mapping experiments, which will enhance their use in characterisation towards the development of improved catalysts.

---

1 Introduction

Proton exchange membrane fuel cells (PEM-FCs), fuelled by hydrogen, provide a zero emission energy source suitable for automotive and a multitude of other uses.^1,2 Widespread adoption of this technology hinges on the availability of hydrogen fuel, as well as improvements to the fuel cell technology itself. Concerns such as power output, efficiency and lifespan are all important, and can be improved via the development of the chemistry involved.

It is understood that one of the major performance bottlenecks for these fuel cells is the oxygen reduction reaction (ORR) that takes place at the cathode.³ Currently, the best commercially available catalysts for the oxygen reduction reaction (ORR) in PEM-FCs are made of Pt.² In this application, Pt is known to overbind oxygen by about 0.2 eV,⁴ leading to a lower than optimal catalytic activity, which was shown using extended Pt(111) surface models. In real fuel cells, finely divided catalytic material in the form of nanoparticles are used, which possess much more complex morphologies than extended surfaces, including many low coordination sites at their edges and vertices. These exacerbate the issue of overbinding as these sites tend to bind oxygen even more strongly.^5–7 It is therefore desirable to develop an improved catalyst for this reaction using alternative materials, and much work is being done to this end.^1,8–10

One promising method for improving ORR catalysts’ performance is to modify the properties of Pt nanoparticles by alloying them with a second transition metal. In this application, Co has been found to have many desirable properties.^11–13 It readily alloys with Pt, has a smaller lattice parameter than Pt (meaning there is a physically driven preference for Co to be in the core of the nanoparticles, rather than at the surface¹⁴), and has been shown to decrease O binding to nanoparticles with a Pt shell and PtCo alloy core, both in experiments and DFT calculations on slab models.^8,15

As Co is easily and irreversibly oxidised, especially in conditions typical in PEM-FCs, any exposed directly to the surrounding environment would be rapidly lost, which is why Pt shell nanoparticles are desirable, as well as the fact that Pt only needs a small O binding adjustment to reach an ideal strength for catalysis.^10,12

It has been suggested by a number of studies that the reason for the increased ORR activity of PtCo alloy nanoparticles is due to the strain effects caused by the mismatched lattice parameters of the two elements.^8,16,17 Indeed, it has been known for some time that there is a correlation between specific activity for oxygen reduction and nearest neighbour distance in Pt alloys.¹⁸

Imaging alloy nanoparticles using annular dark field scanning transmission electron microscopy (ADF-STEM) gives detailed information about their structure, including strain effects. While this method offers a very high resolution, a lack of contrast between the two metal species in the alloy makes full structure determination much more difficult than for monometallic nanoparticles.¹⁹ For pure Pt nanoparticles, full 3D geometries can be derived from the ADF-STEM images,²⁰ but it is difficult to do this for alloys without the use of spectroscopic signals such as electron energy loss spectroscopy (EELS) and energy dispersive X-ray spectroscopy (EDX).^19,21,22

An alternative approach to the single image ADF STEM structure determination is to use tomography as shown by some cases in the literature.^23–26 Tomography is ideal for large nanoparticles where electron beam damage does not affect the morphology of the sample as it is exposed to the electron beam. However, the nanoparticles that we are investigating in this study have a size range between 3 and 4 nm, and due to their small size, they cannot withstand the electron beam for longer than a few minutes without sustaining significant structural damage.

In order to compare our experimental and computational data, we instead work in the reverse direction, starting from 3D structures of alloy nanoparticles produced from our simulations and generating simulated ADF-STEM images from them, using the procedure described by MacArthur et al.²⁷ By comparing the simulated ADF-STEM images to the real ones, we can build a more detailed understanding of alloy nanoparticle structures.

In this work, we investigate the modification of the structural properties of Pt nanoparticles as a result of alloying with Co, particularly with respect to strain, using a combination of computational models and electron microscopy experiments. We perform simulations of PtCo nanoparticles using a combination of large-scale density functional theory (DFT) and classical molecular dynamics (MD). Slab models of Pt₃Co have been investigated with DFT previously in the literature,⁸ and the extension to nanoparticles allows for the assessment of alloying effects while including the added complexity that comes with nanoparticle geometries. The stoichiometry of our systems, due to the way they are constructed (as core–shell structures), varies with nanoparticle diameter, and the nanoparticles we have modelled are somewhat Pt rich compared to Pt₃Co. The experimental nanoparticles were also made with a Pt₃Co stoichiometry, although significant variation among individual nanoparticles is expected.

We include a validation of the Gupta potential²⁸ that we used for the MD simulations, for which we have tested two parametrisations. These are both compared to DFT calculations that we have performed to provide a benchmark from which we assess the suitability of the potential for modelling PtCo nanoparticles. We also discuss the methods used to calculate strain, highlighting some ambiguities with current methods. We thus develop a more robust new approach, which we apply to the 2D ADF-STEM images as well as the 3D models.

We use this approach to investigate, in depth, the strain effects measured in our experimental work, following a layer by layer analysis and comparisons with our computational models. We finish with some conclusions of our findings.

2 Methods

2.1 Experimental

2.1.1 Microscope experimental, image simulation and sample preparation. The experimental nanoparticles used in this study were carbon supported alloy Pt₃Co (with a loading of 3 : 1) nanoparticles provided by Johnson Matthey Technology Centre Sonning. To obtain a dispersed range of isolated particles for strain investigation, the nanoparticles were drop-cast on a holey carbon grid. The carbon grids were then baked in vacuum for 8 hours at 80 °C to minimise hydrocarbon contamination. Atomic resolution imaging of the nanoparticles was performed on a JEOL ARM 200CF electron microscope equipped with a probe corrector for annular dark field (ADF) imaging. The operating voltage was chosen as 200 kV and the probe-convergence angle was 22.46 mrad. The ADF detector collection angles spanned between 72.8 and 271 mrad. Three Pt₃Co nanoparticles with diameters between 3 and 4 nm were chosen for imaging, since the majority of the nanoparticles within this PtCo ensemble were found to be between this size range. Several nanoparticles were imaged at atomic resolution in this size range, however it is experimentally difficult to find ideal on-zone nanoparticles for strain measurements. Out of all the nanoparticles imaged, just three were deemed sufficiently on-zone for measuring displacement and effective lattice parameter shifts. In order to be statistically representative, a wider study is required where several more nanoparticles are imaged. This will be investigated in the future.

In order to minimise damage and compensate for nanoparticle drift, ADF images were recorded in short bursts at 4 μs dwell time. These images were then scan-distortion corrected and non-rigidly aligned using the Smart-Align software.²⁹

As our strain results are highly dependent on an accurate image pixel size, the magnification of the instrument was manually calibrated with a SrTiO₃ standard for every field of view. The scan coil strengths were also adjusted appropriately using the SrTiO₃ standard to maintain pixel squareness along the x and y scan directions.

For the ADF-STEM image simulations the MULTEM software was used.³⁰ A 20 phonon configuration was used with RMS displacements calculated via the parameterisations of Gao and Peng.³¹ The probe forming angle and detector collection angles were chosen to be the same as the experiment.

2.2 Computational modelling

Molecular dynamics simulations were performed with the lammps³² software package, using a tight-binding second moment approximation (TB-SMA) potential.²⁸ For this potential, we used the parameters published by Front et al.³³ for Pt and Co, as well as those of Goyhenex et al.³⁴ as a comparison in the validation section of this paper. All dynamics simulations were done using the canonical (NVT) ensemble, with temperature controlled using a Nosé–Hoover thermostat with a damping parameter of 0.05 ps, while a timestep of 1 fs was used.

The DFT calculations of the (221) Pt slab (where we compare the Gupta potential with DFT) were performed using castep,³⁵ a conventional plane wave code. For these calculations we used the rPBE functional,^36,37 ultrasoft pseudopotentials (USPs)³⁸ and ensemble DFT (EDFT).³⁹ The size of the cell was a = b = 8.765 Å, c = 25.8 Å, with the slab being four layers thick. The Brillouin zone was sampled using a 2 × 2 × 1 Monkhorst–Pack grid.⁴⁰ A kinetic energy cut-off of 650 eV was used, and the systems were treated as spin polarised.

DFT calculations on nanoparticles were performed with onetep,⁴¹ a linear scaling code, using the EDFT method as implemented within the localised orbital framework of onetep.⁴² This allows for large-scale DFT treatment of metallic systems, in the local-orbital machinery of onetep, where the energy is directly minimised with respect to two kinds of variables. These are the density kernel, which is the representation of the single-particle density matrix in the localised orbital basis, and the non-orthogonal generalised Wannier functions (NGWFs), the localised orbital basis itself. The NGWFs are strictly localised and atom centred, and constructed from a psinc (periodic sinc function) basis set. Optimising the NGWFs as well as the density kernel allows for a near-complete basis set accuracy while using a minimal basis set.

As with conventional plane wave DFT codes, onetep makes use of pseudopotentials to model core electrons, and in this work we used projector augmented waves (PAWs).⁴³ The explicitly modelled electrons are 5d⁹6s¹ for Pt and 3p⁶3d⁷4s² for Co. We used 12 NGWFs for each Pt atom, and 10 for each Co, each with a cut-off radius of 9.0 Bohr. Calculations were performed at the Γ-point only. We used the rPBE functional and a kinetic energy cut-off of 650 eV.

2.2.1 Simulated annealing. The annealing process involved a rapid heating and cooling of the nanoparticle systems. We used this firstly to assess the thermal stability of our nanoparticles, as well as to produce less symmetric, potentially more realistic structures.⁴⁴

Following a 10 ns equilibration at 300 K, the temperature is raised to 1500 K over 2 ns (heating rate of 600 K ns⁻¹) and maintained at that temperature for 20 ns. The temperature is then brought down to 300 K at a slower rate of 50 K ns⁻¹ (over 24 ns). Finally, the system is held at 300 K for another 4 ns. This cycle, excluding the 10 ns equilibration, takes 50 ns of simulation time, and is repeated 5 times in total.

Compared to our previous work on pure Pt nanoparticles,⁴⁴ we have increased our high temperature target by 300 K and slowed the rate of cooling substantially. The latter is due to the increased risk of structure frustration in systems with more than one atomic species, while the higher temperature target was chosen to increase the level of deformation of the nanoparticle per cycle, since each cycle takes longer to complete.

2.2.2 Defining atomic layers. We define atomic layers as a series of one-atom-thick shells, starting from the surface of the nanoparticle and moving in towards the centre. Shells are determined, both in 2D and 3D, by calculating the alpha hull (using the qhull library⁴⁵). This generates an alpha shape,⁴⁶ the surface of which is defined as the closest point of approach of a sphere (circle in 2D) with a given radius to the set of atomic positions. The radius is chosen such that this sphere cannot fit between nearest neighbours of atoms. We use a value of 2.1 Å in 3D and a lower value of about 1.6 Å in 2D, which was tweaked as necessary to produce sensible shapes. Calculating such a shape gives the points that define it, which are the set of atoms at the surface. These atoms are assigned to a layer, then removed and the process is repeated. This is continued until all atoms are assigned a layer, or there are no longer enough atoms to construct an alpha hull (at least 4 atoms are required in 3D, but depending on the geometry it must sometimes be stopped with many more atoms remaining). In the latter case, what remains at this point becomes the final layer. Examples of how the defined layers look in the 2D and 3D cases are given in Fig. 1.

Fig. 1 Atomic layers defined via iterative usage of the alpha hull algorithm in (a) 2D and (b) 3D. For the latter, a cross-section is shown.

2.3 Lattice strain calculations

One way to calculate strain effects is to measure atomic displacement from bulk lattice sites. This involves overlaying an ideal reference lattice on the 2D ADF-STEM images or the 3D simulated geometries and measuring the distance from a column or atom, respectively, from this lattice. This must be done carefully, though, since the choice of reference point for the bulk lattice will alter the results greatly.

Previous methods in literature (for 2D ADF-STEM images) have often used a group of atomic columns from the centre of the nanoparticle to create a grid.^47–49 These approaches assume that the centre of the nanoparticle is strain-free and thus can be used as a reliable reference. However, this assumption might not hold true in the case of bimetallic nanoparticles. There is also an issue where strain appears to increase as a function of distance from the reference point, as the displacement of atoms from the projected grid are affected by the displacements of other atoms that lie between them and the reference point. Further discussion of this issue is given in Section S1 of the ESI.†

In order to avoid these issues, the best way to measure strain is with a localised method, where each atom or atomic column is its own reference point. We make use of such a method in this work, assigning each atomic position with an effective lattice parameter based on the location of its first neighbours. We describe how this parameter is defined and measured in the following sections, both in the 2D experimental work and the 3D computational modelling.

2.3.1 Effective lattice parameter in 2D. In order to calculate the effective lattice parameter, a peak finding routine was used to find the atomic column positions. This was followed with a centre of mass refinement and 2D Gaussian fitting.⁵⁰ Atoms with the least amount of hopping observed between the 2D static images were chosen for the strain analysis. Each image frame was checked to see whether atom hopping occurred in-between frames and whether there were any missing columns on the surface. Once the peak positions of the atomic columns were confidently defined, the centre of the nanoparticle was determined by calculating the centre of mass of the column position point cloud. For each atomic column a directional nearest neighbour search is performed along the directions defined by a vector pair. As each atom in a column experiences forces from neighbouring atoms, we calculated the effective lattice parameter from all possible vector pair directions. These measurements were then averaged to obtain the final effective lattice parameter measurements for a nanoparticle. To measure the column displacements and vector cell expansions a generalised gird was created by averaging all the vector lengths from each atom. The grid is then overlaid on top of the atomic positions of the nanoparticles and a least squares refinement is carried out (see Section S1.1 of the ESI† for more details). Using the grid and the atomic positions, the displacement map and the trace of strain tensor can be calculated from.^49,51

2.3.2 Effective lattice parameter in 3D. To calculate the effective lattice parameter in 3D, each atom is considered individually, along with its first neighbours. The set of vectors from the ith atom to each of its neighbours are defined and their lengths measured. The effective lattice parameter is then a simple average of the first neighbour distance multiplied by .

We also considered using only the neighbours within the same layer to calculate the effective lattice parameter, as it was possible to something similar in 2D, but ultimately we did not use these results for our investigation. The differences between using all neighbours and just those in the same layer is, however, shown in the following section, where we compare the tight-binding potential to DFT calculations.

2.4 Validation of tight-binding potential against DFT

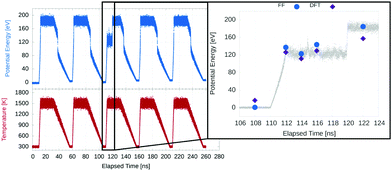
The tight-binding potential was parametrised against DFT calculations (on bulk and slab systems) and experimental data, as described by Front et al. in the article introducing these parameters.³³ We had been interested in using this potential to study PtCo alloy nanoparticles, but found that an older set of parameters³⁴ led to Co atoms favouring lower coordinated sites on nanoparticles and slabs, in contrast to DFT and experimental results. We performed these tests using a (221) cleaved Pt slab, substituting a single Co atom at different sites and relaxing the geometry (though the supercell was not further relaxed, so all cases used the same periodic box size and lattice parameter as the DFT relaxed pure Pt system). The (221) surface consists of regularly stepped (111) terraces, with sites having a minimum coordination of 7 on the step edges.

As shown in Fig. 2, the new parameters lead to a much better agreement with DFT results, with the same energy ordering, meaning MD simulations with this potential will tend to drive Co to higher coordination sites, whereas the old potential led to segregation of Co to the surface, as well as Co edge decoration.

Fig. 2 Comparison of relative energies of a Pt(221) slab with a Co atom in different locations calculated using potentials and DFT. Two parametrisations of the Gupta potential were used: (a) Goyhenex et al.³⁴ (1999) and (b) Front et al.³³ (2019). The latter parametrisation is used in the rest of this work.

DFT single point energy calculations were performed on several snapshots from the annealing cycle of the Pt₅₆₈Co₁₈ L1₀ nanoparticle, in order to compare the two methods. The L1₀ alloy structure shares the basis vectors of an FCC lattice, with two of the four sites occupied by metal A and two by metal B, such that an ABAB layering is formed in the [100] direction.

An unusual feature of the run was chosen, since it provides a more diverse set of structures to compare, and also allows us to determine whether it could be an artefact of the potential. This feature and the calculated energies are shown in Fig. 3. Essentially, during one cycle, a Mark's decahedral.⁵² structure withstood the high temperature part of the anneal for 10 ns, indicating unusually high thermal stability, though such a short-lived structure is unlikely to be observed at high temperatures experimentally.

Fig. 3 The potential energy and temperature as a function of simulation time for Pt₅₆₈Co₁₈ during annealing. The smaller graph on the right hand side is an expanded view of the unusual feature from this simulation. Geometries from this part of the run were sampled and their relative energies compared with DFT (the relaxed, pre-annealed structure was used as the reference point).

Overall, we see a close agreement in relative energy between the new potential and the DFT results. The ordering (in energy) of each snapshot is preserved between both methods, though the difference between the low and high temperature snapshots is smaller in the DFT regime. A final comparison between the potential and DFT calculations was to relax the geometry of a Pt₅₆₈Co₁₈ nanoparticle using both methods. The resulting geometries were compared using a radial distribution function as well as the effective lattice parameter, as described above.

The radial distribution functions for the relaxed geometries, shown in Fig. 4, are very similar, with the force field relaxed nanoparticle having slightly higher and narrower peaks indicative of a more uniformly distributed nanoparticle (less variation between atoms on similar sites). Also, because only one snapshot of a frozen nanoparticle was used, the binning has to be somewhat coarse, and this makes more subtle differences between the two structures more difficult to determine.

Fig. 4 Radial distribution functions of Co₁₈Pt₅₆₈, as relaxed by the force field (FF) and DFT.

The effective lattice parameter of each atom shows the differences between the two structures more clearly, as shown in Fig. 5. When considering the layer only neighbours, the interatomic potential relaxed structure has a 0.02 Å larger average effective lattice parameter than the DFT relaxed one at the surface. We also observe much the same patterns with respect to atomic coordination, the only differences being that the vertices of the potential relaxed structure are slightly more contracted than their DFT relaxed counterparts, while the centres of the (111) facets are slightly less expanded. The first sublayer shows an increase in the discrepancy: up to 0.04 Å. The largest difference, though, is found at the core of the nanoparticles, where the DFT relaxed structure is significantly more contracted, which can be seen from the average lattice parameter in layers 4 and 5 in Fig. 5b.

Fig. 5 Comparison of effective lattice parameter between Pt₅₆₈Co₁₈ after relaxation with DFT and the empirical potential. The structures of the nanoparticle are shown with their atoms (a), coloured according to their nearest neighbour (NN) distance either for all NN or for the NNs in the surface layer. The per layer average as a function of depth is plotted (b), showing both all NN (filled shapes) and layer only NN (hollow shapes) results. Layer 1 is the outermost (surface) layer, with each subsequent layer being further towards the nanoparticle core. The error bars indicate the standard deviation of effective lattice parameter for atoms in the layer.

When considering all neighbours, we see an increase in the average effective lattice parameter of most layers, both in the potential and DFT relaxed structures. The increase is much smaller in the former, with the first two layers remaining the same, and the inner layers each increasing by about 0.015 Å, leading to the peak shifting from the second to the third layer. For the DFT relaxed structure, as well as larger upward shifts in the first, second and fourth layers of 0.035 Å, 0.036 Å, and 0.045 Å, respectively, we see significant changes in the trend. This is largely down to the difference in the third layer, where the average effective lattice parameter decreases slightly. The result is a trend that is almost monotonic from surface to core.

While there are still some discrepancies between this potential and our DFT calculations, both in terms of energy and geometry, we are nevertheless encouraged by the level of agreement we see here. For our uses, primarily concerning strain in alloy nanoparticles, we believe the potential to be sufficiently accurate, though the differences we observe in the contraction at the core of the nanoparticle especially must be kept in mind.

3 Results and discussion

We have performed our simulations on truncated octahedral nanoparticles with PtCo L1₀ intermetallic cores and a 3 atom thick pure Pt shells. These nanoparticles therefore have a core with a Pt : Co ratio of 1 : 1, while overall remaining Pt rich at small sizes, due to the dominance of the Pt shell. Nanoparticles constructed in this way become more Co rich as size increases, and would reach an overall Pt : Co ratio of 3 : 1 at 7.5 nm in diameter. The full set of nanoparticles, spanning a size range of 2.55–5.62 nm in diameter, can be seen in Fig. 6, after they have been annealed. A cross-section, showing the arrangement of atoms in the core, is also shown.

Fig. 6 Each of the model nanoparticles following 5 annealing cycles. The bottom row shows the cross section perpendicular to the (110) lattice direction.

As with our previous work on pure Pt nanoparticles,⁴⁴ we have used a simulated annealing approach to explore the free energy surface of the nanoparticle structures. For the range of nanoparticles we have studied, we find that only the smallest of them (586 atoms/2.55 nm diameter) was fully melted under our annealing conditions. In this case, we observed a partial loss of the intermetallic structure in the core, as well as a small number of Co atoms reaching the nanoparticle surface. We saw a shift from the initial truncated octahedral structure to that of a Mark's decahedron, with the appearance of 5-fold symmetry sites, i.e., 5 (111) facets meeting at a vertex. Features of these multiply twinned decahedral structures were present in subsequent annealed structures, and twinning was also observed to a lesser extent in the next smallest nanoparticle (Pt₁₁₈₄Co₁₀₅).

For the four nanoparticles that did not fully melt, we observed a melting of the surface in this annealing scheme, resulting mainly in a growth of small (101) facets at the intersections of the (111) facets. No Co was exposed to the surface of any of these nanoparticles, indicating good thermal stability of these core–shell structures up to close to the bulk melting temperature of Co. With the constraints on simulation time that come with a 1 fs timestep, we cannot make claims about the long term stability of these nanoparticles at 1500 K, but this is already much hotter than expected operating conditions in a fuel cell.

As seen in Fig. 6, the intermetallic structure of the core was largely unmodified by the annealing for all but the smallest nanoparticle.

3.1 Melting points

In order to find the melting point of these nanoparticles, we have performed simulations in which the temperature is raised at a uniform rate of 50 K ns⁻¹ from 300 K to 2100 K, above the melting point of bulk Pt (2041 K). From this, we constructed caloric curves, determining the melting point to be where the slope (heat capacity) is maximised (Fig. 7).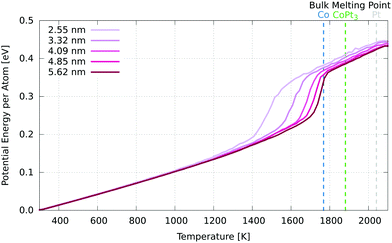

Fig. 7 Caloric curve for each nanoparticle. The melting points are defined as the maxima of the gradient (heat capacity) of these curves. The experimental bulk melting point for Pt is 2041 K, 1768 K for Co and 1881 K for Pt₃Co.⁵³

We see, as expected, that increased nanoparticle size corresponds with an increased melting point. The smallest melted at 1490 K, and each increase in diameter of ∼0.8 nm raised the melting point, but by a smaller amount each time. The largest nanoparticle had a melting point of 1746 K, just below that of bulk Co. We would expect the melting point to converge to the PtCo bulk melting point of 1778 K⁵³ as diameter increases, as the core contribution eventually dominates that of the shell. There was an order/disorder phase transition observed in the PtCo alloy (1 : 1 Pt : Co ratio) experimentally at 1098 K,⁵³ and predicted by this potential at 540 K.³³ Even though the core of our nanoparticles also has a 1 : 1 PtCo ratio, we do not observe any such phase transitions in our simulations, likely due to the short time scales we are working with. The presence of the Pt shell, which acts as a constraint on the core, may also be inhibiting a disorder transition.

3.2 Lattice contraction

It has been suggested that a major contribution to the increased activity of PtCo nanoparticle catalysts (compared to pure Pt) is due to the strain caused by the mismatch between the two metals’ lattice parameters.

Of particular interest is how strain propagates through the nanoparticles, from the core to the shell. To quantify this, we make use of the effective lattice parameter, which we average per layer. This was done both for the simulated and experimental nanoparticles, with interatomic distances measured for the former and intercolumn distances measured for the latter. It should be noted that while layers are defined as a set of atoms or columns in shells, the effective lattice parameter is measured from the (interatomic) distances between atoms, both within the same layer and those neighbouring it. This means that when we refer to layer 1, for example, we are including bonds with atoms in layer 2 as well. Layer 2 is inclusive of bonds between layer 1, 2 and 3, and this continues for each layer to the core.

Fig. 8 shows the 4.44 nm nanoparticle superimposed with coloured dots indicating the effective lattice parameter, as well as displacement from a fitted ideal lattice and change in cell area, calculated directly and from the trace of the strain tensor components. The equivalence of the cell area change as calculated by the two methods indicates that our methodology is consistent. In the future, this opens up scope for studying unit cell expansions along with shear and rotational components.

Fig. 8 Displacement, effective lattice parameter and fractional cell area change measurements for a 4.44 nm Pt₃Co experimental nanoparticle.

3.2.1 Simulated ADF-STEM analysis. While the methods for defining layers and determining effective lattice parameters are as equivalent as we can make them in 2D and 3D, there are still significant differences between the two. To quantify these differences, we have taken the 3D structures from our computational models and derived simulated ADF-STEM images from them. We then performed the 2D analysis in exactly the same way as for the real (measured) ADF-STEM images. The results from one of the nanoparticles (Pt₂₁₂₀Co₂₈₆) can be seen in Fig. 9.

Fig. 9 Effective lattice parameter for the Pt₂₁₂₀Co₂₈₆ model nanoparticle, calculated using the 2D (green) and 3D (red) method. The similar sized 4.44 nm experimental nanoparticle (purple) is also shown for comparison. Layer 1 is the outermost (surface) layer.

The differences between the two methods lead to an extra layer for the 2D version. This is simply due to the extra dimension in 3D, as the alpha surface that defines each layer is not constrained to approach from within one plane. The number of layers is essentially determined by the shortest dimension of the nanoparticle, so unless the dimension that is projected through is the same size or larger than the other two, we would not expect the number of layers to be the same necessarily. To put it another way, in 2D we are, in effect, rolling a cylinder of radius r and of infinite length in the z-direction (the direction in which it remains parallel to) around the nanoparticle to generate a layer, while in 3D we are rolling a sphere of the same radius r around the nanoparticle, and it is free to move in any dimension. There are more opportunities for the sphere to penetrate deeper into the nanoparticle, so it is more likely to reach the centre more rapidly, resulting in fewer layers.

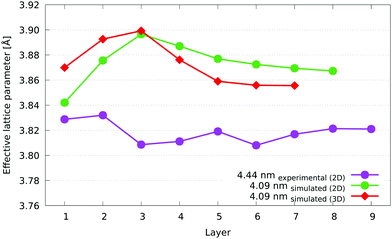
In terms of the numerical differences between the 2D and 3D cases, we see a 0.01 to 0.02 Å larger effective lattice parameter in 2D from the fourth layer inwards, while there is a decrease in the two outermost layers of 0.03 Å and 0.02 Å in the first and second layer, respectively. The third layer is the point of inversion between these behaviours, and as such, there is almost no difference between the 2D and 3D measurements. The reason for these trends is due to the columns of every layer in 2D containing the Pt shell atoms on both the top and bottom sides of the nanoparticle, which leads to an increase compared to the core layers in 3D, which are more Co (with its lower lattice parameter) rich. Also, because of the way the nanoparticle is projected into 2D, each resulting atomic column can contain a different number of atoms. However, when averaging the effective lattice parameter, each column is given equal weighting. This has the effect of reducing the apparent weighting of atoms (compared to the 3D case) in columns that contain more atoms. This is especially true at the surface, where the edges and vertices in the 2D projection have far fewer atoms in their columns. The combination of this biasing and the observation that lower coordinated atoms have shorter nearest neighbour distances means that the average effective lattice parameter in the surface layers is lower in 2D than in 3D. Overall, the differences between the two methods is small, and the layer by layer trends are clearly recognisable between the two.

3.2.2 Experimental and computational comparisons. The behaviour of the effective lattice parameter of the experimental and equivalently sized model nanoparticles as a function of layer is shown in Fig. 10. We observe a fairly distinct range of behaviours across the 3 experimental nanoparticles, especially considering that two of them are very similar in size.

Fig. 10 Comparison of effective lattice parameter per layer simulated and experimental Pt₃Co nanoparticles of similar sizes. Layer 1 is the outermost (surface) layer. For the simulated structures (diamonds), the 3D approach to defining layers and lattice parameter is used. Error bars indicate the standard deviation.

The 3.46 nm experimental nanoparticle has a surface layer average lattice parameter of just over 3.86 Å, equal to that of the 3.32 nm simulated nanoparticle. As a comparison, the lattice parameter of the Pt₃Co alloy, disordered at 1073 K, has a lattice parameter of 3.829 Å after quenching.⁵⁴ Their sublayers, however, diverge from each other, with the experimental nanoparticle showing a decrease in average effective lattice parameter with each layer until the fifth layer. The larger, 4.44 nm experimental nanoparticle shows a fairly similar trend, with similar averages at most layers, while the 3.51 nm nanoparticle is quite different. Although the overall trend of decreasing average effective lattice parameter from the first layer inwards is still present (if to a lesser extent), there is a downward shift of the 3.51 nm nanoparticle across all layers of about 0.03 Å away from what would be a much closer match to the other two experimental nanoparticles. A possible reason for this could be a difference in elemental composition of these nanoparticles, which we are unable to verify. Unleached nanoparticles such as those we have studied can have varying Pt:Co stoichiometry across a given sample population.⁵⁵ The similar trends displayed by the experimental nanoparticles is the most important observation here, although measurements for a larger sample of nanoparticles need to be taken in order to verify that these trends are widely applicable.

For a composition and strain study of these nanoparticles, we would require measurements using ADF imaging and spectroscopy. From the ADF imaging it would be possible to directly observe any structural changes caused by PtCo, CoO, or PtO presence, while with composition it would be possible to measure the percentage of Co with respect to Pt in the surface layers. If the composition measurements were performed using an EELS detector it would be possible to measure the oxidation state around the surface of the nanoparticle as well. This is outside of the scope of this study and has been left for future investigation.

In our experiments, all the nanoparticles we imaged were observed to be FCC, and no oxide layer effects could be seen. To investigate this further, a similar layer by layer measurement as shown in Fig. 1. is required for composition. For such an investigation, the methodologies proposed by MacArthur et al.⁵⁶ and Wang et al.⁵⁵ need to be combined with strain measurements.

Fig. 11 shows how the effective lattice parameter changes in our models as nanoparticle diameter increases. We find that the nanoparticles behave very similarly across the size range. There is an increase in effective lattice parameter moving from the surface of the nanoparticles to the third layer, after which this trend is reversed, with the inner layers contracting again. We see a convergence to the core average of between 3.85 Å and 3.86 Å by the fifth layer, indicating that a bulk-like core is close to being reached at this depth. Finally, there is consistently a greater variation between sites at the surface (as shown by the error bars, which show the standard deviation for the layer), which is simply a reflection of the presence of different facets, edges, vertices, adatoms etc., which lead to a much greater number of inequivalent sites than would be found in the subsurface layers.

Fig. 11 Effective lattice parameter per layer for the range of PtCo L1₀ core nanoparticles. Layer 1 is the outermost (surface) layer. Blue bars show the proportion of Co atoms in each layer.

The core region is expected to have a smaller lattice parameter due to the presence of Co atoms. The proportion of Co atoms in each layer is shown in Fig. 11, from which it can be seen that, with the exception of the smallest nanoparticle, the three layer Pt shell that the models were built with is very much preserved, with only very minor Co presence in the third layer of the smaller nanoparticles. From the fourth layer and inward, the proportion of Co atoms quickly jumps to 50%, meaning the 1 : 1 Co : Pt ratio of the L1₀ lattice is still intact after the annealing process. The smallest nanoparticle shows a small presence of Co at the surface, as well as the second and third layers, with a corresponding reduction of Co in the core.

The discrepancy we see between the computational models and experiment could be explained by a number of factors. Firstly, the tight-binding potential may not be ideal for these systems, and we showed it predicts effective lattice parameters slightly higher than our DFT calculation did, which means DFT calculations, if we were able to do them on larger systems, should give results closer to that of the experiments. However, we feel this is a minor point compared to the issue regarding the locations of Co in our systems. In our computational work, we have built idealised Pt shell, PtCo intermetallic core nanoparticles with roughly the same stoichiometry as the ones we are studying experimentally. However, the experimental nanoparticles are not prepared in such a way as to produce core–shell nanoparticles, as this is difficult to control,⁵⁷ and the Pt–Co distribution is not known. Because of this, we cannot easily assign shifts in the effective lattice parameter in the experimental nanoparticles to regions of low or high Co concentration, as we have in our models. A significant Co presence in the outer shells of the experimental nanoparticles, for instance, would be a likely reason for the discrepancy. Another possibility, and one that could also explain the lack of contraction at the surface layers of the experimental nanoparticles, is the presence of oxide layers at the surface, which are not visible in ADF-STEM images.

3.2.3 Comparison with randomly distributed Co. In order to test the effects of Co presence in the nanoparticle shell, we have built a model nanoparticle with the same stoichiometry as our core–shell nanoparticle, but with a random distribution of Co and Pt atoms. This structure was annealed in the same way, and the resulting structure underwent the same analysis.

The differences between the core–shell nanoparticle and the one with a random distribution of Pt and Co are shown in Fig. 12. The first three layers are similar, with a decrease of just 0.01 Å in the first two layers of the random nanoparticle, and almost no difference in the third layer. In the following layers, where the random nanoparticle has much lower concentrations of Co, there is no decrease in the effective lattice parameter like there is for the core–shell structure, and instead we see a convergence to 3.90 nm. This indicates that average effective lattice parameter of each layer is very much (inversely) correlated with its Co concentration. However, the trend also does not resemble that of the experimental nanoparticles, suggesting a different Co distribution. Another possibility is that the presence of oxygen in the surrounding environment of the experimental nanoparticles could be drawing Co to the surface, resulting in Co rich shells. This would need to be determined via simultaneous ADF-STEM and EELS or EDX experiments, and then compared with revised nanoparticle models, which is beyond the scope of this work, but represents a clear follow up.

Fig. 12 Comparison between the core–shell nanoparticle and a nanoparticle of the same shape (truncated octahedron) and stoichiometry (Pt₂₁₂₀Co₂₈₆). As per Fig. 11, the average lattice parameter is plotted as a function of layer, with layer 1 being the surface. The error bars show the standard deviation from the average at each layer.

3.2.4 Comparison to pure Pt nanoparticles. Comparing our Pt shell, PtCo core nanoparticles to pure Pt nanoparticles of the same size (and initial geometry), our modelling predicts a remarkably similar surface and first subsurface layer, which is shown in Fig. 13. The averaged effective lattice parameter is almost equal at the surface, at around 3.87 Å for the PtCo nanoparticle, and just below that for the pure Pt nanoparticle. Moving to the first sublayer (layer 2), we see an increase of the average effective lattice parameter in both nanoparticles, though the increase is larger for the pure Pt system, reaching 3.90 Å compared to just over 3.89 Å for PtCo. More significant differences appear in the third layer, and become more prominent with each subsequent (more internal) layer. The average effective lattice parameter rises sharply in the pure Pt system, up to 3.92 Å by the third layer, compared to just under 3.90 Å for PtCo, and converges at this value, which is the bulk Pt lattice parameter. The PtCo nanoparticle, meanwhile, shows a monotonic decrease after the third layer, falling to a value close to the L1₀ bulk lattice of 3.86 Å.³³ Although we see a continued decrease in lattice parameter from the fifth layer inwards, the difference between each layer is very small compared to the variation of effective lattice parameter of atoms within each layer.

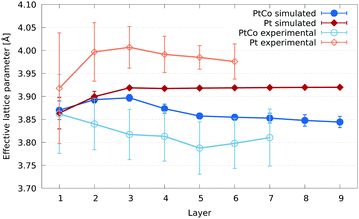Fig. 13 Comparison of the effective lattice parameter per layer between pure Pt and PtCo nanoparticles. For the computational models (filled shapes), two truncated octahedral 4033 atom (4.85 nm diameter) nanoparticles were compared. In blue is the core–shell PtCo nanoparticle described in this paper, while in red is a pure Pt nanoparticle. Both have been annealed and the resulting structures geometry relaxed. A 2.84 nm pure Pt nanoparticle from our experimental work is shown in orange, while in light blue is the 3.46 nm PtCo nanoparticle also shown in Fig. 10. As with previous figures, the error bars show the standard deviation.

The lack of difference between the average effective lattice parameter at the surface of the PtCo and pure Pt nanoparticles seems to be at odds with the prevailing theory in the literature: that the Co rich core induces strain at the Pt surface to alter oxygen binding. However, the lack of difference in the average masks the differences in distribution of surface sites. These differences can be seen in Fig. 14. To better understand the effects of Co in Pt nanoparticles with respect to ORR catalysis, we would need to compare the binding energies of oxygen across the full surface for both the pure Pt and PtCo core nanoparticles. This is currently far too computationally expensive to do with DFT, and reliable potentials and/or parameters are not available for this combination of materials. Instead, the use of descriptors could be used for such a comparison, which is a future stage of this work. A preliminary assessment of the performance in PtCo nanoparticles using an electronic descriptor, first introduced in our earlier work⁷ and successfully applied to metal oxide supported Pt nanoparticles,⁵⁸ is given in Section S2 of the ESI.†

Fig. 14 Effective lattice parameter at the surface of the (a) Pt₃₃₇₆Co₆₅₇ and (b) Pt₄₀₃₃ nanoparticles, as relaxed using the TB-SMA potential. Atoms are coloured according to effective lattice parameter, such that blue represents atoms with shorter average nearest neighbour distances. The scale bar is in units of Å.

In our experimental pure Pt nanoparticles, we see a similar contraction of effective lattice parameter at the surface layer to that of the pure Pt model. A lattice parameter contraction of ∼0.5% of the surface layer of Pt(111) facets has been reported in the literature,⁵⁹ for which a definitive explanation has not been given. While we have not isolated Pt(111) facets in our strain calculations, our results align with this observation, considering that (111) facets, with the lowest surface energy for Pt, are the most predominant in our nanoparticles.⁷ We also expect a contribution to this contraction from atoms in low coordination edge and vertex sites at the surface, which tend to bind to their neighbours slightly more closely than those in the bulk.

Compared to the model, there is a large upward shift of the effective lattice parameter per layer in the experimental nanoparticle of between 0.05 Å and 0.10 Å, with an average shift of 0.07 Å. Shifting all the layers by this average results in a very close agreement between the model and experiment. Some of the reasons for a discrepancy in the experimental lattice parameter could be beam damage, sample drift under the beam, the carbon support and heating for small nanoparticles. These effects contribute to the large error bars seen in Fig. 13.

Unfortunately, such a shift would not resolve the discrepancies observed between theory and experiment for the PtCo nanoparticles, and in fact would only widen the difference if applied in the same way. This is despite the fact that the heating and damage from the beam line will still be present for the alloy nanoparticles.

4 Conclusions

This work aimed to combine experimental and computational methods to determine the effects of introducing Co to Pt nanoparticles, particularly with respect to strain. In order to do this, we developed two near equivalent approaches to determine the strain of real nanoparticles imaged via ADF-STEM, as well as from computational model nanoparticles. We have demonstrated a close level of agreement between these approaches by also generating simulated ADF-STEM images of our model nanoparticles. Good agreement between experiment and our models has also been shown in the case of pure Pt nanoparticles.

Our simulations required the use of an empirical potential, for which we have compared two sets of parameters against DFT calculations. We have shown the suitability of the more recently published set of parameters for use in the study of PtCo alloy nanoparticles, making clear the structural and energetic advantages over the older ones. Better agreement with DFT in these areas, as well as closer consistency with experimental observations are the main improvements. Questions do remain as to how well strain effects are captured by the potential, however, as DFT geometry relaxations show some differences in terms of effective lattice parameter.

Our results show a lower level of agreement between simulation and experiment with regards to strain in PtCo alloy nanoparticles. The observed trend of lattice expansion from the core layers to the surface in the experimental nanoparticles is distinct from the one we see in our models. Since the distribution of Co was not determined in our experimental nanoparticles, we consider this to be the most likely and most significant source of discrepancy. Comparing both Pt-shell, PtCo-core nanoparticles and those with a random distribution of Co with our experimental data shows that neither are a particularly close fit. This could mean that the structure of the real nanoparticles does not resemble either a core–shell or a fully random distribution, and we suggest that oxygen presence in the surrounding environment (something that is ignored in our modelling) could be drawing Co to the surface.

Finally, we see only small changes to strain at the surface layer of our model Pt-shell, PtCo-core nanoparticles compared with pure Pt. This suggests that the contribution to the observed improvement to the catalytic activity for the ORR is not from an average strain induced by the presence of Co in the core. Changes to the electronic structure of the nanoparticles may instead be the dominant effect, or it may be that the process of removing Co from the shell via leaching results in a much different surface structure than what we have in our models.

The observation of distinct distribution of surface strain (despite the average being the same) between the pure and alloy nanoparticles is also important. In future work, we intend to investigate the effects of this on catalytic activity via the use of electronic descriptors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the use of the IRIDIS 5 High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work. We are grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194 and EP/T022213/1), and access was obtained via the UKCP consortium and funded by EPSRC grant ref EP/P022030/1. T. E. would also like to thank Johnson Matthey and the EPSRC for financial support in the form of a PhD studentship. The authors also acknowledge use of characterization facilities within the David Cockayne Centre for Electron Microscopy, Department of Materials, University of Oxford and in particular the EPSRC (EP/K040375/1 “South of England Analytical Electron Microscope”) and additional instrument provision from the Henry Royce Institute (Grant reference EP/R010145/1). We would like to thank Brian Theobald and Jonathan Sharman from JMTC Sonning for provision of the Pt and PtCo samples.

Notes and references

1. R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J. E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K.-i. Kimijima and N. Iwashita, Chem. Rev., 2007, 107, 3904–3951.
2. O. Z. Sharaf and M. F. Orhan, Renewable Sustainable Energy Rev., 2014, 32, 810–853.
3. O. T. Holton and J. W. Stevenson, Platinum Met. Rev., 2013, 57, 259–271.
4. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
5. F. Viñes, Y. Lykhach, T. Staudt, M. P. A. Lorenz, C. Papp, H.-P. Steinrück, J. Libuda, K. M. Neyman and A. Görling, Chem. – Eur. J., 2010, 16, 6530–6539.
6. L. G. Verga, A. E. Russell and C.-K. Skylaris, Phys. Chem. Chem. Phys., 2018, 20, 25918–25930.
7. J. Aarons, L. Jones, A. Varambhia, K. E. MacArthur, D. Ozkaya, M. Sarwar, C.-K. Skylaris and P. D. Nellist, Nano Lett., 2017, 17, 4003–4012.
8. M. Sarwar, J. L. Gavartin, A. M. Bonastre, S. G. Lopez, D. Thompsett, S. C. Ball, A. Krzystala, G. Goldbeck and S. A. French, Phys. Chem. Chem. Phys., 2020, 22, 5902–5914.
9. G. G. Asara, L. O. Paz-Borbón and F. Baletto, ACS Catal., 2016, 6, 4388–4393.
10. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556.
11. J. M. Jaksic, N. M. Ristic, N. V. Krstajic and M. M. Jaksic, Int. J. Hydrogen Energy, 1998, 23, 1121–1156.
12. V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901.
13. Z. Yu, J. Zhang, Z. Liu, J. M. Ziegelbauer, H. Xin, I. Dutta, D. A. Muller and F. T. Wagner, J. Phys. Chem. C, 2012, 116, 19877–19885.
14. L.-L. Wang and D. D. Johnson, J. Am. Chem. Soc., 2009, 131, 14023–14029.
15. P. C. Jennings, H. A. Aleksandrov, K. M. Neyman and R. L. Johnston, Phys. Chem. Chem. Phys., 2014, 16, 26539–26545.
16. M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822.
17. J. Zhang, M. B. Vukmirovic, Y. Xu, M. Mavrikakis and R. R. Adzic, Angew. Chem., Int. Ed., 2005, 44, 2132–2135.
18. V. Jalan and E. J. Taylor, J. Electrochem. Soc., 1983, 130, 2299.
19. A. Varambhia, L. Jones, A. London, D. Ozkaya, P. D. Nellist and S. Lozano-Perez, Micron, 2018, 113, 69–82.
20. L. Jones, K. E. MacArthur, V. T. Fauske, A. T. J. van Helvoort and P. D. Nellist, Nano Lett., 2014, 14, 6336–6341.
21. A. J. Craven, J. Bobynko, B. Sala and I. MacLaren, Ultramicroscopy, 2016, 170, 113–127.
22. H. E, K. E. Macarthur, T. J. Pennycook, E. Okunishi, A. J. D’Alfonso, N. R. Lugg, L. J. Allen and P. D. Nellist, Ultramicroscopy, 2013, 133, 109–119.
23. B. D. A. Levin, E. Padgett, C.-C. Chen, M. C. Scott, R. Xu, W. Theis, Y. Jiang, Y. Yang, C. Ophus, H. Zhang, D.-H. Ha, D. Wang, Y. Yu, H. D. Abruña, R. D. Robinson, P. Ercius, L. F. Kourkoutis, J. Miao, D. A. Muller and R. Hovden, Sci. Data, 2016, 3, 160041.
24. Y. Yang, C.-C. Chen, M. C. Scott, C. Ophus, R. Xu, A. Pryor, L. Wu, F. Sun, W. Theis, J. Zhou, M. Eisenbach, P. R. C. Kent, R. F. Sabirianov, H. Zeng, P. Ercius and J. Miao, Nature, 2017, 542, 75–79.
25. A. D. Backer, L. Jones, I. Lobato, T. Altantzis, B. Goris, P. D. Nellist, S. Bals and S. V. Aert, Nanoscale, 2017, 9, 8791–8798.
26. B. Goris, A. De Backer, S. Van Aert, S. Gómez-Graña, L. M. Liz-Marzán, G. Van Tendeloo and S. Bals, Nano Lett., 2013, 13, 4236–4241.
27. K. E. MacArthur, M. Heggen and R. E. Dunin-Borkowski, Microsc. Microanal., 2018, 24, 1688–1689.
28. R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265.
29. L. Jones, H. Yang, T. J. Pennycook, M. S. J. Marshall, S. Van Aert, N. D. Browning, M. R. Castell and P. D. Nellist, Adv. Struct. Chem. Imaging, 2015, 1, 8.
30. I. Lobato and D. Van Dyck, Ultramicroscopy, 2015, 156, 9–17.
31. H. X. Gao and L.-M. Peng, Acta Crystallogr., Sect. A: Found. Crystallogr., 1999, 55, 926–932.
32. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
33. A. Front, B. Legrand, G. Tréglia and C. Mottet, Surf. Sci., 2019, 679, 128–138.
34. C. Goyhenex, H. Bulou, J.-P. Deville and G. Tréglia, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2781–2788.
35. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
38. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
39. N. Marzari, D. Vanderbilt and M. C. Payne, Phys. Rev. Lett., 1997, 79, 1337–1340.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
41. C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119.
42. Á. Ruiz-Serrano and C.-K. Skylaris, J. Chem. Phys., 2013, 139, 054107.
43. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
44. T. Ellaby, J. Aarons, A. Varambhia, L. Jones, P. Nellist, D. Ozkaya, M. Sarwar, D. Thompsett and C.-K. Skylaris, J. Phys.: Condens. Matter, 2018, 30, 155301.
45. C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Math. Software, 1996, 22, 469–483.
46. H. Edelsbrunner, D. Kirkpatrick and R. Seidel, IEEE Trans. Inf. Theory, 1983, 29, 551–559.
47. T. Nilsson Pingel, M. Jørgensen, A. B. Yankovich, H. Grönbeck and E. Olsson, Nat. Commun., 2018, 9, 2722.
48. B. Goris, J. De Beenhouwer, A. De Backer, D. Zanaga, K. J. Batenburg, A. Sánchez-Iglesias, L. M. Liz-Marzán, S. Van Aert, S. Bals, J. Sijbers and G. Van Tendeloo, Nano Lett., 2015, 15, 6996–7001.
49. A. De Backer, K. H. W. van den Bos, W. Van den Broek, J. Sijbers and S. Van Aert, Ultramicroscopy, 2016, 171, 104–116.
50. M. Nord, P. E. Vullum, I. MacLaren, T. Tybell and R. Holmestad, Adv. Struct. Chem. Imaging, 2017, 3, 9.
51. P. L. Galindo, S. Kret, A. M. Sanchez, J.-Y. Laval, A. Yáñez, J. Pizarro, E. Guerrero, T. Ben and S. I. Molina, Ultramicroscopy, 2007, 107, 1186–1193.
52. L. D. Marks, Rep. Prog. Phys., 1994, 57, 603.
53. H. Okamoto, J. Phase Equilib., 2001, 22, 591.
54. A. S. Darling, Platinum Met. Rev., 1963, 7, 96–104.
55. D. Wang, H. L. Xin, R. Hovden, H. Wang, Y. Yu, D. A. Muller, F. J. DiSalvo and H. D. Abruña, Nat. Mater., 2013, 12, 81–87.
56. K. E. MacArthur, T. J. A. Slater, S. J. Haigh, D. Ozkaya, P. D. Nellist and S. Lozano-Perez, Microsc. Microanal., 2016, 22, 71–81.
57. Z. Liu, H. Xin, Z. Yu, Y. Zhu, J. Zhang, J. A. Mundy, D. A. Muller and F. T. Wagner, J. Electrochem. Soc., 2012, 159, F554.
58. T. Ellaby, L. Briquet, M. Sarwar, D. Thompsett and C.-K. Skylaris, J. Chem. Phys., 2019, 151, 114702.
59. S. Gallego, C. Ocal and F. Soria, Surf. Sci., 1997, 377–379, 18–22.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04318d

---