Effect of Mn doping on the electron injection in CdSe/TiO2 quantum dot sensitized solar cells†
Ning
Du
a,
Yingqi
Cui
b,
Li
Zhang
 *a and
Mingli
Yang
*a and
Mingli
Yang
 *ac
*ac
aInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China. E-mail: lizhang@scu.edu.cn; myang@scu.edu.cn
bSchool of Physics and Electronic Engineering, Zhengzhou Normal University, Zhengzhou 450044, China
cResearch Center for Materials Genome Engineering, Sichuan University, Chengdu 610065, China
First published on 9th December 2020
Abstract
Promotion in power conversion efficiency is an appealing task for quantum dot-sensitized solar cells that have emerged as promising materials for the utilization of clean and sustainable energy. Doping of Mn atoms into quantum dots (QD) has been proven to be one of the effective approaches, although the origin of such a promotion remains controversial. While several procedures are involved in the power conversion process, electron injection from the QD to the semiconductor oxide substrate is focused on in this work using first-principles calculations. Based on the Marcus theory, the electron injection rates are evaluated for the quantum dot-sensitized solar cell models in which the pure and Mn-doped core–shell CdSe clusters are deposited on a semiconductor titanium dioxide substrate. Enhanced rates are obtained for the Mn-doped structure, which is in qualitative agreement with the experiments. A large number of dominant injection channels and strong QD–substrate coupling are responsible for the Mn-induced rate enhancement, which could be achieved by manipulating the band structure mapping between the QD and the semiconductor oxide. By addressing the role of an Mn dopant in the electron injection process, strategies for the promotion of electron injection rates are proposed for the design of quantum dot-sensitized solar cells.
1. Introduction
Solar energy as a clean, cheap and renewable energy source has attracted a great deal of interest in the development of photoelectric conversion materials. Dye-sensitized solar cells (DSSC), firstly proposed by O'Regan et al.1 in 1991, are important devices for collection and utilization of solar energy. The key component of DSSC is a wide band gap oxide semiconductor (usually TiO2, ZnO or SnO2) photoanode, sensitized by a dye monolayer that absorbs incident photons and injects the excited electrons into the conduction band (CB) of the oxide semiconductor.2 However, the low boiling point, volatility and large fluidity of the dye monolayer are unconducive to the long-term stability of solar cells. The use of semiconductor quantum dots (QDs) as the sensitizers instead of dye monolayers has gained growing attention because of the high absorption coefficients and good photostability of the former that are suitable for light harvesting.3 Some semiconductor QDs absorbing a photon can generate multiple excitons and increase the solar cell photocurrent.4,5 Moreover, their band edges can be tuned by changing their sizes and shapes,6 in order to increase their absorption overlap with the solar spectrum. In addition, the staggered alignment of electronic energy levels between QDs and oxide semiconductors can also promote the interfacial electron injection process.7Although much effort has been devoted to QD-sensitized solar cells (QDSSC), their recorded power conversion efficiencies (PCE) are still lower than those of dye-8,9 and perovskite-10–12 sensitized solar cells. When an incident light irradiates on the photoanode, two paths of electron injection, direct and indirect, may occur. In the indirect path, the QD absorbs a photon and excites an electron from its highest occupied molecular orbital (HOMO) to its lowest unoccupied molecular orbital (LUMO), leaving behind a hole and generating an electron–hole pair. The photo-excited electron transfers from the LUMO to one of the conduction bands of oxide semiconductor and then relaxes to the conduction band minimum (CBM). After that, the electron at the CBM moves to the transparent conducting glass and flows into the external circuit. In the direct path, electrons inject from the HOMO of QD to the oxide semiconductor without passing through the LUMO of QD, which often occurs when the QD–substrate distance is shorter than the corresponding van der Waals contact distance.13 Since the indirect path is mostly concerned with in QDSSC studies,14–18,20,21 the indirect electron injection mechanism is focused on in the present work.
All the processes in the indirect path have a considerable effect on the PCE of the cell. In the first process, the optical absorption and the subsequent electron injection are closely related to the QD structures, in particular to their surface structures, which are abundant in defects. These surface defects have a great tendency to trap photo-generated carriers and prevent them from transferring between the QD and the oxide substrate. Encapsulating the QD with a shell to form a core–shell QD can passivate the surface traps and prevent the electron effectively from being trapped. Ågren et al.22 reported the first QDSSC formed with ZnSe/CdS core–shell colloidal particles. Since then a large number of studies7,23–30 have been conducted for the utilization of core–shell QDs in solar cells. For example, Abate et al.23 demonstrated that the double-shell CdS/ZnS in AgInSe2 contributes greatly to the suppression of charge recombination and achieved a maximum PCE of 6.27%. Azpiroz et al.7 investigated ZnSe- and ZnSe/CdS-sensitized TiO2 models using density functional theory (DFT) calculations and found that the core/shell QDs deliver a much better efficiency. Ding et al.24 revealed that suitable bifunctional aromatic linkers connected to the surfaces of CdSe QDs boost the electron injection and weaken the electron–hole recombination in solar cells.
Meanwhile, a number of studies15–18,21,31–46 have pointed out that doping QDs with an optically active transition metal ion results in enhanced electronic and photovoltaic properties of QDSSCs. The doping of transition metal ions, e.g., Mn2+ or Hg2+ into PbS,21,31 Mg2+ into CdS,32 and Mn2+ into CdS33–39 or CdSe,18,36,40–46 increases the current density and PCE of solar cells, and among these Mn is the most commonly used as a dopant. Santra et al.33 found that by doping Mn into CdS/CdSe films nearly 20% enhancement in the PCE is achieved as compared to the corresponding undoped films. Li et al.38 verified that the PCE of Mn–CdS/CdSe co-sensitized cell reaches 7.16%, well above that of 5.54% for the samples without the Mn dopant. Wang et al.41 developed a new route for Mn-doped CdSe0.65Te0.3 sensitized solar cells, achieving a PCE of 9.40% in a champion cell device. Moreover, a 69% enhancement of PCE was reported for the CdS/CdSe co-sensitized solar cell with a Mn-doped ZnSe passivation layer compared to the device without a passivation layer.16
Although many studies have indicated the significant impact of Mn doping on the photovoltaic properties of QDSSC, the role of an Mn dopant remains controversial. For example, Li et al.38 ascribed the high PCE of a doped solar cell to an mid-gap state induced by the Mn dopant, which improves light harvesting and accelerates the charge separation. However, Jung et al.39 believed that the reduction of defects in the Mn doped QD, rather than mid-gap state formation, is one of the main reasons for the enhanced photovoltaic performance of the doped solar cell. In addition, Pimachev et al.44 and Poudyal et al.18 ascribed the large photocurrent enhancement and the short electron injection time constant after Mn doping to the larger wavefunction overlap between the Mn doped CdSe QD and the oxide substrate, which reduces the barrier height for electron injection and favors electron transfer to the photoanode. Chiang et al.17 also demonstrated that Mn doping results in strong electronic coupling at the interfaces and then benefits the electron injection from the QDs into semiconductor oxides. In contrast, Wang et al.41 found that the Mn dopant in CdSe0.65Te0.35 sensitized solar cells has a trade-off effect, retarding electron injection and reducing the electron–hole recombination rates.
It has been well established that first-principles calculations are helpful to understand the electron structures of QDs and the semiconductor oxides. However, computations on the electron flow between them are still scarce because of the complexity of the QD, oxide and their interface for which multi-factor and multi-step computations have to be conducted. In the present work, the Mn doped magic-sized cluster (CdSe)13, which has the smallest core–shell architecture, is deposited on the anatase TiO2 slab surface as the sensitizer. By simulating the electron injection from the pure and Mn-doped CdSe clusters to the TiO2 substrate, the role of the Mn dopant in modulating electron injection process is addressed. Furthermore, the strategy for promoting electron injection is suggested for the CdSe@TiO2 cells.
2. Computational models and methods
The magic-sized cluster (CdSe)13, whose structure has been previously characterized in experiments and computations,14,47–51 is placed over the slab. A vacuum space of 10 Å thickness is added on the top of the QD to avoid the effect of periodicity. Since (CdSe)13 possesses the C3 symmetry with a number of symmetrically equivalent sites, only the unequivalent substitutions of Cd by Mn are explored. Several spin multiplicities for each substitution are examined to locate the lowest-energy Mn-doped structures and spin states. Fig. 1a and b display the structures of the pure and Mn-doped (CdSe)13 clusters.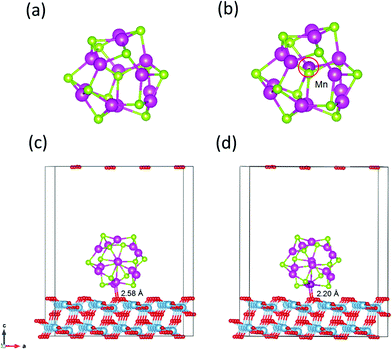 | ||
| Fig. 1 Structures of (CdSe)13 (a), Cd12MnSe13 (b), (CdSe)13@TiO2 (c) and Cd12MnSe13@TiO2 (d). Blue = Ti, red = O, green = Se, light purple = Cd, and deep purple = Mn atoms, respectively. | ||
Two approaches, via in situ and ex situ growth, are used in experiments to deposit QD sensitizers on a photoanode.52 The former includes chemical bath deposition and successive ionic layer adsorption and reaction by which QDs are connected directly to the oxide surface and a high surface coverage can be reached. In the ex situ approach, QDs are first synthesized in a solvent and then deposited on the photoanode. Since they grow in the solvent, their surfaces are usually passivated by ligands. Both bare and ligand-passivated QDs are used in the preparation of solar cells. While this work focuses on the effect of Mn doping on the electron injection process, the direct adsorption model of bare QDs on the oxide surfaces is constructed for simplicity. The stoichiometric anatase TiO2(101) surface, which was characterized as the most stable facet,20,53 is modeled using a periodic slab. The QD may have a lot interaction patterns with the substrate. The exposed O atoms on the substrate surface have a great tendency to interact with the Cd atoms in the QD. Owing to the small size of (CdSe)13, up to two Cd atoms can be bonded to the exposed O atoms. Furthermore, Cd atoms have five unequivalent sites in the symmetric C3 structure. Therefore, a number of candidate structures are created by forming one or two Cd–O bonds at the unequivalent sites. All the created structures including the QD and the substrate are relaxed using DFT calculations under the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE)54 functional, as implemented in the plane-wave PWMat package.55,56 Structural relaxation is converged to the maximum atomic force of less than 0.01 eV Å−1. The ONCV-PWM-PBE norm-conserving pseudopotentials57,58 are adopted with an energy cutoff of 45 Ry, and only the Γ-point is sampled because of the large number of atoms (26 atoms in the QD and 192 atoms in the substrate) in models. Spin-polarized calculations are performed for the open shell structures. The structures of pure and Mn-doped CdSe@TiO2 complexes are depicted in Fig. 1c and d.
The optical adsorption of the pure and doped QDs is calculated using the real-time time-dependent DFT (rt-TDDFT) method.19 The same functional and pseudopotentials as those used in the above structural relaxation are employed. The atom positions are fixed and the total simulation lasts 5 fs at a time step of 0.01 fs. An electric field polarized in the x direction is applied to obtain the absorption spectra.
In a typical electron injection process, the photo-excited electron transfers from the LUMO of the sensitizer to one of the conduction bands of TiO2 and then relaxes to the CBM. Semiclassical Marcus theory59 provides a theoretical model for such an electron transfer process. Suppose the excited electron occupies the LUMO of QD in its initial state i, and occupies the i-th CB state of TiO2 in its final state f, the electron transfer rate from the initial state to the final state is written as
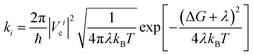 | (1) |
| Gi = EN(RN) + ELUMO − λQD | (2) |
| Gf = EN(RN) + Ei − λTiO2 | (3) |
Marcus theory considers a nonadiabatic electron transfer process in the thermal equilibrium state. When the quantum dots absorbs an incident photon, an electron is excited from an occupied orbital to an unoccupied orbital and subsequently relaxes to the LUMO orbital via an ultrafast phonon-assisted process, which occurs on the picosecond or sub-picosecond scale.60,61 Experiments on quantum dot sensitized solar cells have revealed that the electron injection rate is usually in the range of 1010–1011 s−1,41,62 implying that the relaxation process of the photoexcited electron is completed before the electron injects to the conduction band of the oxide substrate. At room temperature, low-energy vibrations can be easily excited, e.g., with a thermal energy of 26 meV (the minimum vibrational energy level difference).63 This energy corresponds to a vibrational frequency of about 6.3 × 1012 Hz (about 160 fs). This time period increases further at low temperatures. As mentioned above, the measured electron injection rates are in the range of 1010–1011 s−1, which is slower than the vibrational relaxation rate, implying that the vibrational subsystem is in equilibrium before the photoexcited electron injects to the conduction band of the oxide substrate. Therefore, Marcus theory has been employed in many studies62,64–67 to interpret the electron injection processes of quantum dot/dye sensitized solar cells. In addition, the applicability of the Marcus–Levich–Dogonadze expression (i.e., eqn (1)), which ignores contributions from quantum modes, is discussed in the ESI.†
According to eqn (1), electron transfer rate has a close relationship with the energy difference between the LUMO of QD and the CB state of TiO2. Consequently, a precise energy level or band alignment of QD@TiO2 is necessary for subsequent calculations. It is well known on one hand that the conventional local density approximation (LDA) or GGA functionals usually fail to predict the energy levels or bands for most semiconductors. The hybrid exchange–correlation functional Heyd–Scuseria–Ernzerhof (HSE)68 is thus employed in this work in all self-consistent field (SCF) calculations to yield the band alignments. On the other hand, two parts, (CdSe)13/Cd12MnSe13 QDs and the TiO2(101) substrate, are studied in the systems. Precise band energies are difficult to obtain for both QDs and TiO2 with a single parameter in the HSE calculations. A mask function69 is thus used to optimize the parameters that predict precise band energies for both parts at the same time. The mask function has the form
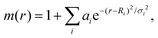 | (4) |
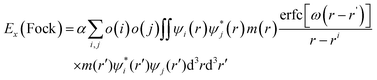 | (5) |
| λ = λQD + λTiO2 | (6) |
| λQD = EN−1(RN) − EN−1(RN−1) | (7) |
| ΔG + λ = Ei − ELUMO + 2λQD | (8) |
The coupling constant, Vci, between the LUMO of QD and the i-th CB state of TiO2 is ascertained using the Landau–Zener anti-crossing energy gap.71 In this approach, an electric field is applied as a perturbation to make the two energy levels get closer until the “anti-crossing” occurs. Their minimum gap is called the anti-crossing energy gap, which is twice their coupling constant (Vc). Finally, the overall electron injection rate is evaluated based on the above calculations.
3. Results and discussion
3.1 Bare and doped (CdSe)13
The relaxed structure of core–shell (CdSe)13 is shown in Fig. 1a. Selected Cd–Se bond-lengths are given in Fig. S2 in the ESI,† which are in agreement with previous studies.47,49 The Mn atom has five unequivalent substitution sites in the C3 symmetric structure. Moreover, the doped structure may have various spin multiplicities 2, 4 and 6. Structure relaxation is performed for all the five doped structures with various spin multiplicities. It is found that the high-spin sextet structure with Mn on the C3 axis has the lowest energy, as shown in Fig. 1b. The structures and energies of other isomers are given Fig. S3 in the ESI.† A stable high-spin structure was identified for Cd9−nMnnSe9 (n = 1, 3 and 5) clusters.72,73 Doping with Mn leads to rather small geometrical changes. The core–shell architecture and C3 symmetry are still retained. The stability of a doped QD is usually measured from its binding energy (Eb), which is defined as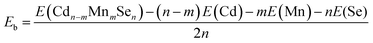 | (9) |
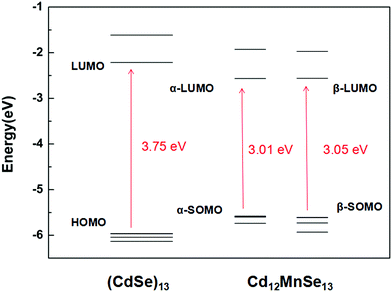
Fig. 2 depicts the frontier molecular orbitals in the bare and doped clusters. In the open-shell structures their HOMOs are singly occupied, which are denoted as SOMOs (singly occupied molecular orbitals). The Mn dopant raises the SOMO, and lowers the LUMO for both α and β spin orbitals, resulting in dramatic decreases from 3.75 eV to 3.01 and 3.05 eV, respectively, in the energy gap. The density of states (DOS) of the pure and doped clusters are given in Fig. S4 in the ESI.† In addition to the total DOS (TDOS), the projected DOS (PDOS) of the Mn atom is also presented. The mid-gap state is however not found in the DOS of the doped structure. Some experiments33,36–38 attributed the narrow band gap of doped QDs to a mid-gap state generated by Mn doping, while other studies16,39,72–74 denied the existence of the mid-gap states. The energy shifts in the SOMO and LUMO mainly result from the contribution of Mn-3d.
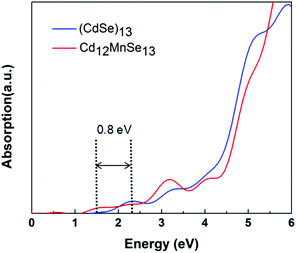
Fig. 3 compares the optical absorption of the bare and Mn-doped clusters, which are computed using the rt-TDDFT method with the PBE functional. The absorption edge is 2.3 eV for the bare, and shifts to 1.5 eV for the doped. For most II–IV QDs their lowest excited states are usually attributed to the HOMO-to-LUMO transitions.75 The redshift of the first peak matches well with the above revealed variations in their frontier molecular orbitals. The broadened light absorption window makes it possible for more photo-excited carriers to be generated in the Mn-doped QD, which have been verified in some experiments.16,33,35,38 For example, Venkata et al.46 demonstrated that doping Mn into CdSe QDSSCs broadens the harvested light range from 612 to 688 nm.
3.2 TiO2 supported QDs
A number of candidate structures of the bare and Mn-doped (CdSe)13 clusters on the TiO2 substrate have been created and screened via DFT computations. The lowest energy structures are shown in Fig. 1c and d. Some other low-lying structures are presented in Fig. S5 (ESI†), along with their relative energies. One or two Cd–O bonds are formed between the QD and the substrate in the low-lying structures. However, two Cd–O bonds are found in the five most stable structures. Similar adsorption patterns were reported by Prezhso’ et al. in the Pb16Se16/TiO2 system.76 In the lowest energy structures, the QD stands vertically on the substrate, about 0.03 and 0.11 eV more stable than the second and third best structures. The distances between the contacting Cd and O atoms are 2.34 and 2.58 Å, respectively. For the Mn doped structure (as shown in Fig. 1d), one of the Cd atoms and the Mn atom interact with the surface oxygen atoms. The Cd–O distance is 2.34 Å, while the Mn–O distance is 2.20 Å. The interaction energy (Eint) between the two parts is computed as| Eint = EQD + ETiO2 − Ecomplex | (10) |
| E int | Δq | E VBM | E HOMO | E LUMO | E CBM | ΔEinj | |
|---|---|---|---|---|---|---|---|
| (CdSe)13@TiO2 | 0.66 | 0.39 | −5.29 | −3.84 | −0.07 | −2.12 | 2.05 |
| Cd12MnSe13@TiO2 | 0.86 | 0.44 | (α) −5.27 | −3.30 | −0.38 | −2.11 | 1.73 |
| (β) −5.27 | −3.49 | −0.38 | −2.11 | 1.73 |
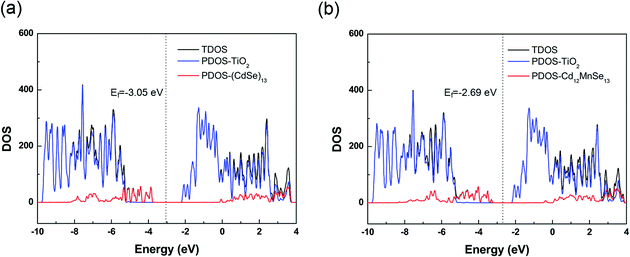
The total density of states (TDOS) of the two complexes are presented in Fig. 4, along with their projection to the TiO2 and the QD parts (PDOS). The TDOS and PDOS give the EVBM, EHOMO, ECBM and ELUMO for the evaluation of electron injection rates. For the undoped complex, the VBM is contributed by the QD, while the CBM by the TiO2 substrate. The valence band from TiO2 is 1.45 eV below the VBM, and the conduction band from QD is 2.05 eV above the CBM. For the Mn-doped open-shell complex, the spin up and spin down densities are almost symmetrically distributed in the vertical direction (Fig. S6, ESI†), except the top of valence bands that is contributed from the spin polarization of CdSe QDs induced by the Mn dopant. Moreover, its band structure is similar to that of the pure-QD complex. Its VBM and CBM are contributed by the QD and TiO2, respectively. The TiO2 contribution to the valence band is 1.97 eV below the VBM, and the QD contribution to the conduction band is 1.73 eV above the CBM. Both complexes belong to the type-II energy level alignment in which the occupied orbitals of QDs intrude into the band gap of the TiO2 substrate, and the unoccupied orbitals are immersed in the CB states of the substrate. Such a staggered band alignment is an important precondition for electron injection.
Table 1 lists the EHOMO(SOMO), ELUMO, EVBM and ECBM of the two complexes. The α-SOMO in Cd12MnSe13 is about 0.1 eV above the corresponding β-SOMO. We use only α-SOMO in the following discussion because they come to similar conclusions. The energy gaps ΔEinj between the LUMO of QDs and the CBM of TiO2 are thus evaluated using the data in Table 1. The Mn substitution leads to an upward shift of the Fermi level Ef, favoring the promotion of the open circuit voltage (VOC), an important quantity that measures the performance of solar cells. Similar to the energy levels of isolated QDs, the ESOMO increases and the ELUMO drops down upon Mn substitution for both α-spin and β-spin.
3.3 Electron injection rates
In a typical electron injection process the electron escapes from the QD, resulting in both structural and orbital relaxations that contribute to the reorganization energy, λQD. The PBE functional predicts similar λQD values, 0.073 eV and 0.067 eV for the pure and doped QDs, respectively. In previous studies,78λQD has been estimated to be 0.03 eV for CdSe QD with 2 nm diameter. It is reasonable that λQD decreases with size because large QDs are usually resistant to changes in their geometrical and electronic structures.In Fig. 4, there are 178 and 154 states between the LUMO and the CBM in the pure and Mn-doped complexes, respectively. To evaluate the coupling constant (Vci) of the LUMO for all these states, external electric fields are applied to find their anti-crossing gaps, which are twicethat the of corresponding Vci. Driven by the applied field, both the conduction band states of TiO2 and LUMO of QD shift upward, but their energy difference decreases continuously until they reach their anti-crossing gap. After that, the LUMO of QD becomes the CBM of the complex, and the states of TiO2 stay in the conduction band if the field strength (F) increases further. Therefore, an appropriate field strength is required to address the point where the anti-crossing gap appears. The field strength can be estimated using
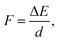 | (11) |
Starting from the estimated F, a number of field strengths are applied on the system to look for the anti-crossing point. Taking the CBM of TiO2 shown in Fig. 4 as an instance, Fig. 5 shows schematically its coupling process with the LUMO of QD. The wave function of LUMO is initially localized at the QD and that of CBM is localized in the TiO2 substrate. In order to make them come closer, an electric field from the substrate to the QD is applied. The two energy levels get closer with increasing field strength, accompanied by the overlap between their wave functions. The coupling reaches a maximum, while the minimum energy gap is obtained at the anti-crossing point. After that, these two states become far away from each other and the characters of the ECBM and ELUMO state are switched. The coupling constant Vc1 between ECBM and ELUMO is then obtained as half of the anti-crossing energy gap. For the first state of the conduction band, its Vc1 is found to be about 0.13 and 5.90 meV for the pure and Mn-doped complexes, respectively.
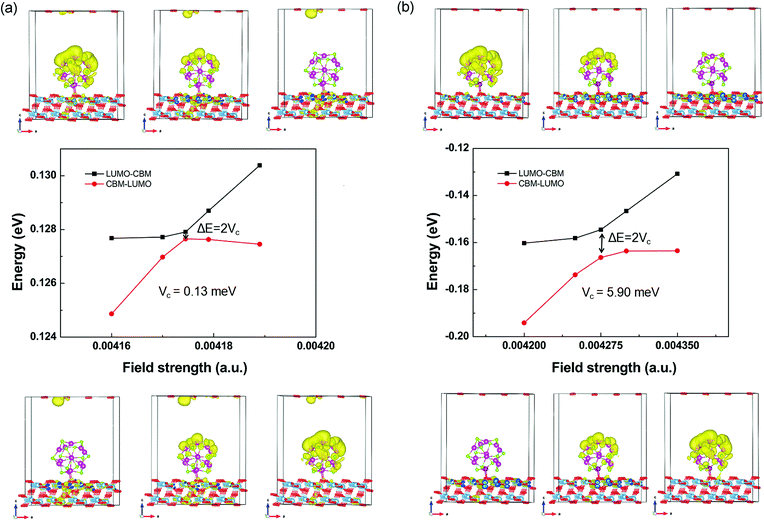 | ||
| Fig. 5 The field-driven coupling process of ECBM and ELUMO in (CdSe)13@TiO2 (a) and Cd12MnSe13@TiO2 (b). | ||
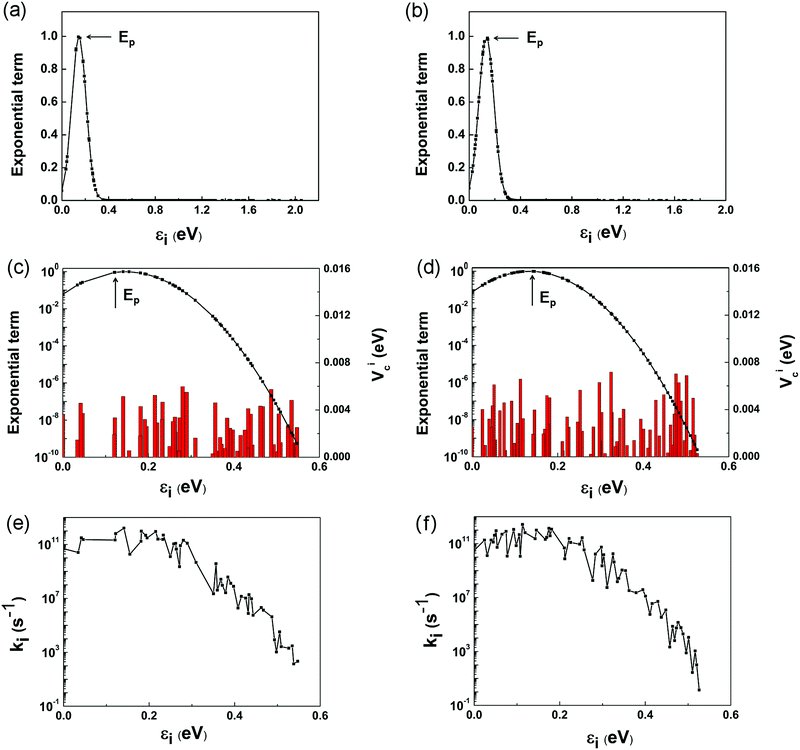
However, it is a computationally demanding job to complete the calculations for the coupling items of all the 179 and 155 states in the two complexes. It is straightforward to select some of the states that dominate the electron transfer rate using eqn (1) and (6). Fig. 6a and b depicts the variation of exponential term exp[−(ΔG + λ)2/4λkBT] with the energy gap between the LUMO and i-th conduction band state of TiO2. For ease of presentation, we define
| εi = ELUMO − Ei. | (12) |
Upon obtaining Ei, ELUMO, λ, and Vci, the electron injection rate kinj is evaluated using
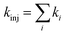 | (13) |
The individual contributions, ki, of the selected channels are shown in Fig. 6e and f. It is interesting to note that ki exhibits roughly similar variations to Vci shown in Fig. 6c and d, which validates our above assumption that kinj can be computed by considering only the channels closer to the Ep point. The points to the left of Ep, εi < 2λQD, are termed as normal Marcus region, while those at the right, εi > 2λQD, as the inverted Marcus region.79ki increases with εi in the normal Marcus region, but decreases in the inverted Marcus region. In both regions, εi alters the Gibbs energy significantly, making ki vary exponentially. As a result, the channels distant from Ep have little influence on kinj, which are reasonably excluded from above computations.
According to Marcus theory, kinj is governed by four factors: coupling constant Vci, reorganization energy λ, energy gap ΔEinj, and available electron transfer channels. Among them, the λ values for these two complexes have similar magnitudes. By intuition, a larger ΔEinj is usually accompanied by more available electron transfer channels, which favors electron injection from QD to TiO2. However, the real scenarios are quite complex. The channels make different contributions to kinj, depending on their gaps from the Ep point. It is only possible for the points around Ep to dominate kinj. Although ΔEinj is narrower (1.73 vs. 2.05 eV), and the number of channels is smaller (155 vs. 179) for the Mn-doped complex, the dominant channels around the Ep point are larger in number than those of the pure complex. Among these dominant channels, Vci takes further effect, which is generally larger in the doped complex. Therefore, the large number of dominant electron-transfer channels and the enhanced Mn–O coupling are the two main reasons for the large kinj in the Mn-doped structure.
It is worth mentioning that the maximum ki appears in the vicinity of the LUMO of QD, and the range of the vicinity depends on the reorganization energy of QD. The electronic structure of QD is size- and structure-dependent. Reorganization energy tends to decrease with size, and ki is mostly determined by the LUMO for large-sized QD. The LUMO shifts from size to size, and varies with the structure. It suggests one way to promote kinj by modulating the QD size and structure, making its LUMO approach the point with the denser density of states. The oxide semiconductor substrates like TiO2 provide abundant electronic structures in their conductive bands, making it possible to find an optimal coupling between the LUMO of QDs and the DOS of the oxides that favors large electron injection rates. One may also note that our calculations are in good agreement in the relative variation with the experiments, but it still does not mean that the adopted models and computations are perfect. In fact, several approximations were applied in the calculations. In addition to those approximations in the charge transfer model in Marcus theory, computations on reorganization energy (λ), coupling constant (Vc), and band structure also depend on the computational models, functionals, and norm-conserving pseudopotentials. Finally, the electron injection is only one of the energy conversion processes in QDSSCs. Other processes, such as electron–hole recombination, also have a considerable effect on the cell performances, which are not studied in the present work.
4. Conclusion
First-principles calculations on the electron injection processes of the pure and Mn-doped QDSSCs are carried out within the frame of Marcus theory, using the TiO2 supported core–shell (CdSe)13 clusters as model systems. For the QD part, Mn doping leads to a redshift in optical absorption, making the QD a wider window for light harvesting. Moreover, the doped cluster has a larger interaction energy and greater amount of charge flow when it deposits on the TiO2 surface. Based on their band structures, the electron injection rates of individual transition channels are computed using the definition of Marcus theory. The channels may make different contributions to the total rate (kinj), depending on their transition energies and the degree of electron coupling. The doped complex has a faster electron injection rate than the undoped one, which is in qualitative agreement with recent observations. The promoted rate mainly results from the dense CB states of the substrate around the transition point and enhanced electron coupling in the Mn-doped complex. The transition point usually appears in the vicinity of the LUMO of QDs, and the dominant range of the vicinity depends on the reorganization energy of QD. It suggests one way to promote kinj by modulating the mapping between the energy levels of the QD and the DOS of the semiconductor oxide, which are tunable for the QDs with diverse structures and sizes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for the financial support from the National Natural Science Foundation of China (No. 21773159) and the Scientific Challenge Program (TZ2016001).References
- B. O’Regan and M. Gratzel, Nature, 1991, 353, 737–740 CrossRef.
- M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2013, 117, 3685–3700 CrossRef.
- A. P. Alivisatos, J. Phys. Chem., 1996, 100, 13226–13239 CrossRef.
- V. I. Klimov, J. Phys. Chem. B, 2006, 110, 16827–16845 CrossRef PubMed.
- M. C. Beard, A. G. Midgett, M. C. Hanna, J. M. Luther, B. K. Hughes and A. J. Nozik, Nano Lett., 2010, 10, 3019–3027 CrossRef PubMed.
- A. P. Alivisatos, J. Phys. Chem., 1996, 100, 13226–13239 CrossRef.
- J. M. Azpiroz, I. Infante and F. De Angelis, J. Phys. Chem. C, 2015, 119, 12739–12748 CrossRef.
- W. Bi, Y. Wu, C. Chen, D. Zhou, Z. Song, D. Li, G. Chen, Q. Dai, Y. Zhu and H. Song, ACS Appl. Mater. Interfaces, 2020, 12, 24737–24746 CrossRef PubMed.
- A. Gupta, K. Sahu, M. Dhonde and V. V. S. Murty, Sol. Energy, 2020, 203, 296–303 CrossRef.
- A. R. B. Mohd Yusoff, P. Gao and M. K. Nazeeruddin, Coord. Chem. Rev., 2018, 373, 258–294 CrossRef.
- A. Venkateswararao, J. K. W. Ho, S. K. So, S.-W. Liu and K.-T. Wong, Mater. Sci. Eng., R, 2020, 139, 100517 CrossRef.
- P. Venkatachalam, T. Kalaivani and N. Krishnakumar, Opt. Mater., 2019, 94, 1–8 CrossRef.
- K. Iida and M. Noda, npj Comput. Mater., 2020, 6(5), 1–8 Search PubMed.
- R. Nadler and J. F. Sanz, Theoret. Claim. Acta, 2018, 137, 12 CrossRef.
- T. Debnath and H. N. Ghosh, J. Phys. Chem. C, 2019, 123, 10703–10719 CrossRef.
- S. Lu, S. Peng, Z. Zhang, Y. Deng, T. Qin, J. Huang, F. Ma, J. Hou and G. Cao, Dalton Trans., 2018, 47, 9634–9642 RSC.
- Y.-H. Chiang, K.-Y. Lin, Y.-H. Chen, K. Waki, M. A. Abate, J.-C. Jiang and J.-Y. Chang, J. Mater. Chem. A, 2018, 6, 9629–9641 RSC.
- U. Poudyal, F. S. Maloney, K. Sapkota and W. Wang, Nanotechnology, 2017, 28, 415401 CrossRef PubMed.
- J. J. Goings, P. J. Lestrange and X. Li, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1341 Search PubMed.
- J. M. Azpiroz, J. M. Ugalde, L. Etgar, I. Infante and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 6076–6086 RSC.
- G. Rimal, A. K. Pimachev, A. J. Yost, U. Poudyal, S. Maloney, W. Wang, T. Chien, Y. Dahnovsky and J. Tang, Appl. Phys. Lett., 2016, 109, 103901 CrossRef.
- Z. Ning, H. Tian, C. Yuan, Y. Fu, H. Qin, L. Sun and H. Agren, Chem. Commun., 2011, 47, 1536–1538 RSC.
- M. A. Abate and J.-Y. Chang, Sol. Energy Mater. Sol. Cells, 2018, 182, 37–44 CrossRef.
- W.-L. Ding, X.-L. Peng, Z.-Z. Sun and Z.-S. Li, J. Mater. Chem. A, 2017, 5, 14319–14330 RSC.
- S. Buhbut, S. Itzhakov, I. Hod, D. Oron and A. Zaban, Nano Lett., 2013, 13, 4456–4461 CrossRef PubMed.
- I. Hod and A. Zaban, Langmuir, 2014, 30, 7264–7273 CrossRef PubMed.
- S. Itzhakov, H. Shen, S. Buhbut, H. Lin and D. Oron, J. Phys. Chem. C, 2013, 117, 22203–22210 CrossRef.
- Z. Ning, C. Yuan, H. Tian, Y. Fu, L. Li, L. Sun and H. Ågren, J. Mater. Chem., 2012, 22, 6032–6037 RSC.
- N. Osada, T. Oshima, S. Kuwahara, T. Toyoda, Q. Shen and K. Katayama, Phys. Chem. Chem. Phys., 2014, 16, 5774–5778 RSC.
- K. E. Roelofs, T. P. Brennan and S. F. Bent, J. Phys. Chem. Lett., 2014, 5, 348–360 CrossRef PubMed.
- J. W. Lee, D. Y. Son, T. K. Ahn, H. W. Shin, I. Y. Kim, S. J. Hwang, M. J. Ko, S. Sul, H. Han and N. G. Park, Sci. Rep., 2013, 3, 1050 CrossRef PubMed.
- F. Khodam, A. R. Amani-Ghadim and S. Aber, Electrochim. Acta, 2019, 308, 25–34 CrossRef.
- P. K. Santra and P. V. Kamat, J. Am. Chem. Soc., 2012, 134, 2508–2511 CrossRef PubMed.
- G. Halder and S. Bhattacharyya, J. Phys. Chem. C, 2015, 119, 13404–13412 CrossRef.
- L. Liu, M. Huang, Z. Lan, J. Wu, G. Shang, G. Liu and J. Lin, J. Mater. Sci.: Mater. Electron., 2013, 25, 754–759 CrossRef.
- S.-K. Kim, C. V. V. M. Gopi, J.-C. Lee and H.-J. Kim, J. Appl. Phys., 2015, 117, 163104 CrossRef.
- X. Lv, C. Hu, J. Shang, P. H. L. Sit, F. L. Y. Lam and W. Y. Teoh, Catal. Today, 2019, 335, 468–476 CrossRef.
- Z. Li, Y. F. Wang, X. W. Wang, Z. Yang and J. H. Zeng, Mater. Lett., 2018, 221, 42–45 CrossRef.
- K. Jung, J. Lee, Y.-M. Kim, Y. Chang Park and M.-J. Lee, Compos. Sci. Technol., 2019, 179, 79–87 CrossRef.
- T. Debnath, P. Maity, S. Maiti and H. N. Ghosh, J. Phys. Chem. Lett., 2014, 5, 2836–2842 CrossRef PubMed.
- J. Wang, Y. Li, Q. Shen, T. Izuishi, Z. Pan, K. Zhao and X. Zhong, J. Mater. Chem. A, 2016, 4, 877–886 RSC.
- B. B. Jin, X. W. Wang, J. L. Cui, L. H. Liu, Y. Cao, T. Chen, D. Wei, Y. F. Wang and J. H. Zeng, Res. Chem. Intermed., 2016, 42, 6255–6263 CrossRef.
- C. Zhang, S. Liu, X. Liu, F. Deng, Y. Xiong and F. C. Tsai, R. Soc. Open Sci., 2018, 5, 171712 CrossRef PubMed.
- A. Pimachev, U. Poudyal, V. Proshchenko, W. Wang and Y. Dahnovsky, Phys. Chem. Chem. Phys., 2016, 18, 26771–26776 RSC.
- J. Hou, H. Zhao, F. Huang, Q. Jing, H. Cao, Q. Wu, S. Peng and G. Cao, J. Power Sources, 2016, 325, 438–445 CrossRef.
- M. Venkata-Haritha, C. V. V. M. Gopi, C. V. Thulasi-Varma, S.-K. Kim and H.-J. Kim, J. Photochem. Photobiol., A, 2016, 315, 34–41 CrossRef.
- J. Sun, X. Zheng, H. He, X. Chen, B. Dong and R. Fei, J. Mol. Struct., 2016, 1114, 123–131 CrossRef.
- J. Yang, R. Fainblat, S. G. Kwon, F. Muckel, J. H. Yu, H. Terlinden, B. H. Kim, D. Iavarone, M. K. Choi, I. Y. Kim, I. Park, H. K. Hong, J. Lee, J. S. Son, Z. Lee, K. Kang, S. J. Hwang, G. Bacher and T. Hyeon, J. Am. Chem. Soc., 2015, 137, 12776–12779 CrossRef PubMed.
- J. M. Azpiroz, J. M. Matxain, I. Infante, X. Lopez and J. M. Ugalde, Phys. Chem. Chem. Phys., 2013, 15, 10996–11005 RSC.
- R. Nadler and J. F. Sanz, Theoret. Claim. Acta, 2013, 132, 1342 CrossRef.
- R. Nadler and J. F. Sanz, J. Phys. Chem. A, 2015, 119, 1218–1227 CrossRef PubMed.
- I. Mora-Seró and J. Bisquert, J. Phys. Chem. Lett., 2010, 1, 3046–3052 CrossRef.
- X. Xin, B. Li, J. Jung, Y. J. Yoon, R. Biswas and Z. Lin, Part. Part. Syst. Charact., 2015, 32, 80–90 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- W. Jia, Z. Cao, L. Wang, J. Fu, X. Chi, W. Gao and L.-W. Wang, Comput. Phys. Commun., 2013, 184, 9–18 CrossRef.
- W. Jia, J. Fu, Z. Cao, L. Wang, X. Chi, W. Gao and L.-W. Wang, J. Comput. Phys., 2013, 251, 102–115 CrossRef.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 2630–2631 CrossRef.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef.
- M. Shim and P. Guyot-Sionnest, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245342 CrossRef.
- L.-W. Wang, M. Califano, A. Zunger and A. Franceschetti, Phys. Rev. Lett., 2003, 91, 056404 CrossRef PubMed.
- K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 29–34 CrossRef PubMed.
- T. Unger, S. Wedler, F.-J. Kahle, U. Scherf, H. Bässler and A. Köhler, J. Phys. Chem. C, 2017, 121, 22739–22752 CrossRef.
- H. Wei, J. W. Luo, S. S. Li and L. W. Wang, J. Am. Chem. Soc., 2016, 138, 8165–8174 CrossRef.
- K. Zheng, K. Žídek, M. Abdellah, P. Chábera, M. S. Abd El-sadek and T. Pullerits, Appl. Phys. Lett., 2013, 102, 163119 CrossRef.
- P. Han, X. Yao, K. Müllen, A. Narita, M. Bonn and E. Cánovas, Nanoscale, 2020, 12, 16046–16052 RSC.
- M. Javad Fahimi, D. Fathi and M. Ansari-Rad, Phys. E, 2015, 73, 148–155 CrossRef.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 120, 7274–7280 CrossRef PubMed.
- Y.-Y. Liu, F. Zheng, X. Jiang, J.-W. Luo, S.-S. Li and L.-W. Wang, Phys. Rev. Appl., 2019, 11, 044058 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B. 01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- V. Coropceanu, D. A. J. Cornil, Y. da, S. Filho, R. S. Olivier and J.-L. Brédas, Chem. Rev., 2007, 107, 926–950 CrossRef PubMed.
- L. G. Gutsev, N. S. Dalal and G. L. Gutsev, Comput. Mater. Sci., 2014, 83, 261–268 CrossRef.
- L. G. Gutsev, N. S. Dalal, G. Maroulis and G. L. Gutsev, Chem. Phys., 2016, 469–470, 105–114 CrossRef.
- L. G. Gutsev, N. S. Dalal and G. L. Gutsev, J. Phys. Chem. C, 2015, 119, 6261–6277 CrossRef.
- N. Du, S. Yu, Y. Xie, Y. Cui, L. Zhang and M. Yang, Eur. Phys. J. B, 2019, 92, 280 CrossRef.
- R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2011, 133, 19240–19249 CrossRef PubMed.
- F. L. Hirshfeld, Theoret. Claim. Acta, 1977, 44, 129–138 CrossRef.
- K. Oshiro, K. Akai and M. Matsuura, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7986–7993 CrossRef.
- J. R. Miller, J. Am. Chem. Soc., 1984, 106, 3047–3049 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03866k |
| This journal is © the Owner Societies 2021 |