Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction-field electrostatics in molecular dynamics simulations: development of a conservative scheme compatible with an atomic cutoff†
Alžbeta
Kubincová
 ,
Sereina
Riniker
,
Sereina
Riniker
 * and
Philippe H.
Hünenberger
*
* and
Philippe H.
Hünenberger
*
Laboratory of Physical Chemistry, ETH Zurich, Vladimir-Prelog-Weg 2, 8093 Zurich, Switzerland. E-mail: sriniker@ethz.ch; phil@igc.phys.chem.ethz.ch
First published on 14th October 2020
Abstract
In molecular dynamics (MD) simulations of condensed-phase systems, straight-cutoff truncation of the non-bonded interactions is well known to cause cutoff noise and serious artifacts in many simulated properties. These effects can be drastically reduced by applying the truncation based on distances between neutral charge groups (CG) rather than between individual atoms (AT). In addition, the mean effect of the omitted electrostatic interactions beyond the cutoff distance can be reintroduced using the reaction-field (RF) method, where the medium outside the cutoff sphere is approximated as a dielectric continuum of permittivity equal to that of the solvent. The RF scheme is generally applied with CG truncation. This is justified for low solvent permittivities, where the RF correction is small and an AT truncation would lead to severe issues, just as in the straight-cutoff case. However, it is less appropriate for solvents with high permittivities, where the RF correction acts as a physically motivated shifting function, and a CG truncation may in turn lead to artifacts and poorer energy conservation. In this study, we assess the impact of truncation artifacts considering the 57 organic liquids which were used in the calibration of the GROMOS-compatible 2016H66 force field. Combinations of shifting or switching schemes with RF-based electrostatic interactions as well as van der Waals (Lennard-Jones) interactions are then introduced to resolve the issues with AT truncation. These shifting and switching schemes have the following properties: (i) they bring the force but not the potential energy to zero at the cutoff; (ii) as a result, they lead to a modification of the interaction that is comparatively small; (iii) they permit to conduct rigorously conservative simulations; (iv) the energies can easily be corrected back to the unmodified form, either on the fly or in a post-processing step. The mathematical formalism of these schemes is presented in detail, and their validation is performed using the 57 organic liquids.
1 Introduction
Classical atomistic simulation and, in particular, molecular dynamics (MD) is nowadays a key component in the investigation of (bio-)chemical processes in the condensed phase.1–6 These simulations rely on a potential-energy function or force field,7–11 constructed as a sum of covalent terms, accounting for interactions between close neighbors within the same molecule, and non-bonded terms, describing the through-space interactions between more remote neighbors as well as between different molecules. The non-bonded interactions include an electrostatic and a van der Waals component, the latter commonly represented using the Lennard-Jones (LJ) function.12 For condensed-phase (bio-)molecular systems, the accuracy of a force field depends most critically on the representation of the dihedral-angle torsions13–16 and of the non-bonded electrostatic and LJ interactions11,17–21 (see Tables 1 and 2 in ref. 20 for an overview of studies investigating the impact of different choices). The calculation of the non-bonded interactions also represents the computational bottleneck in MD simulations, and a trade-off must be established between accuracy and efficiency depending on the system and properties of interest.Restricting the discussion to pairwise-additive force fields and to simulations carried out under periodic boundary conditions, the non-bonded interactions are typically split into short- and long-range components by application of a cutoff distance Rc. A specific calculation scheme is then characterized by the following components:19,20,22–24 (A) the long-range approximation used for the electrostatic and LJ interactions beyond the cutoff; (B) the application modus of the cutoff splitting, i.e. the entities considered for the truncation; (C) the pairlisting procedure for the short-range interaction; (D) the short-range smoothing possibly applied to the interaction; (E) the force-field parameters used for both electrostatic and LJ interactions. These components are discussed in turn below.
For both electrostatic and LJ interactions, there are three main options for the long-range approximation (A), namely: (i) complete omission, leading to a straight-cutoff scheme; (ii) approximation as a continuous medium, leading to a mean-field scheme; (iii) approximation as a periodic medium, leading to a lattice-sum scheme.
For the cutoff distances typically used in simulations (ranging between 0.9 and 1.4 nm), and considering the large magnitude and long-range nature of the electrostatic interactions, abrupt truncation of these interactions in a straight-cutoff approach (Fig. 1a) leads to large errors in many simulated properties.20,25–28 For the LJ interactions, the straight-cutoff scheme is less problematic.29 It mainly causes a cutoff-dependent underestimation (relative to the long-cutoff limit) of the densities, vaporization enthalpies and surface-tension coefficients,21,30,31 due to the neglect of the predominantly dispersive (i.e. attractive) interactions beyond the cutoff. The straight-cutoff approach nevertheless remains the most common scheme for LJ interactions nowadays, as it is consistent with the calibration conditions of many popular force fields. This situation might, however, change in the near future.
In the mean-field approximation, an assumption of homogeneity and isotropy is made for the medium outside the cutoff sphere. The response of this medium is mapped to a constant term added to the system energy and virial, or to a short-range correction added to the pairwise potential energy, force and virial. For the electrostatic interactions, mean-field approaches include in particular the reaction-field (RF),28,32,33 “generalized” reaction-field,34–36 Wolf damping,37 zero multipole,38–42 screening function,43–46 and isotropic periodic sum47–53 methods. For the LJ interactions, available mean-field schemes include the tail-correction1 and LJ isotropic periodic sum47,48,53–55 approaches. Given a sufficiently large cutoff, physically motivated mean-field approximations are appropriate for bulk systems, but may become problematic when the medium outside the cutoff sphere is inhomogeneous and/or anisotropic, e.g. at the surface of a macromolecule or for systems in interfacial/slab geometries.21,56,57 Note that anisotropic mean-field variants have also been proposed for these situations, considering both electrostatic interactions50,57 and LJ interactions.58–67 See also ref. 68 for an alternative route relying on emulating large cutoff distances in mean-field calculations using a lattice-sum scheme.
In the lattice-sum approximation, an assumption of exact periodicity is made for the system simulated under periodic boundary conditions, which is considered to be an infinite pseudo-crystal. By convoluting point charges with a charge-shaping function, the calculation is split into a real- and a reciprocal-space component.69 The range of the former component is made shorter than the cutoff, so that it can be calculated exactly70 (or nearly exactly in the case of a Gaussian charge-shaping function) by pairwise summation. The latter component is long-ranged but periodic and smooth in real-space, so that it converges rapidly in reciprocal-space. For the electrostatic interactions, it can be evaluated either by direct summation over reciprocal-lattice vectors, as in the Ewald71,72 method, or using grid-based fast Fourier transforms, as in the particle–particle–particle–mesh (P3M)73,74 and particle-mesh Ewald (PME)75–78 methods. Both approaches exist as well for the LJ interactions, namely LJ Ewald,30,72,79–82 LJ P3M,83,84 and LJ PME.76,85,86 Note that these lattice-sum LJ schemes may be computationally expensive unless a strict geometric-mean combination rule87 applies to the LJ parameters,30,80 or such a rule is used as an approximation during the calculation.86 The application of a lattice-sum approach is most appropriate for truly periodic systems (crystals, neglecting static and dynamic disorder), but only approximate for inherently non-periodic systems such as liquids and solutions. In practice, for the comparatively short-ranged LJ interactions, lattice-sum and mean-field approximations typically lead to comparably accurate results for bulk systems,21,78 but generally not for interfacial systems, where lattice-sum is to be preferred.30,56,83,85,86,88
Besides reducing the effect of artificial periodicity, there are three additional advantages to the use of mean-field over lattice-sum schemes for both electrostatic and LJ interactions: (i) for large systems, they enable an O(N) scaling of the computational cost, compared to an O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) scaling for FFT-based lattice-sum schemes;74,89 (ii) they enable a pairwise (or groupwise) partitioning of the interaction energy without additional computational cost, whereas such a direct partitioning is not possible in lattice-sum schemes (i.e. it would require additional FFTs69); (iii) for processes involving net-charge changes, the application of lattice-sum schemes is affected by intricate methodological issues.90
N) scaling for FFT-based lattice-sum schemes;74,89 (ii) they enable a pairwise (or groupwise) partitioning of the interaction energy without additional computational cost, whereas such a direct partitioning is not possible in lattice-sum schemes (i.e. it would require additional FFTs69); (iii) for processes involving net-charge changes, the application of lattice-sum schemes is affected by intricate methodological issues.90
A second characteristic of the non-bonded interaction scheme is the application modus (B) of the cutoff splitting, which may be based on distances between: (i) individual atoms, resulting in an atomic (AT) cutoff scheme; (ii) atom groups, resulting in a charge-group (CG) cutoff scheme. Here, charge-groups are small groups of close covalent neighbors within a molecule, for which the partial charges should add up to an integer value. Historically, charge groups truncation was found necessary to permit the simulation of polar liquids using a straight-cutoff scheme for the electrostatic interactions.91–94 In this way, the cutoff noise for Coulombic interactions involving neutral charge groups was reduced from O[Rc−1] for straight-cutoff with AT truncation to O[Rc−3] for straight-cutoff with CG truncation. In addition, the use of a CG-based short-range pairlist95 represented a simple way to reduce memory requirement and computational cost of the pairlist generation. Note, however, that a well-implemented AT scheme relying on a group-based extended pairlist can reach a very comparable level of computational effort and memory usage. In practice, there are several reasons why modern force fields should probably favor AT over CG truncation: (i) if the potential-energy function of a mean-field scheme does not exactly vanish at the cutoff, CG truncation leads to loss of energy conservation and heating,91,92 as well as other artifacts;28,52,96–98 (ii) in the context of lattice-sum and of some mean-field schemes, the short-range potential-energy function actually vanishes at the cutoff, and an AT truncation then becomes the natural choice; (iii) the definition of neutral charge-groups within molecules generally requires charge adjustments that are rather arbitrary as well as difficult to automate in the context of force-field design.99
The third characteristic of the non-bonded interaction scheme concerns the pairlisting procedure (C), which may rely on: (i) a pairwise summation that is exact at each simulation timestep; (ii) a summation dictated by an approximate pairlist. Here, common time-saving techniques include Verlet95 and twin-range100,101 schemes, where the pairlist is only recalculated at periodic intervals. These variants are in principle designed to increase efficiency while negligibly affecting the simulated properties. However, a number of cases have been reported where the implementation of the method and/or the associated parameters may cause serious artifacts in simulations.21,102,103
The fourth important aspect concerns the possible short-range smoothing of the interaction22,23,96 (D), where the options are: (i) no smoothing applied; (ii) application of a shifting (SH) function; (iii) application of a switching (SW) function. The SH approach22,23,104–109 refers to the modification of the short-range interaction over the entire range from 0 to Rc, so as to enforce specific continuity conditions at Rc (e.g. vanishing potential-energy function along with a number of its derivatives). The SW approach104,107,108,110,111 refers to a similar modification applied only over a limited range [Rc − δ, Rc] with 0 < δ < Rc, and enforcing continuity conditions at Rc − δ as well. Switching has the advantage over shifting that the very-short-range interactions (below Rc − δ) remain unmodified, but the drawback that it may induce large forces in the range [Rc − δ, Rc] if δ is chosen small. Historically, SH and SW schemes (with either CG or AT truncation) were applied for the electrostatic interactions to reduce noise and artifacts introduced by straight-cutoff truncation (Fig. 1b). However, the use of such ad hoc schemes without physical motivation may cause major disruptions in the simulated structural, thermodynamic and dynamical properties.96,108,111–115 The SW and SH approaches have also been applied to electrostatic interactions in complement to mean-field schemes, for example in the switched RF approach,116 or in variants of the Wolf-damping method.114,117–122 In view of the small LJ forces at typical cutoff distances, the application of SH or SW schemes to the LJ interactions has been less frequently considered,109,111,123 although it may still be useful if one wishes to enforce a strict energy conservation in simulations. Note that SH and SW schemes are irrelevant in the lattice-sum case, where the cutoff is only a numerical parameter and the level of noise is (nearly) exclusively controlled by the accuracy of the reciprocal-space evaluation.
Finally, the choice of appropriate force-field parameters (E) and the options selected for points A–D above (also including the cutoff distance Rc itself, and the possible use of specific LJ combination rules) are inter-dependent. This is because force-field parameters are effective quantities, which partly compensate for approximations made in the functional-form representation. As a result, a force field is only expected to provide accurate results under simulation conditions that are close to the ones selected during its calibration. For example, the use of a mean-field or lattice-sum long-range component is not recommended for a force field that was calibrated with straight-cutoff, both in the context of LJ interactions21,31,55,85,124–126 and electrostatic interactions.21,127,128 Although the cutoff-dependence of the simulated properties may be reduced, the deviations from experiment are likely to increase, unless an appropriate reparametrization is performed.
The present work focuses on the implementation of one of the best established mean-field approaches for electrostatic interactions, namely the RF method.28,32,33 In the context of molecular liquids, this scheme is underpinned by a particularly sound theoretical basis, as it rests on the Onsager model for a dipole at the center of a cavity immersed in a dielectric medium.129 It is also the standard electrostatic scheme compatible with the GROMOS force field.130–132 The RF scheme depends on the permittivity εRF of the dielectric medium outside the cutoff sphere, which is generally taken to be that of the solvent (or pure liquid) considered. In its usual implementation (see eqn (1) in the Theory section), the potential energy vanishes at the cutoff, but this is generally not the case for the force (Fig. 1c, green curve with non-zero derivative at Rc). In the limit εRF → 1 (vacuum), the RF scheme becomes like a straight-cutoff scheme (Fig. 1a), except for the introduction of a constant offset in −Rc−1 that brings the function to zero at Rc. In the limit εRF → ∞ (conducting), the RF scheme becomes similar to a physically motivated SH scheme (Fig. 1b, orange curve), in which the potential energy and its first derivative vanish at Rc. The RF scheme is generally applied with CG truncation, which is justified for low solvent permittivities. In this case, the RF correction is small and an AT truncation would lead to severe issues, just as in the straight-cutoff case (e.g. noise in O[Rc−1] rather than O[Rc−3] for pairs of neutral charge groups). However, a number of studies28,98,101,133,134 have suggested that the use of a RF/AT scheme gives similar or improved results compared to the RF/CG scheme for aqueous systems.
The goal of this study is to assess the influence of the cutoff treatment on selected properties of pure liquids, as well as to eliminate the need for charge groups by introducing SH and SW schemes in combination with an AT truncation of the RF-based electrostatic interactions (and of the LJ interactions), which are appropriate for low as well as high values of εRF. This work follows analogous developments in the context of Wolf damping119,120 and isotropic periodic sum51 methods. The proposed RF(+LJ)/AT/SH and RF(+LJ)/AT/SW schemes have the following properties: (i) they bring the force but not the potential energy to zero at the cutoff; (ii) as a result, they lead to a modification of the interaction that is comparatively small; (iii) they permit rigorously conservative simulations; (iv) the energies can easily be corrected back to the unmodified form, either on the fly or in a post-processing step. The main idea is to shift/switch the force to zero at Rc, and let the potential energy level-off to a constant (Fig. 1d). This results in an energy contribution involving all atom pairs at a distance larger than Rc. However, this term is easy to calculate and induces neither a force nor a virial contribution. The benefit of this approach is that the continuity of the potential energy as well as that of its first (and second) derivative at Rc can be achieved (conservative scheme), but with a limited perturbation of the original RF forces compared to a corresponding shifting/switching of the potential energy (Fig. 1b).
In this article, the mathematical formalism of these RF(+LJ)/AT/SH and RF(+LJ)/AT/SW schemes is presented in detail. This is followed by their validation in terms of the densities and vaporization enthalpies of the 57 organic liquids considered in the calibration of the GROMOS-compatible 2016H66 force field.135 The effects of different schemes on the radial distribution functions (RDFs) and dipole–dipole orientation correlation functions (DOCs) of some model liquids are also analyzed.
2 Theory
2.1 RF-based electrostatic interactions with AT or CG cutoff schemes
The Coulomb plus RF potential energy vRF,ij between two atoms i and j with charges qi and qj at a distance rij = |rj − ri| is commonly implemented in the form28,32,33,130–132 | (1) |
 | ||
| Fig. 2 Pairwise Coulomb plus RF potential energy and interatomic force close to the cutoff distance. The curves correspond to a cutoff distance Rc = 1.4 nm and atomic charges of the same sign. (a) The potential energy vRF,ij of eqn (1) as a function of the interatomic distance rij. (b) The force fRF,ij as a function of rij, which is the negative derivative of the potential energy and corresponds to the force exerted by atom i on atom j projected along the interatomic vector rij = rj − ri. | ||
In the limit εRF → ∞ (e.g. orange curve for εRF = 80, representative for water), the interatomic force fRF,ij nearly vanishes at the cutoff distance Rc. Thus, in this high-permittivity regime, the RF interaction plays the role of a nearly perfect shifting function, a favorable situation to avoid cutoff noise and pair-distribution artifacts. However, in this regime, the potential energy rises again shortly beyond Rc for charges of the same sign, i.e. the interatomic force becomes unphysically attractive (or repulsive for charges of opposite signs). Such a situation may occur when using CG truncation,28 because interacting CG pairs that have their centers close to Rc may involve some interatomic distances that actually exceed Rc. In contrast, this situation is excluded with AT truncation.
In the limit εRF → 1 (e.g. green curve for εRF = 2, representative for a non-polar organic solvent), the RF interaction becomes progressively closer to a Coulomb interaction with straight-cutoff truncation, i.e. the RF screening no longer acts like a shifting function. In this low-permittivity regime, an AT truncation scheme is expected to induce serious artifacts in the simulated properties.28 These can be largely remedied by a CG-based truncation.
The consequences of these features on simulated pair-distribution functions are illustrated in Fig. 3 for four model liquids, in the form of RDFs calculated using either a RF/CG or a RF/AT scheme for the electrostatic interactions. The results obtained using a lattice-sum scheme are shown for comparison. In addition, the corresponding DOCs and distance-dependent Kirkwood factors G(r) are depicted in Fig. 4 for chloroform and water.
 | ||
| Fig. 3 Radial distribution functions (RDFs) for four model liquids: modified GROMOS CCl4 models136 with a charge of +0.4 e (a) or +0.86 e (b) introduced on the central carbon atom (and neutralized by negative charges on the chlorine atoms), the GROMOS CHCl3 model137 (c), and the SPC water model93 (d). The RDFs g(r) are calculated for the carbon (a–c) or the oxygen (d) atoms. The electrostatic interactions are calculated using RF/CG (blue lines) or RF/AT (red lines), in both cases using a cutoff distance Rc of 1.4 nm (vertical dashed line), as well as with lattice-sum (thick gray lines). For the LJ interactions, the same scheme (i.e. CG or AT) is used as for the electrostatic interactions. The values of εRF are 2.24 for CCl4, 4.81 for CHCl3 and 61 for SPC water. | ||
 | ||
| Fig. 4 Dipole–dipole orientation correlation functions (DOCs) and distance-dependent Kirkwood factors G(r) for (a) CHCl3 (GROMOS CHCl3 model137), and for (b) water (SPC water model93). The DOCs c(r) correspond to the average of the angle-cosine between the dipole-moment vectors of the two molecules, binned as a function of distance based on the carbon (a) or the oxygen (b) atoms. The G(r) function is defined by eqn (23). The electrostatic interactions are calculated using RF/CG (blue lines) or RF/AT (red lines), in both cases using a cutoff distance Rc of 1.4 nm (vertical dashed line), as well as with lattice-sum (thick gray lines). The same settings were used as for Fig. 3. | ||
For the three low-permittivity systems (Fig. 3a–c), the use of AT truncation leads to an artificial peak in the RDF at Rc, particularly pronounced for the CCl4 model with high partial charges. The reason is that molecule pairs at a distance close to Rc can take advantage of a strong potential-energy decrease when they adopt relative positions and orientations that maximize the number of oppositely-charged atom pairs just inside the cutoff and of like-charged atom pairs just outside the cutoff. In contrast, the RF/CG curves are smooth at Rc and very close to the reference lattice-sum curves.
In the high-permittivity case of water (Fig. 3d), the AT scheme results in a small wiggle in the RDF around Rc, which is essentially absent for the RF/CG scheme. However, an opposite difference is observed for the DOC of water (Fig. 4b), where the RF/CG scheme shows negative correlations below Rc and positive ones above, which is also reflected by a dip in the corresponding G(r). In contrast, the RF/AT curve is very close to the reference lattice-sum one. This effect in the RF/CG case is probably related to the slight like-charge attraction between the hydrogen atoms beyond Rc that can occur for molecule pairs in specific orientations with their charge-group centers (oxygen atoms) just below Rc. Note that these observations on the differences between RF/CG and RF/AT for water were already reported previously in ref. 28 (see Fig. 2–4 therein; note that the labels for the CG/1 and AT/2 curves are mistakenly inverted in Fig. 2a; see also ref. 101). For CHCl3, the effect on the DOC is very small (Fig. 4a), likely due to the much smaller partial charges and dipole moment. The Kirkwood factors with lattice-sum and RF/CG are in good agreement up to Rc and diverge afterwards. The use of an AT cutoff causes a slightly stronger alignment of the dipoles close to the cutoff distance compared to the lattice-sum reference.
2.2 Objective of the modification schemes
The observations of the previous section suggest that when applying RF-based electrostatic interactions in their usual implementation,28,32,33,130–132 a CG truncation is to be preferred in the low-permittivity limit, whereas an AT truncation is more adequate for solvents with high permittivity. This is inelegant as well as problematic for intermediate or mixed situations. To address this issue, we introduce here a scheme, which combines RF-based electrostatic interactions with AT truncation, and is designed to fulfill the following requirements (Fig. 1d): (i) the pairwise potential-energy function is unaltered at zero interatomic distance (in a limiting sense); (ii) it is continuous at the cutoff; (iii) it is constant (generally non-zero) at and beyond the cutoff; (iv) its first derivative vanishes at the cutoff (i.e. zero force at Rc); (v) its second derivative also vanishes at the cutoff (i.e. continuous force at Rc). A similar change is also explored for the LJ interactions, so as to achieve non-bonded interaction schemes ensuring a rigorous conservation of the total energy.The proposed AT schemes will be further referred to as modified schemes (mod), to distinguish them from the standard (std) implementation. The modified schemes involve either an additive polynomial shifting function or an additive spline switching function that levels off the force but no the potential energy to zero at Rc. In order to be comparable with the standard energies, a correction can be added to the modified energies, either on the fly or as a post-processing step. These recalculated energies will be referred to as corrected (cor) energies.
2.3 Standard and modified schemes
For the ease of notation, the subscript ω is introduced here to specify the interaction type, namely “RF” for the Coulomb plus reaction-field term, “LJ6” for the dispersive C6 term of the Lennard-Jones interactions, and “LJ12” for the corresponding repulsive C12 term. Defining pairwise topology-dependent prefactors as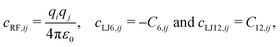 | (2) |
 | (3) |
 | (4) |
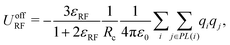 | (5) |
 | (6) |
Turning to the modified schemes, it is convenient to introduce a superscript Ω standing for the modification type, namely “SH” for shifting or “SW” for switching. For these modified schemes, eqn (3) is altered to
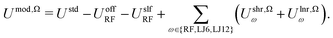 | (7) |
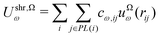 | (8) |
 | (9) |
| ũΩω(r) = uω(r) + uΩω(r) | (10) |
Since the summation in eqn (9) involves a mere constant, this equation can be converted to
 | (11) |
Following the objectives of Section 2.2, the conditions to impose on uΩω(r) are
 | (12) |
| ũΩω(0) = uω(0) i.e. uΩω(0) = 0. | (13) |
In the switching case, conditions similar to eqn (12) are also imposed to enforce corresponding continuity constraints at the onset of the switching range.
The forms of selected functions uΩω(r) satisfying these conditions are detailed in the two following sections for the shifting (Ω = SH, eqn (14)) and switching (Ω = SW, eqn (15)) schemes. Note that the indicated equations only specify these functions in the relevant range up to Rc, as the contribution of ũΩω(r) beyond Rc is already encompassed in the long-range term Ulnr,Ωω. It should also be stressed that the retained functional forms are dictated by considerations related to the above continuity conditions and to computational efficiency, but they are by no means unique.
2.4 Shifting function
The SH scheme relies on a polynomial of the form| uSHω(r) = aω,mrmω + aω,nrnω with 0 < mω < nω, | (14) |
The exponents mω and nω are related to the distance scale of the modification. When the exponents are high, most of the damping of the force towards zero is operated over a small distance range below the cutoff, i.e. the decrease of the force becomes an increasingly close approximation to a step function. When the exponents are low, the force is shifted more progressively towards zero over the entire distance range from 0 to Rc. The choice of even integer exponents is also advantageous in terms of computational efficiency. In this work, only pairs of even integers with nω = mω + 2 are considered. In addition, the condition mω ≥ 4 is imposed, because the choice mRF = 2 for the RF interaction would involve altering the quadratic term of the potential energy, i.e. changing the effective permittivity εRF. This option is nevertheless briefly discussed in the ESI.†
As an illustration, the curves for the modified potential energy cRF,ijũSHRF and the associated interatomic force cRF,ij![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) SHRF are displayed in Fig. 5a and c for two variants with mRF–nRF combinations of 4–6 (purple) and 12–14 (orange), respectively. A more detailed analysis of the amount of change in the influence function introduced by different exponent combinations in the context of RF-based electrostatic interactions is provided in Appendix B. This analysis indicates that mω, the smaller of the two exponents, is the one that predominantly determines the shape of the modified influence function.
SHRF are displayed in Fig. 5a and c for two variants with mRF–nRF combinations of 4–6 (purple) and 12–14 (orange), respectively. A more detailed analysis of the amount of change in the influence function introduced by different exponent combinations in the context of RF-based electrostatic interactions is provided in Appendix B. This analysis indicates that mω, the smaller of the two exponents, is the one that predominantly determines the shape of the modified influence function.
 | ||
Fig. 5 Influence of the SH (left) and SW (right) modifications on the pairwise Coulomb plus RF potential energy cRF,ijũΩRF (top), interatomic force cRF,ij![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) ΩRF (middle), and radial distribution function RDF (bottom) of a model liquid. For the SH scheme (a, c and e), variants with values 4–6 (purple) or 12–14 (orange) for mRF and nRF are shown. For the SW scheme (b, d and f), variants with values 0.78 (purple) or 0.36 (orange) for δsclRF (corresponding to δRF of 0.7 and 0.4 nm, respectively) are shown. Atomic charges of the same sign are considered, i.e. cRF,ij > 0. The cutoff Rc = 1.4 nm is marked (vertical black dashed line) as well as the position of Rc–δRF for the SW scheme (vertical orange and purple dotted lines), and the RF permittivity is εRF = 2.24. The RDFs g(r) (e and f) are calculated for the carbon atoms of the modified GROMOS CCl4 model136 with a charge of +0.86 e on the central carbon atom (neutralized by negative charges on the chlorine atoms). The RDFs corresponding to simulations with standard RF/CG (cyan) or RF/AT (red) are shown for comparison. ΩRF (middle), and radial distribution function RDF (bottom) of a model liquid. For the SH scheme (a, c and e), variants with values 4–6 (purple) or 12–14 (orange) for mRF and nRF are shown. For the SW scheme (b, d and f), variants with values 0.78 (purple) or 0.36 (orange) for δsclRF (corresponding to δRF of 0.7 and 0.4 nm, respectively) are shown. Atomic charges of the same sign are considered, i.e. cRF,ij > 0. The cutoff Rc = 1.4 nm is marked (vertical black dashed line) as well as the position of Rc–δRF for the SW scheme (vertical orange and purple dotted lines), and the RF permittivity is εRF = 2.24. The RDFs g(r) (e and f) are calculated for the carbon atoms of the modified GROMOS CCl4 model136 with a charge of +0.86 e on the central carbon atom (neutralized by negative charges on the chlorine atoms). The RDFs corresponding to simulations with standard RF/CG (cyan) or RF/AT (red) are shown for comparison. | ||
2.5 Switching function
The SW scheme relies on a fourth-order polynomial operating over the distance range from Rc–δω to Rc, namely | (15) |
Similarly to the exponents mω and nω of the SH scheme, the parameter δω specifies the distance scale of the SW scheme. In the limit of a small δω, the decrease of the force becomes an increasingly close approximation to a step function. When δω is chosen larger, the force is shifted more progressively towards zero over a larger distance interval below Rc. However, for values of the parameter δω higher than a given threshold δmaxω, the modified influence function ũSWω presents a spurious minimum in the range [Rc–δω, Rc]. This situation should be avoided as it may lead to artifacts. For this reason, it is preferable to define the switching range by means of a scaled parameter δsclω in the interval (0,1], as
 | (16) |
As an illustration, the curves for the modified potential energy cRF,ijũSWRF and the associated interatomic force cRF,ij![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) SWRF are displayed in Fig. 5b and d for two variants with δsclRF = 0.78 (purple) and 0.36 (orange), respectively. Comparing to the SH scheme in Fig. 5a and c, one sees that for a sensible range of exponents mω and nω in SH or distance parameters δsclω in SW, both modification schemes can yield analogous influence functions.
SWRF are displayed in Fig. 5b and d for two variants with δsclRF = 0.78 (purple) and 0.36 (orange), respectively. Comparing to the SH scheme in Fig. 5a and c, one sees that for a sensible range of exponents mω and nω in SH or distance parameters δsclω in SW, both modification schemes can yield analogous influence functions.
2.6 Corrected energies
The potential energy Umod,Ω in eqn (7), with Ω = SH or SW, is the one relevant for the dynamics of the system when using the corresponding modification scheme. Since the schemes are applied with AT truncation and the potential energy is continuous (up to its second derivative) at the cutoff, strict energy conservation is ensured. However, the potential energy Ustd of the standard scheme in eqn (3) is physically more relevant, because: (i) it excludes the artificial interactions Ulnr,Ωω of eqn (9) beyond Rc; (ii) it excludes the ad hoc interaction modification Ushr,Ωω of eqn (8) within the cutoff sphere; (iii) it is the one compatible with the parametrization conditions of the force field. For this reason, it is useful to calculate not only the modified but also the corrected (to standard) non-bonded potential energy while performing the dynamics or afterwards. This can be done straightforwardly using eqn (7) rewritten for Ucor as | (17) |
Note that neither the standard nor the corrected energies encompass a long-range component for the LJ interactions, e.g. in the sense of a tail-correction,1 in agreement with the calibration conditions for the GROMOS force fields.21,135 Such a tail-correction could (and probably should) be added in the future, but this would require a consistent force-field reparametrization.
3 Computational procedures
3.1 Simulation Details
The proposed modification schemes were implemented into the GROMOS program.132 They were tested using a set of 57 small molecules, previously employed in the calibration of the GROMOS-compatible 2016H66 force field.135 The same force-field parameters were used in the present simulations. The list of compounds, along with key experimental properties, were taken from ref. 135 and are provided in Table S1 of the ESI.† A subset of 11 molecules (marked in the table) was selected as the calibration set, which was used to investigate the effect of parameter variations in the modification schemes. The full set of 57 molecules, referred to as the validation set, was then used to further test the schemes with appropriate parameter choices.The calculations for each compound included 1 ns simulations in the liquid phase and 10 ns simulations in the gas phase. In both cases, the timestep was set to 2 fs, all bond lengths were constrained using SHAKE140 with a relative geometric tolerance of 10−4, and the coordinates and energies were written to file every 1 ps.
The liquid-phase simulations were carried out using MD for a cubic box of 512 molecules under periodic boundary conditions in the isothermal–isobaric ensemble. The average temperature and pressure were maintained close to 298.15 K (unless indicated otherwise in Table S1 of the ESI†) and 1 bar using a Berendsen thermo- and barostat,141 with coupling times of 0.1 and 0.5 ps, respectively, and a compressibility of 4.575 × 10−4 kJ−1 mol nm3 for the barostat. The center-of-mass translational motion was removed every 2 ps. The simulations were started from pre-equilibrated configurations, and an additional 0.1 ns equilibration was performed for every new parameter setting. The gas-phase simulations were carried out using stochastic dynamics (SD) for a single isolated molecule with a friction coefficient of 91 ps−1. The reference temperature was identical to that in the corresponding liquid simulation.
All simulations presented in the main article relied on a cutoff distance Rc = 1.4 nm, a pairlist updated every timestep, the inclusion of long-range electrostatic interactions, and the omission of the long-range LJ component. These settings are compatible with the parametrization conditions of the 2016H66 force field.21,135 The results of analogous simulations with Rc = 1.2 nm instead are provided in the ESI.†
Five schemes were considered for the long-range electrostatic interactions in the liquid-phase simulations: (i) a lattice-sum scheme (LS); (ii) the standard RF scheme with CG cutoff (RF/CG); (iii) the standard RF scheme with AT cutoff (RF/AT); (iv) SH-modified RF schemes with AT cutoff (RF/AT/SH); (v) SW-modified RF schemes with AT cutoff (RF/AT/SW). The lattice-sum scheme relied on the P3M method,73,74 using a Gaussian charge-shaping function of width parameter 0.4 nm−1 and a grid of 64 × 64 × 64 points. For the RF schemes, the permittivity εRF was set to the experimental value for the compound (see Table S1 of the ESI†). For the LJ interactions in the first series of simulations, straight-cutoff truncation was used with a CG truncation when using RF/CG, or an AT truncation in all other cases.
After determining appropriate parameter choices for the SH and SW schemes applied to the electrostatic interactions, a second series of calculations considered the possibility of also modifying the LJ interactions with a SH or SW scheme. The additional schemes are labeled RF+LJ/AT/SH and RF+LJ/AT/SW. They rely on the same parameter choices for the RF modifications, selected as appropriate in the preceding phase.
The gas-phase simulations always relied on the same electrostatic and LJ scheme as used in the corresponding liquid-phase simulation (including the possible application of the SH or SW modifications), with only two differences. The RF permittivity εRF was set to 1, and the lattice-sum case was mapped to exactly Coulombic interactions using straight-cutoff with AT truncation. Note that for the small molecules considered here, intramolecular interatomic distances larger than Rc never occur in the simulations.
In addition, simulations for four model liquids were performed to assess the magnitude of possible cutoff artifacts (shown in Fig. 3, 4, 5, 8 and 9). The corresponding topologies are based on the standard GROMOS models for chloroform137 and carbon tetrachloride,136 as well as the simple-point-charge (SPC) water model.93 For CCl4, the original model does not involve partial charges. Thus, charges of +0.4 e or +0.86e were introduced on the carbon atom (and neutralized by negative charges on the chlorine atoms) to test the effect of a molecular quadrupole. These simulations were carried out in the canonical ensemble at 298.15 K and densities set close to the corresponding experimental values. For water, they involved 2200 molecules instead of 512. For chloroform and water, the simulations lasted 10 ns to obtain converged DOCs and Kirkwood factors. For the other two solvents 1 ns simulations were performed. Besides this, the same parameters were used as for the other liquid simulations.
3.2 Analyses
The analysis of the trajectories was performed using the GROMOS++ analysis programs,142 and involved the calculation of the liquid densities ρliq, vaporization enthalpies ΔHvap, static relative dielectric permittivities ε, and self-diffusion coefficients D. For the four model liquids, RDFs g(r), DOCs c(r), and Kirkwood factor G(r) were calculated.The liquid density ρliq as well as the total potential energies Uliq and Ugas were extracted from the trajectories using the GROMOS++ ene_ana program. The potential energies were corrected according to eqn (17), and the result used to calculate the vaporization enthalpy as
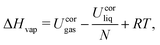 | (18) |
The static relative dielectric permittivities ε were determined using the applied electric-field method.143,144 To this purpose, an external electric field Eextz ranging between 0.01 and 1 e nm−2 was applied along the z-direction of the computational box. For the lattice-sum calculations, the local field determining the forces on the individual charges is equal to Eextz. However, for the RF/CG calculations, this local field must be reduced by a factor 3εRF/(1 + 2εRF) (see eqn (14) in ref. 143). This arises as a consequence of the non-Coulombic nature of the integrated dipole–dipole interaction tensor. For RF/AT, it turns out that the integration of this tensor leads to a result that is very close to the lattice-sum rather than the RF/CG one (see Appendix B in ref. 28). Consequently, for RF/AT, the local field determining the forces on the individual charges is set equal to Eextz, as in the lattice-sum case. The resulting average box dipole moment 〈Mz〉 in the z-direction was evaluated from 0.5 ns simulations at each selected field strength. The permittivity ε was then calculated using the GROMOS++ program eps_field according to
 | (19) |
The self-diffusion coefficients D were calculated based on the liquid simulations using the GROMOS++ program diffus, which relies on the Einstein relation145,146
 | (20) |
The RDFs g(r) were calculated with the GROMOS++ program rdf according to
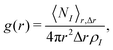 | (21) |
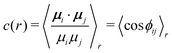 | (22) |
 | (23) |
4 Results and discussion
4.1 Modification schemes for RF-based electrostatic interactions
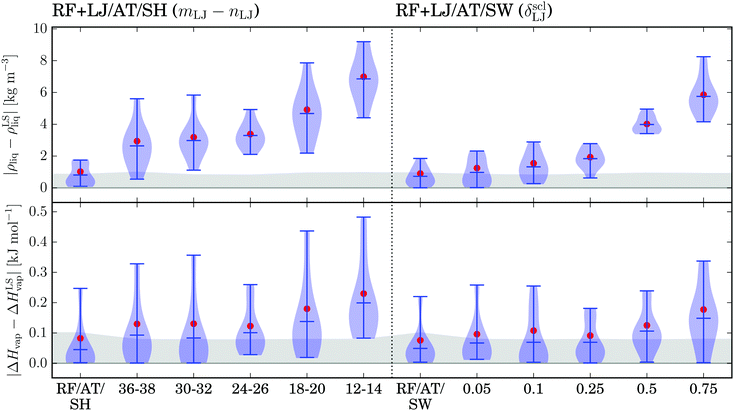
The deviations in the simulated ρliq and ΔHvap values over the calibration set relative to the lattice-sum reference are illustrated in Fig. 6 for the RF/CG, RF/AT, RF/AT/SH and RF/AT/SW schemes with a cutoff distance Rc = 1.4 nm. A number of different parameter combinations are compared for the SH and SW schemes applied to the RF-based electrostatic interactions. The corresponding results for Rc = 1.2 nm are shown in Fig. S1 of the ESI.† For the SH scheme, the lowest exponents considered are mRF = 4 and nRF = 6 (4–6 SH scheme), because the choice mRF = 2 would correspond to changing the effective permittivity εRF. The choice of the highest exponent combination (12–14 SH scheme) is based on the onset of significant deviations from the lattice-sum curves in the RDFs of the model liquids (Fig. 5e and f). For the SW scheme, the entire accessible range (0,1] in terms of the scaled switching distance δsclRF is considered (i.e. 0.05 to 1.0).As can be seen in Fig. 6, the 4–6 SH and the 0.75 SW schemes appear to reproduce the lattice-sum results most accurately with Rc = 1.4 nm. The same holds when considering a 1.2 nm cutoff instead (see Fig. S1 of the ESI†). These specific parameter combinations are thus retained as the most appropriate for the implementation of smooth RF/AT/SH and RF/AT/SW schemes. For these specific schemes, most of the deviations in ρliq and ΔHvap relative to lattice-sum are within one standard deviation of the purely statistical error affecting the calculated properties. Since the smoothing corrects for discontinuities at the cutoff but not for errors related to the instantaneous inhomogeneity/anisotropy of the medium outside the cutoff sphere, the above observation suggests that the errors related to the cutoff discontinuities are more pronounced than those related to the continuum approximation, at least for simple bulk systems and for the longest cutoff distance of 1.4 nm.
The validation of the selected 4–6 SH and 0.75 SW schemes in the context of RF/AT electrostatics on the full set of 57 organic compounds is shown in Fig. 7 for Rc = 1.4 nm (and in Fig. S2 of the ESI† for Rc = 1.2 nm). In addition to ρliq and ΔHvap, the static relative dielectric permittivities ε and the self-diffusion coefficients D are also compared to the lattice-sum results. For both cutoff values, a direct comparison to the experimental data is also shown in Fig. S3 and S4 of the ESI.† However, the comparison against experiment is viewed here as less relevant than the comparison against lattice-sum, because it mixes errors from the force-field parametrization with those resulting exclusively from the non-bonded scheme.
As was observed for the calibration set (Fig. 6), the 4–6 SH and 0.75 SW schemes substantially reduce the deviations in ρliq and ΔHvap relative to lattice-sum for the validation set (Fig. 7a–c). Note, however, that the agreement with lattice-sum was already good for the original RF/CG and RF/AT schemes.
The static relative dielectric permittivities ε (Fig. 7d) calculated using the RF/AT/SH and RF/AT/SW schemes remain close to those obtained with the RF/AT scheme. These values also agree very well with the reference lattice-sum values. The correlation of the RF/CG permittivities with lattice-sum is significantly worse compared to the schemes using an AT cutoff. For a few compounds, the present permittivity results are compared in the ESI† to values calculated using corresponding fluctuation formulae, and found to also agree very well.
The self-diffusion coefficients D (Fig. 7e) obtained using RF/AT tend to be somewhat lower compared to the results obtained using lattice-sum and the three other RF schemes. This reduced diffusion likely results from the preferential positioning of molecule pairs close to the cutoff distance Rc, which appears in the form of an artificial peak in the RDF (Fig. 5e and f). The modification schemes eliminate these RDF artifacts and, as a result, the diffusive behavior in RF/AT/SH and RF/AT/SW matches very well the lattice-sum and RF/CG results.
As mentioned above, the choice mRF = 2 and nRF = 4 was not considered for the SH scheme. However, if one accepts to use a SH scheme corresponding to an altered effective permittivity εRF, the simplest alternative is to use the unmodified RF interaction with εRF → ∞. In this case, the corrected energy Ucor is not evaluated using eqn (17), but by re-calculating the standard potential energy according to the actual permittivity εRF. For completeness, this option was also explored and the corresponding results are shown in Fig. S5 of the ESI† for Rc = 1.4 nm (and Fig. S6 of the ESI† for Rc = 1.2 nm). Even this simple modification leads to a significant improvement of the agreement with the lattice-sum results, although the 4–6 SH scheme still performs slightly better.
Another option to consider is to also apply a correction similar to that of eqn (17) to the virial during the simulation. The results without and with such a correction in the context of the RF/AT/SH scheme are compared in Fig. S7 of the ESI† for Rc = 1.4 nm (and Fig. S8 of the ESI† for Rc = 1.2 nm). The virial correction slightly worsens the results and was thus not adopted. In particular, the values for benzene (like CCl4, a quadrupolar molecule with no dipole moment) differ significantly, due to changes in the RDF at short-range, as shown in Fig. S9 of the ESI.†
Finally, in order to verify that the final RF/AT/SH and RF/AT/SW schemes are indeed exempt of the cutoff artifacts observed in the original RF/CG and RF/AT schemes, the RDFs, DOCs and Kirkwood factors G(r) analogous to those of Fig. 3 and 4 are shown in Fig. 8 and 9, along with the curves from lattice-sum as a reference. Except for the slight oscillation in the RDF for water observed previously for RF/AT, which is still present, the RF/AT artifacts in the RDFs as well as the RF/CG artifact in the DOC of water have both been entirely removed. It can be seen in Fig. 9a that in the low-permittivity regime, the distance-dependent Kirkwood factor still deviates from the lattice-sum reference, resembling the RF/AT case (Fig. 4a). A similar alignment of RF/AT with RF/AT/SH and RF/AT/SW is also observed for the dielectric permittivity (Fig. 7 and Fig. S2 of the ESI†), which is a dipolar property as well. However, it can be argued that due to the poor correlation of static dielectric permittivities with experimental values irrespective of the cutoff treatment (Fig. S3 and S4 of the ESI†), this finding is of little practical relevance.
 | ||
| Fig. 8 Radial distribution functions (RDFs) for four model liquids. This figure is analogous to Fig. 3 (see the corresponding caption for more information). Comparison of results with lattice-sum (thick gray), 4–6 RF/AT/SH (dotted) and 0.75 RF/AT/SW (dashed). Straight-cutoff with AT truncation is used for the LJ interactions in all cases. | ||
 | ||
| Fig. 9 Dipole–dipole orientation correlation functions (DOCs) and distance-dependent Kirkwood factors G(r) for CHCl3 and H2O. This figure is analogous to Fig. 4 (see the corresponding caption for more information). Comparison of results with lattice-sum (thick gray), 4–6 RF/AT/SH (dotted) and 0.75 RF/AT/SW (dashed). Straight-cutoff with AT truncation is used for the LJ interactions in all cases. | ||
4.2 Modification schemes for the LJ interactions
The deviations in the simulated ρliq and ΔHvap values over the calibration set relative to the lattice-sum reference are illustrated in Fig. 10 for RF+LJ/AT/SH and RF+LJ/AT/SW, and compared to the schemes RF/AT/SH and RF/AT/SW. The results for Rc = 1.2 nm are shown in Fig. S10 of the ESI.† For the electrostatic interactions, the previously selected 4–6 SH and 0.75 SW schemes were used. A number of different parameter combinations are tested for the LJ interactions. For simplicity, the same parameters are used for the dispersive (LJ6) and repulsive (LJ12) components of the LJ interactions. The modification applied to the dispersive component actually dominates the influence on the simulated ρliq and ΔHvap (data not shown). For the SH scheme, the extreme values in terms of tested exponents (mLJ6–nLJ6 and mLJ12–nLJ12) correspond to a 12–14 SH and a 36–38 SH scheme. For the SW scheme, scaled switching distances (δsclLJ6 and δsclLJ12) from 0.05 to 0.75 are considered.As can be seen in Fig. 10, the deviations of both ρliq and ΔHvap appear to follow systematic trends with Rc = 1.4 nm (and Rc = 1.2 nm, see Fig. S10 of the ESI†). Relative to the lattice-sum reference, the deviations in both quantities become more limited when the modification scheme acts mainly at large distances, i.e. just below the cutoff (high exponents for SH, short switching distance for SW). The reason for these pronounced trends resides in the fact that the LJ interactions close to the cutoff distance are dominated by the dispersive (attractive) component. As a result, the modification scheme slightly damps the cohesive forces in the system, more so when the modification extends into the shorter distance range. The effect is more significant for ρliq, because the modification influences the virial, provoking a slight expansion of the system and a decrease in the density. It is less significant for ΔHvap, because the potential energy is corrected for the effect of the modification, i.e. the change only reflects the effect of the slightly altered density, not of the altered energetics.
For SW, the choice of a 0.05 SW scheme, which only becomes active at a distance of 0.025 nm from Rc, leads to reasonably small deviations of ρliq and ΔHvap, and was retained for the following. The SH scheme is less suited to achieve similar distance scales for the modification, because the magnitude of the required exponents would give rise to numerical instabilities. For example, the 0.05 SW scheme could be approximated by a SH scheme where the lower exponent is about 200, which would lead to coefficients aLJ6,m and aLJ6,n on the order of 10−30. For the subsequent validation, the 36–38 SH scheme was selected as a good compromise.
The validation of the selected 36–38 SH and 0.05 SW schemes for LJ interactions (along with 4–6 SW or 0.75 SH schemes for RF-based electrostatic interactions) on the full set of 57 organic compounds is shown in Fig. 11 for Rc = 1.4 nm (and for Rc = 1.2 nm in Fig. S11 of the ESI†).
As was observed for the calibration set (Fig. 10), a slight systematic underestimation of ρliq and ΔHvap is observed. As expected, this trend is more pronounced for the SH compared to the SW scheme (Fig. 11a-c). The self-diffusion coefficients D (Fig. 11d) seem to be sensitive to the perturbation introduced in the potential-energy function, but the similar least-square fits to the data indicate that this might be a statistical rather than a systematic effect.
Here again, it is of interest to consider the application of a correction similar to that of eqn (17) to the virial during the simulation. Although this option was not retained in the case of the RF-based electrostatic interactions, in the context of the LJ interactions, it may provide a possibility to counteract the systematic decrease in density resulting from the modification of the potential-energy function. The results without and with such a virial correction, applied only for the LJ interactions in the context of the RF+LJ/AT/SH and RF+LJ/AT/SW schemes are compared in Fig. S12 of the ESI† for Rc = 1.4 nm (and for Rc = 1.2 nm in Fig. S13 of the ESI†). This virial correction noticeably improves the results. For this reason, one might consider adopting it in future work.
5 Conclusion
The RF approach for calculating long-range electrostatic interactions in MD simulations represents a common alternative to the use of lattice-sum methods. Compared to the latter methods, it limits the effect of artificial periodicity in non-periodic systems (liquids and solutions), it involves a more favorable scaling of the computational cost with system size (linear), it enables a pairwise (or groupwise) partitioning of the interaction energy without additional overhead, and it alleviates intricate methodological issues for processes involving net-charge changes. The RF scheme is commonly applied with a CG truncation, to avoid the occurrence of severe artifacts in the context of low-permittivity solvents. However, AT truncation may be preferable when considering high-permittivity solvents, where it reduces the cutoff noise and leads to an improved representation of dipole–dipole correlations. Furthermore, CG truncation relies on the definition of neutral charge groups within molecules, generally requiring charge adjustments that are rather arbitrary as well as difficult to automate in the context of force-field design.To address these issues, simple modification schemes are proposed here, which are compatible with an AT truncation for both RF-based electrostatic as well as LJ interactions. The objective of these modifications is to ensure that the pairwise force and its derivative vanish at the cutoff distance. However, instead of leveling the potential energy to zero, a constant contribution is added for all atom pairs at a distance larger than the cutoff. The calculation of the latter component is inexpensive and the modified potential energy permits to conduct rigorously conservative simulations. The energies can easily be corrected back to the unmodified form, either on the fly or in a post-processing step. Two different types of modification were considered.
The SH schemes rely a two-terms polynomial added to the pairwise interaction energy. The effective range of the shifting is determined by the selected even integer exponents mω and nω (with nω = mω + 2, mω ≥ 4). Due to the restriction to small even integer exponents, the calculation of the modified forces induces only limited overhead in the pairwise interaction calculation, provided that the exponents are pre-selected and hard-coded in the program.
The SW schemes rely on a cubic spline function added to the pairwise force. The perturbation range is determined by a scaled switching distance δsclω, with δsclω in the range (0,1]. The computational overhead of this scheme may be slightly higher, considering that its straightforward implementation adds two conditional (if) statements in the pairwise interaction calculation (or only one if the same switching range is used for the electrostatic and LJ interactions). Alternatively, the use of three separate range-based pairlists would permit to avoid these conditional statements, at the cost of more implementation efforts. In both cases, the scaled switching distance could be given as an input parameter to the simulation, and does not need to be hard-coded.
In practice, using the GROMOS code and RF/AT with 1.4 nm cutoff as a reference, the introduction of a shifting function in RF/AT/SH is found to increase the computational cost of the non-bonded interaction calculation by less than 1%, while the introduction of a switching function in RF/AT/SW increases it by about 8%. In contrast, the reciprocal-space evaluation involved in a lattice-sum P3M calculation (FFT operations) with 64 grid points in each dimension is much more expensive, with an increase in the calculation cost by a factor 2.8.
Simulations involving a set of 11 organic liquids were used to calibrate appropriate distance parameters for both schemes, separately for the RF-based electrostatic and the LJ interactions. Further simulations considering 57 organic liquids were then used to validate the retained SH and SW schemes in terms of liquid density, vaporization enthalpy, relative dielectric permittivity, and diffusion constant.
For the electrostatic interactions, an appropriate modification improves or, at least, does not mitigate the agreement with lattice-sum for all the monitored properties. For the permittivity calculation, it should be noted that the same equations are to be applied for the (modified) RF/AT schemes as for lattice-sum, whereas the equations differ in the RF/CG case. Both the SH and SW schemes can be tuned to give very similar modifications, and are in principle equally adequate for RF-based electrostatic interactions.
For the LJ interactions, even the least disruptive modifications increase the deviations relative to the lattice-sum reference. This is due to the slight damping of the dispersive (cohesive) interactions, and a resulting decrease in density. The effect is more pronounced for the density itself compared to the vaporization enthalpy. Due to the use of corrected energies, the change in vaporization enthalpy only reflects the effect of the altered density, not of the altered energetics. Correcting the virial similarly during the simulation noticeably improves the results for both quantities. One might thus consider adopting this strategy in future work. In the context of LJ interactions, the SW scheme leads to smaller deviations relative to lattice-sum compared to the SH scheme, because it enables shorter modification ranges without giving rise to numerical problems.
The influence of the modification schemes introduced in this work on the simulated properties are limited, suggesting that these schemes can be used together with the GROMOS force fields without requiring a reparametrization and without incurring a pronounced accuracy loss. Further tests on more complex (multi-component, biomolecular) systems will be performed, also considering the occurrence of charged species (ions, ion pairs, charged residues). It is important to stress that the modifications introduced here for the LJ interactions do not account for long-range LJ interactions. In the future, a proper LJ tail correction could (and probably should) be added, which will require a consistent force-field reparametrization.
Conflicts of interest
There are no conflicts to declare.Appendix
A. Coefficients of the shifting function
Given a choice for the exponents mω and nω, analytical expressions are provided here for the coefficients aω,m and aω,n in eqn (14). These coefficients also depend on the cutoff radius Rc and the RF permittivity εRF. The expressions are determined by the conditions of eqn (12), and reported here for ω ∈ {RF,LJ6,LJ12}. The coefficients are given by | (24) |
 | (25) |
 | (26) |
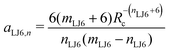 | (27) |
 | (28) |
 | (29) |
B. Amount of change in the RF influence function caused by shifting
Here, we analyze the amount of change introduced in the RF influence function by the use of different combinations for the exponents mRF and nRF in the shifting function of eqn (14). The amount of change can be measured by means of an integral Δu up to the cutoff | (30) |
This unitless quantity is shown in logarithmic form as a function of mRF and nRF in Fig. 12. From this analysis, it appears that mRF, the smaller of the two exponents, is the one that predominantly determines the shape of the modified influence function.
 | ||
| Fig. 12 Amount of change introduced by the shifting function into the RF influence function for different values of its parameters. The integrated deviation Δu of eqn (30) is shown as a function of the exponents mRF and nRF in eqn (14). The graphs rely on a cutoff distance Rc = 1.4 nm and consider four different permittivities εRF. The lower triangle as well as the diagonal are irrelevant given the selected condition 0 < mω < nω specified in eqn (14). | ||
C. Coefficients of the switching function
Given a choice for the range parameter δω, analytical expressions are provided here for the five coefficients bω,0 to bω,4 in eqn (15). These coefficients also depend on the cutoff radius Rc and the RF permittivity εRF. The expressions are determined by the conditions of eqn (12), along with corresponding requirements of continuity up to the second derivative at Rc–δω, and reported here for ω ∈ {RF,LJ6,LJ12}. The coefficients are given by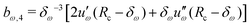 | (31) |
 | (32) |
 | (33) |
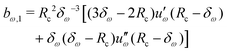 | (34) |
 | (35) |
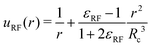 | (36) |
 | (37) |
 | (38) |
| uLJ6(r) = r−6 | (39) |
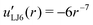 | (40) |
 | (41) |
| uLJ12(r) = r−12 | (42) |
 | (43) |
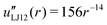 | (44) |
 | (45) |
 | (46) |
Acknowledgements
Financial support by the Swiss National Science Foundation (Grant No. 200021-175944) is gratefully acknowledged.Notes and references
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, New York, USA, 1987 Search PubMed.
- H. J. C. Berendsen, Simulating the physical world, Cambridge University Press, Cambridge, UK, 2007 Search PubMed.
- J. D. Hirst, D. R. Glowacki and M. Baaden, Faraday Discuss., 2014, 169, 9–22 RSC.
- W. F. van Gunsteren and H. J. C. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992–1023 CrossRef.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS.
- W. F. van Gunsteren, D. Bakowies, R. Baron, I. Chandrasekhar, M. Christen, X. Daura, P. Gee, D. P. Geerke, A. Glättli, P. H. Hünenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. A. van der Vegt and H. B. Yu, Angew. Chem., Int. Ed., 2006, 45, 4064–4092 CrossRef CAS.
- T. A. Halgren, Curr. Opin. Struct. Biol., 1995, 5, 205–210 CrossRef CAS.
- P. H. Hünenberger and W. F. van Gunsteren, in Lecture notes in Chemistry, ed. A. F. Sax, Springer Verlag, Berlin, Germany, 1999 Search PubMed.
- A. D. Mackerell Jr., J. Comput. Chem., 2004, 25, 1584–1604 CrossRef.
- L. Monticelli and D. P. Tieleman, Methods Mol. Biol., 2013, 924, 197–213 CrossRef CAS.
- S. Riniker, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS.
- J. E. Lennard-Jones, Physica, 1937, 4, 941–956 CrossRef CAS.
- R. B. Best, N. V. Buchete and G. Hummer, Biophys. J., 2008, 95, L07–L09 CrossRef CAS.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, Biophys. J., 2011, 100, L47–L49 CrossRef CAS.
- K. A. Beauchamp, Y. S. Lin, R. Das and V. S. Pande, J. Chem. Theory Comput., 2012, 8, 1409–1414 CrossRef CAS.
- A. T. Tzanov, M. A. Cuendet and M. E. Tuckerman, J. Phys. Chem. B, 2014, 118, 6539–6552 CrossRef CAS.
- W. Weber, P. H. Hünenberger and J. A. McCammon, J. Phys. Chem. B, 2000, 104, 3668–3675 CrossRef CAS.
- M. A. Kastenholz and P. H. Hünenberger, J. Phys. Chem. B, 2004, 108, 774–788 CrossRef CAS.
- P. Koehl, Curr. Opin. Struct. Biol., 2006, 16, 142–151 CrossRef CAS.
- M. M. Reif, V. Kräutler, M. A. Kastenholz, X. Daura and P. H. Hünenberger, J. Phys. Chem. B, 2009, 113, 3112–3128 CrossRef CAS.
- Y. M. H. Gonçalves, C. Senac, P. F. J. Fuchs, P. H. Hünenberger and B. A. C. Horta, J. Chem. Theory Comput., 2019, 15, 1806–1826 CrossRef.
- H. J. C. Berendsen, in Computer simulation of biomolecular systems, theoretical and experimental applications, ed. W. F. van Gunsteren, P. K. Weiner and A. J. Wilkinson, ESCOM Science Publishers, B.V., Leiden, The Netherlands, 1993, vol. 2 Search PubMed.
- P. E. Smith and W. F. van Gunsteren, in Computer simulation of biomolecular systems, theoretical and experimental applications, ed. W. F. van Gunsteren, P. K. Weiner and A. J. Wilkinson, ESCOM Science Publishers, B.V., Leiden, The Netherlands, 1993, vol. 2 Search PubMed.
- G. A. Cisneros, M. Karttunen, P. Ren and C. Sagui, Chem. Rev., 2014, 114, 779–814 CrossRef CAS.
- C. L. Brooks III, J. Chem. Phys., 1987, 86, 5156–5162 CrossRef.
- H. Schreiber and O. Steinhauser, Biochemistry, 1992, 31, 5856–5860 CrossRef CAS.
- E. Spohr, J. Chem. Phys., 1997, 107, 6342–6348 CrossRef CAS.
- P. H. Hünenberger and W. F. van Gunsteren, J. Chem. Phys., 1998, 108, 6117–6134 CrossRef.
- D. Chandler, J. D. Weeks and H. C. A. Andersen, Science, 1983, 220, 787–794 CrossRef CAS.
- P. J. I. Veld, A. E. Ismail and G. S. Grest, J. Chem. Phys., 2007, 127, 144711 CrossRef.
- N. M. Fischer, P. J. van Maaren, J. C. Ditz, A. Yildirim and D. van der Spoel, J. Chem. Theory Comput., 2015, 11, 2938–2944 CrossRef CAS.
- J. A. Barker and R. O. Watts, Mol. Phys., 1973, 26, 789–792 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- G. Hummer and D. M. Soumpasis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 591–596 CrossRef CAS.
- G. Hummer and D. M. Soumpasis, J. Phys.: Condens. Matter, 1994, 6, A141–A144 CrossRef CAS.
- G. Hummer, L. R. Pratt and A. E. Garcia, J. Phys. Chem., 1996, 100, 1206–1215 CrossRef CAS.
- D. Wolf, S. R. Keblinski, S. R. Phillpot and J. Eggebrecht, J. Chem. Phys., 1999, 110, 8254–8282 CrossRef CAS.
- I. Fukuda, Y. Yonezawa and H. Nakamara, J. Chem. Phys., 2010, 134, 164107 CrossRef.
- I. Fukuda, J. Chem. Phys., 2013, 139, 174107 CrossRef.
- I. Fukuda, N. Kamiya and H. Nakamura, J. Chem. Phys., 2014, 140, 194307 CrossRef.
- H. Wang, H. Nakamura and I. Fukuda, J. Chem. Phys., 2016, 144, 114503 CrossRef.
- S. Sakuraba and I. Fukuda, J. Comput. Chem., 2018, 39, 1551–1560 CrossRef CAS.
- A. Carré, L. Berthier, J. Horbach, S. Ispas and W. Kob, J. Chem. Phys., 2007, 127, 114512 CrossRef.
- S. Izvekov, J. M. J. Swanson and G. A. Voth, J. Phys. Chem. B, 2008, 112, 4711–4724 CrossRef CAS.
- N. A. Denesyuk and J. D. Weeks, J. Chem. Phys., 2008, 128, 124109 CrossRef.
- J. Vatamanu, O. Borodin and D. Bedrov, J. Chem. Theory Comput., 2018, 14, 768–783 CrossRef CAS.
- X. Wu and B. R. Brooks, J. Chem. Phys., 2005, 122, 044107 CrossRef.
- X. Wu and B. R. Brooks, J. Chem. Phys., 2008, 129, 154115 CrossRef.
- C. Y. Tang, Z. Huang and H. C. Allen, J. Phys. Chem. B, 2010, 114, 17068–17076 CrossRef CAS.
- K. Z. Takahashi, T. Narumi, D. Suh and K. Yasuoka, J. Chem. Theory Comput., 2012, 8, 4503–4516 CrossRef CAS.
- K. Z. Takahashi, J. Comput. Chem., 2014, 35, 865–875 CrossRef CAS.
- T. Nozawa, K. Yasuoka and K. Z. Takahashi, Sci. Rep., 2018, 8, 4185 CrossRef.
- X. Wu and B. R. Brooks, J. Chem. Phys., 2019, 150, 214109 CrossRef.
- K. Takahashi, K. Yasuoka and T. Narumi, J. Chem. Phys., 2007, 127, 114511 CrossRef.
- M. R. Shirts, C. Klein, J. M. Swails, J. Yin, M. K. Gilson, D. L. Mobley, D. A. Case and E. D. Zhong, J. Comput.-Aided Mol. Des., 2017, 31, 147–161 CrossRef CAS.
- R. M. Venable, L. E. Chen and R. W. Pastor, J. Phys. Chem. B, 2009, 113, 5855–5862 CrossRef CAS.
- D. Sidler, S. Frasch, M. Cristófol-Clough and S. Riniker, J. Chem. Phys., 2018, 148, 234105 CrossRef.
- A. Lofti, J. Vrabec and J. Fischer, Mol. Simul., 1990, 5, 233–243 CrossRef.
- M. Guo and B. C. Y. Lu, J. Chem. Phys., 1997, 106, 3688–3695 CrossRef CAS.
- P. Lagüe, R. W. Pastor and B. R. Brooks, J. Phys. Chem. B, 2004, 108, 363–368 CrossRef.
- J. Janeček, J. Phys. Chem. B, 2006, 110, 6264–6269 CrossRef.
- L. G. MacDowell and F. J. Blas, J. Chem. Phys., 2009, 131, 074705 CrossRef.
- F. J. Martínez-Ruiz, F. J. Blas, B. Mendiboure and I. M. V. Bravo, J. Chem. Phys., 2014, 141, 184701 CrossRef.
- F. Goujon, A. Ghoufi, P. Malfreyt and D. J. Tildesley, J. Chem. Theory Comput., 2015, 11, 4573–4585 CrossRef CAS.
- L. Lundberg and O. Edholm, J. Chem. Theory Comput., 2016, 12, 4025–4032 CrossRef CAS.
- J. Janeček, O. Said-Aizpuru and P. Paricaud, J. Chem. Theory Comput., 2017, 13, 4482–4491 CrossRef.
- S. V. Lishchuk and J. Fischer, J. Chem. Phys., 2018, 149, 091102 CrossRef.
- T. N. Heinz and P. H. Hünenberger, J. Chem. Phys., 2005, 123, 034107 CrossRef.
- P. H. Hünenberger, in Simulation and theory of electrostatic interactions in solution: Computational chemistry, biophysics, and aqueous solution, ed. G. Hummer and L. R. Pratt, American Institute of Physics, New York, USA, 1999, vol. 492 Search PubMed.
- P. H. Hünenberger, J. Chem. Phys., 2000, 113, 10464–10476 CrossRef.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- B. A. Wells and A. L. Chaffee, J. Chem. Theory Comput., 2015, 11, 3684–3695 CrossRef CAS.
- J. W. Eastwood, R. W. Hockney and D. N. Lawrence, Comput. Phys. Commun., 1980, 19, 215–261 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles., McGraw-Hill, New York, USA, 1981 Search PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. H. Ko and W. H. Fink, J. Comput. Chem., 2002, 23, 477–483 CrossRef CAS.
- W. Z. Ou-Yang, Z. Y. Lu, T. F. Shi, Z. Y. Sun and L. J. An, J. Chem. Phys., 2005, 123, 234502 CrossRef.
- D. E. Williams, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1971, 27, 452–455 CrossRef CAS.
- J. W. Perram, H. G. Petersen and S. W. de Leeuw, Mol. Phys., 1988, 65, 875–893 CrossRef CAS.
- N. Karasawa and W. A. Goddard III, J. Phys. Chem., 1989, 93, 7320–7327 CrossRef CAS.
- Z. M. Chen, T. Çağin and W. A. Goddard III, J. Comput. Chem., 1997, 18, 1365–1370 CrossRef CAS.
- B. Shi, S. Sinha and V. K. Dir, J. Chem. Phys., 2006, 124, 204715 CrossRef.
- R. E. Isele-Holder, W. Mitchell and A. E. Ismail, J. Chem. Phys., 2012, 137, 174107 CrossRef.
- L. C. Wennberg, T. Murtola, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2013, 9, 3527–3537 CrossRef.
- C. L. Wennberg, T. Murtola, S. Páll, M. J. Abraham, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2015, 11, 5737–5746 CrossRef CAS.
- R. J. Good and C. J. Hope, J. Chem. Phys., 1971, 55, 111–116 CrossRef CAS.
- J. Alejandre, D. J. Tildesley and G. A. Chapela, J. Chem. Phys., 1995, 102, 4574–4583 CrossRef CAS.
- T. N. Heinz and P. H. Hünenberger, J. Comput. Chem., 2004, 25, 1474–1486 CrossRef CAS.
- G. J. Rocklin, D. L. Mobley, K. A. Dill and P. H. Hünenberger, J. Chem. Phys., 2013, 139, 184103 CrossRef.
- A. Rahman and F. H. Stillinger, J. Chem. Phys., 1971, 55, 3336–3359 CrossRef CAS.
- D. J. Adams, E. M. Adams and G. J. Hills, Mol. Phys., 1979, 38, 387–400 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces., ed. B. Pullman, Reidel, Dordrecht, The Netherlands, 1981 Search PubMed.
- J. D. Madura and B. M. Pettitt, Chem. Phys. Lett., 1988, 150, 105–108 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- D. van der Spoel and P. J. van Maaren, J. Chem. Theory Comput., 2006, 2, 1–11 CrossRef CAS.
- V. Kräutler and P. H. Hünenberger, Mol. Simul., 2008, 34, 491–499 CrossRef.
- B. Ni and A. Baumketner, J. Mol. Model., 2011, 17, 2883–2893 CrossRef CAS.
- S. Canzar, M. El-Kebir, R. Pool, K. Elbassioni, A. K. Malde, A. E. Mark, D. P. Geerke, L. Stougie and G. W. Klau, J. Comput. Biol., 2013, 20, 188–198 CrossRef CAS.
- H. J. C. Berendsen, W. F. van Gunsteren, H. R. J. Zwinderman and R. G. Geurtsen, Ann. N. Y. Acad. Sci., 1986, 482, 269–285 CrossRef CAS.
- M. Diem and C. Oostenbrink, J. Chem. Theory Comput., 2020, 16, 5985–5990 CrossRef CAS.
- S. Reisser, D. Poger, M. Stroet and A. E. Mark, J. Chem. Theory Comput., 2017, 13, 2367–2372 CrossRef CAS.
- D. Sidler, M. Lehner, S. Frasch, M. Cristófol-Clough and S. Riniker, F1000Res., 2018, 7, 1745 Search PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- K. S. Kim, Chem. Phys. Lett., 1989, 156, 261–268 CrossRef CAS.
- M. Prevost, D. van Belle, G. Lippens and S. Wodak, Mol. Phys., 1990, 71, 587–603 CrossRef CAS.
- R. H. Stote, D. J. States and M. Karplus, J. Chim. Phys., 1991, 88, 2419–2433 CrossRef CAS.
- P. J. Steinbach and B. R. Brooks, J. Comput. Chem., 1994, 15, 667–683 CrossRef CAS.
- S. Toxvaerd and J. C. Dyre, J. Chem. Phys., 2011, 134, 081102 CrossRef.
- R. J. Loncharich and B. R. Brooks, Proteins: Struct., Funct., Genet., 1989, 6, 32–45 CrossRef CAS.
- H. Q. Ding, N. Karasawa and W. A. Goddard III, Chem. Phys. Lett., 1992, 193, 197–201 CrossRef CAS.
- P. E. Smith and B. M. Pettitt, J. Chem. Phys., 1991, 95, 8430–8441 CrossRef CAS.
- K. F. Lau, H. E. Alper, T. S. Thacher and T. E. Stouch, J. Phys. Chem., 1994, 98, 8785–8792 CrossRef CAS.
- D. Zahn, B. Schilling and S. M. Kast, J. Phys. Chem. B, 2002, 106, 10725–10732 CrossRef CAS.
- K. Z. Takahashi, Entropy, 2013, 15, 3249–3264 CrossRef.
- J. W. Essex, Mol. Simul., 1998, 20, 159–178 CrossRef CAS.
- S. M. Kast, K. F. Schmidt and B. Schilling, Chem. Phys. Lett., 2003, 367, 398–404 CrossRef CAS.
- C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104 CrossRef.
- G. S. Fanourgakis, J. Phys. Chem. B, 2015, 119, 1974–1985 CrossRef CAS.
- C. Waibel, M. S. Feinler and J. Gross, J. Chem. Theory Comput., 2019, 14, 572–583 CrossRef.
- I. Fukuda, Y. Yonezawa and H. Nakamura, J. Phys. Soc. Jpn., 2008, 77, 114301 CrossRef.
- V. H. Elvira and L. G. MacDowell, J. Chem. Phys., 2014, 141, 164108 CrossRef.
- M. P. Lautenschlaeger and H. Hasse, Fluid Phase Equilib., 2019, 482, 38–47 CrossRef CAS.
- A. N. Leonard, A. C. Simmonett, F. C. Pickard, J. Huang, R. M. Venable, J. B. Klauda, B. R. Brooks and R. W. Pastor, J. Chem. Theory Comput., 2018, 14, 948–958 CrossRef CAS.
- Z. Bashardanesh and D. van der Spoel, J. Phys. Chem. B, 2018, 122, 8018–8027 CrossRef CAS.
- B. H. Morrow and J. A. Harrison, Energy Fuels, 2019, 33, 848–858 CrossRef CAS.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendsen, J. Chem. Phys., 1998, 108, 10220–10230 CrossRef CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular simulation: The GROMOS96 manual and user guide, Verlag der Fachvereine, Zürich, Switzerland, 1996 Search PubMed.
- M. Christen, P. H. Hünenberger, D. Bakowies, R. Baron, R. Bürgi, D. P. Geerke, T. N. Heinz, M. A. Kastenholz, V. Kräutler, C. Oostenbrink, C. Peter, D. Trzesniak and W. F. van Gunsteren, J. Comput. Chem., 2005, 26, 1719–1751 CrossRef CAS.
- N. Schmid, C. D. Christ, M. Christen, A. P. Eichenberger and W. F. van Gunsteren, Comput. Phys. Commun., 2012, 183, 890–903 CrossRef CAS.
- M. P. M. Lima, M. Nader, D. E. S. Santosa and T. A. Soares, J. Braz. Chem. Soc., 2019, 30, 2219–2230 CAS.
- T. F. D. Silva, D. Vila-Viçosa, P. B. P. S. Reis, B. L. Victor, M. Diem, C. Oostenbrink and M. Machuqueiro, J. Chem. Theory Comput., 2018, 14, 5823–5833 CrossRef CAS.
- B. A. C. Horta, P. T. Merz, P. Fuchs, J. Dolenc, S. Riniker and P. H. Hünenberger, J. Chem. Theory Comput., 2016, 12, 3825–3850 CrossRef CAS.
- I. G. Tironi, P. Fontana and W. F. van Gunsteren, Mol. Simul., 1996, 18, 1–11 CrossRef CAS.
- I. G. Tironi and W. F. van Gunsteren, Mol. Phys., 1994, 83, 381–403 CrossRef CAS.
- M. Bergdorf, C. Peter and P. H. Hünenberger, J. Chem. Phys., 2003, 119, 9129–9144 CrossRef CAS.
- C. de Boor, A practical guide to splines. Applied mathematical sciences, Springer, New York, 2001, vol. 27 Search PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. di Nola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- A. P. Eichenberger, J. R. Allison, J. Dolenc, D. P. Geerke, B. A. C. Horta, K. Meier, C. Oostenbrink, N. Schmid, D. Steiner, D. Wang and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 3379–3390 CrossRef CAS.
- S. Riniker, A. P. E. Kunz and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 1469–1475 CrossRef CAS.
- S. Riniker, B. A. C. Horta, B. Thijssen, S. Gupta, W. F. van Gunsteren and P. H. Hünenberger, ChemPhysChem, 2012, 13, 1182–1190 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- W. Sutherland, Philos. Mag., 1905, 9, 781–785 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03835k |
| This journal is © the Owner Societies 2020 |