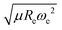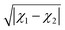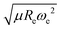Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A data-driven approach to determine dipole moments of diatomic molecules
Xiangyue
Liu
 ,
Gerard
Meijer
and
Jesús
Pérez-Ríos
,
Gerard
Meijer
and
Jesús
Pérez-Ríos
 *
*
Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: jperezri@fhi-berlin.mpg.de
First published on 24th August 2020
Abstract
We present a data-driven approach for the prediction of the electric dipole moment of diatomic molecules, which is one of the most relevant molecular properties. In particular, we apply Gaussian process regression to a novel dataset to show that dipole moments of diatomic molecules can be learned, and hence predicted, with a relative error ≲5%. The dataset contains the dipole moment of 162 diatomic molecules, the most exhaustive and unbiased dataset of dipole moments up to date. Our findings show that the dipole moment of diatomic molecules depends on atomic properties of the constituents atoms: electron affinity and ionization potential, as well as on (a feature related to) the first derivative of the electronic kinetic energy at the equilibrium distance.
1 Introduction
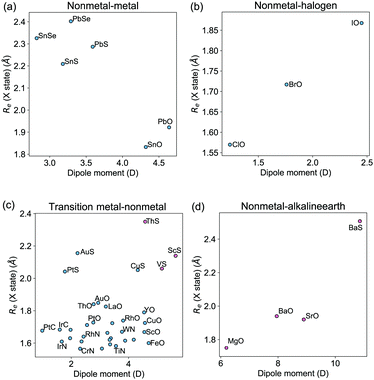
The study of relationships between spectroscopic constants is a traditional topic in chemical physics since the pioneering work of Kratzer and Mecke, among others1–6 and is beautifully summarized by Varshini.7,8 Recently, we have shown that some spectroscopic constants are universally related,9i.e., the relationships between them are independent of the nature of the molecular bond. However, the electric dipole moment of a molecule, despite being an essential molecular property, has not been considered in previous studies about relationships between spectroscopic constants. Only recently, there have been some efforts towards the understanding of the dipole moment in terms of molecular spectroscopic constants. As a result, it has been found by Hou and Bernath that the expression for the dipole moment, d, taught in elementary chemistry courses| d = qRe, | (1) |
In the 2000s the big data-driven science paradigm emerged in the scientific community.12 In this new paradigm, machine learning techniques are among the most prominent tools to assess scientific knowledge. To be precise, adequately formatted data are used to identify unexpected correlations and to predict observables based on patterns and trends of the data. When applied to physics, this novel paradigm lets nature speak up through hidden and intriguing correlations that lead to the formulation of new questions beyond a specific physical model. In particular, in chemical physics, as recently shown, data-driven approaches bring a new perspective to solve some of the most delicate problems of the field.13–16
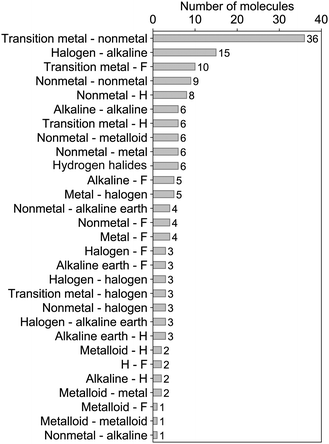
In this paper, we present a data-driven approach to dipole moments of diatomic molecules and its relationship with spectroscopic constants. We show that, after compiling the most exhaustive list of dipole moments for diatomics up to date (to the best of our knowledge) into a dataset, it is possible to learn the dipole moment of diatomic molecules based upon atomic and molecular properties with a relative error ≲5%. The number of molecules in our dataset, classified by the type of the constituent atoms, is given in Fig. 1. Our results reveal that it is not possible to predict the dipole moment of a molecule solely from atomic properties, although this is feasible for the spectroscopic constants,9 but that it is necessary to include molecular features. The molecular spectroscopic constants are needed in a combination that describes the force on the electrons at the equilibrium distance, i.e., in a combination that has the same functional dependence as the first derivative of the electronic kinetic energy at the equilibrium distance.
2 An overview on the nature of the electric dipole moment of molecules
The study of the nature of the electric dipole moment of molecules is a traditional topic in quantum chemistry that has fascinated the chemical physics community for almost a century by now. The first explanation of the nature of the electric dipole moment of molecules is due to Pauling in the 1930s.17 In particular, after studying hydrogen halide molecules, Pauling proposed that the dipole moment of a molecule is correlated with the relevance of the ionic structure with respect to the covalent one at the equilibrium bond length of the molecule. In this model, the dipole moment is a consequence of the charge transfer between the atoms within the molecule. Therefore, the larger the charge transfer, the bigger the dipole moment is. The charge transfer is quantized by the ionic character (IC), which is given by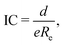 | (2) |
The next step towards understanding the electric dipole moment was the introduction of a new concept: the homopolar dipole moment, dh, by Mulliken. In particular, Mulliken realized that because the atomic orbitals are different in size, the overlap between those leads to a charge displacement with respect to the midpoint of the equilibrium bond length, which affects the electric dipole moment of the molecule.18 Furthermore, Mulliken noticed that the asymmetry in the charge distribution of hybrid orbitals causes the so-called atomic dipole moment, da. The models of Mulliken and Pauling were summarized and further developed by Coulson,19 who proposed the ultimate expression for the dipole moment of a diatomic molecule as
| d = eRe + da + dh + dp, | (3) |
The models of Pauling and Mulliken have been accepted by the physical chemistry community and taught in elementary chemistry courses for a long time, despite the fact that neither one of those is fully satisfactory. Recently, Hou and Bernath,10,11 after studying the experimentally determined dipole moments of an extensive group of molecules and using quantum chemistry calculations, have suggested that the electric dipole moment of a molecule should be given as
| d = qRd | (4) |
3 Machine learning model
3.1 Gaussian process regression
Finding relationships of the dipole moment with spectroscopic constants can be viewed as a regression problem, where the goal is to learn the mapping from the input atomic and molecular features x onto the target property, y, which in this case is the electric dipole moment, by a function y = f(x). In the present work, we use Gaussian process regression (GPR) to approximate the function f(x). As a non-parametric probabilistic method, GPR does not presume a functional form of f(x) before observing the data. Instead, it infers a Gaussian distribution of functions over function space by a Gaussian process21,22| f(x) ∼ GP(m(x),k(x,x′)), | (5) |
The kernel function, k(x,x′), captures the smoothness of the response and intrinsically encodes the behaviour of the model acting on the input. The kernel functions can be chosen by presuming the behaviour of the response to the input feature by observing the data. Its functional form and the possible hyperparameters can also be determined by a cross-validation (CV).23
3.2 Model evaluation
In learning the dipole moments, the dataset is divided into training and test sets. As a data-driven approach, GPR learns the relationship between the input features and dipole moments by observing the training set, while the predictive performance of the GPR models is examined with the test set. In this work, 20 molecules are used in the test set, while the rest are used in the training set. For the training/test splitting, the dataset is first stratified into 20 strata based on the dipole moments’ true values. A Monte Carlo (MC) approach is then performed to select the 20 test data from the dataset randomly. In each MC step, a GPR model is trained based on the training set with 5-fold cross-validation. The generalization performance of the model is then evaluated with the test set. In the end, the mean and standard deviation (STD) of the test-set errors are reported in this work, obtained from 1000 MC training/test splittings. Details about this MC approach will be discussed elsewhere.24The performance evaluation of the GPR models is carried out through three different estimators:
• The mean absolute error (MAE) defined as
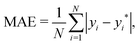 | (6) |
• The root mean square error (RMSE), which reads as
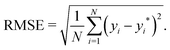 | (7) |
• The normalized error, rE, defined as the ratio of the RMSE to the range of the data
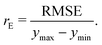 | (8) |
4 The dataset
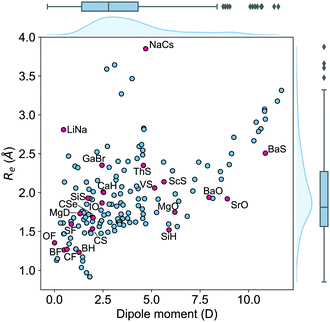
The dataset employed in this work consists of ground-state dipole moments of 162 polar diatomic molecules, 139 of which have both information on the equilibrium bond length, Re, and the harmonic vibrational frequency, ωe. The dataset is presented in Table 4 of the Appendix and it constitutes the most extensive dataset for dipole moments of diatomic molecules that we are aware of. Nevertheless, for more efficient scrutiny of our dataset's generality, we show in Fig. 2 the equilibrium bond length, Re, versus the electric dipole moment of diatomic molecules. The density plots and the box plots show the distribution of Re (right) and dipole moment, d, (top), respectively. The equilibrium bond length of the molecules is distributed between 0.9 and 3.9 Å with a median of around 1.5 Å, although most of the molecules show an equilibrium bond length between 1.2 and 3.2 Å. The dipole moment values in the dataset range from 0.0043 D to 11.69 D with a median of around 2.45 D, which shows the large variety of molecules included in the dataset.The dataset can also be categorized in terms of the type of atoms constituting the molecules, as it is shown in Fig. 1. In this figure, it is noticed that most of the molecules in the dataset present a highly ionic bond resulting from a transition metal and a nonmetal atom. The second most prominent group of molecules contains a halogen atom and an alkaline atom, which shows an ionic bond. The rest of the molecules exhibit a bond from partially ionic to highly ionic, which shows the diversity of the dataset.
5 Results and discussion
We have used a GPR approach to learn the diatomic molecules’ dipole moment employing features coming from different atomic and molecular properties. The atomic properties considered are the electron affinity (EA) taken from ref. 25–27, ionic potential (IP) taken from ref. 28, electronegativity (χ) and polarizability (α) taken from ref. 25, whereas the molecular properties are the reduced mass, μ, equilibrium bond length, Re, and the harmonic vibrational frequency, ωe. The atomic properties employed are related to the intrinsic chemical nature of the dipole moment due to the polarity of a molecular orbital in the molecular-orbital bond theory or to the ionic character of the molecular bond within the valence-bond theory.19 The GPR performance for different features is summarized in Table 1, where we employ 118 out of the 139 molecules from the dataset having values for both Re and ωe. The permutational invariance of the GPR models upon exchanging the two elements in a molecule (e.g., from molecule AB to BA) is ensured by permutation of the training sets.After using different combinations of atomic and molecular properties, we find that the dipole moment of a diatomic molecule can be best learned by a GPR model using (EA1, EA2, IP1, IP2, 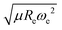 ) as the input features. The performance of this model is shown in Fig. 3. The predicted values reproduce the true values very well with a small deviation that leads to a normalized error rE < 5% (RMSE = 0.56 ± 0.02 D). We have also computed the learning curve of the cited GPR model, which gives an intuitive idea about the model's learning and generalization performance concerning the size of the training set. The results are shown in the inset of Fig. 3. The training RMSE and test RMSE are shown as a function of the number of training data points NTraining. The learning curve's shade shows the variance of training/test RMSE, obtained for each point from a MC approach of 500 training/test splittings. The mean test error decreases with increasing training data. In particular, with 80 training data, the learning curve is almost converged, suggesting that this model can not benefit from more data of the same dataset. The error's variance shows the ability of the model to be employed in different subgroups of molecules. In this case, the variance of test RMSE becomes smaller as the number of training data increases and converges to <0.02 D with 60 training data.
) as the input features. The performance of this model is shown in Fig. 3. The predicted values reproduce the true values very well with a small deviation that leads to a normalized error rE < 5% (RMSE = 0.56 ± 0.02 D). We have also computed the learning curve of the cited GPR model, which gives an intuitive idea about the model's learning and generalization performance concerning the size of the training set. The results are shown in the inset of Fig. 3. The training RMSE and test RMSE are shown as a function of the number of training data points NTraining. The learning curve's shade shows the variance of training/test RMSE, obtained for each point from a MC approach of 500 training/test splittings. The mean test error decreases with increasing training data. In particular, with 80 training data, the learning curve is almost converged, suggesting that this model can not benefit from more data of the same dataset. The error's variance shows the ability of the model to be employed in different subgroups of molecules. In this case, the variance of test RMSE becomes smaller as the number of training data increases and converges to <0.02 D with 60 training data.
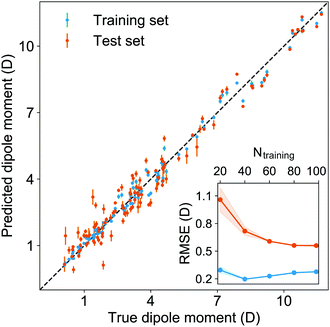 | ||
| Fig. 3 The GPR predictions of the ground-state dipole moments. The values shown in this figure are the average of predictions from 1000 MC sampled training/test splittings.24 The test set contains 20 molecules, while the training set contains 98 molecules. The mean and standard derivation of the predictions are shown for each molecule when they are used as training data (shown in blue) and test data (shown in orange). The inset shows the learning curve, which shows the training and test RMSE of the model with respect to the number of training data Ntraining. The shade in the learning curve shows the variance of training/test RMSE, obtained for each point from a MC approach of 500 training/test splittings. | ||
In previous work, we have shown that Re, ωe, and the binding energy of a diatomic molecule can be learned through groups and periods of the constituent atoms as features.9 However, the same features dramatically fail in learning the dipole moment. In particular, we find that the test errors are RMSE = 1.25 ± 0.02 D and rE = 10.8 ± 0.1%, respectively. In our view, this is an indication of the more intricate nature of the dipole moment compared to the spectroscopic constants of diatomic molecules.
In ref. 29 it is shown that the dipole moment of diatomic alkali–alkaline earth molecules can be empirically calculated from the difference in the electronegativity of the constituent atoms 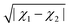 , the mean atomic polarizabilities
, the mean atomic polarizabilities ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) = (α1 + α2)/2 and the dissociation energy De. We have generalized this idea trough a GPR model by using (
= (α1 + α2)/2 and the dissociation energy De. We have generalized this idea trough a GPR model by using (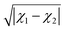 ,
, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) , D0−1) as features and applied it to the present dataset, despite the fact that alkaline earth–alkaline molecules are absent in the dataset. We have used the binding energy, D0, instead of the dissociation energy, as the former is tabulated more frequently. As a result, we find a normalized error rE = 10.5 ± 0.3%, which indicates that some of the physics behind the dipole moment function of alkali–alkaline earth molecules is applicable to any other molecule. This is an unexpected result that shows the underlying universality of the physics of the dipole moment.
, D0−1) as features and applied it to the present dataset, despite the fact that alkaline earth–alkaline molecules are absent in the dataset. We have used the binding energy, D0, instead of the dissociation energy, as the former is tabulated more frequently. As a result, we find a normalized error rE = 10.5 ± 0.3%, which indicates that some of the physics behind the dipole moment function of alkali–alkaline earth molecules is applicable to any other molecule. This is an unexpected result that shows the underlying universality of the physics of the dipole moment.
The outstanding performance of (EA1, EA2, IP1, IP2, 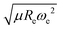 ) as features implies that the accepted picture in chemistry in which the difference of the electronegativity of the atoms within a molecule establishes the ionic character of the molecular bond17,19,30 is not sufficient to characterize the dipole moment of a molecule. When using the electron affinity and the atoms’ ionization potential as features, the performance improves by 25%. However, only if
) as features implies that the accepted picture in chemistry in which the difference of the electronegativity of the atoms within a molecule establishes the ionic character of the molecular bond17,19,30 is not sufficient to characterize the dipole moment of a molecule. When using the electron affinity and the atoms’ ionization potential as features, the performance improves by 25%. However, only if 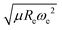 is included as a feature, the dipole moment is predicted with a RMSE below 0.7 D. Therefore, we find that it is essential to add
is included as a feature, the dipole moment is predicted with a RMSE below 0.7 D. Therefore, we find that it is essential to add 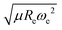 as a feature in describing the dipole moment of a diatomic molecule. It can be shown that this feature is related to the derivative of the electronic kinetic energy, T(R), at the equilibrium bond length as31
as a feature in describing the dipole moment of a diatomic molecule. It can be shown that this feature is related to the derivative of the electronic kinetic energy, T(R), at the equilibrium bond length as31
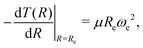 | (9) |
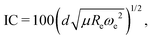 | (10) |
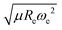 was first introduced by Hou and Bernath10,11 as an empirical relationship, and we use this here to define the ionic character of a molecular bond.
was first introduced by Hou and Bernath10,11 as an empirical relationship, and we use this here to define the ionic character of a molecular bond.
Alternatively, the ionic character can be defined in terms of the electronegativity difference between the two atoms forming a molecule as
| IC = 16|χ1 − χ2| + 3.5|χ1 − χ2|2, | (11) |
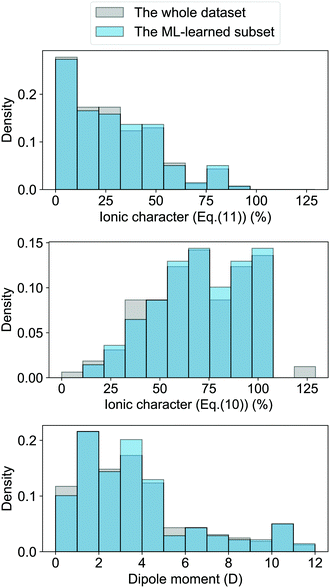 | ||
| Fig. 4 Comparison of the histograms of ionic characters and dipole moments in the whole dataset (shown in grey) and the ML-learned subset of 118 molecules (shown in blue). Panel (a) and (b) show the ionic characters calculated from eqn (10) and (11), respectively. Panel (c) plots the histogram of the dipole moment of the molecules. It is worth noticing that the dark blue regions appear in regions where the grey and light-blue bars overlap. | ||
The GPR model with (EA1, EA2, IP1, IP2, 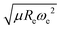 ) as input features shows several outliers. To see the importance of these outliers we have compared the distribution of the ionic character and dipole moment of the molecules in Fig. 4 (shown in grey) with the same magnitudes for the subset of 118 molecules that can be learned in this work (shown in blue). The ML-learned subset has similar overall distributions of dipole moments and ionic characters in comparison with the whole dataset. Therefore the outliers do not significantly modify the underlying distribution that the molecules follow.
) as input features shows several outliers. To see the importance of these outliers we have compared the distribution of the ionic character and dipole moment of the molecules in Fig. 4 (shown in grey) with the same magnitudes for the subset of 118 molecules that can be learned in this work (shown in blue). The ML-learned subset has similar overall distributions of dipole moments and ionic characters in comparison with the whole dataset. Therefore the outliers do not significantly modify the underlying distribution that the molecules follow.
In Table 2, it is shown a classification of the outliers as a function of its molecular bond and constituent atoms. The effective atomic charges of these molecules are also calculated with a density functional theory (DFT) approach, which is shown in Table 3 utilizing different charge partitioning methods. The calculations are performed with the B3LYP functional32 and def2-TZVP basis set,33–35 with the Gaussian 16 package.36 We have noticed that for these outliers, the natural bond orbital (NBO) method gives larger effective atomic charges compares to the Mulliken population. Furthermore, all the molecules showing a NBO charge larger than 1.0 are the ones showing an ionic character in virtue of eqn (10) above 100%. For the outliers within the van der Waals molecules, we find LiNa and NaCs. LiNa has the smallest Re and dipole moment of the bialkaline molecules in this dataset, while NaCs has the largest Re and dipole moment.
| Type of bond | Molecule |
|---|---|
| Nonmetal–nonmetal | IO, CS, SiS, CSe |
| Nonmetal–F | SF, BF, CF, OF |
| Metal–halogen | GaBr |
| Alkaline earth–nonmetal | BaO, SrO, MgO, SrS, BaS |
| Alkaline earth–H | MgD, CaH |
| Metalloid–H | BH, SiH |
| Transition metal–nonmetal | VS, ScS, ThS |
| van der Waals | LiNa, NaCs |
| Molecule | Mulliken | Hirshfeld | NBO |
|---|---|---|---|
| MgO | 0.694 | 0.576 | 1.278 |
| SrO | 0.871 | 0.714 | 1.496 |
| BaO | 0.838 | 0.640 | 1.508 |
| BaS | 0.759 | 0.660 | 1.437 |
| BF | 0.099 | 0.073 | 0.549 |
| CF | 0.030 | 0.014 | 0.315 |
| OF | 0.017 | 0.012 | 0.063 |
| SF | 0.198 | 0.108 | 0.431 |
| MgD | 0.187 | 0.241 | 0.657 |
| CaH | 0.276 | 0.318 | 0.738 |
| BH | −0.036 | 0.072 | 0.349 |
| SiH | 0.048 | 0.122 | 0.349 |
| SiS | 0.231 | 0.222 | 0.656 |
| CS | −0.081 | −0.087 | −0.174 |
| SeC | 0.180 | 0.104 | 0.263 |
| IO | 0.412 | 0.214 | 0.625 |
| GaBr | 0.331 | 0.265 | 0.627 |
| ScS | 0.529 | 0.452 | 0.743 |
| VS | 0.425 | 0.247 | 0.343 |
| CsNa | 0.140 | 0.161 | 0.279 |
| NaLi | −0.074 | 0.001 | 0.007 |
To understand the effect of different bonding types on the dipole moment, we plot in Fig. 5 the relationships between Re and dipole moments for different kinds of molecules in the current dataset, where the outliers are shown in red circles. We observe that the relationships between Re and dipole moments depend on the type of molecule under consideration. As shown in panel (a) of Fig. 5, Re and dipole moments show linear relationship for metal–nonmetal molecules, in which the nonmetals atoms are from the same group in the periodic table. Similarly, linear behaviors have also been observed for the group IV/VI diatomic molecules in ref. 37. For the oxygen halides shown in panel (b), Re increases almost linearly with the dipole moment. In panel (c), the molecules containing a transition metal and a nonmetal atom show a different trend of the equilibrium distance as a function of the dipole moment compared with the molecules formed by the main-group metal elements nonmetal atoms in panel (a). Within these molecules, the outliers are the ones with both the largest dipole moments and Re in panel (c). Interestingly, we find that all the 4 alkaline earth–nonmetal molecules in the dataset are outliers, as shown in panel (d) of Fig. 5, which correlate with an NBO population larger than 1, as shown in Table 3. In particular SrO, BaO and BaS have the largest atomic charges within the molecules in the dataset.
6 Conclusions
In summary, we have shown that through a GPR model, the ground state dipole moments of diatomic molecules can be related to spectroscopic constants, namely Re and ωe. More specifically, without any quantum chemistry calculation, the dipole moments of molecules have been predicted with an error ≲5% by using both atomic features, including electron affinity, and ionic potential, and a combination of molecular spectroscopic constants,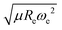 . In addition, we find that the difference in the electronegativity of the constituents atoms is not sufficient to describe the dipole moments of the diatomic molecules in stark contrast with what is generally assumed in general chemistry. Therefore, our data-driven approach shows that the nature of the dipole moment is more intricate than for spectroscopic constants, and it is clearly correlated with the very fundamental nature of the chemical bond. Finally, it is worth emphasizing that our findings have been possible thanks to the development of a complete and unbiased dataset.
. In addition, we find that the difference in the electronegativity of the constituents atoms is not sufficient to describe the dipole moments of the diatomic molecules in stark contrast with what is generally assumed in general chemistry. Therefore, our data-driven approach shows that the nature of the dipole moment is more intricate than for spectroscopic constants, and it is clearly correlated with the very fundamental nature of the chemical bond. Finally, it is worth emphasizing that our findings have been possible thanks to the development of a complete and unbiased dataset.
Conflicts of interest
There are no conflicts to declare.Appendix 1. Details about GPR
The kernel function employed in this work, which gives the best CV scores, is the rational quadratic kernel22 defined by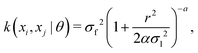 | (12) |
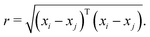 | (13) |
Appendix 2. The dataset for dipole moment of diatomic molecules
The dataset is summarized in Table 4, which consists of dipole moments, d, of 162 polar diatmonic molecules, 156 of which have information about equilibrium bond length, Re, while 139 also have harmonic vibrational frequency, ωe. The references of the dipole moments are also listed in the table.| Molecule | d (D) | R e (Å) | ω e (cm−1) | Ref. | Molecule | d (D) | R e (Å) | ω e (cm−1) | Ref. | Molecule | d (D) | R e (Å) | ω e (cm−1) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a From ref. 127. b From ref. 128. c From ref. 129. d From ref. 130. e From ref. 131. f From ref. 132. g From ref. 133. h From ref. 134. i From ref. 135. j From ref. 136. k From ref. 137. l From ref. 138. m From ref. 139. | ||||||||||||||
| AgBr | 5.62 | 2.393 | 247.7 | 25 | GeTe | 1.06 | 2.34 | 323.9 | 40 | PbSe | 3.29 | 2.402 | 277.6 | 40 |
| AgCl | 6.08 | 2.281 | 343.5 | 25 | DBr | 0.823 | 1.415 | 1884.8 | 41 | PbTe | 2.73 | 2.595 | 212 | 40 |
| AgF | 6.22 | 1.983 | 513.5 | 42 | HBr | 0.8272 | 1.414 | 2649 | 25 | PN | 2.7514 | 1.491 | 1337.2 | 43 |
| AgH | 2.86 | 1.618 | 1759.9 | 44 | DF | 1.819 | 0.917 | 2998.2 | 41 | PO | 1.88 | 1.476 | 1233.3 | 45 |
| AgI | 4.55 | 2.545 | 206.5 | 25 | HF | 1.826526 | 0.917 | 4138.3 | 46 | PtC | 0.99 | 1.677 | 1051.1 | 47 |
| AlF | 1.515 | 1.654 | 802.3 | 48 | HfF | 1.66 | 1.85 | 49 | PtF | 3.42 | 1.868 | 50 | ||
| AuF | 4.32 | 1.918 | 539.4a | 51 | HfO | 3.431 | 1.723 | 974.1 | 52 | PtN | 1.977 | 1.682 | 53 | |
| AuO | 2.94 | 1.849 | 624.59b | 54 | HI | 0.448 | 1.609 | 2309 | 25 | PtO | 2.77 | 1.727 | 851.1 | 47 |
| AuS | 2.22 | 2.156 | 410.19c | 54 | IBr | 0.726 | 2.469 | 268.6 | 25 | PtS | 1.78 | 2.042 | 47 | |
| BaF | 3.17 | 2.163 | 468.9 | 55 | ICl | 1.207 | 2.321 | 384.3 | 56 | RbBr | 10.86 | 2.945 | 169.5 | 57 |
| BaO | 7.955 | 1.94 | 669.8 | 58 | ID | 0.316 | 1.609 | 1639.7 | 59 | RbCl | 10.51 | 2.787 | 228 | 60 |
| BaS | 10.86 | 2.507 | 379.4 | 61 | IF | 1.948 | 1.91 | 610.2 | 25 | RbF | 8.5465 | 2.27 | 376 | 60 |
| BF | 0.5 | 1.263 | 1402.1 | 62 | InCl | 3.79 | 2.401 | 317.4 | 25 | RbI | 11.48 | 3.177 | 138.5 | 57 |
| BH | 1.27 | 1.232 | 2366.9 | 63 | InF | 3.4 | 1.985 | 535.4 | 64 | ReN | 1.96 | 0.61 | 65 | |
| BrCl | 0.519 | 2.136 | 444.3 | 25 | IO | 2.45 | 1.868 | 681.5 | 66 | RhN | 2.43 | 1.64 | 67 | |
| BrF | 1.422 | 1.759 | 670.8 | 25 | IrC | 1.6 | 1.683 | 1060.1 | 68 | RhO | 3.81 | 1.739 | 69 | |
| BrO | 1.76 | 1.717 | 778.7 | 41 | IrF | 2.82 | 1.851 | 70 | RuF | 5.34 | 1.916 | 71 | ||
| CaBr | 4.36 | 2.594 | 285.3d | 72 | IrN | 1.67 | 1.609 | 68 | ScO | 4.55 | 1.668 | 965 | 73 | |
| CaCl | 4.257 | 2.439 | 367.5 | 72 | KBr | 10.6281 | 2.821 | 213 | 74 | ScS | 5.64 | 2.139 | 565.2 | 75 |
| CaD | 2.51 | 2.01 | 76 | KCl | 10.2688 | 2.667 | 281 | 60 | SD | 0.7571 | 1.341 | 1885.5 | 77 | |
| CaF | 3.07 | 1.967 | 581.1 | 78 | KF | 8.59255 | 2.171 | 428 | 74 | SeF | 1.52 | 1.741 | 757 | 66 |
| CaH | 2.53 | 2.003 | 1298.3 | 76 | KI | 10.82 | 3.048 | 186.5 | 57 | SeD | 0.48 | 1.47 | 1708 | 41 |
| CaI | 4.5968 | 2.829 | 238.7 | 79 | LaO | 3.207 | 1.826 | 812.8 | 52 | SeH | 0.5 | 1.47 | 2400 | 41 |
| CF | 0.65 | 1.272 | 1308.1 | 66 | LiBr | 7.2262 | 2.17 | 563.2 | 80 | SF | 0.87 | 1.596 | 837.6 | 66 |
| CH | 1.46 | 1.12 | 2858.5 | 25 | LiCl | 7.1289 | 2.021 | 643.3 | 60 | SH | 0.758 | 1.341 | 2711.6 | 81 |
| ClD | 1.1033 | 1.275 | 2145.2 | 82 | LiF | 6.32736 | 1.564 | 910.3 | 60 | SiH | 5.9 | 1.52 | 2041.8 | 41 |
| ClF | 0.85 | 1.628 | 786.2 | 83 | LiH | 5.882 | 1.596 | 1405.7 | 84 | SiO | 3.0982 | 1.51 | 1241.6 | 85 |
| ClH | 1.1085 | 1.275 | 2990.9 | 82 | LiI | 7.4285 | 2.392 | 498.2 | 86 | SiS | 1.73 | 1.73 | 749.6 | 87 |
| ClO | 1.239 | 1.57 | 853.8 | 88 | LiK | 3.45 | 3.27 | 207 | 25 | SiSe | 1.1 | 2.058 | 580 | 37 |
| CN | 1.45 | 1.172 | 2068.6 | 89 | LiNa | 0.47 | 2.81 | 256.8 | 90 | SnO | 4.32 | 1.833 | 814.6 | 37 |
| CO | 0.112 | 1.128 | 2169.8 | 59 | LiO | 6.84 | 1.695 | 851.5 | 25 | SnS | 3.18 | 2.209 | 487.3 | 37 |
| CoF | 2.82 | 91 | LiRb | 4.0 | 3.466 | 195.2 | 25 | SnSe | 2.82 | 2.326 | 331.2 | 37 | ||
| CoH | 1.88 | 91 | MgD | 1.318 | 1.73 | 1077.9 | 92 | SnTe | 2.19 | 2.523 | 259 | 37 | ||
| CoO | 4.18 | 1.621 | 93 | MgO | 6.2 | 1.749 | 785.1 | 25 | SO | 1.55 | 1.481 | 1149.2 | 94 | |
| CrD | 3.51 | 1.663 | 1182 | 95 | MoC | 6.07 | 96 | SrF | 3.4676 | 2.075 | 502.4 | 97 | ||
| CrN | 2.31 | 1.5652e | 854.0f | 98 | MoN | 3.38 | 1.63 | 99 | SrO | 8.9 | 1.92 | 653.5 | 41 | |
| CrO | 3.88 | 1.615 | 898.4 | 100 | NaBr | 9.1183 | 2.502 | 302.1 | 60 | ThO | 3.534 | 1.84 | 895.8 | 101 |
| CS | 1.958 | 1.535 | 1285.1 | 102 | NaCl | 9.002 | 2.361 | 366 | 60 | ThS | 4.58 | 2.35 | 477g | 103 |
| CsBr | 10.82 | 3.072 | 149.7 | 57 | NaCs | 4.7 | 3.851 | 98.9 | 41 | TiH | 2.455 | 104 | ||
| CsCl | 10.387 | 2.906 | 214.2 | 60 | NaF | 8.1558 | 1.926 | 536 | 105 | TiO | 3.34 | 1.62 | 1009 | 106 |
| CSe | 1.99 | 1.676 | 1035.4 | 107 | NaH | 6.4 | 1.889 | 1176 | 108 | TiN | 3.56 | 1.582h | 1039i | 109 |
| CsF | 7.8839 | 2.345 | 352.6 | 60 | NaI | 9.2357 | 2.711 | 258 | 60 | TlBr | 4.49 | 2.618 | 192.1 | 41 |
| CsI | 11.69 | 3.315 | 119.2 | 57 | NaK | 2.693 | 3.589 | 124.1 | 25 | TlCl | 4.5429 | 2.485 | 283.8 | 37 |
| CuF | 5.26 | 1.745 | 622.7 | 110 | NaRb | 3.1 | 3.644 | 106.9 | 25 | TlF | 4.2282 | 2.084 | 477.3 | 111 |
| CuO | 4.57 | 1.724 | 640.2 | 112 | NbN | 3.26 | 1.663 | 113 | TlI | 4.61 | 2.814 | 143 | 25 | |
| CuS | 4.31 | 2.051 | 415 | 114 | NH | 1.39 | 1.036 | 3282.3 | 25 | VN | 3.07 | 1.566j | 1033k | 98 |
| FeC | 2.36 | 1.61 | 115 | NiH | 2.4 | 1.476 | 1926.6 | 116 | VO | 3.355 | 1.592l | 1011.3 | 117 | |
| FeH | 2.63 | 118 | NO | 0.157 | 1.151 | 1904.2 | 119 | VS | 5.16 | 2.06 | 120 | |||
| FeO | 4.7 | 1.6 | 970 | 121 | NS | 1.86 | 1.494 | 1218.7 | 66 | WC | 3.9 | 122 | ||
| GaF | 2.4 | 1.774 | 622.2 | 41 | OD | 1.653 | 0.97 | 2720.2 | 41 | WN | 3.77 | 1.67m | 65 | |
| GaBr | 2.45 | 2.352 | 263 | 37 | OF | 0.0043 | 1.354 | 1028.7 | 25 | YbF | 3.91 | 2.016 | 501.9 | 123 |
| GeO | 3.2824 | 1.625 | 985.5 | 85 | OH | 1.6498 | 0.97 | 3737.8 | 124 | YF | 1.82 | 1.926 | 631.3 | 125 |
| GeS | 2 | 2.012 | 575.8 | 37 | PbO | 4.64 | 1.922 | 721 | 126 | YO | 4.524 | 1.79 | 861 | 52 |
| GeSe | 1.648 | 2.135 | 408.7 | 40 | PbS | 3.59 | 2.287 | 429.4 | 126 | ZrO | 2.551 | 1.712 | 969.8 | 52 |
Acknowledgements
We thank Dr Stefan Truppe for reading the manuscript and for useful comments and discussion regarding the nature of the electric dipole moment. Open Access funding provided by the Max Planck Society.Notes and references
- A. Kratzer, Z. Phys., 1920, 3, 289 CrossRef CAS.
- R. Mecke, Z. Phys., 1925, 32, 823 CrossRef CAS.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- R. M. Badger, J. Chem. Phys., 1933, 2, 128 CrossRef.
- C. D. Clark and J. L. Stoves, Nature, 1934, 133, 873 CrossRef CAS.
- C. D. Clark, London, Edinburgh Dublin Philos. Mag. J. Sci., 1934, 18, 459–470 CrossRef CAS.
- Y. P. Varshni, Rev. Mod. Phys., 1957, 29, 664 CrossRef CAS.
- Y. P. Varshni, J. Chem. Phys., 1958, 28, 1081 CrossRef CAS.
- X. Liu, G. Meijer and J. Pérez-Ríos, On the universality of spectroscopic constants of diatomic molecules, 2020.
- S. Hou and P. F. Bernath, J. Phys. Chem. A, 2015, 119, 1435–1438 CrossRef CAS.
- S. Hou and P. F. Bernath, Phys. Chem. Chem. Phys., 2015, 17, 4708–4713 RSC.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys. Mater., 2019, 2, 032001 CrossRef.
- P. O. Dral, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef.
- R. V. Krems, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410 RSC.
- L. Pauling, The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry, Cornell University Press, Ithaca, N.Y., 3rd edn, 1986 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1935, 3, 573–585 CrossRef CAS.
- C. A. Coulson, Valence, Clarendon Press, Oxford, Oxford, United Kingdom, 1952 Search PubMed.
- M. Klessinger, Angew. Chem., Int. Ed. Engl., 1970, 9, 500–512 CrossRef CAS.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT press, Cambridge, MA, 2006, vol. 2 Search PubMed.
- MATLAB, 9.7.0 (R2019b), The MathWorks Inc., Natick, Massachusetts, 2019 Search PubMed.
- S. Raschka, arXiv preprint, 2018, arXiv:1811.12808.
- X. Liu, G. Meijer and J. Pérez-Ríos, to be published.
- W. M. Haynes, CRC handbook of chemistry and physics, CRC press, 2014 Search PubMed.
- T. Andersen, H. Haugen and H. Hotop, J. Phys. Chem. Ref. Data, 1999, 28, 1511–1533 CrossRef CAS.
- S. G. Bratsch and J. Lagowski, Polyhedron, 1986, 5, 1763–1770 CrossRef CAS.
- Atomic Spectra Database - Ionization Energies Form, https://physics.nist.gov/PhysRefData/ASD/ionEnergy.html.
- J. V. Pototschnig, A. W. Hauser and W. E. Ernst, Phys. Chem. Chem. Phys., 2016, 18, 5964–5973 RSC.
- N. B. Hannay and C. P. Smyth, J. Am. Chem. Soc., 1946, 68, 171–173 CrossRef CAS.
- R. F. Borkman and R. G. Parr, J. Chem. Phys., 1968, 48, 1116–1126 CrossRef CAS.
- P. J. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. Kaupp, P. v. R. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366 CrossRef CAS.
- T. Leininger, A. Nicklass, W. Küchle, H. Stoll, M. Dolg and A. Bergner, Chem. Phys. Lett., 1996, 255, 274–280 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, J. Chem. Phys., 1970, 53, 2736–2743 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Springer-Verlag, Berlin, Germany, 1979 Search PubMed.
- B. M. Smirnov, Reference Data on Atomic Physics and Atomic Processes, Springer-Verlag, Berlin, Germany, 2008 Search PubMed.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, Z. Naturforsch., A: Phys. Sci., 1970, 25, 539 CAS.
- A. A. Radzig and B. M. Smirnov, Reference data on atoms, molecules, and ions, Springer Science & Business Media, 2012, vol. 31 Search PubMed.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, Z. Naturforsch., A: Phys. Sci., 1970, 25, 35–39 CAS.
- F. Wyse, E. Manson and W. Gordy, J. Chem. Phys., 1972, 57, 1106–1108 CrossRef CAS.
- A. J. Sadlej and M. Urban, Chem. Phys. Lett., 1991, 176, 293–302 CrossRef CAS.
- H. Kanata, S. Yamamoto and S. Saito, J. Mol. Spectrosc., 1988, 131, 89–95 CrossRef CAS.
- J. Muenter and W. Klemperer, J. Chem. Phys., 1970, 52, 6033–6037 CrossRef.
- T. Steimle, K. Jung and B.-Z. Li, J. Chem. Phys., 1995, 103, 1767–1772 CrossRef CAS.
- S. Truppe, S. Marx, S. Kray, M. Doppelbauer, S. Hofsäss, H. C. Schewe, N. Walter, J. Pérez-Ríos, B. G. Sartakov and G. Meijer, Phys. Rev. A, 2019, 100, 052513 CrossRef CAS.
- A. Le, T. C. Steimle, L. Skripnikov and A. V. Titov, J. Chem. Phys., 2013, 138, 124313 CrossRef.
- C. Qin, R. Zhang, F. Wang and T. C. Steimle, J. Chem. Phys., 2012, 137, 054309 CrossRef.
- T. C. Steimle, R. Zhang, C. Qin and T. D. Varberg, J. Phys. Chem. A, 2013, 117, 11737–11744 CrossRef CAS.
- R. Suenram, F. Lovas, G. Fraser and K. Matsumura, J. Chem. Phys., 1990, 92, 4724–4733 CrossRef CAS.
- K. Jung, T. Steimle, D. Dai and K. Balasubramanian, J. Chem. Phys., 1995, 102, 643–652 CrossRef CAS.
- R. Zhang, Y. Yu, T. C. Steimle and L. Cheng, J. Chem. Phys., 2017, 146, 064307 CrossRef.
- W. Ernst, J. Kändler and T. Törring, J. Chem. Phys., 1986, 84, 4769–4773 CrossRef CAS.
- A. Durand, J. Loison and J. Vigué, J. Chem. Phys., 1997, 106, 477–484 CrossRef CAS.
- T. Story Jr and A. Hebert, J. Chem. Phys., 1976, 64, 855–858 CrossRef.
- L. Wharton, M. Kaufman and W. Klemperer, J. Chem. Phys., 1962, 37, 621–626 CrossRef CAS.
- C. A. Burrus, J. Chem. Phys., 1958, 28, 427–429 CrossRef CAS.
- A. Hebert, F. Lovas, C. Melendres, C. Hollowell, T. Story Jr and K. Street Jr, J. Chem. Phys., 1968, 48, 2824–2825 CrossRef CAS.
- C. Melendres, A. Hebert and K. Street Jr, J. Chem. Phys., 1969, 51, 855–856 CrossRef CAS.
- F. J. Lovas and D. R. Johnson, J. Chem. Phys., 1971, 55, 41–44 CrossRef CAS.
- R. Thomson and F. Dalby, Can. J. Phys., 1969, 47, 1155–1158 CrossRef CAS.
- J. Hoeft, F. Lovas, E. Tiemann and T. Törring, Z. Naturforsch., A: Phys. Sci., 1970, 25, 1029–1035 CAS.
- T. C. Steimle and W. L. Virgo, J. Chem. Phys., 2004, 121, 12411–12420 CrossRef CAS.
- C. Byfleet, A. Carrington and D. Russell, Mol. Phys., 1971, 20, 271–277 CrossRef CAS.
- T. Ma, J. Gengler, Z. Wang, H. Wang and T. C. Steimle, J. Chem. Phys., 2007, 126, 244312 CrossRef.
- A. J. Marr, M. Flores and T. Steimle, J. Chem. Phys., 1996, 104, 8183–8196 CrossRef CAS.
- J. Gengler, T. Ma, A. G. Adam and T. C. Steimle, J. Chem. Phys., 2007, 126, 134304 CrossRef.
- X. Zhuang, T. C. Steimle and C. Linton, J. Chem. Phys., 2010, 133, 164310 CrossRef.
- T. C. Steimle, W. L. Virgo and T. Ma, J. Chem. Phys., 2006, 124, 024309 CrossRef.
- T. Törring, W. Ernst and S. Kindt, J. Chem. Phys., 1984, 81, 4614–4619 CrossRef.
- J. Shirley, C. Scurlock and T. Steimle, J. Chem. Phys., 1990, 93, 1568–1575 CrossRef.
- R. Van Wachem, F. De Leeuw and A. Dymanus, J. Chem. Phys., 1967, 47, 2256–2258 CrossRef.
- T. Steimle, A. Marr and D. Goodridge, J. Chem. Phys., 1997, 107, 10406–10414 CrossRef CAS.
- J. Chen and T. C. Steimle, J. Chem. Phys., 2008, 128, 144312 CrossRef.
- W. Meerts and A. Dymanus, Can. J. Phys., 1975, 53, 2123–2141 CrossRef CAS.
- W. Childs, L. Goodman, U. Nielsen and V. Pfeufer, J. Chem. Phys., 1984, 80, 2283–2287 CrossRef CAS.
- W. Ernst, J. Kändler, J. Lüdtke and T. Törring, J. Chem. Phys., 1985, 83, 2744–2747 CrossRef CAS.
- A. Hebert, F. Breivogel Jr and K. Street Jr, J. Chem. Phys., 1964, 41, 2368–2376 CrossRef CAS.
- W. Meerts and A. Dymanus, Astrophys. J., 1974, 187, L45 CrossRef.
- E. W. Kaiser, J. Chem. Phys., 1970, 53, 1686–1703 CrossRef.
- B. Fabricant and J. Muenter, J. Chem. Phys., 1977, 66, 5274–5277 CrossRef.
- L. Wharton, L. P. Gold and W. Klemperer, J. Chem. Phys., 1960, 33, 1255 CrossRef.
- J. W. Raymonda, J. S. Muenter and W. A. Klemperer, J. Chem. Phys., 1970, 52, 3458–3461 CrossRef.
- F. Breivogel Jr, A. Hebert and K. Street Jr, J. Chem. Phys., 1965, 42, 1555–1558 CrossRef.
- J. Lovas, F. Hoeft, E. Tiemann and T. Törring, Z. Naturforsch., A: Phys. Sci., 1969, 24, 1422 Search PubMed.
- T. Amano, S. Saito, E. Hirota, Y. Morino, D. Johnson and F. Powell, J. Mol. Spectrosc., 1969, 30, 275–289 CrossRef.
- R. Thomson and F. Dalby, Can. J. Phys., 1968, 46, 2815–2819 CrossRef.
- P. Dagdigian, J. Graff and L. Wharton, J. Chem. Phys., 1971, 55, 4980–4982 CrossRef.
- H. Wang, X. Zhuang and T. C. Steimle, J. Chem. Phys., 2009, 131, 114315 CrossRef.
- T. C. Steimle, R. Zhang and H. Wang, J. Chem. Phys., 2014, 140, 224308 CrossRef.
- X. Zhuang and T. C. Steimle, J. Chem. Phys., 2014, 140, 124301 CrossRef.
- F. Powell and D. R. Lide Jr, J. Chem. Phys., 1964, 41, 1413–1419 CrossRef.
- J. Chen, T. C. Steimle and A. J. Merer, J. Chem. Phys., 2007, 127, 204307 CrossRef.
- H. Wang, W. L. Virgo, J. Chen and T. C. Steimle, J. Chem. Phys., 2007, 127, 124302 CrossRef.
- W. Ernst, J. Kändler, S. Kindt and T. Törring, Chem. Phys. Lett., 1985, 113, 351–354 CrossRef.
- T. C. Steimle, J. S. Robinson and D. Goodridge, J. Chem. Phys., 1999, 110, 881–889 CrossRef.
- D. Fletcher, K. Jung and T. Steimle, J. Chem. Phys., 1993, 99, 901–905 CrossRef CAS.
- T. C. Steimle, D. F. Nachman, J. E. Shirley, C. W. Bauschlicher Jr and S. R. Langhoff, J. Chem. Phys., 1989, 91, 2049–2053 CrossRef CAS.
- F. Wang, A. Le, T. C. Steimle and M. C. Heaven, Communication: The permanent electric dipole moment of thorium monoxide, ThO, 2011.
- G. Winnewisser and R. L. Cook, J. Mol. Spectrosc., 1968, 28, 266–268 CrossRef CAS.
- A. Le, M. C. Heaven and T. C. Steimle, J. Chem. Phys., 2014, 140, 024307 CrossRef.
- T. Steimle, J. Shirley, B. Simard, M. Vasseur and P. Hackett, J. Chem. Phys., 1991, 95, 7179–7182 CrossRef CAS.
- C. Hollowell, A. Hebert and K. Street Jr, J. Chem. Phys., 1964, 41, 3540–3545 CrossRef.
- T. C. Steimle and W. Virgo, Chem. Phys. Lett., 2003, 381, 30–36 CrossRef.
- J. McGurk, H. Tigelaar, S. Rock, C. Norris and W. Flygare, J. Chem. Phys., 1973, 58, 1420–1424 CrossRef.
- P. J. Dagdigian, J. Chem. Phys., 1979, 71, 2328–2329 CrossRef.
- B. Simard, H. Niki and P. Hackett, J. Chem. Phys., 1990, 92, 7012 CrossRef CAS.
- F. Wang and T. C. Steimle, J. Chem. Phys., 2010, 132, 054301 CrossRef.
- R. v. Boeckh, G. Gräff and R. Ley, Z. Phys., 1964, 179, 285–313 CrossRef CAS.
- X. Zhuang, S. E. Frey and T. C. Steimle, J. Chem. Phys., 2010, 132, 234312 CrossRef.
- D. Fletcher, D. Dai, T. Steimle and K. Balasubramanian, J. Chem. Phys., 1993, 99, 9324–9325 CrossRef.
- T. C. Steimle, W.-L. Chang, D. F. Nachman and J. M. Brown, J. Chem. Phys., 1988, 89, 7172–7179 CrossRef.
- T. C. Steimle, W. L. Virgo and D. A. Hostutler, J. Chem. Phys., 2002, 117, 1511–1516 CrossRef.
- J. A. Gray, S. F. Rice and R. Field, J. Chem. Phys., 1985, 82, 4717–4718 CrossRef.
- R. Suenram, G. T. Fraser, F. J. Lovas and C. Gillies, J. Mol. Spectrosc., 1991, 148, 114–122 CrossRef CAS.
- T. C. Steimle, J. Chen, J. J. Harrison and J. M. Brown, J. Chem. Phys., 2006, 124, 184307 CrossRef.
- A. Hoy, J. Johns and A. McKellar, Can. J. Phys., 1975, 53, 2029–2039 CrossRef.
- X. Zhuang and T. C. Steimle, J. Chem. Phys., 2010, 132, 234304 CrossRef.
- T. C. Steimle, D. F. Nachman, J. E. Shirley and A. J. Merer, J. Chem. Phys., 1989, 90, 5360–5363 CrossRef.
- F. Wang and T. C. Steimle, Communication: Electric dipole moment and hyperfine interaction of tungsten monocarbide, WC, 2011.
- B. Sauer, J. Wang and E. Hinds, J. Chem. Phys., 1996, 105, 7412–7420 CrossRef.
- D. D. Nelson Jr, A. Schiffman and D. J. Nesbitt, J. Chem. Phys., 1989, 90, 5455–5465 CrossRef.
- J. Shirley, C. Scurlock, T. Steimle, B. Simard, M. Vasseur and P. Hackett, J. Chem. Phys., 1990, 93, 8580–8585 CrossRef CAS.
- J. Hoeft, F. Lovas, E. Tiemann, R. Tischer and T. Törring, Z. Naturforsch., A: Phys. Sci., 1969, 24, 1222–1226 CAS.
- P. Schwerdtfeger, J. S. McFeaters, M. J. Liddell, J. Hrušák and H. Schwarz, J. Chem. Phys., 1995, 103, 245–252 CrossRef.
- T. Okabayashi, F. Koto, K. Tsukamoto, E. Yamazaki and M. Tanimoto, Chem. Phys. Lett., 2005, 403, 223–227 CrossRef.
- A. J. Parsons, S. P. Gleason and T. D. Varberg, Mol. Phys., 2018, 116, 3547–3553 CrossRef.
- P. Bernath, R. Field, B. Pinchemel, Y. Lefebvre and J. Schamps, J. Mol. Spectrosc., 1981, 88, 175–193 CrossRef.
- P. Sheridan, M. Brewster and L. M. Ziurys, Astrophys. J., 2002, 576, 1108 CrossRef.
- J. F. Harrison, J. Phys. Chem., 1996, 100, 3513–3519 CrossRef CAS.
- J. H. Bartlett, I. O. Antonov and M. C. Heaven, J. Phys. Chem. A, 2013, 117, 12042–12048 CrossRef CAS.
- T. Dunn, L. K. Hanson and K. A. Rubinson, Can. J. Phys., 1970, 48, 1657–1663 CrossRef CAS.
- A. Douglas and P. Veillette, J. Chem. Phys., 1980, 72, 5378–5380 CrossRef CAS.
- W. J. Balfour, A. J. Merer, H. Niki, B. Simard and P. A. Hackett, J. Chem. Phys., 1993, 99, 3288–3303 CrossRef CAS.
- B. Simard, C. Masoni and P. Hackett, J. Mol. Spectrosc., 1989, 136, 44–55 CrossRef CAS.
- A. J. Merer, Annu. Rev. Phys. Chem., 1989, 40, 407–438 CrossRef CAS.
- R. Ram and P. Bernath, J. Opt. Soc. Am. B, 1994, 11, 225–230 CrossRef CAS.
| This journal is © the Owner Societies 2020 |