 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the separability of large-amplitude motions in anharmonic frequency calculations†
Arman
Nejad
 *a and
Deborah L.
Crittenden
*a and
Deborah L.
Crittenden
 b
b
aInstitute of Physical Chemistry, University of Göttingen, Tammannstr. 6, D-37077 Göttingen, Germany. E-mail: anejad@gwdg.de
bSchool of Physical and Chemical Sciences, University of Canterbury, Christchurch, New Zealand
First published on 4th September 2020
Abstract
Nuclear vibrational theories based upon the Watson Hamiltonian are ubiquitous in quantum chemistry, but are generally unable to model systems in which the wavefunction can delocalise over multiple energy minima, i.e. molecules that have low-energy torsion and inversion barriers. In a 2019 Chemical Reviews article, Puzzarini et al. note that a common workaround is to simply decouple these problematic modes from all other vibrations in the system during anharmonic frequency calculations. They also point out that this approximation can be “ill-suited”, but do not quantify the errors introduced. In this work, we present the first systematic investigation into how separating out or constraining torsion and inversion vibrations within potential energy surface (PES) expansions affects the accuracy of computed fundamental wavenumbers for the remaining vibrational modes, using a test set of 19 tetratomic molecules for which high quality analytic potential energy surfaces and fully-coupled anharmonic reference fundamental frequencies are available. We find that the most effective and efficient strategy is to remove the mode in question from the PES expansion entirely. This introduces errors of up to +10 cm−1 in stretching fundamentals that would otherwise couple to the dropped mode, and ±5 cm−1 in all other fundamentals. These errors are approximately commensurate with, but not necessarily additional to, errors due to the choice of electronic structure model used in constructing spectroscopically accurate PES.
1 Introduction
Harmonic normal mode analysis and scaled harmonic frequencies continue to enjoy great popularity in assisting the assignment of vibrational infrared and Raman spectra,1 but can fail to accurately model anharmonically coupled systems, e.g. the OH stretching spectrum of carboxylic acid dimers.2 Moving beyond the harmonic approximation, the complexity and computational cost associated with constructing anharmonic potential energy surfaces (PES) and solving the nuclear vibrational Schrödinger equation usually demand compromise, and the accuracy of anharmonic models is sensitive both to model ansatz and implementation details.Arguably one of the most important ansatz choices is that of the coordinate system, because this impacts upon both the efficiency of PES construction schemes and the complexity of the nuclear vibrational Hamiltonian. As stressed by Sibert III et al., “exact implementations of the curvilinear and rectilinear descriptions are strictly equivalent. However, a key practical point is that they are not equivalent in low orders of approximation.”3 Usually, this is a choice between Scylla and Charybdis, because the kinetic energy operator is more concisely formulated in rectilinear coordinates, whereas molecular potential energy surface expansions converge faster in curvilinear coordinates.
Anharmonic Watson Hamiltonian models4,5 are widely used but share common limitations when it comes to describing large-amplitude vibrational motions. These limitations arise from the aperiodic nature and shape of rectilinear normal mode coordinates. Watson Hamiltonian models are strictly only suitable for semi-rigid molecules that undergo relatively low-amplitude vibrations from their equilibrium structures, and can yield strongly divergent results when applied to molecules that undergo large-amplitude motions such as torsion or inversion vibrations.
The simplest and most rigorous approximation to circumvent this involves enforcing the required condition of semi-rigidity by ignoring any coupling between the large-amplitude vibrations and all other vibrations. In a recent review, Puzzarini et al. pointed out that this “represents a crude approximation, which can be ill-suited in many situations.”6 However, to the best of our knowledge, the resultant errors have not been systematically investigated or quantified before.
If the large-amplitude vibration itself is of interest, one needs to account for its curvilinear nature using more sophisticated models.7 In some special cases, the Watson Hamiltonian is still suitable if the potential energy surface (PES) and wavefunction can be expanded about a saddle point connecting two symmetric minima. This approach has been used to compute tunnelling splittings for the inversion modes of H3O+ and NH3,8,9 but cannot be extended to other types of motions, such as torsions.9
A more general solution is to numerically map out the PES along one or two large-amplitude coordinates, constrained to remain orthogonal to the remainder of the PES. This idea forms the basis for a series of closely-related methods, including the Hougen–Bunker–Jones Hamiltonian,10 reaction path Hamiltonian,11 reaction surface Hamiltonian12 and internal coordinate path Hamiltonian13,14 models. However, the process of mapping out the PES along these special coordinates is far from routine, and a specialised set of basis functions are required in which to expand the wavefunction. This complicates the evaluation of kinetic and potential energy integrals, decreasing computational efficiency relative to methods based purely on the Watson Hamiltonian.
To investigate the limits of applicability of “pure” Watson Hamiltonian models, we will quantify how omitting or approximating PES-mediated coupling between torsion and inversion vibrations affects fundamental transition wavenumbers of other vibrational modes. In principle, the best way to assess the accuracy of any computational model is to directly benchmark against experimental data. However, in the context of vibrational spectroscopy, problems with this approach arise from both theoretical and experimental perspectives.
From the experimental side, it is not always possible to obtain high-resolution gas phase vibrational spectra and, even if the data is available, unique and unambiguous assignments are not always possible, particularly where there are strong resonances between fundamentals and overtones or combination bands. From the theoretical side, the main problem is that there are multiple sources of error that all contribute to the overall accuracy of the final predictions, including choice of electronic structure model used in constructing the potential energy surface, form and/or completeness of potential energy surface representation, and choice of nuclear vibrational model or form of nuclear vibrational Hamiltonian. It is important to carefully disentangle contributions from each potential source of error to ensure results are robust; i.e. when predictions align with experiment, they are right for the right reasons, not simply due to fortuituous error cancellation.15
Therefore, we will perform a thorough and systematic benchmarking study on a series of 19 tetratomic molecules for which high quality semi-global analytical potential energy surfaces and reference fundamental wavenumbers obtained using alternative nuclear vibrational models are available.16
However, the acid test of any computational model is ultimately its ability to predict and/or interpret experimental data. Informed by the tetratomic benchmarking results, we will construct Watson Hamiltonian models in which the computational sources of error are carefully controlled, and assess their accuracy against high-resolution experimental data for a series of pentatomic and hexatomic molecules, including the textbook example methanol.
2 Theory
The first choice that must be made in any nuclear vibrational calculation is how to represent the potential energy surface. For harmonic frequency calculations this is straightforward; all required information is encoded within the molecular Hessian. However, for anharmonic frequency calculations, there are a number of options for constructing semi-global potential energy surfaces, including force field parameterisation,17–20 numerical mapping on multi-modal grids,8,21 and symmetry-invariant fitting or interpolation.22,23In this work, we choose to use the PyPES and PyVCI program packages16,24 that utilise the Watson Hamiltonian4 in conjunction with sextic force field expansions of the potential energy. Although analytic force field expansions have gone out of fashion in variational calculations, in favour of m-mode grid-based representations of the PES,8,21 we choose to use PyPES because it conveniently offers all necessary tools: PyPES easily facilitates the utilisation of spectroscopically accurate PES compiled from the literature and newly ab initio-generated force fields, allowing theory-theory and theory-experiment benchmarking to be carried out within the same methodological framework. The required PES and wavefunction manipulations to separate out large-amplitude vibrations are trivial to implement in the context of force field-expanded PES and wavefunctions constructed from a basis of harmonic oscillator product functions. Sextic force field expansions in rectilinear normal mode (RNM) coordinates are obtained via coordinate transformation from quartic force fields in curvilinear normal mode (CNM) coordinates, following the formalism established by Allen and Császár.19 This takes advantage of the rapid convergence of force field expansions in CNM coordinates, and provides an efficient and numerically stable procedure for approximating 5th and 6th order RNM force constants.16 Constraints that restrict how force fields describe large-amplitude modes – or indeed, omit them entirely – may be applied in either CNM or RNM space. Because the truncation schemes trialled in this work depend on how the force fields are constructed, we will briefly summarise our approach here.16
2.1 Force field construction
Curvilinear normal mode (CNM) coordinates,![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) , are defined as linear combinations of (possibly redundant) internal coordinates, S, that reproduce rectilinear normal mode (RNM) coordinates, Q, to first order, i.e. whose first derivatives with respect to Cartesian displacements are the same:
, are defined as linear combinations of (possibly redundant) internal coordinates, S, that reproduce rectilinear normal mode (RNM) coordinates, Q, to first order, i.e. whose first derivatives with respect to Cartesian displacements are the same: | (1) |
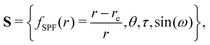 | (2) |
Rectilinear normal mode coordinates (Q) are defined as linear combinations (L−1) of Cartesian displacements (X) that diagonalise the mass-weighted Hessian matrix:27
| Q = L−1X. | (3) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) ) are defined analogously:
) are defined analogously:![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) = (BL)−1S = RS, = (BL)−1S = RS, | (4) |
With curvilinear normal mode coordinates thus defined, the PES can be expanded as a Taylor series in ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) about equilibrium (unrestricted summation):
about equilibrium (unrestricted summation):
 | (5) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , represent derivatives of the energy with respect to displacements along curvilinear normal modes. In general, these force constants may be stably computed to 4th order by numerical differentiation involving analytic ab initio Hessians. However, for molecules contained within the PyPES library, they may instead be obtained by analytical differentiation of implemented reference potentials.28 Our procedures for computing the required force constants, either analytically or numerically, are summarised in Fig. 1.
, represent derivatives of the energy with respect to displacements along curvilinear normal modes. In general, these force constants may be stably computed to 4th order by numerical differentiation involving analytic ab initio Hessians. However, for molecules contained within the PyPES library, they may instead be obtained by analytical differentiation of implemented reference potentials.28 Our procedures for computing the required force constants, either analytically or numerically, are summarised in Fig. 1.
Transforming the 4th order curvilinear normal mode force constants ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) to 6th order rectilinear normal mode force constants F requires derivatives of
to 6th order rectilinear normal mode force constants F requires derivatives of ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) with respect to Q, to 5th order. These are computed via a two-step linear transformation from higher order analogues of the B matrix, using the L and R matrices defined above. Following a non-linear coordinate transformation procedure,19,29 the desired sextic force field in rectilinear normal mode coordinates is obtained (unrestricted summation):
with respect to Q, to 5th order. These are computed via a two-step linear transformation from higher order analogues of the B matrix, using the L and R matrices defined above. Following a non-linear coordinate transformation procedure,19,29 the desired sextic force field in rectilinear normal mode coordinates is obtained (unrestricted summation):
 | (6) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ijklm and
ijklm and ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ijklmn. This approximation can result in errors of up to 10 cm−1 in computed fundamental wavenumbers, but usually they are 1–2 cm−1.16
ijklmn. This approximation can result in errors of up to 10 cm−1 in computed fundamental wavenumbers, but usually they are 1–2 cm−1.16
2.2 Proposed force field truncation schemes
A natural consequence of the semi-local nature of the Watson Hamiltonian is that resultant nuclear vibrational models cannot generally capture tunnelling splittings. Nonetheless, full dimensional Watson Hamiltonian models can – in theory – provide reasonable approximations for higher-frequency modes, provided that tunnelling splittings are small. However, in practice, force field expansions often become unstable when applied to molecules with torsional or inversion modes of vibration.16,20,30Possible sources of instability include:
(1) Unphysical divergences or “holes” in the potential arise along the torsion/inversion coordinate, reflecting the inability of the truncated Taylor series to correctly model the shape of the PES along the vibrationally-accessible region.
(2) The inability of 6th order expansions in RNM coordinates to correctly reproduce the shape of 4th order expansions in CNM coordinates, resulting in unphysical couplings between torsion/inversion coordinates and others within the RNM force field.
(3) Both of the above.
We therefore investigate three possible truncation schemes:
(1) Ṽharm: constraining the problematic coordinate to remain harmonic in the CNM PES expansion, and then transforming to RNM coordinates.
(2) Vdrop: dropping all terms involving the problematic coordinate in the RNM PES expansion, but retaining indirect coupling mediated through the curvilinear-to-rectilinear coordinate transformation process (see ref. 16).
(3) Ṽdrop: dropping all terms involving the problematic coordinate during CNM PES construction prior to transformation into rectilinear normal mode coordinates. This ensures that the dropped mode remains frozen (harmonic and geometrically uncoupled) in the RNM PES expansion. It may become necessary to modify the redundant coordinate set S, which underpins the curvilinear normal mode coordinates ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) (see eqn (4)).
(see eqn (4)).
Transformation procedures used to obtain these truncated PES expansions are summarised in Table 1.
| Name | Definition | Scaling |
|---|---|---|
| V ref |
V
(4)(![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (4)) → V(6)(Q(6)) (4)) → V(6)(Q(6)) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Nvib2) (Nvib2) |
| Ṽ harm |
V
(4)(![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (2)tor/inv, (2)tor/inv,![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (4)bend/str) → V(6)(Q(6)) (4)bend/str) → V(6)(Q(6)) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Nbend/str2) (Nbend/str2) |
| V drop |
V
(4)(![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (4)) → V(6)(Q(0)tor/inv,Q(6)bend/str) (4)) → V(6)(Q(0)tor/inv,Q(6)bend/str) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Nvib2) (Nvib2) |
| Ṽ drop |
V
(4)(![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (0)tor/inv, (0)tor/inv,![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (4)bend/str) → V(6)(Q(0)tor/inv,Q(6)bend/str) (4)bend/str) → V(6)(Q(0)tor/inv,Q(6)bend/str) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Nbend/str2) (Nbend/str2) |
2.3 Vibrational Hamiltonian and wavefunction
Anharmonic fundamental transition wavenumbers are computed with our freely available PyVCI program package, using vibrational configuration interaction (VCI) theory, as detailed in ref. 24. PyVCI utilises the J = 0 Watson Hamiltonian4 for non-linear molecules in rectilinear normal mode coordinates, including first-order Coriolis coupling between rotations and vibrations (in atomic units): | (7) |
The VCI wavefunction is formed as a linear combination of harmonic oscillator product functions:
 | (8) |
 | (9) |
 .
.
VCI fundamentals are identified as those singly-excited states with the largest overlap to the corresponding harmonic oscillator fundamentals, and fundamental transition wavenumbers are computed from the energy difference between these and the VCI ground state.
3 Methods
3.1 Benchmarking – tetratomics
Our benchmarking test set contains 19 tetratomic molecules (plus 5 deuterated isotopologues) that have either a torsion or inversion mode, for which spectroscopically accurate semi-global potential energy surfaces are available in the literature and implemented within the PyPES program package.28 The electronic structure methods, basis sets and nuclear vibrational methods used to obtain the original PES and reference fundamentals are listed in Table 2, and molecular topology classes illustrated in Fig. 2. Trigonal pyramidal molecules (type A) possess symmetry-equivalent minima potentially accessible through inversion. Extended molecules (types C and D), on the other hand, each possess a torsional mode. Trigonal planar molecules (type B) are included as a control group, since they only have a single minimum energy structure accessible through vibrational motion.| Expt.a ref. | Electronic structure method | Nuclear vib. model | Comp. ref. | ||
|---|---|---|---|---|---|
| ICH: internal coordinate Hamiltonian, as implemented in TROVE77 and RVIB4.78 CVPTn: nth order Canonical Van Vleck perturbation theory, as implemented in VANVLK.79,80 VPTn: nth order vibrational perturbation theory, as implemented in SPECTRO.81 VCI: vibrational configuration interaction, as implemented in MULTIMODE.82a High- and low-resolution gas phase experimental data.b With effective core potential (ECP) on metal atom, refer to original reference for details.c Near-complete atomic orbital basis, refer to original reference for details. | |||||
| (A) | |||||
| NH3 | C 3v | 33–36 | CCSD(T)/CBS | ICH (TROVE) | 37 |
| PH3 | C 3v | 38, 39 | CCSD(T)/CBS | ICH (TROVE) | 40 |
| SbH3 | C 3v | 41 | CCSD(T)/aVQZb | ICH (TROVE) | 42 |
| BiH3 | C 3v | 43 | CCSD(T)/aVQZb | ICH (TROVE) | 42 |
| SiH3− | C 3v | CCSD(T)-R12/BS1c | CVPT6 | 44 | |
| (B) | |||||
| BF3 | D 3h | 45–47 | CCSD(T)/VTZ | VPT2 | 48 |
| CF3+ | D 3h | CCSD(T)/VTZ | VPT2 | 48 | |
| AlF3 | D 3h | CCSD(T)/VTZ | CVPT4 | 49 | |
| SiF3+ | D 3h | CCSD(T)/VTZ | CVPT4 | 49 | |
| SO3 | D 3h | 50, 51 | CCSD(T)/aV(Q+d)Z | VPT2 | 52 |
| H2CO | C 2v | 53, 54 | CCSD(T)/aVQZ | ICH (TROVE) | 55 |
| H2SiO | C 2v | CCSD(T)/aV5Z | ICH (RVIB4) | 56 | |
| (C) | |||||
| HOOH | C 2 | 57–61 | CCSD(T)-F12/aV7Z | ICH (RVIB4) | 62 |
| DOOD | C 2 | 63 | CCSD(T)-F12/aV7Z | ICH (RVIB4) | 62 |
| HSOH | C 1 | 64–66 | CCSD(T)/aV(Q+d)Z | ICH (TROVE) | 67 |
| (D) | |||||
| t-HNNH | C 2h | 68 | CCSD(T)/VTZ | VPT2 | 69 |
| c-HSiOH | C s | CCSD(T)/aV5Z | VPT2 | 70 | |
| t-HSiOH | C s | CCSD(T)/aV5Z | VPT2 | 70 | |
| c-DSiOD | C s | CCSD(T)/aV5Z | VPT2 | 70 | |
| t-DSiOD | C s | CCSD(T)/aV5Z | VPT2 | 70 | |
| c-HOCO | C s | CCSD(T)/CBS | VCI | 71 | |
| t-HOCO | C s | 72, 73 | CCSD(T)/CBS | VCI | 74, 75 |
| c-DOCO | C s | CCSD(T)/CBS | VCI | 71 | |
| t-DOCO | C s | 73, 76 | CCSD(T)/CBS | VCI | 74, 75 |
 | ||
| Fig. 2 Topologies of molecules contained within our benchmark set.28 | ||
Full dimensional sextic force fields in rectilinear normal mode coordinates (Vref) and their truncated analogues (Ṽharm, Vdrop and Ṽdrop) are obtained via analytical coordinate transformation from curvilinear normal mode quartic force fields, following the procedures outlined in Section 2.2. The force constants that define these CNM QFFs are themselves obtained by analytical differentiation of the reference PES implemented within PyPES.28
Anharmonic fundamental wavenumbers are computed using VCI at excitation levels (≡ maximum sum of vibrational quanta distributed amongst harmonic oscillator basis states) up to and including VCI(10). A complete set of computed fundamentals is reported in Table S1 of the ESI,† along with benchmark computational and experimental data compiled from the literature.
3.2 Applications – pentatomics and hexatomics
For pentatomic and hexatomic molecules, CNM QFFs are obtained via exact, analytic coordinate transformation from RNM QFFs, whose force constants are computed by numerical differentiation, with second derivative data supplied ab initio. In principle, differentiation could be carried out in curvilinear normal mode coordinates directly but in practice it is easier to make the required atomic displacements in rectilinear space, provided that the computational cost of generating the full QFF is not prohibitive. Full dimensional sextic force fields (Vref) and mode-dropped analogues (Vdrop and Ṽdrop) are generated following exactly the same procedures as used in the benchmarking section.Because the computed fundamentals will be compared directly to experiment, it is important to ensure that the computed RNM QFF is as accurate as possible, to avoid the choice of electronic structure model being the dominant source of error. For this reason, we employ a “hybrid” force field approach, in which the entire PES is computed at a high level of theory for which analytic Hessians are available (fc-CCSD(T)/aVTZ) and the harmonic force constants replaced with values obtained at an even higher level of theory (fc-CCSD(T)-F12a/VTZ-F12). This strategy has been widely used and extensively validated in the vibrational spectroscopy literature.9,83–89 It provides an optimal balance between accuracy and computational cost, and typically reduces electronic structure model errors to <5 cm−1.9,83–89
Frozen-core (fc) CCSD(T) (coupled cluster singles doubles perturbative triples) analytic Hessian calculations90 are carried out in an augmented triple-zeta basis91,92 (fc-CCSD(T)/aVTZ) using the Cfour program package,93,94 version 1. Higher-level fc-CCSD(T)-F12a95/VTZ-F1296 harmonic force constants are computed using Molpro97,98 version 2018.1.
Anharmonic fundamental wavenumbers are computed at excitation levels up to and including VCI(9). A complete set of computed fundamentals is reported in Tables S4–S6 of the ESI,† along with benchmark computational and experimental data compiled from the literature.
4 Benchmarking – tetratomics
The overall aim of this section is to establish how excluding or constraining potentially problematic torsion and inversion modes within the Watson Hamiltonian affects computed fundamental transition frequencies of the remaining modes.4.1 Force field stability
First, it is necessary to establish whether force field expansions can be stabilised by selective truncation along large-amplitude modes, either in curvilinear or rectilinear normal mode coordinates. As stressed by Császár and coworkers in previous works,20,30 truncated force field expansions do not generally have the correct long-range behaviour for large-amplitude vibrational modes and thus should not be employed “for studies on highly excited (ro)vibrational states.”20 However, by using carefully selected sets of internal coordinates and systematic PES construction procedures, it may be possible to ensure correct asymptotic behaviour in all regions of interest. Force field stability is relatively straightforward to assess, by monitoring convergence of computed anharmonic fundamental transition wavenumbers as a function of VCI excitation level.Uncertainties in computed VCI(10) fundamental transition wavenumbers are computed as the difference between values obtained at VCI(9) and VCI(10):
| δcvge(ν) = ν(10) − ν(9) | (10) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm, νdrop or
harm, νdrop or ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop, and the superscript refers to the VCI excitation level at which each set of fundamentals was computed. VCI convergence uncertainties for all bending and stretching fundamentals are illustrated in Fig. 3. Torsion and inversion modes are excluded in all cases to ensure a fair comparison can be made between models.
drop, and the superscript refers to the VCI excitation level at which each set of fundamentals was computed. VCI convergence uncertainties for all bending and stretching fundamentals are illustrated in Fig. 3. Torsion and inversion modes are excluded in all cases to ensure a fair comparison can be made between models.
In agreement with previous work,24νref values converge to within 1 cm−1 for most molecules, except those with large-amplitude torsion or inversion modes: NH3, DOOD and all non-deuterated molecules with large-amplitude torsions, i.e. HSiOH and HOCO, HSOH, and HOOH. The low-barrier, large-amplitude nature of these motions is evident spectroscopically, where tunnelling splittings arise due to wavefunction delocalisation over multiple minima. The largest errors occur in modes that can couple to these problematic modes by symmetry, where errors can propagate from poorly-described torsion/inversion modes into stretching and bending modes through mode coupling within the wavefunction.
The outliers in Fig. 3 (|δcvge(ν)| > 5 cm−1) arise due to resonance mixing with excited inversion/torsion states that cause state assignments to alternate as a function of VCI excitation level. Two examples of this behaviour are shown in Table 3, and the remainder reported in Table S2 of the ESI.† The most extreme example is the OSH bending fundamental of HSOH, which couples strongly to the first torsional overtone via Fermi resonance. Similarly, a large convergence error occurs in the OH stretching fundamental of t-HSiOH, where state assignments vary due to resonance mixing to the seventh torsional overtone.
| V ref | VCI(8) | VCI(9) | VCI(10) | |
|---|---|---|---|---|
| HSOH | Fundamental | 1002.3 | 994.8 | 1016.3 |
| P(ν4) | 87% | 48% | 52% | |
| P(2ν6) | 8% | 39% | 37% | |
| Resonant | 1040.4 | 1016.1 | 992.9 | |
| P(ν4) | 9% | 40% | 44% | |
| P(2ν6) | 72% | 24% | 44% | |
| t-HSiOH | Fundamental | 3666.3 | 3651.0 | 3665.9 |
| P(ν1) | 89 | 42% | 57% | |
| P(3ν3 + ν4) | <1 | <1% | 2% | |
| P(8ν6) | <1 | 21% | <1% | |
| Resonant | 3675.7 | 3661.2 | ||
| P(ν1) | 25% | 28% | ||
| P(3ν3 +ν4) | 20% | 13% | ||
| P(8ν6) | 11% | <1% | ||
Constraining torsion or inversion modes to remain harmonic in curvilinear normal mode coordinates (νref → ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm in Fig. 3) decreases the frequency of outliers, but does not otherwise substantially alter the error distribution. The single outlier corresponds to the OH stretching fundamental of hydrogen peroxide, where a resonance mixing that does not directly involve the torsional mode causes state assignments to alternate as a function of VCI excitation level (see ESI,† Table S3).
harm in Fig. 3) decreases the frequency of outliers, but does not otherwise substantially alter the error distribution. The single outlier corresponds to the OH stretching fundamental of hydrogen peroxide, where a resonance mixing that does not directly involve the torsional mode causes state assignments to alternate as a function of VCI excitation level (see ESI,† Table S3).
From the trialled truncation schemes, the most robust and reliable way to ensure rapid and monotonic VCI convergence is to drop problematic modes entirely. This not only eliminates outliers that arise due to resonance mixing with excited torsion/inversion states, but also reduces all convergence uncertainties to <0.3 cm−1.
Taken together, the results presented in Fig. 3 indicate that force field instabilities are primarily due to using rectilinear coordinates to describe intrinsically curvilinear motions, rather than the accuracy of the force field expansion per se.
If anharmonicity along torsion or inversion modes were the dominant cause of force field instability, then uncertainty profiles for δcvge(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm) would be similar to those of δcvge(νdrop) or δcvge(
harm) would be similar to those of δcvge(νdrop) or δcvge(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop), because in both cases the energy is effectively constrained to change harmonically along the problematic mode. However, Fig. 3 shows that these uncertainty profiles are quite different, indicating significant off-diagonal coordinate-mediated coupling in Ṽharm that is rigorously absent from Vdrop and Ṽdrop. Fundamentally, this arises from the fact that potential energy surface expansions converge slowly in rectilinear normal mode coordinates, particularly when applied to intrinsically curvilinear motions such as torsions and inversions. This limitation in principle affects all PES models based upon rectilinear normal mode coordinates, including numerical m-mode representations.
drop), because in both cases the energy is effectively constrained to change harmonically along the problematic mode. However, Fig. 3 shows that these uncertainty profiles are quite different, indicating significant off-diagonal coordinate-mediated coupling in Ṽharm that is rigorously absent from Vdrop and Ṽdrop. Fundamentally, this arises from the fact that potential energy surface expansions converge slowly in rectilinear normal mode coordinates, particularly when applied to intrinsically curvilinear motions such as torsions and inversions. This limitation in principle affects all PES models based upon rectilinear normal mode coordinates, including numerical m-mode representations.
Conversely, the fact that the δcvge(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ref) and δcvge(
ref) and δcvge(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm) error distributions are similar (excluding resonance-induced outliers) indicates that both models have equally well-behaved PES expansions along the large-amplitude coordinate. This suggests that our force field expansions have inherited appropriate long-range behaviour from the primitive set of internal coordinates from which our curvilinear normal mode quartic force fields are constructed.
harm) error distributions are similar (excluding resonance-induced outliers) indicates that both models have equally well-behaved PES expansions along the large-amplitude coordinate. This suggests that our force field expansions have inherited appropriate long-range behaviour from the primitive set of internal coordinates from which our curvilinear normal mode quartic force fields are constructed.
Overall, dropping problematic modes is the most efficient and robust strategy for stabilising force field expansions, but also represents the most extreme approximation considered here. Thus, it is important to characterise how PES truncation schemes affect the accuracy of computed fundamentals.
4.2 Effect of PES truncation schemes
Errors in computed anharmonic fundamental transition wavenumbers due to force field truncation are computed relative to their fully-coupled all-mode counterparts:| δref(ν) = ν(10) − ν(10)ref | (11) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm, νdrop or
harm, νdrop or ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop, and the superscript refers to the sum of quanta used in the VCI calculation. νref reference results cannot be converged for HOOH, DOOD, HSOH, HSiOH, HOCO (see ESI,† Table S1) and so these molecules are excluded from further analysis in this section. For NH3, although VCI(10) results diverge, VCI(9) results are monotonically converged to within 1 cm−1 so are used instead. Boxplot analysis of errors aggregated by molecular topology are illustrated in Fig. 4, while 5 illustrates error distributions sorted according to vibrational mode type.
drop, and the superscript refers to the sum of quanta used in the VCI calculation. νref reference results cannot be converged for HOOH, DOOD, HSOH, HSiOH, HOCO (see ESI,† Table S1) and so these molecules are excluded from further analysis in this section. For NH3, although VCI(10) results diverge, VCI(9) results are monotonically converged to within 1 cm−1 so are used instead. Boxplot analysis of errors aggregated by molecular topology are illustrated in Fig. 4, while 5 illustrates error distributions sorted according to vibrational mode type.
 | ||
| Fig. 4 Signed errors δref (see eqn (11)) in bending and stretching fundamentals due to applying harmonic constraints on or dropping the torsion/inversion are illustrated in boxplot format, aggregated according to molecular topology for each approximate force field model. Each box extends from the lower quartile to the upper quartile of the data, and whiskers extend out to twice the interquartile range. Outliers are marked with crosses (+) and each box is bisected by a line indicating the median. | ||
 | ||
| Fig. 5 Signed errors δref (see eqn (11)) in bending and stretching fundamentals due to applying harmonic constraints on or dropping the torsion/inversion are illustrated in boxplot format, aggregated according to type of vibration (bending, high frequency X–H and other stretches) for each approximate force field model. Each box extends from the lower quartile to the upper quartile of the data, and whiskers extend out to twice the interquartile range. Outliers are marked with crosses (+) and each box is bisected by a line indicating the median. | ||
Fig. 4 reveals that error distributions are largely independent of molecule type, with all truncated models yielding maximum absolute errors <10 cm−1 in computed fundamentals for all modes except the labelled outliers. In these cases, strong Fermi resonances cause state assignments to vary between Vref, Ṽharm and Vdrop/Ṽdrop models, according to the VCI coefficient data shown in Table 4. However, situations like this can be readily detected by inspection of VCI coefficients, without recourse to reference calculations, and appropriate error bars applied. We suggest applying error bars that stretch between the predicted wavenumbers of the two near-degenerate VCI eigenstates. These outliers will not be included in any further analysis.
| VCI(10) | V ref | Ṽ harm | Ṽ drop | |
|---|---|---|---|---|
| c-DOCO | Fundamental | 969.9 | 944.1 | 960.1 |
| P(ν4) | 62% | 54% | 96% | |
| P(2ν6) | 31% | 40% | — | |
| Resonant | 933.7 | 982.3 | — | |
| P(ν4) | 54% | 42% | — | |
| P(2ν6) | 40% | 53% | — | |
| c-DSiOD | Fundamental | 1375.0 | 1362.3 | 1374.8 |
| P(ν2) | 50% | 55% | 55% | |
| P(ν3 + ν5) | 41% | 36% | 36% | |
| Resonant | 1359.0 | 1378.5 | 1358.9 | |
| P(ν2) | 40% | 35% | 35% | |
| P(ν3 + ν5) | 50% | 57% | 57% | |
Although Fig. 4 suggests that all three truncated models are of approximately equal quality, there are subtle differences in their error distributions that are investigated in more detail by reanalysing the data according to vibrational mode type. Fig. 5 shows that the Ṽharm model tends to produce randomly distributed errors that are similar across all mode types. Mode-dropped models, on the other hand, systematically overestimate stretching wavenumbers, particularly in X–H stretching modes (X = B, C, N, O), which are generally overestimated by 5–10 cm−1. However, mode-dropped models are particularly accurate for bending modes, with randomly distributed errors always within ±5 cm−1. This suggests that neglect of geometric coupling between the dropped large-amplitude mode (e.g. XH torsion) and retained stretching mode (XH stretch) is one of the main accuracy-determining factors of torsion-dropped models.
4.3 Coordinate definitions & coordinate-mediated coupling
V drop and Ṽdrop are particularly attractive models because they are conceptually simple, fully stabilise PES expansions in the relevant energy regime, and/but avoid Fermi resonances between excited torsion/inversion modes and other fundamentals. However, differences and similarities between these truncation schemes are not immediately clear. Inspection of Fig. 3 and 4 even creates the impression that they are the same. Indeed, they often yield very similar results and, in many cases, completely identical results. Because Ṽdrop has the potential to reduce computational cost if curvilinear normal mode force constants are computed ab initio, it is desirable to exploit this similarity where possible.Identical results can only be obtained if the dropped mode is completely uncoupled to other modes geometrically, because the chances of complete energetic decoupling are practically zero. For planar molecules, the large-amplitude mode is the only out-of-plane mode, so is geometrically orthogonal to all other modes by symmetry. Therefore, it is trivial to exclude the inversion (group B) or torsional (group D) internal coordinate and drop the corresponding vibrational mode without affecting any of the remaining coordinate definitions or vibrational wavenumbers. In these cases, Vdrop and Ṽdrop are rigorously identical. For non-planar molecules, non-trivial mappings between internal valence coordinates and curvilinear normal mode coordinates may arise, encoded within the R matrix that defines curvilinear normal mode coordinates as linear combinations of internals (see eqn (4)). Example R matrices for all molecular topologies are provided in the ESI,† Section S2 and computed fundamentals in Table S1.
For example, in ammonia (C3v), the symmetric stretching coordinate acquires substantial bending character after the inversion mode is dropped from CNM space. This is an artefact of redundancy in the internal coordinate basis when it is used to span a reduced CNM space, which leads to a deviation of 5.8 cm−1 between νdrop and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop for the symmetric stretching fundamental. In this case, Vdrop appears to be the more reliable model, because this redundancy problem is avoided.
drop for the symmetric stretching fundamental. In this case, Vdrop appears to be the more reliable model, because this redundancy problem is avoided.
For hydrogen peroxide (C2), although the torsion can couple to three other modes by symmetry, there is a close correspondence between the character of the internal and CNM coordinates, i.e. the torsional mode is defined almost exclusively by displacement along the torsional coordinate. Therefore, excluding the torsional internal coordinate (to ensure numerical stability) and dropping the torsional mode in CNM coordinates prior to coordinate transformation yields almost exactly the same RNM force field as obtained by dropping the torsional mode post-transformation. Hence, the fundamentals computed from Vdrop and Ṽdrop agree to within 0.1 cm−1.
Overall, it is safe to drop modes in CNM space if they are either rigorously orthogonal to other modes by symmetry or there is a (near) one-to-one mapping between the CNM mode to be dropped and a corresponding internal coordinate to be excluded from the internal coordinate basis. Mathematically, this is equivalent to stating that the R matrix must be exactly or very near block-diagonal, with the mode(s) to be dropped contained within its own block. We note that this approach trivially generalises to allow multiple mode-dropping in CNM coordinates, provided that appropriate sets of internal and CNM coordinates to be excluded can be identified separate as sub-blocks of the R matrix.
4.4 Comparison with computational literature
While the internal validation procedures described above have enabled us to assess truncation errors for molecules whose Vref force fields are otherwise stable enough to compute converged fundamental wavefunctions and energies, we have not been able to directly assess accuracy of truncated models for molecules with large-amplitude torsional or inversion modes. However, it is exactly these problematic cases that are most interesting.Fortunately, for many molecules in our data set, alternative reference values are available in the literature, obtained by using more complete and/or accurate representations of the potential energy surface and more appropriate and/or accurate methods for solving the nuclear vibrational Schrödinger equation. Cases in which literature values were obtained using second-order vibrational perturbation theory (VPT2) will be omitted from any further analysis.
Differences between computed VCI(10) fundamentals and literature reference values are defined as:
| δlit(ν) = ν(10) − νlit, | (12) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm, νdrop or
harm, νdrop or ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop. Mean absolute deviations for each molecular topology are illustrated in Fig. 6.
drop. Mean absolute deviations for each molecular topology are illustrated in Fig. 6.
 | ||
| Fig. 6 Mean absolute deviations 〈|δlit|〉 (see eqn (12)) between computed fundamentals and literature reference data, grouped by molecular topology for each different force field model used in this work. Molecules in groups C and D are partitioned into hydrogenated (-h) and deuterated (-d) isotopologues. | ||
For trigonal pyramidal and trigonal planar molecules (groups A and B), force field truncation errors generally increase with the extent of truncation:
|νref − νlit| < |![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm − νlit| < |νdrop − νlit| ≈ | harm − νlit| < |νdrop − νlit| ≈ |![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop − νlit| drop − νlit| |
For hydrogenated molecules with rotatable bonds (groups C and D), νdrop and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop are universally more accurate approximations to νlit than either νref or
drop are universally more accurate approximations to νlit than either νref or ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm. This is because dropped-mode models rigorously eliminate instabilities in the PES both along the torsional mode and by removing coordinate-mediated coupling between the torsional mode and the remaining modes of interest. They have the added advantage of simplifying computed vibrational spectra by also eliminating artificial or mis-assigned resonances involving torsional modes, as found for νref and
harm. This is because dropped-mode models rigorously eliminate instabilities in the PES both along the torsional mode and by removing coordinate-mediated coupling between the torsional mode and the remaining modes of interest. They have the added advantage of simplifying computed vibrational spectra by also eliminating artificial or mis-assigned resonances involving torsional modes, as found for νref and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm.
harm.
Hydrogen peroxide represents a pathological case for Watson Hamiltonian models, with a particularly low-barrier torsional mode, energetic and geometric coupling between modes, and a number of (Fermi) resonances between vibrational states.57–61 As such, all models exhibit large deviations from literature reference values.62 Nonetheless, even in this case, the Vdrop and Ṽdrop models are the “best of the worst”, which implies that ignoring energetic coupling between modes is a reasonable trade-off to make to avoid the pitfalls listed above. On the whole, Fig. 6 shows that νref predictions tend to be about as accurate as ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) harm, νdrop and
harm, νdrop and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) drop.
drop.
5 Applications – pentatomics & hexatomics
Having verified that dropped-mode models are accurate to within 10 cm−1 for stretching and bending modes of tetratomics, it remains to determine whether these models are overall accurate and generalisable enough to reliably assign gas phase vibrational spectra for larger molecules. As a first test of extensibility, we choose pentatomic and hexatomic molecules that all have a torsion vibration and for which full sets of fundamental vibration wavenumbers have been obtained from high-resolution spectroscopy: methyleneimine CH2NH,99–103 hydroxylamine NH2OH,104 formaldoxime CH2NOH,105–108 and methanol CH3OH109–119 (see insets in Fig. 8). Computed fundamental wavenumbers and reference experimental values are reported in the ESI.†Methanol is a useful test case, because it exhibits particularly strong coupling between its low-barrier, large-amplitude torsional mode and other vibrational degrees of freedom. This is reflected in substantial tunnelling splittings (up to 20 cm−1, and inversion of sign) into states of A and E symmetry, as illustrated in Fig. 7.110–115,117–121 As a textbook example of such behaviour, methanol has been the subject of intensive experimental109–119 and computational13,120–126 investigations.
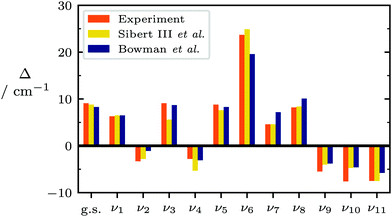 | ||
| Fig. 7 Experimental110,112–115,117–119 and computed120,121 tunneling splittings (Δ = ν(E) − ν(A) + Δg.s.) for all vibrational modes of methanol except the torsion. Raw data is listed in Table S5 of the ESI.† | ||
 | ||
Fig. 8 Error to experiment (δexpt) for computed variational anharmonic fundamentals (this work and selected literature120,121,133) of methyleneimine (CH2NH),99–103 hydroxylamine (NH2OH),104 formaldoxime (CH2NOH)105–108 and methanol (CH3OH).110,113–115,117–119 Irreducible representations are encoded in the font, A′ normal and A′′ in italics. For methanol, computational and experimental data are averaged (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, 2 A, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Raw data is listed in Tables S4–S6 of the ESI.† 1). Raw data is listed in Tables S4–S6 of the ESI.† | ||
At the other extreme, methyleneimine, is relatively rigid and rotationally restricted by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond. This makes it particularly amenable to computational interrogation, and several perturbative127–131 and variational132–134 anharmonic frequency calculations are reported in the literature.
N double bond. This makes it particularly amenable to computational interrogation, and several perturbative127–131 and variational132–134 anharmonic frequency calculations are reported in the literature.
Hydroxylamine and formaldoxime are intermediate in flexibility, capable of rotation about N–O single bonds. For hydroxylamine, perturbative135,136 and sub-space104 anharmonic frequency calculations have been performed. To the best of our knowledge, there are no anharmonic frequency studies on formaldoxime in the literature. Experimentally, no cis–trans delocalisation effects or tunneling splittings have been observed for either molecule.
5.1 Internal validation
As in the benchmarking section above, we first assess force field stability by monitoring VCI convergence:| δcvge(ν) = ν(9) − ν(8) | (13) |
In all cases, fundamentals converge to within 0.1 cm−1 with the exception of the symmetric NH2 stretch ν2 in NH2OH, which undergoes resonance mixing with the first overtone of the NH2 scissor 2ν3 and the second overtone of the NH2 wag 3ν5. Even in this case, fundamental wavenumbers converge to within 2 cm−1 for both Vdrop and Ṽdrop models.
More problematic is the fact that this resonance mixing leads to alternating state assignments between Vdrop and Ṽdrop models, as evidenced by the VCI mixing coefficients presented in Table 5. This is consistent with previous observations that resonance mixing is highly sensitive to even small changes in the underlying PES model, but that this can be readily detected by inspection of VCI coefficients.
| VCI(9) | V drop | Ṽ drop | |
|---|---|---|---|
| NH2OH | Fundamental | 3291.2 | 3303.9 |
| P(ν2) | 45% | 50% | |
| P(3ν5) | 21% | 19% | |
| P(2ν3) | 3% | 9% | |
| Resonant | 3309.5 | 3282.9 | |
| P(ν2) | 27% | 21% | |
| P(3ν5) | 37% | 41% | |
| P(2ν3) | 6% | <1% | |
Aside from the ν2 mode of NH2OH, comparison of the Vdrop and Ṽdrop results in Fig. 8 reveals that these models otherwise agree to within 2 cm−1 for all other fundamentals, and are rigorously identical for modes that are orthogonal to the dropped torsional coordinate by symmetry. The largest errors occur in the CH2 wag of CH2NH and the NH2 wag of NH2OH, with deviations of 1.6 cm−1 and 1.2 cm−1, respectively – vibrations for which the curvilinear normal coordinate definitions change substantially upon dropping the torsional coordinate from the primitive internal basis.
5.2 External validation
Errors to experiment for all four molecules are illustrated in Fig. 8, and corresponding numerical data provided in Tables S4–S6 of the ESI.† Where alternative high quality computational predictions are available in the literature,120,121,133 these are also compared to experiment in Fig. 8. In order to compare the single-reference PyVCI results for methanol with experimental data, the low-resolution band centre is computed by averaging E and A fundamental transitions two to one.For methyleneimine (top panel), all models agree well with experiment and each other, except for the NH stretch fundamental ν1, which the dropped-mode models overestimate by ∼26 cm−1. This is well outside the maximum +10 cm−1 overestimation error expected from the tetratomic benchmark. In this case, our full-dimensional data and reference computational results by Rauhut et al.133 suggest that this disagreement does not stem entirely from the torsion-dropping procedure, because these more rigorous models also significantly overestimate the predicted NH stretching fundamental, albeit to a lesser extent. Inspection of the VCI coefficients reported in Table S5 of the ESI,† reveals a Fermi resonance between ν1 (Vref: 3280.7 cm−1) and the CN stretching overtone 2ν4 (Vref: 3260.0 cm−1), despite the fact that only a single band centre (3262.6 cm−1) is observed experimentally, with very weak rovibrational infrared transitions.101 This raises the possibility that the 2ν4 overtone has been misassigned as the ν1 fundamental. We encourage experimental reinvestigation of this spectral region, perhaps using Raman spectroscopy, because NH stretches tend to be very Raman-active.
For hydroxylamine and formaldoxime (middle two panels), dropped-mode models comfortably reproduce experimental fundamentals to within 10 cm−1 for all modes except the O–H stretches. This even includes the NH2 stretching vibration of hydroxylamine that is strongly resonance-coupled to overtones of its NH2 scissor and NH2 wag. Indeed, in most cases, errors to experiment are within ±5 cm−1. O–H stretches are overestimated by ∼15 cm−1, consistent with previous observations from benchmarking tetratomics.
In methanol (bottom panel), the O–H stretching error-to-experiment is unexpectedly small, at ∼2 cm−1. However, this is almost certainly due to fortuituous error cancellation. Previous benchmark computational studies using full-dimensional electronic structure models for methanol with PES of approximately the same quality underestimate the O–H stretching fundamental by 5–10 cm−1.120,121 If this represents the error due to choice of electronic structure model used in constructing the PES, it suggests that mode-dropping incur an error of 7–12 cm−1, cancelling to give the observed 2 cm−1. The other obvious outlier in this data set is the COH bending mode ν6 that dropped-mode models overestimate by ∼17.5 cm−1. The fact that this fundamental is well modelled in previous full-dimensional studies120,121 suggests that this error is due to mode-dropping. This is supported by the spectroscopic analysis of Lees et al., who report strong resonance mixing between ν6 and torsional combitone states in methanol (ν7 + ν12 and ν8 + ν12).119 It is therefore unsurprising that the missing resonance with torsional combitone states leads to larger deviations for the ν6 fundamental.
6 Conclusions
Three different approaches have been trialled to stabilise rectilinear normal mode force field expansions of the potential energy surface for molecules with large-amplitude torsion or inversion modes which can be performed using our freely available, open-source PyPES and PyVCI program packages.Constraining the problematic mode to remain harmonic and uncoupled in curvilinear normal mode coordinates prior to transformation is not completely effective in stabilising the resultant sextic force field in rectilinear normal mode coordinates. This shows that problems with torsion and inversion modes are not just due to the shape of the potential energy surface along these coordinates, but are also an inherent problem that arises when curvilinear coordinates are expanded in a finite-order rectilinear normal mode basis. We note that this finding applies to all schemes in which potential energy surfaces are expanded or mapped out in rectilinear coordinates.
Removing large-amplitude torsions completely stabilises PES expansions in all cases, introducing errors of up to +15 cm−1 in coupled stretching modes and absolute errors in other fundamentals of ∼5 cm−1. Dropping problematic modes following coordinate transformation (Vdrop) is always numerically robust, but comes with no computational gain during PES construction. Although dropping modes prior to coordinate transformation (Ṽdrop) has the potential to reduce the computational cost of computing the requisite force constants ab initio, care must be taken to exclude matching coordinates from the internal coordinate basis or modify the basis to ensure that the process remains numerically stable. More generally, the R matrices that define curvilinear normal mode coordinates as linear combinations of internal coordinates provide a useful diagnostic of geometric separability of vibrational modes. We anticipate that this could be further utilised to break the “curse of dimensionality” associated with simulating IR spectra more generally by decomposing the full dimensional nuclear vibrational problem into a series of weakly coupled lower dimensional sub-problems.
The rigorous benchmarking procedures carried out in this work confirm the general applicability of the mode-dropping approach. Introduced errors in the remaining fundamentals are approximately commensurate with, but not necessarily additional to, errors associated with using CCSD(T) theory with at least a triple-zeta basis to construct “spectroscopically accurate” PES. Overall, the combined electronic and nuclear vibrational model error when comparing predicted fundamentals directly to experiment is around 5 cm−1 on average but can be up to 15 cm−1 for X–H stretches that couple geometrically to the dropped mode or slightly higher for modes that couple energetically to the dropped mode.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. Nejad thanks the German Academic Scholarship Foundation for funding a six month research stay in Christchurch New Zealand, the Fonds der Chemischen Industrie (FCI) for a generous scholarship, and Martin A. Suhm, Ricardo A. Mata, Benjamin Schröder for many valuable discussions. D. L. Crittenden thanks the DFG and BENCh RTG 2455 for funding a research visit to Germany under the Mercator Fellowship scheme. Funding by the Deutsche Forschungsgemeinschaft (DFG, project numbers 389479699/GRK2455 and 405832858) is gratefully acknowledged.Notes and references
- Over the last decade, the average citation of the paper by Scott and Radom on harmonically scaled harmonic wavenumbers [ A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS ] was 250 per year, according to a Web of Science search.
- C. Emmeluth, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2003, 118, 2242–2255 CrossRef CAS.
- E. L. Sibert III, J. T. Hynes and W. P. Reinhardt, J. Phys. Chem., 1983, 87, 2032–2037 CrossRef.
- J. K. G. Watson, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- J. K. G. Watson, Mol. Phys., 1970, 19, 465–487 CrossRef CAS.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS.
- A. G. Császár, C. Fábri, T. Szidarovszky, E. Mátyus, T. Furtenbacher and G. Czáko, Phys. Chem. Chem. Phys., 2012, 14, 1085–1106 RSC.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- M. Neff and G. Rauhut, Spectrochim. Acta, Part A, 2014, 119, 100–106 CrossRef CAS.
- J. T. Hougen, P. R. Bunker and J. W. C. Johns, J. Mol. Spectrosc., 1970, 34, 136–172 CrossRef CAS.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- T. Carrington Jr. and W. H. Miller, J. Chem. Phys., 1984, 81, 3942–3950 CrossRef.
- D. P. Tew, N. C. Handy, S. Carter, S. Irle and J. Bowman, Mol. Phys., 2003, 101, 3513–3525 CrossRef CAS.
- D. P. Tew, N. C. Handy and S. Carter, J. Chem. Phys., 2006, 125, 084313 CrossRef.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS.
- M. Sibaev and D. L. Crittenden, J. Chem. Phys., 2016, 144, 214107 CrossRef CAS.
- K. Machida, J. Chem. Phys., 1966, 44, 4186–4194 CrossRef CAS.
- A. R. Hoy, I. M. Mills and G. Strey, Mol. Phys., 1972, 24, 1265–1290 CrossRef CAS.
- W. D. Allen and A. G. Császár, J. Chem. Phys., 1993, 98, 2983–3015 CrossRef CAS.
- A. G. Császár, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 273–289 Search PubMed.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- J. Li, K. Song and J. Behler, Phys. Chem. Chem. Phys., 2019, 21, 9672–9682 RSC.
- M. Sibaev and D. L. Crittenden, Comput. Phys. Commun., 2016, 203, 290–297 CrossRef CAS.
- R. E. Tuzun, D. W. Noid and B. G. Sumpter, Macromol. Theory Simul., 1996, 5, 771–788 CrossRef CAS.
- G. Simons, R. G. Parr and J. M. Finlan, J. Chem. Phys., 1973, 59, 3229–3234 CrossRef CAS.
- E. B. Wilson Jr., J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications Inc., New York, 1980 Search PubMed.
- M. Sibaev and D. L. Crittenden, J. Comput. Chem., 2015, 36, 2200–2207 CrossRef CAS.
- W. D. Allen, A. G. Császár, V. Szalay and I. M. Mills, Mol. Phys., 1996, 89, 1213–1221 CrossRef CAS.
- G. Czakó, T. Furtenbacher, A. G. Császár and V. Szalay, Mol. Phys., 2004, 102, 2411–2423 CrossRef.
- J. H. Meal and S. R. Polo, J. Chem. Phys., 1956, 24, 1119–1125 CrossRef CAS.
- J. H. Meal and S. R. Polo, J. Chem. Phys., 1956, 24, 1126–1133 CrossRef CAS.
- Š. Urban, V. Špirko, D. Papoušek, J. Kauppinen, S. P. Belov, L. I. Gershtein and A. F. Krupnov, J. Mol. Spectrosc., 1981, 88, 274–292 CrossRef.
- C. Cottaz, I. Kleiner, G. Tarrago, L. R. Brown, J. S. Margolis, R. L. Poynter, H. M. Pickett, T. Fouchet, P. Drossart and E. Lellouch, J. Mol. Spectrosc., 2000, 203, 285–309 CrossRef CAS.
- G. Guelachvili, A. H. Abdullah, N. Tu, K. N. Rao, Š. Urban and D. Papoušek, J. Mol. Spectrosc., 1989, 133, 345–364 CrossRef CAS.
- I. Kleiner, L. R. Brown, G. Tarrago, Q.-L. Kou, N. Picqué, G. Guelachvili, V. Dana and J.-Y. Mandin, J. Mol. Spectrosc., 1999, 193, 46–71 CrossRef CAS.
- S. N. Yurchenko, J. Zheng, H. Lin, P. Jensen and W. Thiel, J. Chem. Phys., 2005, 123, 134308 CrossRef.
- O. N. Ulenikov, E. S. Bekhtereva, V. A. Kozinskaia, J.-J. Zheng, S.-G. He, S.-M. Hu, Q.-S. Zhu, C. Leroy and L. Pluchart, J. Mol. Spectrosc., 2002, 215, 295–308 CrossRef CAS.
- A. Ainetschian, U. Häring, G. Spiegl and W. A. Kreiner, J. Mol. Spectrosc., 1997, 181, 99–107 CrossRef CAS.
- R. I. Ovsyannikov, W. Thiel, S. N. Yurchenko, M. Carvajal and P. Jensen, J. Chem. Phys., 2008, 129, 044309 CrossRef.
- L. Fusina and G. Di Lonardo, J. Mol. Spectrosc., 2002, 216, 493–500 CrossRef CAS.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2006, 240, 174–187 CrossRef CAS.
- W. Jerzembeck, H. Bürger, J. Breidung and W. Thiel, J. Mol. Spectrosc., 2004, 226, 32–44 CrossRef CAS.
- K. Aarset, A. G. Császár, E. L. Sibert III, W. D. Allen, H. F. Schaefer III, W. Klopper and J. Noga, J. Chem. Phys., 2000, 112, 4053–4063 CrossRef CAS.
- S. Yamamoto, R. Kuwabara, M. Takami and K. Kuchitsu, J. Mol. Spectrosc., 1986, 115, 333–352 CrossRef CAS.
- S. Yamamoto, K. Kuchitsu, T. Nakanaga, H. Takeo, C. Matsumura and M. Takami, J. Chem. Phys., 1986, 84, 6027–6033 CrossRef CAS.
- S. G. W. Ginn, D. Johansen and J. Overend, J. Mol. Spectrosc., 1970, 36, 448–463 CrossRef CAS.
- Y. Pak and R. C. Woods, J. Chem. Phys., 1997, 106, 6424–6429 CrossRef CAS.
- Y. Pak, E. L. Sibert III and R. C. Woods, J. Chem. Phys., 1997, 107, 1717–1724 CrossRef CAS.
- J. Ortigoso, R. Escribano and A. G. Maki, J. Mol. Spectrosc., 1989, 138, 602–613 CrossRef CAS.
- N. F. Henfrey and B. A. Thrush, Chem. Phys. Lett., 1983, 102, 135–138 CrossRef CAS.
- J. M. L. Martin, Spectrochim. Acta, Part A, 1999, 55, 709–718 CrossRef.
- F. K. Tchana, A. Perrin and N. Lacome, J. Mol. Spectrosc., 2007, 245, 141–144 CrossRef CAS.
- A. Perrin, A. Valentin and L. Daumont, J. Mol. Struct., 2006, 780, 28–44 CrossRef.
- A. Yachmenev, S. N. Yurchenko, P. Jensen and W. Thiel, J. Chem. Phys., 2011, 134, 244307 CrossRef.
- J. Koput, S. Carter and N. C. Handy, Chem. Phys. Lett., 1999, 301, 1–9 CrossRef CAS.
- W. B. Olson, R. H. Hunt, B. W. Young, A. G. Maki and J. W. Brault, J. Mol. Spectrosc., 1988, 127, 12–34 CrossRef CAS.
- A. Perrin, A. Valentin, J.-M. Flaud, C. Camypeyret, L. Schriver, A. Schriver and P. Arcas, J. Mol. Spectrosc., 1995, 171, 358–373 CrossRef CAS.
- C. Camy-Peyret, J.-M. Flaud, J. W. C. Johns and M. Noel, J. Mol. Spectrosc., 1992, 155, 84–104 CrossRef CAS.
- W. B. Cook, R. H. Hunt, W. N. Shelton and F. A. Flaherty, J. Mol. Spectrosc., 1995, 171, 91–112 CrossRef CAS.
- J.-M. Flaud, C. Camy-Peyret, J. W. C. Johns and B. Carli, J. Chem. Phys., 1989, 91, 1504–1510 CrossRef CAS.
- P. Małyszek and J. Koput, J. Comput. Chem., 2013, 34, 337–345 CrossRef.
- J.-M. Flaud, J. W. C. Johns, Z. Lu, G. Winnewisser and H. Klein, Can. J. Phys., 2001, 79, 367–374 CrossRef CAS.
- H. Beckers, S. Esser, T. Metzroth, M. Behnke, H. Willner, J. Gauss and J. Hahn, Chem. – Eur. J., 2006, 12, 832–844 CrossRef CAS.
- O. Baum, HSOH: an elusive species with many different traits, PhD thesis, Cuvillier, Göttingen, 1st edn, 2008 Search PubMed.
- O. Baum, T. F. Giesen and S. Schlemmer, J. Mol. Spectrosc., 2008, 247, 25–29 CrossRef CAS.
- S. N. Yurchenko, A. Yachmenev, W. Thiel, O. Baum, T. F. Giesen, V. V. Melnikov and P. Jensen, J. Mol. Spectrosc., 2009, 257, 57–65 CrossRef CAS.
- F. Hegelund, H. Burger and O. Polanz, J. Mol. Spectrosc., 1994, 167, 1–10 CrossRef CAS.
- J. M. L. Martin and P. R. Taylor, Spectrochim. Acta, Part A, 1997, 53, 1039–1050 CrossRef.
- J. M. L. Martin, J. Phys. Chem. A, 1998, 102, 1394–1404 CrossRef CAS.
- R. C. Fortenberry, X. Huang, J. S. Francisco, T. D. Crawford and T. J. Lee, J. Chem. Phys., 2011, 135, 214303 CrossRef.
- J. T. Petty and C. B. Moore, J. Mol. Spectrosc., 1993, 161, 149–156 CrossRef CAS.
- T. J. Sears, W. M. Fawzy and P. M. Johnson, J. Chem. Phys., 1992, 97, 3996–4007 CrossRef CAS.
- R. C. Fortenberry, X. Huang, J. S. Francisco, T. D. Crawford and T. J. Lee, J. Chem. Phys., 2011, 135, 134301 CrossRef.
- X. Huang, R. C. Fortenberry, Y. Wang, J. S. Francisco, T. D. Crawford, J. M. Bowman and T. J. Lee, J. Phys. Chem. A, 2013, 117, 6932–6939 CrossRef CAS.
- J. T. Petty and C. B. Moore, J. Chem. Phys., 1993, 99, 47–55 CrossRef CAS.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- S. M. Colwell, S. Carter and N. C. Handy, Mol. Phys., 2003, 101, 523–544 CrossRef CAS.
- E. L. Sibert III, Comput. Phys. Commun., 1988, 51, 149–160 CrossRef.
- E. L. Sibert III, J. Chem. Phys., 1988, 88, 4378–4390 CrossRef.
- J. F. Gaw, A. Willetts, W. H. Green and N. C. Handy, Advances in molecular vibrations and collision dynamics, Greenwich, CT, 1991, p. 169 Search PubMed.
- J. M. Bowman, S. Carter and X. Huang, Int. Rev. Phys. Chem., 2003, 22, 533–549 Search PubMed.
- A. D. Boese and J. M. L. Martin, J. Phys. Chem. A, 2004, 108, 3085–3096 CrossRef CAS.
- N. Gohaud, D. Begue and C. Pouchan, Int. J. Quantum Chem., 2005, 104, 773–781 CrossRef CAS.
- K. Pflüger, M. Paulus, S. Jagiella, T. Burkert and G. Rauhut, Theor. Chem. Acc., 2005, 114, 327–332 Search PubMed.
- K. Yagi, S. Hirata and K. Hirao, Theor. Chem. Acc., 2007, 118, 681–691 Search PubMed.
- M. Sparta, M. B. Hansen, E. Matito, D. Toffoli and O. Christiansen, J. Chem. Theory Comput., 2010, 6, 3162–3175 CrossRef CAS.
- C. Puzzarini, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2011, 7, 3702–3710 CrossRef CAS.
- S. V. Krasnoshchekov, R. S. Schutski, N. C. Craig, M. Sibaev and D. L. Crittenden, J. Chem. Phys., 2018, 148, 084102 CrossRef.
- J. Gauss and J. F. Stanton, Chem. Phys. Lett., 1997, 276, 70–77 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, For the current version, see https://www.cfour.de.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., MOLPRO, version 2018.1, a package of ab initio programs, 2018, see https://www.molpro.net Search PubMed.
- G. Duxbury, H. Kato and M. L. Le Lerre, Faraday Discuss. Chem. Soc., 1981, 71, 97–110 RSC.
- G. Duxbury and M. L. Le Lerre, J. Mol. Spectrosc., 1982, 92, 326–348 CrossRef CAS.
- L. Halonen and G. Duxbury, Chem. Phys. Lett., 1985, 118, 246–251 CrossRef CAS.
- L. Halonen and G. Duxbury, J. Chem. Phys., 1985, 83, 2091–2096 CrossRef CAS.
- L. Halonen and G. Duxbury, J. Chem. Phys., 1985, 83, 2078–2090 CrossRef CAS.
- D. Luckhaus, J. Chem. Phys., 1997, 106, 8409–8426 CrossRef CAS.
- G. Duxbury, R. M. Percival, D. Devoy and M. R. M. Mahmoud, J. Mol. Spectrosc., 1988, 132, 380–392 CrossRef CAS.
- G. Duxbury, J. Mol. Spectrosc., 1988, 132, 393–406 CrossRef CAS.
- R. A. Bannai and G. Duxbury, J. Opt. Soc. Am. B, 1994, 11, 170–175 CrossRef CAS.
- R. A. Bannai, G. Duxbury, G. Ritchie and S. Klee, J. Mol. Spectrosc., 1996, 178, 84–92 CrossRef CAS.
- I. Kleiner, G. T. Fraser, J. T. Hougen and A. S. Pine, J. Mol. Spectrosc., 1991, 147, 155–172 CrossRef CAS.
- R. H. Hunt, W. N. Shelton, W. B. Cook, O. N. Bignall, J. W. Mirick and F. A. Flaherty, J. Mol. Spectrosc., 1991, 149, 252–256 CrossRef CAS.
- L. Xu and J. Hougen, J. Mol. Spectrosc., 1995, 173, 540–551 CrossRef CAS.
- G. Moruzzi, B. P. Winnewisser, M. Winnewisser, I. Mukhopadhyay and F. Strumia, Microwave, infrared, and laser transitions of methanol: atlas of assigned lines from 0 to 1258 cm−1, CRC Press, Boca Raton, London, New York, 1995 Search PubMed.
- L.-H. Xu, X. Wang, T. J. Cronin, D. S. Perry, G. T. Fraser and A. S. Pine, J. Mol. Spectrosc., 1997, 185, 158–172 CrossRef CAS.
- X. Wang and D. S. Perry, J. Chem. Phys., 1998, 109, 10795–10805 CrossRef CAS.
- R. H. Hunt, W. N. Shelton, F. A. Flaherty and W. B. Cook, J. Mol. Spectrosc., 1998, 192, 277–293 CrossRef CAS.
- R. M. Lees and L.-H. Xu, Phys. Rev. Lett., 2000, 84, 3815–3818 CrossRef CAS.
- R. M. Lees, M. Mollabashi, L.-H. Xu, M. Lock and B. P. Winnewisser, Phys. Rev. A, 2002, 65, 042511 CrossRef.
- M. A. Temsamani, L.-H. Xu and R. M. Lees, J. Mol. Spectrosc., 2003, 218, 220–234 CrossRef.
- R. M. Lees, L.-H. Xu, J. W. C. Johns, Z.-F. Lu, B. P. Winnewisser, M. Lock and R. L. Sams, J. Mol. Spectrosc., 2004, 228, 528–543 CrossRef CAS.
- E. L. Sibert III and J. Castillo-Chará, J. Chem. Phys., 2005, 122, 194306 CrossRef.
- J. M. Bowman, X. Huang, N. C. Handy and S. Carter, J. Phys. Chem. A, 2007, 111, 7317–7321 CrossRef CAS.
- A. Miani, V. Hänninen, M. Horn and L. Halonen, Mol. Phys., 2000, 98, 1737–1748 CrossRef CAS.
- V. Hänninen and L. Halonen, Mol. Phys., 2003, 101, 2907–2916 CrossRef.
- B. Fehrensen, D. Luckhaus, M. Quack, M. Willeke and T. R. Rizzo, J. Chem. Phys., 2003, 119, 5534–5544 CrossRef CAS.
- J. Castillo-Chará and E. L. Sibert III, J. Chem. Phys., 2003, 119, 11671–11681 CrossRef.
- Y. Scribano, D. M. Lauvergnat and D. M. Benoit, J. Chem. Phys., 2010, 133, 094103 CrossRef.
- K. Zaki, M. Gélizé-Duvignau and C. Pouchan, J. Chim. Phys., 1997, 94, 37–53 CrossRef CAS.
- G. de Oliveira, J. M. L. Martin, I. K. C. Silwal and J. F. Liebman, J. Comput. Chem., 2001, 22, 1297–1305 CrossRef CAS.
- P. Carbonniere and V. Barone, Chem. Phys. Lett., 2004, 399, 226–229 CrossRef CAS.
- P. Carbonniere and V. Barone, Chem. Phys. Lett., 2004, 392, 365–371 CrossRef CAS.
- L. Margulès, J. Demaison, P. Sreeja and J.-C. Guillemin, J. Mol. Spectrosc., 2006, 238, 234–240 CrossRef.
- C. Pouchan and K. Zaki, J. Chem. Phys., 1997, 107, 342–345 CrossRef CAS.
- G. Rauhut, G. Knizia and H.-J. Werner, J. Chem. Phys., 2009, 130, 054105 CrossRef.
- S. Heislbetz and G. Rauhut, J. Chem. Phys., 2010, 132, 124102 CrossRef.
- A. T. Kowal, Spectrochim. Acta, Part A, 2002, 58, 1055–1067 CrossRef.
- M. Kumarasiri, C. Swalina and S. Hammes-Schiffer, J. Phys. Chem. B, 2007, 111, 4653–4658 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, computed wavenumbers for all investigated molecules, R matrix definitions, and computational and available gas phase experimental literature data. See DOI: 10.1039/d0cp03515g |
| This journal is © the Owner Societies 2020 |


