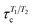Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heterogeneous dynamics in partially disordered proteins†
Salla I.
Virtanen‡
,
Anne M.
Kiirikki‡
,
Kornelia M.
Mikula
,
Hideo
Iwaï
 and
O. H. Samuli
Ollila
and
O. H. Samuli
Ollila
 *
*
Institute of Biotechnology, University of Helsinki, Helsinki, Finland. E-mail: samuli.ollila@helsinki.fi
First published on 4th September 2020
Abstract
Importance of disordered protein regions is increasingly recognized in biology, but their characterization remains challenging due to the lack of suitable experimental and theoretical methods. NMR experiments can detect multiple timescale dynamics and structural details of disordered protein regions, but their detailed interpretation is often difficult. Here we combine protein backbone 15N spin relaxation data with molecular dynamics (MD) simulations to detect not only heterogeneous dynamics of large partially disordered proteins but also their conformational ensembles. We observed that the rotational dynamics of folded regions in partially disordered proteins is dominated by similar rigid body rotation as in globular proteins, thereby being largely independent of flexible disordered linkers. Disordered regions, on the other hand, exhibit complex rotational motions with multiple timescales below ∼30 ns which are difficult to detect from experimental data alone, but can be captured by MD simulations. Combining MD simulations and backbone 15N spin relaxation data, measured applying segmental isotopic labeling with salt-inducible split intein, we resolved the conformational ensemble and dynamics of partially disordered periplasmic domain of TonB protein from Helicobacter pylori containing 250 residues. To demonstrate the universality of our approach, it was applied also to the partially disordered region of chicken Engrailed 2. Our results pave the way in understanding how TonB transfers energy from inner membrane to the outer membrane receptors in Gram-negative bacteria, as well as the function of other proteins with disordered domains.
Introduction
Long (>30 residue) disordered segments that lack the well defined 3D structure are found in 33% of eukaryotic proteins.1 These intrinsically disordered protein regions are associated with various diseases, including cancer, cardiovascular diseases, neurodegenerative diseases, and diabetes,2 yet their importance in biology is probably underestimated because they are difficult to characterize with the available experimental and theoretical methods. Intrinsically disordered proteins and regions participate in important functions also in bacteria, archaea and viruses.3 Furthermore, the importance of disordered linkers attached to folded protein domains is increasingly recognized in allosteric regulation, complex formation, biocatalysis and protein design.4–8 To fully understand the role of disordered protein regions in biology and exploit them in protein design, robust tools to determine their conformational ensembles and dynamics are needed. Average properties and distances between individual residues of disordered proteins can be accessed using small angle X-ray scattering (SAXS), electron paramagnetic resonance (EPR) or fluorescence experiments.9,10 On the other hand, nuclear magnetic resonance (NMR) experiments can detect multiple timescale dynamics and structural details at atomic resolution in disordered and partially disordered proteins. However, NMR experiments are limited by the spectral overlap and complications in the interpretation of the data, especially for large and partially disordered proteins.4,11–14We have recently resolved the problem of spectral overlap for partially disordered TonB protein with 101 folded and 149 disordered residues using segmental isotopic labeling with salt-inducible split intein.16 Moreover, we have used molecular dynamics (MD) simulations to interpret the rotational dynamics of asymmetrically shaped folded proteins from NMR spin relaxation times.15 However, the accuracy of force field parameters limits the applications of MD simulations to interpret the NMR data. For folded proteins, the main issue has been the underestimated water viscosity in the commonly used TIP3P water model, which leads to too fast rotational diffusion of rigid proteins.15,17 Nevertheless, this can be taken into account when calculating NMR parameters even for proteins with anisotropic shape.15 For disordered proteins, canonical force fields predict too condensed conformational ensembles and calculated NMR parameters often disagree with experiments.18–22 Attempts to overcome these issues have been made by reweighting the conformational ensembles23 or rescaling the timescales to reproduce the experimentally measured NMR spin relaxation times.22,24 While these approaches can be useful in the interpretation of individual experiments, they cannot be generally applied for proteins with heterogeneous dynamics in complex environments, such as membrane bound disordered linkers. Furthermore, rescaling of timescales is ambiguous for disordered proteins without clearly distinguishable dynamical processes, and ensemble reweighting can be used only when the original ensemble is not too far from the correct solution.
Here, we show that NMR spin relaxation times and MD simulations can be combined to resolve conformational ensembles of proteins with heterogeneous dynamics such as partially disordered proteins. We resolve conformational ensembles of two large (>100 residues) partially disordered proteins: periplasmic domain (residues 36–285) of TonB protein from Helicobacter pylori (HpTonB) and residues 143–259 of chicken Engrailed 2 (EN2). Periplasmic domain of TonB propagates energy created by proton motive force in the inner membranes of Gram-negative bacteria to the TonB dependent receptors (TBDT) in the outer membranes via unknown mechanism.25 Engrailed 2 is a transcription factor in which partially disordered residues 143–259 are highly conserved and crucial, in particular, in the binding of transcriptional regulators.26–28 The resolved conformational ensembles give novel insight in the rotational timescales of disordered protein regions and in the biological function of TonB proteins. Furthermore, our results pave the way in understanding of relevant properties and functions of disordered protein regions in biology and protein engineering.
Results and discussion
Resolving conformational ensembles of partially disordered proteins using spin relaxation data and MD simulations
The periplasmic domain of TonB protein in Gram-negative bacteria consists of the folded C-terminal region (residues 185–285 in HpTonB) and disordered proline rich region (residues 31–184 in HpTonB, shown in Fig. 1A).16 We have recently determined the NMR structure of the folded C-terminal domain in HpTonB from a construct containing the last 107 residues (HpTonB179–285) and measured the backbone N–H spin relaxation times of almost all residues in the periplasmic region of TonB protein from Helicobacter pylori (HpTonB36–285) using the segmental isotopic labeling with salt-inducible split intein.16,29 The main conclusion from these experiments is that the structure and dynamics of the folded C-terminal domain is largely independent of the proline rich disordered region. However, more detailed interpretation of the conformational ensemble and dynamics of HpTonB36–285 containing disordered region cannot be made from the experimental data alone.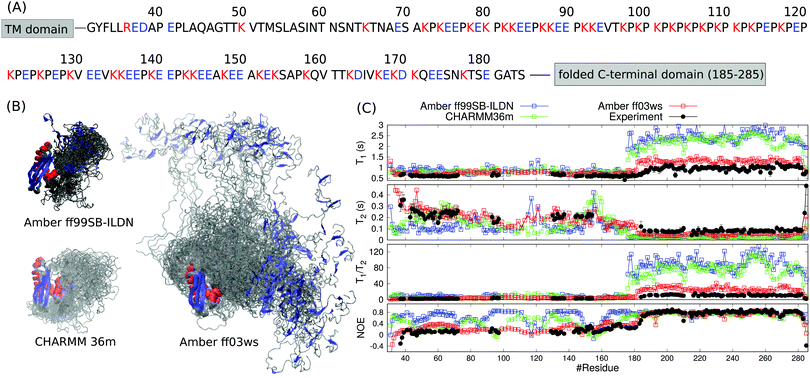 | ||
| Fig. 1 (A) Sequence of the disordered proline rich region (residues 31–184) in HpTonB. The trans membrane (TM) domain is anchored in the inner membrane of Gram-negative bacteria and the folded C-terminal domain interacts with TonB dependent receptors in the outer membrane. Aminoacids bearing positive or negative charge in neutral pH are colored with red and blue, respectively. (B) Overlayed snapshots from MD simulations of HpTonB30–285 with different force fields without additional salt. The orientation of folded domain is fitted in each snapshot. Residues within α-helices and β-strands are red and blue, respectively. (C) Spin relaxation times calculated from simulations with different force fields compared with the experimental values without additional salt. Rotational diffusion of the folded regions in Amber ff99SB-ILDN and CHARMM36m simulations is divided by a factor 2.9 in the spin relaxation time calculation to correct underestimated viscosity of TIP3P water model.15 | ||
To resolve the conformational ensemble of partially disordered periplasmic domain of HpTonB, we initiated MD simulations of TonB30–285 starting from the fully extended linker conformation using three different force fields. In simulations with the Amber ff99SB-ILDN30 and CHARMM36m31 force fields, the linker rapidly collapsed (40 ns and 120 ns, respectively) and the protein formed compact structures with the radius of gyration of 2.29 ± 0.02 nm and 2.32 ± 0.05 nm, respectively (Fig. 1B). The Amber ff03ws force field32 resulted in significantly more extended structure with the radius of gyration of 3.5 ± 0.2 nm. To evaluate the results from different force fields against experimental data, we calculated the backbone 15N spin relaxation times, T1, T2 and NOE relaxation, from simulations taking into account the effect of incorrect water viscosity in TIP3P water model for the folded region (Fig. 1C).15 Amber ff99SB-ILDN and CHARMM36m force fields with the collapsed structures overestimate the T1/T2 ratios for the C-terminal domain, suggesting that the rotation of the folded region is too slow in these simulations. In Amber ff03ws simulations with more extended conformational ensemble, the rotation of C-terminal domain is faster and the spin relaxation times are in better agreement with experiments. Therefore, we conclude that the simulations with Amber ff99SB-ILDN and CHARMM36m force fields predict overcondensated conformations for the disordered proline rich region, and that the whole protein rotates as a single relatively rigid body in these simulations with significantly slower timescales than the C-terminal domain without the disordered region attached. In more realistic Amber ff03ws simulations, the disordered region with more extended conformations has only a marginal effect on the rotational dynamics of C-terminal domain, in line with the interpretation from experimental spin relaxation data.16 Overcondensation of disordered proteins in Amber ff99SB-ILDN and CHARMM36m simulations is reported also previously.19,20
Even though the spin relaxation times from the Amber ff03ws simulation are close to the experimental values in Fig. 1C, they slightly overestimate the T1/T2 ratios for residues in the C-terminal domain suggesting that the rotational dynamics of the folded region is still too slow when compared with experiments. To simulate the protein in conditions closer to experiments, we added 40 mM NaCl to the system, which approximately corresponds to the ionic strength of 20 mM sodium phosphate buffer solution at pH 6 that was used in the experiments. Indeed, the addition of salt led to the further extension of the disordered linker and faster rotational diffusion of the structured C-terminal domain (Table 1). Spin relaxation times from the simulation with 40 mM of NaCl are in good agreement with the experimental values (Fig. 2). Further increase of NaCl concentration to 150 mM did not affect the results neither in experiments nor in simulations (Fig. 2). The radius of gyration from simulations with 150 mM NaCl (5.3 ± 0.7 nm) was close to the experimental value (5.5 ± 0.7 nm) measured with the same salt concentration. In conclusion, both spin relaxation times and radius of gyration from the Amber ff03ws simulation agree with experiments when electrostatic conditions of solvent match with experiments, suggesting that this simulation can be used to interpret the spin relaxation times of partially disordered HpTonB36–285 protein.
| D x | D y | D z | D av | τ c | R g (nm) | |
|---|---|---|---|---|---|---|
| 0 mM | 1.3 ± 0.1 | 1.3 ± 0.1 | 1.4 ± 0.2 | 1.3 ± 0.2 | 13 ± 2 | 3.5 ± 0.2 |
| 40 mM | 1.80 ± 0.01 | 2.1 ± 0.2 | 2.4 ± 0.3 | 2.1 ± 0.2 | 7.9 ± 0.8 | 6.1 ± 0.2 |
| 150 mM | 1.65 ± 0.03 | 1.7 ± 0.1 | 4.1 ± 0.3 | 2.5 ± 0.2 | 6.6 ± 0.6 | 5.3 ± 0.7 |
 | ||
| Fig. 2 (A) Overlayed snapshots from Amber ff03ws MD simulations of HpTonB30–285 with 40 mM NaCl. The orientation of folded domain is fitted in each snapshot and color codes for secondary structure are similar to Fig. 1B. (B) Spin relaxation times calculated from Amber ff03ws simulations with 40 mM and 150 mM NaCl compared with experiments without additional salt (this work) and with 150 mM NaCl (from ref. 16). | ||
Extension of the disordered linker region upon the increase of NaCl concentration from 0 to 40 mM can be explained by the screened attractive interactions between oppositely charged residues in the proline rich linker of HpTonB. This is demonstrated in Fig. 3 by showing the directional correlations of vectors between Cα carbons in consecutive backbone residues in the disordered linker region (residues 31–200). Negative correlations between residues 95–120 and 120–140 in simulation without additional salt can be explained by the hairpin-like turning of the linker due to electrostatic attraction between residues 97–113, bearing a total charge of +9 from lysines, and residues 131–137, bearing a total charge of −2 from glutamic acids. The addition of 40 mM NaCl screens this attraction, thereby straightening the chain and eliminating the negative directional correlations. Our results suggest that the presence of ionic strength corresponding to the typical buffer concentrations used in experiments significantly screens the electrostatic interactions between charged residues in disordered proteins, thereby affecting their conformational ensembles. This should be taken into account when performing MD simulations that mimic the experimental conditions. However, further increase of ion concentration had much smaller effect on directional correlation, spin relaxation times, and conformational ensemble.
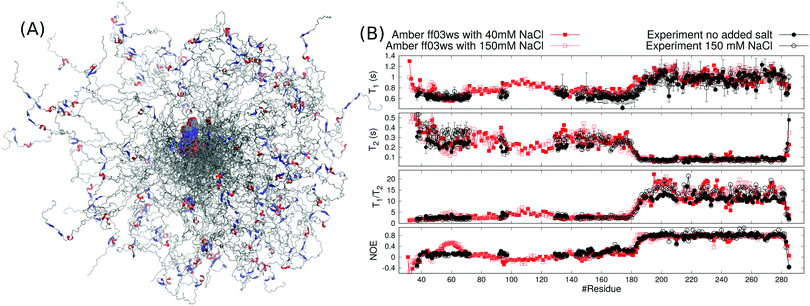
To test our approach also using other protein than HpTonB, we ran simulations of partially disordered region (residues 143–259) of chicken EN2 for which the experimental spin relaxation times measured with multiple magnetic fields are available in the literature.28 In Amber ff03ws simulation of EN2 without additional salt, the oppositely charged residues between N-terminal and C-terminal ends interact and the protein forms a loop-like conformational ensemble (Fig. 4A). Similarly to the TonB simulation without additional salt, T1 times measured with 800 MHz magnet are slightly overestimated in this simulation (Fig. 4C), indicating that the loop-like structure rotates too slowly. Furthermore, residues 151–166 in the N-terminal end form an artificial α-helix, which leads to a poor agreement with experimental spin relaxation times in this region. Because serine and aspartatic acids have overestimated tendencies to form α-helices in this force field,33 we mutated serine (148, 150, 153, 154, 155, 156) and aspartic acid (152 and 154) residues in the N-terminal end to threonine and glutamine, respectively. This mutated protein was then simulated with 40 mM NaCl to mimic the electrostatic conditions in experiments where 40 mM sodium succinate buffer was used.28 As observed for HpTonB, the attraction between charged residues is screened by the addition of salt and more extended conformational ensemble is observed (Fig. 4B). Together with the unfolding of artificial α-helix in residues 151–166, this leads to the improved agreement with experimental spin relaxation data (Fig. 4C). Also the results from different magnetic field strengths support this conclusion (Fig. S1 in the ESI†).
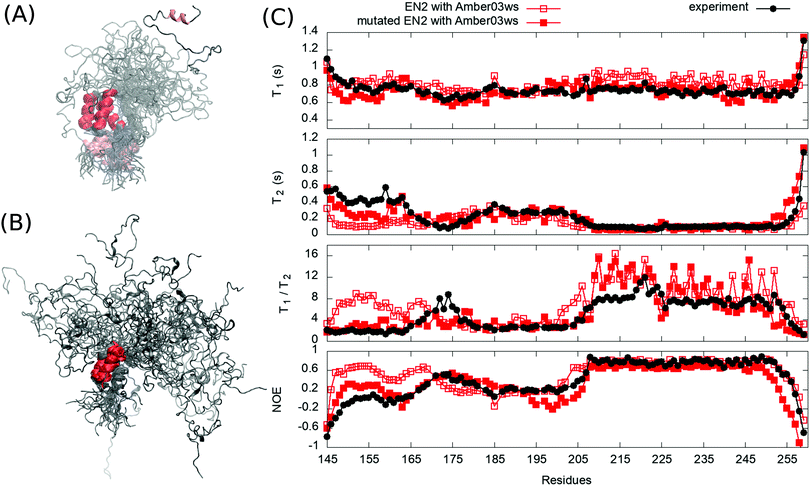 | ||
| Fig. 4 Overlayed snapshots from (A) EN2 simulation without additional salt and (B) from mutated EN2 simulation with 40 mM NaCl. (C) Spin relaxation times from simulations compared with experiments measured in 800 MHz.28 Spin relaxation times with different magnetic field strengths are shown in Fig. S1 (ESI†). Error bars of the experimental data are smaller than the point size. | ||
Our results for HpTonB and EN2 demonstrate that the 15N backbone spin relaxation times are sensitive to the conformational ensembles of partially disordered proteins, and can be therefore used to evaluate MD simulations of such proteins against NMR experiments. Notably, the differences in chemical shifts (calculated using SPARTA+34 or ShiftX35) between simulations with different force fields that predict distinct conformational ensembles for HpTonB (Fig. 1B) were not large enough to evaluate the simulations against experiments (Fig. S2, ESI†). The Amber ff03ws force field captured the essential features of conformational ensembles for both partially disordered proteins studied here when the ionic strength of solvent corresponded to the experimental conditions. However, the known caveats of this force field, such as overestimated tendency of serine and aspartic acid to form α-helices and underestimated stability of folded structures,19,33 may limit its wider usage. In conclusion, our results not only emphasize the necessity of developing better force fields for disordered protein regions, but also demonstrate that the backbone 15N spin relaxation times are good measures to evaluate conformational ensembles predicted by the force fields.
Rotational motions in partially disordered proteins
Rotational dynamics of folded proteins is typically analyzed from spin relaxation data assuming a rigid body motion for overall rotation and independent internal motions for each residue.36–39 Folded proteins exhibit rigid body overall rotational dynamics also in MD simulations and inaccuracies arising from incorrect viscosity of water models can be corrected during spin relaxation time calculations by scaling the overall rotational diffusion coefficients.15,17,40 Because the rigid body approximation is obviously invalid for disordered protein regions, different approaches to analyze rotational motions of disordered proteins have been proposed.13 However, the number and nature of rotational processes occurring in disordered protein regions remains unclear.22,28,41,42Because our HpTonB30–285 simulations with Amber ff03ws force field parameters give spin relaxation times in good agreement with experiments when the ionic strength of solvents match (Fig. 2), we analyzed the underlying rotational timescales of both folded and disordered regions from these simulations using the regularized inverse Laplace transformation (ILT),43 which we used also to perform the Fourier transform of the rotational correlation functions during the spin relaxation time calculations.15 In this approach, each backbone N–H bond rotational correlation function is written as a sum of large number of exponentials (here N = 371)
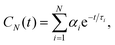 | (1) |
For folded proteins, the timescales related to the overall rigid body rotation dominate the rotation processes with the weight factors between 0.5–0.9 in almost all residues of HpTonB194–285 (Fig. 5 and Fig. S6, ESI†) and PaTonB-96 from Pseudomonas aeruginosa15 (Fig. S7, ESI†). Intermediate (1–4 ns) and very fast (10 ps or faster) timescales have small contributions with the weight factors between 0.1–0.3 in the Amber ff03ws simulation of folded HpTonB194–285 (Fig. 5). In Amber ff99SB-ILDN simulations of folded HpTonB194–285 and PaTonB-96 proteins, the very fast timescales have similar contribution, but intermediate timescales are observed only for few residues (Fig. S6 and S7, ESI†). Therefore, our MD simulations suggest that the two-state (also known as Lipari–Szabo) model36,37 with independent overall and internal rotation timescales is a reasonable approximation for rotational dynamics of folded proteins, even though a third timescale with small weight is observed in simulations with Amber ff03ws force field. Moreover, the αi coefficients for rigid body motions approximately corresponds the Lipari–Szabo order parameters37 in folded regions.
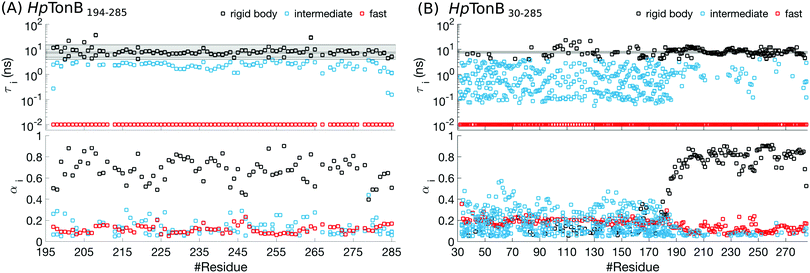 | ||
| Fig. 5 Rotational timescales (top) and related weight coefficients (bottom), defined in eqn (1), from Amber ff03ws simulation of (A) a folded HpTonB194–285 and (B) a partially disordered HpTonB36–285 protein. Only timescales with the weight coefficients larger than αi > 0.05 are shown. Black horizontal lines and the shaded region between the extreme values display timescales from rigid body rotational diffusion coefficients. To guide the eye, the timescales above τi ≈ 4 ns (the fastest rigid body timescale observed for folded HpTonB194–285 protein) are labeled as rigid body motions (black), the timescales corresponding to the saving frequency of coordinates in simulations (τi = 10 ps) are labeled as fast (red), and the timescales in between (10 ps < τi < 4 ns) are labeled as intermediate (turquoise). | ||
Most residues in the folded region (residues 185–285) of partially disordered HpTonB30–285 exhibit similar distribution of rotational timescales as observed in globular proteins: timescales corresponding to rigid body motions dominate, while very fast and intermediate timescales have minor contributions (Fig. 5). Encouraged by this observation, we calculated the rotational diffusion coefficients of folded domains having linkers with different lengths attached. Even though the mean square angle deviations around inertia axes exhibited some non-linear features with increasing linker length (see ESI†), we think that the estimated rotational diffusion coefficients and related timescales can be used to analyze the influence of a disordered linker on rotational dynamics of the folded region. As expected, the rotation of a folded region slows down upon the increasing length of attached linker (Table 2). However, the overall dynamics of folded domain in HpTonB179–285 is only slightly faster than in HpTonB30–285, even though the latter protein has 2.34 times more residues. This is in line with the small changes in experimental spin relaxation times upon increasing the length of linker observed in our previous work.16 These results suggest that the linker is very flexible and that the rotational dynamics of the folded C-terminal domain is almost independent of the attached flexible disordered linker. This conclusion is supported by the similar results for overall timescales estimated from experimental T1/T2 ratios and from MD simulation analysis in Table 2. The analysis using T1/T2 ratio assumes an isotropic rigid body rotational diffusion for protein,45 while MD simulation analysis takes anisotropic effects fully into account.15 Similarity of the results from these two approaches suggests that the assumption of rigid body rotational diffusion is relatively reasonable for folded domains even with long disordered linkers attached.
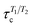 , are taken from our previous work16
, are taken from our previous work16
Disordered region in HpTonB30–285 (residues 30–184) exhibits clearly different distribution of rotational motions than the folded region, having dispersed timescales between approximately 60 ps and 30 ns without any dominating timescales (Fig. 5). Similar differences in distribution of timescales between folded and disordered regions are seen also in HpTonB30–285 with 150 mM NaCl (Fig. S8, ESI†) and EN2 (Fig. S9, ESI†), although intermediate timescales are more pronounced in the folded region of EN2, most likely due to the less rigid structure than in HpTonB simulations. The large number of detected timescales in disordered regions in both proteins suggests that the models assuming two or three timescales for rotational motions are too simple to capture all relevant rotational processes in disordered proteins. This is in line with the recent study where dihedral rotation and rotational tumbling motions of peptide planes were found to have multiple timescales.42 Because large number of parameters are needed to describe such dynamics, the multiple timescale dynamics is very difficult to detect even with the excessive amount of experimental data measured at different conditions.28,41 Khan et al. have analyzed rotational timescales of EN2 by fitting a sum of exponential correlation functions with six fixed timescales to the experimental data detected at different magnetic fields.28 In line with our results (Fig. S9, ESI†), timescales between ∼10 ps and ∼1 ns were not present in the folded region in their analysis. However, their dominant timescale, 5.27 ns, is shorter than ∼10 ns in our results, and they observed significant weight for a very long 21 ns timescale, which is not present in our results. For disordered region of EN2, Khan et al. observed dispersed timescales between 21 ps and 21 ns which is in line with our results. However, the timescale of 1.33 ns dominated the rotation of disordered region in their analysis, while we did not detect any dominant timescale in the disordered region. We believe that these differences may arise because the dynamical model with six fixed timescales that are equal for all residues may be too simple for partially disordered proteins. Our MD simulations suggest that disordered protein regions have more complex distributions of rotational timescales with multiple components that vary between the residues. While this distribution of timescales is very difficult to detect by fitting to even a vast amount of experimental data, MD simulations with realistic force field parameters can capture the relevant rotational processes detected by spin relaxation times for disordered protein regions, thereby giving an interpretation of experimental data with unprecedented details.
Implications to TonB function
TonB proteins are part of TonB complexes, which propagate energy generated by the proton-motive force in the inner membrane of Gram-negative bacteria to the TonB dependent receptors (TBDTs) in the outer membrane with unknown mechanism.25 Because TBDTs use this energy to transport vital nutrients inside bacteria, TonB is a potential target for antibiotics. N-terminal domain of TonB protein is anchored in the inner membrane and the proline rich linker region is expected to span across the approximately 20 nm wide periplasmic space to enable the C-terminal domain to interact with TBDTs in the outer membrane25,46–48 (Fig. 6). The folded domains of proteins in TonB complex have been characterized using cryo-EM, X-ray crystallography, NMR, single molecule experiments and MD simulations.16,29,49–57 However, the role of disordered proline rich linker in TonB function (residues 36–184 in HpTonB, Fig. 1) is poorly understood due to the lack of robust methods to characterize such protein domains. Electron paramagnetic resonance (EPR) and early NMR experiments suggest that the TonB linker in E. coli is disordered but still relatively rigid due to abundant polyproline helices,47,58,59 while some studies assume a completely rigid structure that would enable the mechanical energy transfer across periplasm via rigid rotation.50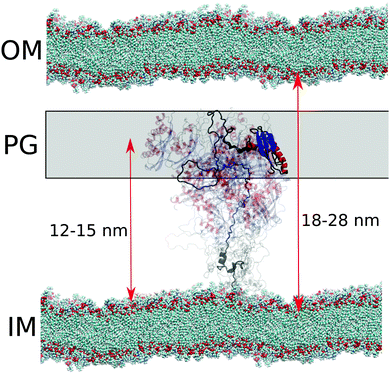 | ||
| Fig. 6 Schematic figure of conformational ensemble sampled by periplasmic TonB in sub-microsecond timescales in cell envelope of Gram-negative bacteria. Distances from the inner membrane (IM) to the outer membrane (OM) and proteoglycan (PG) layer are from ref. 46. | ||
In the conformational ensemble of HpTonB36–285 in solution with physiological ion concentration (Fig. 2), resolved here using Amber ff03ws simulations and NMR spin relaxation experiments, the proline rich linker is very flexible with the rotational timescales faster than 30 ns (Fig. 5) and the folded C-terminal domain rotates almost independently of the linker region (Table 2). On the other hand, significant fractions of polyproline helices (PPII) with the probability up to approximately 70% were observed in the linker region in our simulations (Fig. S17, ESI†). This is in line with the previous NMR and CD measurements of TonB sequence from E. coli.47,58,59 Further data supporting the relatively rigid polyproline helix conformations of the TonB linker in E. coli comes from DEER EPR experiments, where distances between spin labels at different locations in the linker were measured.47 The EPR experiments give average length of 4.6 ± 0.1 nm for the residues 88–106 in E. coli TonB consisting mainly of PK repeats. The corresponding sequence in HpTonB between residues 94–112 (Fig. S16B, ESI†) has the same average length of 4.6 ± 0.2 nm in the Amber ff03ws simulation with 40 mM NaCl. In conclusion, the conformational ensemble from Amber ff03ws simulations (Fig. 2) is in line with the experimental spin relaxation data, as well as with the interpretation of previous NMR and EPR experiments from E. coli sequence,47,58,59 suggesting that the linker is disordered but has relatively extended conformation with high propensity of polyproline helices.
Because crystal structures suggest that TonB interacts with TBDTs via the β3 strand in the folded C-terminal domain of TonB (residues 272–281 in HpTonB),53,54 the linker domain should reach across the approximately 20 nm wide periplasmic space46 to bring the C-terminal domain into contact with TBDTs in outer membrane (Fig. 6). In our conformational ensemble, resolved from Amber ff03ws simulations in 40 mM NaCl solution (Fig. 2), the maximum distance between the β3 strand atoms and the end of transmembrane domain (residue 30) is 15.2 nm with the average value of 11.9 ± 0.3 nm, which is close to the typical distance between inner membrane and proteoglycan layer in Gram-negative bacteria, but shorter than the width of periplasmic space (Fig. 6).
In summary, our results suggest that the periplasmic part of TonB exhibits rapid conformational fluctuations with the timescales faster than 30 ns and that the C-terminal domain locates on average close to the proteoglycan layer (Fig. 6). These results are in line with the previously proposed models where the C-terminal domain of TonB reaches only to the proteoglycan layer, while the binding site in TBDTs extends into periplasm to interact with the β3 helix in CTD of TonB at the proteoglycan layer.50,60 Alternatively, the proton-motive force could be used to increase the linker length to push the C-terminal domain of TonB to interact with the TBDTs in the outer membrane, and the relaxation back to the equilibrium length would then mechanically open the TBDT. On the other hand, the high flexibility of the linker and uncorrelated rotational motions of linker and the folded C-terminal domain do not support models where rotational torque is mediated across periplasmic space via rigid linker.50 Also scanning of TBDTs directly from the outer membrane48 seems less likely due to the short average length of the linker. However, we cannot exclude the possibility that changing pH conditions, TonB dimerization or its interactions with membrane, proteoglycan layer or other proteins in TonB complex would increase the length or rigidity of the linker. We believe that MD simulations with realistic conformational ensembles of disordered linkers, evaluated using experimental spin relaxation times, paves the way for further studies to understand the function of TonB complex, as well as other biological machineries where disordered protein regions play crucial roles.
Conclusions
Our results show that the backbone 15N spin relaxation times are sensitive not only to the protein dynamics at multiple timescales, but also to the conformational ensemble of partially disordered proteins. Using this feature, we evaluated the conformational ensembles of partially disordered HpTonB protein from MD simulations with different force fields against experimental spin relaxation time data. Simulations with Amber ff03ws force field32 predicted the conformational ensemble of periplasmic domain in HpTonB when the ionic strength of solvent corresponded the experimental conditions. The presence of sufficient amount of ions was necessary because they screen electrostatic interactions between charged residues, thereby having a substantial influence on conformational ensemble. These conclusions were further supported by the simulations of EN2 protein compared with previously published spin relaxation data.28MD simulations that reproduced the experimental spin relaxation times revealed that the timescales from overall rigid body rotation dominate in fully folded proteins and folded regions in partially disordered proteins, while very fast (10 ps or faster relaxation times) and intermediate (1–4 ns relaxation times) timescales give small contributions. Furthermore, the rotational dynamics of folded region was almost independent of the attached disordered linker. Therefore, the estimation of overall rotational timescales from experimental T1/T2 ratio using simple model assuming isotropic rotation45 gave reasonable results even for folded region with long disordered linker attached. In contrast, disordered regions exhibit rotational dynamics with multiple dispersed timescales between 60 ps and 30 ns without any dominating contribution, suggesting that the dynamical modes of disordered proteins are very difficult to capture by fitting to even a large amount of experimental data. We suggest that the dynamical modes of disordered protein regions can be captured using MD simulations with accurate force field and solvent ionic strength matching the experimental conditions.
The resolved conformational ensemble of HpTonB36–285 is in line with the previous NMR and EPR studies47,58,59 of TonB linker from E. coli, but gives unprecedented details of periplasmic domain of TonB that helps to understand its function. In our results, the equilibrium length of the TonB linker is not sufficient to reach across the periplasmic space, suggesting that either TBDTs has to extend the periplasmic space,50,60 or the length of linker has to increase, for example, due to changing pH conditions or interactions with other molecules. One possible scenario is that the proton-motive force would be used to induce such increase in the linker length. The energy released by the relaxation of linker to its equilibrium length could be then used to transport nutrients through the TBDT. Our results pave the way for MD simulations that could be combined with experimental approaches to test this, and other hypotheses on the functional mechanism of TonB complex function.
Using MD simulations to interpret the conformational ensembles and dynamics of disordered protein regions from NMR data has two main advantages over the other available methods.11–13,41,61 First, MD simulations that correctly predict the spin relaxation times can be used to interpret the experiments without a priori assumptions about the amount of rotational timescales. Second, MD simulation force fields that give correct conformational ensembles for disordered protein regions can be straightforwardly used to model these regions within complex biomolecules assemblies under various conditions. For example, our results suggest that TonB complex could be simulated by combining the Amber ff03ws force field with Amber compatible lipid force fields62,63 in order to fully understand its function. However, applications of Amber ff03ws force field are limited by its problems to predict the stability of α-helices in some situations.19,33 Therefore, our results also emphasize the necessity of force field development to correctly capture the conformational ensembles of partially disordered proteins in various conditions. Our results suggest that the backbone 15N spin relaxation times are suitable experimental references for these efforts because they are more sensitive to the conformational ensemble than, for example, chemical shifts which are often used in force field optimization or to resolve conformational ensembles of disordered proteins.19,64
Materials and methods
MD simulations
The protein significantly collapsed in both Amber ff99SB-ILDN and CHARMM36m simulations during 40 ns and 120 ns, respectively. Due to the reduced size of the protein, the amount of water molecules were reduced to 45950 and 35892 in these simulations, respectively. The simulation were then continued to have total lengths of 384 ns and 520 ns, respectively. The last 280 ns and 400 ns were used in the analysis, respectively. The size of protein in the Amber ff03ws simulation was much less reduced and the amount of water molecules was reduced to 123497 after 5.3 ns simulation. This system was then simulated 1171 ns and the last 1000 ns was used in the analyzes. The temperature was 310 K in Amber ff99SB-ILDN and CHARMM36m simulations and 298 K in the Amber ff03ws simulation. Simulations were ran using Gromacs versions between 5.0 and 2020 series.67 Rest of the simulation details are described in the ESI.† Simulation files and trajectories are available from ref. 68–70.
Sodium and chloride ions described with parameters containing the electronic continuum correction (ECC),71,72 available from https://bitbucket.org/hseara/ions/, were added into the Amber ff03ws simulation to study the influence of solvent ionic strength on conformational ensemble. The 6 chloride counterions were described by the default Amber ff03ws parameters. Because the protein immediately expanded upon addition of 150 mM NaCl and started to interact with its own periodic image after 200 ns simulation, the number of water molecules was increased for simulations containing ions. Simulation containing 150 mM NaCl had 261780 water molecules with 711 Na+ and Cl− ions, and simulation containing 40 mM NaCl had 262822 water molecules with 190 Na+ and Cl− ions. Simulation files and trajectories with NaCl are available from ref. 73 and 74.
In our previous study, we showed that the underestimated viscosity of TIP3P water model can be corrected during spin relaxation time calculation by dividing the rotational diffusion coefficients of folded proteins with a constant factor of 2.9.15 Here, we apply the same approach to the folded C-terminal domain of HpTonB30–285 when calculating the spin relaxation times from Amber ff99SB-ILDN and CHARMM36m simulations, where TIP3P water was used. For this, we first calculate the rotational diffusion coefficients of the folded C-terminal end (residues 196–280). The rotational correlation functions from N–H bonds of residues 175–285 were then divided to the internal and overall motions, and the contribution of overall motion was corrected during spin relaxation time calculation by dividing the diffusion coefficients with a factor 2.9 as described in our previous work.15 The water viscosity correction was not applied to the disordered linker region because it does not rotate as a rigid body and is therefore expected to be less affected by the fluid viscosity.82 Because spin relaxation times from Amber ff03ws force field are in good agreement with experiments for the folded HpTonB194–285 protein without any correction for the water viscosity (Fig. S3 in the ESI†), the spin relaxation times from Amber ff03ws simulations of HpTonB36–285 and EN2 protein were calculated directly from simulation data without any corrections for water viscosity.
Correlation functions up to one hundredth of the simulation time should give a sufficient statistics for the analysis of rotation from a single molecule MD simulation.83 We observed that insufficient statistics in correlation functions induce artificial timescales with the longest possible timescale (50 ns) when fitting the correlation function to eqn (1). Therefore, when calculating spin relaxation times directly from Amber ff03ws simulations without using diffusion coefficients, we selected the time frames to be analyzed from correlation functions such that the number of weights above 0.05 for artificial 50 ns timescale is minimized. The analyzed time frames from correlation functions were the first 15 ns for HpTonB194–285, the first 10 ns for HpTonB30–285 without NaCl, and the first 25 ns for HpTonB30–285 with NaCl and EN2.
Quantitative error analysis of calculated spin relaxation times is complicated because each step in the analysis has different sources of errors. However, independent simulation replicas of folded PaTonB-96 protein in our previous work15 gives an average deviations of ΔT1 = 0.06 s, ΔT2 = 0.02 s, and ΔNOE = 0.04, which can be considered as the estimates of accuracy of the calculated values.
NMR spin relaxation time experiments
Using segmental labeling with salt-inducible split intein as described in our previous work,16 we prepared HpTonB36–285 with residues 36–154 15N labeled, as well as HpTonB36–285 bearing K154R mutation with residues 155–285 15N labeled. This segmental labeling reduces the overlap of NMR peaks and enables the measurement of spin relaxation times of almost all residues in large partially disordered proteins.16 Spin relaxation times were measured using 5 mm Shigemi tubes filled with 1.37 mM concentration of HpTonB36–285 with residues 36–154 labeled, or 1.56 mM concentration of HpTonB36–285 with residues 155–285 labeled. Both samples were solvated with 20 mM phosphate buffer at pH 6 and 5% of D2O. Experiments were performed on a Bruker Avance 850 MHz spectrometer equipped with a cryogenically cooled probe head using the same pulse sequence45,84,85 and settings as previously16 with the delay times of 50, 100, 200, 300, 500, 700, and 900 ms for T1, and 34, 68, 102, 136, 170, 204, 238, and 272 ms for T2. The sample temperature in experiments was 298 K. The spin relaxation times of HpTonB36–285 with 150 mM NaCl were measured previously.16 The T1 and T2 relaxation data were processed and analyzed using Bruker Dynamic Center software (version 2.5.5) and the NOE relaxation times were processed and analyzed using CcpNmr Analysis software (version 2.4.2).86SAXS experiments
For SAXS experiments, HpTonB36–285 was prepared without isotopic labeling as described previously16 and solvated to 200 μl of 20 mM phosphate buffer at pH 6 with 150 mM NaCl. Concentration of HpTonB36–285 in the sample was 0.36 mM. SAXS experiments coupled with Size-Exclusion Chromatography (SEC-SAXS) were performed at beamline B21, Diamond Light Source, UK. Radius of gyration was calculated from frames with integral of ratio to background larger than 0.255 using Guinier analysis. After discarding the largest and smallest values, the average of these values was calculated and the error bars were determined to cover all the values.Data availability
The simulation trajectories are available from ref. 68–70, 73–77, 79, 80 and collection of derived data and computer codes from ref. 87.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Hannes Beyer and Miska Niemelä for the sample preparation for the SAXS experiments, and Sofia Backlund for the help in processing experimental spin relaxation time data. CSC-IT center for Science Ltd, Finland, is acknowledged for the allocation of computational resources. This work was financially supported by the Academy of Finland (315596, 319902, 277335) and Sigrid Juselius Foundation. The NMR facility has been supported by Biocenter Finland and HiLIFE-INFRA. We thank Diamond Light Source (Didcot, UK) for allowing access to the BioSAXS beamline B21.Notes and references
- J. Ward, J. Sodhi, L. McGuffin, B. Buxton and D. Jones, J. Mol. Biol., 2004, 337, 635–645 CrossRef CAS.
- V. N. Uversky, C. J. Oldfield and A. K. Dunker, Annu. Rev. Biophys., 2008, 37, 215–246 CrossRef CAS.
- B. Xue, A. K. Dunker and V. N. Uversky, J. Biomol. Struct. Dyn., 2012, 30, 137–149 CrossRef CAS.
- Y. E. Shapiro, Prog. Biophys. Mol. Biol., 2013, 112, 58–117 CrossRef CAS.
- X. Chen, J. L. Zaro and W.-C. Shen, Adv. Drug Delivery Rev., 2013, 65, 1357–1369 CrossRef CAS.
- E. Papaleo, G. Saladino, M. Lambrughi, K. Lindorff-Larsen, F. L. Gervasio and R. Nussinov, Chem. Rev., 2016, 116, 6391–6423 CrossRef CAS.
- R. B. Berlow, H. J. Dyson and P. E. Wright, J. Mol. Biol., 2018, 430, 2309–2320 CrossRef CAS.
- N. D. Keul, K. Oruganty, E. T. Schaper Bergman, N. R. Beattie, W. E. McDonald, R. Kadirvelraj, M. L. Gross, R. S. Phillips, S. C. Harvey and Z. A. Wood, Nature, 2018, 563, 584–588 CrossRef CAS.
- D. Eliezer, Curr. Opin. Struct. Biol., 2009, 19, 23–30 CrossRef CAS.
- M. Brucale, B. Schuler and B. Samorí, Chem. Rev., 2014, 114, 3281–3317 CrossRef CAS.
- M. R. Jensen, P. R. Markwick, S. Meier, C. Griesinger, M. Zweckstetter, S. Grzesiek, P. Bernadó and M. Blackledge, Structure, 2009, 17, 1169–1185 CrossRef CAS.
- M. R. Jensen, M. Zweckstetter, J.-R. Huang and M. Blackledge, Chem. Rev., 2014, 114, 6632–6660 CrossRef CAS.
- N. Salvi, A. Abyzov and M. Blackledge, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 43–60 CrossRef CAS.
- S. Milles, N. Salvi, M. Blackledge and M. R. Jensen, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 79–100 CrossRef CAS.
- O. H. S. Ollila, H. A. Heikkinen and H. Iwai, J. Phys. Chem. B, 2018, 122, 6559–6569 CrossRef CAS.
- A. Ciragan, S. M. Backlund, K. M. Mikula, H. M. Beyer, O. H. S. Ollila and H. Iwaï, Front. Chem., 2020, 8, 136 CrossRef.
- V. Wong and D. A. Case, J. Phys. Chem. B, 2008, 112, 6013–6024 CrossRef.
- J. Huang and A. D. MacKerell, Curr. Opin. Struct. Biol., 2018, 48, 40–48 CrossRef.
- P. Robustelli, S. Piana and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4758–E4766 CrossRef.
- J. Henriques, L. Arleth, K. Lindorff-Larsen and M. Skepö, J. Mol. Biol., 2018, 430, 2521–2539 CrossRef.
- K. Kämpf, S. A. Izmailov, S. O. Rabdano, A. T. Groves, I. S. Podkorytov and N. R. Skrynnikov, Biophys. J., 2018, 115, 2348–2367 CrossRef.
- N. Rezaei-Ghaleh, G. Parigi, A. Soranno, A. Holla, S. Becker, B. Schuler, C. Luchinat and M. Zweckstetter, Angew. Chem., 2018, 57, 15262–15266 CrossRef.
- N. Salvi, A. Abyzov and M. Blackledge, J. Phys. Chem. Lett., 2016, 7, 2483–2489 CrossRef.
- Y. Xue and N. R. Skrynnikov, J. Am. Chem. Soc., 2011, 133, 14614–14628 CrossRef.
- H. Celia, N. Noinaj and S. K. Buchanan, Int. J. Mol. Sci., 2020, 21, 375 CrossRef.
- L. T. Peltenburg and C. Murre, EMBO J., 1996, 15, 3385–3393 CrossRef.
- I. Foucher, M. L. Montesinos, M. Volovitch, A. Prochiantz and A. Trembleau, Development, 2003, 130, 1867–1876 CrossRef.
- S. Khan, C. Charlier, R. Augustyniak, N. Salvi, V. Déjean, G. Bodenhausen, O. Lequin, P. Pelupessy and F. Ferrage, Biophys. J., 2015, 109, 988–999 CrossRef.
- A. Ciragan, A. S. Aranko, I. Tascon and H. Iwaï, J. Mol. Biol., 2016, 428, 4573–4588 CrossRef.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CrossRef.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell Jr, Nat. Methods, 2017, 14, 71–73 CrossRef.
- R. B. Best, W. Zheng and J. Mittal, J. Chem. Theory Comput., 2014, 10, 5113–5124 CrossRef.
- R. B. Best, D. de Sancho and J. Mittal, Biophys. J., 2012, 102, 1462–1467 CrossRef.
- Y. Shen and A. Bax, J. Biomol. NMR, 2010, 48, 13–22 CrossRef.
- S. Neal, A. Nip, H. Zhang and D. S. Wishart, J. Biomol. NMR, 2003, 26, 215–240 CrossRef.
- H. Wennerström, B. Lindman, O. Söderman, T. Drakenberg and J. B. Rosenholm, J. Am. Chem. Soc., 1979, 101, 6860–6864 CrossRef.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- D. Korzhnev, M. Billeter, A. Arseniev and V. Orekhov, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 38, 197–266 CrossRef CAS.
- A. G. Palmer, Chem. Rev., 2004, 104, 3623–3640 CrossRef CAS.
- J. J. Prompers and R. Brüschweiler, J. Am. Chem. Soc., 2002, 124, 4522–4534 CrossRef CAS.
- A. Abyzov, N. Salvi, R. Schneider, D. Maurin, R. W. Ruigrok, M. R. Jensen and M. Blackledge, J. Am. Chem. Soc., 2016, 138, 6240–6251 CrossRef CAS.
- N. Salvi, A. Abyzov and M. Blackledge, Angew. Chem., 2017, 56, 14020–14024 CrossRef CAS.
- A. Nowacka, N. Bongartz, O. S. Ollila, T. Nylander and D. Topgaard, J. Magn. Reson., 2013, 230, 165–175 CrossRef CAS.
- A. Ribeiro, N. G. Wade-Jardetzky, R. King and O. Jardetzky, Appl. Spectrosc., 1980, 34, 299–305 CrossRef CAS.
- L. E. Kay, D. A. Torchia and A. Bax, Biochemistry, 1989, 28, 8972–8979 CrossRef CAS.
- V. R. F. Matias, A. Al-Amoudi, J. Dubochet and T. J. Beveridge, J. Bacteriol., 2003, 185, 6112–6118 CrossRef CAS.
- S. Domingo Köhler, A. Weber, S. P. Howard, W. Welte and M. Drescher, Protein Sci., 2010, 19, 625–630 CrossRef.
- A. Sverzhinsky, J. W. Chung, J. C. Deme, L. Fabre, K. T. Levey, M. Plesa, D. M. Carter, P. Lypaczewski and J. W. Coulton, J. Bacteriol., 2015, 197, 1873–1885 CrossRef CAS.
- H. Celia, N. Noinaj, S. D. Zakharov, E. Bordignon, I. Botos, M. Santamaria, T. J. Barnard, W. A. Cramer, R. Lloubes and S. K. Buchanan, Nature, 2016, 538, 60–65 CrossRef CAS.
- P. E. Klebba, J. Bacteriol., 2016, 198, 1013–1021 CrossRef CAS.
- K. Yonekura, S. Maki-Yonekura, R. Matsuoka, Y. Yamashita, H. Shimizu, M. Tanaka and F. Iwabuki, eLife, 2018, 7, e37833 CrossRef.
- R. S. Peacock, A. M. Weljie, S. P. Howard, F. D. Price and H. J. Vogel, J. Mol. Biol., 2005, 345, 1185–1197 CrossRef CAS.
- D. D. Shultis, M. D. Purdy, C. N. Banchs and M. C. Wiener, Science, 2006, 312, 1396–1399 CrossRef CAS.
- P. D. Pawelek, N. Croteau, C. Ng-Thow-Hing, C. M. Khursigara, N. Moiseeva, M. Allaire and J. W. Coulton, Science, 2006, 312, 1399–1402 CrossRef CAS.
- S. J. Hickman, R. E. M. Cooper, L. Bellucci, E. Paci and D. J. Brockwell, Nat. Commun., 2017, 8, 14804 CrossRef.
- J. L. Sarver, M. Zhang, L. Liu, D. Nyenhuis and D. S. Cafiso, Biochemistry, 2018, 57, 1045–1053 CrossRef CAS.
- J. S. Oeemig, O. S. Ollila and H. Iwaï, PeerJ, 2018, 6, e5412 CrossRef.
- J. Evans, B. Levine, I. Trayer, C. Dorman and C. Higgins, FEBS Lett., 1986, 208, 211–216 CrossRef CAS.
- S. Brewer, M. Tolley, I. Trayer, G. Barr, C. Dorman, K. Hannavy, C. Higgins, J. Evans, B. Levine and M. Wormald, J. Mol. Biol., 1990, 216, 883–895 CrossRef CAS.
- D. M. Freed, S. M. Lukasik, A. Sikora, A. Mokdad and D. S. Cafiso, Biochemistry, 2013, 52, 2638–2648 CrossRef CAS.
- M. Krzeminski, J. A. Marsh, C. Neale, W.-Y. Choy and J. D. Forman-Kay, Bioinformatics, 2012, 29, 398–399 CrossRef.
- C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef CAS.
- J. Melcr, H. Martinez-Seara, R. Nencini, J. Kolafa, P. Jungwirth and O. H. S. Ollila, J. Phys. Chem. B, 2018, 122, 4546–4557 CrossRef CAS.
- M. R. Jensen, L. Salmon, G. Nodet and M. Blackledge, J. Am. Chem. Soc., 2010, 132, 1270–1272 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- O. H. S. Ollila, HpTonB(30-285) simulation Amber ff99SB-ILDN, 2020 DOI:10.5281/zenodo.3754109.
- O. H. S. Ollila, HpTonB(30-285) simulation CHARMM36m, 2020 DOI:10.5281/zenodo.3743358.
- O. H. S. Ollila, HpTonB(30-285) simulation Amber ff03ws, 2020 DOI:10.5281/zenodo.3754180.
- M. Kohagen, P. E. Mason and P. Jungwirth, J. Phys. Chem. B, 2016, 120, 1454–1460 CrossRef CAS.
- E. Pluhařová, H. E. Fischer, P. E. Mason and P. Jungwirth, Mol. Phys., 2014, 112, 1230–1240 CrossRef.
- I. S. Virtanen and O. H. S. Ollila, MD simulation of HpTonB(30-285) in 40 mM NaCl with Amber ff03ws force field, 2020 DOI:10.5281/zenodo.3756664.
- I. S. Virtanen and O. H. S. Ollila, MD simulation of HpTonB(30-285) in 150 mM NaCl with Amber ff03ws force field, 2020 DOI:10.5281/zenodo.3756668.
- O. H. S. Ollila, HpTonB(179-285) simulation Amber ff99SB-ILDN, 2020 DOI:10.5281/zenodo.3754253.
- O. H. S. Ollila, HpTonB(179-285) simulation Amber ff03ws, 2020 DOI:10.5281/zenodo.3754230.
- O. H. S. Ollila, HpTonB(194-285) simulation Amber ff03ws, 2020 DOI:10.5281/zenodo.3754272.
- L. Carlier, S. Balayssac, F.-X. Cantrelle, L. Khemtémourian, G. Chassaing, A. Joliot and O. Lequin, Biophys. J., 2013, 105, 667–678 CrossRef CAS.
- M. A. Kiirikki and O. H. S. Ollila, EN2(143-259) simulation with Amber ff03ws, 2020 DOI:10.5281/zenodo.3778216.
- M. A. Kiirikki and O. H. S. Ollila, Mutated EN2(143-259) simulation with Amber ff03ws, 2020 DOI:10.5281/zenodo.3778112.
- O. H. S. Ollila, ProteinDynamics, 2018 DOI:10.5281/zenodo.1288574.
- S.-H. Bae, H. J. Dyson and P. E. Wright, J. Am. Chem. Soc., 2009, 131, 6814–6821 CrossRef CAS.
- C.-Y. Lu and D. A. V. Bout, J. Chem. Phys., 2006, 125, 124701 CrossRef.
- G. Barbato, M. Ikura, L. E. Kay, R. W. Pastor and A. Bax, Biochemistry, 1992, 31, 5269–5278 CrossRef CAS.
- N. A. Farrow, R. Muhandiram, A. U. Singer, S. M. Pascal, C. M. Kay, G. Gish, S. E. Shoelson, T. Pawson, J. D. Forman-Kay and L. E. Kay, Biochemistry, 1994, 33, 5984–6003 CrossRef CAS.
- W. F. Vranken, W. Boucher, T. J. Stevens, R. H. Fogh, A. Pajon, M. Llinas, E. L. Ulrich, J. L. Markley, J. Ionides and E. D. Laue, Proteins, 2005, 59, 687–696 CrossRef CAS.
- O. H. S. Ollila, Data related to manuscript titled “Heterogeneous dynamics in partially disordered proteins”, 2020 DOI:10.5281/zenodo.3975900.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03473h |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2020 |