Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilization of proteins embedded in sugars and water as studied by dielectric spectroscopy†
Christoffer
Olsson
 ,
Rano
Zangana
and
Jan
Swenson
,
Rano
Zangana
and
Jan
Swenson
 *
*
Department of Physics, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: jan.swenson@chalmers.se
First published on 8th September 2020
Abstract
In many products proteins have become an important component, and the long-term properties of these products are directly dependent on the stability of their proteins. To enhance this stability it has become common to add disaccharides in general, and trehalose in particular. However, the mechanisms by which disaccharides stabilize proteins and other biological materials are still not fully understood, and therefore we have here used broadband dielectric spectroscopy to investigate the stabilizing effect of the disaccharides trehalose and sucrose on myoglobin, with the aim to enhance this understanding in general and to obtain specific insights into why trehalose exhibits extraordinary stabilizing properties. The results show the existence of three or four clearly observed relaxation processes, where the three common relaxations are the local (β) water relaxation below the glass transition temperature (Tg), the structural α-relaxation of the solvent, observed above Tg, and an even slower protein relaxation due to large-scale conformational protein motions. For the trehalose containing samples with less than 50 wt% myoglobin a fourth relaxation process was observed due to a β-relaxation of trehalose below Tg. This latter process, which was assigned to intramolecular rotations of the monosaccharide rings in trehalose, could not be detected for high protein concentrations or for the sucrose containing samples. Since sucrose has previously been found to form more intramolecular hydrogen bonds at the present hydration levels, it is likely that this rotation becomes too slow to be observed in the case of sucrose. However, this sugar relaxation has probably less influence on the protein stability below Tg, where the better stabilizing effect of trehalose on proteins can be explained by our observation that trehalose slows down the water relaxation more than sucrose does. Finally, we show that the α-relaxation of the solvent and the large-scale protein motions exhibit similar temperature dependences, which suggests that these protein motions are slaved by the α-relaxation. Furthermore, the α-relaxation of the trehalose solution is slower than for the corresponding sucrose solution, and thereby also the protein motions become slower in the trehalose solution, which explains the more efficient stabilizing effect of trehalose on proteins above Tg.
Introduction
Modern pharmaceutical molecules are becoming more and more structurally complex. It is becoming more common for a drug to consist of large protein structures, and with such large structures comes a decrease in stability, affecting the shelf life of these drugs. For this purpose, disaccharides in general, and trehalose in particular, are often used as stabilizing agent. Trehalose is a molecule which has been shown to exhibit many different bioprotective properties.1–8 The exact mechanisms for how disaccharides stabilize biological materials are however questions of active discussion and research.9–14 Several different structural and dynamical aspects of these mechanisms have been investigated. For example, from a structural point of view, trehalose and sucrose molecules are generally preferentially excluded from the protein surfaces,13–19 thus maintaining the proteins native hydration layer. This exclusion has also been shown to persist even at extremely low water concentrations,17,20 where an important aspect of trehalose is its natural capability of moisture control.21From a molecular dynamics point of view, it has been suggested that trehalose has a stronger reducing effect on the water dynamics.22–25 It has also been shown that trehalose exhibits a stronger coupling of its dynamics to the dynamics of the proteins, compared to other disaccharides.26,27 In order to study molecular dynamics of proteins and disaccharides in the presence of water, many different methods are commonly used, such as molecular dynamics simulations,13,18,25 neutron scattering techniques,19,22,28–39 Raman-spectroscopy17,40–43 and many others. One particular method which has often been used, particularly for the purpose of studying disaccharides44–48 and proteins, is dielectric spectroscopy.35,49–55 Dielectric spectroscopy measurements give insights into relatively slow molecular processes, which are related to the stability of the protein, such as the large-scale motions of the protein back-bone, or fluctuations of protein side-chains. However, mixtures of proteins and disaccharides in aqueous solutions have rarely been studied by dielectric spectroscopy, despite such studies should give answers regarding how these molecules affect each other.
For proteins in aqueous solutions multiple different relaxation processes have been observed.51,55 Examples of such relaxation processes include: a fast relaxation commonly attributed to methyl-group rotations, local protein side-chain relaxations, and large-scale conformational changes of the protein related to protein function (see e.g.ref. 55 and references therein). In recent years, there have been a number of studies which have suggested that the protein dynamics is “slaved” by the solvent.34,50–52,56–58 The concept of slaving was first introduced by Fenimore and co-workers,56 and it highlights the importance of the environment of the protein for its functions. More specifically, it has been shown that the large-scale conformational changes of the protein exhibit the same non-Arrhenius temperature dependence as the cooperative motions of the bulk solvent, whereas more local internal protein motions are slaved by the local β-relaxation of the hydration water, although the latter occurs at faster rates. According to this slaving behavior a large number of solvent fluctuations are required to cause larger fluctuations in the protein.51,59,60
For disaccharides in aqueous solutions, three types of relaxation processes are typically found. A β-relaxation of the hydration water, the viscosity and glass transition related structural α-process, and another β-relaxation in between these which origin is not fully understood but is often attributed to rotation of the disaccharide molecule around its glycosidic bond.45–49,61,62
In the present study, we investigate how protein dynamics is affected by the addition of disaccharide molecules to the aqueous environment. For trehalose samples, two β-relaxations are found, however at high protein concentrations the β-relaxation due to intramolecular rotations of the monosaccharide rings in trehalose could not be detected. This β-relaxation is neither visible for the sucrose samples, and we discuss a possible explanation for its appeared absence. Above the glass transition temperature, Tg, the α-relaxation of the solvent and a slower protein relaxation, due to large-scale conformational motions, are observed. We show that this protein relaxation is slaved by the solvent α-relaxation, which implies that storing proteins below Tg stabilizes the protein by preventing these conformational changes to occur and furthermore that the addition of trehalose leads to a more efficient stabilization of proteins than sucrose.
Experimental section
Sample preparation
The investigated samples were different concentrations of myoglobin and water, with either α,α-trehalose or α,β-sucrose. Trehalose was purchased (Sigma-Aldrich) in crystalline, dihydrate form, sucrose was purchased (Sigma-Aldrich) in crystalline form, and myoglobin was purchased (Sigma-Aldrich) as a lyophilized powder. The protein and the disaccharide were mixed to desired ratios in an aqueous solution (Milli-Q water) and left to stir for ∼12 h to ensure homogeneous mixtures. The solutions were subsequently dried in vacuum to desired water concentrations, which were checked using thermo-gravimetric analysis (TGA).Five samples of different compositions, as presented in Table 1, were used for the analysis in this paper. All samples were viscous liquids at room temperature, with varying viscosities depending on the composition. In order to avoid ice formation during cooling, the samples had to contain relatively low water concentrations. To ensure no ice was formed during cooling, the samples were measured with a differential scanning calorimeter (DSC) over a temperature span of 120–300 K. For these DSC measurements, the samples were first cooled with a cooling rate of 20 K min−1 (similar to that of the subsequent quenching done in the dielectric measurements), and heated with a rate of 5 K min−1, using a DSC Q1000 from TA instruments. The bulk part of the DSC measurements were originally presented in a previous paper by the authors.14
| Sample name | Myoglobin (Mb) wt% | Disaccharide wt% | Water wt% | Water per sugar |
|---|---|---|---|---|
| 11 Wat. per Sug. 10% Mb | 10 | 56 | 34 | 11.5 |
| 11 Wat. per Sug. 33% Mb | 33 | 43 | 24 | 10.6 |
| 11 Wat. per Sug. 56% Mb | 56 | 28 | 16 | 10.9 |
| 7 Wat. per Sug. 10% Mb | 10 | 67 | 23 | 6.5 |
| 7 Wat. per Sug. 33% Mb | 33 | 49 | 17 | 6.5 |
| 7 Wat. per Sug. 56% Mb | 56 | 32 | 12 | 6.5 |
Dielectric measurements
For all measurements the prepared samples were placed between two gold plated electrodes, separated by 0.1 mm thick Teflon strips, and were then placed inside of the sample holder of a broadband spectrometer from Novocontrol (Concept 80). This sample holder was then put into a cryostat in which the measurements were performed. The cryostat uses cold nitrogen gas to cool, and before putting in the samples, the gas was pre-cooled to ∼100 K, which resulted in a rapid cooling of the sample (∼20 K min−1). Once an initial temperature of ∼120 K was reached, measurements began by sweeping over a frequency range of 10−2 to 107 Hz using an Alpha-S high resolution dielectric analyzer. This sweep was repeated for every 5 K up to room-temperature, with an isothermal stability of ±0.2 K.BDS fitting
The complex permittivity (ε*) from the dielectric spectra were fitted using a sum of Havriliak–Negami (HN) functions63 plus a conductivity-term: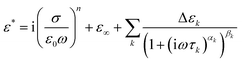 | (1) |
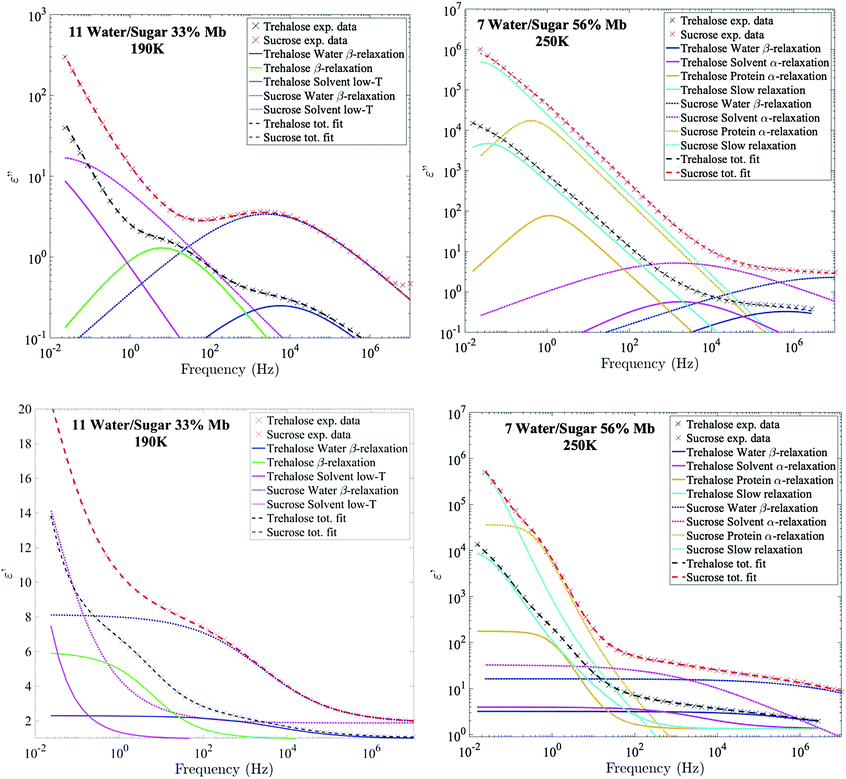
The relaxation times of the different relaxation processes were first determined by analysis of the logarithmic derivative of the real part of the dielectric permittivity, which is approximately the imaginary part but without the conductivity-term (see Fig. 1).64 This representation can highlight certain processes which are otherwise difficult to detect in either the real or the imaginary part of the complex permittivity. The spectra were then fitted simultaneously in the real part of ε* (where the conductivity-contribution is absent), and in the imaginary part (with an additional appropriate conductivity term).
The temperature dependences of the relaxation times (as presented in Fig. 2) were fitted using either the Arrhenius equation:
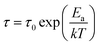 | (2) |
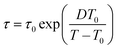 | (3) |
Results and discussion
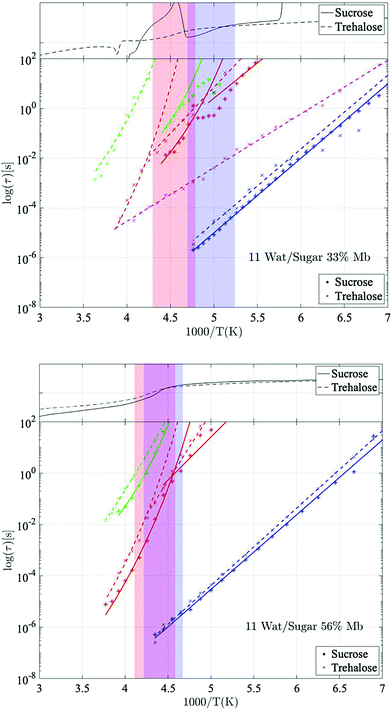
Fig. 2 shows Arrhenius plots of two selected investigated samples, which highlights the investigated relaxation processes. The Arrhenius plots for the remaining samples are shown in the ESI† (Fig. S1). In general, all samples exhibit two or three fast β-relaxations clearly detectable below Tg, and multiple VFT-like processes above Tg. Typically, an even faster Arrhenius-process than the ones shown in Fig. 2 is detected in protein-containing systems. This process has been attributed to the reorientation of hydroxyl groups on the protein. In the present study, this process was difficult to detect, if present at all. In most samples it was however used for the fitting of the high-frequency part at the lowest temperatures (∼below 150 K), but since the other processes are mainly analyzed above those temperatures, and are several times stronger than the hydroxyl group reorientation process, this process has been omitted from the analysis, and from the Arrhenius plots.The fastest process shown in Fig. 2 is attributed to a water β-relaxation (here denoted water relaxation) and the second fastest (found here only for some of the trehalose-containing samples) is attributed to a trehalose-related β-relaxation, and is here denoted as sugar β-relaxation since it is expected to exist for sucrose as well, although not detected in the present study. Whether or not this sugar β-relaxation can be observed in the trehalose-containing samples depends on the trehalose and protein concentrations of the system, which will be discussed in further detail below. All samples also exhibit another Arrhenius-like process below Tg, which is slower than both the water relaxation and the sugar β-relaxation (at least in the case of trehalose when it can be observed) and is denoted as “solvent low-T” relaxation, since it seems to be caused mainly by solvent motions that decouples from the cooperative α-relaxation of the solvent. Similar decoupling at about the calorimetric Tg has also been observed for other aqueous solutions.65,66 The origin of it is not fully clear, but it has been discussed in these previous publications and since the behavior is not unique for sugar or protein solutions, we find further discussion about it to be outside the scope of this paper.
Above Tg the “solvent low-T” relaxation exhibits a VFT temperature dependence and it can, as mentioned above, be attributed to the viscosity related α-relaxation of the solvent. There are also other, even slower, relaxation processes, above Tg, where, at least, the fastest and most clearly observed process is attributed to large-scale protein motions, and therefore denoted protein α-relaxation. One or some of the other and even slower processes (omitted from Fig. 2 and Fig. S1, ESI†) may also, at least partly, be due to protein relaxations, but more likely they are mainly caused by polarization effects. These slow processes will not be further discussed in the present study. In the following sections, the water β-relaxation, sugar β-relaxation, solvent α-relaxation and protein α-relaxation will be discussed in more detail, with the emphasis on how they are affected by the concentrations of the three components in the samples.
Water β-relaxation
Below the glass transition the process which is most clearly observed is the water relaxation. The assignment of this process to a β-relaxation (most likely the so-called Johari–Goldstein β-relaxation67) is easy since it is universal for water-containing systems, such as aqueous solutions and water confined in different types of porous materials.47,68–73 In fact, even bulk water exhibits a similar relaxation process,74 and it is therefore likely that this is an intrinsic relaxation process of water, which implies that all water in the systems participate in this low temperature relaxation. However, although this relaxation process is mainly due to water, which is further supported by the fact that its intensity increases with increasing water content, it should be noted that certain protein moieties may also exhibit local motions on a similar time scale (see e.g.ref. 55). Furthermore, in systems of high sugar concentrations and low water contents, this process has also been shown to merge with the relaxation of exocyclic hydroxymethyl groups of the sugars, since these have very similar dynamics.49The water β-relaxation is a broad and symmetric Cole–Cole process, with a broadening parameter αk of ∼0.35–0.45. It has approximately the same activation energy of ∼0.55 eV (see Table S2, ESI†) for all concentrations, similar to those obtained in other studies of aqueous solutions.47,58,66,75 However, from Fig. 3 and Table S1 (ESI†) it is evident that its time-scale and activation energy are affected by interactions with both the protein and the disaccharide. As is typical for aqueous solutions47,52,58,66,68,72,75–77 both its time-scale and activation energy tend to increase with decreasing water concentration, particularly in the case of trehalose. It has been shown that the stability of proteins in its glassy state below Tg is directly coupled to the dynamics of the solvent β-relaxation.53 Thus, reducing the water relaxation time by increasing the disaccharide content is highly important for improving protein stability below Tg. Since the addition of trehalose slows down the water relaxation more than sucrose,‡ particularly at low protein contents, our results explain why trehalose is a more efficient stabilizer of proteins below Tg. In addition to reducing the water relaxation time, a low water content also ensures that detrimental ice formation is avoided.
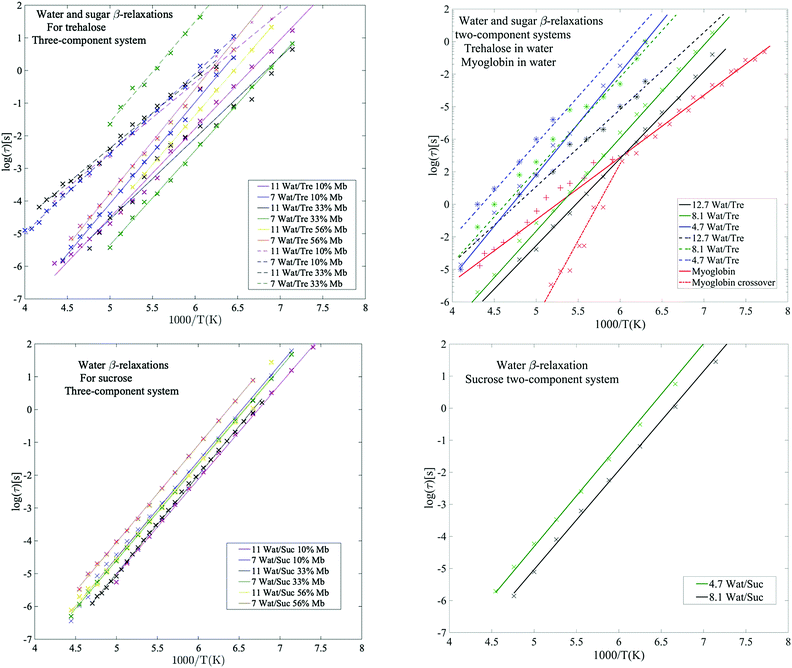 | ||
| Fig. 3 Water β-relaxations (solid lines) and sugar β-relaxations (dashed lines) with corresponding Arrhenius fits. Upper left panel: Three-component systems with trehalose as obtained from the present study. Upper right panel: Two-component systems for trehalose in water, obtained from Pagnotta et al.47 (obtained by extracting values by hand from Fig. 4 and 5 from ref. 47 small deviations presented here may occur and to get more accuracy here the reader is referred to the original publication), and protein in water (66 wt% myoglobin) as obtained from Jansson et al.69 Here, the water β-relaxation for the myoglobin sample partly exhibit a crossover to a VFT behavior at Tg, as shown by the dashed-dotted red line. Lower left panel: Three-component systems with sucrose as obtained from the present study. Lower right panel: Two-component systems for sucrose in water, based on data from Jansson et al.44 The sugar β-relaxation was not found in the samples containing sucrose. | ||
Sugar β-relaxation
From the example data fit of trehalose in Fig. 1(Upper Left) it can be seen that close to the water β-relaxation, there is a slower relaxation which approaches the water relaxation at low temperatures. Since this relaxation process has similar time-scale and activation energy as previously observed in multiple studies of both binary water–trehalose solutions47,78 (see Fig. 3(Upper Right) for water/trehalose data as obtained from ref. 47), and is furthermore observed also for anhydrous disaccharide samples (including both trehalose and sucrose),45,46,61,62 we are making the same assignment of it. In these previous studies the authors have suggested that this relaxation process is due to the rotation of the two monosaccharide rings of the disaccharide around its glycosidic bond.§ However, this process was not observed for all the presently investigated samples. It was not observed for the trehalose samples containing 56 wt% myoglobin and neither it could be detected for samples containing both sucrose and myoglobin. This can be directly seen from the example data sets shown in Fig. 1 (which can also be seen in the Arrhenius plots of Fig. 2 and Fig. S1 (ESI†), and also in further examples of dielectric data given in Fig. S2, ESI†), where only the trehalose containing sample with 33 wt% myoglobin exhibits a “shoulder” at frequencies below the water β-relaxation. Interestingly, an opposite observation was made in a recent study by Starciuc and co-workers,49 where a freeze dried sample of lysozyme and sucrose was found to exhibit this process, in contrast to a similar sample with trehalose. In that study,49 the water content was however much lower (7.8 wt% and 3.8 wt% for lysozyme in trehalose and sucrose respectively) than in the present case. Thus, the sugar β-relaxation we observe here is likely to exist also in the present sucrose–myoglobin samples, but it is most probably slower than for trehalose and therefore hidden under the low-frequency α-relaxation and/or protein relaxation. On the other hand, in the Starciuc's study,49 it was suggested that the trehalose relaxation instead was hidden under the low-frequency processes. This suggests that, at the relatively high hydrations presented in this work, and in the presence of protein, trehalose rotates around its glycosidic linkage more freely than sucrose, but when similar systems are freeze-dried the sucrose molecules are more mobile instead. One could thus argue that the intramolecular rotation of trehalose is more sensitive to the water concentration than sucrose.Multiple studies79,80 have shown that sucrose has a greater tendency to form intramolecular bonds than trehalose, thus forming more of a closed structure, which fits well with the present observations; intramolecular bonds between the monosaccharide rings prevents the monosaccharide rings from rotating. The reverse observation, made in Starciuc's study49 for freeze-dried samples, however would suggest that trehalose formed stronger intramolecular bonds than sucrose in that scenario. This could be explained by that trehalose has a lower tendency than sucrose to form intramolecular bonds between the monosaccharide rings, but when they do form, the bonds are stronger. It also explains why the sugar β-relaxation is not detected in the drier scenarios with trehalose and 56 wt% myoglobin, where a greater portion of the water content has been forced to adsorb onto the protein surface, thus leaving the trehalose molecules sufficiently dry to form this more rigorous strongly intramolecular state.
The solvent α-relaxation
Fig. 4 shows the temperature dependence of the α-relaxation and the crossover to the “solvent low-T” relaxation around Tg, as mentioned above. This crossover is not a unique observation for aqueous solutions65,66 and will not be discussed further in this paper (see previous works by e.g. Cerveny et al.,66 for a more thorough study of this cross-over). Instead we focus on the cooperative α-relaxation of the solvent, which is more relevant for the purpose of protein stability above the glass transition temperature. The α-relaxation of the solvent is clearly seen above Tg, and by extrapolating this process to lower temperatures, it can be seen that it reaches approximately 100 s (i.e. a time-scale corresponding to the calorimetric Tg) at the midpoint or low-temperature region of the glass transition's temperature span, which supports our assignment of this relaxation as a cooperative α-relaxation. Its dynamics is affected by protein interactions and dynamics, and it is also possible that some protein side chains move cooperatively with the solvent and therefore also contribute to this α-relaxation. This can be seen by analyzing the results shown in Fig. 4. In Fig. 4 it can be seen that the solvent α-relaxation becomes somewhat faster with increasing water content, but that the difference is much smaller for the trehalose containing samples compared to the sucrose containing samples. It is particularly evident that an increasing protein content has no effect, or even a slight speeding-up, on the α-relaxation of the trehalose samples, whereas it slows down the solvent α-relaxation of the sucrose samples considerably. The reason for this is that the solvent α-relaxation of the pure water–trehalose solutions are substantially slower than the corresponding sucrose solutions, which implies that the protein may act as a plasticizer in the case of trehalose and as an anti-plasticizer for aqueous sucrose solutions. From the fitting parameters provided in Table S2 of ESI† it is also evident that the addition of protein increases the fragility of the α-relaxation, which suggests that the protein weakens the network character of the water–disaccharide solvent.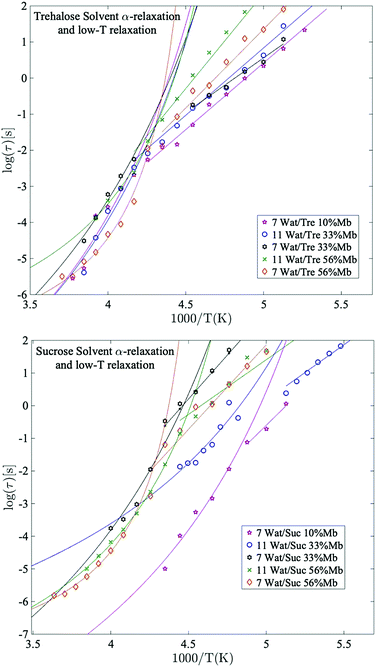 | ||
| Fig. 4 Arrhenius plots of the main solvent relaxation for selected trehalose samples (upper panel) and sucrose samples (lower panel), with corresponding Arrhenius- and VFT-fits. | ||
The protein α-relaxation
The fastest and most clearly observed relaxation of the processes slower than the α-relaxation of the solvent is in analogy to interpretations made in previous studies51,69 assigned to large-scale conformational motions of the protein. The temperature dependence of this process is shown in Fig. 5. This relaxation participates also in the calorimetric glass transition and reaches a relaxation time of about 100 s at the high temperature region of the glass transition. From previous studies51,69 it has been shown that protein solutions exhibit a glass transition which is mainly due to the surrounding solvent (provided that the solvent is not pure water, which does not contribute to the observed glass transition51,69), but that slower conformational fluctuations of the protein also contribute to the glass transition and broadens it to higher temperatures. Thus, the protein dynamics is related to the high temperature region of the calorimetric glass transition. This broadening effect of the glass transition, due to the addition of protein, can also be seen from the calorimetric measurements of the present study, as shown in the upper parts of the panels in Fig. 2. In fact, the calorimetric glass transition is so broad that it likely is caused by several different types of large-scale internal protein motions occurring on slightly different time-scales. The protein α-relaxation observed here can therefore be regarded as a superposition of several large-scale protein motions, and since these are a few orders of magnitude slower than the cooperative solvent relaxation they reach a relaxation time of approximately 100 s at a higher temperature than Tg of the solvent. Overall, this gives rise to a broad Tg, where the α-relaxation of the solvent is responsible for the low temperature part of it and all the different large-scale protein motions are responsible for the remaining part of Tg.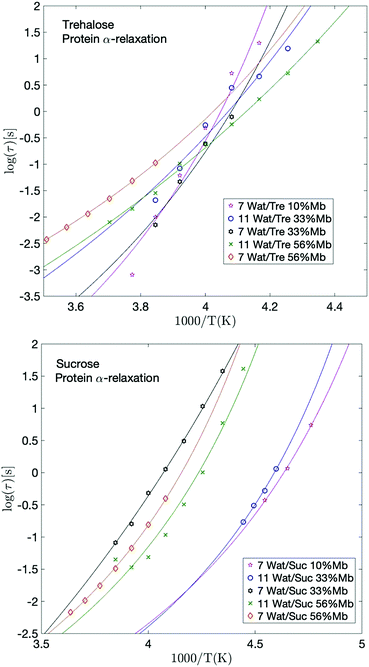 | ||
| Fig. 5 Arrhenius plots of the protein relaxation for selected trehalose samples (upper panel) and selected sucrose samples (lower panel), with corresponding VFT-fits. | ||
Giuffrida et al.81 showed in a recent study that the protein becomes most stabilized at an optimal sugar per protein (S/P) ratio. In their study they showed that both too high and too low S/P ratios resulted in a deformation of the heme pocket of myoglobin. That study was conducted at even lower water contents than in the present study, and is therefore not directly comparable; at too high S/P ratios the detrimental effect most likely stems from a microphase separation to high sugar domains and high protein domains, as shown in ref. 82 and 83. In the present study, the water content at the highest S/P ratios is relatively high, and thus such inhomogeneities should not be present to a large extent (as indicated by a previous study by our group84), and the fast dynamics (and the protein stabilization by extension) in these samples is dominated by the water dynamics. However, the present samples containing 33 and 56 wt% myoglobin are comparable with the samples in the study by Giuffrida et al. (albeit still at a higher water content here). According to their study, the samples with 33 wt% myoglobin should have a more optimal sugar to protein ratio than the samples with 56 wt% myoglobin. This is due to that in the lower S/P regime, the protein dominates the system and there are not enough sugar molecules per protein to prevent protein–protein interactions, which may lead to protein deformations and aggregations. In the present study it can be seen that for both the solvent and the protein α-relaxation (Fig. 4 and 5), for both sugars containing 7 waters per sugar molecule, there is a tendency for the intermediate sugar to protein ratio (33 wt% Mb) to have the highest relaxation time, implying a more stable system for this intermediate S/P ratio. The study by Giuffrida et al.81 also showed how the protein stability due to the presence of trehalose is less dependent on the S/P ratio than in the case of sucrose. Similarly, in the present study, the relaxation times of both the solvent and the protein α-relaxation are less dependent on the sample composition for the trehalose containing samples, compared to those with sucrose (Fig. 4 and 5). This implies that trehalose is able to provide effective protein stabilization over a substantially broader composition range than sucrose.
Slaving behavior
It has been previously shown by multiple studies that internal conformational protein fluctuations and different peptide-chain relaxations are “slaved” by a faster α-relaxation process in the surrounding solvent.52,56–58,66 This has been established by, for example, showing that these protein and solvent relaxations exhibit identical temperature dependences, although where the solvent-associated α-relaxation is 102–105 times faster than the protein relaxations. A similar behavior can be seen in the present study, which is highlighted in Fig. 6. In Fig. 6 the logarithmic relaxation times of the protein relaxation are plotted as a function of the logarithmic relaxation times of the solvent α-relaxation, and from there it can be seen that the slope is roughly equal to 1, meaning that they exhibit almost the same temperature dependence, in consistency with the slaving model. The slight deviations from a slope of exactly 1 can likely be explained by the fact that the dielectric data in the frequency range of these processes is affected by conductivity and electrode polarization effects, which introduces some errors in the exact values of the obtained relaxation times. The deviations are, however, so small that the slaving behavior can be regarded as valid also for these sugar solutions.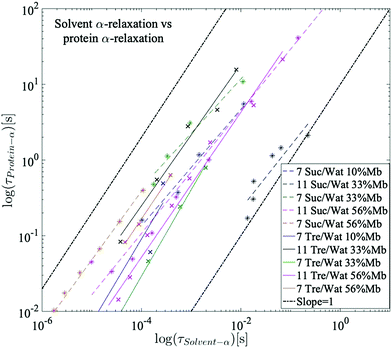 | ||
| Fig. 6 Logarithmic relaxation times of the protein relaxation as a function of the logarithmic relaxation times of the solvent α-relaxation. A slope of 1 indicates a perfect slaving behavior. | ||
Since trehalose causes a stronger slowing down of the solvent dynamics than sucrose, due to a stronger dynamic coupling between water and trehalose than for water and sucrose,22,24,25,49 the slaving phenomenon implies that also of the large-scale protein motions slows down more by trehalose than by sucrose. This explains why trehalose is more efficient at protein stabilization than sucrose above Tg. This correlation between solvent dynamics and protein stabilization has however been shown to be invalid below Tg, where other, more complex, mechanisms, such as how the disaccharides interact with the protein surface and the role of the β-relaxations of water and the disaccharides, play substantial roles in explaining the phenomena of protein stabilization.85,86
From the results, as shown in e.g.Fig. 2 and Fig. S1 (ESI†) it can be seen that most relaxations of trehalose and sucrose converge with increasing myoglobin concentration. This is not surprising since higher concentrations of protein also means that the signal strength – and also the dynamics of the system – is governed by the protein motions to a greater extent. Thus, the stabilizing effect of using trehalose rather than sucrose naturally cancels out when there are insufficient sugar molecules per protein.
Conclusions
Below the glass transition temperature, the dielectric spectra of the aqueous sugar–protein solutions are dominated by a water β-relaxation. However, for the trehalose samples with a sufficiently low protein concentration another local β-relaxation, in this case arising from the rotation of the monosaccharide rings around their glycosidic linkage, is observed. This process is interestingly not visible for the present samples containing sucrose. This can be explained by that sucrose has previously been found to form more intramolecular hydrogen bonds, and thus rotates more slowly at the present hydrations. Furthermore, for samples containing over 50 wt% myoglobin, this process disappeared also for the samples with trehalose. The reason for this is most likely that the water concentration is sufficiently low at these concentrations to force trehalose molecules to also form intramolecular hydrogen bonds. Another possible explanation could be that the high concentration of protein prevents these rotations due to macromolecular crowding effects. How this sugar β-relaxation affects the protein stability below Tg is however difficult to determine since the water β-relaxation is expected to have a much stronger influence on the stability.Above the calorimetric glass transition, two relaxation processes are clearly observed, due to the α-relaxation of the solvent and large-scale conformational protein motions. These protein motions are “slaved” by the solvent α-relaxation, which implies that they would not occur without the presence of the solvent relaxation, which thereby is responsible for the protein motions. It was also found that the protein α-relaxation tends to slow down and become more sensitive to changes in temperature with increasing trehalose concentration. These findings may explain its excellent stabilizing effect on proteins since they increase the time for a protein to reach another conformational stage. In the case of sucrose all these effects of adding the disaccharide are smaller. This can be explained by the fact that the α-relaxation of the aqueous sucrose solution is faster than for the corresponding trehalose solution, i.e. its viscosity is lower, and due to the slaving phenomenon also the large-scale protein motions are also faster, leading to a less stabilized protein above Tg. This finding does however only explain why trehalose is more efficient than sucrose above Tg, Below Tg it has been shown85,86 that the protein stability is mainly determined by the β-relaxation of the surrounding water. Furthermore, it is likely that a more detailed understanding of the stabilizing role of disaccharides requires also deeper insights into the solvent structure around the protein molecules and how the disaccharides interact with the protein. However, the present study does provide insights into how large complex molecules, such as proteins, are stabilized by disaccharides due to the slaving behavior above Tg and the slowing down of the water β-relaxation below Tg.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Wera Larsson, Sonia Esko, and Jonas Ericsson for assistance in measurements of trehalose samples. We would also like to thank Helén Jansson for helpful discussions and instructions regarding dielectric spectroscopy measurements and fitting. This work was financially supported by the Swedish Research Council.Notes and references
- C. Colaço, S. Sen, M. Thangavelu, S. Pinder and B. Roser, Bio/Technology, 1992, 10, 1007 Search PubMed.
- M. Uritani, M. Takai and K. Yoshinaga, J. Biochem., 1995, 117, 774–779 CrossRef CAS.
- T. Duong, R. Barrangou, W. M. Russell and T. R. Klaenhammer, Appl. Environ. Microbiol., 2006, 72, 1218–1225 CrossRef CAS.
- A. Wiemken, Antonie van Leeuwenhoek, 1990, 58, 209–217 CrossRef CAS.
- G. Bellavia, G. Cottone, S. Giuffrida, A. Cupane and L. Cordone, J. Phys. Chem. B, 2009, 113, 11543–11549 CrossRef CAS.
- D. Barreca, G. Laganà, S. Magazù, F. Migliardo, G. Gattuso and E. Bellocco, Int. J. Biol. Macromol., 2014, 63, 225–232 CrossRef CAS.
- J. H. Crowe, L. M. Crowe, J. F. Carpenter and C. Aurell Wistrom, Biochem. J., 1987, 242, 1–10 CrossRef CAS.
- W. Q. Sun and A. C. Leopold, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1997, 117, 327–333 CrossRef.
- L. Lupi, L. Comez, M. Paolantoni, D. Fioretto and B. M. Ladanyi, J. Phys. Chem. B, 2012, 116, 7499–7508 CrossRef CAS.
- M. Malferrari, A. Nalepa, G. Venturoli, F. Francia, W. Lubitz, K. Mobius and A. Savitsky, Phys. Chem. Chem. Phys., 2014, 16, 9831–9848 RSC.
- S. Giuffrida, G. Cottone, G. Bellavia and L. Cordone, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 1–12 CrossRef.
- L. Cordone, G. Cottone, A. Cupane, A. Emanuele, S. Giuffrida and M. Levantino, Curr. Org. Chem., 2015, 19, 1684–1706 CrossRef CAS.
- D. Corradini, E. G. Strekalova, H. E. Stanley and P. Gallo, Sci. Rep., 2013, 3, 1218 CrossRef.
- C. Olsson, H. Jansson and J. Swenson, J. Phys. Chem. B, 2016, 120, 4723–4731 CrossRef CAS.
- T. Arakawa and S. N. Timasheff, Biophys. J., 1985, 47, 411–414 CrossRef CAS.
- G. Xie and S. N. Timasheff, Biophys. Chem., 1997, 64, 25–43 CrossRef CAS.
- P. S. Belton and A. M. Gil, Biopolymers, 1994, 34, 957–961 CrossRef CAS.
- R. D. Lins, C. S. Pereira and P. H. Hünenberger, Proteins: Struct., Funct., Bioinf., 2004, 55, 177–186 CrossRef CAS.
- C. Olsson, S. Genheden, V. García Sakai and J. Swenson, J. Phys. Chem. B, 2019, 123, 3679–3687 CrossRef CAS.
- G. Cottone, G. Ciccotti and L. Cordone, J. Chem. Phys., 2002, 117, 9862–9866 CrossRef CAS.
- D. Kilburn, S. Townrow, V. Meunier, R. Richardson, A. Alam and J. Ubbink, Nat. Mater., 2006, 5, 632–635 CrossRef CAS.
- S. Magazù, F. Migliardo and M. T. F. Telling, Eur. Biophys. J., 2006, 36, 163–171 CrossRef.
- S. Magazù, F. Migliardo and M. T. F. Telling, Food Chem., 2008, 106, 1460–1466 CrossRef.
- P. Bordat, A. Lerbret, J. P. Demaret, F. Affouard and M. Descamps, EPL, 2004, 65, 41 CrossRef CAS.
- Y. Choi, K. W. Cho, K. Jeong and S. Jung, Carbohydr. Res., 2006, 341, 1020–1028 CrossRef CAS.
- G. Cottone, J. Phys. Chem. B, 2007, 111, 3563–3569 CrossRef CAS.
- S. Giuffrida, G. Cottone and L. Cordone, Biophys. J., 2006, 91, 968–980 CrossRef CAS.
- S. Magazù, G. Maisano, F. Migliardo and C. Mondelli, Biophys. J., 2004, 86, 3241–3249 CrossRef.
- S. Magazu, V. Villari, P. Migliardo, G. Maisano, M. T. F. Telling and H. D. Middendorf, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 301, 130–133 CrossRef CAS.
- S. Magazu, F. Migliardo and M. T. F. Telling, Food Chem., 2007, 106, 1460–1466 CrossRef.
- F. Affouard, P. Bordat, M. Descamps, A. Lerbret, S. Magazù, F. Migliardo, A. J. Ramirez-Cuesta and M. F. T. Telling, Chem. Phys., 2005, 317, 258–266 CrossRef CAS.
- C. Branca, V. Magazu, G. Maisano, F. Migliardo and A. K. Soper, Appl. Phys. A: Mater. Sci. Process., 2002, 74, s450–s451 CrossRef CAS.
- V. G. Sakai, S. Khodadadi, M. T. Cicerone, J. E. Curtis, A. P. Sokolov and J. H. Roh, Soft Matter, 2013, 9, 5336–5340 RSC.
- H. Jansson, F. Kargl, F. Fernandez-Alonso and J. Swenson, J. Chem. Phys., 2009, 130, 205101 CrossRef CAS.
- H. Jansson, R. Bergman and J. Swenson, J. Non-Cryst. Solids, 2006, 352, 4410–4416 CrossRef CAS.
- S. E. Pagnotta, M. A. Ricci, F. Bruni, S. McLain and S. Magazu, Chem. Phys., 2008, 345, 159–163 CrossRef CAS.
- S. E. Pagnotta, S. E. McLain, A. K. Soper, F. Bruni and M. A. Ricci, J. Phys. Chem. B, 2010, 114, 4904–4908 CrossRef CAS.
- C. Olsson, H. Jansson, T. Youngs and J. Swenson, J. Phys. Chem. B, 2016, 120, 12669–12678 CrossRef CAS.
- F. Migliardo, M. T. Caccamo and S. Magazù, J. Non-Cryst. Solids, 2013, 378, 144–151 CrossRef CAS.
- G. Caliskan, D. Mechtani, J. H. Roh, A. Kisliuk, A. P. Sokolov, S. Azzam, M. T. Cicerone, S. Lin-Gibson and I. Peral, J. Chem. Phys., 2004, 121, 1978–1983 CrossRef CAS.
- G. Caliskan, A. Kisliuk and A. P. Sokolov, J. Non-Cryst. Solids, 2002, 307, 868–873 CrossRef.
- C. Branca, S. Magazù, G. Maisano and P. Migliardo, J. Chem. Phys., 1999, 111, 281–287 CrossRef CAS.
- C. Branca, S. Magazu, F. Migliardo and P. Migliardo, Phys. A, 2002, 304, 314–318 CrossRef CAS.
- H. Jansson, R. Bergman and J. Swenson, J. Non-Cryst. Solids, 2005, 351, 2858–2863 CrossRef CAS.
- K. Kaminski, E. Kaminska, P. Wlodarczyk, S. Pawlus, D. Kimla, A. Kasprzycka, M. Paluch, J. Ziolo, W. Szeja and K. L. Ngai, J. Phys. Chem. B, 2008, 112, 12816–12823 CrossRef CAS.
- K. Kaminski, E. Kaminska, S. Hensel-Bielowka, E. Chelmecka, M. Paluch, J. Ziolo, P. Wlodarczyk and K. L. Ngai, J. Phys. Chem. B, 2008, 112, 7662–7668 CrossRef CAS.
- S. E. Pagnotta, A. Alegría and J. Colmenero, Phys. Chem. Chem. Phys., 2012, 14, 2991–2996 RSC.
- K. Fuchs and U. Kaatze, J. Chem. Phys., 2002, 116, 7137–7144 CrossRef CAS.
- T. Starciuc, B. Malfait, F. Danede, L. Paccou, Y. Guinet, N. T. Correia and A. Hedoux, J. Pharm. Sci., 2020, 109, 496–504 CrossRef CAS.
- H. Jansson, R. Bergman and J. Swenson, J. Phys. Chem. B, 2005, 109, 24134–24141 CrossRef CAS.
- H. Jansson, R. Bergman and J. Swenson, J. Phys. Chem. B, 2011, 115, 4099–4109 CrossRef CAS.
- J. Swenson, H. Jansson, J. Hedström and R. Bergman, J. Phys.: Condens. Matter, 2007, 19, 205109 CrossRef.
- M. T. Cicerone and J. F. Douglas, Soft Matter, 2012, 8, 2983–2991 RSC.
- A. Bonincontro and G. Risuleo, Spectrochim. Acta, Part A, 2003, 59, 2677–2684 CrossRef.
- S. Khodadadi and A. P. Sokolov, Soft Matter, 2015, 11, 4984–4998 RSC.
- P. W. Fenimore, H. Frauenfelder, B. H. McMahon and F. G. Parak, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16047–16051 CrossRef CAS.
- H. Frauenfelder, P. W. Fenimore, G. Chen and B. H. McMahon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15469–15472 CrossRef CAS.
- S. Cerveny, I. Combarro-Palacios and J. Swenson, J. Phys. Chem. Lett., 2016, 7, 4093–4098 CrossRef CAS.
- P. W. Fenimore, H. Frauenfelder, B. H. McMahon and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408 CrossRef CAS.
- H. Frauenfelder, G. Chen, J. Berendzen, P. W. Fenimore, H. Jansson, B. H. McMahon, I. R. Stroe, J. Swenson and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5129–5134 CrossRef CAS.
- I. Ermolina, E. Polygalov, C. Bland and G. Smith, J. Non-Cryst. Solids, 2007, 353, 4485–4491 CrossRef CAS.
- I. Ermolina and G. Smith, J. Non-Cryst. Solids, 2011, 357, 671–676 CrossRef CAS.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- M. Wübbenhorst and J. van Turnhout, J. Non-Cryst. Solids, 2002, 305, 40–49 CrossRef.
- J. Sjöström, J. Mattsson, R. Bergman, E. Johansson, K. Josefsson, D. Svantesson and J. Swenson, Phys. Chem. Chem. Phys., 2010, 12, 10452–10456 RSC.
- S. Cerveny and J. Swenson, Phys. Chem. Chem. Phys., 2014, 16, 22382–22390 RSC.
- G. P. Johari and M. Goldstein, J. Chem. Phys., 1970, 53, 2372–2388 CrossRef CAS.
- A. Panagopoulou, A. Kyritsis, M. Vodina and P. Pissis, Biochim. Biophys. Acta, Proteins Proteomics, 2013, 1834, 977–988 CrossRef CAS.
- H. Jansson and J. Swenson, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 20–26 CrossRef CAS.
- S. Cerveny, Á. Alegría and J. Colmenero, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 31803 CrossRef.
- K. Elamin, H. Jansson, S. Kittaka and J. Swenson, Phys. Chem. Chem. Phys., 2013, 15, 18437–18444 RSC.
- S. Cerveny, G. A. Schwartz, A. Alegria, R. Bergman and J. Swenson, J. Chem. Phys., 2006, 124, 194501 CrossRef CAS.
- J. Sjöström, J. Swenson, R. Bergman and S. Kittaka, J. Chem. Phys., 2008, 128, 154503 CrossRef.
- K. Amann-Winkel, C. Gainaru, P. H. Handle, M. Seidl, H. Nelson, R. Böhmer and T. Loerting, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17720–17725 CrossRef CAS.
- S. Khodadadi, S. Pawlus and A. P. Sokolov, J. Phys. Chem. B, 2008, 112, 14273–14280 CrossRef CAS.
- J. Swenson, H. Jansson and R. Bergman, Phys. Rev. Lett., 2006, 96, 247802 CrossRef.
- J. Swenson, K. Elamin, H. Jansson and S. Kittaka, Chem. Phys., 2013, 424, 20–25 CrossRef CAS.
- L. Lupi, L. Comez, M. Paolantoni, S. Perticaroli, P. Sassi, A. Morresi, B. M. Ladanyi and D. Fioretto, J. Phys. Chem. B, 2012, 116, 14760–14767 CrossRef CAS.
- A. Lerbret, P. Bordat, F. Affouard, M. Descamps and F. Migliardo, J. Phys. Chem. B, 2005, 109, 11046–11057 CrossRef CAS.
- M. Mathlouthi, Carbohydr. Res., 1981, 91, 113–123 CrossRef CAS.
- S. Giuffrida, L. Cordone and G. Cottone, J. Phys. Chem. B, 2018, 122, 8642–8653 CrossRef CAS.
- A. Longo, S. Giuffrida, G. Cottone and L. Cordone, Phys. Chem. Chem. Phys., 2010, 12, 6852–6858 RSC.
- S. Giuffrida, M. Panzica, F. M. Giordano and A. Longo, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 87 CrossRef CAS.
- C. Olsson and J. Swenson, Mol. Phys., 2019, 117, 3408–3416 CrossRef CAS.
- L. M. Crowe, D. S. Reid and J. H. Crowe, Biophys. J., 1996, 71, 2087–2093 CrossRef CAS.
- K. Tanaka, T. Takeda and K. Miyajima, Chem. Pharm. Bull., 1991, 39, 1091–1094 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03281f |
| ‡ As was the case in all samples, apart from 7 Wat./sugar with 33% Mb, as shown in Fig. S1 (ESI†), where the water β-relaxation is slower than for sucrose. This result is surprising, but the authors believe that this is an outlier which might have been caused by problems in the fitting due to the presence of the sugar β-relaxation in trehalose. The apparent lack of sugar β-relaxation in sucrose makes the water β-relaxation simpler to fit for sucrose. |
| § Alternative explanations for this process has also been suggested, such as it is originating from confined water clusters.47 |
| This journal is © the Owner Societies 2020 |