Pressure-dependent kinetics of peroxy radicals formed in isobutanol combustion

Abstract

Bio-derived isobutanol has been approved as a gasoline additive in the US, but our understanding of its combustion chemistry still has significant uncertainties. Detailed quantum calculations could improve model accuracy leading to better estimation of isobutanol's combustion properties and its environmental impacts. This work examines 47 molecules and 38 reactions involved in the first oxygen addition to isobutanol's three alkyl radicals located α, β, and γ to the hydroxide. Quantum calculations are mostly done at CCSD(T)-F12/cc-pVTZ-F12//B3LYP/CBSB7, with 1-D hindered rotor corrections obtained at B3LYP/6-31G(d). The resulting potential energy surfaces are the most comprehensive isobutanol peroxy networks published to date. Canonical transition state theory and a 1-D microcanonical master equation are used to derive high-pressure-limit and pressure-dependent rate coefficients, respectively. At all conditions studied, the recombination of γ-isobutanol radical with O₂ forms HO₂ + isobutanal. The recombination of β-isobutanol radical with O₂ forms a stabilized hydroperoxy alkyl radical below 400 K, water + an alkoxy radical at higher temperatures, and HO₂ + an alkene above 1200 K. The recombination of β-isobutanol radical with O₂ results in a mixture of products between 700–1100 K, forming acetone + formaldehyde + OH at lower temperatures and forming HO₂ + alkenes at higher temperatures. The barrier heights, high-pressure-limit rates, and pressure-dependent kinetics generally agree with the results from previous quantum chemistry calculations. Six reaction rates in this work deviate by over three orders of magnitude from kinetics in detailed models of isobutanol combustion, suggesting the rates calculated here can help improve modeling of isobutanol combustion and its environmental fate.

---

1 Introduction

In June 2018, the U.S. Environmental Protection Agency approved the large scale blending of bio-derived isobutanol into gasoline at concentrations up to 16%.^1,2 This newly approved oxygenate has multiple advantages over ethanol, such as lower volatility,³ lower hydroscopicity,⁴ and higher energy density,³ while providing similar knock resistance.⁵ Relative to larger alcohol additives, isobutanol also shows longer ignition delay times with lower CO and NO_x emissions,⁶ indicating it could help boost the octane numbers of fuel while lowering other emissions. With this approval, isobutanol could become a major component of transportation fuel in the United States.

While extensive experimental testing was necessary prior to the approval,⁴ detailed isobutanol combustion models are still inaccurate at engine-relevant conditions, indicating a gap in our understanding of isobutanol combustion. Detailed isobutanol mechanisms typically deviate more from experiments than do models of n-butanol, tert-butanol, and sec-butanol.^7,8 Multiple inter-model comparisons using detailed isobutanol models have showed that at lean, low-temperature conditions the models yield a wide range of ignition timings that deviate from experimental ignition delay measurements in homogeneous charge compression⁹ and shock tube setups.¹⁰ One mechanism shows the largest deviations from experiments below 850 K and at fuel lean conditions, indicating that the dependence on O₂ might be incorrectly described.¹¹

Such shortcomings indicate a need for improving our understanding of isobutanol combustion in combustion regimes, especially where peroxy radical chemistry is important.¹² The dominant degradation pathway of peroxy radicals at various temperatures and pressures impacts overall ignition properties such as the negative temperature coefficient region, in which ignition slows with increasing temperature.

While several aspects of isobutanol combustion chemistry have been studied in detail, such as the initial hydrogen abstraction by OH¹³ and the oxidation of its smaller oxidation products,¹⁴ accurate pressure-dependent kinetics of peroxy radicals formed in isobutanol combustion has not been fully developed nor incorporated into detailed models. This is in spite of some isobutanol studies showing that ignition delay is sensitive to peroxy radical reactions.^8,10 Given the sensitivity of this fuel to equivalence ratio and pressure,⁵ the formation and fate of peroxy radicals can significantly impact ignition timing and multi-stage heat release.^12,15 Peroxy radical chemistry is also expected to control the environmental fate of isobutanol emitted into the environment because peroxy radicals are also key intermediates in atmospheric degradation processes.

Fig. 1 shows the peroxy radicals studied in this work, which correspond to the three predominant hydrogen abstractions that isobutanol can undergo. The alkoxy radical formed from hydrogen abstraction of isobutanol by OH is expected to be much less common¹³ and thus not included in this work. For each of the three isomers studied, various unimolecular reactions can occur, as shown in Fig. 2. The peroxy radicals (RO₂) can isomerize through intramolecular hydrogen abstractions to form various alkyl hydroperoxide radicals (QOOH), or can unimolecularly decompose to form HO₂ and an alcohol with a double bond. QOOH can decompose in a variety of ways. Some decomposition pathways are highly structure-specific requiring additional functional groups, such as the pathway forming H₂O and an ketoalkoxy radical.¹⁶ β-scission pathways are more general and can lead QOOH to form the same products as HO₂ elimination (if a C–O bond breaks) or an alkyl radical and double bond (if a C–C bond breaks).¹⁷ Multiple simultaneous β-scissions are also possible, forming three or more fragments. Cyclic ethers and OH can also result from QOOH decomposition. Like the alkyl radicals, QOOH can also undergo O₂ addition, which is important for fast, low-temperature combustion. However, these pathways were not examined because calculations in this work suggest stabilized QOOH does not appear in appreciable quantities above 500 K.

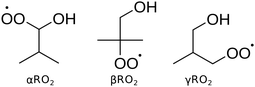Fig. 1 The three peroxy isomers derived from isobutanol correspond to the three main sites for hydrogen abstraction from isobutanol.

Fig. 2 Unimolecular reaction pathways available for alcohol-based peroxy radicals.

Previous quantum calculations of these important radicals have mostly focused on βRO₂ since it is also formed in the OH-initiated oxidation of isobutene. Sun et al. and Lizardo-Huerta et al. report high-pressure-limit rates obtained from CBSQ//B3LYP/6-31G(d,p) and CBS-QB3, respectively.^18,19

Similar work has not been conducted for the other two isomers, αRO₂ and γRO₂, but studies on similar species have been done. Zádor et al. have studied the fate of the α-peroxy radical derived from ethanol, though the full surface of αRO₂ derived from isobutanol has not, to our knowledge, been evaluated.²⁰ Welz et al. calculated a potential energy surface for the γRO₂ isomer, but did not include reactions of all isomers nor report reaction rates.¹⁶

Given the errors for isobutanol models at low temperature and the lack of quantum calculations for the peroxy intermediates, we present thermodynamic and kinetic parameters for isomers, reactants, and products on the α-, β-, and γ-isobutanol peroxy surfaces. Since there is potential for some for these reactions to be dependent on pressure,²¹ both pressure-dependent and high-pressure-limit rate coefficients are reported. Comparison to other work and sensitivity analysis are conducted to determine the robustness of the rates.

2 Methods

To quantify the rates of reaction of isobutanol peroxy radicals, we conducted quantum calculations of the lowest-energy stable conformers and transition states and used those calculations in deriving rate coefficients with both transition state theory (TST) and the 1-D master equation.

2.1 Quantum calculations

To efficiently obtain accurate rate coefficients necessary for our analysis, we conducted geometry optimization, hindered rotor scans, and frequency calculations with B3LYP/CBSB7 or BMK/6-31g(d) using Gaussian 03.²² Energy was calculated with CCSD(T)-F12/cc-pVTZ-F12 using either Molpro 2012.1.21 or Molpro 2015.1.37, including scaling the triples energy to the ratio of correlation energies from F12 and MP2.²³ For each molecule and transition state, we first conducted a geometry optimization of an initial guess. Transition states were verified to have one imaginary frequency. Internal Reaction Coordinate (IRC) calculations were conducted at B3LYP/CBSB7 level theory and visualized to ensure the transition states correspond with the correct reactants and products (see ESI,† for trajectories of each IRC calculation). For each rotatable dihedral, we calculated relaxed hindered rotor scans using 10-degree increments. When hindered rotor scans ended in a different conformer than the lowest-energy conformer, hindered rotor scans were rerun with the fixed dihedral angles and/or bond lengths to ensure an the scan proceeded as intended. While most geometry, hindered rotor and frequency calculations used the B3LYP method, calculations for compounds with a hydroperoxy group on the α carbon used BMK because B3LYP proved difficult to converge on these structures.

At each stationary point geometry, single-point CCSD(T)-F12a/cc-pVTZ-F12 were performed. Quantum chemistry outputs necessary to reproduce the thermodynamic and kinetic calculations are available in the ESI.†

Of the 85 calculations performed, over a third had T₁ diagnostic values above 0.02, indicating that many of these structures likely have multireference character.²⁴ Three of these had T₁ diagnostic values above 0.05, corresponding to the formation of alkoxy radicals from RO₂. The D₁ values also show similar effects with over a third of structures having a value greater than 0.1. The potential for multireference behavior, as indicated by these diagnostics, is thought to increase the uncertainties in the final energies to approximately 21 kJ mol⁻¹.²⁰ Based on work that compared single reference and multireference energies for a very similar system (oxygen addition to hydroxyethyl radical),²⁰ the difference in energies did not have any convincing systematic trend.

2.2 Thermodynamic and kinetic calculations

For thermodynamic and kinetic parameters, this work used Arkane, which is freely available as part of the Reaction Mechanism Generator software suite.²⁵ The partition function for each molecule and transition state was obtained using the rigid-rotor harmonic oscillator approximation with independent 1-D hindered rotor corrections. The data from the scans were fit using a Fourier series and separated from vibrations following Goldsmith et al.²⁶ In a few cases, relaxed scans broke hydrogen bonds but did not reform them during the scan and rigid scans were not accurate. The Fourier fits from these calculations gave unrealistic negative energies, so a cosine fit was used instead. Moments of inertia for each rotation were estimated using the lowest-energy conformer geometry. Vibrations were treated harmonically and their frequencies were scaled differently based on the usage.²⁷ Scale factors of 0.99²⁸ and 1.004²⁹ were applied to the frequencies for zero-point energy and the vibrational partition function, respectively.

Standard enthalpies, entropies, and heat capacity were obtained from the partition function, with energy adjustments based on atoms,³⁰ bonds,³⁰ and zero-point energies. These were fit over the range 10 to 3000 K using two NASA polynomials in the standard CHEMKIN II format.³¹

High-pressure-limit kinetics used canonical transition state theory with 1-D Eckart tunneling corrections. Unlike the thermodynamic calculations, atom and bond corrections were not applied when determining kinetic parameters. Twenty data points from 180 to 1500 K were fit to the modified Arrhenius form (k = ATⁿexp(−E_a/RT)).

Pressure-dependent networks were constructed for α-, β-, and γ-isobutanol radicals. Pressure-dependent rate coefficients for each network were obtained from the master equation at 20 temperatures from 180 K to 1500 K and 20 pressures from 0.01 bar to 100 bar. The reservoir state method was used to compute the phenomenological rate coefficients,³² based on the implementation described in Allen et al.³³ However, since Eckart tunneling was used in this work, the method was modified slightly; the cutoff between Boltzmann-distributed reservoir and the excited states was taken at the energy where the microcanonical reaction rate was 1% of the rate at the transition state's zero-point energy. This allows the transition point between excited states and Boltzmann-distributed states to adjust with the amount of tunneling. The maximum energy separation was 2 kJ mol⁻¹ with at least 200 energy grains per well. Lennard–Jones parameters of σ = 4.64 Å and ε = 318 cm⁻¹ were calculated using the 1-D minimization method with γRO₂ and N₂ as a bath gas.³⁴ Collisional energy transfer parameters of 〈ΔE_down〉 = 250 × (T/300 K)^0.85 cm⁻¹ were used, a value that has been used for a similar system of 2-butanol radicals in helium.³⁵

For the three barrierless entrance channels of R + O₂, inverse Laplace transform (ILT) of analogous reaction rates was used to obtain k(E) from k(T).³³ For αR + O₂, we used the high-pressure-limit rate of the analogous ethanol reaction, CH₃CHOH + O₂, from Zádor et al.²⁰ Rates for oxygen addition to βR and γR were taken from the rate rules developed by Miyoshi for tertiary and primary additions, respectively.³⁶

Pressure-dependent rates were fit at each temperature and pressure to Chebyshev polynomials. Thermodynamic parameters, pressure-dependent and high-pressure-limit rate coefficients are available in CHEMKIN II format in the ESI.†

2.3 Monte Carlo uncertainty analysis

Previous work has highlighted important sources of uncertainty in similar systems. Uncertainty analysis for oxygen addition to the propyl radical in Goldsmith et al. showed collisional energy transfer rates, zero-point corrected energies, and location of barrierless reactions to be important.³⁷ Xing et al. also found the Lennard-Jones parameter and tunnelling frequency important in their study of ethanol decomposition.³⁸ Allen et al. showed that the method of solving for phenomenological rates can also impact pressure-dependent rates.³³

To bound the accuracy of the results in this work, multiple input parameters into the pressure-dependent solver were varied for each of the networks using a Monte Carlo approach. From these calculations, distributions of net rates of oxygen addition and branching ratios of the hydroxyalkly + O₂ reaction and the unimolecular RO₂ reaction can be computed.

In this work, seven categories of parameters were varied: zero point energies, rate of reactions input into ILT, negative frequencies of transition states, preexponential factor of collisional energy transfer, temperature exponent of collisional energy transfer. Lennard-Jones parameter, and the method of solving for phenomenological rates. The zero point energies of each stationary point were treated with a normal distribution with standard deviation of 10 kJ mol⁻¹, which gives a 95% confidence interval similar to the error reported by Zádor et al. for highly multi-reference energies. The rate of each reaction input into the ILT algorithm was varied with a lognormal distribution with a standard deviation of two, given the rate used was for a similar barrierless reaction. Negative frequencies of transition states, which impacts tunnelling, were treated as a lognormal distribution with standard deviation of 0.2. The preexponential factor of the collisional energy transfer was taken as a lognormal distribution with standard deviation of 0.5, and its exponent was a normal distribution with standard deviation of 0.15. The Lennard-Jones σ parameter was assumed to be a lognormal distribution with a standard deviation of 0.2. The last four uncertainties described were used in Goldsmith et al. and Xing et al.^37,38 Two methods to solve phenomenological rates were used: modified strong collision and reservoir state. Reservoir state method was weighted with three times the probability of modified strong collision because it was seen as potentially more accurate.³³

2.4 Species and reaction naming

In total, this study involves 47 species and 38 transition states, so there is a need to develop a succinct and descriptive nomenclature. To ease discussion, α, β, and γ always refer to the carbon location relative to the alcohol group, even if multiple functional groups are present.

All compound names are listed next to their corresponding structure on the three networks in Fig. 3, 6 and 9. Stable compound names are italicized throughout the text.

Fig. 3 The potential energy surface for α-peroxy radical, showing pathways involving αQOOH (red), αQOOH (yellow) and αQOOH[O] (blue). Energy includes zero-point energy and atom corrections.

For contrast, reaction names are bolded. Each reaction starts with the Greek letter of the network to which it belongs. All reaction names are listed on the potential energy surfaces in Fig. 3, 6 and 9.

3 Results and discussion

For each peroxy radical, the pathways shown in Fig. 2 were evaluated. A QOOH species was found for each unique abstractable hydrogen. For each of these intermediates, the lowest-energy β-scission reaction, cyclic ether formation, and, if available, water formation pathways were found. In total 38 transition states were obtained.

In the following sections we describe major results from each peroxy radical individually, showing potential energy surfaces, microcanonical rates, pressure-dependent branching ratios, and comparisons to other quantum calculations. We then discuss the uncertainty of the pressure-dependent branching ratios and overall rates. We end by comparing the rates to a detailed combustion mechanism.

3.1 α-Peroxy network

The lowest-energy pathway in the α-peroxy network, shown in Fig. 3 involves a two-step HO₂ elimination of the peroxy radical. The first step, called αAdductFromRO2, forms a hydrogen bonded complex, called αadduct. This has an activation energy lower in energy than the separated products. The second step, αAdductSplit, involves breaking the hydrogen bond to form isobutanal and HO₂. This barrierless reaction was included in the master equation by using an ILT of the collision-limited rate of the products.^33,39 The TS for αAdductFromRO2 is a concerted reaction with the SOMO perpendicular to the COO plane; the analogous reaction of other α-hydroxy peroxy radicals has been discussed previously.²⁰

The α-peroxy network also includes three intramolecular hydrogen abstraction reactions from the peroxy radical to form alkyl or alkoxy radicals. The lowest-energy direct hydrogen abstraction involves the formation of the alkoxy product, αQOOH[O]. Unlike the formation of αQOOHβ and αQOOHγ, this does not require the breaking of a hydrogen bond, allowing for a lower barrier despite a higher ring strain and larger bond dissociation energy.⁴⁰ For the other hydrogen abstraction reactions, the reaction with a six-membered transition state forming αQOOHγ has a lower barrier than the one with a five-membered transition state forming αQOOHβ, due differences in ring strain.

This network also includes subsequent isomerization reactions, αAlkoxyIsomFromβ and αAlkoxyIsomFromγ, forming αQOOH[O]. These subsequent isomerization reactions have even higher barriers than both the direct isomerization from αRO₂ (αAlkoxyIsom) and the lowest-energy decomposition pathways (αEpoxyFrom and αC4EtherFrom). Due to the high barriers of these alkyl-based isomerizations, they were not calculated for the β- and γ-networks.

The products formed from the isomerizations, αQOOHβ, αQOOHγ, and αQOOH[O], each have a number of decomposition pathways. The alkoxy pathway has three β-scission reactions that break a bond connected to the α-carbon. The αQOOHβ behaves similar to peroxy radicals from non-oxygenated fuels, with the formation of an epoxide (in this case trisub_epoxy) + OH, or an alkene (ibutenol) + HO₂ as the main channels. The αQOOHγ decomposition can undergo reactions αDoubleβ-scission, αC4EtherFromγ, and α-βscissionFromγ. The last of these reactions has the highest barrier and forms a methyl radical and alkene. Since this reaction is unlikely to dominate at any realistic condition, reactions forming both alkenes and methyl radicals were excluded for the other peroxy networks. The other β-scission reaction involves the simultaneous breaking of two bonds, similar to the Waddington mechanism described for β-peroxy radicals,¹⁷ but with a higher barrier. αC4EtherFromγ has the lowest decomposition barrier for αQOOHγ, but it is still significantly higher than the decomposition reactions of αQOOHβ and αQOOH[O].

From the quantum calculations, we derived density of states and microcanonical rates, with selected microcanonical rates shown in Fig. 4. The formation of αAdduct is the dominant pathway, as it is faster than other channels by at least an order of magnitude at all energy levels. For αAdduct, shown in Fig. 4b, most energies result in the breaking of the hydrogen bond to form HO₂ and isobutanal. Since this rate is based on the ILT for forming αAdduct from HO₂ and isobutanal through microcanonical equilibrium, the reaction rate reported here has only order of magnitude accuracy. However, given the wide gap in Fig. 4b, one or two orders of magnitude change in the αAdductSplit rate will not shift the major product.

Fig. 4 Microcanonical rates for all the reaction channels coming from (a) αRO₂ and (b) αadduct. The reaction names correspond to those in Fig. 3, with αR + O2 being the reverse of αRO2Form, and αRO2Isom being the reverse of αAdductFromRO2. The energy values correspond to those in Fig. 3 and are relative to that of αR + O₂.

Fig. 5a shows the major products from phenomenological rate coefficients. Under practically all conditions studied, αR + O₂ proceeds via a well-skipping reaction to form HO₂ and isobutanal. Even the stabilized αRO₂ formed at low temperature and high pressure forms the same product or the hydrogen-bonded adduct, as shown in Fig. 5b. This result is consistent with isobutanol oxidation experiments between 500–700 K, which show isobutanal as a major product.⁴¹

Fig. 5 Major stabilized products for the reactions of (a) αR + O₂ and (b) αRO₂ at various temperatures and pressures. Shading indicates the fraction going to the major pathway.

The main products, HO₂ and isobutanal, could also form by direct hydrogen abstraction of αR by O₂, which was not studied in this work. However, based on the work of an analogous ethanol network by Zádor et al., this channel is unlikely to be important even at temperatures as high as 1000 K.²⁰

Because the dominant channel from αR + O₂ makes HO₂, and not a carbon-centered radical, αR does not lead to significant low-T chain-branching via second O₂ addition. (The HO₂ can lead to chain branching via H₂O₂, but typically that only becomes important above 750 K). Since the αR is predicted to be the dominant radical from isobutanol combustion,^11,13,15 a large negative temperature coefficient effect is not expected. This is in agreement with previous experiments that found no negative temperature coefficient region in isobutanol combustion.^5,8

3.2 β-Peroxy network

Fig. 6 shows three isomerization reactions of βRO₂, forming βQOOHα, βQOOHγ, and βQOOH[O]. βQOOHγ can undergo β-scission and cyclic ether formation. βQOOHα can undergo both of those pathways as well as water + alkoxy formation. The β-scission of the alkoxy radical, βQOOH[O], commonly refered to as the Waddington mechanism,¹⁷ is often the major sink of βRO₂ radicals.^18,41

Fig. 6 The potential energy surface for β-peroxy radical, showing pathways involving βQOOHγ (red), βQOOHα (blue) and βQOOH[O] (yellow). Energy includes zero-point energy and atom corrections.

The microcanonical rates of the major intermediates are shown in Fig. 7. Of all the pathways available to βRO₂, three pathways dominate at different energies. At the lowest energies (<−65 kJ mol⁻¹, i.e. below the zero-point energy of βQOOH[O]), β-αQOOHIsom, which occurs through tunneling, is the fastest reaction. After forming βQOOHα at this low energy, it will likely form trisub_epoxy + OH through βEpoxyFromα, as shown in Fig. 7c.

Fig. 7 Microcanonical rates for all the reaction channels coming from (a) βRO₂, (b) βQOOH[O], and (c) βQOOHα. The reaction names correspond to those in Fig. 6, with βR + O2 being the reverse of βRO2Form, and βRO2Isom being the reverse of βAlkoxyIsom (for subplot b) and β-αQOOHIsom (for subplot c). The energy values correspond to those in Fig. 6 and are relative to that of βR + O₂.

At moderate energies, the fastest reaction involving βRO₂ is βAlkoxyIsom. The rates of the alkoxy intermediate are given in Fig. 7b. The reverse reaction for βQOOH[O] re-forming βRO₂ (βAlkoxyIsom) is favored at most energies and the β-βscissionFromAlkoxy is favored only at high energies. The strong reversibility of the alkoxy isomerization allows for other secondary pathways to contribute to product formation.

The reverse reaction rate re-forming βRO₂ in Fig. 7b is nonmonotonic, decreasing at higher energies. This is because the zero-point-corrected energies of βQOOH[O] and βRO2Isom are similar (differing by only 2 kJ mol⁻¹) and because βQOOH[O] has more freedom of motion than βRO2Isom. This causes the ratio of density of states between transition state and reactant to reach a peak around −60 kJ mol⁻¹. Because this isomerization is so fast, in the energy range from −60 kJ mol⁻¹ through −10 kJ mol⁻¹, βRO₂ and βQOOH[O] equilibrate on a 10 ps timescale.

Based on Fig. 7a, most high-energy βRO₂ will dissociate back into βR and O₂, which is essentially non-reactive. The fraction that does react mostly forms alkene, ibutenol, and HO₂ through β-αHO2ElimFromRO2 and β-γHO2ElimFromRO2.

Fig. 8a shows the major products from phenomenological rate coefficients. In the case of βR + O₂, the two HO₂ pathways become dominant at higher temperatures. The Waddington pathway (forming acetone, CH₂O, and OH) will dominate at moderate temperatures and low pressures. Stabilized βRO₂ forms at the moderate and lower temperatures.

Fig. 8 Major stabilized products for the reactions of (a) βR + O₂ and (b) βRO₂ at various temperatures and pressures. Shading indicates the fraction going to the major pathway.

The products of a stabilized βRO₂ look quite different than for the entrance channel due to lower available energy. For example, epoxides only form in substantial amounts at low temperatures and when βRO₂ is stabilized. While epoxides have not been observed in isobutanol oxidation,⁴¹ most studies have focused mostly on temperatures higher than 500 K.

At temperatures between 500 and 1000 K and pressures above 10⁵ Pa, Fig. 8 shows that βR + O₂ primarily forms stabilized βRO₂, and stabilized βRO₂ primarily forms βR + O₂, indicating a partial equilibrium between βR + O₂ and βRO₂. Under these conditions, the secondary products, not explicitly shown in Fig. 8, would be the dominant net pathways. At lower temperatures, the calculations in this work suggest that the dominant secondary products are trisub_epoxy and OH at low temperatures and acetone, CH₂O, and OH at higher temperatures.

With the exception of temperatures below 250 K and above 10⁵ Pa, very few stabilized QOOH radicals are predicted to be formed. As with the α-network, the lack of QOOH radicals suggests slow preignition chemistry.

3.2.1 Comparison with previous calculations. There have been more previous quantum calculations of the βRO₂ surface than of the other two isomers’ surfaces because βR can also form from OH addition to isobutene.^18,19,42 This section compares this work's results with those of two other quantum studies. They include all the reactions in this work except for βH2OForm,¹⁶ which has not been published for the β-isobutanol surface before.

The barrier heights in this work generally agree with those previously published, though with a few slight differences (see Table 1).^18,19 For βEpoxyFromγ, our reaction barrier is 5 kJ mol⁻¹ and 15 kJ mol⁻¹ lower than the barriers computed by Lizardo-Huerta et al. and Sun et al., respectively. This may be due to the presence of intramolecular hydrogen bonding in the TS conformers in this work and that of Lizardo-Huerta et al. but not in Sun et al.^18,19 For β-γHO2elimFromRO2, the barrier in this work is 10 kJ mol⁻¹ lower than the rate computed by Sun et al., but only 3 kJ mol⁻¹ lower than the barrier computed by Lizardo-Huerta et al. The barrier height for βHO2elimFromα determined in this study is between those calculated in the other two studies. The calculated barriers for the rest of the reactions fell within 8 kJ mol⁻¹ of those in the other two studies. A recent study by Li et al. looked at βAlkoxyIsom and β-βscissionFromAlkoxy using two methods, CCSD(T) and DLPNO-CCSD(T), with basis set extrapolation.⁴² Relative to the current work, DLPNO-CCSD(T) resulted in a larger difference in barrier heights than CCSD(T) did (see Table 1). For these two reactions larger barrier hight differences exist between the present work and that of Li et al. than between this work and that of Sun et al.¹⁸ or Lizardo-Huerta et al.¹⁹

Table 1 Reaction barriers at 0 K of reactions in the β-network (kJ mol⁻¹) in this work and other published works

Reaction	This work	Sun et al.^18	Lizardo-Huerta et al.^19	Li et al. DLPNO^42	Li et al. CCSD(T)^42
β-γQOOHIsom	147	149	149
βEpoxyFromα	29	21	35
βEpoxyFromγ	40	55	45
βHO2elimFromγ	64	63	62
β-γHO2elimFromRO2	123	134	127
β-αHO2elimFromRO2	133	134	136
βHO2elimFromα	54	49	66
β-αQOOHIsom	119	120	116
βAlkoxyIsom	89	92	94	105	96
β-βscissionFromAlkoxy	35	38	28	24	26

---

The high-pressure-limit rates in this network can be compared to those presented in Sun et al., Lizardo-Huerta et al. and Li et al.^18,19,42 Nine out of the ten rates in Lizardo-Huerta et al. come within one order of magnitude with the rates of corresponding reactions in this work over the temperature range 500–1000 K, indicating good agreement. The rate coefficients by Sun et al. over the same temperature range differed from this work by an average factor of 23. Adjusting the activation energy of the Sun et al. rates based on the differences in energies shown in Table 1 reduced this difference in rates to an average factor of 15, indicating that energy differences do not entirely account for the difference in rates; this indicates that differences in calculated partition functions are also contributing. In the work of Li et al., only the βAlkoxyIsom using the DLPNO-CCSD(T) method, differed by more than a factor of 10 over the same temperature range, due in part to the 16 kJ mol⁻¹ barrier height difference.

The major pressure-dependent pathways in this work, shown in Fig. 8, show general agreement with the conclusions drawn in Sun et al., though our calculations predict more alkene formation. Both studies predict that βR + O₂ gives stabilized βRO₂ at higher pressures and lower temperatures, with the switching of the major pathway at around 10⁵ Pa and 1000 K. With lower pressures (T = 1000 K), our calculations suggest alkene formation will dominate over the Waddington reaction, whereas those of Sun et al. suggest the reverse. Other major products in this work include ibutenol and trisub_epoxy, which Sun et al. also found as large secondary pathways.¹⁸

For the reactions of stabilized βRO₂, this work and that of Sun et al. find the reaction forming βR + O₂ to dominate for all pressures at 800 K. For lower pressures (at 800 K), this work and that of Sun et al. predict the main secondary channel to be the Waddington pathway.¹⁸ However, at high pressures, Sun et al. found βQOOH[O] formation to be the main secondary channel, but this work finds it to be one of the slower pathways. This difference may have arisen from the approximations made to get phenomenological rates. If we use the modified strong collision method to obtain pressure-dependent rates from the master equation instead of the reservoir state method, we obtain more rapid formation of βQOOH[O], in better agreement with the results of Sun et al. (see Fig. S3 in the ESI,† for the major products obtained using the modified strong collision method).

The reactions shown in Fig. 8 do not explicitly include the non-reaction path, in which excited βRO₂ reforms βR and O₂ (though this is taken into account implicitly by an overall decrease in reaction rate). This non-reaction can be important when determining how much of βR will β-scission to form isobutene instead of adding O₂, which the model by Merchant et al. had trouble accurately predicting.¹¹ Fig. S45 in the ESI,† shows the fraction of excited βRO₂ which decomposes back to the βR. For the β-network at high temperatures, over 95% of excited βRO₂ re-forms βR + O₂, in agreement with the results in Sun et al.¹⁸

Given the small region showing the formation of acetone, CH₂O, and OH in Fig. 8a, the Waddington pathway appears less important than has been suggested previously.^41,43 This is due to sensitivity in the kinetic rates and the masking of secondary products in Fig. 8. The fraction going to this path is highly dependent on the barrier heights. A sensitivity study in which the barrier height of β-γHO2FromRO2 was raised by 10 kJ mol⁻¹, to correspond to that of Sun et al., increased the range of conditions where the Waddington pathway was most dominant (Fig. S1 of the ESI†). In addition, in the region around 800 K and 50 bar, where βR + O₂ and stabilized βRO₂ are essentially reversible, the major secondary pathway is the Waddington path.

3.3 γ-Peroxy network

As shown in Fig. 9, γRO₂ has four isomerization reactions and a direct path to form HO₂. The lowest-energy isomerization involves a 6-member transition state to form γQOOHα, which can decompose via a number of pathways: γDoubleβscissionFromα, γAldolFromα, γC4EtherFromα, and γH2OForm.

Fig. 9 The potential energy surface for the γ-peroxy radical. Energy includes zero-point energy and atom corrections. Species name and structures appear in black near the structure energy level. Reaction names appear in gray above the transition state energy.

The other isomerization reactions are less important. Despite only slightly higher product energies, the decomposition pathways of γQOOH and γQOOH[O] all have high barriers, making them unlikely to be important at most conditions. The isomerization reaction with the highest barrier, γ-βQOOHIsom, forms γQOOHβ. This intermediate has two lower-energy decomposition paths forming either an alkene or a cyclic ether. The direct HO₂ elimination pathway from γRO₂ has a similar barrier to γ-βQOOHIsom.

Fig. 10 shows the microcanonical rates for relevant intermediates. For γRO₂, the γ-αQOOHIsom pathway is dominant at the lower energies and is taken over by the rate to reform γR + O₂ only at higher energies. At high energies, other product channels such as γ-γQOOHIsom and γHO2ElimFromRO2 also have competitive rates.

Fig. 10 Microcanonical rates for all the reaction channels coming from (a) γRO₂ and (b) γQOOHα. The reaction names correspond to those in Fig. 6, with γR + O2 being the reverse of γRO2Form, and γRO2Isom being the reverse of γ-αQOOHIsom. The energy values correspond to those in Fig. 9 and are relative to that of γR + O₂.

At the lowest energies shown in Fig. 10b, γQOOHα will reform γRO₂, though this is taken over at slightly higher energies by γH2OForm. At the highest energies, many reactions can effectively compete, as is the case for the microcanonical rates of γRO₂.

The large number of potential pathways at high energies is shown by the dark shading at high temperatures in Fig. 11a. This includes a mixture of HO₂ + γalkene, CH₂O + OH + propene1ol, and OH + disub_c4ether. Between 800–1100 K, the dominant product is H₂O + γaldoxy, which agrees with the results of Welz et al.¹⁶ Below 600 K, the major product is stabilized γRO₂.

Fig. 11 Major stabilized products for the reactions of (a) γR + O₂ and (b) γRO₂ at various temperatures and pressures. Shading indicates the fraction going to the major pathway.

Stabilized γRO₂ starts with much lower internal energy, which prohibits the higher-energy reactions that are available to the entrance channel γR + O₂. At the lowest temperatures simulated, shown in Fig. 11b, stabilized γQOOHα radical is formed. Above 400 K, the well-skipping reaction forming water and the alkoxy radical is the major pathway. At the highest temperatures and pressures, dissociation to reform γR + O₂ is the dominant pathway.

Relative to the other two networks, the γ-network is most likely to produce a stabilized QOOH radical. This species can undergo unimolecular reaction or reaction with O₂ (via addition of H-atom abstraction). Comparison of these reaction rates (high-pressure unimolecular reactions from this work, bimolecular reactions with O₂ by Sarathy et al.¹⁵) indicates that γQOOHα reacts almost entirely through bimolecular H-abstraction channel in air, forming HO₂ and a ketohydroperoxide, over the range of conditions in this study. The ketohydroperoxide will likely decompose into two OH radicals, two carbonyls, and a carbon monoxide, which is the dominant decomposition pathway for other γ-separated, aldehyde-containing ketohydroperoxides.¹² Overall, this pathway for isobutanol oxidation can produce one HO₂ and two OH radicals from a single initiation. If important enough, this radical branching could create a negative temperature coefficient region. However, since our calculations show γQOOHα only forming below 500 K, this channel is unlikely to impact combustion significantly.

3.3.1 Comparison with previous calculations. Welz et al. calculated an extensive potential energy surface for the γ-network, but did not calculate the corresponding kinetic rates. The present work includes all but one of the reactions examined by Welz et al. for the γ-network and added also includes decomposition pathways for three isomers: γQOOH[O], γQOOHγ, and γQOOHβ.¹⁶ The reaction not included in this present work, which involved a direct path from γRO₂ to γaldol + OH, was instead replaced by a reaction from γQOOH[O] to form the same products: γaldol and OH, based on the IRC trajectory (view IRC trajectories in the ESI†). This reaction, named γAldoxyHabs, involves a hydrogen abstraction of the α-hydrogen with a simultaneous breaking of the O–O bond.

Table 2 shows the barrier height differences between this work and that of Welz et al. Decent agreement, within 8 kJ mol⁻¹, occurs for all but three reactions. We report barrier heights for γAlkoxyIsom to be 20 kJ mol⁻¹ lower and that of γAldolFromα to be 20 kJ mol⁻¹ higher than those in Welz et al. The barrier for γC4EtherFromα was calculated to be 12 kJ mol⁻¹ higher than that in Welz et al. A smaller difference of 6 kJ mol⁻¹ occurs for γH2OForm, the dominant pathway at most conditions. These differences may be due to different level of theory used in the two studies, possibly amplified by multireference effects. Using the barriers given by Welz for the γH2OForm reactions does not lead to significant shifts in predicted product distribution (see Fig. S1 in the ESI†).

Table 2 Reaction barriers at 0 K of reactions in the γRO₂ network (kJ mol⁻¹), compared to CBS-QB3 calculations by Welz et al.¹⁶

Reaction	This work	Welz et al.^41
γAlkoxyIsom	99	123
γ-αQOOHIsom	84	85
γ-γQOOHIsom	102	99
γ-βQOOHIsom	124	127
γHO2elimFromRO2	126	133
γH2OForm	47	41
γC4EtherFromα	73	61
γDouble scissionFromα	102	94
γAldolFromα	91	69

---

3.4 Uncertainty analysis

We evaluated how the inputs into the pressure-dependent kinetic solver impact the product branching ratios using two methods. The first involved changing an input parameter a specified amount and viewing how it would change the branching ratios across the range of temperatures and pressures shown in Fig. 5, 8 and 11. This was done for three input parameters: barrier heights, collisional energy transfer, and the method of solving phenomenological rates. The results appear in Fig. S1–S3 of the ESI.† From these sensitivity studies, the largest change appeared when changing the method used in solving phenomenological rate constants, and the smallest change ocurred when varying the collisional energy transfer. This methodology was particularly useful when evaluating how a difference in barrier heights between this work and previous works impacted the conclusions in this work. This method does not give an overall uncertainty of the branching ratio given the multiple sources of uncertainty.

To evaluate this overall uncertainty, Monte Carlo calculations were conducted varying seven types of parameters: electronic energies, tunneling frequency, Lennard-Jones parameters, collisional energy transfer parameters, rates of reaction used for barrierless reactions, and the method of solving for phenomenological rates. Of the 2000 runs for each network, 1008, 932, and 1194 were successful for the α-, β-, and γ-networks, respectively. Unsuccessful calculations typically resulted from initial conditions where a transition state is lower in energy than the corresponding reactants or products, which occurred more frequently in this work than it would in other work³⁷ due to the larger network size and a higher uncertainty value being placed on single-point energies.

Branching ratios from the resulting models were calculated for bimolecular R + O₂ and unimolecular RO₂ reactions at three conditions: 300 K and 1 × 10⁵ Pa, 600 K and 3 × 10⁵ Pa, and 900 K and 1 × 10⁶ Pa. The median value and 90% confidence limits are reported in Tables S1–S18 of the ESI.† Also included are the two inputs parameters that had the highest absolute value of Spearman rank coefficient, indicating they had a large impact on the branching ratio.

In general, branching ratio uncertainty was higher in regions where the original model showed competing pathways. For example, the reaction of βR + O₂ at 300 K ant 10⁵ Pa in Fig. 8a shows that βRO₂ is the only major product. The 90% confidence interval for the branching ratio of βR + O₂ forming βRO₂, as determined from Monte Carlo, is 0.96–1.00, indicating there is also little uncertainty in this value. On the other hand, the reaction of γRO₂ at 600 K and 3 × 10⁵ Pa has three major pathways, shown in Fig. 11b. For each of these three pathways, the 90% confidence intervals for the branching ratio spans at least 0.01 to 0.90, indicating that any one of these reactions could reasonably be the dominant product at these conditions. Given this uncertainty, any user of this model should ensure their conclusions are not sensitive to the branching ratios discussed in this work when the original model predicts a branching ratio of the dominant channel less than 90% (demarcated with darker shading in Fig. 5, 8 and 11).

The factors that most contributed to branching ratio uncertainty were single-point energies, the rate used in ILT, the method used to solve phenomenological rates, and negative frequencies of transition states. Single-point energies and the frequency of transition states were more important at lower temperature, whereas the rates used to solve for the ILT were important for the branching ratio of RO₂ at higher temperatures. The method used to solve for phenomenological rates was important where well skipping occurs, including for reactions of RO₂ at high temperatures and reactions of R + O₂ at all three temperatures. Relative to these sources of uncertainty, collisional energy transfer and Lennard-Jones parameters were not large sources of uncertainty when determining branching ratios.

Tables S19–S21 (ESI†) show the uncertainty in overall reaction rate for various pathways and the major factors contributing to them. For the oxygen addition reaction, the only major source of uncertainty comes from the rate used in the ILT. For stabilized RO₂ the uncertainty came from three sources: the electronic energy of the peroxy radical, the electronic energy of the isomerization transition state, and the rate used in the ILT, with the last being more important at higher temperatures.

While the uncertainty analysis here was conducted at only three conditions, the ESI,† contains the models and code to estimate uncertainty anywhere within 180–1500 K and 10³–10⁷ Pa, enabling such an uncertainty assessment to be conducted for any given set of reaction conditions.

3.5 Comparison with a detailed combustion mechanism

The reaction rates from these calculations can be compared to estimates from the detailed isobutanol mechanism by Sarathy et al.¹⁵ Two other isobutanol mechanisms, published by Hui et al.⁷ and Merchant et al.,¹¹ do not include explicit representation of peroxy radicals, so these cannot be compared directly to the calculations here.

The Sarathy mechanism uses pressure-independent rate coefficients, which were compared to our high-pressure-limit rate coefficients. Of our 38 reactions, only 25 correspond directly to reactions in the Sarathy mechanism. The Waddington mechanism, which the Sarathy mechanism represents as one step, was also added and is compared to the βAlkoxyIsom reaction in this work. These reactions were compared at 50 temperatures between 500 and 1000 K. At each temperature, a ratio was taken of the rate in this work to rates in the Sarathy mechanism, and the mean of the ratios at the 50 temperatures is designated as the deviation between the two models. Fig. 12 shows the deviation for the 25 reactions as a histogram, with color coding indicating different types of reactions.

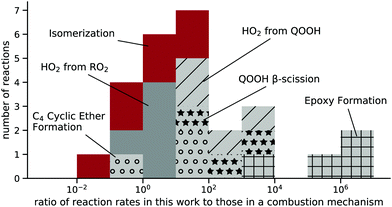Fig. 12 Histogram of the average ratio of rates calculated in this work and those estimated in the Sarathy mechanism¹⁵ between 500–1000 K, grouped by reaction type.

Given that the rates in Sarathy et al. consist of estimates, obtaining a rate within two orders of magnitude is reasonable. Good agreement is found for HO₂ elimination reactions from RO₂ and most of the RO₂ isomerization reactions.

Other reaction types deviate more strongly, with Sarathy et al. estimating epoxy formation around a million times slower than this work suggests. In the Sarathy mechanism, these rates originate from rate rules based on alkane fuels; such reactions have an activation energy of around 92 kJ mol⁻¹,⁴⁴ which is substantially higher than activation energies given from quantum calculations for ethane oxidation, between 50–70 kJ mol⁻¹.⁴⁵ In addition, the rates in Sarathy et al. are 2–3 orders of magnitude slower than those recommended by a more recent structure–activity relationship.⁴⁶ The barrier heights for epoxy formation reactions from isobutanol in this present work and other studies^18,19 are also approximately 20 kJ mol⁻¹ lower than those reported for alkane and ethanol oxidation.^20,45,46 The large differences between the estimates in Sarathy et al. and those in this work can be attributed to the use of older structure–activity relationships and/or differences between alkane chemistry (on which the Sarathy et al. rate rule is based) and the chemistry of isobutanol oxidation.

The two classes of QOOH decomposition shown in Fig. 12, ‘QOOH β-scission’ and ‘HO₂ from QOOH’, are also predicted by Sarathy et al. to be 10–10⁴ times slower than determined in this work. The slower decomposition of QOOH would increase the predicted concentrations of QOOH; this would lead to an increased predicted importance of O₂ addition to QOOH, which can leading to a faster simulated ignition than what would be predicted based on this present work.

4 Conclusion

The calculations in this work update the chemistry of peroxy radicals formed in isobutanol oxidation using pressure-dependent rates for all three peroxy radical isomers. We obtain general agreement with the potential energy surface proposed by Zádor et al. for αRO₂, the studies of Sun et al. and Lizardo-Huerta et al. for βRO₂, and the work of Welz et al. for γRO₂.

The three isomers in this work react through different channels. The fate of αR + O₂ almost entirely results in HO₂ + isobutanal, which agrees with the results of Zádor et al.²⁰ The reaction of γR + O₂ almost entirely forms H₂O and alkoxy at lower temperatures, as suggested by Welz et al., with a mixture of products at higher temperatures. The β-network predominately proceeds via the Waddington pathway at lower temperatures, though there is much more competition with other pathways at higher temperatures than other studies suggest. The rates from this work can explain the lack of two-stage ignition from isobutanol combustion.

Given the potential use of isobutanol as a biofuel, these rates can be integrated into detailed kinetic mechanisms to help improve the accuracy of combustion models for low-temperature combustion (500–700 K). Refining the oxidation chemistry of key products predicted in this work, such as alkenols and larger aldehydes, might help improve accuracy of detailed models still further. Due to the potential for multireference characteristics, important reactions in this work (such as βAlkoxyIsom, β-βscissionFromAlkoxy, and β-γHO2elimFromRO2) could be better constrained using multireference calculations. Further, an improved understanding of low-temperature isobutanol oxidation may require the inclusion of the O₂ reactions with stabilized QOOH radicals, such as γQOOHα.

Conflicts of interest

This fundamental research was funded by grants to MIT from the NSF and from BP. We note that BP is a part owner of BUTAMAX, a company commercializing the biofuel isobutanol. The authors declare that they have no financial interest in isobutanol commercialization and no conflict of interest.

Acknowledgements

M. J. G., J. H. K., and W. H. G. gratefully acknowledge financial support from the National Science Foundation's Environmental Chemical Sciences Program through grant 1709993. M. J. G. also acknowledges NSF support through a Graduate Research Fellowship (Grant No. 1122374). N. W. Y. and W. H. G. acknowledge financial support from BP through its participation as a Founding Member of the MIT Energy Initiative. The authors gratefully acknowledge Shamel Merchant for helpful guidance on the quantum calculations, and Oliver Welz for sharing the geometries from his calculations with us.

Notes and references

1. U. S. Environmental Protection Agency, Fed. Regist., 2018, 83, 13460–13463.
2. S. E. Pruitt, Letter of Approval of Isobutanol Fuel Additive to Butamax Advanced Biofuels, LLC, 2018.
3. L. M. Rodríguez-Antón, F. Gutíerrez-Martín and Y. Doce, Fuel, 2016, 166, 73–78.
4. U.S. eRulemaking Management Office, https://www.regulations.gov/document?D=EPA-HQ-OAR-2018-0131-0045, (accessed June 2019).
5. J. H. Mack, D. Schuler, R. H. Butt and R. W. Dibble, Appl. Energy, 2016, 165, 612–626.
6. B. Rajesh Kumar, S. Saravanan, D. Rana and A. Nagendran, Energ. Convers. Manage., 2016, 119, 246–256.
7. X. Hui, K. E. Niemeyer, K. B. Brady and C.-J. Sung, Energy Fuels, 2017, 31, 867–881.
8. B. W. Weber and C.-J. Sung, Energy Fuels, 2013, 27, 1688–1698.
9. M. Shahsavan and J. H. Mack, Energ. Convers. Manage., 2018, 157, 28–40.
10. L. Pan, Y. Zhang, Z. Tian, F. Yang and Z. Huang, Energy Fuels, 2014, 28, 2160–2169.
11. S. S. Merchant, E. F. Zanoelo, R. L. Speth, M. R. Harper, K. M. Van Geem and W. H. Green, Combust. Flame, 2013, 160, 1907–1929.
12. S. S. Merchant, C. F. Goldsmith, A. G. Vandeputte, M. P. Burke, S. Klippenstein and W. H. Green, Combust. Flame, 2015, 162, 3658–3673.
13. J. Zheng, R. Meana-Pañeda and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 5150–5160.
14. G. P. Smith, D. M. Golden, M. Frenklach, N. W. Moriarty, B. Eiteneer, M. Goldenberg, C. T. Bowman, R. K. Hanson, S. Song, W. C. Gardiner, V. Lissianski and Z. Qin, GRI-MECH 3.0, http://www.me.berkeley.edu/gri_mech/.
15. S. M. Sarathy, S. Vranckx, K. Yasunaga, M. Mehl, P. Oßwald, W. K. Metcalfe, C. K. Westbrook, W. J. Pitz, K. Kohse-Höinghaus, R. X. Fernandes and H. J. Curran, Combust. Flame, 2012, 159, 2028–2055.
16. O. Welz, S. J. Klippenstein, L. B. Harding, C. A. Taatjes and J. Zádor, J. Phys. Chem. Lett., 2013, 4, 350–354.
17. D. J. M. Ray, A. Redfearn and D. J. Waddington, J. Chem. Soc., Perkin Trans. 2, 1973, 540–543.
18. H. Sun, J. W. Bozzelli and C. K. Law, J. Phys. Chem. A, 2007, 111, 4974–4986.
19. J. C. Lizardo-Huerta, B. Sirjean, R. Bounaceur and R. Fournet, Phys. Chem. Chem. Phys., 2016, 18, 12231–12251.
20. J. Zádor, R. X. Fernandes, Y. Georgievskii, G. Meloni, C. A. Taatjes and J. A. Miller, Proc. Combust. Inst., 2009, 32, 271–277.
21. B. M. Wong, D. M. Matheu and W. H. Green, J. Phys. Chem. A, 2003, 107, 6206–6211.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03 (Revision D.01), Gaussian Inc., Pittsburg, PA, 2004.
23. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
24. U. R. Fogueri, S. Kozuch, A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2013, 132, 1291.
25. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225.
26. C. F. Goldsmith, W. H. Green and S. J. Klippenstein, J. Phys. Chem. A, 2012, 116, 3325–3346.
27. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
28. J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827.
29. M. K. Kesharwani, B. Brauer and J. M. L. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714.
30. A. G. Dana, B. Buesser, S. S. Merchant and W. H. Green, Int. J. Chem. Kinet., 2018, 50, 243–258.
31. CHEMKIN Theory Manual, Reaction Design Technical Report CK-THE-10131-1307-UG-1, 2013.
32. N. J. B. Green and Z. A. Bhatti, Phys. Chem. Chem. Phys., 2007, 9, 4275–4290.
33. J. W. Allen, C. F. Goldsmith and W. H. Green, Phys. Chem. Chem. Phys., 2012, 14, 1131.
34. A. W. Jasper and J. A. Miller, Combust. Flame, 2014, 161, 101–110.
35. I. O. Antonov, J. Kwok, J. Zádor and L. Sheps, J. Phys. Chem. A, 2015, 119, 7742–7752.
36. A. Miyoshi, J. Phys. Chem. A, 2011, 115, 3301–3325.
37. C. F. Goldsmith, A. S. Tomlin and S. J. Klippenstein, Proc. Combust. Inst., 2013, 34, 177–185.
38. L. Xing, S. Li, Z. Wang, B. Yang, S. J. Klippenstein and F. Zhang, Combust. Flame, 2015, 162, 3427–3436.
39. D. Chen, K. Wang and H. Wang, Combust. Flame, 2017, 186, 208–210.
40. Y. R. Luo and J.-P. Cheng, in CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, 100th edn, 2019, ch. 9, pp. 73–104.
41. O. Welz, J. D. Savee, A. J. Eskola, L. Sheps, D. L. Osborn and C. A. Taatjes, Proc. Combust. Inst., 2013, 34, 493–500.
42. Y. Li, Q. Zhao, Y. Zhang, Z. Huang and S. M. Sarathy, J. Phys. Chem. A, 2020, 124, 5646–5656.
43. O. Welz, J. Zádor, J. D. Savee, M. Y. Ng, G. Meloni, R. X. Fernandes, L. Sheps, B. A. Simmons, T. S. Lee, D. L. Osborn and C. A. Taatjes, Phys. Chem. Chem. Phys., 2012, 14, 3112–3127.
44. H. J. Curran, P. Gaffuri, W. J. Pitz and C. K. Westbrook, Combust. Flame, 2002, 129, 253–280.
45. L. H. Oakley, F. Casadio, K. R. Shull and L. J. Broadbelt, Ind. Eng. Chem. Res., 2017, 56, 7454–7461.
46. J. Bugler, J. Power and H. J. Curran, Proc. Combust. Inst., 2017, 36, 161–167.

---

Footnote

† Electronic supplementary information (ESI) available: A pdf file contains videos of internal reaction coordinates, graphs of the major products in sensitivity studies, and data about the reversibility of excited RO₂. A CHEMKIN II file contains species thermo and high-pressure-limit and pressure-dependent reaction rates. Machine readable text files contain information with the atom coordinates of each molecule and transition state, their energies, energies from the hindered rotor scans, and other parameters used to determine kinetics, like molecular symmetry. One zenodo data repository (DOI http://10.5281/zenodo.3858424) contains all the quantum calculations as well as the scripts used to reproduce the analysis and figures in this paper using the docker framework. Another zenodo data repository (DOI http://10.5281/zenodo.3970278) contains methods to do Monte Carlo uncertainty analysis. See DOI: 10.1039/d0cp02872j

---