 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating ultrafast two-pulse experiments on single DNQDI fluorophores: a stochastic quantum approach†
Giulia
Dall'Osto
 a,
Emanuele
Coccia
a,
Emanuele
Coccia
 b,
Ciro A.
Guido
b,
Ciro A.
Guido
 a and
Stefano
Corni
a and
Stefano
Corni
 *ac
*ac
aDepartment of Chemical Sciences, University of Padova, via Marzolo 1, Padova, Italy. E-mail: stefano.corni@unipd.it
bDepartment of Chemical and Pharmaceutical Sciences, University of Trieste, via Giorgieri 1, Trieste, Italy
cCNR Institute of Nanoscience, via Campi 213/A, Modena, Italy
First published on 13th July 2020
Abstract
Ultrafast two-pulse experiments on single molecules are invaluable tools to investigate the microscopic dynamics of a fluorophore. The first pulse generates electronic or vibronic coherence and the second pulse probes the time-evolution of the coherence. A protocol that is able to simulate ultrafast experiments on single molecules is applied in this study. It is based on a coupled quantum-mechanical description of the fluorophore and real-time dynamics of the system vibronic wave packet interacting with an electric field, described by means of the stochastic Schrödinger equation within the Markovian limit. This approach is applied to the DNQDI fluorophore, previously investigated experimentally [D. Brinks et al., Nature, 2010, 465, 905–908]. We find this to be in good agreement with the experimental outcomes and provide microscopic and atomistic interpretation.
1 Introduction
In the last decade, ultrafast spectroscopy on single molecules has become a powerful tool to investigate different features of microscopic dynamics as quantum coherence.1–8 A possible strategy to study processes at the atomic scale is to set up techniques which have appropriate sensitivity. Ultrafast spectroscopy employs ultrashort pulses whose duration has the same time scale (ideally shorter) as the processes one wants to investigate.9 Pulses resolved at the femtosecond timescale are essential to detect very fast molecular processes such as electronic dephasing, charge transfer, excitation energy transfer, and vibrational energy relaxation.10,11 Many of these ultrafast processes play a relevant role in biological processes: indeed one of the applications of ultrafast experiments is the detection of electronic and vibrational coherences12,13 in light-harvesting complexes involved in photosynthesis.14–16In order to detect femtosecond molecular processes, different ultrafast techniques based on ensemble measurements have been developed. In particular in the framework of non-linear optics, multidimensional electronic spectroscopy has allowed the investigation of the vibrational structure of a system and the detection of coherence decay.17,18 Different from multidimensional spectroscopy, single-molecule techniques1–3,19–23 have the advantage of preventing ensemble-average effects, detecting the intrinsic inhomogeneity due to different conformations and local environments experienced by each molecule. The outcomes of two-pulse ultrafast experiments may be strongly affected by quantum coherence whose persistence depends on the interaction between the system (i.e., the molecule under study) and the environment. For this reason the effects of the surrounding environment cannot be neglected, and the system is described as open.17
Approaches based on the time-dependent Schrödinger equation have been widely employed to perform a time-resolved analysis of the optical processes of interest, also coupled with a quantum chemical description of the molecule,24–26 usually focusing on a close system. A description of the spectroscopic target in terms of open quantum systems27,28 is required in order to include the presence of a surrounding environment. Most of the approaches present in the literature are based on density matrix master equations29–32 involving phenomenological parameters,33,34 in some cases including a vibronic analysis.35,36 The density matrix approach has been also coupled with a TDDFT37,38 or quantum-chemistry-based39 description of the spectroscopic target. The protocol here employed is based on existing methodologies that, when combined, allow the investigation of ultrafast processes preserving a refined description of the fluorophore. The fluorophore time propagation is computed through the stochastic Schrödinger equation (SSE)40–42 within the Markovian limit.43,44 In this model, dissipation and fluctuations due to the environment are included by means of stochastic terms in every realization of the wave function evolution. Averaging over a number of realizations leads to results equivalent to the Lindblad master equation solution with the advantage of less computational effort.45 The density matrix terms (i.e. populations and coherences), computed starting from the coefficients of wave function expansion, are used to interpret the experimental results.
The SSE is coupled with a quantum mechanical description of the vibronic structure of the molecular target, such as vibronic energies and transition dipole moments. This information can be obtained by fitting experimental results. However, this method usually leads to no univocal sets of input data. On the other hand a quantum chemistry computation of the fluorophore leads to a univocal system description. In the present work the electronic ground and first-excited states of DNQDI have been characterized in terms of energies, dipole moments and normal mode frequencies employing DFT/TDDFT methods. A vibrational structure has been included by means of harmonic vibrational levels and related Franck–Condon factors.
The whole protocol, schematized in Fig. 1, has been applied in the present work to a two-pulse experiment performed on the DNQDI fluorophore,1 in order to clarify the interpretation of the experimental results. In the experiment,1 fluorophore molecules embedded in a thin polymeric matrix interact with two identical pulses 15 fs long separated by a controlled delay time Δt of the order of femtoseconds. Moreover a phase difference Δϕ between the two pulses is applied. Ultrashort pulses have a bandwidth large enough in the frequency domain to excite various vibrational levels of the electronic excited state. The fluorescence signal of single molecules (proportional to the population in the excited state after the two pulses) has been detected for fixed phase differences. Their profile as a function of delay time has a dumped oscillating behaviour with frequencies distributed between 670 and 1500 cm−1 and a peak at 1070 cm−1.1 The signal decay is the result of pure electronic and/or vibronic dephasing of the wave packet:20,46 typical dephasing times T2 for this molecule under the experimental conditions reported in ref. 1 are around 60 fs. Oscillations were explained in terms of wave packet interference and interpreted as an excited-state vibrational signature of DNQDI.1 In detail, the first pulse populates a manifold of vibrational levels of the excited state, generating a vibronic wave packet and it creates a coherence between the electronic ground state and the excited state, which evolves with time. The second pulse interacts with the system generating another wave packet that can interfere constructively or destructively with the first one, depending on Δϕ and Δt values. The excited state population after the second pulse depends on such interference that in turn is sensitive to the decoherence taking place during Δt. Thus the emission signal provides signature of the coherence dynamics.
This paper is organized as follows: the theoretical framework employed to simulate the ultrafast dynamics induced by two pulses is described in Section 2, computational details are briefly summarized in Section 3, the present results are reported and discussed in Section 4, and our final comments and perspectives are summarized in conclusions.
2 Theory
Our theoretical and computational approach is hierarchically based on three steps (Fig. 1): (i) description of the electronic structure of the spectroscopic target by means of DFT/TDDFT; (ii) electronic properties (excitation energies and transition dipole moments) are then “dressed” by a proper vibrational structure, using the quantities computed at step (i); (iii) a real-time propagation of the vibronic wave packet is performed, in terms of close (“standard” time-dependent Schrödinger equation) and open quantum (SSE) systems, using the quantities from steps (i) and (ii) as input parameters.43,44 Using DFT/TDDFT to characterize states for many-electron dynamics has been performed before.24,25,47In this section, we briefly review the SSE protocol and the methodology to vibrationally dress the electronic states.
2.1 Stochastic Schrödinger equation
The stochastic Schrödinger equation (SSE)48–50 is an approach equivalent to master equation for the density matrix, as Lindblad equation,51 that is able to perform the real-time propagation of the system wave function.45 The SSE employed in this work is thoroughly described in ref. 43, while we report here only the main equations and the new features included. The SSE in a Markovian regime reads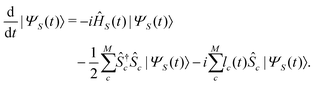 | (1) |
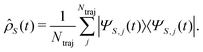 | (2) |
 | (3) |
 , with Nel, Nm and Nvib being the number of electronic states, the number of included normal modes, and the number of vibrational states per normal mode, respectively. Eqn (1) returns the coefficients of the wave function expansion, allowing one to compute all the elements of the density matrix at a certain time t, averaging over the Ntraj SSE trajectories.43 Diagonal elements of the density matrix are the population of states
, with Nel, Nm and Nvib being the number of electronic states, the number of included normal modes, and the number of vibrational states per normal mode, respectively. Eqn (1) returns the coefficients of the wave function expansion, allowing one to compute all the elements of the density matrix at a certain time t, averaging over the Ntraj SSE trajectories.43 Diagonal elements of the density matrix are the population of states | (4) |
The Ŝq operators in eqn (1) describe the relaxation and dephasing processes. In the model developed before43 relaxation has been included via radiative (spontaneous) emission and nonradiative decay processes. According to previous studies,43,44,48,56 relaxation has been included by the operator
 | (5) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b7.gif) S(t))qq of the q-th state exponentially decays with the rate constant Γq. Such decay rates can be included as phenomenological parameters for non-radiative processes or according to Fermi's Golden rule in fluorescence processes. Here we choose Γq = T1−1, with T1 phenomenological relaxation time, for all the q states.
S(t))qq of the q-th state exponentially decays with the rate constant Γq. Such decay rates can be included as phenomenological parameters for non-radiative processes or according to Fermi's Golden rule in fluorescence processes. Here we choose Γq = T1−1, with T1 phenomenological relaxation time, for all the q states.
Vibrational and electronic coherences decay with different time scales.57 Following the treatment in ref. 58, the (pure) dephasing of the quantum state of the molecular target originates from the random time fluctuations of the energy difference between the states of interest, due to the interaction with degrees of freedom not treated explicitly. For electronic levels of a molecule in a matrix, the differential interaction of the ground and excited-state charge densities with the environment fluctuating polarization is an important source of excitation energy fluctuations and thus electronic dephasing. Vibrational dephasing may have various origins,59 but the anharmonic coupling among vibrational modes (of the composite molecule-environment system) is certainly relevant in modulating vibrational frequencies and thus inducing dephasing.60
Here we include them with different operators. For vibrational dephasing we exploit the generic operators defined before,43 specialized for vibronic states k and q:
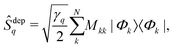 | (6) |
To account for a purely electronic dephasing (i.e., a dephasing that does not affect the coherence between different vibrational states belonging to the same electronic state), in the present work we also introduce the following dephasing operator:
 | (7) |
The form of the two operators in eqn (6) and (7) assures that coherences between vibrational levels of the same electronic state exponentially decay with a rate equal to γvib (i.e., only vibrational dephasing matters) whereas, for coherences between vibrational levels of different electronic states the decay rate is γvib + γel (i.e., both vibrational and electronic decoherences are at work).
2.2 Vibronic structure
Electronic-state potential energies are approximated by harmonic oscillators, as shown in the upper panel of Fig. 2.61 The transition dipole moments are calculated assuming the Franck–Condon (FC) approximation and the integrals between vibrational states are computed using the Sharp and Rosenstock approach.61–65 It allows the explicit calculation of the 〈0g|0e〉 FC integral taking into account the displacement of the equilibrium position due to all the normal modes. The FC integrals between the vibrational ground state of the electronic ground state and any other vibrational levels in an excited electronic state are evaluated recursively from 〈0g|0e〉. | ||
| Fig. 2 Schematic structure of the DNQDI vibronic system and molecular structure of the reduced model of DNQDI employed in the simulations. | ||
When more than one normal mode is considered to describe the molecule, all the possible combinations between different quanta of different normal modes give a total number of states with N equal to 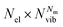 , as already shown. Including the complete set of normal mode frequencies in the vibrational structure of a large system translates into prohibitive computational costs of the wave function propagation. Therefore, a selected number of vibronic states can be included based on the analysis of the equilibrium position displacement vector (within the harmonic approximation), as it will be shown in Section 4. Approaches able to describe the molecular vibronic structure beyond the harmonic approximations and including non-adiabatic coupling can be found in the literature.66–68 However, since pulses employed in the target experiment are temporarily very close (largest delay time of 120 fs), slower processes driven by non-adiabatic coupling are unlikely. For DNQDI in particular, nonradiative decay induced by non-adiabatic coupling takes place on the much longer ns time scale. For this reason, neglecting non-adiabatic coupling is considered accurate for our goal.
, as already shown. Including the complete set of normal mode frequencies in the vibrational structure of a large system translates into prohibitive computational costs of the wave function propagation. Therefore, a selected number of vibronic states can be included based on the analysis of the equilibrium position displacement vector (within the harmonic approximation), as it will be shown in Section 4. Approaches able to describe the molecular vibronic structure beyond the harmonic approximations and including non-adiabatic coupling can be found in the literature.66–68 However, since pulses employed in the target experiment are temporarily very close (largest delay time of 120 fs), slower processes driven by non-adiabatic coupling are unlikely. For DNQDI in particular, nonradiative decay induced by non-adiabatic coupling takes place on the much longer ns time scale. For this reason, neglecting non-adiabatic coupling is considered accurate for our goal.
3 Computational details
In order to vibrationally characterize the molecule, ground and excited state energy and vibrational normal modes of DNQDI have been calculated using DFT and TDDFT methods at the B3LYP/6-31G(d) level of theory performed by means of Gaussian16.69 Quantum mechanical calculations were performed for a reduced model of the fluorophore (lower panel of Fig. 2) where alkyl lateral chains have been replaced with hydrogen atoms in order to decrease the computational cost (see Fig. S1 in the ESI†).The vibrationally resolved optical spectrum has been computed with the FCclasses code.61 FCclasses allows the calculation of the displacements of excited-state normal modes coordinates with respect to the ground state normal modes coordinates and FC integrals. FC integrals have been computed between the vibrational ground states of the electronic states 〈0g|0e〉 and also between the ground and the vibrational excited states of the excited singlet state 〈0g|νe〉, up to 19th vibrational quantum number.
SSE simulations were performed by using the homemade WaveT code.43 A time step equal to δt = 1.21 as has been employed while the whole dynamics takes 1 ps. A shorter dynamics, e.g., around 200 fs, would have been large enough to properly reproduce the ultrafast dynamics of DNQDI, since delay times are limited to 120 fs. Yet, in the initial numerical assessment of our approach we tested larger delay times that required 1 ps duration, and we kept this value for all the simulations. When specified, relaxation is included in the simulation viaeqn (5) assuming a fluorescence emission time T1 = 3 ns (corresponding to Γq = 3.3 × 10−1 ns−1 for each q). Unless specified otherwise, dephasing is included viaeqn (6) with γq = 2.01 × 10−4 fs−1 for each q. This decay rate leads to a T2 of 60 fs, chosen on the basis of a phenomenological analysis of experimental data.1
100 SSE trajectories were calculated for each delay time and then the averaged populations of the excited states were computed. When compared with the outcomes of Lindblad master equation (Fig. S2 of ESI†), the results with 100 SSE trajectories show a relative error of less than 1%. A numerical test carried out with 200 SSE trajectories (Fig. S2, ESI†) confirms that accurate and reliable results are obtained by using 100 SSE trajectories.
All the dynamics start from the vibrational ground state, since vibrational excited states for the normal modes of interest (reported in Table 1) are not thermally populated.
| GS frequency (cm−1) | ES frequency (cm−1) | Displacement (Å) |
|---|---|---|
| 1368 | 1370 | 7.52 × 10−2 |
| 1629 | 1632 | 4.53 × 10−2 |
| 1265 | 1271 | 3.56 × 10−2 |
| 1647 | 1638 | 3.14 × 10−2 |
| 1583 | 1570 | 2.65 × 10−2 |
The field parameters are modeled after the experimental set-up.1 Pulses have an enveloped Gaussian sinusoidal shape, with the FWHM equal to 15 fs to have a bandwidth of 120 nm while the maximum intensity of the electric field is Imax = 1 × 109 W cm−2, unless otherwise specified. The pulse frequency ωexc employed in the experiment is shifted from the maximum absorption energy by 507 cm−1. Assuming that the calculated vertical absorption energy is the maximum absorption energy, a detuning of 1090 cm−1 between ωexc and the |0g〉 − |0e〉 transition can be estimated in the simulations. We have used such detuning to set the central frequency of the pulse (1.76 eV, 703 nm).
4 Results
In this section our results are presented. We first show the simulation of the vibrationally resolved optical absorption spectrum of DNQDI and its comparison with the experimental one. Then we report the results of the simulations of the real-time dynamics of the system interacting with two delayed pulses, compared with the experimental findings. Simulations have been performed by assuming either a pure electronic system or including a vibronic structure. We have systematically investigated several key aspects: the vibronic structure of the fluorophore, the possible interplay of electronic and vibrational dephasing effects, and the roles of pulse shape and pulse intensity.4.1 Optical spectrum
Fig. 3 reports the comparison between the computed (our work) and the experimental70 vibrationally resolved absorption spectrum of DNQDI (the experimental one has been shifted in order to superpose the two spectra). Although the simulated spectrum (in vacuo) is rigidly red-shifted by 0.13 eV with respect to the experimental one70 (in toluene), the general features are properly maintained: the distance between the two peaks is around 1370 cm−1 in both spectra, which is a typical value of vibrational modes in aromatic compounds.71 Generally speaking, the lower-energy peak may be related to the |0g〉 − |0e〉 transition (from the vibrational ground state of the electronic ground state to the vibrational ground state of the electronic excited state) and the other one to a |0g〉 − |1e〉 transition (from the vibrational ground state of the electronic ground state to the first vibrational state of the electronic excited state). We also calculated the absorption energy of DNQDI in toluene within the PCM model, red-shifted to 0.24 eV with respect to the maximum absorption in the experimental spectrum. The PCM calculation of absorption energy of DNQDI in PMMA (the matrix polymer employed in the ultrafast experiment1) provided the same result as in toluene. The analysis of the displacements of the excited-state parabolas along each one of the 3N − 6 normal mode coordinates (with N being the number of atoms) allows us to establish which normal modes contribute to the |0g〉 − |1e〉 band of the absorption spectrum. Indeed only if a normal mode is characterized by a sufficiently large displacement of the excited-state parabola with respect to the ground state, the vibrational ν = 1 state (|1e〉) of the electronic excited state has a non-negligible overlap with the ground state |0g〉. As one can see in Table 1, the normal mode with the largest displacement (7.52 × 10−2 Å) has a frequency of 1368 cm−1 (1370 cm−1) in the electronic ground (excited) state, fully compatible with the separation of the two peaks in the absorption spectrum of Fig. 3. The two normal modes with the largest displacement (with frequencies 1368 and 1629 cm−1 in the GS) have been considered for the vibronic dynamics, reported below in Section 4.3. | ||
| Fig. 3 Experimental70 (exp., in toluene) and calculated (calc.) absorption spectrum of DNQDI. The calculated spectrum has been blue-shifted by 0.13 eV in order to superpose the experimental and simulated spectra. | ||
4.2 Pure electron dynamics
We first propagated SSE trajectories, only involving the ground and the first-excited electronic states; the pulse bandwidth, taken from the experimental work,1 allows us to appreciably populate only the first excited state (as reported in Fig. S3 of the ESI†) since the other electronic excited states are too high in energy (Table S1, ESI†). Two-photon absorption under the conditions of the experiment is also unlikely, as discussed in the ESI.† The delay time has been varied between 0 fs and 120 fs and Δϕ is equal to 0 or π. SSE real-time dynamics were performed including dephasing and relaxation effects. The excited-state population, after the pulse sequence, as a function of delay time has a damped oscillating profile as shown in panel (a) of Fig. 4. The decay of population is due to the dephasing1,43 with decay time T2(el) = 60 fs, as a consequence of the interference (constructive or destructive) between the two pulses interacting with the system. On the other hand the dynamics is short enough to prevent population relaxation, and thus the effect of decay time T1 = 3 ns is negligible. Moreover the excited-state population oscillates with a frequency (1090 cm−1, 0.13 eV) equal to detuning δ = |ωexc − ω0–0| (ω0–0 is the frequency of the 0–0 excitation). The FT of the signal is reported in panel (b) of Fig. 4. The profile of excited state population is analogous to the experimental fluorescence signal reported in panel (c) of Fig. 4. A vibrational structure is not therefore needed to produce fluorescence oscillations: also for a pure electronic two-level system the population of the excited state oscillates with the detuning frequency. This was already noted in ref. 72.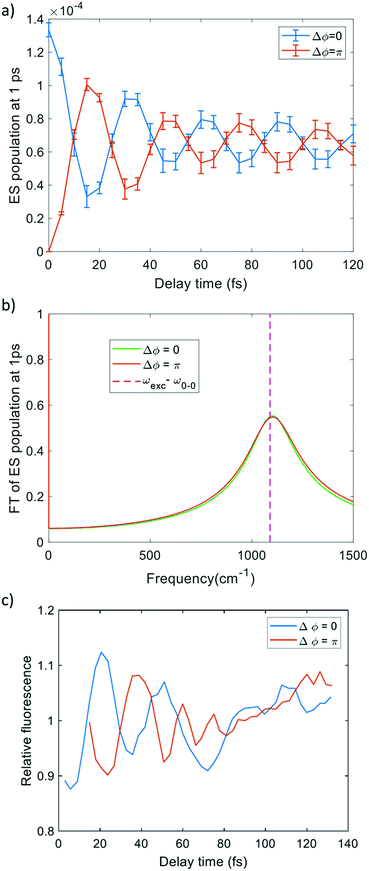 | ||
| Fig. 4 (a) Population of excited states at the end of simulation as a function of delay time in pure electronic dynamics. (b) FT of (a). (c) Fluorescence emission signal as a function of delay time from ref. 1. ω0–0 is the excitation energy of the excited state, ωexc is the pulse frequency. | ||
4.3 Vibronic dynamics
The next step in our investigation was the inclusion of vibrational states in the molecular description. We took into account only the two normal modes responsible for the largest displacement along the nuclear coordinate, as shown in Table 1. These two normal modes, schematically represented in Fig. S4 and S5 of ESI† and labeled as NM1 and NM2, are characterized by the “breathing” of the aromatic structure and by the C–H bending.For each normal mode, 20 vibrational levels were considered to compute FC integrals. Transition dipole moments between the state levels and ground vibrational states of electronic ground and excited states were calculated within the FC approximation. According to the values of the FC integrals for the two selected normal modes (Table 2), vibrational levels higher in energy were neglected in the SSE propagations. The 〈0g|0e〉 contribution is dominant for both normal modes.
| State (νe) | NM1 〈0g|νe〉 | NM2 〈0g|νe〉 |
|---|---|---|
| |0e〉 | 0.222 | 0.222 |
| |1e〉 | 7.43 × 10−2 | 4.89 × 10−2 |
| |2e〉 | 1.76 × 10−2 | 7.78 × 10−3 |
| |3e〉 | 3.40 × 10−3 | 1.03 × 10−3 |
| |4e〉 | 5.69 × 10−4 | 1.21 × 10−4 |
| |5e〉 | 8.5 × 10−5 | 1.3 × 10−5 |
| |6e〉 | 1.2 × 10−5 | 1 × 10−5 |
 is significantly lower (one order of magnitude) than
is significantly lower (one order of magnitude) than  (see Table 2). Including the population of state |1e〉 produces a modulation of the original |0e〉 population as could be noticed in panel (a) of Fig. 5.
(see Table 2). Including the population of state |1e〉 produces a modulation of the original |0e〉 population as could be noticed in panel (a) of Fig. 5.
 | ||
| Fig. 5 Sum of excited-state populations at the end of simulation as a function of delay time without (panel (a)) and with (panel (b)) relaxation and dephasing effects. (c) FT of (a). (d) FT of (b). Only the NM1 normal mode was added to the wave packet of eqn (3). ω0g−0e (ω0g−1e) is the excitation energy of state |0e〉 (|1e〉), and ωexc is the pulse frequency. | ||
The FT of the sum of populations (panel (c) of Fig. 5) reveals a frequency peak of around 1090 cm−1, namely the already observed detuning δ discussed previously. A smaller frequency peak (about 280 cm−1) is also present, related to detuning between pulse frequency and excitation frequency of state |1e〉: it has a lower intensity because the |1e〉 state is much less populated than |0e〉. The same results are observed with the FT of the SSE signal (panel (d) of Fig. 5), with only a broadening of the frequency peaks. Signals with Δϕ = 0 and π give approximately the same information.
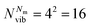 vibrational levels. Fig. 6 shows the sum of excited state populations at the end of simulation as a function of delay time for simulations obtained including dephasing and relaxation effects. The result is very close to panel (b) of Fig. 5 since the contribution of NM2 is smaller in terms of transition dipole moment than the contribution of NM1 (see Table 2). Moreover, the profile of the sum of excited-state populations is not very different with respect to that of the pure electronic system shown in panel (a) of Fig. 4: FC integrals between state |0g〉 and excited vibrational levels of the electronic excited state are much smaller than the FC integral 〈0g|0e〉. Vibronic dynamics does not change the interpretation: the observed oscillations in the fluorescence profile are due to detuning rather than to a normal-mode frequency of DNQDI.
vibrational levels. Fig. 6 shows the sum of excited state populations at the end of simulation as a function of delay time for simulations obtained including dephasing and relaxation effects. The result is very close to panel (b) of Fig. 5 since the contribution of NM2 is smaller in terms of transition dipole moment than the contribution of NM1 (see Table 2). Moreover, the profile of the sum of excited-state populations is not very different with respect to that of the pure electronic system shown in panel (a) of Fig. 4: FC integrals between state |0g〉 and excited vibrational levels of the electronic excited state are much smaller than the FC integral 〈0g|0e〉. Vibronic dynamics does not change the interpretation: the observed oscillations in the fluorescence profile are due to detuning rather than to a normal-mode frequency of DNQDI.
 | ||
| Fig. 6 Sum of excited-state populations at the end of the SSE simulation as a function of delay time. Normal modes NM1 and NM2 were added to the wave packet of eqn (3). | ||
The sum of populations of excited states as a function of delay time is shown in Fig. 7. In both cases the decay is dominated by the electronic dephasing time. The result may be easily understood in terms of the faster electronic loss of coherence between the states |0g〉 and |0e〉 or |0g〉 and |1e〉, created by the first pulse. These numerical results show that under the conditions of the experiment, vibrational coherences (between |0g〉 and |1g〉 or |0e〉 and |1e〉), i.e., the coherent motions of the nuclear wave packet, do not play any appreciable role. Again, for both cases reported in Fig. 7 the fluorescence oscillations are produced by the dominant contribution of the detuning δ between pulse frequency and the excitation frequency for the |0g〉 →|0e〉 transition. A different value of detuning was also tested and the results of the corresponding simulations are reported in the ESI† (Fig. S6–S8).
Vibronic dynamics in the presence of this pulse, only including NM1, was carried out. Since the goal is to investigate the possible effect of the pulse shape on the fluorescence oscillations, the calculation was performed without dephasing and relaxation effects. Panel (b) of Fig. 8 shows the total excited-state population (i.e. P0e + P1e + P2e + P3e) at the end of the simulation as a function of delay time: the profile is very close to panel (a) of Fig. 5. The observed oscillations have a frequency equal to the detuning between ωexc1 and ω0g−0e (ω0g−1e), as already observed with the “simple” pulse shape (Fig. 8). Detuning between the added pulse frequency ωexc2 and the transition frequencies |0g〉 → |0e〉 and |0g〉 → |1e〉 was not detected probably because of out of the considered frequency domain, and because the excitation to state |1e〉 is included only in the tail of pulse frequency bandwidth, respectively. As a conclusion, varying the shape of the applied field does not modify our physical interpretation.
4.4 Higher-order responses
All the conditions explored in the previous paragraphs do not allow us to directly detect vibrational signatures of DNQDI encoded in the time profile of the fluorescence. Of course when the detuning is zero, then the vibrational frequency can be detected as a fluorescence signal due to the excitation of the off-resonance vibrational states, but can vibrational frequencies be revealed by two-pulse experiments on a single molecule even in the presence of a detuning? All the simulations reported so far have been carried out in a linear response regime (Imax = 1 × 109 W cm−2, used in the experimental work1). We focus on the higher-order responses of DNQDI to the applied field, going beyond the linear regime. Additional components should be added to the present model in order to take into account high-intensity phenomena such as ionization, nonlinear optical responses and multi-photon processes. However, our aim is the interpretation of the experimental work,1 performed in the linear low-intensity regime, and the study of the possible role of vibrational coherence in the modulation of the fluorescence signal. In all the following simulations a four-level model for DNQDI was considered: two electronic states and two vibrational levels from NM1 normal mode for each electronic state. Dephasing and relaxation effects were neglected.The excited-state populations after the pulses are larger when the higher-intensity field is applied, as expected. The FT of the sum of excited-state populations is shown in panel (c) (Imax = 2.5 × 1012 W cm−2) and panel (d) (Imax = 1 × 1013 W cm−2) of Fig. 9. In both cases, two peaks at 1090 and 280 cm−1 are present, which are due to the detuning between pulse frequency and |0g〉 − |0e〉 transition frequency, and between pulse frequency and |0g〉 − |1e〉 transition frequency, as in the linear response. Only for Imax = 1 × 1013 W cm−2, the FT of the time-resolved signal reveals the presence of a peak at around 1380 cm−1, very close to the normal mode frequency in both electronic ground and excited states. An additional simulation on a model system neglecting vibrational levels in the ground state confirms that the detected frequency in the nonlinear regime is the excited-state vibrational frequency (Fig. S10 in ESI†).
 | (8) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (τ) is the electric field (which includes ωexc, labelled as ω in the following equations), ω0e and ω1e are respectively the excitation frequencies of states |0e〉 and |1e〉,
(τ) is the electric field (which includes ωexc, labelled as ω in the following equations), ω0e and ω1e are respectively the excitation frequencies of states |0e〉 and |1e〉,  and
and  are the transition dipole moments from |0g〉 and C0g(0) is the coefficient of the ground state at the beginning of the simulation (t = 0). In the approximation of an electric field composed of two delayed Dirac functions, the first-order response of excited-state coefficients is a function of delay time and it depends on the detuning between pulse frequency and excitation frequency (see ref. 72) and on the corresponding transition dipole moment, as resulting from the integral solution
are the transition dipole moments from |0g〉 and C0g(0) is the coefficient of the ground state at the beginning of the simulation (t = 0). In the approximation of an electric field composed of two delayed Dirac functions, the first-order response of excited-state coefficients is a function of delay time and it depends on the detuning between pulse frequency and excitation frequency (see ref. 72) and on the corresponding transition dipole moment, as resulting from the integral solution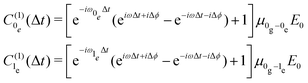 | (9) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) related to field intensity as
related to field intensity as  . Population of states |0e〉 and |1e〉 are given by
. Population of states |0e〉 and |1e〉 are given by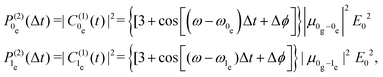 | (10) |
Field-induced transitions between states |0e〉 and |1e〉 are not possible (the related frequency is not included in the pulse frequency band), therefore only in the third-order correction of the excited-state coefficients, with respect to the electric field, the vibrational frequency of the excited state appears. Indeed the third-order coefficients of excited states depend on the second-order coefficients of the ground state, including oscillating terms with detuning frequency with respect to excitation energy of both states |0e〉 and |1e〉:
 | (11) |
In particular the terms of |0e〉 coefficients oscillating with the normal mode frequency depend on the product μ0g−1e2·μ0g−0e and on the third power of the electric field amplitude E0: as a consequence, the population of excited states depends on the sixth power of the electric field (third power of the intensity) and transition dipole moments.
The excited-state populations at the sixth order with respect to the electric field amplitude (within the RWA approximation) include oscillating terms with detuning frequency with respect to excitation energy of both states |0e〉 and |1e〉, and also include oscillations at normal mode frequency (ω1e − ω0e) in the electronic excited state:
 | (12) |
In conclusion, perturbative analytical results agree with the SSE numerical result simulations and confirm that excited-state normal mode frequencies of a single molecule can be only detected in the nonlinear regime, except when, trivially, the pulse and the vibronic transition frequencies coincide.
5 Conclusions
We have set-up a protocol that is able to simulate ultrafast experiments on single molecules by coupling the DFT/TDDFT description of the fluorophore and the real-time dynamics of the system by means of SSE. Based on quantum mechanical calculations, we have introduced a vibrational structure in the system description in terms of harmonic-oscillator levels and FC factors. Analysis on single molecules is a powerful tool to study the effects which are usually hindered by the ensemble average,35,36 as reported in Fig. S11 of the ESI.†The protocol has been applied to simulate a two-pulse experiment performed on DNQDI.1 Our results are in agreement with the experimental findings, providing also microscopic interpretation: the observed oscillations of the fluorescence signal as a function of delay time are due to detuning rather than the vibrational frequency under the conditions of the original work.1 In this particular case the two frequencies are of the same order of magnitude (around 1090 and 1370 cm−1, respectively). SSE simulations and the perturbative analysis show that the oscillation at the detuning frequencies is given by the linear response of excited-state populations as a function of delay time,72 while the excited state vibrational frequency can be directly detected only at the nonlinear regime.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from the ERC under the Grant ERC-CoG-2015 No. 681285 “TAME-Plasmons” is gratefully acknowledged. Computational support from C3P high-performance computing facility of the Department of Chemistry of the University of Padova and from CINECA (Iscra C project “VIBCOSTO”) is also acknowledged.References
- D. Brinks, F. D. Stefani, F. Kulzer, R. Hildner, T. H. Taminiau, Y. Avlasevich, K. Müllen and N. F. Van Hulst, Nature, 2010, 465, 905–908 CrossRef CAS PubMed.
- D. Brinks, R. Hildner, F. D. Stefani and N. F. van Hulst, Faraday Discuss., 2011, 153, 51–60 RSC.
- M. Liebel, C. Toninelli and N. F. van Hulst, Nat. Photonics, 2018, 12, 45–49 CrossRef CAS.
- D. Brinks, R. Hildner, E. M. H. P. van Dijk, F. D. Stefani, J. B. Nieder, J. Hernando and N. F. van Hulst, Chem. Soc. Rev., 2014, 43, 2476–2491 RSC.
- R. Hildner, D. Brinks, J. B. Nieder, R. J. Cogdell and N. F. van Hulst, Science, 2013, 340, 1448–1451 CrossRef CAS PubMed.
- A. De Sio, F. Troiani, M. Maiuri, J. Réhault, E. Sommer, J. Lim, S. F. Huelga, M. B. Plenio, C. A. Rozzi, G. Cerullo, E. Molinari and C. Lienau, Nat. Commun., 2016, 7, 13742 CrossRef CAS PubMed.
- W. E. Moerner and L. Kador, Phys. Rev. Lett., 1989, 62, 2535–2538 CrossRef CAS PubMed.
- J. J. Macklin, J. K. Trautman, T. D. Harris and L. E. Brus, Science, 1996, 272, 255–258 CrossRef CAS.
- A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS.
- C. V. Shank, Science, 1986, 233, 1276–1280 CrossRef CAS PubMed.
- C. V. Shank, Science, 1983, 219, 1027–1031 CrossRef CAS PubMed.
- M. B. Plenio, J. Almeida and S. F. Huelga, J. Chem. Phys., 2013, 139, 235102 CrossRef CAS PubMed.
- F. Schweighöfer, L. Dworak, M. Braun, M. Zastrow, J. Wahl, I. Burghardt, K. Rück Braun and J. Wachtveitl, Sci. Rep., 2015, 5, 1–6 Search PubMed.
- R. Croce, R. van Grondelle, H. van Amerongen and I. van Stokkum, Light Harvesting in Photosynthesis, CRC Press, Boca Rata, 2018 Search PubMed.
- H. Lee, Y. C. Cheng and G. R. Fleming, Science, 2007, 316, 1462–1465 CrossRef CAS PubMed.
- G. S. Engel, T. R. Calhoun, E. L. Read, T. K. Ahn, T. Mančal, Y. C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782 CrossRef CAS PubMed.
- E. Collini, Chem. Soc. Rev., 2013, 42, 4932–4947 RSC.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644 CrossRef CAS PubMed.
- X. S. Xie and J. K. Trautman, Annu. Rev. Phys. Chem., 1998, 49, 441–480 CrossRef CAS PubMed.
- R. Hildner, D. Brinks and N. F. van Hulst, Nat. Phys., 2010, 7, 172 Search PubMed.
- R. Hildner, D. Brinks, F. D. Stefani and N. F. van Hulst, Phys. Chem. Chem. Phys., 2011, 13, 1888–1894 RSC.
- W. E. Moerner and M. Orrit, Science, 1999, 283, 1670–1676 CrossRef CAS PubMed.
- M. Orrit and J. Bernard, Phys. Rev. Lett., 1990, 65, 2716–2719 CrossRef CAS PubMed.
- J. A. Sonk, M. Caricato and H. B. Schlegel, J. Phys. Chem. A, 2011, 115, 4678–4690 CrossRef CAS PubMed.
- J. A. Sonk and H. B. Schlegel, J. Phys. Chem. A, 2011, 115, 11832–11840 CrossRef CAS PubMed.
- J. A. Sonk and H. B. Schlegel, J. Phys. Chem. A, 2012, 116, 7161–7168 CrossRef CAS PubMed.
- H. P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, Oxford, 2006 Search PubMed.
- R. Kosloff, M. A. Ratner and W. B. Davis, J. Chem. Phys., 1997, 106, 7036–7043 CrossRef CAS.
- J. C. Tremblay, T. Klamroth and P. Saalfrank, J. Chem. Phys., 2008, 129, 84302 CrossRef PubMed.
- G. Hermann and J. C. Tremblay, J. Phys. Chem. C, 2015, 119, 25606–25614 CrossRef CAS.
- J. C. Tremblay, P. Krause, T. Klamroth and P. Saalfrank, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 63420 CrossRef.
- L. Uranga-Piña and J. C. Tremblay, J. Chem. Phys., 2014, 141, 74703 CrossRef PubMed.
- W. Domcke and G. Stock, Theory of Ultrafast Nonadiabatic Excited State Processes and their Spectroscopic Detection in Real Time, 1997 Search PubMed.
- M. J. Tao, Q. Ai, F. G. Deng and Y. C. Cheng, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- E. Palacino González, M. F. Gelin and W. Domcke, Phys. Chem. Chem. Phys., 2017, 19, 32296–32306 RSC.
- E. Palacino González, M. F. Gelin and W. Domcke, Phys. Chem. Chem. Phys., 2017, 19, 32307–32319 RSC.
- Y. Shinohara, K. Yabana, Y. Kawashita, J. I. Iwata, T. Otobe and G. F. Bertsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155110 CrossRef.
- D. G. Tempel, M. A. Watson, R. Olivares Amaya and A. Aspuru Guzik, J. Chem. Phys., 2011, 134, 74116 CrossRef PubMed.
- C. A. Rozzi, F. Troiani and I. Tavernelli, J. Phys.: Condens. Matter, 2017, 30, 13002 CrossRef PubMed.
- K. Mølmer, Y. Castin and J. Dalibard, J. Opt. Soc. Am. B, 1993, 10, 524–538 CrossRef.
- J. Dalibard, Y. Castin and K. Mølmer, Phys. Rev. Lett., 1992, 68, 580–583 CrossRef CAS PubMed.
- N. Gisin and I. C. Percival, J. Phys. A: Math. Gen., 1992, 25, 5677 CrossRef.
- E. Coccia, F. Troiani and S. Corni, J. Chem. Phys., 2018, 148, 204112 CrossRef PubMed.
- E. Coccia and S. Corni, J. Chem. Phys., 2019, 151, 044703 CrossRef PubMed.
- R. Biele and R. D'Agosta, J. Phys.: Condens. Matter, 2012, 24, 273201 CrossRef CAS PubMed.
- G. Stock and W. Domcke, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 3032–3040 CrossRef CAS PubMed.
- G. Hermann, V. Pohl and J. C. Tremblay, J. Comput. Chem., 2017, 38, 2378–2387 CrossRef CAS PubMed.
- N. G. Van Kampen, Stochastic Processes in Physics and Chemistry, North Holland, 2007 Search PubMed.
- H. J. Carmichael, An Open Systems Approach to Quantum Optics, Springer, Berlin, 1993 Search PubMed.
- H. J. Carmichael, Statistical Methods in Quantum Optics 1: Master Equations and Fokker Planck Equations, Physics and Astronomy Online Library, Springer, Berlin, 1999 Search PubMed.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130 CrossRef.
- C. W. Gardiner and P. Zoller, Quantum Noise, Springer, Berlin, 2005 Search PubMed.
- M. B. Plenio, J. Almeida and S. F. Huelga, J. Chem. Phys., 2013, 139, 235102 CrossRef CAS PubMed.
- M. B. Plenio and P. L. Knight, Rev. Mod. Phys., 1998, 70, 101–144 CrossRef CAS.
- B. Wolfseder and W. Domcke, Chem. Phys. Lett., 1995, 235, 370–376 CrossRef CAS.
- J. C. Tremblay, T. Klamroth and P. Saalfrank, J. Chem. Phys., 2008, 129, 84302 CrossRef PubMed.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647–656 CrossRef CAS PubMed.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1995, vol. 6 Search PubMed.
- A. H. Zewail, Advances in Laser Chemistry, 1978 Search PubMed.
- R. Shelby, C. Harris and P. Cornelius, J. Chem. Phys., 1979, 70, 34–41 CrossRef CAS.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 84509 CrossRef PubMed.
- T. E. Sharp and H. M. Rosenstock, J. Chem. Phys., 1964, 41, 3453–3463 CrossRef CAS.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- R. Improta, V. Barone and F. Santoro, J. Phys. Chem. B, 2007, 111, 14080–14082 CrossRef CAS PubMed.
- R. Improta, V. Barone and F. Santoro, Angew. Chem., Int. Ed., 2007, 46, 405–408 CrossRef CAS PubMed.
- H. Köppel, W. Domcke, L. S. Cederbaum and W. V. Niessen, J. Chem. Phys., 1978, 69, 4252–4263 CrossRef.
- D. Egorova, M. F. Gelin and W. Domcke, J. Chem. Phys., 2005, 122, 134504 CrossRef PubMed.
- M. F. Gelin, D. Egorova and W. Domcke, J. Chem. Phys., 2009, 131, 124505 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B.01, 2016 Search PubMed.
- Y. Avlasevich, S. Müller, P. Erk and K. Müllen, Chem. – Eur. J., 2007, 13, 6555–6561 CrossRef CAS PubMed.
- D. Padula, M. H. Lee, K. Claridge and A. Troisi, J. Phys. Chem. B, 2017, 121, 10026–10035 CrossRef CAS PubMed.
- N. F. Scherer, R. J. Carlson, A. Matro, M. Du, A. J. Ruggiero, V. Romero Rochin, J. A. Cina, G. R. Fleming and S. A. Rice, J. Chem. Phys., 1991, 95, 1487–1511 CrossRef CAS.
- S. Mukamel, A. Piryatinski and V. Chernyak, Acc. Chem. Res., 1999, 32, 145–154 CrossRef CAS.
- S. Mukamel, Annu. Rev. Phys. Chem., 2000, 51, 691–729 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison between full and reduced models of DNQDI (Fig. S1). Comparison between SSE and Lindblad master equation (Fig. S2). Results of electronic dynamics of DNQDI with 5 excited states (Fig. S3). Excitation energies at TDDFT/B3LYP level of theory (Table S1). Analysis of high-energy processes (Table S2). NM1 and NM2 normal modes (Fig. S4 and S5). Results of simulations performed on DNQDI with a different value of detuning with respect to the one employed in the main text (Fig. S6–S8). Time profile of the pulse employed in Section 4.3.4 (Fig. S9). Results for the three level system in the nonlinear regime (Fig. S10). Simulation of ensemble effects (Fig. S11). See DOI: 10.1039/d0cp02557g |
| This journal is © the Owner Societies 2020 |




