Non-adiabatic quantum dynamics of the electronic quenching OH(A²Σ⁺) + Kr

Abstract

We present the dynamics of the electronic quenching OH(A²Σ⁺) + Kr(¹S) → OH(X²Π) + Kr(¹S), with OH(A²Σ⁺) in the ground ro-vibrational state. This study relies on a new non-adiabatic quantum theory that uses three diabatic electronic states Σ⁺, Π′, and Π′′, coupled by one conical-intersection and nine Renner–Teller matrix elements, all of which are explicitly considered in the equation of the motion. The time-dependent mechanism and initial-state-resolved quenching probabilities, integral cross sections, thermal rate constants, and thermally-averaged cross sections are calculated via the real wavepacket method. The results point out a competition among three non-adiabatic pathways: Σ⁺ ↔ Π′, Σ⁺ ↔ Π′′, and Π′ ↔ Π′′. In particular, the conical-intersection effects Σ⁺–Π′ are more important than the Renner–Teller couplings Σ⁺–Π′, Σ⁺–Π′′, and Π′–Π′′. Therefore, Π′ is the preferred product channel. The quenching occurs via an indirect insertion mechanism, opening many collision complexes, and the probabilities thus present many oscillations. Some resonances are still observable in the cross sections, which are in good agreement with previous experimental and quasi-classical findings. We also discuss the validity of more approximate quantum methods.

---

1. Introduction

The role of the hydroxyl radical is paramount in atmospheric and combustion chemistry. It is also the product of many elementary reactions that in turn contribute to more complex processes involving the OH radical. Because its efficiency, its detection is usually carried out by laser induced fluorescence on the OH A²Σ⁺–X²Π electronic band,^1,2 that can be used to measure the radical concentration very accurately.³ Hence, collisional electronic quenching of the A²Σ⁺ state is a process of considerable practical interest since it reduces radiative lifetimes and fluorescence quantum yield. It is thus not surprising that the quenching of OH(A²Σ⁺) has received a great deal of attention especially devoted to measure quenching cross sections with different collision partners^4–7 and to investigate the mechanism associated with the transit through the conical intersection.^8–12 Among other processes involving electronic quenching with OH(A²Σ⁺), collisions with rare gases (Rg) has received a special attention in the last few years as examples of processes in which collisional energy transfer and rotational depolarization may compete with electronic deactivation.^13–23 In addition, Rg + OH(A²Σ⁺) collisions are amenable to rigorous electronic and dynamical calculations^{16–19,21–23} that can be compared with a considerable amount of experimental information, ranging from thermal rate coefficients⁷ and cross sections for selected spin-rotational initial states^{5,6,18,19,21,23} to rotational and lambda-doublet state resolved cross sections.²¹ Interestingly, whereas quenching cross sections for He, Ne, and Ar are almost negligible when compared with rotational energy transfer on the excited potential energy surface (PES), for Kr and Xe quenching cross sections are similar or larger than those with H₂, O₂, or N₂.^18,21,23 As such, adiabatic calculations carried out on the 2A′ excited PES for Kr and Xe cannot account for rotational initial state depopulation.^21–23

Previous calculations for the Kr + OH(A²Σ⁺) system using quasiclassical trajectories (QCT) and surface hopping (SH) on ab initio PESs^21,22 demonstrated that the sole consideration of 2-PES transition (2A′–1A′) could not reproduced the magnitude of the quenching cross section dependence on the initial rotational state of OH(A²Σ⁺). It was necessary to include the participation of the 1A′′ and the roto-electronic couplings between 2A′ and 1A′′, and 1A′ and 1A′′, to recover the experimental values and the rotational state dependence. However, in that work the PESs and their couplings were calculated at a fixed O–H internuclear distance corresponding to its equilibrium value on the A²Σ⁺ electronic state. It remains to be seen how the approximate results on two-dimensional (2D) PESs compare with those obtained on 3D PESs. More importantly, the results reported in ref. 22 obtained using QCT-SH need to be validated with quantum dynamics calculations.

We here investigate the non-adiabatic quantum dynamics of the electronic quenching OH(A²Σ⁺) + Kr(¹S) → OH(X²Π) + Kr(¹S), extending experimental and quasi-classical previous works by Lehman et al.²¹ and by Perkins et al.²² Using reactant Jacobi coordinates r, R, and γ, where γ = 0 corresponds to the direction from O to H, we plot in Fig. 1R cuts of the three PESs required for this study for better understanding the present definitions some of which are different from those in ref. 22.

Fig. 1 R cuts of PESs for OH(A²Σ⁺) + Kr → OH(X²Π) + Kr. Adiabatic states 1A′, 2A′, and A′′. Diabatic states Σ⁺(1), Π′(2), and Π′′(3). Energy from this work, with respect to the reactants. Lower/higher energy in red/blue. The black dot labels the CI₁₂ conical intersection.

The doublet electronic states are labeled according to ref. 21 and 22, in both adiabatic and diabatic representations, and the non-adiabatic couplings between them are schematically shown.

Adiabatically, the reactants correlate with the excited 2A′ electronic species of OHKr and the products correlate with the nearly degenerate ground states 1A′ and 1A′′. 2A′ is considerably bound at γ = 180°, i.e. for a linear Kr–OH geometry, whereas 1A′ and A′′ are unbound and lie well below the reactant energy. At large R, the main configurations of 2A′ and 1A′ are Σ⁺ and Π′, respectively, and at small R these configurations exchange to Π′ and Σ⁺, respectively, owing to a conical intersection of the A′ states at R ∼ 3.8a₀ and γ = 180°. Therefore, Fig. 1 shows that the electronic states can be also described in a diabatic representation as Σ⁺(1), Π′(2), and Π′′(3), which belong to the C_s irreducible representations A′, A′, and A′′, respectively. At linearity (z) these diabats are the eigenstates of the z component of the total and spinless electronic angular momentum L̂ with eigenvalues 0 and ±1, respectively.

The electronic quenching is barrierless but closed in the Born–Oppenheimer approximation. Nevertheless, the electronic states interact via non-adiabatic effects that open the quenching channel: the linear conical intersection (CI₁₂) between the A′ states [Σ⁺(1) and Π′(2)]^21,22 and the L̂-induced Renner–Teller^24,25 couplings among all three species (i.e., RT₁₂, RT₁₃, and RT₂₃).²² This is depicted in Fig. 1 which also shows that the 2A′ minimum and the CI₁₂ point are very near, both in geometry and in energy, as we shall discuss in Section 3.

Extending the previous studies,^21,22 the present work reports time-dependent wavepacket (WP) quantum dynamics of the electronic quenching OH(A²Σ⁺) + Kr(¹S) → OH(X²Π) + Kr(¹S), including three 3D PESs and all the non-adiabatic interactions (i.e., one CI and nine RT coupling surfaces) all of them at multi-reference configuration-interaction (MRCI) level. The paper is organized as follows. Section 2 presents theory and computational methods. Section 3 shows the results of the electronic calculations, the time-dependent quenching mechanism, initial-state-resolved reaction probabilities with OH(²Σ⁺) in the ground ro-vibrational state, some model probabilities, and initial-state-resolved cross sections, rate constants, and thermally-averaged cross sections. We finally report our main conclusions in Section 4 and other results in the ESI.†

2. Theory and computational methods

Unless otherwise specified, we employ atomic units (a.u.), Jacobi reactant coordinates, and a counter-clockwise body-fixed frame with the origin at the center of the nuclear masses, where OHKr lies in the z,x plane and the z axis is either along r (r-embedding) or R (R-embedding).

We investigate the collision dynamics of the OH(A²Σ⁺) + Kr electronic quenching following our previous works^22,26 on non-adiabatic effects in triatoms. The present theoretical treatment is somewhat similar to that of Zhou et al.,²⁷ who considered three diabats coupled by both conical-intersection and Renner–Teller effects. Spin–orbit interactions are non negligible for this system, and accounting for them would permit to consider additional routes for the quenching, by coupling the 2A′(Σ⁺) to 1A′(Π′) and A′′(Π′′) states. In the vicinity of the conical intersection, spin–orbit couplings are of the order 200 cm⁻¹ approximately, being slightly stronger between the two A′ states (230 versus 170 cm⁻¹). Those values of ∼0.0009 a.u. are nevertheless three orders of magnitude smaller than other couplings here considered, as we shall see in Section 3, and including them is not expected to significantly change the results. Due to the huge additional cost required to include them in the treatment for a small expected change in the results, make us prefer to work within the non-relativistic approximation.

We therefore use a total spinless Ĥ containing all rovibronic couplings: (1) electronic, with diabatic electronic states coupled by the electronic Hamiltonian Ĥ^el; (2) vibrational-electronic, with adiabatic or diabatic states coupled by the vibrational Hamiltonian T̂^vib; and (3) roto-electronic, with adiabatic or diabatic species coupled by the total electronic angular momentum L̂. In the last case, at least one electronic state is degenerate when the molecule is linear. We here employ strictly diabatic electronic states whose vibronic couplings are much smaller than other couplings, and are thus safely neglected. The electronic and roto-electronic couplings between these diabats are associated with conical-intersection (CI) and Renner–Teller (RT) effects, respectively. The former depend on just one operator, Ĥ^el, but the latters correspond to seven operators, L̂², L̂²_z, L̂_xL̂_z, L̂_y∂/∂γ, L̂_y, L̂_z, and L̂_x, whose matrix elements are rarely computed on initio MRCI states.

2.1. Electronic structure calculations and computational details

Using the MOLPRO suite of ab initio codes,²⁸ we have calculated twelve 3D adiabatic surfaces: three PESs 1A′, 2A′, and A′′, and nine r-embedding matrix elements of L̂. Labeling r- or R-embedding with or without a bar, respectively, these are , , , , 〈1A′|L̂_y|2A′〉, , , 〈1A′|L̂²_y|2A′〉, and , where the L̂_y and L̂²_y terms are the same in both embeddings. Using again MOLPRO,²⁸ we then obtain the 3D diabatic PESs Σ⁺, Π′, and Π′′, the 〈Σ⁺|Ĥ^el|Π′〉 diabatic coupling, and the surface of the adiabat-to-diabat transformation angle χ.

As already pointed out, to treat the quenching of OH(Σ⁺ → Π), three electronic states have to be considered. The Π state is doubly degenerated, but this degeneracy is broken by the presence of the Kr atom when the three atoms are not aligned. This occurs because OH presents an unpaired electron, which can be located in a p orbital in the plane of the triatomic system (A′) or one perpendicular to the plane (A′′). Asymptotically, when Kr is too far to interact with OH, the two orthogonal p orbitals are equivalent and both states are degenerated. For symmetry reasons, when the three atoms are in a collinear configuration, the orbitals are also equivalent and both A′ and A′′ components are degenerated.

Previous calculations of the ground and first excited state PESs^21,22 were performed at a fixed OH internuclear distance at its equilibrium value of the excited A²Σ⁺ state. Considering that this value is similar to that of the minimum of the ground X²Π state, and that collisional quenching was studied at thermal temperatures (0.025–0.039 eV), this was deemed as a reliable approximation. However, the effect of the OH vibration must be included for a more accurate and reliable description of the processes, especially if calculations are performed at higher collision energies. Therefore, to obtain the 3D analytical PESs and couplings, ab initio calculations were performed over a regular grid in Jacobi coordinates (R,r,γ) referred to the Kr + OH channel with γ = 180° corresponding to the HO–Kr linear configuration. The considered grid elements are R = [3.4, 3.6, 3.8, 4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8, 6.0, 6.4, 6.8, 7.2, 7.6, 8.0, 8.5, 9.0, 9.5, 10, 15]a₀, r = [1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.1, 2.2, 2.4]a₀, and γ = [0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180] degrees for a total of 2808 points. Electronic structure calculations at each point of the grid were performed with a full electron Douglas–Kroll aug-cc-pVTZ basis set²⁹ and using the Douglas–Kroll Hamiltonian to account for relativistic effects of Kr inner electrons. In a first step, the two A′ states and the A′′ state associated to the Σ⁺ and two components of the Π state of OH are calculated in a state-average CASSCF calculation³⁰ using an active space of 5 electrons in 4 orbitals (16–18a′,6a′′). This active space ensures a good accuracy with an affordable computation time and, most importantly, keeps the continuity in the electronic wavefunctions in all the configuration space and for the three electronic states considered. The generated configurations and orbitals are then employed for an internally contracted MRCI treatment³¹ including Davidson correction.³² This scheme was employed within the quasi-diabatization procedure available in the MOLPRO program²⁸ which allowed us to obtain directly the diabatic PESs of the states Σ⁺ and Π′, as well as the 〈Σ⁺|Ĥ^el|Π′〉 non-adiabatic coupling, and the surface of the mixing angle χ [see below, eqn (2.1)]. By construction, the diabatic Π′′ state corresponds to the adiabatic A′′ state. Finally, the nine r-embedding matrix elements of L̂ were computed at CASSCF level. Here we should remind that these elements are calculated in reference to the adiabatic states. When a change of character of the electronic wavefunction happens along a coordinate of the PES (after an avoided crossing for example), some of the r-embedding matrix elements are swapped. When this happens, they need to be rearranged properly in order to fulfill the conditions of continuity and derivability in the configuration space, if this requirement is not met, it would be impossible to obtain a reliable three dimensional fit.

The three diabatic PESs, the 〈Σ⁺|Ĥ^el|Π′〉 coupling surface, and the nine r-embedding L̂ surfaces in the adiabatic representation were then fitted independently using the Reproducing Kernel Hilbert Space (RKHS) method.³³ This method is known to be well suited for fitting 3D PESs, and it is even better adapted to fit couplings surfaces. The advantage of this method stems from the use of its angle-like kernels which are convenient to fit angular variables such as Jacobi angle from which couplings between PESs are highly dependent. Angle-like kernels are also well adapted to obtain a good extrapolation for distance variables when surfaces converge to a fixed value in the asymptotic region, which is also the case of couplings (i.e. for Kr far away, one should recover the couplings of isolated OH).

The fitting procedure is extensively described in ref. 34 and 35. Here, only the most relevant details will be described. To fit the various PESs, the energy was decomposed in 1-, 2- and 3-body terms. 1- and 2-body terms were fitted implicitly together referring the zero of energy to the asymptotic value of the dissociated diatom. To account properly for the asymptotic limits of the three electronic states considered, five diatoms were considered: OH(X²Π), OH(A²Σ⁺), and three van der Waals diatomic clusters Kr–H, Kr–O(³P) and Kr–O(¹D). Once the energy for each diatom is subtracted from the corresponding electronic states, the 3-body term, which also vanishes in asymptotic regions, are fitted independently. The global PESs over the whole configuration space are then obtained as the sum of the corresponding fitted 2- and 3-body terms. We should point out here that since all the fitted diatomics go to zero asymptotically; the ∼2 eV separation between O(³P) and O(¹D) is added when the total PESs are reconstructed, a necessary step to keep the good relative energy differences between the three states. For the couplings, most of the terms were fitted directly (without decomposition) since most of them vanish in the asymptotic regions. Only the couplings elements depending on the OH bond length and which do not vanish asymptotically were decomposed in order to apply efficiently the 3D RKHS fitting. In all the cases, angle-like kernels were used for the 3D fitting. Three new angular variables (i.e. limited in the [0,1] interval) were thus defined from the Jacobi coordinates as follow: x = exp(−br), y = exp(−aR) and z = (1 + cos γ)/2.

2.2. Hamiltonian theory

2.2.1. Electronic states, r-embedding, and roto-electronic representation. Our adiabatic, real and ortho-normal electronic states 1A′, 2A′, and A′′ and their strictly diabatic transforms Σ⁺, Π′, and Π′′, are linked by²²We also label these real diabatic species as ,²⁶ where σ is their parity and Λ their L̂_z eigenvalue at linearity. Note that they do not correspond to the complex species labelled in the same way in ref. 22.

The total Ĥ, the CI electronic operator Ĥ^el, the RT operators L̂² and L̂_y, the vibrational operator T̂^vib, and the Jacobi coordinates do not depend on the embedding used but many operators of Ĥ become different in r- or R-embedding. Thus, for practical purposes we have labeled the operators with or without a bar depending on they are expressed in r- or R-embedding, respectively (the invariant operators are also unbarred). Like Ĥ^el, we define a RT roto-electronic operator as the sum of all rotational terms of Ĥ that contain . Writing the full spinless rotational operator²⁶ as , where contains terms that depend only on the total angular momentum Ĵ, the r-embedding full RT operator is equal to

with b = 1/(2μ_rr²), B = 1/(2μ_RR²), and μ_r and μ_R are the reduced masses associated to the r or R, respectively. Since the first two lines of this eqn belong to the A′ irreducible representation of the C_s point group and the others to A′′, the first and second give rise to both potential and coupling surfaces and the others only to couplings. Note the interactions between the total Ĵ and electronic rotations and between both rotations and the angular coordinate γ. The most important operators are and because they are multiplied by 1/sin²γ that diverges quadratically at the linearity. Nevertheless this degeneracy is analytically removed at linearity²⁶ where Ĵ_z = L̂_z. The terms of are called Coriolis operators.

Real electronic species |e〉 fulfill

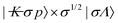since the second term is negligible in a strictly diabatic representation. Employing then the symmetry-adapted roto-electronic diabatic representation ,²⁶ where is the r-embedding helicity, p is the total parity and σ^1/2 = + or i for σ = + or −, respectively, the matrix elements of are presented in eqn (2.5):We use eqn (2.4) with . These matrix elements are real as the states, those of L̂_x, L̂_y, and L̂_z are purely imaginary, and the others are real. This equation defines both |σΛ〉-diagonal potential terms and off-diagonal coupling terms; it is also obtained by summing eqn (4.6) and (4.7) of ref. 26, changing appropriately the notation and omitting the unnecessary terms. It is also similar to eqn (44)–(46) of ref. 22, taking into account that the present diabatic states are real and that we call here “RT couplings” also A_ij and C_ij of eqn (44) and (46),²² following ref. 24 and 25.

2.2.2. R-Embedding, diabats, and quenching approximation. We investigate the collision dynamics transforming the r-embedding, diabatic representation in eqn (2.5) to the R-embedding by exchanging b and B.³⁶ We also make a quenching approximation in 〈Σ⁺| − − |Π′〉, assuming that the diagonal terms 〈1A′| − − |1A′〉 and 〈2A′| − − |2A′〉 are equal and cancel each other. According to this, only the off-diagonal matrix elements of L̂ need to be considered since they rule the quenching dynamics.³⁷Eqn (2.5) then simplifies and specializes for the off-diagonal elements aswhere |+Λ〉 = Σ⁺ or Π′ for Λ = 0 or 1, respectively.

2.2.3. Roto-electronic-angular representation. We obtain the Ĥ roto-electronic-angular representation considering T̂^J, the vibrational operator T̂^vib that does not work on strictly diabatic electronic states, and the normalized associated Legendre states |jK〉 with³⁸The three Born–Oppenheimer diabatic and diagonal blocks of the Hamiltonian are equal towhere |σΛ〉 = Σ⁺, Π′, or Π′′, the radial kinetic Hamiltonian is T̂^rad = −B∂²/∂R² − b∂²/∂r², and 〈σΛ|Ĥ^el|σΛ〉 are the diabatic potential energy surfaces.

The non-adiabatic CI and RT interactions between the diabats Σ⁺, Π′, and Π′′ are

2.2.4. K approximation. The coupled-channel eqn (2.9)–(2.12) contain λ^±_JK Coriolis terms that are very hard to implement in a huge-time demanding computer code with six large blocks (three Born–Oppenheimer plus three coupling terms) and they are thus simplified via the K approximation²²where K₀ is the K value of the OH reactant and l = J or j. The Born–Oppenheimer eqn (2.9) thus becomesRepresenting the Ĥ^el and L̂ operators on the roto-electronic basis, the non-adiabatic couplings in Fig. 1 are equal to

CI₁₂ = 〈Σ⁺|Ĥ^el|Π′〉, (2.15)

Note that the K approximation removes the λ^±_jK|j,K ± 1〉 terms of eqn (2.10). The couplings eqn (2.10)–(2.12) therefore simplify respectively as

〈j′K₀| 〈Σ⁺|〈K₀ + p|Ĥ|K₀ + p〉|Π′〉|jK₀〉 = 〈j′K₀|CI₁₂ + RT₁₂|jK₀〉, (2.19)

〈j′K₀|〈Σ⁺|〈K₀ + p|Ĥ|K₀ − p〉|iΠ′′〉 |jK₀〉 = 〈j′K₀|RT₁₃|jK₀〉, (2.20)

〈j′K₀|〈Π′|〈K₀ + p|Ĥ|K₀ − p〉|iΠ′′〉|jK₀〉 = 〈j′K₀|RT₂₃|jK₀〉, (2.21)

and Ĥ is real and symmetric, since the matrix elements of L̂_x, L̂_y, and L̂_z are purely imaginary and the others are real. In block-matrix form we have

The coefficients of the L̂ components increase with J and depend on K₀, those of L̂²_z, L̂_xL̂_z, L̂_z, and L̂_x diverge at C_∞v geometries, mainly for L̂²_z and L̂_z, and their relative strength depends on the system under study and can be assessed only via numerical calculations. The centrifugal-sudden approximation is obtained with . If J = 0, the RT₁₂L̂_y term of eqn (2.16) vanishes and the Π′′ product channel in eqn (2.17) and (2.18) is closed. If K₀ = 0, also the first lines of eqn (2.17) and (2.18) vanish. On the other hand, all RT couplings are present if K₀ > 0.

We represent this roto-electronic angular Hamiltonian on a (R,r) 2D radial grid, where the T̂^rad matrix elements are obtained via a Fourier transform from the coordinate to the momentum representation, calculating the matrix elements in the latter space, and returning back to the former representation via an inverse Fourier transform. In conclusion, the full representation includes three diabats, two radial coordinates, Legendre states, and overall-rotational species, and it is used for computing the quenching dynamics as we briefly report in the next Section.

In closing this Section we summarize all our approximations.

(1) Spinless Hamiltonian: the spin is considered only in the calculation of the electronic states.

(2) OH(X²Π): the electronic angular momentum is omitted.

(3) Strictly diabatic electronic representation: ∂|e〉/∂Q ≡ 0, where |e〉 is an electronic state and Q is a Jacobi coordinate.

(4) Quenching approximation: only couplings 〈e′|Ô|e〉, e′ ≠ e.

(5) Diagonal approximation: 〈1A′| − − |1A′〉 = 〈2A′| − − |2A′〉 in the calculation of 〈Σ⁺| − − |Π′〉.

(6) K approximation: K′ = K ± 1 ≈ K = K₀.

2.3. Wavepacket collision dynamics

Initial-state-resolved reaction probabilities are obtained through the time-dependent real wavepacket (WP) formalism of Gray and Balint-Kurti,³⁹ essentially equal to the Chebyshev approach of Guo.⁴⁰ To this end we scale and shift the Hamiltonian of Section 2.2.4, obtaining Ĥ_s, whose arccos mapping of the equation of the motion is solved recursively. We employ a complex initial WP

|ψ₀〉 = |a₀〉 + i|b₀〉 = |Σ⁺〉|s₀(R)〉|v₀j₀(r)〉|j₀K₀〉, (2.23)

that contains the sinc⁴¹R-dependent termtimes the OH(²Σ⁺) vibrational and rotational states |v₀j₀(r)〉 and |j₀K₀〉. The recursions are

|a₁〉 = Ĥ_s|a₀〉 − (1 − Ĥ_s²)^1/2|b₀〉, first complex propagation, (2.25)

|a_n+2〉 = 2Ĥ_s|a_n+1〉 − |a_n〉, other real Chebyshev propagations. (2.26)

The WP is propagated in all the reactant Jacobi coordinates and the quenching probabilities are calculated at the end through a time-to-energy Fourier transform and an asymptotic analysis on the Π′ and Π′′ PESs at R_∞.³⁹

We have converged quenching probabilities and of OH(²Σ⁺), from the ground vibrational state and the ground rotational state j₀ = K₀ = 0 to the OH(²Π) final diabatic states Π′ and Π′′, propagating WPs at all J ≤ 140 with the numerical parameters of Table 1, that correspond to 7 227 394 basis states, and using 330 values of the collision energy E_col, from 0.001 to 0.33 eV.

Table 1 Parameters of the quantum dynamics calculations. Values in a.u., unless otherwise specified

Initial sinc s0(R): α, E0, R0, β	17, 0.039 eV, 11, 0.01
R range and number of grid points	2.95–16 and 307
r range and number of grid points	1.45–7 and 79
Number of Legendre states	100
R and r absorption start at	12 and 5
R and r absorption strengths	0.05 and 0.01
Asymptotic analysis at R∞	11

---

Finally, initial-state-resolved cross sections σ(E_col) and thermal rate constants at the temperature T, k(T), are calculated via the usual expressions. Following ref. 21 and 42, we also obtain thermally averaged cross sections from the mean relative velocity, 〈v(T)〉 = (8k_BT/πμ_R)^1/2, as 〈σ(T)〉 = k(T)/〈v(T)〉. For analyzing some probabilities we also use thermally averaged partial cross sections 〈σ^J(300)〉 resolved on the quantum numbers J and j₀ = K₀ = 0, at 300 K.

3. R-Embedding results and discussion

3.1. Electronic calculations

The present diabatic PESs and the respective couplings can be considered as 3D extensions of the previous 2D PESs and couplings presented in ref. 21, in which the OH bond distance r was fixed at its equilibrium value on the A²Σ⁺ state. The effect of varying r is best seen near the 2A′–1A′ CI seam at linearity, where the adiabats belong exactly to the Σ⁺ and Π′ irreps, respectively, and their Ĥ^el coupling vanishes by symmetry. As already pointed out in ref. 21 and 22, and also below Fig. 3, that seam plays a central role in the quenching and it is presented in Fig. 2 at γ = 180° (Kr–OH configuration). We clearly see that the initial Σ⁺ PES becomes fully repulsive at r > 2.5a₀ and that the CI seam lies very near the PES minimum and then moves at larger R and r values and higher energies. We report further details and the implications of this result by discussing Fig. 3.

Fig. 2 γ = 180°. Σ⁺ PES (eV with respect to the reactants). The Σ⁺–Π′ CI seam is labeled by a green line.

Fig. 3 r = 1.916a₀. Σ⁺ PES (eV with respect to the reactants), conical-intersection coupling CI₁₂ = 〈Σ⁺|Ĥ^el|Π′〉, Renner–Teller matrix element 〈Σ⁺|L̂²|Π′〉. J = 70 and K₀ = 0, total coupling CI₁₂ + RT₁₂ of eqn (2.15) + (2.16). Negative/zero/positive levels in red/black/blue. The Σ⁺–Π′ diabatic crossing is labeled by a green line.

Nevertheless the main topographic characteristics of the three PESs are essentially the same and will be described mainly at the calculated equilibrium bond length of the OH asymptote in the Σ⁺ PES: r = 1.916a₀. The top-left panel of Fig. 3 shows that the Σ⁺ PES (2A′ in C_s symmetry), which correlates with OH(A²Σ⁺), exhibits two pronounced van der Waals (vdW) wells in linear configurations. The global minimum corresponds to a collinear Kr–OH vdW complex at R_vdW = 3.847a₀, r_vdW = 1.900a₀, γ_vdW = 180°, and V_vdW = −0.990 eV. This minimum is very near to a conical-intersection point with the Π′ species, at R_CI = 3.827a₀, r_CI = 1.916a₀, γ_CI = 180°, and V_CI = −0.984 eV. It is the presence of this deep Kr–OH minimum that allows collisions at thermal energies to access the conical intersection, boosting the quenching cross sections to values comparable to those of collisions with H₂ and somewhat higher than those with N₂. This is in contrast to other Rg + OH(A) systems with lighter rare gases (He, Ne, Ar), whose Rg–OH(A) minima are much shallower and their conical intersection lies well above the respective asymptotes at a much shorter R distance, above the strong repulsive wall of the Rg–OH(X) PES. As a consequence, their respective quenching cross sections are two to three orders of magnitude smaller than those for Kr + OH(A). As can be expected, however, for Xe + OH(A) the situation is analogous to the Kr + OH(A), but the quenching cross section are almost a factor of two bigger for the former.^5,23

The origin of the well between OH Σ⁺ state and the noble gas can be traced back to the electronic structure of the system. OH(Σ⁺) is characterized by the excitation of one electron from the σ bonding to the π orbital. In the same time, σ presents a favourable overlap with the collinear p orbital of Kr. This deficit of electron in the σ bonding orbital allows it to drag the electronic density of the p orbital providing a partial charge transfer of about −0.4 a.u., according to a Mulliken population analysis of the MRCI wavefunction, and therefore stabilizing the system. In the OH(Π) ground state, the σ bonding orbital is filled and cannot drag electronic density: in this case, Krypton remains neutral and the interaction with OH is purely repulsive. The OH Σ⁺ state can thus be considered as partial Lewis acid when it interacts with Krypton.

The secondary minimum, at a linear OH–Kr configuration with γ = 0, occurs at R ∼ 5.3a₀, is shallower (V ∼ −0.28 eV), and is therefore less important for the quenching dynamics. In the adiabatic representation, both minima are the result of avoided crossings of the Σ⁺ and the repulsive wall of the Π′ ground state, which can cross in C_∞v linear configuration where the A′ species take exactly their Σ⁺ and Π′ character and their electronic coupling vanishes. However, when the system departs from linearity, the A′ component of the Π state couples with the Σ⁺ state and crossing becomes avoided.

We also see that the Σ⁺ PES is strongly anisotropic: the linear configurations are indeed preferred whereas the Kr perpendicular approach to OH is inhibited. In contrast, the Π′ PES that correlates with OH(X²Π), shown in Fig. S1 (ESI†), is unbound, fairly isotropic, symmetric with respect to γ = 90°, and very similar to the Π′′ one that it is not shown. Our 3D results confirm essentially the previous 2D calculations^21,22 at constant r, except that the present global minimum is deeper and takes place at somewhat smaller value of R than that of ref. 21, where R_vdW = 4.16a₀, r = 1.913a₀, and V_vdW = −0.754 eV.

Due to the topographic singularities at the conical intersections, the adiabatic representation is not ideally suited for dynamical calculations and the fit is much more problematic. The diabatic representation, where the Σ⁺ and Π′ character are preserved in the whole PES, becomes a much better option. In this representation, Σ⁺ and Π′ states can cross not only in linear conformation, but everywhere. However, the crossings only occur in the regions of the Σ⁺ wells. When Kr approaches perpendicularly to OH, the interaction is repulsive for both Σ⁺ and Π′ and they never cross. Since the couplings become effective only when the energy difference between the coupled states is small, the regions of the two wells will be more relevant for the efficiency of the quenching. In addition of the PESs, it is therefore interesting to discuss the evolution of the couplings depending on the geometry of the system, and in particular the L̂ couplings. We thus plot in Fig. 3 also some relevant couplings, at r = 1.916a₀, and at J = 70 and K₀ = 0 when they depend on these quantum numbers.

The CI₁₂ term 〈Σ⁺|Ĥ^el|Π′〉 on the top-right panel of Fig. 3 vanishes by symmetry in C_∞v and is nearly antisymmetric with respect to γ = 90°, with a maximum value equal to 0.14 a.u. at R = 3a₀ and γ = 117° at the r value here considered. Nevertheless, this configuration is at a repulsive Σ⁺ energy, not important for the low-energy quenching that is favored by the Σ⁺ attractive region and by rather large coupling values near R ∼ 3.8a₀ and γ ∼ 160°.

The eqn (2.14)–(2.21) use the R-embedding and the matrix elements of L̂ between diabatic states, which are calculated from the MOLPRO r-embedding and adiabatic species in two steps, through the properties of L̂.²⁶ (1) The R-embedding L̂ components are obtained from the r-ones by rotating counter-clockwise the body-fixed axes around y by γ. (2) The diabatic matrix elements are then calculated viaeqn (2.1) and (2.2), and the quenching approximation 〈1A′| − − |1A′〉 = 〈2A′| − − |2A′〉. For example

and

〈Σ⁺|L̂²_z|Π′〉 = 〈1A′|L̂²_z|2A′〉(cos²χ − sin²χ). (3.2)

Another example of these transformations is in Fig. S2 (ESI†) that reports the angle χ(R) of eqn (2.2), three L̂_x(R) couplings in both embeddings and representations, and two couplings in the r-embed and adiabatic representation, at r = 1.916a₀ and γ = 175°. This figure also shows that our r-embed, adiab matrix elements , , and are nearly equal to those of Fig. 2 of ref. 22, provided a A′′ change of sign, but that R_AC is larger by ∼0.32a₀ due to the present variation of r and to the sensitivity of the CI seam to the calculation accuracy.

Among the eight matrix elements of L̂ in eqn (2.16)–(2.18), the largest one is 〈Σ⁺|L̂²|Π′〉 plotted in the bottom-left panel of Fig. 3. It is approximately antisymmetric with respect to γ = 90°, as the electronic coupling due to Ĥ^el, and varies sharply both in value and in sign near the linear conical intersections where it attains large absolute values. This result is due to sudden changes of χ in these regions where both numerator and denominator of eqn (2.2) almost vanish, as the above-left panel of Fig. S2 (ESI†) shows. Fig. S3 (ESI†) then reports the L̂²_z, L̂_xL̂_z, and L̂_y matrix elements. The decidedly smaller L̂²_z values with respect to L̂² point out that the latter term is essentially due to L̂²_x + L̂²_y, and L̂_xL̂_z and L̂_y are nearly constant at R > 4a₀.

According to eqn (2.16)–(2.18), all Renner–Teller couplings do not depend solely on the L̂ matrix elements but also on their coefficients, all of which are functions of the Jacobi coordinates and those of the L̂ components depend also on the overall-rotation quantum numbers J and K₀. For example, the B coefficient of L̂² in eqn (2.16) is 1/(2μ_RR²) ≤ 10⁻⁶ a.u. in the considered R range, and the coefficients of L̂²_z, L̂_xL̂_z, L̂_z, and L̂_x are large near linear geometries if K₀ > 0, especially that of L̂_z. We thus plot in the bottom-right panel of Fig. 3 the overall non-adiabatic Σ⁺(1)–Π′(2) coupling CI₁₂ + RT₁₂, eqn (2.15) + (2.16), at J = 70 and K₀ = 0, showing that it is very similar to the Ĥ^el coupling. This fact implies that the Σ⁺–Π′ interaction is essentially due to the conical intersection, as we shall see also in Section 3.3.2.

After the non-adiabatic CI and RT matrix elements of operators belonging to the A′ irreducible representation of the C_s point group, we close this Session by presenting in Fig. 4 the total couplings Σ⁺(1)–Π′′(3) RT₁₃, (2.17), and Π′(2)–Π′′(3) RT₂₃, (2.18), due to L̂_z and L̂_x ∼ A′′.

Fig. 4 r = 1.916a₀, J = 70 and K₀ = 0. RT₁₃, eqn (2.17), and RT₂₃, eqn (2.18). Details as in Fig. 3.

Even at J = 70 and K₀ = 0, where λ⁰_70,0 is large and equal to 70.5 a.u., these Renner–Teller couplings RT₁₃ and RT₂₃ are smaller than the conical-intersection term CI₁₂, confirming that the latter effects are more important than the former when OH(A²Σ⁺) is in the ground ro-vibrational state. In particular, both RT₁₃ and RT₂₃ are different from zero at large R values and RT₂₃ is rather important at linearity, because L̂_z couples the nearly degenerate Π′ and Π′′ components of the OH(²Π) product via the cot γ factor of eqn (2.18). This is different from CI₁₂ that is larger far from the linearity where it vanishes by symmetry. Since RT₁₃ < RT₂₃, these results show that the relative strength of the non-adiabatic couplings is CI₁₂ ≫ RT₂₃ > RT₁₃ > RT₁₂. Finally, other L̂ matrix operators are plotted in Fig. S4 (ESI†) and it is easy to check that all fulfill the C_∞v selection rules at γ = 0 and 180°.

3.2. Time-dependent reaction mechanism

The time-dependent reaction mechanism on the three coupled diabats |e〉 is shown in Fig. 5 that presents normalized electronic norms and snapshots of the j-summed (R,r) densityof a WP at J = 70, j₀ = K₀ = 0, and at five times t ≤ 573 fs. The time is proportional⁴³ to the propagation number n in eqn (2.26) but this proportionality is lost afterwards and the WP spreads on all the conformational space at larger times, masking the mechanism.

Fig. 5 J = 70 and j₀ = K₀ = 0. WP norms and γ-averaged (R,r) densities at 5 times.

The initial Σ⁺ WP remains essentially on this PES up to ∼180 fs, moving towards the interaction region without being affected by the non-adiabatic couplings with the Π states. Contrasting this finding with other barrierless quenchings with smaller or equal exoergicity, as OH(X) + H⁺³⁷ and OH(A) + H,⁴⁴ we see that this collision is much slower than the others owing to the larger mass of the Kr atom. During this early stage of the reaction, only R decreases while both r and γ do not vary appreciably.

The attack of Kr to the O atom and the quenching process begins at ∼180 fs, when part of the WP enters into the strong interaction region at R < 5a₀, where the WP jumps on the Π′ PES at R ∼ 3.8a₀ and γ ∼ 160° owing to the Σ⁺–Π′ conical intersection. At 181 fs the hops from Σ⁺ to Π′ occur mainly at R_hop ∼ 3.5–4 and 4.5–5a₀, where the WP forms KrOH metastable complexes near the CI seam. Nearly 20 fs later, that is at ∼200 fs, also the Π′′ surface begins to be populated at R_hop ∼ 3.5–4a₀ and the collision complex reveals now its full non-adiabatic nature, spreading on all the three PESs.

At larger times we see both the non reactive WP on Σ⁺, due to recrossings of the CI seam, and the reactive densities on Π′ and Π′′, together with the formation of the quenching products resolved on these final states. Nevertheless, the major part of the WP is not reactive and is reflected back into the reactant channel.

By transforming the WP from the Legendre representation j to the angular one γ,⁴⁵ Fig. S5 (ESI†) shows a complementary picture of the mechanism plotting r-summed (R,γ) densities. Because we are considering a rotationless OH(²Σ⁺) diatom with j₀ = 0, the initial r-averaged density depends only on R, as the top panel of Fig. S5 (ESI†) shows. During the OH(A) + Kr collision many Legendre polynomials are occupied and the WP thus spreads on all the γ values, mainly at 180° near the Σ⁺ minimum and the most important CI point. Therefore, the Π metastable complexes begin at ∼180 fs with a Kr–OH linear geometry.

In conclusion, these results reflect nicely the non-adiabatic couplings and extend to three coupled electronic states and to (R,γ) densities the findings found with just two of them,^37,44 showing the different role played by two final electronic states here investigated in two different conformational subspaces.

3.3. Initial-state-resolved quenching probabilities

3.3.1. Full calculations. We present in Fig. 6 quenching probabilities , , and , resolved and summed on the final Π states, at J = 0, 30, 70, 100, and 140 and at j₀ = K₀ = 0. Contrarily to the OH + H⁺ quenching,³⁷ where only the 〈Π′|L̂_z|Π′′〉 matrix element was considered but it is closed at J = 0, the OH(A) + Kr quenching is open at any J value owing to other couplings. As Fig. 3 shows, this finding is mainly due to the 〈Σ⁺|Ĥ^el|Π′〉 conical intersection coupling, and the Π′′ channel is closed at J = 0 according to eqn (2.17) and (2.18).

Fig. 6 J = 0, 30, 70, 100, 140, and j₀ = K₀ = 0. Quenching probabilities, resolved and summed on the final Π diabats.

The most striking feature of the probabilities is their resonance structure in all the energy range and at all J values, decreasing however as J increases, similar to that observed in other electronic quenchings.³⁷ Many causes can contribute to this finding: (1) The strong exoergic character of the quenching, associated with an indirect Kr insertion, with the formation of many long-lived intermediate complexes on the Π surfaces as Fig. 5 and Fig. S5 (ESI†) show, and with an electronic-to-translational energy transfer. (2) The formation of OH(²Π) rotational states.^21,22 (3) The presence of the van der Waals minimum on the Σ⁺ PES. (4) The K approximation used which enhances the oscillatory structure by omitting all K ≠ K₀ terms that in general average the probability oscillations.

Because the quenching is barrierless, low-J probabilities do not present any threshold, which appears only around J = 30 and increases very slowly with the overall rotation. This J shifting is simply due to the centrifugal barrier BJ(J + 1) of the Born–Oppenheimer matrix elements, where B is small owing to the Kr large mass and to R ≥ 2.95a₀, as we already found in comparing CI₁₂ and CI₁₂ + RT₁₂ in Fig. 3. We also see that the Π′ electronic component is preferred with respect to Π′′, on account of the important Ĥ^el electronic coupling CI₁₂, and that the Π′ and Π′′ populations decrease or increase with J, respectively. In fact, the former channel in essentially due to conical-intersection effects and the latter depends only on Renner–Teller couplings that increase with J.

3.3.2. Model calculations. In ref. 22 the quenching cross sections were calculated through the quasi-classical trajectory surface hopping method, using space-fixed cartesian coordinates, adiabatic electronic states, first-derivative radial couplings, and hopping probabilities obtained from non-adiabatic couplings. Results of both full and model calculations were presented to assess the relative importance of the different couplings.²² This is quite different from the present quantum formalism which relies on body-fixed Jacobi coordinates, on diabats, on a R-embedding Hamiltonian Ĥ containing all couplings, and on the Ĥ_s equation of the motion. Nevertheless, we here follow this idea at the probability level, contrasting full and model calculations of some representative total quenching probabilities at J = 70 and j₀ = K₀ = 0. In fact, calculations of cross sections at j₀ > 0 is beyond our computer facilities.

We plot in Fig. 7 the results of four models: (1) centrifugal sudden (CS) with λ⁰_70,0 = 0 in eqn (2.14)–(2.18); (2) L̂_x = L̂_y = 0 in eqn (2.16)–(2.18); (3) conical-intersection only (CI) with L̂ = 0; (4) Renner–Teller only (RT) with χ = 0 in eqn (2.1). The sharp and strong resonances make it difficult in some cases to compare quantitatively different probabilities. To this aim, we use the thermally averaged partial cross sections of Table 2, resolved on the quantum numbers J = 70 and j₀ = K₀ = 0, and at T = 300 K.

Fig. 7 J = 70 and j₀ = K₀ = 0. Full and model total probabilities.

Table 2 J = 70 and j₀ = K₀ = 0. Thermally averaged partial cross sections at 300 K

Calculation	/Å^2
CS	0.11
L̂ x = L̂y = 0	0.14
CI	0.13
RT	0.01
Full	0.14

---

The left panel presents two widely used approximations. The CS one does not work well at this high J value, with the Π′′ channel closed at K₀ = 0, according to eqn (2.17) and (2.18), and with larger resonances shifted to higher energies. Nevertheless, the Maxwell averaging on E_col reduces strongly these differences with a CS lower by ∼20%. On the other hand, the model probability obtained with L̂_x = L̂_y = 0 is practically equal to the full results and indistinguishable on the scale of Fig. 7. The right panel reports model probabilities when some non-adiabatic couplings are switched off. We see that both and are large by considering only CI effects, and the opposite is true if only RT effects are taken into account. These two effects are not addictive and CI is by far the most important coupling when j₀ = K₀ = 0, because the geometries where Σ⁺ is attractive and the term 〈Σ⁺|Ĥ^el|Π′〉 is large are near, as we have seen in Fig. 3. The CI model slightly overestimates some resonances with respect to the full calculations. This finding implies that CI and RT effects can be in mutual competition because they are large at different geometries as we have seen in Section 3, and RT couplings can induce a few recrossings from Π′ and Π′′ to Σ⁺, which are small when K₀ = 0 according to eqn (2.16) and (2.17). These findings are essentially confirmed by other model calculations at different values of J, j₀, and K₀.

Therefore, the general trend of model probabilities, with respect to full calculations, is that the CS approximation cannot be used at large J, the L̂_x = L̂_y = 0 approximation works very well at low K₀ values, and CI effects are larger than those RT which are enhanced when OH(A) is in an excited rotational state, as it is usually found.³⁷ On the overall, the effects of model calculations are larger in quantum than in quasi-classical calculations²² where these effects are considered indirectly, via hopping probabilities from the couplings, and they are summed over J by the cross sections results.

3.4. Initial-state-resolved quenching cross sections and rate constants

Fig. 8 shows quenching cross sections σ at j₀ = 0, from 0.001 to 0.33 eV, and Table 3 reports some representative numerical values.

Fig. 8 j ₀ = 0. Quenching cross sections, resolved (black) and summed (red) on the final Π diabats.

Table 3 j ₀ = 0. Quenching cross sections^a

E col/eV	σ Π′/Å^2	σ Π′′/Å^2	σ Π′+Π′′/Å^2
a All resonances, except at 0.039 eV.
0.011	5.6	1.0	6.6
0.029	10.1	2.7	12.8
0.039	11.2	2.9	14.1 (17.2 ± 0.4)^22
0.045	11.6	3.2	14.8
0.052	11.1	3.4	14.5
0.081	9.2	4.2	13.4
0.140	8.6	4.0	12.6
0.176	8.1	3.9	12.0
0.225	7.2	3.4	10.6
0.240	7.1	3.4	10.5

---

The Π′ channel is strongly preferred at low E_col, in agreement with the reaction probabilities and with the bottom-left panel of Fig. 6 of ref. 22, and the collision energy enhances the Π′′ weight with a branching ratio σ_Π′′/σ_Π′ increasing from ∼0.1 at the threshold to ∼0.6 at 0.33 eV. We also see that at least nine resonances survive the partial wave sum of the probabilities, mainly for the quenching on the Π′ surface. The Π′ + Π′′ and Π′ cross sections increase sharply from the threshold up to maximum values equal to 14.8 Ų at 0.045 eV and to 11.6 Ų at 0.044 eV, respectively, that is at the third resonance. Their average values then decrease at larger energies because the quenching is barrierless and exoergic. This trend is less evident for σ_Π′′ that presents smother variations with a maximum value equal to 4.2 Ų at 0.083 eV, near the forth resonance. At 0.039 eV the total quantum cross section σ_{Π′+Π′′} is equal to 14.1 Ų, whereas quasi-classical²² value is 17.2 ± 0.4 Ų. We believe that this difference is mainly due to many and sharp oscillations of the quantum probabilities which are averaged by quasi-classical calculations.

We also report in Fig. 9 and Table 4 initial-state-resolved non-adiabatic thermal rate constants and thermally averaged cross sections at j₀ = 0. Total and Π′-resolved k and 〈σ〉 increase sharply at low temperature and reach their asymptotic values at 900 K: 12.4 × 10⁻¹¹ and 8.8 × 10⁻¹¹ cm³ s⁻¹ for k, and 10.7 and 7.6 Ų for 〈σ〉. The rate constants increase monotonically whereas 〈σ_{Π′+Π′′}〉 has a maximum at 450 K, equal to 11.9 Ų. At 300 K, 〈σ_{Π′+Π′′}(300)〉 = 11.6 Ų in good agreement with the experimental value²¹ of 10 ± 1 Ų.

Fig. 9 j ₀ = 0. Thermal rate constants (left) and thermally averaged cross sections (right), resolved (black) and summed (red) on the final Π diabats.

Table 4 j ₀ = 0. Thermal rate constant k_{Π′+Π′′} and thermally averaged cross section 〈σ_{Π′+Π′′}〉

T/K	k Π′+Π′′/10^−11 cm^3 s^−1	〈σΠ′+Π′′〉/Å^2
100	3.1	8.0
200	5.8	10.7
300	7.8	11.6 (10 ± 1)^21
400	9.2	11.8
500	10.3	11.8
700	11.7	11.4
900	12.4	10.7

---

Quantum σ_{Π′+Π′′}(0.039) and 〈σ_{Π′+Π′′}(300)〉 differ by 2.5 Ų, owing to the averaging of the latter on its resonances, whereas quasi-classical²² observables are nearly equal since the oscillations are washed out in the quasi-classical opacities. We fit the total rate constant from 100 to 900 K to the extended Arrhenius expression k^Arr = A(T/K)^x exp(−E_a/k_BT), finding A = 3.02 × 10⁻¹¹ cm³ s⁻¹, x = 0.230, and E_a = 0.0094 eV. This is a small activation energy, because the Σ⁺ PES is barrierless, the centrifugal barrier is little important, the quenching is exoergic, and the WPs do not feel any repulsive potential on the Π′ and Π′′ PESs.

4. Summary and conclusions

Following a previous quasi-classical trajectory surface hopping study,²² this paper presents the non-adiabatic quantum dynamics of the electronic quenching OH(A²Σ⁺) + Kr(¹S) → OH(X²Π) + Kr(¹S), with OH(A²Σ⁺) in the ground ro-vibrational state. We use a new non-adiabatic quantum theory based on three diabatic electronic states, Σ⁺(1), Π′(2), and Π′′(3), coupled by nine conical-intersection (CI) and Renner–Teller (RT) matrix elements. Using a triatomic Hamiltonian Ĥ, all the matrix elements of the electronic Hamiltonian Ĥ^el and of the total electronic angular momentum L̂ are taken into account and ab initio calculated in three dimensions. The time-dependent mechanism, initial-state-resolved quenching probabilities, integral cross sections, thermal rate constants, and thermally averaged cross sections are calculated through the real wavepacket (WP) method and an asymptotic analysis.

Since the minimum structure of the initial Σ⁺ PES and its CI seam with the Π′ surface are very near, the quenching is opened by the Σ⁺–Π′ CI₁₂ coupling at γ ∼ 160°, whereas RT couplings are more important near the linearity. When OH(A²Σ⁺) is in the ground ro-vibrational state, CI₁₂ is the preferred non-adiabatic pathway, much more than those Σ⁺–Π′ RT₁₂, Σ⁺–Π′′ RT₁₃ and Π′–Π′′ RT₂₃. In particular, the relative strength of the non-adiabatic couplings is CI₁₂ ≫ RT₂₃ > RT₁₃ > RT₁₂, with 〈Π′|L̂_z|Π′′〉 in RT₂₃ more important than other L̂ matrix elements.

These electronic results are confirmed and strengthened by the analysis of the quantum dynamics, showing that the Π′ channel is preferred with respect to Π′′, and that conical-intersection and Renner–Teller effects are non-additive and in competition at some collision energies E_col. When OH(A²Σ⁺) is in the ground ro-vibrational state, the quantum results also suggest that the conical-intersection coupling rules the dynamics but can overestimate the reactivity, which is reduced by the Renner–Teller effects that modulate the dynamics.

Time-dependent WP snapshots show that the quenching is rather slow and that the opening rates of the Π′ and Π′′ channels are ∼180 and 200 fs⁻¹, respectively. Quenching probabilities P(E_col) present many sharp oscillations that imply an insertion, complex-forming mechanism that is reflected on some smooth resonances of the cross sections σ(E_col), as in other electronic quenching processes.³⁷ We obtain total σ(E_col = 0.039 eV) = 14.1 Ų and thermally averaged 〈σ(300 K)〉 = 11.6 Ų. These quantum findings compare well with previous quasi-classical²² and experimental results,²¹ which are equal to 17.2 ± 0.4 and 10 ± 1 Ų, respectively. The total cross sections increase from small values at the threshold up to the maximum values σ(E_col = 0.045 eV) = 14.8 Ų and 〈σ(450 K)〉 = 11.9 Ų. On the other hand, the total rate constant increases monotonically in the temperature range here investigated, with a ∼T^1/4 temperature dependence and a small activation energy.

In closing, we contrast the present quenching OH(A²Σ⁺) + Kr with other quenchings we investigated with similar quantum methods, namely O(¹D) + N₂,⁴⁶ OH(A²Σ⁺) + H,⁴⁴ and OH(X²Π) + H^{+ 37} with the reactant diatom also in the ground rotational state. When the quenching is due to non-adiabatic couplings of different nature, as in O(¹D) + N₂ with Spin–Orbit and Renner–Teller effects or in OH(A) + Kr, the RT couplings are less important, because they are significantly different from zero near the linearity whereas the others are important in larger geometry ranges. This is confirmed by the H₂O photodissociation²⁷ where CI and RT terms are in competition, like here. OH(A) + H has a smaller resonance structure and larger cross sections than those found here, probably because its reduced mass μ_R is 15 times smaller, giving both a faster collision with shorter-lived intermediate complexes and larger cross sections. On the other hand OH + H⁺ presents many resonances, like OH(A) + Kr, and larger cross sections owing to its smaller μ_R.

Clearly, this work should be extended to a coupled-channel formalism, to excited OH(A) rotational states, and to other cross sections investigated in ref. 21 and 22. Nevertheless, these quantum calculations are very expensive and much beyond our present computer resources. A final comment concerns the comparison of full 3D calculations with respect to those 2D^21,22 with constant r. The real WP method of Gray and Balint-Kurti³⁹ relies on the projection of the WP at R_∞ onto the final ro-vibrational states of the products OH(Π′) and OH(Π′′) and it cannot used in reduced dimensionality. Nevertheless, we are planning to carry out surface-hopping QCT calculations on the new PESs with a fixed OH distance and with the full 3D PESs. In addition, not only the quenching cross section will be calculated but also the rotational energy transfer cross sections and the OH rotational distributions on the 1A′ and A′′ PESs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are very grateful to A. Bernini, P. Defazio, M. Olivucci, and to the Dipartimento di Biotecnologie, Chimica, e Farmacia, Università di Siena, Italy, for invaluable computing resources. This research is supported by the Spanish Ministry of Science, Innovation, and Universities through grants RTI2018-094757-B-I00, MCIU/AEI/FEDER, UE and MDM-2017-0767, and in part, by the Generalitat de Catalunya (2017SGR0013 and XRQTC). PG thanks Generalitat de Catalunya for his Serra Húnter Associate Professorship. Funding by the Spanish Ministry of Innovation and Universities (MCIU/FEDER-PGC2018-096444-B-100) is also acknowledged.

References

1. D. R. Crosley, Adv. Ser. Phys. Chem., 1995, 3, 256.
2. D. R. Crosley, J. Phys. Chem., 1989, 93, 6273.
3. D. R. Crosley, J. Atmos. Sci., 1995, 52, 3299.
4. D. E. Heard and D. A. Henderson, Phys. Chem. Chem. Phys., 2000, 2, 67.
5. B. L. Hemming, D. R. Crosley, J. E. Harrington and V. Sick, J. Chem. Phys., 2001, 115, 3099.
6. B. L. Hemming and D. R. Crosley, J. Phys. Chem. A, 2002, 106, 8992.
7. P. H. Paul, J. L. Durant, Jr., J. A. Gray and M. R. Furlanetto, J. Chem. Phys., 1995, 102, 8378.
8. B. C. Hoffman and D. R. Yarkony, J. Chem. Phys., 2000, 113, 10091.
9. P. A. Cleary, L. P. Dempsey, C. Murray, M. I. Lester, J. Kłos and M. H. Alexander, J. Chem. Phys., 2007, 126, 204316.
10. B. Fu, E. Kamarchik and J. M. Bowman, J. Chem. Phys., 2010, 133, 164306.
11. J. H. Lehman, L. P. Dempsey, M. I. Lester, B. Fu, E. Kamarchik and J. M. Bowman, J. Chem. Phys., 2010, 133, 164307.
12. J. H. Lehman and M. I. Lester, Annu. Rev. Phys. Chem., 2014, 65, 537.
13. M. L. Costen, S. Marinakis and K. G. McKendrick, Chem. Soc. Rev., 2008, 37, 732.
14. M. Brouard, A. Bryant, Y.-P. Chang, R. Cireasa, C. J. Eyles, A. M. Green, S. Marinakis, F. J. Aoiz and J. Kłos, J. Chem. Phys., 2009, 130, 044306.
15. M. L. Costen, R. Livingstone, K. G. McKendrick, G. Paterson, M. Brouard, H. Chadwick, Y.-P. Chang, C. J. Eyles, F. J. Aoiz and J. Kłos, J. Phys. Chem. A, 2009, 113, 15156.
16. J. Kłos, M. H. Alexander, M. Brouard, C. J. Eyles and F. J. Aoiz, J. Chem. Phys., 2008, 129, 054301.
17. M. Brouard, H. Chadwick, Y.-P. Chang, C. J. Eyles, F. J. Aoiz and J. Kłos, J. Chem. Phys., 2011, 135, 084306.
18. H. Chadwick, M. Brouard, Y.-P. Chang, C. J. Eyles, T. Perkins, S. A. Seamons, J. Kłos, M. H. Alexander and F. J. Aoiz, J. Chem. Phys., 2012, 137, 154305.
19. H. Chadwick, M. Brouard, Y.-P. Chang, C. J. Eyles, G. McCrudden, T. Perkins, S. A. Seamons, J. Kłos, M. H. Alexander, P. J. Dagdigian, D. Herráez-Aguilar and F. J. Aoiz, J. Chem. Phys., 2014, 140, 054306.
20. H. Chadwick, M. Brouard, T. Perkins and F. J. Aoiz, Int. Rev. Phys. Chem., 2014, 33, 79.
21. J. H. Lehman, M. I. Lester, J. Kłos, M. H. Alexander, P. J. Dagdigian, D. Herráez-Aguilar, F. J. Aoiz, M. Brouard, H. Chadwick, T. Perkins and S. A. Seamons, J. Phys. Chem. A, 2013, 117, 13481.
22. T. Perkins, D. Herráez-Aguilar, G. McCrudden, J. Kłos, F. J. Aoiz and M. Brouard, J. Chem. Phys., 2015, 142, 144307.
23. J. Kłos, G. McCrudden, M. Brouard, T. Perkins, S. A. Seamons, D. Herráez-Aguilar and F. J. Aoiz, J. Chem. Phys., 2018, 149, 184301.
24. P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, Canada, 2nd edn, 1998, p. 370.
25. Ch. Jungen, J. Mol. Spectrosc., 2019, 363, 111172.
26. C. Petrongolo, J. Chem. Phys., 1988, 89, 1297.
27. L. Zhou, B. Jiang, D. Xie and H. Guo, J. Phys. Chem. A, 2013, 117, 6940.
28. H.-J. Werner, P. J. Knowles, G. Knizia, F. T. Manby, M. Schülz, et al., MOLPRO version 2012.1, a package of ab initio programs, 2012, http://www.molpro.net.
29. V. Kellö and A. J. Sadlej, Theor. Chim. Acta, 1996, 94, 93.
30. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
31. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514.
32. E. R. Davidson, J. Comput. Phys., 1975, 17, 87.
33. T.-S. Ho and H. J. Rabitz, Chem. Phys., 1996, 104, 2584.
34. A. Zanchet, B. Bussery-Honvault and P. Honvault, J. Phys. Chem. A, 2006, 110, 12017.
35. A. Zanchet, B. Bussery-Honvault, M. Jorfi and P. Honvault, Phys. Chem. Chem. Phys., 2009, 11, 6182.
36. B. T. Sutcliffe and J. Tennyson, Mol. Phys., 1986, 58, 1053.
37. P. Gamallo, S. Akpinar, P. Defazio and C. Petrongolo, Phys. Chem. Chem. Phys., 2017, 19, 4454 and refs therein.
38. E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, Cambridge University Press, Cambridge, UK, 1984, p. 52.
39. S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950.
40. H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1 and refs therein.
41. M. Hankel, G. G. Balint-Kurti and S. K. Gray, Int. J. Quantum Chem., 2003, 92, 205.
42. H. Chadwick, M. Brouard, Y.-P. Chang, C. J. Eyles, T. Perkins, S. A. Seamons, J. Kłos, M. H. Alexander and F. J. Aoiz, J. Chem. Phys., 2012, 137, 154305.
43. G. G. Balint-Kurti, A. I. Gonzalez, E. M. Goldfield and S. K. Gray, Faraday Discuss., 1998, 110, 169.
44. P. Gamallo, S. Akpinar, P. Defazio and C. Petrongolo, J. Chem. Phys., 2013, 139, 094303.
45. Z. Bacic and J. C. Light, J. Chem. Phys., 1986, 85, 4594.
46. P. Gamallo, S. Akpinar, P. Defazio and C. Petrongolo, J. Chem. Phys., 2012, 136, 054308.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02512g

---