Mechanism of powellite crystallite expansion within nano-phase separated amorphous matrices under Au-irradiation

Abstract

A fundamental approach was taken to understand the implications of increased nuclear waste loading in the search for new materials for long-term radioisotope encapsulation. This study focused on the formation and radiation tolerance of glass ceramics with selectively induced CaMoO₄ as a form to trap the problematic fission product molybdenum. Several samples were synthesised with up to 10 mol% MoO₃ within a soda lime borosilicate matrix, exhibiting phase separation on the nano scale according to thermal analysis, which detected two glass transition temperatures. It is predicted that these two phases are a result of spinodal decomposition with Si–O–Ca–O–Si and Si–O–Ca–O–B units, with the latter phase acting as a carrier for MoO₃. The solubility limit of molybdenum within this matrix was 1 mol%, after which crystallisation of CaMoO₄ occurred, with crystallite size (CS) increasing and cell parameters decreasing as a function of [MoO₃]. These materials were then subjected to irradiation with 7 MeV Au³⁺ ions to replicate the nuclear interactions resulting from α-decay. A dose of 3 × 10¹⁴ ions per cm² was achieved, resulting in 1 dpa of damage within a depth of ∼1.5 μm, according to TRIM calculations. Glasses and glass ceramics were then analysed using BSE imaging, XRD refinement, and Raman spectroscopy to monitor changes induced by accumulated damage. Irradiation was not observed to cause any significant changes to the residual amorphous network, nor did it cause amorphisation of CaMoO₄ based on the relative changes to particle size and density. Furthermore, the substitution of Ca²⁺ to form water-soluble Na₂/NaGd–MoO₄ assemblages did not occur, indicating that CaMoO₄ is resilient to chemical modification following ion interactions. Au-irradiation did however cause CaMoO₄ lattice parameter expansion, concurrent to growth in CS. This is predicted to be a dual parameter mechanism of alteration based on thermal expansion from electronic coupling, and the accumulation of defects arising from atomic displacements.

---

1. Introduction

As new developments are made to nuclear reactor design and performance, greater stress will be placed on materials for waste storage, as these new developments will create different waste streams.^1–3 This shift is concurrent with a general desire to decrease the final volume of waste for storage, as more countries turn to nuclear power as a method of decarbonisation.⁴ This has led to a renewed interest in the development of alternative glass or glass ceramic compositions for the encapsulation of waste streams that contain a higher concentration of compounds with a limited solubility in borosilicates, such as molybdenum, platinoids, and rare earths (REs).

These compounds have been problematic in the traditional process of vitrification^5–9 as they lead to uncontrolled precipitation of crystalline phases within the glassy matrix that can act as carriers for radioactive caesium, strontium, or minor actinides and lanthanides (Ce³⁺, La³⁺, Sm³⁺, Nd³⁺, Gd³⁺, Y³⁺),^7,10 that will subsequently alter the psychochemical properties of the wasteform.¹¹ This type of precipitation can also increase the fracture potential at the interface between these phases, which would similarly affect material properties.^12–14 While glasses prove to be useful containment matrices as they can be easily synthesised on a large scale, and show good thermal and radiation resistance, as well as chemical durability when exposed to aqueous environments,^10,15,16 these properties are dependent on the material remaining an amorphous monolith. Thus, limitations arise when increased waste loading or waste from weapons decommissioning, post operation clean out, or Generation IV reactors is considered.^10,17,18 In response to this problem single or poly-phase ceramics based on natural analogues, such as apatites, zirconolites or synroc were developed for the encapsulation of specific radioisotopes with desired material properties.^10,19–22 Unfortunately, they required high temperatures and pressures during synthesis, making them both time-consuming and costly to manufacture on an industrial scale.

As a result, a new ideology has emerged of inducing controlled crystallisation of predesigned phases within a glass matrix using the existing vitrification infrastructure. These glass ceramics (GCs) or glass composite materials are able to incorporate poorly soluble waste components such as sulfates, chlorides, molybdates and actinides in a durable crystalline phase, while the majority of other shorter-lived radioisotopes can be trapped in a flexible amorphous network.^10,17,23,24 In the context of molybdenum incorporation, selective formation of CaMoO₄, which is 13 500× less soluble than alkali molybdates²⁵ within a borosilicate framework is of interest.

In reprocessed waste streams, the fission product molybdenum is usually found as Mo⁶⁺ in oxidizing or neutral conditions.^26–28 It forms the oxyanion (MoO₄)²⁻ according to Mo EXAFS, which are found to be unconnected to each other and to the glassy framework when dissolved into an amorphous structure.^27,29,30 According to Greaves’ structural model, this is because they are located in non-bridging oxygen (NBO) channels.³¹ Mobile alkali or alkaline earth cations are also found to cluster is these channels, and can coordinate octahedrally to (MoO₄)²⁻ entities by weak long-range ionic forces.³² A similar configuration is also found for crystalline complexes,^8,30,32 where the process of phase separation stems from the accumulation of (MoO₄)²⁻ oxyanions in close proximity to charge-balancing cations within these depolymerized regions.^33–36

The preferred formation of crystalline CaMoO₄ over alkali molybdates can be driven by composition,^30,32,34 external heat treatments,^8,34,37 increasing the quench rate during synthesis,³⁸ or through redox chemistry.^35,39 Compositionally, molybdate speciation is influenced by the preferential charge balancing of BO₄⁻ and (MoO₄)²⁻ anionic entities by Na⁺ and Ca²⁺ ions.⁴⁰ Owing to ion charge, mobility, size and sterics both anions prefer Na⁺ as a charge balancer, but BO₄⁻ will have a stronger affinity to Na⁺, thus enabling the incorporation of Ca²⁺ into CaMoO₄.^29,41,42 This trend has been observed to increase for increasing amounts of B₂O₃ or CaO, as it affects the population of BO₄⁻ species.^32,34,40

Composition is also a significant factor in controlling glass-in-glass phase separation within the residual matrix, which will have subsequent effects on molybdate precipitation. In past phase separation studies focusing on molybdate formation, the concentration of CaO in soda lime borosilicate glasses has been limited to ∼11 mol%, as it is known to cause glass-in-glass phase separation.³⁴ This limitation has resulted in Na₂MoO₄ production in most studies, despite the manipulation of other factors affecting speciation. In the calcium borosilicate system, low concentrations of CaO will generally lead to phase separation of calcium borate and calcium silicate-based phases.^43,44 This is also true for alkali borosilicates.⁴⁵ For either alkali or alkaline earth borosilicates, the regions of immiscibility decrease with the atomic size of the cation, and increased incorporation can be achieved by rapid quenching, according to temperature profiles.

Base glasses formed solely of network formers can also show phase separation with a dependence on SiO₂/B₂O₃,^46,47 hence the need for cations to induce homogeneity. However, at low alkali or alkaline earth concentrations, regions of immiscibility within borosilicates are evident with temperature-dependent transitions.^43–45 Approaching these regions of immiscibility through composition or heat treatments can cause a multicomponent system to separate into distinct phases with different chemical compositions, and therefore different physical properties.⁴⁸ It can proceed through spinodal decomposition, or via a nucleation and growth process, as the system moves from metastable to unstable within the immiscibility dome. The first process is a result of small stochastic fluctuations in composition with temperature that occurs without a thermodynamic barrier.⁴⁹ It arises within a chemical spinodal area that may be present within a bimodal immiscibility region. Within the spinodal dome, homogeneous phase separation will occur. In contrast, nucleation and growth is a two-step process in which larger fluctuations cause the discrete nucleation of separated regions, which grow as a result of diffusion. This process can occur anywhere in the immiscibility region as the temperature of the system decreases. The distribution and size of secondary phases in this mechanism are governed by the kinetics of these two steps, which are assumed to follow Gaussian profiles with regards to temperature^49,50 and will determine many structural properties of the glass.⁵¹ Phases can be identified through a unique enthalpy signature associated with the glass transition temperature (T_g), which is the process at which a liquid “freezes” into a metastable solid.⁵²

While several factors can impact glass-in-glass phase separation and the speciation of molydates during synthesis, their durability against internal radiation is of considerable importance in determining its viability as a GC wasteform. Materials containing radioisotopes will continuously undergo α-decay of minor actinides and Pu, β-decay of fission products, and transitional γ-decay, which is a secondary process following α and β-decay. These collective decay processes can cause significant changes to long-range ordering through atomic displacements, ionisation, and electronic excitation.

Macroscopically, these structural modifications can cause changes to volume, where both swelling and densification have been observed,^6,53,54 and to mechanical properties, such as hardness, fracture toughness and elasticity.^55–57 They can also induce phase transformations, such as devitrification of the amorphous network, precipitation, amorphisation of crystalline phases, redistribution of radionuclides to existing molybdenum assemblages, glass-in-glass phase separation, or the clustering of cations.^{5,6,13,58–60} The range of effects is of course dependent on composition, and can sometimes result in favourable properties like an increase in fracture toughness, or re-vitrification of unwanted crystalline phases.^5,6

The α-decay process, and specifically the heavy recoil nuclei, are responsible for the for the bulk of these changes.^5,6,61 During α-decay, a fast moving α (or He²⁺) particle with kinetic energy between 4.5 to 5.5 MeV, and a heavy daughter isotope with kinetic energy between 70–100 keV referred to as the α-recoil are created from a stationary parent isotope. The small α-particle will interact with electrons in a substrate and typically travel 10 to 20 μm, while the α-recoil will interact primarily through nuclear collisions and stop after ∼30 nm.⁵ These nuclear collisions will have a billiard ball-type effect that will initiate a chain reaction, referred to as a displacement cascade. While this process will generate substantial structural reorganization, it is partly mitigated by the α-particle that will initiate some recovery processes through the creation of latent ion tracks that can be considered to mimic high temperature effects.^6,62,63

These competing processes of damage creation and defect annealing have been observed to result in a saturation of changes to mechanical properties, internal energy, and density for a cumulative dose of 4 × 10¹⁸α g⁻¹.^6,64,65 Given current waste loading standards and waste streams, this is expected to occur following ∼1000 years of storage,^2,6 which corresponds to approximately 1 displacement per atom (dpa).^64,66 By replicating the damage in this timeframe, long-term structural projections can be produced to test the durability of GCs against internal radiation and to understand how radiation damage can be used as a tool to design specific structural components adaptable for transmuted waste created through decay processes, or to increase the solubility of non-radioactive fission products.

This paper specifically aimed to answer the question of if irradiation would: (1) lead to powellite (CaMoO₄) amorphisation; (2) modify the crystalline structure or induce cationic substitution; or (3) result in modifications to the borosilicate network that would enable precipitation. It further sought to identify the mechanism in which any of the above would occur as a function of composition. It therefore attempts to validate a CaMoO₄ bearing GC as a candidate wasteform with a higher waste loading efficiency on a fundamental level.

2. Experimental

2.1 Composition and synthesis technique

The GCs in this study were created to test the formation of molybdates when MoO₃ was added in a 1 : 1 ratio to CaO in a borosilicate glass normalised to French nuclear waste glass SON68 (non-active form of R7T7) with respect to SiO₂, B₂O₃ and Na₂O. The excess Ca²⁺ ions were required to promote powellite production with the aim of preventing any water soluble Na₂MoO₄ from forming. See Table 1 for the normalised compositions.

Table 1 Normalised sample composition in mol%

Sample ID	SiO2	B2O3	Na2O	CaO	MoO3	Gd2O3
CNO	63.39	16.88	13.70	6.03	—	—
CNG1	61.94	16.49	13.39	7.03	1.00	0.15
CNG1.75	60.93	16.22	13.17	7.78	1.75	0.15
CNG2.5	59.93	15.96	12.95	8.52	2.50	0.15
CNG7	53.84	14.34	11.64	13.03	7.00	0.15
CN10	49.90	13.29	10.78	16.03	10.00	—

---

Several of the samples also contained a fixed amount of gadolinium. RE dopants can be considered as an actinide surrogate, and can therefore act as an indicator for potential incorporation sites of radioactive elements. They can further be used to investigate how incorporation would affect powellite crystallinity.

Glass batches of ∼30 g were prepared by mixing and then sintering powders of SiO₂, H₃BO₃, CaCO₃, Na₂CO₃, MoO₃ and Gd₂O₃ in a platinum–rhodium (90/10) crucible at 1500 °C. Compositions were first melted for 30 min. They were then cooled, crushed and re-melted for 20 min. A double melt with short melt times was used to try and ensure homogeneity, while minimizing volatilization. Specimens were annealed for 24 h at 520 °C to reduce internal stresses, after which they were cut to ∼3/4 mm × 3/4 mm in order to fit the irradiation sample holder (see Fig. 1). These pieces were all hand polished successively using P600, 800, 1200, 2400 and 4000 SiC grit paper, followed by 3 μm and 1 μm diamond polishing to achieve a uniform thickness of approximately 500 μm, and a surface appropriate for analysis.

Fig. 1 Samples of CNO, CNG1, CNG1.75, CNG2.5 and CN10 prior to (top) and following Au-irradiation (bottom). Discolouration observed for samples with MoO₃ and opalescence in Gd-containing GCs.

2.2 Irradiation experiment

Irradiation with medium energy ions can be used to simulate some of the damage created by α-decay observed on long timescales. While this method does not simulate the α-particle, which can induce healing,^11,62 the nuclear stopping power of ions such as Pt, Au, and Pb is similar to that of the α-recoil (5 keV per nm),⁶⁷ which as previously mentioned is responsible for creating displacement cascades that result in the greatest degree of structural changes.

The radiation experiment conducted in this study was performed with 7 MeV Au³⁺ ions at a flux of 2 × 10¹⁰ ions per cm² s on the ARAMIS beamline at CSNSM in France. A total dose of 3 × 10¹⁴ ions per cm² was achieved, which corresponds to approximately 1 dpa with a ion penetration depth of ∼1.5 μm, as estimated from TRIM simulations⁶⁶ (see ESI† for results of simulation). This level of damage should test the stability of any crystalline phases, as well as the flexibility of the residual amorphous phase. Fig. 1 shows the sample prior to and following irradiation.

2.3 Characterisation techniques

The primary points of interest in this investigation were radiation affects on crystallinity and the Mo environment. This required use of several analytical techniques as GCs contain multiple phases, which can create complexity when studying modifications following irradiation.

Crystal phase and crystallite size identification were performed using X-ray diffraction (XRD) with CuK_α1 (λ = 0.15406 nm) and CuK_α2 (λ = 0.15444 nm) wavelengths on a Bruker D8 ADVANCE. The diffractometer was equipped with Göbel mirrors for a parallel primary beam, and a Vantec position sensitive detector. For each sample, data was acquired for a 2θ = 10–90° spectral range with a 0.02° step size, and a 10 s per step dwell time. Samples were analysed as monoliths instead of powders to isolate irradiation effects at the surface, and rotated to find the maximum diffracting orientation before final acquisition in order to compare samples containing randomly orientated crystals with some accuracy. Scherrer crystallite size (CS) valuations were determined from structural analysis based on whole pattern Rietveld refinements with the software Topas v4.1.⁶⁸ A single parameter approach was utilized based on the quality of data available and the large amorphous content in most samples.^69,70 In this fitting approach, CS is presumed to incorporate contributions from both size and strain, as correlation issues prevented the independent deconvolution and quantification of these two physical properties in GCs.

In order to characterise and assess structural changes to both the crystalline and non-diffracting amorphous phases following irradiation, Raman spectroscopy was utilized. Spectra were collected with a 300 μm confocal Horiba Jobin Yvon LabRam300 spectrometer coupled to a Peltier cooled front illuminated CCD detector over the 150–1600 cm⁻¹ spectral range with a 2 μm spot size and a holographic grating of 1800 grooves mm⁻¹. The 532 nm excitation line used in this experiment was produced using a diode-pumped solid-state laser (Laser Quantum) with an incident power of 100 mW focused with an Olympus 50× objective. This set-up enabled a spectral resolution of ∼1.4 cm⁻¹ per pixel (1024 × 256 pixels in size), and an estimated penetration depth of ∼22 μm based on depth profile analysis. This means results also showed a contribution from the pristine layer under the irradiation zone. Despite this fact, these parameters were used based on a number of factors including acquisition time, spectral resolution, minimization of damage, and a desire to describe the amorphous phase. As a result, the recorded trends are indicative of those induced by irradiation, but the magnitude of these trends will be more pronounced if measurements were solely collected from the irradiation zone. Raman spectra of GCs were analysed with PeakFit software using pseudo-Voigt profiles to characterise bands, while spectra of amorphous phases were analysed qualitatively due to uncertainties with comparing overlapping broad bands.

Multi-phase GCs present varying morphologies and phases for quantification. This was analysed using SEM backscattered (BSE) imaging and energy dispersive X-ray spectroscopy (EDS) on a Quanta-650F held at low vacuum (0.06–0.08 mbar) and performed with a 5–7.5 keV beam. This configuration resulted in a maximum penetration depth of ∼0.05 μm. For EDS analysis, measurements were collected with a 8 mm cone in order to reduce skirting effects when analysing small particles. Images were collected using FEI Maps software, while acquisition and analysis for EDS was performed using Bruker ESPRIT software from mapped areas or 10–15 points. Quantification of particle size and density at the surface was determined by image analysis using ImageJ.⁷¹

While these analytical techniques were useful for comparative analysis of glasses and GCs prior to and following irradiation, addition characterisation of synthesised materials prior to irradiation was required to help explain subsequent modifications. The two bulk characterisation techniques employed for this purpose were ¹¹B MAS NMR and simultaneous differential scanning calorimetry – thermogravimetric analysis (SDT). In both cases, analysis following irradiation was limited owing to the small irradiation volume and the requirement to powder monoliths, thus creating additional defects and limiting further investigation.

¹¹B MAS NMR (μ_z = 2.6887; γ = 8.5847 × 10⁷ rad T⁻¹ s⁻¹) experiments were conducted on a Varian Infinity Plus spectrometer with a 11.74 T superconducting magnet, tuned to the Larmor frequency of ∼160.37 MHz using 2.5 mm probes. For each measurement, approximately 9–13 mg of powdered solids were packed in zirconia rotors, and spun at 20 kHz. 90° pulses with a 0.7 s pulse delay, and 5 μs receiver and acquisition delays were used. Chemical shifts were then measured relative to the primary liquid standard BF₃Et₂O (0 ppm), and the secondary solid standard of NaBH₄ (−42 ppm).

Thermal SDT analysis was performed on a TA Instruments Q600 with Pt/Rh thermocouples arranged for a dual beam balance under nitrogen gas to ensure no weight changes resulted from oxidation at high temperature. The equipment configuration resulted in a standard balance sensitivity of ±0.1 μg, and a ±2% calorimetric accuracy. Two measurements were taken per sample using 10–18 mg of powdered material in alumina pans. A 10 °C min⁻¹ heating rate to a maximum temperature of 1500 °C was applied to each experiment, after which the system was air-cooled. All observable thermal transitions were analysed using TA Instruments Universal Analysis 2000 software.

3. Results

3.1 Bulk material characteristics

The addition of MoO₃ can lead not only to crystallisation of alkali or alkaline earth molybdates, but it can also cause changes to the residual glass matrix. These changes will have subsequent effects on thermal properties, which can be used as metrics for phase separation and crystallisation. The events of interest measured by SDT are T_g and the melting temperature T_M of crystallites, both of which are summarised in Table 2 (spectra provided in ESI†).

Table 2 Glass transition temperature(s) and melting temperature determined by SDT analysis

Sample ID	T g1		T g2		T M
	T (°C)	H (J g^−1)	T (°C)	H (J g^−1)	T (°C)	H (J g^−1)
CNO	599.56	5.08	741.54	89.95
CNG1	595.39	6.70	725.80	42.29	1015.85	115.40
CNG1.75	591.10	16.82	738.91	55.53	1042.78	137.70
CNG2.5	593.86	19.76	742.93	54.35	1041.41	125.70
CNG7	586.05	23.80	757.88	69.47	1087.64	310.00
CN10	599.81	6.35	760.26	80.56	1067.87	327.00

---

Interestingly two T_gs were detected for glasses and GCs. The first transition, T_g1 around 600 °C is closer to the value of T_g found for similar soda lime borosilicate systems with [SiO₂]/[B₂O₃] > 3.^72,73 This transition also exhibits the previously observed inverse relationship to increasing [MoO₃].³⁵ The outlier to this rule was CN10, which most closely emulated the temperature and enthalpy of transition seen in CNO suggesting that with excess MoO₃ the conversion of phase separated Mo–O–Ca–O–B/Si to CaMoO₄ increases, thereby reducing the amount of molybdenum in the amorphous phase. It may also be related to the gadolinium dopant present in the other compositions, though previous studies have indicated that this dopant would reduce primary phase separation instead of increasing it.⁸ A tertiary reasoning could be sampling in heterogeneous GCs skewing results.

In contrast, the second transition, T_g2, is similar to glasses with [SiO₂]/[B₂O₃] < 0.2.^74,75 Like T_g1, T_g2 also experienced a composition-induced shift with [MoO₃]. In this case, there appeared to be a logarithmic relationship between the two, where inclusion of MoO₃ first caused a drop in T_g2, after which growth was seen in proportion to [MoO₃].

While the composition dependent shifts of these transitions imply that MoO₃ altered the glass structure, the presence of these two glass transitions implies a degree of heterogeneity. Furthermore, the relative enthalpies of transition suggest that MoO₃ can increase the domain size of separated phases. It is speculated that the relationship observed between T_g2 and [MoO₃] is correlated to molybdenum phase separation and eventual crystallisation primarily within this higher refractory phase. As more [MoO₃] is added to the system, (MoO₄)²⁻ oxyanions accumulate leading to additional phase separation and the tendency for CaMoO₄ crystallisation subsequently increases, which would increase T_g of the encapsulating phase. Correspondingly, the number of Ca²⁺ ions in the residual glassy matrix of the phase associated with T_g1 decreases as they are pulled towards phase 2, thereby allowing T_g1 of phase 1 to increase.

Multiple phases cannot be clearly resolved in the micrographs of CNG1 in Fig. 2. This suggests that phase separation proceeded through spinodal decomposition, which would result in two phases that cannot clearly diffuse light due to the nano-domain size, as has been previously found experimentally.^51,76 Further investigations using TEM and utilization of heat treatments above T_g1 could be used to confirm this theory.

Fig. 2 BSE micrographs of CNG1: (a) following synthesis, and (b) following Au-irradiation.

While a complex relationship was observed for glass transitions with composition, a more straightforward observation was made with respect to the liquidus or melting temperature (T_M) of CaMoO₄ or a CaMo-rich precursor environment (see Fig. 3). Given that CNG1, which appears to be a glass also produced a T_M, it is assumed that there is an amorphous precursor environment to crystallisation in which the structure of clustered (MoO₄)²⁻ oxyanions in relation to cations is very similar to that of crystalline powellite, as has been previously observed.³² It can therefore also produces a similar “melting” transition. The presence of this transition could also indicate that there are very small crystallites (<50 nm) in CNG1 that are beyond XRD and SEM detection (<1 vol%).

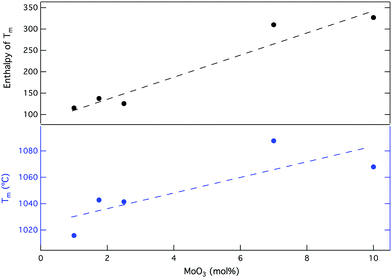Fig. 3 Melting temperature (T_M) of CaMoO₄ and the enthalpy of transition for soda lime borosilicate with increasing amounts of MoO₃.

Generally, T_M and the enthalpy of this thermal event (H_Tm) increase with the quantity of crystal matter, which increases with [MoO₃] as Fig. 3 indicates. Prior to crystallisation on a detectable level, T_M is found at a lower temperature (CNG1). As [MoO₃] increases forming GCs, a corresponding increase in T_M and H_Tm can be correlated to a predicted increase in the crystal content. This reflects the fact that motion in an amorphous precursor environment is easier than in an analogous phase with denser atomic packing and higher ordering resulting in increased CaMoO₄ formation.

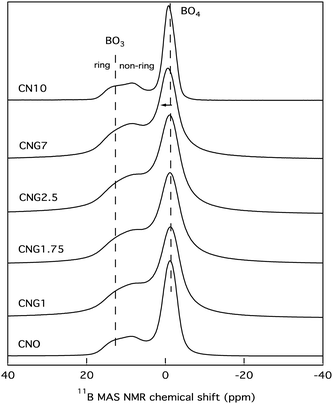
The results in Table 2 suggest a level of phase separation within the bulk residual glass matrix, which can be correlated to the extent of Si–O–B mixing within the short-range order of the glass. Initial phase separation is independent of MoO₃, but inclusion of MoO₃ causes additional phase separation of within the borosilicate phase in addition to the formation of a Ca–Mo-rich environment associated with T_M. ¹¹B MAS NMR has long since been considered one of the primary tools to elucidate this type of mixing and phase separation, and thus was employed in this study, the results of which can be seen in Fig. 4. There are two main contributions detected. The first is from (BO₄)⁻ groups centred around −1 ppm, with downfield shifts expected for an increasing number of boron nearest neighbours as opposed to silicon, and an upfield shift expected for more silicon nearest neighbours.^33,34,77 The second detected group of overlapping peaks is from BO₃ units centred around 10 ppm. The quadrupolar BO₃ peak is composed of two contributions from ring and non-ring configurations,^34,78 as the labels on Fig. 4 indicate.

Fig. 4 Mass normalised ¹¹B MAS NMR spectra for samples with increasing amounts of MoO₃. The samples with the letter G in the name contain a gadolinium dopant, which can account for the observed peak broadening in these samples.

While there are no drastic changes to the mass normalised ¹¹B MAS NMR spectra, some minor modifications occurred. Firstly, the spectra for CN10 and CNO are similar, indicating that MoO₃ has minimal effects on the coordination of boron when molybdenum is primarily found in a crystalline phase. The main modifications observed were a minor increase in non-ring over ring BO₃ units similar to that observed in the spectra for CNG7, in addition to a marginal increase in [BO₃] over [BO₄⁻]. A minor downfield shift of the peak associated with BO₄⁻ units was also found for [MoO₃] ≥ 7 mol%, indicative of a higher fraction of BO₄⁻(2B,2B) relative to the primary BO₄⁻(3Si,1B), but none of these changes were occurring on a significant scale.

Secondly, a visible spectral broadening for samples CNG1, CNG1.75, CNG2.5, and CNG7 is evident. This is caused by the gadolinium, which with 7 unpaired electrons (spin 7/2) can create a local magnetic field that will induce spectral broadening. The slow electron flipping of gadolinium ions can also cause fluctuations in the relaxation of boron with spin 3/2, which would similarly cause spectral broadening. The inclusion of a dopant also appeared to increase the relative [BO₃]/[BO₄⁻] fraction in all of these samples, with a preference for non-ring BO₃ units as [MoO₃] increases. This could perhaps be tied to structural units in the nano-phase associated with T_g1, as the relative enthalpies of transition follow a similar trend.

3.2 Crystallisation

In soda lime borosilicate glasses normalised to SON68, the selective formation of water-durable CaMoO₄ was achieved by introducing up to 10 mol% MoO₃ in a 1 : 1 ratio to CaO for a fixed melting process according to XRD (see ESI† for raw XRD patterns). Spherical particles containing CaMoO₄ crystallites were found to be homogeneously distributed within the amorphous network indicative of a nucleation and growth process (see Fig. 5). The particle sizes (PS) observed were proportional to MoO₃, with two groups identifiable for low and high [MoO₃], as Table 3 indicates. This was also true of the Scherrer CS determined from Rietveld refinements of XRD patterns (see Table 4). Increasing [MoO₃] was also observed to be inversely related to the a and c cell parameters of powellite.

Fig. 5 BSE micrographs of GCs: (a) CNG1.75, (b) CNG2.5, (c) CNG7, and (d) CN10 following synthesis; and of (e) CNG1.75, (f) CNG2.5, (g) CNG7, and (h) CN10 following Au-irradiation.

Table 3 Range of particles sizes (PS) and calculated surface particle density based on image analysis using ImageJ of BSE micrographs

Sample	Pristine		Au-Irradiated
	PS (nm)	Surface particle density (μm^−2)	PS (nm)	Surface particle density (μm^−2)
CNG1.75	92–135	3.51	79–151	3.14
CNG2.5	91–151	6.38	92–165	5.09
CNG7	186–308	2.74	195–321	2.30
CN10	247–363	2.38	263–395	2.21

---

Table 4 Scherrer CS in diameter and cell parameters of CaMoO₄ prior to and following Au-irradiation with the estimated standard deviation from fitting given in brackets

Sample	Dose (ions per cm^2)	CS (nm)	a (Å)	c (Å)
CNG1.75	0	51.27 (±2.26)	5.2289 (±0.0011)	11.4606 (±0.0034)
	3 × 10^14	80.96 (±3.16)	5.2294 (±0.0006)	11.4621 (±0.0019)
CNG2.5	0	55.09 (±2.08)	5.2280 (±0.0080)	11.4593 (±0.0025)
	3 × 10^14	71.62 (±4.99)	5.2326 (±0.0012)	11.4669 (±0.0039)
CNG7	0	143.38 (±2.54)	5.2265 (±0.0001)	11.4558 (±0.0003)
	3 × 10^14	236.24 (±9.68)	5.2312 (±0.0002)	11.4630 (±0.0005)
CN10	0	125.24 (±1.94)	5.2264 (±0.0001)	11.4554 (±0.0030)
	3 × 10^14	176.26 (±6.70)	5.2310 (±0.0002)	11.4648 (±0.0006)

---

An exception to the proportional dependence of CS with [MoO₃] occurred in CN10, which mirrors deviations observed in bulk characterisation. This may result from the absence of a Gd₂O₃ dopant in this composition, which is predicted to improve crystallisation kinetics in the other GCs, or could be a result of sampling variations. For compositions with [MoO₃] < 1.75 mol%, samples did not show the formation of distinctive particles according to BSE imagining and showed no diffraction peaks (see Fig. 2 and ESI†), indicating that they were completely amorphous. This retention limit of molybdenum is similar to that observed in previous compositional studies of SON68-type borosilicates.^8,29,30

Following Au-irradiation, CNO and CNG1 remained amorphous with no CaMoO₄ precipitation detected by XRD. Similarly, GCs contained a single powellite crystal phase, with no identifiable Na⁺ or Na–Gd substitution of Ca²⁺ within the CaMoO₄ structure. The powellite phase remained spherical in particle morphology and evenly distributed within the amorphous matrix, but a marginal increase in the range of PS was determined, as Table 3 summarises. This coincided with a reduction in the number of particles per unit area, which suggests that PS growth is diffusion based.

This shift in PS was mirrored by growth in both the powellite CS and cell parameters, as can be seen in Table 4. While irradiation-induced growth of both CS and cell parameters occurred for all samples (see Fig. 6), the expansion of the unit cell cannot alone account for the changes in CS, therefore an additional process must be taking place to enable CS growth. This is especially true for high Mo-bearing samples with [MoO₃] ≥ 7 mol%, where ΔCS > 50 nm. These results imply either that there was some diffusion-assisted growth of crystallites, which changes to the range and density of PS support, or that some bulk-to-surface precipitation of powellite took place in these compositions. Alternatively, it could indicate a greater sensitivity of these compositions towards accumulated defects and a propensity for void formation within the crystal structure. This latter effect can be a direct result of displaced atoms following nuclear collisions, and would have a similar effect on PS as particles are made out of crystallites.

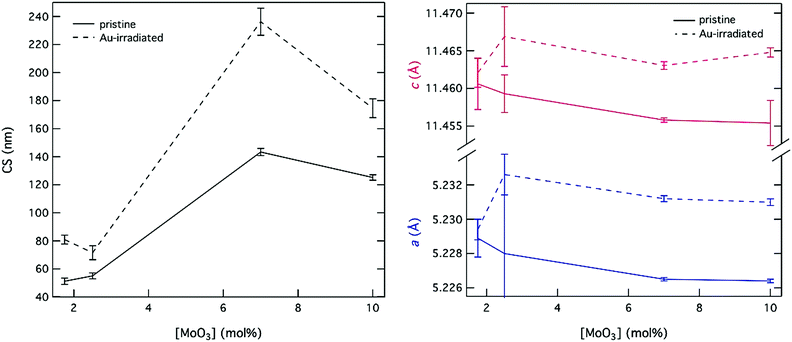Fig. 6 Changes to CS and the a and c powellite cell parameters following Au-irradiation with a dose of 3 × 10¹⁴ ions per cm².

The magnitude of change for powellite cell parameters was also larger as [MoO₃] increased (see Fig. 6). This result corroborates the theory that the crystal phase becomes more susceptible to alteration as [CaMoO₄] increases. In contrast, changes to the powellite cell parameters often fell within the estimated standard deviation for compositions with [MoO₃] ≤ 2.5 mol%. Nevertheless, expansion occurred in both unit cell directions and growth of CS was always observed in these compositions. Growth of the unit cell also occurred isotropically, which mirrors a temperature based response.

It is interesting that the CS growth induced by Au-irradiation was smallest for CNG2.5. This is an anomaly that has been seen in other studies on compositions with 1.5–4.5 mol% MoO₃ where an initial GC containing 2.5 mol% MoO₃ showed broader diffraction peaks indicative of increased Mo solubility in comparison to other compositions with CaMoO₄ formation.^8,70 This is mirrored by SDT, XRD and SEM results in this study, which show an increased retention of MoO₃. A similar such property in CNG2.5 could subsequently have inhibited radiation-induced CS growth as well.

3.3 Composition and Raman modifications

Changes to CS are concurrent to shifts in the Raman bands associated with internal (MoO₄)²⁻ lattice vibrational modes for powellite with C_4h point symmetry. The main bands of interest are ν₁(A_g) 878 cm⁻¹, ν₃(B_g) 848 cm⁻¹, ν₃(E_g) 795 cm⁻¹, ν₄(E_g) 405 cm⁻¹, ν₄(B_g) 393 cm⁻¹ and ν₂(A_g + B_g) 330 cm⁻¹.^79–81 These vibrations are associated to: symmetric elongation of the molybdenum tetrahedron, unsymmetrical translation of double degenerate modes, symmetric and unsymmetrical bending. There are three supplementary vibrations at 206 cm⁻¹, 188 cm⁻¹ and 141 cm⁻¹ assigned to external translational modes of Ca–O and MoO₄,⁷⁹ referred to as ν_def(A_g) deformation modes of the cationic sublattice.⁸¹ Prior to irradiation, these modes are all present for GCs with [MoO₃] ≥ 1 mol% (see Fig. 7), but are found at lower wavenumbers in comparison to the listed vibrations for single crystals. As MoO₃ increased from 1.75–10 mol%, these vibrational modes experience a ∼0.8 cm⁻¹ shift to higher wavenumbers, thus approaching theoretical values as the powellite cell parameters decreased towards an ideal crystal structure.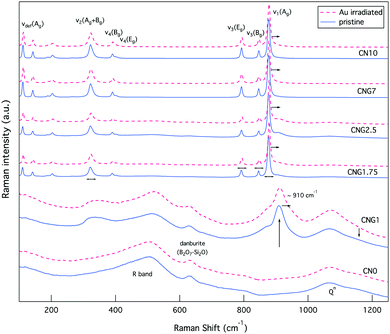

Fig. 7 Raman spectra of both glasses and GCs prior to (blue solid line), and following irradiation (red dashed line).

Following Au-irradiation these vibrational modes are all still present, indicative of rigidity of the molybdenum tetrahedron, and thus resilience of the crystal phase. However, a shift of ∼1–2 cm⁻¹ to higher wavenumbers was observed for all (MoO₄)²⁻ lattice vibrational modes, an example of which can be seen in Fig. 8. This is associated to an increase in the Mo–O bond length,⁸² which has similarly been observed for CaMoO₄ under increasing temperature or pressure.^83,84

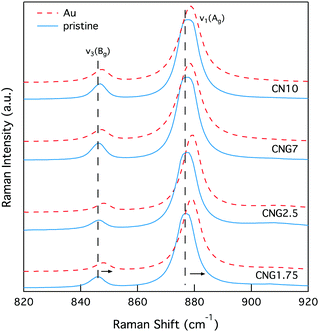Fig. 8 Raman spectra of select MoO₄²⁻ vibrational modes (ν₁(A_g) 878 cm⁻¹ and ν₃(B_g) 848 cm⁻¹) in GCs illustrating a spectral shift to higher wavenumbers.

The effect of radiation on vibrational modes via a shift to higher wavenumbers was also dependent on composition, with a more significant change found at low [MoO₃], as Fig. 9 indicates. This could be attributed to existing defects within the crystal structures following synthesis that resulted in the (MoO₄)²⁻ lattice vibrational modes starting off at lower wavenumbers.

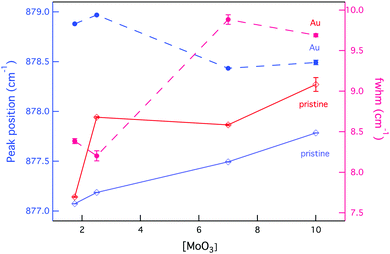Fig. 9 Changes to the position and broadening of the Raman vibrational band ν₁(A_g) as a function of composition and external radiation.

Simultaneous to a change in peak position was an observed peak broadening for all GC compositions, except CNG2.5 where the peak full-width decreased (see Fig. 9). Peak broadening can be associated with distortion within the molybdenum tetrahedron or increased disorder in the stacking of (MoO₄)²⁻ units, whereas a decrease in broadening is associated with greater order within the crystalline environment.⁸⁵ Given that this composition showed some anomalies with an increased fraction of molybdenum anion incorporation, it also appeared to modify the radiation response, as CS changes confer. The increased incorporation of (MoO₄)²⁻ units is supported by the band at ∼910 cm⁻¹ being largest for this composition (see Fig. 7). This is predicted to occur owing to the initial metastable equilibrium state of this composition, which is hypothesized to be associated with a higher fictive temperature (T_f) from internal quenching processes. Therefore, radiation serves initially as a relaxing agent increasing the order within the crystalline phase in this composition, after which structural defects form.

While evident modification was observed for the vibrational modes of powellite, very little change was detected from the Raman spectra of fully amorphous samples (CNO and CNG1), as Fig. 7 indicates. In these samples there are several bands classically assigned to silicates or borates. The most significant of which is the R band at ∼450–520 cm⁻¹, which at lower wavenumbers is assigned to mixed Si–O–Si and Si–O–B bending and rocking,^77,86,87 and at higher wavenumbers to B–O–B rocking.⁸⁸ The second band of interest is at ∼633 cm⁻¹ and can be attributed to Si–O–B vibrations in danburite-like B₂O₇–Si₂O groups.^64,79 This band experiences minor damping relative to the R band following Au-irradiation indicative of modified ring structures. The last collection of overlapping characteristic bands can be found between ∼850–1250 cm⁻¹, and are representative of Si–O stretching vibrational modes for Qⁿ units that represent SiO₄ tetrahedra with n bridging oxygen.⁸⁹ The maintenance of the first and last grouping of broad bands in their existing proportions indicates that the borosilicate network experiences little modification on average.

The Raman spectra for the glass containing 1 mol% MoO₃ also showed three broad bands at ∼330 cm⁻¹, ∼870 cm⁻¹ and ∼910 cm⁻¹ in addition to those listed above. The first two broad bands indicate that while crystallisation has not been observed in this composition, (MoO₄)²⁻ tetrahedron are similarly clustered and coordinated to Ca²⁺ ions.³² The broadness of these bands reflects that they nonetheless remained in an amorphous state. Following irradiation, these bands became even broader, indicative of increased disorder in the molybdenum environment, which can be associated to increased molybdenum dissolution. The band at ∼910 cm⁻¹ representing Mo–O bond elongation in tetrahedral (MoO₄)²⁻ chains is a metric of this.³⁰ As this band moves to higher wavenumbers it indicates the dissolution of isolated (MoO₄)²⁻ units in the amorphous network or significantly distorted Ca²⁺–(MoO₄)²⁻ assemblies. In contrast, as it moves to lower wavenumbers crystallisation commences.^82,90 Following irradiation this band underwent the first transformation, with a shift of ∼2 cm⁻¹ to higher wavenumbers. These results collectively imply that the molybdenum local environment was sensitive to radiation damage, while the borosilicate matrix showed resilience to modification.

In order to understand how the observed change to crystallinity and bonding occurred, EDS analysis was employed. Results in Table 5 indicate that as MoO₃ increased, Ca and Mo ions were leached out of the amorphous phase and clustered in the crystalline phase prior to irradiation. Furthermore, the fairly constant [Ca]/[Mo] ratio of ∼3.5 in the amorphous phase of all GCs implies that the influence of network modifying ions is independent of [MoO₃] following an initial concentration of 1 mol% MoO₃.

Table 5 Calculated [Si]/[Ca] and [Ca]/[Mo] ratios from EDS analysis for amorphous and crystalline phases

Sample ID	Dose (ions/cm^2)	Amorphous		Crystalline
		Si/Ca	Ca/Mo	Si/Ca	Ca/Mo
CNO	0	26.36 (±4.00)
	3 × 10^14	33.79 (±4.91)
CNG1	0	15.63 (±1.29)	6.99 (±0.62)
	3 × 10^14	24.09 (±4.60)	3.34 (±0.70)
CNG1.75	0	11.43 (±0.75)	3.46 (±0.86)	11.09 (±0.71)	2.99 (±0.62)
	3 × 10^14	13.67 (±0.86)	2.61 (±0.52)	14.07 (±0.91)	2.63 (±0.54)
CNG2.5	0	10.48 (±0.63)	3.53 (±0.82)	10.44 (±0.63)	3.44 (±0.78)
	3 × 10^14	18.19 (±1.52)	2.32 (±0.55)	16.59 (±1.29)	2.00 (±0.39)
CNG7	0	8.19 (±0.40)	3.68 (±0.70)	4.24 (±0.14)	1.52 (±0.09)
	3 × 10^14	12.74 (±0.75)	0.80 (±0.02)	5.29 (±0.17)	0.97 (±0.03)
CN10	0	7.00 (±0.30)	3.38 (±0.52)	2.83 (±0.09)	1.31 (±0.05)
	3 × 10^14	11.89 (±0.66)	2.12 (±0.31)	3.24 (±0.09)	1.11 (±0.04)

---

Prior to irradiation, some oddities in concentration were noted representative of equipment limitations. Si was found in the “crystalline phase”, and the [Ca]/[Mo] ratio was often greater that one, which is the expected value for powellite. Although this ratio approached unity and smaller amounts of Si were detected as MoO₃ increased, this result reflects the relative spot size versus particle volume. Most measurements for the “crystalline phase” would have incorporated some of the residual amorphous matrix, hence the disparity. Nevertheless comparative results can be used to gauge ion diffusion initiated by irradiation.

Following Au-irradiation all samples showed an increase in [Si]/[Ca] and a decrease in [Ca]/[Mo] in both the amorphous and “crystalline” phases (see Table 5). This implies cationic depletion at the surface, which has also been observed to occur with alkali ions,^63,91 and irradiation with both β-particles^69,70 and Xe²³⁺ ions,^92,93 which simulate the electronic components of β and α-decay. This type of surface depletion is due to an electric field gradient created from bombarding ions, which appears translational to irradiation with Au³⁺ ions.

While an increase in [Si]/[Ca] and a decrease in [Ca]/[Mo] occurred in both phases, the fractional differences are larger in the amorphous phase. This could be a result of minor changes in the Ca-rich amorphous phase around crystalline particles, while the crystallites themselves remained compositionally unchanged. It could also suggests a secondary effect of cross phase diffusion of Ca ions from the amorphous to the “crystalline” phase, though this is difficult to ascertain owing to the significant mechanism of surface to bulk diffusion.

Based on a comparison between the changes seen for CNG7 and CN10, which initially have particles of a similar size, it can be concluded that the mobility of Ca ions increases for Gd-doped samples when exposed to irradiation. Moreover, the normalised [Gd] increases from ∼0.10 to ∼0.15 atm% in CNG1.75, CNG2.5 and CNG7 following irradiation. This increase could indicate a charge balancing substitution of Ca²⁺ ions for Gd³⁺ within the borosilicate network, which would subsequently enable the free migration of Ca²⁺ ions, though this effect would be small given the relative dopant concentration.

4. Discussion

4.1 Multi-scale phase separation

The compositions used in this study facilitated an excess of calcium for CaMoO₄ formation, and had a high enough concentration of B₂O₃ to ensure that Na⁺ ions were unavailable for Na₂MoO₄ formation. In excess of 1 mol% MoO₃, phase separation and consecutive crystallisation occurred during cooling and a single powellite (CaMoO₄) phase was observed within an amorphous network. A uniform distribution of spherical and unconnected powellite particles are indicative of a nucleation and growth process.⁹⁴ The first stage of this process involves liquid–liquid phase separation of the borosilicate network that created depolymerized regions of the glass where (MoO₄)²⁻ entities accumulate. The initiation of phase separation can be correlated to the field strength of modifying ions, such as Na⁺, Ca²⁺, and Mo⁶⁺, with the degree of phase separation proportional to the modifier field strength.^29,35 The second stage of this process involves Ca–O–Mo bond formation leading to crystallisation inside these regions during cooling.³²

The resultant CaMoO₄ crystallites were observed to precipitate on the micron scale following synthesis and took the form of scheelite-type powellite with a tetragonal structure. The CS values and cell parameters for these synthesised crystals align with studies for similar soda lime borosilicate GC compositions,^8,30,34 as well as calcium borosilicate GCs with a high MoO₃ content.⁶⁹ A variance was found to exists between the lattice parameters for crystals within an amorphous matrix, and those of a monocrystal (a = 5.222 Å and c = 11.425 Å).⁹⁵ In general, synthesised GCs had a larger unit cell compared to powellite single crystals in both this and previous studies, which suggests that the very nature of an amorphous structure independent of composition causes this effect. It is predicted that contraction of the borosilicate framework during the glass transition process subsequently creates tensile stress on CaMoO₄ crystals. This transition inhibits a full relaxation of powellite crystals to room temperature equilibrium, thus creating the discrepancies in lattice parameters.

In this study, a compositional effect was observed for both of these metrics with CS expansion and lattice parameter contraction occurring for increasing [MoO₃]. PS was similarly proportional to increasing [MoO₃]. These composition-dependent shifts can be correlated to a change in the temperature of phase transitions that consequently controls the molybdenum environment. In previous studies of sodium borosilicates, the phase separation temperature (T_PS) was observed to increase by ∼18 °C per mol of MoO₃.³⁵ Comparatively, Magnin et al. observed a ∼50 °C increase in T_PS and a ∼40 °C increase in the crystallisation temperature (T_C) of CaMoO₄ for every 0.5mol% increase in [MoO₃].³⁴ Increases in T_PS and T_C would produce larger crystallites that form into larger particles for a fixed synthesis temperature. These crystallites would also have a longer period of relaxation before a glass transition occurred and the matrix goes from liquid to solid. This longer relaxation would subsequently result in smaller lattice parameters. Given that these trends were recorded for increasing [MoO₃] in this study, it can be concluded that these principles of increasing T_PS and T_C apply to these GCs.

Similar trends were also observed for T_M and H_Tm with increasing amounts of MoO₃, indicating that T_PS and T_C are related to the melting of crystallites. When T_PS and T_C increase, larger crystallites with smaller cell parameters are formed, which represent embedded powellite crystals approaching single crystal ideality. A larger amount of these crystals are also formed, which is supported by the larger (∼3× in size) PS found for higher [MoO₃]. As a growing number of crystals that are approaching ideality in structure form, a higher temperature would be required to induce thermal motion and eventual melting. The less ordered crystal structures formed when T_C is closer to T_g would in comparison require less thermal energy to induce amorphisation. For this reason T_M is predicted to increase with T_PS and T_C, and therefore [MoO₃]. Theoretically T_C and T_M are presented as overlapping Gaussian profiles on the Gibbs free energy versus temperature plot.⁵⁰ Accordingly, the proportional relationships observed here are not unexpected.

While this trend with respect to [MoO₃] held for PS and powellite lattice parameters, a deviation occurred with respect to CS and T_M. In this study, CS was initially ∼20 nm larger for CNG7 than for CN10 despite a 3 mol% difference in [MoO₃], and the rate of change following irradiation was likewise larger. Similarly T_M was ∼20 °C cooler for CN10 than for CNG7. These differences can be attributed to the gadolinium dopant, which is predicted to improve crystallisation kinetics during synthesis, in addition to growth kinetics following external radiation. This is in contrast to the theory that REs such as neodymium prevent the initial phase separation of molybdenum-rich regions by disrupting coordination in depolymerized regions of the glass.³⁰ However, melt crystallisation tendency has been observed to vary with both the type of alkaline earth and RE.^37,40 This observation thus outlines the effects of specie dependent trace incorporation of REs, which may or may not translate to actinides in nuclear waste glasses or GCs.

Crystallisation of CaMoO₄ was a clear process taking place in GCs, however results interestingly suggest that the residual matrix was also phase separated. This is based on the presence of two T_gs, which imply the formalization of two distinct structural states.⁵² Yet, glasses and the residual matrix of GCs were not characterised by distinct micro-phase separation and remained amorphous, according to SEM and XRD respectively. Furthermore, random Raman spot analysis at the surface gave almost identical spectra (see ESI†), as opposed to those with different proportions of silica and borate-type features indicating that any type of phase separation in these glasses occurred uniformly within the spot size.

It is therefore hypothesized that phase separation in CNO occurred through spinodal decomposition. This process results in strongly interconnected phases with a similar chemical composition that are separated by a diffuse interface, and are thus difficult to discern using SEM microscopy and EDS analysis.⁹⁶ This type of heterogeneity on the nano-scale can result in multiple glass transitions, as has been previously predicted.⁷⁸ Kobayashi et al. theorised that multiple transitions would occur through the emergence of very small variations in the intermediate-range order (IRO) resulting in a bimodal nano-structure periodically distributed throughout the amorphous network.⁹⁷

Moreover, these types of transitions have shown a dependency on composition and the relative cationic content, which determines structural mobility.^98,99 In silicates, the addition of alkali and alkaline earth oxides causes a decrease in T_g, through the formation of additional NBOs that increase thermal motion of the glass network with temperature. Whereas, low alkali or alkaline earth concentrations can increase T_g in borates through the creation of BO₄⁻ entities with a proportional dependence on the cationic size as this affects spatial hindrance.⁹⁹ Therefore, the population of bridging oxygen and the [BO₃]/[BO₄⁻] fraction, which was observed to vary with composition in this study are important factors in determining the IRO, and therefore the transition temperature.¹⁰⁰

Based on this existing knowledge a model is put forth to explain the type of nano-phase separation occurring in these compositions. It is predicted that the two interconnected phases in CNO are attributed to a variations in Si–O–Ca²⁺–O⁻–Si and Si–O–Ca²⁺–O⁻–B units. As the CaO content increases with MoO₃, the separation of borate groups from the silicate network increases, thus resulting in de-mixing of Si–O–Ca²⁺–O⁻–B units, as has been observed to occur in similar compositions.^51,76 This shift causes the relative changes to the enthalpies of T_g1 and T_g2 observed in Table 2.

The simultaneous inclusion of MoO₃ distributed between these two phases causes a secondary process of nucleation and growth evident on the sub-micron scale. It is predicted that the first step in this process requires the separation of a MoO₃–CaO–B₂O₃–NaO₂ rich phase associated with T_M or the liquidus temperature. Therefore, it is theorised that MoO₃ relies on the de-mixing of Si–O–Ca²⁺–O⁻–B units. It can further be deduced that decreasing the initial [SiO₂], while increasing [CaO] could promote mixing of these two IRO units and therefore reduce secondary Mo phase separation.

4.2 Crystallite modification

Radiation was observed to modify the crystal phase in a process of significant CS and lattice parameter expansion. It is hypothesized that this is occurring due to two reasons. The first is a temperature-based component, and the second is an accumulation of defects induced by atomic displacements.

Although Au-irradiation was primarily employed to replicate ballistic collisions, it does not omit electronic interactions, which EDS results indicate are occurring from the observed cationic depletion at the surface. As 7 MeV Au³⁺ ions travel through a material, energy from the ion can be transferred to the host lattice electrons via electron–electron and electron–phonon coupling. The thermal spike model translates these interactions into a small cylinder of energy characterised by a temperature of ∼1000 K.¹⁰¹ It was later theorised that electronic coupling at the site of a nuclear interaction could also create a melt halo around every collision.⁶⁰ Therefore, external radiation can theoretically induce temperature-like effects. In this study, changes to the powellite lattice parameters following irradiation are similar to those typically seen for heat treatments between 100–200 °C.^102,103 Furthermore, the isotropic nature in which expansion occurred supports a temperature-like effect.

Thermal expansion is predicted to contribute to the radiation-induced alteration of crystallites, yet changes to powellite lattice parameters cannot alone account for changes to CS in compositions with [MoO₃] ≥ 7 mol% (where ΔCS > 50 nm). Theoretically, additional crystallite growth could have been initiated by a high-temperature diffusion of ions, but this kinetic process has an activation barrier that is affected by the glass structure and requires time at temperature.¹⁰⁴ It is therefore predicted that the accumulation of damage is the driving force to additional structural changes.

As previously mentioned, internal radiation can cause structural modifications that result in changes to mechanical properties and to volume.^6,53–57 In a crystal structure, these modifications can present themselves as swelling through the displacement of atoms, which can create voids, mobile interstitials that can cluster, and other structural defects such as dislocations and interfacial cracking.^10,105,106 The accumulation of this type of damage from elastic collisions has experimentally been observed to increase T_f through a process of ballistic disorder and fast quenching.^65,107

Unit cell expansion and swelling has been previously observed to occur in powellite single crystals undergoing Ar-irradiation, though alteration occurred anisotropically.⁸⁵ In this case, expansion occurred through the formation of defect clusters that turned into dislocations as the dose increased to 1 dpa. In this study, increasing disorder was supported by shifts in Raman vibrational modes of (MoO₄)², which suggests defects in the stacking of Ca polyhedra along the c axis and the Mo tetrahedra along the a axis. It is therefore assumed that this type of transformation was occurring in irradiated GCs, as opposed to simply a thermal process resulting from electronic coupling, but that it is not the only process given the isotropic nature of modifications observed here.

The mechanism of CS alteration in this study thus combines elements of thermal expansion and defect accumulation leading to crystallite swelling. It can further be summarised that increasing [MoO₃], and therefore the fraction of CaMoO₄ within the borosilicate matrix, accelerated damage accumulation within the crystalline structure, and therefore CS expansion.

It can further be deduced from comparison of studies examining the irradiation of GCs with other ions that expansion of powellite CS and lattice parameters has only been found for damage emulating nuclear interactions. β-Irradiation was observed to result in a unit cell contraction with a non-linear CS trend with respect to dose.^69,70 Here the unit cell alteration was hypothesized to occur from thermal relaxation of the crystalline lattice following the energy inputted from irradiation, with changes to CS resulting from the accumulation of point defects. In contrast, irradiation with Xe²³⁺ ions,^92,93 which replicated the electronic component of α-decay, caused a reduction of CS concurrent to a dose dependent anisotropic unit cell expansion along the c-axis, which led to partial amorphisation.^92,93 Combined, these results suggest that the components of internal radiation will produce opposing forces on structural modifications within powellite crystallites, and that electronic interactions may reduce displacement induced swelling and unit cell expansion.

4.3 Ion impact on phase transformations

Following Au-irradiation results confirm a single crystalline phase of powellite (CaMoO₄). Had incorporation of Gd³⁺ ions into CaMoO₄ taken place, or if Na₂ or Na_0.5Gd_0.5 substitution of Ca²⁺ occurred this would have been reflected in XRD and Raman results. Refinement of the calcium site occupancy in CaMoO₄ would have revealed substitution, particularly for Gd³⁺, where the covalent sizes are substantially different, as has been previously determined.^37,90 Moreover, substitution of Gd³⁺ into the powellite structure would have converted the point group symmetry of the octahedrally coordinated Ca²⁺ end-member from S₄ to C₂, which would have altered spectroscopic emissions, in addition to XRD.¹⁰⁸ In this study, no such substitution was detected following refinement of XRD patterns, nor was such inclusion evident in Raman peak analysis.

In addition to a lack of detected Ca²⁺ substitution, SEM imaging reported the growth of particles, which coincided with CS expansion for all GCs. This occurred alongside isotropic lattice parameter expansion, most evident in compositions with [MoO₃] > 2.5 mol%. The collective results answers the first two questions posed in this paper in that radiation damage did not induce significant amorphisation, nor did it induce cationic substitution of CaMoO₄. If amorphisation were occurring, the opposite trend in PS and CS would have been produced, in addition to XRD whole pattern damping, and growth of the Raman band at ∼910 cm⁻¹ assigned to (MoO₄)²⁻ dissolved in the amorphous network. These changes have been seen for irradiation-induced amorphisation with higher energy ions,⁹³ though no amorphisation of CaMoO₄ has been previously reported for irradiation with medium-energy ions like 7 MeV Au³⁺.^85,109

The third question to be answered was whether irradiation damage would induce precipitation. Increases in the range of PS, together with a decrease in the particle density at the surface suggest a rearrangement of crystallites as opposed to additional precipitation. This result is supported by cationic depletion at the surface, whereas CaMoO₄ formation would have required Ca²⁺ ions to be in excess within the molybdenum environment.

In terms of the amorphous phase very little changes were observed in terms of short to medium-range order. In glasses, the residual matrix showed a minor reformation of ring structures away from danburite-like units and the molybdenum environment showed increasing disorder, which is predicted to discourage crystallisation. Unfortunately, no information could be gained on how microheterogeneities of the matrix changed following irradiation and if this could have played a role in the observed modifications to the powellite phase.

5. Conclusions

This paper focused on the fundamental processes occurring in glasses and GCs containing MoO₃ as a method to investigate matrices that can increase the incorporation of the fission product molybdenum. Several glasses and GCs were synthesised with up to 10 mol% MoO₃ within a soda lime borosilicate matrix. Two types of phase separation were observed in these systems. The residual glassy matrix is predicted to be phase separated on the nano-scale through a mechanism of spinodal decomposition resulting in small variations in the amount of Si–O–Ca²⁺–O⁻–Si relative to Si–O–Ca²⁺–O⁻–B units, with increases in [CaO] causing the de-mixing of these two types of IRO units. Above 1 mol% MoO₃, a secondary process of nucleation and growth of CaMoO₄ crystals occurred, which pulled Ca and Mo ions out of the residual matrix and toward crystal centres, according to EDS analysis. This process did not significantly alter the presence of heterogeneities in the glass matrix according to thermal analysis, nor the coordination of boron according to ¹¹B MAS NMR.

These materials were then subjected to a dose of 3 × 10¹⁴ ions per cm² using 7 MeV Au³⁺ ions to replicate the damage caused by internal α-decay and thus determine radiation tolerance. This created 1 dpa of damage for a depth of ∼1.5 μm, according to TRIM calculations. Using this experiment we could test the theory of whether irradiation would: (1) cause amorphisation of CaMoO₄, (2) change the crystal structure or induce cationic substitution of CaMoO₄, or (3) induce precipitation of alternative phases. Results imply that amorphisation or precipitation did not occur based on changes to the size and density of crystalline particles. Furthermore, Na₂/NaGd–MoO₄ assemblages were likewise found not to form through direct crystallisation or substitution, as both would have introduced new XRD and Raman peaks, which were not detected. Au-irradiation was however found to cause expansion of both the unit cell and CS of CaMoO₄. The mechanism in which this occurs is based on two processes. The first is a thermal expansion resulting from heat generated by electronic interactions. The second is swelling from the creation of defect clusters, such as voids resulting from the accumulation of atomic displacements following ballistic collisions. The collective results suggest that while modification to the crystalline phase of interest may be occurring, they do not alter the nature of this phase, therefore proving that these GCs are tolerant to radiation damage.

Conflicts of interest

The authors declare that are no conflicts of interest.

Acknowledgements

The authors would like to thank Cyril Bachelet at CSNSM for assistance with the irradiation experiment. They would also like to acknowledge the help of several members in the Department of Earth Sciences (Sébastien Facq, Robin Clarke, Chris Parish, and Iris Buisman) and those from the Department of Material Science and Metallurgy (Lata Sahonta, Rachel Olivier) that aided in access to facilities and sample preparation, as well as training on analytical equipment. This work was funded by the University of Cambridge, Department of Earth Sciences and EPSRC (Grant No. EP/K007882/1) for an IDS. Additional financial support provided by FfWG and the Cambridge Philosophical Society.

References

1. R. C. Ewing, W. J. Weber and F. W. Clinard, Radiation effects in nuclear waste forms for high-level radioactive waste, Prog. Nucl. Energy, 1995, 29, 63–127.
2. W. J. Weber, R. C. Ewing, C. R. A. Catlow, T. D. de la Rubia, L. W. Hobbs, C. Kinoshita, H. Matzke, A. T. Motta, M. Nastasi, E. K. H. Salje, E. R. Vance and S. J. Zinkle, Radiation effects in crystalline ceramics for the immobilization of high-level nuclear waste and plutonium, J. Mater. Res., 1998, 13, 1434–1484.
3. K. Brinkman, K. Fox, J. Marra, J. Reppert, J. Crum and M. Tang, Single phase melt processed powellite (Ba,Ca)MoO4 for the immobilization of Mo-rich nuclear waste, J. Alloys Compd., 2013, 551, 136–142.
4. S. Chu and A. Majumdar, Opportunities and challenges for a sustainable energy future, Nature, 2012, 488, 294–303.
5. W. J. Weber, R. C. Ewing, C. A. Angell, G. W. Arnold, J. M. Delaye, L. W. Hobbs and D. L. Price, Radiation effects in glasses used for immobilization of high-level waste and plutonium disposition, J. Mater. Res., 1997, 12, 1946–1978.
6. S. Peuget, J. M. Delaye and C. Jégou, Specific outcomes of the research on the radiation stability of the French nuclear glass towards alpha decay accumulation, J. Nucl. Mater., 2014, 444, 76–91.
7. E. R. Vance, J. Davis, K. Olufson, D. J. Gregg, M. G. Blackford, G. R. Griffiths, I. Farnan, J. Sullivan, D. Sprouster, C. Campbell and J. Hughes, Leaching behaviour of and Cs disposition in a UMo powellite glass-ceramic, J. Nucl. Mater., 2014, 448, 325–329.
8. T. Taurines and B. Boizot, Microstructure of powellite-rich glass-ceramics: A model system for high level waste immobilization, J. Am. Ceram. Soc., 2012, 95, 1105–1111.
9. S. Gin, C. Guittonneau, N. Godon, D. Neff, D. Rebiscoul, M. Cabí and S. Mostefaoui, Nuclear glass durability: New insight into alteration layer properties, J. Phys. Chem. C, 2011, 115, 18696–18706.
10. W. E. Lee, M. I. Ojovan, M. C. Stennett and N. C. Hyatt, Immobilisation of radioactive waste in glasses, glass composite materials and ceramics, Adv. Appl. Ceram., 2006, 105, 3–12.
11. S. Peuget, M. Tribet, S. Mougnaud, S. Miro and C. Jégou, Radiations effects in ISG glass: from structural changes to long-term aqueous behavior, npj Mater. Degrad., 2018, 2, 23.
12. P. Lv, L. Chen, B. T. Zhang, W. Yuan, B. H. Duan, Y. D. Guan, Y. Zhao, X. Y. Zhang, L. M. Zhang and T. S. Wang, Composition-dependent mechanical property changes in Au-ion- irradiatd borosilicate glasses, J. Nucl. Mater., 2019, 520, 218–225.
13. Y. Inagaki, H. Furuya and K. Idemitsu, Microstructure of simulated high-level waste glass doped with short-lived actinides, ²³⁸Pu and ²⁴⁴Cm, Mater. Res. Soc. Symp. Proc., 1992, 257, 199–206.
14. P. B. Rose, D. I. Woodward, M. I. Ojovan, N. C. Hyatt and W. E. Lee, Crystallisation of a simulated borosilicate high-level waste glass produced on a full-scale vitrification line, J. Non-Cryst. Solids, 2011, 357, 2989–3001.
15. S. Peuget, J.-N. Cachia, C. Jégou, X. Deschanels, D. Roudil, V. Broudic, J. M. Delaye and J.-M. Bart, Irradiation stability of R7T7-type borosilicate glass, J. Nucl. Mater., 2006, 354, 1–13.
16. P. Frugier, C. Martin, I. Ribet, T. Advocat and S. Gin, The effect of composition on the leaching of three nuclear waste glasses: R7T7, AVM and VRZ, J. Nucl. Mater., 2005, 346, 194–207.
17. J. V. Crum, B. J. Riley, L. R. Turo, M. Tang and A. Kossoy, Summary Report: Glass-Ceramic Waste Forms for Combined Fission Products, Richland, 2011.
18. B. F. Dunnett, N. R. Gribble, R. Short, E. Turner, C. J. Steele and A. D. Riley, Vitrification of high molybdenum waste, Glass Technol.: Eur. J. Glass Sci. Technol., Part A, 2012, 53, 166–171.
19. F. Gauthier-Lafaye, P. Holliger and P.-L. Blanc, Natural fission reactors in the Franceville basin, Gabon: A review of the conditions and results of a ‘critical event’ in a geologic system, Geochim. Cosmochim. Acta, 1996, 60, 4831–4852.
20. P. Loiseau, D. Caurant, N. Baffier, L. Mazerolles and C. Fillet, Glass – ceramic nuclear waste forms obtained from lanthanides (Ce, Nd, Eu, Gd, Yb) and actinides (Th): study of internal crystallisation, J. Nucl. Mater., 2004, 335, 14–32.
21. E. R. Vance, J. Davis, K. Olufson, I. Chironi, I. Karatchevtseva and I. Farnan, Candidate waste forms for immobilisation of waste chloride salt from pyroprocessing of spent nuclear fuel, J. Nucl. Mater., 2012, 420, 396–404.
22. J. Lian, L. M. Wang, R. C. Ewing, S. V. Yudintsev and S. V. Stefanovsky, Thermally induced phase decomposition and nanocrystal formation in murataite ceramics, J. Mater. Chem., 2004, 15, 709–714.
23. B. Camara, W. Lutze and J. Lux, in Advances in Nuclear Science & Technology: Scientific Basis for Nuclear Waste Management, ed. C. J. M. Northrup, Springer, Boston, MA, 1979, pp. 93–102.
24. I. W. Donald, B. L. Metcalfe, S. K. Fong, L. A. Gerrard, D. M. Strachan and R. D. Scheele, A glass-encapsulated calcium phosphate wasteform for the immobilization of actinide-, fluoride-, and chloride-containing radioactive wastes from the pyrochemical reprocessing of plutonium metal, J. Nucl. Mater., 2007, 361, 78–93.
25. W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 94th edn, 2013.
26. B. J. Greer and S. Kroeker, Characterisation of heterogeneous molybdate and chromate phase assemblages in model nuclear waste glasses by multinuclear magnetic resonance spectroscopy, Phys. Chem. Chem. Phys., 2012, 14, 7375–7383.
27. R. J. Short, R. J. Hand, N. C. Hyatt and G. Möbus, Environment and oxidation state of molybdenum in simulated high level nuclear waste glass compositions, J. Nucl. Mater., 2005, 340, 179–186.
28. A. Horneber, B. Camara and W. Lutze, Investigation on the Oxidation State and The Behaviour of Molybdenum in Silicate Glass, MRS Proc. Sci. Basis Nucl. Waste Manag. V, 1982, 11, 279–288.
29. D. Caurant, O. Majérus, E. Fadel, M. Lenoir, C. Gervais and O. Pinet, Effect of molybdenum on the structure and on the crystallisation of SiO₂-Na₂O-CaO-B₂O₃ glasses, J. Am. Ceram. Soc., 2007, 90, 774–783.
30. N. Chouard, D. Caurant, O. Majérus, J. L. Dussossoy, S. Klimin, D. Pytalev, R. Baddour-Hadjean and J. P. Pereira-Ramos, Effect of MoO₃, Nd₂O₃, and RuO₂ on the crystallisation of soda–lime aluminoborosilicate glasses, J. Mater. Sci., 2015, 50, 219–241.
31. G. N. Greaves and K. L. Ngai, Reconciling ionic-transport properties with atomic structure in oxide glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 6358–6380.
32. D. Caurant, O. Majérus, E. Fadel, A. Quintas, C. Gervais, T. Charpentier and D. Neuville, Structural investigations of borosilicate glasses containing MoO₃ by MAS NMR and Raman spectroscopies, J. Nucl. Mater., 2010, 396, 94–101.
33. C. Martineau, V. K. Michaelis, S. Schuller and S. Kroeker, Liquid-liquid phase separation in model nuclear waste glasses: A solid-state double-resonance NMR study, Chem. Mater., 2010, 22, 4896–4903.
34. M. Magnin, S. Schuller, C. Mercier, J. Trébosc, D. Caurant, O. Majérus, F. Angéli and T. Charpentier, Modification of molybdenum structural environment in borosilicate glasses with increasing content of boron and calcium oxide by ⁹⁵Mo MAS NMR, J. Am. Ceram. Soc., 2011, 94, 4274–4282.
35. Y. Kawamoto, K. Clemens and M. Tomozawa, Effects of MoO₃ on phase separation of Na₂0-B₂0₃-Si0₂ glasses, J. Am. Ceram. Soc., 1981, 64, 292–296.
36. S. Gossé, C. Guéneau, S. Bordier, S. Schuller, A. Laplace and J. Rogez, 2nd International Summer School on Nuclear Glass Wasteform: Structure, Properties and Long-Term Behavior, SumGLASS 2013, Elsevier B.V., 2014, vol. 7, pp. 79–86.
37. N. Henry, P. Deniard, S. Jobic, R. Brec, C. Fillet, F. Bart, A. Grandjean and O. Pinet, Heat treatments versus microstructure in a molybdenum-rich borosilicate, J. Non-Cryst. Solids, 2004, 333, 199–205.
38. S. Schuller, O. Pinet, A. Grandjean and T. Blisson, Phase separation and crystallisation of borosilicate glass enriched in MoO₃, P₂O₅, ZrO₂, CaO, J. Non-Cryst. Solids, 2008, 354, 296–300.
39. K. Ishiguro, N. Kawanishi, H. Nagaki and A. Naito, Chemical states of molybdenum in radioactive waste glass (PNCT-N–831-82-01), Tokyo, Japan, 1982.
40. A. Quintas, D. Caurant, O. Majérus, T. Charpentier and J. L. Dussossoy, Effect of compositional variations on charge compensation of AlO₄ and BO₄ entities and on crystallisation tendency of a rare-earth-rich aluminoborosilicate glass, Mater. Res. Bull., 2009, 44, 1895–1898.
41. F. Angeli, O. Villain, S. Schuller, S. Ispas and T. Charpentier, Insight into sodium silicate glass structural organization by multinuclear NMR combined with first-principles calculations, Geochim. Cosmochim. Acta, 2011, 75, 2453–2469.
42. G. Calas, M. Le Grand, L. Galoisy and D. Ghaleb, Structural role of molybdenum in nuclear glasses: an EXAFS study, J. Nucl. Mater., 2003, 322, 15–20.
43. G. W. Morey and E. Ingerson, The melting of danburite: a study of liquid immiscibility in the system, CaO-B₂O₃-SiO₂, Am. Mineral., 1937, 22, 37–47.
44. W. Vogel, Glass Chemistry, Springer-Verlag, Berlin Heidelberg, 2nd edn, 1994.
45. O. Mazurin and E. A. Porai-Koshits, Phase Separation in Glass, Volume 5, Elsevier, North Holland, 1st edn, 1984.
46. H. Liu, R. E. Youngman, S. Kapoor, L. R. Jensen, M. M. Smedskjaer and Y. Yue, Nano-phase separation and structural ordering in silica-rich mixed network former glasses, Phys. Chem. Chem. Phys., 2018, 20, 15707–15717.
47. P. Hudon and D. R. Baker, The nature of phase separation in binary oxide melts and glasses. I. Silicate systems, J. Non-Cryst. Solids, 2002, 303, 299–345.
48. T. Yazawa, K. Kuraoka, T. Akai, N. Umesaki and W. Du, Clarification of Phase Separation Mechanism of Sodium Borosilicate Glasses in Early Stage by Nuclear Magnetic Resonance, J. Phys. Chem. B, 2000, 104, 2109–2116.
49. E. P. Favvas and A. C. Mitropoulos, What is Spinodal Decomposition?, J. Eng. Sci. Technol. Rev., 2008, 25–27.
50. N. Okui, Relationship between crystallisation temperature and melting temperature in crystalline materials, J. Mater. Sci., 1990, 25, 1623–1631.
51. L. Martel, M. Allix, F. Millot, V. Sarou-Kanian, E. Véron, S. Ory, D. Massiot and M. Deschamps, Controlling the size of nanodomains in calcium aluminosilicate glasses, J. Phys. Chem. C, 2011, 115, 18935–18945.
52. J. Kieffer, Structural Transitions and Glass Formation, J. Phys. Chem. B, 1999, 103, 4153–4158.
53. J.-M. Delaye, S. Peuget, G. Bureau and G. Calas, Molecular dynamics simulation of radiation damage in glasses, J. Non-Cryst. Solids, 2011, 357, 2763–2768.
54. R. A. B. Devine, Macroscopic and microscopic effects of radiation in amorphous SiO₂, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 91, 378–390.
55. W. Yuan, H. Peng, M. Sun, X. Du, P. Lv, Y. Zhao, F. Liu, B. Zhang, L. Chen, T. Wang, W. Yuan, H. Peng, M. Sun, X. Du, P. Lv, Y. Zhao and F. Liu, Structural origin of hardness decrease in irradiated sodium borosilicate glass Structural origin of hardness decrease in irradiated sodium borosilicate glass, J. Chem. Phys., 2017, 147, 7.
56. O. Gedeon, J. Lukeš and K. Jurek, Reduced Young modulus and hardness of electron irradiated binary potassium-silicate glass, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 275, 7–10.
57. H. B. Peng, M. L. Sun, K. J. Yang, H. Chen, D. Yang, W. Yuan, L. Chen, B. H. Duan and T. S. Wang, Effect of irradiation on hardness of borosilicate glass, J. Non-Cryst. Solids, 2016, 443, 143–147.
58. B. Boizot, G. Petite, D. Ghaleb and G. Calas, Radiation induced paramagnetic centres in nuclear glasses by EPR spectroscopy, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141, 580–584.
59. T. S. Wang, X. Du, W. Yuan, B. H. Duan, J. D. Zhang, L. Chen, H. B. Peng, D. Yang, G. F. Zhang and Z. H. Zhu, Morphological study of borosilicate glass surface irradiated by heavy ions, Surf. Coat. Technol., 2016, 306, 245–250.
60. G. García, A. Rivera, M. L. Crespillo, N. Gordillo, J. Olivares and F. Agulló-López, Amorphization kinetics under swift heavy ion irradiation: A cumulative overlapping-track approach, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 492–497.
61. J. F. DeNatale, D. K. McElfresh and D. G. Howitt, Radiation Effects in Nuclear Waste Glasses, MRS Proc., 1982, 6, 697–702.
62. T. Charpentier, L. Martel, A. H. Mir, J. Somers, C. Jégou and S. Peuget, Self-healing capacity of nuclear glass observed by NMR spectroscopy, Sci. Rep., 2016, 6, 25499.
63. A. H. Mir, B. Boizot, T. Charpentier, M. Gennisson, M. Odorico, R. Podor, C. Jégou, S. Bouffard and S. Peuget, Surface and bulk electron irradiation effects in simple and complex glasses, J. Non-Cryst. Solids, 2016, 453, 141–149.
64. J. de Bonfils, S. Peuget, G. Panczer, D. de Ligny, S. Henry, P.-Y. Noël, A. Chenet and B. Champagnon, Effect of chemical composition on borosilicate glass behavior under irradiation, J. Non-Cryst. Solids, 2010, 356, 388–393.
65. E. A. Maugeri, S. Peuget, D. Staicu, A. Zappia, C. Jegou and T. Wiss, Calorimetric study of glass structure modification induced by α decay, J. Am. Ceram. Soc., 2012, 95, 2869–2875.
66. J. F. Ziegler, M. D. Ziegler and J. P. Biersack, SRIM - The stopping and range of ions in matter (2010), Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823.
67. Y. Zhang, I. T. Bae, K. Sun, C. Wang, M. Ishimaru, Z. Zhu, W. Jiang and W. J. Weber, Damage profile and ion distribution of slow heavy ions in compounds, J. Appl. Phys., 2009, 105, 12.
68. R. W. Cheary, A. a. Coelho and J. P. Cline, Fundamental parameters line profile fitting in laboratory diffractometers, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 1–25.
69. K. B. Patel, B. Boizot, S. P. Facq, S. Peuget, S. Schuller and I. Farnan, Impacts of composition and beta irradiation on phase separation in multiphase amorphous calcium borosilicates, J. Non-Cryst. Solids, 2017, 473, 1–16.
70. K. B. Patel, B. Boizot, S. P. Facq, G. I. Lampronti, S. Peuget, S. Schuller and I. Farnan, β-Irradiation Effects on the Formation and Stability of CaMoO₄ in a Soda Lime Borosilicate Glass Ceramic for Nuclear Waste Storage, Inorg. Chem., 2017, 56, 1558–1573.
71. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9, 671–675.
72. Y. Hattori, T. Wakasugi, H. Shiomi, J. Nishii and K. Kadono, Li+ for Na+ ion-exchange-induced phase separation in borosilicate glass, J. Mater. Res., 2012, 27, 999–1005.
73. N. Chouard, D. Caurant, O. Majérus, N. Guezi-Hasni, J. L. Dussossoy, R. Baddour-Hadjean and J. P. Pereira-Ramos, Thermal stability of SiO2-B2O3-Al2O3-Na2O-CaO glasses with high Nd2O3 and MoO3 concentrations, J. Alloys Compd., 2016, 671, 84–99.
74. H. Liu, M. M. Smedskjaer, H. Tao, L. R. Jensen, X. Zhao and Y. Yue, A medium range order structural connection to the configurational heat capacity of borate-silicate mixed glasses, Phys. Chem. Chem. Phys., 2016, 18, 10887–10895.
75. M. M. Smedskjaer, J. C. Mauro, R. E. Youngman, C. L. Hogue, M. Potuzak and Y. Yue, Topological Principles of Borosilicate Glass Chemistry, J. Phys. Chem. B, 2011, 115, 12930–12946.
76. H. Miyoshi, D. Chen, H. Masui, T. Yazawa and T. Akai, Effect of calcium additive on structural changes under heat treatment in sodium borosilicate glasses, J. Non-Cryst. Solids, 2004, 345–346, 99–103.
77. M. H. Manghnani, A. Hushur, T. Sekine, J. Wu, J. F. Stebbins and Q. Williams, Raman, Brillouin, and nuclear magnetic resonance spectroscopic studies on shocked borosilicate glass, J. Appl. Phys., 2011, 109, 113509.
78. L. S. Du and J. F. Stebbins, Solid-state NMR study of metastable immiscibility in alkali borosilicate glasses, J. Non-Cryst. Solids, 2003, 315, 239–255.
79. R. L. Frost, J. Bouzaid and I. S. Butler, Raman spectroscopic study of the molybdate mineral szenicsite and com- pared with other paragenetically related molybdate minerals, Spectrosc. Lett., 2007, 40, 603–614.
80. S. P. S. Porto and J. F. Scott, Raman spectra of CaWO₄, SrWO₄, CaMoO₄, and SrMoO₄, Phys. Rev., 1967, 157, 716–719.
81. M. Crane, R. L. Frost, P. A. Williams and J. T. Kloprogge, Raman spectroscopy of the molybdate minerals chillagite (tungsteinian wulfenite-I4), stolzite, scheelite, wolframite and wulfenite, J. Raman Spectrosc., 2002, 33, 62–66.
82. F. D. Hardcastle and I. E. Wachs, Determination of molybdenum-oxygen bond distances and bond orders by Raman spectroscopy, J. Raman Spectrosc., 1990, 21, 683–691.
83. D. Errandonea and F. J. Manjon, Pressure effects on the structural and electronic properties of ABX4 scintillating crystals, Prog. Mater. Sci., 2008, 53, 711–773.
84. E. Sarantopoulou, C. Raptis, S. Ves, D. Christofilos and G. A. Kourouklis, Temperature and pressure dependence of Raman-active phonons of CaMoO4: an anharmonicity study, J. Phys.: Condens. Matter, 2002, 14, 8925–8938.
85. X. Wang, G. Panczer, D. de Ligny, V. Motto-Ros, J. Yu, J. L. Dussossoy, S. Peuget, I. Jóźwik-Biala, N. Bérerd and J. Jagielski, Irradiated rare-earth-doped powellite single crystal probed by confocal Raman mapping and transmission electron microscopy, J. Raman Spectrosc., 2014, 45, 383–391.
86. T. Furukawa and W. B. White, Raman spectroscopic investigation of sodium borosilicate glass structure, J. Mater. Sci., 1981, 16, 2689–2700.
87. D. R. Neuville, L. Cormier, B. Boizot and A. M. Flank, Structure of β-irradiated glasses studied by X-ray absorption and Raman spectroscopies, J. Non-Cryst. Solids, 2003, 323, 207–213.
88. G. E. Walrafen, S. R. Samanta and P. N. Krishnan, Raman investigation of vitreous and molten boric oxide, J. Chem. Phys., 1980, 72, 113–120.
89. D. Manara, A. Grandjean and D. R. Neuville, Advances in understanding the structure of borosilicate glasses: A Raman spectroscopy study, Am. Mineral., 2009, 94, 777–784.
90. T. Taurines, D. Neff and B. Boizot, Powellite-rich glass-ceramics: A spectroscopic study by EPR and Raman spectroscopy, J. Am. Ceram. Soc., 2013, 96, 3001–3007.
91. B. Boizot, G. Petite, D. Ghaleb, N. Pellerin, F. Fayon, B. Reynard and G. Calas, Migration and segregation of sodium under β-irradiation in nuclear glasses, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 166–167, 500–504.
92. K. B. Patel, S. Peuget and S. Schuller, Swift heavy ion-irradiated multi-phase calcium borosilicates: implications to molybdenum incorporation, microstructure, and network topology, J. Mater. Sci., 2019, 54, 11763–11783.
93. K. B. Patel, S. Peuget, S. Schuller, G. I. Lampronti, S. P. Facq, C. Grygiel, I. Monnet and I. Farnan, Discovery of a maximum damage structure for Xe-irradiated borosilicate glass ceramics containing powellite, J. Nucl. Mater., 2018, 510, 229–242.
94. C. Cousi, F. Bart, E. De Base, C. E. A. Valrhô, M. D. E. N. Dtcd, B. Cedex, L. Verres and U. De Montpellier, Proc. VII Symp. on Crystallisation in Glasses and Liquids, Sheffield, 6–9 July 2003, 2004, vol. 45, pp. 65–67.
95. R. M. Hazen, L. W. Finger and J. W. E. Mariathasan, High-pressure crystal chemistry of scheelite-type tungstates and molybdates, J. Phys. Chem. Solids, 1985, 46, 253–263.
96. S. Schuller, in From glass to crystal, ed. D. R. Neuville, L. Cornier, D. Caurant and L. Montagne, EDP Sciences, 2017, pp. 125–150.
97. H. Kobayashi and H. Takahashi, Roles of intermediate-range orders on the glass transition process: Fictive temperature, residual entropy, relaxation time and boson peak, J. Non-Cryst. Solids, 2015, 427, 34–40.
98. C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, Relaxation in glassforming liquids and amorphous solids, J. Appl. Phys., 2000, 88, 3113–3157.
99. I. Avramov, T. Vassilev and I. Penkov, The glass transition temperature of silicate and borate glasses, J. Non-Cryst. Solids, 2005, 351, 472–476.
100. S. Takahashi, D. R. Neuville and H. Takebe, Thermal properties, density and structure of percalcic and peraluminus CaO-Al₂O₃-SiO₂ glasses, J. Non-Cryst. Solids, 2015, 411, 5–12.
101. M. Toulemonde, E. Paumier and C. Dufour, Thermal spike model in the electronic stopping power regime, Radiat. Eff. Defects Solids, 1993, 126, 201–206.
102. S. N. Achary, S. J. Patwe, M. D. Mathews and A. K. Tyagi, High temperature crystal chemistry and thermal expansion of synthetic powellite (CaMoO4): A high temperature X-ray diffraction (HT-XRD) study, J. Phys. Chem. Solids, 2006, 67, 774–781.
103. A. Abdel-Rehim, Thermal Analysis and X-ray Diffraction of Synthesis of Scheelite, J. Therm. Anal. Calorim., 2004, 64, 557–569.
104. X. Orlhac, C. Fillet and J. Phalippou, Mat. Res. Soc. Symp. Proc., 1999, vol. 556, pp. 263–270.
105. K. E. Sickafus, R. W. Grimes, J. A. Valdez, A. Cleave, M. Tang, M. Ishimaru, S. M. Corish, C. R. Stanek and B. P. Uberuaga, Radiation-induced amorphization resistance and radiation tolerance in structurally related oxides, Nat. Mater., 2007, 6, 217–223.
106. W. J. Weber, R. C. Ewing and L. M. Wang, The radiation-induced crystalline-to-amorphous transition in zircon, J. Mater. Res., 1994, 9, 688–698.
107. D. L. Griscom and W. J. Weber, Electron spin resonance study of Fe³⁺ and Mn²⁺ ions in 17-year-old nuclear-waste-glass simulants containing PuO2 with different degrees of ²³⁸Pu substitution, J. Non-Cryst. Solids, 2011, 357, 1437–1451.
108. M. Schmidt, S. Heck, D. Bosbach, S. Ganschow, C. Walther and T. Stumpf, Characterization of powellite-based solid solutions by site-selective time resolved laser fluorescence spectroscopy, Dalton Trans., 2013, 42, 8387.
109. M. Tang, A. Kossoy, G. Jarvinen, J. Crum, L. Turo, B. Riley, K. Brinkman, K. Fox, J. Amoroso and J. Marra, Radiation stability test on multiphase glass ceramic and crystalline ceramic waste forms, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 326, 293–297.

---

Footnote

† Electronic supplementary information (ESI) available: TRIM calculations, an example SDT spectrum, SEM micrographs of CNO and CNG1, raw XRD patterns, and a Raman spectra with overlapping measurements taken for a single composition. See DOI: 10.1039/d0cp02447c

---