Exploring cycling induced crystallographic change in NMC with X-ray diffraction computed tomography

Abstract

This study presents the application of X-ray diffraction computed tomography for the first time to analyze the crystal dimensions of LiNi_0.33Mn_0.33Co_0.33O₂ electrodes cycled to 4.2 and 4.7 V in full cells with graphite as negative electrodes at 1 μm spatial resolution to determine the change in unit cell dimensions as a result of electrochemical cycling. The nature of the technique permits the spatial localization of the diffraction information in 3D and mapping of heterogeneities from the electrode to the particle level. An overall decrease of 0.4% and 0.6% was observed for the unit cell volume after 100 cycles for the electrodes cycled to 4.2 and 4.7 V. Additionally, focused ion beam-scanning electron microscope cross-sections indicate extensive particle cracking as a function of upper cut-off voltage, further confirming that severe cycling stresses exacerbate degradation. Finally, the technique facilitates the detection of parts of the electrode that have inhomogeneous lattice parameters that deviate from the bulk of the sample, further highlighting the effectiveness of the technique as a diagnostic tool, bridging the gap between crystal structure and electrochemical performance.

---

Introduction

Environmental considerations and a further electrification of the global automotive fleet and energy grid systems are driving the need for robust electrochemical energy storage devices.^1,2 While lithium-ion (Li-ion) batteries have emerged over the last few decades as the prime choice for powering portable consumer electronics, they are also being employed for a wider range of applications due to their high energy densities and specific capacities. Since its discovery, lithium cobalt oxide (LCO) has been one of the most commonly used materials in Li-ion electrochemical storage devices and has been employed in numerous applications.³ High cobalt costs and its inherent toxicity have driven the exploration of other chemistries with reduced Co content, such as lithium nickel manganese cobalt oxide (NMC), where the slightly lower capacity is compensated by excellent power and low self-heating during cycling.⁴ However, to meet the demands of modern applications, improvements are required to increase the cycle life, capacity and safety of these materials.

Intercalation battery cathodes are formed by transition metal oxide solid matrices from which Li-ions travel from and intercalate into a carbonaceous anode during charging (and vice versa during discharge).⁵ Repeated intercalation of Li-ions during electrochemical cycling can lead to internal stresses within particles of active material due to cyclical expansion and shrinking. Furthermore, Li-ion concentration gradients within individual particles, caused by uneven active lithium loss during extended cycling can contribute to these internal stresses, which ultimately may result in particle cracking.⁶ An approach to increase the capacity per cycle with intercalation electrode materials consists in forcing a larger number of Li-ions to participate in the electrochemical process by cycling to a higher upper cut-off voltage, which corresponds to a greater fraction of Li removal from the transition metal oxide crystal structure at higher voltages. This not only accentuates the aforementioned phenomena, but is also likely to affect the stability of the electrolyte over extended cycling.⁷ Moreover, cycling at high voltages can cause the release of oxygen from the cathode lattice, which then reacts with the electrolyte, and transition metal dissolution, which can subsequently deposit onto the anode increasing its resistivity and reducing the utilizable capacity.^8,9 A previous study, by Mao et al., uses a combination of X-ray spectroscopic and crystallographic techniques to highlight how different regions with increased oxidation or reduction states are present within a particle as a function of the upper cycling voltage.¹⁰

X-ray-based characterisation techniques have emerged over the last few decades as excellent tools for electrode analysis.¹¹ Their non-destructive nature allows studying of phenomena of interest across different length and time-scales and obtaining both chemical and microstructural information that can be used to further the fundamental understanding of these materials during operation, and ultimately improve their performance. Techniques such as transmission X-ray microscopy,^12–14 X-ray absorption near edge spectroscopy (XANES),^15–17 X-ray computed tomography (X-ray CT)^18–20 and X-ray diffraction (XRD)^21–23 have all been extensively used to study battery materials.²⁴ Of particular interest for this study are X-ray CT and XRD: X-ray CT relies on resolving the attenuation of X-ray photons caused by interacting with the sample.²⁵ While this technique provides qualitative and quantitative microstructural information, it is typically unable to provide information regarding the chemical or crystal state of the sample. XRD is one of the most commonly used techniques in the field of material characterisation; it operates by resolving the scattering of the incoming X-ray photons by the periodic structure of a crystalline sample.²⁶ While detailed information regarding crystal structure and different phases present in the sample can be obtained with XRD, the technique does not typically provide any spatial information. There are numerous studies in which these techniques are used both to understand the fundamental principles of electrode materials, and to characterize, quantify and model how different factors such as manufacturing and cycling regimes impact the morphology and crystal structure.^27–35

X-ray diffraction computed tomography (XRD-CT) can be described as the combination of these techniques: in XRD-CT, multidimensional measurements are taken where several spatial dimensions are combined with one containing diffraction information.^36–38 The resulting dataset provides a 3-dimensional (3D) map where each pixel/voxel contains a distinct diffraction pattern.³⁹ By analysing the diffraction patterns, localized information regarding the crystallographic properties of the sample can be calculated. Over the last decade, the potential of XRD-CT as a characterization tool has been realized, especially for functional materials, such as heterogeneous catalysts and fuel cells.^40–44 The technique has also been used to characterize different aspects of battery materials.^45–50 Jensen et al. have used the technique to single out individual elements of a commercial Li-ion coin cell and nickel metal hydride AAA battery.⁴⁵Via ex situ XRD-CT, the internal structure of both types of batteries and the individual components within them were isolated. Furthermore, the heterogeneous crystal structure of the LCO cathode was visualized. A more recent study, by Finegan et al., uses the technique to analyse silicon and graphite particles in a composite anode where a 1 μm pencil beam was used to observe the electrochemical interaction between the silicon and graphite after the lithiation of the electrode. This was the first implementation of region-of-interest (ROI) XRD-CT.⁴⁶ Finegan et al. also studied crystallographic heterogeneities in Li_xMn₂O₄ (LMO) electrode using in situ and ex situ XRD-CT to identify the stoichiometric differences within and between different particles. Through this study it was possible to spatially localize different phases and interlink their transitions to the electrochemical cycling of the cell.⁴⁷

Here we present the first report, to the authors’ knowledge, of the application of XRD-CT to analyse the evolution of the NMC crystal structure as a result of electrochemical cycling. In this work, electrodes were cycled up to 100 cycles in full-cells with upper cut-off voltages of 4.2 and 4.7 V. These results provide new insights into NMC materials, and demonstrate the potential of XRD-CT as a complementary tool to more traditional X-ray CT, where both can be used synergistically to quantify and analyse the electrode morphology and the underlying crystallographic structure. The stoichiometry and crystallographic structure of Li-ion electrodes has a deterministic effect on the long-term performance of these materials. Hence, the potential of this technique to reconcile morphology and crystallography provides compelling opportunities to understand the complex processes associated with the performance and degradation of battery materials.

Materials and methods

Electrode and coin cell preparation

The NMC electrode was prepared to a formula containing 90% active material (NMC111, Targray), with 5% conductive carbon (Timcal Super C65, Imerys, Switzerland) and 5% polyvinylidene fluoride (PVDF). The slurry was processed using N-methyl-2-pyrrolidone (NMP) as a solvent with a dual asymmetric centrifuge system (SpeedMixer DAC 150.1 FVZ-K, Hauschild, Germany) and cast onto an aluminum sheet with a doctor blade with a 150 μm blade gap for a target active mass loading of 10 mg cm⁻². Pre-prepared graphite electrodes (Warwick Manufacturing Group) with 95% active material and an active mass loading of 9.5 mg cm⁻² were used as counter electrodes. As the theoretical capacity of graphite is approximately double that of NMC, for similar loading, the anode capacity is sufficient to avoid Li plating on the surface of the anode during charge, even for the electrodes cycled to 4.7 V.

For coin cells, the cathode and anode discs were cut to 10 and 11 mm respectively to ensure that the anode disk fully covered the cathode. These were then dried under dynamic vacuum in an oven at 120 °C and transferred into the argon filled glovebox for cell assembly without exposure to air. The coin cells were assembled using polymer separator (2400, Celgard) and 150 μl 1.2 M LiPF₆ in ethylene carbonate (EC) : ethyl methyl carbonate (EMC) (1 : 2 v/v, Soulbrain, MI) as electrolyte. After cycling, the cells were de-crimped in the glovebox and the electrode was extracted and subsequently washed in dimethyl carbonate (DMC) to remove the electrolyte residues. The electrodes were allowed to dry overnight and extracted from the glovebox. A 1 mm disk was punched from the electrode using a biopsy punch and attached on the flat end of a 1 mm dowel pin for imaging.

Electrochemical testing

The coin cells were cycled on various battery cyclers (Basytec CTS; Maccor 4300; Interface Gamry Interface 1000E). The extended cycling was preceded by two formation steps at C/10 to allow for solid electrolyte interphase (SEI) formation on the graphite electrode. The coin cells were cycled at C/2 between 3 to 4.2 V or 3 to 4.7 V for 25, 50, 75 and 100 cycles in constant current–constant voltage (CCCV) mode. A voltage hold step was carried out at the upper cut-off voltage at the end of charge, with a current limitation step of C/20. Two coin cells were cycled for each cycle number–voltage combination. However, due to time constraints during the beam time, only one electrode was scanned per cycle number, except for the electrodes cycled to 100 cycles.

XRD-CT measurements

The XRD-CT scanning was carried out at the European Synchrotron Radiation Facility (ESRF) beam line ID15A.⁵¹ For the electrode disc, ROI and coarse scans were carried out: the coarse scan encompassed the entirety of the electrode disk, whereas the ROI scans targeted an internal slice of electrode particles. The coarse scans are required to subtract the contributing signal outside the field-of-view (FOV) in the ROI scan. The electrode samples are prone to ‘cupping’ as a result of cutting them using a biopsy punch; a second utility of the coarse scan is hence to ensure that sufficient material is present in the FOV to carry out an ROI scan. The diffraction measurements were taken with a monochromatic 50 keV (0.2480 Å) X-ray beam, focused to 1 μm using a Kirkpatrick–Baez mirror. A high-energy photon counting Pilatus3 X CdTe 2 M detector was utilized to record the diffracted X-ray beam. The ROI scan for the electrode discs were carried out with 251 translation steps for 250 rotation steps over 180° with a 1 μm step size. This resulted in 251 × 251 × 1 voxel horizontal slices of the sample. The coarse slices were taken with the same parameters, but using a 10 μm step size. Each slice consists of a 4D matrix, consisting of three spacial dimensions and one containing diffraction information. The spatial dimensions contain a map of diffraction intensities, with each pixel presenting a distinct diffraction pattern. Every 2D diffraction image was converted to a 1D powder diffraction pattern after applying a 10% trimmed mean filter to remove outliers with the nDTomo and pyFAI software packages using a fast GPU processor.^52–54 The final XRD-CT images (i.e. reconstructed data volume) were reconstructed using the filtered back projection algorithm.

X-ray CT imaging conditions. The X-ray CT slice was collected on a lab-based micro-CT instrument (Xradia Versa 520, Carl Zeiss Inc.) using a 60 s exposure, 3201 projections and a pixel binning of 1. An effective pixel size of 237 nm was obtained over a FOV of 400 μm. The radiographs were reconstructed using a filtered back-projection algorithm (FDK).

Focused ion beam-scanning electron microscope (FIB-SEM) imaging conditions. The sample was sandwiched between two pieces of high-conductivity thin silicon wafers using Ag-conductive epoxy. The cross section was mechanically polished and then ion milled using Ar ions. The SEM images were recorded with 1024 × 844 pixels at 3 keV electron beam energy using the through-the-lens (TLD) detector in a SEM (Thermo Fisher Scientific Nova NanoSEM 630).

Data processing, Rietveld refinement and lattice parameter analysis. The mean diffraction pattern per XRD-CT dataset was analysed using the X’Pert HighScore Plus software for phase identification. Rietveld analysis was then performed using the Topas v5 software. The last step involved the use of in-house developed Matlab and Topas scripts for the batch full profile analysis of the reconstructed diffraction patterns, on a voxel by voxel basis using as a starting model the one refined using the mean diffraction pattern.⁵⁵ In this work, the Rietveld analysis of the XRD-CT data presented in this work was based on the intensity of the scale factors and should be treated as a semi-quantitative analysis. The results from the refinements were then imported into MALTAB to create the various images (e.g. phase distribution maps based on the scale factors, lattice parameters etc.). The strategy applied for the Rietveld analysis of the collected XRD-CT data is presented in the EIS.† No phase change was observed for the samples and the R3̄m space group was used for the refinement. A MultiTool GUI was used to extract the diffraction pattern for visualization.⁵⁶

After refinement, a masking procedure was developed to highlight the outlines of individual particles for further analysis. This entailed in obtaining a mask from the mean diffraction intensity image and overlaying this mask on the lattice parameter maps to isolate single particles. The single particle analysis was carried out on the masked lattice parameter maps, by plotting an Euclidean distance map and calculating the average lattice parameter with increasing distance into the core of the particle. The details of both these approaches can be found in the ESI.†

Results and discussion

Electrochemical data

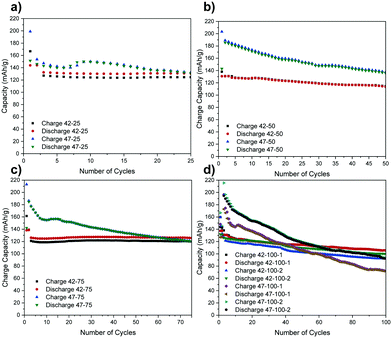
The following electrochemical data is collected for coin cells in a full-cell arrangement from which the electrodes were harvested. These cells were cycled to 4.2 and 4.7 V for up to 100 cycles at C/2. A full description of process is presented in the methodology section. For brevity, the electrodes are denominated according to the cut-off voltage (V) used and cycle number (CN) and repeat number (N), where there are multiple electrodes, in the format “V–CN–N” (for example, a cell with a cut off voltage of 4.7 V, cycled to 100 cycles and a second repeat would be denoted ‘47–100–2’). The charge and discharge capacities for the cells from which the electrodes were harvested are presented in Fig. 1.

Fig. 1 Discharge capacities versus number of cycles for the cells cycled to (a) 25, (b) 50, (c) 75 and (d) 100 cycles. Cells are named according to their cut-off voltage (V), cycle number (CN), in the order V–CN. For the electrodes cycled to 100 cycles, the repeat number (N) is included in the order V–CN–N.

A higher capacity reported for the very first cycles represents the formation step. Due to time constraints at the synchrotron, only the repeats for the cells cycled to 100 cycles were scanned so the rest are omitted from the following graphs for brevity.

While a certain degree of consistency can be observed in the discharge capacity for different cells cycled to 4.2 V (e.g. 42–25, 42–75), a higher capacity loss compared to literature is also observed (e.g. 42–50, 42–100).⁸ The percentage of discharge capacity loss for each cell between the first cycle after formation and last cycles is presented in Table S1 in the ESI.†

The higher capacity loss observed for the cells cycled to 4.7 V can be attributed to the expected enhanced cathode degradation but also to side reactions between the cathode and the electrolyte.⁶ The uneven performance of the cells cycled to 4.2 V, with 42–50 exhibiting a higher capacity loss than 42–25 and 42–75, suggests that there are other factors affecting electrode performance for cells cycled to both voltages. As the same materials are used, and some cells are performing as expected, the inconsistent performance is thought to result from uneven sealing and moisture ingress over extended cycling that negatively impacts some cells more than others. This is also confirmed by a lower capacity loss for the first 3 cycles for 42–50 and 42–100–1 and an increasingly severe drop thereafter. If the time for formation cycles is also taken into account, this indicates that moisture ingress may have started occurring after ca. 50 h of cycling. Furthermore, a temporary capacity recovery can be observed after the initial 10 to 20 cycles for 47–25, 47–75 and 47–100–1 and this again could be due to side-reactions with moisture that could be accentuated at higher voltages. Further factors affecting cell performance have been ruled out from the analysis of the diffraction data in the following section.

The above issues with uneven degradation, as well as the lack of in situ data, hinder the direct correlation of the lattice parameter with the exact lithiation state and associated electrode degradation. However, the results presented hereafter, highlight the first known attempt in using XRD-CT to characterize NMC, as well as the inherent potential of the technique to spatially localize heterogeneities in the crystal structure both on an electrode and particle level.

Electrode level characterisation

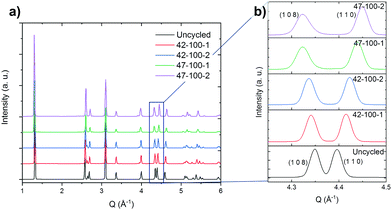
The diffraction pattern for the uncycled electrode and electrodes harvested from coin cells cycled to 4.2 and 4.7 V upper cut-off voltages are presented in Fig. 2(a). The cells were discharged to 3 V prior to disassembly. The reader is referred to the methodology section for a detailed overview of the process.

Fig. 2 (a) Diffraction pattern for the uncycled electrodes and those cycled to 100 cycles. Intensity in arbitrary units (a.u.). (b) Expanded view of the (1 0 8) and (1 1 0) reflections. Diffraction measurements taken with a beam energy of 50 keV, corresponding to a wavelength of 0.2480 Å.

The expanded region of interest of the diffraction pattern for 4.2 < Q Å⁻¹ < 4.5 is presented in Fig. 2(b).

From the expanded pattern, a change in position can be observed for several peaks as cycling progresses. Specifically, the splitting of the (1 0 8) and (1 1 0) peaks with progressive cycling is observed. As reported in literature, this indicates the shrinkage along the a and b directions and expansion along c.^8,57,58 The quality of the fits and procedure for Rietveld refinement is discussed in the ESI† in Fig. S5 and S6. An excellent fit can be observed for all electrodes except 47–100–1 and 47–100–2, with a weighted profile R-factor (RWP) value below 3. For 47–100–1 and 47–100–2, a higher RWP may indicate the formation of surface rock salt structures due to cycling at higher voltage and resulting loss of oxygen.⁵⁹

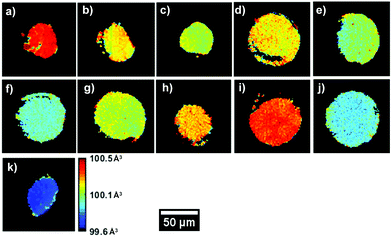
Fig. 3 presents the unit volume (V) distribution map for the coarse scans for both upper cut-off voltages, as a means to both obtain an overview of the material within the region of interest (ROI) but also have a first indication of lattice evolution with cycling. These were taken with a resolution of 10 μm and 251 × 251 voxels per direction. Ignoring the edges of the sample, the coarse scans indicate that a sufficiently uniform central area of the sample was identified for all datasets. It is important to note that the following lattice parameter analysis was carried out on cathodes that were lithiated as a last cycling step.

Fig. 3 Unit volume V obtained from the refinement of the coarse scans for (a) the uncycled electrode, (b) 42–25, (c) 42–50, (d) 42–75, (e) 42–100–1, (f) 42–100–2, (g) 47–25, (h) 47–50, (i) 47–75, (j) 47–100–1 and (k) 47–100–2.

A V of 100.5 ų, uniform throughout the slice of the electrode, can be observed for the uncycled dataset, in line with values reported in the literature. A decrease in V can be observed between the uncycled electrodes and those cycled 100 times. This effect is more pronounced for the 4.7 V electrodes, with V decreasing up to ca. 0.8% after 100 cycles, from ca. 100.5 ų to 99.7 ų. However, certain anomalies can be observed in the overall V trend, with samples such as 42–75 and 47–75 presenting a higher average value than electrode samples with fewer cycles. From the maps in Fig. 3 it is clear that V is not completely uniform across the electrode slice as cycling proceeds: samples such as 42–75 and 47–50 present a ‘spotty’ V distribution, compared to the uncycled electrode, indicating zones of uneven lithiation. This could be the result of microstructural heterogeneities present in the electrode or areas with poorer conductivity influencing participation in the electrochemical reaction. From the mean diffraction patterns of the coarse scans, the ratio between the (0 0 3)/(1 0 4) peak intensities was calculated as presented in Table S4 (ESI†). As reported in literature, values below 1.2 indicate possible Ni/Li cation intermixing which is not observed for these samples.⁶⁰

Fig. 4 presents a comparison between through-plane slices obtained from X-ray CT and XRD-CT to provide a comparison of what the resulting datasets from the two techniques represent: the former contains microstructural information obtained from the attenuation of the incoming beam by the sample, the latter presents maps of the lattice parameters of the electrode particles. While XRD-CT can be collected in three spatial dimensions, the below maps only represent a slice through the electrode and visualize the cross-sectional lattice parameters of the particles.

Fig. 4 (a) Absorption micro X-ray CT slice in the through-plane direction for the uncycled NMC electrode. ROI XRD-CT maps for (b) a, (c) c lattice parameters and the (d) unit volume V.

Further information on the crystal structure of the electrode can be obtained by examining the detailed ROI maps for a, c and V. These are presented in Fig. 5 and 6 for the 4.2 and 4.7 V electrodes, respectively.

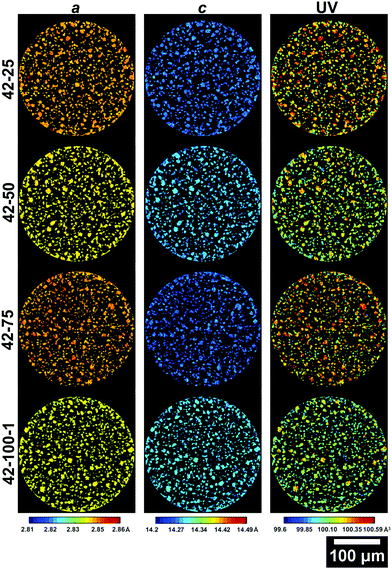Fig. 5 Slices from the ROI scans of electrodes cycled to 4.2 V presenting the a (left column), c (central column) lattice parameters and the unit volume V (right column). The slice for 42–100–2 is presented in the ESI.†

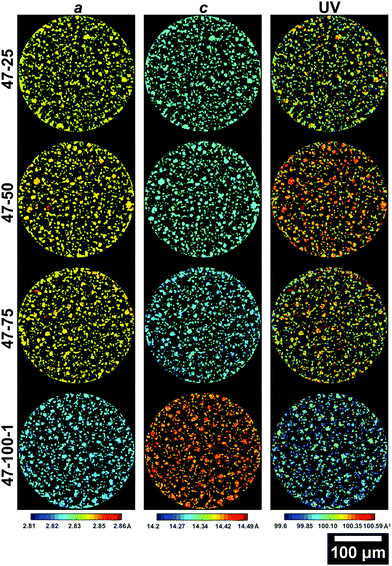Fig. 6 Slices from the ROI scans of electrodes cycled to 4.7 V presenting the a (left column), c (central column) lattice parameters and the unit volume V (right column). The slice for 47–100–2 is presented in the ESI.†

The 42–100–2 and 47–100–2 maps are placed in the ESI† in Fig. S1 and S2, respectively. As the electrodes have been discharged to 3 V prior to cell disassembly, the variations in lattice dimensions are affected both by the amount of Li that re-intercalated in the crystal matrix but also any other changes to the crystal structure imparted by cycling such as phase transitions discussed previously for the electrodes cycled to 4.7 V.

From the maps shown in Fig. 5, it is clear that the resolution allows resolving larger particles, with radii >5 μm. As cycling progresses, the V starts varying greatly across the slice. It is important to note that due to the 2D nature of the data, only large particles are taken into account for future analysis to ensure that the cross section is representative. Smaller fragments could represent either smaller particles, or edges of larger particles on a plane above or below the analysed slice. The average lattice parameters for each slice of the electrodes cycled to 4.2 V and 4.7 V are summarized in Table S2 in the ESI.†

Values of 2.856, 14.221 Å and 100.442 ų for a, c and V are in line with those observed in literature for NMC in its pristine state.^8,23,58 The overall trend, with decreasing a and increasing c between 0 and 100 cycles, is in line with what is reported in literature, with the a lattice parameter decreasing by ca. 0.5%, the c lattice parameter increasing by ca. 0.6% and the overall V decreasing by ca. 0.4%.^23,34 Two main dominating effects behind these lattice parameter changes are the expansion in one direction and shrinkage in the other. As Li-ions are removed from the interlayer spaces, the repulsion of oxygen atoms on opposing transition metal slabs causes the expansion observed along the c-axis. Concurrently, the transition metal oxide layers shrink as Li-ions are extracted, due to the increased oxidation state of the transition metal oxides, which causes them to reduce their ionic radius.³⁴ The higher a lattice parameter for 42–75 compared to 42–25 and 42–50, suggests that other factors are influencing the performance of the cell.

Similar observations can be made for the 4.7 V electrodes presented in Fig. 6. The extent of volume shrinkage is more severe, as expected for a larger degree of active Li loss due to increased capacity decay because of the higher upper cut-off voltage. As presented in Table S2 (ESI†), the a lattice parameter decreases by ca. 1%, c increases by ca. 1.5% and the overall V decreases by ca. 0.6%. A larger change in lattice parameters compared to the 4.2 V electrodes is expected, due to the larger amount of Li extracted during cycling due to the higher upper cut-off voltage used and the resulting accentuated degradation. Interestingly, there is a particle with anomalous lattice parameters for sample 47–100–2 as viewable in Fig. S2 in the ESI,† which will be discussed in the following section. Further information on the variations in lattice parameters can be obtained by analysing their frequency distribution and the associated discharge capacity loss for the electrode as presented in Fig. 7.

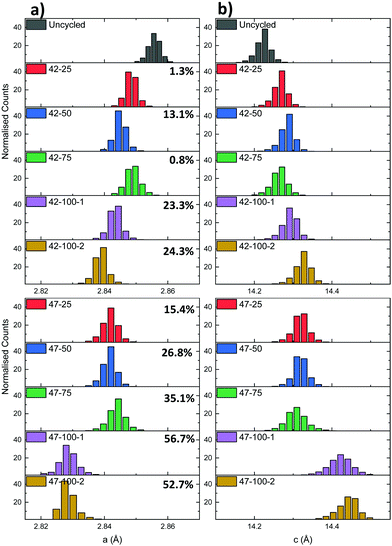Fig. 7 (a) a and (b) c lattice parameter distributions for the electrodes cycled to 4.2 and 4.7 V respectively. The percentages represent the cell discharge capacity loss.

A mismatch can be observed between the expected capacity loss due to progressing cycle number and lattice parameter evolution for some of the electrodes. Two cases can be identified for the different upper cut-off voltages used. For the 4.2 V electrodes, the capacity loss for the 42–25 and 42–75 cells is comparable at ca. 1%, indicating that increased capacity fade for the other cells with higher cycle count is more dependent on performance degradation mechanisms described previously such as moisture ingress. As reported in literature, the LiPF₆ contained in the electrolyte can react with trace amounts of moisture forming hydrofluoric acid (HF).⁶¹ HF degrades both the anode and the cathode by eroding the SEI layer. This can cause a continuous loss of Li-ions to replenish the lost SEI as cycling proceeds.⁶²

For the 4.7 V electrodes, a larger discharge capacity loss can be observed for all electrodes, but again a mismatch is present between the expected lattice parameter trend and overall discharge capacity loss. In this case the 47–25, 47–50 and 47–75 electrodes have a discharge capacity loss varying between ca. 15 to 35%, but similar average lattice parameters of ca. 2.844 Å and 14.310 Å for a and c. As these electrodes were cycled to a higher voltage, two additional mechanisms, additional to those described previously, could contribute to the capacity fade. In battery electrodes, secondary NMC particles are composed of agglomerates of smaller primary crystallites.⁶³ Firstly, the anisotropic shrinkage and expansion of primary particles contained in the NMC cathode can lead to intergranular cracking. This in turn can lead to a loss of electrical conductivity between primary particle grains and loss of active material.⁶ The combined effect of these degradation mechanisms is thought to then affect the effective capacity, irrespective of cycle number, and lead to the discrepancies between lattice parameter and discharge capacities. As a larger amount of Li is extracted from the cathode matrix due to the higher upper cut-off voltage, the primary particles are subjected to higher cyclical strains leading to cathode degradation. Evidence of particle cracking is presented hereafter through FIB-SEM cross-sections. Cycling to higher voltages can also lead to electrolyte instability as mentioned previously. After 100 cycles at 4.7 V, there is both a considerable capacity loss and a decrease in both lattice parameters compared to the 4.2 V electrodes. While the correlation of the exact amount of lithium to the lattice parameter cannot be determined due to a lack of in situ data and the aforementioned degradation mechanisms, XRD-CT allows detailed crystallographic information to be obtained on the overall lattice of the active material. Overall, the inconsistencies in the electrochemical performance (due to suspected moisture ingress and other competing degradation mechanisms), pose some limitations to the interpretation of the data in terms of active Li loss from the cathode matrix. However the previous methodology and resulting findings highlight the potential of this technique to spatially localize diffraction information for bulk electrodes. This approach can also be applied to gain sub-secondary particle information as presented in the following section.

Particle level characterisation

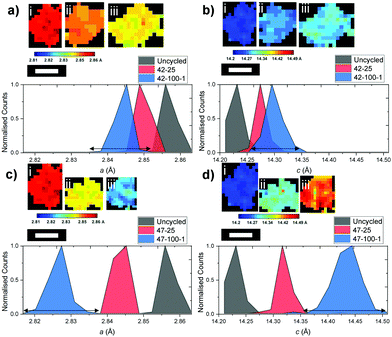
While the previous analysis offers insight on full electrodes, detailed information can also be obtained on individual particles. The diagram in Fig. 8 presents six particles for the uncycled, 42–25, 42–100–1, 47–25 and 47–100–1 electrodes and their associated a and c lattice parameter distributions.

Fig. 8 Normalized distributions of (a) the a lattice parameter for the (i) uncycled, (ii) 42–25 and (iii) 42–100–1 particles, (b) the c lattice parameter for the (i) uncycled, (ii) 42–25 and (iii) 42–100–1 particles, (c) the a lattice parameter for the (i) uncycled, (ii) 47–25 and (iii) 47–100–1 particles and (d) the c lattice parameter for the (i) uncycled, (ii) 47–25 and (iii) 47–100–1 particles. Broadening at the base for the electrodes cycled 100 times is indicated by an arrow. Scale bar represents 10 μm.

The above particles were cropped by taking into account their shape and radius: while the limiting factor in clearly resolving the particles is the beam versus particle size, particles were chosen so that a cross section of the particles is more likely to be close to their middle, as opposed to smaller fragments that could be unrepresentative of the full particle mass. A uniform lattice parameter can be observed for the uncycled electrode across the particle cross-section. This homogeneity is lost as cycling proceeds, with different sections of the particle shrinking according to different local change in the crystal structure, partly caused by the amount of Li that re-intercalates in the electrode particles after the final discharge cycle. This can also be visualized by the broadening of the lattice parameter distributions, particularly visible when comparing those of 42–25 and 42–100–1 in Fig. 8(a and b) to the uncycled electrode.

The above observations are also valid for the particles cropped from the electrodes cycled to 4.7 V, as presented in Fig. 8(c and d). While no repeating geometrical trend or core–shell structure can clearly be identified from the above diagrams, local variations in lattice parameters could give an indication as to local heterogeneities present within secondary particles and could indicate the location of hotspots of microstructural degradation as a result of extended cycling.^6,64 The broadening of the curve for the electrodes cycled to 100 cycles is more severe for both a and c, further proving that as cycling proceeds, different areas of the particles present inhomogeneous underlying lattice structures.

To further explore the possibility of any trends of the lattice parameter distributions, the ratio between the lattice parameter of interest and the mean particle lattice parameter versus the radial depth within the particle is presented in Fig. S3 and S4 in the ESI.† No consistent trend can be observed between the particles from different electrodes, suggesting that localized shrinkage of the electrode particles depends on factors other than spatial positioning of the lattice points within the particles as discussed hereafter.

Further evidence of the effect of non-uniform shrinkage is provided by the FIB-SEM slices, presented in Fig. 9, where extensive cracking can be observed as a function of upper cut-off voltage. Additional slices with an overview of the electrode for all three samples are placed in the ESI† in Fig. S11–S13.

Fig. 9 FIB-SEM cross-sectional slices of the (a) uncycled electrode taken at 2k×, (b) uncycled particle taken at 8k×, and particles extracted from (c) 42–100–1 taken at 8k× and (d) 47–100–1 taken at 6.5k×.

From Fig. 9(a and b), no cracks can be observed in the uncycled particles. However, numerous internal voids and an array of polydispersed primary particles reveal the complex internal structure of the secondary agglomerates. For 42–100–1 and 47–100–1 on the other hand, the extent of internal cracks within particles increases as a function of upper cut-off voltage as presented in Fig. 9(c and d). While the resolution and image clarity do not allow for establishing whether crack propagation preferentially occurs along grain boundaries, an overall increase of intraparticle crack density can be observed as a function of cut-off voltage. As shown in the early stage cracking of 42–100–1 in Fig. 9(c), the cracks seem to originate at the centre of the particle and then to propagate towards the edges of the particle for 47–100–1 in Fig. 9(d). As described by Yan et al., edge dislocations within primary particles act as crack nucleation points and additional crack propagation is an electrochemically driven process.⁶ These results complement previous observations and confirm that cyclical expansion and shrinkage, due to non-uniform Li-ion intercalation and concentrations, are partly responsible for stress distribution that ultimately results in particle cracking and performance degradation over extended cycling. While several discrepancies can be observed in the discharge capacities as discussed in the previous sections, the larger extent of cracking observable in the electrodes cycled to 4.7 V confirms that cycling to a higher upper cut-off voltage has a direct influence on the degradation of the cathode particles.

Li-ion diffusion during battery cycling can also be affected by grain size and orientation.⁶⁵ It is important to note that the overall size of the secondary particles may play an important role in the overall variation of crystal dimensions: for example, a core–shell structure might be observable if the overall size of the particle increases. A source of error may arise from the XRD-CT beam being close to the primary particle size. Further improvements in the measuring technique may lead to a reduction in beam size which in turn may help in resolving smaller primary crystals more accurately. However when reducing the beam size, an increase in the probability of obtaining numerous single crystal artefacts will also have to be taken into account. Other techniques such as pair distribution function (PDF) can also help in overcoming these issues.⁶⁶ Furthermore, as the size of the secondary particles increases, different Li-gradients may form depending on local internal conductivities. The internal structure of the particles is also likely to have an effect on their structural integrity over extended cycling, with larger voids acting as a buffer to uneven internal strains.¹⁰ These observations further highlight the potential of this technique to elucidate the link between the internal structure of the particles and electrochemical behaviour: while the beam size is critical in determining the resolution of the measurement, further development of this technique will allow a direct observation of individual crystallites and their lattice dimensions.

An outlying particle, presented in Fig. S14 in the ESI,† is isolated from 47–100–2. Interestingly, this underwent moderate shrinkage compared to the rest of the electrode. Average values of 2.832 Å, 14.418 Å and 100.155 ų for a, c and the V are calculated for this particle, versus 2.824 Å, 14.437 Å and 99.718 ų for the rest of the electrode slice. This may have been caused by electrochemical inactivity of the particle or a different composition compared to the bulk of the electrode. These results further highlight the potential of the technique, not only to quantify the crystallographic structure of electrode materials, but also identify particles or areas with heterogeneous characteristics compared to the majority of the sample.

Conclusions

This work has presented the first application of an XRD-CT technique to analyse the lattice evolution of NMC electrodes as a result of electrochemical cycling. The technique allows spatially resolved physico-chemical characterization of electrodes by analysing local diffraction patterns from sample voxels corresponding to 1 μm³ in size. A wealth of information was obtained from analysing 3D slices taken from electrodes harvested from previously cycled cells; the effect of two upper cut-off voltages, namely 4.2 and 4.7 V. Through full profile analysis of the XRD data contained in the datasets, a localized map of the lattice parameter and V was obtained.

XRD-CT has allowed spatially resolved characterisation of local heterogeneities of the unit cell volume by analysing the expansion along the c-axis and shrinkage along the a-axis as a result of extended cycling. The crystal structure of the electrodes cycled to 4.7 V underwent larger shrinkage. The overall capacity fade observed across the different cells was thought to be caused by a combination of poor cell sealing, electrolyte and cathode degradation. When individual particles were analysed, no distribution that correlates local shrinkage to radial depth within the particle was identified. This was attributed to the highly heterogeneous internal structure of the secondary particles, which was also examined with FIB-SEM, revealing extensive cracking as a result of high voltage cycling.

Further potential of the technique was also demonstrated by its ability to identify outlying particles with different crystal dimensions compared to the bulk. Overall, the results in this work indicate that this technique can be successfully used to obtain detailed spatially resolved chemical information. Its further development will enable using it to elucidate the bidirectional link between crystallographic structure and performance of functional materials, thus contributing to advancing their use in demanding applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge funding from the EPSRC (EP/N032888/1, EP/K005030/1, and EP/M009394/1), the Royal Academy of Engineering (CIET1718/59). SD acknowledges EPSRC and JM for funding via the CASE studentship scheme. This work was also carried out with funding from the Faraday Institution (faraday.ac.uk; EP/S003053/1), grant number FIRG001. UCL is grateful to Warwick Manufacturing Group for supplying coated graphite anodes for use in this work.

References

1. F. Schipper, E. M. Erickson, C. Erk, J.-Y. Shin, F. F. Chesneau and D. Aurbach, J. Electrochem. Soc., 2017, 164, A6220–A6228.
2. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2014, 18, 252–264.
3. G. G. Amatucci, J. M. Tarascon and L. C. Klein, J. Electrochem. Soc., 1996, 143, 1114–1123.
4. S. B. Chikkannanavar, D. M. Bernardi and L. Liu, J. Power Sources, 2014, 248, 91–100.
5. Z. Ma, X. Yuan, L. Li, Z.-F. Ma, D. P. Wilkinson, L. Zhang and J. Zhang, Energy Environ. Sci., 2015, 8, 2144–2198.
6. P. Yan, J. Zheng, M. Gu, J. Xiao, J.-G. Zhang and C.-M. Wang, Nat. Commun., 2017, 8, 14101.
7. I. Buchberger, S. Seidlmayer, A. Pokharel, M. Piana, J. Hattendorff, P. Kudejova, R. Gilles and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, A2737–A2746.
8. I. Buchberger, S. Seidlmayer, A. Pokharel, M. Piana, J. Hattendorff, P. Kudejova, R. Gilles and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, A2737–A2746.
9. R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164(7), A1361–A1377.
10. Y. Mao, X. Wang, S. Xia, K. Zhang, C. Wei, S. Bak, Z. Shadike, X. Liu, Y. Yang, R. Xu, P. Pianetta, S. Ermon, E. Stavitski, K. Zhao, Z. Xu, F. Lin, X. Q. Yang, E. Hu and Y. Liu, Adv. Funct. Mater., 2019, 29, 1–11.
11. T. M. M. Heenan, C. Tan, J. Hack, D. J. L. Brett and P. R. Shearing, Mater. Today, 2019, 31, 69–85,  DOI:10.1016/j.mattod.2019.05.019.
12. J. Nelson, S. Misra, Y. Yang, A. Jackson, Y. Liu, H. Wang, H. Dai, J. C. Andrews, Y. Cui and M. F. Toney, J. Am. Chem. Soc., 2012, 134, 6337–6343.
13. K. W. Nam, S. M. Bak, E. Hu, X. Yu, Y. Zhou, X. Wang, L. Wu, Y. Zhu, K. Y. Chung and X. Q. Yang, Adv. Funct. Mater., 2013, 23, 1047–1063.
14. S. C. Chao, Y. F. Song, C. C. Wang, H. S. Sheu, H. C. Wu and N. L. Wu, J. Phys. Chem. C, 2011, 115, 22040–22047.
15. G. X. Wang, S. Needham, J. Yao, J. Z. Wang, R. S. Liu and H. K. Liu, J. Power Sources, 2006, 159, 282–286.
16. S. Kobayashi, I. R. M. Kottegoda, Y. Uchimoto and M. Wakihara, J. Mater. Chem., 2004, 14, 1843.
17. M. Balasubramanian, X. Sun, X. Yang and J. McBreen, J. Power Sources, 2001, 92, 1–8.
18. S. Randjbar Daemi, D. J. L. Brett and P. R. Shearing, ECS Trans., 2017, 77, 1119–1124.
19. D. P. Finegan, E. Tudisco, M. Scheel, J. B. Robinson, O. O. Taiwo, D. S. Eastwood, P. D. Lee, M. Di Michiel, B. Bay, S. A. Hall, G. Hinds, D. J. L. Brett and P. R. Shearing, Adv. Sci., 2015, 2198–3844.
20. D. Kehrwald, P. R. Shearing, N. P. Brandon, P. K. Sinha and S. J. Harris, J. Electrochem. Soc., 2011, 158, A1393.
21. T. R. Thurston, N. M. Jisrawi, S. Mukerjee, X. Q. Yang, J. McBreen, M. L. Daroux and X. K. Xing, Appl. Phys. Lett., 1996, 69, 194–196.
22. S.-M. Bak, E. Hu, Y. Zhou, X. Yu, S. D. Senanayake, S.-J. Cho, K.-B. Kim, K. Y. Chung, X.-Q. Yang and K.-W. Nam, ACS Appl. Mater. Interfaces, 2014, 6, 22594–22601.
23. N. Yabuuchi, Y. Makimura and T. Ohzuku, J. Electrochem. Soc., 2007, 154, A314.
24. C. Cao, M. F. Toney, T.-K. Sham, R. Harder, P. R. Shearing, X. Xiao and J. Wang, Mater. Today, 2020, 34, 132–147,  DOI:10.1016/j.mattod.2019.08.011.
25. E. N. Landis and D. T. Keane, Mater. Charact., 2010, 61, 1305–1316.
26. Y. Waseda, E. Matsubara and K. Shinoda, X-Ray Diffraction Crystallography, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011.
27. P. R. Shearing, L. E. Howard, P. S. Jørgensen, N. P. Brandon and S. J. Harris, Electrochem. Commun., 2010, 12, 374–377.
28. S. R. Daemi, C. Tan, T. Volkenandt, S. J. Cooper, A. Palacios-Padros, J. Cookson, D. J. L. Brett and P. R. Shearing, ACS Appl. Energy Mater., 2018, 1, 3702–3710.
29. C. Tan, M. D. R. Kok, S. R. Daemi, D. J. L. Brett and P. R. Shearing, Phys. Chem. Chem. Phys., 2019, 21, 4145–4154.
30. O. O. Taiwo, D. P. Finegan, J. Gelb, C. Holzner, D. J. L. Brett and P. R. Shearing, Chem. Eng. Sci., 2016, 154, 27–33.
31. M. Ebner, F. Geldmacher, F. Marone, M. Stampanoni and V. Wood, Adv. Energy Mater., 2013, 3, 845–850.
32. F. Lin, Y. Liu, X. Yu, L. Cheng, A. Singer, O. G. Shpyrko, H. L. Xin, N. Tamura, C. Tian, T.-C. Weng, X.-Q. Yang, Y. S. Meng, D. Nordlund, W. Yang and M. M. Doeff, Chem. Rev., 2017, 117, 13123–13186.
33. A. A. A. Al-Tabbakh, A. B. Al-Zubaidi and N. Kamarulzaman, Indian J. Phys., 2016, 90(3), 297–305,  DOI:10.1007/s12648-015-0748-y.
34. K. Min, K. Kim, C. Jung, S. W. Seo, Y. Y. Song, H. S. Lee, J. Shin and E. Cho, J. Power Sources, 2016, 315, 111–119.
35. S.-C. Yin, Y.-H. Rho, I. Swainson and L. F. Nazar, Chem. Mater., 2006, 18, 1901–1910.
36. U. Kleuker, P. Suortti, W. Weyrich and P. Spanne, Phys. Med. Biol., 1998, 43, 2911–2923.
37. P. Bleuet, E. Welcomme, E. Dooryhée, J. Susini, J. L. Hodeau and P. Walter, Nat. Mater., 2008, 7, 468–472.
38. G. Harding, J. Kosanetzky and U. Neitzel, Med. Phys., 1987, 14, 515–525.
39. A. M. Beale, S. D. M. Jacques, E. K. Gibson and M. Di Michiel, Coord. Chem. Rev., 2014, 277, 208–223.
40. A. Vamvakeros, S. D. M. Jacques, M. Di Michiel, D. Matras, V. Middelkoop, I. Z. Ismagilov, E. V. Matus, V. V. Kuznetsov, J. Drnec, P. Senecal and A. M. Beale, Nat. Commun., 2018, 9, 4751.
41. I. Martens, A. Vamvakeros, R. Chattot, M. V. Blanco, M. Rasola, J. Pusa, S. D. M. Jacques, D. Bizzotto, D. P. Wilkinson, B. Ruffmann, S. Heidemann, V. Honkimäki and J. Drnec, J. Power Sources, 2019, 437, 226906–226914,  DOI:10.1016/j.jpowsour.2019.226906.
42. T. Li, T. M. M. Heenan, M. F. Rabuni, B. Wang, N. M. Farandos, G. H. Kelsall, D. Matras, C. Tan, X. Lu, S. D. M. Jacques, D. J. L. Brett, P. R. Shearing, M. Di Michiel, A. M. Beale, A. Vamvakeros and K. Li, Nat. Commun., 2019, 10, 1–11.
43. S. D. M. Jacques, M. Di Michiel, A. M. Beale, T. Sochi, M. G. O’Brien, L. Espinosa-Alonso, B. M. Weckhuysen and P. Barnes, Angew. Chem., Int. Ed., 2011, 50, 10148–10152.
44. A. M. Beale, S. D. M. Jacques, M. Di Michiel, J. F. W. Mosselmans, S. W. T. Price, P. Senecal, A. Vamvakeros and J. Paterson, Philos. Trans. R. Soc., A, 2018, 376, 20170057.
45. K. M. O. Jensen, X. Yang, J. V. Laveda, W. G. Zeier, K. A. See, M. D. Michiel, B. C. Melot, S. A. Corr and S. J. L. Billinge, J. Electrochem. Soc., 2015, 162, A1310–A1314.
46. D. Finegan, A. Vamvakeros, L. Cao, C. Tan, T. Heenan, S. Daemi, S. Jacques, A. M. Beale, M. Di Michiel, K. Smith, D. J. L. Brett, P. R. Shearing and C. Ban, Nano Lett., 2019, 19(6), 3811–3820,  DOI:10.1021/acs.nanolett.9b00955.
47. D. P. Finegan, A. Vamvakeros, C. Tan, T. M. M. Heenan, S. R. Daemi, N. Seitzman, M. Di Michiel, S. Jacques, A. M. Beale, D. J. L. Brett, P. R. Shearing and K. Smith, Nat. Commun., 2020, 11, 1–11.
48. H. Liu, S. Kazemiabnavi, A. Grenier, G. Vaughan, M. Di Michiel, B. J. Polzin, K. Thornton, K. W. Chapman and P. J. Chupas, ACS Appl. Mater. Interfaces, 2019, 11, 18386–18394.
49. O. O. Taiwo, T. M. M. Heenan, D. P. Finegan, D. J. L. Brett, P. R. Shearing, J. M. Paz-García, S. A. Hall, R. Mokso, P. Villanueva-Pérez and A. Patera, J. Power Sources, 2017, 342, 904–912.
50. G. Tonin, G. B. M. Vaughan, R. Bouchet, F. Alloin, M. Di Michiel and C. Barchasz, J. Power Sources, 2020, 468, 1–8.
51. G. B. M. Vaughan, R. Baker, R. Barret, J. Bonnefoy, T. Buslaps, S. Checchia, D. Duran, F. Fihman, P. Got, J. Kieffer, S. A. J. Kimber, K. Martel, C. Morawe, D. Mottin, E. Papillon, S. Petitdemange, A. Vamvakeros, J.-P. Vieux and M. Di Michiel, J. Synchrotron Radiat., 2020, 27, 515–528.
52. A. Vamvakeros, S. D. M. Jacques, M. Di Michiel, V. Middelkoop, C. K. Egan, R. J. Cernik and A. M. Beale, J. Appl. Crystallogr., 2015, 48, 1943–1955.
53. J. Kieffer, S. Petitdemange and T. Vincent, J. Synchrotron Radiat., 2018, 25, 612–617.
54. A. Vamvakeros, nDTomo Software Suite, Github, 2019.
55. D. Matras, S. D. M. Jacques, H. R. Godini, M. Khadivi, J. Drnec, A. Poulain, R. J. Cernik and A. M. Beale, J. Phys. Chem. C, 2018, 122, 2221–2230.
56. A. Vamvakeros, S. D. M. Jacques, M. Di Michiel, P. Senecal, V. Middelkoop, R. J. Cernik and A. M. Beale, J. Appl. Crystallogr., 2016, 49, 485–496.
57. J. Li, R. Shunmugasundaram, R. Doig and J. R. Dahn, Chem. Mater., 2016, 28, 162–171.
58. R. Weber, C. R. Fell, J. R. Dahn and S. Hy, J. Electrochem. Soc., 2017, 164, A2992–A2999.
59. C. Tian, F. Lin and M. M. Doeff, Acc. Chem. Res., 2018, 51, 89–96.
60. X. Zhang, W. J. Jiang, A. Mauger, Qilu, F. Gendron and C. M. Julien, J. Power Sources, 2010, 195(5), 1292–1301.
61. Z. Chen, Y. Ren, A. N. Jansen, C. K. Lin, W. Weng and K. Amine, Nat. Commun., 2013, 4, 1513–1518.
62. P. Voelker, R&D Mag., 2014, 1–5.
63. P. C. Tsai, B. Wen, M. Wolfman, M. J. Choe, M. S. Pan, L. Su, K. Thornton, J. Cabana and Y. M. Chiang, Energy Environ. Sci., 2018, 11, 860–871.
64. A. Mukhopadhyay and B. W. Sheldon, Prog. Mater. Sci., 2014, 63, 58–116.
65. N. Balke, S. Jesse, A. N. Morozovska, E. Eliseev, D. W. Chung, Y. Kim, L. Adamczyk, R. E. García, N. Dudney and S. V. Kalinin, Nat. Nanotechnol., 2010, 5, 749–754.
66. S. Grangeon, A. Fernandez-Martinez, A. Baronnet, N. Marty, A. Poulain, E. Elkaïm, C. Roosz, S. Gaboreau, P. Henocq and F. Claret, J. Appl. Crystallogr., 2017, 50, 14–21.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01851a

---