 Open Access Article
Open Access ArticleThe transformation of cuboctahedral to icosahedral nanoparticles: atomic structure and dynamics†
Philipp N.
Plessow

Institute of Catalysis Research and Technology (IKFT), Karlsruher Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: plessow@kit.edu; Tel: +49 721 608-24413
First published on 1st June 2020
Abstract
The rearrangement of transition metal nanoparticles from cuboctahedral to icosahedral structures is studied for up to 923 atoms. The atomic structure and temperature dependence of the transition are investigated with a well-defined collective variable. This collective variable describes the folding of the square fcc(100) facets into two triangular facets through a linear combination of the diagonals of all fcc(100) facets of all shells of the particle. Activation barriers are determined through harmonic transition state theory and constrained molecular dynamics simulations based on force field potentials. These calculations predict an activation entropy larger than 1 meV K−1, leading to strongly temperature dependent activation barriers. Density functional theory calculations were additionally performed both as single point calculations and as full optimizations. Cu, Ag, Au and Ni clusters show low barriers for concerted, symmetric transition up to the 309-atomic clusters. In contrast, for Pd, Pt, Rh and Ir higher barriers are required, already for the 147-atomic clusters. With increasing barriers, an asymmetric but still concerted rearrangement becomes energetically more favorable than the fully symmetric transformation. The material-dependence of the transition can be correlated with the melting point of the bulk metals.
1 Introduction
In the limit of large clusters (>104 atoms), the thermodynamically most stable metal particles generally have the structure of the bulk material, in particular fcc for fcc metals. For smaller particles, different structural motifs can be more stable, for example decahedral and icosahedral structures.1–6 Many properties, in particular the reactivity7,8 have been shown to depend on the particle shape. Which particle structures are observable is not only determined by their thermodynamic stability, but also by the rate with which they are formed or rearrange.9–11 This has implications also for supported nanoparticles, where it has been shown that transition metal particles can dynamically adapt to reaction conditions.12,13 On the other hand, the persistence of defects such as stacking faults in copper particles14 and grain boundaries in gold electrodes15 have also been proposed as the origin of the catalytic activity. Shape changes within a certain crystal structure can occur via single atom diffusion and can be modeled with 3D-lattice kinetic Monte Carlo simulations.16,17 For rearrangements between fcc and icosahedral clusters, the lattice changes and a concerted transformation is possible, which is more challenging to model.The Mackay icosahedron was proposed in 1962 as a potential cluster shape along with the realization that it can be generated by the distortion of a cuboctahedron.18 Icosahedral clusters have since then indeed been observed many times and have been found to be stable mainly in the range of small to intermediate clusters (<1000 atoms).19 The stability of different cluster morphologies was also shown to depend on the interaction with the support for Ni and Cu clusters.20 The transition from fcc to icosahedral particles itself has also been studied, mainly as a spontaneous process in molecular dynamics simulations (MDs).21 When studying the melting process of a gold cluster, Landman and coworkers have found clusters to form intermediate icosahedral structures prior to melting.22 Icosahedral gold clusters were also found upon simulated freezing.23 Similiar observations were made for nickel24,25 and palladium26 clusters, where transitions involving icosahedral structures were also found prior to melting. Baletto and coworkers used MD and metadynamics simulations to study the transitions between decahedral, cuboctahedral and icosahedral clusters. Barriers were found to be accessible at room temperature up to Ni561 and Cu561, while higher barriers were found for Pd, Pt, Au and Ag.27–29 Barreteau et al. found energy barriers for Pd147 and Rh147 to be larger than 4 eV and larger than 10 eV for Pd309 and Rh309 using a tight binding approach.30
This work is organized as follows. We will first introduce a new collective variable that is used to study the atomic structure of the rearrangement between cuboctahedral and icosahedral structures of copper particles. The energy barriers for this transformation are computed using DFT and various empirical force fields. The temperature dependence of the rearrangement is then analyzed based on force field MD simulations. Last, the barrier is compared for different transition and coinage metals.
2 Results and discussion
The transformation from cuboctahedral to icosahedral structures is shown for Cu309 in Fig. 1(a). The structural transformation can be described as a folding of the six square fcc(100)-facets into twelve triangular facets. For boranes, this mechanism was termed the diamond–square–diamond mechanism.31 This turns the cuboctahedron that consists of eight fcc(111)-facets and six fcc(100) facets into an icosahedron with 20 identical, triangular facets. In this process, the initially equally long diagonals of the fcc(100) facets distort so that one becomes longer, while the other becomes shorter, forming an edge. This is shown in Fig. 1(a) and the difference of these diagonals, d+–d−, which we measure between the corner atoms, can actually be used to construct a collective variable. In the collective variable ξ(s), we simply sum over these differences for all six fcc(100) facets of a given shell s. Optimizations are only robust, when this is done for all shells of the cuboctahedral particles, since all of these shells need to transform individually: | (1) |
It is important to stress, that ξ is only a single degree of freedom despite containing the linear combination of many atomic distances. Furthermore, ξ(s) is only introduced for the sake of analysis, but is in fact never varied or fixed for an individual shell, since ξ is always applied as a sum over all ξ(s). For Cu309, four shells with six fcc(100) facets and two diagonals each lead to a linear combination of 48 atomic distances for the collective variable ξ. For the cuboctahedron, ξ equals zero, since the fcc(100) facets are squares. During the transition to the icosahedron, ξ grows to a final value which we choose to be ξ = 1, using an appropriate normalization constant N in eqn (1). Although all shells have to transform, they do not need to do so simultaneously and we indeed find that the outer shells transform first, when going from cuboctahedron to icosahedron. This can be seen in Fig. 1(b), where ξ(s) is shown (with appropriate normalization for each shell) as a function of the collective variable for the overall particle ξ. The value of ξ(s) for the outer shells clearly changes first and faster. The shell-by-shell rearrangement can be explained by the fact that this requires less atomic displacements at the same time. The order of the transformation can be rationalized by the fact that the entire particle slightly contracts when forming an icosahedron. In this respect it is interesting, that for Fe-clusters, DFT calculations have predicted structures to be stable which are only partially Mackay transformed.32
In the present form, ξ is limited to specific cluster shapes, here cuboctahedral and closed-shell icosahedral. In this respect, geometric descriptors such as average coordination numbers and related quantities, as used in metadynamics simulations by Baletto and coworkers are more generally applicable.27,28 The advantage of the collective variable used here is that it allows to selectively drive only the cuboctahedral-to-icosahedral transition and gives very detailed insights into its atomic structure.
Fig. 1(c) shows the relaxed potential energy surface E(ξ) for Cu561 obtained for various methods through constrained optimizations, where ξ is held fixed and E is minimized with respect to all other degrees of freedom. As the shape of the curve suggests, there is only a single, well-defined transition state, which has been verified through normal mode analysis for the force-field methods. DFT-calculations have been carried out with the PBE functional33 along with the D3 dispersion correction.34 For Cu561, PBE-D3 shows a moderately high barrier of 2.4 eV, while the formation of the icosahedral particle is strongly exothermic (ΔE = −15 eV). Simple, classical force fields such as Lennard-Jones and Morse potentials give a completely different description, resulting in a much higher barrier and much less exothermic reaction. While Fig. 1(c) shows only one set of parameters for these potentials, this discrepancy with DFT cannot be resolved, since changing parameters for these two force fields will increase or lower both Ea and ΔE at the same time. Better agreement with DFT is reached with effective medium theory (EMT)35 and the potential suggested by Gupta:36,37
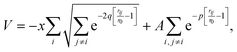 | (2) |
For the larger, 561- and 923-atomic copper nanoparticles we find that a less symmetric transformation is energetically more favorable and this will be referred to as the asymmetric transition. In this asymmetric transition, the six fcc(100) facets change no longer simultaneously but in two groups, consisting of three facets each. The variable ξ can be split into two components ξ1 and ξ2 in order to describe this behavior. The splitting of the six fcc(100) facets (f = 1,…,6) into two groups again applies to all shells, so that one can rewrite eqn (1) for ξ1:
 | (3) |
This is illustrated in Fig. 1(e), where the asymmetric TS is shown for Cu923. In the transition state, the faster changing three fcc(100) facets (constituting ξ2) have diagonal distances of 16.7 and 24.0 Å, while the slower changing three facets (constituting ξ1) have diagonal distances of 19.3 and 22.8 Å. Fig. 1(f) shows a contour plot of the potential energy surface E(ξ1,ξ2) as a function of the two collective variables ξ1 and ξ2. The symmetric transformation ξ1 = ξ2, as observed for Cu309 has a barrier that is higher by 0.6 eV for Cu923 and by 0.1 eV for Cu561.
When asymmetric transition is favored, as for Cu923, only the asymmetric transition state is a true first order saddle point. In these cases, the highest point of the symmetric path is no longer a true transition state but a higher-order saddle point. This is because there are four different ways to group the six fcc(100) facets into the two coordinates ξ1 and ξ2. When symmetric transition is favored, as for Cu309, only the symmetric transition state is a true first order saddle point. In these cases, there is no stationary point for asymmetric transition, meaning that a more asymmetric transition is simply increasingly less favorable.
To study kinetics, it is crucial to take into account thermal corrections and we have therefore performed MD simulations for Cu561. Calculations were carried in the NVT ensemble with a Nosé–Hoover-thermostat and a timestep of 5 fs. All simulations use the Gupta potential that has been implemented into a local version of LAMMPS.40 We have first performed unconstrained MD simulations and determined the rate constant for the cuboctahedral-to-icosahedral transition from the average time after which it occurred. The transition was detected by a characteristic decrease of the maximum Cu–Cu distance (corresponding to opposite corners) below 12.3 Å. Activation barriers Fa were then calculated from these rate constants based on transition state theory (TST). Transitions are easily observed within a few thousand MD steps at T > 500 K. This corresponds to an activation free energy of Fa < 0.5 eV, which is surprisingly low given the computed activation energy of Ea = 2.6 eV. The activation free energy Fa increases significantly with lower temperatures, as shown in Fig. 2(a). At 450 K, transitions happen on average after around 600 ns (120 million MD steps), which requires multiple trajectories of 6 million steps each, to obtain sufficient transitions to determine the rate constant.
Investigations at lower temperatures therefore require the use of constrained MD simulations. Using the collective variable ξ defined above, this was done with Umbrella Integration (UI). The Helmholtz free energy curves F(ξ) were obtained from trajectories at 46 different values of ξ0, each 500 ps long, and are shown in Fig. 2(b) for various temperatures. With increasing temperature, the free energy barrier drops significantly, until the barrier almost disappears at 600 K. Activation free energies were obtained as described in ref. 41 from the free energy difference ΔF0→ξ* = F(ξ = ξ*) − F(ξ = 0), where ξ* refers to the maximum in the free energy diagram:
 | (4) |
 . The obtained barriers Fa are shown in Fig. 2(a) as a function of temperature and agree well with the predictions obtained both from harmonic transition state theory and unconstrained MD simulations. A similar temperature-dependence is found for other metals and parameterizations of the Gupta potential from the literature9,37 (see the ESI†).
. The obtained barriers Fa are shown in Fig. 2(a) as a function of temperature and agree well with the predictions obtained both from harmonic transition state theory and unconstrained MD simulations. A similar temperature-dependence is found for other metals and parameterizations of the Gupta potential from the literature9,37 (see the ESI†).
This clearly shows that the activation free energy is strongly temperature dependent, going from high barriers (>1 eV) below 300 K to negligible barriers at 500 K. This gives the appearance of a temperature-driven phase transition like melting, which is clearly not the case, but is due to the high activation entropy. It is also worth noting that previous investigations have found the stability of nanoparticles, as modeled with force fields, to depend significantly on temperature.42,43 While the cuboctahedral particles studied in this work are in all cases less stable than the icosahedral structures, it is worth noting that cuboctahedral particles are not particularly stable fcc structures. This is because they correspond to Wulff constructions with equal 100- and 111-surface energies, while the actual surface energies of 111-surfaces are generally lower.
In addition to Cu clusters, other fcc metals have been studied. Ag, Au and Ni behave very similarly to Cu in that they show low barriers for the cuboctahedral-to-icosahedral transition up to the 309-atomic cluster and rearrange symmetrically up to these sizes (Table 1). They can also be very well described with the discussed collective variable and full DFT-optimization is feasible up to the 309-atomic clusters. Pd, Pt, Rh and Ir, however, behave very differently, as they show generally higher barriers and rearrange asymmetrically already at smaller cluster sizes. Here, DFT-optimizations were carried out with the NEB method44 using 7 to 12 images (see also Fig. S3, ESI†). The barriers for the 147-atomic clusters are higher than 1.5 eV and the asymmetric transition is energetically more favorable, for Rh and Ir by more than 1 eV. Again, similar results are obtained with the PBEsol and BEEF-vdW functionals. Fig. 3 shows the barriers of the 147-atomic clusters as a function of the experimental melting point.45 It can be seen that the barrier generally increases with the melting point. The elements with the lowest melting points, Ag, Au, Cu and Ni show a negligible barrier. The activation energy increases dramatically from Pd and Pt (both 1.8 eV) to Rh (4.7 eV) and Ir (6.4 eV). While the activation barrier for the cuboctahedral-to-icosahedral transition is clearly correlated with the bulk melting point, the underlying reason is not obvious. Although the rearrangement to the icosahedral structure is not a melting transition, it has two properties in common: an increase in energy caused by distortion/destruction of the fcc-structure and an (intermediate) gain in entropy. One can speculate that both the energetic cost and the entropic gain are related for melting and the cuboctahedral-to-icosahedral transition and therefore change systematically between different metals.
 | ||
| Fig. 3 Activation energy Ea at the PBE-D3 level of theory for the cuboctahedral-to-icosahedral transition of the 147-atomic cluster of various fcc-metals as a function of the experimental bulk melting temperature.45 | ||
3 Conclusions
We have proposed a reaction coordinate that allows the systematic investigation of the cuboctahedral-to-icosahedral transition. The transformation occurs via a single transition state, albeit shell-wise and, for higher barriers, also in an asymmetric fashion, where the six fcc(100) facets transform in two groups. The concept of the collective variable in this work that is adapted specifically to a certain transition should also be applicable to other transitions and more challenging situations, such as nanoparticles interacting with supports or adsorbates. Cu, Ag, Au and Ni show low activation barriers (<1 eV) for the transition from cuboctahedron to icosahedron up to the 309-atomic clusters. Using constrained MD simulations, the transformation can be studied over a wide temperature range and the free energy barrier is shown to be strongly temperature dependent. The high activation entropy lowers the activation free energy for the case of Cu561 from 2.6 eV at T = 0 K to 0.5 eV at T = 500 K. Pd, Pt, Rh and Ir show barriers higher than 1.5 eV already for the 147-atomic cluster, where the asymmetric transition is clearly preferred. While all calculations in this work were carried out for isolated particles, it can be expected that many results, such as the strong temperature dependence and the correlation of barriers with the bulk melting point also apply to supported nanoparticles.4 Computational details
4.1 DFT calculations
DFT-calculations were carried out with a plane-wave cutoff of 300 eV, Gaussian smearing with σ = 0.05 eV using the projector augmented wave method (PAW) with standard PAW potentials and the VASP program in version 5.4.1.46,47 Clusters were separated by at least 12 Å and k-point sampling was restricted to the Γ-point. DFT calculations for nickel particles were performed spin-polarized. The barrier from constrained optimizations was determined as the maximum energy along ξ. Optimizations have been carried out with the ASE,48 where the constraint was implemented in a local version.49 Optimizations were carried with a convergence criterion of 0.01 eV Å−1 for minimizations and constrained optimizations and 0.05 eV Å−1 for NEB calculations.4.2 Force field calculations
All optimizations were carried out with the ASE48 and a convergence criterion of 0.1 meV Å−1. Tight convergence thresholds are necessary due to the very low curvatures and the resulting low frequency vibrations. The imaginary frequencies for the transition mode are on the order of 10 cm−1. All transition states were verified to have only a single imaginary frequency. The connectivity was furthermore checked through small displacements along the transition mode followed by optimizations that led to icosahedron and cuboctahedron, respectively. Harmonic frequencies were calculated from a numerical Hessian computed using finite differences.4.3 MD simulations
All MD simulations were performed using LAMMPS40 with the Gupta potential and the parameters in Table S1 in the ESI.† The Gupta potential was implemented into a local version of LAMMPS and the additional subroutine is also provided as ESI.† Unconstrained MDs were analyzed based on the average transition time 〈t〉, which was used to determine the rate constant k = 1/〈t〉. The activation free energy Fa was then determined from transition state theory, k = kBTh−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Fa/(kBT)).
exp(−Fa/(kBT)).
Umbrella integration50 was performed using a harmonic potential κ/2(ξ − ξ0)2 with κ = 5 eV (NÅ2)−1, where N is the normalization constant in eqn (1). At T ≥ 500 K, additional potentials are required to prevent artificial reconstructions that cause the corner atoms, for which ξ is defined, to diffuse over the cluster surface. These additional pairwise potentials can be chosen to act only from interatomic distances large enough to not perturb regular vibrations. The constraints were applied between all pairs of atoms in the outer shell (atom 1) and all atoms in the outer or second shell (atom 2) if the distance d between atom 1 and 2 is smaller than d1 both in the icosahedron and in the cuboctahedron. A quadratic attractive potential k/2(d − d2)2 with k = 50 eV Å−2 was applied for these pairs for distances d > d2. The distance d1 = 3.0 Å was chosen to capture the nearest neighbor distance and d2 = 3.4 Å was chosen larger, to not significantly perturb regular vibrations. The effect of these additional potentials was carefully checked by varying these parameters. For example for Cu561, at a temperature of 500 K, increasing d2 to 3.8 Å changes the final free energy barrier by 0.02 eV.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author acknowledges support by the state of Baden-Württemberg through bwHPC (bwunicluster and JUSTUS, RV bw17D011). Financial support from the Helmholtz Association is also gratefully acknowledged.References
- K. Koga, T. Ikeshoji and K. I. Sugawara, Phys. Rev. Lett., 2004, 92, 115507 CrossRef PubMed.
- J. M. Rahm and P. Erhart, Nano Lett., 2017, 17, 5775–5781 CrossRef CAS PubMed.
- B. Fleury, R. Cortes-Huerto, O. Tache, F. Testard, N. Menguy and O. Spalla, Nano Lett., 2015, 15, 6088–6094 CrossRef CAS PubMed.
- A. L. Garden, A. Pedersen and H. Jonsson, Nanoscale, 2018, 10, 5124–5132 RSC.
- H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jonsson and X. C. Zeng, Nano Lett., 2015, 15, 682–688 CrossRef CAS PubMed.
- D. M. Foster, R. Ferrando and R. E. Palmer, Nat. Commun., 2018, 9, 1323 CrossRef CAS PubMed.
- R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343–1348 CrossRef CAS.
- K. Sytwu, F. Hayee, T. C. Narayan, A. L. Koh, R. Sinclair and J. A. Dionne, Nano Lett., 2018, 18, 5357–5363 CrossRef CAS PubMed.
- F. Baletto, A. Rapallo, G. Rossi and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 235421 CrossRef.
- D. M. Wells, G. Rossi, R. Ferrando and R. E. Palmer, Nanoscale, 2015, 7, 6498–6503 RSC.
- D. Pearmain, S. J. Park, A. Abdela, R. E. Palmer and Z. Y. Li, Nanoscale, 2015, 7, 19647–19652 RSC.
- P. L. Hansen, J. B. Wagner, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen and H. Topsoe, Science, 2002, 295, 2053–2055 CrossRef CAS PubMed.
- P. Nolte, A. Stierle, N. Y. Jin-Phillipp, N. Kasper, T. U. Schulli and H. Dosch, Science, 2008, 321, 1654–1658 CrossRef CAS PubMed.
- M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B. L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlogl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- R. G. Mariano, K. McKelvey, H. S. White and M. W. Kanan, Science, 2017, 358, 1187–1191 CrossRef CAS PubMed.
- L. Li, P. N. Plessow, M. Rieger, S. Sauer, R. S. Sanchez-Carrera, A. Schaefer and F. Abild-Pedersen, J. Phys. Chem. C, 2017, 121, 4261–4269 CrossRef CAS.
- K. C. Lai and J. W. Evans, Phys. Rev. Mater., 2019, 3, 026001 CrossRef CAS.
- A. L. Mackay, Acta Crystallogr., 1962, 15, 916–918 CrossRef CAS.
- T. Ikeshoji, G. Torchet, M. F. de Feraudy and K. Koga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031101 CrossRef CAS PubMed.
- M. Eckhoff, D. Schebarchov and D. J. Wales, J. Phys. Chem. Lett., 2017, 8, 5402–5407 CrossRef CAS PubMed.
- H.-S. Nam, N. M. Hwang, B. D. Yu, D.-Y. Kim and J.-K. Yoon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 233401 CrossRef.
- C. L. Cleveland, W. D. Luedtke and U. Landman, Phys. Rev. Lett., 1998, 81, 2036 CrossRef CAS.
- H. S. Nam, N. M. Hwang, B. D. Yu and J. K. Yoon, Phys. Rev. Lett., 2002, 89, 275502 CrossRef PubMed.
- D. Schebarchov and S. C. Hendy, Phys. Rev. Lett., 2005, 95, 116101 CrossRef CAS PubMed.
- Z. Zhang, W. Hu and S. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125443 CrossRef.
- D. Schebarchov and S. C. Hendy, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 121402(R) CrossRef.
- L. Pavan, K. Rossi and F. Baletto, J. Chem. Phys., 2015, 143, 184304 CrossRef CAS PubMed.
- K. Rossi, L. Pavan, Y. Soon and F. Baletto, Eur. Phys. J. B, 2018, 91, 33 CrossRef.
- F. Baletto, J. Phys.: Condens. Matter, 2019, 31, 113001 CrossRef PubMed.
- C. Barreteau, M. C. Desjonqueres and D. Spanjaard, Eur. Phys. J. D, 2000, 11, 395–402 CrossRef CAS.
- W. N. Lipscomb, Science, 1966, 153, 373–378 CrossRef CAS PubMed.
- G. Rollmann, M. E. Gruner, A. Hucht, R. Meyer, P. Entel, M. L. Tiago and J. R. Chelikowsky, Phys. Rev. Lett., 2007, 99, 083402 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. K. Nørskov and N. D. Lang, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 2131–2136 CrossRef.
- R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265–6270 CrossRef CAS.
- F. Cleri and V. V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Mogelhoj, V. Petzold, D. D. Landis, J. K. Norskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- T. Bucko, S. Chibani, J. F. Paul, L. Cantrel and M. Badawi, Phys. Chem. Chem. Phys., 2017, 19, 27530–27543 RSC.
- J. P. K. Doye and F. Calvo, Phys. Rev. Lett., 2001, 86, 3570–3573 CrossRef CAS PubMed.
- A. Šiber, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 075407 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley, Hoboken, NJ, USA, 7th edn, 1996 Search PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Hjorth Larsen, J. Jorgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiotz, O. Schutt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- P. N. Plessow, J. Chem. Theory Comput., 2018, 14, 981–990 CrossRef CAS PubMed.
- J. Kastner and W. Thiel, J. Chem. Phys., 2005, 123, 144104 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fitted parameters for the Gupta potential, an extensive study using parameters for the Gupta potential from the literature and the source code used for the Gupta potential. See DOI: 10.1039/d0cp01651a |
| This journal is © the Owner Societies 2020 |


