Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Grand canonical simulations of ions between charged conducting surfaces using exact 3D Ewald summations†
Samuel
Stenberg
 a,
Björn
Stenqvist
a,
Björn
Stenqvist
 b,
Cliff
Woodward
b,
Cliff
Woodward
 c and
Jan
Forsman
c and
Jan
Forsman
 *a
*a
aTheoretical Chemistry, Naturvetarvägen 14, 22362 Lund, Sweden. E-mail: samuel.stenberg@teokem.lu.se; jan.forsman@teokem.lu.se
bPhysical Chemistry, Naturvetarvägen 14, 22362 Lund, Sweden. E-mail: bjorn.stenqvist@teokem.lu.se
cUniversity College, University of New South Wales (ADFA), Canberra ACT 2600, Australia. E-mail: c.woodward@adfa.edu.au
First published on 2nd June 2020
Abstract
We present a useful methodology to simulate ionic fluids confined by two charged and perfectly conducting surfaces. Electrostatic interactions are treated using a modified 3D Ewald sum, which accounts for all image charges across the conductors, as well as the 2D periodicity, parallel to the surfaces. The energy expression is exact, and the method is trivial to implement in existing Ewald codes. We furthermore invoke a grand canonical scheme that utilizes a bias potential, that regulates the surface charge density. The applied bias potential also enables us to calculate individual chemical potentials of the ions. Finally, we argue that our approach leads to a pedagogically appealing description of the Donnan potential, and what it measures in these systems.
1 Introduction
Mechanisms underlying different electrochemical properties of ionic systems confined by polarizable surfaces has attracted much attention recently due to their application in electric double layers capacitors.1–3 Simulating such systems provides a number of challenges, associated mainly with treating the long-range electrostatic interactions that are used to obtain electrochemical properties such as surface potentials and capacitance. Many different methods have been developed to manage electrostatic interactions in ionic fluids confined between two flat conducting electrodes. Examples include solutions to the Poisson equation using expansion methods,4 the ICMMM2D method,5 the ELCIC method,6 mapping schemes,7 direct summations of the image charges8,9 and Gaussian representation of the surface charges.10 However, generally such methods can be difficult to implement with slow convergence. Instead, in this work we implement a different approach which utilizes a double cell that includes the ions and their nearest images to simulate the many-reflected full system via Ewald summation. The Ewald summation has a long history in the simulation of coulombic fluids and has been developed over many decades to become an efficient and valuable tool for researchers. As such, optimized implementations, such as particle mesh Ewald11 and smooth particle mesh Ewald12 can be put to good use to efficiently treat the problem of charged fluids confined by conducting surfaces.One of the difficulties associated with calculating properties such as the capacitance in these systems is that knowledge of the electrode potential relative to a fixed reference is required. While the latter is often chosen to be the bulk fluid, this is not a requirement. Here we show that a generalization of the Ewald approach,13,14 utilizing a grand canonical treatment with single ion insertions and deletions, allows us to maintain a given surface potential relative to a fixed reference, which will generally not be that of the bulk fluid. Single ion insertion and deletions are not usual in grand canonical schemes for charged fluids, due to obvious problems associated with non-electroneutrality. However, this is avoided in the presence of conducting surfaces by the counterbalancing charge of the images.
A specific example, where we expect our method to be particularly useful, is the theoretical study of electric double layer capacitors, sometimes called “supercapacitors”.15–19 This area has attracted substantial experimental and theoretical work.3,15–31 Some experimental data20,21 support the existence of an electrode pore size (typically of the order of nanometers), which maximizes the capacitance of the system. However, controlling and measuring size distributions of nanoporous electrodes is difficult, and the measurements would strongly benefit by complementing theoretical modelling. Mean-field analyses have indeed suggested the presence of “superionic states” in these systems, whereby a very strong electrostatic screening in narrow pores of conducting materials might facilitate dense packing of equally charged species, which in turn can generate a huge capacitance.32 Still, such simple mean-field predictions need validation by more exact treatments, such as simulations. Simulation studies of porous electrodes are notoriously difficult due to the presence of multiple image charges. Dudka et al. have made attempts to circumvent these problems by simulating lattice models of ionic liquids, where interactions are restricted to nearest-neighbours.31 While such models certainly can generate interesting insight, it is nevertheless of considerable interest to be able to utilize a continuum space fluid model, in which Coulomb interactions (including surface polarization) are properly treated.
In the next section, we describe the Ewald method we use to treat the ionic fluid between two conducting surfaces. The original derivation of this model was given by Hautman et al.33 some three decades earlier, but it seems not to have been widely adopted in recent treatments of these systems. The description contained here has some slight differences, in particular, we define a different unit cell which is useful for charged electrodes. Furthermore, as mentioned earlier, we describe the use of a grand canonical ensemble simulation scheme to create charged electrodes with a potential relative to a well-defined reference.
2 Method
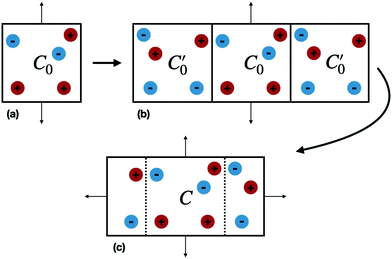
Our system consists of an ionic fluid confined between two infinite and flat perfectly conducting surfaces (electrodes), parallel to the (x, y) plane, and positioned at z = ±h/2. The electrode surface is defined by the dielectric discontinuity, which is assumed to be sharp. In simulations we necessarily restrict the system size to a unit cell, C0, defined by |x| ≤ Lx/2 and |y| ≤ Ly/2, containing a finite number of ions. The simulation box need not be electro-neutral.Periodic boundary conditions (PBC) in the (x, y) directions give an infinite number of adjacent replicas of C0 parallel to the confining electrodes (see Fig. 1(a)), which can be treated using a suitable 2-dimensional (2D) Ewald scheme. The polarization of the two conducting electrodes can be described with image charges, resulting in an infinite number of reflections34 in the two subspaces z > h/2 and z < −h/2. These images give rise to a perpendicular electrostatic field at the dielectric discontinuity, which mimics the equilibrium response of electrons in the conductors. The electrodes thus have a constant potential over their surfaces. The combination of a 2D Ewald scheme with a very large number of explicit image reflections, amounts to a significant computational task for most reasonably sized systems and alternatives to such a straightforward approach are desirable. For example, Santos et al.4 have recently described a more efficient but complex treatment for this system, which utilizes periodic Greens functions and a modified 3D Ewald summation, combined with a separate evaluation of the contribution from surface polarizations.
We now consider the basic isolated unit cell C0 (without images). The images are reintroduced by defining a complementary unit cell, C0′, which consists of the mirror image of C0 reflected in say the left-hand electrode surface. This process not only reflects the particle positions but also reverses the sign of the charges, so the total charge of both cells always add to zero. A similar complementary cell can be obtained by reflection in the right hand surface of C0, see Fig. 1(b). We now define a symmetric electroneutral super-cell, C, consisting of the central cell C0 and the nearest halves of the adjacent complementary cells, see Fig. 1(c). Thus C contains open boundaries, but possesses internal bounding surfaces which correspond to the positions of the original electrodes. Furthermore, though C contains 2N particles, only N are independent, therefore we can write the energy of particles in C as a function of the co-ordinates of particles in the sub-cell C0.
An infinite 3-dimensional array of replicas of C reproduces the original ionic fluid, between two conducting electrodes, and with PBCs along the (x, y) directions. Such an array can be easily treated with usual 3D Ewald methods to obtain the energy of the ions in C, which is numerically equal to the sum of the energy of a sub-cell C0 and a complementary cell, C0′, i.e.,
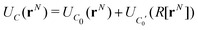 | (1) |
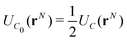 | (2) |
We shall denote this approach as the “Image Ewald” method (IE). We note that in the direction parallel to the surfaces the periodicity may induce crystal artifacts, yet by utilizing isotropic periodic boundary conditions35 in these directions such effects will be mitigated. A direct effect from such a scheme is that the reciprocal-space Ewald forces in the xy-directions will be zero, yet there will be a long-range contribution to the total energy. In our simulations, however, we did not use isotropic boundary conditions.
The total Ewald energy for the cell C will have the general form
| UC(rN) = UC′(rN) + Usurf(rN) | (3) |
However, for the general case of charged electrodes, one needs to take cognizance of the slab geometry. This is because, the surface term will be responsible for creating a potential difference between electrodes. For the slab geometry the surface term is given by,
| Usurf(rN) = 2πMz2/Vcell | (4) |
The IE method described here offers significant computational advantages over many other recent approaches that have been used to deal with such systems, both in terms of efficiency and simplicity of coding. As mentioned earlier, Hautman et al.33 originally described this approach some years ago, however, that work seems not to have gained wide recognition. Since we developed the methodology without prior knowledge of the earlier work by Hautman et al.,33 there are actually some conceptual differences. For example, Hautman et al. used a different type of unit cell consisting of C0 and its adjacent complement C0′. It is clear that even for symmetric, charged electrodes the average dipole moment in such a cell is not zero, giving a non-zero average surface energy in the slab geometry. This would lead to a spurious electric field within the cell that would need to be removed in an ad hoc fashion. We therefore, argue that our choice of unit cell is conceptually preferable. Furthermore, as far as we are aware, the method of Hautman et al. has not been applied to the case of electrodes with a net total surface charge. This is likely because the original formulation uses a Hamiltonian wherein the electrode potentials are specified. Such an approach is precluded when these potentials (relative to a fixed reference) are unknown. We will now show how the IE can be used in a grand canonical ensemble simulation, which naturally gives rise to net charged electrodes and solves the problem of specifying a fixed reference potential.
2.1 Grand canonical simulations
To simulate ionic fluids bound by electrodes we used the Grand Canonical (Metropolis) Monte Carlo (GCMC) method. When employing the GCMC method it is usual to choose an initially electroneutral configuration with subsequent insertions and deletions of electroneutral combinations of ions. These ions are imagined to be taken to or from a fictitious bulk, and it is useful to define an “average” (experimentally measurable) chemical potential per ion, μsalt. This can be obtained by averaging the individual chemical potentials, μind, i.e.,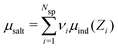 , where Nsp is the number of species with different valencies Zi. The coefficients νi satisfy
, where Nsp is the number of species with different valencies Zi. The coefficients νi satisfy 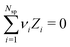 and
and 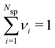 . Individual ion chemical potentials are experimentally elusive to measure, but it is relevant to note that, given the definition of μsalt, it is possible to write the individual ion chemical potentials as,
. Individual ion chemical potentials are experimentally elusive to measure, but it is relevant to note that, given the definition of μsalt, it is possible to write the individual ion chemical potentials as,| μind(Zi) = μsalt − ZieΨref | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z electrolyte in the restricted primitive model (RPM) Ψref = 0, (see ESI†) but it is non-zero in a 2
Z electrolyte in the restricted primitive model (RPM) Ψref = 0, (see ESI†) but it is non-zero in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 model, for example. Hence, the IE provides a method to determine μind(Zi), as we will explicitly demonstrate below, where we also compare IE results with those from the established modified Widom technique.36
1 model, for example. Hence, the IE provides a method to determine μind(Zi), as we will explicitly demonstrate below, where we also compare IE results with those from the established modified Widom technique.36
In our simulation method, electroneutrality is always maintained by the correlated presence of oppositely charged ions in the complementary C0′ sub-cell. This is physically equivalent to the creation of counter-balancing image charges in the conducting electrodes and allows us to perform simulations at constant electrode potential, rather than constant electrode charge, using single ion insertions and deletions. Constant potential systems are arguably more relevant to real experimental scenarios. The fluctuating electrode surface charge density, σS, will have an average value 〈σS〉 that can be regulated by application of a constant potential that will bias either anions or cations via the chemical potentials. With a μsalt for a given bulk electrolyte, “effective” individual ion chemical potentials are constructed using
| μeff(Zi) = μsalt − ZieΨbias | (6) |
2.2 Simulation details
The ionic fluid was modelled using the RPM wherein the solvent only enters via the dielectric constant, εr = 78.3. At a temperature of 298 K, this gives a Bjerrum length of about 7.16 Å. In order to highlight some interesting aspects of asymmetric electrolytes, we assumed a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt, consisting of divalent and opposing monovalent charges embedded in hard spheres of diameter 5 Å. Generalization to other kinds of salt is straightforward. The Ewald sums used a minimum image cutoff in the real space sum. We set Lx = Ly = 200 Å, and used an equal number of reciprocal wave vectors in the Fourier sum along the reciprocal z as in the reciprocal (x, y) directions, with a suitable symmetrization in the latter case.37 A total of 1800 vectors were used for the Fourier component. The Ewald splitting parameter, often denoted as α, was set to 7/Lx. At least 2 × 107 configurations were used for the final production runs, subsequent to equilibrations, which used even more configurations.
1 salt, consisting of divalent and opposing monovalent charges embedded in hard spheres of diameter 5 Å. Generalization to other kinds of salt is straightforward. The Ewald sums used a minimum image cutoff in the real space sum. We set Lx = Ly = 200 Å, and used an equal number of reciprocal wave vectors in the Fourier sum along the reciprocal z as in the reciprocal (x, y) directions, with a suitable symmetrization in the latter case.37 A total of 1800 vectors were used for the Fourier component. The Ewald splitting parameter, often denoted as α, was set to 7/Lx. At least 2 × 107 configurations were used for the final production runs, subsequent to equilibrations, which used even more configurations.
For all simulation results presented in the main article, we have set βμsalt = −10.7 where β is the inverse thermal energy. In the ESI,† we provide results for other scenarios, including a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt, and a monovalent salt where the cations carry a non-central charge.
1 salt, and a monovalent salt where the cations carry a non-central charge.
3 Results
A quantity of interest is the average electrostatic potential, Ψ(z), which can be evaluated by integration of the average charge density profile, as described in the ESI.† This calculation simply adds the direct contributions from the charge densities and (due to symmetry) will always give a value of zero, for the potential at the electrode surfaces. Fig. 2(a) and (b) shows the average electrostatic potential Ψ(z) profiles from our GCMC simulations, using IE, with a slit of width, h = 145 Å. This is obviously large enough to produce a bulk fluid in the mid-plane region as evidenced by the flat profile there. Two different Ψbias are chosen, and these are compared with the result for Ψbias = 0. Normally, we measure Ψ(z) relative to the bulk, which requires addition of a constant potential correction, called the “Donnan potential”,38ΨDonn, due to charge distributions external to the slit. Due to the asymmetry of the electrolyte model, ΨDonn is not simply equal to Ψbias, since there is a finite Ψref in the bulk. From eqn (6) and (5) can write,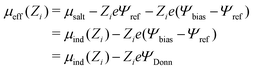 | (7) |
| Ψ(z = 0) → −ΨDonn | (8) |
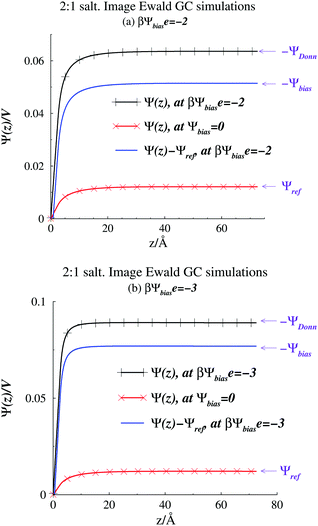 | ||
| Fig. 2 Average potential profiles, as obtained from Image Ewald simulations. (a) βΨbiase = −2. The profile for Ψbias = 0 is also shown. (b) βΨbiase = −3. The profile for Ψbias = 0 is also shown. | ||
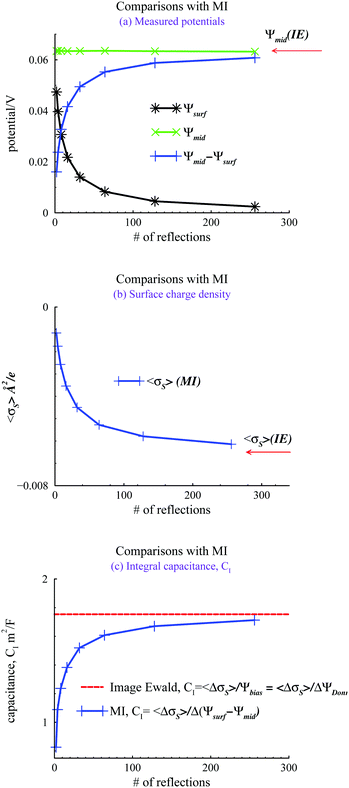
We evaluated the IE by comparing it with a more straightforward approach, where we use GCMC simulations, as discussed above, but explicitly evaluate a finite number of multiple image reflections between the electrodes. Previous work has noted that convergence of the sum of reflected images is facilitated by using an even number of terms.9 Further details are also provided in the ESI.† We also used the minimum image (MI) convention to treat the PBC in the x, y directions, rather than Ewald sums. Hence we use the acronym MI to denote this approach. In the MI method, long-range interactions outside the MI truncation were estimated by an “external” mean-field potential,39,40 from previously established average charge densities, appropriately symmetrized, and adjusted so that the external potential vanishes at the surfaces. It should be noted that the inclusion of this long-range correction only had a small influence on the properties investigated here, i.e. the results were very similar to those obtained with a simple MI truncation, without any long-range correction. Fig. 3 summarizes our comparisons between the IE and MI approaches for βΨbiase = −2 and h = 145 Å. As noted above this width is sufficient to produce bulk conditions in the center of the slit.
In Fig. 3(a), we note how the MI method gives a surface value of Ψ(z), which varies significantly from zero, with the number of reflections used. The potential difference between the mid-plane and the surface in the MI does approach the IE result asymptotically but the convergence is quite slow. Surprisingly, these results indicate that the mid-plane potential from the MI actually displays only a modest variation with the number of image reflections, and is in all cases rather close to the value obtained by the IE. One could then be tempted to just assume that Ψ(z) is zero at the surface and use the mid-plane value to set the surface potential relative to the bulk (recall that the negative of the mid-plane value is equal to the proper reference surface potential). However, such a strategy belies other serious errors obtained with too few reflections. For example, in Fig. 3(b), we see that the average surface charge density varies strongly with the number of image reflections, only slowly converging towards the IE value. In Fig. 3(c), we compare predictions of the integral capacitance CI. Using Image Ewald, this is simply obtained as CI = 〈ΔσS〉/Ψbias, where 〈ΔσS〉 is the difference between the average surface charge density at Ψbias and the average surface charge density at with a vanishing bias potential (i.e. Ψbias = 0). However, with the MI approach, we have to account for truncation errors, which leads to a finite (local) surface potential. Interestingly enough, the capacitance converges faster towards the Image Ewald value than the net potential, or the average surface charge density. This is obviously due to a cancellation of errors. It should be emphasized that since we generally would define the differential capacitance (CD) as CD = Δσs/ΔΨDonn = Δσs/ΔΨbias, we do not need to establish Ψref, to generate a CD curve. This is a significant advantage for narrow pores (slits).
We now turn our attention to the individual chemical potentials, μind. Using eqn (5) we calculate μind for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 RPM salt using our method, by setting Ψbias = 0 and measuring Ψref. We compare with results from the modified Widom technique using canonical bulk simulations, a cubic box, and Coulomb interactions that are truncated by the minimum image convention. The canonical densities were given by the mid-plane density from grand canonical IE simulations, at zero applied bias potential. Size convergence was estimated by simulating three different simulation box sizes, using the modified Widom method. The results are summarized in Fig. 4, where the standard deviations from the canonical simulations are smaller than the size of the symbols, and therefore not indicated. We note a modest but significant size dependence of the modified Widom simulations, but also that the large size limit seems to approach the Image Ewald result.
1 RPM salt using our method, by setting Ψbias = 0 and measuring Ψref. We compare with results from the modified Widom technique using canonical bulk simulations, a cubic box, and Coulomb interactions that are truncated by the minimum image convention. The canonical densities were given by the mid-plane density from grand canonical IE simulations, at zero applied bias potential. Size convergence was estimated by simulating three different simulation box sizes, using the modified Widom method. The results are summarized in Fig. 4, where the standard deviations from the canonical simulations are smaller than the size of the symbols, and therefore not indicated. We note a modest but significant size dependence of the modified Widom simulations, but also that the large size limit seems to approach the Image Ewald result.
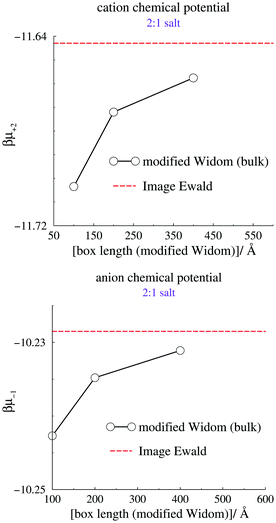 | ||
| Fig. 4 Calculated individual chemical potentials for the cation (top) and anion (bottom). The dashed line indicates the value acquired using Image Ewald simulations, combined with eqn (5). | ||
4 Conclusions
In summary, we have utilized a simple and effective way to manage long-range interactions, using an exact model of infinite image reflections, in systems where an ionic fluid is confined between two charged (in general), planar, and perfectly conducting surfaces, or electrodes. Note that “confined” should be interpreted with some care, since our grand canonical method ensures that the fluid is in chemical equilibrium with a bulk solution, at some prescribed chemical potential. Using wide surface separations, our system will accurately approximate the behaviours at a single electrode surface and we are able to calculate the individual chemical potentials. An important advantage is that we are also able to model a porous electrode, by utilizing a short surface separation. Our method relies on straightforward 3D Ewald techniques, which are wide-spread, and can therefore be highly optimized using particle-mesh Ewald, smooth particle-mesh Ewald etc., to achieve a computational scaling of![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N
(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N), where N is the number of charges in the system. Hence, the Image Ewald method is suitable for a multitude of system setups. One such case is the study of electrochemical behaviours of salt solutions and ionic liquids, in the presence of nanoporous electrodes. Finally, we note that while we have utilized the Metropolis Monte Carlo technique in this work, the IE method can naturally be directly implemented in molecular dynamics codes.
N), where N is the number of charges in the system. Hence, the Image Ewald method is suitable for a multitude of system setups. One such case is the study of electrochemical behaviours of salt solutions and ionic liquids, in the presence of nanoporous electrodes. Finally, we note that while we have utilized the Metropolis Monte Carlo technique in this work, the IE method can naturally be directly implemented in molecular dynamics codes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. F. acknowledges financial support by the Swedish Research Council.Notes and references
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- E. Frackowiak, Phys. Chem. Chem. Phys., 2007, 9, 1774–1785 RSC.
- S. Kondrat, N. Georgi, M. V. Fedorov and A. A. Kornyshev, Phys. Chem. Chem. Phys., 2011, 13, 11359–11366 RSC.
- A. P. dos Santos, M. Girotto and Y. Levin, J. Chem. Phys., 2017, 147, 184105 CrossRef PubMed.
- S. Tyagi, A. Arnold and C. Holm, J. Chem. Phys., 2007, 127, 154723 CrossRef PubMed.
- S. Tyagi, A. Arnold and C. Holm, J. Chem. Phys., 2008, 129, 204102 CrossRef PubMed.
- R. Kjellander and S. Marcelja, J. Chem. Phys., 1985, 82, 2122–2135 CrossRef CAS.
- D. Bratko, B. Jönsson and H. Wennerström, Chem. Phys. Lett., 1986, 128, 449–454 CrossRef CAS.
- R. Szparaga, C. E. Woodward and J. Forsman, Soft Matter, 2015, 11, 4011–4021 RSC.
- S. K. Reed, O. J. Lanning and P. A. Madden, J. Chem. Phys., 2007, 126, 084704 CrossRef PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- T. M. Nymand and P. Linse, J. Chem. Phys., 2000, 112, 6152–6160 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- Y. Bai, Y. Cao, J. Zhang, M. Wang, R. Li, P. Wang, S. M. Zakeeruddin and M. Grätzel, Nat. Mater., 2008, 7, 626–630 CrossRef CAS PubMed.
- S. Ito, S. M. Zakeeruddin, P. Comte, P. Liska, D. Kuang and M. Grätzel, Nat. Photonics, 2008, 2, 693–698 CrossRef CAS.
- V. Lockett, R. Sedev, J. Ralston, M. Horne and T. Rodopoulos, J. Phys. Chem. C, 2008, 112, 7486–7495 CrossRef CAS.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- J. Chimola, G. Yushin, Y. Gogotsi, C. Portret, P. Simon and P. Taberna, Science, 2006, 313, 1760 CrossRef PubMed.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 12629–12631 CrossRef CAS PubMed.
- J. Forsman, C. E. Woodward and M. Trulsson, J. Phys. Chem. B, 2011, 115, 4606–4612 CrossRef CAS PubMed.
- D.-e. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- C. E. Szparaga, R. Woodward and J. Forsman, J. Phys. Chem. C, 2012, 116, 15946 CrossRef.
- C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687–7693 CrossRef CAS.
- C. Merlet, D. T. Limmer, M. Salanne, R. van Roij, P. A. Madden, D. Chandler and B. Rotenberg, J. Phys. Chem. C, 2014, 118, 18291–18298 CrossRef CAS.
- A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2753–2757 CrossRef CAS PubMed.
- M. Dudka, S. Kondrat, O. Benichou, A. A. Kornyshev and G. Oshanin, J. Chem. Phys., 2019, 151, 184105 CrossRef PubMed.
- S. Kondrat and A. Kornyshev, J. Phys.: Condens. Matter, 2010, 23, 022201 CrossRef PubMed.
- J. Hautman, J. W. Halley and Y. Rhee, J. Chem. Phys., 1989, 91, 467–472 CrossRef CAS.
- M. M. Hatlo and L. Lue, Soft Matter, 2008, 4, 1582–1596 RSC.
- B. Stenqvist and M. Lund, EPL, 2018, 123, 10003 CrossRef.
- B. R. Svensson and C. E. Woodward, Mol. Phys., 1988, 64, 247–259 CrossRef CAS.
- B. A. Wells and A. L. Chaffee, J. Chem. Theory Comput., 2015, 11, 3684–3695 CrossRef CAS PubMed.
- F. G. Donnan, Z. Elektrochem. Angew. Phys. Chem., 1911, 17, 572 CAS.
- G. M. Torrie and J. P. Valleau, J. Chem. Phys., 1980, 73, 5807–5816 CrossRef CAS.
- B. Jönsson, H. Wennerström and B. Halle, J. Phys. Chem., 1980, 84, 2179 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01640c |
| This journal is © the Owner Societies 2020 |