Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A molecular perspective on Tully models for nonadiabatic dynamics†
Lea M.
Ibele
and
Basile F. E.
Curchod
 *
*
Department of Chemistry, Durham University, South Road, Durham DH1 3LE, UK. E-mail: basile.f.curchod@durham.ac.uk
First published on 25th June 2020
Abstract
Over the past decades, an important number of methods have been developed to simulate the nonadiabatic dynamics of molecules, that is, the dynamics of molecules beyond the Born–Oppenheimer approximation. These nonadiabatic methods differ in the way they approximate the dynamics emanating from the time-dependent molecular Schrödinger equation. In 1990, Tully devised a series of three one-dimensional model systems to test the approximations of the method called trajectory surface hopping. The Tully models were designed to probe different scenarios of nonadiabatic processes, such as single and multiple nonadiabatic (re)crossings. These one-dimensional models rapidly became the testbed for any new nonadiabatic dynamics strategy. In this work, we present a molecular perspective to the Tully models by highlighting a correspondence between these simple one-dimensional models and processes happening during the excited-state dynamics of molecules. More importantly, each of these nonadiabatic processes can be connected to a given exemplary molecular system, and we propose here three molecules that could serve as molecular Tully models, reproducing some of the key features of the original models but this time in a high-dimensional space. We compare trajectory surface hopping with the ab initio multiple spawning for the three molecular Tully models and highlight particular features and differences between these methods resulting from their distinct approximations. We also provide all the necessary information – initial conditions and all required parameters for the dynamics as well as the electronic structure – employed in our simulations such that the molecular Tully models can become in the future a unified and standardized test for ab initio nonadiabatic molecular dynamics methods. The molecular Tully models also offer an exciting link between the world of low-dimensional model systems for nonadiabatic dynamics and the excited-state dynamics of molecular systems in their full dimensionality.
I Introduction
Simulating the dynamics of photoexcited molecules is often hampered by the complexity brought about by the breakdown of the Born–Oppenheimer approximation.1,2 As a result, one should account explicitly for the coupling between electronic and nuclear motion in the dynamics – the nonadiabatic effects – as well as some additional quantum nuclear effects. Achieving this implies, in principle, the solution of the time-dependent molecular Schrödinger equation – a task hardly possible for anything but the smallest molecular systems or models. Approximations to this equation are required to investigate the photochemistry and photophysics of molecules in their full dimensionality, and often imply to choose a representation for the molecular wavefunction.3Most methods for nonadiabatic dynamics start by expressing the molecular wavefunction in the Born–Huang representation, leading to a picture of photochemistry where a nuclear wavefunction evolves on a given potential energy surface and can transfer nuclear amplitude in regions of strong nonadiabaticity to a different electronic state. Within this framework, the most accurate methods represent the electronic structure quantities and the nuclear wavefunctions on a grid and solve the nuclear time-dependent Schrödinger equations in a numerically exact manner. The multiconfigurational time-dependent Hartree (MCTDH) method4–7 belongs to this family of techniques and is perceived as the gold standard for nonadiabatic dynamics. Due to their computational cost and the fact that they require the precalculation of potential energy surfaces, grid-based approaches for quantum dynamics cannot treat molecules of more than six or seven atoms in their full dimensionality and are therefore limited to a subset of the total number of nuclear degrees of freedom for larger molecular systems.
Hence, additional approximations are required if one wishes to simulate the nonadiabatic dynamics of molecules in their full configuration space – what we call here nonadiabatic molecular dynamics. An impressive number of methods have been proposed for this task over the last decades, and we focus our attention here only on the most employed techniques. One strategy consists in expanding the nuclear wavefunctions using trajectory basis functions (TBFs).8 Members of this family of methods include the variational multiconfigurational Gaussian (vMCG),9–11 the multiconfigurational Ehrenfest (MCE),12–14 or the Full and Ab Initio Multiple Spawning (FMS and AIMS).15–17 While being formally exact, the overall accuracy of these methods depends on the number of basis functions used and the way the TBFs are coupled together. At a more approximate level of theory, the mixed quantum/classical method called trajectory surface hopping (TSH)18–21 offers an appealing (yet intrinsically approximated) description of nonadiabatic molecular processes. TSH will be described in more detail below, but it is sufficient to picture it at this stage as a way to represent the dynamics of nuclear wavepackets by using independent classical trajectories that can hop between electronic states, mimicking nonadiabatic transitions. Owing to its simplicity, TSH has become the preferred method for nonadiabatic molecular dynamics.20,22 While all the strategies described in this paragraph can employ precomputed potential energy surfaces and nonadiabatic couplings for the nuclear dynamics, they are also compatible with on-the-fly dynamics, that is, when the electronic-structure quantities required to perform the nuclear dynamics are not precomputed but calculated at each time step.
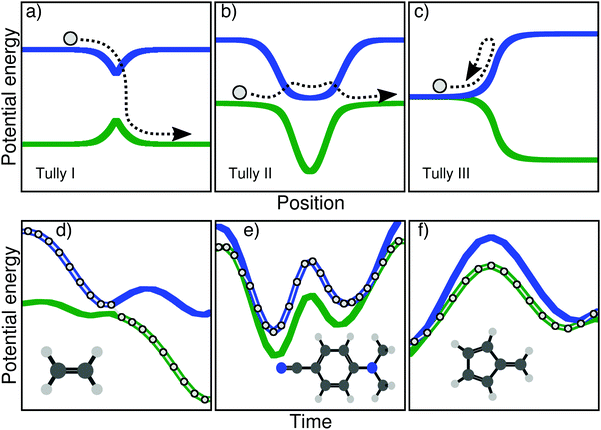
But prior to any actual application aiming at either explaining experimental observations or predicting a particular molecular behavior, one has to duly test the approximations of a given nonadiabatic method and determine the limitations that such approximations impose on the use of the technique. To this end, Tully proposed a series of three tests in his seminal article on TSH, later called the Tully models, which are depicted in the upper panel of Fig. 1. A model in this context corresponds to (i) predefined potential energy curves and nonadiabatic couplings between electronic states – the focus here being on the nuclear dynamics and not the electronic structure – and (ii) initial conditions for the nuclear dynamics – initial position and momentum of the nuclear wavepacket/trajectories. The Tully models are one-dimensional, and the potential energy curves and couplings are expressed analytically (in a diabatic representation).
The main goal of these three models (upper panel of Fig. 1) was to test different processes observed during a typical nonadiabatic dynamics and see how approximate methods performed in comparison to exact quantum dynamics simulations. We describe here briefly the main ideas of each model and will give more details on the physics they probe in Section III. The Tully model I (Fig. 1a) exemplifies a simple nonadiabatic event where a one-dimensional particle, whose initial state is described by a nuclear wavepacket in say the first excited electronic state (blue curve), reaches an avoided crossing and can transfer towards the ground electronic state (green curve). The Tully model II (Fig. 1b) depicts a somewhat more complicated process, where the particle encounters two different nonadiabatic regions (dual avoided crossing). The nuclear wavepacket describing the state of the particle can ‘branch’ in the first coupling region – part of the amplitude in the original electronic state is transferred to the coupled state – and the two wavepackets can meet again in the second coupling region. Interferences are possible if the two nuclear wavepackets recohere at the second coupling, and their importance will vary as a function of the initial momentum of the particle. The Tully model III (Fig. 1c) offers a way to test reflection processes: the two potential energy curves are nearly degenerate at the beginning of the dynamics, and a nonadiabatic coupling region is located just before the near-degeneracy is lifted. When the particle, initially on the ground state, is transferred onto the upper state after the crossing, it may reflect back towards the coupling region if its momentum is too small to overcome the repulsive potential. We will discuss later how these different processes stress the approximation of nonadiabatic methods.
Since their publication in 1990, the simple model systems described above have been extensively used to assess the quality of newly-developed methods or test new approximations or corrections proposed for existing ones. The diversity of strategies tested with some or all of Tully models is astonishing. It includes, among others, full multiple spawning,15 semiclassical initial value representation,23 symmetrical quasi-classical windowing combined with Meyer–Miller mapping Hamiltonian,24 surface hopping Herman–Kluk semiclassical initial value representation method,25 semiclassical Monte-Carlo,26 dephasing representation of quantum fidelity,27 counter-propagating wave methods trajectories,28 Ehrenfest-Plus,29 coupled-trajectory mixed quantum/classical dynamics,30,31 quantum trajectory mean-field approach,32 iterative linearized approach to nonadiabatic dynamics,33 mean-field dynamics with stochastic decoherence,34 nonadiabatic Bohmian dynamics,35,36 mean-field molecular dynamics with surface hopping,37 non-Hermitian surface hopping,38 multi-state trajectory approach to nonadiabatic dynamics,39 partial linearized density matrix dynamics,40 ring polymer surface hopping,41 quantum trajectory surface hopping,42 consensus surface hopping,43 or quasiclassical mapping Hamiltonian methods.44 The Tully models were also used to assess decoherence in nonadiabatic dynamics or to test newly-developed decoherence corrections for the TSH, see ref. 45–52 for examples.
As mentioned earlier, the Tully models probe interesting physical phenomena caused by nonadiabatic effects, but how well do these one-dimensional models connect with the nonadiabatic processes observed in (high-dimensional) molecules? In other words, the original one-dimensional Tully models are employed to test the approximations of nonadiabatic methods which will be used for high-dimensional molecular systems, but are the nonadiabatic mechanisms probed in one dimension representative of the coupled electron–nuclear processes a molecule can suffer? This question is legitimate already from an electronic structure perspective, as moving from one to two nuclear degrees of freedom forces us to account for conical intersections (in the adiabatic representation).53–56 Moving to an even higher number of nuclear degrees of freedom allows us to define a two-dimensional branching space – coordinates along which the electronic degeneracy is lifted – as well as the 3Nn − 8 dimensional intersection seam – along which the electronic degeneracy is preserved, Nn being the number of nuclei. Conical intersections are known to be ubiquitous in the photodynamics of molecular systems and responsible for ultrafast funneling processes between electronic states. Hence, can we connect some typical nonadiabatic processes occurring in molecular systems to some of the features of the simpler one-dimensional Tully model? Achieving this goal will offer a series of molecular models to compare nonadiabatic molecular dynamics methods among each other in the full nuclear dimensionality of molecules. There is a consensus in the community that such unified hard benchmark tests,57 using models in higher dimensions, would be highly beneficial for benchmarking the different methods available and dissect their approximations. The Libra library is a project going towards this direction.58 We propose here three molecules, serving as typical examples of key nonadiabatic processes for molecular systems, that can be seen as a set of molecular Tully models and a new tool towards a more general mean of comparison between methods for nonadiabatic dynamics.
Let us start by highlighting different nonadiabatic processes that can take place during the excited-state dynamics of a molecule and be connected to key features of the original Tully models. A caveat is needed at this stage: the categories discussed below are not intended to fully represent the huge diversity of mechanisms in nonadiabatic molecular dynamics but are only meant to draw some (hopefully general) parallels with the nonadiabatic processes probed in the original Tully models. Upon photoexcitation, certain molecules exhibit an efficient decay back to the ground electronic state mediated by one or more (peaked) conical intersections. A characteristic of such nonadiabatic dynamics is that electronic states are connected by mostly one efficient nonadiabatic event – or one passage through a conical intersection. Such ultrafast and efficient decay processes are clearly connected with the Tully model I – a single crossing event between a pair of electronic states (Fig. 1a). Examples from the literature of such photodynamics could be simple photoisomerization processes like the one of ethylene,59 protonated formaldimine,60 or retinal.61 Other molecules may suffer a nonradiative decay characterized by numerous passages through a given intersection seam between a pair of electronic states. This behaviour is observed when a pair of electronic states remain close in energy, such that the photoexcited molecule can exchange between them several times. This kind of photodynamics can be related to the Tully model II – multiple crossings between two electronic states (Fig. 1b). As examples of this category, one can mention molecules having coupled electronic states with different characters close in energy (4-N,N′-dimethylaminobenzonitrile, DMABN, see below), or molecules suffering photodissociation with electronic states getting close in energy, stimulating multiple crossings (see for example 1,2-dithiane62). Another possible outcome of a nonadiabatic dynamics can be observed when a molecule hits a sloped conical intersection with a specific topography. The molecule can transfer to a different electronic state following the passage through the intersection, but soon after will reflect back towards the same region of the intersection seam where a novel nonadiabatic event can take place. Such a nonradiative decay, involving subsequent passages through a nonadiabatic region caused by a reflection process, is reminiscent to the dynamics observed at low kinetic energy in the Tully model III (Fig. 1c). As compared to efficient funneling processes involving peaked conical intersections (as mentioned above), sloped intersections are known to slow down the transfer of populations between the coupled electronic states.63 Such nonadiabatic dynamics proceeding via a sloped intersection and involving a form or reflection process was observed for example in up-funnelings during collision processes,64 as one contribution to the nonradiative deactivation of fulvene,65 or in diabatic trappings.66
In this work, we present three molecules that, upon electronic excitation, exemplify the typical nonadiabatic processes described above and therefore constitute a molecular version of the original Tully models. The original model potentials proposed by Tully may look somehow ‘artificial’ (in particular the second and third model), but the correspondence with the processes described in the previous paragraph becomes clearer if, instead of looking at the potential energy curves as a function of position, one plots them as a function of time. In other words, one could compare the potential energy curves as a function of time, drawn by the dynamics of a molecule. In the upper panel of Fig. 1, we show this dynamics in the Tully models by sketching the trajectory of a particle. The lower panel of Fig. 1 shows the electronic energies as a function of time for a full atomistic nonadiabatic molecular dynamics of ethylene, DMABN, and fulvene. In the simple case of ethylene (Fig. 1d), one sees a trivial correspondence between the molecular trajectory and the one of the particle, both exhibiting a single nonadiabatic event. For the case of DMABN (Fig. 1e), the molecule, originally on the green (potential energy) curve, jumps to the blue curve after a nonadiabatic transition, before going back to the green curve due to a passage through a second different nonadiabatic region. The fulvene case (Fig. 1f) shows an example of reflection following nonadiabatic transition, where the molecule transfers from the blue to the green curve, reflects, and goes back to the same region of the intersection space, mimicking the one-dimensional trajectory of the Tully model III. (We note that in this latter case, the reflection for fulvene occurs on the ground state while it takes place on the excited state in the original Tully model III.) At this stage, it is worth noting that several deactivations paths can compete in any nonadiabatic processes. For example, the particle in the Tully model II could also remain adiabatically on the lower potential energy curve – a branching of the initial nuclear wavepacket in two contributions after the first nonadiabatic event. Such a diversity in the possible outcomes after a nonadiabatic transition is likely to be further enhanced for molecular systems as a natural consequence of the larger number of nuclear degrees of freedom. The increase in nuclear degrees of freedom also comes with alternative fates for the photoexcited molecule. Coming back to the previous example, the original Tully model II offers the possibility to observe a recoherence in the second nonadiabatic region, when the branched nuclear wavepackets recombine. In molecular systems, it is likely that, while the molecule may hit multiple times the same intersection seam, it will do so at a different region of the seam, limiting the possibilities of interferences between the branched nuclear wavepackets. Hence, Fig. 1 is only an illustration of selected possible trajectories that depict some of the interesting phenomena observed in the original Tully models (a more detailed comparison between the molecular and original models will be proposed below).
In the following, we show that ethylene, DMABN, and fulvene offer an interesting molecular version of the original Tully models for testing nonadiabatic molecular dynamics methods. For each molecule, we propose a detailed comparison of the nonadiabatic dynamics obtained with TSH, TSH with decoherence correction, and AIMS, using the same level of electronic-structure theory and defining a common set of initial conditions. While an exact solution of the time-dependent molecular Schrödinger equation is clearly out of reach for such large molecular systems, we highlight specific features of the nonadiabatic dynamics for each molecule that can be used to probe the approximations of other nonadiabatic methods. As mentioned earlier, one of the key interests of the Tully models is that they are easily transferable to any nonadiabatic methods, being based on analytical potential energy curves and couplings as well as a clear definition of the initial conditions. While such transferability is more challenging to achieve for ab initio nonadiabatic dynamics, we give access here to all the initial conditions, parameters, and simulation protocol for our simulations, hoping that it will render the use of our molecular models as straightforward as possible and stimulate the community to employ them as a test set for ab initio nonadiabatic molecular dynamics.
II Methodology
A. Theoretical considerations
In the following, we introduce three molecular Tully models to test methods for nonadiabatic molecular dynamics. We use two of the most commonly employed strategies for nonadiabatic dynamics, TSH and AIMS, to test these models and extract some interesting features that can be used for comparison with other methods in the future. We propose here a brief introduction to AIMS and TSH in the context of nonadiabatic dynamics, highlighting their respective approximations. The interested reader is referred to ref. 8 and 67 for general reviews on AIMS, including a comparison of its formalism with that of TSH, ref. 21 for a presentation of TSH and its different flavors, and ref. 3 for a general overview of nonadiabatic molecular dynamics.A typical TSH run is started in a similar way as AIMS: an independent classical trajectory is initiated in a selected electronic state, with initial conditions for the nuclear positions and momenta also chosen from a given quantum distribution. The classical trajectory is propagated adiabatically and, after each nuclear time step, the fewest-switches algorithm dictates stochastically whether the TSH trajectory has to remain on this electronic state or hop to another one. The TSH trajectory is propagated until a particular predefined criterion is reached. This full sequence is repeated for many independent trajectories to converge the TSH result with respect to (i) the initial conditions and (ii) the stochastic algorithm triggering the nonadiabatic transitions.
As stated above, the number of TBFs will grow during an AIMS run as a result of nonadiabatic transitions. As such, AIMS does require fewer runs than TSH to converge, as the latter needs more runs to ensure a proper convergence of the hopping algorithm.82 For an optimal comparison between AIMS and TSH, we adopt a strategy where a given number of initial conditions are sampled from a Wigner distribution (for uncoupled harmonic oscillators) and used for both TSH and AIMS. However, ten TSH runs are generated for each set of initial conditions by altering the seed for the random number generator used in the hopping algorithm.83 As a result, each TSH run starting from the same initial condition can produce different trajectories due to a different hopping pattern. The strategy of using multiple TSH runs for each initial condition allows for a better convergence of the fewest-switches algorithm and dramatically improves the comparison with the AIMS result while using a common set of initial conditions.83
B. Computational details
The AIMS dynamics were performed with the AIMS/MOLPRO interface.97 The TBFs were propagated with a time step of 20 a.u., reduced to 5 a.u. in coupling regions. The threshold to enter the spawning mode was fixed to 3.0 a.u.−1 for ethylene and 10.0 a.u.−1 for fulvene (norm of the nonadiabatic coupling vector). Spawning was only allowed for TBFs with a minimum population of 0.01. For ethylene, TBFs spawned on the ground state were removed from the propagation if they had been uncoupled to any other TBFs for more than 200 a.u., and the limit of allowed violation of classical energy was set to 0.03 a.u. This limit for energy conservation was set to 0.01 a.u. for fulvene. The results of AIMS dynamics for DMABN were taken from ref. 98, where the spawning threshold (defined in this case as the scalar product of the nonadiabatic coupling vectors and the nuclear velocities) was set to 0.005 a.u.−1, and the minimum TBF population required to spawn was 0.1.
The TSH simulations were carried out with the SHARC 2.0 program.99–101 The same initial conditions as in the AIMS dynamics were used, but every trajectory was repeated using 10 different random seeds to improve the convergence of the fewest-switches stochastic process associated to nonadiabatic transitions as described above. Hence, a total of 660 TSH runs were performed for ethylene, 210 for DMABN, and 180 for fulvene. A nuclear time step of 0.5 fs was used (∼20 a.u.), a local diabatization scheme was employed, and nonadiabatic couplings were obtained from wavefunction overlaps instead of computing explicitly the nonadiabatic coupling vectors.102 Velocity rescaling following a surface hop was performed along the nuclear momenta (unless otherwise stated).
The TSH simulations were carried out with and without the energy-based decoherence correction80,83 (EDC), which dampens the electronic amplitudes of TSH in case of decoherence. The EDC was used as implemented by default in SHARC, and the same set of random seeds were used for the simulation with and without decoherence correction to ensure a proper comparison. We note here that we used the original implementation of the EDC, where the TSH amplitudes of the non-running states are damped. Recent discussions revealed that the TSH populations, instead of amplitudes, should have been corrected, as done for example in Newton-X.80,103,104 We tested the stability of our results with respect to both ways of imposing the EDC and did not observe major variations. We finally note that all the TSH trajectories employing the EDC strictly satisfy the internal consistency criterion detailed in ref. 83.
III Description of the molecular Tully models – results and discussion
In the following, we discuss the three molecular Tully models, the resulting nonadiabatic molecular dynamics using TSH and AIMS, as well as interesting observations for each dynamics.A. Molecular Tully model I – ethylene
Ethylene is the simplest example of a molecule showing photoinduced isomerization through conical intersections, and its photodynamics highlighted the importance of moving beyond a simple one-dimensional model to study qualitatively this photoisomerization.59 The nonadiabatic dynamics of ethylene from its first excited singlet state has been the subject of numerous theoretical studies, employing a variety of approaches such as wavepacket propagation,105 TSH (see e.g., ref. 106–111), AIMS (see for example ref. 69, 112–116), MCTDH,117 MCE,13 or the partial linearized path-integral and symmetrical quasi-classical approach within a quasi-diabatic propagation.89All methods predict a very similar behavior for the excited ethylene: after photoexcitation to the bright ππ* state (S1), internal conversion to the ground state occurs rapidly through two possible conical intersections. However, the ultrafast deactivation occurs in a Tully-I like manner, that is, the nuclear wavepacket only undergoes a single nonadiabatic event via one or the other conical intersection. Thanks to its straightforward dynamical behavior, ethylene has already been used in several studies to demonstrate the performance of on-the-fly nonadiabatic molecular dynamics methods, for example in ref. 13, 88, 89 and 110. However, these benchmarks were not performed on a common set of initial conditions or using similar electronic structure methods, and with the exception of ref. 89 have not been consistently compared to other nonadiabatic dynamics methods.
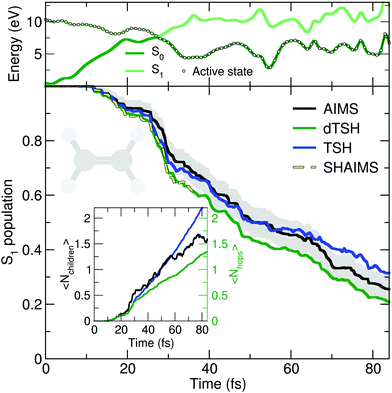
The deactivation of ethylene from its S1 state was simulated with the original TSH, decoherence-corrected TSH (dTSH, see computational details for more information), and AIMS, using a set of common initial conditions and the strategy discussed in Sections II.A.2 and II.A.3 for an improved comparison. Coining the photodynamics of ethylene a molecular Tully I model is validated by looking at the average number of hops performed in dTSH (〈Nhops〉, inset of Fig. 2): within the first 82 fs of dynamics, 80% of the trajectories have decayed to the ground state and the average cumulative number of hops has only reached 1.3, indicating that most trajectories perform a single hop from S1 to the ground state S0. Thus, the nonadiabatic dynamics of ethylene towards the ground state involves mostly a single crossing event, followed by a stable dynamics in S0, i.e., without hops back to S1. This behavior is illustrated by an exemplary TSH trajectory (top panel of Fig. 2). The two electronic states come energetically close and, following the nonadiabatic transition at around 28 fs when the trajectory hopped to the ground state, they separate again in energy, and the trajectory remains in the ground state. Focusing now on the AIMS dynamics, we observe that the average number of child TBFs (〈Nchildren〉), while rising slightly above the average number of hops, remains below two as expected from a dynamics dominated by a single avoided crossing.
The time traces of the S1 population obtained with the different methods are overall in good agreement (Fig. 2). The decay starts after 11 fs of dynamics and the ground state is largely populated within 80 fs. Despite the overall agreement between the different methods, small differences can be observed. dTSH predicts the fastest decay (with around 20% of population remaining in the S1 after 82 fs). It was proposed in previous studies that the more rapid population decay predicted by (d)TSH in comparison to AIMS could be attributed to the intrinsic overcoherence of TSH. Even though the population traces obtained with the different methods are close to each other in the present simulations, we wanted to test whether we could reproduce the result obtained with (d)TSH by applying additional approximations to AIMS. We therefore enforced the following approximations to the AIMS dynamics: (i) setting intrastate couplings between TBFs to zero, (ii) propagating the amplitudes of the spawned TBFs on the support of the parent TBF, and (iii) enforcing a perfect overlap between TBFs. These approximations intend to bridge the equations of motion for the amplitudes in AIMS to those of TSH, and was hence coined Surface Hopping Approach to AIMS (SHAIMS). Interestingly, the nonadiabatic dynamics described by SHAIMS closely follows that of dTSH (dashed line in Fig. 2) and shows a faster decay of the S1 population as compared to AIMS. While care has to be taken when assessing the difference in population decay due to the close agreement of the methods, SHAIMS appears to indicate that a perfect overlap between TBFs would indeed tend to speed up the transfer of population towards the ground state, as observed for TSH and dTSH. We note that TSH and dTSH, while exhibiting a similar population time trace over the first 35 fs of dynamics, start to diverge noticeably after this time. This point of divergence is also observed in the average number of hops between the two TSH methods and can be correlated with some hops back to S1 taking place in the TSH dynamics but prevented in dTSH thanks to the use of the decoherence correction. The fact that the hops back do not take place in dTSH also explains why the SHAIMS strategy agrees more with dTSH after 35 fs (as back spawns are artificially prevented in this analysis method).
In summary, the molecular Tully model I appears to be a good general first test for any newly-developed nonadiabatic dynamics strategy.
B. Molecular Tully model II – DMABN
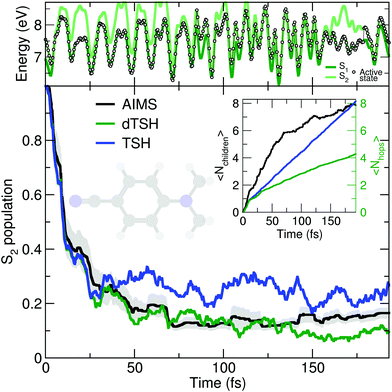
As discussed earlier, the original Tully model II depicts a somewhat more complicated case of nonadiabatic dynamics than the model I, where more than one avoided crossings can be encountered during the dynamics. We show here that a comparable behavior is observed at the molecular level during the photodynamics of DMABN. This molecule has been the subject of different studies looking into the details of its ultrafast decay from the photoexcited S2 state and using different levels of theory for the electronic structure and the nuclear dynamics.98,118–120 All previous work agreed on the ultrafast relaxation from the S2 to the S1 occurring within the first 50 fs of dynamics. This ultrafast decay is also in line with the photodynamics of the parent molecule 4-aminobenzonitrile, studied with MCTDH.121 However, the S2 and S1 states remain close in energy during the excited-state dynamics, and the nuclear wavepackets visit subsequent nonadiabatic regions leading to oscillations of population between these two states after the initial ultrafast decay. Such multiple crossings between a pair of electronic states link the photodynamics of DMABN to the Tully model II.The average number of hops during the dTSH dynamics of DMABN rises to more than four within the first 200 fs of dynamics (inset of Fig. 3). In stark contrast with the dynamics of ethylene, the (d)TSH dynamics of DMABN is characterized by a significant number of nonadiabatic transitions between the same pair of electronic states, further exemplified by the exemplary trajectory shown in the upper panel of Fig. 3. Hops between the two states occur at 7, 85.5, 96, 103, 112, 121, 157, and 179 fs. Importantly, the nonadiabatic transitions do not happen in the same region of the intersection seam (the electronic energies at the different hopping points are different). This observation is crucial as it indicates that the dTSH trajectories do not hop back and forth between S2 and S1 in the same region of the intersection seam but instead visit different points of such crossing seam, analogously to the two avoided crossings in Tully model II. As a corollary to this observation, we would expect a branching of the nuclear wavepackets after each nonadiabatic transition without them interfering again at a later time, i.e., with no recoherence.122 This nonadiabatic dynamics contrasts with the Stueckelberg oscillations observed in the original Tully model II18 that are caused by a modulation of the nonadiabatic interferences between the two wavepackets at the second avoided crossings as a function of the initial momentum of the wavepacket.123
All methods – TSH, dTSH, and AIMS (from ref. 98) – predict an ultrafast decay of the S2 population and the corresponding population traces are similar during the first 30 fs. After this time, the result of the TSH dynamics starts to deviate more strongly from that of the other two methods. Interestingly, this specific behavior of TSH starts to appear when the average number of hops is reaching 2, indicating that, in average, a TSH trajectory has experienced two hopping events between the same pair of states. Combining this information with the one discussed above (hops in different regions of the intersection space) allows us to assume that TSH, in this particular case, suffers from its lack of decoherence. While the nuclear wavepackets should branch after each nonadiabatic transitions, the ITA forces each TSH trajectories to propagate their amplitudes on the support of a unique trajectory, leading to an overcoherence propagation.72 Importantly, a large average number of hops between the same pair of states may also defeat the fewest-switches idea of TSH and insufflate a mean-field character to the excited-state dynamics.18 The described failure of TSH is, however, easily addressed by enforcing decoherence on the amplitudes carried by each trajectory, as showed by the excellent agreement of dTSH with AIMS during the entire nonadiabatic dynamics and its reduced number of average hops. We note that decoherence corrections may not offer an adequate patch to TSH if recoherences were present in the dynamics.122 We also would like to point out that the difference between TSH and dTSH is not caused by the limited number of initial conditions sampled. The same behavior – and, more importantly, differences – between these two flavors of TSH is also observed for a common set of 100 random initial conditions (see ESI,† Fig. S1).
The molecular Tully model II can be used to study the behavior of a given nonadiabatic molecular dynamics method during an excited-state dynamics with multiple crossings between the same pair of electronic states. It also offers an exciting test for novel strategies that aim at incorporating decoherence effects in mixed quantum/classical methods beyond the somehow ad hoc corrections of the TSH algorithm.
C. Molecular Tully model III – fulvene
Previous theoretical work on the fulvene molecule has unraveled two possible decay channels upon photoexcitation on the first excited electronic state S1, see for example ref. 65 and 124–126. The first deactivation pathway is driven by a stretch of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 moiety and involves a strongly sloped conical intersection with S0, while the second one relies on a twist of the same C
CH2 moiety and involves a strongly sloped conical intersection with S0, while the second one relies on a twist of the same C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 moiety and a decay through a peaked conical intersection. In the first mechanism, the photogenerated nuclear wavepacket passes through the sloped conical intersection and is subsequently reflected on the lower electronic state back towards the nonadiabatic region where a recrossing takes place, leading to a stepwise decay of the S1 population. Such a nonadiabatic transition involving a reflection is reminiscent of the dynamics generated by the Tully model III (see Fig. 1c). More importantly, the previous theoretical studies also highlighted the strong correlation between the initial dynamics of the nuclear wavepacket and the decay channel followed.65 Hence, one of the two deactivation pathways can be privileged by altering the initial conditions for the dynamics – an observation that we will use in the following to probe the reflection mechanism in the nonadiabatic dynamics of fulvene. To ensure a favored decay of the nuclear wavepacket through the sloped conical intersections, we sampled the initial geometries for the dynamics from a Wigner distribution but set their initial momenta to zero in the first place.
CH2 moiety and a decay through a peaked conical intersection. In the first mechanism, the photogenerated nuclear wavepacket passes through the sloped conical intersection and is subsequently reflected on the lower electronic state back towards the nonadiabatic region where a recrossing takes place, leading to a stepwise decay of the S1 population. Such a nonadiabatic transition involving a reflection is reminiscent of the dynamics generated by the Tully model III (see Fig. 1c). More importantly, the previous theoretical studies also highlighted the strong correlation between the initial dynamics of the nuclear wavepacket and the decay channel followed.65 Hence, one of the two deactivation pathways can be privileged by altering the initial conditions for the dynamics – an observation that we will use in the following to probe the reflection mechanism in the nonadiabatic dynamics of fulvene. To ensure a favored decay of the nuclear wavepacket through the sloped conical intersections, we sampled the initial geometries for the dynamics from a Wigner distribution but set their initial momenta to zero in the first place.
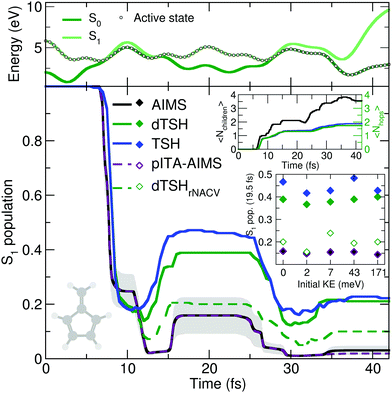
The reflective nature of the nonadiabatic dynamics through the sloped conical intersection is illustrated by the exemplary dTSH trajectory presented in the top panel of Fig. 4. During the dynamics, the two electronic states get closer in energy until the conical intersection is reached at around 7 fs, leading to a net transfer of population from S1 to S0. However, the trajectory rapidly reflects and reaches the same region of configuration space again after only 5 fs, where a recrossing occurs and leads to a population back transfer towards S1. The coupling region is met again after 28 fs of dynamics, this time leading to a stable trajectory in S0. Importantly, all the recrossings occur at close electronic energies, indicating that the nuclear wavepacket hits each time a similar region of the intersection seam.
AIMS, dTSH, and TSH show all a significant S1 population decay after 7 fs of dynamics and agree on the remaining population in the excited state: ∼20% after 10 fs. The recrossing leading to back population transfer occurs in all methods shortly after, but its related population transfer depends on the nonadiabatic dynamics method employed. While AIMS predicts that only around 16% of population is in the S1 state between 15 and 25 fs, the repopulation process of S1 starts earlier and lasts longer with TSH and dTSH (at around 12 to 30 fs) and the resulting excited-state population plateaus at higher values (40% and 50% of S1 population with dTSH and TSH, respectively). This difference of S1 population between TSH/dTSH and AIMS can also be observed during the subsequent nonadiabatic event occurring between 35 and 42 fs. We note that the average number of hops tends towards two for TSH and dTSH within the timescale of our simulation. In contrast, the average number of child TBFs increases stepwise to a value of 3.5 over the same period of time, highlighting that AIMS spawns new TBFs for the different recrossing events.
To ensure a conservation of total energy along a (d)TSH trajectory, it is necessary to adjust the nuclear kinetic energy after each surface hop to account for the loss or gain in potential energy. Several strategies have been proposed for this task: the most straightforward approach (implemented as default in several TSH codes) is to rescale the nuclear velocity vectors isotropically – a strategy used in all (d)TSH runs above. Alternatively, nuclear velocities can be scaled along the nonadiabatic coupling vectors. This latter strategy is usually encouraged as it can be justified by semiclassical arguments, but in practice it implies the explicit calculation of the nonadiabatic coupling vectors, which might increase the computational cost of the dynamics. In AIMS, the nuclear kinetic energy of a newly spawned TBF is by default rescaled along the nondiabatic coupling vectors, but can also be done isotropically. We tested the influence of the nuclear velocity rescaling on the result presented above for dTSH and AIMS. In dTSH, rescaling the nuclear velocities along the nonadiabatic coupling vectors (dTSHrNACV in Fig. 4) drastically alters the population dynamics: the S1 population decays to around 5% during the first nonadiabatic transition and the amount of repopulation of the S1 state is reduced to only around 20%, in closer agreement with AIMS. In contrast, the AIMS dynamics is mostly unchanged when the child TBFs nuclear velocities are rescaled along the nonadiabatic coupling vectors or isotropically (see ESI,† Fig. S2).
A key difference between AIMS and (d)TSH is that the TBFs in the former are coupled, while the trajectories of the latter are all propagated independently as a result of the ITA (see Section II.A). As we could observe the creation of numerous TBFs in S0, some of them exhibiting a non-negligible overlap between each other, we wanted to investigate the role played by the intrastate couplings between TBFs in AIMS, that is, the coupling between the TBFs evolving on the same electronic state. To do so, we repeated the AIMS dynamics with all direct intrastate couplings removed by setting the overlap between the TBFs belonging to the same electronic state to zero. This pseudo independent trajectory approximation in AIMS (pITA-AIMS, palatinate dashed line in Fig. 4) does not appear to significantly affect the S1 population trace as compared to that obtained with AIMS (we note a slightly more noticeable deviation after 35 fs). This observation indicates that the difference between AIMS and (d)TSH is likely to be caused by the interstate coupling between the TBFs evolving in S1 and S0. However, it is important to remember at this stage that, while AIMS accounts for both intra- and interstate couplings between the TBFs emanating from a given parent TBF, the Hamiltonian matrix elements responsible for such couplings are approximated using the SPA0 (see Section II.A). Interestingly, we found that improving the description of the intrastate couplings to the SPA1 instead of the SPA0 does not alter the AIMS dynamics (see ESI,† Fig. S2), suggesting that the SPA0 may provide a reasonable description of the coupling between the TBFs present in the simulation (see below for an additional discussion on these results). We note that we propose in the ESI† (Table S1) some comments on the computational costs of AIMS and dTSH for the fulvene photodynamics.
An exciting aspect of the original one-dimensional Tully models is the possibility to change the initial momentum of the nuclear wavepacket. Such a variation of the initial kinetic energy of the nuclear wavepacket permits to probe the nonadiabatic dynamics in different regimes and also to create specific situations involving nonadiabatic interferences for example (see the discussion on Stueckelberg oscillations above) or transfer of the nuclear wavepacket above a barrier on the potential energy curves. Playing with the initial momenta for a molecular system is more challenging to achieve in a controlled way but was proposed for different molecules as a mean of investigating specific photochemical reaction pathways.65,126,127 We propose here to reproduce this specific feature of the original Tully models by testing the influence of the initial momenta on the nonadiabatic dynamics of fulvene.
To achieve this goal, we propose here a simplified scheme where the same set of initial conditions (described earlier) is used for the nuclear configurations, but to which we attached a (single) set of nuclear momenta sampled according to a Wigner distribution were only the contribution of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 stretching mode is incorporated while all other contributions are set to zero (overall kinetic energy of 1.71 meV). This choice is motivated by the discussion above on the deactivation pathways of fulvene: the sloped intersection is reached by a coordinate containing a substantial contribution from the C
CH2 stretching mode is incorporated while all other contributions are set to zero (overall kinetic energy of 1.71 meV). This choice is motivated by the discussion above on the deactivation pathways of fulvene: the sloped intersection is reached by a coordinate containing a substantial contribution from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 stretching. Hence, adding more kinetic energy along this mode will affect the dynamics of fulvene along the reactive coordinate leading to the sloped conical intersection – a test reminiscent to the idea of altering the nuclear momentum of a nuclear wavepacket in the original one-dimensional Tully models. To further enhance the effect of this kick in kinetic energy, we also propose to apply a multiplicative factor to the initial set of nuclear velocities (of the (d)TSH trajectories or AIMS TBFs) to generate additional initial conditions with an increasing amount of nuclear kinetic energy. While this offers a simple testbed for the influence of the initial kinetic energy of the system on the branching ratio between electronic states, it has to be duly noted that methods incorporating a more accurate description of the nuclear wavepacket dynamics (such as FMS or vMCG) would also need to correct the initial wavefunction, that is, the amplitudes carried by each traveling Gaussian, to adequately perform such a test (see for example ref. 126). The inset of Fig. 4 shows the S1 population after 19.5 fs of dynamics for AIMS and (d)TSH as a function of the initial kinetic energy of the trajectories or TBFs, respectively. While the S1 population given by AIMS at this time only slightly varies with different initial kinetic energies, the S1 population obtained with TSH or dTSH appears to fluctuate slightly more. The difference between the population decay in dTSH and dTSHrNACV discussed above for the case with zero initial kinetic energy is also clearly visible over the full range of nuclear kinetic energies: a significantly lower population in S1 is observed after 19.5 fs in dTSHrNACV in all cases. In addition, the improved correlation between the result of dTSHrNACV and AIMS highlighted earlier is also observed for most tests with higher initial kinetic energy – both predicting a significantly lower S1 population after 19.5 fs than the other flavors of (d)TSH. Judging from the perfect agreement between pITA-AIMS and AIMS, the difference in S1 populations observed between AIMS and (d)TSH appears, as described above, to be linked to the description of interstate couplings between TBFs. It has to be noted that dTSHrNACV shows a stronger repopulation of the S1 in the case of an initial kinetic energy of 7 meV, deviating more from the result obtained with AIMS.
CH2 stretching. Hence, adding more kinetic energy along this mode will affect the dynamics of fulvene along the reactive coordinate leading to the sloped conical intersection – a test reminiscent to the idea of altering the nuclear momentum of a nuclear wavepacket in the original one-dimensional Tully models. To further enhance the effect of this kick in kinetic energy, we also propose to apply a multiplicative factor to the initial set of nuclear velocities (of the (d)TSH trajectories or AIMS TBFs) to generate additional initial conditions with an increasing amount of nuclear kinetic energy. While this offers a simple testbed for the influence of the initial kinetic energy of the system on the branching ratio between electronic states, it has to be duly noted that methods incorporating a more accurate description of the nuclear wavepacket dynamics (such as FMS or vMCG) would also need to correct the initial wavefunction, that is, the amplitudes carried by each traveling Gaussian, to adequately perform such a test (see for example ref. 126). The inset of Fig. 4 shows the S1 population after 19.5 fs of dynamics for AIMS and (d)TSH as a function of the initial kinetic energy of the trajectories or TBFs, respectively. While the S1 population given by AIMS at this time only slightly varies with different initial kinetic energies, the S1 population obtained with TSH or dTSH appears to fluctuate slightly more. The difference between the population decay in dTSH and dTSHrNACV discussed above for the case with zero initial kinetic energy is also clearly visible over the full range of nuclear kinetic energies: a significantly lower population in S1 is observed after 19.5 fs in dTSHrNACV in all cases. In addition, the improved correlation between the result of dTSHrNACV and AIMS highlighted earlier is also observed for most tests with higher initial kinetic energy – both predicting a significantly lower S1 population after 19.5 fs than the other flavors of (d)TSH. Judging from the perfect agreement between pITA-AIMS and AIMS, the difference in S1 populations observed between AIMS and (d)TSH appears, as described above, to be linked to the description of interstate couplings between TBFs. It has to be noted that dTSHrNACV shows a stronger repopulation of the S1 in the case of an initial kinetic energy of 7 meV, deviating more from the result obtained with AIMS.
From the dynamics proposed here, it appears that the molecular Tully model III may require a proper description of the non-local behavior of the nuclear wavepackets involved in the dynamics. This is translated in AIMS by the importance of (interstate) couplings between the TBFs. While this could constitute an exciting test for methods describing such couplings11,14,128 and an example of potential issues with the independent trajectory approximation of (d)TSH, we would like to repeat at this stage our earlier caveat. AIMS can describe both intra- and interstate couplings between TBFs, but the integral mediating such couplings are approximated – see the brief discussion on the SPA in Section II.A and ref. 71 for more details – and a sufficient number of TBFs are required to ensure an adequate convergence of the result. More specifically, the intrastate coupling is only crudely approximated and higher order of the SPA can be required in cases where such couplings are critical (see also the discussion on time-dependent dipole moments in ref. 71). As mentioned above, we ran additional calculations using the SPA up to first order for the set of initial conditions with zero initial kinetic energy, and only negligible differences in the population dynamics were observed (see Fig. S2 in the ESI†). While the test comparing the SPA0 and SPA1 is reassuring, the molecular Tully model III will surely stimulate further development of AIMS to ensure that intrastate (and interstate) couplings are adequately described in such cases and to investigate the importance of spawning more child TBFs when intrastate couplings appear to be important.
IV Conclusions
In this work, we proposed a molecular version of the original Tully models, aiming at offering a unified mean of comparison between the different strategies for on-the-fly nonadiabatic molecular dynamics. We used these tests to compare the most commonly employed methods for excited-state dynamics: trajectory surface hopping and ab initio multiple spawning.The molecular Tully model I, ethylene, offers a simple test for nonadiabatic molecular dynamics as it depicts a photodynamics dominated by a single nonadiabatic crossing event. As such, all methods tested are in good agreement, with a potential tendency for (d)TSH to exhibit a slightly faster S1 population decay in the early stage of the excited-state dynamics. The molecular Tully model II, DMABN, stresses the nonadiabatic methods slightly more as the photodynamics from the S2 excited state involves multiple crossings between S2 and S1 – a rather challenging dynamics to describe for TSH without a correction for decoherence. The molecular Tully model III, fulvene, paves the way for numerous ways of playing with nonadiabatic methods. The reflection of the nuclear wavepacket following passage through the sloped conical intersection as well as the possible intra- and interstate coupling between the nuclear wavepackets makes it a rather stringent test for all methods tested. The population dynamics can be altered by varying the initial conditions (nuclear kinetic energy) of the nonadiabatic dynamics à la Tully. The S1 population trace obtained AIMS dynamics differs from the one obtained with (d)TSH. While the AIMS dynamics creates numerous TBFs on the ground electronic state, their (intrastate) couplings do not appear to affect the population trace significantly – indicating that the difference in population observed between AIMS and (d)TSH can be linked to the interstate couplings between TBFs. However, while previous dynamics using vMCG seem to confirm the importance of these couplings, the photodynamics of fulvene exemplifies one of the important limitations of the molecular Tully models presented here: the lack of exact solutions for these nonadiabatic processes. Nevertheless, we do believe that the central goals of these molecular Tully models are to (i) compare the strengths and weaknesses of different nonadiabatic molecular dynamics and (ii) stimulate the detection of potential improvements by highlighting processes that stress the existing approximations of a given method – for example, the saddle-point approximation of AIMS in the present case of fulvene.
Interestingly, the original Tully models highlighted specific features of nonadiabatic dynamics that were observed in the molecular version of this models, further reinforcing – if needed – the need for challenging models in low dimensions and providing an essential connection between the world of chemical physics (exactly-solvable models) and physical chemistry (photodynamics of molecules).
Last but not least, all the necessary details of our simulations are provided in the ESI† of this article – all initial conditions as well as the parameters for the nonadiabatic dynamics as well as those for the electronic structure methods – to ensure that these molecular Tully models can be broadly used by the community developing methods for nonadiabatic molecular dynamics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 803718, project SINDAM). LMI acknowledges the EPSRC for an EPSRC Doctoral Studentship (EP/R513039/1). This work made use of the facilities of the Hamilton HPC Service of Durham University and benefited from workshops organized by the E-CAM project (European Union's Horizon 2020 research and innovation program [676531]). The authors thank Federica Agostini and Yorick Lassmann for stimulating discussions.References
- J. C. Tully, Theor. Chem. Acc., 2000, 103, 173–176 Search PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- F. Agostini and B. F. E. Curchod, WIREs Comput. Mol. Sci., 2019, 9, e1417 CrossRef.
- H. D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H. D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- G. A. Worth, H. D. Meyer and L. S. Cederbaum, in Conical Intersections: Electronic Structure, Dynamics & Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, Advanced Series in Physical Chemistry, World Scientific, 2004, ch. 14, vol. 15, pp. 583–617 Search PubMed.
- H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional quantum dynamics, John Wiley & Sons, 2009 Search PubMed.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS PubMed.
- G. Worth, M. Robb and I. Burghardt, Faraday Discuss., 2004, 127, 307–323 RSC.
- B. Lasorne, M. J. Bearpark, M. A. Robb and G. A. Worth, Chem. Phys. Lett., 2006, 432, 604–609 CrossRef CAS.
- G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- D. Shalashilin, J. Chem. Phys., 2009, 130, 244101 CrossRef PubMed.
- K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- D. Makhov, C. Symonds, S. Fernandez-Alberti and D. Shalashilin, Chem. Phys., 2017, 493, 200 CrossRef CAS.
- T. J. Martínez, M. Ben-Nun and R. D. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef.
- T. J. Martínez, M. Ben-Nun and R. D. Levine, J. Phys. Chem. A, 1997, 101, 6389–6402 CrossRef.
- T. J. Martínez and R. D. Levine, J. Chem. Soc., Faraday Trans., 1997, 93, 941–947 RSC.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657 CrossRef CAS.
- M. Barbatti, WIREs Comput. Mol. Sci., 2011, 1, 620–633 CrossRef CAS.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- X. Sun and W. H. Miller, J. Chem. Phys., 1997, 106, 6346–6353 CrossRef CAS.
- S. J. Cotton and W. H. Miller, J. Phys. Chem. A, 2015, 119, 12138–12145 CrossRef CAS PubMed.
- Y. Wu and M. F. Herman, J. Chem. Phys., 2005, 123, 144106 CrossRef PubMed.
- V. N. Gorshkov, S. Tretiak and D. Mozyrsky, Nat. Commun., 2013, 4, 2144 CrossRef PubMed.
- T. Zimmermann and J. Vaníček, J. Chem. Phys., 2010, 132, 241101 CrossRef PubMed.
- B. Poirier and G. Parlant, J. Phys. Chem. A, 2007, 111, 10400–10408 CrossRef CAS PubMed.
- R. Baskov, A. J. White and D. Mozyrsky, J. Phys. Chem. Lett., 2019, 10, 433–440 CrossRef PubMed.
- F. Agostini, S. K. Min, A. Abedi and E. K. U. Gross, J. Chem. Theory Comput., 2016, 12, 2127–2143 CrossRef CAS PubMed.
- G. H. Gossel, F. Agostini and N. T. Maitra, J. Chem. Theory Comput., 2018, 14, 4513–4529 CrossRef CAS PubMed.
- W. Feng, L. Xu, X.-Q. Li, W. Fang and Y. Yan, AIP Adv., 2014, 4, 077131 CrossRef.
- E. R. Dunkel, S. Bonella and D. F. Coker, J. Chem. Phys., 2008, 129, 114106 CrossRef CAS PubMed.
- M. Bedard-Hearn, R. Larsen and B. Schwartz, J. Chem. Phys., 2005, 123, 234106 CrossRef PubMed.
- B. F. E. Curchod, I. Tavernelli and U. Rothlisberger, Phys. Chem. Chem. Phys., 2011, 13, 3231–3236 RSC.
- J. C. Burant and J. C. Tully, J. Chem. Phys., 2000, 112, 6097 CrossRef CAS.
- O. V. Prezhdo and P. J. Rossky, J. Chem. Phys., 1997, 107, 825–834 CrossRef CAS.
- X. Gao and W. Thiel, Phys. Rev. E, 2017, 95, 013308 CrossRef PubMed.
- G. Tao, J. Chem. Phys., 2017, 147, 044107 CrossRef PubMed.
- P. Huo and D. F. Coker, J. Chem. Phys., 2011, 135, 201101 CrossRef PubMed.
- F. A. Shakib and P. Huo, J. Phys. Chem. Lett., 2017, 8, 3073–3080 CrossRef CAS PubMed.
- C. C. Martens, J. Phys. Chem. A, 2019, 123, 1110–1128 CrossRef CAS PubMed.
- C. C. Martens, J. Phys. Chem. Lett., 2016, 7, 2610–2615 CrossRef CAS PubMed.
- X. Gao, M. A. Sallerr, Y. Liu, A. Kelly, J. O. Richardson and E. Geva, J. Chem. Theory Comput., 2020, 16, 2883–2895 CrossRef CAS PubMed.
- E. R. Bittner and P. J. Rossky, J. Chem. Phys., 1995, 103, 8130–8143 CrossRef CAS.
- J. Subotnik and N. Shenvi, J. Chem. Phys., 2011, 134, 024105 CrossRef PubMed.
- J. Subotnik and N. Shenvi, J. Chem. Phys., 2011, 134, 244114 CrossRef PubMed.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- N. Shenvi and W. Yang, J. Chem. Phys., 2012, 137, 22A528 CrossRef PubMed.
- M. J. Falk, B. R. Landry and J. E. Subotnik, J. Phys. Chem. B, 2014, 118, 8108–8117 CrossRef CAS PubMed.
- J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang and N. Bellonzi, Annu. Rev. Phys. Chem., 2016, 67, 387–417 CrossRef CAS PubMed.
- F. Agostini, Eur. Phys. J. B, 2018, 91, 143 CrossRef.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985 CrossRef CAS.
- Conical Intersections: Electronic Structure, Dynamics & Spectroscopy, ed. W. Domcke, D. Yarkony and H. Köppel, World Scientific Pub Co Inc, 2004, vol. 15 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- S. C. Althorpe, W. Barford, J. Blumberger, C. Bungey, I. Burghardt, A. Datta, S. Ghosh, S. Giannini, T. Grünbaum and S. Habershon, et al. , Faraday Discuss., 2020, 221, 564–581 RSC.
- A. V. Akimov, J. Comput. Chem., 2016, 37, 1626–1649 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martínez, Annu. Rev. Phys. Chem., 2007, 58, 613–634 CrossRef CAS PubMed.
- M. Barbatti, A. J. A. Aquino and H. Lischka, Mol. Phys., 2006, 104, 1053–1060 CrossRef CAS.
- D. Polli, P. Altoè, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura and R. A. Mathies, et al. , Nature, 2010, 467, 440 CrossRef CAS PubMed.
- C. D. Rankine, J. P. F. Nunes, M. S. Robinson, P. D. Lane and D. A. Wann, Phys. Chem. Chem. Phys., 2016, 18, 27170–27174 RSC.
- D. R. Yarkony, J. Chem. Phys., 2001, 114, 2601–2613 CrossRef CAS.
- T. J. Martínez, Chem. Phys. Lett., 1997, 272, 139–147 CrossRef.
- D. Mendive-Tapia, B. Lasorne, G. A. Worth, M. J. Bearpark and M. A. Robb, Phys. Chem. Chem. Phys., 2010, 12, 15725–15733 RSC.
- L. Blancafort, P. Hunt and M. A. Robb, J. Am. Chem. Soc., 2005, 127, 3391–3399 CrossRef CAS PubMed.
- L. M. Ibele, A. Nicolson and B. F. E. Curchod, Mol. Phys., 2020, 118, e1665199 CrossRef.
- M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 1998, 108, 7244–7257 CrossRef CAS.
- M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef CAS.
- B. Mignolet and B. F. E. Curchod, J. Chem. Phys., 2018, 148, 134110 CrossRef PubMed.
- B. Mignolet and B. F. E. Curchod, J. Phys. Chem. A, 2019, 123, 3582–3591 CrossRef CAS PubMed.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- A. Bjerre and E. Nikitin, Chem. Phys. Lett., 1967, 1, 179–181 CrossRef CAS.
- M. Thachuk, M. Y. Ivanov and D. M. Wardlaw, J. Chem. Phys., 1998, 109, 5747–5760 CrossRef CAS.
- J. Y. Fang and S. Hammes-Schiffer, J. Phys. Chem. A, 1999, 103, 9399–9407 CrossRef CAS.
- A. W. Jasper, S. Nangia, C. Zhu and D. G. Truhlar, Acc. Chem. Res., 2006, 39, 101–108 CrossRef CAS PubMed.
- M. Persico and G. Granucci, Theor. Chem. Acc., 2014, 133, 1–28 Search PubMed.
- B. F. E. Curchod and I. Tavernelli, J. Chem. Phys., 2013, 138, 184112 CrossRef PubMed.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- J. E. Subotnik, W. Ouyang and B. R. Landry, J. Chem. Phys., 2013, 139, 214107 CrossRef PubMed.
- A. Toniolo, C. Ciminelli, M. Persico and T. J. Martínez, J. Chem. Phys., 2005, 123, 234308 CrossRef CAS PubMed.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef.
- H.-J. Werner, Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 1987, vol. 69, pp. 1–62 Search PubMed.
- B. O. Roos, Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 1987, vol. 69, pp. 399–445 Search PubMed.
- R. H. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222 Search PubMed.
- D. V. Makhov, W. J. Glover, R. J. Martinez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- W. Zhou, A. Mandal and P. Huo, J. Phys. Chem. Lett., 2019, 10, 7062–7070 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- M. E. Casida, Recent Advances in Density Functional Methods, 1995, p. 155 Search PubMed.
- M. Petersilka, U. J. Gossmann and E. K. U. Gross, Phys. Rev. Lett., 1996, 76, 1212–1215 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, A. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision A.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012 Search PubMed.
- B. G. Levine, J. D. Coe, A. M. Virshup and T. J. Martínez, Chem. Phys., 2008, 347, 3–16 CrossRef CAS.
- B. F. E. Curchod, A. Sisto and T. J. Martínez, J. Phys. Chem. A, 2017, 121, 265–276 CrossRef CAS PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, WIREs Comput. Mol. Sci., 2018, 8, e1370 CrossRef PubMed.
- S. Mai, M. Richter, M. Heindl, M. F. S. J. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, M. Oppel, P. Marquetand and L. González, SHARC2.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, http://sharc-md.org, 2018 Search PubMed.
- F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. González, J. Chem. Theory Comput., 2016, 12, 1207–1219 CrossRef CAS PubMed.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, WIREs Comput. Mol. Sci., 2014, 4, 26–33 CrossRef CAS.
- A. Prlj, NEWTON-X forum: Implementation of decoherence correction, 2019 Search PubMed.
- A. Viel, R. P. Krawczyk, U. Manthe and W. Domcke, Angew. Chem., Int. Ed., 2003, 42, 3434–3436 CrossRef CAS PubMed.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608 CrossRef CAS.
- M. Barbatti, M. Ruckenbauer and H. Lischka, J. Chem. Phys., 2005, 122, 174307 CrossRef CAS PubMed.
- M. Barbatti, J. Paier and H. Lischka, J. Chem. Phys., 2004, 121, 11614–11624 CrossRef CAS PubMed.
- M. Barbatti, G. Granucci, M. Persico and H. Lischka, Chem. Phys. Lett., 2005, 401, 276–281 CrossRef CAS.
- E. Fabiano, T. Keal and W. Thiel, Chem. Phys., 2008, 349, 334–347 CrossRef CAS.
- B. Sellner, M. Barbatti, T. Müller, W. Domcke and H. Lischka, Mol. Phys., 2013, 111, 2439–2450 CrossRef CAS.
- M. Ben-Nun and T. J. Martínez, Chem. Phys. Lett., 1998, 298, 57–65 CrossRef CAS.
- J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2003, 107, 829–837 CrossRef CAS.
- H. Tao, B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2009, 113, 13656–13662 CrossRef CAS PubMed.
- H. Tao, T. Allison, T. Wright, A. Stooke, C. Khurmi, J. Van Tilborg, Y. Liu, R. Falcone, A. Belkacem and T. Martinez, J. Chem. Phys., 2011, 134, 244306 CrossRef CAS PubMed.
- T. Mori, W. J. Glover, M. S. Schuurman and T. J. Martínez, J. Phys. Chem. A, 2012, 116, 2808–2818 CrossRef CAS PubMed.
- A. Viel, R. P. Krawczyk, U. Manthe and W. Domcke, J. Chem. Phys., 2004, 120, 11000–11010 CrossRef CAS PubMed.
- L. Du and Z. Lan, J. Chem. Theory Comput., 2015, 11, 1360–1374 CrossRef CAS PubMed.
- M. A. Kochman, A. Tajti, C. A. Morrison and R. J. D. Miller, J. Chem. Theory Comput., 2015, 11, 1118–1128 CrossRef CAS PubMed.
- G. R. Medders, E. C. Alguire, A. Jain and J. E. Subotnik, J. Phys. Chem. A, 2017, 121, 1425–1434 CrossRef CAS PubMed.
- P. J. Castro, A. Perveaux, D. Lauvergnat, M. Reguero and B. Lasorne, Chem. Phys., 2018, 509, 30–36 CrossRef CAS.
- G. Miao and J. Subotnik, J. Phys. Chem. A, 2019, 123, 5428–5435 CrossRef CAS PubMed.
- B. F. E. Curchod, F. Agostini and E. K. U. Gross, J. Chem. Phys., 2016, 145, 034103 CrossRef PubMed.
- M. J. Bearpark, F. Bernardi, M. Olivucci, M. A. Robb and B. R. Smith, J. Am. Chem. Soc., 1996, 118, 5254–5260 CrossRef CAS.
- S. Alfalah, S. Belz, O. Deeb, M. Leibscher, J. Manz and S. Zilberg, J. Chem. Phys., 2009, 130, 124318 CrossRef CAS PubMed.
- D. Mendive-Tapia, B. Lasorne, G. A. Worth, M. A. Robb and M. J. Bearpark, J. Chem. Phys., 2012, 137, 22A548 CrossRef PubMed.
- M. Araújo, B. Lasorne, A. L. Magalhaes, M. J. Bearpark and M. A. Robb, J. Phys. Chem. A, 2010, 114, 12016–12020 CrossRef PubMed.
- S. K. Min, F. Agostini, I. Tavernelli and E. K. Gross, J. Phys. Chem. Lett., 2017, 8, 3048–3055 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on the (d)TSH dynamics of DMABN and the AIMS dynamics of fulvene. Comment on the computational cost of the fulvene dynamics with dTSH and AIMS. Initial conditions (nuclear geometries and velocities) for all the molecular Tully models and population traces are available as a zip file (molecular_tully_models.zip). See DOI: 10.1039/d0cp01353f |
| This journal is © the Owner Societies 2020 |