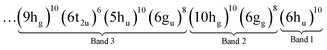VUV photoionization dynamics of the C₆₀ buckminsterfullerene: 2D-matrix photoelectron spectroscopy in an astrophysical context

Abstract

We present the photoionization dynamics of the C₆₀ buckminsterfullerene from threshold up to 14.0 eV recorded with VUV synchrotron radiation at the DESIRS beamline at the SOLEIL synchrotron. The recorded data is obtained using a double-imaging photoelectron photoion coincidence spectrometer and is presented as a two-dimensional photoelectron matrix which contains a wealth of spectroscopic data. We present these data in an astrophysical context which relates to (i) the threshold photoelectron spectrum which is compared to data relevant to the diffuse interstellar bands (DIBs), (ii) the kinetic photoelectron distribution at the Lyman-α line which is relevant to the dominant heating source in the ISM, and (iii) the absolute photoionization cross section of C₆₀ up to approx. 10.5 eV. The photoelectron spectrum implies that the symmetry of the ground state is different than previous theoretical models have predicted, and this result is discussed in context of recent experimental and theoretical findings. Also presented are partial photoionization cross sections of the first two photoelectron bands and their anisotropy parameters. These data are compared with previous theoretical values and discussed where appropriate.

---

1. Introduction

The discovery of the buckminsterfullerene C₆₀¹ was in sorts a prescient affair. The experimental conditions under which C₆₀ was formed, were devised in order to understand the formation mechanisms of long-chain carbon molecules whose presence had been confirmed in various interstellar regions in the preceding years.^2–5 It was predicted that C₆₀ should be as abundant in space as well, but it took over three decades before C₆₀ could be unambiguously identified; first in various types of nebulae,^6–8 and later on in H II regions,⁹ circumstellar shells,¹⁰ post-asymptotic giant-branch (post-AGB) objects,¹¹ and various other Photon Dominated Regions (PDRs).¹² Furthermore, with the identification of its cation, C₆₀⁺, as the carrier of initially two and later four diffuse interstellar bands (DIBs) in the near-infrared of the diffuse interstellar medium (ISM),^13–15 research into this molecule is forcing us to reevaluate our understanding of interstellar molecular complexity. For a long time C₃ was the largest pure carbon species identified in diffuse clouds^16,17 and thus, the detection of C₆₀⁺ substantially stretches the size-limit for carbon-containing molecules in the diffuse ISM which could hold the key to unravelling the rest of the DIB mystery which has remained unsolved for almost a century at the time of writing.^18–21

The question of how C₆₀ forms in interstellar space has given rise to some convincing hypotheses,²² especially in light of the apparent inverse relationship between the abundance of polycyclic aromatic hydrocarbons (PAHs) and C₆₀ at decreasing distances towards stars.²³ Among the formation mechanisms for interstellar fullerenes that have gained much traction are (i) dehydrogenation of hydrogenated amorphous carbon nanoparticles²⁴ and (ii) the formation of graphene through photo-stripping H-atoms off larger PAHs. In the second scenario the bare carbon skeleton then undergoes further photo-excitation via VUV photons and self-stabilizes via IR photon emission or carbon loss leading to pentagonal defects; a prerequisite for the sheet to fold into a fullerene.²³ Indeed, mass-resolved laboratory data have shown that upon UV irradiation, PAHs undergo H-stripping to reveal bare carbon skeletons which form stable cluster ions, indicative of fullerene formation.²⁵ For this reason, several recent studies have been focusing on PAH pentagon formation schemes, to further exploit bowling mechanisms under interstellar conditions.^26,27

With the tenuous connection between PAHs and fullerenes in space, it is worth noting that fullerenes may contribute to the ionization balance of the ISM and the photoelectric heating of PDRs in a similar way as PAHs have been found to be.²⁸ In and of itself C₆₀ has been proposed as a diagnostic tool to estimate the temperature and/or UV flux inside molecular clouds²⁹ but such data is dependent on measurements of solid C₆₀ rather than gas-phase measurements as those relative to DIBs studies.^13–15

The ground state electronic structure of neutral C₆₀ possesses an icosahedral I_h symmetry. The highest occupied molecular orbital (HOMO) is fully occupied which results in a closed-shell ground state that is both fully symmetric and nondegenerate with ten valence electrons in an electronic quintet level labelled 6h_u. The relevant portion of the valence electronic configuration of the first three photoelectron bands of C₆₀ are:^30,31

Upon ionization the icosahedral symmetry is broken and a hole in the HOMO results in the cation possessing a h_u symmetric fivefold degenerate ground state which is Jahn–Teller (JT) active.³² The electron density relevant to the JT-active modes is akin to a band along an imaginary waistline of the C₆₀ structure³³ and when spontaneous symmetry breaking takes place upon ionization, the electron density around the molecule is best described by an oblate spheroid. Thus, a singly charged C₆₀⁺ ion possesses a ²H_u ground state and ²H_g and ²G_g low-lying excited states which are all capable of JT-distortions along h_g and g_g normal coordinates.³⁴

For C₆₀⁺, one can discern JT-active modes from the I_h character table.³⁵ These are H_g, G_g, and A_g. Though the A_g mode does not reduce the symmetry, it does shift the total energy of the molecule. The H_g and G_g modes, however, break the I_h symmetry and produce a multisheet adiabatic potential energy surface with a conical intersection in the symmetric geometry and extrema in configurations of D_5d and D_3d lowered symmetry.⁸ While matrix isolation studies of C₆₀⁺ have favored D_5d symmetry from interpretation of the results,^36–38 evidence has been found that free gas-phase C₆₀⁺ molecules display D_3d symmetry in their ground state.³⁹ The theoretical community seems to currently favor the results of the matrix isolation studies^40–42 and the application of a D_5d symmetric ground state has been used to speculate on the origins of the DIBs relative to C₆₀⁺.⁴³

Despite all this recent progress, several elemental physical chemical questions concerning C₆₀ and C₆₀⁺ remain. One is linked to the intensity ratios of the astronomically recorded C₆₀⁺ transitions that are not yet fully understood and that is possibly related to our present understanding of the symmetry of ground state C₆₀⁺ ions in the gas phase.^44,45 Another question is that in the diffuse interstellar medium, only C₆₀⁺ signals have been found and no neutral precursor signals. The present work, which focuses on the photoionization dynamics of C₆₀ (in)directly addresses these questions.

The use of photoelectron spectroscopy in tandem with synchrotron radiation has been somewhat of a hallmark in the history of spectroscopic investigations of C₆₀,^39,46–52 but so far, the threshold photoelectron spectrum (TPES) has still eluded closer inspection. By utilizing the double-imaging photoelectron photoion coincidence (i²PEPICO) technique, a wealth of information besides the TPES can be retrieved regarding the electronic structure and properties of C₆₀ and here we will present a 2D photoelectron dynamics matrix, from which are extracted the first measured TPES of C₆₀, the electron kinetic energy distributions, an estimation of the absolute photoionization cross section, and partial photoionization yields from threshold and above the Lyman-α limit (up to 14 eV), and discuss them within the context of the presence of C₆₀ and C₆₀⁺ in space.

2. Experimental

Experiments were performed at the DESIRS VUV beamline⁵³ at the Synchrotron SOLEIL facility. Horizontally polarized radiation in the photon energy range 7–14 eV was generated by an undulator (OPHELIE2)⁵⁴ whose higher harmonics are subsequently suppressed by four to five orders of magnitude with a gas filter filled with Krypton which is transparent in the aforementioned photon energy range.⁵⁵ The purified photon beam was then dispersed by a 6.65 normal incidence monochromator equipped with a 200 grooves per mm grating. The photon flux delivered was between 10¹² and 10¹³ photons per s and was calibrated with an AXUV100, IRD Si photodiode. For the slit width used for the experiments, the photon energy resolution scales from 6 meV at 7.3 eV to 23 meV at 14.0 eV. Downstream the monochromator, the photon beam intersected a supersonic molecular beam at a right angle inside the double imaging DELICIOUS III spectrometer⁵⁶ of the permanent end-station SAPHIRS.⁵⁷ Inside DELICIOUS III, photoions and photoelectrons were accelerated in opposite directions with a DC electric field and then detected in coincidence with delay line anode-based position sensitive detectors (PSDs). The electrons passed through a velocity map imaging spectrometer and the ions went through a modified Wiley McLaren time-of-flight (WM-TOF) 3D momentum imaging spectrometer. The PEPICO scheme allows mass-tagging the electron images allowing to discard any spurious/background compounds. Further filtering was also achieved by using the ion imaging capability of the set-up (see below).

C₆₀ was obtained commercially (Sigma-Aldrich ≥99% purity) and was sublimated in an in-vacuum temperature-controlled oven heated up to 600 °C. The oven was placed inside the differentially pumped SAPHIRS chamber which is connected to the DELICIOUS III ionization chamber via a two-stage differential pumping.⁵⁷ Argon was used as a carrier gas with a backing pressure of 1.0 bar. Exiting the oven, the sample expanded supersonically through a 200 μm nozzle. Between the oven and the first skimmer (ϕ = 1.0 mm) leading to the differential chamber, a cold trap utilizing the flow of chilled ethylene glycol (set to −20 °C) was placed to attract any thermalized C₆₀ that was not engulfed in the molecular beam. Passing through the first skimmer onward through the differential pumping chamber, the molecular beam encountered a second skimmer (ϕ = 2.0 mm) that led to the ionization chamber. Under these relatively mild expansion conditions we expect no aggregation processes and indeed no masses heavier than 720 amu were observed.

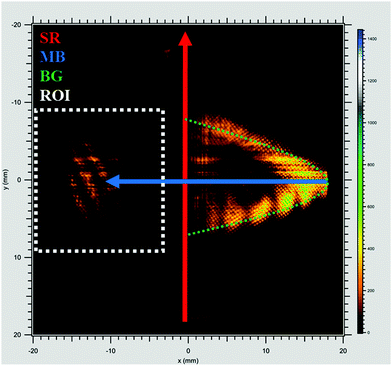
Once the components of the molecular beam were ionized inside the DELICIOUS III chamber, the charged particles were accelerated with an electric field of 88 V cm⁻¹. To ensure the detection of all the C₆₀ ions passing through the modified WM-TOF setup, an additional electrostatic deflection was applied along the molecular beam axis so that no high-mass particles would miss the PSD because of their initial velocity. Visually, this shifting effect is akin to pulling the thermal background ions towards one side of the ionization chamber, being stretched to the visible “D-shaped” pattern, while “pulling” the supersonic part of the molecular beam, i.e. the region of interest which contains the heaviest species, further towards the center of the PSD (Fig. 1).

Fig. 1 An example of the ion image with the deflection voltage applied. The red arrow shows the direction of the synchrotron radiation (SR) beam, the blue arrow shows the direction of the molecular beam (MB) and the green dashed line shows the background signals that were ionized by the SR. The deflection voltage causes the generated ions to travel further towards the right side of the PSD instead of travelling directly through the mass spectrometer. Hence, the background appears like a stretched rubber band instead of being aligned with the SR. The blue arrow points to the heaviest contents of the MB, namely the signals pertaining to ionized C₆₀. The white dashed rectangle indicates the region of interest (ROI). The background is filtered away by removing all coincidence signals outside of the chosen ROI, leaving only coincidence signals pertaining to the contents of the molecular beam.

Energy calibration was achieved using various ionization energies of background contaminants such as O₂ (12.07 eV), H₂O (12.62 eV) and the residual second harmonic ionization of argon (7.88 eV). This results in a 5 meV accuracy of the energy scale, or approximately half the scan step. Such energy calibrations using higher harmonic ionizations of the contents of the molecular beam have been performed previously and discussed in detail elsewhere.^58,59 In order to correct for possible drifts in the C₆₀ neutral density, i.e. the relative intensities of the bands between the scans, a “fast” scan was performed over the entire energy range with 0.1 eV step sizes with the same acquisition time per point as in the aforementioned scans which had significantly smaller step sizes. Thus, when plotted together, the intensities of the individual scans could be scaled to the intensities from the fast scan. Subsequently, the absolute intensity was normalized for the photon flux with measurements obtained from the photodiode to give a flat photon flux response.

Electron images were Abel inverted using the pBasex algorithm.⁶⁰ Following inversion of the mass-filtered electron images pertaining to the ROI in Fig. 1, the ionization intensities can be plotted in matrix form as a function of the electron kinetic energy and photon energy. By integrating the pixel intensities along the electron signals in the matrix, from KE_max = 0 up to a fairly small value (50 meV in this work), the threshold photoelectron spectrum is obtained. A more detailed description of the TPES abstraction from the 2D-matrix has been given elsewhere.⁵⁹

The 50 meV integration window is chosen as the best compromise between signal and resolution. The total energy resolution is in fact a convolution of the electron bandwidth that is used to obtain the TPES and the photon resolution. This issue has been discussed previously^58,59 and we have found that the 50 meV electron bandwidth translates into a resolution of 13 meV. Due to spectral congestion, the width of the peaks in the TPES well exceed the total energy resolution which is the convoluted value of the electron resolution and photon resolution.

3. Results and discussion

3.1 TOF-MS

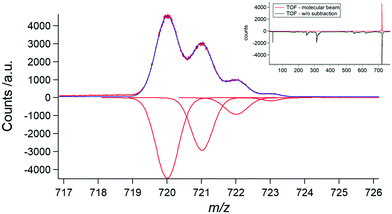
Fig. 2 shows the accumulated time-of-flight mass spectrum (TOFMS) for the 7.3–10.0 eV photon energy scan, zoomed-in around the mass of C₆₀. The inset shows the full mass spectrum with and without the subtraction of the background signals outside the ROI. In the background there is a signal at 40 amu that corresponds to the second harmonic ionization of Argon which was used to calibrate the energy scale (see above). The broad peaks visible in the m/z 150–650 range are due to spurious compounds present as thermal gas in the chamber.

Fig. 2 Zoomed in figure of the portion of the signal pertaining to C₆₀ and its isotopologues in the time-of-flight mass spectrum (TOFMS) obtained by integrating all signals in the ion image of the energy scan from 7.3 eV up to 10.0 eV. Presented in blue is the combined fit from Gaussian curves for each mass peak from 720 amu to 723 amu, which are individually presented in the mirrored mass spectrum. On the inset in the right corner, the entirety of the TOFMS is presented up to 1050 amu, with (red curve) and without correction (black curve) by the ion ROI.

From a molecule containing sixty carbon atoms, a significant amount of the sample contains one or more ¹³C isotopes. The expected natural abundances of ¹³C¹²C₅₉, ¹³C₂¹²C₅₈, ¹³C₃¹²C₅₇ are, respectively, 64.9%, 20.7%, and 4.3% out of the natural abundance of ¹²C₆₀. These are well reproduced as the abundances observed for the 721 amu, 722 amu, and 723 amu signals are 65.2%, 20.5% and 2.7%, respectively.

It has been shown that isotopic distribution within the molecule is truly random⁶¹ but more importantly, the mass perturbation does not affect the electronic structure of C₆₀ so force constants are unchanged.⁶² To capitalize on this observation, we integrate over the entire visible isotopic pattern (720–723 amu) to obtain the best possible signal to noise ratio in our PES signals.

3.2 2D-Photoelectron matrix

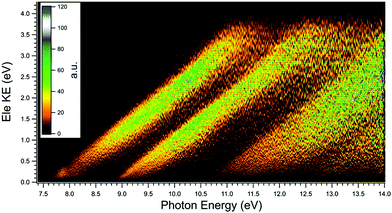
The two-dimensional coincident signal as a function of electron and photon energy for C₆₀, i.e. the ROI and mass-filtered signal pertaining to the C₆₀ isotopologues is shown in Fig. 3. There are three strong bands visible with onsets at 7.58 eV, 8.82 eV and 10.58 eV. Above the third band (around 12.20 eV) there seem to be other bands, but these are not as well resolved as the first three bands and appear very diffuse. As has been discussed previously, the second photoelectron band is expected to arise from the ionization of two states, namely 6g_g (²G_g) and 10h_g (²H_g). The third band is expected to include four different electronic states and the fourth band eight (see Table 1).

Fig. 3 Photoelectron intensity matrix of C₆₀. The colors represent the electron signal as a function of the electron kinetic energy (Ele KE) and photon energy in eV. Energy steps below 10 eV are 8 meV and above 10 eV they are 10 meV.

Table 1 Valence ionization potentials of the electronic bands observed up to 14.0 eV and comparisons with the theoretical framework

Band	Band positions (this work)/eV	Calculated IEv (Colavita et al.^30)/eV	Calculated IEv (Zakrzewski et al.^64)/eV	Calculated IEv (Ponzi et al.^65)/eV	Label	Symmetry
1	0 (7.65)	0	0	0	6hu	π
2	1.31 (8.96)	1.13	1.56	1.11	6gg	π
		1.24	1.53	1.21	10hg	π
3	3.07 (10.72)	2.80	3.48	2.72	6gu	π
		3.10	4.08	2.32	5hu	σ
		3.30	4.21	3.24	6t2u	π
		3.39	4.24	2.62	9hg	σ
4	4.69 (12.34)	4.42	5.65	3.58	5gu	σ
		4.58	5.88	4.49	8hg	π
		4.89	6.38	4.15	2t2g	σ
		5.16	7.19	4.36	5gg	σ
		5.53		4.74	7hg	σ
		5.65		5.57	6t1u	π
		6.01		5.29	4gu	σ
		6.20		6.10	4ag	π

---

The theoretical results that are presented in Table 1 for comparisons used different methodologies to arrive at their respective ionization energies. Colavita et al. used a local density correlation approximation (VWN TS) to calculate the ionization energies and their orbital energies are presented relative to that of the calculated ground state. Ponzi et al. did the same with their DFT & TD-DFT results. Zakrzewski et al. employed electron propagator methods which gave a perfect comparison of the absolute energies of the ground state, but this methodology is ill-suited to finding ionization energies beyond the third photoelectron band.

Several literature values for the adiabatic ionization potential (IE_ad) of C₆₀ – all determined from total ion yield measurements – can be found, e.g. 7.58^+0.04_−0.02,⁵⁰ 7.54 ± 0.04 eV,⁴⁸ and 7.57 ± 0.01 eV.⁶³ Our measurement allows us to determine both a vertical and adiabatic value of the IP, namely IE_v = 7.648 ± 0.010 eV and IE_ad = 7.511 ± 0.010 eV. The adiabatic value was obtained from the total ion yield as the first point where the ion signal surpasses the noise level. However, obtaining the adiabatic IE using this method is imprecise and must be viewed as an approximation since hot bands and other temperature effects such as conformer population, will affect the signal onset. Adiabatic IEs are more precisely obtained from the TPES by comparison with simulations that account for the Franck–Condon factors, but as mentioned further down the text, this is not possible with the current experimental resolution and the vibronic congestion on the first band. For the higher electronic bands, our results compare well with previous computations.^30,64,65

3.3 Threshold photoelectron spectrum (TPES)

Diagonal integration along the 2D-matrix in Fig. 3 up to KE_max = 50 meV yields the TPES of C₆₀ (see Fig. 4) according to a procedure documented previously.⁶⁶ The TPES allows comparisons with the theoretical valence vertical ionization potentials of all the electronic states in the first four bands as well as theoretically simulated PES. Our results compare relatively well for the first two bands but less so for the third and fourth bands. Between 12.0 and 14.0 eV, eight electronic states are expected from theory but in this region, we are unable to obtain a good S/N ratio to decipher anything regarding these states. It is also noteworthy that there are discrepancies between the theoretical works of Colavita et al.³⁰ and Gao et al.⁶⁷ in this region. Note that comparing the branching ratios between different electronic states intensities between this work and the simulated PES at 14 eV of Gao et al. is not straightforward because of the kinetic energy effect on the partial cross sections and the possible presence of autoionization resonances in the TPES. Lastly, a comparison with the measured PES from Korica et al.⁶⁸ is presented which was collected at 50 eV and compares reasonably well with our TPES in terms of shape and energies although the lower resolution of this spectrum precludes a more precise comparison. For instance, the first band of Korica et al. is noticeably shifted to the red by about 400 meV which could either be a resolution effect or due to other experimental issues.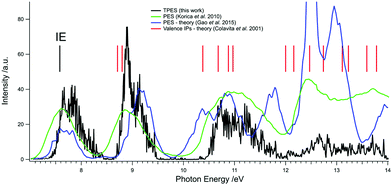

Fig. 4 Threshold photoelectron spectrum (TPES) of C₆₀ from threshold up to 14.0 eV (black). Superimposed is the PES of C₆₀ at 50 eV from ref. 68 (green) and the theoretically simulated PES of C₆₀ at 14 eV from ref. 67 (blue). The ionization potential is indicated with a black vertical stick and the red vertical sticks are the valence ionization potentials calculated by Colavita et al.³⁰

From past experiments on the infrared spectra of C₆₀⁺ cations, there are up to twelve active vibrational bands expected in the ground state alone which vary in their fundamental frequencies between 350 cm⁻¹ (43 meV) and 1550 cm⁻¹ (192 meV).³⁷ It has furthermore been shown that sublimated C₆₀ molecules embedded in a supersonic expansion do not efficiently cool vibrationally.⁶⁹ With step sizes ranging from 8 meV up to 10 meV covering an energy range that includes a dozen different vibrational modes it is thus impossible to resolve any of the vibrational structure from the electronic bands we observe in the TPES. However, the bands themselves display some interesting structures on which we will elaborate.

The first electronic band we observe resembles the convolution of three distinct peaks which is very similar to that observed in the PES from Canton et al.³⁹ As mentioned in the introduction, they showed evidence in the shape of the photoelectron spectrum of the first electronic band that suggests that the C₆₀⁺ ion portrays D_3d symmetry in the gas phase but not D_5d, as has been derived from matrix experiments backed up by theoretical calculations.^36–38 The problem with media such as noble gas matrices is that they can be quite perturbative and previous electronic and IR spectra of C₆₀⁺ from such media displayed features that had to be attributed to another unidentified geometry.⁷⁰ The D_3d symmetry claim was called into question⁷¹ where it was argued that the three-way splitting of the tunneling states observed in the photoelectron spectrum was too large to be due to tunneling states. This was counterargued as large spacings between vibronic states is not an uncommon occurrence in free ions.⁷² Indeed it has been stipulated more recently that symmetries of C₆₀ anions and cations are lower than I_h and D_5d⁷³ and it has also been shown with scanning tunneling spectroscopy that the fundamental frequencies of C₆₀⁺ are insufficient to explain the complete appearance of the PES of C₆₀⁷⁴ bringing further validity to the idea of a split C₆₀⁺ ground state.

In relation to C₆₀⁺, the theory developed by Moate et al.³⁴ in which the ground electronic state ²H_u is JT-active, the symmetries of the vibrations capable of coupling with it are determined from the symmetrized direct product, [H_u⊗H_u] = A_g⊕G_g⊕2H_g. As a_g modes do not inflict symmetry changes, the linearly JT active modes form a basis of the G_g and H_g irreducible representations in the I_h point group which leads to a H⊗(g + 2h) JT problem comprising eight h_g and six g_g modes which could in principle give rise to multimode coupling. For an in-depth discussion of the theoretical treatment, see ref. 34, 75 and 76. The theory predicts that the tunneling splitting between A and H states in the D_3d geometry ranges from 0 to 2ħω for the multimode H⊗(g + 2h) system (ħω is the frequency of the JT active mode) and this is what was reported,^39,72 with the relative intensities of the H_u, G_u, and A_u states being 5 : 4 : 1 in their experiment which compares well with the 4 : 3 : 1 ratio of contributing JT active modes of h_g, g_g, and a_g, respectively.⁷⁶

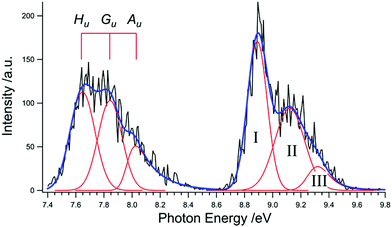
A close-up of our measured TPES of the first two bands is presented in Fig. 5. The bands are fitted internally with Gaussians for the H_u and G_u states whereas the best fit was obtained by employing a modified Gaussian to the A_u states, similar to the methodology of Canton et al.³⁹ The observed spectral structures appear very noisy with typical widths of the noise being around 8–12 meV. An energy scan with a step size of 4 meV revealed the same structures but the noise between scans was not reproducible which made rovibrational assignments impossible.

Fig. 5 Close-up of the first two electronic bands observed in the TPES of C₆₀. Each band is fitted with two Gaussians (for the H_u and G_u states in the first band and structures I and II in the second band) and one modified asymmetric Gaussian (for the A_u state in the first band and the structure III in the second band) and are presented in red. The convoluted fit is presented in blue.

When our results for the first band are analyzed in terms of the H_u, G_u, A_u splitting, our TPES shows the same basic structure as Canton et al. from their PES recorded at 50 eV, with reasonably similar energy positioning considering our S/N, and with slightly dissimilar ratios between the peak intensities. The numerical results and the comparisons with the work of Canton et al. are presented in Table 2. As previously mentioned, the results favor a D_3d interpretation of the ground state whereas in D_5d symmetry the ground state would be split into two bands with a 5 : 1 intensity ratio.³⁴ As the participating modes include eight h_g, six g_g modes and two a_g modes, the expected ratios are 4 : 3 : 1 in a D_3d symmetric ground state. Direct comparison shows that in our TPES, the H_u state appears weaker than in the PES³⁹ while a greater contribution is observed in the A_u state. The differences in intensities are interesting nonetheless as they can be indicators of differences in the possible contributions of autoionizing states converging to the different states. Besides this, we do not expect any photon energy dependence in the branching ratio since the JT-induced splitting occurs in the final cation state.

Table 2 Energies (in eV) and relative intensities of the JT split bands from the curve fitting of the threshold photoelectron spectrum in Fig. 5 of the first electronic band along with comparison with the results from Canton et al.

	E b – this work^a	E b – Canton et al.	ΔEb – this work	ΔEb – Canton et al.	I rel – this work^b	I rel – Canton et al.
a Estimated error is ±0.012 eV. b Estimated error is ±0.020.
Hu	7.648	7.75	0	0	0.423	0.55
Gu	7.843	7.98	0.195	0.23	0.386	0.36
Au	7.970	8.14	0.322	0.40	0.191	0.05

---

Regarding the second band, previous experiments from the early 1990's actually alluded to this sort of three way split structure as two distinct peaks at electron binding energies of 8.89 and 9.12 eV and an obscure peak at roughly 9.3 eV were seen.⁷⁷ Furthermore, it has been suggested that these three peaks are closely related to peaks at 7.87, 8.12, and 8.29 eV in the absorption spectrum of C₆₀ because the spacing between the peaks are quite similar.⁷⁸ It is therefore entirely reasonable that the absorption measurements evidence a Feshbach resonance involving superexcited states originating from inner valence-excited Rydberg states of C₆₀ converging to the two split excited states of the cation.

Assigning the second electronic band specifically is not straight-forward, however. To simplify our analysis, we fit the second band in the same manner as that of the first band – with three different peaks – to extract information about the states from the relative intensities of the fitted peaks. The results are presented in Table 3.

Table 3 Energies (in eV) and relative intensities of the split bands from the curve fitting of the threshold photoelectron spectrum in Fig. 5 of the second electronic band. The estimated errors are the same as the values presented in Table 2

	E b	ΔEb	I rel
I	8.891	0	0.583
II	9.121	0.23	0.321
III	9.270	0.379	0.096

---

Within the second band there are two electronic states anticipated which are labeled 6g_g and 10h_g.^30,64,65 Depending on the theory, it is not clear whether the 6g_g state or the 10h_g state is higher in energy. While Zakrzewski et al. predict the 10h_g state to be 30 meV lower in energy than 6g_g, Colavita et al. predict the 10h_g state to be 110 meV higher than the 6g_g state. Meanwhile, gas-phase research into the C₆₀⁺ DIBs (Campbell et al. 2015; Kuhn et al. 2016) shows a splitting of 60 cm⁻¹ (7.4 meV) between the two strongest DIBs assigned to transitions from the ground state of C₆₀⁺ to its excited states. Assignment of this second band is of capital interest to the astronomical community as several of the elusive diffuse interstellar bands have recently been assigned to transitions from the electronic ground state of C₆₀⁺. Thus, ascribing an accurate assignment to the electronic states of the C₆₀⁺ ion might become helpful in assigning even more of the recorded DIBs.

If we, for a moment, assume that both of the electronic states in the second band are split into three tunneling states like the ground state (i.e. they are both D_3d symmetric), we would expect the same basic convoluted structure of three peaks of decreasing intensity. While we observe what could be construed as a three-way splitting, the first peak is significantly stronger than that of the ground state. Between the first band and the second band, the relative intensity of the first peak increases from 0.423 to 0.583. Meanwhile, the relative intensities of the second and third peaks decrease from 0.386 to 0.321 and 0.191 to 0.096, respectively. These differences call for a different approach to explain the structure of this band.

Some significant progress has been made recently in assigning the electronic transitions that give rise to the DIBs. In their theoretical approach, Lykhin et al.⁴³ employed electronic structure methods to describe a pseudo-JT effect in C₆₀⁺ through the interaction with low-lying excited states.⁷⁹ Lykhin et al. found the D_5d to be energetically the most favorable ground state symmetry in accordance with prior calculations. Applying a pseudo-JT distortion to this configuration lifts the degeneracy of the first (bright) excited state giving rise to two symmetry-allowed transitions: ²A_u → ²A_g and ²A_u → ²B_g. This is made possible via a distortion along the lowest e_1g vibrational mode pertaining to D_5d symmetry. According to the epikernel principle,⁸⁰ this distortion lifts the degeneracy of the excited state and distorts the D_5d fullerene cage toward the C_2h minima.

Since our TPES results show evidence of a D_3d symmetric ground state of C₆₀⁺, the question arises what impact it has on these findings. The answer is none at all. The epikernel principle dictates that a distortion of both D_3d and D_5d symmetries lead to C_2h minima with the only difference being that from D_3d symmetry, the ground state is “softened” by mixing the e_g vibrational mode pertaining to D_3d symmetry, rather than the lowest-lying e_1g vibrational mode for D_5d symmetry.

Analogous situations involving pseudo-JT distortions have been described previously.⁷⁹e.g. A similar pseudo-JT effect was employed to resolve the issue of the ground state symmetry of CO₃ where the ground state exhibits D_3h symmetry which undergoes distortion along the e′ coordinate towards a C_2v geometry which is observed in the first excited state/s.⁸¹

In terms of an exact assignment of the features of the second photoelectron band, however, the more relaxed rules of direct ionization add a level of complication since more transitions from the ground neutral state to both JT split electronic states are possible, as compared to the limited number of two bright states.⁴³ With the added congestion from possible vibrational progressions and our current energy resolution, we can only note that the predicted JT splitting is too small to account for the peak separation in Table 3, so that most likely, and based on the calculated ionization energies, the first two bands can be attributed to direct ionization to the 6g_g and 10h_g states. Thus, the third band might represent vibrational progression on the cation, as already postulated.⁷⁷ Confirmation of this would need FC simulations on excited states, which is a challenging theoretical task and out of the scope of the present paper.

In terms of astrophysical implications, these speculations may imply that DIBs higher in energy corresponding to excitations from the ground state to either higher vibrational progressions of the A_g and B_g states, or from the ground state to either the h_g or g_g excited states, are possible in principle, but in astronomical settings – particularly as cold as the diffuse ISM – these may be too weak for detection.

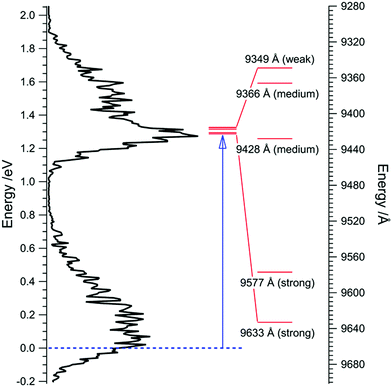
Exact vibrational assignments within the second band are troublesome for the same reasons as in the ground state. The vibrational structure is difficult to reproduce because a supersonic expansion does not vibrationally cool the molecule.⁶⁹ As a result the intensities of the bands are not indicative of interstellar conditions (with very low temperature) and we can see in Fig. 6 that the strongest DIB transitions (9633 Å = 1.287 eV) do not exactly converge to the difference between our measured values of the vertical IP (7.648 eV) and the maximum of band I (8.891 eV) which equals 9975 Å (1.243 eV).

Fig. 6 (left axis) The first two bands observed in the TPES are plotted vertically with the energy scale calibrated to zero around the IP_v value of the H_u state. The blue arrow is representative of the excitations to the strongest feature in the second PES band which reflects the transitions behind the DIBs. Although the energy level correspondence between the ground state and the maximum of the second photoelectron band is good, it is not perfect as the intensities from the experiment may not be reflective of interstellar conditions.

While there is definitely some observable structure in the third electronic band, no effort was made to disentangle it as the number of electronic states is double that of the states within the second band. It is noteworthy that the third band seems to be similarly structured as the ground state (i.e. split into tunneling states) and with similar intensities so an invocation of D_3d symmetric states might be appropriate but a confirmation would require more work, and is beyond the scope of this paper. There are also some severe discrepancies between its appearance and that of simulated PES,⁶⁷ indicating that there is still ground to be made up in the convergence of experiment and theory to the photoelectron spectrum of C₆₀.

In effort to extract more information about the nature of these states several fixed photon energy i²PEPICO acquisitions at different energies (from 8.5 eV to 13.5 eV) were performed to measure the anisotropy parameter β of these bands. The results are presented in the ESI† and compared (where applicable) to theoretically obtained values.^65,82 The recent results from Ponzi et al.⁶⁵ predict a much more negative value of β for the HOMO 6h_u band for slow photoelectrons (KE < 4 eV), while the agreement for faster photoelectrons is more reasonable. As for the second band, the calculations predict negative anisotropy values ranging from −0.7 to −0.1 for both 6g_g and 10h_g states in our photon energy range, while our experimental values start at −0.5 at 10.5 eV and progress towards slightly positive values at 13.5 eV. All in all the agreement is good considering the theoretical approximations and our experimental error bars (±0.2), but the fact that the calculated anisotropies of both 6g_g and 10h_g states are very similar does not allow further progress in the assignment of the second photoelectron band.

4. Further astrophysical implications

4.1 Photoionization around the Lyman-α limit

The 2D-matrix presented in Fig. 3 holds a lot of information. Relevant to the presence of C₆₀ in photodissociation regions where Lyman-α radiation dominates, we can extract the photoelectron energy distribution, i.e. the PES corresponding to photoionization by the Lyman-α line (10.2 eV). This is achieved by taking a vertical cut of the matrix intensities at 10.2 eV (see Fig. 7). The PES shown in Fig. 7, is to our knowledge the first ever measured at this astrophysically-relevant photon energy.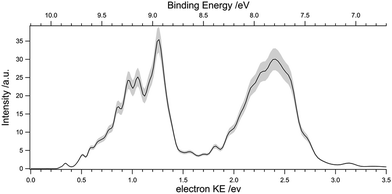

Fig. 7 Photoelectron spectrum recorded at the Lyman-α line (10.2 eV), showing the electron energy distribution produced at this energy. The curve is obtained by vertical cut of the 2D intensity matrix in Fig. 3 at 10.2 eV which has been smoothed with a three-point smoothing. The shaded region is representative of the error bars.

When the C₆₀ photoelectron distribution for a Lyman-α like radiation is inspected more closely, two structures arise, corresponding to ionization to the ground and first two electronically excited states of C₆₀⁺. The two bands have now similar intensities, unlike the case of the TPES in Fig. 5. These discrepancies are due to kinetic energy effects in the photoionization cross sections, but the overall vibrational envelope of each electronic state is quite similar, although the PES offers a lower resolution.

The UV/VUV interstellar radiation field processes the entire ISM and either electronically excites PAHs and fullerenes or ionizes them. This photoelectric effect is thought to be the dominant heating source of the ISM where the photoelectrons may carry additional kinetic energy leftover from the photoionization process, and this kinetic energy heats up the ISM.⁸³ This is especially important for big systems, such as C₆₀, where absolute cross-sections are expected to be relatively large (see below). The kinetic energy of the photoelectrons has been roughly evaluated by models^84,85 which include some experimental information,⁸⁶ but this information is still in need of an update and it requires checking whether more PAHs and fullerenes exhibit the same behavior as has been used in these models. Thus, we present here the photoelectron kinetic energy distribution of the ionization of C₆₀ for the Lyman-α limit, which can be directly utilized by astrochemical models dealing with photoelectric emission processes from isolated carbon grains.

4.2 Absolute photoionization cross section around the Lyman-α limit

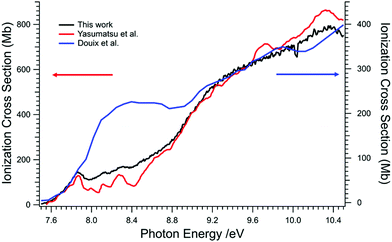
The total absolute absorption cross section of C₆₀ in this energy range has been recorded previously,⁷⁸ from which a photoionization quantum yield was deduced. The measurements were subsequently used to obtain the absolute photoionization cross section of C₆₀ from 25 eV up to 120 eV.⁸⁷ Recently, the total photoionization cross section of C₆₀⁺ was measured and calculated and it was found that the absorption cross sections of neutral C₆₀ and its cation are nearly identical, and differ from a simple 60 carbon atoms sum rule.⁸⁸ This raises the question of whether the photoionization cross sections of neutral C₆₀ and its cation display the same level of similarity as their absorption cross sections.

Here, we present the cross section from threshold up to approximately 10.5 eV (Fig. 8). The reason is that above 10.5 eV, the collection of the produced photoelectrons is not 100% as the extraction field was not set high enough to collect electrons with kinetic energy release above approximately 3.5 eV (see Fig. 3). Firstly, we directly compare our results with those of Yasumatsu et al.⁷⁸ by taking their absolute photoabsorption cross section multiplied with its photoionization quantum yield to obtain the absolute photoionization cross section. This is presented on the left y-axis. Secondly, we plot the absolute photoionization cross section of C₆₀⁺ from Douix et al.,⁸⁸ shifted down in energy (by approximately 3 eV) to coincide with the ionization onset of neutral C₆₀. This is plotted on the right y-axis.

Fig. 8 The absolute photoionization cross section from the results from Yasumatsu et al. are presented in red and is plotted on the left y-axis, as indicated with the red arrow. In blue, the absolute photoionization cross section from Douix et al. is plotted on the right y-axis, as indicated with the blue arrow. Meanwhile the total ion yield from this work is plotted in black and is scaled to match the general shapes of the two curves.

There are some discrepancies between the two comparisons. The cross section obtained from Yasumatsu et al. is approximately two times larger than the one from Douix et al. It is likely that the results from Yasumatsu et al. are overestimated but they indicate an approximate 100% uncertainty value in their absolute absorption cross section. Since the calculated absorption cross-sections of neutral and cationic C₆₀ are very similar,⁸⁸ the difference seen in Fig. 8 should arise from the different ionization quantum yields. However, measuring experimental absolute ionization cross-sections is extremely challenging so that the typical error bars do not leave room for further discussion.

The total ion yield (TIY) from this work is set on an absolute scale in the VUV, calibrated at around 9 eV to the curve of Yasumatsu et al. As compared to previous work, such as the TIY of Hertel et al.⁴⁸ or the absorption spectrum of Yasumatsu et al., we also observe a peak at 7.87 eV attributed to the autoionization of Rydberg series converging to the ionization limits of the first excited states of the cation. This feature is slightly visible on the 2D matrix presented in Fig. 3 on which a brighter spot is discernible at the beginning of the diagonal line corresponding to the ground state. They also assigned a vibrational progression that is associated with the peak around 8.12 eV and they attributed the slight dip at 8.45 eV to a Feshbach–Fano antiresonance due to the interaction of a superexcited state with an ionization continuum. Overall the shape of our TIY is in very good agreement with the one previously derived data.⁷⁸

There is also an interesting difference in the cross sections of C₆₀ and C₆₀⁺ around a photon energy of 8.3 eV, where there seems to be a resonance present in the cross section of C₆₀⁺. Undeniably the shape of our TIY compares very well with the results of Douix et al.⁸⁸ apart from this region. We can only speculate on the origins of this broad resonance. It is possible that shape or confinement resonances, which have been calculated to be present in the continuum,⁶⁵ are stronger in the cation due to the increased attractiveness of the potential as felt by the departing electron.

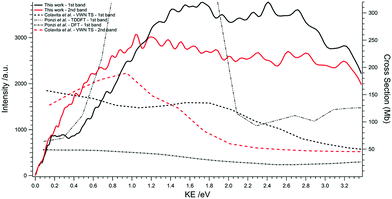
Further manipulation of the 2D photoelectron matrix can also reveal the partial photoionization cross sections of the first two bands up to 3.3 eV KE (i.e. ∼10.8 eV). Integrating along the diagonal lines (constant ionic state lines) provides the partial photoionization yield of the two bands (see Fig. 9) as a function of the electron KE. Both bands suggest the presence of shape resonances above the ionization threshold, around 1–3 eV KE.^65,82 The partial cross sections of the first two bands have been previously calculated by Colavita et al.³⁰ and more recently by Ponzi et al.⁶⁵ The shapes differ quite significantly (see Fig. 9) and they, furthermore, do not account for all the shape resonances that are evident in our measurement. There are also significant differences in the DFT and TDDFT results from Ponzi et al. in this region which are due to autoionizing resonances being included in the TDDFT treatment and according to our findings it seems that these autoionizing resonances are greatly exaggerated in the TDDFT treatment where the calculations predict a value of 900 Mb at 8.7 eV (or 1.3 eV on the KE scale in Fig. 9). These exaggerations stem from the frozen core approximation where nuclear motion is not considered, and the strong geometry dependence of the resonances.

Fig. 9 Partial photoionization yields of the first two electronic bands plotted in arbitrary units (left y-axis). Drawn in comparison are the calculated partial absolute photoionization cross sections by Colavita et al. and Ponzi et al. (right y-axis).

5. Conclusions

By utilizing the i²PEPICO spectroscopic method in tandem with synchrotron radiation in the VUV range, we have uncovered a wealth of information regarding the photoionization dynamics of C₆₀. This method provided us with a 2D-photoelectron matrix from which by horizontal, vertical, and diagonal projections/cuts of different regions of the matrix, we could obtain information relevant to the TPES, the total ion yield (normalized on an absolute scale in the VUV range), the electron kinetic energy distribution at various photon energies, and the partial photoionization cross sections of individual electronic bands.

The information we have presented here on the C₆₀ buckminsterfullerene has direct and indirect applications to ongoing astrochemical work related to DIBs and astrochemical models that include C₆₀ photoionization and photoelectric heating with photoelectrons from PAHs and fullerenes alike, as well as addressing some fundamental questions about the symmetry of the ground state of C₆₀⁺.

The results of our TPES of C₆₀ imply a different symmetry of the ground state ion than calculations seem to favor, which is in line with some other previous experimental findings.^39,74 Although this work implies that the ground state of the C₆₀⁺ ion belongs to the D_3d symmetry group rather than the D_5d symmetry group, the recent theoretical progress⁴³ in assigning the transitions at the heart of the DIBs that have been assigned to C₆₀⁺, are not diminished – on the contrary – as both D_5d and D_3d symmetry groups undergo the same pseudo-JT distortion to give rise to C_2h symmetry and, moreover, there does seem to be a connection between the DIBs assigned to C₆₀⁺ and the most intense structure we observe in the second photoelectron band in our recorded TPES. This does not tell the whole story, however, as the energetics of the 6g_g and 10h_g excited states have not been definitively accounted for and it is likely that their structure in the second photoelectron band is due to photoionization converging to unresolvable vibrational modes of these states. This brings to light the temperature issue in our experiment which we expect to be higher than in a typical diffuse interstellar cloud. Next generation photoionization experiments should aim at circumventing the hot vibrational temperature issue using cryogenic methods to cool C₆₀ molecules, as has been successfully achieved for IR spectroscopy.⁸⁹

Finally, although scarce, the results on the electron continuum suggest differences between calculated and experimental cross sections and anisotropy values, which in turn highlight the difficulties of calculating continuum properties in large systems and could be used as benchmarks for further theoretical advancements.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We are grateful to the whole SOLEIL for provision of synchrotron radiation under proposal number 20180297, as well as to J.-F. Gil for his technical assistance on the SAPHIRS endstation. H. R. H. is grateful for support from the Marie Sklodowska Curie Actions, proposal ID: 838372.

References

1. H. Kroto, J. Heath, S. Obrien, R. Curl and R. Smalley, C₆₀ Buckminsterfullerene, Nature, 1985, 318, 162–163.
2. H. Kroto, C. Kirby, D. Walton, L. Avery, N. Broten, J. Macleod and T. Oka, Detection of Cyanohexatriyne, H(C=C)₃CN, in Heiles Cloud 2, Astrophys. J., 1978, 219, L133–L137.
3. N. Broten, T. Oka, L. Avery, J. Macleod and H. Kroto, Detection of HC₉N in Interstellar Space, Astrophys. J., 1978, 223, L105–L107.
4. G. Winnewisser and C. Walmsley, Detection of HC₅N and HC₇N in IRC + 10216, Astron. Astrophys., 1978, 70, L37–L39.
5. L. Little, G. Macdonald, P. Riley and D. Matheson, Observations of Interstellar HC₅N and HC₇N in Dark Dust Clouds, Mon. Not. R. Astron. Soc., 1978, 183, P45–P50.
6. K. Sellgren, M. W. Werner, J. G. Ingalls, J. D. T. Smith, T. M. Carleton and C. Joblin, C₆₀ in Reflection Nebulae, Astrophys. J., Lett., 2010, 722, L54–L57.
7. J. Cami, J. Bernard-Salas, E. Peeters and S. E. Malek, Detection of C₆₀ and C₇₀ in a Young Planetary Nebula, Science, 2010, 329, 1180–1182.
8. O. Berne, G. Mulas and C. Joblin, Interstellar C₆₀⁺, Astron. Astrophys., 2013, 550, L4,  DOI:10.1051/0004-6361/201220730.
9. C. Boersma, R. H. Rubin and L. J. Allamandola, Spatial Analysis of the Polycyclic Aromatic Hydrocarbon Features Southeast of the Orion Bar, Astrophys. J., 2012, 753(2), 168,  DOI:10.1088/0004-637X/753/2/168.
10. D. A. Garcia-Hernandez, N. K. Rao and D. L. Lambert, Are C₆₀ Molecules Detectable in Circumstellar Shells of R Coronae Borealis Stars?, Astrophys. J., 2011, 729(2), 126,  DOI:10.1088/0004-637X/729/2/126.
11. C. Gielen, J. Cami, J. Bouwman, E. Peeters and M. Min, Carbonaceous Molecules in the Oxygen-Rich Circumstellar Environment of Binary Post-AGB Stars – C₆₀ Fullerenes and Polycyclic Aromatic Hydrocarbons, Astron. Astrophys., 2011, 536, A54,  DOI:10.1051/0004-6361/201117961.
12. P. Castellanos, O. Berne, Y. Sheffer, M. G. Wolfire and A. G. G. M. Tielens, C₆₀ in Photodissociation Regions, Astrophys. J., 2014, 794(1), 83,  DOI:10.1088/0004-637X/794/1/83.
13. E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Laboratory Confirmation of C₆₀⁺ as the Carrier of Two Diffuse Interstellar Bands, Nature, 2015, 523, 322.
14. M. Kuhn, M. Renzler, J. Postler, S. Ralser, S. Spieler, M. Simpson, H. Linnartz, A. G. G. M. Tielens, J. Cami, A. Mauracher, Y. Wang, M. Alcami, F. Martin, M. K. Beyer, R. Wester, A. Lindinger and P. Scheier, Atomically Resolved Phase Transition of Fullerene Cations Solvated in Helium Droplets, Nat. Commun., 2016, 7, 13550,  DOI:10.1038/ncomms13550.
15. M. A. Cordiner, H. Linnartz, N. L. J. Cox, J. Cami, F. Najarro, C. R. Proffitt, R. Lallement, P. Ehrenfreund, B. H. Foing, T. R. Gull, P. J. Sarre and S. B. Charnley, Confirming Interstellar C₆₀⁺ Using the Hubble Space Telescope, Astrophys. J., 2019, 875, L28.
16. J. Maier, N. Lakin, G. Walker and D. Bohlender, Detection of C₃ in Diffuse Interstellar Clouds, Astrophys. J., 2001, 553, 267–273.
17. M. R. Schmidt, J. Krelowski, G. A. Galazutdinov, D. Zhao, M. A. Haddad, W. Ubachs and H. Linnartz, Detection of Vibronic Bands of C₃ in a Translucent Cloud Towards HD 169454, Mon. Not. R. Astron. Soc., 2014, 441, 1134–1146.
18. G. Herbig, The Diffuse Interstellar Bands, Annu. Rev. Astron. Astrophys., 1995, 33, 19–73.
19. P. J. Sarre, The Diffuse Interstellar Bands: A Major Problem in Astronomical Spectroscopy, J. Mol. Spectrosc., 2006, 238, 1–10.
20. N. L. J. Cox, J. Cami, L. Kaper, P. Ehrenfreund, B. H. Foing, B. B. Ochsendorf, S. H. M. van Hooff and F. Salama, VLT/X-Shooter Survey of Near-Infrared Diffuse Interstellar Bands, Astron. Astrophys., 2014, 569, A117,  DOI:10.1051/0004-6361/201323061.
21. H. Linnartz, J. Cami, M. Cordiner, N. L. J. Cox, P. Ehrenfreund, B. Foing, M. Gatchell and P. Scheier, C₆₀⁺ as a Diffuse Interstellar Band Carrier; A Spectroscopic Story in 6 Acts, J. Mol. Spectrosc., 2020, 367, 111243.
22. A. G. G. M. Tielens, The Molecular Universe, Rev. Mod. Phys., 2013, 85, 1021–1081.
23. O. Berne and A. G. G. M. Tielens, Formation of Buckminsterfullerene (C₆₀) in Interstellar Space, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 401–406.
24. W. W. Duley and A. Hu, Fullerenes and Proto-Fullerenes in Interstellar Carbon Dust, Astrophys. J., Lett., 2012, 745(1), L11,  DOI:10.1088/2041-8205/745/1/L11.
25. J. Zhen, P. Castellanos, D. M. Paardekooper, H. Linnartz and A. G. G. M. Tielens, Laboratory Formation of Fullerenes from PAHS: Top-Down Interstellar Chemistry, Astrophys. J., Lett., 2014, 797(2), L30,  DOI:10.1088/2041-8205/797/2/L30.
26. T. Chen, J. Zhen, Y. Wang, H. Linnartz and A. G. G. M. Tielens, From Planes to Bowls: Photodissociation of the Bisanthenequinone Cation, Chem. Phys. Lett., 2018, 692, 298–303.
27. W. Zhang, Y. Si, J. Zhen, T. Chen, H. Linnartz and A. G. G. M. Tielens, Laboratory Photochemistry of Covalently Bonded Fluorene Clusters: Observation of an Interesting PAH Bowl-forming Mechanism, Astrophys. J., 2019, 872, 38.
28. A. G. G. M. Tielens, Interstellar Polycyclic Aromatic Hydrocarbon Molecules, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
29. A. C. Brieva, R. Gredel, C. Jaeger, F. Huisken and T. Henning, C₆₀ as a Probe for Astrophysical Environments, Astrophys. J., 2016, 826(2), 112,  DOI:10.3847/0004-637X/826/2/122.
30. P. Colavita, G. De Alti, G. Fronzoni, M. Stener and P. Decleva, Theoretical Study of the Valence and Core Photoemission Spectra of C₆₀, Phys. Chem. Chem. Phys., 2001, 3, 4481–4487.
31. D. Toffoli, M. Stener, G. Fronzoni and P. Decleva, Computational Characterization of the HOMO-2 Photoemission Intensity Oscillations in C₆₀, Chem. Phys. Lett., 2011, 516, 154–157.
32. C. C. Chancey and M. C. M. O’Brien, The Jahn–Teller Effect in C₆₀ and Other Icosahedral Complexes, Princeton University Press, Princeton, N.J., 1997.
33. N. Manini, A. Dal Corso, M. Fabrizio and E. Tosatti, Electron-Vibration Coupling Constants in Positively Charged Fullerene, Philos. Mag. B, 2001, 81, 793–812.
34. C. Moate, J. Dunn, C. Bates and Y. Liu, An Analytical Model for the H⊗(h⊕g) Jahn–Teller System, J. Phys.: Condens. Matter, 1997, 9, 6049–6060.
35. G. Dresselhaus, M. Dresselhaus and P. Eklund, Symmetry for Lattice Modes in C₆₀ and Alkali-Metal-Doped C₆₀, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 6923–6930.
36. J. Fulara, M. Jakobi and J. Maier, Electronic and Infrared-Spectra of C₆₀⁺ and C₆₀⁻ in Neon and Argon Matrices, Chem. Phys. Lett., 1993, 211, 227–234.
37. B. Kern, D. Strelnikov, P. Weis, A. Boettcher and M. M. Kappes, IR Absorptions of C₆₀⁺ and C₆₀⁻ in Neon Matrixes, J. Phys. Chem. A, 2013, 117, 8251–8255.
38. D. Strelnikov, B. Kern and M. M. Kappes, On Observing C₆₀⁺ and C₆₀²⁺ in Laboratory and Space, Astron. Astrophys., 2015, 584, A55,  DOI:10.1051/0004-6361/201527234.
39. S. Canton, A. Yencha, E. Kukk, J. Bozek, M. Lopes, G. Snell and N. Berrah, Experimental Evidence of a Dynamic Jahn–Teller Effect in C₆₀⁺, Phys. Rev. Lett., 2002, 89(4), 045502,  DOI:10.1103/PhysRevLett.89.045502.
40. R. Bendale, J. Stanton and M. Zerner, Investigation of the Electronic-Structure and Spectroscopy of Jahn–Teller Distorted C₆₀⁺, Chem. Phys. Lett., 1992, 194, 467–471.
41. M. Luders, N. Manini, P. Gattari and E. Tosatti, Hund's Rule Magnetism in C₆₀ Ions?, Eur. Phys. J. B, 2003, 35, 57–68.
42. I. D. Hands, L. M. Sindi, J. L. Dunn and C. A. Bates, Theoretical Treatment of Pseudorotation in the Jahn–Teller C₆₀⁺ Ion, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(11), 115410,  DOI:10.1103/PhysRevB.74.115410.
43. A. O. Lykhin, S. Ahmadvand and S. A. Varganov, Electronic Transitions Responsible for C₆₀⁺ Diffuse Interstellar Bands, J. Phys. Chem. Lett., 2019, 10, 115–120.
44. G. A. Galazutdinov, V. V. Shimansky, A. Bondar, G. Valyavin and J. Krelowski, C₆₀⁺ – Looking for the Bucky-Ball in Interstellar Space, Mon. Not. R. Astron. Soc., 2017, 465, 3956–3964.
45. R. Lallement, N. L. J. Cox, J. Cami, J. Smoker, A. Fahrang, M. Elyajouri, M. A. Cordiner, H. Linnartz, K. T. Smith, P. Ehrenfreund and B. H. Foing, The EDIBLES Survey II. The Detectability of C₆₀⁺ Bands, Astron. Astrophys., 2018, 614, A28.
46. P. Benning, D. Poirier, N. Troullier, J. Martins, J. Weaver, R. Haufler, L. Chibante and R. Smalley, Electronic States of Solid C₆₀ – Symmetries and Photoionization Cross-Sections, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 1962–1965.
47. J. Weaver, J. Martins, T. Komeda, Y. Chen, T. Ohno, G. Kroll, N. Troullier, R. Haufler and R. Smalley, Electronic-Structure of Solid C₆₀ – Experiment and Theory, Phys. Rev. Lett., 1991, 66, 1741–1744.
48. I. Hertel, H. Steger, J. De Vries, B. Weisser, C. Menzel, B. Kamke and W. Kamke, Giant Plasmon Excitation in Free C₆₀ and C₇₀ Molecules Studied by Photoionization, Phys. Rev. Lett., 1992, 68, 784–787.
49. H. Steger, J. De Vries, B. Kamke, W. Kamke and T. Drewello, Direct Double Ionization of C₆₀ and C₇₀ Fullerenes Using Synchrotron Radiation, Chem. Phys. Lett., 1992, 194, 452–456.
50. J. De Vries, H. Steger, B. Kamke, C. Menzel, B. Weisser, W. Kamke and I. Hertel, Single-Photon Ionization of C₆₀-Fullerene and C₇₀-Fullerene with Synchrotron Radiation – Determination of the Ionization-Potential of C₆₀, Chem. Phys. Lett., 1992, 188, 159–162.
51. T. Liebsch, O. Plotzke, F. Heiser, U. Hergenhahn, O. Hemmers, R. Wehlitz, J. Viefhaus, B. Langer, S. Whitfield and U. Becker, Angle-Resolved Photoelectron-Spectroscopy of C₆₀, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 457–464.
52. K. Hansen, R. Richter, M. Alagia, S. Stranges, L. Schio, P. Salen, V. Yatsyna, R. Feifel and V. Zhaunerchyk, Single Photon Thermal Ionization of C₆₀, Phys. Rev. Lett., 2017, 118(10), 103001,  DOI:10.1103/PhysRevLett.118.103001.
53. L. Nahon, N. de Oliveira, G. A. Garcia, J.-F. Gil, B. Pilette, O. Marcouille, B. Lagarde and F. Polack, DESIRS: A State-of-the-Art VUV Beamline Featuring High Resolution and Variable Polarization for Spectroscopy and Dichroism at SOLEIL, J. Synchrotron Radiat., 2012, 19, 508–520.
54. O. Marcouille, P. Brunelle, O. Chubar, F. Marteau, M. Massal, L. Nahon, K. Tavakoli, J. Veteran and J.-M. Filhol, in Synchrotron Radiation Instrumentation Pts 1 & 2, ed. J. Y. Choi and S. Rah, AMER Inst. Physics, 2 Huntington Quadrangle, Ste 1NO1, Melville, NY 11747-4501 USA, 2007, vol. 879, pp. 311–314.
55. B. Mercier, M. Compin, C. Prevost, G. Bellec, R. Thissen, O. Dutuit and L. Nahon, Experimental and Theoretical Study of a Differentially Pumped Absorption Gas Cell Used as a Low Energy-Pass Filter in the Vacuum Ultraviolet Photon Energy Range, J. Vac. Sci. Technol., A, 2000, 18, 2533–2541.
56. G. A. Garcia, B. K. C. de Miranda, M. Tia, S. Daly and L. Nahon, DELICIOUS III: A Multipurpose Double Imaging Particle Coincidence Spectrometer for Gas Phase Vacuum Ultraviolet Photodynamics Studies, Rev. Sci. Instrum., 2013, 84(5), 053112,  DOI:10.1063/1.4807751.
57. X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Vacuum Upgrade and Enhanced Performances of the Double Imaging Electron/Ion Coincidence End-station at the Vacuum Ultraviolet Beamline DESIRS, Rev. Sci. Instrum., 2015, 86(12), 123108,  DOI:10.1063/1.4937624.
58. H. R. Hrodmarsson, J.-C. Loison, U. Jacovella, D. M. P. Holland, S. Boye-Peronne, B. Gans, G. A. Garcia, L. Nahon and S. T. Pratt, Valence-Shell Photoionization of C₄H₅: The 2-Butyn-1-yl Radical, J. Phys. Chem. A, 2019, 123, 1521–1528.
59. H. R. Hrodmarsson, G. A. Garcia, L. Nahon, B. Gans and J.-C. Loison, Threshold Photoelectron Spectrum of the Anilino Radical, J. Phys. Chem. A, 2019, 123, 9193–9198.
60. G. Garcia, L. Nahon and I. Powis, Two-Dimensional Charged Particle Image Inversion Using a Polar Basis Function Expansion, Rev. Sci. Instrum., 2004, 75, 4989–4996.
61. J. Hawkins, A. Meyer, S. Loren and R. Nunlist, Statistical Incorporation of C-13(2) Units into C₆₀, J. Am. Chem. Soc., 1991, 113, 9394–9395.
62. J. Menendez and J. Page, Light Scattering in Solids VIII, Springer-Verlag Berlin, Heidelberger Platz 3, D-14197 Berlin, Germany, 2000, vol. 76, pp. 27–95.
63. R. Yoo, B. Ruscic and J. Berkowitz, Vacuum Ultraviolet Photoionization Mass-Spectrometric Study of C₆₀, J. Chem. Phys., 1992, 96, 911–918.
64. V. G. Zakrzewski, O. Dolgounitcheva and J. V. Ortiza, Electron Propagator Calculations on C₆₀ and C₇₀ Photoelectron Spectra, J. Chem. Phys., 2008, 129, 104306.
65. A. Ponzi, S. T. Manson and P. Decleva, Photoionization of C₆₀: Effects of Correlation on Cross Sections and Angular Distributions of Valence Subshells, J. Phys. Chem. A, 2020, 124, 108–125.
66. J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Gregoire, C. Desfrancois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Photoionization of 2-pyridone and 2-hydroxypyridine, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572.
67. C.-Z. Gao, P. Wopperer, P. M. Dinh, E. Suraud and P.-G. Reinhard, On the Dynamics of Photo-Electrons in C₆₀, J. Phys. B: At., Mol. Opt. Phys., 2015, 48(10), 105102,  DOI:10.1088/0953-4075/48/10/105102.
68. S. Korica, A. Reinkoester, M. Braune, J. Viefhaus, D. Rolles, B. Langer, G. Fronzoni, D. Toffoli, M. Stener, P. Decleva, O. M. Al-Dossary and U. Becker, Partial Photoionization Cross Sections of C₆₀ and C₇₀: A Gas versus Adsorbed Phase Comparison, Surf. Sci., 2010, 604, 1940–1944.
69. J. T. Stewart, B. E. Brumfeld, B. M. Gibson and B. J. McCall, Inefficient Vibrational Cooling of C₆₀ in a Supersonic Expansion, ISRN Phys. Chem., 2013, 2013, 675138.
70. Z. Gasyna, L. Andrews and P. Schatz, Near-Infrared Absorption-Spectra of C₆₀ Radical Cations and Anions Prepared Simultaneously in Solid Argon, J. Phys. Chem., 1992, 96, 1525–1527.
71. N. Manini and E. Tosatti, Comment on “Experimental Evidence of a Dynamic Jahn–Teller Effect in C₆₀⁺”, Phys. Rev. Lett., 2003, 90(24), 249601,  DOI:10.1103/PhysRevLett.90.249601.
72. S. Canton, A. Yencha, E. Kukk, J. Bozek, M. Lopes, G. Snell and N. Berrah, Comment of “Experimental Evidence of a Dynamic Jahn–Teller Effect in C₆₀⁺”, Phys. Rev. Lett., 2003, 90(24), 249602,  DOI:10.1103/PhysRevLett.90.249602.
73. J. Tamuliene, Electronic and Vibrational Spectra of C₆₀ and Its Ions, Fullerenes, Nanotubes, Carbon Nanostruct., 2015, 23, 187–195.
74. T. Frederiksen, K. J. Franke, A. Arnau, G. Schulze, J. I. Pascual and N. Lorente, Dynamic Jahn–Teller Effect in Electronic Transport through Single C₆₀ Molecules, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(23), 233401,  DOI:10.1103/PhysRevB.78.233401.
75. A. Ceulemams and P. Fowler, The Jahn–Teller Instability of Fivefold Degenerate States in Icosahedral Molecules, J. Chem. Phys., 1990, 93, 1221–1234.
76. H. Ramanantoanina, M. Zlatar, P. Garcia-Fernandez, C. Daul and M. Gruden-Pavlovic, General Treatment of the Multimode Jahn–Teller Effect: Study of Fullerene Cations, Phys. Chem. Chem. Phys., 2013, 15, 1252–1259.
77. D. Lichtenberger, K. Nebesny, C. Ray, D. Huffman and L. Lamb, Valence and Core Photoelectron-Spectroscopy of C₆₀, Buckminsterfullerene, Chem. Phys. Lett., 1991, 176, 203–208.
78. H. Yasumatsu, T. Kondow, H. Kitagawa, K. Tabayashi and K. Shobatake, Absorption Spectrum of C₆₀ in the Gas Phase: Autoionization via Core-Excited Rydberg States, J. Chem. Phys., 1996, 104, 899–902.
79. I. B. Bersuker, Pseudo-Jahn–Teller Effect—A Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids, Chem. Rev., 2013, 113, 1351–1390.
80. A. Ceulemans and L. G. Vanquickenborne, Stereochemistry and Bonding, Springer Berlin Heidelberg, Berlin, Heidelberg, 1989, vol. 71, pp. 125–159.
81. D. A. Hrovat, G.-L. Hou, B. Chen, X.-B. Wang and W. T. Borden, Negative Ion Photoelectron Spectroscopy Confirms the Prediction that D_3h Carbon Trioxide (CO₃) has a Singlet Ground State, Chem. Sci., 2016, 7, 1142–1150.
82. M. Venuti, M. Stener, G. De Alti and P. Decleva, Photoionization of C₆₀ by Large Scale One-Center Density Functional Explicit Continuum Wave-Function, J. Chem. Phys., 1999, 111, 4589–4597.
83. E. Bakes and A. Tielens, The Photoelectric Heating Mechanism for Very Small Graphitic Grains and Polycyclic Aromatic-Hydrocarbons, Astrophys. J., 1994, 427, 822–838.
84. E. Habart, L. Verstraete, F. Boulanger, G. P. des Forets, F. Le Peintre and J. P. Bernard, Photoelectric Effect on Dust Grains across the L1721 Cloud in the Rho Ophiuchi Molecular Complex, Astron. Astrophys., 2001, 373, 702–713.
85. J. C. Weingartner and B. T. Draine, Photoelectric Emission from Interstellar Dust: Grain Charging and Gas Heating, Astrophys. J., 2001, 134(Suppl. Ser), 263–281.
86. L. Verstraete, A. Leger, L. Dhendecourt, O. Dutuit and D. Defourneau, Ionization Cross-Section Measurements for 2 PAH Molecules – Implications for the Heating of Diffuse Interstellar Gas, Astron. Astrophys., 1990, 237, 436–444.
87. B. P. Kafle, H. Katayanagi, Md. S. I. Prodhan, H. Yagi, C. Huang and K. Mitsuke, Absolute Total Photoionization Cross Section of C₆₀ in the Range of 25–120 eV: Revisited, J. Phys. Soc. Jpn., 2008, 77(1), 014302,  DOI:10.1143/JPSJ.77.014302.
88. S. Douix, D. Duflot, D. Cubaynes, J.-M. Bizau and A. Giuliani, Photoionization of the Buckminsterfullerene Cation, J. Phys. Chem. Lett., 2017, 8, 7–12.
89. P. B. Changala, M. L. Weichman, K. F. Lee, M. E. Fermann and J. Ye, Rovibrational Quantum State Resolution of the C₆₀ Fullerene, Science, 2019, 363, 49–54.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01210f

---