Cold and controlled chemical reaction dynamics
Jutta
Toscano
 a,
H. J.
Lewandowski
a,
H. J.
Lewandowski
 a and
Brianna R.
Heazlewood
a and
Brianna R.
Heazlewood
 *b
*b
aJILA and the Department of Physics, University of Colorado, Boulder, Colorado 80309, USA
bPhysical and Theoretical Chemistry Laboratory (PTCL), Department of Chemistry, University of Oxford, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: brianna.heazlewood@chem.ox.ac.uk
First published on 17th April 2020
Abstract
The prospect of studying state-to-state chemical reaction dynamics, with full control over all of the reaction parameters, is becoming a reality for a small number of systems. Thanks to the rapid development of new experimental techniques (alongside novel combinations of existing methods), an increasingly diverse range of reactants can be prepared under cold conditions and manipulated with external fields. These tools are enabling the study of reactions at previously inaccessible collision energies; the role of long-range forces and quantum effects are beginning to be experimentally probed—challenging the accuracy of theoretical predictions and fundamental models of reactivity. In this perspective article, we outline the key methodologies that are adopted for the study of cold and controlled reaction dynamics. We discuss the motivation for these studies, detail the progress made to date, and highlight the future prospects for the field.
1 Introduction
Historically, a major drive to study reactions at low temperatures has been the desire to understand the chemistry of the coldest parts of the Universe. In regions such as the interstellar medium and planetary atmospheres, temperatures can be as low as a few Kelvin. Investigating the properties of reactions that take place in naturally-occurring cold environments is necessary in order to accurately model their chemistry.1–10 Even now, many of the reactions postulated to be of astrochemical importance are yet to be experimentally measured under cold conditions.As experimental methods have developed—enabling reactions to be examined at ever-lower temperatures—the motivation for studying cold chemistry has also evolved. Increasingly, cold conditions have been employed as a means of controlling how chemical reactions occur. While the direct application to astrochemistry remains a motivation in many cases, there are numerous other advantages associated with studying reactions at low temperatures.
• Minimising thermal averaging means that few partial waves contribute to the collision process, greatly simplifying the reaction dynamics. By controlling and manipulating the properties of the reactants, and sensitively detecting the properties of the products, we can probe the role that each reaction parameter plays in determining the outcome of a collision.
• We can examine the transition from classical to quantum reaction dynamics. As excess energy is removed from the system, quantum effects become increasingly important; particles display wave-like behaviour, giving rise to phenomena such as tunnelling and scattering resonances.11,12
• The relative importance of long-range interactions, non-adiabatic effects and subtle features on the underlying potential energy surface(s) can be established.13
• Precision measurements of reaction systems can be undertaken. Long interaction times and perturbation-free environments (alongside sensitive detection methods) enable us to measure reaction properties such as rate coefficients, collision cross sections and branching ratios with exceptional precision.
• Long-standing theories of reactivity can be experimentally tested. It is only very recently that decades-old theories of reactivity (for example, statistically adiabatic capture theory) have started to be experimentally challenged at low temperatures.14 The close interplay between theory and experiment has, in many cases, been critical in developing our understanding of reaction dynamics.
• New chemistry and unexpected chemical behaviour can be discovered.
In essence, cold temperatures allow us to manipulate many of the variables associated with a reactive collision. The field is now equipped with tools that enable us to control almost all aspects of a gas-phase reactive collision.15,16 We can routinely select the quantum state of the reactants; we can frequently control the energy at which a collision occurs; we can even control the orientation of certain reactants.17–24 The rationale for controlling these various reaction parameters is to improve our understanding of how reactions occur at a fundamental level, and to elucidate the influence that each variable has on the outcome of a reactive collision.
In this work, the key experimental methods used to achieve cold and controlled reaction conditions are discussed, accompanied by a description of the range of detection methods adopted to analyse the resulting products. While this review focuses on experimental measurements, one must not overlook the importance of detailed theory work in predicting systems of interest, guiding the interpretation of experimental results, and identifying the limitations of experiments.25 The significant contributions made by theoretical studies are therefore highlighted at various points throughout the document. We do not attempt to review all previous work related to the field of cold chemistry. As the goal of this work is to discuss cold and controlled chemical reaction dynamics, we focus on (predominantly) reactive collisions and on systems that involve at least one molecular species (i.e. systems involving exclusively atomic species are not explicitly considered). We also limit ourselves to considering (primarily) gas-phase reactions; while there is a large and interesting body of research related to reactions at surfaces, such work is beyond the scope of this review.
2 Reactions in beams
2.1 Intra-beam studies
Numerous chemical reactions of interstellar relevance have been experimentally studied within beams using flow methods such as CRESU (cinétique de réaction en ecoulement supersonique uniforme—reaction kinetics in uniform supersonic flow).26 The CRESU technique relies on the simultaneous expansion of the reactants (or their precursors) into a single beam where the reaction occurs. Cooling of the flow is achieved by supersonically expanding gas through a Laval nozzle. This particular type of nozzle is composed of a convergent section, where the gas is accelerated towards a lower pressure chamber without being compressed, and a divergent section, where it expands adiabatically. The resulting uniform, thermally-equilibrated flow is comparable to that of a flow tube without walls. The reaction is initiated, for instance by photolysis with a laser, shortly after the nozzle and the products are detected further downstream. In contrast to trap-based methods (discussed in Section 3), a limitation that is common to all flow-based methods is the intrinsic restriction to measuring relatively fast reactions—the flow moves rapidly and the flow tube is finite in length.Reactions have been investigated using the CRESU method at temperatures as low as 5.8 K.27 Many of the processes involving a highly reactive species—for example, the N+ + H2O and N+ + NH3 reactions—have been observed to proceed faster as the temperature is lowered.28–30 Quantum mechanical tunnelling has been shown by CRESU experiments to play a key role in low temperature chemistry, featuring in reactions such as OH + CH3OH and F + H2.31,32 In recent years, the CRESU approach has been combined with Chirped-Pulse Fourier-Transform Microwave (CP-FTMW) spectroscopy to measure channel-specific rate coefficients. Using this combination of techniques, all the products of the low-temperature reaction between CN and propyne have been observed, and the product branching ratios established.33 Measuring the reaction dynamics and kinetics of thermally-equilibrated systems at low temperatures, such as those described above, affords a number of advantages. In particular, such studies are able to directly inform us about how chemical reactions proceed under conditions comparable to those found in complex interstellar environments. In order to gain a more detailed understanding of the reaction dynamics on a fundamental, state-to-state level, we typically require more control over the properties of the reactants.
A higher degree of control over the intra-beam collision energy can be achieved by exploiting the velocity difference between different species within the same beam (velocity slip). Sub-Kelvin collision temperatures have been attained by initiating the formation of the faster-moving particles at the back of the beam (or gas pulse) such that they catch up and collide with the slower-moving reactants at the front of the beam. Collisions of atoms and molecules with Rydberg atoms have been studied in this way.34,35 In a related intra-beam study, control over both the rotational population and alignment of one of the colliding molecules has been achieved, permitting the observation of a strong stereodynamic effect.36 Stark-induced adiabatic Raman passage (SARP) was used to prepare ro-vibrationally excited HD molecules in the v = 1, j = 2 state, with the molecular bond axis preferentially aligned either parallel or perpendicular to the molecular beam axis. Upon collision with D2 (v = 0, j = 0) molecules, the rotational relaxation of HD to the v = 1, j = 1 state was three times more likely to occur when HD was aligned perpendicular rather than parallel to the flight axis. Extracting such remarkable levels of detail from the collision process is only possible with very precise control over the reaction parameters—specifically, the internal and external (orbital angular momentum) quantum states of the colliding molecules, together with the minimisation of the number of partial waves (orbital angular momentum states) contributing to the collision process.
2.2 Crossed beams
Generally speaking, the relative velocities of two reacting species can be better controlled if the reactants are introduced as two separate beams, as opposed to both reactants being entrained in the same beam.37 Whereas particles in effusive beams maintain the thermal internal energy and velocity distributions of the source, beams of internally cold particles can be formed by supersonic expansion methods. When the mean free path of a particle becomes smaller than the orifice from which it is escaping, frequent collisions occur during the expansion process and adiabatic cooling takes place. The decrease in translational (velocity spread), rotational and, to a lesser extent, vibrational energy is compensated by an increase in the kinetic energy of the beam in the laboratory frame.38 The obvious challenge that arises from studying the reactions of two supersonic beams at low temperatures is the need to cross these beams in order for the reaction to occur; crossing two supersonic beams at 90° typically results in high collision energies. Two different approaches have been adopted to mitigate the high forward velocities of supersonic beams and enable the study of reactions at low collision energies. The first consists of crossing two supersonic beams at a very shallow angle, such that the relative velocity of the cold species within each beam is minimised (as described below).39,40 The second approach involves removing the superfluous kinetic energy by decelerating a supersonic beam41–43 before it undergoes collisions (either with another beam, or with a static target of trapped particles, as discussed in Section 3).Since the pioneering work of Herschbach and Lee,44,45 crossed molecular beams have become a cornerstone of gas-phase chemical reaction dynamics studies.12,16,21,46–50 Such experiments have traditionally seen the collision of two collimated beams of particles, usually at a 90° crossing angle, with the properties of the resulting products probed using laser-based detection methods. At high collision energies, a large number of quantum states can be populated as a result of the collision and, therefore, many partial waves contribute to the scattering process. As the collision energy is decreased—for example, by decreasing the crossing angle between the two beams and matching their velocities—progressively fewer partial waves play a role in the scattering process and it becomes possible to disentangle their individual contributions. In this regime, resonances in the scattering cross section as a function of collision energy can be observed: a sharp enhancement in the cross section occurs when the collision energy of the colliding particles matches the energy of a long-lived collision complex or quasi-bound state. The position and shape of these resonances is exceptionally sensitive to the long-range, attractive part of the underlying potential energy surface (PES) and, as a result, low-crossing-angle beam scattering experiments provide stringent tests for quantum scattering theory.12,16,21,50
Scattering resonances have been observed in the state-to-state inelastic cross sections of several systems, including CO + H2 and O2 + H2, using a crossed molecular beam apparatus with a variable angle of intersection.51,52 The lowest crossing angle of 12.5° enabled collision energies as low as 3 cm−1 (≈4 K) to be studied. Recently, the same apparatus has been employed to study inelastic collisions in the more computationally-challenging H2O + H2 system. These experiments have seen the first experimental verification of the accuracy with which long-range interactions are described by the H2O + H2 intermolecular PES.53 In the reactive scattering of the F + H2 system, the observation of a resonance peak resulting from tunnelling-enhanced reactivity has led to the identification and characterisation of a resonance state present behind the reaction barrier.54
A complementary approach to varying the crossing angle of two supersonic beams is to change the velocity of one of the beams. This has been achieved with a Stark decelerator, where inhomogeneous time-varying electric fields are applied to a series of electrodes to manipulate the velocity of low-field-seeking (LFS) polar molecules using the Stark effect. In this way, packets of particles with a well-defined (and adjustable) velocity can be generated, significantly enhancing the energy resolution of collision studies.38,55 By crossing two molecular beams at 45°, and carefully varying the velocity of one of these beams, scattering resonances have been observed in the state-to-state inelastic integral and differential cross sections of NO + He and NO + H2.56,57 In these experiments, the angular distribution of the scattered particles (that is, the differential cross section) was probed using velocity map imaging (VMI) (Fig. 1).58,59 The high resolution afforded by the combination of Stark deceleration and VMI detection has also facilitated the study of product-pair correlations following inelastic scattering events. For example, the likelihood of one product ending up in a specific rotational state given the final rotational state of its collision partner has been investigated for the NO + O2 system.60 The ability to study product-pair correlations in bimolecular collisions opens the door to new exciting experiments that will deepen our understanding of the interactions between molecules.
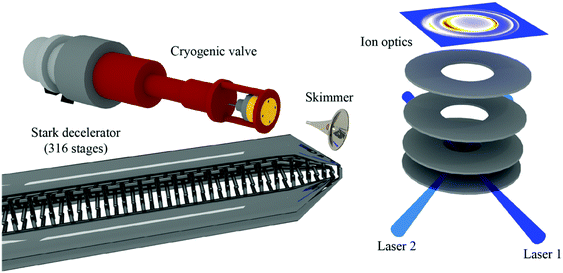 | ||
| Fig. 1 Schematic representation of a crossed beam apparatus. A beam of NO radicals is passed through a Stark decelerator and scattered with a pulsed beam of para-H2 or ortho-D2. The inelastically scattered NO radicals are state-selectively ionised using two pulsed lasers and detected using velocity map imaging. Only the last section of the Stark decelerator is shown. Reprinted with permission from Gao et al.,58 copyright 2017 American Chemical Society. | ||
2.3 Merged beams
In order to reach collision energies corresponding to temperatures below 1 K, two supersonic beams travelling at the same speed need to be crossed at an angle close to 0°.61 This can be achieved by merging two reactant beams into a single beam—for example, by bending one beam onto the other such that they converge to the same axis. In systems where one of the species has no magnetic moment, a curved magnetic guide can be employed to direct LFS paramagnetic species onto the axis of a second (non-paramagnetic) beam of particles (Fig. 2).62 State selectivity of both reactants can be attained by using two curved guides, such as a magnetic and an electric guide, to overlap the reactant beams.63 The collision energy in a merged beam experiment is typically dictated by the relative velocity of the two beams, and their velocity spread. By carefully tuning the velocity of the beams, collisions have been recorded at temperatures as low as 8.7 ± 0.8 mK, allowing the observation of orbiting resonances in the Penning ionisation reaction of Ar and H2 with metastable He.62 Although the collision energy is normally limited by the velocity distribution of the hottest beam, which is usually ≥0.1 K, lower energies can be obtained by using very short gas pulses generated by Even-Lavie valves.64 When the flight time of the gas packet is considerably longer than the initial duration of the pulse, the position of the particles within the pulse is correlated to their velocity: faster particles move to the front of the pulse and slower particles lag behind. Selectively addressing a narrow portion of this velocity distribution in space results in lower collision energies and better resolution than would otherwise be possible.65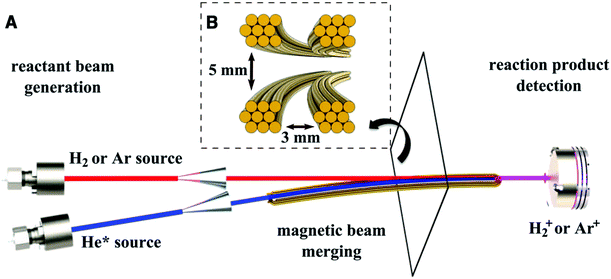 | ||
| Fig. 2 Schematic representation of a merged beam apparatus. (A) Two supersonic valves followed by skimmers produce the collimated beams to be merged. A curved magnetic guide bends the metastable helium beam (blue) onto the axis of the undeflected H2 or Ar beam (red) to give a single, merged beam (purple). (B) Cross section of the magnetic guide. Precise adjustment of the relative velocities of the two beams allows collision energies in the order of milliKelvin to be achieved. Reprinted with permission from Henson et al.,62 copyright 2012 Science. | ||
Merged beams have been employed to investigate a variety of chemi-ionisation reactions, where collision of the target species with an electronically-excited species results in either Penning ionisation (A* + B → A + B+ + e−) or associative ionisation (A* + B → AB+ + e−). These studies, which have so far featured metastable helium or metastable neon as the electronically-excited reactant, have yielded a wealth of information on the dynamics of ionisation processes at low temperatures. Collisions of metastable helium with H2, HD and D2 have permitted the observation of the quantum kinetic isotope effect—which sees scattering resonances appearing at different collision energies for the different isotopologues—setting valuable constraints on ab initio calculations of the interaction potential.66 Furthermore, the rotationally-excited spin isomer ortho-H2 has been shown to ionise faster than ground state para-H2. The addition of one quantum of rotational excitation modifies the long-range intermolecular interaction potential, from being isotropic to anisotropic, thereby strengthening the long-range attractive forces.67,68 Recently, the branching ratio of Penning to associative ionisation for the Ne* + N2 reaction has been adjusted by manipulating the orientation of the metastable reactant, in addition to controlling the collision energy.69 A strong steric effect has been observed at collision energies above 30 K, where the propensity for one reaction channel over the other is distinctively orientation dependent. Specifically, associative ionisation is found to take place exclusively when the singly-occupied p orbital in Ne* is oriented along the interatomic axis. In contrast, the reaction outcome at collision energies below 30 K is observed to be independent of the Ne* orientation and the stereodynamics of the reaction is shown to be dominated by the interatomic potential instead. With a longer timescale of approach for the slower-moving reactants, more time is spent exploring the long-range part of the interaction potential—resulting in an enhanced ability to induce the dynamical reorientation of Ne* into the energetically most favourable geometry.69,70
Chemi-ionisation of polyatomic molecules features the added complexity of multiple reaction channels. The internal structure of the reactants has been found to play a crucial role in low temperature reaction dynamics experiments. Reactive scattering in the CHF3 + He* (or Ne*) system is suppressed in favour of inelastic scattering where the collision leads to the rotational excitation of the molecule instead of leading to its ionisation. The relatively small rotational constant of CHF3 gives rise to a high density of rotational states which, in turn, opens inelastic collision channels that dominate the reaction dynamics—even at low collision energies. This is not the case for lighter systems featuring larger rotational constants, such as NH3 and CH3F.71,72 State-selective detection of the reaction products, which has not yet been possible for this system, would enable the rotational population of CHF3 to be probed directly following the collision.
Extending the merged beam technique to study ion–molecule reactions presents the additional challenge of considering stray electric fields, which can affect the kinetic energy of the ionic reactants and therefore reduce the collision energy resolution. This issue has been cleverly overcome by using a highly-excited Rydberg molecule in place of the ion to investigate the reaction H2+ + H2 → H3+ + H.73,74 The Rydberg molecule H2* (with principal quantum number n = 22) behaves chemically as if it is an H2+ ion, with the Rydberg electron shielding the ionic core of the molecule from stray fields. The reaction cross section for the H2* + H2 system has been found to deviate from the classical Langevin-capture model for ion-induced-dipole interactions below 1 K, where a 15% increase in the rate coefficient has been observed. This departure from the classical model has been attributed to the long-range scattering potential becoming anisotropic at low collision energies, due to the interaction between the H2+ ion core and the rotational quadrupole moment of ortho-H2 (j = 1; 75% in the statistical mixture used). At higher collision energies, the anisotropic contributions to the potential average out; at low collision energies, the collision complex tends to adiabatically follow the lowest-energy pathway along the anisotropic potential, leading to the observed enhancement in the rate coefficient.
With a view to improving the sensitivity of merged beam experiments, a magnetic synchrotron has been proposed,75 and an electric version has been developed.76,77 Particles are confined in packets within the storage ring. The packets of particles traversing the ring can interact with a tangential supersonic beam multiple times (over numerous round trips), leading to an enhanced signal-to-noise ratio. So far, collisions between ND3 and Ar have been studied using a molecular synchrotron apparatus, with the observed collision cross sections in good agreement with theoretical predictions.76 Following a similar principle, but on a larger scale, a cryogenic storage ring for molecular ions has been built featuring a neutral atom beam set-up for merged beam studies.78 The state-specific dissociative recombination of HeH+ ions merged with an un-deflected beam of quasi-monoenergetic electrons has very recently been studied with this apparatus.79 Rotational excitation of the ions has been observed to have a strong influence on the reaction rate at low temperatures, with the ground rotational state reacting considerably slower than expected. A smaller-than-predicted rate coefficient for the dissociative recombination of HeH+ (j = 0) will have a significant effect on the abundance of such ions in models of the early Universe. Further studies of astrochemically-relevant reactions between ro-vibrationally cold molecular ions, such as H3+, and neutral atoms are envisaged to follow.80
3 Reactions in traps
3.1 Ion-neutral reactions
The ability to trap the reactant(s)—and, in many cases, also the product(s)—of a chemical reaction offers a number of benefits for the study of chemical dynamics. These benefits include extended interaction times (enabling very slow reactions to be examined), ultra-high vacuum conditions, excellent detection sensitivity and control over the reaction conditions. There are many different trap designs available, suited to confining species with a range of different properties. Of these different trap designs, traps for charged particles—and, in particular, radiofrequency (RF) ion traps—have been the most widely employed for reaction studies. One of the advantages of RF ion traps is their significant trap depth (on the order of 1–10 eV; several orders of magnitude larger than the depth of traps typically employed to confine neutral species), which can enable the ionic products of exoergic reactions to be trapped.81Reactions between ions and neutrals have been studied over an extended temperature range, spanning approximately 10–300 K, using a cryogenic 22-pole trap set-up. Trapped ions can be collisionally cooled by a buffer gas, a process that is efficient in a multi-pole RF trap (compared to, say, a quadrupole trap) as there is minimal interaction between the ions and the confining RF field in the central trapping region.81 A number of astrochemically-relevant reactions have been studied in multi-pole traps over the past few decades.82 In particular, instruments such as the atomic beam 22-pole trap apparatus have facilitated the detailed study of reactions between H (or D) atoms and a range of molecular ions at low temperatures.83,84 While it is challenging to reach temperatures below 10–20 K, the use of buffer gas cooling (a “universal” cooling method; see Section 4) within a cryogenic 22-pole trap has enabled the reactions of both anions and cations to be investigated.85,86
To achieve translational temperatures below 10 K, one can employ laser-based cooling methods. Coulomb crystals can be formed upon the laser cooling of trapped ions; once sufficient kinetic energy has been removed from the ions, they adopt a (typically) spheroidal lattice structure—a Coulomb crystal—that is stable for an extended period of time. The positively charged ions repel one another, but these repulsive forces are balanced by the confining forces of the trapping fields. Neighbouring ions in the resulting Coulomb crystal are separated by some 10–20 μm. The laser-cooled ions constantly fluoresce as part of the laser cooling cycle, and so can be directly imaged using a charge-coupled device (CCD) camera system (see Fig. 3). Non-laser-cooled ions can also be incorporated into Coulomb crystals, provided they are able to be confined by the trapping potential and exhibit a mass-to-charge ratio that is sufficiently close to the laser-cooled ion for efficient “sympathetic” cooling. Elastic collisions between laser-cooled ions and co-trapped ions remove excess kinetic energy from the co-trapped species (so-called sympathetic cooling), integrating the co-trapped ions into the Coulomb crystal framework.87 A diverse range of effectively stationary ionic reactants can therefore be prepared within Coulomb crystals.
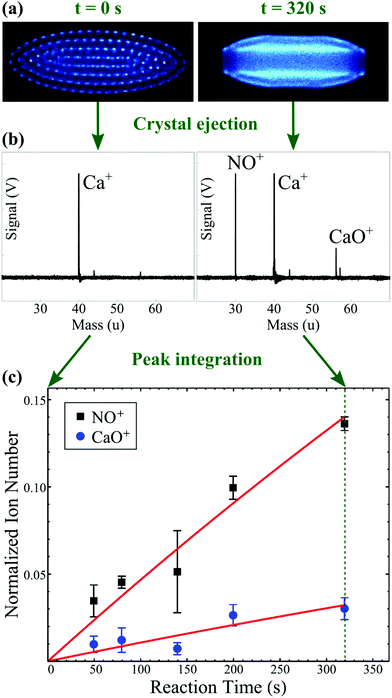 | ||
| Fig. 3 Schematic representation of the Ca+ + NO reaction system. The two competing reaction pathways yield NO+ (charge transfer) and CaO+ (O addition) products. (a) Experimental images of the fluorescing calcium ions within a Coulomb crystal are collected as a function of time using a CCD camera. The reaction begins with a crystal that contains only Ca+ ions (left panel); as NO is introduced to the reaction chamber, the accumulation of non-fluorescing, sympathetically-cooled ionic products can be inferred from the flattening of the crystal and the appearance of a dark core in its centre (right panel). (b) At various reaction times, all ions within the Coulomb crystal are ejected into a time-of-flight mass spectrometer. The area under each peak in the resulting mass spectrum is proportional to the number of ions of each species at the time of ejection. (c) Fitting the number product ions as a function of reaction time enables the rate coefficients and product branching ratios to be calculated. Panel (c) has been modified and reprinted with permission from Greenberg et al.,88 copyright 2018 American Physical Society. | ||
Since the first reaction observed within a Coulomb crystal, Mg+(3p2P3/2) + H2 → MgH+ + H,89 a range of ion–molecule reaction processes have been examined. These include reactions between ions and radical molecules, such as Ca+ with NO or O2, where the internal quantum state of the ion changes the reactivity.88,90 Studying reactions in Coulomb crystals has also enabled the accuracy of rotationally adiabatic capture theories to be experimentally tested,91–93 and has highlighted the importance of subtle features on potential energy surfaces in dictating the outcomes of chemical reactions.92,94–96 A number of these reactions have been discussed in previous review articles on cold ion chemistry—most recently in 2019.87,97–99 Many of the earlier studies of ion–molecule reactions in Coulomb crystals focused on the reactions of laser-cooled ions. For example, the reactivity of electronically excited Be+ with H2, HD and D2 was investigated, alongside a study of the H3+ + O2 reaction in a Be+ Coulomb crystal.100 The rate coefficients for these reactions were found to be well described by Langevin's theory—unsurprisingly, given the non-polar nature of the neutral reactants.
More recent studies have shifted the focus to the reactions of sympathetically-cooled, co-trapped ions, exploring increasingly complex chemical systems. The detection of products from the reaction of CCl+ with C2H2 has demonstrated a possible pathway for creating larger carbocations in the interstellar medium.101 Additionally, the relative reactivity of C2H2+ with two isomers of C3H4, propyne and allene, has unveiled two distinct reaction mechanisms.102 For the C2H2+ + allene (H2C3H2) reaction, it is proposed that the first step is charge transfer that occurs at long range and with no intermediate complex formed en route to products. In contrast, the reaction C2H2+ + propyne (HC3H3) often begins with charge transfer at short range, which leads to the formation of a reaction complex. As a result, the propyne reaction leads to additional products being formed compared to the allene reaction.102
Isomer-specific reaction studies have also been conducted using an electrostatic deflector combined with a linear Paul ion trap. The two nuclear spin isomers of water, para- and ortho-H2O, were found to exhibit different reactivities with trapped N2H+ ions.93 This difference in reactivity can be explained by considering the differences in the ion–dipole interactions, and was accurately predicted by rotationally adiabatic capture theory.93 An ion-neutral reaction system that has provided some unexpected results—findings that cannot be rationalised by capture theory models—is the charge exchange between Xe+ ions and NH3 or ND3 molecules. A significant inverse kinetic isotope effect was observed in the reaction rate coefficients, with ND3 found to undergo charge exchange more than three times faster than NH3. Classical capture theories cannot account for this difference in reactivity. A possible explanation has been proposed, based on the higher density of states and anticipated lifetime of the deuterated reaction complex.96
While it is relatively straightforward to prepare an effectively stationary target of ionic reactants, it is challenging to study bimolecular reactions with trapped ions under truly cold conditions. For example, even when studying the reactions of laser-cooled ions in small crystals—under conditions where micromotion can be neglected—one must account for contributions arising from electronically excited ions (populated as part of the laser cooling process).90 Non-laser-cooled ionic species can often be prepared in selected quantum states using methods such as resonance-enhanced multiphoton ionisation (REMPI). However, the majority of molecular ions (i.e. species other than homonuclear diatomics) interact with black-body radiation (BBR), leading to BBR-induced population redistribution within tens of seconds in traps operated at ambient (300 K) conditions. There have been a number of methods proposed to maintain internal state selectivity in sympathetically-cooled molecular ions. For example, laser-based cooling schemes have been demonstrated for a few specific molecular ions,103–107 and the superposition of an ion trap with a magneto-optical trap (MOT) has facilitated inelastic collisions between BaCl+ molecular ions and ultracold Ca atoms.108,109 Cryogenic ion trap chambers, with nested temperature stages maintaining optical access to the trap centre for lasers and imaging purposes, offer the most generally applicable and versatile approach to maintaining state selectivity in molecular ions.110–113
Armed with these tools and techniques, the community is now beginning to examine the reactions of a range of state-selected molecular ions in Coulomb crystals. Ion traps are being combined with a diverse range of cold neutral sources,94,99,114–117 equipping the field with the tools needed to experimentally probe elusive ion-neutral reactions. Systems of interest include fundamental reaction processes that are important to astrochemistry and atmospheric chemistry—such as the reaction between N2+ and H, which (in spite of multiple attempts spanning several decades) is yet to be precisely measured.9,83,118 We anticipate that the coming years will see a range of increasingly complex ion-neutral reaction systems probed under truly cold and controlled conditions for the first time.
A related field that has received significant attention in recent years is the study of reactions in “hybrid” ion-atom traps (see Fig. 4), where an ensemble of trapped ions is spatially and temporally overlapped with a cloud of ultracold atoms.119 A comprehensive review of cold ion-atom interactions has recently been published, providing a detailed overview of the ion-atom systems that have been studied in hybrid trap environments prior to 2019.120 We direct readers to this excellent resource for an in-depth analysis of both the experimental and theoretical work undertaken on ion-atom collisions in hybrid traps. Here, we highlight a few (very recent) examples that showcase interesting chemical dynamics and involve at least one molecular partner.
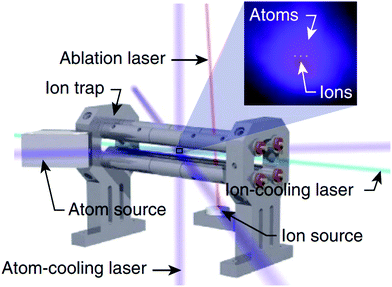 | ||
| Fig. 4 Schematic depiction of a hybrid atom-ion trap. With careful alignment of the two trap centres, an ensemble of trapped ions can be spatially overlapped with a cloud of laser-cooled atoms. Reprinted from Schowalter et al.,121 under the terms of the Creative Commons CC BY license. Copyright 2016, Springer Nature. | ||
As the field explores more complex systems in hybrid traps, the focus is beginning to expand beyond atom-atomic ion interactions to consider atom-molecular ion collisions, unveiling some unexpected results. A “reaction blockading” effect has been reported in the low-energy collisions of electronically excited Ca atoms with BaCl+ ions in a hybrid MOT-ion trap. The radiative lifetime of the Ca quantum state was reported to dictate the reaction dynamics at the lowest collision energies, in contrast to capture theory predictions, resulting in a suppression of the reactivity of Ca atoms in short-lived excited states.122 Hybrid traps have also identified striking differences in the reaction dynamics of charge transfer collisions in Rb + N2+ and Rb + O2+—systems where one might intuitively expect to see comparable behaviour. With the assistance of classical-capture, quasiclassical-trajectory and quantum-scattering calculations, the delicate interaction between short-range and long-range effects has been identified as the cause of the different charge transfer reaction mechanisms observed for the different reaction channels.123 Beyond examining reactive ion-atom collisions, hybrid traps have also seen the synthesis of novel forms of matter. A hypermetallic alkaline earth oxide, BaOCa+, has been produced from the barrierless reaction of ultracold Ca(3PJ) atoms with BaOCH3+ ions in a hybrid trap set-up.124
3.2 Collisions of cold neutral molecules
Cold collisions of neutral molecules have also been explored using trap environments. The trapping potentials for neutral molecules rely on interactions between a permanent or induced dipole moment and an external field. Electrostatic traps, which confine molecules using the interaction of an induced electric dipole moment with an electric field, have been demonstrated for many species and are typically the deepest traps for neutral molecules. This is due to the ease of producing strong laboratory electric fields, combined with the large dipole moments of small polar molecules. Magnetostatic traps are typically weaker when created using electromagnets, but can be sufficiently deep if created through the use of permanent-magnetic or superconducting materials.125–130 Finally, neutral molecules have been trapped in optical fields by taking advantage of the polarisability of a molecule in a focused optical field (far from resonance with any molecular transitions). This method is most applicable to ultracold molecules (corresponding to T < 1 mK), as the trap depths are typically in the 1 mK regime. The reaction dynamics of ultracold molecules are discussed in Section 3.3; this section focuses on the collisions of cold molecules (covering an approximate temperature range of 1 mK ≤ T ≤ 1 K).Overall, trap depths for neutral molecules are significantly lower than for ions. The result is that collisions with room-temperature background gas atoms and molecules can impart enough energy to the trapped molecules to eject them from the trap. Thus, the lifetimes of neutral trapped molecules are in the 1–10 s range for room temperature systems operated at pressures on the order of 10−9–10−10 Torr. Longer lifetimes can be achieved within cryogenic traps, as the background gas pressure is significantly lower in these systems.
One of the consequences of limited trap lifetimes is the restriction it places on the timescale over which processes can be monitored. There is only a small window of time for rare interactions—such as chemical reactions—to take place. The combination of limited interaction times, decreased reactivity (compared to ionic species), and low densities has led to experiments with trapped neutral molecules demonstrating mostly non-reactive collisions. Non-reactive collisions can be categorised into two groups: elastic and inelastic. Elastic collisions refer to collisions where only momentum transfer occurs, while inelastic collisions refer to interactions where the internal state of at least one of the particles changes. For cold, trapped systems, elastic collisions are usually deemed “favourable”, as they thermalise the sample; inelastic collisions are deemed “unfavourable”, since a change in internal quantum state often means the particle will be transferred into a state that cannot be confined by the trap.
Experiments can be designed where a molecular beam is directed at an ensemble of cold, trapped neutral molecules. The advantage of such a system is that the trapped species can interact with many packets of a pulsed molecular beam (or for an extended period of time with a continuous beam), increasing the likelihood of collisions. Additionally, the relative collision energy can be tuned by adjusting the mean speed of the molecular beam. In one such experimental set-up, a supersonic beam of OH radicals was slowed using a Stark decelerator and then loaded into a magnetic trap created by permanent magnets inside the vacuum system. The second collision partner, D2, was entrained within a seeded supersonic molecular beam, which was directed at the centre of the trapping region. The mean speed of the D2 reactants was modified by adjusting the temperature of the solenoid valve producing the supersonic beam. In this way, the collision energy could be tuned from 145 cm−1 to 510 cm−1.131 The total collision cross section of OH with D2 was determined by measuring the loss of OH from the magnetic trap after the pulsed beam of D2 passed through the trapping region. When plotting the collision cross section as a function of collision energy, a peak was observed in the scattering cross section at 305 cm−1—suggested as possible evidence of resonant energy transfer.131 In a similar experiment, a buffer-gas-cooled132 and velocity-filtered beam of cold ND3 molecules (generated using an electrostatic hexapole guide with a 90° bend) was collided with magnetically trapped OH molecules.133 The resulting collision energy of the OH + ND3 system was calculated to be 3.6 cm−1 (≈5 K).133 The total trap loss cross section was measured with and without electric fields present to probe the effect of polarising the molecules and to look for evidence of electric dipole–dipole collisions. A small enhancement of the cross section was observed when an electric field was applied.133
To study collisions at even lower energies, it is often convenient to trap both reactants. Co-trapping experiments have been used to study atom-molecule and molecule-molecule collisions. NH molecules and N atoms have been cooled inside a helium buffer gas cell and co-trapped in a magnetic trap.134 Helium gas was pulsed into the cell, reaching densities of 1015 cm−3 for efficient collisional cooling of the atoms and molecules to 600 mK. The He valve was then closed and the He escaped the cell, reducing the density to 1012 cm−3—corresponding to trap lifetimes on the order of a few seconds. Trapped NH molecules were detected using laser induced fluorescence. By measuring the trap lifetime with a range of different N atom densities, the loss rate coefficient could be calculated.134 The loss rate coefficient arises from a combination of elastic collisions (producing NH molecules with kinetic energy higher than the trap depth) and inelastic collisions (transferring population into an untrapped NH quantum state). Quantum scattering calculations suggest that the dominant inelastic channel occurs via magnetic dipole interactions.134 The calculations also indicated that, over a large temperature range (10 mK to 1 K), the ratio of elastic to inelastic collisions could be large enough to possibly sympathetically cool NH molecules with spin-polarised and evaporatively-cooled N atoms.
To directly explore the possibility of sympathetically cooling trapped molecules with ultracold atoms, a dual trapping experiment was constructed: ND3 molecules were Stark decelerated and electrostatically trapped alongside laser-cooled and magnetically-trapped Rb atoms.135 The atom trap was loaded in a differentially-pumped portion of the vacuum system and then translated such that the atom trap overlapped the molecular trap to initialise collisions. The peak density of the trapped ND3 molecules was measured as a function of time using ionisation detection, and compared to Monte Carlo simulations of the co-trapped samples. From this combination of experimental measurements and simulations, the inelastic cross section was determined and an upper limit was placed on the elastic cross section. These cross sections were inconsistent with theoretical calculations without an electric field present, illustrating the significant influence of electric fields on collisions even in the 100 mK temperature regime.135 These measurements and calculations showed that the ratio of elastic to inelastic collisions was not favourable for sympathetic cooling of these species in the 100 mK temperature regime. Another experiment created a co-trapped system of O2 molecules with lithium atoms. Atoms and molecules in a supersonic beam were decelerated using time-varying inhomogeneous magnetic fields and trapped in a magnetic trap formed by two high-temperature superconducting coils.126 The column density of both species was determined by ionising the trapped particles, extracting them from the trap using electric fields, and detecting them on a micro-channel plate detector. The signature of atom-molecule collisions was a decreased lifetime of the lithium atoms in the trap. The decay curve fit well to a two-body loss process.126
The most challenging experiments involve the study of collisions between trapped molecules. The challenge arises from obtaining a high enough density to see the effects of collisions from co-trapped molecules before trap losses (arising from background gas collisions) cause significant depletion. One way to tackle this problem is to decrease the background pressure—for example, by working in a cryogenic environment. In the same experimental apparatus used to study collisions between O2 and Li, researchers were also able to study O2–O2 bi-molecular collisions.126 In the absence of O2–O2 collisions, trap lifetimes of 52 s were recorded. By increasing the trap depth, and thus the density of molecules, the two-body trapping lifetime was found to be 9 s. Using measurements of the time dependence of the column density at different radial positions in the trap, along with Monte Carlo simulations, the ratio of elastic to inelastic cross sections was estimated to be around 4–8 for collisions at 800 mK. This ratio is critical to predicting if evaporative cooling might be possible. Here, evaporative cooling refers to the method of selectively removing high-energy particles from a trap and allowing elastic collisions to re-thermalise the sample to a new, lower temperature. Although the O2–O2 collision cross section ratio is too low for evaporative cooling to be efficient, other isotopologues (such as 17O17O) may exhibit more favourable collisional properties.126
Collisions between co-trapped species have also been seen with magnetically trapped OH molecules in a room temperature apparatus. Encouraged by calculations that showed favourable elastic to inelastic collision rates between OH molecules in the presence of a magnetic field, forced radio frequency (RF) evaporation has been attempted.136 This method selectively removes molecules with a higher-than-average energy using RF fields tuned to resonance for transitions in high magnetic fields. The RF-induced removal of molecules produced a modified density distribution in the trap. Fitting Boltzmann distributions to these measurements produced estimates of the elastic collision rates between 100–1000 s−1.136 The impact of electric fields on the inelastic collision rate was also investigated.137
A related experiment was able to study collisions between molecules in an electrostatic guide. An electrostatic quadrupole guide was loaded from a cryogenic buffer gas beam source. The guide was bent into a circle and rotated in the lab frame to decelerate molecules using the centrifugal potential. This apparatus, called a cryofuge, was used to study ND3–ND3 and CH3F–CH3F collisions.138 Collisions between molecules gave rise to increasing loss of molecular signal as the velocity was decreased. Both inelastic and elastic collisions can lead to loss of molecules from the guide. Rate coefficients for the collisions were calculated using the Langevin capture model (inelastic) and semiclassical eikonal approximation (elastic). Theoretical calculations indicated that dipole–dipole interactions were the dominant cause of the experimentally observed collisions.138
3.3 Reactions of ultracold neutral molecules
Magnetoassociation methods have seen the production of ultracold neutral molecules, where pairs of ultracold alkali metal atoms are combined to form weakly-bound diatomic molecules through the careful tuning of an external magnetic field across a Feshbach resonance. A laser can coherently transfer these weakly-bound species into the deeply-bound ground state, yielding an ultracold molecule. It has been possible to (indirectly) study reactions between two ultracold neutral molecules for over a decade, with the loss of reactants monitored as a function of time.139,140 It has long been proposed that the quantum state of a given ultracold molecule will play an important role in their reactivity. For example, reactive collisions between two 40K87Rb molecules held within an optical trap can produce K2 + Rb2 products, with the reaction rate coefficient reported to exhibit a dependence on the reactant quantum state. The KRb reactants are fermions; the Pauli principle tells us that two identical fermions will avoid each other, thereby suppressing the rate of reaction when all KRb reactants are in a single quantum state. When some KRb molecules are prepared in a different quantum state (by flipping the orientation of the nuclear spin), the reaction rate could be enhanced by a factor of 10 to 100.139In addition to association methods (combining two ultracold atoms),141–146 ultracold molecules can also be prepared by direct laser-cooling processes.147,148 Laser-cooled 40Ca19F molecules have been successfully loaded into an optical tweezer array, enabling individual molecules to be addressed and the collisions of two CaF molecules to be studied.149,150 This impressive feat was achieved by transferring CaF molecules from a MOT, to an optical dipole trap, and ultimately into the optical tweezer traps (formed by tightly-focused 780 nm laser beams and manipulated using an acousto-optical deflector).149 A single state-selected CaF molecule was held in each optical tweezer trap within the array. By merging two of these optical tweezer traps into a single trap, it was possible to achieve near-ideal conditions for the study of collision events in an exact two-body system.150 After a certain collision time, the combined optical tweezer trap was separated and the remaining CaF particle(s) detected. The two-body collisional loss rate could then be calculated from the single-particle and two-particle survival probabilities. In this way, CaF + CaF collisional loss rates were able to be calculated for molecules in their absolute ro-vibrational ground state, and for selected excited hyperfine states. No dependence on the hyperfine state was found. Chemical reactions (CaF + CaF → CaF2 + Ca) or the formation of long-lived reaction intermediates were identified as the likely collisional trap loss mechanisms.150
Until very recently, the study of ultracold bimolecular reactions has been hampered by the inability to directly probe product formation. In spite of the extreme control that has been exerted over the properties of ultracold molecules, and the presence of ultra-high vacuum conditions, all experiments have observed fast loss rates.151 Ultracold dipolar molecules can typically only be held in crossed optical dipole traps for up to a few seconds, even in non-reactive systems. The mechanism by which molecules are lost from the trap—in particular, in systems where there are no open reaction channels—is an ongoing area of research.
The collisional dissociation of 6Li2 Feshbach molecules, Li2 + Li2 → 2Li + Li2, was found to exhibit a temperature dependence in line with the Arrhenius law. However, the universal constant (C) derived from the experimental rate coefficient measurements was unable to be reconciled with theoretical predictions.152 A detailed study of (non-reactive) ultracold 87Rb133Cs molecules found that the experimentally-observed loss rate of ground state molecules could be described by second-order rate equations—in agreement with the “sticky collision” model (invoking the idea that long-lived collision complexes are formed), but significantly lower than the universal limit (where all two-body collisions at short range lead to trap loss).151 An alternative explanation attributes trap loss to the unintentional electronic excitation of bimolecular collision complexes by the trapping lasers. This theory is based on the study of non-reactive collisions between ultracold 23Na40K molecules, where the loss rate could be explained by trapping-laser-driven excitation (and subsequent loss) of the NaK–NaK collision complexes.153 Recently, additional experimental evidence supporting this idea was presented in a system of ultracold 87Rb133Cs molecules.154
While the models outlined above (amongst others) propose possible explanations, there is yet to be a consensus on the mechanism(s) responsible for the high two-body trap loss rates observed with ultracold molecules for all bialkali species. What is clear is the advantage of directly monitoring product formation—rather than reactant consumption—when studying ultracold bimolecular reactions. The first direct observation of a bimolecular reaction in the ultracold regime has very recently been reported.155 Through the use of sensitive spectroscopic and VMI detection methods, all species involved in the KRb + KRb → K2Rb2* → K2 + Rb2 reaction have been unambiguously observed: the reactants, the reaction intermediates and the products. The experimental detection of all species involved in an ultracold bimolecular reaction is a truly exciting result. The ability to probe the properties of the transient intermediate species (for example, by measuring the lifetime and quantum state of the intermediate) coupled with state-selective product detection will likely see the validity of established theories of reaction dynamics tested. In particular, one could begin to experimentally examine the transition from classical behaviour to the quantum regime in bimolecular reactions—providing a stringent test of existing universal models of reactivity.156
4 Other cold environments
4.1 Helium nanodroplets
In contrast to the gas phase molecular beam or trap-based methods discussed above, helium nanodroplets offer a rather different environment for the study of cold chemical reactions. Helium nanodroplets are formed by the supersonic expansion of He gas through a cryogenic nozzle. The droplets cool by evaporating atoms off the surface, reaching a final temperature of 0.37 K (for nanodroplets containing 4He, with this temperature determined by the surface binding energy of the He atoms).157,158 Droplet beams can be directed through one or more regions containing the reactant species of interest, with these dopant species readily picked up by (and incorporated into, or bound on the surface of) the droplets. One can select the experimental conditions—for example, by designing an apparatus with several pick-up cells—to ensure that the reactant species are incorporated into each droplet in a controlled fashion.159 The internal and kinetic energy of the reactants can be efficiently transferred to the nanodroplet through collisions, with this energy subsequently dissipated by the evaporation of helium atoms from the droplet surface (provided there are >103 He atoms per droplet).160,161 One of the key benefits of studying processes in helium nanodroplets is the broad applicability of the technique; the only practical requirement is that a sufficient amount of each reactant species must be present in the gas phase in order to be successfully picked up by a droplet.158The chemically inert behaviour and superfluid nature of helium nanodroplets make them attractive for a range of different applications.162 For example, the low temperature environment and spectroscopic transparency have seen He droplets widely used as a spectroscopic matrix for high-resolution studies of clusters and complexes.159,160,163 Receiving somewhat less attention, but of most relevance to this review, is the employment of helium nanodroplets for the study of chemical reaction dynamics. As the field of helium nanodroplets has been recently reviewed,161 with the study of chemical dynamics in helium droplets the topic of an earlier review,164 we will only mention a few recent examples here.
The helium matrix can influence how a reaction proceeds—for example, by collisionally stabilising reaction intermediates in local minima along a reaction co-ordinate (in reactions where a submerged barrier is present).161 This enables one to study the formation of collision complexes and to probe transient intermediates. In this way, the sequential capture of reactants has facilitated a detailed study of the O–HCN complex formed by the O(3P) + HCN reaction,165 and of the ethylperoxy radicals (CH3CH2OO) formed following CH3CH2 + O2 collisions within a He droplet (see Fig. 5).166 Helium nanodroplets also provide an attractive environment for the monitoring of reactions involving large molecular species. The sequential addition of C atoms to C60 molecules has been examined in helium nanodroplets, yielding carbenes of the form C60(C:)n (with n ≤ 6) and C60![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C60 “dumbell”-shaped adducts.167
C60 “dumbell”-shaped adducts.167
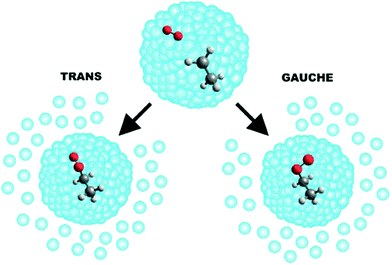 | ||
| Fig. 5 A schematic illustration of the reaction that occurs when a helium nanodroplet picks up a single ethyl radical followed by a single O2 molecule. The resulting CH3CH2 + O2 reaction is exothermic and barrierless. The evaporation of approximately 2700 He atoms from the droplet quenches the energy released by the formation of an ethylperoxy radical. Reprinted with permission from Franke et al.,166 copyright 2019 American Chemical Society. | ||
4.2 Cryogenic buffer gas cells
Similar to helium nanodroplets, buffer gas cooling experiments use cryogenically cooled noble gases to cool reactants. However, in this case, the cold buffer gas (typically helium) is in the gas phase inside a metal cell that is in thermal contact with a cryostat. As the helium is in thermal equilibrium with the walls of the cell, it can collisionally cool reactants introduced to the system via ablation,168 a beam,169 or a gas inlet.170 Buffer gas cooling is universal as it does not depend on the internal structure of the molecules—relying entirely on elastic and inelastic collisions between the buffer gas and the molecular reactants. As with all collisional cooling processes, the translational and rotational degrees of freedom are cooled more rapidly than any vibrational excitations. Although the reactants are not trapped, the density of helium in the cell is sufficiently high (1015–1018 cm−3) that the diffusion of reactants to the cell wall is slow; there is ample time for reactions to occur before the reactants diffuse to the cell walls (where they freeze and are lost from the system).132One example of a chemical reaction studied within a buffer gas cell is the association of lithium and helium atoms to form a weakly-bound diatomic molecule, arising from a three-body collision event.171 These van der Waals molecules were created following the ablation of a lithium target inside a helium cryogenic buffer gas cell. The appearance of LiHe molecules was detected by laser induced fluorescence. By varying the temperature of the cell, the binding energy of the LiHe product was found to be 0.024 ± 0.025 cm−1, which is consistent with the theoretically calculated binding energy of 0.0039 cm−1.171
In a similar experiment, the barrierless hydrogen abstraction reaction Li + CaH → LiH + Ca was explored at temperatures of 1–2 K.172 The reduction in density of the CaH reactant and the increase in density of the LiH product was monitored using laser absorption and fluorescence spectroscopy, respectively. A related experimental system used a combination of cold helium and naphthalene gas flowed through a helium vapour cell anchored to a cryostat to study bimolecular reactions. The naphthalene reached a temperature of around 6 K and had a density of 2 × 1011 cm−3.173 The naphthalene was detected at two locations in the flow tube; a decrease in the naphthalene signal at the downstream location indicated that reactions had occurred. Modelling of the system suggested the dominant loss mechanism was due to naphthalene-naphthalene dimerisation reactive collisions.173
5 Conclusions
Over the past few decades, remarkable progress has been made in the development of experimental techniques that enable us to control the conditions under which reactions occur. The use of external electric or magnetic fields, often in combination with lasers, has enabled the properties of a range of reactant species to be precisely manipulated. Alongside these advances in the preparation of reactants, the field has also seen a range of sensitive detection methods adopted and detailed theoretical models proposed. Reactions are now being studied at temperatures as low as a few mK, and single reactive collision events can be monitored. The prospect of improving our fundamental understanding of chemical reaction dynamics—and the related fields of molecular physics, quantum chemistry and chemical physics—is becoming a reality in certain systems. In spite of this impressive progress, it should be noted that many of the techniques employed to control and manipulate reactants have only been applied to a very small subset of molecules (with particularly attractive properties). While applying these methods to study the reaction dynamics of larger molecules remains an ongoing challenge, progress is already underway. As experimental techniques are combined in new and exciting ways, and the state-of-the-art advances, it will be possible to examine increasingly complex and chemically interesting systems under cold and controlled conditions.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. T. gratefully acknowledges the support of the Lindemann Trust in the form of a Postdoctoral Fellowship. B. R. H. thanks the Engineering and Physical Sciences Research Council (EPSRC, EP/N032950/1 and EP/N004647/1) and the Royal Society (RGS\R2\192210) for ongoing financial support. H. J. L. acknowledges support from NSF PHY-1734006, CHE-1900294, and AFOSR FA9550-16-1-0117.References
- D. Williams and S. Viti, Philos. Trans. R. Soc., A, 2013, 371, 20110587 CrossRef PubMed.
- P. Ehrenfreund, M. Spaans and N. G. Holm, Philos. Trans. R. Soc., A, 2011, 369, 538–554 CrossRef CAS PubMed.
- W. Klemperer, Annu. Rev. Phys. Chem., 2011, 62, 173–184 CrossRef CAS PubMed.
- V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13–72 CrossRef CAS.
- E. Herbst and E. F. van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480 CrossRef CAS.
- D. A. Williams, W. A. Brown, S. D. Price, J. M. C. Rawlings and S. Viti, Astron. Geophys., 2007, 48, 25–34 Search PubMed.
- E. Herbst, Chem. Soc. Rev., 2001, 30, 168–176 RSC.
- P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427–483 CrossRef CAS.
- V. G. Anicich, J. Phys. Chem. Ref. Data, 1993, 22, 1469 CrossRef CAS.
- M. Sablier and C. Rolando, Mass Spectrom. Rev., 1993, 12, 285 CrossRef CAS.
- D. W. Chandler, J. Chem. Phys., 2010, 132, 110901 CrossRef PubMed.
- C. Naulin and M. Costes, Int. Rev. Phys. Chem., 2014, 33, 427–446 Search PubMed.
- P. F. Weck and N. Balakrishnan, Int. Rev. Phys. Chem., 2006, 25, 283–311 Search PubMed.
- D. C. Clary, Annu. Rev. Phys. Chem., 1990, 41, 61–90 CrossRef CAS.
- P. F. Weck and N. Balakrishnan, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, S1215–S1227 CrossRef CAS.
- M. Costes and C. Naulin, Chem. Sci., 2016, 7, 2462–2469 RSC.
- R. V. Krems, Phys. Chem. Chem. Phys., 2008, 10, 4079–4092 RSC.
- M. Schnell and G. Meijer, Angew. Chem., Int. Ed., 2009, 48, 6010–6031 CrossRef CAS PubMed.
- G. Quemener and P. S. Julienne, Chem. Rev., 2012, 112, 4949–5011 CrossRef CAS PubMed.
- M. Lemeshko, R. V. Krems, J. M. Doyle and S. Kais, Mol. Phys., 2013, 111, 1648–1682 CrossRef CAS.
- M. Brouard, D. H. Parker and S. Y. T. van de Meerakker, Chem. Soc. Rev., 2014, 43, 7279–7294 RSC.
- B. K. Stuhl, M. T. Hummon and J. Ye, Annu. Rev. Phys. Chem., 2014, 65, 501–518 CrossRef CAS PubMed.
- Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero, ed. O. Dulieu and A. Osterwalder, RSC publishing, 2018 Search PubMed.
- C. P. Koch, M. Lemeshko and D. Sugny, Rev. Mod. Phys., 2019, 91, 035005 CrossRef CAS.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS PubMed.
- M. Fournier, S. D. Le Picard and I. R. Sims, Low-temperature Chemistry in Uniform Supersonic Flows, in Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero, ed. O. Dulieu and A. Osterwalder, RSC publishing, 2018 Search PubMed.
- C. Berteloite, M. Lara, A. Bergeat, S. D. Le Picard, F. Dayou, K. M. Hickson, A. Canosa, C. Naulin, J.-M. Launay, I. R. Sims and M. Costes, Phys. Rev. Lett., 2010, 105, 203201 CrossRef PubMed.
- J. Marquette, B. Rowe, G. Dupeyrat, G. Poissant and C. Rebrion, Chem. Phys. Lett., 1985, 122, 431–435 CrossRef CAS.
- B. Rowe, A. Canosa and V. Le Page, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 573–596 CrossRef.
- I. W. M. Smith, Annu. Rev. Astron. Astrophys., 2011, 49, 29–66 CrossRef CAS.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745–749 CrossRef CAS PubMed.
- M. Tizniti, S. D. Le Picard, F. Lique, C. Berteloite, A. Canosa, M. H. Alexander and I. R. Sims, Nat. Chem., 2014, 6, 141–145 CrossRef CAS PubMed.
- C. Abeysekera, B. Joalland, N. Ariyasingha, L. N. Zack, I. R. Sims, R. W. Field and A. G. Suits, J. Phys. Chem. Lett., 2015, 6, 1599–1604 CrossRef CAS PubMed.
- C. Amarasinghe and A. G. Suits, J. Phys. Chem. Lett., 2017, 8, 5153–5159 CrossRef CAS PubMed.
- K. Gawlas and S. D. Hogan, J. Phys. Chem. Lett., 2020, 11, 83–87 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356–359 CrossRef CAS PubMed.
- J. L. Bohn, A. M. Rey and J. Ye, Science, 2017, 357, 1002–1010 CrossRef CAS PubMed.
- S. Y. T. van de Meerakker, H. L. Bethlem and G. Meijer, Nat. Phys., 2008, 4, 595–602 Search PubMed.
- A. Osterwalder, EPJ Tech. Instrum., 2015, 2, 10 Search PubMed.
- J. Jankunas and A. Osterwalder, Annu. Rev. Phys. Chem., 2014, 66, 241–262 CrossRef PubMed.
- S. D. Hogan, M. Motsch and F. Merkt, Phys. Chem. Chem. Phys., 2011, 13, 18705–18723 RSC.
- S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878 CrossRef CAS PubMed.
- E. Narevicius and M. G. Raizen, Chem. Rev., 2012, 112, 4879–4889 CrossRef CAS PubMed.
- D. R. Herschbach, Angew. Chem., Int. Ed. Engl., 1987, 26, 1221–1243 CrossRef.
- Y. T. Lee, Science, 1987, 236, 793–798 CrossRef CAS PubMed.
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, 2005 Search PubMed.
- Tutorials in Molecular Reaction Dynamics, ed. M. Brouard and C. Vallance, RSC Publishing, 2012 Search PubMed.
- P. Casavecchia, N. Balucani and G. G. Volpi, Annu. Rev. Phys. Chem., 1999, 50, 347–376 CrossRef CAS PubMed.
- X. Yang, Annu. Rev. Phys. Chem., 2007, 58, 433–459 CrossRef CAS PubMed.
- J. Onvlee, S. N. Vogels and S. Y. T. van de Meerakker, Chem. Phys. Chem., 2016, 17, 3583–3595 CrossRef CAS PubMed.
- S. Chefdeville, T. Stoecklin, A. Bergeat, K. M. Hickson, C. Naulin and M. Costes, Phys. Rev. Lett., 2012, 109, 023201 CrossRef PubMed.
- S. Chefdeville, Y. Kalugina, S. Y. T. van de Meerakker, C. Naulin, F. Lique and M. Costes, Science, 2013, 341, 1094–1096 CrossRef CAS PubMed.
- A. Bergeat, A. Faure, S. B. Morales, A. Moudens and C. Naulin, J. Phys. Chem. A, 2020, 124, 259–264 CrossRef CAS PubMed.
- T. Yang, L. Huang, C. Xiao, J. Chen, T. Wang, D. Dai, F. Lique, M. H. Alexander, Z. Sun, D. H. Zhang, X. Yang and D. M. Neumark, Nat. Chem., 2019, 11, 774–781 Search PubMed.
- H. L. Bethlem, G. Berden and G. Meijer, Phys. Rev. Lett., 1999, 83, 1558 CrossRef CAS.
- S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790 CrossRef CAS PubMed.
- S. N. Vogels, T. Karman, J. Kłos, M. Besemer, J. Onvlee, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2018, 10, 435–440 CrossRef CAS PubMed.
- Z. Gao, S. N. Vogels, M. Besemer, T. Karman, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, J. Phys. Chem. A, 2017, 121, 7446–7454 CrossRef CAS PubMed.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- Z. Gao, T. Karman, S. N. Vogels, M. Besemer, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2018, 10, 469–473 CrossRef CAS PubMed.
- Q. Wei, I. Lyuksyutov and D. Herschbach, J. Chem. Phys., 2012, 137, 054202 CrossRef PubMed.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234–238 CrossRef CAS PubMed.
- J. Jankunas, B. Bertsche, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2014, 140, 244302 CrossRef PubMed.
- U. Even, Eur. Phys. J. Tech. Instrum., 2015, 2, 17 Search PubMed.
- Y. Shagam and E. Narevicius, J. Phys. Chem. C, 2013, 117, 22454–22461 CrossRef CAS.
- E. Lavert-Ofir, Y. Shagam, A. B. Henson, S. Gersten, J. Kłos, P. S. Zuchowski, J. Narevicius and E. Narevicius, Nat. Chem., 2014, 6, 332–335 CrossRef CAS PubMed.
- Y. Shagam, A. Klein, W. Skomorowski, R. Yun, V. Averbukh, C. P. Koch and E. Narevicius, Nat. Chem., 2015, 7, 921–926 CrossRef CAS PubMed.
- A. Klein, Y. Shagam, W. Skomorowski, P. S. Zuchowski, M. Pawlak, L. M. C. Janssen, N. Moiseyev, S. Y. T. van de Meerakker, A. van der Avoird, C. P. Koch and E. Narevicius, Nat. Phys., 2017, 13, 35–38 Search PubMed.
- J. Zou, S. D. S. Gordon and A. Osterwalder, Phys. Rev. Lett., 2019, 123, 133401 CrossRef CAS PubMed.
- S. D. S. Gordon, J. J. Omiste, J. Zou, S. Tanteri, P. Brumer and A. Osterwalder, Nat. Chem., 2018, 10, 1190–1195 CrossRef CAS PubMed.
- J. Jankunas, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2016, 144, 221102 CrossRef PubMed.
- K. Jachymski, M. Hapka, J. Jankunas and A. Osterwalder, Chem. Phys. Chem., 2016, 17, 3776–3782 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, O. Schullian, K. Hoveler, J. A. Agner, H. Schmutz and F. Merkt, Chem. Phys. Chem., 2016, 17, 3596–3608 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, K. Hoveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316 CrossRef PubMed.
- A. P. P. van der Poel, K. Dulitz, T. P. Softley and H. L. Bethlem, New J. Phys., 2015, 17, 055012 CrossRef.
- A. P. P. van der Poel, P. C. Zieger, S. Y. T. van de Meerakker, J. Loreau, A. van der Avoird and H. L. Bethlem, Phys. Rev. Lett., 2018, 120, 033402 CrossRef CAS PubMed.
- A. P. P. van der Poel and H. L. Bethlem, EPJ Tech. Instrum., 2018, 5, 6 CrossRef PubMed.
- R. von Hahn, A. Becker, F. Berg, K. Blaum, C. Breitenfeldt, H. Fadil, F. Fellenberger, M. Froese, S. George, J. Göck, M. Grieser, F. Grussie, E. A. Guerin, O. Heber, P. Herwig, J. Karthein, C. Krantz, H. Kreckel, M. Lange, F. Laux, S. Lohmann, S. Menk, C. Meyer, P. M. Mishra, O. Novotný, A. P. O'Connor, D. A. Orlov, M. L. Rappaport, R. Repnow, S. Saurabh, S. Schippers, C. D. Schröter, D. Schwalm, L. Schweikhard, T. Sieber, A. Shornikov, K. Spruck, S. Sunil Kumar, J. Ullrich, X. Urbain, S. Vogel, P. Wilhelm, A. Wolf and D. Zajfman, Rev. Sci. Instrum., 2016, 87, 063115 CrossRef CAS PubMed.
- O. Novotný, P. Wilhelm, D. Paul, Á. Kálosi, S. Saurabh, A. Becker, K. Blaum, S. George, J. Göck, M. Grieser, F. Grussie, R. von Hahn, C. Krantz, H. Kreckel, C. Meyer, P. M. Mishra, D. Muell, F. Nuesslein, D. A. Orlov, M. Rimmler, V. C. Schmidt, A. Shornikov, A. S. Terekhov, S. Vogel, D. Zajfman and A. Wolf, Science, 2019, 365, 676–679 CrossRef PubMed.
- H. Kreckel, O. Novotný and A. Wolf, Philos. Trans. R. Soc., A, 2019, 377, 20180412 CrossRef CAS PubMed.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- D. Gerlich and M. Smith, Phys. Scr., 2006, 73, C25–C31 CrossRef CAS.
- G. Borodi, A. Luca and D. Gerlich, Int. J. Mass Spectrom., 2009, 280, 218–225 CrossRef CAS.
- R. Plašil, T. Mehner, P. Dohnal, T. Kotrik, J. Glosík and D. Gerlich, Astrophys. J., 2011, 737, 60 CrossRef.
- R. Plašil, T. D. Tran, Š. Roučka, P. Jusko, D. Mulin, I. Zymak, S. Rednyk, A. Kovalenko, P. Dohnal, J. Glosík, K. Houfek, J. Táborský and M. Čížek, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 96, 062703 CrossRef.
- T. D. Tran, S. Rednyk, A. Kovalenko, Š. Roučka, P. Dohnal, R. Plašil, D. Gerlich and J. Glosík, Astrophys. J., 2018, 854, 25 CrossRef.
- B. R. Heazlewood and T. P. Softley, Annu. Rev. Phys. Chem., 2015, 66, 475–495 CrossRef CAS PubMed.
- J. Greenberg, P. C. Schmid, M. Miller, J. F. Stanton and H. J. Lewandowski, Phys. Rev. A: At., Mol., Opt. Phys., 2018, 98, 032702 CrossRef CAS.
- K. Mølhave and M. Drewsen, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 011401(R) CrossRef.
- P. Schmid, M. Miller, J. Greenberg, T. L. Nguyen, J. F. Stanton and H. J. Lewandowski, Mol. Phys., 2019, 117, 3036–3042 CrossRef CAS.
- D. Clary, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 139–148 RSC.
- A. D. Gingell, M. T. Bell, J. M. Oldham, T. P. Softley and J. N. Harvey, J. Chem. Phys., 2010, 133, 194302 CrossRef PubMed.
- A. Kilaj, H. Gao, D. Rösch, U. Rivero, J. Küpper and S. Willitsch, Nat. Commun., 2018, 9, 2096 CrossRef PubMed.
- Y.-P. Chang, K. Długołęcki, J. Küpper, D. Rösch, D. Wild and S. Willitsch, Science, 2013, 342, 98–101 CrossRef CAS PubMed.
- T. Yang, A. Li, G. K. Chen, C. Xie, A. G. Suits, W. C. Campbell, H. Guo and E. R. Hudson, J. Phys. Chem. Lett., 2018, 9, 3555 CrossRef CAS PubMed.
- L. S. Petralia, A. Tsikritea, J. Loreau, T. P. Softley and B. R. Heazlewood, Nat. Commun., 2020, 11, 173 CrossRef CAS PubMed.
- S. Willitsch, Int. Rev. Phys. Chem., 2012, 31, 175–199 Search PubMed.
- D. Zhang and S. Willitsch, Cold ion chemistry, in Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero, ed. O. Dulieu and A. Osterwalder, RSC Publishing, 2018 Search PubMed.
- B. R. Heazlewood, Mol. Phys., 2019, 117, 1934–1941 CrossRef CAS.
- B. Roth, P. Blythe, H. Wenz, H. Daerr and S. Schiller, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 042712 CrossRef.
- K. J. Catani, J. Greenberg, B. V. Saarel and H. J. Lewandowski, arXiv:2003.12102v1, 2020.
- P. C. Schmid, J. Greenberg, M. I. Miller, T. L. Nguyen, J. H. Thorpe, J. F. Stanton and H. J. Lewandowski, 2020, in preparation.
- P. F. Staanum, K. Højbjerre, P. S. Skyt, A. K. Hansen and M. Drewsen, Nat. Phys., 2010, 6, 271–274 Search PubMed.
- T. Schneider, B. Roth, H. Duncker, I. Ernsting and S. Schiller, Nat. Phys., 2010, 6, 275–278 Search PubMed.
- N. Deb, B. R. Heazlewood, M. T. Bell and T. P. Softley, Phys. Chem. Chem. Phys., 2013, 15, 14270–14281 RSC.
- N. Deb, B. R. Heazlewood, C. J. Rennick and T. P. Softley, J. Chem. Phys., 2014, 140, 164314 CrossRef PubMed.
- C.-Y. Lien, C. M. Seck, Y.-W. Lin, J. H. V. Nguyen, D. A. Tabor and B. C. Odom, Nat. Commun., 2014, 5, 4783 CrossRef CAS PubMed.
- E. R. Hudson, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 032716 CrossRef.
- W. G. Rellergert, S. T. Sullivan, S. J. Schowalter, S. Kotochigova, K. Chen and E. R. Hudson, Nature, 2013, 495, 490–494 CrossRef CAS PubMed.
- M. Schwarz, O. O. Versolato, A. Windberger, F. R. Brunner, T. Ballance, S. N. Eberle, J. Ullrich, P. O. Schmidt, A. K. Hansen, A. D. Gingell, M. Drewsen and J. R. C. López-Urrutia, Rev. Sci. Instrum., 2012, 83, 083115 CrossRef CAS PubMed.
- A. K. Hansen, O. O. Versolato, Ł. Kłosowski, S. B. Kristensen, A. Gingell, M. Schwarz, A. Windberger, J. Ullrich, J. R. Crespo López-Urrutia and M. Drewsen, Nature, 2014, 508, 76–79 CrossRef CAS PubMed.
- T. Leopold, S. A. King, P. Micke, A. Bautista-Salvador, J. C. Heip, C. Ospelkaus, J. R. Crespo López-Urrutia and P. O. Schmidt, Rev. Sci. Instrum., 2019, 90, 073201 CrossRef CAS PubMed.
- M. Hejduk and B. R. Heazlewood, Rev. Sci. Instrum., 2020, 90, 123701 CrossRef PubMed.
- K. S. Twyman, M. T. Bell, B. R. Heazlewood and T. P. Softley, J. Chem. Phys., 2014, 141, 024308 CrossRef PubMed.
- K. Okada, Y. Takada, N. Kimura, M. Wada and H. A. Schuessler, Rev. Sci. Instrum., 2017, 88, 083106 CrossRef PubMed.
- J. Toscano, C. J. Rennick, T. P. Softley and B. R. Heazlewood, J. Chem. Phys., 2018, 149, 174201 CrossRef PubMed.
- D. Haas, C. von Planta, T. Kierspel, D. Zhang and S. Willitsch, Commun. Phys., 2019, 2, 101 CrossRef.
- M. Schwarzer, A. Hansel, W. Freysinger, N. Oberhofer, W. Lindinger and E. E. Ferguson, J. Chem. Phys., 1991, 95, 7344–7347 CrossRef CAS.
- A. Härter and J. Hecker Denschlag, Contemp. Phys., 2014, 55, 33–45 CrossRef.
- M. Tomza, K. Jachymski, R. Gerritsma, A. Negretti, T. Calarco, Z. Idziaszek and P. S. Julienne, Rev. Mod. Phys., 2019, 91, 035001 CrossRef CAS.
- S. J. Schowalter, A. J. Dunning, K. Chen, P. Puri, C. Schneider and E. R. Hudson, Nat. Commun., 2016, 7, 12448 CrossRef CAS PubMed.
- P. Puri, M. Mills, I. Simbotin, J. A. Montgomery Jr., R. Côté, C. Schneider, A. G. Suits and E. R. Hudson, Nat. Chem., 2019, 11, 615–621 CrossRef CAS PubMed.
- A. D. D. Dörfler, P. Eberle, D. Koner, M. Tomza, M. Meuwly and S. Willitsch, Nat. Commun., 2019, 10, 5429 CrossRef PubMed.
- P. Puri, M. Mills, C. Schneider, I. Simbotin, J. A. Montgomery Jr., R. Côté, A. G. Suits and E. R. Hudson, Science, 2017, 357, 1370–1375 CrossRef CAS PubMed.
- N. Akerman, M. Karpov, Y. Segev, N. Bibelnik, J. Narevicius and E. Narevicius, Phys. Rev. Lett., 2017, 119, 073204 CrossRef PubMed.
- Y. Segev, M. Pitzer, M. Karpov, N. Akerman, J. Narevicius and E. Narevicius, Nature, 2019, 572, 189–193 CrossRef CAS PubMed.
- Y. Liu, M. Vashishta, P. Djuricanin, S. Zhou, W. Zhong, T. Mittertreiner, D. Carty and T. Momose, Phys. Rev. Lett., 2017, 118, 093201 CrossRef PubMed.
- J. Riedel, S. Hoekstra, W. Jäger, J. J. Gilijamse, S. Y. T. van de Meerakker and G. Meijer, Eur. Phys. J. D, 2011, 65, 161–166 CrossRef CAS.
- L. Caldwell, H. J. Williams, N. J. Fitch, J. Aldegunde, J. M. Hutson, B. E. Sauer and M. R. Tarbutt, Phys. Rev. Lett., 2020, 124, 063001 CrossRef CAS PubMed.
- H. J. Williams, L. Caldwell, N. J. Fitch, S. Truppe, J. Rodewald, E. A. Hinds, B. E. Sauer and M. R. Tarbutt, Phys. Rev. Lett., 2018, 120, 163201 CrossRef CAS PubMed.
- B. C. Sawyer, B. K. Stuhl, D. Wang, M. Yeo and J. Ye, Phys. Rev. Lett., 2008, 101, 203203 CrossRef PubMed.
- N. R. Hutzler, H.-I. Lu and J. M. Doyle, Chem. Rev., 2012, 112, 4803–4827 CrossRef CAS PubMed.
- B. C. Sawyer, B. K. Stuhl, M. Yeo, T. V. Tscherbul, M. T. Hummon, Y. Xia, J. Kłos, D. Patterson, J. M. Doyle and J. Ye, Phys. Chem. Chem. Phys., 2011, 13, 19059–19066 RSC.
- M. T. Hummon, T. V. Tscherbul, J. Kłos, H.-I. Lu, E. Tsikata, W. C. Campbell, A. Dalgarno and J. M. Doyle, Phys. Rev. Lett., 2011, 106, 053201 CrossRef PubMed.
- L. P. Parazzoli, N. J. Fitch, P. S. Żuchowski, J. M. Hutson and H. J. Lewandowski, Phys. Rev. Lett., 2011, 106, 193201 CrossRef CAS PubMed.
- B. K. Stuhl, M. T. Hummon, M. Yeo, G. Quéméner, J. L. Bohn and J. Ye, Nature, 2012, 492, 396–400 CrossRef CAS PubMed.
- B. K. Stuhl, M. Yeo, M. T. Hummon and J. Ye, Mol. Phys., 2013, 111, 1798–1804 CrossRef CAS.
- X. Wu, T. Gantner, M. Koller, M. Zeppenfeld, S. Chervenkov and G. Rempe, Science, 2017, 358, 645–648 CrossRef CAS PubMed.
- S. Ospelkaus, K.-K. Ni, D. Wang, M. H. G. de Miranda, B. Neyenhuis, G. Quéméner, P. S. Julienne, J. L. Bohn, D. S. Jin and J. Ye, Science, 2010, 327, 853–857 CrossRef CAS PubMed.
- L. De Marco, G. Valtolina, K. Matsuda, W. G. Tobias, J. P. Covey and J. Ye, Science, 2019, 363, 853–856 CrossRef CAS PubMed.
- F. Lang, K. Winkler, C. Strauss, R. Grimm and J. Hecker Denschlag, Phys. Rev. Lett., 2008, 101, 133005 CrossRef CAS PubMed.
- T. Takekoshi, L. Reichsöllner, A. Schindewolf, J. M. Hutson, C. R. L. Sueur, O. Dulieu, F. Ferlaino, R. Grimm and H.-C. Nägerl, Phys. Rev. Lett., 2014, 113, 205301 CrossRef PubMed.
- P. K. Molony, P. D. Gregory, Z. Ji, B. Lu, M. P. Köppinger, C. R. L. Sueur, C. L. Blackley, J. M. Hutson and S. L. Cornish, Phys. Rev. Lett., 2014, 113, 255301 CrossRef PubMed.
- M. Guo, B. Zhu, B. Lu, X. Ye, F. Wang, R. Vexiau, N. Bouloufa-Maafa, G. Quéméner, O. Dulieu and D. Wang, Phys. Rev. Lett., 2016, 116, 205303 CrossRef PubMed.
- J. W. Park, S. A. Will and M. W. Zwierlein, Phys. Rev. Lett., 2015, 114, 205302 CrossRef PubMed.
- F. Seeßelberg, N. Buchheim, Z.-K. Lu, T. Schneider, X.-Y. Luo, E. Tiemann, I. Bloch and C. Gohle, Phys. Rev. A: At., Mol., Opt. Phys., 2018, 97, 013405 CrossRef.
- S. Truppe, H. J. Williams, M. Hambach, L. Caldwell, N. J. Fitch, E. A. Hinds, B. E. Sauer and M. R. Tarbutt, Nat. Phys., 2017, 13, 1173–1176 Search PubMed.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, Nat. Phys., 2018, 14, 890–893 Search PubMed.
- L. Anderegg, L. W. Cheuk, Y. Bao, S. Burchesky, W. Ketterle, K.-K. Ni and J. M. Doyle, Science, 2019, 365, 1156–1158 CrossRef CAS PubMed.
- L. W. Cheuk, L. Anderegg, Y. Bao, S. Burchesky, S. Yu, W. Ketterle, K.-K. Ni and J. M. Doyle, arXiv:2002.00048v1, 2020.
- P. D. Gregory, M. D. Frye, J. A. Blackmore, E. M. Bridge, R. Sawant, J. M. Hutson and S. L. Cornish, Nat. Commun., 2019, 10, 3104 CrossRef PubMed.
- D. K. Hoffmann, T. Paintner, W. Limmer, D. S. Petrov and J. Hecker Denschlag, Nat. Commun., 2018, 9, 5244 CrossRef CAS PubMed.
- A. Christianen, M. W. Zwierlein, G. C. Groenenboom and T. Karman, Phys. Rev. Lett., 2019, 123, 123402 CrossRef CAS PubMed.
- P. D. Gregory, J. A. Blackmore, S. L. Bromley and S. L. Cornish, arXiv:2002.04431v2, 2020.
- M.-G. Hu, Y. Liu, D. D. Grimes, Y.-W. Lin, A. H. Gheorghe, R. Vexiau, N. Boulufa-Maafa, O. Dulieu, T. Rosenband and K.-K. Ni, Science, 2019, 366, 1111–1115 CrossRef CAS PubMed.
- B. Gao, Phys. Rev. Lett., 2010, 105, 263203 CrossRef PubMed.
- D. M. Brink and S. Stringari, Z. Phys. D, 1990, 15, 257–263 CrossRef CAS.
- J. W. Niman, B. S. Kamerin, D. J. Merthe, L. Kranabetter and V. V. Kresin, Phys. Rev. Lett., 2019, 123, 043203 CrossRef CAS PubMed.
- S. Yang and A. M. Ellis, Chem. Soc. Rev., 2013, 42, 472–484 RSC.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90 CrossRef CAS.
- A. Vilà and M. González, Phys. Chem. Chem. Phys., 2016, 18, 31869–31880 RSC.
- K. K. Lehmann and G. Scoles, Science, 1998, 279, 2065–2066 CrossRef CAS.
- A. Slenczka and J. P. Toennies, Chemical dynamics inside superfluid helium nanodroplets at 0.37 K, in Low Temperatures and Cold Molecules, ed. I. W. M. Smith, Imperial College Press, 2008, pp. 345–392 Search PubMed.
- J. T. Brice, P. R. Franke and G. E. Douberly, J. Phys. Chem. A, 2017, 121, 9466–9473 CrossRef CAS PubMed.
- P. R. Franke, J. T. Brice, C. P. Moradi, H. F. Schaefer III and G. E. Douberly, J. Phys. Chem. A, 2019, 123, 3558–3568 CrossRef CAS PubMed.
- S. A. Krasnokutski, M. Kuhn, A. Kaiser, A. Mauracher, M. Renzler, D. K. Bohme and P. Scheier, J. Phys. Chem. Lett., 2016, 7, 1440–1445 CrossRef CAS PubMed.
- J. D. Weinstein, R. deCarvalho, T. Guillet, B. Friedrich and J. M. Doyle, Nature, 1998, 395, 148–150 CrossRef CAS.
- D. Egorov, W. C. Campbell, B. Friedrich, S. E. Maxwell, E. Tsikata, L. D. van Buuren and J. M. Doyle, Eur. Phys. J. D, 2004, 31, 307–311 CrossRef CAS.
- W. C. Campbell and J. M. Doyle, Cooling, trap loading, and beam production using a cryogenic helium buffer gas, in Cold Molecules: Theory, Experiment, Applications, ed. R. V. Krems, W. C. Stwalley and B. Friedrich, CRC Press, 2009 Search PubMed.
- N. Tariq, N. Al Taisan, V. Singh and J. D. Weinstein, Phys. Rev. Lett., 2013, 110, 153201 CrossRef PubMed.
- V. Singh, K. S. Hardman, N. Tariq, M.-J. Lu, A. Ellis, M. J. Morrison and J. D. Weinstein, Phys. Rev. Lett., 2012, 108, 203201 CrossRef PubMed.
- D. Patterson, E. Tsikata and J. M. Doyle, Phys. Chem. Chem. Phys., 2010, 12, 9736–9741 RSC.
| This journal is © the Owner Societies 2020 |