Temperature- and pressure-dependent kinetics of the competing C–O bond fission reactions of dimethoxymethane

Abstract

Oxymethylene ethers are often considered as promising fuel additives to reduce the emissions of soot and NO_x from diesel engines. Dimethoxymethane (DMM) is the smallest member of this class of compounds and therefore particularly suitable to study the reactivity of the characteristic methylenedioxy group (O–CH₂–O). In this context, we investigated the pyrolysis of DMM behind reflected shock waves at temperatures between 1100 and 1600 K and nominal pressures of 0.4 and 4.7 bar by monitoring the formation of H atoms with time-resolved atom resonance absorption spectroscopy. Rate coefficients for the C–O bond fission reactions of DMM were inferred from the recorded [H](t) profiles, and a pronounced temperature and pressure dependence of the rate coefficients was found. To rationalize this finding, we characterized the relevant parts of the potential energy surface of DMM by performing quantum chemical calculations at the CCSD(F12*)(T*)/cc-pVQZ-F12//B2PLYP-D3/def2-TZVPP level of theory. On the basis of the results, a two-channel master equation accounting for the two different C–O bond-fission reactions of DMM was set up and solved. Specific rate coefficients were calculated from the simplified Statistical Adiabatic Channel Model. The branching between the two reaction channels was modeled, and the CH₃OCH₂O + CH₃ product channel was found to be clearly dominating. A Troe parameterization for the pressure dependence of this channel was derived. To enable implementation of both channels into kinetic mechanisms for combustion modeling, ‘log p’ parameterizations of the rate coefficients for both reaction channels are also given and were implemented into a literature mechanism for DMM oxidation. With this slightly modified mechanism, the results of our experiments could be adequately modeled. The role of competing molecular (i.e. nonradical) decomposition channels of DMM was also quantum-chemically checked, but no indications for such channels could be found.

---

1. Introduction

Exhaust gas pollution from diesel engines is one of today's major challenges faced by highly motorized societies and their automotive industry. Various approaches to reduce pollutant emission have been discussed. One is the use of mixtures of conventional diesel fuels with additives that reduce the formation of soot and nitric oxides (NO_x). In this context, oxymethylene ethers (OMEs) are currently considered as promising candidates,^1–3 also because they can be produced from nonfossil carbon sources.^4,5 Their comparatively high oxygen content and the absence of C–C bonds lead to a reduced formation of soot and NO_x in the combustion of OME/fuel mixtures.⁶

Dimethoxymethane (DMM) as the smallest OME is particularly suitable to study the reactivity of the characteristic methylenedioxy group (O–CH₂–O). The first kinetic mechanism (511 reactions, 75 species) to describe the oxidation of DMM was developed by Daly et al.⁷ in 2001. For the initial reactions of DMM, all rate coefficients were estimated in analogy to the corresponding reactions of dimethyl (DME) and diethyl ether (DEE). The model developed in this way was able to describe quite well concentration profiles measured in jet-stirred reactor/gas chromatography (JSR/GC) experiments (T = 800–1200 K, p = 5.07 bar).

Nine years later, Dias et al.⁸ recorded mole-fraction profiles of different species in two DMM/O₂/Ar flames (p = 50 mbar, equivalence ratios of Φ = 0.24 and 1.72), using electron impact molecular beam mass spectrometry (EI-MBMS). A kinetic scheme consisting of 90 species and 480 reactions was proposed with rate coefficients for DMM-specific reactions adopted from ref. 7.

On the basis of ref. 8, two further mechanisms for DMM combustion were proposed by Marrodán et al.^9,10 and Alexandrino et al.¹¹ In ref. 9 and 10 the oxidation of DMM was studied in a flow reactor over wide ranges of temperature and pressure (T = 373–1073 K, p = 20–60 bar ⁹ and T = 573–1573 K, p = 1–60 bar ¹⁰) by using GC to determine species mole fraction profiles. Alexandrino et al.¹¹ studied the formation of soot from DMM under pyrolytic conditions with a flow reactor/GC experiment (T = 1075–1475 K, p ∼ 1 bar). The obtained experimental results were described with a kinetic mechanism consisting of the DMM-specific part taken from ref. 8 with adjustments for the different pressure range studied, the C₁–C₂ base mechanism from Glarborg et al.,^12–14 and additional submechanisms (for details see ref. 11).

In 2018, Vermeire et al.¹⁵ published a combined experimental and theoretical study on DMM oxidation. To obtain thermochemical data for the most important peroxy species involved, the authors performed quantum chemical calculations at the CBS-QB3 level of theory. Rate coefficients for important reactions were derived and implemented into a new DMM combustion model consisting of a DMM-specific submechanism that was set up with the automatic mechanism generator Genesys,¹⁶ and the AramcoMech V. 1.3¹⁷ as base mechanism. Simulation results obtained on the basis of this novel mechanism were compared to concentration profiles recorded with GC and GC/MS in JSR experiments (T = 500–1100 K, p = 1.07 bar).

One year later, Sun et al.¹⁸ published another detailed discussion of DMM combustion. The authors studied the oxidation of DMM in two JSR setups by using photoionization time-of-flight mass spectrometry (PI-TOF-MS), Fourier transform infra-red (FTIR) spectroscopy, and GC/MS for detection (JSR/PI-TOF-MS experiment: T = 460–820 K, p ∼ 1 bar, JSR/FTIR and JSR/GC/MS experiments: T = 500–1200 K, p = 10 bar). To further analyze the obtained mole fraction profiles, the authors developed a kinetic model (2821 reactions, 524 species) on the basis of AramcoMech V. 2.0. Rate coefficients for the reactions of DMM were adopted from earlier studies by Kopp et al.,¹⁹ Vermeire et al.,¹⁵ and Glaude et al..²⁰

Under pyrolytic conditions, the decomposition of DMM mainly proceeds via C–O bond fissions, yielding either CH₃ and CH₃OCH₂O, reaction (R1), or OCH₃ and CH₃OCH₂, reaction (R2):^{7,8,15,21–23}

CH₃OCH₂OCH₃ → CH₃OCH₂O + CH₃ (R1)

CH₃OCH₂OCH₃ → CH₃OCH₂ + OCH₃ (R2)

In the literature, the direct formation of CH₃OH, reaction (R3), and DME, reaction (R4), are also discussed as DMM consumption pathways under pyrolytic conditions:^18,24

CH₃OCH₂OCH₃ → CH₃OH + CH₃ + HCO (R3)

CH₃OCH₂OCH₃ → CH₃OCH₃ + CH₂O (R4)

Currently, the branching between the simple C–O bond fission reactions (R1) and (R2) and the complex elimination reactions (R3) and (R4) are not well characterized in the literature, and in different works, different reaction channels are discussed to be dominating (see below). Moreover, the pressure dependence even of the total rate coefficient has not been experimentally studied so far.

To the best of our knowledge, only two detailed experimental investigations of the initial C–O bond fission reactions (R1) and (R2) have been published so far. Recently in this laboratory, the pyrolysis of DMM behind reflected shock waves was studied by hydrogen atom resonance absorption spectroscopy (H-ARAS) and high-repetition time-of-flight mass spectrometry (HR-TOF-MS) (T = 1100–1700 K, p = 0.9–1.3 bar).²² From the initial slope of the recorded H atom concentration–time profiles, a total rate coefficient k₁₊₂ ≡ k₁ + k₂ = (6.2 ± 1.9) × 10¹³ exp(−31 830 K/T) s⁻¹ (T = 1100–1550 K, p ∼ 1.1 bar, x_DMM ∼ 3.4 ppm, bath gas: Ar) was inferred by assuming that the initial C–O bond fission reactions are the rate determining steps for H-atom production from DMM. In this analysis, the authors followed the DMM oxidation mechanism from ref. 9, in which reactions (R5) and (R6) are the major consecutive decomposition reactions of the radicals produced in reactions (R1) and (R2), and identified reactions (R6) to (R8) as the most important steps in the formation of H atoms from DMM:

CH₃OCH₂ → CH₂O + CH₃ (R5)

CH₃OCH₂O → CH₃OCHO + H (R6)

CH₃OCH₂O → CH₃O + CH₂O (R7)

CH₃O → CH₂O + H (R8)

In both DMM consumption pathways, reactions (R1) + (R6) + (R7) + (R8) and (R2) + (R8), one H atom per consumed molecule DMM is produced. Accordingly, a relative branching fraction k₁/(k₁ + k₂) cannot be inferred from H atom concentration–time profiles alone. Golka et al.²² assumed a relative branching fraction of 0.5 to implement the obtained rate coefficient k₁₊₂ into the DMM combustion model of ref. 9. With this modified kinetic mechanism, the authors were able to well predict the concentration–time profiles obtained in shock tube/H-ARAS and shock tube/TOF-MS experiments.²²

Also in 2018, Peukert et al.²³ published a study on DMM pyrolysis behind reflected shock waves, using H-ARAS, HR-TOF-MS, and GC/MS for detection. The experiments cover temperatures between 1100 and 1430 K at pressures between 1.2 and 2.5 bar. Initial DMM mole fractions range from 0.5 ppm in the shock tube/H-ARAS and 10 000 ppm in the shock tube/TOF-MS experiments. Total rate coefficients k₁₊₂ were deduced from the measured H atom and DMM concentration–time profiles on the basis of simulations with a small kinetic mechanism (16 reactions, 15 species, H-ARAS results) and the mechanism by Vermeire et al.¹⁵ (TOF-MS and GC/MS results). Because the rate coefficients obtained from the different experiments were found to be consistent, one overall Arrhenius expression was given: k₁₊₂(T) = 10^{13.28 ± 0.27} × exp[−(247.90 ± 6.36) kJ mol⁻¹/(RT)] s⁻¹ (T = 1100–1400 K, p = 1.2–2.5 bar). In addition, the authors analyzed the pressure dependence of reaction (R2) by a restricted rotor Rice–Ramsperger–Kassel–Marcus(RRKM)-Gorin model, whereas an analogous analysis for reaction (R1) was not performed because, according to the mechanism from Vermeire et al.,¹⁵reaction (R1) is of negligible importance (branching fraction k₂/(k₁ + k₂) ∼ 0.98).

The first and so far only purely theoretical study on DMM reactions relevant in combustion was published by Kopp et al.¹⁹ in 2018. On the basis of potential energy surfaces calculated at the CCSD(T)/aug-cc-pV(D+T)Z//B2PLYPD3BJ/6-311++g(d,p) level of theory, these authors obtained rate coefficients for the H-atom abstraction reactions from DMM by H and CH₃ radicals from transition state theory (TST), and for the consecutive isomerization and β-scission reactions from RRKM/master equation calculations. In addition, important thermochemical data e.g. heat capacities for DMM and DMM radicals were predicted. On the basis of ref. 19, a novel kinetic mechanism for DMM oxidation was proposed by Jacobs et al.²⁴ consisting of 2889 reactions and 355 species. Additionally, calculations at the same level of theory were conducted in ref. 24 to compute rate coefficients for reactions that were not covered in ref. 19 such as decomposition channels of peroxy radicals. Simulations with the proposed mechanism were compared to the results of ignition delay time and laminar burning velocity measurements (T = 590–1215 K; p = 1–40 bar), and good agreement was found.

In the current work, we present a detailed discussion of the pressure dependence of the C–O bond fission reactions in DMM. We measured H atom concentration–time profiles by ARAS behind reflected shock waves at two different nominal pressures, p ∼ 0.4 bar and p ∼ 4.7 bar over the temperature range T = 1100–1600 K. The deduced overall rate coefficient k₁₊₂ exhibits a pronounced temperature and pressure dependence. To further analyze our experimental results and also to gain information on the relative importance of reactions (R1) and (R2), we conducted master equation analyses with specific rate coefficients from the simplified Statistical Adiabatic Channel Model (s-SACM). To this end, we characterized the reaction paths for reactions (R1) and (R2) as well as the consecutive radical decomposition channels (R5) and (R7) by exploring the relevant potential energy surface with quantum chemical calculations at the CCSD(F12*)(T*)/cc-pVQZF12//B2PLYP-D3/def2-TZVPP level of theory. A search for competing molecular decomposition channels of DMM was also performed.

2. Methodology

2.1. Shock tube/H-ARAS experiments

Experiments were conducted in a stainless steel shock tube behind reflected shock waves at temperatures between 1100 and 1600 K at nominal pressures of 0.4 and 4.7 bar with Ar as bath gas. To obtain comparable initial concentrations of DMM behind the reflected shock wave, reaction mixtures contained between 1.5 and 24.5 ppm DMM depending on the nominal pressure. To exclude any influence of possible contaminations, in particular from unwanted H-atom sources, we daily performed blank experiments in pure Ar. Calibration and DMM pyrolysis experiments were only conducted after no absorbance could be determined in these blank experiments.

Since the experimental setup has been described in detail elsewhere (see ref. 22, 25 and 26 and references cited therein), only a brief overview is given here. The shock tube (inner diameter: 10 cm) consisted of a high-pressure (length: 3.05 m) and a low-pressure section (length: 4.20 m) that were separated by an aluminum foil (thickness: 20 μm or 100 μm). Shock waves were initiated by pressure bursting of the aluminum foil with H₂ as driver gas. Post-shock conditions were calculated from the initial conditions and the shock wave velocity on the basis of one-dimensional conservation equations and the ideal gas law (see e.g.ref. 27). The shock velocity was measured with four piezo-electric pressure transducers mounted at the low-pressure section. Error margins for temperature and pressure were estimated to be ±10 K and ±0.1 bar, respectively.

H-atom concentrations were monitored by ARAS at the Lyman-α-line (wavelength: 121.6 nm). Vacuum ultraviolet (VUV) radiation was generated in a microwave-discharge lamp operated with mixtures of 1% H₂ in He. To reduce the wavelength range transmitted to the detector, an oxygen filter operated with 30 to 40 mbar O₂ was used. The transmitted radiation was detected with a solar-blind photomultiplier. The data were sampled with a digital storage oscilloscope and further processed on a personal computer. Calibration experiments to derive a relation between measured absorbances and absolute H-atom concentrations in the shock tube were daily performed with N₂O/H₂ mixtures that served as a well characterized H-atom source.^28,29

Mixtures were prepared manometrically in stainless steel mixing vessels. The purities of the chemicals used were as follows: DMM (Sigma-Aldrich) ≥99.0%, N₂O (Air Liquide) ≥99.5%, H₂ for calibration (Messer Griesheim) ≥99.999%, H₂ as driver gas (Air Liquide) ≥99.9%, O₂ (Air Liquide) ≥99.998%, Ar as bath gas (Air Liquide) ≥99.999%, He (Air Liquide) ≥99.999%. DMM was degassed in several freeze–pump–thaw cycles prior to use.

2.2. Quantum chemical calculations

For all species considered, geometries and harmonic vibrational frequencies were calculated with density functional theory (DFT) at the B2PLYP-D3/def2-TZVPP level of theory^30–33 by using the Gaussian 09 program package.³⁴ Accurate electronic energies were calculated with explicitly correlated coupled cluster theory at the CCSD(F12*)(T*)/cc-pVQZ-F12 level of theory^35–37 by using the TURBOMOLE 7.3 package of programs.³⁸ Neither vibrational frequencies nor zero-point vibrational energies were scaled because no scaling factors are available for the dispersion-corrected double-hybrid functional and, moreover, scaling factors tend to cancel in rate coefficients calculated with statistical rate theory.

The uncertainties of reaction energies from explicitly correlated coupled cluster calculations were recently demonstrated to be on the order of ±2 kJ mol⁻¹ (mean absolute deviation of 0.833 kJ mol⁻¹ for reaction energies calculated at the CCSD(T)-F12a/AVTZ level of theory³⁹ multiplied by a conversion factor of 2.5 to obtain the 95% confidence limit⁴⁰).

2.3 Kinetic modeling

All kinetic modeling calculations were performed with the program package OpenSMOKE++.⁴¹ Concentration–time profiles were predicted on the basis of numerical solutions of the coupled differential equation system describing a given reaction mechanism (elementary reactions, rate parameters, and thermodynamic quantities). We chose the model of a homogeneous batch reactor under adiabatic conditions in the constant-volume regime to describe our experiments. Heat loss and other non-idealities are negligible due to the very low reactant concentrations and the short reaction times on the order of 2 ms.

3. Results and discussion

3.1. Experimental determination of rate coefficients

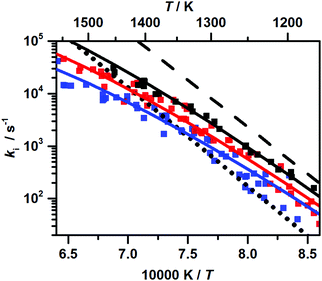
Representative H atom concentration–time profiles obtained from our experiments are depicted in Fig. 1. We deduced rate coefficients k₁₊₂(T) directly from the initial slope of the recorded profiles, assuming that at early reaction times the rate of H-atom production from DMM is mainly determined by the rate of the initial C–O bond-fission reactions (see the discussions on sensitivity in ref. 22). The first-order rate coefficient k₁₊₂ is related to the initial slope of the recorded concentration–time profiles via k₁₊₂ = [DMM]₀⁻¹(d[H]/dt)_t→0, with [DMM]₀ denoting the initial concentration of DMM. As discussed earlier, it cannot be distinguished between the two reactions (R1) and (R2) alone on the basis of the results from the H-ARAS experiments, and hence the obtained rate coefficient corresponds to the sum k₁₊₂ = k₁ + k₂. The maximum error of k₁₊₂ was estimated to be ±30% mainly due to uncertainties in the calibration of H-atom concentrations.

Fig. 1 Measured H atom concentration–time profiles (black noisy lines) and results of simulations with the mechanism of this study (cf. Section 3.3) (red solid lines). Experimental conditions: T = 1230 K, p = 0.4 bar, [DMM]₀ = 9.19 × 10⁻¹¹ mol cm⁻³, [Ar]₀ = 3.77 × 10⁻⁶ mol cm⁻³ (left panel), T = 1330 K, p = 4.6 bar, [DMM]₀ = 8.16 × 10⁻¹¹ mol cm⁻³, [Ar]₀ = 4.16 × 10⁻⁵ mol cm⁻³ (right panel).

The rate coefficients obtained are shown in Fig. 2. For a detailed list of the experimental conditions along with the numerical values of the rate coefficients at p ∼ 0.4 bar and p ∼ 4.7 bar see Table S1 of the ESI.† Note that the analogous data for p ∼ 1.1 bar were already given in Table S1 of the Supplemental material of ref. 22. The rate coefficients exhibit a pronounced temperature and pressure dependence. From linear least-squares fits with equal weight for each data point, we obtained the following Arrhenius expressions (for p ∼ 1.1 bar taken from ref. 22):

k₁₊₂(T, p ∼ 0.4 bar) = (2.2 ± 0.7) × 10¹³ exp(−31 500 K/T) s⁻¹ (1)

k₁₊₂(T, p ∼ 1.1 bar) = (6.2 ± 1.9) × 10¹³ exp(−31 830 K/T) s⁻¹ (2)

k₁₊₂(T, p ∼ 4.7 bar) = (1.2 ± 0.4) × 10¹⁴ exp(−31 940 K/T) s⁻¹ (3)

Fig. 2 Experimentally determined overall rate coefficients k₁₊₂ = k₁ + k₂ of the unimolecular C–O bond fission reactions of DMM at p ∼ 0.4 bar (blue), p ∼ 1.1 bar (red, data from ref. 22), and p ∼ 4.7 bar (black); error bars ± 30%; solid lines: linear least-squares fits, eqn (1)–(3).

3.2. Quantum chemical calculations

To further analyze our experimental results, we characterized the reaction paths for the two homolytic C–O bond fission reactions of DMM, reactions (R1) and (R2), and the consecutive reactions (R6) and (R8), following the approach described in Section 2.2. Numerical values for the optimized structures, rotational constants, and vibrational frequencies are presented in Tables S2–S4 of the ESI.† Though extensively searched for at the B2PLYP-D3/def2-TZVPP level of theory, no indications for competing molecular (i.e. nonradical) channels, including reactions (R3) and (R4), could be found. Note that energies of possible transition states with multireference character, which are not accounted for by DFT, are expected to be significantly higher than the thresholds of the homolytic bond dissociation steps. We also note that possible roaming pathways were not considered in this work (for a discussion on the relevance of roaming pathways in the decomposition of dimethyl ether, see ref. 42).

BDEs have a particularly large effect on the calculated rate coefficients of bond dissociation reactions. The BDEs obtained in this work for the two C–O bonds in DMM are compared to values from the literature in Table 1.

Table 1 Bond-dissociation energies (in kJ mol⁻¹) of the C–O bonds in DMM

	BDE(CH3–OCH2OCH3)	BDE(CH3O–CH2OCH3)	Ref.
a CCSD(F12*)(T*)/cc-pVQZ-F12//B2PLYP-D3/def2-TZVPP. b CCSD(T)/aug-cc-pV(D+T)Z//B2PLYP-D3/6-311g++(d,p). c G4. d Derived from tabulated heats of formation.
T = 0 K	343.7 ± 2^a	368.6 ± 2^a	This work
	344.5^b	361.2^b	24
	337.5^c	363.9^c	43
T = 298.15 K	350.0 ± 2^a	373.6 ± 2^a	This work
		365.7 ± 8.4^d	44

---

The BDE(CH₃–OCH₂OCH₃) calculated in this work is very close to the value from Jacobs et al.²⁴ who employed a similar approach based on coupled cluster theory but with smaller basis sets and without explicitly correlated terms. The G4 method used by Sun et al.⁴³ yields a lower value. The calculated BDE(CH₃O–CH₂OCH₃) from this work is about 5 kJ mol⁻¹ higher than the value from Sun et al.,⁴³ a finding that is in line with the difference in the BDEs(CH₃–OCH₂OCH₃). The value calculated by Jacobs et al.²⁴ for BDE(CH₃O–CH₂OCH₃) is even lower. The data compilation by Luo⁴⁴ recommends a BDE(CH₃O–CH₂OCH₃) of (365.7 ± 8.4) kJ mol⁻¹ at 298.15 K, which is lower than the value obtained in this work but with overlapping error margins.

Fig. 3 shows the potential energy diagrams of reactions (R1) and (R2) and the consecutive C–O bond fission reactions of the formed radicals, reactions (R6) and (R8). The energy thresholds of these consecutive reactions are low compared to the thresholds of reactions (R1) and (R2) (R5: 29.9 kJ mol⁻¹; R7: 54.8 kJ mol⁻¹). Accordingly, reactions (R1) and (R2) can indeed be assumed to represent the rate-limiting steps along the unimolecular decomposition pathways starting from DMM and, hence, in the formation of H atoms from DMM.

Fig. 3 Potential energy diagram for the unimolecular C–O bond fission reactions of DMM, reactions (R1) (black) and (R2) (blue), and the consecutive radical decomposition reactions (R6) (black) and (R8) (blue).

3.3. Statistical rate theory calculations and master equation analysis

To rationalize the observed pressure dependence of the rate coefficients, we performed statistical rate theory calculations on the basis of molecular data from our quantum chemical calculations. Rate coefficients were calculated by solving a thermal two-channel master equation with a detailed balanced stepladder model for collisional energy transfer.^45,46 For more details of our specific implementation see ref. 47–49 and the literature cited therein.

Energy-specific rate coefficients for the two barrierless decomposition channels (R1) and (R2) were calculated by using the simplified statistical adiabatic channel model (s-SACM)^50,51 with the SACM anisotropy ratio set to its standard value of α/β = 0.5.⁵² Energy- and angular momentum-resolved sums and densities of states were determined by direct counting procedures.^53,54 We assumed an angular momentum quantum number of J = 65 corresponding to the thermal average at T = 1350 K, a temperature close to the center of the temperature range covered in our experiments.

From the canonical version of the s-SACM, the following high-pressure limiting rate coefficients for reactions (R1) and (R2) were obtained:

k^∞₁(T) = 4.36 × 10¹⁷ exp (−341.8 kJ mol⁻¹/RT) s⁻¹ (4)

k^∞₂(T) = 2.20 × 10¹⁷ exp (−361.7 kJ mol⁻¹/RT) s⁻¹ (5)

Lennard-Jones parameters for DMM and Ar were taken from ref. 23 and 55, respectively. The step size, ΔE_SL, of the stepladder model, which corresponds to the average energy transferred per downward collision,⁴⁶ was treated as the only adjustable parameter. We obtained the best agreement of experimental and calculated rate coefficients for ΔE_SL = 230 cm⁻¹ (cf.Fig. 4). It should be noted, however, that the rate coefficients obtained from the experimental data exhibit a somewhat stronger temperature dependence for T < 1250 K than the corresponding calculated values. Nonetheless, we refrained from introducing a second fit parameter as e.g. the anisotropy ratio α/β from s-SACM because no reliable experimentally determined high-pressure limiting rate coefficients of reactions (R1) and (R2) for adjustment are currently available.

Fig. 4 Experimental (symbols) and calculated (solid lines) rate coefficients k₁₊₂ at p ∼ 4.7 bar (black), p ∼ 1.1 bar (red), and p ∼ 0.4 bar (blue); calculated high-pressure limiting rate coefficients: k₁ (dashed line) and k₂ (dotted line).

For a compact representation of the master equation results, we parameterized the calculated rate coefficient k₁(T, p), using the formalism described in Gilbert et al.⁵⁶ (also known as Troe parameterization, see ref. 57) The following expressions were obtained for the second-order low-pressure limiting rate coefficient, k^bim₁(T), and the center broadening factor, F_cent,1(T), valid for the temperature range 1100–1600 K:

k^bim₁(T) = 1.22 × 10⁹¹ × (T/K)^−21.31 exp(−46 538/T) cm³ mol⁻¹ s⁻¹ (6)

F_cent,1(T) = (1 − 0.7294) exp(−T/643 K) + 0.7294 exp(−T/16 K) + exp(−3538 K/T) (7)

One should note that an analogous approach does not work for k₂(T, p), the rate coefficient of the reaction with the higher threshold energy. Rate coefficients for such reactions exhibit a stronger fall-off behavior and a stronger than linear pressure dependence at low pressures. This was discussed in some detail in ref. 58, and a compact parameterization was recently proposed in ref. 59. The situation is illustrated in Fig. 5. Due to the more significant decrease of k₂(p) with decreasing pressure and the remaining curvature of the fall-off curve even for vanishing pressure, a conventional low-pressure limiting rate coefficient proportional to the pressure cannot be given for reaction (R2). Accordingly, a traditional Troe parameterization, analogous to that for k₁(T, p), is not possible for k₂(T, p). To still enable an implementation of both k₁(T, p) and k₂(T, p) into kinetic mechanisms for combustion modeling, we derived from our master equation calculations a ‘log p’ representation (see e.g.ref. 60) for k₁ and k₂. The resulting expressions are given in Table S5 of the ESI.†

Fig. 5 Calculated pressure dependence of the rate coefficients k₁ (black squares) and k₂ (grey squares) at T = 1400 K from the master-equation analysis; red line: Troe parameterization of k₁ (T = 1400 K, p).

To describe the relative importance of the two C–O bond fission channels (R1) and (R2) at different temperatures, we calculated relative branching fractions ϕ_i(T) = k_i(T)/[k₁(T) + k₂(T)] at p = 1 bar from the results of our master equation analysis. As can be expected from the lower BDE (cf.Table 1), reaction (R1) is the dominant reaction channel under the conditions of the present work (1100 K < T < 1600 K). In Fig. 6, the branching fractions from this work are compared to values obtained from rate coefficients given in the literature. Arrhenius representations from the different references are compared in Fig. S1 of the ESI.†

Fig. 6 Relative branching fractions ϕ_i = k_i/(k₁ + k₂) at p = 1 bar; black: ϕ₁, blue: ϕ₂; solid lines: from master-equation analysis of this work; dashed lines: from Vermeire et al.,¹⁵ dash-dotted lines: from Marrodán et al.,⁹ dotted lines: from Sun et al.¹⁸ with ϕ_i = k_i/(k₁ + k₂ + k₃), black: ϕ₁, blue: ϕ₂, red: ϕ₃.

According to the expressions for the rate coefficients used by Marrodán et al.,⁹reaction (R1) is the dominating C–O bond fission channel for T > 1200 K. For 1100 K < T < 1200 K, reactions (R1) and (R2) are of almost equal importance (ϕ₁ ≈ ϕ₂ = 0.5 ± 0.04), whereas for T < 1100 K reaction (R2) prevails. We note that in ref. 9, the rate coefficients k₁ and k₂ were adopted from the work of Dias et al.⁸ who, in turn, used values estimated by Daly et al.⁷ on the basis of analogous reactions for DME and DEE.

In contrast to the branching fractions from the present work and those derived in ref. 9, Vermeire et al.¹⁵ assumed reaction (R2) as being the dominating C–O bond fission reaction. This result was obviously obtained on the basis of the Genesys automatic mechanism generator and contradicts the expectations resulting from the BDEs (cf.Table 1), which would clearly favor reaction (R1). It is interesting to note here that Peukert et al.²³ were able to describe the temperature dependence of the total rate coefficient with a Gorin model, assuming the branching ratio from Vermeire et al.¹⁵ to be correct. While this proves the flexibility of the Gorin model with respect to its adjustable parameters, it also demonstrates that great care should be taken if mechanistic conclusions are to be drawn and/or extrapolations to other temperature and pressure ranges are to be made.

Sun et al.¹⁸ consider the molecular DMM decomposition channel (R3) as non-negligible besides reactions (R1) and (R2). Accordingly, the relative branching fractions from ref. 18 depicted in Fig. 6 correspond to ϕ_i(T) = k_i(T)/[k₁(T) + k₂(T) + k₃(T)]. From the quantum chemical calculations of the present work, however, no indications for relevance of reaction (R3) could be found. Among reactions (R1) and (R2), Sun et al.¹⁸ also found reactions (R1) to be the dominating step with increasing importance for increasing temperature.

3.4. Kinetic modeling

To extend the applicability of the DMM pyrolysis mechanism proposed in ref. 22 to a wider pressure range, we implemented the ‘log p’-parametrized rate coefficients for reactions (R1) and (R2) (cf. ESI,† Table S5) into the mechanism given in ref. 22. It turned out, however, that this has a negligible influence on the simulated H atom concentration–time profiles at p ∼ 1 bar. This finding is in line with the low sensitivity of the simulated H-atom concentrations towards variations of the branching ratio as was already pointed out in our earlier work.²² For p ∼ 0.4 and p ∼ 4.7 bar, we observed a generally good agreement between measured and simulated concentration–time profiles, in particular for short reaction times, where the C–O bond fission reactions are rate-determining. This behavior is illustrated in Fig. 1. Toward longer reactions times, the deviations between simulations and measurements increase to up to 50%. At these reaction times, the consumption of DMM and the production and consumption of H atoms is dominated by secondary reactions of DMM decomposition products. Accordingly, the observed deviations probably result from uncertainties in the implemented base mechanism. A further analysis of the base mechanism, however, is beyond the scope of the present work.

4. Summary

The pyrolysis of DMM was studied behind reflected shock waves at temperatures between 1100 and 1600 K at two different nominal pressures of p ∼ 0.4 and p ∼ 4.7 bar by time-resolved monitoring H-atom concentrations with ARAS. Rate coefficients for the C–O bond fission reactions were inferred from the recorded [H](t)-profiles and exhibit a pronounced temperature and pressure dependence. We further characterized the reaction paths for these reactions by quantum chemical calculations at the CCSD(F12*)(T*)/cc-pVQZ-F12//B2PLYP-D3/def2-TZVPP level of theory. On the basis of these calculations, we solved a thermal two-channel master equation, using specific rate coefficients obtained from the s-SACM. The results clearly indicate the dominance of reaction (R1) in the thermal decomposition of DMM. Due to the higher threshold energy and the pronounced falloff effect, reaction (R2) is virtually negligible under the conditions of the present work. Also no indications for competing molecular decomposition channels were found. The pressure dependence of the rate coefficient for the unimolecular C–O bond fission reaction (R1) was parameterized using the Troe formalism. Additionally, a ‘log p’ representation of rate coefficients for both channel (R1) and channel (R2) was derived and implemented into an earlier DMM oxidation mechanism. Results of simulations with this modified mechanism are in good agreement with the experimentally determined H atom concentration–time profiles over the entire pressure range covered.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 237267381 – TRR 150. The authors also acknowledge generous allocation of computer time by the state of Baden-Württemberg through bwHPC and the DFG through grant no INST 40/467-1 FUGG (JUSTUS cluster); they furthermore thank Mr Patrick Bügel for help with the quantum chemical calculations. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.

References

1. H. J. Curran, E. M. Fisher, P.-A. Glaude, N. M. Marinov, W. Pitz, C. Westbrook, D. Layton, P. F. Flynn, R. P. Durrett, A. Zur Loye, O. C. Akinyemi and F. L. Dryer, SAE Tech. Pap. Ser., 2001-01-0653.
2. H. Liu, Z. Wang, J. Wang and X. He, Energy, 2016, 97, 105–112.
3. M. Härtl, P. Seidenspinner, E. Jacob and G. Wachtmeister, Fuel, 2015, 153, 328–335.
4. X. Zhang, A. O. Oyedun, A. Kumar, D. Oestreich, U. Arnold and J. Sauer, Biomass Bioenergy, 2016, 90, 7–14.
5. R. Sun, I. Delidovich and R. Palkovits, ACS Catal., 2019, 9, 1298–1318.
6. Z. Wang, H. Liu, X. Ma, J. Wang, S. Shuai and R. D. Reitz, Fuel, 2016, 183, 206–213.
7. C. A. Daly, J. M. Simmie, P. Dagaut and M. Cathonnet, Combust. Flame, 2001, 125, 1106–1117.
8. V. Dias, X. Lories and J. Vandooren, Combust. Sci. Technol., 2010, 182, 350–364.
9. L. Marrodán, E. Royo, Á. Millera, R. Bilbao and M. U. Alzueta, Energy Fuels, 2015, 29, 3507–3517.
10. L. Marrodán, F. Monge, Á. Millera, R. Bilbao and M. U. Alzueta, Combust. Sci. Technol., 2016, 188, 719–729.
11. K. Alexandrino, Á. Millera, R. Bilbao and M. U. Alzueta, Fuel Process. Technol., 2018, 179, 369–377.
12. P. Glarborg, M. U. Alzueta, K. Dam-Johansen and J. A. Miller, Combust. Flame, 1998, 115, 1–27.
13. P. Glarborg, M. U. Alzueta, K. Kjærgaard and K. Dam-Johansen, Combust. Flame, 2003, 132, 629–638.
14. M. S. Skjøth-Rasmussen, P. Glarborg, M. Østberg, J. T. Johannessen, H. Livbjerg, A. D. Jensen and T. S. Christensen, Combust. Flame, 2004, 136, 91–128.
15. F. H. Vermeire, H.-H. Carstensen, O. Herbinet, F. Battin-Leclerc, G. B. Marin and K. M. Van Geem, Combust. Flame, 2018, 190, 270–283.
16. N. M. Vandewiele, K. M. Van Geem, M.-F. Reyniers and G. B. Marin, Chem. Eng. J., 2012, 207, 526–538.
17. W. K. Metcalfe, S. M. Burke, S. S. Ahmed and H. J. Curran, Int. J. Chem. Kinet., 2013, 45, 638–675.
18. W. Sun, T. Tao, M. Lailliau, N. Hansen, B. Yang and P. Dagaut, Combust. Flame, 2018, 193, 491–501.
19. W. A. Kopp, L. C. Kröger, M. Döntgen, S. Jacobs, U. Burke, H. J. Curran, K. A. Heufer and K. Leonhard, Combust. Flame, 2018, 189, 433–442.
20. P. A. Glaude, W. J. Pitz and M. J. Thomson, Proc. Combust. Inst., 2005, 30, 1111–1118.
21. L. Marrodán, Á. Millera, R. Bilbao and M. U. Alzueta, Energy Fuels, 2014, 28, 6107–6115.
22. L. Golka, I. Weber and M. Olzmann, Proc. Combust. Inst., 2019, 37, 179–187.
23. S. Peukert, P. Sela, D. Nativel, J. Herzler, M. Fikri and C. Schulz, J. Phys. Chem. A, 2018, 122, 7559–7571.
24. S. Jacobs, M. Döntgen, A. B. S. Alquaity, W. A. Kopp, L. C. Kröger, U. Burke, H. Pitsch, K. Leonhard, H. J. Curran and K. A. Heufer, Combust. Flame, 2019, 205, 522–533.
25. T. Bentz, B. R. Giri, H. Hippler, M. Olzmann, F. Striebel and M. Szöri, J. Phys. Chem. A, 2007, 111, 3812–3818.
26. I. Weber and M. Olzmann, Int. J. Chem. Kinet., 2019, 51, 367–376.
27. W. C. Gardiner, Jr., B. F. Walker and C. B. Wakefield, Shock Waves in Chemistry, ed. A. Lifshitz, Marcel Dekker, New York, 1981, pp. 319–374.
28. D. Appel and J. P. Appleton, Proc. Combust. Inst., 1975, 15, 701–715.
29. J. V. Michael and A. Lifshitz, in Handbook of Shock Waves, ed. G. Ben-Dor, O. Igra and T. Elperin, Academic Press, San Diego, 2001, pp. 77–105.
30. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
31. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
32. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
33. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
34. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, Revision D.01, Gaussian Inc., Wallingford CT, 2013.
35. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
36. R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comput. Chem., 2011, 32, 2492–2513.
37. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
38. TURBOMOLE V7.3 2018, a development of University Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com, accessed 04 January 2020.
39. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
40. B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097–1101.
41. A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, Comput. Phys. Commun., 2015, 192, 237–264.
42. R. Sivaramakrishnan, J. V. Michael, A. F. Wagner, R. Dawes, A. W. Jasper, L. B. Harding, Y. Georgievskii and S. J. Klippenstein, Combust. Flame, 2011, 158, 618–632.
43. W. Sun, G. Wang, S. Li, R. Zhang, B. Yang, J. Yang, Y. Li, C. K. Westbrook and C. K. Law, Proc. Combust. Inst., 2017, 36, 1269–1278.
44. Y.-R. Luo, Handbook of Bond Dissociation Energies in Organic Compounds, CRC Press, Boca Raton, 2002.
45. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell, Oxford, 1990.
46. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, 2nd edn, 1996.
47. M. Olzmann, in Cleaner Combustion, ed. F. Battin-Leclerc, J. M. Simmie and E. Blurock, Springer-Verlag, London, 2013, pp. 549–576.
48. M. Pfeifle and M. Olzmann, Int. J. Chem. Kinet., 2014, 46, 231–244.
49. A. Busch, N. González-García, G. Lendvay and M. Olzmann, J. Phys. Chem. A, 2015, 119, 7838–7846.
50. M. Quack and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1974, 78, 240–252.
51. J. Troe, J. Chem. Phys., 1983, 79, 6017–6029.
52. C. J. Cobos and J. Troe, J. Chem. Phys., 1985, 83, 1010–1015.
53. M. Olzmann and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1992, 96, 1327–1332.
54. M. Olzmann and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1994, 98, 1563–1574.
55. R. C. Reid, J. M. Prausnitz and B. E. Poling, The Properties of Gases and Liquids, Mc Graw Hill, Boston, 4th edn, 1987.
56. R. G. Gilbert, K. Luther and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1983, 87, 169–177.
57. J. Troe, J. Phys. Chem., 1979, 83, 114–126.
58. G. Friedrichs, M. Colberg, J. Dammeier, T. Bentz and M. Olzmann, Phys. Chem. Chem. Phys., 2008, 10, 6520–6533.
59. J. Troe, J. Phys. Chem. A, 2019, 123, 1007–1014.
60. T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer, Berlin, 2014.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00136h

‡ Present address: Laboratoire PC2A, Université de Lille 1 - Bàtiment C11, 59655 Villeneuve dÁscq, France.

---