Vibrations of the guanine–cytosine pair in chloroform: an anharmonic computational study

Abstract

We compute at the anharmonic level the vibrational spectra of the Watson–Crick dimer formed by guanosine (G) and cytidine (C) in chloroform, together with those of G, C and the most populated GG dimer. The spectra for deuterated and partially deuterated GC are also computed. We use DFT calculations, with B3LYP and CAM-B3LYP as reference functionals. Solvent effects from chloroform are included via the Polarizable Continuum Model (PCM), and by performing tests on models including up two chloroform molecules. Both B3LYP and CAM-B3LYP calculations reproduce the shape of the experimental spectra well in the fingerprint region (1500–1700 cm⁻¹) and in the N–H stretching region (2800–3600 cm⁻¹), with B3LYP providing better quantitative agreement with experiments. According to our calculations, the N–H amido streching mode of G falls at ∼2900 cm⁻¹, while the N–H amino of G and C falls at ∼3100 cm⁻¹ when hydrogen-bonded, or ∼3500 cm⁻¹ when free. Overtone and combination bands strongly contribute to the absorption band at ∼3300 cm⁻¹. Inclusion of bulk solvent effects significantly increases the accuracy of the computed spectra, while solute–solvent interactions have a smaller, though still noticeable, effect. Some key aspects of the anharmonic treatment of strongly vibrationally coupled supermolecular systems and the related methodological issues are also discussed.

---

1 Introduction

Vibrational spectroscopy of nucleic acids has attracted significant attention, especially after the breakthrough developments in 2 dimensional-infrared (2D-IR) spectroscopy,^1–5 as the potential to monitor the structural dynamics of DNA and RNA, their folding and denaturation and their interaction with other systems (drugs, protein, metal surfaces etc.) has been recognized.^3,6–11

More recently, thanks to the advances in time resolved (TR) pump probe UV-IR spectroscopy, the analysis of differential IR spectra has become a key tool to investigate the photoactivated dynamics of DNA, providing fundamental information, inter alia, on the photophysics of nucleobases,^12–17 the photodimerization of dipyrimidine steps,¹⁸ the formation of charge transfer excited states,^19–24 and the occurrence of proton coupled electron transfer (PCET) processes.^25–29 In many of these studies, the assignment of the spectra has been made with the help of quantum mechanical calculations, in most of the cases limited to harmonic treatments.^{14,16,24,28,29} However, an unambiguous interpretation of the TR spectra requires a full assessment of the ground state properties, including anharmonicities, which are fundamental to assigning the ultrafast (sub-ps) part and could strongly affect the differential spectra, since it cannot be taken for granted that anharmonicity affects ground- and excited-state vibrational modes in a similar way. While the inclusion of anharmonic effects in excited state spectra is still in its infancy,³⁰ several reliable procedures to include anharmonic effects in the calculation of vibrational spectra have been developed and applied to many molecular systems (too many to be exhaustively reviewed here, see for example ref. 31–37 and references therein). However, most of the studies on DNA focus on isolated bases^38–47 or molecular crystals,^41,48,49 whereas those focusing on hydrogen bonded pairs are much more limited^38,50–54 and, to the best of our knowledge, in the literature there is no detailed comparison with the experimental spectra, which would be very important to assess the reliability of the different methods. In this respect, the large complexity of the IR spectra of oligonucleotides, which are affected by several factors, including conformational equilibria, makes the study of smaller model systems particularly attractive, since they are more suitable for the assessment of computational procedures. Previously, Temps et al. have shown that modified guanosine and deoxycytidine (as well as adenosine and thymidine⁵⁵), in which bulky tert-butyldimethylsilyl (TBDMS) groups were attached to dangling OH groups, hereafter simply called GC, can form stable hydrogen bonded pairs, with the Watson and Crick pattern (see Fig. 1), in chloroform solution.^9,56,57

Fig. 1 (top) Schematic description and atom labelling of the cG≡cC computational model. In the mG≡mC model, the five member cycles are substituted by a simple methyl group. Experimental IR spectra have been obtained of tert-butyldimethylsilyl (TBDMS) derivatives of cG and cC, where TBMDS is attached to the OH groups in the C2, C3 and C5 position of the sugar. (bottom) Schematic description of the conformer used to model the GG dimer.

GC in chloroform is a fundamental model system for understanding PCET in DNA,^58–61 since it allows the decoupling of stacking from hydrogen bond (HB) effects and does not include the backbone, though the sugar is present. The moderately polar environment obviously cannot capture the complexity of the strongly anisotropic character of a DNA duplex, however it can still be a reasonably reliable model for the ‘effective’ dielectric constant experienced by bases within a duplex, given that the dielectric constant of chloroform, ε = 4.9, and that in a DNA double helix ε ∼ 3–5.⁶²

The 1D-IR and 2D-IR spectra of GC in chloroform have been investigated in detail in a series of seminal papers, which provides a fundamental benchmark for anharmonic calculations in the condensed phase.^{9,15,17,57,63,64} Therefore, in the present work, we report a thorough computational analysis of the IR spectra of this system in chloroform, both at the harmonic and the anharmonic level. In order to analyse the effect of the formation of the WC pair on the vibrational modes, we shall compare the IR spectra of GC with those of the monomers and of the most populated GG isomer in chloroform, as G is prone to dimerisation.¹⁷ Particular attention has been devoted to disentangling the role of different effects, such as substituent or solvent, on the spectra and to examine their dependence on the adopted computational approach (density functional, basis set, etc.). In the Discussion section, we shall critically compare our predictions with the existing assignment of the experimental spectra and discuss the strengths and limitations of our approach.

Besides its significance for the study of DNA and, in particular, for the forthcoming studies dealing with the excited state vibrational characterization in polynucleotides, our study provides general insights into the importance of anharmonic treatment of the vibrations in strongly hydrogen bonded supramolecular systems.

2 Computational details

As anticipated above, the experimental spectra have been obtained on (TBDMS) modified guanosine and deoxycytidine. In TBDMS, there is a silicon atom, with one tert-butyl and two methyl substituents. In order to decrease the computational cost and aid the interpretation of the IR spectra, we studied two different computational models. Using the first, more realistic model, we studied the system depicted in Fig. 1, where the O–Si(TB) groups of G and C nucleosides are substituted by a hydrogen atom. In the following, we label this system cG≡cC. This model, though lacking the bulky substituents of the sugar ring, should include the effect of the sugar ring on the bases’ vibrations. Most of our anharmonic analysis is performed on a simpler model (mG≡mC), where the five member-cycle substituent is replaced by a methyl group.

Since G in chloroform has a strong tendency to dimerize, we have also studied the most stable GG tautomer in chloroform, calculated to have a Boltzmann population of >90% compared to other tautomers at 298 K,¹⁷ with hydrogen bonds between each of the C6=O11 and N1–H1 groups (see Fig. 1).

Our analysis has been based on two widely used density functionals, B3LYP⁶⁵ and its long-range corrected analogous CAM-B3LYP.⁶⁶ The former has been thoroughly validated for the calculation of anharmonic vibrational spectra.^{32,39,51,67–69} On the other hand, it suffers from the traditional deficiencies of standard functionals in the treatment of charge transfer transitions⁷⁰ and, therefore, it is not suitable for the study of PCET and, more generally, of DNA excited states. CAM-B3LYP, on the other hand, has already been profitably used in the study of the photoactivated dynamics, including the study of PCET in GC base pairs.^71,72 Test calculations by including Grimme's D3 dispersion correction with Becke–Johnson dampling⁷³ and using the M05-2X and M06-2X functionals,⁷⁴ which have been developed with a different philosophy compared to B3LYP and CAM-B3LYP, have also been performed.

We have computed the IR spectra by using basis sets of different size, 6-311+G(d,p), 6-311G(d,p), 6-31+G(d,p), and 6-31G(d), complemented by N07D, which has been extensively used, together with the B3LYP functional, for the computation of IR spectra.^{32,39,51,68,69}

The effect of solvent has been modeled by using the polarizable continuum model (PCM).^75,76 We performed some test calculations on computational models including up to two explicit chloroform molecules, hydrogen bonded to the carbonyl groups of G and C, according to the results of our previous MD simulations.⁶¹

The second-order vibrational perturbation theory (VPT2)^{31,33,77–79} has been used for our anharmonic vibrational analysis (frequency and intensities), obtaining semidiagonal quartic force fields by numerical differentiation of the analytical second derivatives along each active normal coordinate, at the geometries optimized with tight convergence criteria. Fermi resonances have been treated in the framework of the generalized VPT2 scheme (GVPT2).^31,33,79 For mC (in chloroform and in the gas phase), all the vibrational modes have been included in the anharmonic calculations. For mG≡mC, most of our anharmonic analysis has been performed by including all the vibrational modes with frequency ≥1000 cm⁻¹, and test calculations including all the vibrational modes have also been performed. The standard 0.01 Å step has been used in the numerical differentiation procedure, but test calculations using different values have also been made, showing that our conclusions are robust with respect to this parameter. This procedure, also recently extended to excited electronic states,³⁰ has been profitably used to compute the anharmonic spectra in several systems (see ref. 31–33, 48, 51 and 80 and references therein).

When not otherwise specified, the calculated spectra have been plotted by convoluting each peak with a Lorentzian function with a half width at half maximum of 4 cm⁻¹. We have also checked that convolution with a Gaussian function does not significantly affect the spectra shown. For a given level of theory in a particular spectral range, the spectra are shown normalised to the most intense peak unless otherwise stated. When labels appear to identify peaks, they indicate the predominant normal mode contribution(s) to the closest peak to them, unless otherwise indicated by arrows. When multiple local vibrations contribute to a normal mode, they will be indicated with a ‘+’ and listed in order of importance. The following labelling convention is used for the local vibrations: ωⁿ_m(X–Y), where ω is the type of vibration, with ν = stretch and δ = scissor; m is the nucleobase where the vibration is localised on (C or G, irrespective of the molecular model); n contains additional information about the vibration, with s = symmetric, as = antisymmetric, and ot = overtone; and X–Y are the atoms involved in the vibration, with atomic numbering according to Fig. 1. Combination bands are shown with the notation ([mode 1],[mode 2]). Any other notation will be indicated in figure captions.

All the calculations have been performed by the Gaussian16 program.⁸¹

3 Results

3.1 Harmonic spectrum of GC in chloroform

3.1.1 The fingerprint region. In Fig. 2, we report the experimental spectrum of GC in chloroform in the fingerprint region (i.e. at 1550–1800 cm⁻¹), together with those of solutions containing only the two components.⁶³ Our computed harmonic infrared spectrum of cG≡cC, and that of the individual components cC and cG are reported in Fig. 3.

Fig. 2 Experimental vibrational spectrum of GC in CHCl₃. G (blue line, 3.2 mM), C (red line, 2.3 mM), and G=C (black line, 50 mM) in the fingerprint region. Reproduced from ref. 63. Labels correspond to the latest experimental assignment of the vibration(s) contributing to each peak, colour coded to match the experimental spectrum they describe.

Fig. 3 Linear harmonic infrared spectra computed in chloroform for cG≡cC, cG and cC at the 6-311G(d,p) level in the fingerprint region with (a) CAM-B3LYP and (b) B3LYP functionals. Black curve: cG≡cC; red-curve: cC; blue curve: cG; blue dashed curve: cG=cG. Coloured labels indicate the predominant local mode vibration(s) contributing to each peak of the cG≡cC, cG and cC spectra (full assignment is shown in the ESI† in Table S1, cG=cG spectra are also included in the ESI†). Spectra normalised to cG≡cC rather than cG=cG.

Our calculated spectral line-shape for cG≡cC, both at the B3LYP and CAM-B3LYP levels, is fairly close to the experimental spectrum of GC except for the expected blue-shift of the spectra computed in harmonic approximation. The assignment of the different peaks is mostly consistent with a previous proposal,⁶³ though our calculations indicate that the formation of a WC pair leads to significant couplings between the vibrational modes of G and C. For example, the peak at ∼1765 cm⁻¹ in the CAM-B3LYP calculation has a predominant contribution from the C=O stretching mode on cG (labelled ν_G(C6=O11) and compared to 1689 cm⁻¹ experimentally⁶³), however the NH bend (δ_G(N1–H1)) and NH₂ bends on both G (δ_G(N10–H2)) and C (δ_C(N8′–H2)) are also significantly involved. This coupling of carbonyl stretching modes to NH bending motions has been observed previously,⁶ and the full assignment including all local vibrations is given in the ESI,† Table S1.

Our calculations capture the effect of WC formation on the spectra of G and C, apart from the apparent exception of the ν_G(C6=O11) peak of cG at ∼1800 cm⁻¹, which is ∼50 cm⁻¹ blue-shifted from the predominant ν_G(C6=O11) peak in cG≡cC. Experiments show, instead, that the ν_G(C6=O11) peaks are virtually co-incident on G and GC. This may be explained by the fact that for G in chloroform at a concentration of 3.2 mM, the degree of association to form a GG dimer has been estimated to be larger than 0.6.¹⁷ As a consequence, in the experimental spectrum of ‘free’ G, the carbonyl group is involved in many intermolecular hydrogen bond interactions. In the computed IR spectra of the most stable cG=cG tautomer in chloroform (dashed curve in Fig. 3), the ν_G(C6=O11) peak is indeed shifted to 1757 cm⁻¹, i.e. very close to the value found in cG≡cC. A detailed assignment of cG=cG is shown in the ESI,† Fig. S1 and Table S1.

C does not exhibit as large a propensity to dimerise as G,⁵⁷ so we can regard the experimental spectrum of C as being composed entirely of the monomer, and we can compare it directly with our calculated spectrum of cC. The main discrepancy between the two is that experimentally there is a broad, structured peak at ∼1650 cm⁻¹ assigned to two transitions, whereas our calculated spectrum has two separate peaks at 1705 and 1750 cm⁻¹. In addition to the lack of anharmonic effects, this may simply be a consequence of insufficient broadening of the calculated peaks, so that they appear separately.

From the methodological point of view, the CAM-B3LYP and B3LYP spectra are very similar. The latter functional predicts slightly red-shifted vibrational frequencies, thus being in better agreement with experiments, confirming the general trends previously highlighted.⁸² The spectra reported in the ESI,† Fig. S2, show that, even in a non polar solvent such as CHCl₃, the inclusion of bulk solvent effects (by PCM) affects the computed spectra and improves the agreement with the experiments. The spectra computed in the gas phase are blue-shifted by 40–50 cm⁻¹ with respect to those in CHCl₃ and their relative intensity is in worse agreement with the experimental one. Substitution of the bulky sugar rings with the smaller methyl groups does not significantly affect the position of the peaks in the fingerprint region. However, the computed intensities are in worse agreement with the experimental one, confirming the importance of the use of molecular models as close as possible to the experimental one. On the other hand, using the mG≡mC computational model should not dramatically affect the qualitative reliability of our prediction. Analogously, the spectra computed with the 6-31G(d) basis set, though being further blue-shifted with respect to the experiments, are fairly similar to those obtained with the larger basis set.

3.1.2 The NH stretching region. We now focus on the high energy part of the vibrational spectrum, i.e. that around 3000 cm⁻¹. In Fig. 4, we report the experimental spectra for GC, G and C in that region obtained in CDCl₃, but without allowing the exchange with the hydrogen atoms of the bases.⁹

Fig. 4 Linear infrared spectra of GC base pairs and C and G monomers dissolved in CDCl₃. Reproduced from ref. 9. Labels correspond to the latest experimental assignment of the vibration(s) contributing to each peak, colour coded to match the experimental spectrum they describe. Fr indicates a Fermi resonance. Intense absorptions below 3000 cm⁻¹ from TBDMS groups, and spectra are normalised to the most intense non TBDMS group peak on GC.

According to our calculated spectra shown in Fig. 5, for cG≡cC, the peaks at 3160 cm⁻¹ in CAM-B3LYP and 3147 cm⁻¹ in B3LYP are assigned to the ν_G(N1–H1) stretch, two close lying features between 3250–3400 cm⁻¹ are assigned to the bonded amino groups stretches ν_C(N8′–H8′) and ν_G(N10–H10) while the band around 3700 cm⁻¹ is assigned to the free NH bond stretches ν_G(N10–H10_f) and ν_C(N8′–H8′_f). In addition to the expected general blue-shift, the most significant discrepancy with respect to the experiments concerns the position of the bonded amino NH stretch ν_C(N8′–H8′), which is closer to the ν_G(N10–H10) stretch than to the ν_G(N1–H1) one. The authors of ref. 63 assign the 3303 cm⁻¹ band to the hydrogen-bonded stretch of ν_G(N10–H10) and the 3145 cm⁻¹ band to a superposition of the two N–H stretches ν_G(N1–H1) and ν_C(N8′–H8′). The lack in the computed spectra of a very large absorption band below 3000 cm⁻¹ is simply due to the absence in our model of the many CH stretching modes of the TBDMS-ribose groups.⁶²

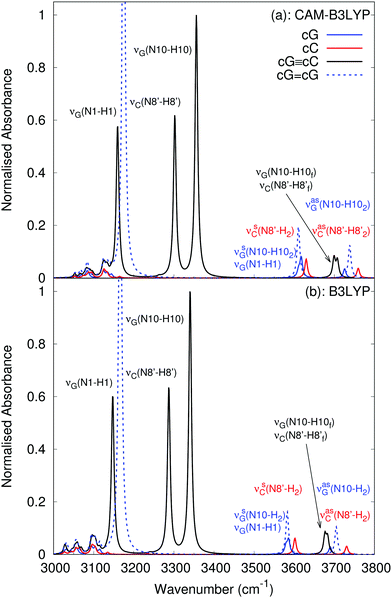Fig. 5 Linear harmonic infrared spectra computed in chloroform for cG≡cC, cG and cC at the 6-311G(d,p) level in the NH stretching region with (a) CAM-B3LYP and (b) B3LYP functionals. Black curve: cG≡cC; red-curve: cC; blue curve: cG; blue dashed curve cG=cG. Coloured labels indicate the predominant local mode vibration(s) contributing to each peak of the cG≡cC, cG and cC spectra (full assignment is shown in the ESI† in Table S1, cG=cG spectra are also assigned in the ESI†). Spectra normalised to cG≡cC rather than cG=cG.

With regards to free C, our calculations reproduce the energy difference between the symmetric and antisymmetric ν_C(N8′–H₂) stretching modes well, though with the expected blue-shift.

Analogously to the fingerprint region, the B3LYP and CAM-B3LYP spectra are very similar, except for an almost uniform red-shift of the former, by 30–40 cm⁻¹.

The inclusion of bulk solvent effects at PCM level also significantly modulates this spectral region. Fig. S3 in the ESI,† shows that the spectrum computed in the gas phase is quite different with respect to that obtained in chloroform. Firstly, the gas phase spectrum is blue-shifted with respect to that in PCM(chloroform). Secondly, confirming the previous calculations,³⁸ in the gas phase, the HB formed by G(N10–H10) is significantly less stiff than that of C(N8′–H8′), as suggested by the longer HB distance and larger (by ∼200 cm⁻¹) stretching frequency. As a consequence, the frequencies of the C(N8′–H8′) and G(N1–H1) stretches are closer to one another in the gas phase.³⁸

The substitution of the five-member cycles with the methyl groups does not noticeably affect the computed spectra in this region, whereas the 6-31G(d) spectra are simply red-shifted, but the predicted spectral pattern does not change with respect to the results obtained with larger basis sets.

3.2 Anharmonic IR spectra

Our analysis confirms that the computed harmonic spectra can provide useful insights into the assignment of the experimental spectra. On the other hand, without using any scaling factor, the quantitative discrepancy with the experimental frequencies is fairly large. Furthermore, we have seen that in some cases, the disagreement with the experimental picture is also qualitative, indicating that simply applying a scaling factor may not remedy the issue properly, prompting us to carry out an anharmonic study of the IR spectrum of mG≡mC. To begin with, however, we first compute the spectra of monomeric mC, followed by those of monomeric mG and the mG=mG dimer in its most populated tautomer.¹⁷ The monomeric spectra permit us to evaluate the effect of hydrogen bonding on the mG≡mC spectrum, and to compare the harmonic spectra, whilst the mG=mG spectrum allows the comparison with another hydrogen bonded system, as well as its effect on modulating the experimental G spectrum. Following the mG≡mC spectrum, we also compute its deuterated form, and experimental data on deuterated GC is available for comparison.⁶³

We shall focus on the N–H stretching region, for a number of reasons: firstly, the N–H stretching region has been investigated more thoroughly by 2D-IR experiments;^9,17,63 secondly, the majority of the qualitative disagreement between the harmonic spectra and experiment concerned this region; and thirdly, this region is the most relevant to the PCET process.

3.2.1 Anharmonic IR spectrum of C. Initially, we compute the spectrum of C in the gas-phase, exploiting the availability of high resolution IR spectra in gas phase matrices for 1-methyl-cytosine.^83,84 For this compound, the most stable tautomer in the gas phase is the keto-amino, making our analysis relevant for the study of mG≡mC in chloroform. This analysis will also provide useful indications on the expected accuracy of calculations employing the small 6-31G(d) basis set.

The spectra reported in Fig. 6 show that inclusion of anharmonic effects remarkably improves the agreement with experiments.^83,84 The NH stretching region is very well reproduced by calculation, in regards to both the relative intensity and the energy difference between the peak associated with the amino C(N8′–H₂) antisymmetric and symmetric stretching modes, the former at the blue end of the spectrum, and the latter at the red end.

Fig. 6 Linear anharmonic infrared spectra computed in the gas phase for 1-methylcytosine in the NH stretching region with the (a) CAM-B3LYP and (b) B3LYP functionals. Black curve: 6-31G(d); red-curve: 6-311G(d,p); blue curve: 6-311+G(d,p). Dashed lines show the harmonic computations. The experimental spectrum reproduced from ref. 83 is shown in grey. Full assignments are given in Table S2 in the ESI.†

In Fig. 7, we also report the anharmonic spectrum computed for mC in PCM chloroform solution using CAM-B3LYP and B3LYP functionals with different basis sets and compare it with the experiments on C, considering that the NH stretching is less sensitive to the substitution of the sugar than the fingerprint region. The experimental spectra⁹ are well reproduced by the anharmonic calculations, being significantly red-shifted with respect to the harmonic computations shown in Fig. 5 for the cC model.

Fig. 7 Linear anharmonic infrared spectra computed in PCM(chloroform) for 1-methylcytosine in the NH stretching region with the (a) CAM-B3LYP and (b) B3LYP functionals. Black curve: 6-31G(d); red-curve: 6-311G(d,p); blue curve: 6-311+G(d,p). The experimental spectrum from Fig. 4 reproduced from ref. 9 is shown in grey, where it has been normalised to the most intense peak to permit better comparison. Full assignments are given in Table S3 in the ESI.†

As with the gas phase results presented above, the B3LYP results are in better agreement with the experimental results with the 6-31G(d) basis than those of the larger 6-311G(d,p) and 6-311+G(d,p) results, both in terms of the frequency and relative intensity of the peaks. However, the same is not true of the CAM-B3LYP results, with the 6-31G(d) peaks blue shifted by 50 cm⁻¹ relative to the other basis sets, and ∼100 cm⁻¹ relative to the experimental results. The relative intensity of the peaks is however in better agreement with experiment than the other basis sets.

3.2.2 Anharmonic IR spectra of G and GG. In Fig. 8, the computed anharmonic spectrum for the monomeric mG model is shown, as well as the mG=mG model in its most populated tautomer.¹⁷ Both are calculated in PCM(chloroform) with a 6-31G(d) basis by CAM-B3LYP and B3LYP. The mG anharmonic spectra are similar to the harmonic cG spectra shown in Fig. 5 albeit ∼200 cm⁻¹ red-shifted, with a peak at 3555 cm⁻¹ for CAM-B3LYP and 3494 cm⁻¹ for B3LYP due to the antisymmetric N10–H₂ stretch, and two close peaks at 3450 cm⁻¹ for CAM-B3LYP and ∼3400 cm⁻¹ for B3LYP due to the symmetric N10–H₂ stretch and the N1–H1 stretch.

Fig. 8 Anharmonic vibrational spectrum in the N–H stretching region of mG=mG (black) and mG (blue) with anharmonic fundamentals of mG=mG (red, dashed) computed by (a) CAM-B3LYP and (b) B3LYP in PCM(chloroform) with a 6-31G(d) basis. When a peak is due to multiple combination bands with in phase (ip) and out of phase (oop) combinations of vibrations, they are separated by a ‘/’ in the label. The label ν_GG indicates that the vibration in parentheses occurs on both mG molecules in the mG=mG dimer. * Corresponds to a possible anomalous peak, discussed in the text.

For mG=mG, the position of the fundamentals resembles the harmonic cG=cG spectra (again, with an ∼200 cm⁻¹ red-shift), with the antisymmetric and symmetric N10–H₂ stretches falling at similar frequencies to those of the monomer, whilst the peak due to the hydrogen bonded N1–H1 stretch is significantly red-shifted and more intense with respect to the monomer, falling at ∼2900 cm⁻¹. The out of phase combination of the N1–H1 stretches on each mG in the mG=mG dimer is more intense than that in phase combination, in particular for CAM-B3LYP where the in phase combination is barely apparent on the red shoulder of the out of phase peak, and so is unlabeled. The full assignment, including dipole strengths, is given in the ESI.†

Our predictions are extremely close to the experimental indications, which show a broader peak at ∼3500 cm⁻¹ and sharper one at 3400 cm⁻¹ (see Fig. 4). Experimental spectra also exhibit a broad absorption band with peaks at 3300 and 3100 cm⁻¹. As a matter of fact, in contrast to monomeric mG, the anharmonic mG=mG spectrum exhibits a broad feature at 3000–3400 cm⁻¹ due to a number of combination bands between ring stretches, C6=O11 stretches, and N1–H1 and N10–H₂ scissoring motions. The combinations are predominantly between one normal mode with in phase vibrations on each mG in the dimer, and a second normal mode with out of phase vibrations on each mG in the dimer. The B3LYP spectrum also exhibits a possible artefact (marked with a *) due to the experimental model chosen, as it involves an umbrella motion on the methyl group attached to N9 on G, which would not be present with a -TBDMS group.

These anharmonic spectra indicate that an experimental IR spectrum of G, in which there is significant dimerisation, is likely to be considerably modulated by the GG dimer. For a nominal G concentration of 2 mM, as is the case in the experimental spectrum in Fig. 4, using the relationships in ref. 17, we have [G] = 0.778 mM and [GG] = 0.611 mM. Scaling the anharmonic spectra of mG and mG=mG by these concentrations (see Fig. S6 in the ESI†) demonstrates a much better comparison with experiment than with monomeric mG alone. We note that we do not take into account other tautomers of the mG=mG dimer, whose relative population at 298 K is <10%,¹⁷ and that the relative intensity of the peaks associated with the combination bands is likely to be overestimated with respect to experiments, which is discussed further in a later section.

3.2.3 Anharmonic IR spectrum of GC. In the previous sections, we have shown that anharmonic B3LYP and CAM-B3LYP calculations, even with the 6-31G(d) basis set, can provide a reliable basis for the interpretation of the IR spectra of 1-methylcytosine in gas matrices, as well as C and G in chloroform, with the latter being modulated by the effects of dimerisation.

We can now proceed with the computation of the anharmonic spectrum of mG≡mC in chloroform, using those previously computed anharmonic spectra to assess the effect of WC pair formation on the vibrational behaviour of G and C. As previously stated, we focus on the NH stretching region of the spectrum, however test calculations (see ESI,† Fig. S9) show that the computed anharmonic spectrum is also consistent with the experimental one in the fingerprint region, albeit with a blue shift of ∼50 cm⁻¹.

The calculated anharmonic spectra in the NH stretching region are shown in Fig. 9. Both functionals predict a rather similar picture of the fundamental transitions. Around 3500 cm⁻¹, we find an absorption band due to the ‘free’ amino N–H stretching of G and C. According to CAM-B3LYP calculations, the amino N–H stretching modes involved in the HB, C(N8′–H8′) and G(N10–H10), contribute to peaks falling either side of 3100 cm⁻¹, whereas the G(N1–H1) stretching falls at ∼2900 cm⁻¹, similar to the position of the G(N1–H1) stretch in the mG=mG dimer. For what concerns the differences between the two functionals appearing in Fig. 9, the predicted B3LYP frequencies are 40–50 cm⁻¹ red-shifted, confirming the trends highlighted in the previous sections. Moreover, the intensity of the combination bands is much larger at the CAM-B3LYP level, likely due to shorter HB distances.

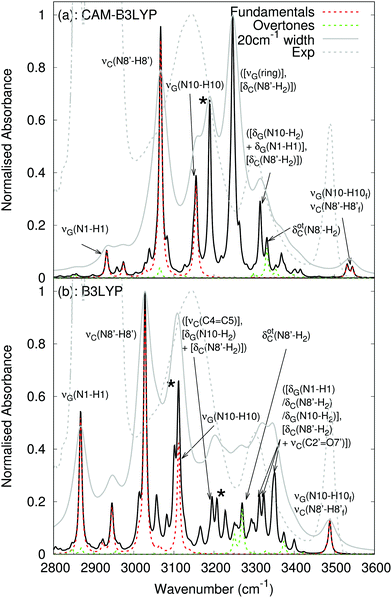Fig. 9 Linear infrared spectra computed in PCM(chloroform) for mG≡mC at the (a) CAM-B3LYP and (b) B3LYP levels of theory with a 6-31G(d) basis. Black curve: anharmonic spectrum; red dashed curve: anharmonic fundamentals; green dashed curve: overtones. In solid gray is the spectrum obtained by using a value of 20 cm⁻¹ for the convoluting Lorentzian function. Experimental spectrum⁹ in dashed grey for comparison. * Corresponds to possible anomalous peaks, discussed in the text.

The spectra feature the overtone of an N8′–H₂ scissoring motion on C, and a number of combination bands in the 3200–3400 cm⁻¹ region that, whilst the exact assignment differs for both functionals, all involve the N8′–H₂ scissoring motion on C. The most intense contribution to the CAM-B3LYP spectrum is at 3246 cm⁻¹ from a combination of ring stretching modes on G, and the N8′–H₂ scissoring motion on C. Whilst for B3LYP, the most intense contribution is from three combination bands at 3310–3350 cm⁻¹ between NH₂ scissoring modes on C and G, C2′=O7′ stretch on C and the N1–H1 stretching on G. The precise assignment, including all local vibrational contributions, is shown in the ESI† in Table S8. Both spectra also feature peaks (marked with a *) that may be artefacts due to the experimental model chosen, as they involve umbrella motions of the methyl group attached to N9 on G, and N1′ on C, which would not be present with a -TBDMS group.

The anharmonic calculations on the models including one or two explicit CDCl₃ molecules, hydrogen bonded to the carbonyl groups of G and C, reveal interesting trends. As shown in Fig. S13 in the ESI,† the ‘free’ N–H bonds are red-shifted by 30–50 cm⁻¹ with respect to the ‘PCM only’ calculations, the shift being larger in the presence of one explicit solvent molecule for CAM-B3LYP and two explicit solvent molecules for B3LYP.

For the hydrogen bonded NH, the peak due to the G(N10–H10) stretch is blue shifted both for the system with one CDCl₃ and the system with two CDCl₃ molecules; the peak due to the C(N8′–H8′) stretch is red shifted for the system with one CDCl₃ and blue shifted for the system with two CDCl₃ molecules; whilst the peak due to G(N1–H1) is blue shifted more for the system with one CDCl₃ than the system with two CDCl₃. This may be explained by the position of the explicit CDCl₃ molecules (see Fig. S12 in the ESI†), with the model with one CDCl₃ on the G(N10–H10) side, whilst the model with two CDCl₃ has an additional CDCl₃ on the C(N8′–H8′) side. The explicit solute/solvent hydrogen bond causes a decrease of the nearby WC HB strength, whilst the HB further away becomes stronger to compensate. This is demonstrated with the G(N10–H10)–OC and C(N8′–H8′)–OC HB distances for CAM-B3LYP (B3LYP), which are 1.84 (1.87) and 1.82 (1.85) Å for the PCM only model, 1.87 (1.90) and 1.81 (1.84) Å for 1 CDCl₃, and 1.86 (1.89) and 1.83 (1.86) Å for the 2 CDCl₃ model.

We have also performed some test B3LYP calculations on cG≡cC with a 6-31G(d) basis and on mG≡mC by using the larger 6-311G(d,p) basis set. Inclusion of the sugar does not strongly affect the position of the peaks in the N–H stretching region, although their relative intensity exhibits some changes, with the overtone and combination bands on average increasing in intensity relative to the fundamentals. The anomalous peaks due to the methyl group are also removed. Increasing the basis set for the mG≡mC model does not significantly affect the position of the fundamental transitions, although once more the relative intensity of the combination and overtone bands increases relative to the fundamentals. See ESI,† Fig. S11 for full details.

Finally, the results of M05-2X and M06-2X calculations are fully in line with those of B3LYP and CAM-B3LYP (see Fig. S10 in the ESI†). Inclusion of D3 corrections leads to a small red-shift of B3LYP and CAM-B3LYP spectra, without significantly affecting the picture just described.

3.2.4 Deuterated anharmonic IR spectra of GC. In Fig. 10, the anharmonic spectrum computed for fully deuterated mG≡mC, in which all the acidic protons are substituted by deuterium, is reported. As observed with previous spectra, the CAM-B3LYP results are slightly blue shifted with respect to B3LYP.

Fig. 10 Linear infrared spectra computed for deuterated mG=mC with CAM-B3LYP (black, with fundamentals in dashed red) and B3LYP (blue, with fundamentals in dashed green) in PCM(CDCl₃) with the 6-31G(d) basis. Experimental spectrum⁶³ shown in grey. The labels for the fundamental modes apply to both functionals, whilst the combination bands are colour coded to match the functional. * Labels a possible anomalous combination band, involving a rocking motion of the methyl group in the N9 position of mG.

Since under the experimental conditions, full deuteration cannot be achieved, due to fast H/D exchange with atmospheric water vapor, we have also computed the spectra in which only the proton involved in intermolecular hydrogen bonds is deuterated, whereas the ‘free’ N–H bonds are not, which is shown in the ESI,† Fig. S14.

The computed spectra are in very good agreement with the experimental one,⁶³ albeit with a red shift of the calculated fundamentals at ∼2280 cm⁻¹ relative to the broad experimental feature at 2338 cm⁻¹. These fundamentals are assigned to an intense hydrogen bonded C–ND stretching mode, i.e. C(N8′–D8′), and less intense hydrogen bonded G–ND stretching mode, i.e. G(N10–D10) (dipole strengths given in Table S9 in the ESI†). The partially deuterated spectra calculate these stretching modes to be ∼30 cm⁻¹ blue shifted compared to the fully deuterated spectra, which could contribute to this discrepancy. The partially deuterated spectra also predict the higher frequency G(N10–D10) stretching mode to have a more comparable intensity to C(N8′–D8′) than the fully deuterated one, which again could contribute to the discrepancy.

Concerning the other peaks in the fully deuterated spectra, CAM-B3LYP and B3LYP both predict a peak at ∼2200 cm⁻¹ due to the G(N1–D1) stretching, which compares nicely with experiment, and the partially deuterated spectra have a more modest ∼10 cm⁻¹ blue shift. The peaks at ∼2600 cm⁻¹ are due to the ‘free’ amino stretching modes of G and C, which also compare nicely with the experimental peak at 2603 cm⁻¹.

Combination bands contribute to the region between the hydrogen bonded amino stretches and the non-hydrogen bonded amino stretches to a lesser degree than the undeuterated spectra, although a few are still present. The most intense combination band for CAM-B3LYP is due to a combination between the deuterated C(N8′–D₂) scissoring motion and C–H scissoring modes on C5′ and C6′, with a small contribution from the N–C stretch of the methyl group in the N1′ position. For B3LYP, the most intense combination band is due to a combination between the deuterated G(N10–D₂) scissoring motion, with a contribution from ring stretching on G, and the scissoring motion of the H atom attached to C8 on G.

4 Discussion

4.1 Comparison of experimental and computational assignment

We shall focus mainly on the analysis of the NH fundamental transitions, whose features are less sensitive to the adopted computational model (e.g. the substitution of the sugar with a methyl group or the presence of explicit solvent molecules) than overtones and especially combination bands. Furthermore, it is likely that the frequencies of the overtone/combination bands computed at the 6-31G(d) level are overestimated, since we know that, at this level of theory, the fundamental bands in the fingerprint region are on average too large, even when including anharmonic corrections.

According to our calculations, the ‘free’ amino N–H stretching of G and C absorbs at 3500 cm⁻¹; this prediction is in nice agreement with the experimental band at 3491 cm⁻¹. Interestingly, the hydrogen bond of CDCl₃ molecules leads to a weak red-shift of these modes, in line with the experimental indications obtained for DNA in water.⁷ In this latter system, the stronger hydrogen bonds with the solvent lead to a much larger red-shift.

With regards to the WC hydrogen bonded NH, we predict that C(N8′–H8′) and G(N10–H10) are responsible for the experimental absorption band at 3145 cm⁻¹, in contrast to the experimental assignment of C(N8′–H8′) and G(N1–H1) stretches.^9,57

Our anharmonic computations reveal instead that the the G(N1–H1) stretching falls at ∼2900 cm⁻¹. Though this region is obscured by the strong TBDMS group absorptions, the subtraction of the GC spectrum by those of G and C revealed no significant absorption below 3000 cm⁻¹.⁹ On the other hand, as we have shown in a previous section, the GG dimer can make a significant contribution to the ‘monomeric’ G spectrum, including a peak at ∼2900 cm⁻¹ due to the hydrogen bonded N1–H1 stretches of its most populated tautomer. The subtraction procedure could therefore remove the peak due to the N1–H1 stretch in GC, as well as those due to the TBDMS groups.

Further support for our assignment comes from the deuterated spectra, with the experimental spectra⁶³ not being affected by the TBDMS group in the region of interest. Calculated and experimental spectra are in good agreement: the ‘free’ amino N–D stretching of G and C is coincident with the experimental peak at 2603 cm⁻¹, our peak due to the hydrogen bonded C(N8′–D8′) and D(N10–D10) is slightly red-shifted with respect to the experimental one at 2338 cm⁻¹, and our peak due to G(N1–D1) almost coincides with the experimental peak at 2179 cm⁻¹. Interestingly, on the grounds of the results on the deuterated system, the authors of ref. 63 compute a ‘scaling’ factor and estimate the position of the corresponding N–H peaks in the non-deuterated system. They suggest a correspondence between the peaks at 2603 and 3491 cm⁻¹, and those at 2338 and 3145 cm⁻¹, whilst the peak at 2179 cm⁻¹ should correspond with the one at 2940 cm⁻¹, which is in line with our prediction.

Turning to the broad experimental peak at ∼3300 cm⁻¹, the red end of this at 3303 cm⁻¹ was assigned to the hydrogen bonded G(N10–H10) stretch, whilst the blue end at 3380 cm⁻¹ was assigned to an overtone of the G(C6=O11) stretch. For the former, whilst we have assigned the G(N10–H10) stretch to the peak at 3145 cm⁻¹, we cannot rule out that the tail of this vibration contributes to the 3303 cm⁻¹ peak. As we will discuss in more detail in the following section, our treatment could overestimate GC HB interaction and therefore underestimate the hydrogen bonded NH stretches. Furthermore, while the experimental spectra of the deuterated GC clearly show a low-energy peak we assign to G(N1–D1), increasing our confidence on the computed G(N1–H1) frequency (∼2900 cm⁻¹), G(N10–D10) is very close to C(N8–H8) and therefore cannot provide additional information on the reliability of our estimates.

Concerning the blue end of the experimental band at 3380 cm⁻¹, our spectra reveal a number of combination bands and overtones in the 3200–3400 cm⁻¹ region, however the most intense ones predominantly involve a C(N8′–H8′₂) scissoring motion, rather than a G(C6=O11) stretch. The experimental assignment of the peak of the overtone of the G(C6=O11) stretch was aided by a 2D-IR spectrum that estimated the diagonal anharmonicity of the mode to be Δ_ii = 21 ± 5 cm⁻¹, via an excited state absorption peak. This value does not compare well with what we estimated for this overtone (11.8 cm⁻¹), but it is consistent with that estimated for GC in the gas phase (13.2 cm⁻¹).³⁸

Our calculated diagonal anharmonicity for the C(N8′–H8′₂) scissoring motion is −5.8 cm⁻¹ for CAM-B3LYP, and −9.3 cm⁻¹ for B3LYP. This appears to be even further from agreement with the experimental observation; however, as we see many combination bands involving the C(N8′–H8′₂) scissoring motion, as well as the overtone in that spectral region, it is plausible that the peak in the 2D-IR spectrum is a result of a cross-peak between one of the combination bands and the overtone, rather than an excited state absorption of the overtone.

Actually, the 3300 cm⁻¹ band could be described as a ‘collective mode’ where the amino N–H scissoring modes are strongly coupled to the N–H and C=O stretches. This feature could be related to the very fast disappearance of the 3301 peak (≤1 ps),⁹i.e. faster than that at ∼3100 cm⁻¹. This finding would be more difficult to reconcile if the peak is assigned to the G(N10–H10) stretch, as it is usually assumed that the lifetime of N–H bond vibrations decreases with increasing hydrogen bond strength. Therefore, it should be expected that the lifetime of the peak related to G(N10–H10) stretching, which has the weakest hydrogen bond, is intermediate between those of the other hydrogen bonded N–H stretches and the ‘free’ N–H stretches, rather than faster than the other hydrogen bonded N–H stretches.

However, as stated previously, the fundamental frequencies in the fingerprint range are not as well reproduced by our model as those in the NH stretching region. Therefore, the combination bands and overtones may be subject to error, both in terms of their frequency and identity of contributing vibrations. What our calculations do indicate with more certainty, however, is that hydrogen bonding leads to significant mixing of local vibrations that gives rise to combination bands and overtones, as evidenced by the difference between the monomeric mG and mC spectra, and that of the hydrogen bonded pair mG≡mC.

The spectra for the mG=mG dimer also contain multiple peaks due to the combination bands and, as we have shown, the dimer is likely to contribute to the experimental spectrum of G. These combination bands occur in the regions of the spectrum that have experimental peaks at 3180 cm⁻¹ and 3310 cm⁻¹, which were assigned to the GG(N1–H1) stretch, and a Fermi resonance between the GG(N1–H1) stretch and the GG(C6=O11) stretch.¹⁷ As previously stated, our anharmonic computations indicate that the GG(N1–H1) stretch occurs at ∼2900 cm⁻¹, disagreeing with this assignment. Interestingly, the authors of ref. 17 conducted scaled harmonic DFT calculations, which predicted the GG(N1–H1) peak at 2804 cm⁻¹, in line with our anharmonic computation. We therefore propose that the experimental peaks at 3180 cm⁻¹ and 3310 cm⁻¹ are due to the combination bands involving ring stretches, C6=O11 stretches, and N1–H1 and N10–H₂ scissoring motions on the GG dimer. This is akin to what we propose for the peak at 3303 cm⁻¹ in GC, and as was the case there, we must also specify the caveat that the fingerprint vibrations are subject to error, so the combination bands will be also.

4.2 Some considerations on our methodological approach

A full anharmonic computational characterization of a system containing many dozens of atoms in the condensed phase, such as TBDMS-GC in chloroform, is a very difficult task and, at the moment, some approximations are necessary. Many of these issues are general and concern any theoretical study of large size systems, so here we simply highlight some points that are more directly relevant to the IR study of oligonucleotides.

A first very basic one, whose importance is sometimes overlooked, involves the decrease of the size of the system to be computed. In our case, for example, we first discard the bulky TBDMS groups and then the entire ring, the latter of which is substituted by a methyl group. These kinds of approximations are at the base of any QM/MM approach.^85,86 Our analysis shows that these choices are not anodyne, and they affect vibrational modes that are not directly concerned with the substitution, with the relative intensity of the peaks being more sensitive than their position. For example, we have shown that the relative intensity of the main peaks noticeably changes when the sugar is modeled by a methyl group. This is an important caveat for any study on DNA vibrations, suggesting that a bare base is probably not sufficient.

Furthermore, the replacement of groups may also introduce features into the spectrum that would not otherwise be present. This is the case, for example, in the anharmonic spectra of mG≡mC and mG=mG where there are combination bands that involve an umbrella motion on the methyl group, which would not be present with the sugar ring.

Another important issue is related to the inclusion of environmental/solvent effects. In this study, we resorted to PCM⁷⁵ because solute–solvent interactions in chloroform are expected to be less directional than in other solvents, such as the strongly hydrogen bonding ones.^40,45,46 Nonetheless, we have checked that the explicit inclusion of two solvent molecules that are most strongly bound to GC does not dramatically affect the position of the harmonic fundamentals. This mixed discrete-continuum approach, adopted also in other recent papers on hydroxyl vibrational modes,^87,88 whose extension to studying IR spectra of small/medium systems in water would be rather cumbersome, is instead more suitable to study the IR spectra of larger DNA fragments in water, where a relatively small number of solvent molecules can affect the spectra via the hydrogen bonded to the ‘dangling’ NH bonds.⁷ In these cases, the inclusion of solvent molecules at the full QM level, without relying on a simplified classical force field, is particularly attractive, since it can better model the mixing between the solute and solvent vibrational wave-functions.^40,89 On the other hand, our results clearly show that, even in a moderately polar solvent, inclusion of the solvent effect is very important when looking for an accurate description of the IR spectrum, especially at the anharmonic level, which is sensitive to small variations of the equilibrium geometry.

For what concerns the reference electronic method, an exhaustive review of the performances of many different functionals falls outside the aims of the present paper, and we simply checked that our main conclusions do not depend on the choice of the functional. Density functional calculations based on B3LYP are confirmed to provide a reliable description of the IR spectra.^32,67,82 For GC, the agreement with experiments, at least for the peaks that can be more easily assigned, such as the free N–H or the N–D vibrations, is almost quantitative. The comparison with the high-resolution spectra in the gas matrices is also encouraging, although discrepancies can occur due to the lack of interactions with the gas matrix. On the other hand, inclusion of the dispersion interaction could be very important to treat hydrogen bonded systems as GC.^73,90,91 In this respect more extensive benchmarking at an anharmonic level is highly desirable, since, as shown in the present study, anharmonic corrections, not only on the position but also on the intensity of the different bands, can be larger than the differences due to the functional. These effects should be considered when examining the performances of CAM-B3LYP. CAM-B3LYP provides spectral patterns rather similar to those of B3LYP, but the quantitative agreement with the experiments is slightly worse, with a blue-shift of a few tens of cm⁻¹. Since CAM-B3LYP provides a reliable description of DNA excited states, including those with CT characters, this is an encouraging indication for using this functional in the interpretation of pump/probe IR experiments in polynucleotides. CAM-B3LYP likely overestimates the intensity of some combination bands, and this feature could be related to an underestimation of the GC HB distance, and hence an overestimation of the HB strength. Interestingly, inclusion of D3 corrections strongly reduces the intensity of the CAM-B3LYP combination bands (see ESI†). However, this could also be due to the approach followed in the anharmonic vibrational calculations, where a perturbative approach to treat strongly vibrationally coupled systems can lead to inconsistencies concerning the intensity of the combination bands.

Regarding the basis set, 6-31G(d) calculations overestimate the frequencies in the fingerprint region (and most likely the corresponding combination/overtone), but they deliver a rather accurate description of the NH stretches. Indeed, as discussed above, the picture we provide is in good agreement with experiments and our treatment can also be rather straightforwardly adopted for larger polynucleotides.

Finally, concerning the time-independent approach adopted here for the spectra, we note some considerations. First, it is possible that hydrogen bond strength may be overestimated due to the neglect of thermal/conformational effects. Second, the coupling between the fast vibrational modes of the NH stretches is severely modulated by the slow ones. For example, the ‘spacing’ between the peaks related to the hydrogen bonded C(N8′–H8′) and G(N10–H10) fundamentals is twice as large in the spectra computed in the gas phase compared to that in chloroform, simply due to small differences in the HB geometry. This HB geometry would be affected by the low energy large amplitude intermolecular modes of the rings, and these modes are not well described at the harmonic level, and so may be even less well described after perturbation in the anharmonic method. Analogously, the N–H stretching modes are expected to be modulated by the inversion motion of the hydrogen atoms, which affects the ‘delocalization’ of the amino L.P. in the rings and, therefore, the ‘stiffness’ of the C–N bond. These issues may be remedied by a time-dependent approach, i.e. based on the results of molecular dynamics simulations (see for example, ref. 40 and 92–96 and references therein). The computational cost of long simulation runs can, however, be very high and a classical treatment of the nuclei can lead to inconsistencies, especially when relying on classical force fields, often necessary to treat large size systems. A proper combination of ‘time-independent’ and ‘time-dependent’ approaches, based on a separate treatment of the ‘slow’ and ‘fast’ vibrational degrees of freedom, like those recently adopted to study electronic spectra,⁹⁷ could therefore be a promising path to follow in the future.

5 Conclusions

In this paper, we have reported a computational study of the GC dimer in chloroform solution, trying to assess how different factors, e.g. the sugar ring, the solvent (both bulk solvent effects and solute–solvent hydrogen bonds) and deuteration modulate its vibrational spectra, focusing in particular on the high energy region of the spectra, i.e. that associated with NH stretching modes. At the same time, from the methodological point of view, we have verified the applicability of perturbative approaches to the anharmonic vibrational treatment of a strongly coupled hydrogen bonded system and the accuracy of B3LYP and CAM-B3LYP functionals. The computed spectra are in good agreement with the experimental ones and indicate that the G(N1–H1) stretch absorbs around 2900 cm⁻¹, the C amino N–H stretch involved in the hydrogen bond with G absorbs around 3100 cm⁻¹, and the corresponding group of G absorbs between 3100 and 3200 cm⁻¹. The first two assignments are solid and confirmed by the very good agreement between experiments and calculations found for deuterated G–C. The smaller intensity predicted for the hydrogen bonded G-amino group and its sensitivity to the inclusion of explicit solute–solvent interactions does not yet allow an unambiguous assignment, and the predicted frequency could be slightly underestimated. Our calculations show that the inclusion of anharmonic effects is fundamental to get a good agreement with the experimental spectral patterns, and that combination and overtone transitions strongly contribute to the spectra. Interpretative models based on local vibrational modes cannot be easily adopted to analyse the vibrational spectra of strongly coupled supramolecular systems such as GC in chloroform, as many local modes contribute to the normal mode picture obtained. Furthermore, a proper account of dynamical conformational effects is also desirable. Nonetheless, the good agreement with the experimental spectrum, especially when using relatively small basis sets, provides encouraging indications of a possible extension of our approach to studying the vibrational behavior of larger polynucleotides and/or excited electronic states.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No. 765266 (LightDyNAmics). The authors thank Dr F. Santoro and L. Martinez Fernandez for very useful discussion.

Notes and references

1. P. Hamm, M. Lim and R. M. Hochstrasser, J. Phys. Chem. B, 1998, 102, 6123.
2. O. Golonzka, M. Khalil, N. Demirdöven and A. Tokmakoff, Phys. Rev. Lett., 2001, 86, 2154.
3. A. T. Krummel, P. Mukherjee and M. T. Zanni, J. Phys. Chem. B, 2003, 107, 9165.
4. E. T. J. Nibbering and T. Elsaesser, Chem. Rev., 2004, 104, 1887.
5. T. Elsaesser, Acc. Chem. Res., 2009, 42, 1220.
6. A. T. Krummel and M. T. Zanni, J. Phys. Chem. B, 2006, 110, 13991–14000.
7. C. Greve and T. Elsaesser, J. Phys. Chem. B, 2013, 117, 14009–14017.
8. V. Kozich, L. Szyc, E. T. J. Nibbering, W. Werncke and T. Elsaesser, Chem. Phys. Lett., 2009, 473, 171.
9. M. Yang, L. Szyc, K. Röttger, H. Fidder, E. T. J. Nibbering, T. Elsaesser and F. Temps, J. Phys. Chem. B, 2011, 115, 5484.
10. L. Szyc, M. Yang, E. T. J. Nibbering and T. Elsaesser, Angew. Chem., Int. Ed., 2010, 49, 3598.
11. C. S. Peng, K. C. Jones and A. Tokmakoff, J. Am. Chem. Soc., 2011, 133, 15650.
12. M. K. Kuimova, J. Dyer, M. W. George, D. C. Grills, J. M. Kelly, P. Matousek, A. W. Parker, X. Z. Sun, M. Towrie and A. M. Whelan, Chem. Commun., 2005, 1182.
13. S. Quinn, G. W. Doorley, G. W. Watson, A. J. Cowan, M. W. George, A. W. Parker, K. L. Ronayne, M. Towrie and J. M. Kelly, Chem. Commun., 2007, 2130.
14. B. M. Pilles, B. Maerz, J. Chen, D. B. Bucher, P. Gilch, B. Kohler, W. Zinth, B. P. Fingerhut and W. J. Schreier, J. Phys. Chem. A, 2018, 122, 4819–4828.
15. K. Röttger, H. J. B. Marroux, H. Böhnke, D. T. J. Morris, A. T. Voice, F. Temps, G. M. Roberts and A. J. Orr-Ewing, Faraday Discuss., 2016, 194, 683–708.
16. Y. Zhang, R. Improta and B. Kohler, Phys. Chem. Chem. Phys., 2014, 16, 1487.
17. R. A. Ingle, G. M. Roberts, K. Röttger, H. J. Marroux, F. Dönnichsen, M. Yang, L. Szyc, Y. Harabuchi, S. Maeda, F. Temps and A. J. Orr-Ewing, Chem. Phys., 2018, 515, 480–492.
18. W. J. Schreier, T. E. Schrader, F. O. Koller, P. Gilch, C. E. Crespo-Hernandez, V. N. Swaminathan, T. Carell, W. Zinth and B. Kohler, Science, 2007, 315, 625.
19. D. B. Bucher, B. M. Pilles, T. Carell and W. Zinth, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4369.
20. B. M. Pilles, D. B. Bucher, L. Liu, P. Gilch, W. Zinth and W. J. Schreier, Chem. Commun., 2014, 50, 15623.
21. G. W. Doorley, M. Wojdyla, G. W. Watson, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, J. Phys. Chem. Lett., 2013, 4, 2739.
22. Y. Zhang, J. Dood, A. A. Beckstead, X.-B. Li, K. V. Nguyen, C. J. Burrows, R. Improta and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11612.
23. M. Duchi, M. P. O’Hagan, R. Kumar, S. J. Bennie, M. C. Galan, B. F. E. Curchod and T. A. A. Oliver, Phys. Chem. Chem. Phys., 2019, 21, 14407–14417.
24. Y. Zhang, J. Dood, A. A. Beckstead, X.-B. Li, K. V. Nguyen, C. J. Burrows, R. Improta and B. Kohler, J. Phys. Chem. B, 2015, 119, 7491.
25. D. B. Bucher, A. Schlueter, T. Carell and W. Zinth, Angew. Chem., Int. Ed., 2014, 53, 11366.
26. Y. Zhang, X.-B. Li, A. M. Fleming, J. Dood, A. A. Beckstead, A. M. Orendt, C. J. Burrows and B. Kohler, J. Am. Chem. Soc., 2016, 138, 7395–7401.
27. Y. Zhang, K. de La Harpe, A. A. Beckstead, L. Martinez-Fernandez, R. Improta and B. Kohler, J. Phys. Chem. Lett., 2016, 7, 950.
28. Y. Zhang, K. de La Harpe, A. A. Beckstead, R. Improta and B. Kohler, J. Am. Chem. Soc., 2015, 137, 7059.
29. L. Martínez-Fernández, Y. Zhang, K. de La Harpe, A. A. Beckstead, B. Kohler and R. Improta, Phys. Chem. Chem. Phys., 2016, 18, 21241.
30. F. Egidi, D. B. Williams-Young, A. Baiardi, J. Bloino, G. Scalmani, M. J. Frisch, X. Li and V. Barone, J. Chem. Theory Comput., 2017, 13, 2789.
31. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108.
32. V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759.
33. J. Bloino, J. Phys. Chem. A, 2015, 119, 5269–5287.
34. P. Carbonniere, A. Dargelos and C. Pouchan, Theor. Chem. Acc., 2010, 125, 543–554.
35. O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953.
36. D. Madsen, O. Christiansen and C. Konig, Phys. Chem. Chem. Phys., 2018, 20, 3445–3456.
37. D. Madsen, O. Christiansen, P. Norman and C. Konig, Phys. Chem. Chem. Phys., 2019, 21, 17410–17422.
38. G. Wang, X. Ma and J. Wang, Chin. J. Chem. Phys., 2009, 22, 563.
39. C. Puzzarini, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2011, 7, 3702.
40. C. Pouchan, S. Thicoipe and M. De La Pierre, Theor. Chem. Acc., 2019, 138, 36.
41. M. De La Pierre and C. Pouchan, Theor. Chem. Acc., 2018, 137, 25.
42. S. V. Krasnoshchekov, N. Vogt and N. F. Stepanov, J. Phys. Chem. A, 2015, 119, 6723–6737.
43. T. Rasheed, S. Ahmad, S. M. Afzal and K. Rahimullah, THEOCHEM, 2009, 895, 18.
44. G. N. Ten, V. V. Nechaev and S. V. Krasnoshchekov, Opt. Spectrosc., 2010, 108, 37.
45. S. Thicoipe, P. Carbonniere and C. Pouchan, Phys. Chem. Chem. Phys., 2013, 15, 11646–11652.
46. S. Thicoipe, P. Carbonniere and C. Pouchan, Chem. Phys. Lett., 2014, 591, 243–247.
47. S. Thicoipe, P. Carbonniere and C. Pouchan, Theor. Chem. Acc., 2017, 136, 44.
48. T. Fornaro, I. Carnimeo and M. Biczysko, J. Phys. Chem. A, 2015, 119, 5313–5326.
49. K. B. Beć, J. Grabska, M. A. Czarnecki, C. W. Huck, M. J. Wojcik, T. Nakajima and Y. Ozaki, J. Phys. Chem. B, 2019, 123, 10001–10013.
50. T. Fornaro, D. Burini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 4224–4236.
51. T. Fornaro, M. Biczysko, J. Bloino and V. Barone, Phys. Chem. Chem. Phys., 2016, 18, 8479.
52. A. Bende and C. M. Muntean, J. Mol. Model., 2014, 20, 2113.
53. A. Bende, D. Bogdan, C. M. Muntean and C. Morari, J. Mol. Model., 2011, 17, 3265–3274.
54. G. N. Ten, V. V. Nechaev, A. N. Pankratov and V. I. Baranov, J. Struct. Chem., 2010, 51, 453.
55. C. Greve, N. K. Preketes, H. Fidder, R. Costard, B. Koeppe, I. A. Heisler, S. Mukamel, F. Temps, E. T. J. Nibbering and T. Elsaesser, J. Phys. Chem. A, 2013, 117, 594.
56. N. K. Schwalb and F. Temps, J. Am. Chem. Soc., 2007, 129, 9272.
57. N. K. Schwalb, T. Michalak and F. Temps, J. Phys. Chem. B, 2009, 113, 16365.
58. A. L. Sobolewski, W. Domcke and C. Hättig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906.
59. A. Kumar and M. D. Sevilla, Chem. Rev., 2010, 110, 7002–7023.
60. A. Francés-Monerris, H. Gattuso, D. Roca-Sanjuán, I. n. Tuñón, M. Marazzi, E. Dumont and A. Monari, Chem. Sci., 2018, 9, 7902–7911.
61. L. Martinez-Fernandez, G. Prampolini, J. Cerezo, Y. Liu, F. Santoro and R. Improta, Chem. Phys., 2018, 515, 493–501.
62. K. Siriwong, A. A. Voityuk, M. D. Newton and N. Rösch, J. Phys. Chem. B, 2003, 107, 2595–2601.
63. H. Fidder, M. Yang, E. T. J. Nibbering, T. Elsaesser, K. Röttger and F. Temps, J. Phys. Chem. B, 2013, 117, 845.
64. K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Bohnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Angew. Chem., Int. Ed., 2015, 54, 14719.
65. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
66. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
67. P. Carbonniere, T. Lucca, C. Pouchan, N. Rega and V. Barone, J. Comput. Chem., 2005, 26, 384.
68. I. Carnimeo, C. Puzzarini, N. Tasinato, P. Stoppa, A. P. Charmet, M. Biczysko, C. Cappelli and V. Barone, J. Chem. Phys., 2013, 139, 074310.
69. C. Puzzarini, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2010, 6, 828.
70. A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037.
71. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540.
72. L. Biemann, S. A. Kovalenko, K. Kleinermanns, R. Mahrwald, M. Markert and R. Improta, J. Am. Chem. Soc., 2011, 133, 19664.
73. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
74. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
75. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
76. C. Cappelli, F. Lipparini, J. Bloino and V. Barone, J. Chem. Phys., 2011, 135, 104505.
77. V. Barone, J. Chem. Phys., 2004, 120, 3059.
78. V. Barone, J. Chem. Phys., 2005, 122, 014108.
79. J. Bloino, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 11862.
80. C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191.
81. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
82. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
83. M. Szczesniak, M. Nowak and K. Szczepaniak, J. Mol. Struct., 1984, 115, 221–224.
84. K. Kuczera, M. Szczesniak and K. Szczepaniak, J. Mol. Struct., 1988, 172, 73–88.
85. Combining Quantum Mechanics and Molecular Mechanics. Some Recent Progresses in QM/MM Methods, ed. J. R. Sabin and E. Brändas, Academic Press, 2010, vol. 59.
86. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
87. M. J. Schuler, T. S. Hofer and C. W. Huck, Phys. Chem. Chem. Phys., 2017, 19, 11990–12001.
88. K. B. Beć and C. W. Huck, Front. Chem., 2019, 7, 48.
89. A. Petrone, J. Cerezo, F. J. A. Ferrer, G. Donati, R. Improta, N. Rega and F. Santoro, J. Phys. Chem. A, 2015, 119, 5426–5438.
90. S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154.
91. S. A. Katsyuba, E. E. Zvereva and S. Grimme, J. Phys. Chem. A, 2019, 123, 3802–3808.
92. Y.-a. Yan and O. Kühn, J. Phys. Chem. B, 2011, 115, 5254–5259.
93. Y. Yan and O. Kühn, Phys. Chem. Chem. Phys., 2010, 12, 15695.
94. Y. Yan, G. M. Krishnan and O. Kühn, Chem. Phys. Lett., 2008, 464, 230.
95. M. Schmitz and P. Tavan, J. Chem. Phys., 2004, 121, 12233–12246.
96. M. Schmitz and P. Tavan, J. Chem. Phys., 2004, 121, 12247–12258.
97. R. Improta, F. J. A. Ferrer, E. Stendardo and F. Santoro, ChemPhysChem, 2014, 15, 3320.

---

Footnote

† Electronic supplementary information (ESI) available: Additional harmonic and anharmonic IR spectra. Tables with the detailed assignment of the IR spectra. Cartesian coordinates of cG=cC. See DOI: 10.1039/c9cp06373k

---